The influence of the noise on the exact solutions of a Kuramoto-Sivashinsky equation

Sahar Albosaily; Wael W. Mohammed; Ali Rezaiguia; Mahmoud El-Morshedy; Elsayed M. Elsayed

doi:10.1515/math-2022-0012

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

The influence of the noise on the exact solutions of a Kuramoto-Sivashinsky equation

Sahar Albosaily , Wael W. Mohammed , Ali Rezaiguia , Mahmoud El-Morshedy and Elsayed M. Elsayed

Published/Copyright: March 17, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

$Open Mathematics$

From the journal Open Mathematics Volume 20 Issue 1

Abstract

In this article, we take into account the stochastic Kuramoto-Sivashinsky equation forced by multiplicative noise in the Itô sense. To obtain the exact stochastic solutions of the stochastic Kuramoto-Sivashinsky equation, we apply the G ′ G -expansion method. Furthermore, we extend some previous results where this equation has not been previously studied in the presence of multiplicative noise. Also, we show the influence of multiplicative noise on the analytical solutions of the stochastic Kuramoto-Sivashinsky equation.

Keywords: stochastic Kuramoto-Sivashinsky; multiplicative noise; stochastic exact solutions; (G′/G)-expansion method

MSC 2010: 35Q51; 35A20; 60H10; 60H15; 83C15

1 Introduction

Nonlinear partial differential equations (NLPDEs) are applied to describe a wide range of phenomena in biology, fluid mechanics, chemical physics, chemical kinematics, solid-state physics, optical fibers, plasma physics, geochemistry, and a lot of other fields. The research of analytical solutions for NLPDEs is important in the investigation of nonlinear physical phenomena. Throughout the past several decades, the discovery of new phenomena has been aided by new exact solutions. Thus, the seeking of exact solutions to those equations of NLPDEs has long been a feature of mathematics and science. To obtain exact solutions of NLPDEs, a variety of effective techniques have been applied, for instance, the Exp-function method [1,2], the G ′ G -expansion method [3,4], the tanh–sech method [5,6], the improved tanh-function method [7], the exp ( − φ ( η ) ) -expansion method [8], the perturbation method [9,10, 11,12], the extended tanh method [13,14], the sine-cosine method [15,16], the Adomian decomposition method [17,18, 19,20].

Until the 1950s, deterministic models of differential equations were commonly used to describe the dynamics of the system in implementations. However, it is evident that the phenomena that exist in today’s world are not always deterministic.

Noise has now been shown to be important in many phenomena, also called randomness or fluctuations. Therefore, random effects have become significant when modeling different physical phenomena that take place in oceanography, physics, biology, meteorology, environmental sciences, and so on. Equations that consider random fluctuations in time are referred to as stochastic differential equations.

Here, we treat the stochastic Kuramoto-Sivashinsky (SKS) equation in one dimension with multiplicative noise in the Itô sense as follows:

(1) d u + [ α u ∂ x u + p ∂ x 2 u + q ∂ x 4 u ] d t = σ u d β ,

where α , p , and q are nonzero real constants, σ is a noise strength, and β ( t ) is the standard Wiener process and it depends only on t .

The Kuramoto-Sivashinsky (KS) equation (1) with σ = 0 was first proposed in the mid-1970s. Kuramoto was the first to derive the equations for the Belousov-Zabotinskii reaction using reaction-diffusion equations. Also, Sivashinsky used it to describe tiny thermal diffusive instabilities in laminar flamence Poiseuille flow of a film layer on an inclined surface in higher space dimensions. It may also be used to represent Benard convection in an elongated box in one space dimension, and it can be utilized to illustrate long waves at the interface between two viscous fluids and unstable drift waves in plasmas. The KS equation can be applied to control surface roughness in the growth of thin solid films by sputtering, step dynamics in epitaxy, amorphous film formation, and population dynamics models [21,22,23, 24,25].

The deterministic Kuramoto-Sivashinsky equation (1) (i.e., σ = 0 ) has been studied by a number of authors to attain its exact solutions by different methods such as the modified tanh–coth method [26], the tanh method and the extended tanh method [27], homotopy analysis method [28], the truncated expansion method [29], the G ′ G -expansion [30], the polynomial expansion method [31,32, 33,34], the perturbation method [35], the Painlevé expansions methods [36]. However, the analytical stochastic solutions of the stochastic Kuramoto-Sivashinsky have never been obtained till this moment.

Our motivation of this article is to obtain the analytical stochastic solutions of the SKS (1) with multiplicative noise by using the G ′ G -expansion method. The results introduced here extend earlier studies, for instance, those reported in [27]. Also, we address the effects of multiplicative noise on these solutions.

The format of this paper is as follows: In Section 2, we obtain the wave equation for SKS equation (1), while in Section 3, we have the exact stochastic solutions of the SKS (1) by applying the G ′ G -expansion method. In Section 4, we show several graphical representations to demonstrate the effect of multiplicative noise on the obtained solutions of SKS. Finally, the conclusions of this paper are shown.

2 Wave equation for SKS equation

To obtain the wave equation for SKS equation (1), we use the following wave transformation:

(2) u ( x , t ) = φ ( η ) e ( σ β ( t ) − 1 2 σ 2 t ) , η = x − c t ,

where c is the wave speed and φ is the deterministic function. Substituting equation (2) into equation (1) and using

(3) d u = − c φ ′ + 1 2 σ 2 φ − 1 2 σ 2 φ e ( σ β ( t ) − 1 2 σ 2 t ) d t + σ φ e ( σ β ( t ) − 1 2 σ 2 t ) d β , u x = φ ′ e ( σ β ( t ) − 1 2 σ 2 t ) , u x x = φ ″ e ( σ β ( t ) − 1 2 σ 2 t ) u x x x = φ ‴ e ( σ β ( t ) − 1 2 σ 2 t ) , u x x x x = φ ⁗ e ( σ β ( t ) − 1 2 σ 2 t ) ,

where + 1 2 σ 2 φ is the Itô correction term, we obtain

(4) − c φ ′ + α φ φ ′ e ( σ β ( t ) − 1 2 σ 2 t ) + p φ ″ + q φ ⁗ = 0 .

Taking expectation on both sides and considering that φ is the deterministic function, we have

(5) − c φ ′ + α φ φ ′ e − 1 2 σ 2 t E ( e σ β ( t ) ) + p φ ″ + q φ ⁗ = 0 ,

Since β ( t ) is the standard Gaussian random variable, then for any real constant γ , we have E ( e γ β ( t ) ) = e γ 2 2 t . Now equation (5) has the form

(6) − c φ ′ + α φ φ ′ + p φ ″ + q φ ⁗ = 0 ,

Integrating equation (6) once in terms of η yields

(7) q φ ‴ + p φ ′ + α 2 φ 2 − c φ = 0 ,

where we put the constant of integration equal zero.

3 The stochastic exact solutions of SKS equation

In this section, we use the G ′ G -expansion method [3] to find the solutions of equation (7). As a result, we have the exact stochastic solutions of the SKS (1). First, we assume that the solution of equation (7) has the form:

(8) φ = ∑ k = 0 M ℏ k G ′ G k ,

where ℏ 0 , ℏ 1 , … , ℏ M are uncertain constants that must be calculated later, and G solves

(9) G ″ + λ G ′ + μ G = 0 ,

where λ , μ are unknown constants. Let us now calculate the parameter M by balancing φ 2 with φ ‴ in equation (7) as follows:

2 M = M + 3 ,

and hence,

(10) M = 3 .

From (10), we can rewrite equation (8) as follows:

(11) φ = ℏ 0 + ℏ 1 G ′ G + ℏ 2 G ′ G 2 + ℏ 3 G ′ G 3 .

Substituting equation (11) into equation (7) and using equation (9) , we obtain a polynomial with degree 6 of G ′ G as follows:

1 2 α ℏ 3 2 − 60 q ℏ 3 G ′ G 6 + ( − 24 q ℏ 2 + α ℏ 2 ℏ 3 − 144 q λ ℏ 3 ) G ′ G 5 + 1 2 α ℏ 2 2 − 3 p ℏ 3 − 6 q ℏ 1 + α ℏ 1 ℏ 3 − 111 q λ 2 ℏ 3 − 114 q μ ℏ 3 − 54 q λ ℏ 2 G ′ G 4 + ( − c ℏ 3 + 2 p ℏ 2 + α ℏ 0 ℏ 3 + α ℏ 1 ℏ 2 − 3 p λ ℏ 3 − 38 q λ 2 ℏ 2 − 40 q μ ℏ 2 − 27 λ 3 ℏ 3 − 12 q λ ℏ 1 − 168 q λ μ ℏ 3 ) G ′ G 3

+ ( − c ℏ 2 + 1 2 α ℏ 1 2 − p ℏ 1 + α ℏ 0 ℏ 2 − 2 p λ ℏ 2 − 3 p μ ℏ 3 − 7 q λ 2 ℏ 1 − 8 q μ ℏ 1 − 8 q λ 3 ℏ 2 − 52 q λ μ ℏ 2 − 60 q μ 2 ℏ 3 − 57 q λ 2 μ ℏ 3 ) G ′ G 2 + ( − c ℏ 1 + α ℏ 0 ℏ 1 − p λ ℏ 1 − 2 p μ ℏ 2 − q λ 3 ℏ 1 − 16 q μ 2 ℏ 2 − 8 q λ μ ℏ 1 − 14 q λ 2 μ ℏ 2 − 36 q μ 2 λ ℏ 3 ) G ′ G + − c ℏ 0 + 1 2 α ℏ 0 2 − p μ ℏ 1 − q λ 2 μ ℏ 1 − 6 q μ 2 λ ℏ 2 − 2 q μ 2 ℏ 1 − 6 q μ 3 ℏ 3 = 0 .

Assuming coefficient of G ′ G i ( i = 0 , 1 , 2 , 3 , 4 , 5 , 6 ) to zero, we obtain a system of algebraic equations. Solving this system by using Maple, we obtain two cases:

First case:

(12) ℏ 0 = ± 30 p 19 α − p 19 q , ℏ 1 = 90 p 19 α , ℏ 2 = 0 , ℏ 3 = 120 q α , c = ± 30 p 19 − p 19 q , λ = 0 , μ = p 76 q , if p q < 0 .

In this situation, the solution of equation (7) is

(13) φ ( η ) = ℏ 0 + ℏ 1 G ′ G + ℏ 3 G ′ G 3 .

Solving equation (9) with λ = 0 , μ = p 76 q if p q < 0 , we obtain

(14) G ( η ) = c 1 exp − p 76 q η + c 2 exp − − p 76 q η ,

where c 1 and c 1 are arbitrary constants. Substituting equation (14) into equation (13), we have

φ ( η ) = ± 30 p 19 α − p 19 q + 90 p 19 α − p 76 q c 1 exp − p 76 q η − c 2 exp − − p 76 q η c 1 exp − p 76 q η + c 2 exp − − p 76 q η + 120 q α − p 76 q 3 c 1 exp − p 76 q η − c 2 exp − − p 76 q η c 1 exp − p 76 q η + c 2 exp − − p 76 q η 3 .

Hence, the exact stochastic solution in this case of the SKS (1), by using (2), has the following form:

(15) u 1 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α − p 19 q + 90 p 19 α − p 76 q c 1 exp − p 76 q ( x − c t ) − c 2 exp − − p 76 q ( x − c t ) c 1 exp − p 76 q ( x − c t ) + c 2 exp − − p 76 q ( x − c t ) + 120 q α − p 76 q 3 c 1 exp − p 76 q ( x − c t ) − c 2 exp − − p 76 q ( x − c t ) c 1 exp − p 76 q ( x − c t ) + c 2 exp − − p 76 q ( x − c t ) 3 ,

where c = ± 30 p 19 − p 19 q and p q < 0 .

Second case:

(16) ℏ 0 = ± 30 p 19 α 11 19 q , ℏ 1 = − 270 p 19 α , ℏ 2 = 0 , ℏ 3 = 120 q α , c = ± 30 p 19 11 p 19 q , λ = 0 , μ = − 11 p 76 q , if p q > 0 .

In this situation, the solution of equation (7) is expressed as follows:

(17) φ ( η ) = ℏ 0 + ℏ 1 G ′ G + ℏ 3 G ′ G 3 .

Solving equation (9) with λ = 0 , μ = − 11 p 76 q , if p q > 0 , we obtain

(18) G ( η ) = c 1 exp 11 p 76 q η + c 2 exp − 11 p 76 q η .

Substituting equation (14) into equation (13), we have

φ ( η ) = ± 30 p 19 α 11 p 19 q − 270 p 19 α 11 p 76 q c 1 exp 11 p 76 q η − c 2 exp − 11 p 76 q η c 1 exp 11 p 76 q η + c 2 exp − 11 p 76 q η + 120 q α 11 p 76 q 3 c 1 exp 11 p 76 q η − c 2 exp − 11 p 76 q η c 1 exp 11 p 76 q η + c 2 exp − 11 p 76 q η 3 .

Therefore, by using (2), the exact stochastic solution in this case of the SKS (1) has the following form:

(19) u 2 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α 11 p 19 q − 270 p 19 α 11 p 76 q c 1 exp 11 p 76 q ( x − c t ) − c 2 exp − 11 p 76 q ( x − c t ) c 1 exp 11 p 76 q ( x − c t ) + c 2 exp − 11 p 76 q ( x − c t ) + 120 q α 11 p 76 q 3 c 1 exp 11 p 76 q ( x − c t ) − c 2 exp − 11 p 76 q ( x − c t ) c 1 exp 11 p 76 q ( x − c t ) + c 2 exp − 11 p 76 q ( x − c t ) 3 ,

where c = ± 30 p 19 11 p 19 q and p q > 0 .

Special cases:

Case 1: If we choose c 1 = c 2 = 1 , then equations (15) and (19) become

(20) u 1 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α − p 19 q + 90 p 19 α − p 76 q tanh − p 76 q ( x − c t ) + 120 q α − p 76 q 3 tanh 3 − p 76 q ( x − c t ) ,

where c = ± 30 p 19 − p 19 q and p q < 0 , and

(21) u 2 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α 11 p 19 q − 270 p 19 α 11 p 76 q tanh 11 p 76 q ( x − c t ) + 120 q α 11 p 76 q 3 tanh 3 11 p 76 q ( x − c t ) ,

where c = ± 30 p 19 11 p 19 q and p q > 0 .

Case 2: If we choose c 1 = 1 and c 2 = − 1 , then equations (15) and (19) become

(22) u 1 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α − p 19 q + 90 p 19 α − p 76 q coth − p 76 q ( x − c t ) + 120 q α − p 76 q 3 coth 3 − p 76 q ( x − c t ) ,

where c = ± 30 p 19 − p 19 q and p q < 0 , and

(23) u 2 ( x , t ) = e ( σ β ( t ) − 1 2 σ 2 t ) ± 30 p 19 α 11 p 19 q − 270 p 19 α 11 p 76 q coth 11 p 76 q ( x − c t ) + 120 q α 11 p 76 q 3 coth 3 11 p 76 q ( x − c t ) ,

where c = ± 30 p 19 11 p 19 q and p q > 0 .

Remark 1

If we put σ = 0 (i.e., equation (1) without noise) in equations (20)–(23), then we obtain the same results stated in [27].

4 The influence of noise on SKS solutions

Here, we discuss the influence of multiplicative noise on the exact solutions of the SKS equation (1). Fix the parameters α = p = q = 1 . We present a number of simulations for different values of σ (noise intensity). We utilize the MATLAB package to simulate our figures as follows:

In Figure 1, we can see that there is a kink solution, which indicates that the solution is not planar when σ = 0 . But in Figure 2, when the noise appears and the intensity of the noise increases, we find that the surface becomes much more planar after small transit patterns. This means that the multiplicative noise affects and stabilizes the solutions.

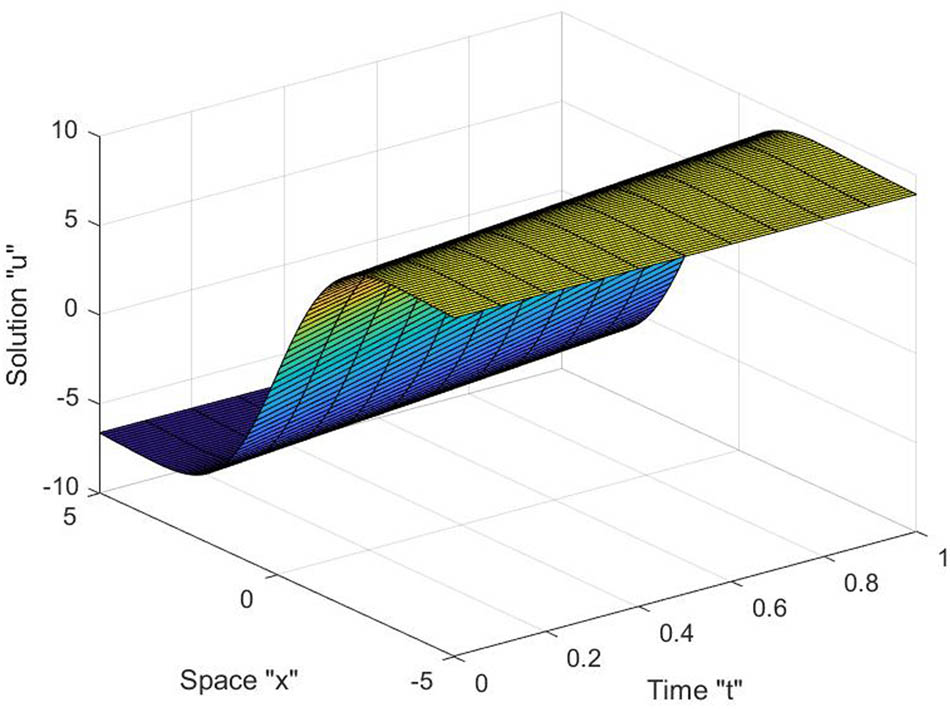
$Figure 1 Graph of solution u 2 {u}_{2} in equation (21) with σ = 0 \sigma =0 .$

Figure 1

Graph of solution u 2 in equation (21) with σ = 0 .

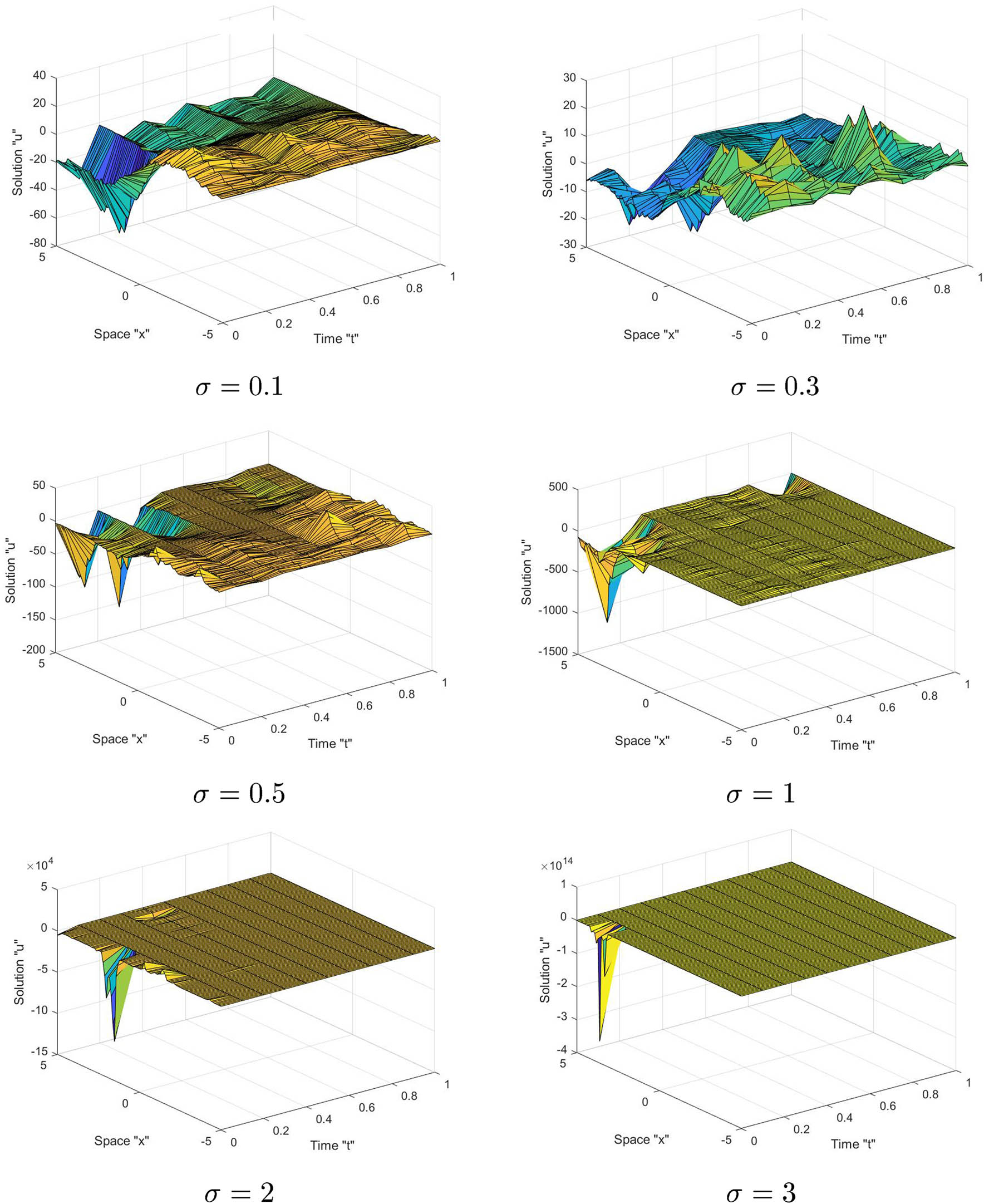
$Figure 2 Graph of solution u 2 {u}_{2} in equation (21) with σ = 0.1 , 0.3 , 0.5 , 1 , 2 , 3 \sigma =0.1,0.3,0.5,1,2,3 .$

Figure 2

Graph of solution u 2 in equation (21) with σ = 0.1 , 0.3 , 0.5 , 1 , 2 , 3 .

5 Conclusion

In this paper, we presented a large variety of exact stochastic solutions of the Kuramoto-Sivashinsky equation (1) forced by multiplicative noise. Moreover, several results were extended such as those described in [27]. These types of solutions can be utilized to explain a variety of fascinating and complex physical phenomena. Finally, we used the MATLAB program to generate some graphical representations to show the impact of multiplicative noise on the solutions of the SKS (1). In the future work, we can consider the multiplicative noise with more dimensions or we can take this equation with additive noise.

Acknowledgments

This research has been funded by Scientific Research Deanship at University of Ha’il - Saudi Arabia through project number RG-21001.

Funding information: This research has been funded by Scientific Research Deanship at University of Ha’il - Saudi Arabia through project number RG-21001.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors declare no coflict of interest.
Data availability statement All data are available in this paper.

References

[1] X. H. Wu, Exp-function method for nonlinear wave equations, Chaos Solitons Fractals 30 (2006), 700–708. 10.1016/j.chaos.2006.03.020Search in Google Scholar

[2] J. H. He and M. A. Abdou, New periodic solutions for nonlinear evolution equations using exp-function method, Chaos Solitons Fractal 34 (2007), 1421–1429. 10.1016/j.chaos.2006.05.072Search in Google Scholar

[3] M. L. Wang, X. Z. Li, and J. L. Zhang, The (G′G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A 372 (2008), no. 4, 417–423. 10.1016/j.physleta.2007.07.051Search in Google Scholar

[4] H. Zhang, New application of the (G′G)-expansion method, Commun. Nonlinear Sci. Numer. Simul. 14 (2009), 3220–3225. 10.1016/j.cnsns.2009.01.006Search in Google Scholar

[5] A. M. Wazwaz, The tanh method: exact solutions of the Sine-Gordon and Sinh-Gordon equations, Appl. Math. Comput. 167 (2005), 1196–1210. 10.1016/j.amc.2004.08.005Search in Google Scholar

[6] W. Malfliet and W. Hereman, The tanh method. I. Exact solutions of nonlinear evolution and wave equations, Phys. Scr. 54 (1996), no. 6, 563–568. 10.1088/0031-8949/54/6/003Search in Google Scholar

[7] S. A. El-Wakil and M. A. Abdou, New exact travelling wave solutions of two nonlinear physical models, Nonlinear Anal. 68 (2008), 235–245. 10.1016/j.na.2006.10.045Search in Google Scholar

[8] K. Khan and M. A. Akbar, The exp(−φ(η))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation, Int. J. Dyn. Syst. Differ. Equ. 5 (2014), 72–83. 10.1504/IJDSDE.2014.067119Search in Google Scholar

[9] W. W. Mohammed, Modulation equation for the stochastic Swift–Hohenberg equation with cubic and quintic nonlinearities on the real line, Mathematics 7 (2019), no. 12, 1217. 10.3390/math7121217Search in Google Scholar

[10] W. W. Mohammed, Approximate solutions for stochastic time-fractional reaction-diffusion equations with multiplicative noise, Math. Methods Appl. Sci. 44 (2021), no. 2, 2140–2157. 10.1002/mma.6925Search in Google Scholar

[11] W. W. Mohammed and N. Iqbal, Impact of the same degenerate additive noise on a coupled system of fractional space diffusion equations, Fractals 30 (2022), 2240033. 10.1142/S0218348X22400333Search in Google Scholar

[12] W. W. Mohammed, Amplitude equation for the stochastic reaction-diffusion equations with random Neumann boundary conditions, Math. Methods Appl. Sci 38 (2015), 4867–4878. 10.1002/mma.3402Search in Google Scholar

[13] S. A. El-Wakil and M. A. Abdou, New exact travelling wave solutions using modified extended tanh-function method, Chaos Solitons Fractals 31 (2007), 840–852. 10.1016/j.chaos.2005.10.032Search in Google Scholar

[14] A. M. Wazwaz, The extended tanh method for abundant solitary wave solutions of nonlinear wave equations, Appl. Math. Comput. 187 (2007), no. 2, 1131–1142. 10.1016/j.amc.2006.09.013Search in Google Scholar

[15] A. M. Wazwaz, A sine-cosine method for handling nonlinear wave equations, Math. Comput. Model. 40 (2004), no. 5–6, 499–508. 10.1016/j.mcm.2003.12.010Search in Google Scholar

[16] C. Yan, A simple transformation for nonlinear waves, Phys. Lett. A 224 (1996), 77–84. 10.1016/S0375-9601(96)00770-0Search in Google Scholar

[17] H. Khan, R. Shah, P. Kumam, D. Baleanu, and M. Arif, Laplace decomposition for solving nonlinear system of fractional order partial differential equations, Adv. Differ. Equ. 2020 (2020), 375. 10.1186/s13662-020-02839-ySearch in Google Scholar

[18] R. Shah, H. Khan, D. Baleanu, P. Kumam, and M. Arifa, The analytical investigation of time-fractional multi-dimensional Navier-Stokes equation, Alex. Eng. J. 59 (2020), no. 5, 2941–2956. 10.1016/j.aej.2020.03.029Search in Google Scholar

[19] A. A. Alderremy, H. Khan, R. Shah, S. Aly, and D. Baleanu, The analytical analysis of time-fractional Fornberg-Whitham equations, Mathematics 8 (2020), no. 6, 987. 10.3390/math8060987Search in Google Scholar

[20] N. Iqbal, H. Yasmin, A. Ali, A. Bariq, M. M. Al-Sawalha, and W. W. Mohammed, Numerical methods for fractional-order Fornberg-Whitham equations in the sense of Atangana-Baleanu derivative, J. Funct. Spaces 2021 (2021), 2197247. 10.1155/2021/2197247Search in Google Scholar

[21] R. Cuerno and A. L. Barabasi, Dynamic scaling of ion-sputtered surfaces, Phys. Rev. Lett. 74 (1995), 4746. 10.1103/PhysRevLett.74.4746Search in Google Scholar PubMed

[22] A. Karma and C. Misbah, Competition between noise and determinism in step flow growth, Phys. Rev. Lett. 71 (1993), 3810. 10.1103/PhysRevLett.71.3810Search in Google Scholar

[23] Y. Kuramoto and T. Tsuzuki, Persistent propagation of concentration waves in dissipative media far from thermal equilibrium, Prog. Theor. Phys. 55 (1976), 356–369. 10.1143/PTP.55.356Search in Google Scholar

[24] D. T. Papageorgiou, C. Maldarelli, and D. S. Rumschitzki, Nonlinear interfacial stability of core-annular film flows, Phys. Fluids A 2 (1990), 340–352. 10.1063/1.857784Search in Google Scholar

[25] G. I. Sivashinsky, Nonlinear analysis of hydrodynamic instability in laminar flames: I. Derivation of basic equations, Acta Astronautica 4 (1977), 1176–1206. 10.1016/0094-5765(77)90096-0Search in Google Scholar

[26] L. Wazzan, A modified tanh-coth method for solving the general Burgers-Fisher and Kuramoto-Sivashinsky equations, Commun. Nonlinear Sci. Numer. Simul. 14 (2009), no. 6, 2642–2652. 10.1016/j.cnsns.2008.08.004Search in Google Scholar

[27] A. M. Wazwaz, New solitary wave solutions to the Kuramoto-Sivashinsky and the Kawahara equations, Appl. Math. Comput. 182 (2006), 1642–1650. 10.1016/j.amc.2006.06.002Search in Google Scholar

[28] S. Abbasbandy, Solitary wave solutions to the Kuramoto-Sivashinsky equation by means of the homotopy analysis method, Nonlinear Dyn. 52 (2008), 35–40. 10.1007/s11071-007-9255-9Search in Google Scholar

[29] N. A. Kudryashov and M. B. Soukharev, Popular ansatz methods and solitary wave solutions of the Kuramoto-Sivashinsky equation, Regul. Chaotic Dyn. 14 (2009), 407–409. 10.1134/S1560354709030046Search in Google Scholar

[30] H. Kheiri and A. Jabbari, Application of the xxxx-expansion method for two nonlinear evolution equations, Int. J. Nonlinear Dyn. Eng. Sci. 2 (2010), 57–67. Search in Google Scholar

[31] Y. Z. Peng, A polynomial expansion method and new general solitary wave solutions to KS equation, Commun. Theor. Phys. 39 (2003), no. 6, 641–642. 10.1088/0253-6102/39/6/641Search in Google Scholar

[32] N. A. Kudryashov, Solitary and periodic solutions of the generalized Kuramoto-Sivashinsky equation, Regul. Chaotic Dyn. 13 (2008), 234–238. 10.1134/S1560354708030088Search in Google Scholar

[33] N. A. Kudryashov, Exact soliton solutions of the generalized evolution equation of wave dynamics, J. Appl. Math. Mech. 52 (1988), 361–365. 10.1016/0021-8928(88)90090-1Search in Google Scholar

[34] C. M. Khalique, Exact solutions of the generalized Kuramoto-Sivashinsky equation, Casp. J. Math. Sci. 1 (2012), 109–116. Search in Google Scholar

[35] W. W. Mohammed, Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain, Chin. Ann. Math. Ser. B 39 (2018), 145–162. 10.1007/s11401-018-1057-5Search in Google Scholar

[36] N. A. Kudryashov, On types of nonlinear nonintegrable equations with exact solutions, Phys. Lett. A 155 (1991), 269–275. 10.1016/0375-9601(91)90481-MSearch in Google Scholar

Received: 2021-09-30

Revised: 2022-01-15

Accepted: 2022-01-24

Published Online: 2022-03-17

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/math-2022-0012

Keywords for this article

stochastic Kuramoto-Sivashinsky; multiplicative noise; stochastic exact solutions; (G′/G)-expansion method

Creative Commons

BY 4.0