Seeing the unseen: Laser speckles as a tool for coagulation tracking

2.1 Materials

Skimmed milk powder (low heat treatment), and the commercially available enzymes Marzyme XT 220 PF (440 IMCU/L) and Chymostar (714 IMCU/L) were obtained by IFF internally. Calcium chloride dihydrate (technical grade) was purchased from Sigma-Aldrich (St. Louis, USA). All experiments were performed using deionized water (PURELAB flex 1, ELGA LabWater, High Wycombe, UK).

2.2 Sample preparation

The milk for the coagulation experiments was prepared by mixing milk powder with a 0.009 M calcium chloride solution at a concentration of 60 g/L (referred to as regular protein content) or 120 g/L (referred to as high-protein [HP]content).

The solution was stirred for 30 min, achieving complete dissolution of the milk powder. Subsequently, the milk was rested for at least 30 min at the coagulation test temperature using a heating chamber at 21°C to temper the milk to the test temperature.

The coagulants were diluted prior to inoculating the milk samples. Marzyme and Chymostar were diluted 5-fold and 10-fold, respectively, achieving enzyme concentrations of 40 and 71.4 IMCU/L. The diluted enzyme solutions were used for further experiments within 10 min after preparation.

2.3 Time sweep

The rheological changes upon the rennet coagulation of milk were tracked by time sweeps. The time sweeps were performed with a stress-controlled rheometer (Anton-Paar MCR 302) equipped with a concentric cylinder (27 mm; V sample = 19 mL) geometry. The storage modulus ( G ′ ), loss modulus ( G ″ ), complex modulus ( G * = G ′ 2 + G ″ 2 ), and loss factor ( δ = G ″ / G ′ ) were captured within a period of 40 min at a shear strain of 1%, well within the linear viscoelastic regime (LVR) (Figure S2), at a frequency ω = 1 Hz. All measurements were performed with a solvent trap to minimize evaporation. All measurements were performed at 21°C in triplicate.

Our test methodology proceeded as follows. First, 50 mL of milk, prepared according to Section 2.2, was inoculated at a concentration of 40 or 80 IMCU/L using the diluted coagulants. Second, the sample was transferred to the pre-heated measuring geometry, and the time sweep was started after a resting period of 5 min.

2.4 Laser speckle rheology

The laser speckle rheology optical setup is schematically displayed in Figure 1. Light from a randomly polarized laser diode (650 nm, 5 mW, Global Laser, Abertillery, UK) was polarized and focused onto the sample, which resulted in a laser spot of approximately 1 cm in diameter. The sample had a volume of 15 mL and a corresponding height of approximately 1 cm. The cross-polarized component of the light back-scattered at an angle of approximately 50° was collected by a complementary metal-oxide semiconductor (CMOS) camera (BFS-U3-51S5M-C, FLIR Systems, USA), equipped with a TV lens (25 mm, f1.4, Pentax, Rungis, France). To minimize external light interference, the experimental setup was enclosed using blackout curtains. The speckle frames were acquired at 199 fps, over an ROI of 200 × 200 pixels, for approximately 0.5 s unless specified differently. The camera parameters and image acquisition were controlled through a home-written Python-based code. The sample temperature was controlled through a heating jacket with constant water exchange from an external water bath.

Figure 1

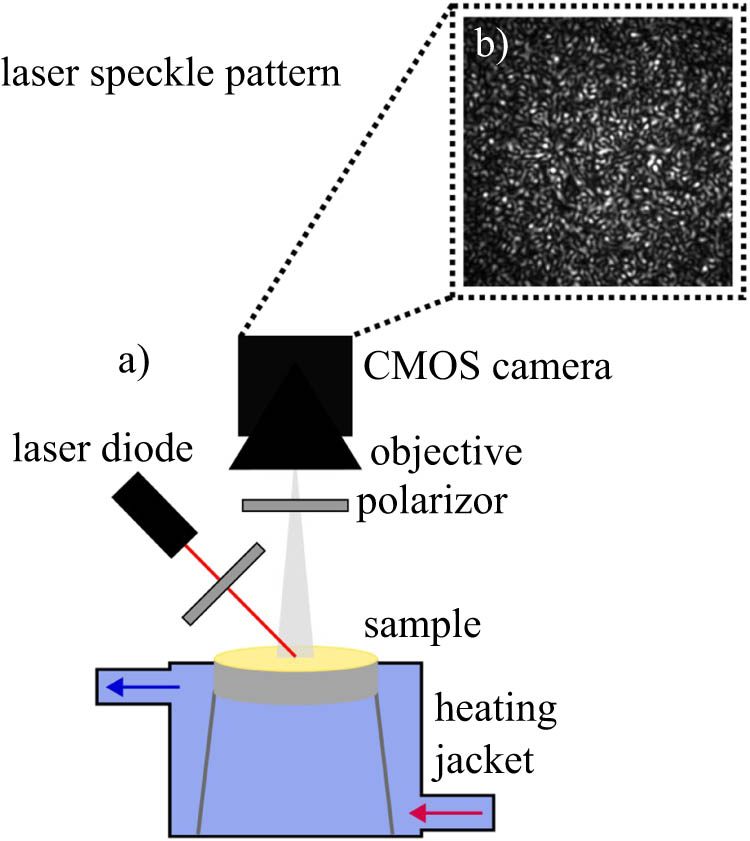
(a) Schematic of the laser speckle rheology setup and (b) laser speckle pattern.

2.5 Data processing

The acquired laser speckle images were analyzed using a custom Python script. First, the temporal evolution of the acquired speckle frames was analyzed by the two-dimensional linear correlation shown in equation (frames correlation),

where I ‾ ( t ) and I ‾ ( t + τ ) are the mean intensities of the corresponding frames. The frames correlation coefficient C indicates, similar to the Pearson correlation coefficient, the degree of linear correlation between two frames separated by the lag time τ . C is 1 if the pixel intensities I at t and t + τ are linearly related, whereas C is 0 if the speckle patterns separated by τ are uncorrelated. As the movement of the scatterers causes random changes in the speckle pattern, the frames correlation coefficient reflects the relative number of displacements in the sample between two frames [18]. Contrary to speckle autocorrelation, the frames correlation is less time-consuming, independent of the speckle contrast, and less vulnerable to acquisition noise [18], facilitating the simplification of the laser speckle rheology setup. Second, to quantify the frame-to-frame two-dimensional linear correlation, we use the viscoelasticity index V I τ , which was previously introduced in literature as viscosity index [18]:

where M τ and σ τ are the median and standard deviation, respectively, for all frames correlation coeficients between frames within a time period of Δ t separated by τ . The VI represents the filtered average frames correlation coefficient for a specific τ , with the filter criterion of one standard deviation from the median, providing a robust measure of the scatterer mobility [18]. In particular, the VI calculated as follows: The frames correlation was calculated for all consecutive frames within a time period of 100 frames according to equation (frames correlation). Hence, τ was set to approximately 5 ms, unless specified differently. The selected τ ≈ 5 ms has no significant impact on the overall captured coagulation dynamics. The impact of τ is further discussed in Section 3.3. To reduce the computational load, the frames correlation was calculated using only the centered 50 × 50 pixels. Subsequently, the frames correlation coefficients were used to compute the VI according to equation (VI).

To compare laser speckle rheology with SAOS rheology as methods to track the rheological changes during rennet coagulation of milk, we extract characteristic features from the temporal VI and G * evolution curves. The coagulation times t c , VI and t c , G * were determined as the first points deviating more than 500 and 100%, respectively, from the moving average. The onset of the VI plateau, t 2 nd plt . , was extracted by finding the first point deviating more than 150% from the reversed moving average. The value of the second VI plateau, V I 2 nd plt . , was calculated as the mean of all VI data points following t 2 nd plt . . The steepest VI slope, dVI d t max , was chosen to represent the curd firming rate of the laser speckle rheology and was determined by calculating the slope for each consecutive pair of points. The curd firming rate measured by the SAOS, d G * d t , was approximated as the average slope of the linear G * section after the coagulation point. The cross-over point between G ′ and G ″ was defined as the point at which G ′ becomes larger than G ″ . A graphical representation of the characteristic features is provided in Figures S4 and S5 of the supplementary information.

3.1 Temporal evolution of laser speckle patterns during rennet coagulation

Upon the rennet addition to milk, chymosin starts to cleave the stabilizing κ-casein located on the outside of the casein micelles. The cleavage of the κ-casein leads to the destabilization of the casein micelles. This, in turn, results in the aggregation of the destabilized casein micelles and, eventually, in the formation of a percolating casein gel network [26,28]. The rheology of the milk systems changes drastically as a consequence of this coagulation process, from being a low-viscosity liquid to a firm viscoelastic gel [26,28,29]. As the scatterers’, i.e., casein micelles, mobility is reduced by the formation of aggregates and the subsequently formed space-spanning gel network, we hypothesize that the laser speckle pattern fluctuation slows down simultaneously (refer supplementary video). The frames correlation coefficient as a function of the delay time τ within a range of 5,000 ms at various time points during the rennet coagulation by 40 IMCU/L Marzyme at 21°C is shown in Figure 2.

Figure 2

Frames correlation coefficient C as a function of the delay time τ within a τ range of 5,000 ms at various points in time during the rennet coagulation of milk by 40 IMCU/L Marzyme at 21°C. The inset shows the initial decay between τ of 0 and 50 ms for improved visibility.

With increasing time after the coagulant addition, the frames correlation coefficient decays slower, as shown in Figure 2. Within the first 12 min, decorrelation of the laser speckle pattern occurs within a single τ of approximately 5 ms. Thus, within this time frame, the laser speckle fluctuations are sufficiently fast such that two subsequent images are uncorrelated at the acquisition frame rate of 199 fps. Thus, the maximum frame rate determines the lower detection limit. On the other extreme, after 40 min, the frames correlation function only decays to approximately 0.5 within 5,000 ms. The increased decorrelation time suggests a reduction in the scatterer mobility with increasing time after rennet addition. It is necessary to point out that the frames correlation coefficient is not only affected by the rheological properties but also by the optical properties of the sample [30,31]. For instance, Tripathi et al. [31] attributed an increase in the temporal speckle intensity autocorrelation at longer lag times to changing optical properties resulting from blood coagulation. During the rennet coagulation process, the casein micelles destabilize, aggregate, and eventually form a space-spanning gel network [26,28]. Consequently, we expect the optical properties of the milk samples to change during the coagulation process. We acknowledge the importance of the optical properties for deriving the viscoelastic moduli, but they are not considered in this study due to the inherent complexity of milk and the focus on comparing the relative rheological changes in compositionally similar samples. In Figure S1, we discuss the backscattered light intensity during the coagulation process and its implications on the optical properties of the sample. Further, we must note the presence of periodic perturbations with a constant frequency of 11 Hz, suggesting a non-random origin. Potential sources of the observed periodic perturbations are discussed in the supplementary information.

To quantify the linear correlation of the speckle patterns during the coagulation process, thereby providing insights into the simultaneous rheological transitions, we use the VI. SAOS was chosen as the comparison method to laser speckle rheology, as it is the industry standard for detailed rheological characterization and directly probes the mechanical changes during rennet coagulation [32,33]. Therefore, comparing shear and laser speckle rheology data enables the interpretation of laser speckle rheology measurements. However, it is important to note that the laser speckle approach probes scatterer mobility and thus, only indirectly reflects the rheological properties of the surrounding matrix, whereas SAOS directly probes the bulk rheological behavior. Consequently, the two methods do not probe the system at the same length or time scales. As such, comparisons and interpretations of the two methods must be carried out with caution. The temporal evolution of the VI, as well as the storage modulus G ′ , loss modulus G ″ , and complex modulus G * , during the rennet coagulation by 40 IMCU/L at 21°C is shown in Figure 3. Each data point represents the mean of three independent experimental realizations, while the error bars denote one standard deviation.

Figure 3

Storage modulus G ′ , loss modulus G ″ , complex modulus G * , and VI as a function of the time after rennet addition t during the rennet coagulation by 40 IMCU/L at 21°C.

In SAOS, an oscillatory shear stress or strain is applied, and the resulting response from the developing gel is measured [26]. The applied shear strain must remain within the LVR during the entire gel development, ensuring a linear proportionality between stress and strain. Yet, initially, the curd is very weak, and consequently, strongly limiting the LVR. Regardless, we argue that the gel strength develops sufficiently fast, thereby ensuring the linear viscoelasticity. To ensure that the time sweeps were performed within the LVR, an amplitude sweep was conducted and is shown in Figure S2 of the supplementary information.

Within the first 13 min, both G ′ and G ″ are nearly constant with G ′ < G ″ , indicating a dominant liquid-like behavior. After 13 min, both G ′ and G ″ increase apparently linearly (note that G ′ and G ″ are plotted on a semilog scale). Further, a cross-over occurs after approximately 15 min, indicating the gel point [34]. To understand the rheological changes upon rennet addition, we will view the system as a developing particle gel with the casein micelles being the particles. For such a system, the shear modulus G can be approximated as [35]:

where C is the characteristic length, N is the number of stress-bearing strands per unit area perpendicular to the direction of the applied deformation x , and d F is the change in free Gibbs energy when particles are moved by d x , i.e., bond strength. According to the modulus formula, during the coagulation process, G depends on both the incorporation of new particles into the gel network and the bond strength. The ratio between the storage and loss moduli, i.e., the loss factor, reflects the nature of the bonds within the network [26]. Consequently, the loss factor, which approaches a constant value after the cross-over (Figure 4c), suggests that the increasing gel firmness is caused by the increasing number of casein micelles being incorporated into the gel network. Similar to the shear moduli, VI remains constant at approximately zero within the first 13 min. Subsequently, VI increases rapidly. After approximately 16 min, the growth rate begins to decline. After 40 min, at the end of the observation window, VI increased to a maximum value of about 0.75.

Figure 4

(a) VI, (b) complex modulus G*, and (c) loss factor δ as a function of time after rennet addition t during the rennet coagulation of regular and HP milk by either Marzyme or Chymostar at various concentrations at 21°C.

The initial VI regime around 0 is temporally well aligned with the liquid-like behavior dominated plateau observed for the shear moduli. The dominant liquid-like behavior indicates that the system remains within that time frame in the primary enzymatic phase. The absence of structures resisting the casein micelle mobility within the primary enzymatic phase explains the nearly instant decorrelation of the frame’s correlation coefficient, responsible for the VI value of 0. The onset of the observed increase in both the moduli and VI at 13 min, commonly referred to as the coagulation point [26], indicates the formation of structures restricting the scatterer mobility, which is simultaneously linked to an increasing resistance to deformation. Thus, this transition implies the onset of the secondary enzymatic phase. Over time, the casein aggregates grow further and eventually form a coherent space-spanning gel. The cross-over point was reached after 15.5 min, indicating the transition from liquid-like to gel-like behavior, as expected, resulting from the gel formation. Interestingly, the maximum VI growth rate occurred simultaneously at 15.5 min. The increasing shear moduli and VI after 15.5 min, known as curd firming, are caused by an increasing number of casein micelles incorporated into the particle gel network [26,28,29]. We propose that the incorporation of casein micelles, and also larger casein aggregates, reduces the number of freely moving casein micelles in solution. Concurrently, the resulting network further hinders the movement of free micelles. Consequently, the number of scatterers that moved between two frames, thereby changing the speckle pattern, characterized by the frames correlation coefficient [18], is expected to decrease. Thus, the frames correlation coefficient and consequently VI increase due to the curd firming.

Yet, we must note that the curd firming dynamics captured by the shear moduli and VI differed fundamentally. While the moduli increase visibly linearly (note that Figure 3 is plotted on a semilog scale), the slope of the VI seems to decrease with increasing coagulation duration, characteristic of a sigmoidal curve. Generally, one expects that the shear moduli reach a plateau at long times, i.e., a sigmoidal curve, as all casein micelles are incorporated into the gel network [26]. Hence, the SAOS coagulation curve indicates that this last coagulation stage was not reached within the observation window of 40 min. Despite the apparent different curd firming dynamics, both the laser speckle rheology and SAOS are temporally well-aligned in terms of the coagulation point and cross-over.

3.2 Tracking under various coagulation conditions

The generic behavior of both the shear moduli and the VI, and their connection, in response to the rennet coagulation of milk was discussed in Section 3.1. We further proceed by comparing the response of the two methods to the rennet coagulation of milk under various industry-relevant coagulation conditions. The VI, complex modulus G * , and loss factor δ as a function of time after rennet addition during the rennet coagulation of regular and “HP” milk by various concentrations of Marzyme or Chymostar at 21°C are shown in Figure 4. Here each data point represents the mean value of three independent experimental realizations, while the error bars denote ± one standard deviation. As visible in Figure 4, the rennet coagulation process under all investigated coagulation conditions follows the same stages, as discussed in detail for the rennet coagulation by 40 IMCU/L at 21°C (Figure 3). Yet, despite the same overall behavior, the temporal occurrence of aggregation, gelation, and subsequent gel firming dynamics differs along the investigated coagulation conditions. To characterize these apparent coagulation dynamics differences, characteristic features were extracted from the coagulation curves shown in Figure 4 and are presented in Figure 5. A graphical representation of the characteristic features is provided in Figures S4 and S5 of the supplementary information.

Figure 5

Characteristic features, extracted from the VI and moduli as a function of time after rennet addition during the rennet coagulation of regular and HP milk by either Marzyme or Chymostar at various concentrations at 21°C, as a function of the enzyme concentration. Filled and open markers represent measures extracted from the laser speckle rheology and shear rheometry, respectively. (a) Coagulation times t c , VI (filled markers) and t c , G * (open markers), (b) time of maximum VI slope t dVI d t max (filled markers) and cross-over time t G ′ = G ″ (open markers), (c) curd firming rates dVI d t max (filled markers) and d G * d t (open markers), (d) onset of late VI plateau t 2 nd plt . , and (e) late VI plateau value V I 2 nd plt . .

The experimental results indicate an inverse relation between coagulation time and enzyme concentration, as shown in Figure 5a. The coagulation time of the Marzyme-containing samples decreased from approximately 31 to 18 min and 5 min for enzyme concentrations of 20, 40, and 80 IMCU/L, respectively. A similar trend was found for the Chymostar-containing samples, where the coagulation time decreased from around 15–8 min for enzyme concentrations of 40 and 80 IMCU/L, respectively. Principally, milk coagulation initiates when a sufficiently high degree of κ -casein is hydrolyzed [36]. A higher enzyme concentration results in an increased enzymatic activity and consequently reduces the time required to reach the κ -casein hydrolysis threshold, known as coagulation time. Comparing the two enzymes at a given enzymatic activity, i.e., 40 or 80 IMCU/L, it is noticeable that the Chymostar-containing samples coagulated consistently slightly delayed compared to the Marzyme-containing samples (Figure 5a). Despite the theoretical enzymatic activity, experimental conditions like pH and temperature deviating from the standard test definition may have resulted in the different coagulation times. Further, for a fixed enzyme concentration, i.e., 80 IMCU/L Marzyme, doubling the casein fraction resulted in a coagulation time increase from 5 to 18 min. This observed coagulation time increase with increasing protein content is due to the reduced enzyme/casein ratio. This, in turn, results in relatively less available enzyme to cleave the κ -casein. Consequently, the κ -casein threshold required for coagulation is reached only after longer times [28,29]. Comparing the two methods, we note that the coagulation times determined through SAOS, i.e., t c , G * , and laser speckle rheology, i.e., t c , VI , are approximately the same with margins of about 2 min, corresponding to 5% of the experimental window. As the laser speckle patterns were acquired only every minute, the inter-method coagulation time difference seems negligible, indicating that the two methods are temporally well aligned regarding rheological changes.

Similar to the coagulation point, the time of the G ′ − G ″ cross-over, shown in Figure 5b, decreased with increasing enzyme concentration. The increased κ -casein hydrolysis rate with higher enzyme concentrations results in a shorter enzymatic phase, and thus, an earlier gel point [26]. As discussed for Figure 3, the occurrence of the maximum VI growth rate aligns temporally well with the cross-over time for all tested samples, indicating a potential connection between the formation of a space-spanning casein network and the subsequent continuously decreasing VI slope.

Further, the gel network development, captured by both methods, was compared by extracting the characteristic curd firming rates, which are shown in Figure 5c. As outlined in Section 2.5, the maximum VI slope and the slope of the linear G * section after the coagulation point were extracted for the laser speckle rheology and SAOS, respectively. Again, both methods clearly measured an increase in the curd firming rate with increasing enzyme concentration. The observed proportionality between curd firming rate and enzyme concentration was previously linked to the higher κ -casein hydrolysis rate [29]. Both laser speckle rheology and SAOS indicated that the curd firming rate of the Marzyme-containing sample slightly exceeded the Chymostar-containing samples at any investigated enzyme concentration. Yet, despite the consensus regarding the enzyme concentration and type, we note that the two methods indicated an opposing protein content effect on the curd firming rate. The curd firming rate determined by SAOS increased from 0.43 to 0.74 Pa/min as a result of a two-fold increase in the casein content during the coagulation by 80 IMCU/L Marzyme. The distance between casein micelles is reduced with increasing casein concentration. Consequently, aggregation between casein micelles is promoted, resulting in the observed increased curd firming rate [37]. In contrast, under the same coagulation conditions, the curd firming rate determined by laser speckle rheology decreased from 0.18 to 0.08 min⁻¹. We speculate that the apparent decreased firming rate does not reflect the actual gel-firming process. Rather, we hypothesize, as VI reflects the number of moved scatterers between two frames [18], that the elevated number of free casein micelles dominates the increased inclusion of casein into the gel network.

A substantial difference in the apparent coagulation dynamics captured by laser speckle rheology and SAOS is the behavior at the advanced coagulation stage, i.e., as t approached 40 min. Within the observation window of 40 min, G * increased linearly. Yet, VI showed sigmoidal behavior with an apparent late-stage VI plateau of approximately 0.75 for all tested conditions (Figure 5e). In principle, one expects a sigmoidal G * coagulation curve, as eventually all casein micelles are incorporated into the gel network [26]. Yet, as we observed a linear G * increase within the experimental timeframe, suggesting that the casein micelles were not depleted yet, the shared late VI plateau value seems to be unrelated to the gel firmness. Interestingly, the onset time of the VI plateau seems to decrease with increasing enzyme concentration, except for the HP milk sample (Figure 5d). The twofold casein concentration increase resulted in a time difference increase from approximately 10 to 21 min for the coagulation by 80 IMCU/L. Rather than being directly related to the gel strength, we hypothesize that the VI plateau is linked to a change in scatterer mobility timescale. This timescale transition may be caused by the formation of a space-spanning gel network, drastically hindering the scatterer mobility. Thus, the τ of 5 ms used for the VI computations were presumably insufficient to capture sufficient scatterer movements to resolve the firmness development during the advanced coagulation stage.

3.3 Influence of lag time τ

The lag time τ is a critical parameter in the laser speckle pattern correlation analysis and must be carefully chosen with respect to the scatterers’ timescale [38]. If τ is too short (τ ≪ Brownian motion), insufficient scatterer movement will occur between the two time points, and thus, the laser speckle pattern will appear unchanged. Conversely, if τ is too long (τ ≫ Brownian motion), the laser speckle patterns will appear completely uncorrelated as too many scatterer movements occurred within that timeframe. Hence, in both cases, we are unable to quantify the speed of the laser speckle fluctuations and, consequently, unable to derive any rheological properties. To investigate the impact of the lag time τ on the VI during the rennet coagulation of milk, we determined VI for various values of τ . The VI for 5 ms ≤ τ ≤ 2,500 ms as a function of time after rennet addition during the rennet coagulation of milk by 40 IMCU/L Marzyme at 21°C is shown in Figure 6. Each data point represents the mean value of three independent experimental realizations, while the error bars denote ± one standard deviation.

Figure 6

(a) VI for lag times 5 ms ≤ τ ≤ 2,500 ms as a function of time after rennet addition, and (b) normalized VI / V I max for lag times 5 ms ≤ τ ≤ 2,500 ms as a function of time after rennet addition, corrected for the difference in the coagulation time relative to τ = 5 ms, during the rennet coagulation of milk by 40 IMCU/L Marzyme at 21°C.

The impact of the lag time τ was quantified by extracting the characteristic features from the VI coagulation curves, as outlined in Section 2.5, and is shown in Table 1. The apparent coagulation time seems to be delayed with increasing τ . The coagulation time increased by 5 min, from approximately 13 to 18 min, as a result of the τ increase from 5 to 2,500 ms. A dependency between τ and the coagulation time was anticipated. The coagulation point is related to the formation of casein structures that reduce casein mobility. Thus, in turn, fewer scatterer movements occur within a fixed timeframe, leading to the VI increase. Consequently, a longer τ requires a higher degree of mobility reduction so that the number of scatterer movements is limited sufficiently to avoid complete decorrelation of the two laser speckle patterns. Enhanced mobility reduction is related to a higher degree of structure formation, which requires longer times to develop.

Moreover, the onset of the late VI plateau seems to be delayed, while its value decreases, with increasing τ . The delayed onset of the late VI plateau appears to be related to the extended range in which differentiation between scatterer mobility is possible. A larger τ decreases the VI plateau value due to a greater number of scatterer movements being captured. Furthermore, we observe that the curd firming rate seems to decrease with increasing τ , potentially related to the reduced VI range with increasing τ .

To compare the underlying coagulation dynamics suggested by the VI coagulation curves at various τ , we normalized VI and t . The VI was normalized by dividing it by V I max , removing the differences in the second plateau height and ensuring that the range of the curves is the same for all, i.e., 0–1. Additionally, we introduced the shift factor Δ t c = t c , τ − t c , 5 ms , which represents the difference in coagulation time relative to the coagulation time of the VI curve at τ = 5 ms. The normalized VI for 5 ms ≤ τ ≤ 2,500 ms as a function of time after rennet addition during the rennet coagulation of milk by 40 IMCU/L Marzyme at 21°C is shown in Figure 6b). Each data point represents the mean of three independent experimental realizations, while the error bars denote ± one standard deviation. Rescaling VI to the range 0–1 and temporally aligning the coagulation points leads to the collapse of the curves onto a single master curve. The alignment of the curves through the normalization process reveals that the underlying dynamics captured are inherently similar, regardless of τ . Hence, by combining different values of τ , one can potentially extend the measurable range of VI values that qualitatively reflect the gel firming behavior, as larger τ values delay the onset of the second plateau. A similar adaptive speckle imaging approach was previously presented to investigate film formation and drying processes [39].

3.4 Scaling analysis

In Sections 3.1–3.3, we compared the coagulation curves captured by SAOS and laser speckle rheology, and discussed the influence of coagulation conditions on these features. Despite the temporal alignment of key features, such as the coagulation point, and the ability of both methods to capture the effects of various coagulation conditions, we noted that the apparent gel firming dynamics differed between the two techniques. The G * evolution suggests apparent linear gel firming within the experimental window, while VI shows a decreasing firming rate at later stages, characteristic of the sigmoidal VI coagulation curve. To understand the complex relationship between G * and VI, we plot the complex modulus G * as a function of the corresponding VI during the rennet coagulation under various coagulation conditions in Figure 7. Each data point represents the mean of three independent experimental realizations, with the error bars denoting ± one standard deviation.

Figure 7

Complex modulus G * as a function of the VI for the corresponding time points during the rennet coagulation by variable concentrations of Marzyme or Chymostar at 21°C. The inset shows an exponential function (dashed line) fitted to the data after the coagulation point, indicated by the light gray shading.

Interestingly, when plotting G * as a function of VI, all data collapse onto a single master curve for all coagulation conditions, except for the HP sample. The collapse of all data from samples with the same composition onto a single master curve indicates that VI can serve as a reliable measure of G * under fixed sample composition and acquisition parameters, following an appropriate calibration. The deviation of the HP content data from the master curve may be related to the increased scatterer fraction resulting from the twofold increase in solids. We speculate that VI is inversely proportional to the amount of freely moving scatterers, namely, mostly the non-aggregated casein micelles. Therefore, at higher casein concentrations, a larger fraction of casein must be incorporated into the network to produce the same reduction in speckle activity as observed in the regular milk samples. Consequently, the increased incorporation of casein at higher solid fractions leads to an increase in G * at a given VI. As clearly shown in the inset for coagulation by 40 IMCU/L Marzyme at 21°C, G * appears to be an exponential function of VI. The apparent exponential relationship arises from the sigmoidal shape of the VI coagulation curve, with its growth rate decreasing as it approaches the upper limit of VI ≈ 0.75, resembling exponential decay. The exponential nature implied by Figure 7 highlights the sensitivity of the laser speckle rheology method in detecting the initial increase in resistance to deformation caused by the formation of casein aggregates. However, we note that the differentiation of gel firmness is limited by VI at a constant τ . Thus, laser speckle rheology appears to be a viable method for tracking and differentiating protein aggregation under various conditions, provided the samples have similar compositions and fixed acquisition parameters.