The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions

1 Introduction

The world around us is basically nonlinear. In this regards nonlinear partial differential equations (NPDEs) are main significance to describe the complex physical phenomena; for example, nonlinear wave propagation can occur in the scopes of elasticity theory, fluid dynamics, plasma physics, and nonlinear optics. The exploration of analytical, exact solutions for NPDEs has become quite prominent due to the recently great advances gained in the computational techniques. Several efficient and powerful methods can be

applied for finding the analytical solutions such as; Ricatti Bernoulli’s sub-ODE method [1, 2], Modified extended direct algebraic method [3, 4, 6], the homogeneous balance method, the modified simple equation method [7, 8, 9], auxiliary equation method [10], the modified extended mapping method [11, 12, 13, 14], extended Jacobian elliptic function expansion method, the modified extended tanh-function method, the generalized Kudryashov method, the sine-cosine method [15], the Hirota’s bilinear method [16], Darboux transformation [17, 18], semi-inverse variational principle [19], the hyperbolic tangent expansion method [20], the inverse scattering transform [21], the tanhsech method and the extended tanhcoth method, the first integral method [22], the symmetry method, the soliton ansatz methods [23, 24, 25, 26,27, 28, 29, 30, 31, 32, 33, 34, 35, 38].

Article purpose is to investigate exact solutions of integro-differential Ito equation by employing the three analytical modified mathematical methods. The integro-differential Ito equation having fruitful applications in mathematical physics.In previous authors [39, 40] applied generalized Kudryashov and (G^′/G, 1/G) methods respectively for exact traveling wave solutions for Eq. (10). But the aspire our presented work is that, we give concentration for finding analytical solutions of Eq. (10) by generalized direct algebraic, extended simple equation and modified F-expansion methods. The derived solutions are productive tools for solving numerous problems in the field applied sciences.

The reminant article arranged sections (2-5) as, Description of proposed steps in 2, apply methods in 3. Results discussion in 4 and Summary in 5.

2 Description proposed methods

Consider

Let

Put (2) in (1),

3 Applications

3.2 Applications of Extended Simple Equation Method

Let (12) has solution,

(21) v=A1Ψ+A−1Ψ+A0

Put (21) in (12) along with (7) and after solving obained system of equations, we have

Case I

l₃ = 0,

Family - I

(22) A1=−2l2,   A−1=0,      ω=l12−4l0l2

Substitute (22) in (21) with (7), then solution of Eq. (10) achieved,

(23) v4=A0    +(l1−4l0l2−l12tan(4l0l2−l122(ξ+ξ0))),4l0l2>l12

(24) u4=−12( 4l0l2     −l12 )(ξ+ξ0)sec2(124l0l2−l12(ξ+ξ0)),     4l0l2>l12

Family - II

(25) A1=0,   A−1=2l0,   ω=l12−4l0l2

Figure 1

Exact traveling waves of solution (20).

Figure 2

Traveling waves of solution of (30).

Put (25) in (21),

(26) v5=A0       −4l2l0(l1−4l2l0−l12tan(124l2l0−l12(ξ+ξ.0))),4l0l2>l12.

(27) u5=2l0l2(4l0l2−l12)(ξ+ξ0)sec2(124l0l2−l12(ξ+ξ0))(l1−4l0l2−l12tan(124l0l2−l12(ξ+ξ0)))2,4l0l2>l12

Case II

l₀ = l₃ = 0,

(28) ω=l12,  A1=−2l2,   A−1=0

Put (28) in (21),

(29) v6=−2l2l1el1(ξ+ξ0)(1−l2el1(ξ+ξ0)),   l1>0.

(30) u6=−2l12l22(ξ+ξ0)el1(ξ+ξ0)(1−l2eli(ξ+ξ0))2,   l1>0.

(31) v7=2l2l1el1(ξ+ξ0)(1+l2el1(ξ+ξ0)),       l1<0.

(32) u7=−2l12l22(ξ+ξ0)el1(ξ+ξ0)(l2el1(ξ+ξ0)+1)2,    l1<0.

Case III

l₁ = l₃ = 0,

Family - I

(33) ω=−4l0l2,   A1=−2l2,    A−1=0

Put (33) in (21),

(34) v8=A0−2l0l2(tanl0l2(ξ+ξ0)),        l2l0>0.

(35)  u8=−2l0l2(ξ+ξ0)sec2(l0l2(ξ+ξ0)),l2l0>0.

(36)   v9=A0+2−l0l2(tanh−l0l2(ξ+ξ0)),l2l0<0.

(37)   u9=−2l0l2(ξ+ξ0)sech2(−l0l2(ξ+ξ0)),l2l0<0.

Family - II

(38) ω=−4l0l2,   A1=0,    A−1=2l0

Put (38) in (21),

(39) v10=A0−2l0l2l0l2(tanl0l2(ξ+ξ0)),    l0l2>0,

(40) u10=−2l0l2(ξ+ξ0)csc2(l0l2(ξ+ξ0)),l0l2>0,

(41)  v11=A0+2l0l2(−l0l2tanh−l0l2(ξ+ξ0)),l0l2<0,

(42) u11=2l0l2(ξ+ξ0)csch2(−l0l2(ξ+ξ0)),l0l2<0,

Family - III

(43) ω=−16l0l2,   A1=−2l2,   A−1=2l0

Put (43) in (21),

Figure 3

Traveling waves of solution (32).

(44) v12=A0−2l0l2(tanl0l2(ξ+ξ0))     −2l0l2l0l2(tanl0l2(ξ+ξ0)),     l0l2>0.

(45) u12=−2l0l2(ξ+ξ0)sec2(l0l2(ξ+ξ0))     −2l0l2(ξ+ξ0)csc2(l0l2(ξ+ξ0)),          l0l2>0.

(46) v13=A0+2−l0l2(tan−l0l2(ξ+ξ0))     +2l0l2(−l0l2tanh−l0l2(ξ+ξ0)),      l0l2<0.

(47) u13=−2l0l2(ξ+ξ0)sech2(−l0l2(ξ+ξ0))    +2l0l2(ξ+ξ0)csch2(−l0l2(ξ+ξ0)),      l0l2<0.

3.3 Applications of Modified F-expansion Method

Let solution of (12) is;

(48) v=a0+a1F+b1F

Substitute (48) in (12) with (11),

For A = 0, B = 1, C = −1, we have,

(49) ω=1,  a1=2,   b1=0

Put (49) in (48),

(50) v14=a0+(1+tanh(12ξ))

(51) u14=12ξsech2(ξ2)

When A = 0, B = −1, C = 1, then we have,

(52) ω=1,   a1=−2,   b1=0

Substitute (52) into (48),

(53) v15=a0−(1−coth(12ξ))

(54) u15=12ξcsch2(ξ2)

For A=12,  B=0,C=−12, then we have,

Figure 4

Traveling waves of solution of (42).

Family - I

(55) ω=1,   a1=0,    b1=1

Put (55) in (48),

(56) v16=a0+(1coth(ξ)±csch(ξ))

(57) u16=−−ξcsch2(ξ)−ξcoth(ξ)csch(ξ)(coth(ξ)+csch(ξ))2

Family - II

(58) ω=−1,   a1=1,  b1=0

Put (58) in (48),

(59) v17=a0+(±csch(ξ)+coth(ξ))

(60) u17=−ξcsch2(ξ)−ξcoth(ξ)csch(ξ)

Family - III

(61) ω=−4,  a1=1,  b1=−1

Put (61) in (48),

(62) v18=a0+(1(±csch(ξ)+coth(ξ)))     +(±csch(ξ)+coth(ξ))

(63) u18=−ξcsch2(ξ)−−ξcsch2(ξ)−ξcoth(ξ)csch(ξ)(coth(ξ)+csch(ξ))2     −ξcoth(ξ)csch(ξ)

For C = −1, B = 0, A = 1,

Family - I

(64) ω=4,  a1=0, b1=2

Put (64) in (48),

(65) v19=a0+2(1tanh(ξ)),   or  a0+2(1coth(ξ))

(66) u19=−ξcsch2(ξ),    or    ξsech2(ξ)

Family - II

(67) ω=4,  a1=2,   b1=0

Put (67) in (48),

(68) v20(ξ)=a0+2(tanh(ξ))   or   a0+(coth(ξ))

(69) u20(ξ)=ξsech2(ξ)   or   −ξcsch2(ξ)

Family - III

(70) ω=16,    a1=2,  b1=2

Put (70) in (29),

(71) v21=a0+2(tanh(ξ)+1tanh(ξ)),or  a0+2(coth(ξ)+1coth(ξ))

(72) u21=2ξsech2(ξ)−ξcsch2(ξ),or  2ξsech2(ξ)−ξcsch2(ξ)

When A=12,C=12,B=0,

Family - I

(73) ω=−1,    a1=−1,     b1=0

Put (73) in (48),

(74) v22=a0−(sec(ξ)+tanh(ξ))

(75) u22=ξsec2(ξ)+ξtan(ξ)sec(ξ)

Family - II

(76) ω=−1,   a1=0,  b1=1

Put (76) in (48),

(77) v23=a0+(1tan(ξ)+sec(ξ))

(78) u23=−ξsec2(ξ)+ξtan(ξ)sec(ξ)(tan(ξ)+sec(ξ))2

Family - III

(79) ω=−4,   a1=−1,    b1=1

By putting Eq. (79) in (48),

(80) v24=a0−(tan(ξ)+sec(ξ))+(1tan(ξ)+sec(ξ))

(81) u24=ξsec2(ξ)+ξsec2(ξ)+ξtan(ξ)sec(ξ)(tan(ξ)+sec(ξ))2     +ξtan(ξ)sec(ξ)

A=−12,B=0,C=−12,

Family - I

(82) ω=−1,  a1=1,   b1=0

Put (82) in (48),

(83) v25=a0+(sec(ξ)−tan(ξ))

(84) u25=ξtan(ξ)sec(ξ)−ξsec2(ξ)

Family - II

(85) ω=−1,   a1=0,         b1=−1

Put (85) in (48),

(86) v226=a0−(1tan(ξ)−sec(ξ))

(87) u26=ξsec2(ξ)−ξtan(ξ)sec(ξ)(tan(ξ)−sec(ξ))2

Family - III

(88) ω=−4,   a1=1,   b1=−1

Put (88) in (48),

(89) v27=a0+(sec(ξ)−tan(ξ))−32(1tan(ξ)−sec(ξ))

(90) u27=−ξsec2(ξ)−ξtan(ξ)sec(ξ)−ξsec2(ξ)(sec(ξ)−tan(ξ))2     −ξtan(ξ)sec(ξ)

C = A = −1, B = 0,

Family - I

(91) ω=−4,    a1=2,   b1=0

Put (91) in (48),

(92) v28=a0+2(tan(ξ)),    or   a0+2(cot(ξ))

(93) u28=2ξsec2(ξ),  or   −2ξcsc2(ξ)

Family - II

(94) ω=−4,   a1=0,    b1=−2

Put (94) in (48),

(95) v29=a0−2(1( tan(ξ)),    or     a0−2(1( cot(ξ))

(96) u29=2ξcsc2(ξx),     or    −2ξsec2(ξ)

Family - III

(97) ω=−16,   a1=2,   b1=−2

Put (97) in (48),

(98) v30(x,t)=a0+2(1( tan(ξ))−2(tan(ξ))

(99) u30(x,t)=−2ξcsc2(ξ)−2ξsec2(ξ)

When A = 0, B = 1, C₃ ≠ 0, then we have,

(100) ω=1,   a1=−2C,     b1=0

Put (100) in (48),

(101) v31=a0+2C(1Cξ+ϵ)

(102) u31=−2C2ξ(Cξ+ϵ)2

When B = 0, C = 0, then we have,

(103) a1=ω3A,   b1=0

Put (103) in (48),

(104) v32=ωξ3

(105) u32=13(ωξ)

When A ≠ 0, B ≠ 0, C = 0, then we have,

(106) ω=B2,   a1=0,    b1=2A

Put (106) in (48),

(107) v33=a0+2A(B(exp(Bξ)−A))

(108) u33=−2AB2ξeBξ(eBξ−A)2

4 Results and Discussion

Different researchers used distinct schemes for the determination of solutions of integro-differential Ito model [39, 40]. But here we have investigated serval types solutions nonlinear Eq. (12) via three analytical modified mathematical mathematical methods. With different values of the parameters in Eq. (4), Eq. (6) and Eq. (6) respectively obtained many different types solutions. However, some our investigated results are likely similar to with other researchers results in [39, 40]. Our solution (30) and(32) are approximate similar to the solutions (18) and (21) in [39]. Solution (18) and (20) likely similar to (3.17) and (3.18) in [40].

Figure 1-5 are plotted after assigning these particular values to the parameters such that, solution u₃(x, t) at η = 1, p = −1, r₁ = 0.9, r₂ = 2 r₃ = 5, ξ₀ = 0.07, ∈ = −1, ω = r₁ and u₆(x, t) at 4l₀ = 1, l₁ = 0.9, l₂ = 1 ∈ = 0.5 and u₇(x, t) at l₀ = 1, l₁ = −0.3, l₂ = 1, ∈ = 0.5, ω=l12 and u₁₁(x, t) l₀ = 0.05, l₂ = −0.5, ∈ = 0.5, ω = −4l₀l₂ and u₃₁ at B = 6, ω = 1, ∈ = 1 respectively. From results discussion and graphical representations of u₃, u₆, u₇, u₁₁ u₃₁ by assigning the particular values with the assistance of Mathematica sofware, we have found that our techniques provide a rich plate form as a mathematical tools for solving nonlinear wave problem in Mathematics, physics and engineerings.

Figure 5

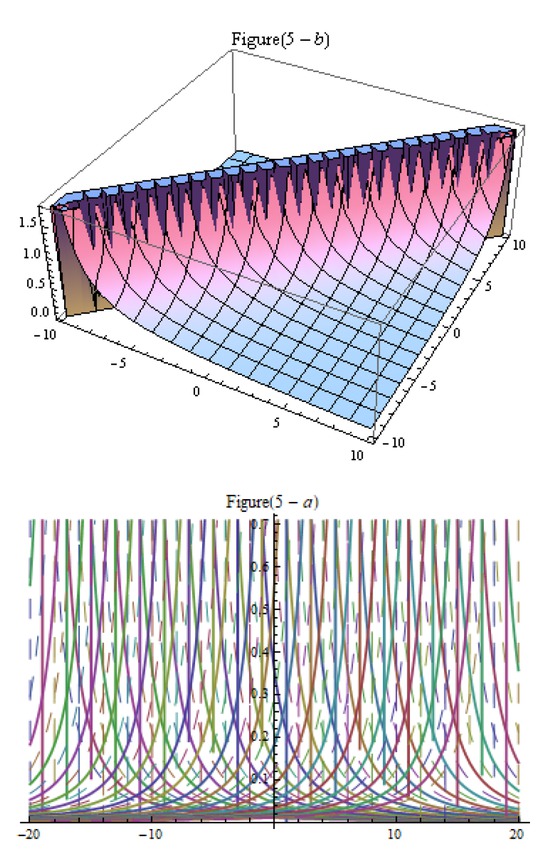
Traveling waves of solution (102).

5 Conclusion

In this work, three analytical modified mathematical methods so called generalized direct algebraic, extended simplest equation and modified F-expansion methods are serve for the construction of the wave solutions of integro-differential Ito equation, having important applications in mathematical physics. The investigated results are more general and provide a basic ground for solving many nonlinear problems.