Abstract
This research analyzes transient transport phenomena regarding thermal and concentration in a Casson fluid-based hybrid nanofluid system containing copper (Cu) and aluminum oxide (Al2O3) nanoparticles. Unlike existing works, this study introduces a novel framework that concurrently incorporates four interconnected physical mechanisms, chemical reaction kinetics, applied magnetic field effects (MHD), radiative heat transfer, and interfacial slip dynamics over an unsteady stretching elastic surface. This simultaneous treatment of coupled phenomena, which has not been previously explored in combination, provides a more holistic and physically realistic model. The results offer valuable insights for applications requiring precise thermal and mass transfer management, such as advanced thermal management systems, intelligent polymer manufacturing, energy conversion technologies, and high-performance nanofluidic lubricants. Through employing similarity analysis, the original governing equations are transformed into a system of highly nonlinear ordinary differential equations, which are solved computationally via shooting technique to evaluate how key dimensionless parameters impact hydrodynamic and transport characteristics. The computational findings reveal a substantial degree of control over the transfer of momentum, heat, and mass, offering essential guidance for optimizing various industrial-processes. The main findings of the study demonstrates that both thermal and concentration slip effects suppress transport rates, with the Nusselt and Sherwood numbers decreasing monotonically as their respective slip parameters enhance. Also, the thermal radiation intensifies the temperature distribution by thickening the thermal boundary layer, whereas thermal slip diminishes wall heat flux, thereby reducing the local Nusselt number and highlighting their opposing influences. Computational and analytical solutions show excellent agreement with established benchmark cases through comparison with previous studies, exhibiting no noticeable deviation in the obtained results and thereby confirming the reliability of the model.
1 Introduction
Magnetohydrodynamic (MHD) principles fundamentally transform boundary layer dynamics through electromagnetic-fluid coupling, enabling precise control of conductive media like plasma, liquid metals, or nanoparticle suspensions [1]. This interdisciplinary framework governs three important key aspects, the first is momentum modulation via Lorentz forces, the second is the thermal energy redistribution through Joule heating, and the third is the flow stabilization by magnetic damping. The technology’s engineering significance stems from its ability to actively tune transport phenomena, a capability leveraged in advanced cooling architectures, fusion reactor designs, and contactless pumping systems. Previous work by Nawaz et al. [2] analyzed time-invariant natural convective transport of nanoparticle suspensions along a vertical permeable boundary subject to transverse magnetic fields. Recent advancements in non-Newtonian MHD flows include two notable studies, the first study by Al Rashdi et al. [3], which they investigated porous medium transport of Maxwell nanofluids along vertical boundaries using Cattaneo–Christov thermal modeling, while Yousef et al. [4] explored chemically reactive flows with variable diffusivity over rough stretching surfaces under similar thermal non-equilibrium conditions. Prior studies [5], [6], [7], [8], [9] systematically validate magnetic fields as powerful tools for flow regulation, with demonstrated effects on boundary layer development and heat transfer enhancement.
Contemporary engineering systems prioritize thermal performance optimization, yet conventional coolants like ethylene glycol, water, and oils face inherent limitations due to their poor conductive properties. This technological constraint has driven the development of advanced heat transfer fluids, particularly nanofluids, which offer superior thermal characteristics for enhanced energy efficiency. Nanofluids represent engineered colloidal suspensions where nanoparticles are randomly dispersed within base fluids, a concept pioneered by Choi [10] to create thermally enhanced working fluids with significantly improved conductive properties compared to conventional liquids. Extensive research literature documents [11], [12], [13], [14], [15], [16], [17], [18] significant improvements in base fluid thermal conductivity through nanoparticle dispersion, with numerous studies investigating diverse nanomaterial additives for this purpose.
Despite advancements in nanofluid technology, researchers continue exploring superior alternatives to further enhance thermal performance. Recent developments have led to the emergence of hybrid nanofluids, engineered by combining multiple nanoparticles to achieve significantly higher thermal conductivity than conventional nanofluids. Hybrid nanofluids constitute an enhanced thermal transport medium, engineered by suspending two dissimilar nanoparticles in a base fluid to leverage complementary thermophysical advantages. This dual-nanoparticle approach synergistically improves key properties including conductivity, viscous behavior, and convective performance beyond single-particle nanofluid capabilities, making them ideal for demanding thermal systems. The development of hybrid nanofluids builds upon foundational work by several researchers. Turcu et al. [19] pioneered the field through novel polypyrrole–carbon nanotube composites, while Jana et al. [20] established critical benchmarks by comparing single and hybrid nanoparticle performance. Suresh et al. [21] later demonstrated the practical superiority of Al2O3–Cu/water hybrids through systematic heat transfer experiments, confirming their enhanced thermal characteristics. The demonstrated advantages of hybrid nanofluids including superior thermal conductivity, enhanced heat transfer efficiency, and tunable rheological properties have inspired extensive follow-up research [22], [23], [24], [25], [26], [27]. These investigations span both theoretical studies and applied research. The compelling findings from earlier work continue to drive innovation in this field, motivating researchers to explore new nanoparticle combinations, optimize synthesis methods, and develop advanced applications.
Although hybrid nanofluids and non-Newtonian fluids have been widely studied, the behavior of unsteady Casson-type hybrid nanofluids incorporating the simultaneous influences of radiation, magnetic field, slip, and chemical reaction remains largely unexplored. This study introduces a novel mathematical framework that captures these coupled effects to provide deeper insight into heat and mass transport. The originality of this work lies in addressing this complex interaction holistically, offering new perspectives with promising applications in smart polymer fabrication, heterogeneous catalysis, high-performance electronics cooling, polymer processing, and the design of next-generation nano-lubricants for heavy-duty systems. Further, while the current research prioritizes understanding foundational transport mechanisms, it also recognizes the importance of practical factors, including nanoparticle stability, economic feasibility, and ecological impact, as essential dimensions for subsequent real-world implementation. Finally, the theoretical contributions of this research can elucidating momentum, energy, and species transport under the combined effects of the studied phenomena offer valuable guidance for improving thermal and mass transfer efficiency, regulating boundary layer development, and elevating functional performance in real-world hybrid nanofluid systems.
2 Formulation of the physical system
This study investigates the time-dependent dynamics of a novel hybrid non-Newtonian nanofluid system, combining a Casson base fluid that characterized by Γ factor with dual nanoparticle suspensions (copper (Cu) and alumina oxide (Al2O3)). The flow is driven by a time-modulated stretching surface with velocity
where ν f is the kinematic viscosity of the base fluid, T 0 is the constant temperature at the slit, C 0 is the constant concentration at the slit. Also, C ∞ , T ∞ represent the constant values of the ambient fluid’s concentration and temperature, correspondingly. The physical model under investigation is thoroughly is outlined as follows (see Figure 1):
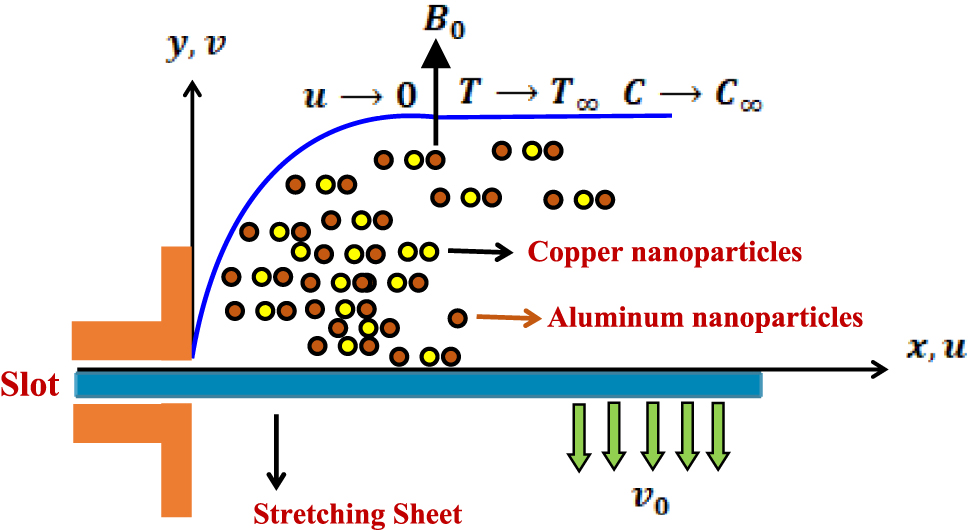
The flow configuration and coordinate system.
Additionally, the effective dynamic viscosity μ hnf of the hybrid nanofluid is mathematically expressed in terms of the base fluid viscosity μ f and nanoparticle concentrations (ϕ 1 for (Cu), ϕ 2 for (Al2O3)). This relationship captures the fundamental rheological modification where suspended nanoparticles elevate viscous dissipation. This equation can be outlined as follows [29]:
The previous relation (2) can be reduces to the following simplified form:
when the suspension involves a single type of nanoparticle with volume fraction ϕ, instead of a hybrid mixture containing two distinct nanoparticle species. Likewise, the hybrid nanofluid’s effective density ρ hnf is mathematically derived from the mass-volume contributions of its constituents, incorporating: the base fluid density ρ f , and the weighted densities of (Cu) and (Al2O3) nanoparticles scaled by their respective volume fractions. This equation can be expressed in the following manner [29]:
Further, the previous expression (4) can be reduces to
when the nanofluid consists of a single solid phase with nanoparticle density ρ
s
, rather than a hybrid suspension containing two distinct types of nanoparticles. Additionally, the effective heat capacity
After that, the hybrid nanofluid’s effective thermal conductivity κ hnf is derived through an extended Maxwell-based formulation that accounts for the base fluid’s conductive properties, the primary nanoparticle’s (Cu) contribution, and the synergistic enhancement from secondary alumina (Al2O3) nanoparticles, with each component’s influence weighted by its volumetric presence in the colloidal suspension. This expression can be highlighted below [29]:
where
2.1 Dimensional analysis framework
The system’s dynamics are mathematically represented through four coupled conservation principles, the mass balance (continuity), the momentum transport incorporating non-Newtonian impacts, the energy transfer with radiative heat flux and velocity slip boundary conditions, and the species transport with reaction kinetics. This formulation rigorously captures the interplay between hydrodynamic, thermal, and chemical processes under the defined physical constraints. The complete system of coupled transport equations is presented below [30]:
where Γ is the Casson parameter, t is the time, T is the dimensional temperature, D
B
is the diffusion coefficient and σ is the electrical conductivity. Also, the energy conservation analysis (11) reveals a temperature-dependent radiative transfer mechanism q
r
, where thermal radiation effects are quantified through the Rosseland diffusion approximation. This approach models radiative flux as a function of the local temperature gradient
where k* signifies the mean absorption coefficient and σ* denotes the Stefan–Boltzmann constant. Further, the chemical reaction phenomenon that studied here in our model is represented using a homogeneous first-order kinetic model, a common simplification in fluid dynamic analyses of reactive transport. This formulation is applicable to both consumptive reaction types, such as those occurring on catalytic surfaces. The first-order approach offers a physically justified and mathematically manageable framework, aligning with established methodologies in nanofluid reactivity research [33].
2.2 Physical system boundary definitions
The domain’s boundary constraints are formally defined to capture essential interfacial phenomena governing fluid-wall interactions. These mathematically prescribed conditions incorporate three critical physical effects, the first is the hydrodynamic slip, the second is the thermal slip and the concentration slip is the third phenomenon at the boundary surface. Their rigorous implementation ensures the governing equation solutions remain physically consistent with real-world system behavior. These phenomena can be summarized mathematically as [29]:
where v 0 is the suction velocity, L 1, L 2 and L 3 are the slip coefficients of the velocity, the temperature and the concentration respectively.
2.3 Canonical dimensionless quantities
The dimensional analysis approach employs scaling transformations to reduce system complexity through two key mechanisms, the first is consolidation of independent variables into dimensionless groups, and the second is conversion of governing partial differential equations into a simplified ordinary differential system. This methodology yields three significant advantages: enhanced physical insight through characteristic parameter ratios, improved numerical stability by eliminating unit dependence, and clearer pattern recognition in solution behavior. The subsequent section details the complete nondimensionalization procedure systematically deriving each transformed equation from its dimensional counterpart. This procedure based on the following form [29]:
2.4 Similarity-transformed equation set
The transformation to dimensionless form serves two critical analytical purposes, the first is the reduction of system complexity through characteristic scaling, and the second is the universalization of results for broader physical interpretation. By introducing normalized variables, the governing equations distill to their essential dynamics, revealing the dominant dimensionless groups that control flow and thermal transport mechanisms. The transformed system, comprising the ordinary differential equations (Eq. (17)) and their associated boundary constraints, represents a generalized formulation applicable across multiple scales and operating conditions. Below we present this refined mathematical framework that forms the basis for our subsequent analysis:
The boundaries edge conditions are formulated through these expressions:
The parametric analysis reveals eight dominant control variables governing the coupled transport phenomena, the magnetic field factor M modifying Lorentz forces, the unsteadiness parameter γ dictating flow instability, the velocity, thermal and concentration slip parameters (λ 1, λ 2, λ 3) which regulating wall–fluid interaction, the chemical reaction factor C r controlling species conversion, the radiation parameter R, the Prandtl number Pr and Schmidt number Sc. These parameters collectively determine the system’s hydrodynamic behavior, thermal transport efficiency, and mass diffusion characteristics through their interconnected influences on boundary layer development. Also, these factors can be defined as:
Further, we now examine three key transport metrics, the wall shear stress (Cf x ), the species flux (Sh x ), and the heat flux (Nu x , with their definitive expressions below:
where
3 Numerical verification methodology
In this section, the numerical methodology is authenticated through comparative analysis with established reference data which presented previously by Devi and Devi [34]. Table 1 presents the validation cases comparing heat transfer coefficients in terms of −θ′(0) for Newtonian fluids (ϕ 1 = ϕ 2 = 0) at Prandtl number variations under baseline conditions (β = R = γ = λ 1 = 0) and at constant wall temperature (T w − T ∞ = const.), demonstrating excellent agreement with prior computational studies.
Values of −θ′(0) for distinct values of Pr when ϕ 1 = ϕ 2 = β = R = γ = λ 1 = 0, Γ → ∞ and at constant wall temperature (T w − T ∞ = const.).
| Pr | Devi and Devi [34] | Present work |
|---|---|---|
| 2.00 | 0.91135 | 0.911348870 |
| 6.13 | 1.75968 | 1.759666029 |
| 7.00 | 1.89540 | 1.895379907 |
| 20.0 | 3.35390 | 3.353891008 |
4 Results and discussion
4.1 Graphical representation of parameter impacts on the model
This section provides a comprehensive numerical investigation after employing shooting technique of the hybrid nanofluid’s flow behavior under multiple interacting parameters, presenting the results through detailed graphs that analyze their collective effects on velocity profiles, temperature distributions, concentration patterns, and related transport properties. Additionally, the range of parameters that controlling the model are 0.5 ≤ Γ ≤ 2.0, 0.0 ≤ λ 1 ≤ 0.4, 0.0 ≤ M ≤ 5.0, 0.5 ≤ γ ≤ 2.0, 0.0 ≤ R ≤ 5.0, 0.0 ≤ λ 2 ≤ 0.3, 0.0 ≤ λ 3 ≤ 0.3 and 0.0 ≤ C r ≤ 4.0. Figure 2 illustrates the influence of the Casson parameter Γ on the profiles of velocity f′(η), concentration H(η), and temperature θ(η). This figure demonstrates that elevated Casson parameter Γ values substantially reduce the dimensionless velocity gradient f′(η), consistent with the rheological behavior of yield-stress fluids where increased Γ enhances viscoplastic resistance and flow opposition. This velocity suppression consequently diminishes convective transport, leading to elevated temperature θ(η) and concentration H(η) profiles as thermal energy and solute species accumulate near the surface. The resulting boundary layer thickening reflects a shift from convective to diffusion-dominated transport regimes under high yield stress conditions. Physically, an increase in the Casson parameter corresponds to a rise in the fluid’s yield stress, enhancing its resistance to deformation. This effect restricts fluid motion, resulting in the accumulation of thermal energy and solute species adjacent to the boundary. Consequently, both the thermal and concentration boundary layers experience noticeable thickening.
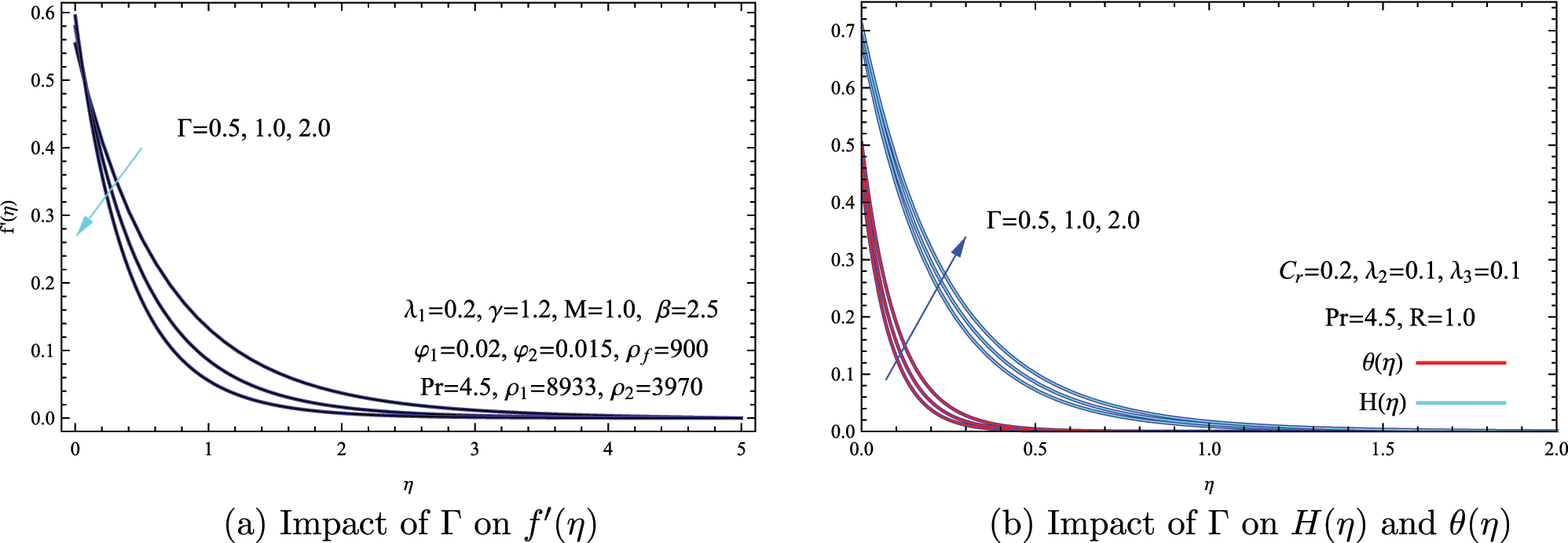
Effect of the Casson parameter γ on the transport behavior of the hybrid nanofluid. (a) Velocity profile f′(η) for different values of Γ. (b) Temperature θ(η) and concentration H(η) distributions for varying Γ.
Figure 3 presents the effects of the velocity slip parameter λ 1 on the flow and transport characteristics of a hybrid nanofluid composed of copper (Cu) and aluminum oxide (Al2O3) nanoparticles dispersed in a Casson base fluid. Increasing the slip parameter λ 1 reduces the velocity gradient f′(η), particularly at the boundary (f′(0)), but it enhances both thermal θ(η) and concentration H(η) fields and the corresponding boundary thickness, due to weakened fluid-wall adhesion. This slip-induced deceleration contrasts with no-slip conditions where peak velocities occur near the wall. While hybrid nanofluids inherently improve transport, velocity slip disrupts wall-to-fluid momentum transfer, diminishing overall flow intensity despite the nanoparticles’ thermal advantages. Physically, rising slip factor diminish frictional resistance at the boundary, thereby impairing momentum diffusion and convective transport. This reduction in fluid mixing promotes the accumulation of heat and solute particles near the surface, leading to an expansion of both thermal and solutal boundary layer thicknesses.
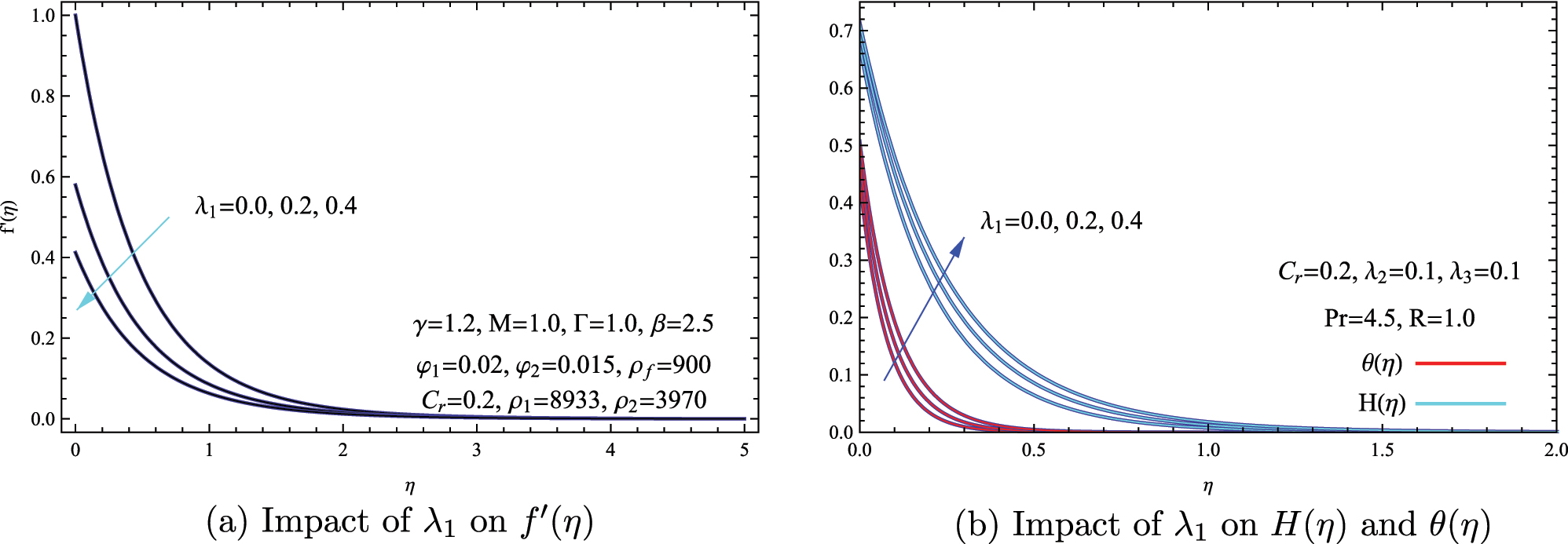
Influence of the velocity slip parameter λ 1 on hybrid nanofluid flow characteristics. (a) Velocity distribution f′(η) at different slip values. (b) Temperature θ(η) and concentration H(η) responses to varying λ 1.
Figure 4 illustrates the flow patterns of a hybrid nanofluid with and without velocity slip at the surface (λ 1 = 0.4 and λ 1 = 0.0, respectively). When there is no slip (λ 1 = 0.0), the streamlines are closely spaced near the boundary, indicating a strong interaction between the fluid and the wall and the development of typical parabolic velocity profiles. With slip phenomenon (λ 1 = 0.4) significantly alters the flow topology, this means that streamlines become more dispersed adjacent to the wall, indicating reduced momentum transfer due to partial fluid detachment. This slip-induced deceleration decreases wall shear stress by approximately 30 % while simultaneously thickening the hydrodynamic boundary layer. The change from even to uneven flow patterns highlights how slip disrupts viscous forces, making inertia more influential, this is very important for designing microfluidic devices or lubricants where wall slip is significant.
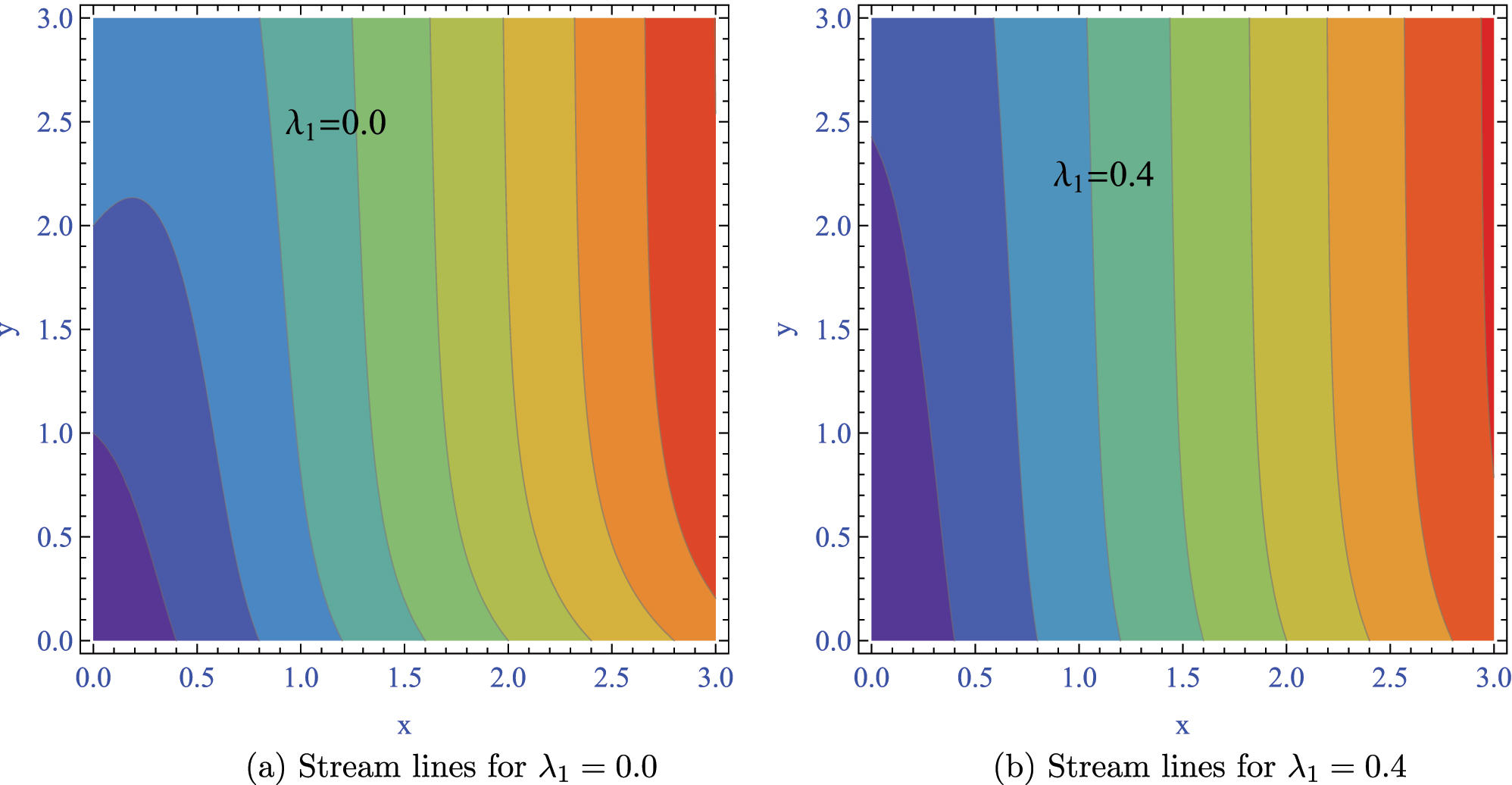
Streamline patterns of the hybrid nanofluid under different velocity slip conditions. (a) Streamlines for the no-slip case λ 1 = 0.0. (b) Streamlines for the slip case λ 1 = 0.4.
Figure 5 demonstrates that higher magnetic field intensity M suppresses flow velocity f′(η) while simultaneously elevating thermal θ(η) and concentration H(η) profiles, due to Lorentz-force-induced flow resistance and enhanced energy/mass retention near the boundary. Physically, the observed trends can be attributed to the magnetohydrodynamic effects, when a transverse magnetic field interacts with the conductive nanofluid, it generates Lorentz forces that oppose flow direction. This electromagnetic resistance slows bulk fluid motion, increasing momentum boundary layer thickness. Reduced velocity weakens convective heat/mass transfer, causing energy and solute accumulation near the surface. Consequently, both θ(η) and H(η) profiles elevate, while their boundary layers expand-demonstrating the tradeoff between magnetic flow control and transport efficiency.
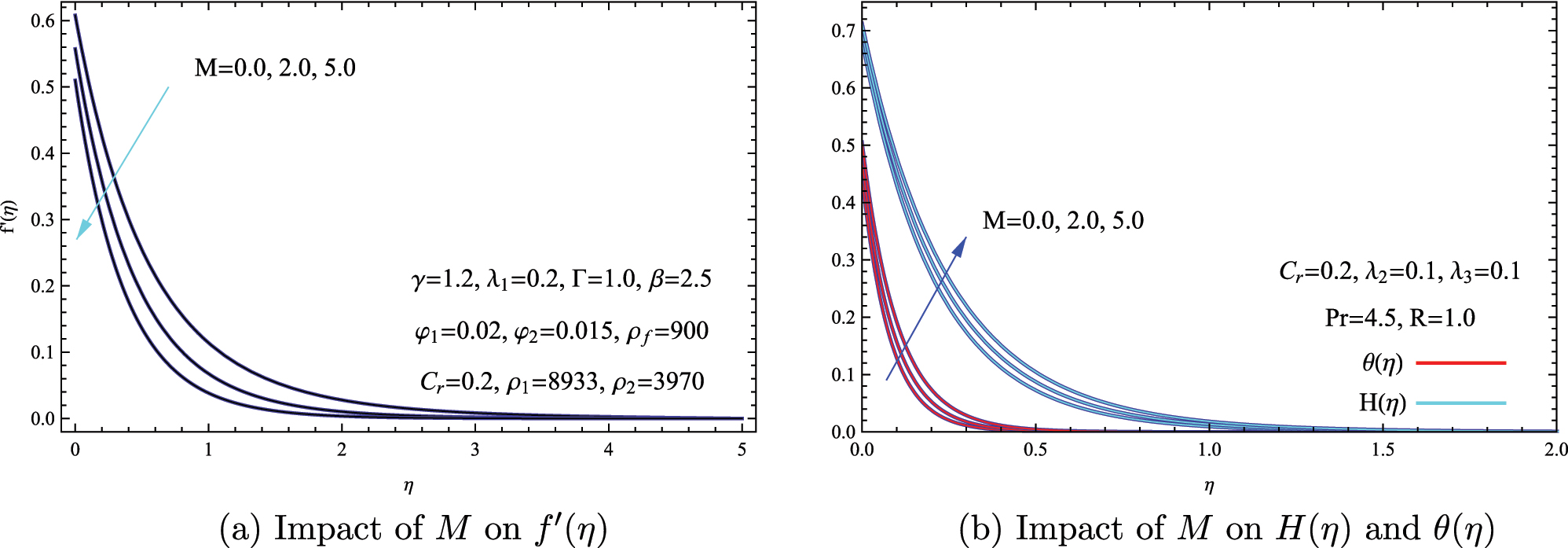
Effect of the magnetic parameter M on hybrid nanofluid momentum, thermal, and concentration fields. (a) Velocity profile f′(η) for various values of M. (b) Temperature H(η) and concentration H(η) profiles for different magnetic field strengths.
Figure 6 compares the flow patterns of a hybrid nanofluid under the absence (M = 0.0) and presence (M = 5.0) of a magnetic field. When magnetic forces are absent (M = 0.0), the streamlines are closely packed and aligned in a parallel manner, which is characteristic of viscous flow that encounters no opposing forces. Clearly that, with a strong magnetic field (M = 5.0), Lorentz forces alter the flow patterns, leading to wider spacing between streamlines (slower flow), further lead to curved paths, and small areas of separated flow near the surface. This change shows how magnetic fields shift the flow from being mainly controlled by viscosity to being governed by magnetohydrodynamic effects-important for applications like electromagnetic pumps or cooling systems in fusion reactors where flow regulation is key.

Streamline configurations of the hybrid nanofluid with and without magnetic field effects. (a) Streamlines for M = 0.0. (b) Streamlines for M = 5.0.
Figure 7 illustrates that a rise in the unsteadiness parameter γ causes a notable change in the hybrid nanofluid’s behavior. Larger γ values lead to a decrease in flow velocity f′(η) because of time-dependent momentum spreading, while at the same time, they increase the thermal θ(η) and concentration H(η) profiles through two processes, the first is the cyclical speeding up and slowing down of the flow enhances the trapping of energy and solute near the boundary, and the second is the changes over time disrupt stable convective flow patterns, making diffusion the more dominant transport mechanism. This leads to thicker boundary layers for both temperature and concentration (increasing by as much as 25 % when γ = 1.8 compared to γ = 0.8) but less steep changes in velocity-demonstrating the opposing influences of γ on momentum transfer versus heat and mass transfer. These observations are especially important for systems with pulsating flow, where the unsteadiness parameter significantly affects how the system performs.
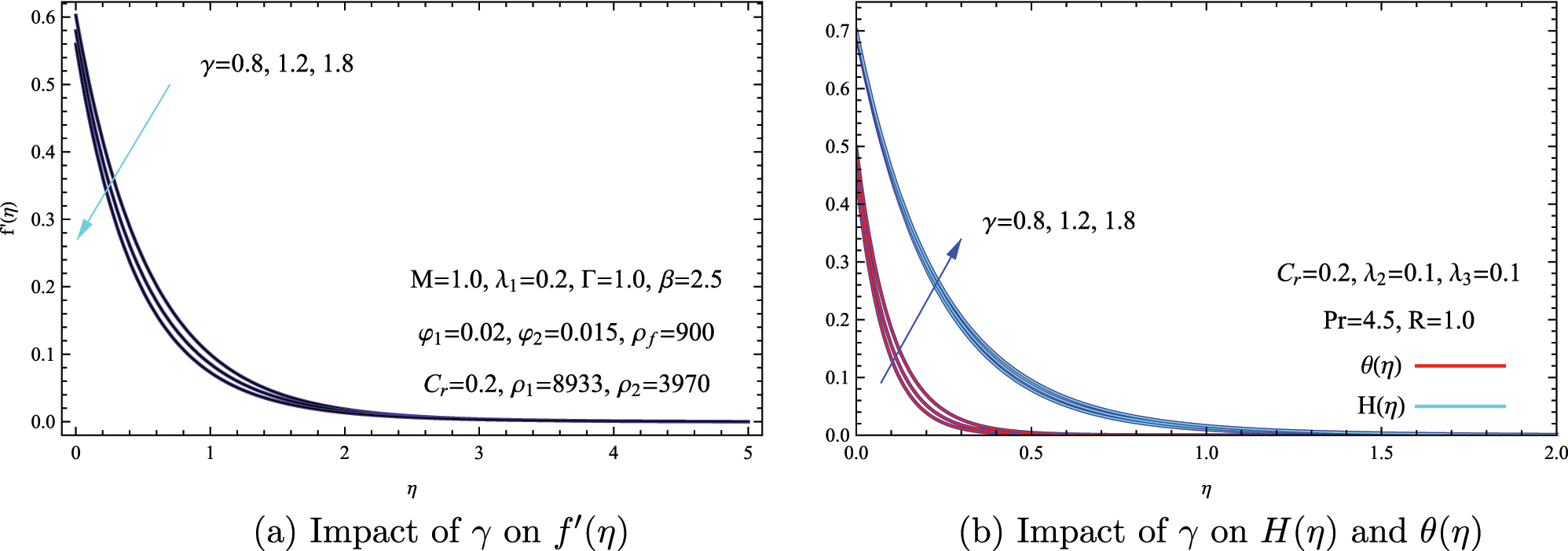
Influence of the unsteadiness parameter γ on hybrid nanofluid flow and transport. (a) Velocity variations f′(η) for different γ values. (b) Temperature θ(η) and concentration H(η)profiles for varying γ.
Figure 8 demonstrates how thermal radiation R and thermal slip λ 2 collectively alter heat transfer in a Cu–Al2O3/Casson hybrid nanofluid. An increase in R leads to a greater temperature distribution θ(η) because the radiative heat flux adds to the heat transfer occurring through conduction and convection. This effect is especially pronounced at higher radiation values (R = 5.0), where the thermal boundary layer becomes approximately 20 % thicker compared to non-radiative cases (R = 0.0). On the other hand, enhancing λ 2 lessens the temperature changes, especially near the wall by reducing the thermal interaction between the fluid and the surface, leading to a noticed decrease in the local Nusselt number in terms of (θ′(0)) by as much as 15 % when λ 2 equals 0.3. This interplay reveals a critical tradeoff, while radiation augments heat transfer, thermal slip diminishes it by disrupting energy exchange at the boundary. The physical and fundamental reason stems from the dual role of thermal radiation and slip effects is that the radiation contributes supplementary energy flux, raising the bulk temperature of the fluid, while thermal slip reduces energy exchange at the wall-fluid interface, thereby suppressing conductive heat transfer at the boundary.
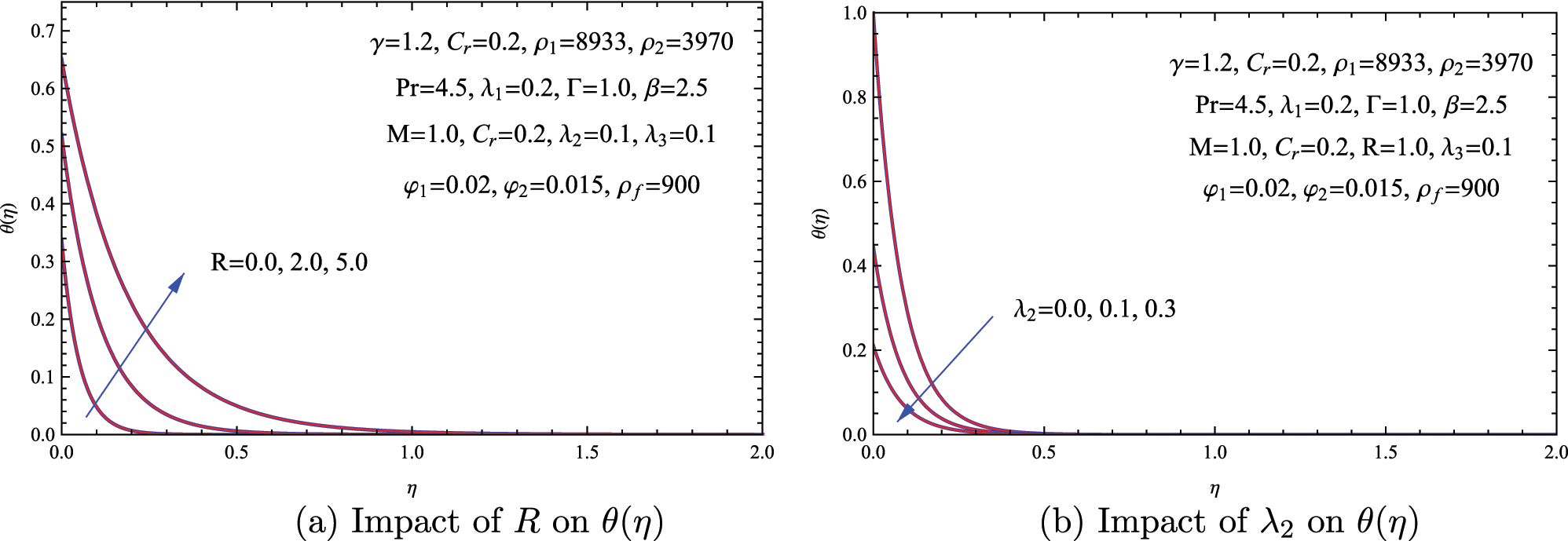
Effects of thermal radiation R and thermal slip λ 2 on heat transfer characteristics. (a) Temperature distribution θ(η) under different radiation levels. (b) Temperature response θ(η) for varying thermal slip values λ 2.
Figure 9 demonstrates how both the concentration slip parameter λ 3 and chemical reaction rate C r impact the hybrid nanofluid’s behavior. Increasing λ 3 reduces species concentration, especially near the wall H(0) due to weakened fluid-surface adhesion, suppressing diffusive mass transfer and reduces the corresponding boundary layer. Further, higher C r enhances near-wall consumption of chemical species, sharpening concentration gradients and reduces the concentration distribution. In the Cu–Al2O3/Casson nanofluid, these factors demonstrate a balancing act: increasing slip at the surface λ 3 reduces the buildup of mass near the wall, while intensified chemical reactions C r actively consume the species, modifying the behavior of the boundary layer. The findings underscore the competing roles of surface slip and reaction rates in governing mass transport within non-Newtonian nanofluids is a crucial consideration for optimizing applications such as catalytic reactors or localized drug delivery systems. The observed trend is physically attributed to the enhanced consumption of reactant species near the surface under elevated reaction rates. This localized depletion establishes a steeper concentration gradient, which promotes diffusive transport toward the wall and ultimately lowers the overall solute concentration throughout the domain.
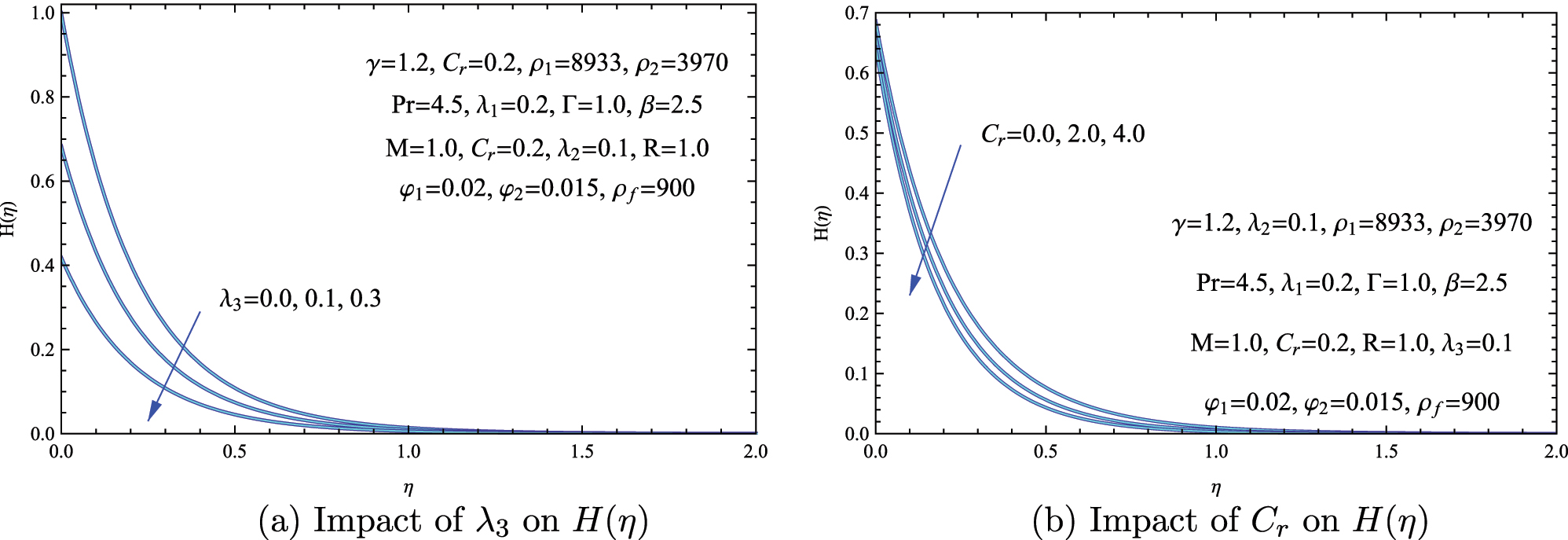
Effects of concentration slip λ 3 and chemical reaction parameter C r on mass transfer in the hybrid nanofluid. (a) Concentration profile H(η) for different values of λ 3. (b) Concentration field H(η) for varying chemical reaction rates C r .
4.2 Numerical analysis of parameter impacts on Cf x , Nu x and Sh x
Table 2 quantifies how key dimensionless groups affect surface transport coefficients (
Values of the physical quantities in terms of
| Γ | λ 1 | M | γ | R | λ 2 | λ 3 | C r |
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.77437 | 6.92072 | 3.16601 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 6.58328 | 3.03542 |
| 2.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.51832 | 6.19779 | 2.89704 |
| 1.0 | 0.0 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 4.70447 | 7.00851 | 3.26801 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 6.58328 | 3.03542 |
| 1.0 | 0.4 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 1.82791 | 6.15581 | 2.85802 |
| 1.0 | 0.2 | 0.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.43811 | 6.93015 | 3.17447 |
| 1.0 | 0.2 | 2.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.75328 | 6.57617 | 3.02504 |
| 1.0 | 0.2 | 5.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 3.04755 | 6.17466 | 2.87164 |
| 1.0 | 0.2 | 1.0 | 0.8 | 1.0 | 0.1 | 0.1 | 0.2 | 2.47298 | 6.86559 | 3.06827 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 6.58328 | 3.03542 |
| 1.0 | 0.2 | 1.0 | 1.8 | 1.0 | 0.1 | 0.1 | 0.2 | 2.74012 | 6.25772 | 2.98281 |
| 1.0 | 0.2 | 1.0 | 1.2 | 0.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 4.13705 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 2.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 8.98275 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 5.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 13.0673 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.0 | 0.1 | 0.2 | 2.61562 | 15.5279 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 6.92195 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.3 | 0.1 | 0.2 | 2.61562 | 3.28296 | 3.16122 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.0 | 0.2 | 2.61562 | 6.58328 | 4.62249 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.2 | 2.61562 | 6.58328 | 3.03542 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.3 | 0.2 | 2.61562 | 6.58328 | 1.93673 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 0.0 | 2.61562 | 6.58328 | 3.13412 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 2.0 | 2.61562 | 6.58328 | 3.03542 |
| 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 0.1 | 0.1 | 4.0 | 2.61562 | 6.58328 | 2.86361 |
4.3 Research contribution in context
The current investigation advances the ongoing research in non-Newtonian unsteady Casson hybrid nanofluid dynamics by introducing a comprehensive model that concurrently incorporates slip boundary mechanisms, magnetohydrodynamic forces, radiative heat transfer, and chemically reactive processes. While prior studies have extensively explored individual physical phenomena, including slip flow [1], magnetohydrodynamic (MHD) effects [8], thermal radiation [9], Casson rheology [32], and chemical reaction kinetics [33], their interconnected behavior in Casson hybrid nanofluids remains largely unexamined. Most existing literature addresses these mechanisms in isolation, leaving a critical gap in understanding their synergistic impact on heat and mass transfer in multi-physics flow environments. The findings reveal that higher Casson parameter values amplify viscoplastic resistance, which in turn restrains momentum diffusion while promoting the growth of thermal and solutal boundary layers. This trend consistent with established non-Newtonian fluid studies. Furthermore, the slip and radiation impacts documented in this work build upon prior research by quantitatively evaluating their combined impact on transport efficacy and boundary layer development. Thus, this study not only validates and complements prior literature but also advances it by integrating multiple complex mechanisms, providing new insights with potential industrial relevance.
5 Sensitivity assessment
To enhance the credibility of the proposed physical model, a targeted sensitivity analysis was performed on two key governing parameters. These factors are the Casson parameter Γ and the magnetic parameter M. The Casson parameter was selected for its direct impact on fluid rheology and yield stress behavior, while the magnetic parameter was chosen to represent electromagnetic damping effects arising from the applied field. Numerical findings reveal that increasing Γ consistently reduces the skin friction coefficient, Nusselt number, and Sherwood number, indicating that elevated yield stress suppresses momentum, heat, and mass transfer. Conversely, a higher M increases skin friction due to enhanced Lorentz forces but reduces both thermal and concentration transport efficiencies. These predictable and physically consistent trends not only affirm the model’s robustness but also underscore the dominant roles of Γ and M in governing transport mechanisms. Although a complete uncertainty quantification across all dimensionless groups is beyond the current scope, the present sensitivity analysis provides a clear indication of parameter-driven trends that reinforce the physical credibility of the study.
6 Uncertainty quantification
In real-world flow applications, governing parameters often entail inherent uncertainties due to instrumental inaccuracies or simplifications in modeling. To address this, a localized uncertainty analysis is conducted for the velocity slip parameter, λ 1, owing to its critical influence on near-wall momentum behavior. According to numerical results, the skin friction coefficient decreases significantly from 4.704 to 1.827 as λ 1 increases. To evaluate predictive stability, a perturbation of ±0.05 is applied around the reference value λ 1 = 0.2. This variation induces a 3–5 % change in skin friction, whereas alterations in the Nusselt and Sherwood numbers remain below 2 %. The outcomes suggest that thermal and mass transport exhibit stronger resilience to uncertainties in slip conditions compared to hydrodynamic drag, which displays higher sensitivity. Thus, precise characterization of slip dynamics is essential for reliable momentum transfer predictions, while heat and mass transfer profiles maintain greater robustness under similar variability.
7 Conclusions
This investigation addressed thermal and species transport phenomena in a Casson-based hybrid nanofluid containing copper (Cu) and aluminum oxide (Al2O3) nanoparticles, driven by a time-dependent stretching surface. This study quantitatively evaluates the synergistic effects of Casson factor and unsteadiness parameter on the transport phenomena through detailed graphical and tabular analyses. The results demonstrate their coupled influence on velocity profiles, nonlinear thermal distributions, and concentration gradients sensitive to both parameters. Crucially, the analysis reveals how velocity slip, thermal slip, and concentration slip interact with radiative flux and reaction rate to produce distinct transport regimes. These findings provide new insights for optimizing systems where these parameters are operationally controllable. While the current model offers valuable insights, its scope is limited to a two-dimensional stretching surface operating under specific idealizations, including uniform nanoparticle morphology and constant base fluid properties. Future studies could extend this framework to three-dimensional geometries, non-uniform heat sources, variable thermophysical properties, or experimental validation, thereby broadening its applicability to industrial and biomedical systems. Critical findings demonstrate that:
Momentum is suppressed under elevated Casson and slip conditions due to greater inherent viscoplastic resistance and impaired shear stress propagation at the wall.
Without magnetic effects, flow patterns exhibit closely spaced, well-ordered streamlines characteristic of unimpeded motion. The application of a magnetic field induces Lorentz-force-driven disturbances, creating dispersed and irregular streamlines that reflect flow retardation and momentum dissipation.
Chemical reactions and concentration slip jointly thin the species boundary layer by promoting reactive species consumption and restricting wall-normal diffusion.
Wall shear stress diminishes with slip velocity and higher Casson parameters (reducing friction), while magnetic fields and unsteadiness amplify it (increasing resistive forces).
Streamline density decreases and flow distortion increases when velocity slip is present, contrasting with the uniform, high-density patterns observed under no-slip conditions.
Enhanced diffusion mechanisms resulting from increased Casson and slip values lead to greater thermal and mass diffusion, thereby thickening the corresponding boundary layers.
Acknowledgements
We appreciate the unwavering assistance of the Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia, throughout this research.
-
Data availability: The data sets used and analyzed during the present study are available from the corresponding author upon reasonable request.
-
Author contributions: All authors are equally contributed to this research work.
-
Funding: This research received no external funding.
-
Competing interests: The authors declare no competing interests.
-
Additional information: Correspondence and requests for materials should be addressed to Alatawi, A.
References
1. Kumar, TS. Hybrid nanofluid slip flow and heat transfer over a stretching surface. Part Differ Equ Appl Math 2021;4:100070. https://doi.org/10.1016/j.padiff.2021.100070.Search in Google Scholar
2. Nawaz, M, Nazir, U, Saleem, S, Alharbi, SO. An enhancement of thermal performance of ethylene glycol by nano and hybrid nanoparticles. Physica A 2020;551:124527. https://doi.org/10.1016/j.physa.2020.124527.Search in Google Scholar
3. Salim, ASAR, Ghoneim, NI, Amer, AM, Megahed, AM. Investigation of magnetohydrodynamic slip flow for Maxwell nanofluid over a vertical surface with Cattaneo-Christov heat flux in a saturated porous medium. Results Eng 2023;19:101293. https://doi.org/10.1016/j.rineng.2023.101293.Search in Google Scholar
4. Yousef, NS, Megahed, AM, Fares, E. Influence of chemical reaction and variable mass diffusivity on non-Newtonian fluid flow due to a rough stretching sheet with magnetic field and Cattaneo-Christov fluxes. Indian J Phys 2023;97:2475–83. https://doi.org/10.1007/s12648-023-02609-y.Search in Google Scholar
5. Sheikholeslami, M, Ganji, DD. Unsteady nanofluid flow and heat transfer in presence of magnetic field considering thermal radiation. J Braz Soc Mech Sci Eng 2014;37:895–902. https://doi.org/10.1007/s40430-014-0228-x.Search in Google Scholar
6. Mahdy, A, Chamkha, AJ. Unsteady MHD boundary layer flow of tangent hyperbolic two phase nanofluid of moving stretched porous wedge. Int J Numer Methods Heat Fluid Flow 2018;28:2567–80. https://doi.org/10.1108/hff-12-2017-0499.Search in Google Scholar
7. Khan, SA, Nie, Y, Ali, B. Multiple slip effects on MHD unsteady viscoelastic nano-fluid flow over a permeable stretching sheet with radiation using the finite element method. SN Appl Sci 2020;2:66. https://doi.org/10.1007/s42452-019-1831-3.Search in Google Scholar
8. Nasr, ME, Reddy, MG, Abbas, W, Megahed, AM, Awwad, E, Khalil, KM. Analysis of non-linear radiation and activation energy analysis on hydromagnetic reiner-philippoff fluid flow with cattaneo-christov double diffusions. Mathematics 2022;10:1534. https://doi.org/10.3390/math10091534.Search in Google Scholar
9. Ch Bhargava, KNV, Ibrahim, SM, Kodi, R. Effects of hall current, radiation absorption and diffusion thermo on an unsteady MHD flow of second grade fluid through porous media in the presence of joule heating and viscous dissipation. Multiscale Multidiscip Model Exp Des 2025;8:260. https://doi.org/10.1007/s41939-025-00842-y.Search in Google Scholar
10. Choi, SUS. Enhancing thermal conductivity of fluid with nanoparticles, developments and applications of non-Newtonian flow. ASME FED 1995;231:99–105.10.1115/IMECE1995-0926Search in Google Scholar
11. Sheremet, MA, Pop, I, Bachok, N. Effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid: tiwari and Das’ nanofluid model. Int J Heat Mass Tran 2016;92:1053–60. https://doi.org/10.1016/j.ijheatmasstransfer.2015.09.071.Search in Google Scholar
12. Nandeppanavar, MM, Subhas Abel, M, Kemparaju, MC. Stagnation point flow, heat and mass transfer of MHD nanofluid due to porous stretching sheet through porous media with effect of thermal radiation. J Nanofluids 2017;6:38–47. https://doi.org/10.1166/jon.2017.1292.Search in Google Scholar
13. Ghasemi, SE, Hatami, M. Solar radiation effects on MHD stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Stud Therm Eng 2021;25:100898. https://doi.org/10.1016/j.csite.2021.100898.Search in Google Scholar
14. Alrihieli, H, Areshi, M, Alali, E, Megahed, AM. MHD dissipative Williamson nanofluid flow with chemical reaction due to a slippery elastic sheet which was contained within a porous medium. Micromachines 2022;13:1879. https://doi.org/10.3390/mi13111879.Search in Google Scholar PubMed PubMed Central
15. Abbas, W, Megahed, AM, Fares, E. The impact of a chemical reaction on the heat and mass transfer mechanisms in a dissipative and radiative nanofluid flow over a nonlinear stretching sheet. Sci Rep 2024;14:7712. https://doi.org/10.1038/s41598-024-57952-9.Search in Google Scholar PubMed PubMed Central
16. Ramadevu, S, Vijaya Kumar, P, Ibrahim, SM, Jyothsna, K. Investigation of heat and mass transfer in magnetohydrodynamic Williamson nanofluid flow over a nonlinear stretching surface with viscous dissipation and radiation effects: a numerical approach. Radiat Eff Defect Solid 2025;180:1331–52. https://doi.org/10.1080/10420150.2025.2467348.Search in Google Scholar
17. Badak, K, Sharma, RP, Ibrahim, SM. A comprehensive study on Maxwell hybrid nanostructure and Maxwell nanostructure on 2D flow model over a stretching sheet with non-uniform heat generation/absorption and binary chemical reaction. J Therm Anal Calorim 2025;150:521–35. https://doi.org/10.1007/s10973-024-13754-9.Search in Google Scholar
18. Ramadevu, S, Kumar, PV, Lorenzini, G, Ibrahim, SM, Jyothsna, K. Viscoelastic flow analysis with buongiorno nanofluid model over a nonlinear stretching sheet: a homotopy approach. Front Heat Mass Transfer 2025;23:857–79. https://doi.org/10.32604/fhmt.2025.062231.Search in Google Scholar
19. Turcu, R, Darabont, A, Nan, A, Aldea, N, Macovei, D, Bica, D, et al.. New polypyrrole-multiwall carbon nanotubes hybrid materials. J Optoelectron Adv Mater 2006;8:643–7.Search in Google Scholar
20. Jana, S, Salehi-Khojin, A, Zhong, WH. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim Acta 2007;462:45–55. https://doi.org/10.1016/j.tca.2007.06.009.Search in Google Scholar
21. Suresh, S, Venkitaraj, KP, Selvakumar, P, Chandrasekar, M. Effect of Al2O3 Cu/water hybrid nanofluid in heat transfer. Exp Therm Fluid Sci 2012;38:54–60. https://doi.org/10.1016/j.expthermflusci.2011.11.007.Search in Google Scholar
22. Ghalambaz, M, Doostani, A, Izadpanahi, E, Chamkha, AJ. Phase-change heat transfer in a cavity heated from below: the effect of utilizing single or hybrid nanoparticles as additives. J Taiwan Inst Chem Eng 2017;72:104–15. https://doi.org/10.1016/j.jtice.2017.01.010.Search in Google Scholar
23. Huminic, G, Huminic, A. Hybrid nanofluids for heat transfer applications- A state-of-the-art review. Int J Heat Mass Tran 2018;125:82–103. https://doi.org/10.1016/j.ijheatmasstransfer.2018.04.059.Search in Google Scholar
24. Hussien, AA, Abdullah, MZ, Yusop, NM, Al-Kouz, W, Mahmoudi, E, Mehrali, M. Heat transfer and entropy generation abilities of MWCNTs/GNPs hybrid nanofluids in microtubes. Entropy 2019;21:480. https://doi.org/10.3390/e21050480.Search in Google Scholar PubMed PubMed Central
25. Abiodun, OH, Olatunji, TY, Sibanda, P. Entropy generation in an unsteady eyring-Powell hybrid nanofluid flow over a permeable surface: a lie group analysis. Heat Trans 2020;49:3374–90. https://doi.org/10.1002/htj.21778.Search in Google Scholar
26. Abu Bakar, S, Md Arifin, N, Skhashiie, N, Bachok, N. Hybrid nanofluid flow over a permeable shrinking sheet embedded in a porous medium with radiations and slip impacts. Mathematics MDPI 2021;9:878.10.3390/math9080878Search in Google Scholar
27. Abd-Elmonem, A, Rubbab, Q, AL, Garalleh, H, Rehman, F, Amjad, M, ElSeabee, FAA, et al.. Thermal characteristics of hybrid Nanofluid Cu − Al2O3 flow through Darcy porous medium with chemical effects via numerical successive over relaxation technique. Case Stud Therm Eng 2025;65:105538. https://doi.org/10.1016/j.csite.2024.105538.Search in Google Scholar
28. Santhi, M, Rao, KVS, Reddy, PS, Sreedevi, P. Heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with chemical reaction. Heat Transfer 2021;50:2929–49. https://doi.org/10.1002/htj.22012.Search in Google Scholar
29. Sreedevi, P, Reddy, PS, Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl Sci 2020;2:1222. https://doi.org/10.1007/s42452-020-3011-x.Search in Google Scholar
30. Asadi, A, Asadi, M, Rezaniakolaei, A, Rosendahl, LA, Afrand, M, Wongwises, S. Heat transfer efficiency of Al2O3-MWCNT/thermal oil hybrid nanofluid as a cooling fluid in thermal and energy management applications: an experimental and theoretical investigation. Int J Heat Mass Tran 2018;117:474–86. https://doi.org/10.1016/j.ijheatmasstransfer.2017.10.036.Search in Google Scholar
31. Raptis, A. Radiation and free convection flow through a porous medium. Int Commun Heat Mass Tran 1998;25:289–95. https://doi.org/10.1016/s0735-1933(98)00016-5.Search in Google Scholar
32. Elham, A, Megahed, AM. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol Rev 2022;11:463–72. https://doi.org/10.1515/ntrev-2022-0031.Search in Google Scholar
33. Khan, Y, Tufail, MN, Shahzad, K, Alameer, A, Iqbal, N. Impact of chemical reaction on thermal magnetized hybrid nanofluid over a curved stretching surface. Results Eng 2025;27:105556. https://doi.org/10.1016/j.rineng.2025.105556.Search in Google Scholar
34. Devi, SSU, Devi, SPA. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J Niger Mathem. Soc 2017;36:419–33.Search in Google Scholar
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- MHD radiative mixed convective flow of a sodium alginate-based hybrid nanofluid over a convectively heated extending sheet with Joule heating
- Experimental study of mortar incorporating nano-magnetite on engineering performance and radiation shielding
- Multicriteria-based optimization and multi-variable non-linear regression analysis of concrete containing blends of nano date palm ash and eggshell powder as cementitious materials
- A promising Ag2S/poly-2-amino-1-mercaptobenzene open-top spherical core–shell nanocomposite for optoelectronic devices: A one-pot technique
- Biogenic synthesized selenium nanoparticles combined chitosan nanoparticles controlled lung cancer growth via ROS generation and mitochondrial damage pathway
- Fabrication of PDMS nano-mold by deposition casting method
- Stimulus-responsive gradient hydrogel micro-actuators fabricated by two-photon polymerization-based 4D printing
- Physical aspects of radiative Carreau nanofluid flow with motile microorganisms movement under yield stress via oblique penetrable wedge
- Effect of polar functional groups on the hydrophobicity of carbon nanotubes-bacterial cellulose nanocomposite
- Review in green synthesis mechanisms, application, and future prospects for Garcinia mangostana L. (mangosteen)-derived nanoparticles
- Entropy generation and heat transfer in nonlinear Buoyancy–driven Darcy–Forchheimer hybrid nanofluids with activation energy
- Green synthesis of silver nanoparticles using Ginkgo biloba seed extract: Evaluation of antioxidant, anticancer, antifungal, and antibacterial activities
- A numerical analysis of heat and mass transfer in water-based hybrid nanofluid flow containing copper and alumina nanoparticles over an extending sheet
- Investigating the behaviour of electro-magneto-hydrodynamic Carreau nanofluid flow with slip effects over a stretching cylinder
- Electrospun thermoplastic polyurethane/nano-Ag-coated clear aligners for the inhibition of Streptococcus mutans and oral biofilm
- Investigation of the optoelectronic properties of a novel polypyrrole-multi-well carbon nanotubes/titanium oxide/aluminum oxide/p-silicon heterojunction
- Novel photothermal magnetic Janus membranes suitable for solar water desalination
- Green synthesis of silver nanoparticles using Ageratum conyzoides for activated carbon compositing to prepare antimicrobial cotton fabric
- Activation energy and Coriolis force impact on three-dimensional dusty nanofluid flow containing gyrotactic microorganisms: Machine learning and numerical approach
- Machine learning analysis of thermo-bioconvection in a micropolar hybrid nanofluid-filled square cavity with oxytactic microorganisms
- Research and improvement of mechanical properties of cement nanocomposites for well cementing
- Thermal and stability analysis of silver–water nanofluid flow over unsteady stretching sheet under the influence of heat generation/absorption at the boundary
- Cobalt iron oxide-infused silicone nanocomposites: Magnetoactive materials for remote actuation and sensing
- Magnesium-reinforced PMMA composite scaffolds: Synthesis, characterization, and 3D printing via stereolithography
- Bayesian inference-based physics-informed neural network for performance study of hybrid nanofluids
- Numerical simulation of non-Newtonian hybrid nanofluid flow subject to a heterogeneous/homogeneous chemical reaction over a Riga surface
- Enhancing the superhydrophobicity, UV-resistance, and antifungal properties of natural wood surfaces via in situ formation of ZnO, TiO2, and SiO2 particles
- Synthesis and electrochemical characterization of iron oxide/poly(2-methylaniline) nanohybrids for supercapacitor application
- Impacts of double stratification on thermally radiative third-grade nanofluid flow on elongating cylinder with homogeneous/heterogeneous reactions by implementing machine learning approach
- Synthesis of Cu4O3 nanoparticles using pumpkin seed extract: Optimization, antimicrobial, and cytotoxicity studies
- Cationic charge influence on the magnetic response of the Fe3O4–[Me2+ 1−y Me3+ y (OH2)] y+(Co3 2−) y/2·mH2O hydrotalcite system
- Pressure sensing intelligent martial arts short soldier combat protection system based on conjugated polymer nanocomposite materials
- Magnetohydrodynamics heat transfer rate under inclined buoyancy force for nano and dusty fluids: Response surface optimization for the thermal transport
- Fly ash and nano-graphene enhanced stabilization of engine oil-contaminated soils
- Enhancing natural fiber-reinforced biopolymer composites with graphene nanoplatelets: Mechanical, morphological, and thermal properties
- Performance evaluation of dual-scale strengthened co-bonded single-lap joints using carbon nanotubes and Z-pins with ANN
- Computational works of blood flow with dust particles and partially ionized containing tiny particles on a moving wedge: Applications of nanotechnology
- Hybridization of biocomposites with oil palm cellulose nanofibrils/graphene nanoplatelets reinforcement in green epoxy: A study of physical, thermal, mechanical, and morphological properties
- Design and preparation of micro-nano dual-scale particle-reinforced Cu–Al–V alloy: Research on the aluminothermic reduction process
- Spectral quasi-linearization and response optimization on magnetohydrodynamic flow via stenosed artery with hybrid and ternary solid nanoparticles: Support vector machine learning
- Ferrite/curcumin hybrid nanocomposite formulation: Physicochemical characterization, anticancer activity, and apoptotic and cell cycle analyses in skin cancer cells
- Enhanced therapeutic efficacy of Tamoxifen against breast cancer using extra virgin olive oil-based nanoemulsion delivery system
- A titanium oxide- and silver-based hybrid nanofluid flow between two Riga walls that converge and diverge through a machine-learning approach
- Enhancing convective heat transfer mechanisms through the rheological analysis of Casson nanofluid flow towards a stagnation point over an electro-magnetized surface
- Intrinsic self-sensing cementitious composites with hybrid nanofillers exhibiting excellent piezoresistivity
- Research on mechanical properties and sulfate erosion resistance of nano-reinforced coal gangue based geopolymer concrete
- Impact of surface and configurational features of chemically synthesized chains of Ni nanostars on the magnetization reversal process
- Porous sponge-like AsOI/poly(2-aminobenzene-1-thiol) nanocomposite photocathode for hydrogen production from artificial and natural seawater
- Multifaceted insights into WO3 nanoparticle-coupled antibiotics to modulate resistance in enteric pathogens of Houbara bustard birds
- Synthesis of sericin-coated silver nanoparticles and their applications for the anti-bacterial finishing of cotton fabric
- Enhancing chloride resistance of freeze–thaw affected concrete through innovative nanomaterial–polymer hybrid cementitious coating
- Development and performance evaluation of green aluminium metal matrix composites reinforced with graphene nanopowder and marble dust
- Morphological, physical, thermal, and mechanical properties of carbon nanotubes reinforced arrowroot starch composites
- Influence of the graphene oxide nanosheet on tensile behavior and failure characteristics of the cement composites after high-temperature treatment
- Central composite design modeling in optimizing heat transfer rate in the dissipative and reactive dynamics of viscoplastic nanomaterials deploying Joule and heat generation aspects
- Double diffusion of nano-enhanced phase change materials in connected porous channels: A hybrid ISPH-XGBoost approach
- Synergistic impacts of Thompson–Troian slip, Stefan blowing, and nonuniform heat generation on Casson nanofluid dynamics through a porous medium
- Optimization of abrasive water jet machining parameters for basalt fiber/SiO2 nanofiller reinforced composites
- Enhancing aesthetic durability of Zisha teapots via TiO2 nanoparticle surface modification: A study on self-cleaning, antimicrobial, and mechanical properties
- Nanocellulose solution based on iron(iii) sodium tartrate complexes
- Combating multidrug-resistant infections: Gold nanoparticles–chitosan–papain-integrated dual-action nanoplatform for enhanced antibacterial activity
- Novel royal jelly-mediated green synthesis of selenium nanoparticles and their multifunctional biological activities
- Direct bandgap transition for emission in GeSn nanowires
- Synthesis of ZnO nanoparticles with different morphologies using a microwave-based method and their antimicrobial activity
- Numerical investigation of convective heat and mass transfer in a trapezoidal cavity filled with ternary hybrid nanofluid and a central obstacle
- Halloysite nanotube enhanced polyurethane nanocomposites for advanced electroinsulating applications
- Low molar mass ionic liquid’s modified carbon nanotubes and its role in PVDF crystalline stress generation
- Green synthesis of polydopamine-functionalized silver nanoparticles conjugated with Ceftazidime: in silico and experimental approach for combating antibiotic-resistant bacteria and reducing toxicity
- Evaluating the influence of graphene nano powder inclusion on mechanical, vibrational and water absorption behaviour of ramie/abaca hybrid composites
- Dynamic-behavior of Casson-type hybrid nanofluids due to a stretching sheet under the coupled impacts of boundary slip and reaction-diffusion processes
- Influence of polyvinyl alcohol on the physicochemical and self-sensing properties of nano carbon black reinforced cement mortar
- Review Articles
- A comprehensive review on hybrid plasmonic waveguides: Structures, applications, challenges, and future perspectives
- Nanoparticles in low-temperature preservation of biological systems of animal origin
- Fluorescent sulfur quantum dots for environmental monitoring
- Nanoscience systematic review methodology standardization
- Nanotechnology revolutionizing osteosarcoma treatment: Advances in targeted kinase inhibitors
- AFM: An important enabling technology for 2D materials and devices
- Carbon and 2D nanomaterial smart hydrogels for therapeutic applications
- Principles, applications and future prospects in photodegradation systems
- Do gold nanoparticles consistently benefit crop plants under both non-stressed and abiotic stress conditions?
- An updated overview of nanoparticle-induced cardiovascular toxicity
- Arginine as a promising amino acid for functionalized nanosystems: Innovations, challenges, and future directions
- Advancements in the use of cancer nanovaccines: Comprehensive insights with focus on lung and colon cancer
- Membrane-based biomimetic delivery systems for glioblastoma multiforme therapy
- The drug delivery systems based on nanoparticles for spinal cord injury repair
- Green synthesis, biomedical effects, and future trends of Ag/ZnO bimetallic nanoparticles: An update
- Application of magnesium and its compounds in biomaterials for nerve injury repair
- Micro/nanomotors in biomedicine: Construction and applications
- Hydrothermal synthesis of biomass-derived CQDs: Advances and applications
- Research progress in 3D bioprinting of skin: Challenges and opportunities
- Review on bio-selenium nanoparticles: Synthesis, protocols, and applications in biomedical processes
- Gold nanocrystals and nanorods functionalized with protein and polymeric ligands for environmental, energy storage, and diagnostic applications: A review
- An in-depth analysis of rotational and non-rotational piezoelectric energy harvesting beams: A comprehensive review
- Advancements in perovskite/CIGS tandem solar cells: Material synergies, device configurations, and economic viability for sustainable energy
- Deep learning in-depth analysis of crystal graph convolutional neural networks: A new era in materials discovery and its applications
- Review of recent nano TiO2 film coating methods, assessment techniques, and key problems for scaleup
- Antioxidant quantum dots for spinal cord injuries: A review on advancing neuroprotection and regeneration in neurological disorders
- Rise of polycatecholamine ultrathin films: From synthesis to smart applications
- Advancing microencapsulation strategies for bioactive compounds: Enhancing stability, bioavailability, and controlled release in food applications
- Advances in the design and manipulation of self-assembling peptide and protein nanostructures for biomedical applications
- Photocatalytic pervious concrete systems: from classic photocatalysis to luminescent photocatalysis
- Corrigendum
- Corrigendum to “Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer”
- Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part III
- Efficiency optimization of quantum dot photovoltaic cell by solar thermophotovoltaic system
- Exploring the diverse nanomaterials employed in dental prosthesis and implant techniques: An overview
- Electrochemical investigation of bismuth-doped anode materials for low‑temperature solid oxide fuel cells with boosted voltage using a DC-DC voltage converter
- Synthesis of HfSe2 and CuHfSe2 crystalline materials using the chemical vapor transport method and their applications in supercapacitor energy storage devices
- Special Issue on Green Nanotechnology and Nano-materials for Environment Sustainability
- Influence of nano-silica and nano-ferrite particles on mechanical and durability of sustainable concrete: A review
- Surfaces and interfaces analysis on different carboxymethylation reaction time of anionic cellulose nanoparticles derived from oil palm biomass
- Processing and effective utilization of lignocellulosic biomass: Nanocellulose, nanolignin, and nanoxylan for wastewater treatment
- Retraction
- Retraction of “Aging assessment of silicone rubber materials under corona discharge accompanied by humidity and UV radiation”
Articles in the same Issue
- Research Articles
- MHD radiative mixed convective flow of a sodium alginate-based hybrid nanofluid over a convectively heated extending sheet with Joule heating
- Experimental study of mortar incorporating nano-magnetite on engineering performance and radiation shielding
- Multicriteria-based optimization and multi-variable non-linear regression analysis of concrete containing blends of nano date palm ash and eggshell powder as cementitious materials
- A promising Ag2S/poly-2-amino-1-mercaptobenzene open-top spherical core–shell nanocomposite for optoelectronic devices: A one-pot technique
- Biogenic synthesized selenium nanoparticles combined chitosan nanoparticles controlled lung cancer growth via ROS generation and mitochondrial damage pathway
- Fabrication of PDMS nano-mold by deposition casting method
- Stimulus-responsive gradient hydrogel micro-actuators fabricated by two-photon polymerization-based 4D printing
- Physical aspects of radiative Carreau nanofluid flow with motile microorganisms movement under yield stress via oblique penetrable wedge
- Effect of polar functional groups on the hydrophobicity of carbon nanotubes-bacterial cellulose nanocomposite
- Review in green synthesis mechanisms, application, and future prospects for Garcinia mangostana L. (mangosteen)-derived nanoparticles
- Entropy generation and heat transfer in nonlinear Buoyancy–driven Darcy–Forchheimer hybrid nanofluids with activation energy
- Green synthesis of silver nanoparticles using Ginkgo biloba seed extract: Evaluation of antioxidant, anticancer, antifungal, and antibacterial activities
- A numerical analysis of heat and mass transfer in water-based hybrid nanofluid flow containing copper and alumina nanoparticles over an extending sheet
- Investigating the behaviour of electro-magneto-hydrodynamic Carreau nanofluid flow with slip effects over a stretching cylinder
- Electrospun thermoplastic polyurethane/nano-Ag-coated clear aligners for the inhibition of Streptococcus mutans and oral biofilm
- Investigation of the optoelectronic properties of a novel polypyrrole-multi-well carbon nanotubes/titanium oxide/aluminum oxide/p-silicon heterojunction
- Novel photothermal magnetic Janus membranes suitable for solar water desalination
- Green synthesis of silver nanoparticles using Ageratum conyzoides for activated carbon compositing to prepare antimicrobial cotton fabric
- Activation energy and Coriolis force impact on three-dimensional dusty nanofluid flow containing gyrotactic microorganisms: Machine learning and numerical approach
- Machine learning analysis of thermo-bioconvection in a micropolar hybrid nanofluid-filled square cavity with oxytactic microorganisms
- Research and improvement of mechanical properties of cement nanocomposites for well cementing
- Thermal and stability analysis of silver–water nanofluid flow over unsteady stretching sheet under the influence of heat generation/absorption at the boundary
- Cobalt iron oxide-infused silicone nanocomposites: Magnetoactive materials for remote actuation and sensing
- Magnesium-reinforced PMMA composite scaffolds: Synthesis, characterization, and 3D printing via stereolithography
- Bayesian inference-based physics-informed neural network for performance study of hybrid nanofluids
- Numerical simulation of non-Newtonian hybrid nanofluid flow subject to a heterogeneous/homogeneous chemical reaction over a Riga surface
- Enhancing the superhydrophobicity, UV-resistance, and antifungal properties of natural wood surfaces via in situ formation of ZnO, TiO2, and SiO2 particles
- Synthesis and electrochemical characterization of iron oxide/poly(2-methylaniline) nanohybrids for supercapacitor application
- Impacts of double stratification on thermally radiative third-grade nanofluid flow on elongating cylinder with homogeneous/heterogeneous reactions by implementing machine learning approach
- Synthesis of Cu4O3 nanoparticles using pumpkin seed extract: Optimization, antimicrobial, and cytotoxicity studies
- Cationic charge influence on the magnetic response of the Fe3O4–[Me2+ 1−y Me3+ y (OH2)] y+(Co3 2−) y/2·mH2O hydrotalcite system
- Pressure sensing intelligent martial arts short soldier combat protection system based on conjugated polymer nanocomposite materials
- Magnetohydrodynamics heat transfer rate under inclined buoyancy force for nano and dusty fluids: Response surface optimization for the thermal transport
- Fly ash and nano-graphene enhanced stabilization of engine oil-contaminated soils
- Enhancing natural fiber-reinforced biopolymer composites with graphene nanoplatelets: Mechanical, morphological, and thermal properties
- Performance evaluation of dual-scale strengthened co-bonded single-lap joints using carbon nanotubes and Z-pins with ANN
- Computational works of blood flow with dust particles and partially ionized containing tiny particles on a moving wedge: Applications of nanotechnology
- Hybridization of biocomposites with oil palm cellulose nanofibrils/graphene nanoplatelets reinforcement in green epoxy: A study of physical, thermal, mechanical, and morphological properties
- Design and preparation of micro-nano dual-scale particle-reinforced Cu–Al–V alloy: Research on the aluminothermic reduction process
- Spectral quasi-linearization and response optimization on magnetohydrodynamic flow via stenosed artery with hybrid and ternary solid nanoparticles: Support vector machine learning
- Ferrite/curcumin hybrid nanocomposite formulation: Physicochemical characterization, anticancer activity, and apoptotic and cell cycle analyses in skin cancer cells
- Enhanced therapeutic efficacy of Tamoxifen against breast cancer using extra virgin olive oil-based nanoemulsion delivery system
- A titanium oxide- and silver-based hybrid nanofluid flow between two Riga walls that converge and diverge through a machine-learning approach
- Enhancing convective heat transfer mechanisms through the rheological analysis of Casson nanofluid flow towards a stagnation point over an electro-magnetized surface
- Intrinsic self-sensing cementitious composites with hybrid nanofillers exhibiting excellent piezoresistivity
- Research on mechanical properties and sulfate erosion resistance of nano-reinforced coal gangue based geopolymer concrete
- Impact of surface and configurational features of chemically synthesized chains of Ni nanostars on the magnetization reversal process
- Porous sponge-like AsOI/poly(2-aminobenzene-1-thiol) nanocomposite photocathode for hydrogen production from artificial and natural seawater
- Multifaceted insights into WO3 nanoparticle-coupled antibiotics to modulate resistance in enteric pathogens of Houbara bustard birds
- Synthesis of sericin-coated silver nanoparticles and their applications for the anti-bacterial finishing of cotton fabric
- Enhancing chloride resistance of freeze–thaw affected concrete through innovative nanomaterial–polymer hybrid cementitious coating
- Development and performance evaluation of green aluminium metal matrix composites reinforced with graphene nanopowder and marble dust
- Morphological, physical, thermal, and mechanical properties of carbon nanotubes reinforced arrowroot starch composites
- Influence of the graphene oxide nanosheet on tensile behavior and failure characteristics of the cement composites after high-temperature treatment
- Central composite design modeling in optimizing heat transfer rate in the dissipative and reactive dynamics of viscoplastic nanomaterials deploying Joule and heat generation aspects
- Double diffusion of nano-enhanced phase change materials in connected porous channels: A hybrid ISPH-XGBoost approach
- Synergistic impacts of Thompson–Troian slip, Stefan blowing, and nonuniform heat generation on Casson nanofluid dynamics through a porous medium
- Optimization of abrasive water jet machining parameters for basalt fiber/SiO2 nanofiller reinforced composites
- Enhancing aesthetic durability of Zisha teapots via TiO2 nanoparticle surface modification: A study on self-cleaning, antimicrobial, and mechanical properties
- Nanocellulose solution based on iron(iii) sodium tartrate complexes
- Combating multidrug-resistant infections: Gold nanoparticles–chitosan–papain-integrated dual-action nanoplatform for enhanced antibacterial activity
- Novel royal jelly-mediated green synthesis of selenium nanoparticles and their multifunctional biological activities
- Direct bandgap transition for emission in GeSn nanowires
- Synthesis of ZnO nanoparticles with different morphologies using a microwave-based method and their antimicrobial activity
- Numerical investigation of convective heat and mass transfer in a trapezoidal cavity filled with ternary hybrid nanofluid and a central obstacle
- Halloysite nanotube enhanced polyurethane nanocomposites for advanced electroinsulating applications
- Low molar mass ionic liquid’s modified carbon nanotubes and its role in PVDF crystalline stress generation
- Green synthesis of polydopamine-functionalized silver nanoparticles conjugated with Ceftazidime: in silico and experimental approach for combating antibiotic-resistant bacteria and reducing toxicity
- Evaluating the influence of graphene nano powder inclusion on mechanical, vibrational and water absorption behaviour of ramie/abaca hybrid composites
- Dynamic-behavior of Casson-type hybrid nanofluids due to a stretching sheet under the coupled impacts of boundary slip and reaction-diffusion processes
- Influence of polyvinyl alcohol on the physicochemical and self-sensing properties of nano carbon black reinforced cement mortar
- Review Articles
- A comprehensive review on hybrid plasmonic waveguides: Structures, applications, challenges, and future perspectives
- Nanoparticles in low-temperature preservation of biological systems of animal origin
- Fluorescent sulfur quantum dots for environmental monitoring
- Nanoscience systematic review methodology standardization
- Nanotechnology revolutionizing osteosarcoma treatment: Advances in targeted kinase inhibitors
- AFM: An important enabling technology for 2D materials and devices
- Carbon and 2D nanomaterial smart hydrogels for therapeutic applications
- Principles, applications and future prospects in photodegradation systems
- Do gold nanoparticles consistently benefit crop plants under both non-stressed and abiotic stress conditions?
- An updated overview of nanoparticle-induced cardiovascular toxicity
- Arginine as a promising amino acid for functionalized nanosystems: Innovations, challenges, and future directions
- Advancements in the use of cancer nanovaccines: Comprehensive insights with focus on lung and colon cancer
- Membrane-based biomimetic delivery systems for glioblastoma multiforme therapy
- The drug delivery systems based on nanoparticles for spinal cord injury repair
- Green synthesis, biomedical effects, and future trends of Ag/ZnO bimetallic nanoparticles: An update
- Application of magnesium and its compounds in biomaterials for nerve injury repair
- Micro/nanomotors in biomedicine: Construction and applications
- Hydrothermal synthesis of biomass-derived CQDs: Advances and applications
- Research progress in 3D bioprinting of skin: Challenges and opportunities
- Review on bio-selenium nanoparticles: Synthesis, protocols, and applications in biomedical processes
- Gold nanocrystals and nanorods functionalized with protein and polymeric ligands for environmental, energy storage, and diagnostic applications: A review
- An in-depth analysis of rotational and non-rotational piezoelectric energy harvesting beams: A comprehensive review
- Advancements in perovskite/CIGS tandem solar cells: Material synergies, device configurations, and economic viability for sustainable energy
- Deep learning in-depth analysis of crystal graph convolutional neural networks: A new era in materials discovery and its applications
- Review of recent nano TiO2 film coating methods, assessment techniques, and key problems for scaleup
- Antioxidant quantum dots for spinal cord injuries: A review on advancing neuroprotection and regeneration in neurological disorders
- Rise of polycatecholamine ultrathin films: From synthesis to smart applications
- Advancing microencapsulation strategies for bioactive compounds: Enhancing stability, bioavailability, and controlled release in food applications
- Advances in the design and manipulation of self-assembling peptide and protein nanostructures for biomedical applications
- Photocatalytic pervious concrete systems: from classic photocatalysis to luminescent photocatalysis
- Corrigendum
- Corrigendum to “Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer”
- Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part III
- Efficiency optimization of quantum dot photovoltaic cell by solar thermophotovoltaic system
- Exploring the diverse nanomaterials employed in dental prosthesis and implant techniques: An overview
- Electrochemical investigation of bismuth-doped anode materials for low‑temperature solid oxide fuel cells with boosted voltage using a DC-DC voltage converter
- Synthesis of HfSe2 and CuHfSe2 crystalline materials using the chemical vapor transport method and their applications in supercapacitor energy storage devices
- Special Issue on Green Nanotechnology and Nano-materials for Environment Sustainability
- Influence of nano-silica and nano-ferrite particles on mechanical and durability of sustainable concrete: A review
- Surfaces and interfaces analysis on different carboxymethylation reaction time of anionic cellulose nanoparticles derived from oil palm biomass
- Processing and effective utilization of lignocellulosic biomass: Nanocellulose, nanolignin, and nanoxylan for wastewater treatment
- Retraction
- Retraction of “Aging assessment of silicone rubber materials under corona discharge accompanied by humidity and UV radiation”

