Theoretical study of the effect of orientations and fibre volume on the thermal insulation capability of reinforced polymer composites

Abdullah Shalwan; Abdalrahman Alajmi; Belal Yousif

doi:10.1515/rams-2023-0190

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

Theoretical study of the effect of orientations and fibre volume on the thermal insulation capability of reinforced polymer composites

Abdullah Shalwan , Abdalrahman Alajmi and Belal Yousif

Published/Copyright: April 2, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 63 Issue 1

Abstract

In industry, synthetic fibre reinforcements are popular due to their cost-effectiveness and lightweight nature. However, the non-reusability and non-degradability have raised environmental concerns and prompted scientists to explore more environmentally friendly alternatives. Natural fibres are being investigated as potential replacements to address these issues and promote sustainability. This study investigated the effect of fibre loading and orientation on the heat conductivity of polymer resins using a finite element-based numerical model developed in our previous research. The numerical analysis was conducted in ANSYS® modelling and simulation using glass and sisal fibres in combination with three distinct matrix materials (epoxy, polyester, and vinyl ester). Different orientations (parallel, perpendicular, 45°, and normal) and volume of fibre fractions (20–35%) were used for the analysis. The properties of the materials were incorporated into the ANSYS Engineering database, and the composite model was divided into five segments to analyse the heat transfer. The thermal boundary condition was implemented by keeping one side of the cylinder at 120°C. The results showed that the thermal conductivity of the composites decreased as the volume fraction of natural fibres increased. Epoxy-based composites exhibited better insulation performance than polyester and vinyl ester-based composites. This study demonstrated the potential of using natural fibres to improve the thermal insulation properties of composites.

Keywords: natural fibres; sisal; synthetic fibres; glass; composites; thermal properties; orientations; volume; ANSYS

1 Introduction

Composites are unique engineering materials that can be tailor-made from various materials to suit specific applications. A composite material is created by integrating two or more different materials, one acting as the matrix and the other as reinforcement. Composite materials are used for their thermal, electrical, mechanical, and tribological properties. They have several applications in modern industries because of their advantages, such as their small weight and thermal resistance. From a thermal point of view, fibre orientation and loading are the main determinants of their thermal properties. These factors determine the thermal conductivity and distribution of heat flux throughout the composite material [1,2,3,4,5].

Synthetic reinforcements like glass and carbon fibres are widely used in fibre reinforce composite (FRC) as a cost-effective alternative to expensive metal-based materials [6]. This is primarily attributed to their lightweight and cost-effectiveness. However, being non-recyclable and non-degradable led to increasingly facing strict environmental regulations. To solve this problem, researchers are trying to replace them with natural fibres and biodegradable materials. Natural fibres such as sisal, kenaf, bagasse, and hemp have been studied as reinforcing materials for conventional polymer resins. Such composites are often termed green composites and have unique properties compared to conventional composites. Natural fibres are also obtained from sustainable sources, are cheaply available, weigh much less, and are biodegradable [7,8]. In addition, natural fibres can also offer unique thermal insulation properties. Due to these attractive features, natural fibres are increasingly researched for use in the automotive, aerospace, textile, and construction industries.

For instance, Liu et al. [9] researched the transverse heat conductivity of unidirectional epoxy composites reinforced with bamboo and abaca fibres through resin transfer moulding. The study found a clear correlation between the dosage of bamboo and abaca fibres and the composites’ thermal conductivity. An increase in bamboo fibre dosage made the composite more thermally conductive, and vice versa was observed with the abaca fibres. Additionally, the transverse thermal conductivity was significantly influenced by the lumen structure rather than the structures and chemical components of the composites. Similar findings were obtained by Zheng [10] in a study investigating the thermal properties of hemp fibre bundles by focusing on their anisotropic thermal conductivities. Their analysis used a 2D computational composite model of unidirectional hemp fibre bundles in a hypothetical matrix in ABAQUS. The same model was incorporated with equivalent solid fibre, replacing the bundle to check the influence of bundle homogeneity. It was observed that the effective thermal conductivity of the composite depends on the proportion of solid region and lumen in the fibre.

The derived optional interrelationship’s predictions were validated through comparison with an analytical model derived from the interface interaction between circular matrix and circular inclusions embedded in the matrix, showing good agreement with the analytical results. The key findings include the establishment of an optional interrelationship between the thermal conductivity of the solid region and the fibre bundle through curve-fitting techniques.

Rahman et al. [11] have studied the effects of fibre orientation and volume fraction on the thermal properties of the laminated jute-reinforced polyester composite. It is found that the thermal conductivity of the laminated jute-reinforced polyester composite is increased with fibre volume fraction and varied with fibre orientation.

Also, Ramanaiah et al. [12] have studied Sansevieria natural fibre as reinforcement in preparing partially biodegradable green composites. The effect of fibre direction and content on the thermal properties of composite was investigated. The thermal conductivity of the composite decreased with an increase in fibre content, and the opposite trend was observed with respect to temperature. In addition, the experimental results of thermal conductivity at different volume fractions were compared with the theoretical model. The response of the specific heat capacity of the composite with temperature as measured by differential scanning calorimeter was discussed. The lowest thermal diffusivity of the composite was observed at 90°C, and its value is 0.9948 × 10⁻⁰⁷ m²·s⁻¹.

Several similar studies are available on the manufacturing and analysis of FRC using natural fibres such as jute [13,14], hemp [15], kenaf [16], bamboo [17], banana [18,19], and sisal fibres [20,21,22]. However, most focused on these composites’ mechanical performance and structural characteristics [23].

A modern approach in this regard to optimize properties and standardize processing methods of natural fibre-reinforced composites (NFRCs) is finite element modelling (FEM). FEM is a sophisticated computational tool that enables engineers to simulate experiments in a virtual environment. The benefits include ease of interpretation of resulting graphs and a clear understanding of the output of their designs under different conditions. Additionally, it facilitates iterative analysis, enabling refinement and optimization of the designs with high accuracy. As such, FEM has become an invaluable tool for engineers across a wide range of industries, and it can be utilized to evaluate and design FRCs with superior thermal insulation properties [24,25,26].

In this context, the temperature change of NFRC has mostly been studied by modelling Fourier’s heat conduction equation [27,28,29]. A study by Shokrieh and Ghanei-Mohammadi [30] presented a unit cell FEM for analysing the thermal behaviour of composites. They focused on the effects of different representative volume element configurations on the results. Similarly, Wang and Qin [31] developed a 2D hybrid finite element formulation for predicting the effective thermal conductivity of FRCs. In another study, Ahmadi et al. [6] used FEM to investigate the thermal conductivities of multiphase composites reinforced by carbon fibres. They examined the effects of interphase features, fibre volume fraction, orientation, and arrangement on thermal conductivity. Likewise, Javanbakht, Hall [32] introduced a correction factor for fine-tuning, self-updating capability of NFRCs’ numerical models considering the size-effect of fibres.

In all of these studies, FEM proved to be a valuable tool for studying the thermal behaviour of NFRCs. One particular aspect that has garnered significant attention is the effect of the reinforcement’s orientation and volume on the thermal conductivity of composites. The reinforcement phase in composites, such as fibres or particles, can be aligned in different directions relative to the applied heat flux. The orientation of the reinforcement significantly impacts the pathways available for heat conduction within the composite material. It is pivotal in various applications, including heat exchangers, thermal management systems, electronic devices, and aerospace structures [20,33,34].

In numerical research on NFRC, ANSYS® modelling and simulation has emerged as the predominant platform for FEM analysis employing solid and shell elements. However, from both industrial and academic perspectives, a noticeable research gap exists regarding the thermal characteristics of these composites [35,36], particularly the impact of reinforcement orientation and volume on NFRC’s thermal conductivity. Although previous research efforts have explored 2D and 3D modelling of NFRC using FEM [33,37,38,39], there is a dominance of 2D analyses [35], indicating an unexplored avenue in terms of comprehensive understanding and characterization of NFRC’s thermal behaviour [37,38,39,40]. The transition to 3D modelling using ANSYS is essential for capturing the intricacies of heat transfer in NFRC and enabling more accurate thermal conductivity predictions. Furthermore, optimising algorithms for determining the ideal dosage and orientation of fibres in NFRC is essential for tailoring the material’s thermal properties according to specific requirements.

2 Methodology

2.1 Numerical process methodology

A rigorous methodology was used to obtain numerical outcomes on the thermal characteristics of various matrix/fibre composites. The research study forming the theoretical background of our modelling and simulation approach can be reviewed in our previous work [40]. Also, this study and our previous work [40] have been built based on experimental work achieved in the last period and published [41,42]. The FEM is a powerful computational tool for estimating solutions to real-life engineering problems. Physical phenomena occur in a continuum of matter ranging from solid to gas, subject to field variables. These field variables usually vary between points and possess a finite number of solutions within that domain. This tool simplifies the problems by converting the whole domain into a finite number of pieces or elements. An approximate function could be associated with the unknown field variables. Modelling of thermal can be carried out using FEM programs such as ANSYS [41].

This research used ANSYS to analyse conductive heat transfer through fibre composite bodies. Many practical heat transfer problems require numerical methods, which allow problems to be solved quickly. The effect of changes in parameters can often be seen when a problem is modelled numerically. A numerical formulation can also be performed using partial differential equations. These equations are replaced by discrete approximations, such as temperature fields that are approximated by the values at discrete points. As a result, a computational mesh is formed (in Cartesian or cylindrical coordinates), and the field is considered at consecutive time steps with a time increment ∆t [43]. This type of modelling of a cylindrical composite is explained in this chapter. In Figure 1, the flow of the numerical programmer of a cylindrical model is summarized.

Figure 1

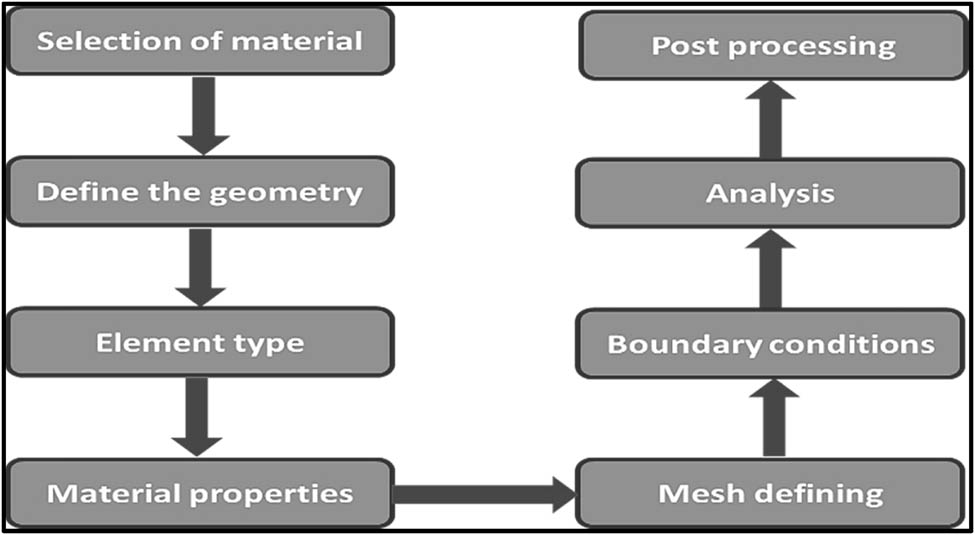
Key steps involved in developing a cylindrical model.

Here, numerical tests were conducted using glass and sisal fibres combined with three distinct matrix materials. Our goal was to study the thermal properties of these composites and determine the impact of different matrix/fibre combinations on the resulting characteristics. The details of their components and fibre orientation procedures of the study are illustrated in Table 1.

Table 1

Types of fibre orientation in different composites

Type of fibre	Fibre orientation	Composite samples	Volume fraction (%)
Glass	Parallel, perpendicular, 45°, normal	Glass–epoxy	20–35
		Glass–polyester
		Glass–vinyl ester
Sisal	Parallel, perpendicular, 45°, normal	Sisal–epoxy	20–35
		Sisal–polyester
		Sisal–vinyl ester

This study tools several assumptions to reduce the complexity and successful convergence of the numerical model to a solution. These are listed as follows:

The heat transfer process within the composite material is a steady state.
Fibres are perfectly organized in the matrix in a specific pattern (parallel, perpendicular, 45°, normal)
There are no imperfections in the composite samples.
The interfaces between fibre and matrix are perfectly bonded.
During the analysis, no phase changes or material transformations occurred within the composite material.
The thermal conductivities of the materials are assumed to be constant in all directions.
Heat source applied to one end of the composite material generates a uniform heat flux or heat generation rate.

2.2 Simulation setup

The development and execution of the numerical model were carried out in the ANSYS programming design language. It is the main interface of the ANSYS software and involves stages such as geometry design, meshing, application of boundary conditions, and solution. These steps make it possible to successfully observe the effects of parametric variations on the developed model. The numerical formulation can be achieved through partial differential equations, which are then transformed into discrete approximations, like the approximation of temperature fields, using values at different points. This procedure produces a computational mesh, which may be represented using cylindrical or Cartesian coordinates. The field is then examined in a series of time steps with an interval of ∆t. The following diagram summarizes the main steps and the order of the numerical program for a cylindrical model.

2.3 Engineering data

The materials were incorporated into the ANSYS engineering data bank through manual addition, as these were not available through other means. This was necessary to ensure that information was available for the respective simulations and analyses. Table 2 lists the properties.

Table 2

Properties of fibres and resins used in the composites

Properties	Sisal fibres	Glass fibres	Resin epoxy	Resin polyester	Resin vinyl ester
Density (kg·m⁻³)	1,330	2,550	1,160	1,200	1,200
Young’s modulus (GPa)	20	72	3.7	3	3
Specific heat (kJ·kg·⁻¹·C⁻¹)	—	0.16	0.24	1.3	0.24
Poisson’s ratio	0.3	0.33	0.35	0.316	0.316
Shear modulus (GPa)	7.5	27	1.4	1.14	1.13
Bulk modulus (GPa)	19	70	4.2	2.7	2.7
Tensile yield strength (GPa)	650	2.05	—	—	—
Isotropic thermal conductivity (W·m⁻¹·K⁻¹)	0.07	0.04	0.35	0.05	0.15

2.4 Numerical modelling of cylindrical coordinates

Numerical modelling of cylindrical coordinates and heat transfer has been investigated and researched by many researchers [43,44,45]. Consider heat transfer across a cylinder whose radius is r, and the heat transfer occurs in vertical and radial directions in rotational symmetry around the z-axis. Here, the temperature along with r in the z-direction at a specific time t is given by [48,49]:

(1) T = T ( r , z , t ) .

A radial and a vertical thermal process, which is rotationally symmetric around the z-axis, is considered for this modelling. Here, the interval along “r” is divided into a mesh having cell widths (as shown in Figure 2a) as follows [44,45]:

(2) ∆ ri , i = 1 , N .

Figure 2

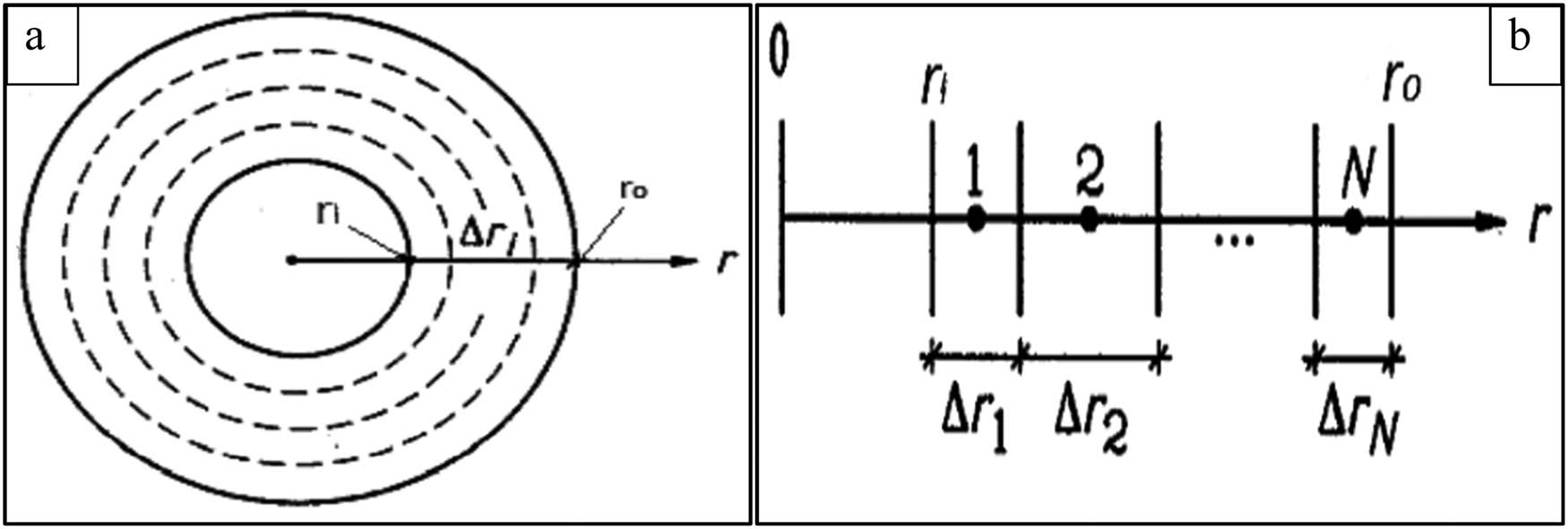
(a) Proposed cylinder for heat transfer study and (b) details of the meshes in the radial direction.

The inner boundary is at r = rI, the outer boundary is at r = ro, and the midpoint is at r = ri. Here, rI may be at the z-axis and hence zero (as shown in Figure 2b).

Here, we have [44,45]

(3) r 1 = rI + ∆ r 1 2 ,

(4) ri = ri − 1 + ∆ ri − 1 2 + ∆ ri 2 .

In the aforementioned equation, “i” ranges from 2 to N. If the widths of the individual cells are summed up, we obtain the total annulus width as follows [44,45]:

(5) ∑ i = 1 N ∆ r = r 0 − r ₗ .

The dimensions in the z-direction are shown in Figure 3a, and the cell widths in the z-direction are given as ∆zj. At the middle point of cell (i, j), the temperature at a time step of “n” is given by the following relation [44,45]:

(6) Ti , j = T ( ri , zj , n ∆ t ) ,

Figure 3

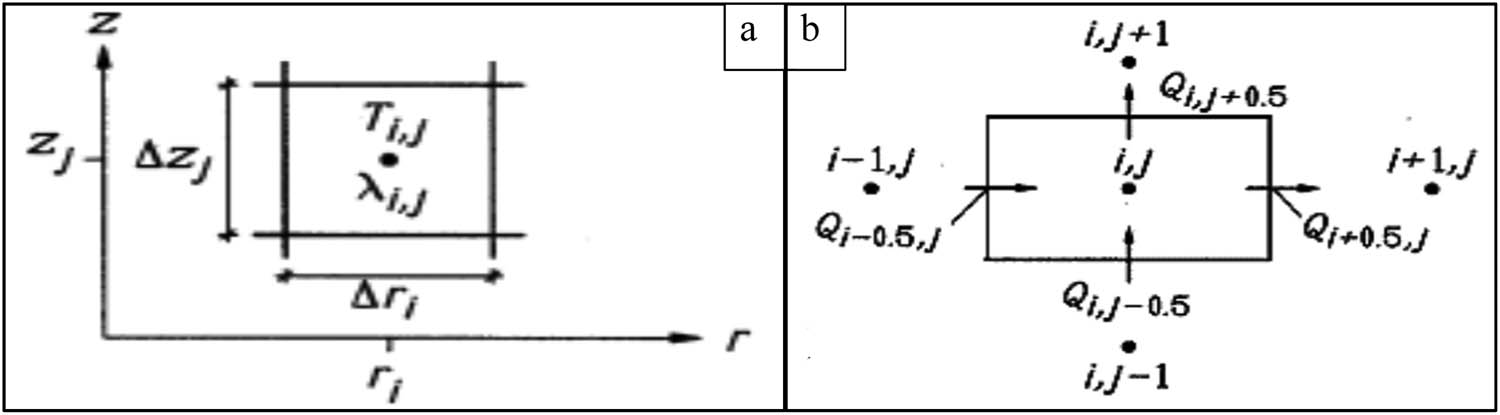
(a) A mesh element in the cylindrical coordinates and (b) illustration of heat flows (W) to and from the cell (i, j).

where the cell (i, j) shown in the figure is an annular section of cylindrical shape and its dimensions are given as [44,45]:

(7) ri − Δ ri 2 ≤ r ≤ ri + ri 2 ′ ,

(8) zj − ∆ zj 2 ≤ z ≤ zj + ∆ zj 2 .

The volume of the cell can be given by using the dimensions of the cell by the following relationship [44,45]:

(9) ∆ ri ∆ zj 2 π ri = π ri + ∆ ri 2 2 − π ri − ri 2 2 ∆ zj .

The conductance (K) between two successive cells, i.e., cell (i, j) and l (i−1,), could be given as [44,45]:

(10) Ki − 0.5 j = ∆ zj ln ri − 0.5 ri − 1 1 2 π λ i − 1 , j + ln ri ri − 0.5 1 2 π λ i , j + ri − 0.5 2 π ri − 0.5 .

The conductance in the aforementioned equation is in watts per kelvin (W·K). The thermal conductivity is given by the term for cells, respectively. In addition, Ri−0.5 and j represent an optional thermal resistance present at the interface of two cells. The first term in the denominator gives the value of the thermal resistance per unit height of the ri − 1 ≤ r ≤ ri − 0.5 annulus.

The heat conductance in the direction of the z-axis can be given as a product of the area of the cell perpendicular to the z-axis (2πri∆ri) and unidimensional conductance. The equation is given as follows [44,45]:

(11) Ki , j − 0.5 = 2 π ri Δ ri 0.5 Δ zj − 1 λ i , j − 1 + 0.5 Δ zj λ i , j + ri − 0.5 , j .

The heat flows are shown in Figure 3b. The product of temperature difference and conductance gives them. These flows are used for all “i” and “j” and are as follows [44,45]:

(12) Qi − 0.5 , j = Ki − 0.5 , j ( Ti − 1 , j − Ti , j ) ,

(13) Qi , j − 0.5 = Ki , j − 0.5 ( Ti , j − 1 − Ti , j ) .

In a time-step of ∆t, an increase or a decrease in the temperature takes place, and as a result, Ti is used for the next time-step. Hence, the heat balance equation takes the form as follows [44,45]:

(14) ∆ ri ∆ zj 2 π riCi , j ( Ti , j − Ti , j ) = [ Qi − 0.5 , j − Qi + 0.5 , j + Qi , j − 0.5 − Qi , j + 0.5 ] ∆ t .

The choice of a stable time-step for the cell (i,) is made by using the stability criteria given as [44,45]:

(15) ∆ t < ∆ ri ∆ zj 2 π riCi , j ∑ K .

Here, ∑ K = K i − 0.5 , j + K i + 0.5 , j + K i , j − 0.5 + K i , j + 0.5 .

The aforementioned criteria for numerical stability must be satisfied for the cell (i,), and the smallest time-step obtained is used to guarantee stability for all cells.

2.5 Numerical theory behind ANSYS modelling

The first law of thermodynamics states that thermal energy is conserved. Specializing this to a differential control volume, the equation of the following form can be given as (SAS, 2012) [44,45]:

(16) Q = ∇ . { q } + ∂ T ∂ t + { v } T ∇ T ρ c .

In the aforementioned equation, the vector functions are further explained as [44,45]:

(17) Vector operator = ∇ = ∂ ∂ x ∂ ∂ y ∂ ∂ z { ∂ ∂ x / ∂ ∂ y / ∂ ∂ z ,

(18) Velocity vector for mass transport of heat = { v } = Vx Vy Vz .

In the next step, the heat flux vector is related to the thermal gradients by using the Fourier’s law of heat conduction as follows [44,45]:

(19) { q } = − [ D ] ∇ T ,

where [D] is the conductivity matrix, which is given as follows [44,45]:

(20) [ D ] = k ᵪ ᵧ 0 0 0 k ᵧ ᵧ 0 0 0 kzz .

In the aforementioned matrix, the k _xx, k _yy, and k _zz are the conductivity elements in the x, y, and z dimensions, respectively. The equations could be combined to form a compound equation as follows [44,45]:

(21) Q = ( − [ D ] ∇ T ) + ( ∂ T ∂ t + ∂ T ∂ t + { v } T ∇ T ) ρ c ,

(22) Q + ∇ . ( [ D ] ∇ T ) = ∂ T ∂ t + { v } T ∇ T ρ c .

The aforementioned equation can be expanded to a more familiar form as follows [44,45]:

(23) ∂ T ∂ t + v ∂ T ∂ x + v ∂ T ∂ y + v ∂ T ∂ z ρ c = Q + ∂ ∂ x K ∂ T ∂ x + ∂ ∂ y K ∂ T ∂ y + ∂ ∂ z K ∂ T ∂ z .

Here, it has been assumed that all effects are in the global Cartesian system. Three boundary conditions are considered for this system, and it has been presumed that these conditions cover the entire element. These are given as follows:

Specified temperatures acting over the surface S1, T = T*
The T* above is the specified temperature.
Specified heat flows acting over the surface S2, as shown in Figure 4, is given as [44,45]:

(24) − Q * = { n } { q } T ,

Figure 4

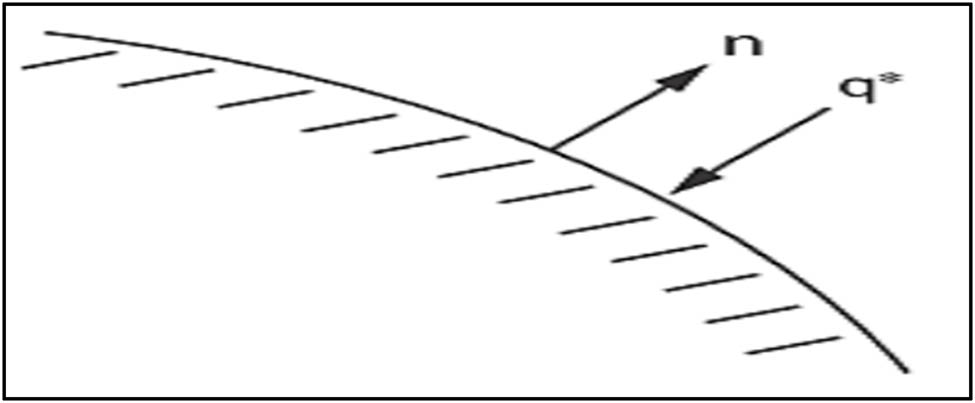
Specified convection surfaces.

where {n} is the unit outward normal vector and Q* is the specified heat flow.

2.6 Development of the model

The initial models were created by inputting information on the constituent elements and components. The properties of the composites were incorporated into the ANSYS Engineering database per the previously specified table. In this case, thermal conductivity and specific heat were the most critical properties. The modelled composite cylinder was divided into five segments to analyse the heat transfer. A meshed geometry of the composite cylinder is shown in Figure 5.

Figure 5

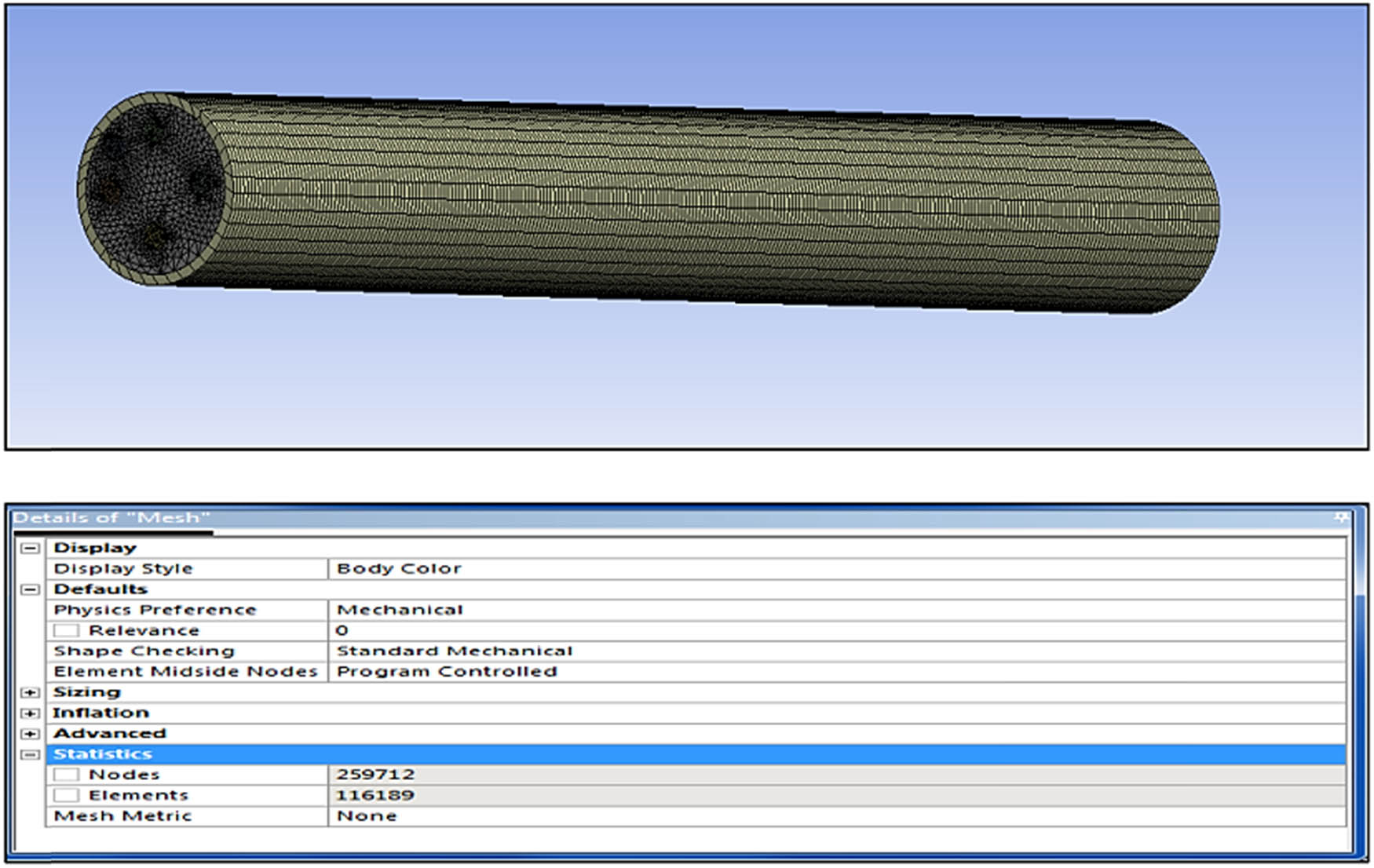
Meshed model of the composite cylinder with details on nodes and elements.

The cylinder’s overall length was fixed at 10 cm, while the length of each segment was set at 2 cm. The thermal boundary condition was implemented by setting the temperature of one side of the cylinder to 120°C. This is known as a Dirichlet boundary condition, specifying the exact temperature value at the boundary. The other side of the cylinder was set to a natural boundary condition, which specifies that the heat flux at the boundary is zero. This means that no heat can flow through the boundary. Figure 6 depicts the investigation results into temperature differences over the length of the cylinders with various fibre orientations.

Figure 6

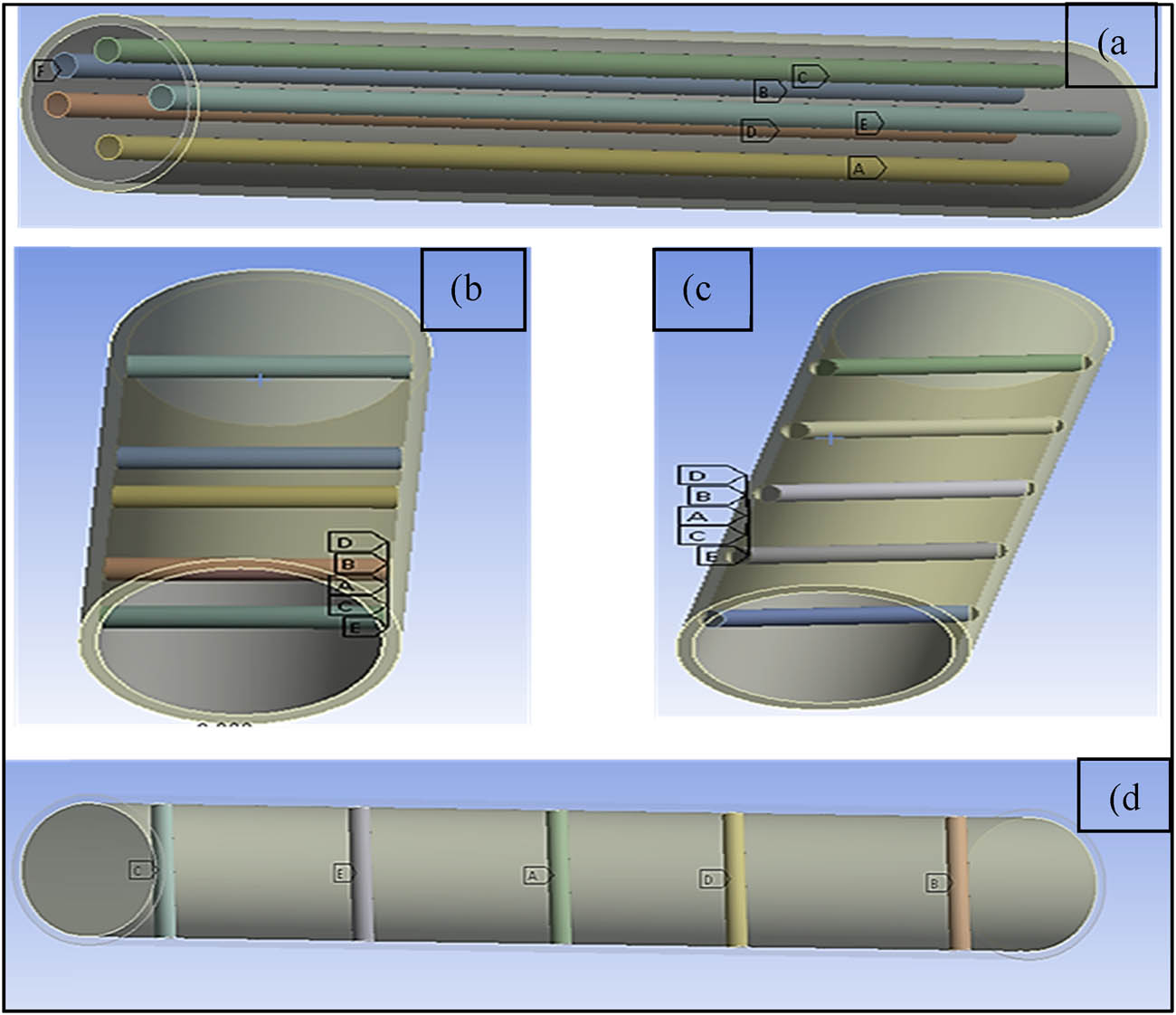
Developed models with different fibre orientations: (a) Normal, (b) perpendicular, (c) 45°, and (d) parallel.

2.7 Preliminary results

The preliminary results obtained in this study are shown in Figures 7–9, and these results confirmed a successful construction of theoretical models concerning various composites in ANSYS. The results also enabled a comparison of the synthetic and natural fibre-based FRC about their thermal insulation or conductance. The volume percentage of the fibres and their orientation both had a considerable impact on the composites’ thermal conductivity.

Figure 7

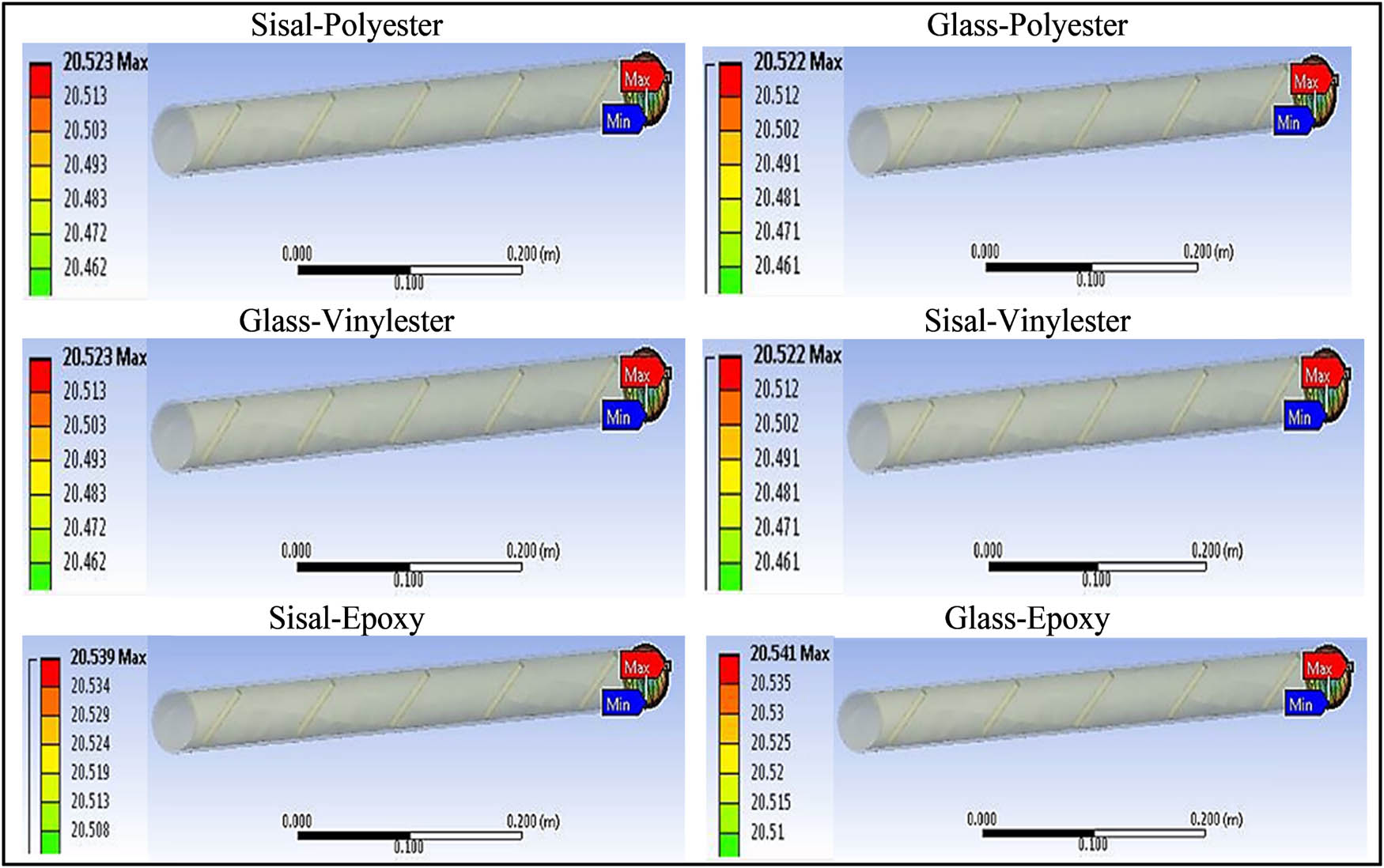
Preliminary results of the different composites, each with 20% of fibres oriented perpendicularly.

Figure 8

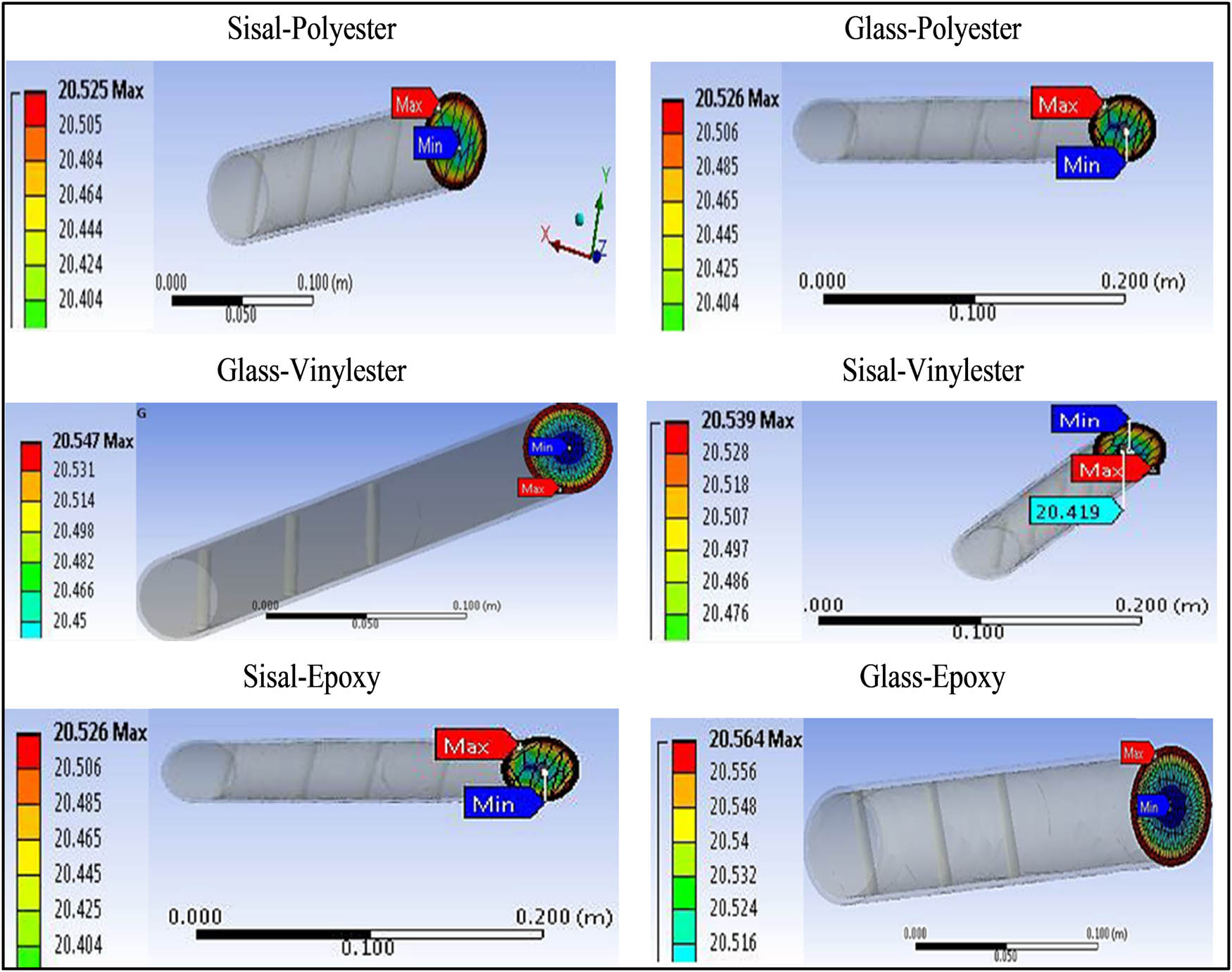
Preliminary results of the different composites, each having 20% of fibres oriented in the parallel direction.

Figure 9

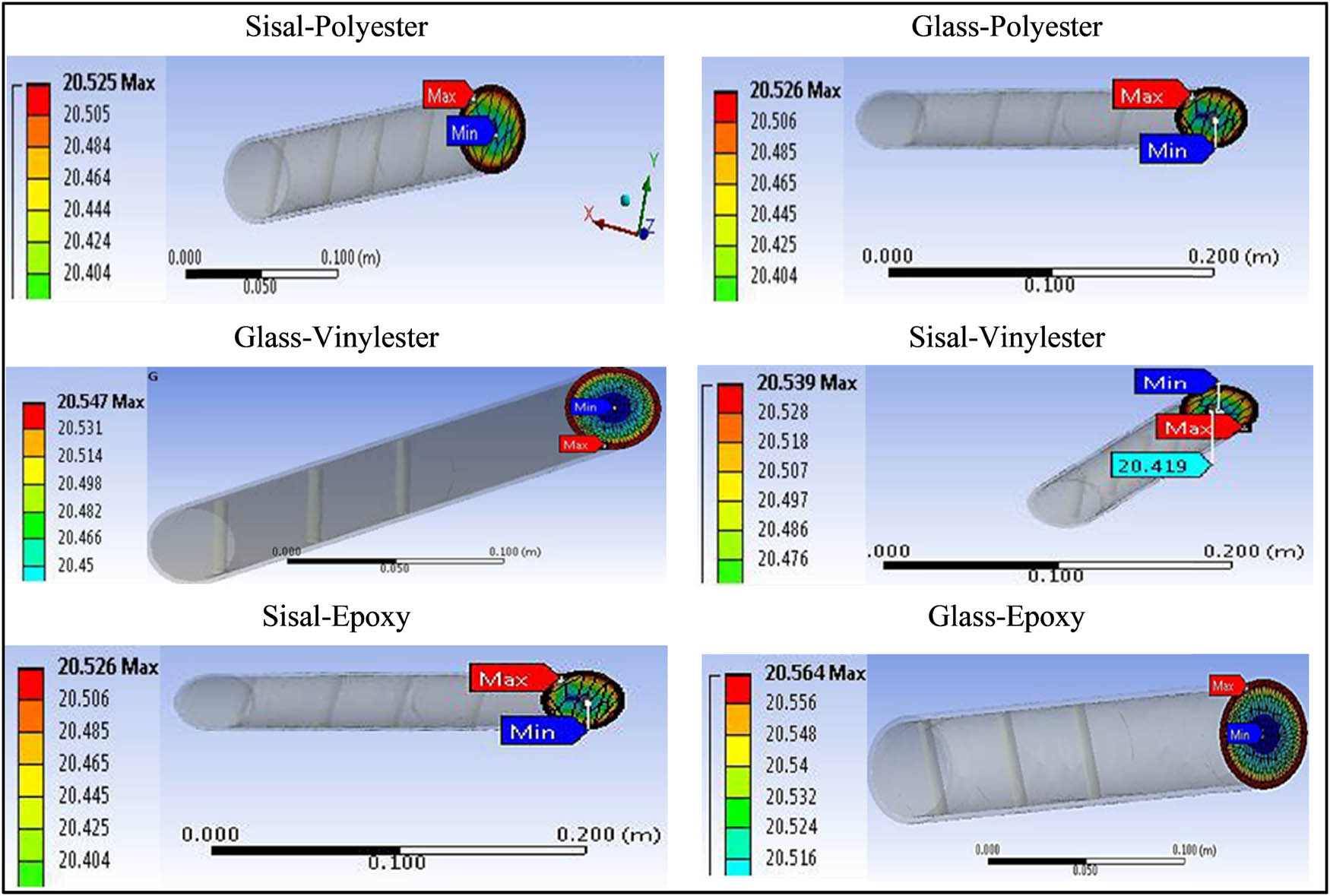
Preliminary results of the different composites, each having 20% of fibres oriented in 45° direction.

3 Results and discussion

3.1 Effect of orientation and volume in sisal fibre/epoxy & glass fibre/epoxy

The sisal fibre orientation effect at various loadings on the insulating capabilities of the epoxy-based composite is shown in Figure 10. The insulation percentage of composites increased for all kinds of fibre orientations at all loadings. This decrease in thermal conductivity can be attributed to the most significant influence of fibre loadings on the thermal conductivity of composites compared to the epoxy matrix. Each loading developed a smooth curve with time, and a consistent rise in the insulation % was attained. For all time intervals, the fibre orientations of perpendicular, parallel, and 45° exhibited values with proximity, indicating slightly higher insulation percentages than the normal orientation.

Figure 10

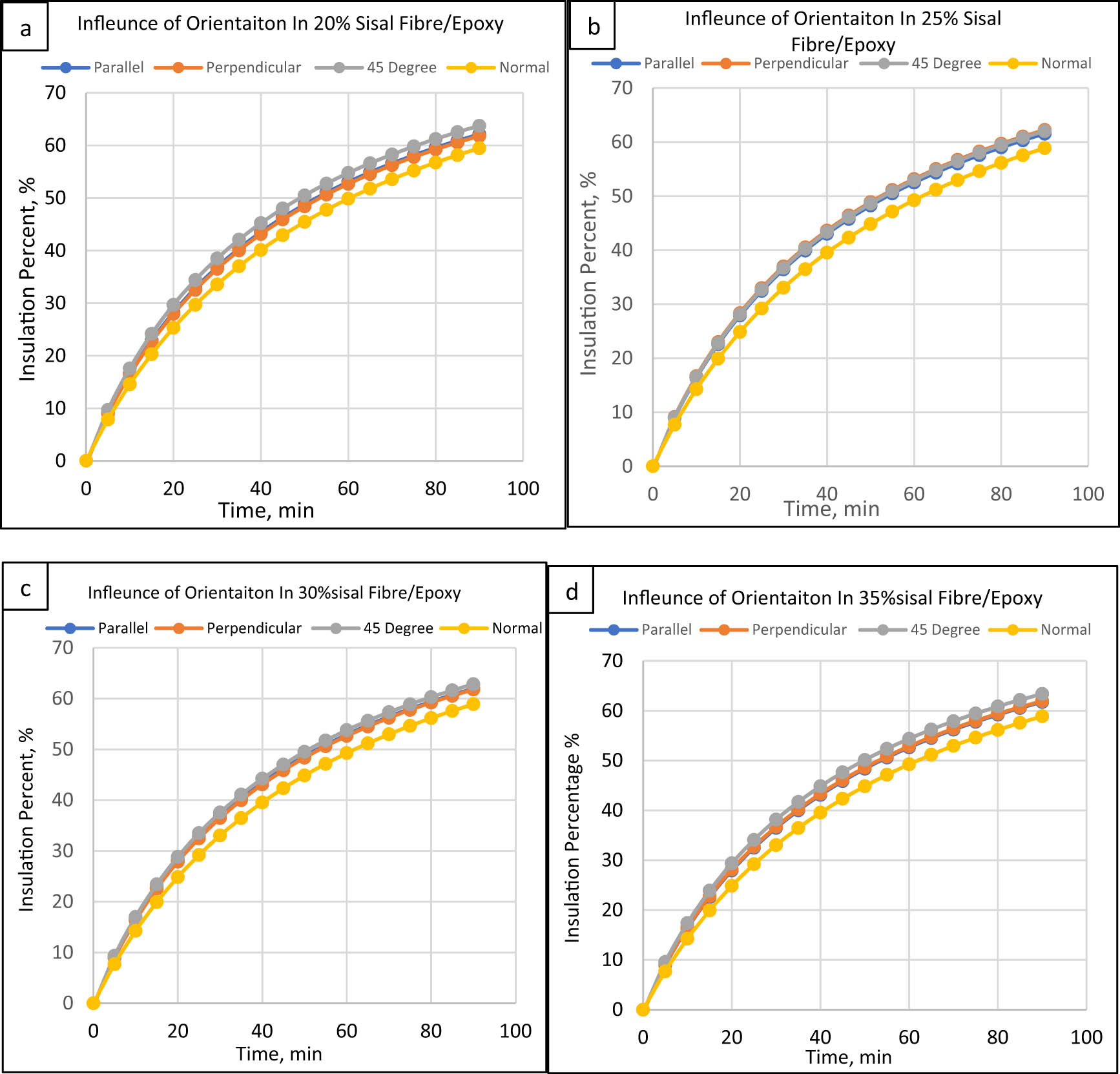
Orientation effect on sisal epoxy/fibre composites: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

The insulating capability of the composites was improved by increasing the fibre loading from 20 to 25%. For example, after 90 minutes, the insulation percentage of the 30% fibre loading was 0.1% higher than that of the 20% loading. Similar variations, like increases or decreases in insulation percentage, were observed at other times. This is consistent with the findings of Kalaprasad et al. [46], who found that the insulating capability of a composite improves as the fibre content increases. This is because the fibres have a lower thermal conductivity than the epoxy matrix, and they form disrupted heat transfer pathways via fibre–matrix interfaces. Moreover, they introduce porosity and voids into the composite structure. These voids act as thermal insulators to interrupt the heat flow, decreasing thermal conductivity [34,38,47,48].

In a similar study, Devireddy and Biswas [19] also investigated the impact of fibre orientation on the thermal properties of natural fibre-reinforced epoxy composites. They determined thermal conductivity following steady-state heat transport simulations using the ANSYS software. The loadings of fibres varied between 10 and 30% with orientations in both normal and transverse directions to the heat flow. A substantial decrease in heat conductivity was observed after adding fibres to the epoxy resin, and outcomes comparable to our study were achieved. NFRC with fibres normally orientated (35%) instead of transversally (44%). The fibre alignment parallel to the heat flow direction is the primary cause of the usual orientation’s lower insulation capabilities.

The glass fibre orientation effect at various loadings on these insulating characteristics of the epoxy composite is shown in Figure 11. As apparent, all loadings and orientations of glass fibre composites produced considerable insulating patterns. In contrast, these parameters had a negligible impact on the thermal conductivities of the composites. Such behaviour may be explained by the glass fibres’ comparatively high thermal conductivity (>1 W·m⁻¹·K⁻¹) and isotropic nature, as opposed to sisal fibres’ thermal conductivity of only 0.07 W·m⁻¹·K⁻¹ [46].

Figure 11

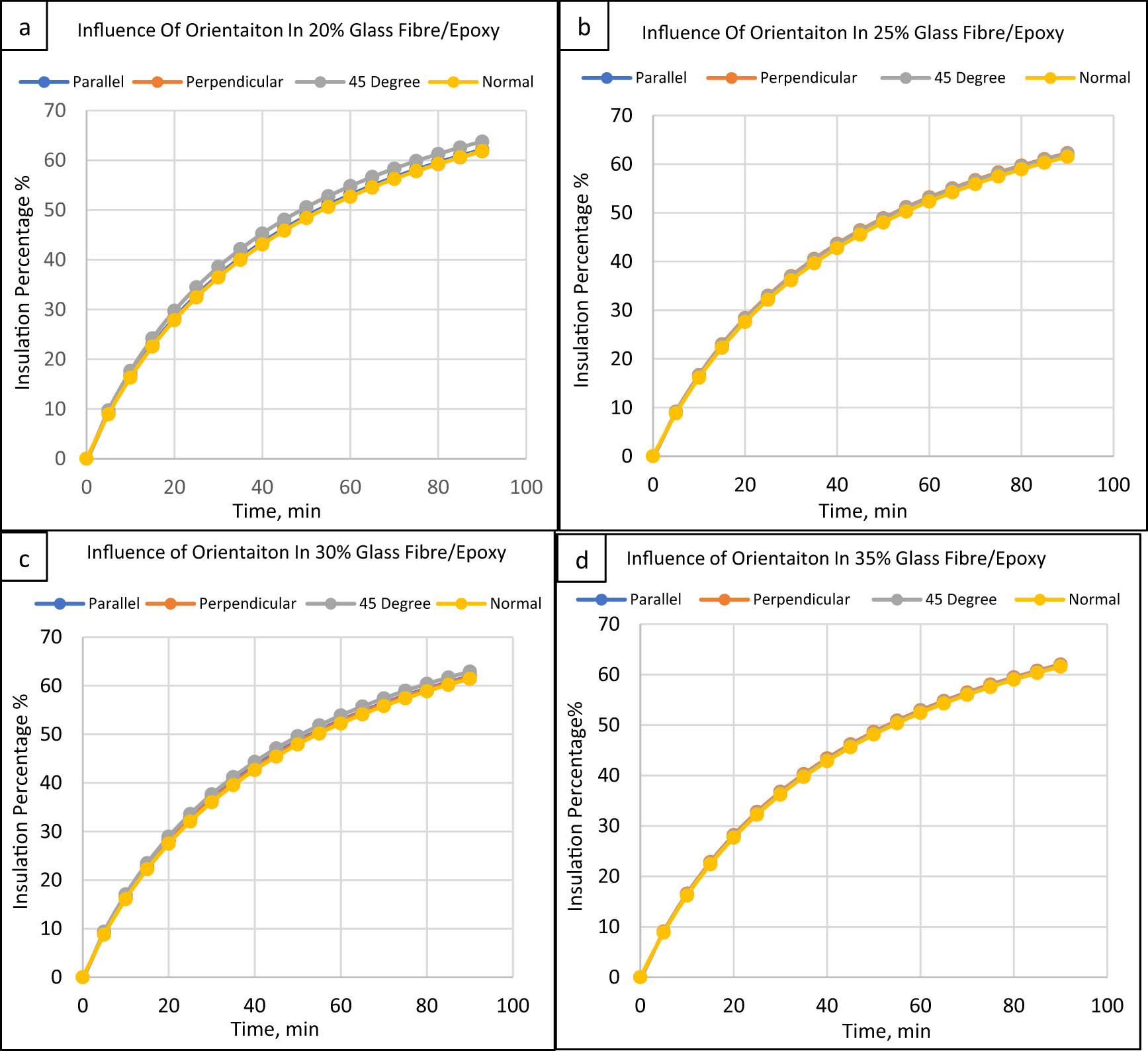
Orientation effect on glass epoxy/fibre composites: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

The thermal insulation properties of glass fibres are isotropic, independent of fibre orientation. This is because the iron ions (Fe²⁺) commonly found in glass fibres provide the electrons needed for thermal conduction [46]. Similarly, a slight disparity in insulation percentage among the four composites was observed at a specific time interval (90 min). This observation indicates that an increase in glass fibre concentration leads to a minor reduction in thermal conductivity at a given temperature. This behaviour aligns with the findings of Cao et al. [49], who conducted modelling and practical investigations on the thermal performance of glass fibre-reinforced boards. It has been noted that the amount of glass fibre improves thermal conductivity as the temperature changes [46]. This is because the iron ions in the glass fibres become more mobile at higher temperatures, increasing the composite’s thermal conductivity.

3.2 Effect of orientation and volume in sisal fibre/polyester and glass fibre/polyester

The sisal fibre orientation effect at various loadings on the insulating capabilities of the polyester-based composite is shown in Figure 12. The efficiency of sisal fibre-reinforced polyester resin in thermal insulation is comparable to that of epoxy resin composites. In a study by Mounika et al. [50], the effect of bamboo fibre orientations on the thermal properties of polyester-based composites was investigated. The thermal conductivity of composites was measured with bamboo fibres oriented at 0°, 45°, and 90° to the heat flow direction. The results showed that the thermal insulation capabilities decreased as the fibre orientation angle increased. This is because the bamboo fibres aligned parallel to the heat flow direction acted as thermal barriers, preventing heat from flowing through the composite. However, the present study observed no such behaviour for sisal–polyester composites. It may be due to the different properties of sisal fibres compared to bamboo fibres.

Figure 12

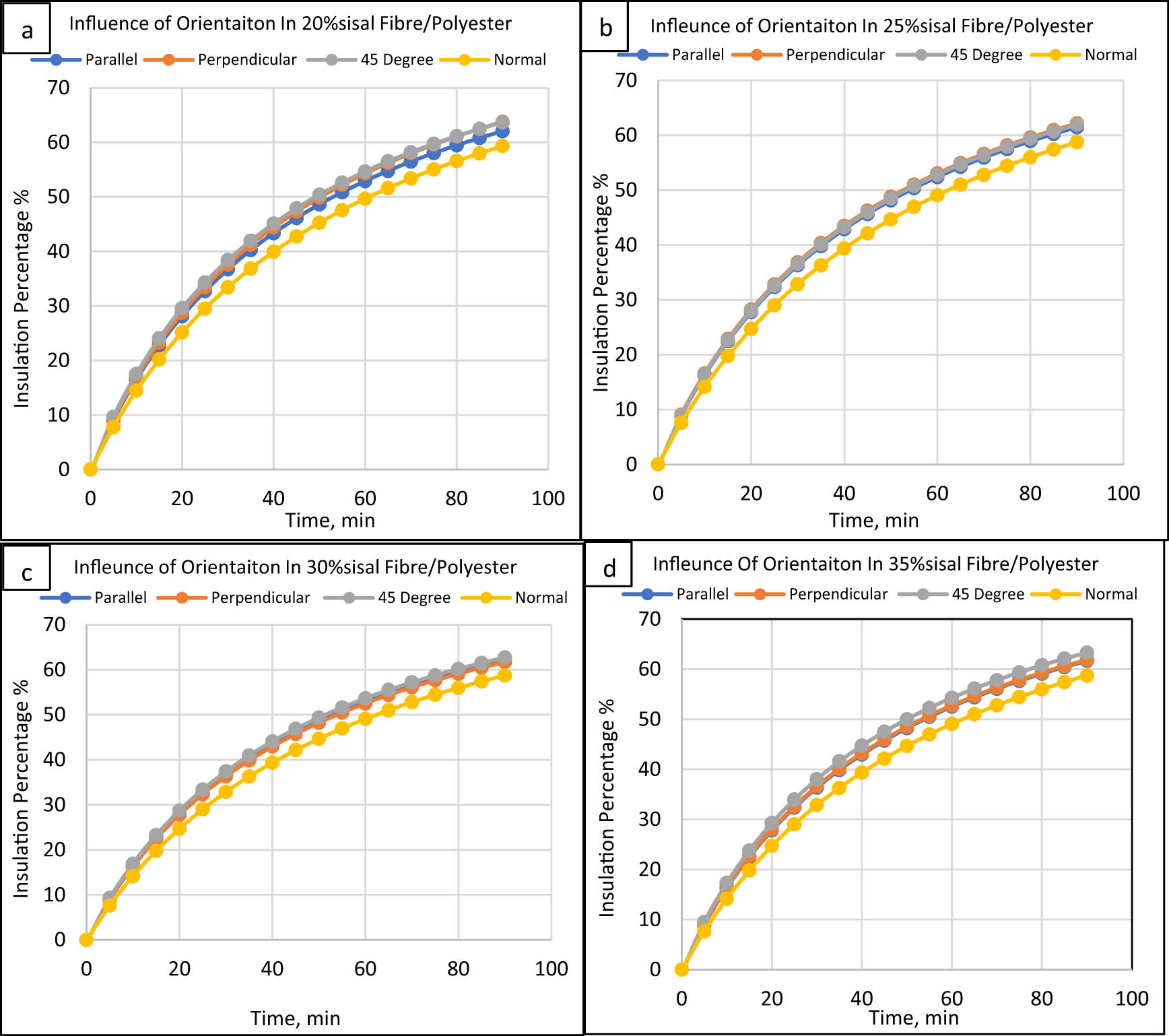
Orientation effect on polyester composites/sisal fibre: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

Figure 13 illustrates the impact of glass fibre orientation at different loadings on the insulation capabilities of the polyester-based composite. Orientations b to d exhibited higher insulation percentages across all time intervals. In contrast, orientation deviated from this trend, possibly due to the disparity in fibre loading compared to the other cases. Previous studies employing ANSYS modelling have similarly demonstrated the influence of fibre content on thermal conductivity in glass fibre-based composites. Moreover, the insulation level increases at 25 wt% loadings and slightly decreases beyond 45 wt% [51].

Figure 13

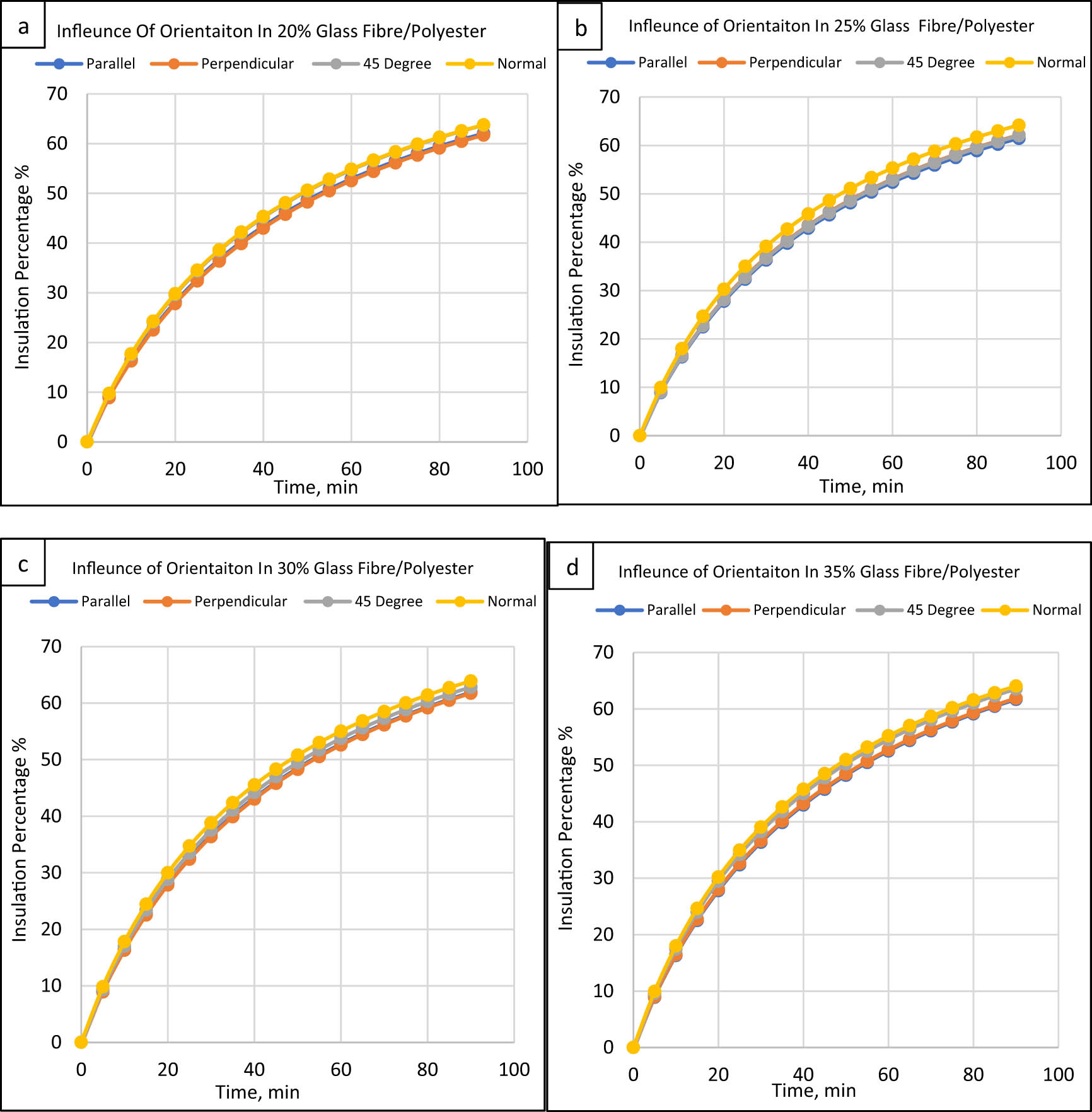
Orientation effect on polyester composites/glass fibre: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

These finding also aligns with the study outcomes by Idicula et al. [52]. They strengthened polyester resins using glass and sisal fibres. The thermal properties (specific heat, thermal conductivity, and diffusivity) were examined with fibre loading from 20 to 40%. The heat conductivity of NFRC was reduced by 16 to 22% compared to pure polyester resin. On the other hand, adding glass fibres reduced the thermal insulation provided by polyester resin. The reason for this behaviour was the glass fibre’s high thermal transfer characteristics.

3.3 Effect of orientation and volume in sisal fibre/vinyl ester and glass fibre/vinyl ester

The sisal fibre orientation effect on the insulating capabilities of the vinyl ester-based composites at various loadings is shown in Figure 14. The insulation characteristics of these composites were also similar to polyester and epoxy-based composites. As stated earlier, adding sisal fibres decreases the overall thermal conductivity of vinyl ester resin – the usual orientation resulted in poor insulating values with various sisal loadings. The insulation percentages obtained in the other three orientations were similar and followed the same pattern.

Figure 14

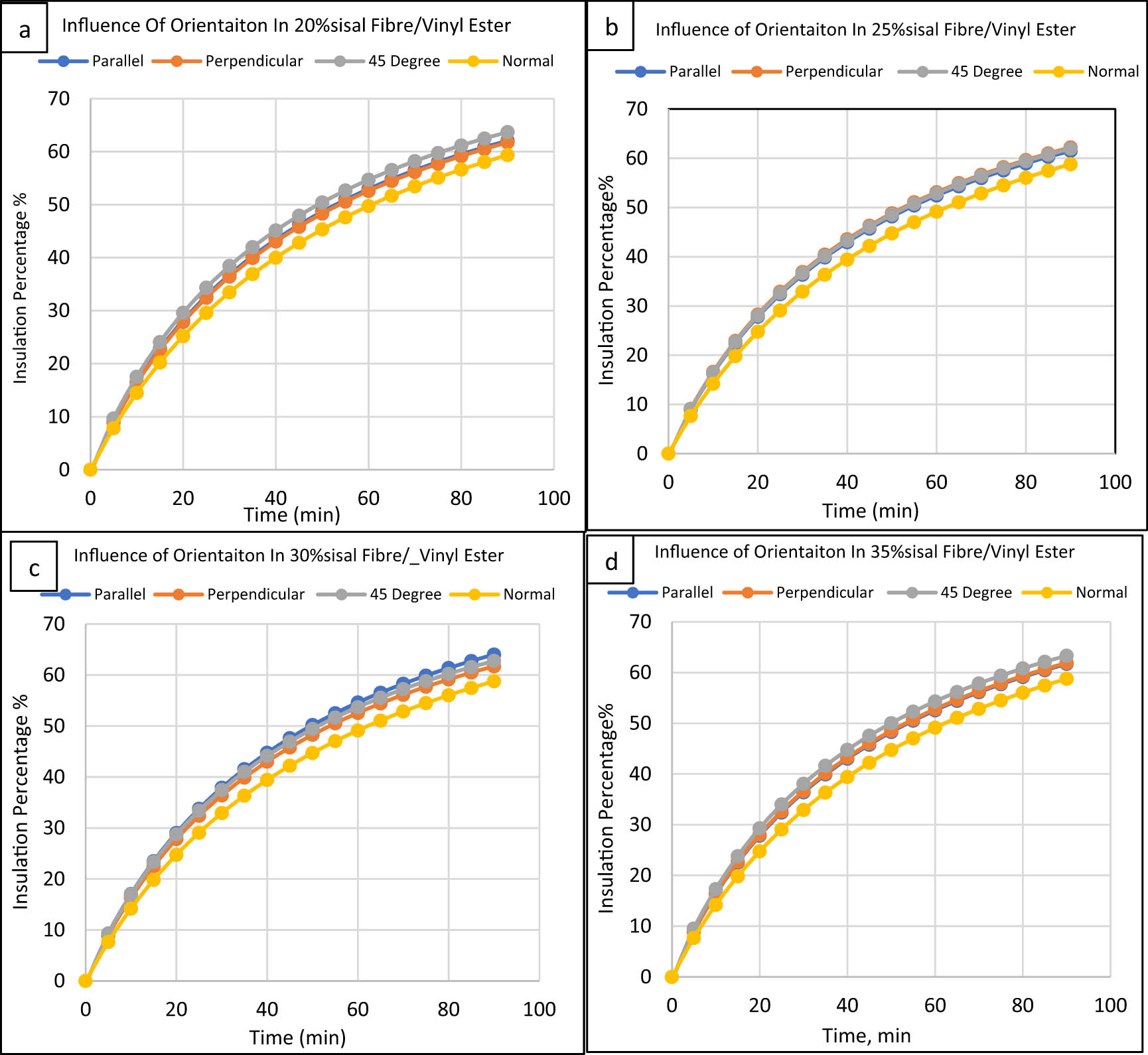
Orientation effect on vinyl ester composites/sisal fibre: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

Figure 15 depicts how the glass fibre orientation affects the insulating characteristics of the vinyl ester-based composites at various loadings. The insulation capabilities of these composites were similar to the glass fibre–epoxy composites at all loadings. A recent study used glass and natural fibres (vetiver, basalt) to make hybrid composites based on the vinyl ester. ANSYS Workbench was used to analyse these composites for thermal loadings that could occur during the machining process. Both kinds of fibres had similar results, and the vinyl ester’s thermal conductivity was significantly reduced. Modelling findings showed that the natural fibre-based hybrid composites had lower heat flux during machining than the glass fibre-based hybrid composites [53].

Figure 15

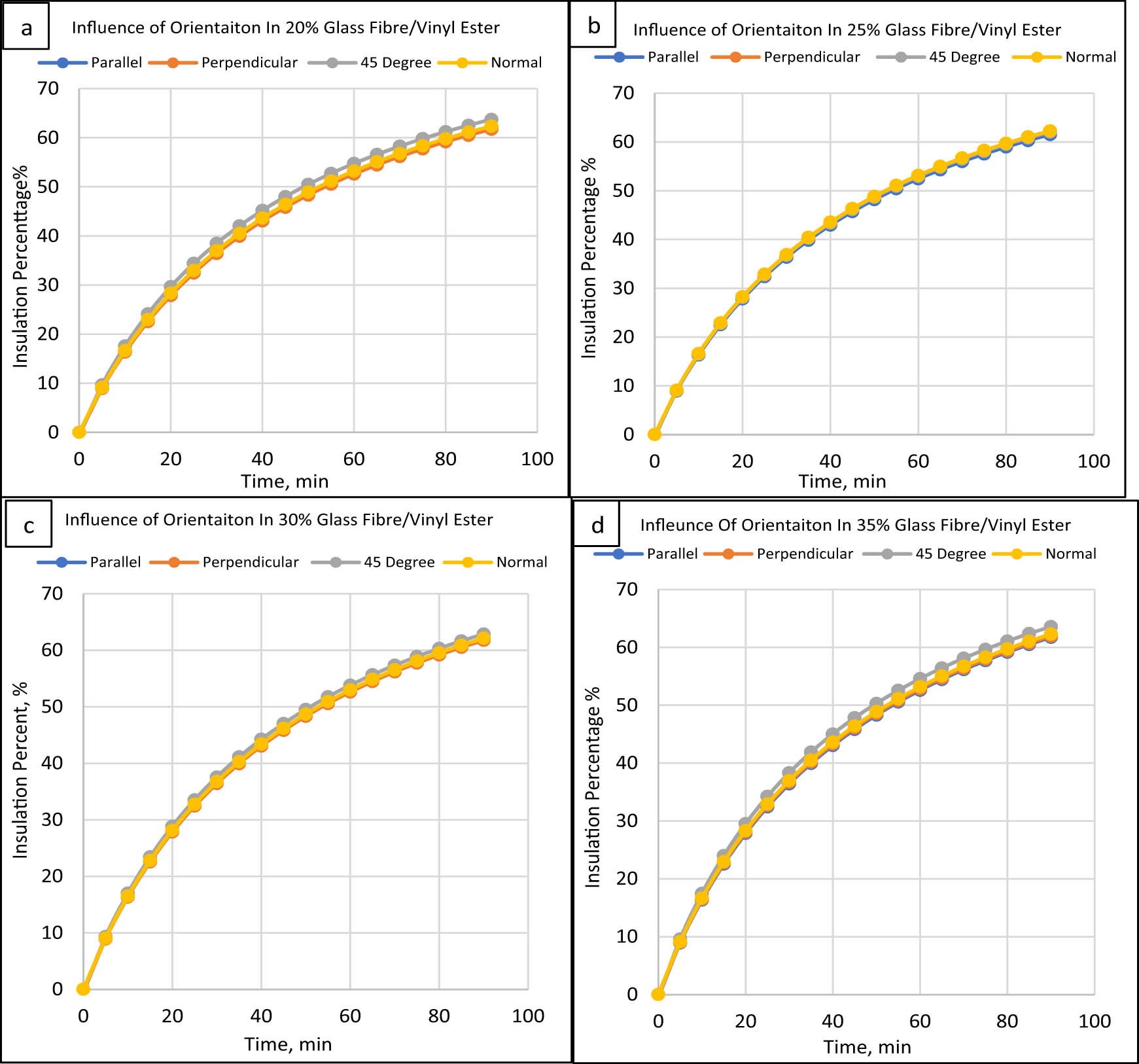
Orientation effect on vinyl ester composites/glass fibre: (a) 20%, (b) 25%, (c) 30%, and (d) 35%.

3.4 Effect of fibre orientation

Figures 16 and 17 show the effect of sisal and glass fibre orientation (45°) on the insulating properties of resins with a 35% fibre loading. The results show that sisal fibres provide all three resins with insulating properties. However, all three types of composites (sisal with three resins) exhibit the same insulating characteristics across the entire time spectrum. A closer look at the graph revealed that sisal fibre provides slightly higher insulation capability with epoxy, compared to polyester resin and vinyl ester, by 0.078 and 0.05%, respectively. With glass fibres–epoxy, similar findings were obtained under the same conditions, and they showed 1.7 and 0.03% higher insulation percentages than vinyl ester and polyester, respectively.

Figure 16

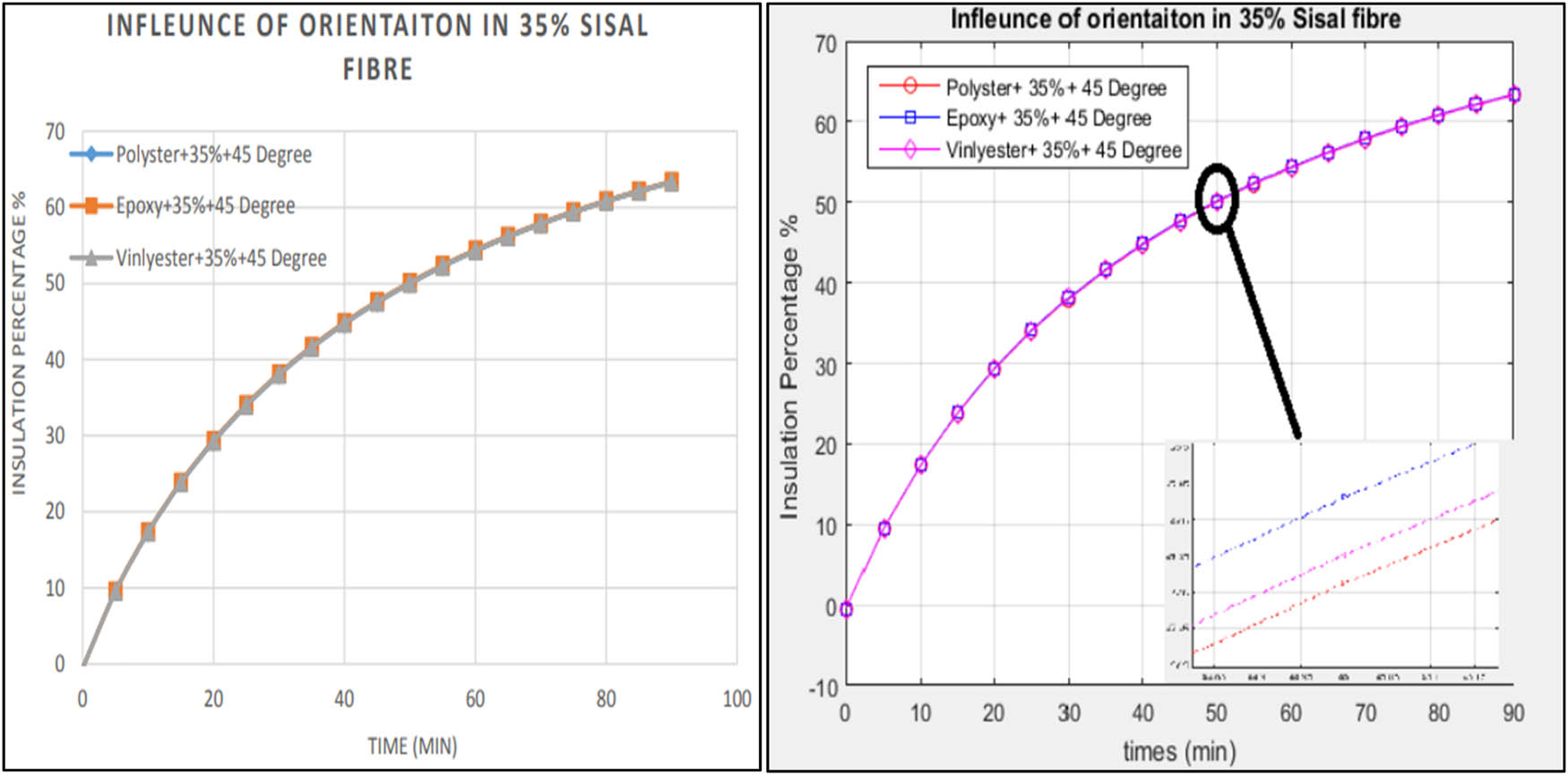
Sisal fibre (loading of 35%) orientation effects on resin insulating characteristics by drawing the plot in MATLAB to represent the variations.

Figure 17

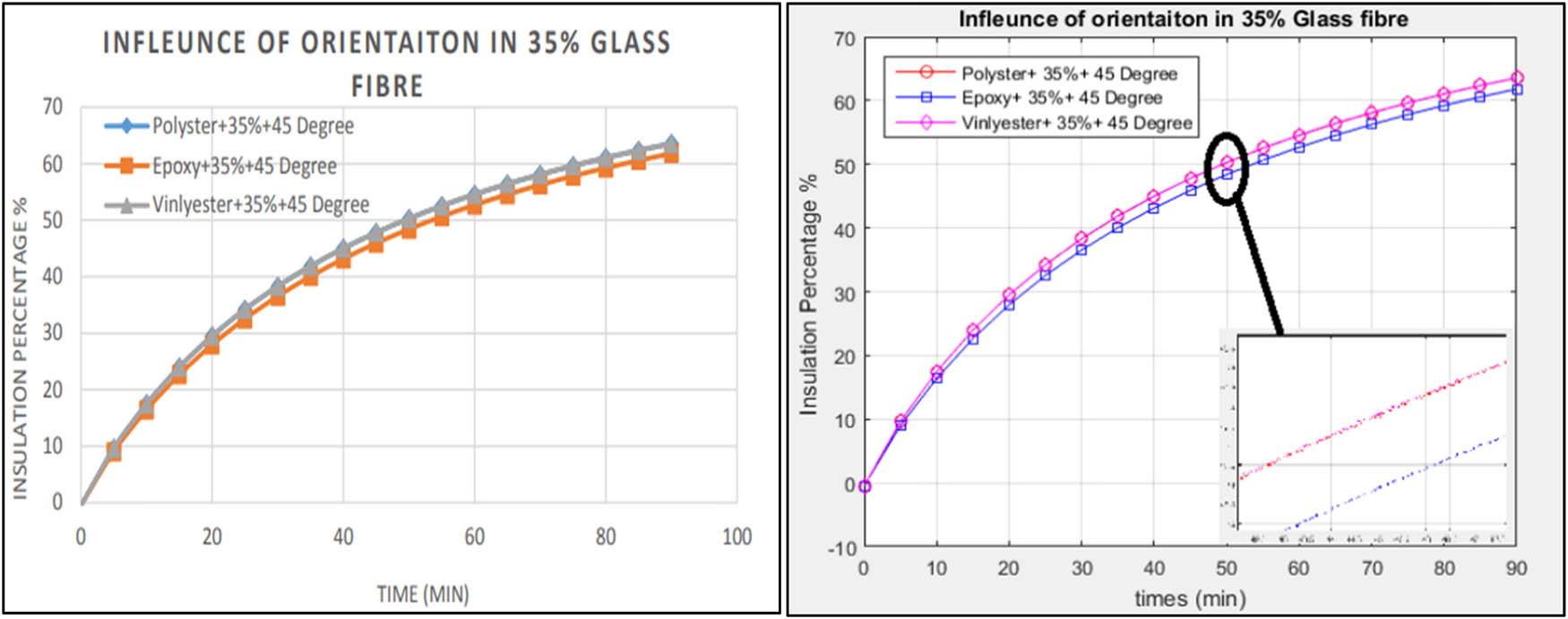
Draw the plot in MATLAB to represent the variations in glass fibre (loading of 35%) orientation effects on resin insulating characteristics.

The fibre orientation effect on the insulation percentage of the three different resins is seen in Figure 18. Unlike epoxy, vinyl ester and glass fibre-reinforced polyester composites demonstrated a maximum insulating percentage of about 63.5% (comparatively more than the sisal fibre). In contrast, such composites reached a maximum insulating percentage of approximately 63% when sisal fibres were included. Consequently, there was little to no difference between the two groups of composites. In contrast to sisal and glass fibre-based composites, which perform well as insulators, the epoxy resin obtained a significant performance disparity. These observations align with the findings of other research works [54,55]. Previous research has shown that polyester composites have better thermal insulation properties than pure polymer resin or glass fibres [52,53]. This may be attributed to the interaction between the fibre and resin. Sisal and other natural fibres often adhere to polymer resin less effectively than glass fibres [56,57,58]. This weak interaction between the two phases may explain the poor insulating capability of vinyl ester/sisal–polyester composites. Future research is needed to investigate the properties of natural fibres in more detail.

Figure 18

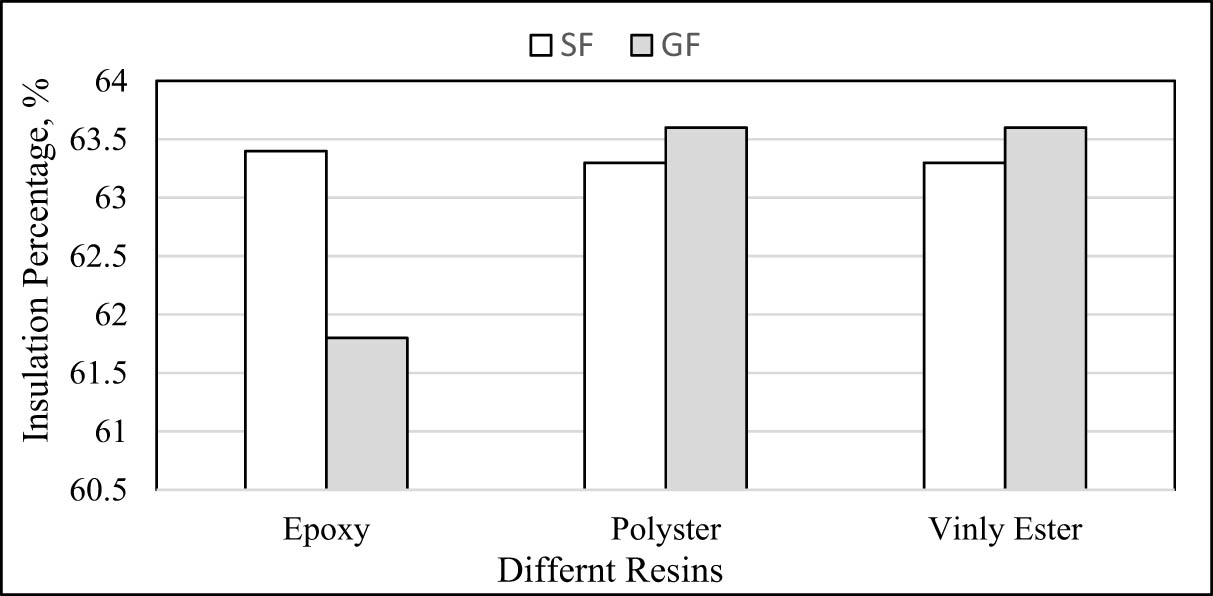
Effect of sisal and glass fibre (loading of 35%) orientation on insulating characteristics of three resins.

4 Conclusion

This research study successfully demonstrated the capability of ANSYS software in testing and validating theoretical models derived from our previous experimental works. By employing this approach, we compared the thermal efficiency of various natural and synthetic fibres. Our objective was to quantify the heat conductivity of each sample and test the mathematical model that correlates fibre orientation and volume with heat conductivity. The results indicated that composites containing more natural fibres exhibited superior insulation properties. In contrast, composites with a higher volume fraction of synthetic fibres displayed poorer insulation characteristics. Remarkably, we achieved the fabrication of composites with significantly enhanced insulation efficiency by orienting both natural and synthetic fibres at a 45° angle.

Furthermore, the epoxy-based composites demonstrated superior insulation performance compared to polyester and vinyl ester. This study showcased various thermal capabilities in composites comprising natural and synthetic fibres. These findings can contribute to bio-composite development via numerical analyses. This study introduces significant view that could help in designing better thermal insulation materials for buildings, aircraft, and spacecraft. Additionally, it can help in designing better thermal insulation materials for high-temperature industrial processes.

Acknowledgments

The authors appreciate the support from the Faculty of Health, Engineering and Surveying, University Southern Queensland, Australia

Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Nandhakumar, S., K. M. Kanna, A. M. Riyas, and M. N. Bharath. Experimental investigations on natural fiber reinforced composites. Materials Today: Proceedings, Vol. 37, 2021, pp. 2905–2908.Search in Google Scholar

[2] Ramakrishna, G., K. Purushothaman, E. Sivakumar, and M. Sreenivasan. An analysis on natural fiber composite materials. Materials Today: Proceedings, Vol. 45, 2021, pp. 6794–6799.Search in Google Scholar

[3] Dress, G. A., M. Woldemariam, and D. Redda. Influence of fiber orientation on impact resistance behavior of woven sisal fiber reinforced polyester composite. Advances in Materials Science and Engineering, Vol. 2021, 2021, pp. 1–11.Search in Google Scholar

[4] Gupta, U. S., A. Dharkar, M. Dhamarikar, A. Choudhary, D. Wasnik, P. Chouhan, et al. Study on the effects of fiber orientation on the mechanical properties of natural fiber reinforced epoxy composite by finite element method. Materials Today: Proceedings, Vol. 45, 2021, pp. 7885–7893.Search in Google Scholar

[5] Yousif, B., A. Shalwan, C. W. Chin, and K. Ming. Flexural properties of treated and untreated kenaf/epoxy composites. Materials & Design, Vol. 40, 2012, pp. 378–385.Search in Google Scholar

[6] Ahmadi, M., R. Ansari, and M. K. Hassanzadeh-Aghdam. Finite element analysis of thermal conductivities of unidirectional multiphase composites. Composite Interfaces, Vol. 26, 2019, pp. 1035–1055.Search in Google Scholar

[7] Shalwan, A., T. Alsaeed, and B. Yousif. Machinability of polymeric composites and future reinforcements—A review. Journal of Materials Science and Chemical Engineering, Vol. 10, No. 5, 2022, pp. 40–72.Search in Google Scholar

[8] Alajmi, R., B. F. Yousif, F. M. Alajmi, and A. Shalwan. Study the possibility of using sisal fibres in building applications. Advanced Materials Letters, Vol. 10, No. 3, 2019, pp. 222–229.Search in Google Scholar

[9] Liu, K., H. Takagi, R. Osugi, and Z. Yang. Effect of physicochemical structure of natural fiber on transverse thermal conductivity of unidirectional abaca/bamboo fiber composites. Composites Part A: Applied Science and Manufacturing, Vol. 43, No. 8, 2012, pp. 1234–1241.Search in Google Scholar

[10] Zheng, G.-Y. Numerical investigation of characteristic of anisotropic thermal conductivity of natural fiber bundle with numbered lumens. Mathematical Problems in Engineering, Vol. 2014, 2014, pp. 1–8.Search in Google Scholar

[11] Rahman, F., A. Eiamin, M. R. Hasan, S. Islam, M. M. Haque, M. A. Gafur, et al. Effect of fiber loading and orientation on mechanical and thermal properties of jute-polyester laminated composite. Journal of Natural Fibers, Vol. 19, No. 5, 2022, pp. 1741–1755.Search in Google Scholar

[12] Ramanaiah, K., A. R. Prasad, and K. H. C. Reddy. Mechanical, thermophysical and fire properties of sansevieria fiber-reinforced polyester composites. Materials & Design, Vol. 49, 2013, pp. 986–991.Search in Google Scholar

[13] Braga, R. and P. Magalhaes Jr. Analysis of the mechanical and thermal properties of jute and glass fiber as reinforcement epoxy hybrid composites. Materials science and Engineering: C, Vol. 56, 2015, pp. 269–273.Search in Google Scholar

[14] Mohanavel, V., T. Raja, A. Yadav, M. Ravichandran, and J. Winczek. Evaluation of mechanical and thermal properties of jute and ramie reinforced epoxy-based hybrid composites. Journal of Natural Fibers, Vol. 19, No. 14, 2022, pp. 8022–8032.Search in Google Scholar

[15] Stelea, L., I. Filip, G. Lisa, M. Ichim, M. Drobotă, C. Sava, et al. Characterisation of hemp fibres reinforced composites using thermoplastic polymers as matrices. Polymers, Vol. 14, No. 3, 2022, id. 481.Search in Google Scholar

[16] Vijaya Ramnath, B., S. Rajesh, C. Elanchezhian, and G. Pon Senthil Kumar. Determination of impact and hardness properties of neem-kenaf fiber reinforced polymer composites. In Advances in Materials and Manufacturing Engineering: Select Proceedings of ICMME, 2020, Springer, 2019, pp. 293–302.Search in Google Scholar

[17] Biswas, S., S. Shahinur, M. Hasan, and Q. Ahsan. Physical, mechanical and thermal properties of jute and bamboo fiber reinforced unidirectional epoxy composites. Procedia Engineering, Vol. 105, 2015, pp. 933–939.Search in Google Scholar

[18] Kenned, J. J., K. Sankaranarayanasamy, J. S. Binoj, and S. K. Chelliah. Thermo-mechanical and morphological characterization of needle punched non-woven banana fiber reinforced polymer composites. Composites Science and Technology, Vol. 185, 2020, id. 107890.Search in Google Scholar

[19] Devireddy, S. B. R. and S. Biswas. Physical and thermal properties of unidirectional banana–jute hybrid fiber-reinforced epoxy composites. Journal of Reinforced Plastics and Composites, Vol. 35, No. 15, 2016, pp. 1157–1172.Search in Google Scholar

[20] Rawi, S. M., S. A. Wahid, and N. Awang. A review on fiber orientation of natural fiber reinforced polymer composite. Proceeding of the Malaysia TVET on Research via Exposition 2017, Dungun, Terengganu, 2017, pp. 287–297.Search in Google Scholar

[21] Kumaresan, M., S. Sathish, and N. Karthi. Effect of fiber orientation on mechanical properties of sisal fiber reinforced epoxy composites. Journal of Applied Science and Engineering, Vol. 18, No. 3, 2015, pp. 289–294.Search in Google Scholar

[22] Alajmi, A., R. Abousnina, A. Shalwan, S. Alajmi, G. Alipour, T. Tafsirojjaman, et al. An experimental and numerical investigation into the durability of fibre/polymer composites with synthetic and natural fibres. Polymers, Vol. 14, No. 10, 2022, id. 2024.Search in Google Scholar

[23] Chen, Y., L. Xin, Y. Liu, Z. Guo, L. Dong, and Z. Zhong. A viscoelastic model for particle-reinforced composites in finite deformations. Applied Mathematical Modelling, Vol. 72, 2019, pp. 499–512.Search in Google Scholar

[24] Gao, W., Z. Qin, and F. Chu. Wave propagation in functionally graded porous plates reinforced with graphene platelets. Aerospace Science and Technology, Vol. 102, 2020, id. 105860.Search in Google Scholar

[25] Li, C., P. Li, B. Zhong, and B. Wen. Geometrically nonlinear vibration of laminated composite cylindrical thin shells with non-continuous elastic boundary conditions. Nonlinear Dynamics, Vol. 95, 2019, pp. 1903–1921.Search in Google Scholar

[26] Zhang, Y. and D. Shi. Vibration analysis of laminated composite coupled double cylindrical shell-annular-rectangular plate system. Composite Structures, Vol. 281, 2022, id. 115020.Search in Google Scholar

[27] Meyghani, B., and M. Awang. Developing a finite element model for thermal analysis of friction stir welding by calculating temperature dependent friction coefficient. In 2nd International Conference on Mechanical, Manufacturing and Process Plant Engineering Lecture Notes in Mechanical Engineering, Springer, Singapore, 2020.Search in Google Scholar

[28] Zhao, X., W. Tu, Q. Chen, and G. Wang. Progressive modeling of transverse thermal conductivity of unidirectional natural fiber composites. International Journal of Thermal Sciences, Vol. 162, 2021, id. 106782.Search in Google Scholar

[29] Hao, X., H. Zhou, B. Mu, L. Chen, Q. Guo, X. Yi, et al. Effects of fiber geometry and orientation distribution on the anisotropy of mechanical properties, creep behavior, and thermal expansion of natural fiber/HDPE composites. Composites Part B: Engineering, Vol. 185, 2020, id. 107778.Search in Google Scholar

[30] Shokrieh, M. and A. Ghanei-Mohammadi. Finite element modeling of residual thermal stresses in fiber-reinforced composites using different representative volume elements. In Proceedings of the World Congress on Engineering, 2010.Search in Google Scholar

[31] Wang, H. and Q. Qin. Special fiber elements for thermal analysis of fiber‐reinforced composites. Engineering Computations, Vol. 28, No. 8, 2011, pp. 1079–1097.Search in Google Scholar

[32] Javanbakht, Z., W. Hall, A. S. Virk, J. Summerscales, and A. Öchsner. Finite elemen analysis of natural fiber composites using a self-updating model. Journal of Composite Materials, Vol. 54, No. 23, 2020, pp. 3275–3286.Search in Google Scholar

[33] Xiong, X., S. Z. Shen, L. Hua, J. Z. Liu, X. Li, X. Wan, et al. Finite element models of natural fibers and their composites: A review. Journal of Reinforced Plastics and Composites, Vol. 37, No. 9, 2018, pp. 617–635.Search in Google Scholar

[34] Wang, B., S. Zhong, T. L. Lee, K. S. Fancey, and J. Mi. Non-destructive testing and evaluation of composite materials/structures: A state-of-the-art review. Advances in Mechanical Engineering, Vol. 12, No. 4, 2020, id. 1687814020913761.Search in Google Scholar

[35] Alhijazi, M., Q. Zeeshan, Z. Qin, B. Safaei, and M. Asmael. Finite element analysis of natural fibers composites: A review. Nanotechnology Reviews, Vol. 9, No. 1, 2020, pp. 853–875.Search in Google Scholar

[36] Mulenga, T. K., A. U. Ude, and C. Vivekanandhan. Techniques for modelling and optimizing the mechanical properties of natural fiber composites: A review. Fibers, Vol. 9, No. 1, 2021, id. 6.Search in Google Scholar

[37] Dixit, S. and S. Padhee. Finite element analysis of fiber reinforced hybrid composites. Materials Today: Proceedings, Vol. 18, 2019, pp. 3340–3347.Search in Google Scholar

[38] Sharma, A., M. Choudhary, P. Agarwal, T. K. Patnaik, S. K. Biswas, and A. Patnaik. Experimental and numerical investigation of thermal conductivity of marble dust filled needle punched nonwoven jute-epoxy hybrid composite. Materials Today: Proceedings, Vol. 38, 2021, pp. 248–252.Search in Google Scholar

[39] Parashar, S. and V. Chawla. Kenaf-Coir based hybrid nano-composite: an analytical and representative volume element analysis. Engineering Solid Mechanics, Vol. 11, No. 1, 2023, pp. 103–118.Search in Google Scholar

[40] Shalwan, A., A. Alajmi, and B. Yousif. Theoretical study of the effect of fibre porosity on the heat conductivity of reinforced gypsum composite material. Polymers, Vol. 14, No. 19, 2022, id. 3973.Search in Google Scholar

[41] Subramani, T. and S. Vishnupriya. Finite element analysis of a natural fiber (Maize) composite beam. International Journal of Modern Engineering Research, Vol. 4, No. 6, 2014, pp. 1–7.Search in Google Scholar

[42] Dewangan, K. K. and A. Satapathy. A numerical study on enhancement of thermal insulation capability of polyester by reinforcement of micro-sized rice husk particles, In International Conference on Advancements in Polymeric Materials, Ahmedabad, 2012.Search in Google Scholar

[43] Blomberg, T. R. Heat conduction in two and three dimensions: Computer modelling of building physics applications, Doctoral Thesis (monograph), Division of Building Physics, Byggnadsfysik LTH, Lunds Tekniska Högskola, 1996.Search in Google Scholar

[44] Taler, D. Numerical modelling and experimental testing of heat exchangers, Springer International Publishing, Cham, Switzerland, Vol. 161, 2019.Search in Google Scholar

[45] Miidla, P. E. Numerical modelling, IntechOpen, Rijeka, 2012.Search in Google Scholar

[46] Kalaprasad, G., P. Pradeep, G. Mathew, C. Pavithran, and S. Thomas. Thermal conductivity and thermal diffusivity analyses of low-density polyethylene composites reinforced with sisal, glass and intimately mixed sisal/glass fibres. Composites Science and Technology, Vol. 60, No. 16, 2000, pp. 2967–2977.Search in Google Scholar

[47] Gibson, R. F. Principles of composite material mechanics (2nd ed.), CRC Press, Boca Raton, 2007.Search in Google Scholar

[48] Lomov, S. V., C. Breite, D. Carrella-Payan, V. Carvelli, N. Ersoy, M. Gigliotti M, et al. Multi-instrument multi-scale experimental damage mechanics for fibre reinforced composites. In IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2018.Search in Google Scholar

[49] Cao, X., J. Liu, X. Cao, Q. Li, E. Hu, and F. Fan. Study of the thermal insulation properties of the glass fiber board used for interior building envelope. Energy and Buildings, Vol. 107, 2015, pp. 49–58.Search in Google Scholar

[50] Mounika, M., P. Anusha, K. Ramanaiah, A. Ratnaprasad, K. H. C. Reddy. Thermal properties of Bamboo fiber reinforced polyester composite. IJERST-International Journal of Engineering Research and Science & Technology, Vol. 3, No. 4, 2014, pp. 87–93.Search in Google Scholar

[51] Patnaik, A., P. Kumar, S. Biswas, and M. Kumar. Investigations on micro-mechanical and thermal characteristics of glass fiber reinforced epoxy based binary composite structure using finite element method. Computational Materials Science, Vol. 62, 2012, pp. 142–151.Search in Google Scholar

[52] Idicula, M., A. Boudenne, L. Umadevi, L. Ibos, Y. Candau, and S. Thomas. Thermophysical properties of natural fibre reinforced polyester composites. Composites science and technology, Vol. 66, No. 15, 2006, pp. 2719–2725.Search in Google Scholar

[53] Rathinavel, S., G. Vigneshkumar, and U. Sathishkumar. Optimization of thermal analysis of hybrid fibre composite on drilling process. International Journal of Science Technology & Engineering, Vol. 2, No. 5, 2015, pp. 2–5.Search in Google Scholar

[54] Devireddy, S. B. R. and S. Biswas. Physical and mechanical behavior of unidirectional banana/jute fiber reinforced epoxy based hybrid composites. Polymer Composites, Vol. 38, No. 7, 2017, pp. 1396–1403.Search in Google Scholar

[55] Sahu, Y. K. Study on the effective thermal conductivity of fiber reinforced epoxy composites, National Institute of Technology, Odisha, India, 2014.Search in Google Scholar

[56] Watt, A., A. Goodwin, and A. Mouritz. Thermal degradation of the mode I interlaminar fracture properties of stitched glass fibre/vinyl ester composites. Journal of Materials Science, Vol. 33, 1998, pp. 2629–2638.Search in Google Scholar

[57] Li, Y., Y.-W. Mai, and L. Ye. Sisal fibre and its composites: A review of recent developments. Composites Science and Technology, Vol. 60, No. 11, 2000, pp. 2037–2055.Search in Google Scholar

[58] Njuguna, J., P. Wambua, K. Pielichowski, and K. Kayvantash. Natural fibre-reinforced polymer composites and nanocomposites for automotive applications. In: Cellulose Fibers: Bio-and Nano-Polymer Composites: Green Chemistry and Technology, Springer, Berlin, Heidelberg, 2011, pp. 661–700.Search in Google Scholar

Received: 2023-04-18

Revised: 2024-01-09

Accepted: 2024-02-22

Published Online: 2024-04-02

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/rams-2023-0190

Keywords for this article

natural fibres; sisal; synthetic fibres; glass; composites; thermal properties; orientations; volume; ANSYS

Creative Commons

BY 4.0