Home A magnetohydrodynamic flow of a water-based hybrid nanofluid past a convectively heated rotating disk surface: A passive control of nanoparticles
Article Open Access

A magnetohydrodynamic flow of a water-based hybrid nanofluid past a convectively heated rotating disk surface: A passive control of nanoparticles

  • Humaira Yasmin EMAIL logo , Laila A. AL-Essa , Ali M. Mahnashi , Waleed Hamali and Anwar Saeed EMAIL logo
Published/Copyright: October 7, 2024
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 63 Issue 1

Abstract

One of the basic fluid mechanics problems of fluid flows over a revolving disk has both theoretical and real-world applications. The flow over a rotating disk has been the subject of numerous theoretical studies because it has many real-world applications in areas like rotating machinery, medical equipment, electronic devices, and computer storage. It is also crucial for engineering processes. Therefore, this article deals with a time-independent water-based hybrid nanofluid flow containing copper oxide and silver nanoparticles past a spinning disk. The Newtonian flow is taken into consideration in this analysis. The influence of magnetic field, thermophoresis, nonlinear thermal radiation, Brownian motion, and activation energy has been considered. The present analysis is modeled in a partial differential equation form and is then converted to ordinary differential equations using appropriate variables. A numerical solution using the bvp4c technique is accomplished using MATLAB software. The current results are matched with the previous literature and established a close relationship with previous studies. The purpose of this investigation is to numerically investigate the time-independent hybrid nanofluid flow comprising copper oxide and silver nanoparticles over a rotating disk surface. The results show that the increased magnetic parameters increase the friction force at the surface, which decreases the radial and azimuthal velocity distribution. At the sheet surface, the radial velocity of the hybrid nanofluid shows dominant performance compared to the nanofluid. On the other hand, the magnetic factor has dominant behavior on the azimuthal velocity component of the nanofluid flow compared to the hybrid nanofluid flow. The higher volume fraction and magnetic factor enhance the skin friction at the disk surface. Furthermore, greater surface drag is found for the hybrid nanofluid flow. The higher solid volume fraction, temperature ratio, and Biot number enhance the rate of heat transmission. Also, a higher rate of heat transmission is observed for the hybrid nanofluid flow.

Keywords: MHD; hybrid nanofluid; nonlinear thermal radiation; activation energy; heat source

Nomenclature

r, ψ, z

coordinate system

u, w, v

velocity components

Ω

angular velocity

B 0

strength of the magnetic field

T f ,T w ,T ∞

reference, surface, and ambient temperatures

C f, C w, C ∞

reference, surface, and ambient concentrations

δ

exponential index

p

pressure

μ

dynamic viscosity

σ, k

electrical and thermal conductivities

C p

specific heat

Q

coefficient of heat source

ν

kinematic viscosity

D T

thermophoretic coefficient

D B

Brownian diffusion coefficient

k r

chemical reaction coefficient

M

magnetic factor

Pr

Prandtl number

ω

temperature difference factor

Q e

exponential heat source factor

Bi

thermal Biot number

Rd

radiation factor

Nt

thermophoresis factor

Nb

Brownian motion factor

Sc

Schmidt number

E

activation energy factor

K r

chemical reaction factor

θ w

temperature ratio factor

F(η)

radial velocity component

G(η)

azimuthal velocity component

Subscripts

f, nf, hnf

base fluid, nanofluid, and hybrid nanofluid

s 1

CuO nanoparticle

s 2

Ag nanoparticle

1 Introduction

In the past, the cooling of various devices in industry and different engineering applications was challenging. Pure fluids like water and engine oil have lower thermal flow characteristics. Therefore, there was a need to enhance such flow characteristics of pure fluids. Scientists and researchers have performed various experiments to attain this goal and have modeled various approaches in this regard. The mixture of tiny-sized particles with pure fluid is one such approach, as introduced by Choi and Eastman [1]. Afterward, a new door opened in the literature to enhance the thermal characteristics of pure fluids in a variety of ways. Shahzad et al. [2] examined the convergence of second order for EMHD nanofluid on a rotating disk with the Hall effect and concluded that the volume fraction has a tremendous impact on fluid motion and heat transportation. Shamshuddin et al. [3] deliberated on dissipative and radiation mechanisms for nanofluid flow upon a disk where the flow was encountered by the Hall current. Pasha et al. [4] investigated statistically the viscous nanofluid flow on an elongating sheet and uncovered that fluid velocity deteriorated and heat flow improved for growth at nanoparticle concentration. Shah et al. [5] used nanoparticles of gold in blood to optimize its thermal flow characteristics subject to thermally radiative effects between two plates. Asghar and Ying [6] studied 2-D radiative and mixed convective nanofluid flow on an exponentially contracting surface with impacts of partial slip constraints and observed that an upsurge in radiation factor supported the growth in thermal characteristics. Khan et al. [7] debated the nanofluid flow on a heated moving needle using chemically reactive and viscous dissipative effects. Haider et al. [8] discussed computationally a comparative work for a blood-mathematical model with impacts of magnetic field and nanoparticles. Akhtar et al. [9] carried out a dynamical analysis with computational evaluation for endoscopy of the left artery and simulated that flow arriving at the slender section of stenosis attained a maximum velocity. Naveed Khan et al. [10] studied stagnant point flow for the nanofluid of second grade on an exponentially elongating surface and established that thermal distribution augmented for higher Brownian and thermophoresis factors. Ahsan et al. [11] discussed bio-convective Darcy flow on a curved elongating surface with impacts of heterogeneous and homogenous reactions and observed that the velocity of fluid declined with growth in magnetic and porosity factors. Kanwal et al. [12] studied the dynamics of nanofluid flow with nonlinear and linear mixed convective thermal radiations and activated energy on a gyrating disk.

Recently, it has been proved that the thermal conductivities of pure fluid can be upgraded more by collaborating two types of nanoparticles in these fluids, which are known as hybrid nanofluids. Waseem et al. [13] scrutinized the mixed convective flow of hybrid nanofluid with the combined impression of the magnetic field, homogenous and heterogeneous reactions. Hussain et al. [14] used a sintered copper wick pipe to discuss experimentally the thermal performance of hybrid nanoparticles. Guedri et al. [15] discussed nanofluid flow over a nonlinear stretched sheet using various effects of the flow of the fluid. Zhang et al. [16] examined the magnetohydrodynamics (MHD) nanofluid flow on an elastic surface by mixing nanoparticles of tantalum and nickel and proved that the velocity of fluid increased with growth in tantalum nanoparticles and Darcy number while magnetic effects opposed the fluid motion. Ojjela [17] investigated numerically the heat transference of nanofluid and depicted that the thermal transportation rate increased with alumina nanoparticles compared with silica nanoparticles. Gumber et al. [18] debated the thermal characteristics of the hybrid nanoparticles past a plate and concluded that the growth in suction had a positive impact on the fluid velocity. Sriharan et al. [19] used the hybrid nanofluid flow through a tube subject to the heat source and concluded that the Nusselt number improved by 28.4% for the Al2O3/CuO−DIW hybrid nanofluid. Ullah et al. [20] examined thermal and mass flow characteristics for magnetized nanofluid flow on a cone with convective conditions at the boundary. Zawawi et al. [21] used a hybrid nano-lubricant flow with different composition ratios of nanoparticles to augment the thermal behavior of the air-conditioned system. Asghar et al. [22] inspected magnetized 3-D gyratory nanofluid flow on contracting and expanding surfaces and noticed that thermal panels augmented with growth in Eckert number and radiation factor. Babar et al. [23] inspected the effectiveness of H2O-based ferric oxide−silica hybrid nanofluid flow to investigate the airfoil-designed pin-fin with a heat sink. They deduced that the Nusselt number enhanced with a thermal power of 75 W. Akbar et al. [24] studied magnetized thermal transportation for a dual-phase nanofluid flow model using the impacts of thermal radiations and ANN approach for the solution and noticed that thermal flow augmented with an increase in the radiation factor. Ullah et al. [25] evaluated analytically the 3-D problem of a condensed film on a gyrating disk. Raja et al. [26] studied nanofluid flow on a gyratory disk with impacts of particle slip and magnetic field effects and matched the efficiency of their designed LMB-NN methodology through a comparative study and performance by utilizing error histograms, regression, and correlation. Ullah et al. [27] discussed computationally the magnetized squeezed flow for the Jeffery fluid in a gyrating frame with the mass and heat flux model suggested by Cattaneo-Christov.

MHD, a discipline at the intersection of fluid dynamics and electromagnetism, investigates the intricate interplay between magnetic fields and electrically conductive fluids [28]. In the specific perspective of heat transfer for fluid flow on a disk, MHD manifests profound impacts on the thermal behavior. As a magnetic field permeates the electrically conductive fluid, it induces electric currents, creating a dynamic coupling between the magnetic field and the fluid motion. This interaction significantly alters the flow patterns around the disk, influencing the velocity profiles and modifying the thickness of the boundary layer. MHD normally enhances heat transfer, contingent upon factors such as the orientation and strength of the magnetic field, as well as fluid properties [29,30]. In instances where MHD promotes enhanced heat transfer, it does so by fostering better mixing and circulation of the fluid near the disk’s surface [31]. Additionally, the magnetic Reynolds number, indicative of the dominance of magnetic effects, plays a crucial role in determining the overall impact on heat transfer. The complex relationship of these factors is further compounded by the potential development of instabilities and turbulence within the fluid flow induced by MHD, thereby influencing the stability and proficiency of heat transfer phenomena [32]. Solving the complex system of coupled fluid flow problem, heat transfer, and electromagnetic fields is fundamental in comprehending the multifaceted implications of MHD on heat transfer. Asghar et al. [33] evaluated double solutions for rotary convective 3-D nanofluid flow on contracting and expanding surfaces. Rasool et al. [34] examined time-based double solutions for hybrid nanofluid flow subject to slip and magnetic constraints and found that flow is retarded in the first solution with an increase in nanoparticles’ volumetric fraction of copper. Lund et al. [35] discussed Casson magnetized nanofluid flow on a moveable and permeable surface subject to Joule heating and thermally radiative effects.

Nonlinear thermal radiation is the process of heat transfer through electromagnetic waves emitted by a surface that displays a non-linear association between the temperature and radiative heat flux. In traditional linear thermal radiation, the Stefan−Boltzmann law is employed to describe the radiant heat exchange, assuming a linear proportionality between the temperature and emitted radiation. However, in nonlinear thermal radiation, the radiative properties of the material, such as emissivity and absorptivity, are temperature-dependent in a non-linear manner [36]. This nonlinearity introduces complexities in predicting and analyzing heat transfer phenomena. The impacts of nonlinear thermal radiation on heat transfer are profound, influencing several key aspects. First, it alters the radiative heat transfer rates between surfaces, deviating from the simpler linear relationships. This can lead to significant variations in temperature distributions and thermal gradients within a system. Second, nonlinear thermal radiation complicates the design and optimization of heat exchange systems, as traditional linear models may not accurately capture the intricate temperature-dependent radiative properties of the materials. In applications such as high-temperature processes, combustion, or space exploration, where radiative heat transfer plays a critical role, accounting for nonlinear thermal radiation becomes essential for precise and reliable thermal analysis [37]. Additionally, in scenarios involving materials with temperature-sensitive optical properties, nonlinearity can impact the overall energy balance and thermal performance of the system. Accurate modeling of nonlinear thermal radiation is crucial for advancing technologies in fields, such as aerospace, materials science, and energy systems, where a nuanced understanding of heat transfer phenomena is vital for optimizing efficiency, durability, and safety. Shaw et al. [38] examined the features of linear and nonlinear radiations on MHD liquid flow on a cylinder and scrutinized the thermal flow characteristics using the values of Prandtl number in the range 10−10 ≤ Pr ≤ 104.

An exponential heat source denotes a heat generation term in the energy equation, which is proportional to an exponential function of temperature. The exponential nature of the heat source implies that as the temperature increases, the heat generation rate diminishes exponentially [39]. The impact of an exponential heat source on the heat transfer phenomena is significant, introducing nonlinearity and influencing temperature distributions within a system [40]. As the temperature increases, the heat generation decreases rapidly, potentially leading to complex spatial and temporal variations in the temperature field [41]. The impact of an exponential heat source is crucial in applications like electronics cooling, combustion processes, and materials processing, where accurate prediction of temperature profiles is essential for optimizing efficiency, preventing overheating, and ensuring the integrity of the system [42]. Modeling of exponential heat sources in heat transfer simulations is imperative for designing and engineering systems that effectively manage thermal loads and maintain desired temperature conditions in diverse technological contexts [43]. Haq et al. [44] explored the impact of exponential heating sources on second-grade MHD fluid flow subject to chemically reactive effects.

A lower quantity of energy, mandatory to start a reaction chemically, is called activation energy. Alqarni et al. [45] inspected the motivation of activated energy on a Casson fluid flow over a spinning disk. Rekha et al. [46] debated the activation energy influence on the motion of nanoparticles through wedge, cone, and plate and deduced that mass transportation augmented more slowly for the flow of fluid past a cone in comparison to flow on a wedge or plate. Abbasi et al. [47] scrutinized the fluid flow at the stagnant point of a horizontal cylinder subject to activation energy and perceived that with augmentation in the chemical reaction and temperature gradient factors, the mass diffusion declined. Ayub et al. [48] investigated the activation energy impact upon nanofluid flow on a cylindrical surface using inclined magnetic effects and deduced that an increase in the magnetic factor amplified the energy and weakened the velocity of the fluid flow (Table 1).

Table 1

Thermophysical features of the water nanofluid, copper oxide, and silver nanoparticles [55]

Base fluid and nanoparticles H2O CuO Ag
σ [Ω·m−1] 0.05 2.70 × 10−8 6.30 × 107
k [W·m−1·K−1] 0.613 76.5 429
C p [J·kg−1·K−1] 4,179 531.8 235
ρ [kg·m−3] 997.1 6,320 10,500
Pr 6.2 — —

One of the basic fluid mechanics problems of fluid flows over a revolving disk has both theoretical and real-world applications. The flow on a gyrating disk has remained the subject of numerous theoretical studies because it has many real-world applications in areas like rotating machinery, medical equipment, electronic devices, and computer storage. It is also crucial to engineering processes. In this attempt, we have considered the time-independent hybrid nanofluid flow over a rotating disk. Newtonian flow is taken into consideration in this analysis. The fluid flow is influenced by the magnetic field, exponential heat source, Brownian motion, chemical reaction, activation energy, thermophoresis, and nonlinear thermal radiation. By incorporating a number of complex phenomena into the modeling of hybrid nanofluid flow, this work improves the field and provides a more comprehensive knowledge of the dynamics at play. Nonlinear thermal radiation and exponential heat sources are included, which is a major improvement over earlier models that frequently omitted these features. We obtain high precision in our numerical solutions using the bvp4c technique to solve the ordinary differential equations (ODEs). This provides a solid foundation for further research into similar systems. The thorough validation procedure guarantees the validity of our results, significantly advancing the current state of fluid dynamics and heat transfer research. A mathematical model is presented in the partial differential equation form and is converted to ODEs using appropriate transformations in Section 2. The numerical solution of the existing model is obtained using the bvp4c technique in Section 3. The model validation is done in Section 4. The results of embedded factors on velocity profiles and detailed discussion are provided in Section 5, while the closing comments are listed in Section 6.

2 Formulation of the problem

Assume a time-independent water-based hybrid nanofluid containing copper oxide and silver nanoparticles on a gyrating disk with angular velocity Ω along the z-direction. The cylindrical coordinates system (r, ψ, z) along the u-,v-, and w-directions is chosen for the existing problem. In the normal direction of the fluid flow, a magnetic field of strength B 0 is employed. The fluid, surface, and ambient temperatures and concentrations are T f, C f, T w, C w, T ∞, and C ∞ such that T f > T w, C f > C w. A geometrical representation is displayed in Figure 1. Additionally, to understand the flow behavior, the following suppositions are made in this investigation:

  • The flow is Newtonian.

  • Impacts of the Hall current and induced magnetic field have been ignored.

  • The significance of nonlinear linear thermal radiation, Brownian motion, and thermophoresis are accounted for.

  • The flow is impacted by the chemical reaction with activation energy.

Figure 1 Geometry of flow problem.
Figure 1

Geometry of flow problem.

Thus, the main equations are defined as follows [49,50,51]:

(1) ∂ u ∂ r + ∂ w ∂ z + u r = 0 ,

(2) u ∂ u ∂ r − v 2 r + w ∂ u ∂ z = − 1 ρ hnf ∂ p ∂ r + μ hnf ρ hnf ∂ 2 u ∂ r 2 + 1 r ∂ u ∂ r − u r 2 + ∂ 2 u ∂ z 2 − σ hnf ρ hnf B 0 2 u ,

(3) u ∂ v ∂ r + w ∂ v ∂ z + u v r = μ hnf ρ hnf ∂ 2 v ∂ r 2 − v r 2 + 1 r ∂ v ∂ r + ∂ 2 v ∂ z 2 − σ hnf ρ hnf B 0 2 v ,

(4) w ∂ w ∂ z + u ∂ w ∂ r = − 1 ρ hnf ∂ p ∂ z + μ hnf ρ hnf ∂ 2 w ∂ r 2 + ∂ 2 w ∂ z 2 + 1 r ∂ w ∂ r ,

(5) u ∂ T ∂ r + w ∂ T ∂ z = k hnf ( ρ C p ) hnf ∂ 2 T ∂ r 2 + 1 r ∂ T ∂ r + ∂ 2 T ∂ z 2 + 1 ( ρ C p ) hnf 16 σ ⁎ T 2 3 k ⁎ T ∂ 2 T ∂ z 2 + 3 ∂ T ∂ z 2 + ( ρ C p ) np ( ρ C p ) hnf D B ∂ T ∂ r ∂ C ∂ r + ∂ T ∂ z ∂ C ∂ z + D T T ∞ ∂ T ∂ r 2 + ∂ T ∂ z 2 + Q ( ρ C p ) hnf ( T f − T ∞ ) exp − δ Ω ν f z ,

(6) u ∂ C ∂ r + w ∂ C ∂ z = D B ∂ 2 C ∂ z 2 + ∂ 2 C ∂ r 2 + 1 r ∂ C ∂ r + D T T ∞ ∂ 2 T ∂ z 2 + ∂ 2 T ∂ r 2 + 1 r ∂ T ∂ r − k r 2 ( C − C ∞ ) T T ∞ n exp − E a k b T .

The constraints at the boundary are [52]

(7) u = 0 , w = 0 , v = Ω r , − k hnf ∂ T ∂ z = h f ( T f − T ) , D T T ∞ ∂ T ∂ z + D B ∂ C ∂ z = 0 at z = 0 , u → 0 , T → T ∞ , v → 0 , C → C ∞ as z → ∞ .

The thermophysical features of the nanofluid/hybrid nanoparticles are expressed as follows [52,53,54]:

(8) μ = 1 ( 1 − χ ) 2.5 , ( ρ C p ) nf = ( ρ C p ) f ( 1 − χ ) + χ ( ρ C p ) s , ρ nf = χ ρ s + ρ f ( 1 − χ ) , σ nf = σ s + 2 σ f − 2 ( σ f − σ s ) χ σ s + 2 σ f + ( σ f − σ s ) χ σ f , k nf = k s − 2 ( k f − k s ) χ + 2 k f k s + ( k f − k s ) χ + 2 k f k f ,

(9) k hnf = χ 1 k s 1 + χ 2 k s 2 ( χ 2 + χ 1 ) + 2 k f + 2 ( χ 1 k s 1 + χ 2 k s 2 ) − 2 k f ( χ 2 + χ 1 ) χ 1 k s1 + χ 2 k s 2 ( χ 2 + χ 1 ) + 2 k f − 2 ( χ 1 k s 1 + χ 2 k s 2 ) + k f ( χ 2 + χ 1 ) k f , ρ hnf = ( 1 − χ 1 − χ 2 ) ρ f + χ 1 ρ s 1 + χ 2 ρ s 2 , μ hnf = μ f ( 1 − χ 1 − χ 2 ) 2.5 , ( ρ C p ) hnf = ( 1 − χ 1 − χ 2 ) ( ρ C p ) f + ( ρ C p ) 2 ρ s 2 + χ 1 ( ρ C p ) s 1 , σ hnf = χ 1 σ s 1 + χ 2 σ s 2 ( χ 2 + χ 1 ) + 2 σ f + 2 ( σ s 1 χ 1 + σ s 2 χ 2 ) − 2 σ f ( χ 2 + χ 1 ) χ 1 σ s 1 + χ 2 σ s 2 ( χ 2 + χ 1 ) + 2 σ f − 2 ( σ s 1 χ 1 + σ s 2 χ 2 ) + σ f ( χ 2 + χ 1 ) σ f .

A set of appropriate [49,56,57]:

(10) u = r Ω F ( η ) , v = r Ω G ( η ) , w = Ω ν f H ( η ) , p − p ∞ = 2 μ f Ω p ( η ) T = T ∞ ( 1 + ( θ w − 1 ) θ ( η ) ) , ϕ ( η ) = C − C ∞ C ∞ , η = Ω ν f z .

Using Eq. (10) in Eqs. (1)–(6), we have

(11) H ′ + 2 F = 0 ,

(12) μ hnf / μ f ρ hnf / ρ f F ″ − F 2 + G 2 − H F ′ − σ hnf / σ f ρ hnf / ρ f M F = 0 ,

(13) μ hnf / μ f ρ hnf / ρ f G ″ − 2 F G − H G ′ − σ hnf / σ f ρ hnf / ρ f M G = 0 ,

(14) k hnf k f + Rd ( 1 + θ ( θ w − 1 ) ) 3 θ ″ + 4 Rd ( θ w − 1 ) ( 1 + ( θ w − 1 ) θ ) 2 θ ′ 2 − Pr ( ρ C p ) hnf ( ρ C p ) f H θ ′ + Pr Nt θ ′ 2 + Pr Nb θ ′ ϕ ′ + Q e exp ( − δ η ) = 0 ,

(15) ϕ ″ + Nt Nb θ ″ − Sc H ϕ ′ − KrSc ( 1 + ω θ ) n ϕ exp − E ( 1 + ω θ ) = 0 .

Transformed constraints at the boundary are as follows:

(16) F ( 0 ) = 0 , H ( 0 ) = 0 , G ( 0 ) = 1 , k hnf k f θ ′ ( 0 ) = − Bi ( 1 − θ ( 0 ) ) , ϕ ′ ( 0 ) + Nt Nb θ ′ ( 0 ) = 0 , F ( ∞ ) = 0 , G ( ∞ ) = 0 , θ ( ∞ ) = 0 , ϕ ( ∞ ) = 0 .

The emerging factors are as follows:

(17) M = σ f B 0 2 ρ f Ω , Pr = ν f ( ρ C p ) f k f , ω = T f − T ∞ T ∞ , Q e = Q Ω ( ρ C p ) f , Bi = h f k f ν f Ω , Rd = 16 σ * T ∞ 3 3 k * k f , N t = ( ρ C p ) np D T ( T f − T ∞ ) ( ρ C p ) f T ∞ ν f , Nb = ( ρ C p ) np D B C ∞ ( ρ C p ) f ν f , Sc = ν f D B , E = E a k b T ∞ , K r = k r 2 Ω , θ w = T f T ∞ . .

The skin friction (coefficient) and Nusselt number are described mathematically as

(18) C fr = τ wr 2 + τ wz 2 ρ f ( Ω r ) 2 , Nu r = r q w k f ( T f − T ∞ ) ,

where

(19) τ wr = μ hnf ∂ u ∂ z + ∂ w ∂ r z = 0 , τ wz = μ hnf 1 r ∂ w ∂ ψ + ∂ v ∂ z z = 0 .

Thus, the above equation is reduced to

(20) Re r C f = G ′ 2 ( 0 ) + F ′ 2 ( 0 ) , 1 Re r Nu = − k hnf k f + Rd ( 1 + ( θ w − 1 ) θ ( 0 ) ) 3 θ ′ ( 0 ) ,

where Re r Ω r 2 ν f is the local Reynolds number.

3 Numerical solution

The bvp4c procedure, coded in MATLAB software, is practical and simple to use and is capable of handling problems that are somewhat complex. For the purpose of resolving nonlinear equations, this iterative approach is used [58,59,60]. The present numerical technique is implemented in Eqs. (11)–(15) subject to Eq. (16). First, we convert the nonlinear equations into a first-order system as follows:

(21) H = ℜ ( 1 ) , H ′ = ℜ ′ ( 1 ) , F = ℜ ( 2 ) , F ′ = ℜ ( 3 ) , F ″ = ℜ ′ ( 3 ) , G = ℜ ( 4 ) , G ′ = ℜ ( 5 ) , G ″ = ℜ ′ ( 5 ) , θ = ℜ ( 6 ) , θ ′ = ℜ ( 7 ) , θ ″ = ℜ ′ ( 7 ) , ϕ = ℜ ( 8 ) , ϕ ′ = ℜ ( 9 ) , ϕ ″ = ℜ ′ ( 9 ) , ,

(22) ℜ ′ ( 1 ) = − 2 ℜ ( 2 ) ,

(23) ℜ ′ ( 3 ) = − ( ℜ ( 4 ) ) 2 − ( ℜ ( 2 ) ) 2 − ℜ ( 1 ) ℜ ( 3 ) − σ hnf / σ f ρ hnf / ρ f M ℜ ( 2 ) μ hnf / μ f ρ hnf / ρ f ,

(24) ℜ ′ ( 5 ) = 2 ℜ ( 2 ) ℜ ( 4 ) + ℜ ( 1 ) ℜ ( 5 ) + σ hnf / σ f ρ hnf / ρ f M ℜ ( 4 ) μ hnf / μ f ρ hnf / ρ f ,

(25) ℜ ′ ( 7 ) = − Rd ( θ w − 1 ) ( 1 + ( θ w − 1 ) ℜ ( 6 ) ) 2 ( ℜ ( 7 ) ) 2 − Pr ( ρ C p ) hnf ( ρ C p ) f ℜ ( 1 ) ℜ ( 7 ) + Pr Nt ( ℜ ( 7 ) ) 2 + Pr Nb ℜ ( 7 ) ℜ ( 9 ) + Q e exp ( − δ η ) k hnf k f + Rd ( 1 + ( θ w − 1 ) ℜ ( 6 ) ) 3 ,

(26) ℜ ′ ( 9 ) − Nt Nb ℜ ′ ( 7 ) − S c ℜ ( 1 ) ℜ ( 9 ) − K r Sc ( 1 + ω ℜ ( 6 ) ) n ℜ ( 8 ) exp − E ( 1 + ω ℜ ( 6 ) ) .

with the boundary conditions

(27) ℜ 0 ( 1 ) − 0 , ℜ 0 ( 2 ) − 0 , ℜ 0 ( 4 ) − 1 , k hnf k f ℜ 0 ( 7 ) − Bi ( 1 − ℜ 0 ( 6 ) ) , ℜ 0 ( 9 ) + Nt Nb ℜ 0 ( 7 ) , ℜ inf ( 2 ) − 0 , ℜ inf ( 6 ) − 0 , ℜ inf ( 8 ) − 0 , ℜ inf ( 4 ) − 0 , ,

where ℜ 0 and ℜ inf are used for the initial and boundary conditions.

4 Present validation

When all other factors are zero, the existing results are compared with the results of Rashidi et al. [61] and Turkyilmazoglu [62], who also published their findings. As shown in Table 2, a similar result has been found in our present exploration.

Table 2

Validation of the current data with the available results of Turkyilmazoglu [62] and Rashidi et al. [61] when χ 1 = χ 2 = 0.0

F(0)
M 1 4
Rashidi et al. [61] 0.309237 0.165701
Turkyilmazoglu [62] 0.309258 0.165703
Present results 0.309258 0.165703

5 Results and discussions

5.1 Results

5.1.1 Discussion of results

This section compacts with the impacts of embedded factors on radial and azimuthal velocity, thermal, and concentration distributions of the fluid flow past a revolving disk. The numerical solution for the problem is evaluated using the bvp4c method. The influence of embedded factors on the flow distributions and quantities of interest is shown in Figures 2–16 and Tables 2–8. Table 2 describes a comparative analysis. Figures 2 and 3 display the influence of magnetic parameter (M) over radial velocity (F(η)) and azimuthal velocity (G(η)). From these figures, it can be observed that F(η) and G(η) reduce due to an increase of M. Actually, growth in M heightens the Lorentz force as created in the flow system, which augments the friction farce at the sheet surface and decelerates the flow. Therefore, the magnetic parameter opposes the transport phenomena, which results in the reduction of the velocity profiles, as shown in Figures 2 and 3. Hence, the velocity of the fluid in both radial and azimuthal directions decreases due to the augmenting magnetic factor. At the sheet surface, the radial velocity of the hybrid nanofluid shows a dominant behavior compared to the nanofluid. However, this effect is reversed above the surface. Figures 4 and 5 demonstrate the impact of the radiation factor (Rd) on (θ(η)) and (ϕ(η)), respectively. From these figures, it can be observed that both θ(η) and ϕ(η) reduce due to an increase of Rd. Generally, Rd is the source of external energy that provides heat to the working fluid in the electromagnetic waveform, and as a result, the temperature and concentration boundary layer thicknesses increase. Thus, θ(η) and ϕ(η) increase with an increase in the thermal radiation factor. At the sheet surface, the temperature of the nanofluid shows a dominant behavior compared to the nanofluid. However, this effect is reversed above the surface. Figure 6 shows the influence of the temperature difference factor θ w on θ(η). It is noticed that the thermal distribution increases with increasing θ w. The temperature difference factor shows the ratio of T f with T ∞ (i.e., θ w = T f/T ∞). It is also obvious that θ w must be greater than 1. According to this definition, as we increase θ w, the reference heat of fluid flow also increases, which results in a higher thermal distribution of the fluid flow. Thus, an increase in θ w increases θ(η). At the surface of the sheet, the temperature of the nanofluid shows a dominant behavior compared to the hybrid nanofluid. However, this effect is reversed above the surface. Figure 7 shows the impact of the heat source factor (Q e) on θ(η). It is noticed that θ(η) increases with increasing Q e. Actually, Q e plays an imperative role in the form of extra heat to the flow system. Because of the fundamental principles of thermodynamics, adding a heat source to a system improves its thermal profile. According to the law of conservation of energy, energy cannot be generated or destroyed, but rather transferred or changed from one form to another. As a result, the heat source provides thermal energy to the system, causing a temperature increase throughout its geographical extent. This thermal energy transfer occurs when heat naturally flows from higher temperatures (the heat source) to lower temperatures (the surroundings or the system itself), resulting in a detectable increase in the temperature throughout the system. Thus, the thermal profile reflects how the new heat is redistributed and changes the system’s thermal state. Thus, an increase in Q e increases θ(η). Similarly, ϕ(η) also increases with an increase in Q e, as displayed in Figure 8. At the sheet surface, the temperature of the nanofluid shows a dominant behavior compared to the hybrid nanofluid. However, this effect is reversed above the surface. Figures 9 and 10 show the influence of Nt on θ(η) and ϕ(η). It is observed that both θ(η) and ϕ(η) increase with increasing Nt. This occurs because the particles near the heated surfaces generate a thermophoretic force that pushes the particles to break down away from the fluid regime, increasing the thicknesses of concentration and temperature boundary layers. At the sheet surface, the temperature and concentration of the nanofluid show a dominant behavior compared to the hybrid nanofluid. However, this consequence is reversed above the surface. Figure 11 shows the impact of the Brownian factor (Nb) on ϕ(η). It is found that an increase of Nb reduces ϕ(η). As Nb values increase, the concentration profile decreases, in turn the concentration layer at the boundary likewise drops. Increasing values of Nb have an impact on the Brownian motion, which also restricts the nanoparticle diffusion in the flow regime and reduces the concentration of the fluid. Thus, an increase in Nb reduces ϕ(η). At the sheet surface, the concentration of the nanofluid shows dominant behavior compared to the hybrid nanofluid. However, this effect is reversed above the surface. Figures 12 and 13 show the impression of thermal Biot number (Bi) on θ(η) and ϕ(η). Both θ(η) and ϕ(η) augment with increasing values of Bi. The reason is that increasing Bi augments the thermal flow, which results in intensification in the heat transfer rate. The increase in the thermal flow rate leads to the enhancement of the thickness of the thermal boundary layer. Thus, θ(η) increases with increasing Bi. Similarly, Bi also augments the concentration boundary layer thickness and thus ϕ(η) increases. At the sheet surface, the concentration of the nanofluid shows a dominant behavior compared to the hybrid nanofluid. However, this effect is reversed above the surface. Figure 14 shows the influence of E on ϕ(η). It was found that an increase in E augments ϕ(η). It was observed that at lower temperatures and higher E, the reaction rate decreases, thereby slowing the chemical process; as a result, the thickness of the concentration boundary layer increases, which increases ϕ(η). Furthermore, the impact of E is higher for the hybrid nanofluid compared to the nanofluid flow. Figure 15 shows the influence of the reaction factor (K r) on ϕ(η). It was found that an increase in K r reduces ϕ(η). Actually, the increase in the chemical reaction factor improves K rSc(1 + ωθ) n ϕ exp(−E/(1 + ωθ)). Thus, increasing chemical reaction takes place and reduces the thickness of the concentration boundary layer, which results in the reduction of the concentration distribution. Thus, an increase in K r reduces ϕ(η). Furthermore, the concentration of the nanofluid flow is lower than the flow of the hybrid nanoliquid. Figure 16 demonstrates the impact of Sc on ϕ(η). An increase in Sc reduces the diffusion of mass. Therefore, an increase in Sc diminishes ϕ(η). Moreover, the concentration of the hybrid nanoparticles flow is greater than the flow of the nanofluid. Table 3 shows the influences of χ 1 and M on Re r C f . The increasing χ 1 and M augment Re r C f . The reason is that the higher volume fraction of the solid nanoparticles increases the shear stress, which consequently increases the skin friction at the surface. Thus, Re r C f increases with an increase in χ 1. Also, an increase in M increases Re r C f . An increase in M generates Lorentz force, which results in higher friction force at the surface. Thus, an increase in M reduces Re r C f . The same findings can be found in Tables 4 and 5. From these tables, it can be found that the friction force for the hybrid nanofluid was found to be the highest. Table 6 shows the impacts of χ 1, Bi, and θ w on 1 Re r Nu . An increase in χ 1, Bi and θ w augments 1 Re r Nu . Thus, 1 Re r Nu increases with increasing χ 1. Similarly, an increase in Bi enhances the coefficient of heat transmission, which consequently augments the rate of thermal flow of the nanofluid. Hence, the higher Bi heightens 1 Re r Nu . The same impact of θ w is found for 1 Re r Nu . The same findings can be found in Tables 7 and 8. As shown in the tables, the heat transmission rate for the hybrid nanofluid was found to be the highest. The Ag−H2O nanofluid has a 3% greater impact on Re r C f than the CuO−H2O nanofluid. Similarly, the CuO−Ag/H2O hybrid nanofluid has a 28% higher impact on Re r C f than the Ag−H2O nanofluid. Also, the CuO−Ag/H2O hybrid nanofluid has a 26% higher impact on Re r C f than the CuO−H2O nanofluid. The heat transfer rate of the Ag−H2O nanofluid is 3% greater than the CuO−H2O nanofluid. Also, the heat transfer rate of the CuO−Ag/H2O hybrid nanofluid is 28% higher than the Ag−H2O nanofluid.

Figure 2 Influence of M on F(η).
Figure 2

Influence of M on F(η).

Figure 3 Influence of M on G(η).
Figure 3

Influence of M on G(η).

Figure 4 Influence of Rd on θ(η).
Figure 4

Influence of Rd on θ(η).

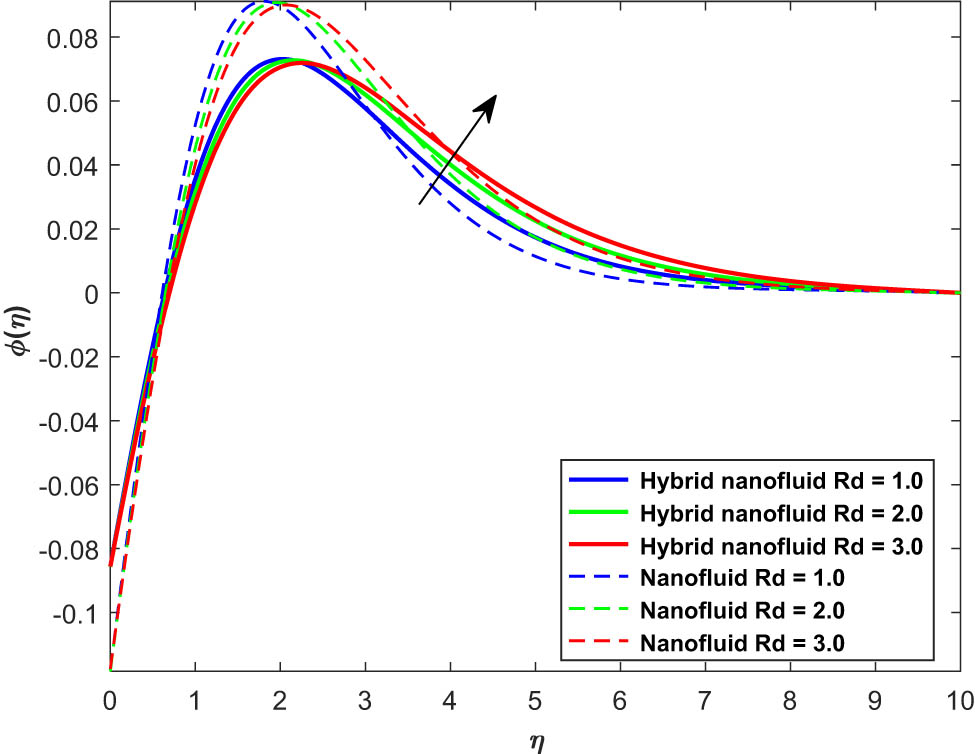
Figure 5 Influence of Rd on ϕ(η).
Figure 5

Influence of Rd on ϕ(η).

Figure 6 Influence of θ w on θ(η).
Figure 6

Influence of θ w on θ(η).

Figure 7 Influence of Q e on θ(η).
Figure 7

Influence of Q e on θ(η).

Table 3

Impacts of χ 1 and M on Re r C f

χ 1 M CuO−H2O nanofluid
0.01 0.1 0.467647
0.02 0.476437
0.03 0.487643
0.04 0.498738
0.3 0.397647
0.7 0.456784
1.3 0.549720
Table 4

Impacts of χ 2 and M on Re r C f

χ 2 M Ag−H2O nanofluid
0.01 0.1 0.470863
0.02 0.480849
0.03 0.495185
0.04 0.515890
0.3 0.415759
0.7 0.479058
1.3 0.568561
Table 5

Impacts of χ 1 = χ 2 and M on Re r C f

χ 1 = χ 2 M CuO−Ag/H2O hybrid nanofluid
0.01 0.1 0.588648
0.02 0.607529
0.03 0.598620
0.04 0.637863
0.3 0.654264
0.7 0.670834
1.3 0.696431
Table 6

Impacts of χ 1, Bi, and θ w on 1 Re r Nu

χ 1 Bi θ w CuO−H2O nanofluid
0.01 0.1 1.1 0.467647
0.02 0.476437
0.03 0.487643
0.04 0.498738
0.3 0.397647
0.7 0.456784
1.3 0.549720
1.1 0.476536
1.2 0.486525
1.3 0.497533
Table 7

Impacts of χ 2, Bi, and θ w on 1 Re r Nu

χ 2 Bi θ w Ag−H2O nanofluid
0.01 0.1 1.1 0.470863
0.02 0.480849
0.03 0.495185
0.04 0.515890
0.3 0.415759
0.7 0.479058
1.3 0.568561
1.1 0.487657
1.2 0.496426
1.3 0.509264
Table 8

Impacts of χ 1 = χ 2, Bi, and θ w on 1 Re r Nu

χ 1 = χ 2 Bi θ w CuO−Ag/H2O hybrid nanofluid
0.01 0.1 1.1 0.588648
0.02 0.607529
0.03 0.598620
0.04 0.637863
0.3 0.654264
0.7 0.670834
1.3 0.696431
1.1 0.523574
1.2 0.547627
1.3 0.568973
Figure 8 Influence of Q e on ϕ(η).
Figure 8

Influence of Q e on ϕ(η).

Figure 9 Influence of Nt on θ(η).
Figure 9

Influence of Nt on θ(η).

Figure 10 Influence of Nt on ϕ(η).
Figure 10

Influence of Nt on ϕ(η).

Figure 11 Influence of Nb on ϕ(η).
Figure 11

Influence of Nb on ϕ(η).

Figure 12 Influence of Bi on θ(η).
Figure 12

Influence of Bi on θ(η).

Figure 13 Influence of Bi on ϕ(η).
Figure 13

Influence of Bi on ϕ(η).

Figure 14 Influence of E on ϕ(η).
Figure 14

Influence of E on ϕ(η).

Figure 15 Influence of K r on ϕ(η).
Figure 15

Influence of K r on ϕ(η).

Figure 16 Influence of Sc on ϕ(η).
Figure 16

Influence of Sc on ϕ(η).

6 Conclusion

This section presents the concluding remarks that are observed from the present analysis. The current study is done for a time-independent water-based hybrid nanofluid flow over a rotating disk surface. In this investigation, two different nanoparticles, namely copper oxide and silver, are chosen. In the present analysis, the flow is considered to be Newtonian. The influence of the magnetic field, thermophoresis, nonlinear thermal radiation, chemical reaction, Brownian motion, and activation energy is taken into account. A numerical solution using the bvp4c technique is accomplished using MATLAB software. The present results are compared with the previous literature and it is found to have a close relationship with previous studies. From this investigation, the following concluding points are found:

  1. A higher magnetic parameter causes the surface to experience more friction, which lowers the radial and azimuthal velocity profiles. When compared to the nanofluid, the hybrid nanofluid’s radial velocity at the sheet surface exhibits dominant behavior.

  2. The thermal and concentration profiles are enhanced by the higher thermal radiation factor. In comparison to the nanofluid, the temperature and concentration of the nanofluid exhibit dominant behavior near the sheet surface. Above the surface, though, this impact is the opposite.

  3. The temperature profiles are enhanced when thermophoresis, temperature ratio, and heat source parameters increase. When compared to a hybrid nanofluid, the temperature of the nanofluid exhibits dominant behavior near the sheet surface. Above the surface, though, this impact is the opposite.

  4. The concentration profile is enhanced by the thermophoresis factor and decreased by the Brownian motion factor. When compared to a hybrid nanofluid, the concentration profiles of the former exhibit dominant behavior at the sheet surface. Above the surface, though, this impact is the opposite.

  5. The Biot number increases with the concentration and temperature profiles. Additionally, in comparison to the hybrid nanofluid, the concentration of the nanofluid exhibits dominant behavior near the sheet surface. Above the surface, though, this impact is the opposite.

  6. The skin friction at the disk’s surface is increased by the increase in the solid volume fraction and magnetic component. Moreover, the hybrid nanofluid flow is observed to have a greater surface drag.

  7. The rate of heat transmission is accelerated by a greater solid volume fraction, temperature ratio, and Biot number. Furthermore, a greater rate of heat transfer is observed in the case of the hybrid nanofluid flow.

7 Future recommendations

In the future, the present mathematical model can be extended to study ternary hybrid nanofluid flow over a rotating disk surface by including three different metallic and nonmetallic nanoparticles. Furthermore, the addition of the Cattaneo-Christov heat and mass flux model can be studied to analyze heat and mass transport phenomena.

Acknowledgments

This study was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R443), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was also supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU241370).

  1. Funding information: This study was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R443), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU241370).

  2. Author contributions: Humaira Yasmin: conceptualization, methodology, software, funding, reviewing, and editing. Laila A. AL-Essa: data curation, writing – reviewing, and editing. Ali M. Mahnashi: visualization and investigation. Waleed Hamali: software, validation, and supervision. Anwar Saeed: writing – original draft preparation. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

  4. Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Choi, S. U. S. and J. A. Eastman. Enhancing thermal conductivity of fluids with nanoparticles. 1995 International mechanical engineering congress and exhibition, San Francisco, CA, United States, Nov 1995.Search in Google Scholar

[2] Shahzad, F., W. Jamshed, S. M. El Din, M. Shamshuddin, R. W. Ibrahim, and Z. Raizah. Second-order convergence analysis for Hall effect and electromagnetic force on ternary nanofluid flowing via rotating disk. Scientific Reports, Vol. 12, 2022, pp. 1–21.10.1038/s41598-022-23561-7Search in Google Scholar PubMed PubMed Central

[3] Shamshuddin, M. D., N. Akkurt, A. Saeed, and P. Kumam. Radiation mechanism on dissipative ternary hybrid nanoliquid flow through rotating disk encountered by Hall currents: HAM solution. Alexandria Engineering Journal, 2022.10.1016/j.aej.2022.10.021Search in Google Scholar

[4] Pasha, A. A., N. Islam, W. Jamshed, M. I. Alam, A. G. A. Jameel, K. A. Juhany, et al. Statistical analysis of viscous hybridized nanofluid flowing via Galerkin finite element technique. The International Communications in Heat and Mass Transfer, Vol. 137, 2022, id. 106244.10.1016/j.icheatmasstransfer.2022.106244Search in Google Scholar

[5] Shah, Z., A. Khan, W. Khan, M. K. Alam, S. Islam, P. Kumam, et al. Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Computer Methods and Programs in Biomedicine, Vol. 186, 2020, id. 105197.10.1016/j.cmpb.2019.105197Search in Google Scholar PubMed

[6] Asghar, A. and T. Y. Ying. Zaimi WMKAW. Two-dimensional mixed convection and radiative Al2O3-Cu/H2O hybrid nanofluid flow over a vertical exponentially shrinking sheet with partial slip conditions. CFD Letter, Vol. 14, 2022, pp. 22–38.10.37934/cfdl.14.3.2238Search in Google Scholar

[7] Khan, A., W. Kumam, I. Khan, A. Saeed, T. Gul, P. Kumam, et al. Chemically reactive nanofluid flow past a thin moving needle with viscous dissipation, magnetic effects and hall current. PLoS One, Vol. 16, 2021, id. e0249264.10.1371/journal.pone.0249264Search in Google Scholar PubMed PubMed Central

[8] Haider, J. A., S. Ahmad, H. A. Ghazwani, M. Hussien, M. Y. Almusawa, and E. A. Az-Zo’bi. Results validation by using finite volume method for the blood flow with magnetohydrodynamics and hybrid nanofluids. Modern Physics Letters B, 2024, id. 2450208.10.1142/S0217984924502087Search in Google Scholar

[9] Akhtar, S., Z. Hussain, H. A. Ghazwani, S. A. Lone, and E. A. Az-Zo’bi. Computational fluid dynamics analysis on endoscopy of main left coronary artery: An application of applied mathematics. Heliyon, 2024.10.1016/j.heliyon.2024.e26628Search in Google Scholar PubMed PubMed Central

[10] Naveed Khan, M., A. A. Khan, M., A. Alqahtani, Z. Wang, H. A. Hejazi, and E. A. Az-Zo’bi. Chemically reactive aspects of stagnation-point boundary layer flow of second-grade nanofluid over an exponentially stretching surface. Numerical Heat Transfer, Part B: Fundamentals, 2024, pp. 1–17.10.1080/10407790.2024.2318456Search in Google Scholar

[11] Ahsan, N., M. N. Aslam, M. N. Khan, and E. A. Az-Zo’bi. Bioconvective flow analysis of non-newtonian fluid over a porous curved stretching surface. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, 2024, 23977914241231892.10.1177/23977914241231891Search in Google Scholar

[12] Kanwal, S., S. A. A. Shah, A. Bariq, B. Ali, A. E. Ragab, and E. A. Az-Zo’bi. Insight into the dynamics of heat and mass transfer in nanofluid flow with linear/nonlinear mixed convection, thermal radiation, and activation energy effects over the rotating disk. Scientific Reports, Vol. 13, 2023, id. 23031.10.1038/s41598-023-49988-0Search in Google Scholar PubMed PubMed Central

[13] Waseem, M., T. Gul, I. Khan, A. Khan, A. Saeed, I. Ali, et al. Gravity-driven hydromagnetic flow of couple stress hybrid nanofluid with homogenous-heterogeneous reactions. Scientific Reports, Vol. 11, 2021, pp. 1–12.10.1038/s41598-021-97045-5Search in Google Scholar PubMed PubMed Central

[14] Hussain, M. A., F. Jamil, A. Ejaz, A. Wakeel, S. Khalid, H. M. Ali, et al. Thermal performance of sintered copper wick heat pipe using water-based hybrid nanofluids: an experimental study. Journal of Porous Materials, 2022, id. 25.10.1615/JPorMedia.2022040519Search in Google Scholar

[15] Guedri, K., A. Khan, N. Sene, Z. Raizah, A. Saeed, and A. M. Galal. Thermal Flow for radiative ternary hybrid nanofluid over nonlinear stretching sheet subject to Darcy–Forchheimer phenomenon. Mathematical Problems in Engineering, 2022, id. 2022.10.1155/2022/3429439Search in Google Scholar

[16] Zhang, L., M. M. Bhatti, E. E. Michaelides, M. Marin, and R. Ellahi. Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. European Physical Journal: Special Topics, Vol. 231, 2022, pp. 521–33.10.1140/epjs/s11734-021-00409-1Search in Google Scholar

[17] Ojjela, O. Numerical investigation of heat transport in Alumina–Silica hybrid nanofluid flow with modeling and simulation. Mathematics and Computers in Simulation, Vol. 193, 2022, pp. 100–22.10.1016/j.matcom.2021.09.022Search in Google Scholar

[18] Gumber, P., M. Yaseen, S. K. Rawat, and M. Kumar. Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differential Equations in Applied Mathematics, Vol. 5, 2022, id. 100240.10.1016/j.padiff.2021.100240Search in Google Scholar

[19] Sriharan, G., S. Harikrishnan, and H. M. Ali. Enhanced heat transfer characteristics of the mini hexagonal tube heat sink using hybrid nanofluids. Nanotechnology, Vol. 33, 2022, id. 475403.10.1088/1361-6528/ac8995Search in Google Scholar PubMed

[20] Ullah, H., M. Shoaib, R. A. Khan, K. S. Nisar, M. A. Z. Raja, and S. Islam. Soft computing paradigm for heat and mass transfer characteristics of nanofluid in magnetohydrodynamic (MHD) boundary layer over a vertical cone under the convective boundary condition. International journal of simulation modelling, 2023, pp. 1–25.10.1080/02286203.2023.2191586Search in Google Scholar

[21] Zawawi, N. N. M., W. H. Azmi, M. F. Ghazali, and H. M. Ali. Performance of air-conditioning system with different nanoparticle composition ratio of hybrid nanolubricant. Micromachines, Vol. 13, 2022, id. 1871.10.3390/mi13111871Search in Google Scholar PubMed PubMed Central

[22] Asghar, A., L. A. Lund, Z. Shah, N. Vrinceanu, W. Deebani, and M. Shutaywi. Effect of thermal radiation on three-dimensional magnetized rotating flow of a hybrid nanofluid. Nanomaterials, Vol. 12, 2022, id. 1566.10.3390/nano12091566Search in Google Scholar PubMed PubMed Central

[23] Babar, H., H. Wu, H. M. Ali, T. R. Shah, and W. Zhang. Staggered oriented airfoil shaped pin-fin heat sink: Investigating the efficacy of novel water based ferric oxide-silica hybrid nanofluid. International Journal of Heat and Mass Transfer, Vol. 194, 2022, id. 123085.10.1016/j.ijheatmasstransfer.2022.123085Search in Google Scholar

[24] Akbar, A., H. Ullah, M. A. Z. Raja, K. S. Nisar, S. Islam, and M. Shoaib. A design of neural networks to study MHD and heat transfer in two phase model of nano-fluid flow in the presence of thermal radiation. Waves in Random and Complex Media, 2022, pp. 1–24.10.1080/17455030.2022.2152905Search in Google Scholar

[25] Ullah, H., S. Islam, and M. Fiza. Analytical solution for three-dimensional problem of condensation film on inclined rotating disk by extended optimal homotopy asymptotic method. The Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, Vol. 40, 2016, pp. 265–73.10.1007/s40997-016-0030-8Search in Google Scholar

[26] Raja, M. A. Z., K. S. Nisar, M. Shoaib, A. Akbar, H. Ullah, and S. Islam. A predictive neuro-computing approach for micro-polar nanofluid flow along rotating disk in the presence of magnetic field and partial slip. AIMS Mathematics, Vol. 8, 2023, pp. 12062–92.10.3934/math.2023608Search in Google Scholar

[27] Ullah, H., K. Ullah, M. A. Z. Raja, M. Shoaib, K. S. Nisar, S. Islam, et al. Numerical treatment of squeezed MHD Jeffrey fluid flow with Cattaneo Chrisstov heat flux in a rotating frame using Levnberg-Marquard method. Alexandria Engineering Journal, Vol. 66, 2023, pp. 1031–50.10.1016/j.aej.2022.12.034Search in Google Scholar

[28] Vishalakshi, A. B., U. S. Mahabaleshwar, and I. E. Sarris. An MHD fluid flow over a porous stretching/shrinking sheet with slips and mass transpiration. Micromachines, Vol. 13, 2022, id. 116.10.3390/mi13010116Search in Google Scholar PubMed PubMed Central

[29] Asjad, M. I., M. Zahid, M. Inc, D. Baleanu, and B. Almohsen. Impact of activation energy and MHD on Williamson fluid flow in the presence of bioconvection. Alexandria Engineering Journal, Vol. 61, 2022, pp. 8715–27.10.1016/j.aej.2022.02.013Search in Google Scholar

[30] Bejawada, S. G., Y. D. Reddy, W. Jamshed, K. S. Nisar, A. N. Alharbi, and R. Chouikh. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alexandria Engineering Journal, Vol. 61, 2022, pp. 8207–20.10.1016/j.aej.2022.01.043Search in Google Scholar

[31] Usman, M., T. Gul, A. Khan, A. Alsubie, and M. Z. Ullah. Electromagnetic couple stress film flow of hybrid nanofluid over an unsteady rotating disc. The International Communications in Heat and Mass Transfer, Vol. 127, 2021, id. 105562.10.1016/j.icheatmasstransfer.2021.105562Search in Google Scholar

[32] Sharma, K., S. Kumar, A. Narwal, F. Mebarek-Oudina, and I. L. Animasaun. Convective MHD fluid flow over stretchable rotating disks with dufour and Soret effects. International Journal of Applied and Computational Mathematics, Vol. 8, 2022, pp. 1–12.10.1007/s40819-022-01357-7Search in Google Scholar

[33] Asghar, A., N. Vrinceanu, T. Y. Ying, L. A. Lund, Z. Shah, and V. Tirth. Dual solutions of convective rotating flow of three-dimensional hybrid nanofluid across the linear stretching/shrinking sheet. Alexandria Engineering Journal, Vol. 75, 2023, pp. 297–312.10.1016/j.aej.2023.05.089Search in Google Scholar

[34] Rasool, G., W. Xinhua, L. A. Lund, U. Yashkun, A. Wakif, and A. Asghar. Dual solutions of unsteady flow of copper-alumina/water based hybrid nanofluid with acute magnetic force and slip condition. Heliyon, Vol. 9, 2023.10.1016/j.heliyon.2023.e22737Search in Google Scholar PubMed PubMed Central

[35] Lund, L. A., A. Asghar, G. Rasool, and U. Yashkun. Magnetized casson SA-hybrid nanofluid flow over a permeable moving surface with thermal radiation and Joule heating effect. Case Stud. Thermal Engineering, Vol. 50, 2023, id. 103510.10.1016/j.csite.2023.103510Search in Google Scholar

[36] Tarakaramu, N., P. V. Satya Narayana, R. Sivajothi, K. Bhagya Lakshmi, D. Harish Babu, and B. Venkateswarlu. Three‐dimensional non‐Newtonian couple stress fluid flow over a permeable stretching surface with nonlinear thermal radiation and heat source effects. Heat Transfer, Vol. 51, 2022, pp. 5348–67.10.1002/htj.22550Search in Google Scholar

[37] Nasir, S., S. Sirisubtawee, P. Juntharee, A. S. Berrouk, S. Mukhtar, and T. Gul. Heat transport study of ternary hybrid nanofluid flow under magnetic dipole together with nonlinear thermal radiation. Applied Nanoscience, Vol. 12, 2022, pp. 2777–88.10.1007/s13204-022-02583-7Search in Google Scholar

[38] Shaw, S., S. S. Samantaray, A. Misra, M. K. Nayak, and O. D. Makinde. Hydromagnetic flow and thermal interpretations of Cross hybrid nanofluid influenced by linear, nonlinear and quadratic thermal radiations for any Prandtl number. The International Communications in Heat and Mass Transfer, Vol. 130, 2022, id. 105816.10.1016/j.icheatmasstransfer.2021.105816Search in Google Scholar

[39] Owhaib, W. and W. Al-Kouz. Three-dimensional numerical analysis of flow and heat transfer of bi-directional stretched nanofluid film exposed to an exponential heat generation using modified Buongiorno model. Science Reports, Vol. 12, 2022, pp. 1–20.10.1038/s41598-022-13351-6Search in Google Scholar PubMed PubMed Central

[40] Waqas, H., M. Oreijah, K. Guedri, S. U. Khan, S. Yang, S. Yasmin, et al. Gyrotactic motile microorganisms impact on pseudoplastic nanofluid flow over a moving Riga surface with exponential heat flux. Crystals, Vol. 12, 2022, id. 1308.10.3390/cryst12091308Search in Google Scholar

[41] Samrat, S. P., Y. H. Gangadharaiah, G. P. Ashwinkumar, and N. Sandeep. Effect of exponential heat source on parabolic flow of three different non-Newtonian fluids. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 2022, id. 09544089221083468.10.1177/09544089221083468Search in Google Scholar

[42] Qian, W.-M., M. I. Khan, F. Shah, M. Khan, Y.-M. Chu, W. A. Khan, et al. Mathematical modeling and MHD flow of micropolar fluid toward an exponential curved surface: heat analysis via ohmic heating and heat source/sink. Arabian Journal for Science and Engineering, Vol. 47, 2022, pp. 867–78.10.1007/s13369-021-05673-wSearch in Google Scholar

[43] Ramzan, M., J. Ali, N. Shahmir, H. A. S. Ghazwani, K. S. Nisar, and C. A. Saleel. Thermophoretic particle deposition impact in the Oldroyd-B fluid flow influenced by a magnetic dipole with an exponential thermal heat source. International Journal of Modern Physics B: Condensed Matter Physics, Statistical Physics, Applied Physics, 2022, id. 2350059.10.1142/S0217979223500595Search in Google Scholar

[44] Haq, S. U., S. U. Jan, R. Bilal, J. H. Alzahrani, I. Khan, and A. Alzahrani. Heat-mass transfer of MHD second grade fluid flow with exponential heating, chemical reaction and porosity by using fractional Caputo-Fabrizio derivatives. Case Studies in Thermal Engineering, Vol. 36, 2022, id. 102104.10.1016/j.csite.2022.102104Search in Google Scholar

[45] Alqarni, M. M., M. Bilal, R. Allogmany, E. Tag-Eldin, M. E. Ghoneim, and M. F. Yassen. Mathematical analysis of Casson fluid flow with energy and mass transfer under the influence of activation energy from a non-coaxially spinning disc. Frontiers in Energy Research, 2022, id. 10.10.3389/fenrg.2022.986284Search in Google Scholar

[46] Rekha, M. B., I. E. Sarris, J. K. Madhukesh, K. R. Raghunatha, and B. C. Prasannakumara. Activation energy impact on flow of AA7072-AA7075/Water-Based hybrid nanofluid through a cone, wedge and plate. Micromachines, Vol. 13, 2022, id. 302.10.3390/mi13020302Search in Google Scholar PubMed PubMed Central

[47] Abbasi, A., S. U. Khan, K. Al-Khaled, M. I. Khan, W. Farooq, A. M. Galal, et al. Thermal prospective of Casson nano-materials in radiative binary reactive flow near oblique stagnation point flow with activation energy applications. Chemical Physics Letters, Vol. 786, 2022, id. 139172.10.1016/j.cplett.2021.139172Search in Google Scholar

[48] Ayub, A., T. Sajid, W. Jamshed, W. R. M. Zamora, L. A. V. More, L. M. G. Talledo, et al. Activation energy and inclination magnetic dipole influences on Carreau nanofluid flowing via cylindrical channel with an infinite shearing rate. Applied Science, Vol. 12, 2022, id. 8779.10.3390/app12178779Search in Google Scholar

[49] Khan, U., S. Bilal, A. Zaib, O. D. Makinde, and A. Wakif. Numerical simulation of a nonlinear coupled differential system describing a convective flow of Casson gold–blood nanofluid through a stretched rotating rigid disk in the presence of Lorentz forces and nonlinear thermal radiation. Numerical Methods for Partial Differential Equations, 2020.10.1002/num.22620Search in Google Scholar

[50] Turkyilmazoglu, M. MHD fluid flow and heat transfer due to a stretching rotating disk. International Journal of Thermal Sciences, Vol. 51, 2012, pp. 195–201.10.1016/j.ijthermalsci.2011.08.016Search in Google Scholar

[51] Mustafa, I., T. Javed, and A. Ghaffari. Heat transfer in MHD stagnation point flow of a ferrofluid over a stretchable rotating disk. Journal of Molecular Liquids, Vol. 219, 2016, pp. 526–32.10.1016/j.molliq.2016.03.046Search in Google Scholar

[52] Dawar, A., S. Islam, Z. Shah, and S. R. Mahmuod. A passive control of casson hybrid nanofluid flow over a curved surface with alumina and copper nanomaterials: a study on sodium alginate-based fluid. Journal of Molecular Liquids, 2023, id. 122018.10.1016/j.molliq.2023.122018Search in Google Scholar

[53] Dawar, A., A. Wakif, T. Thumma, and N. A. Shah. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. The International Communications in Heat and Mass Transfer, Vol. 130, 2022, id. 105800.10.1016/j.icheatmasstransfer.2021.105800Search in Google Scholar

[54] Shafiq, A., G. Rasool, H. Alotaibi, H. M. Aljohani, A. Wakif, I. Khan, et al. Thermally enhanced Darcy-Forchheimer Casson-water/glycerine rotating nanofluid flow with uniform magnetic field. Micromachines, Vol. 12, 2021, id. 605.10.3390/mi12060605Search in Google Scholar PubMed PubMed Central

[55] Alghamdi, M., A. Wakif, T. Thumma, U. Khan, D. Baleanu, and G. Rasool. Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Studies in Thermal Engineering, Vol. 28, 2021, id. 101428.10.1016/j.csite.2021.101428Search in Google Scholar

[56] Von Kármán, T. Uber laminare und turbulente Reibung. Zeitschrift fuer Angewandte Mathematik und Mechanik, Vol. 1, 1921, pp. 233–52.10.1002/zamm.19210010401Search in Google Scholar

[57] Ragupathi, P., T. Muhammad, S. Islam, and A. Wakif. Application of Arrhenius kinetics on MHD radiative Von Kármán Casson nanofluid flow occurring in a Darcy-Forchheimer porous medium in the presence of an adjustable heat source. Physica Scripta, Vol. 96, 2021, id. 125228.10.1088/1402-4896/ac297cSearch in Google Scholar

[58] Shampine, L. F., J. Kierzenka, and M. W. Reichelt. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutorial Notes, Vol. 2000, 2000, pp. 1–27.Search in Google Scholar

[59] Dharmaiah, G., S. Dinarvand, P. Durgaprasad, and S. Noeiaghdam. Arrhenius activation energy of tangent hyperbolic nanofluid over a cone with radiation absorption. Results Engineering, Vol. 16, 2022, id. 100745.10.1016/j.rineng.2022.100745Search in Google Scholar

[60] Xia, W.-F., S. Ahmad, M. N. Khan, H. Ahmad, A. Rehman, J. Baili, et al. Heat and mass transfer analysis of nonlinear mixed convective hybrid nanofluid flow with multiple slip boundary conditions. Case Studies in Thermal Engineering, Vol. 32, 2022, id. 101893.10.1016/j.csite.2022.101893Search in Google Scholar

[61] Rashidi, M. M., S. Abelman, and N. F. Mehr. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. International Journal of Heat and Mass Transfer, Vol. 62, 2013, pp. 515–25.10.1016/j.ijheatmasstransfer.2013.03.004Search in Google Scholar

[62] Turkyilmazoglu, M. Purely analytic solutions of magnetohydrodynamic swirling boundary layer flow over a porous rotating disk. Computers and Fluids, Vol. 39, 2010, pp. 793–9.10.1016/j.compfluid.2009.12.007Search in Google Scholar
Received: 2024-04-23
Accepted: 2024-08-13
Published Online: 2024-10-07

© 2024 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. Effect of superplasticizer in geopolymer and alkali-activated cement mortar/concrete: A review
  3. Experimenting the influence of corncob ash on the mechanical strength of slag-based geopolymer concrete
  4. Powder metallurgy processing of high entropy alloys: Bibliometric analysis and systematic review
  5. Exploring the potential of agricultural waste as an additive in ultra-high-performance concrete for sustainable construction: A comprehensive review
  6. A review on partial substitution of nanosilica in concrete
  7. Foam concrete for lightweight construction applications: A comprehensive review of the research development and material characteristics
  8. Modification of PEEK for implants: Strategies to improve mechanical, antibacterial, and osteogenic properties
  9. Interfacing the IoT in composite manufacturing: An overview
  10. Advances in processing and ablation properties of carbon fiber reinforced ultra-high temperature ceramic composites
  11. Advancing auxetic materials: Emerging development and innovative applications
  12. Revolutionizing energy harvesting: A comprehensive review of thermoelectric devices
  13. Exploring polyetheretherketone in dental implants and abutments: A focus on biomechanics and finite element methods
  14. Smart technologies and textiles and their potential use and application in the care and support of elderly individuals: A systematic review
  15. Reinforcement mechanisms and current research status of silicon carbide whisker-reinforced composites: A comprehensive review
  16. Innovative eco-friendly bio-composites: A comprehensive review of the fabrication, characterization, and applications
  17. Review on geopolymer concrete incorporating Alccofine-1203
  18. Advancements in surface treatments for aluminum alloys in sports equipment
  19. Ionic liquid-modified carbon-based fillers and their polymer composites – A Raman spectroscopy analysis
  20. Emerging boron nitride nanosheets: A review on synthesis, corrosion resistance coatings, and their impacts on the environment and health
  21. Mechanism, models, and influence of heterogeneous factors of the microarc oxidation process: A comprehensive review
  22. Synthesizing sustainable construction paradigms: A comprehensive review and bibliometric analysis of granite waste powder utilization and moisture correction in concrete
  23. 10.1515/rams-2025-0086
  24. Research Articles
  25. Coverage and reliability improvement of copper metallization layer in through hole at BGA area during load board manufacture
  26. Study on dynamic response of cushion layer-reinforced concrete slab under rockfall impact based on smoothed particle hydrodynamics and finite-element method coupling
  27. Study on the mechanical properties and microstructure of recycled brick aggregate concrete with waste fiber
  28. Multiscale characterization of the UV aging resistance and mechanism of light stabilizer-modified asphalt
  29. Characterization of sandwich materials – Nomex-Aramid carbon fiber performances under mechanical loadings: Nonlinear FE and convergence studies
  30. Effect of grain boundary segregation and oxygen vacancy annihilation on aging resistance of cobalt oxide-doped 3Y-TZP ceramics for biomedical applications
  31. Mechanical damage mechanism investigation on CFRP strengthened recycled red brick concrete
  32. Finite element analysis of deterioration of axial compression behavior of corroded steel-reinforced concrete middle-length columns
  33. Grinding force model for ultrasonic assisted grinding of γ-TiAl intermetallic compounds and experimental validation
  34. Enhancement of hardness and wear strength of pure Cu and Cu–TiO2 composites via a friction stir process while maintaining electrical resistivity
  35. Effect of sand–precursor ratio on mechanical properties and durability of geopolymer mortar with manufactured sand
  36. Research on the strength prediction for pervious concrete based on design porosity and water-to-cement ratio
  37. Development of a new damping ratio prediction model for recycled aggregate concrete: Incorporating modified admixtures and carbonation effects
  38. Exploring the viability of AI-aided genetic algorithms in estimating the crack repair rate of self-healing concrete
  39. Modification of methacrylate bone cement with eugenol – A new material with antibacterial properties
  40. Numerical investigations on constitutive model parameters of HRB400 and HTRB600 steel bars based on tensile and fatigue tests
  41. Research progress on Fe3+-activated near-infrared phosphor
  42. Discrete element simulation study on effects of grain preferred orientation on micro-cracking and macro-mechanical behavior of crystalline rocks
  43. Ultrasonic resonance evaluation method for deep interfacial debonding defects of multilayer adhesive bonded materials
  44. Effect of impurity components in titanium gypsum on the setting time and mechanical properties of gypsum-slag cementitious materials
  45. Bending energy absorption performance of composite fender piles with different winding angles
  46. Theoretical study of the effect of orientations and fibre volume on the thermal insulation capability of reinforced polymer composites
  47. Synthesis and characterization of a novel ternary magnetic composite for the enhanced adsorption capacity to remove organic dyes
  48. Couple effects of multi-impact damage and CAI capability on NCF composites
  49. Mechanical testing and engineering applicability analysis of SAP concrete used in buffer layer design for tunnels in active fault zones
  50. Investigating the rheological characteristics of alkali-activated concrete using contemporary artificial intelligence approaches
  51. Integrating micro- and nanowaste glass with waste foundry sand in ultra-high-performance concrete to enhance material performance and sustainability
  52. Effect of water immersion on shear strength of epoxy adhesive filled with graphene nanoplatelets
  53. Impact of carbon content on the phase structure and mechanical properties of TiBCN coatings via direct current magnetron sputtering
  54. Investigating the anti-aging properties of asphalt modified with polyphosphoric acid and tire pyrolysis oil
  55. Biomedical and therapeutic potential of marine-derived Pseudomonas sp. strain AHG22 exopolysaccharide: A novel bioactive microbial metabolite
  56. Effect of basalt fiber length on the behavior of natural hydraulic lime-based mortars
  57. Optimizing the performance of TPCB/SCA composite-modified asphalt using improved response surface methodology
  58. Compressive strength of waste-derived cementitious composites using machine learning
  59. Melting phenomenon of thermally stratified MHD Powell–Eyring nanofluid with variable porosity past a stretching Riga plate
  60. Development and characterization of a coaxial strain-sensing cable integrated steel strand for wide-range stress monitoring
  61. Compressive and tensile strength estimation of sustainable geopolymer concrete using contemporary boosting ensemble techniques
  62. Customized 3D printed porous titanium scaffolds with nanotubes loading antibacterial drugs for bone tissue engineering
  63. Facile design of PTFE-kaolin-based ternary nanocomposite as a hydrophobic and high corrosion-barrier coating
  64. Effects of C and heat treatment on microstructure, mechanical, and tribo-corrosion properties of VAlTiMoSi high-entropy alloy coating
  65. Study on the damage mechanism and evolution model of preloaded sandstone subjected to freezing–thawing action based on the NMR technology
  66. Promoting low carbon construction using alkali-activated materials: A modeling study for strength prediction and feature interaction
  67. Entropy generation analysis of MHD convection flow of hybrid nanofluid in a wavy enclosure with heat generation and thermal radiation
  68. Friction stir welding of dissimilar Al–Mg alloys for aerospace applications: Prospects and future potential
  69. Fe nanoparticle-functionalized ordered mesoporous carbon with tailored mesostructures and their applications in magnetic removal of Ag(i)
  70. Study on physical and mechanical properties of complex-phase conductive fiber cementitious materials
  71. Evaluating the strength loss and the effectiveness of glass and eggshell powder for cement mortar under acidic conditions
  72. Effect of fly ash on properties and hydration of calcium sulphoaluminate cement-based materials with high water content
  73. Analyzing the efficacy of waste marble and glass powder for the compressive strength of self-compacting concrete using machine learning strategies
  74. Experimental study on municipal solid waste incineration ash micro-powder as concrete admixture
  75. Parameter optimization for ultrasonic-assisted grinding of γ-TiAl intermetallics: A gray relational analysis approach with surface integrity evaluation
  76. Producing sustainable binding materials using marble waste blended with fly ash and rice husk ash for building materials
  77. Effect of steam curing system on compressive strength of recycled aggregate concrete
  78. A sawtooth constitutive model describing strain hardening and multiple cracking of ECC under uniaxial tension
  79. Predicting mechanical properties of sustainable green concrete using novel machine learning: Stacking and gene expression programming
  80. Toward sustainability: Integrating experimental study and data-driven modeling for eco-friendly paver blocks containing plastic waste
  81. A numerical analysis of the rotational flow of a hybrid nanofluid past a unidirectional extending surface with velocity and thermal slip conditions
  82. A magnetohydrodynamic flow of a water-based hybrid nanofluid past a convectively heated rotating disk surface: A passive control of nanoparticles
  83. Prediction of flexural strength of concrete with eggshell and glass powders: Advanced cutting-edge approach for sustainable materials
  84. Efficacy of sustainable cementitious materials on concrete porosity for enhancing the durability of building materials
  85. Phase and microstructural characterization of swat soapstone (Mg3Si4O10(OH)2)
  86. Effect of waste crab shell powder on matrix asphalt
  87. Improving effect and mechanism on service performance of asphalt binder modified by PW polymer
  88. Influence of pH on the synthesis of carbon spheres and the application of carbon sphere-based solid catalysts in esterification
  89. Experimenting the compressive performance of low-carbon alkali-activated materials using advanced modeling techniques
  90. Thermogravimetric (TG/DTG) characterization of cold-pressed oil blends and Saccharomyces cerevisiae-based microcapsules obtained with them
  91. Investigation of temperature effect on thermo-mechanical property of carbon fiber/PEEK composites
  92. Computational approaches for structural analysis of wood specimens
  93. Integrated structure–function design of 3D-printed porous polydimethylsiloxane for superhydrophobic engineering
  94. Exploring the impact of seashell powder and nano-silica on ultra-high-performance self-curing concrete: Insights into mechanical strength, durability, and high-temperature resilience
  95. Axial compression damage constitutive model and damage characteristics of fly ash/silica fume modified magnesium phosphate cement after being treated at different temperatures
  96. Integrating testing and modeling methods to examine the feasibility of blended waste materials for the compressive strength of rubberized mortar
  97. Special Issue on 3D and 4D Printing of Advanced Functional Materials - Part II
  98. Energy absorption of gradient triply periodic minimal surface structure manufactured by stereolithography
  99. Marine polymers in tissue bioprinting: Current achievements and challenges
  100. Quick insight into the dynamic dimensions of 4D printing in polymeric composite mechanics
  101. Recent advances in 4D printing of hydrogels
  102. Mechanically sustainable and primary recycled thermo-responsive ABS–PLA polymer composites for 4D printing applications: Fabrication and studies
  103. Special Issue on Materials and Technologies for Low-carbon Biomass Processing and Upgrading
  104. Low-carbon embodied alkali-activated materials for sustainable construction: A comparative study of single and ensemble learners
  105. Study on bending performance of prefabricated glulam-cross laminated timber composite floor
  106. Special Issue on Recent Advancement in Low-carbon Cement-based Materials - Part I
  107. Supplementary cementitious materials-based concrete porosity estimation using modeling approaches: A comparative study of GEP and MEP
  108. Modeling the strength parameters of agro waste-derived geopolymer concrete using advanced machine intelligence techniques
  109. Promoting the sustainable construction: A scientometric review on the utilization of waste glass in concrete
  110. Incorporating geranium plant waste into ultra-high performance concrete prepared with crumb rubber as fine aggregate in the presence of polypropylene fibers
  111. Investigation of nano-basic oxygen furnace slag and nano-banded iron formation on properties of high-performance geopolymer concrete
  112. Effect of incorporating ultrafine palm oil fuel ash on the resistance to corrosion of steel bars embedded in high-strength green concrete
  113. Influence of nanomaterials on properties and durability of ultra-high-performance geopolymer concrete
  114. Influence of palm oil ash and palm oil clinker on the properties of lightweight concrete
https://doi.org/10.1515/rams-2024-0054
Keywords for this article
MHD; hybrid nanofluid; nonlinear thermal radiation; activation energy; heat source
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. Effect of superplasticizer in geopolymer and alkali-activated cement mortar/concrete: A review
  3. Experimenting the influence of corncob ash on the mechanical strength of slag-based geopolymer concrete
  4. Powder metallurgy processing of high entropy alloys: Bibliometric analysis and systematic review
  5. Exploring the potential of agricultural waste as an additive in ultra-high-performance concrete for sustainable construction: A comprehensive review
  6. A review on partial substitution of nanosilica in concrete
  7. Foam concrete for lightweight construction applications: A comprehensive review of the research development and material characteristics
  8. Modification of PEEK for implants: Strategies to improve mechanical, antibacterial, and osteogenic properties
  9. Interfacing the IoT in composite manufacturing: An overview
  10. Advances in processing and ablation properties of carbon fiber reinforced ultra-high temperature ceramic composites
  11. Advancing auxetic materials: Emerging development and innovative applications
  12. Revolutionizing energy harvesting: A comprehensive review of thermoelectric devices
  13. Exploring polyetheretherketone in dental implants and abutments: A focus on biomechanics and finite element methods
  14. Smart technologies and textiles and their potential use and application in the care and support of elderly individuals: A systematic review
  15. Reinforcement mechanisms and current research status of silicon carbide whisker-reinforced composites: A comprehensive review
  16. Innovative eco-friendly bio-composites: A comprehensive review of the fabrication, characterization, and applications
  17. Review on geopolymer concrete incorporating Alccofine-1203
  18. Advancements in surface treatments for aluminum alloys in sports equipment
  19. Ionic liquid-modified carbon-based fillers and their polymer composites – A Raman spectroscopy analysis
  20. Emerging boron nitride nanosheets: A review on synthesis, corrosion resistance coatings, and their impacts on the environment and health
  21. Mechanism, models, and influence of heterogeneous factors of the microarc oxidation process: A comprehensive review
  22. Synthesizing sustainable construction paradigms: A comprehensive review and bibliometric analysis of granite waste powder utilization and moisture correction in concrete
  23. 10.1515/rams-2025-0086
  24. Research Articles
  25. Coverage and reliability improvement of copper metallization layer in through hole at BGA area during load board manufacture
  26. Study on dynamic response of cushion layer-reinforced concrete slab under rockfall impact based on smoothed particle hydrodynamics and finite-element method coupling
  27. Study on the mechanical properties and microstructure of recycled brick aggregate concrete with waste fiber
  28. Multiscale characterization of the UV aging resistance and mechanism of light stabilizer-modified asphalt
  29. Characterization of sandwich materials – Nomex-Aramid carbon fiber performances under mechanical loadings: Nonlinear FE and convergence studies
  30. Effect of grain boundary segregation and oxygen vacancy annihilation on aging resistance of cobalt oxide-doped 3Y-TZP ceramics for biomedical applications
  31. Mechanical damage mechanism investigation on CFRP strengthened recycled red brick concrete
  32. Finite element analysis of deterioration of axial compression behavior of corroded steel-reinforced concrete middle-length columns
  33. Grinding force model for ultrasonic assisted grinding of γ-TiAl intermetallic compounds and experimental validation
  34. Enhancement of hardness and wear strength of pure Cu and Cu–TiO2 composites via a friction stir process while maintaining electrical resistivity
  35. Effect of sand–precursor ratio on mechanical properties and durability of geopolymer mortar with manufactured sand
  36. Research on the strength prediction for pervious concrete based on design porosity and water-to-cement ratio
  37. Development of a new damping ratio prediction model for recycled aggregate concrete: Incorporating modified admixtures and carbonation effects
  38. Exploring the viability of AI-aided genetic algorithms in estimating the crack repair rate of self-healing concrete
  39. Modification of methacrylate bone cement with eugenol – A new material with antibacterial properties
  40. Numerical investigations on constitutive model parameters of HRB400 and HTRB600 steel bars based on tensile and fatigue tests
  41. Research progress on Fe3+-activated near-infrared phosphor
  42. Discrete element simulation study on effects of grain preferred orientation on micro-cracking and macro-mechanical behavior of crystalline rocks
  43. Ultrasonic resonance evaluation method for deep interfacial debonding defects of multilayer adhesive bonded materials
  44. Effect of impurity components in titanium gypsum on the setting time and mechanical properties of gypsum-slag cementitious materials
  45. Bending energy absorption performance of composite fender piles with different winding angles
  46. Theoretical study of the effect of orientations and fibre volume on the thermal insulation capability of reinforced polymer composites
  47. Synthesis and characterization of a novel ternary magnetic composite for the enhanced adsorption capacity to remove organic dyes
  48. Couple effects of multi-impact damage and CAI capability on NCF composites
  49. Mechanical testing and engineering applicability analysis of SAP concrete used in buffer layer design for tunnels in active fault zones
  50. Investigating the rheological characteristics of alkali-activated concrete using contemporary artificial intelligence approaches
  51. Integrating micro- and nanowaste glass with waste foundry sand in ultra-high-performance concrete to enhance material performance and sustainability
  52. Effect of water immersion on shear strength of epoxy adhesive filled with graphene nanoplatelets
  53. Impact of carbon content on the phase structure and mechanical properties of TiBCN coatings via direct current magnetron sputtering
  54. Investigating the anti-aging properties of asphalt modified with polyphosphoric acid and tire pyrolysis oil
  55. Biomedical and therapeutic potential of marine-derived Pseudomonas sp. strain AHG22 exopolysaccharide: A novel bioactive microbial metabolite
  56. Effect of basalt fiber length on the behavior of natural hydraulic lime-based mortars
  57. Optimizing the performance of TPCB/SCA composite-modified asphalt using improved response surface methodology
  58. Compressive strength of waste-derived cementitious composites using machine learning
  59. Melting phenomenon of thermally stratified MHD Powell–Eyring nanofluid with variable porosity past a stretching Riga plate
  60. Development and characterization of a coaxial strain-sensing cable integrated steel strand for wide-range stress monitoring
  61. Compressive and tensile strength estimation of sustainable geopolymer concrete using contemporary boosting ensemble techniques
  62. Customized 3D printed porous titanium scaffolds with nanotubes loading antibacterial drugs for bone tissue engineering
  63. Facile design of PTFE-kaolin-based ternary nanocomposite as a hydrophobic and high corrosion-barrier coating
  64. Effects of C and heat treatment on microstructure, mechanical, and tribo-corrosion properties of VAlTiMoSi high-entropy alloy coating
  65. Study on the damage mechanism and evolution model of preloaded sandstone subjected to freezing–thawing action based on the NMR technology
  66. Promoting low carbon construction using alkali-activated materials: A modeling study for strength prediction and feature interaction
  67. Entropy generation analysis of MHD convection flow of hybrid nanofluid in a wavy enclosure with heat generation and thermal radiation
  68. Friction stir welding of dissimilar Al–Mg alloys for aerospace applications: Prospects and future potential
  69. Fe nanoparticle-functionalized ordered mesoporous carbon with tailored mesostructures and their applications in magnetic removal of Ag(i)
  70. Study on physical and mechanical properties of complex-phase conductive fiber cementitious materials
  71. Evaluating the strength loss and the effectiveness of glass and eggshell powder for cement mortar under acidic conditions
  72. Effect of fly ash on properties and hydration of calcium sulphoaluminate cement-based materials with high water content
  73. Analyzing the efficacy of waste marble and glass powder for the compressive strength of self-compacting concrete using machine learning strategies
  74. Experimental study on municipal solid waste incineration ash micro-powder as concrete admixture
  75. Parameter optimization for ultrasonic-assisted grinding of γ-TiAl intermetallics: A gray relational analysis approach with surface integrity evaluation
  76. Producing sustainable binding materials using marble waste blended with fly ash and rice husk ash for building materials
  77. Effect of steam curing system on compressive strength of recycled aggregate concrete
  78. A sawtooth constitutive model describing strain hardening and multiple cracking of ECC under uniaxial tension
  79. Predicting mechanical properties of sustainable green concrete using novel machine learning: Stacking and gene expression programming
  80. Toward sustainability: Integrating experimental study and data-driven modeling for eco-friendly paver blocks containing plastic waste
  81. A numerical analysis of the rotational flow of a hybrid nanofluid past a unidirectional extending surface with velocity and thermal slip conditions
  82. A magnetohydrodynamic flow of a water-based hybrid nanofluid past a convectively heated rotating disk surface: A passive control of nanoparticles
  83. Prediction of flexural strength of concrete with eggshell and glass powders: Advanced cutting-edge approach for sustainable materials
  84. Efficacy of sustainable cementitious materials on concrete porosity for enhancing the durability of building materials
  85. Phase and microstructural characterization of swat soapstone (Mg3Si4O10(OH)2)
  86. Effect of waste crab shell powder on matrix asphalt
  87. Improving effect and mechanism on service performance of asphalt binder modified by PW polymer
  88. Influence of pH on the synthesis of carbon spheres and the application of carbon sphere-based solid catalysts in esterification
  89. Experimenting the compressive performance of low-carbon alkali-activated materials using advanced modeling techniques
  90. Thermogravimetric (TG/DTG) characterization of cold-pressed oil blends and Saccharomyces cerevisiae-based microcapsules obtained with them
  91. Investigation of temperature effect on thermo-mechanical property of carbon fiber/PEEK composites
  92. Computational approaches for structural analysis of wood specimens
  93. Integrated structure–function design of 3D-printed porous polydimethylsiloxane for superhydrophobic engineering
  94. Exploring the impact of seashell powder and nano-silica on ultra-high-performance self-curing concrete: Insights into mechanical strength, durability, and high-temperature resilience
  95. Axial compression damage constitutive model and damage characteristics of fly ash/silica fume modified magnesium phosphate cement after being treated at different temperatures
  96. Integrating testing and modeling methods to examine the feasibility of blended waste materials for the compressive strength of rubberized mortar
  97. Special Issue on 3D and 4D Printing of Advanced Functional Materials - Part II
  98. Energy absorption of gradient triply periodic minimal surface structure manufactured by stereolithography
  99. Marine polymers in tissue bioprinting: Current achievements and challenges
  100. Quick insight into the dynamic dimensions of 4D printing in polymeric composite mechanics
  101. Recent advances in 4D printing of hydrogels
  102. Mechanically sustainable and primary recycled thermo-responsive ABS–PLA polymer composites for 4D printing applications: Fabrication and studies
  103. Special Issue on Materials and Technologies for Low-carbon Biomass Processing and Upgrading
  104. Low-carbon embodied alkali-activated materials for sustainable construction: A comparative study of single and ensemble learners
  105. Study on bending performance of prefabricated glulam-cross laminated timber composite floor
  106. Special Issue on Recent Advancement in Low-carbon Cement-based Materials - Part I
  107. Supplementary cementitious materials-based concrete porosity estimation using modeling approaches: A comparative study of GEP and MEP
  108. Modeling the strength parameters of agro waste-derived geopolymer concrete using advanced machine intelligence techniques
  109. Promoting the sustainable construction: A scientometric review on the utilization of waste glass in concrete
  110. Incorporating geranium plant waste into ultra-high performance concrete prepared with crumb rubber as fine aggregate in the presence of polypropylene fibers
  111. Investigation of nano-basic oxygen furnace slag and nano-banded iron formation on properties of high-performance geopolymer concrete
  112. Effect of incorporating ultrafine palm oil fuel ash on the resistance to corrosion of steel bars embedded in high-strength green concrete
  113. Influence of nanomaterials on properties and durability of ultra-high-performance geopolymer concrete
  114. Influence of palm oil ash and palm oil clinker on the properties of lightweight concrete
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 13.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2024-0054/html
Scroll to top button