Startseite Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes
Artikel Open Access

Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes

  • Ting-Yun Kuo , Cuei-Fang Jhang , Che-Min Lin , Tzu-Yang Hsien und Hsyue-Jen Hsieh EMAIL logo
Veröffentlicht/Copyright: 29. Dezember 2017
Artikel downloaden (PDF)
Open Physics
Aus der Zeitschrift Open Physics Band 15 Heft 1

Abstract

It is difficult to fabricate chitosan-wrapped coaxial nanofibers, because highly viscous chitosan solutions might hinder the manufacturing process. To overcome this difficulty, our newly developed method, which included the addition of a small amount of gum arabic, was utilized to prepare much less viscous chitosan solutions. In this way, coaxial polyvinyl alcohol (PVA)/chitosan (as core/shell) nanofiber membranes were fabricated successfully by coaxial electrospinning. The core/shell structures were confirmed by TEM, and the existence of PVA and chitosan was also verified using FT-IR and TGA. The tensile strength of the nanofiber membranes was increased from 0.6-0.7 MPa to 0.8-0.9 MPa after being crosslinked with glutaraldehyde. The application potential of the PVA/chitosan nanofiber membranes was tested in drug release experiments by loading the core (PVA) with theophylline as a model drug. The use of the coaxial PVA/chitosan nanofiber membranes in drug release extended the release time of theophylline from 5 minutes to 24 hours. Further, the release mechanisms could be described by the Korsmeyer-Peppas model. In summary, by combining the advantages of PVA and chitosan (good mechanical strength and good biocompatibility respectively), the coaxial PVA/chitosan nanofiber membranes are potential biomaterials for various biomedical applications.

Keywords: electrospinning; core/shell structures; gum arabic; drug release; Korsmeyer-Peppas model
PACS: 81.07.-b

1 Introduction

Electrospinning is a commonly used technology to obtain polymer nanofibers with diameters in the range of several nanometers to micrometers [1, 2, 3, 4]. During the electrospinning process electrostatic repulsion is used to overcome the surface tension of a solution droplet at the needle tip, thus stretching the droplet to form a jet, which dries while flying toward a collector, to produce nanofibers [5]. The accumulation of electrospun nanofibers forms a membrane with high porosity and specific surface area. This membrane is suitable for use in tissue engineering, drug release and separation process [6]. Coaxial electrospinning is a modified electrospinning method which uses a blunt-tip coaxial needle to extrude core and shell solutions without mixing during electrospinning, thus producing nanofibers with a core/shell structure [7, 8, 9, 10]. There are several advantages associated with the core/shell structure. For example, by using a material easy to be electrospun as core layer, another material, which cannot be electrospun alone, may have a chance to be spun successfully as shell layer. On the other hand, if the core layer contains drugs, the outer shell layer can act as a barrier to give a slow and sustained drug release. Furthermore, the mechanical properties of the coaxial nanofibers can be improved by choosing a material with good strength as the core layer. Therefore, in the application of tissue engineering, natural materials with good biocompatibility can be used as shell layer material to wrap the core material with low biocompatibility but good mechanical strength, thus generating biocompatible coaxial nanofibers that also possess suitable strength.

In the present study, polyvinyl alcohol (PVA) and chitosan were selected as major core and shell materials, respectively. PVA is a water-soluble polymer that can be used as an excipient for drug delivery. PVA is also a material easy to be electrospun and thus can be used as core material for coaxial electrospinning [11, 12]. Chitosan is a natural basic polysaccharide composed of glucosamine and N-acetyl glucosamine [13]. It has been used in drug delivery, tissue engineering, and other biomedical applications because it is biocompatible, biodegradable and antimicrobial. Chitosan is soluble in acidic solution but the chitosan solution becomes highly viscous when its concentration goes high, making the preparation of chitosan nanofibers by electrospinning quite problematic. To overcome this difficulty, chitosan has to dissolve in high concentration of acetic acid or organic solvents such as trifluotoacetic acid (TFA) and hexafluoroisopropanol (HFIP) [14, 15, 16]. However, TFA and HFIP are highly corrosive and expensive. To prevent the use of TFA and HFIP, we employed our newly developed method (i.e., the addition of gum arabic) to prepare a solution with a high chitosan content but a much lower viscosity, thus making the electrospinning process feasible [17, 18]. Gum arabic is a branched biopolymer. In our previous research, we found that gum arabic can interact with chitosan to form globe-like microstructures and thus remarkably decrease the viscosity of the resulting chitosan solution [19].

Similarly, this research demonstrated that the addition of a small amount of gum arabic significantly decreased the viscosity of chitosan solutions even though chitosan was dissolved in a mild (5 wt%) aqueous acetic acid solution. The chitosan solution thus prepared was then used as the shell solution in the coaxial electrospinning while the PVA solution was selected as the core solution. The parameters affecting the electrospinning process such as the flow rates and compositions of core and shell solutions were optimized. The mechanical properties and the application of the coaxial PVA/chitosan nanofiber membranes were also investigated.

2 Materials and methods

2.1 Materials

Chitosan (molecular weight: about 300 kDa; degree of deacetylation: about 90%) was purchased from Kiotek Co. (Taipei, Taiwan). Polyvinyl alcohol (PVA) (degree of hydrolysis: 98.5-99.2%) was supplied by Chang Chun Petrochemical Co. Ltd (Taiwan). Gum arabic, acetic acid and other chemicals of reagent grade were purchased from Sigma-Aldrich (St. Louis, MO, USA).

2.2 Preparation of solutions

The abbreviations and compositions of various PVA and chitosan solutions prepared in this study are shown in Table 1. PVA solutions were prepared by dissolving PVA in 90 °C water. 8, 10 and 12 wt% PVA solutions were prepared and designated as P8, P10 and P12, respectively. The preparation of chitosan solutions suitable for electrospinning was carried out by using our newly developed method [17, 18, 19]. Our method included the addition of a small amount of gum arabic (10 wt% of chitosan) that significantly decreased the viscosity of chitosan solutions when using a mild aqueous acetic acid solution as a solvent. To prepare various chitosan solutions, chitosan powder was dissolved in acetic acid solution, and then gum arabic (10 wt% of chitosan) was added into the solution to greatly decrease the viscosity of chitosan solution. 4, 6, 8, 10 and 12 wt% chitosan solutions (containing gum arabic) were prepared using 5, 10 or 20 wt% aqueous acetic acid solution as a solvent. These chitosan solutions were designated as Cm-n (m representing the concentration of chitosan and n representing the concentration of acetic acid). For example, C4-5 represents a chitosan solution containing 4wt% chitosan, 0.4wt% gum arabic and 5 wt% acetic acid.

Table 1

The abbreviations and compositions of various PVA and chitosan solutions

Composition (wt%)
Abbreviation
ChitosanGum arabicAcetic acidPVAH2O
PVA solutionsP8---892
P10---1090
P12---1288
P10-20--201070
Chitosan solutionsC4-540.45-90.6
C6-560.65-88.4
C8-580.85-86.2
C10-5101.05-84.0
C12-5121.25-81.8
C4-1040.410-85.6
C6-1060.610-83.4
C8-1080.810-81.2
C1O-10101.010-79.0
C12-10121.210-76.8
C4-2040.420-75.6
C6-2060.620-73.4
C8-2080.820-71.2
C1O-20101.020-69.0
C12-20121.220-66.8

2.3 Characterization of solutions

A pH meter (model 420A, Orion, USA) was used to determine the pH of various solutions. The viscosity of various solutions was measured by a viscometer (model DV-II+, Brookfield, USA), and the rotation speed of spindle was fixed at 2 rpm. The conductivity and surface tension of various solutions were also measured by using a conductivity meter (model COND6 plus, Eutech, Singapore) and a tesiometer (model 514-B, Itoh Seisakusho, Japan), respectively.

2.4 Coaxial electrospinning of solutions

Coaxial electrospun nanofibers with core/shell structures were fabricated by using an electrospinning unit (Jyi-Goang Enterprise, Taipei, Taiwan). The blunt-tip coaxial needle was composed of a 23G (i.d. 0.33 mm, o.d. 0.63 mm) inner needle concentrically mounted on an 18G (i.d. 0.96 mm, o.d. 1.26 mm) outer needle. PVA and chitosan solutions were loaded in two individual syringes and fed by two separate syringe pumps. The applied voltage and working distance between needle tip and collector were 25 KV and 15 cm, respectively. The environmental temperature and relative humidity were controlled at 32 °C and 40-50%.

2.5 Analysis of coaxial nanofibers

A scanning electron microscope (SEM, JSM-5310, Jeol, Japan) and a transmission electron microscope (TEM, JEM-1230, Jeol, Japan) were used to observe the morphology of coaxial nanofibers. Fourier transform infrared spectroscopy (FT-IR) analysis was carried out using an FT-IR spectrometer (Spectrum One, Perkin-Elmer, USA).

Thermal behavior of various samples was investigated by a thermogravimetric analysis meter (TGA, model Pyris 1, Perkin-Elmer, USA). For TGA analysis, about 5 mg sample was hold at 50 °C for 20 min to remove residual water in the sample, and then was heated from 50 °C to 600 °C at a rate of 10 °C/min. The process of TGA analysis was under continuous nitrogen purge at a rate of 20 ml/min.

2.6 Mechanical properties of coaxial nanofiber membranes

To analyze mechanical properties of nanofiber membranes, the membranes were cut into a dumbbell shape, and the thicknesses of membranes were measured with a micrometer. The mechanical properties including tensile strength (stress at maximum load) and elongation (strain at maximum load) were measured with a tensile strength instrument (model LRX, Lloyd, Hampshire, UK). The stretching rate of the measurement was 10 mm/min.

2.7 Drug release experiments

The application potential of the PVA/chitosan coaxial nanofiber membranes was tested in drug release experiments when the core (PVA) was loaded with theophylline (5 mg/ml) as a model drug. For comparison purposes, conventional (non-coaxial) PVA nanofiber membranes were also fabricated and used as controls. The theophylline containing nanofiber membranes were crosslinked with glutaraldehyde vapor for 8 hours, followed by drying in a vacuum oven for 12 hours. The drug release experiments were carried out by immersing the nanofiber membranes in phosphate-buffered saline (PBS). PBS samples (1 ml) were withdrawn periodically at predetermined time intervals and the theophylline concentrations in the PBS samples were determined using a spectrophotometer (model U-2001, Hitachi, Japan) at 274 nm. The “percentage of drug released” was calculated using the following formula:

Percentageofdrugreleased%==AmountofdrugreleasedaftertimetAmountofdrugreleasedafter24hours×100%

Since theophylline was initially present in the core (PVA), the shell (chitosan) acted as a barrier to the release of theophylline. It was expected that the use of drug-loaded coaxial nanofiber membranes would give a gradual and sustained drug release. However, several phenomena such as nanofiber swelling, disintegration, and drug diffusion were involved in the release of theophylline. To investigate these anomalous transport phenomena, a semi-empirical model called “Korsmeyer-Peppas model” was utilized to correlate the theophylline release from the coaxial nanofiber membranes because the above-mentioned anomalous phenomena were considered in this model, as shown below [20, 21, 22]:

MtM∞=ktn

where Mt is the cumulative amount of drug at any time t, M∞ is the cumulative amount of drug at the last time of the measurement, k is the release rate constant, and n is the release exponent. To obtain the parameters of release kinetics (k and n), data obtained from drug release experiments were plotted as log percentage of drug released vs. log time [21, 23].

3 Results and discussion

3.1 Properties of PVA and chitosan solutions

To search for polymer solutions suitable for electrospinning, the pH, surface tension and conductivity of various PVA and chitosan solutions were determined, as shown in Table 2. The pH of PVA solutions slightly decreased as the concentration of PVA increased, probably due to the residual acetyl groups in PVA that might be hydrolyzed to yield acetic acid. On the other hand, since chitosan is a basic polysaccharide, increasing the concentration of chitosan elevated the pH of chitosan solutions (containing chitosan, gum Arabic, and acetic acid) (Table 2).

Table 2

The pH, surface tension and conductivity of various PVA and chitosan solutions

SamplepHSurface tension (mN/m)Conductivity (S/m)
PVA solutionsP86.0151.43±1.100.065±0.000
P105.9550.13±0.770.074±0.000
P125.7448.15±0.290.083±0.000
Chitosan solutionsC4-53.2944.82±0.440.543±0.001
C6-53.4544.67±1.330.731±0.001
C8-53.9144.55±0.630.921±0.002
C10-54.1743.36±0.351.002±0.001
C12-54.6342.30±0.211.150±0.002
C4-103.1943.11±0.660.545±0.000
C6-103.3942.69±0.270.717±0.001
C8-103.6142.03±0.440.870±0.001
C10-103.7241.44±0.210.937±0.001
C12-104.0040.72±0.961.060±0.002
C4-202.6538.37±1.470.460±0.001
C6-202.8236.96±0.950.606±0.002
C8-203.0735.66±0.840.746±0.001
C10-203.1234.70±0.200.854±0.003
C12-203.2133.57±0.740.895±0.004

During the electrospinning process electrostatic repulsion is used to overcome the surface tension of a solution droplet at the needle tip [24], suggesting that both surface tension and conductivity may influence the morphology of nanofibers. As shown in Table 2, surface tension of various PVA and chitosan solutions decreased while the concentrations of PVA and chitosan increased. The use of acetic acid solution at higher concentrations also decreased the surface tension of chitosan solutions, since the surface tension of pure acetic acid (27.08 mN/m) [25] is lower than that of pure water (71.97 mN/m). As for theconductivity of solutions, increasing the concentrations of PVA and chitosan improved the conductivity of solutions, especially for chitosan (Table 2). Since PVA is a relatively neutral polymer, however, chitosan is a basic polysaccharide which contains positive charge in an acidic solution, thus enhancing the conductivity of solutions.

The viscosity of polymer solutions plays an important role in electrospinning. A low-viscosity polymer solution implies less entanglement of polymer chains in the solution which may lead to poor electrospinning, resulting in the formation of beads or spindle-like structures. However, if solution viscosity is too high, the solution will become too sticky to be electrospun. Figure 1 shows the influence of concentration on the viscosity of PVA and chitosan solutions. As shown in Figure 1(a), the viscosity of PVA solutions increased as the concentration of PVA increased, possibly due to more entanglement of polymer chains. Figure 1(b) shows a similar trend for chitosan solutions. It should be noted that without the addition of gum arabic in chitosan solution, the viscosity of chitosan solution dramatically increased when the concentration of chitosan solution increased to 8 wt% (hollow symbols in Figure 1(b)). Therefore, the preparation of high-content (10-12 wt%) chitosan solutions would be impossible unless using our newly developed method, i.e., the addition of a small amount of gum arabic (10 wt% of chitosan) to greatly decrease the viscosity of chitosan solutions (solid symbols in Figure 1(b)) [17, 18]. Gum arabic is a branched biopolymer. In our previous research, we found that gum arabic can interact with chitosan to form globe-like microstructures and thus remarkably decrease the viscosity of the resulting chitosan solution [19]. As a result, the use of our newly developed method (i.e., the addition of gum arabic) to prepare a chitosan solution with a high chitosan content (up to 12 wt%) but a much lower viscosity made the following electrospinning process feasible. Figure 1(b) also shows that the viscosity of chitosan solutions can be further lowered by decreasing the concentration of acetic acid from 20 to 5 wt%.

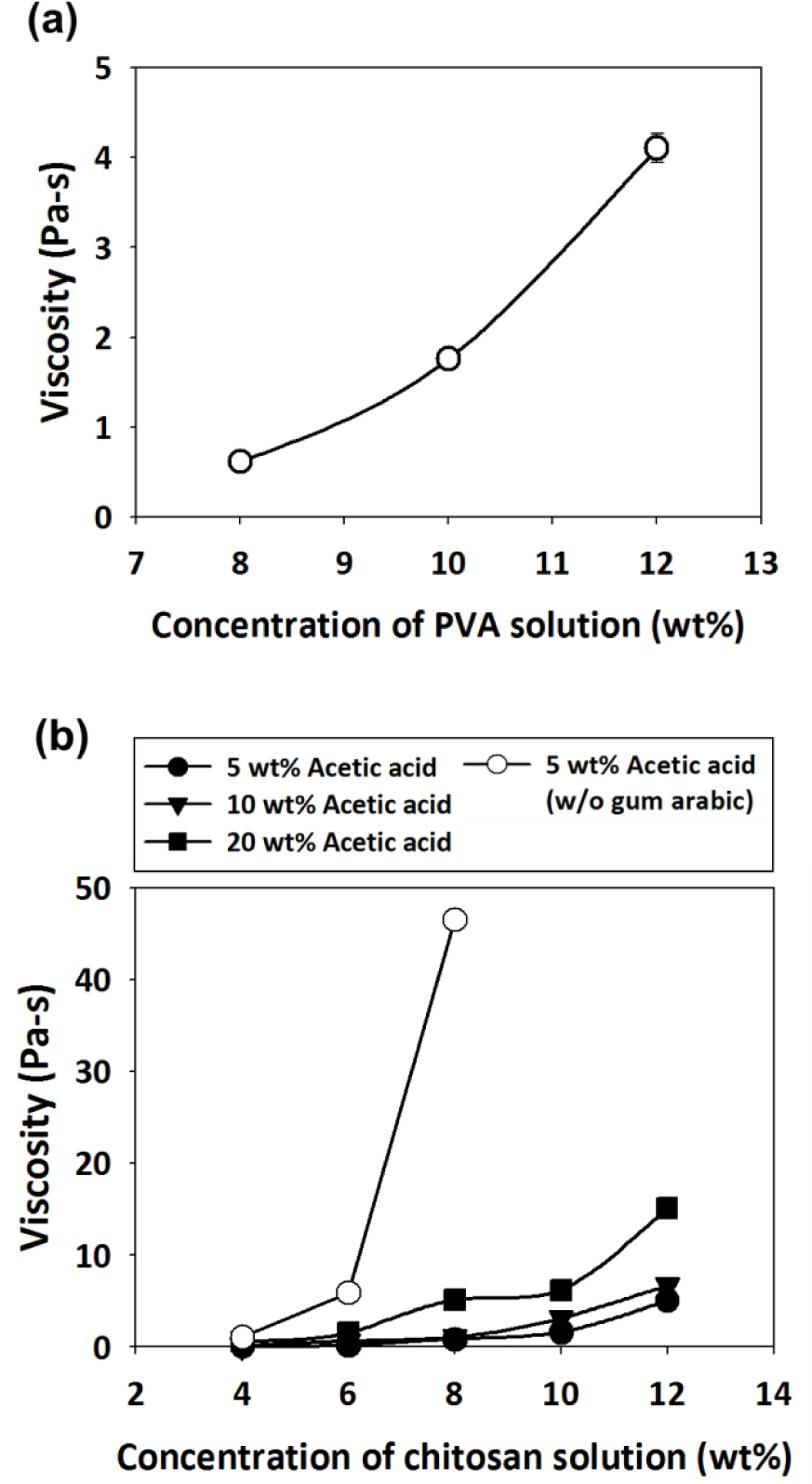
Figure 1 Viscosity of: (a) PVA solutions, (b) chitosan solutions, prepared as shown in Table 1. Chitosan was dissolved in 5 wt%, 10 wt%, or 20 wt% aqueous acetic acid solutions containing gum arabic (solid symbols). For comparison, the viscosity of chitosan solutions without gum arabic (hollow symbols) was also measured.
Figure 1

Viscosity of: (a) PVA solutions, (b) chitosan solutions, prepared as shown in Table 1. Chitosan was dissolved in 5 wt%, 10 wt%, or 20 wt% aqueous acetic acid solutions containing gum arabic (solid symbols). For comparison, the viscosity of chitosan solutions without gum arabic (hollow symbols) was also measured.

3.2 Influence of process parameters

Process parameters affecting the coaxial electrospinning such as the flow rates and compositions of core and shell solutions were investigated and optimized.

3.2.1 Flow rate ratio of core and shell solutions

Figure 2 shows the SEM images of coaxial PVA/chitosan (P10/C8-20 as core/shell) nanofibers prepared under different flow rate ratios of core and shell solutions. Nanofibers with better morphology were found when flow rate ratios of core:shell solutions were 0.15:0.15 and 0.15:0.3 (mL/h). Further increase in the flow rate of shell (chitosan) solution might interrupt the formation of PVA nanofibers. Repeating the experiment indicated that the best flow rate ratio of core:shell solution was 0.15:0.15 (mL/h) which was then utilized to carry out the following experiments.

Figure 2 SEM images of coaxial PVA/chitosan (P10/C8-20 as core/shell) nanofibers prepared under the same core flow rate (0.15 mL/h) but different shell flow rates (0.15-0.9 mL/h). Flow rates are designated on the top of each image by “core: shell” flow rates (mL/h). (Scale bar = 60 μm)
Figure 2

SEM images of coaxial PVA/chitosan (P10/C8-20 as core/shell) nanofibers prepared under the same core flow rate (0.15 mL/h) but different shell flow rates (0.15-0.9 mL/h). Flow rates are designated on the top of each image by “core: shell” flow rates (mL/h). (Scale bar = 60 μm)

3.2.2 Composition of core (PVA) solution

Figure 3(a) shows the SEM images of coaxial PVA/chitosan nanofibers prepared using different core (PVA) solutions (P8, P10, P12) but the same shell solution (C8-20). No nanofibers were found in P8/C8-20 group since the viscosity of P8 solution was too low to form nanofibers (see Figure 1(a)). Few nanofibers were found in P12/C8-20 group since the viscosity of P12 solution was slightly too high and thus not favorable for nanofiber formation. In contrast, more nanofibers were found in P10/C8-20 group and thus P10 was selected as the composition of core solution for coaxial electrospinning in this research.

Figure 3 SEM images of coaxial PVA/chitosan (as core/shell) nanofibers prepared using: (a) different core solutions but the same shell solution (C8-20), (b) the same core solution (P10) but different shell solutions. The core and shell flow rates were the same (0.15 mL/h). (Scale bar = 60 μm)
Figure 3

SEM images of coaxial PVA/chitosan (as core/shell) nanofibers prepared using: (a) different core solutions but the same shell solution (C8-20), (b) the same core solution (P10) but different shell solutions. The core and shell flow rates were the same (0.15 mL/h). (Scale bar = 60 μm)

3.2.3 Composition of shell (chitosan) solution

Figure 3(b) shows the SEM images of coaxial PVA/chitosan nanofibers prepared using the same core solution (P10) but different shell solutions (C4-20, C6-20, C8-20, C10-20, C12-20). Few nanofibers were found in P10/C10-20 and P10/C12-20 groups since the viscosity of C10-20 and C12-20 solutions was quite high and thus not favorable for nanofiber formation. In contrast, more nanofibers were found in P10/C4-20, P10/C6-20, and P10/C8-20 groups and thus these three groups were selected as the compositions of shell solutions for further investigation.

3.2.4 Concentration of acetic acid

One of the parameters affecting electrospinning is the solvent utilized to prepare a polymer solution [26]. It was found that better coaxial nanofibers were obtained when the solvent of core solution was more similar to the solvent of shell solution [27]. So far the solvents of core (PVA) and shell (chitosan) solutions were water and 20 wt% aqueous acetic acid solution, respectively. In order to make these two solvents more similar to each other, two methods were considered. The first method was to replace the solvent of core solution by 20 wt% aqueous acetic acid solution. The second method was to replace the solvent of shell solution by water, but it was unfeasible because chitosan was water-insoluble. The alternative method was to use acetic acid solution at lower concentration (5 or 10 wt%) as the solvent of shell solution.

About the first method, Figure 4(a) shows the SEM images of coaxial PVA/chitosan nanofibers obtained when the solvents of core and shell solutions were the same (20 wt% aqueous acetic acid solution). However, very few nanofibers were found in these groups (P10-20/C4-20, P10-20/C6-20 and P10-20/C8-20), indicating that acetic acid solution might not be a suitable solvent for PVA.

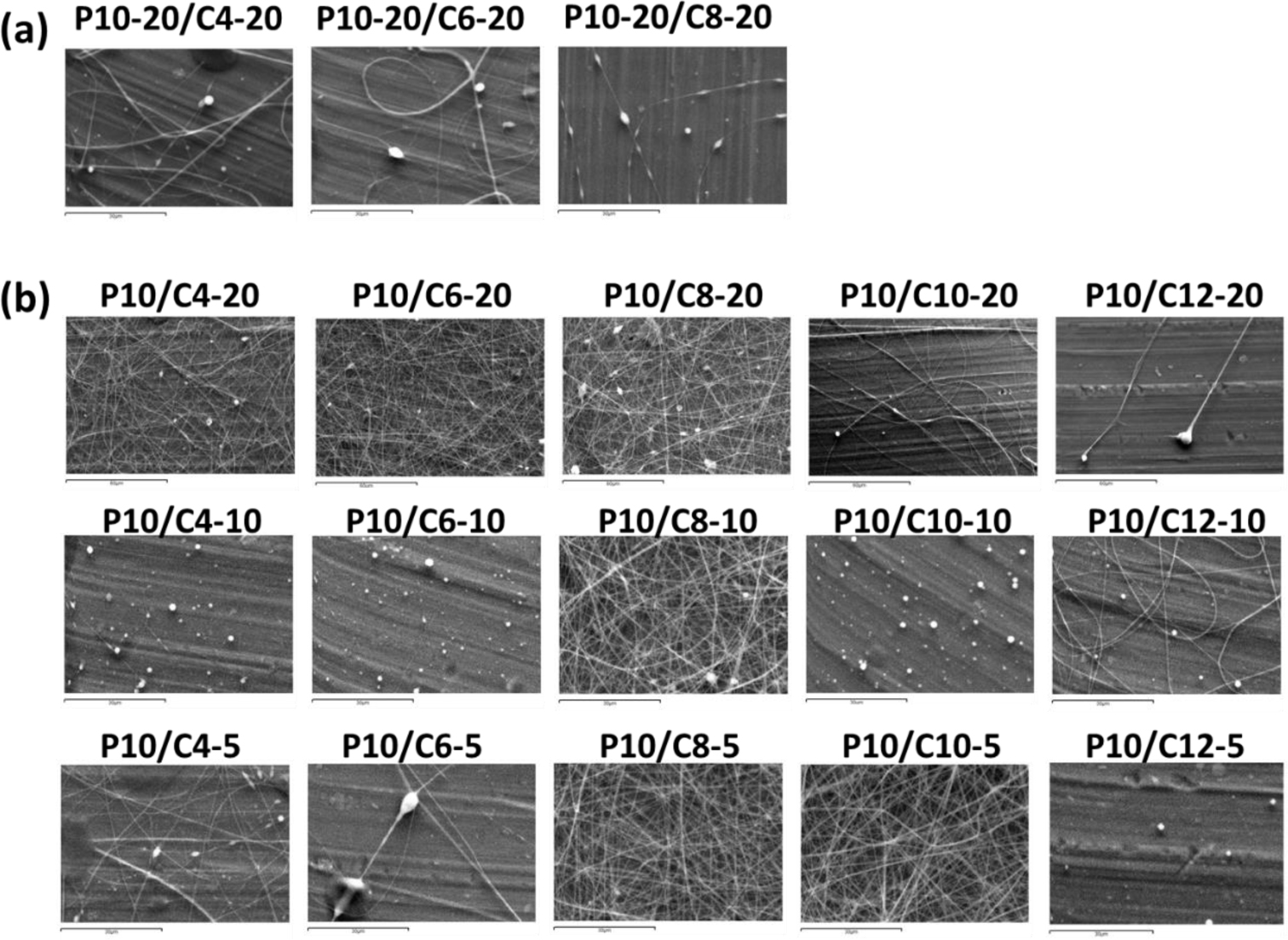
Figure 4 SEM images of coaxial PVA/chitosan (as core/shell) nanofibers prepared using: (a) the same core solution (P10-20) but different shell solutions, (b) the same core solution (P10) but different shell solutions. The core and shell flow rates were the same (0.15 mL/h). (Scale bar = 60 μm)
Figure 4

SEM images of coaxial PVA/chitosan (as core/shell) nanofibers prepared using: (a) the same core solution (P10-20) but different shell solutions, (b) the same core solution (P10) but different shell solutions. The core and shell flow rates were the same (0.15 mL/h). (Scale bar = 60 μm)

About the second method, Figure 4(b) shows the SEM images of coaxial PVA/chitosan nanofibers obtained when acetic acid solution at lower concentration (5 or 10 wt%) was utilized as the solvent of shell (chitosan) solution. When the concentration of acetic acid decreased to 10 wt%, nanofibers were found only in P10/C8-10 group (see the second row in Figure 4(b)). When the concentration of acetic acid decreased further to 5 wt%, nanofibers were found in P10/C8-5 and P10/C10-5 groups (see the third row in Figure 4(b)). In comparison with the results of nanofibers obtained using 20 wt% acetic acid solution as the solvent of shell solution (see the first row in Figure 4(b)), a similar amount of nanofibers but less beads and spindle-like structures were found when using 5 wt% acetic acid solution as the solvent. Hence, P10/C8-5 and P10/C10-5 groups were selected for further investigation.

3.3 Characteristics of coaxial PVA/chitosan nanofibers

Figure 5 shows the TEM images of various coaxial PVA/chitosan (as core/shell) nanofibers. The coaxial structures of electrospun nanofibers can be found in all five groups. However, among these chitosan-wrapped coaxial nanofibers better coverage of chitosan was present in P10/C8-5 group.

Figure 5 TEM images of various coaxial PVA/chitosan (as core/shell) nanofibers. (Scale bar = 0.1 μm)
Figure 5

TEM images of various coaxial PVA/chitosan (as core/shell) nanofibers. (Scale bar = 0.1 μm)

To confirm the existence of PVA and chitosan, FT-IR analysis was carried out, as shown in Figure 6. PVA shows a characteristic peak at 3248 −1 (O–H stretching) and two peaks at 2923 cm−1 (C–H stretching) and 1077 cm−1 (C–O stretching). On the other hand, chitosan shows a peak at 1647 cm−1 (C=O stretching) and another peak at 1581 cm−1 (N–H bending). Gum arabic shows a peak at 1610 cm−1 (COO-symmetric stretching) [28]. Coaxial P10/C8-5 nanofiber membrane shows characteristic peaks of PVA at 3273 cm−1 (O–H stretching), 2925 cm−1 (C–H stretching) and 1080 cm−1 (C–O stretching), and also characteristic peaks of chitosan at 1661 cm−1 (C=O stretching) and another peak at 1584 cm−1 (N–H bending). P10/C10-5 nanofiber membrane shows similar results, thus confirming the existence of PVA and chitosan in coaxial nanofibers.

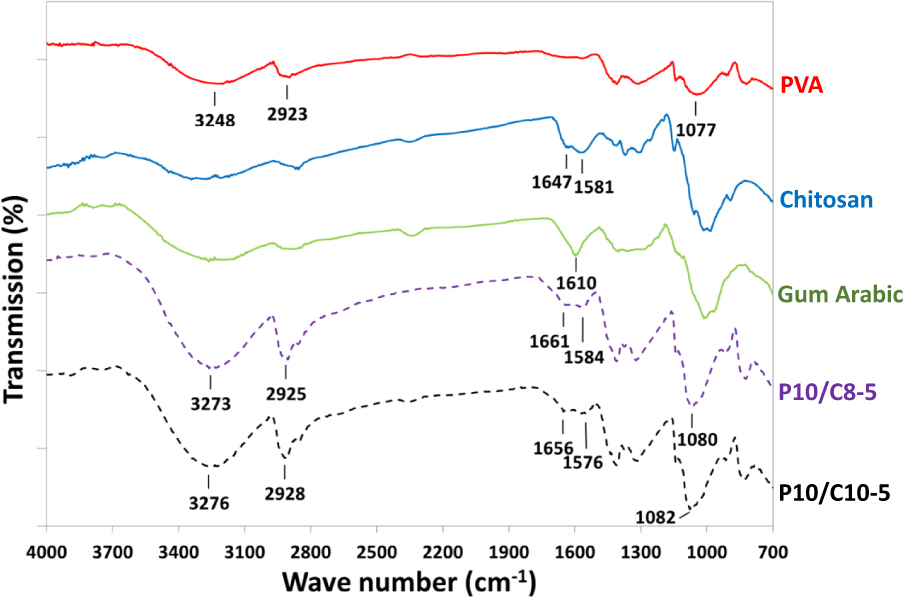
Figure 6 FT-IR spectra of PVA, chitosan, gum arabic, coaxial P10/C8-5 nanofiber membranes, and coaxial P10/C10-5 nanofiber membranes.
Figure 6

FT-IR spectra of PVA, chitosan, gum arabic, coaxial P10/C8-5 nanofiber membranes, and coaxial P10/C10-5 nanofiber membranes.

3.4 Thermal properties of coaxial PVA/chitosan nanofibers

TGA thermograms of PVA powder, chitosan powder and coaxial nanofibers (P10/C8-5 and P10/C10-5) are shown in Figure 7. According to the literature, the thermal degradation of PVA is approximately a two-step degradation [29], which is consistent with the PVA curve in Figure 7. The thermal degradation of chitosan is also a two-step degradation. In the first step, 50% weight loss occurs between 220°C and 320°C [30], which is also consistent with the chitosan curve in Figure 7. Interestingly, if comparing all four TGA curves in Figure 7, the P10/C8-5 curve is more similar to the chitosan curve while the P10/C10-5 curve is more similar to the PVA curve. The reason could be that the shell solution of P10/C8-5 was less viscous than that of P10/C10-5 andit might be easier to form coaxial P10/C8-5 nanofibers with better coverage of chitosan. Hence in comparison with P10/C10-5, the TGA thermogram of P10/C8-5 is more similar to that of chitosan. On the contrary, P10/C10-5 might have a thinner coverage of chitosan, thus making the TGA thermogram of P10/C10-5 more similar to that of PVA.

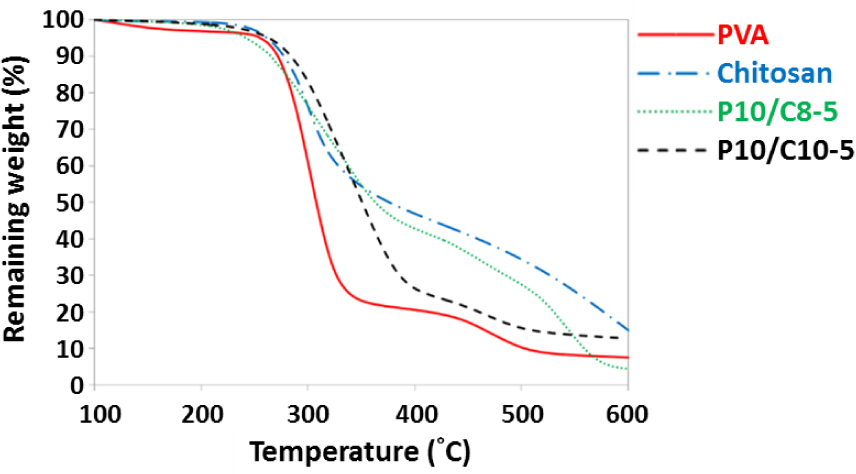
Figure 7 TGA thermograms of PVA, chitosan, coaxial P10/C8-5 nanofiber membranes, and coaxial P10/C10-5 nanofiber membranes.
Figure 7

TGA thermograms of PVA, chitosan, coaxial P10/C8-5 nanofiber membranes, and coaxial P10/C10-5 nanofiber membranes.

3.5 Mechanical properties of coaxial PVA/chitosan nanofiber membranes

To enhance the mechanical properties of coaxial PVA/chitosan (P10/C8-5 and P10/C10-5) nanofiber membranes, the membranes were crosslinked by glutaraldehyde for 8 hours [31]. Figure 8 shows the mechanical properties (tensile strength and elongation) of coaxial P10/C10-5 and P10/C8-5 nanofiber membranes (uncrosslinked and crosslinked). The tensile strength (stress at maximum load) of P10/C8-5 and P10/C10-5 membranes increased from 0.77 and 0.66 MPa to 0.91 and 0.83 MPa, respectively (Figure 8(a)). The tensile strength of P10/C8-5 (uncrosslinked and crosslinked) was higher than that of P10/C10-5, possibly due to the better coverage of shell (chitosan) layer (see the second row in Figure 5) that enhanced the tensile strength of P10/C8-5 especially after crosslinking.

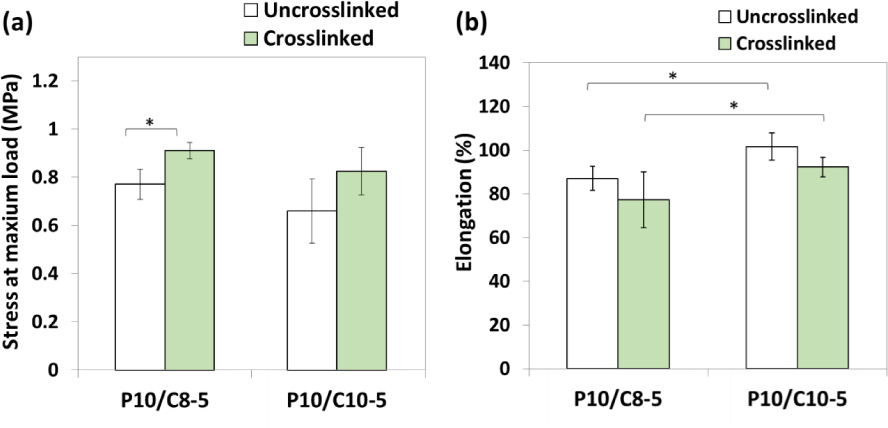
Figure 8 Mechanical properties of coaxial P10/C10-5 and P10/C8-5 nanofiber membranes: (a) Tensile strength (stress at maximum load), (b) elongation (strain at maximum load).* p< 0.05.
Figure 8

Mechanical properties of coaxial P10/C10-5 and P10/C8-5 nanofiber membranes: (a) Tensile strength (stress at maximum load), (b) elongation (strain at maximum load).* p< 0.05.

As shown in Figure 8(b), crosslinking also caused a slight decrease in the elongation (strain at maximum load) of P10/C8-5 and P10/C10-5 membranes, i.e., from 87% and 102% down to 77% and 92% (still ductile), respectively. Taken together, coaxial P10/C8-5 and P10/C10-5 nanofiber membranes exhibited favorable mechanical properties (good tensile strength and good ductility), but P10/C8-5 membranes were better and thus utilized in the following drug release experiments.

3.6 Drug release from coaxial PVA/chitosan nanofiber membranes

Theophylline is a small molecule drug (a bronchodilator) and can be easily released from a dense film [32]. The use of coaxial PVA/chitosan (P10/C8-5) nanofiber membranes in drug release was carried out by loading the core (PVA) with theophylline (5 mg/ml) as a model drug. For comparison purposes, conventional (non-coaxial) PVA (P10) nanofiber membranes loaded with theophylline were also prepared. Figure 9 shows the release profiles of theophylline from coaxial P10/C8-5 nanofiber membranes and also from non-coaxial P10 nanofiber membranes. During the first 3 minutes, 95% of theophylline was released from P10 membranes (Figure 9(b)). In contrast, 95% release of theophylline from P10/C8-5 (as core/shell) membranes was prolonged to 24 hours (Figure 9(a)). In Figure 9(c), both P10/C8-5 and P10 were confirmed as nanofiber membranes, but the average diameter of P10/C8-5 nanofibers (about 620 nm) was larger than that of P10 nanofibers (about 506 nm). Since theophylline was initially present in the core (PVA), the shell (chitosan) acted as a barrier, thus slowing down the release of theophylline. Besides, due to the larger nanofiber diameter, the specific area of P10/C8-5 nanofibers should be smaller than the specific area of P10 nanofibers. The smaller specific area also caused the release of theophylline from P10/C8-5 membranes to become slower. The drug release behavior of coaxial P10/C8-5 nanofiber membranes might be divided into three stages. The first stage was the swelling of nanofibers that gave a burst release of theophylline. The second stage was the disintegration of nanofiber membranes that gave a continuous theophylline release at a rate lower than the first stage. The third stage was the gradual diffusion of theophylline from the core that permeated through the shell of nanofibers and eventually reached equilibrium [33]. In the third stage, the chitosan shell layer was a barrier of mass transfer and thus decreased the release rate of theophylline.

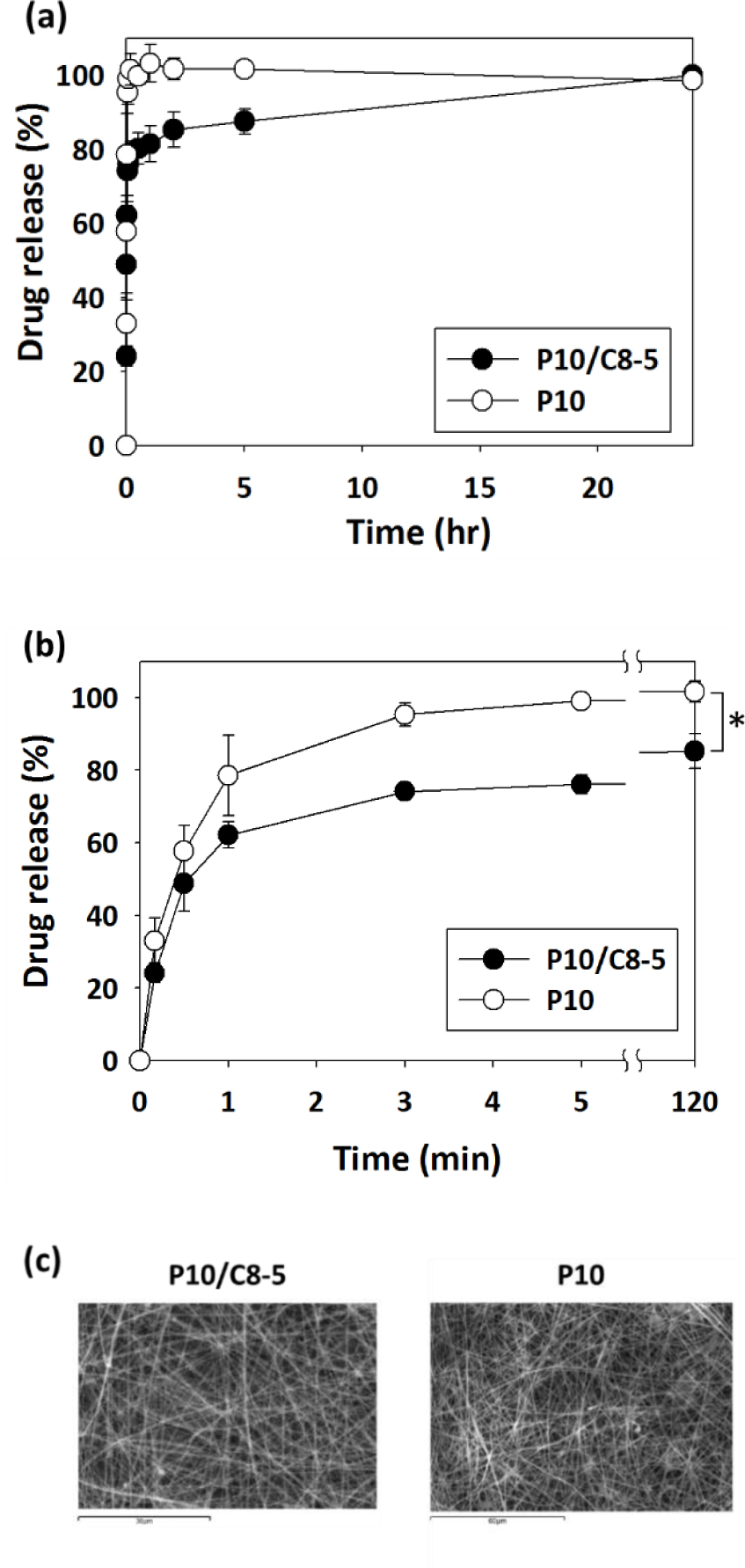
Figure 9 The release profiles of theophylline (as a model drug) from coaxial P10/C8-5 nanofiber membranes and from conventional (non-coaxial) P10 nanofiber membranes, and the SEM images of membranes: (a) from 0 to 24 hours, (b) the initial 120 minutes * p < 0.05, (c) The SEM images of P10/C8-5 and P10 nanofiber membranes. (Scale bar = 60 μm)
Figure 9

The release profiles of theophylline (as a model drug) from coaxial P10/C8-5 nanofiber membranes and from conventional (non-coaxial) P10 nanofiber membranes, and the SEM images of membranes: (a) from 0 to 24 hours, (b) the initial 120 minutes * p < 0.05, (c) The SEM images of P10/C8-5 and P10 nanofiber membranes. (Scale bar = 60 μm)

As described above, several phenomena such as nanofiber swelling, disintegration, and drug diffusion were involved in the release of theophylline. To investigate these anomalous transport phenomena, a semi-empirical model called “Korsmeyer-Peppas model” was utilized to correlate the theophylline release from coaxial P10/C8-5 nanofiber membranes because the above-mentioned anomalous phenomena were considered in this model (see Section 2.7) [20, 21, 22, 23]. To obtain the parameters of release kinetics (k and n), the initial 65% of theophylline release data shown in Figure 9(b) were plotted as log drug release (%) vs. log time (min) [21, 23]. By fitting the theophylline release data with the Korsmeyer-Peppas model, the release rate constant (k) of 65.34 and release exponent (n) of 0.54 were obtained with a correlation coefficient (r2) of 0.979, as shown in Table 3. In Korsmeyer-Peppas model, for drug release from swellable cylindrical systems n ≤ 0.45 corresponds to Fickian diffusion, 0.45<n < 0.89 corresponding to anomalous (non-Fickian) transport [23]. The release exponent (n) of 0.54 obtained in this study suggests that the release mechanisms of theophylline from coaxial P10/C8-5 nanofiber membranes may involve several anomalous transport phenomena including nanofiber swelling and disintegration as well as drug diffusion.

Table 3

The parameters of release kinetics (k, n) obtained by using the Korsmeyer-Peppas model to correlate the theophylline release data

Korsmeyer-Peppas model
Release rate constant (k)65.34
Release exponent (n)0.54

  1. *Correlation coefficient (r2): 0.979

4 Conclusion

By adding a small amount of gum arabic to prepare much less viscous chitosan solutions, coaxial PVA/chitosan electrospun nanofiber membranes with core/shell structures were successfully fabricated in this research. The core/shell structures were confirmed by TEM. The existence of PVA and chitosan in the nanofiber membranes was established by FT-IR analysis. Among several groups of PVA/chitosan (as core/shell) nanofiber membranes prepared in this study, P10/C8-5 membranes showed a higher tensile strength than P10/C10-5 and other membranes possibly due to the better coverage of shell (chitosan) layer. The use of coaxial P10/C8-5 nanofiber membranes in drug release extended the release time of theophylline from 5 minutes to 24 hours. Further, the Korsmeyer-Peppas model was selected to fit the data of theophylline release, giving a release exponent (n) of 0.54, suggesting that the release mechanisms may involve several anomalous transport phenomena including nanofiber swelling and disintegration as well as drug diffusion. In brief, by combining the advantages of PVA and chitosan (good mechanical strength and good biocompatibility respectively), coaxial PVA/chitosan nanofiber membranes have great potential in many biomedical applications.

Acknowledgement

Ting-Yun Kuo and Cuei-Fang Jhang contributed equally to the present work. This study was financially supported in part by the Ministry of Science and Technology, Taiwan (grants: MOST 104-2221-E-002-174 & MOST 105-2221-E-002-202).

References

[1] Reneker D.H., Chun I., Nanometre diameter fibres of polymer, produced by electrospinning, Nanotechnology, 1996, 7, 216-223.10.1088/0957-4484/7/3/009Suche in Google Scholar

[2] Doshi J., Reneker D.H., Electrospinning process and applications of electrospun fibers, J. Electrostat., 1995, 35, 151-160.10.1109/IAS.1993.299067Suche in Google Scholar

[3] Huang Z.M., Zhang Y.Z., Kotaki M., Ramakrishna S., A review on polymer nanofibers by electrospinning and their applications in nanocomposites, Compos. Sci. Technol., 2003, 63, 2223-2253.10.1016/S0266-3538(03)00178-7Suche in Google Scholar

[4] Noh H.K., Lee S.W., Kim J.M., Oh J.E., Kim K.H., Chung C.P., et al., Electrospinning of chitin nanofibers: Degradation behavior and cellular response to normal human keratinocytes and fibroblasts, Biomaterials, 2006, 27, 3934-3944.10.1016/j.biomaterials.2006.03.016Suche in Google Scholar

[5] Haider A., Haider S., Kang I.-K., A comprehensive review summarizing the effect of electrospinning parameters and potential applications of nanofibers in biomedical and biotechnology, Arab. J. Chem., (in press), https://doi.org/10.1016/j.arabjc.2015.11.01510.1016/j.arabjc.2015.11.015Suche in Google Scholar

[6] Huang Z.-M., Zhang Y.Z., Kotaki M., Ramakrishna S., A review on polymer nanofibers by electrospinning and their applications in nanocomposites, Compos. Sci. Technol., 2003, 63, 2223-2253.10.1016/S0266-3538(03)00178-7Suche in Google Scholar

[7] Sun Z., Zussman E., Yarin A.L., Wendorff J.H., Greiner A., Compound core–shell polymer nanofibers by co-electrospinning, Adv. Mater., 2003, 15, 1929-1932.10.1002/adma.200305136Suche in Google Scholar

[8] Zhang Y., Huang Z.-M., Xu X., Lim C.T., Ramakrishna S., Preparation of core-shell structured PCL-r-gelatin bi-component nanofibers by coaxial electrospinning, Chem. Mater., 2004, 16, 3406-3409.10.1021/cm049580fSuche in Google Scholar

[9] Chen H., Wang N., Di J., Zhao Y., Song Y., Jiang L., Nanowire-in-microtube structured core/shell fibers via multifluidic coaxial electrospinning, Langmuir, 2010, 26, 11291-11296.10.1021/la100611fSuche in Google Scholar PubMed

[10] Moghe A.K., Gupta B.S., Co-axial electrospinning for nanofiber structures: Preparation and applications, Polymer Reviews, 2008, 48, 353-377.10.1080/15583720802022257Suche in Google Scholar

[11] Yan E.Y., Cao M.L., Wang Y.W., Meng Y., Zheng H., Hao X.Y., et al., Degradable polyvinyl alcohol/poly(butylene carbonate) core-shell nanofibers for chemotherapy and tissue engineering, Mater. Lett., 2016, 167, 13-17.10.1016/j.matlet.2015.12.113Suche in Google Scholar

[12] Zupancic S., Sinha-Ray S., Sinha-Ray S., Kristl J., Yarin A.L., Controlled release of ciprofloxacin from core-shell nanofibers with monolithic or blended core, Molecular Pharmaceutics, 2016, 13, 1393-1404.10.1021/acs.molpharmaceut.6b00039Suche in Google Scholar

[13] Kubota N., Tatsumoto N., Sano T., Toya K., A simple preparation of half N-acetylated chitosan highly soluble in water and aqueous organic solvents, Carbohydr. Res., 2000, 324, 268-274.10.1016/S0008-6215(99)00263-3Suche in Google Scholar

[14] Ohkawa K., Cha D.I., Kim H., Nishida A., Yamamoto H., Electrospinning of chitosan, Macromol. Rapid Commun., 2004, 25, 1600-1605.10.1002/marc.200400253Suche in Google Scholar

[15] Schiffman J.D., Schauer C.L., Cross-linking chitosan nanofibers, Biomacromolecules, 2007, 8, 594-601.10.1021/bm060804sSuche in Google Scholar

[16] Chen Z.G., Wang P.W., Wei B., Mo X.M., Cui F.Z., Electrospun collagen-chitosan nanofiber: A biomimetic extracellular matrix for endothelial cell and smooth muscle cell, Acta Biomater., 2010, 6, 372-382.10.1016/j.actbio.2009.07.024Suche in Google Scholar

[17] Tsai R.Y., Hung S.C., Lai J.Y., Wang D.M., Hsieh H.J., Electrospun chitosan-gelatin-polyvinyl alcohol hybrid nanofibrous mats: Production and characterization, J. Taiwan Inst. Chem. Eng., 2014, 45, 1975-1981.10.1016/j.jtice.2013.11.003Suche in Google Scholar

[18] Tsai R.Y., Kuo T.Y., Hung S.C., Lin C.M., Hsien T.Y., Wang D.M., Hsieh H.J., Use of gum arabic to improve the fabrication of chitosan-gelatin-based nanofibers for tissue engineering, Carbohydr. Polym., 2015, 115, 525-532.10.1016/j.carbpol.2014.08.108Suche in Google Scholar

[19] Tsai R.Y., Chen P.W., Kuo T.Y., Lin C.M., Wang D.M., Hsien T.Y., Hsieh H.J., Chitosan/pectin/gum Arabic polyelectrolyte complex: Process-dependent appearance, microstructure analysis and its application, Carbohydr. Polym., 2014, 101, 752-759.10.1016/j.carbpol.2013.10.008Suche in Google Scholar

[20] Costa P., Sousa Lobo J.M., Modeling and comparison of dissolution profiles, Eur. J. Pharm. Sci., 2001, 13, 123-133.10.1016/S0928-0987(01)00095-1Suche in Google Scholar

[21] Dash S., Murthy P.N., Nath L., Chowdhury P., Kinetic modeling on drug release from controlled drug delivery systems, Acta Pol. Pharm., 2010, 67, 217-223.Suche in Google Scholar

[22] Shaikh H.K., Kshirsagar R.V., Patil S.G., Mathematical models for drug release characterization: a review, World J. Pharm. Pharm. Sci., 2015, 4, 324-338.Suche in Google Scholar

[23] Ritger P.L., Peppas N.A., A simple equation for description of solute release II. Fickian and anomalous release from swellable devices, J. Controlled Release, 1987, 5, 37-42.10.1016/0168-3659(87)90035-6Suche in Google Scholar

[24] Shin Y.M., Hohman M.M., Brenner M.P., Rutledge G.C., Experimental characterization of electrospinning: the electrically forced jet and instabilities, Polymer, 2001, 42, 09955-09967.10.1016/S0032-3861(01)00540-7Suche in Google Scholar

[25] Granados K., Gracia-Fadrique J., Amigo A., Bravo R., Refractive index, surface tension, and density of aqueous mixtures of carboxylic acids at 298.15 K, J. Chem. Eng. Data, 2006, 51, 1356-1360.10.1021/je060084cSuche in Google Scholar

[26] Moghe A.K., Gupta B.S., Co-axial electrospinning for nanofiber structures: Preparation and applications, Polymer Reviews, 2008, 48, 353-377.10.1080/15583720802022257Suche in Google Scholar

[27] Pakravan M., Heuzey M.C., Ajji A., Core-shell Structured PEO-chitosan nanofibers by coaxial electrospinning, Biomacromolecules, 2012, 13, 412-421.10.1021/bm201444vSuche in Google Scholar

[28] Ibekwe C.A., Oyatogun G.M., Esan T.A., Oluwasegun K.M., Synthesis and characterization of chitosan/gum arabic nanoparticles for bone regeneration, American Journal of Materials Science and Engineering, 2017, 5, 28-36.10.12691/ajmse-5-1-4Suche in Google Scholar

[29] Gilman J.W., Vanderhart D.L., Kashiwagi T., Thermal decomposition chemistry of poly (vinyl alcohol), fire and polymers II: Materials and test for hazard prevention, ACS Symposium Series, 1994, 599, 161-185.10.1021/bk-1995-0599.ch011Suche in Google Scholar

[30] Diab M.A., El-Sonbati A.Z., Bader D.M.D., Zoromba M.S., Thermal stability and degradation of chitosan modified by acetophenone, J. Polym. Environ., 2012, 20, 29-36.10.1007/s10924-011-0330-4Suche in Google Scholar

[31] Hennink W.E., Van Nostrum C.F., Novel crosslinking methods to design hydrogels, Adv. Drug Deliv. Rev., 2002, 54, 13-36.10.1016/S0169-409X(01)00240-XSuche in Google Scholar

[32] Asada M., Takahashi H., Okamoto H., Tanino H., Danjo K., Theophylline particle design using chitosan by the spray drying, Int. J. Pharm., 2004, 270, 167-174.10.1016/j.ijpharm.2003.11.001Suche in Google Scholar PubMed

[33] Yang D., Li Y., Nie J., Preparation of gelatin/PVA nanofibers and their potential application in controlled release of drugs, Carbohydr. Polym., 2007, 69, 538-543.10.1016/j.carbpol.2007.01.008Suche in Google Scholar

Received: 2017-10-29
Accepted: 2017-11-27
Published Online: 2017-12-29

© 2017 Ting-Yun Kuo et al.

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Artikel in diesem Heft

  1. Regular Articles
  2. Analysis of a New Fractional Model for Damped Bergers’ Equation
  3. Regular Articles
  4. Optimal homotopy perturbation method for nonlinear differential equations governing MHD Jeffery-Hamel flow with heat transfer problem
  5. Regular Articles
  6. Semi- analytic numerical method for solution of time-space fractional heat and wave type equations with variable coefficients
  7. Regular Articles
  8. Investigation of a curve using Frenet frame in the lightlike cone
  9. Regular Articles
  10. Construction of complex networks from time series based on the cross correlation interval
  11. Regular Articles
  12. Nonlinear Schrödinger approach to European option pricing
  13. Regular Articles
  14. A modified cubic B-spline differential quadrature method for three-dimensional non-linear diffusion equations
  15. Regular Articles
  16. A new miniaturized negative-index meta-atom for tri-band applications
  17. Regular Articles
  18. Seismic stability of the survey areas of potential sites for the deep geological repository of the spent nuclear fuel
  19. Regular Articles
  20. Distributed containment control of heterogeneous fractional-order multi-agent systems with communication delays
  21. Regular Articles
  22. Sensitivity analysis and economic optimization studies of inverted five-spot gas cycling in gas condensate reservoir
  23. Regular Articles
  24. Quantum mechanics with geometric constraints of Friedmann type
  25. Regular Articles
  26. Modeling and Simulation for an 8 kW Three-Phase Grid-Connected Photo-Voltaic Power System
  27. Regular Articles
  28. Application of the optimal homotopy asymptotic method to nonlinear Bingham fluid dampers
  29. Regular Articles
  30. Analysis of Drude model using fractional derivatives without singular kernels
  31. Regular Articles
  32. An unsteady MHD Maxwell nanofluid flow with convective boundary conditions using spectral local linearization method
  33. Regular Articles
  34. New analytical solutions for conformable fractional PDEs arising in mathematical physics by exp-function method
  35. Regular Articles
  36. Quantum mechanical calculation of electron spin
  37. Regular Articles
  38. CO2 capture by polymeric membranes composed of hyper-branched polymers with dense poly(oxyethylene) comb and poly(amidoamine)
  39. Regular Articles
  40. Chain on a cone
  41. Regular Articles
  42. Multi-task feature learning by using trace norm regularization
  43. Regular Articles
  44. Superluminal tunneling of a relativistic half-integer spin particle through a potential barrier
  45. Regular Articles
  46. Neutrosophic triplet normed space
  47. Regular Articles
  48. Lie algebraic discussion for affinity based information diffusion in social networks
  49. Regular Articles
  50. Radiation dose and cancer risk estimates in helical CT for pulmonary tuberculosis infections
  51. Regular Articles
  52. A comparison study of steady-state vibrations with single fractional-order and distributed-order derivatives
  53. Regular Articles
  54. Some new remarks on MHD Jeffery-Hamel fluid flow problem
  55. Regular Articles
  56. Numerical investigation of magnetohydrodynamic slip flow of power-law nanofluid with temperature dependent viscosity and thermal conductivity over a permeable surface
  57. Regular Articles
  58. Charge conservation in a gravitational field in the scalar ether theory
  59. Regular Articles
  60. Measurement problem and local hidden variables with entangled photons
  61. Regular Articles
  62. Compression of hyper-spectral images using an accelerated nonnegative tensor decomposition
  63. Regular Articles
  64. Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes
  65. Regular Articles
  66. Calculating degree-based topological indices of dominating David derived networks
  67. Regular Articles
  68. The structure and conductivity of polyelectrolyte based on MEH-PPV and potassium iodide (KI) for dye-sensitized solar cells
  69. Regular Articles
  70. Chiral symmetry restoration and the critical end point in QCD
  71. Regular Articles
  72. Numerical solution for fractional Bratu’s initial value problem
  73. Regular Articles
  74. Structure and optical properties of TiO2 thin films deposited by ALD method
  75. Regular Articles
  76. Quadruple multi-wavelength conversion for access network scalability based on cross-phase modulation in an SOA-MZI
  77. Regular Articles
  78. Application of ANNs approach for wave-like and heat-like equations
  79. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  80. Study on node importance evaluation of the high-speed passenger traffic complex network based on the Structural Hole Theory
  81. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  82. A mathematical/physics model to measure the role of information and communication technology in some economies: the Chinese case
  83. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  84. Numerical modeling of the thermoelectric cooler with a complementary equation for heat circulation in air gaps
  85. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  86. On the libration collinear points in the restricted three – body problem
  87. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  88. Research on Critical Nodes Algorithm in Social Complex Networks
  89. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  90. A simulation based research on chance constrained programming in robust facility location problem
  91. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  92. A mathematical/physics carbon emission reduction strategy for building supply chain network based on carbon tax policy
  93. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  94. Mathematical analysis of the impact mechanism of information platform on agro-product supply chain and agro-product competitiveness
  95. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  96. A real negative selection algorithm with evolutionary preference for anomaly detection
  97. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  98. A privacy-preserving parallel and homomorphic encryption scheme
  99. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  100. Random walk-based similarity measure method for patterns in complex object
  101. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  102. A Mathematical Study of Accessibility and Cohesion Degree in a High-Speed Rail Station Connected to an Urban Bus Transport Network
  103. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  104. Design and Simulation of the Integrated Navigation System based on Extended Kalman Filter
  105. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  106. Oil exploration oriented multi-sensor image fusion algorithm
  107. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  108. Analysis of Product Distribution Strategy in Digital Publishing Industry Based on Game-Theory
  109. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  110. Expanded Study on the accumulation effect of tourism under the constraint of structure
  111. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  112. Unstructured P2P Network Load Balance Strategy Based on Multilevel Partitioning of Hypergraph
  113. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  114. Research on the method of information system risk state estimation based on clustering particle filter
  115. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  116. Demand forecasting and information platform in tourism
  117. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  118. Physical-chemical properties studying of molecular structures via topological index calculating
  119. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  120. Local kernel nonparametric discriminant analysis for adaptive extraction of complex structures
  121. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  122. City traffic flow breakdown prediction based on fuzzy rough set
  123. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  124. Conservation laws for a strongly damped wave equation
  125. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  126. Blending type approximation by Stancu-Kantorovich operators based on Pólya-Eggenberger distribution
  127. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  128. Computing the Ediz eccentric connectivity index of discrete dynamic structures
  129. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  130. A discrete epidemic model for bovine Babesiosis disease and tick populations
  131. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  132. Study on maintaining formations during satellite formation flying based on SDRE and LQR
  133. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  134. Relationship between solitary pulmonary nodule lung cancer and CT image features based on gradual clustering
  135. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  136. A novel fast target tracking method for UAV aerial image
  137. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  138. Fuzzy comprehensive evaluation model of interuniversity collaborative learning based on network
  139. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  140. Conservation laws, classical symmetries and exact solutions of the generalized KdV-Burgers-Kuramoto equation
  141. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  142. After notes on self-similarity exponent for fractal structures
  143. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  144. Excitation probability and effective temperature in the stationary regime of conductivity for Coulomb Glasses
  145. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  146. Comparisons of feature extraction algorithm based on unmanned aerial vehicle image
  147. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  148. Research on identification method of heavy vehicle rollover based on hidden Markov model
  149. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  150. Classifying BCI signals from novice users with extreme learning machine
  151. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  152. Topics on data transmission problem in software definition network
  153. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  154. Statistical inferences with jointly type-II censored samples from two Pareto distributions
  155. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  156. Estimation for coefficient of variation of an extension of the exponential distribution under type-II censoring scheme
  157. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  158. Analysis on trust influencing factors and trust model from multiple perspectives of online Auction
  159. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  160. Coupling of two-phase flow in fractured-vuggy reservoir with filling medium
  161. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  162. Production decline type curves analysis of a finite conductivity fractured well in coalbed methane reservoirs
  163. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  164. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions
  165. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  166. The size prediction of potential inclusions embedded in the sub-surface of fused silica by damage morphology
  167. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  168. Research on carbonate reservoir interwell connectivity based on a modified diffusivity filter model
  169. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  170. The method of the spatial locating of macroscopic throats based-on the inversion of dynamic interwell connectivity
  171. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  172. Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method
  173. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  174. A volumetric ablation model of EPDM considering complex physicochemical process in porous structure of char layer
  175. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  176. Numerical simulation on ferrofluid flow in fractured porous media based on discrete-fracture model
  177. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  178. Macroscopic lattice Boltzmann model for heat and moisture transfer process with phase transformation in unsaturated porous media during freezing process
  179. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  180. Modelling of intermittent microwave convective drying: parameter sensitivity
  181. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  182. Simulating gas-water relative permeabilities for nanoscale porous media with interfacial effects
  183. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  184. Simulation of counter-current imbibition in water-wet fractured reservoirs based on discrete-fracture model
  185. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  186. Investigation effect of wettability and heterogeneity in water flooding and on microscopic residual oil distribution in tight sandstone cores with NMR technique
  187. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  188. Analytical modeling of coupled flow and geomechanics for vertical fractured well in tight gas reservoirs
  189. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  190. Special Issue: Ever New "Loopholes" in Bell’s Argument and Experimental Tests
  191. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  192. The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  193. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  194. Erratum to: The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  195. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  196. Rhetoric, logic, and experiment in the quantum nonlocality debate
  197. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  198. What If Quantum Theory Violates All Mathematics?
  199. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  200. Relativity, anomalies and objectivity loophole in recent tests of local realism
  201. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  202. The photon identification loophole in EPRB experiments: computer models with single-wing selection
  203. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  204. Bohr against Bell: complementarity versus nonlocality
  205. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  206. Is Einsteinian no-signalling violated in Bell tests?
  207. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  208. Bell’s “Theorem”: loopholes vs. conceptual flaws
  209. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  210. Nonrecurrence and Bell-like inequalities
  211. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  212. Three-dimensional computer models of electrospinning systems
  213. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  214. Electric field computation and measurements in the electroporation of inhomogeneous samples
  215. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  216. Modelling of magnetostriction of transformer magnetic core for vibration analysis
  217. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  218. Comparison of the fractional power motor with cores made of various magnetic materials
  219. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  220. Dynamics of the line-start reluctance motor with rotor made of SMC material
  221. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  222. Inhomogeneous dielectrics: conformal mapping and finite-element models
  223. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  224. Topology optimization of induction heating model using sequential linear programming based on move limit with adaptive relaxation
  225. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  226. Detection of inter-turn short-circuit at start-up of induction machine based on torque analysis
  227. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  228. Current superimposition variable flux reluctance motor with 8 salient poles
  229. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  230. Modelling axial vibration in windings of power transformers
  231. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  232. Field analysis & eddy current losses calculation in five-phase tubular actuator
  233. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  234. Hybrid excited claw pole generator with skewed and non-skewed permanent magnets
  235. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  236. Electromagnetic phenomena analysis in brushless DC motor with speed control using PWM method
  237. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  238. Field-circuit analysis and measurements of a single-phase self-excited induction generator
  239. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  240. A comparative analysis between classical and modified approach of description of the electrical machine windings by means of T0 method
  241. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  242. Field-based optimal-design of an electric motor: a new sensitivity formulation
  243. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  244. Application of the parametric proper generalized decomposition to the frequency-dependent calculation of the impedance of an AC line with rectangular conductors
  245. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  246. Virtual reality as a new trend in mechanical and electrical engineering education
  247. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  248. Holonomicity analysis of electromechanical systems
  249. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  250. An accurate reactive power control study in virtual flux droop control
  251. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  252. Localized probability of improvement for kriging based multi-objective optimization
  253. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  254. Research of influence of open-winding faults on properties of brushless permanent magnets motor
  255. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  256. Optimal design of the rotor geometry of line-start permanent magnet synchronous motor using the bat algorithm
  257. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  258. Model of depositing layer on cylindrical surface produced by induction-assisted laser cladding process
  259. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  260. Detection of inter-turn faults in transformer winding using the capacitor discharge method
  261. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  262. A novel hybrid genetic algorithm for optimal design of IPM machines for electric vehicle
  263. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  264. Lamination effects on a 3D model of the magnetic core of power transformers
  265. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  266. Detection of vertical disparity in three-dimensional visualizations
  267. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  268. Calculations of magnetic field in dynamo sheets taking into account their texture
  269. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  270. 3-dimensional computer model of electrospinning multicapillary unit used for electrostatic field analysis
  271. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  272. Optimization of wearable microwave antenna with simplified electromagnetic model of the human body
  273. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  274. Induction heating process of ferromagnetic filled carbon nanotubes based on 3-D model
  275. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  276. Speed control of an induction motor by 6-switched 3-level inverter
https://doi.org/10.1515/phys-2017-0125
Schlagwörter für diesen Artikel
electrospinning; core/shell structures; gum arabic; drug release; Korsmeyer-Peppas model
Creative Commons
BY-NC-ND 4.0

Artikel in diesem Heft

  1. Regular Articles
  2. Analysis of a New Fractional Model for Damped Bergers’ Equation
  3. Regular Articles
  4. Optimal homotopy perturbation method for nonlinear differential equations governing MHD Jeffery-Hamel flow with heat transfer problem
  5. Regular Articles
  6. Semi- analytic numerical method for solution of time-space fractional heat and wave type equations with variable coefficients
  7. Regular Articles
  8. Investigation of a curve using Frenet frame in the lightlike cone
  9. Regular Articles
  10. Construction of complex networks from time series based on the cross correlation interval
  11. Regular Articles
  12. Nonlinear Schrödinger approach to European option pricing
  13. Regular Articles
  14. A modified cubic B-spline differential quadrature method for three-dimensional non-linear diffusion equations
  15. Regular Articles
  16. A new miniaturized negative-index meta-atom for tri-band applications
  17. Regular Articles
  18. Seismic stability of the survey areas of potential sites for the deep geological repository of the spent nuclear fuel
  19. Regular Articles
  20. Distributed containment control of heterogeneous fractional-order multi-agent systems with communication delays
  21. Regular Articles
  22. Sensitivity analysis and economic optimization studies of inverted five-spot gas cycling in gas condensate reservoir
  23. Regular Articles
  24. Quantum mechanics with geometric constraints of Friedmann type
  25. Regular Articles
  26. Modeling and Simulation for an 8 kW Three-Phase Grid-Connected Photo-Voltaic Power System
  27. Regular Articles
  28. Application of the optimal homotopy asymptotic method to nonlinear Bingham fluid dampers
  29. Regular Articles
  30. Analysis of Drude model using fractional derivatives without singular kernels
  31. Regular Articles
  32. An unsteady MHD Maxwell nanofluid flow with convective boundary conditions using spectral local linearization method
  33. Regular Articles
  34. New analytical solutions for conformable fractional PDEs arising in mathematical physics by exp-function method
  35. Regular Articles
  36. Quantum mechanical calculation of electron spin
  37. Regular Articles
  38. CO2 capture by polymeric membranes composed of hyper-branched polymers with dense poly(oxyethylene) comb and poly(amidoamine)
  39. Regular Articles
  40. Chain on a cone
  41. Regular Articles
  42. Multi-task feature learning by using trace norm regularization
  43. Regular Articles
  44. Superluminal tunneling of a relativistic half-integer spin particle through a potential barrier
  45. Regular Articles
  46. Neutrosophic triplet normed space
  47. Regular Articles
  48. Lie algebraic discussion for affinity based information diffusion in social networks
  49. Regular Articles
  50. Radiation dose and cancer risk estimates in helical CT for pulmonary tuberculosis infections
  51. Regular Articles
  52. A comparison study of steady-state vibrations with single fractional-order and distributed-order derivatives
  53. Regular Articles
  54. Some new remarks on MHD Jeffery-Hamel fluid flow problem
  55. Regular Articles
  56. Numerical investigation of magnetohydrodynamic slip flow of power-law nanofluid with temperature dependent viscosity and thermal conductivity over a permeable surface
  57. Regular Articles
  58. Charge conservation in a gravitational field in the scalar ether theory
  59. Regular Articles
  60. Measurement problem and local hidden variables with entangled photons
  61. Regular Articles
  62. Compression of hyper-spectral images using an accelerated nonnegative tensor decomposition
  63. Regular Articles
  64. Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes
  65. Regular Articles
  66. Calculating degree-based topological indices of dominating David derived networks
  67. Regular Articles
  68. The structure and conductivity of polyelectrolyte based on MEH-PPV and potassium iodide (KI) for dye-sensitized solar cells
  69. Regular Articles
  70. Chiral symmetry restoration and the critical end point in QCD
  71. Regular Articles
  72. Numerical solution for fractional Bratu’s initial value problem
  73. Regular Articles
  74. Structure and optical properties of TiO2 thin films deposited by ALD method
  75. Regular Articles
  76. Quadruple multi-wavelength conversion for access network scalability based on cross-phase modulation in an SOA-MZI
  77. Regular Articles
  78. Application of ANNs approach for wave-like and heat-like equations
  79. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  80. Study on node importance evaluation of the high-speed passenger traffic complex network based on the Structural Hole Theory
  81. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  82. A mathematical/physics model to measure the role of information and communication technology in some economies: the Chinese case
  83. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  84. Numerical modeling of the thermoelectric cooler with a complementary equation for heat circulation in air gaps
  85. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  86. On the libration collinear points in the restricted three – body problem
  87. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  88. Research on Critical Nodes Algorithm in Social Complex Networks
  89. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  90. A simulation based research on chance constrained programming in robust facility location problem
  91. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  92. A mathematical/physics carbon emission reduction strategy for building supply chain network based on carbon tax policy
  93. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  94. Mathematical analysis of the impact mechanism of information platform on agro-product supply chain and agro-product competitiveness
  95. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  96. A real negative selection algorithm with evolutionary preference for anomaly detection
  97. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  98. A privacy-preserving parallel and homomorphic encryption scheme
  99. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  100. Random walk-based similarity measure method for patterns in complex object
  101. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  102. A Mathematical Study of Accessibility and Cohesion Degree in a High-Speed Rail Station Connected to an Urban Bus Transport Network
  103. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  104. Design and Simulation of the Integrated Navigation System based on Extended Kalman Filter
  105. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  106. Oil exploration oriented multi-sensor image fusion algorithm
  107. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  108. Analysis of Product Distribution Strategy in Digital Publishing Industry Based on Game-Theory
  109. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  110. Expanded Study on the accumulation effect of tourism under the constraint of structure
  111. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  112. Unstructured P2P Network Load Balance Strategy Based on Multilevel Partitioning of Hypergraph
  113. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  114. Research on the method of information system risk state estimation based on clustering particle filter
  115. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  116. Demand forecasting and information platform in tourism
  117. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  118. Physical-chemical properties studying of molecular structures via topological index calculating
  119. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  120. Local kernel nonparametric discriminant analysis for adaptive extraction of complex structures
  121. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  122. City traffic flow breakdown prediction based on fuzzy rough set
  123. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  124. Conservation laws for a strongly damped wave equation
  125. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  126. Blending type approximation by Stancu-Kantorovich operators based on Pólya-Eggenberger distribution
  127. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  128. Computing the Ediz eccentric connectivity index of discrete dynamic structures
  129. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  130. A discrete epidemic model for bovine Babesiosis disease and tick populations
  131. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  132. Study on maintaining formations during satellite formation flying based on SDRE and LQR
  133. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  134. Relationship between solitary pulmonary nodule lung cancer and CT image features based on gradual clustering
  135. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  136. A novel fast target tracking method for UAV aerial image
  137. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  138. Fuzzy comprehensive evaluation model of interuniversity collaborative learning based on network
  139. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  140. Conservation laws, classical symmetries and exact solutions of the generalized KdV-Burgers-Kuramoto equation
  141. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  142. After notes on self-similarity exponent for fractal structures
  143. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  144. Excitation probability and effective temperature in the stationary regime of conductivity for Coulomb Glasses
  145. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  146. Comparisons of feature extraction algorithm based on unmanned aerial vehicle image
  147. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  148. Research on identification method of heavy vehicle rollover based on hidden Markov model
  149. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  150. Classifying BCI signals from novice users with extreme learning machine
  151. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  152. Topics on data transmission problem in software definition network
  153. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  154. Statistical inferences with jointly type-II censored samples from two Pareto distributions
  155. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  156. Estimation for coefficient of variation of an extension of the exponential distribution under type-II censoring scheme
  157. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  158. Analysis on trust influencing factors and trust model from multiple perspectives of online Auction
  159. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  160. Coupling of two-phase flow in fractured-vuggy reservoir with filling medium
  161. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  162. Production decline type curves analysis of a finite conductivity fractured well in coalbed methane reservoirs
  163. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  164. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions
  165. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  166. The size prediction of potential inclusions embedded in the sub-surface of fused silica by damage morphology
  167. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  168. Research on carbonate reservoir interwell connectivity based on a modified diffusivity filter model
  169. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  170. The method of the spatial locating of macroscopic throats based-on the inversion of dynamic interwell connectivity
  171. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  172. Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method
  173. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  174. A volumetric ablation model of EPDM considering complex physicochemical process in porous structure of char layer
  175. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  176. Numerical simulation on ferrofluid flow in fractured porous media based on discrete-fracture model
  177. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  178. Macroscopic lattice Boltzmann model for heat and moisture transfer process with phase transformation in unsaturated porous media during freezing process
  179. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  180. Modelling of intermittent microwave convective drying: parameter sensitivity
  181. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  182. Simulating gas-water relative permeabilities for nanoscale porous media with interfacial effects
  183. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  184. Simulation of counter-current imbibition in water-wet fractured reservoirs based on discrete-fracture model
  185. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  186. Investigation effect of wettability and heterogeneity in water flooding and on microscopic residual oil distribution in tight sandstone cores with NMR technique
  187. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  188. Analytical modeling of coupled flow and geomechanics for vertical fractured well in tight gas reservoirs
  189. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  190. Special Issue: Ever New "Loopholes" in Bell’s Argument and Experimental Tests
  191. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  192. The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  193. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  194. Erratum to: The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  195. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  196. Rhetoric, logic, and experiment in the quantum nonlocality debate
  197. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  198. What If Quantum Theory Violates All Mathematics?
  199. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  200. Relativity, anomalies and objectivity loophole in recent tests of local realism
  201. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  202. The photon identification loophole in EPRB experiments: computer models with single-wing selection
  203. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  204. Bohr against Bell: complementarity versus nonlocality
  205. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  206. Is Einsteinian no-signalling violated in Bell tests?
  207. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  208. Bell’s “Theorem”: loopholes vs. conceptual flaws
  209. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  210. Nonrecurrence and Bell-like inequalities
  211. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  212. Three-dimensional computer models of electrospinning systems
  213. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  214. Electric field computation and measurements in the electroporation of inhomogeneous samples
  215. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  216. Modelling of magnetostriction of transformer magnetic core for vibration analysis
  217. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  218. Comparison of the fractional power motor with cores made of various magnetic materials
  219. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  220. Dynamics of the line-start reluctance motor with rotor made of SMC material
  221. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  222. Inhomogeneous dielectrics: conformal mapping and finite-element models
  223. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  224. Topology optimization of induction heating model using sequential linear programming based on move limit with adaptive relaxation
  225. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  226. Detection of inter-turn short-circuit at start-up of induction machine based on torque analysis
  227. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  228. Current superimposition variable flux reluctance motor with 8 salient poles
  229. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  230. Modelling axial vibration in windings of power transformers
  231. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  232. Field analysis & eddy current losses calculation in five-phase tubular actuator
  233. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  234. Hybrid excited claw pole generator with skewed and non-skewed permanent magnets
  235. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  236. Electromagnetic phenomena analysis in brushless DC motor with speed control using PWM method
  237. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  238. Field-circuit analysis and measurements of a single-phase self-excited induction generator
  239. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  240. A comparative analysis between classical and modified approach of description of the electrical machine windings by means of T0 method
  241. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  242. Field-based optimal-design of an electric motor: a new sensitivity formulation
  243. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  244. Application of the parametric proper generalized decomposition to the frequency-dependent calculation of the impedance of an AC line with rectangular conductors
  245. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  246. Virtual reality as a new trend in mechanical and electrical engineering education
  247. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  248. Holonomicity analysis of electromechanical systems
  249. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  250. An accurate reactive power control study in virtual flux droop control
  251. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  252. Localized probability of improvement for kriging based multi-objective optimization
  253. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  254. Research of influence of open-winding faults on properties of brushless permanent magnets motor
  255. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  256. Optimal design of the rotor geometry of line-start permanent magnet synchronous motor using the bat algorithm
  257. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  258. Model of depositing layer on cylindrical surface produced by induction-assisted laser cladding process
  259. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  260. Detection of inter-turn faults in transformer winding using the capacitor discharge method
  261. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  262. A novel hybrid genetic algorithm for optimal design of IPM machines for electric vehicle
  263. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  264. Lamination effects on a 3D model of the magnetic core of power transformers
  265. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  266. Detection of vertical disparity in three-dimensional visualizations
  267. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  268. Calculations of magnetic field in dynamo sheets taking into account their texture
  269. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  270. 3-dimensional computer model of electrospinning multicapillary unit used for electrostatic field analysis
  271. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  272. Optimization of wearable microwave antenna with simplified electromagnetic model of the human body
  273. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  274. Induction heating process of ferromagnetic filled carbon nanotubes based on 3-D model
  275. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  276. Speed control of an induction motor by 6-switched 3-level inverter
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 12.10.2025 von https://www.degruyterbrill.com/document/doi/10.1515/phys-2017-0125/html?lang=de
Button zum nach oben scrollen