Home Mathematics KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy
Article Open Access

KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy

  • Shahram Golzari EMAIL logo , Mohammad Nourmohammadi Zardehsavar , Amin Mousavi , Mahmoud Reza Saybani , Abdullah Khalili and Shahaboddin Shamshirband EMAIL logo
Published/Copyright: December 31, 2018
Download Article (PDF)
Open Mathematics
From the journal Open Mathematics Volume 16 Issue 1

Abstract

Gravitational Search Algorithm (GSA) is a metaheuristic for solving unimodal problems. In this paper, a K-means based GSA (KGSA) for multimodal optimization is proposed. This algorithm incorporates K-means and a new elitism strategy called “loop in loop” into the GSA. First in KGSA, the members of the initial population are clustered by K-means. Afterwards, new population is created and divided in different niches (or clusters) to expand the search space. The “loop in loop” technique guides the members of each niche to the optimum direction according to their clusters. This means that lighter members move faster towards the optimum direction of each cluster than the heavier members. For evaluations, KGSA is benchmarked on well-known functions and is compared with some of the state-of-the-art algorithms. Experiments show that KGSA provides better results than the other algorithms in finding local and global optima of constrained and unconstrained multimodal functions.

Keywords: Gravitational Search Algorithm (GSA); multimodal optimization; K-means; niching methods

1 Introduction

In addition to the need for finding several optima in many applications, solving multimodal problems can be useful at least for two reasons; first, it can increase the chance of finding the global optimum and second, it can help the researcher to become more familiar with the nature of the problem [1]. Population-based (or meta-heuristic) algorithms have been used to solve optimization problems. Some of these algorithms are: Genetic Algorithm (GA) by [2, 3], Simulated Annealing (SA) by [4], Artificial Immune Systems (AIS) by [5], Ant Colony Optimization (ACO) by [6], Particle Swarm Optimization (PSO) by [7], and Gravitational Search Algorithm (GSA) by [8, 9]. Generally speaking, these algorithms are inspired by nature and are effective in solving unimodal optimization problems. However, they have not been very successful in solving multimodal problems. To resolve this, two solutions have been provided: 1- Niching techniques to converge to more than one solution by dividing the main population into non-overlapping areas and 2- Elitism strategy to accelerate the convergence by selecting the best individuals from the current population and its offspring.

In this study, the Gravitational Search Algorithm (GSA) is boosted with the K-means niching and a new elitism strategy called “loop in loop” to make an efficient algorithm (called KGSA) in solving multimodal problems. GSA was selected since it is less dependent on parameters and can find existing optima with less iterations without trapping in local minimum. In addition, K-means clustering technique was chosen for its simplicity, effectiveness and, low time complexity in dividing the main population into non-overlapping subpopulations. Results show that by incorporating K-means and “loop in loop” into the GSA, the proposed algorithm has increased both ‘exploration’ and ‘exploitation’.

This paper is structured as follows: in section 2, some recent works regarding solving multimodal problems are studied. Afterwards, in section 3, GSA, niching concepts and K-means clustering techniques are described. Section 4, describes how the proposed algorithm is designed and how is “loop in loop” used. In section 5, after introducing constrained and unconstrained benchmark functions, evaluation criteria and parameters required for the suggestive algorithm are presented and results of implementation of the suggestive algorithm on the benchmark functions are analyzed, and then the sensitivity of parameter Tl relevant to the suggestive algorithm on some functions is measured. At the end, in section 6, strengths and weaknesses of the proposed algorithm are analyzed and some future works are suggested.

2 Literature review

Solving multimodal problems has always been one of the important and interesting issues for computer science researchers. Authors in [10] presented NichePSO algorithm to solve multimodal problems and showed its efficiency by solving some multimodal functions. In this algorithm, Guaranteed Convergence Particle Swarm Optimization (GCPSO) and Faure-sequences [11] were used to optimize the sub-swarms and the population initialization, respectively. In addition, two parameters δ and μ were defined in this algorithm. If an individual’s variance was less than δ or, in other words, if an individual did not change over several generations, it may be an optimum member. Therefore, the individual and its closest member build a sub-swarm. On the other hand, parameter μ was used to merge the sub-swarms. Results indicated that NichePSO is highly dependent on parameter μ to explore the optimal solutions and this is a major weakness.

Authors in [12] presented Clustering-Based Niching (CBN) method to find global and local optima. The main idea of this method for exploring optima and keeping variety of population was to use sub-populations instead of one population. Species were formed using sub-populations and sub-populations were separated by a density-based clustering algorithm which is appropriate for populations with different sizes and for problems in which the number of clusters is not predetermined. In order to attach two members during the clustering process in CBN, their distance should be less than parameter σdist. Results showed that this algorithm is highly dependent on σdist which is a major drawback.

Authors in [13] presented a method in which PSO and cleansing technique were used. In this method, population was divided into different species based on similarity of its members. Each species was then formed around a dominant individual (or the ‘specie-seed’). In each phase, particles were selected from the whole population and the species were formed adaptively based on the feedback of fitness space. The method was named as Species based Particle Swarm Optimization (SPSO). Although SPSO was proven to be effective in solving multimodal problems with small dimensions, the dependency on species’ radius is among its weaknesses.

Authors in [14] presented an algorithm for solving multimodal optimization problems. This new method was named Multi-Grouped Particle Swarm Optimization (MGPSO) in which, if the number of groups is N, PSO can search N peaks. The efficiency of this method was shown in [14]. Weaknesses of this algorithm are: 1) Determining the number of groups that is determining the number of optimal solutions by user while initializing the algorithm. It is also possible that the function is unknown and no information about the number of optimal points exists. 2) Determining the number of individuals for each group and selecting an appropriate initial value for the radius of each gbest.

Authors in [15] used a new algorithm called NGSA for solving multimodal problems. The main idea was that the initial swarm is divided into several sub-swarms. NGSA used following three strategies: i) an elitism strategy, ii) a K-NN strategy, and iii) amendment of active gravitational mass formulation [15]. This algorithm was applied on two important groups of constrained and unconstrained multimodal benchmark functions and obtained good results, but this algorithm suffers from high dependency on two parameters Ki and Kf.

Authors in [16] proposed Multimodal Cuckoo Search (MCS), a modified version of Cuckoo Search (CS) with multimodal capacities provided by the following three mechanisms: (1) incorporating a memory mechanism which efficiently registers potential local optima based on their fitness value and the distance to other potential solutions, (2) modifying of the original CS individual selection strategy for accelerating the detection process of new local minima, and (3) including a depuration procedure for cyclically elimination of duplicated memory elements. Experiments indicated that MCS provides competitive results compared to other algorithms for multimodal optimization.

Author of [17] modified the original PSO by dividing the original population into several subpopulations based on the order of particles. After this, the best particle in each subpopulation was employed in the velocity updating formula instead of the global best particle in PSO. Evaluations showed that after modifying the velocity updating formula, convergence behaviour of particles in terms of the number of iterations, and the local and global solutions was improved.

Authors in [18] combined exploration mechanism of the Gravitational search algorithm with the exploitation mechanism of Cuckoo search and called their method Cuckoo Search-Gravitational Search Algorithm (CS-GSA). Evaluations on standard test functions showed that CS-GSA converges with less number of fitness evaluations than both Cuckoo Search and GSA algorithms.

Authors in [19] proposed a multimodal optimization method based on firefly algorithm. In their method, the optimal points are detected by evolving each sub-population separately. For determining the stability of sub-populations, a stability criterion is used. Based on the criterion, stable sub-populations are found and since they have optimal points, they are stored in the archive. After several iterations, all the optimums are included in the archive. This algorithm also incorporates a simulated annealing local optimization algorithm to enhance search power, accuracy and speed. Experiments show that the proposed algorithm can successfully find optimums in multimodal optimization problems.

Authors in [20] proposed a niching method for Chaos Optimization Algorithm (COA) called NCOA. Their method utilizes a number of techniques including simultaneously contracted multiple search scopes, deterministic crowding, and clearing for niching. Experiments demonstrated that by using niching, NCOA can compete the state-of-the-art multimodal optimization algorithms.

Authors in [21] presented a novel evolutionary algorithm called Negatively Correlated Search (NCS) which parallels multiple individual search and models the behaviour of each individual search as a probability distribution. Experiments showed that NCS provides competitive results to the state-of-the-art multimodal optimization algorithms in the sense that NCS achieved the best overall performance on 20 non-convex benchmark functions.

Author of [22] presented a modified PSO which in the first step randomly divides the original population into two groups with one group focusing on the maximum optimization of the multimodal function and the other on minimization. After this, each group is divided into subgroups for finding optimum points simultaneously. The important point is that subgroups are not related and each one seeks for one optimum individually. Similar to [17], the velocity updating formula is modified in the proposed method by replacing the best particle of each subgroup instead of the global best. Evaluations on different kinds of multimodal optimization functions and one complex engineering problem demonstrated the applicability of the proposed method.

Authors in [1] incorporated a novel niching method into PSO (named NNGSA) by using Nearest Neighbour (NN) mechanism for forming species inside the population. They also employed the hill valley algorithm without a pairwise comparison between any pair of solutions for detecting niches inside the population. Experiments showed the effectiveness of NNGSA compared to the well-known niching methods.

3 Basic concepts

3.1 Gravitational search algorithm

GSA was presented in [8] based on Newton’s law of gravitation. Agents in this algorithm are similar to particles in the universe. The heavier the mass of an agent, the more efficient is that agent. This means that agents with heavier mass have higher attractions and walk more slowly (Figure 1). The location of an agent i in GSA is shown by Equation (1). Considering a system of N agents, the whole system can be formulated as Equation (2).

Xi←(xi1,xi2,…,xid,.....,xin)(1)
X←(X1,X2,…,Xi,.....,XN)(2)
Figure 1 General principle of GSA [8]
Figure 1

General principle of GSA [8]

In the above equations, xid is the location of agent i in dimension d, n is the dimension of the search space and N is the number of individuals (or agents). At a given time t, the applied force on agent i by agent j is calculated using Equation (3).

Fijd←GtMpit×MajtRijt+ϵ(xjdt−xid(t))(3)

where Maj is the active gravitational mass of agent j, Mpi is the passive gravitational mass of agent i, G(t) is gravitational constant at time t, ϵ is a small constant and Rij is the Euclidian distance between the two agents determined by Equation (4).

Rijt←Xit,Xj(t)(4)

Assuming that Kbest is the set of K agents with the best fitness value and thus the biggest mass, the whole applied force to the agent i in dimension d from agents in Kbest is computed by Equation (5).

Fidt←∑jϵKbest,j≠irandjFijd(5)

where randj is a random number in [0,1]. It should be noted that Kbest changes with time, its initial value is K0 and as time passes it decreases. The acceleration of the agent i in dimension d at time t is calculated by Equation (6).

aidt←Fid(t)Mii(t)(6)

where Mii is the inertia mass of the agent i. In addition, the velocity and position of the agent i in dimension d at time t + 1 are calculated by Equations (7) and (8) respectively. In equation (7), randi is a random number in [0,1].

vidt+1←randi×vidt+aid(t)(7)
xidt+1←xidt+vidt(8)

Gravitational fixed G is a function of time that is started with the initial value G0 and as time passes, it decreases to control the accuracy of search. The value of this function is calculated by Equations (9) and (10).

Gt←(G0,t)(9)
G(t)←G0e−αtT(10)

where α and G0 are fixed values and T indicates all iterations. In addition, inertia and gravitational masses are updated using Equations (11)–(13)

Mai=Mpi=Mii=Mii=1,2,…,N(11)
mit←fitit−worst(t)bestt−worst(t)(12)
Mit←mit∑j=1Nmjt(13)

where fiti(t) shows fitness value of the agent i at time t and worst(t) and best(t) are calculated using Equations (14) and (15).

bestt←maxj∈{1,…..,N}fitjt(14)
worstt←minj∈{1,…..,N}fitjt(15)

3.2 Niching

As mentioned previously, niching is the concept of dividing the search space into different areas or niches in a way that these areas are not overlapped. Evolutionary algorithm with niching technique search for optimal solutions in each separated area to efficiently explore the search space for finding global optimal solutions. Some of the well-known niching techniques are: fitness sharing [23], clearing [24], crowding [25], deterministic crowding [26, 27, 28] and probabilistic crowding [29].

3.3 K-means algorithm

K-means is employed as the niching technique in KGSA. The most important parameter in K-means is the number of clusters which is manually determined by the user. Clusters are represented by their centers which are randomly selected at the beginning of K-means. Then, K-means works as follows: each point (or agent) is assigned to the closest center, and in this way members of each cluster are determined. The mean of members in each cluster is calculated as the new center of that cluster (Equation 16). This process continues until the maximum number of iterations is reached or the members of clusters do not change.

ck←1Sk∑∀Xi∈SkXi(16)

In the above equation, Xi is agent i which belongs to cluster Sk, ck is the center of Sk and ∣Sk∣ is the number of members (agents) in Sk. A pseudocode of K-means algorithm is shown in Figure 2. Simplicity, flexibility and being easy to understand are among the advantages of this algorithm, but determining the number of clusters at the beginning of the algorithm is a weakness. In addition, since initial centers are randomly selected, results are different in different runs.

Figure 2 Pseudocode of K-means algorithm for clustering population members
Figure 2

Pseudocode of K-means algorithm for clustering population members

4 Proposed algorithm

GSA, K-means and a new elitism strategy called “loop in loop” are used to design the suggestive algorithm. This algorithm is called KGSA (K-means gravitational search algorithm) owing to the use of K-means and GSA. In this algorithm, firstly, the members of the initial population are clustered by K-means. Afterwards, the population is created and divided into different niches or clusters, the reinforced GSA with “loop in loop” technique guide the members of each niche to the optimum direction according to their clusters. More specifically, members of each cluster apply force to each other so that lighter members move towards the optimum direction of each cluster with higher velocity and heavier ones move to the direction slower. The principle of KGSA is shown in Figure 3. Different parts of the KGSA are separately described in order to explain more details.

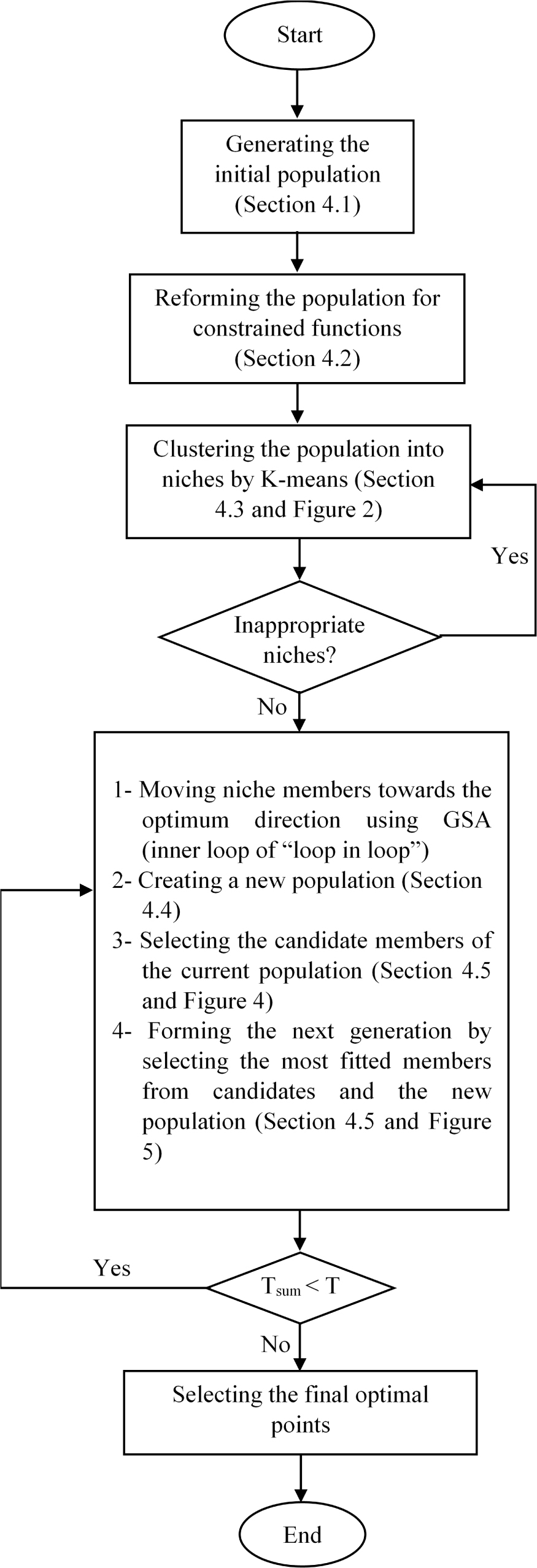
Figure 3 General principle of KGSA
Figure 3

General principle of KGSA

4.1 Population initialization

Before initializing the population, the structure of individuals must be specified. In this research, phenotypic structure is used where each member in each dimension gets a numerical value. To form the initial population, uniform and partition methods adopted from [15] are used. In the uniform method, members are initialized using Equation (17):

xid=Low+rand∗(High−Low)(17)

where xid is the location of agent (member) i in dimension d, Low and High are respectively the lowest and highest possible values in dimension d, and rand is a random number in [0,1]. Although the uniform method is simple, members initialized with this approach may be placed close to each other resulting in poor distribution in the search space.

In the partition method, the legal [Low, High] period in each dimension d is first divided into N smaller sub-periods with equal length where N is the size of population. Then for each dimension d, members are assigned to different sub-periods and similar to Equation (17), get a random value in that sub-period. With this approach, the main problem of the uniform method is solved and members are better distributed in the search space.

4.2 Population reformation

Population reformation is used for constrained functions so that infeasible solutions are avoided. It is clear that infeasible solutions may be produced when the initial population or new population are created. In the first case, the infeasible solutions are replaced by new solutions (members) created over and over again using uniform or partition methods. This process continues until possible solutions are found. In the latter case, the infeasible solutions are replaced by the most fitted members of the previous generation [30].

4.3 Production of appropriate clusters from population

Inappropriate clusters when initializing the population are either single-member or empty clusters. In other phases of KGSA, only empty clusters are considered inappropriate. Depending on the type of population initialization especially uniform method, some clusters may be inappropriate after executing the K-means algorithm, resulting in losing niches. To resolve this problem, when a cluster is inappropriate in population initialization, the population is rejected and the initial population is formed and clustered again until some appropriate clusters are created. But in other phases of KGSA, clustering is iterated until none of the clusters are inappropriate.

4.4 Calculation of mass, force, velocity and production of the next generation

Before calculating the mass of each member (agent), its neighbours should be determined. Since members have been clustered before, other members within the cluster of each member are considered as its neighbours. Then, using Equations (11)-(13), the mass of each member is calculated. After the mass of all members were specified, according to the Equation (5), the total force on agent i in dimension d is determined. Applied force to a member is only from its neighbours. When members apply force to each other, each member moves towards a direction with different velocity which can be calculated using Equation (7). As a result of the movement, new population is created. As will be discussed in the next section, this new population competes with the candidate members of the current population to form the next generation.

4.5 Use of innovative method “loop in loop” and discovery of optima

As described in the previous section, after the current population was developed by Tl iterations using GSA algorithm, the new population is created (section 4.4). Since this process needs Tl iterations, it is called the first (or inner) loop in the “loop in loop” method. Then, the most fitted members of the current population are selected as candidates (Section 4.5.1) and they compete with members of the new population (Section 4.5.2) to form the initial population for the next generation. This process continues until the maximum number of repetitions or the maximum number of permitted evaluations is reached. This is actually the second (or outer) loop of the “loop in loop”.

4.5.1 Selecting the candidate members from the current population

Since after developing the current population via Tl iterations using GSA, members of the current population are closer to the optimal solutions, the two closest members of each cluster (niche) are found, the most fitted one is selected and kept and the other one is removed. This process continues until the number of selected members reaches the number of optimal solutions (niches). These selected members along with the most fitted members of the current population (i.e. the best individual in the whole population and those having at least 80% of the fitness of the best individual) are candidate members for the next generation. The described process is based on the work of [30] and illustrated in Figure 4.

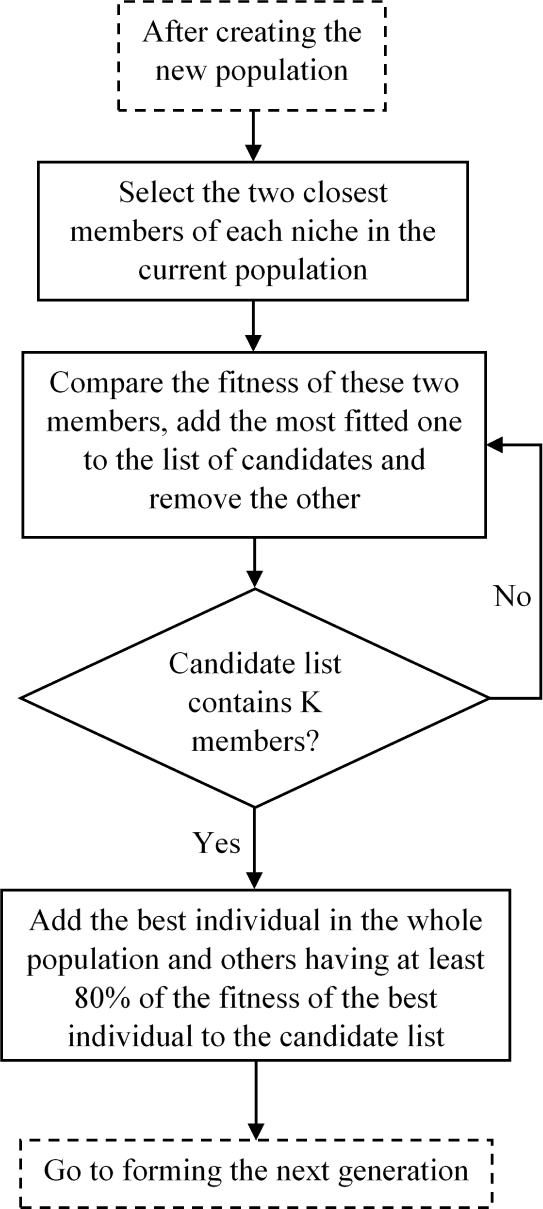
Figure 4 Preparing candidate list at the end of inner loop of “loop in loop”
Figure 4

Preparing candidate list at the end of inner loop of “loop in loop”

4.5.2 Forming the next generation by selecting the best members of candidates and the new population

The candidate members of the current population compete with the new population in the following way: for each candidate, the closest member of the new population is found. If the candidate is more fitted, it replaces the closest member of the new population; otherwise, it is ignored (Figure 5). After all the candidates were checked, the initial population for the next generation has been formed, so the next iteration of the inner loop of the “loop in loop” is started. It is worth to mention that when going from one generation to the next, niches are also transferred to the next generation.

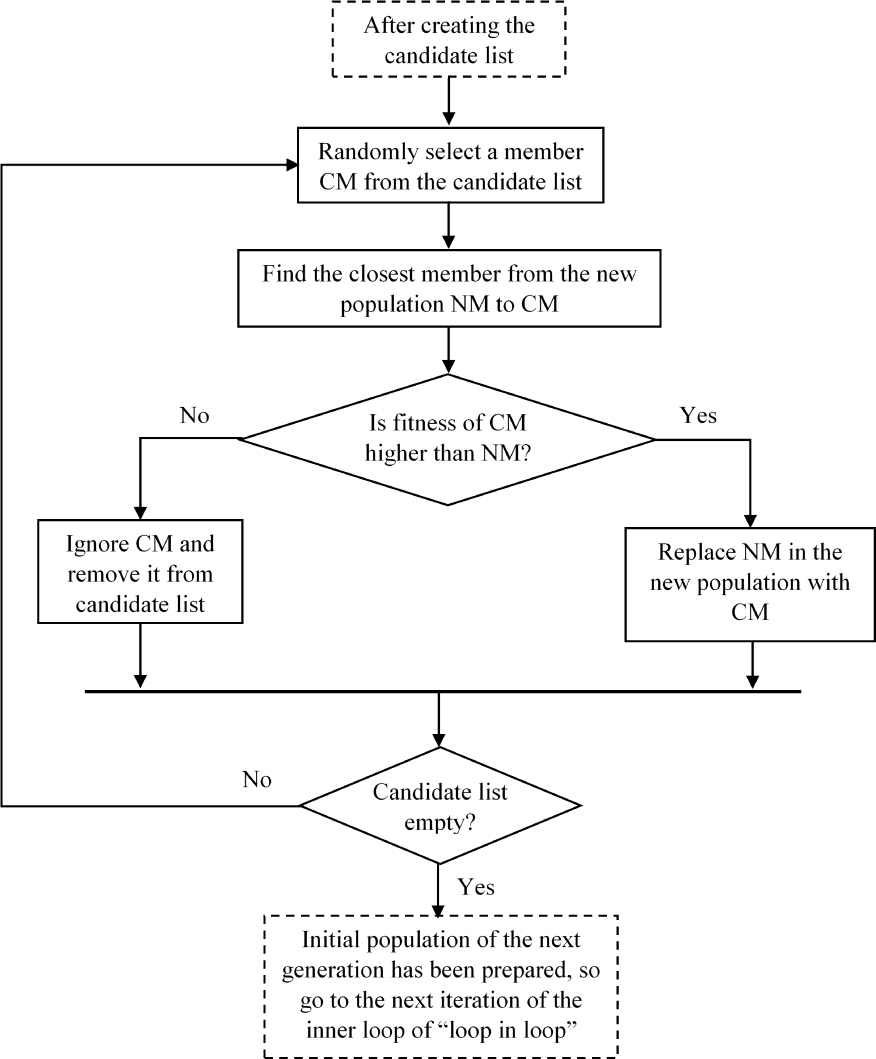
Figure 5 Forming the initial population of the next generation by selecting the most fitted members of the candidate list and the new population
Figure 5

Forming the initial population of the next generation by selecting the most fitted members of the candidate list and the new population

4.6 Conditions of ending the “loop in loop” algorithm

As illustrated in Figure 3, the maximum number of generations in “loop in loop” algorithm is fixed number T, but for the K-means algorithm, stopping criteria is when, the center of clusters does not change anymore.

5 Experimental results

To evaluate KGSA, some standard constrained and unconstrained functions are used. These functions are extracted from [15]. Results of benchmarking KGSA on these functions are compared to a number of algorithms including r3PSO [31], r2PSO-lhc [31], r3PSO-lhc [31], SPSO [32], FER-PSO [33], NichePSO [10], deterministic crowding [27], sequential niche [34], NGSA [15], NCOA [20], Firefly [19], and NNGSA [1]. It should be noted that some benchmark functions of this study have not been used in NCOA [20], Firefly [19], and NNGSA [1] and thus, the corresponding cells in tables showing the results are empty.

At the end of section 5, KGSA is statistically compared with other algorithms using Friedman test to show whether this algorithm is statistically superior or not.

5.1 Constrained and unconstrained benchmark functions

Unlike the constrained functions, when the domain is not considered in unconstrained functions, solutions do not follow a specific pattern. Tables 1A and 2A in Appendix show, respectively, unconstrained and constrained benchmark functions used in this study. Some of these benchmark functions along with the position of their optimal solutions are presented in Figures 6-9.

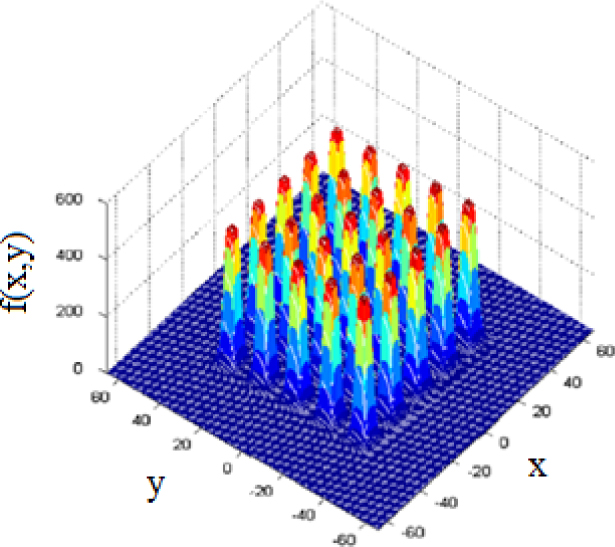
Figure 6 Shekel’s Foxholes function
Figure 6

Shekel’s Foxholes function

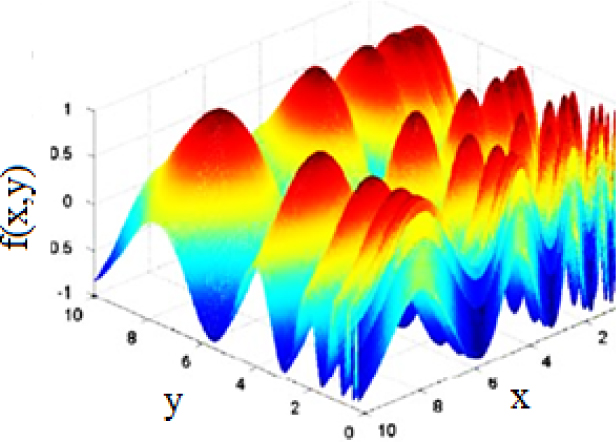
Figure 7 Inverted Vincent function
Figure 7

Inverted Vincent function

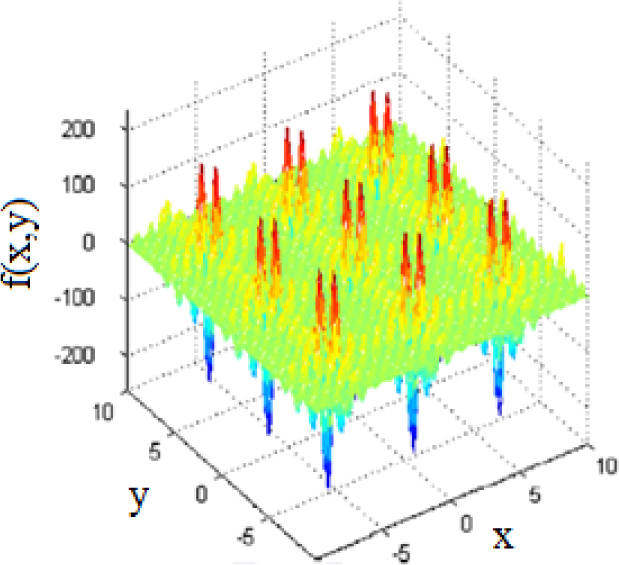
Figure 8 Inverted Shubert function
Figure 8

Inverted Shubert function

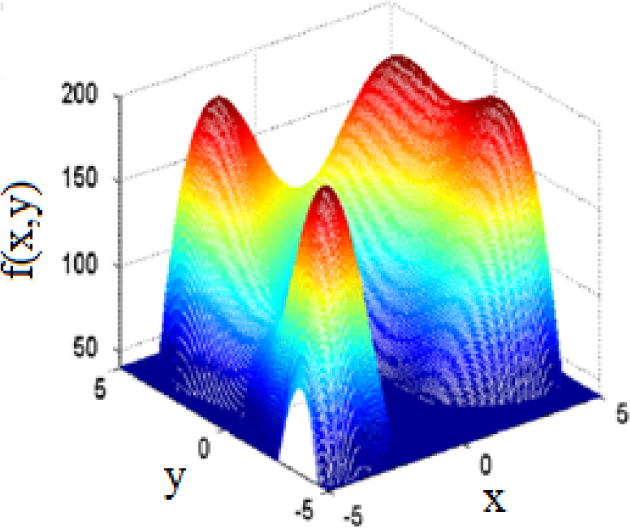
Figure 9 Himmelblau’s function
Figure 9

Himmelblau’s function

Table 1A

Unconstrained test functions in the experiments (see [15])

NameTest functionRangeNumber of global peakNumber of all peak
Equal maximaF1(x) = sin6(5πx)0≤x≤155
Decreasing maximaF2(x)=e−2log(2)(x−0.10.8)2sin6⁡(5πx)0≤x≤115
Uneven maximaF3(x) = sin6 (5π (x3/4 – 0.05))0≤x≤155
Uneven decreasing maximaF4(x)=e−2log(2)(x−0.080.854)2sin6⁡(5π(x3/4x−0.05))0≤x≤115
Himmelblau’s functionF5(x1,x2)=200−(x12+x2−11)2−(x1+x22−7)2−6 ≤ x1, x2 ≤ 644
Two-peak trapF6(x)=160/15(15−x)for0≤x≤15200/5(x−15)for15≤x≤200 ≤ x ≤ 2012
Central two-peak trapF7(x)=  160/10xfor0≤x≤10160/5(15−x)for10≤x≤15200/5(x−15)for15≤x≤200 ≤ x ≤ 2012
Five-uneven-peak- trapF8(x)={80(2.5−x)for0.0≤x≤2.564(x−2.5)for2.5≤x≤5.064(7.5−x)for5.0≤x≤7.528(x−7.5)for7.5≤x≤12.528(17.5−x)for12.5≤x≤17.532(x−17.5)for17.5≤x≤22.532(27.5−x)for22.5≤x≤27.580(x−27.5)for27.5≤x≤300 ≤ x ≤ 3025
Six-Hump Camel BackF9(x1,x2)=−4[(4−2.1x12+x143)x12+x1x2+(−4+4x22)x22]−1.9 ≤ x1 ≤ 1.9 −1.1 ≤ x2 ≤ 1.124
Shekel’s FoxholesF10(x1,x2)=500−{0.002+∑i=024[1+i+(x1−a(i))6+(x2−b(i))6]−1}−1wherea(i)=16((imod5)−2),andb(i)=16(⌊(i/5)⌋−2)−65.536 ≤ x1, x2 ≤ 65.536125
Inverted ShubertF11(x)=−∏i=1n∑j=15jcos⁡[(j+1)xi+j]−10 ≤ xi ≤ 103na
Inverted VincentF12(x)=1/n∑i=1nsin⁡(10log⁡(xi))0.25 ≤ xi ≤ 106n6n

Table 2A

Constrained test functions in the experiments (see [15])

NameTest functionRangeNumber of global peakNumber of all peak
cRastriginF13(x)=10n+∑i=1n[xi2−10cos⁡(2nxi)]s.t.h(x)=∑i=1nxi=0−5.12 ≤ xi ≤ 5.1222
cGriewankF14(x)=1/4000∑i=1nxi2−∏i=1ncos⁡(xii)+1s.t.h(x)=1512(n−1)∑i=2nxi2−|x1|=0−512 ≤ xi ≤ 51244
Deb’s constrainedF15(x)=(x1+a1)2+(x2+a2)2+...+(xn+an)2s.t.[(x1+b1)2+...(xn+bn)2]≥n2,−(n+1)≤xi≤n+1−3 ≤ xi ≤ 314

5.2 Evaluation Criteria of Algorithms

The KGSA algorithm is run multiple times and results of these independent runs are averaged. The evaluation criteria are success rate, error rate, and the number of fitness evaluations.

5.2.1 Success rate

In each run of the algorithm, if all peaks are found, the run is successful. When an agent reaches 99% of its highest value, it is considered as to have reached the peak value [15]. In addition, for a fair comparison, in cases that the error rate is reported, they are taken into account in KGSA. The success rate or the Average Discovering Rate (ADR) is calculated by averaging the results of different runs.

5.2.2 Error rate

Suppose that an algorithm finds a number of optimal solutions in an n dimensional space. The error rate is the mean of the Euclidian distance of the position of the discovered solutions from the position of the real optimum and is calculated using Equation (18).

ζ←1m∑i=1m∑j=1nsij−φij212(18)

where m is the number of the optimal solutions found by the algorithm and n is the dimension of the problem. In addition, s indicates the position of the optimum found by the algorithm and φ is the position of the real optimum of the problem. Similar to the ADR, error rate for different runs are averaged.

5.2.3 Number of fitness evaluations

In each generation, when the algorithm finds the niches, number of times that the evaluation function has been called is reported as the number of fitness evaluation. In another words, this number is the number of times that fitness agent has been calculated from the beginning. Similar to success and error rates, this value is also averaged for different runs.

5.3 Parameters and results of other algorithms

The results and parameters of other algorithms including the number of population members or N, number of iteration and maximum number of evaluations can be obtained from [15].

In KGSA, K is the number of clusters and is considered to be the total number of optimal solutions. In cases that the number of optimal solutions is higher than 25, K is equal to the number of the optima that must be discovered. G0 is set to 0.1 of the domain value and α is equal to 8. In both iterations, K-means algorithm is executed once. In each generation, 70% of the best individuals of each cluster apply force to co-cluster members. Other values from 20% to 95% (with step size 5%) were also tested for this. However, experiments showed that values lower than 70% result in virtual (incorrect) niches and values higher than 85% lead to losing some actual niches. Thus, the least appropriate value (70%) was selected since in addition to providing the desired results, it has less computational cost.

5.4 Finding optimal solutions

5.4.1 Finding global optimum in unconstrained functions

For finding global optima, KGSA was executed on functions F1 to F12 with partitioning initialization. Success rate is reported in Table 1 and the number of fitness evaluations for discovering the global optima are reported in Tables 3A and 4A in Appendix. Table 3A in Appendix compares KGSA with the well-known swarm-based methods for multimodal optimization and Table 4A in Appendix presents the result of comparison with NNGSA and some of the other evolutionary approaches. It should be mentioned that results are averaged over 50 runs. In Table 2, the required parameters for algorithms NGSA and KGSA are shown. Unlike the other algorithms, when executing NGSA on functions F6 to F9, the number of the initial population was set to 100 instead of 50, but the maximum number of iterations was decreased such that the maximum number of all evaluations is not exceeded.

Table 1

Comparison of found global maximum (%ADR) obtained with KGSA, NGSA, r2PSO, r3PSO, r2PSO-lhc, r3PSO-lhc, FER-PSO and SPSO using functions F1 to F12. The results were averaged after fifty independent runs of algorithms.

NCOAFireFly
FunctionKGSANGSAr2 PSOr3 PSOr2 PSO -lhcr3 PSO -lhcFER-PSOSPSO
[20][19]
F1100100100100100100100100100100
F210010010010098100100100100100
F31001001001009898100100100100
F4100100100100100100100100100100
F510010010010092741009898100
F61001001001009810094788824
F710010010010010096988810022
F8100100100941009696969840
F9100100100100100100100100100100
F1010090100100100100727810050
F11(2D)100931001009098981005649
F12(1D)100--9292948692908884

Table 2

List of required parameters for discovering global optima in unconstrained functions

FunctionF1F2F3F4F5F6F7F8F9F10F11F12
KGSAN1010201020108301540100500
Max eval8006008007502400180012803600135010006000090000
Tl201510152090806030506045
NGSAN5050505050100100100100500250100
Max100001000010000100001000010000100001000010000100001000010000
eval000000000000
ε0.010.010.010.010.10.10.150.010.010.10.01

Table 3A

Mean value of fitness function assessments needed to converge for each PSO based algorithm for the results shown in Table 1. The results were averaged over fifty independent runs of algorithms

FunctionKGSANGSAr2 PSOr3 PSOr2 PSO -lhcr3 PSO -lhcFER-PSOSPSO
F1214±133263±89376±30443±51396±51447±52384±29355±30
F2105±108300±1072120±1999141±11143±14144±13170±12127±9
F3263±140334±812430±19942440±1994456±33623±273317±31343±23
F4130±124316±76175±17160±20178±18162±16189±20144±13
F5864±3821632±3307870±289121400±54671490±1387380±33475070±19451250±45
F6304±110477±4093460±1972620±8747390±334023200±583414400±453577200±5859
F7290±130234±1082960±15205340±27644340±222913100±45882110±22778300±5856
F8557±346694±853978±1864650±27844710±27836730±30882660±199263300±6773
F9230±1211032±892619±24684±30618±30650±25965±53653±32
F103119±21724164±17684360±5595310±45329700±627724800±57383470±33642800±6968
F11(2D)33344±80995369±193055900±267639100±164837800±148032400±58194900±126161600±4463
F12(1D)12480±181752134±4308310±337115400±49069600±382414700±434413000±460117000±5162

Table 4A

Average number of fitness function evaluations required to converge for each of the evolutionary algorithms. The results were averaged over fifty independent runs of algorithms

FunctionKGSANCOA [20]Firefly [19]NNGSA [1]
F1214±133607±31182±94-
F2105±108614±22206±91-
F3263±140622±34186±101-
F4130±124620±31180±88-
F5864±3821180±501152±2741466±513
F6304±110498±76460±178-
F7290±130477±63489±184-
F8557±346580±39528±215200±0
F9230±1212196±72692±402200±0
F103119±217227539±1431-15740±8313
F11(2D)33344±809929397±25551260±39430840±7254
F12(1D)12480±18175-1002±404-

As illustrated in Table 1, the KGSA has performed much better than the well-known swarm-based algorithms in discovering all global optima for all functions. Table 3A in Appendix shows that the results of Table 1 were obtained with less number of evaluations in most cases. Furthermore, as can be seen in Table 2, the initial population size for KGSA was lower in all cases, except for function F12.

5.4.2 Finding local and global optima in unconstrained functions

In order to find global and local optima, KGSA is developed with different population sizes in at most 120 generations. Results of this evaluation is compared with that of NGSA algorithm with two different initializations: 1) uniform initialization where the comparative results are presented in Table 3 and 2) partitioning initialization where the results are shown in Table 4. Table 3 shows that the proposed algorithm performed much better when the initialization is uniform. However, with partitioning initialization, both KGSA and NGSA algorithms were equally successful in finding the global and local optima. In order to fine-tune the population size, it was set to 20 and the error rates of KGSA and NGSA were recorded in Table 5. As can be seen from this table, KGSA had lower error rate than NGSA for both initialization methods in this setting. The results were averaged for 30 independent runs of both algorithms. It should be noted that Tl for all experiments was set to 15.

Table 3

%ADR obtained with the KGSA and NGSA using different population sizes, and uniform initialization for finding all local and global maxima.

FunctionN=75N=50N=35N=20
KGSANGSAKGSANGSAKGSANGSAKGSANGSA
F11001001001001009310080
F21001001001001009610073
F31001001001001008610073
F4100100100961009010066
F51001001001001009610076

Table 4

%ADR obtained with the KGSA and NGSA using different population sizes and partitioning initialization for finding all local and global maxima.

N=75N=50N=35N=20
Function
KGSANGSAKGSANGSAKGSANGSAKGSANGSA
F1100100100100100100100100
F2100100100100100100100100
F3100100100100100100100100
F4100100100100100100100100
F5100100100100100100100100

Table 5

The mean error ζobtained with the KGSA and NGSA using N=20, T=120

Average ζ
FunctionKGSA uniform initializationKGSA partitioning initializationNGSA partitioning initialization
F11.75e - 6 ± 1.03e - 61.78e - 6 ± 9.41e - 71.62e - 5 ± 3.47e - 5
F24.96e - 7 ± 1.54e - 62.75e - 7 ± 2.94e - 70.001± 1.66e - 4
F32.41e - 6 ± 2.12e - 62.35e - 6 ± 1.29e - 60.0012 ± 5.04e - 4
F46.87e - 7 ± 1.98e - 65.34e - 7 ± 6.81e - 72.37e - 4 ± 3.38e - 4
F53.59e - 3 ± 2.13e - 34.29e - 3 ± 4.22e - 30.0570 ± 0.0262

Considering the results presented in Tables 3-5, one can see that KGSA outperforms NGSA in terms of finding global and local optima and lower error rate. In addition, when reducing the population size, NGSA was sensitive to the initialization type but not the KGSA algorithm since it uses the “loop in loop” method resulting in a larger search space.

In order to evaluate the algorithms in other settings and on more functions, the number of members was set to 20, maximum numbers of iterations was set to 2000, initialization method was partitioning and evaluations were performed on functions F1 to F5. Results of this evaluation for KGSA are presented in Tables 6 and 7, and results of other algorithms can be obtained from [15]. Table 6 shows that the proposed algorithm has performed better than other algorithms in terms of finding global and local optima. The number of necessary evaluations for finding optimal solutions is reported in Table 7. This table shows that for 100% discovering the optima, KGSA needed less number of evaluations than the other algorithms. Furthermore, Table 5A in Appendix shows that KGSA achieved the results presented in Tables 6 and 7 with lower population size and lower “maximum number of iterations” compared to the other algorithms.

Table 6

Comparison of KGSA, NGSA, deterministic crowding, sequential niche and NichePSO algorithms in terms of %ADR for functions F1 to F5. The results were averaged after thirty independent runs of algorithms.

FunctionKGSANGSADeterministic CrowdingSequential NicheNichePSO
F1100100100100100
F2100100938393
F310010090100100
F4100100909393
F51001009086100

Table 7

Average number of fitness function assessments needed to converge for each niching algorithm for functions F1 to F5. The results were averaged after thirty independent runs of algorithms.

FunctionKGSANGSADeterministic CrowdingSequential NicheNichePSO
F1208 ± 1151786 ± 20414647 ± 46124102 ± 5772372 ± 109
F2211±1031892±56113052 ± 25073505 ± 4632934 ± 475
F3286 ± 1361752 ± 27313930 ± 32844141 ± 5542404 ± 195
F4272 ±1491806 ± 30713929 ± 29963464 ± 2872820±517
F5897 ± 4462033 ± 20114296 ± 34083423 ± 4022151 ± 200

Table 5A

List of required parameters for discovering local and global optima in Tables 6, 7

FunctionF1F2F3F4F5
KGSAN1010201020
T80604075120
Tl2015101520
Other AlgorithmsN2020202020
T20002000200020002000

Also, the KGSA algorithm was applied to functions F6 to F10 using partitioning initialization. Results of this comparison are presented in Tables 8 and 9. The first table shows comparisons with NGSA and the latter presents comparisons with NNGSA. As can be seen from Table 8, KGSA has higher success rate in all situations, and the lower error-rate and the “number of evaluations” in most cases. Moreover, Table 6A in Appendix shows that results presented in Table 8 were achieved with lower population size and lower “number of evaluations” than those of NGSA. All parameters and results for NGSA and KGSA were adopted from [15].

Table 8

Results of KGSA and NGSA in terms of %ADR and the number of fitness assessments needed to converge for each niching algorithm using functions F6 to F10. The results were averaged after fifty independent runs of algorithms.

KGSANGSA
FunctionNumber of fitness evaluationsAverage ζADR(%)Number of fitness evaluationsAverage ζADR(%)
F6413 ±1131.02e - 4 ± 1.38e - 4100542±3864.27e - 4 ± 4.18e - 4100
F7267 ± 1285.12e - 6 ± 5.66e - 6100321 ± 1187.44e - 6 ± 6.01e - 6100
F8873 ± 7216.51e - 5 ± 2.08e - 4100966 ±7652.19e - 3 ± 1.37e - 294
F91097±8567.29e - 5 ± 1.88e - 41001122 ± 3531.50e - 3 ± 3.33e - 298
F1011318 ± 28614.51e - 2 ± 6.73e - 31006186 ± 21339.66e - 4 ± 1.18e - 3100

Table 9

Results of KGSA and NNGSA in terms of %ADR and the number of fitness assessments needed to converge for each niching algorithm using functions F6 to F10. The results were averaged after fifty independent runs of algorithms.

KGSANNGSA [1]
FunctionNumber of fitness evaluationsAverage ζNumber of fitness evaluationsAverage ζ
F6413 ±1131.02e - 4 ± 1.38e - 4--
F7267 ± 1285.12e - 6 ± 5.66e - 6--
F8873 ± 7216.51e - 5 ± 2.08e - 4--
F91,097 ± 8567.29e - 5 ± 1.88e - 4200 ± 00 ± 0
F1011,318 ± 28614.51e - 2 ± 6.73e - 31,5740e + 4 ± 8.313e + 33,6015e - 4 ± 0.151 e - 1

Table 6A

List of required parameters for discovering local and global optima in Table 8

FunctionF6F7F8F9F10
KGSAN158301580
Max eval270056003600525020000
Tl9070605050
NGSAN100100100100500
Max eval100000100000100000100000100000
ε0.10.150.010.01

5.4.3 Finding global optima in constrained functions

KGSA was also evaluated on constrained functions F13 to F15. Average results of 50 runs using partitioning initialization are shown in Table 10. This table illustrates that KGSA achieved 100% success rate for all the constrained functions in addition to having a lower error-rate than the other algorithms in most cases. Moreover, this algorithm had the lowest “number of evaluations” on two out of three of these functions. In case of function F15, “number of evaluations” for KGSA was only greater than that of NGSA. Table 7A in Appendix shows parameter settings used for these experiments and indicates that results of KGSA were achieved with lower population size and less iterations.

Table 10

Performance comparison when constrained test functions were used.

FunctionMethodsAverage ζNumber of fitness evaluationsADR(%)
Fl3r2PSO3.1586e - 04±0.0080510±438.1082100
r3PSO6.3425e - 04±0.0105546±396.0056100
r2PSO-lhc5.5256e - 04±0.0067474±383.7569100
r3PSO-lhc1.2619e - 03±0.0083450±292.2498100
Deterministic crowding4.3717e - 04±0.01031,098±662.8602100
NGSA3.1255e - 04±0.010778±146.0919100
NNGSA2.5352 - 04 ± 6.1e - 032,080±19,110100
KGSA6.04e - 05 ± 5.67e - 0592±43100
F14r2PSO2.3313e - 02±2.25222,396±0.1469100
r3PSO7.1531e - 03±0.98352,092±0.5050100
r2PSO-lhc8.9047e - 03±1.83142,476±0.5123100
r3PSO-lhc1.3116e - 02±2.10652,232±0.5539100
Deterministic crowding1.6902e - 02±0.495621,552±1.0056100
NGSA1.9672e - 02±0.37901,944 ± 1.2944e + 03100
NNGSA2.0176e-03±0.0365e- 021,413±1,080100
KGSA5.79e - 03 ± 0.040981,395 ± 587100
F15r2PSO0.3966±0.2352788±0.0849100
r3PSO0.381±0.1997792±0.0849100
r2PSO-lhc4.9832e - 03±0.2081812±0.0396100
r3PSO-lhc0.3237±0.1873796±0.0480100
Deterministic crowding6.2571e - 04±0.05526,672±0.0283100
NGSA5.0262e - 04±0.02033,116±1.0135100
NNGSA1.4415e-03±3.02e-025,183±1,560100
KGSA3.37e - 04 ± 6.37 e - 04480 ± 103100

Table 7A

List of required parameters for discovering global optima in Table 10

FunctionFl3F14F15
KGSAN104025
T8010045
Ti405045
NGSAN300200200
T200100100

5.5 Sensitivity analysis of parameter Tl in KGSA

In this section, sensitivity of KGSA to Tl is evaluated. As stated previously, Tlrepresents the number of repetitions of the inner loop of “loop in loop” method. This parameter can affect the performance of KGSA since loops have a major role in finding optima; therefore, correct setting of Tl is very important. If Tl is too small, few generations will be created in a loop and therefore, the population will not develop adequately and candidates with lower fitness will go to the next generation. On the other hand, if Tl is too large, the number of loops will reduce and consequently, search space will be small. Therefore, it is necessary to select an appropriate value for Tl. For doing this, an experiment was conducted to evaluate KGSA on functions F1 to F5with different values for Tl. In this experiment, the population number was set to 20, the first population was initialized by the partitioning method, and the maximum number of generations was set to 120. Result of 50 independent runs of KGSA in this setting is shown in Table 8A in Appendix. As can be seen from this table, KGSA success rate on F1to F4 has not been changed for different values of Tl. However, for function F5, result is different. When Tl is 10, the success rate is 96% which indicates that the number of repetitions for building the population is not enough. On the other hand, when Tl is 40 and 60, the success rate is 98% and 94% respectively. This points out the excessive number of repetitions in a loop for building the population. This means that the search space has been reduced in this case. Overall, it can be concluded that the success rate is not significantly affected by Tl, showing the low sensitivity of KGSA to Tl.

Table 8A

Success rate of the KGSA for the different values of Tl

FunctionTl = 10Tl = 15Tl = 20Tl = 30Tl = 40Tl = 60
Fl100100100100100100
F2100100100100100100
F3100100100100100100
F4100100100100100100
F5961001001009894

5.6 Statistical Tests

In the final test, KGSA is statistically compared with other methods. For this purpose, Friedman test has been performed on possible metrics between KGSA and other methods. It is known that Friedman test is based on the chi-square distribution with for analyzing the statistical significant difference between the results of several methods [35]. The Friedman test is a non-parametric statistical test for ranking the algorithms and evaluating whether their results are statistically significantly different or not. It computes a score for each algorithm on a specific criterion and finally ranks them based on the scores. In the Friedman test, the null hypothesis states that the methods are not statistically significantly different. If the p-value is less than a predetermined level, null hypothesis is rejected which shows that results of the methods are significantly different. In this paper, p-value was set to 0.05.

Results of Friedman test are provided in Table 11. In this table, the best method in each column is shown in bold face and the second best is underlined. This table indicates that KGSA and Firefly [19] algorithms are the most successful. It must be noted that since we did not have access to the codes of other algorithms and some of the benchmark functions used in this study were different, all tests could not be performed on all algorithms and thus, some of the cells in Table 11 are empty.

Table 11

Friedman test on KGSA and the other algorithms

Finding all global maximaNumber of Function Evaluations
r2 PSO3.777.25
r3 PSO5.328.50
r2 PSO lhc4.736.25
r3 PSO lhc5.097.25
FER PSO4.828.75
SPSO4.777.75
NGSA6.366.00
NCOA6.235.25
Firefly6.953.25
NNGSA---2.75
KGSA6.952.50
P-value0.0060.033
Degree of Freedom910

6 Conclusions and Future Works

In this paper, KSGA, a novel Gravitational Search Algorithm for multimodal problems was proposed. KSGA incorporated k-means and a new elitism strategy called “loop in loop” into the conventional Gravitational Search Algorithm (GSA). First in KGSA, the initial population was clustered by K-means and after that, the first population was created by selecting the members from different clusters (niches). This resulted in a large search space and thus increased the chance of finding local and global optima in KGSA. “loop in loop” technique was used to guide the members of each niche to the optimum direction according to their clusters. With these modifications, KGSA does not need the following items: the type of population initialization and parameter “radius of niche”. Evaluations on different benchmark functions showed that KGSA is superior to other GSA based evolutionary algorithms in finding both local and global optima. We intend to exploit fuzzy methods to determine the number of optima at the beginning of KGSA and incorporating the “loop in loop” technique into unimodal problems for future works.

References

[1] Haghbayan P., Nezamabadi-Pour H., Kamyab S., A niche GSA method with nearest neighbor scheme for multimodal optimization, Swarm and Evolutionary Computation, 35, 2017, 78-9210.1016/j.swevo.2017.03.002Search in Google Scholar

[2] Subhrajit R., Minhazul I., Das S., Ghosh S., Multimodal optimization by artificial weed colonies enhanced with localized group search optimizers, Applied Soft Computing, 13, 2013, 27-4610.1016/j.asoc.2012.08.038Search in Google Scholar

[3] Tang K. S., Man K., Kwong S., He Q., Genetic algorithms and their applications, IEEE Signal Processing Magazine, 13, 1996, 6, 22-3710.1109/79.543973Search in Google Scholar

[4] Kirkpatrick S., Vecchi M., Optimization by simmulated annealing, Science, 220, 1983, 4598, 671-68010.1126/science.220.4598.671Search in Google Scholar

[5] Farmer J. D., Packard N. H., Perelson A. S., The immune system, adaptation, and machine learning, Physica D: Nonlinear Phenomena, 22, 1986, 1, 187-20410.1016/0167-2789(86)90240-XSearch in Google Scholar

[6] Dorigo M., Maniezzo V., Colorni A., Ant system: optimization by a colony of cooperating agents, IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 26, 1996, 1, 29-4110.1109/3477.484436Search in Google Scholar PubMed

[7] Kenndy J., Particle Swarm Optimization, in “Encyclopedia of machine learning”, Sammut C., Webb G. I., eds., Springer, Boston, MA, 2011, 760-76610.1007/978-0-387-30164-8_630Search in Google Scholar

[8] Rashedi E., Nezamabadi-Pour H., Saryazdi S., GSA: a Gravitational Search Algorithm, Information sciences, 179, 2009, 13, 2232-224810.1016/j.ins.2009.03.004Search in Google Scholar

[9] Rashedi E., Nezamabadi-Pour H., Saryazdi S., BGSA: binary gravitational search algorithm, Natural Computing, 9, 2010, 3, 727-74510.1007/s11047-009-9175-3Search in Google Scholar

[10] Brits R., Engelbrecht A. P., Van den Bergh F., A niching particle swarm optimizer, In: Proceedings of the 4th Asia-Pacific conference on simulated evolution and learning, Paper Presented at Proceedings of the 4th Asia-Pacific conference on simulated evolution and learning (Orchid Country Club, Singapore), 2002, November 18, Orchid Country Club, 692-696Search in Google Scholar

[11] Thiemard E., Economic generation of low-discrepancy sequences with a b-ary Gray code, Technical Report, 1998, Department of Mathematics, Ecole Polytechnique Fédérale de Lausanne, Lausanne, SwitzerlandSearch in Google Scholar

[12] Streichert F., Stein G., Ulmer H., Zell A., A clustering based niching method for evolutionary algorithms, In: Genetic and Evolutionary Computation Conference, Paper Presented at Genetic and Evolutionary Computation Conference (Chicago, USA), 2003, July 9-11, Springer, 644-64510.1007/3-540-45105-6_79Search in Google Scholar

[13] Li X., Adaptively choosing neighbourhood bests using species in a particle swarm optimizer for multimodal function optimization, In: Genetic and Evolutionary Computation Conference, Paper Presented at Genetic and Evolutionary Computation Conference, (Seattle, USA), 2004, June 26-30, Springer, 105-11610.1007/978-3-540-24854-5_10Search in Google Scholar

[14] Seo J. H., Im C. H, Heo C. G., Kim J. K., Jung H. K., Lee C. G., Multimodal function optimization based on particle swarm optimization, IEEE Transactions on Magnetics, 42, 2006, 4, 1095-109810.1109/TMAG.2006.871568Search in Google Scholar

[15] Yazdani S., Nezamabadi-Pour H., Kamyab S., A gravitational search algorithm for multimodal optimization, Swarm and Evolutionary Computation, 14, 2014, 1-1410.1016/j.swevo.2013.08.001Search in Google Scholar

[16] Cuevas E., Reyna-Orta A., A cuckoo search algorithm for multimodal optimization, 2014, The Scientific World Journal, 201410.1155/2014/497514Search in Google Scholar PubMed PubMed Central

[17] Chang W. D., A modified particle swarm optimization with multiple subpopulations for multimodal function optimization problems, Applied Soft Computing, 33, 2014, 170-18210.1016/j.asoc.2015.04.002Search in Google Scholar

[18] Naik M. K., Panda R., A new hybrid CS-GSA algorithm for function optimization, In: Proceedings of the IEEE International Conference on Electrical, Electronics, Signals, Communication and Optimization, Paper Presented at IEEE International Conference on Electrical, Electronics, Signals, Communication and Optimization, (Visakhapatnam, India), 2015, January 24-25, IEEE, 1-610.1109/EESCO.2015.7253661Search in Google Scholar

[19] Nekouie N., Yaghoobi M., A new method in multimodal optimization based on firefly algorithm, Artificial Intelligence Review, 46, 2016, 2, 267-28710.1007/s10462-016-9463-0Search in Google Scholar

[20] Rim C., Piao S., Li G., Pak U., A niching chaos optimization algorithm for multimodal optimization, Soft Computing, 22, 2016, 2, 621-63310.1007/s00500-016-2360-2Search in Google Scholar

[21] Tang K., Yang P., Yao S., Negatively correlated search, IEEE Journal on Selected Areas in Communications, 34, 2016, 3, 542-55010.1109/JSAC.2016.2525458Search in Google Scholar

[22] Chang W. D., Multimodal function optimizations with multiple maximums and multiple minimums using an improved PSO algorithm, Applied Soft Computing, 60, 2017, 60-7210.1016/j.asoc.2017.06.039Search in Google Scholar

[23] Goldberg D. E., Richardson J., Genetic algorithms with sharing for multimodal function optimization, In: Proceedings of the Second International Conference on Genetic Algorithms and their applications, Paper Presented at the Second International Conference on Genetic Algorithms and their applications, (Cambridge, USA), 1987, Hillsdale: Lawrence Erlbaum, 41-49Search in Google Scholar

[24] Pétrowski A., A clearing procedure as a niching method for genetic algorithms, In: Proceedings of IEEE International Conference on Evolutionary Computation, Paper Presented at Proceedings of IEEE International Conference on Evolutionary Computation, (Nagoya, Japan), 1996, IEEE, May 20-22, 798-80310.1109/ICEC.1996.542703Search in Google Scholar

[25] De Jong K. A., An Analysis of the Behavior of a Class of Genetic Adaptive Systems, In: Techincal Report, 1975, Computer and Communication Sciences Department, College of Literature, Science, and the Arts, University of MichiganSearch in Google Scholar

[26] Mahfoud S. W., Simple Analytical Models of Genetic Algorithms for Multimodal Function Optimization, In: Proceedings of the 5th International Conference on Genetic Algorithms, Paper Presented at Proceedings of the 5th International Conference on Genetic Algorithms (San Fransisco, USA), 1993, San Fransisco: Morgan Kaufman Publishers, 643Search in Google Scholar

[27] Mahfoud S. W., Crossover Interactions Among Niches, In: Proceedings of the First IEEE Conference on Evolutionary Computation, Paper Presented at the First IEEE Conference on Evolutionary Computation, (Orlando, USA), 1994, June 27-29, IEEE, 188-193Search in Google Scholar

[28] Mahfoud S. W., Niching methods for genetic algorithms, Urbana, 51, 1994, 95001, 62-94Search in Google Scholar

[29] Mengshoel O. J., Goldberg D. E., Probabilistic crowding: Deterministic crowding with probabilistic replacement. In: Genetic and Evolutionary Computation Conference, Paper Presented at Genetic and Evolutionary Computation Conference, (San Fransisco, USA), 1999, July 8-12, San Fransisco: Morgan Kaufman Publishers, 409Search in Google Scholar

[30] Kimura S., Matsumura K., Constrained multimodal function optimization using a simple evolutionary algorithm, In: IEEE Congress on Evolutionary Computation, Paper Presented at IEEE Congress on Evolutionary Computation, (New Orleans, USA), 2011, June 5-8, IEEE, 447-45410.1109/CEC.2011.5949652Search in Google Scholar

[31] Li X., Niching without niching parameters: particle swarm optimization using a ring topology, IEEE Transactions on Evolutionary Computation, 14, 2010, 1, 150-16910.1109/TEVC.2009.2026270Search in Google Scholar

[32] Parrott D., Li X., Locating and tracking multiple dynamic optima by a particle swarm model using speciation, IEEE Transactions on Evolutionary Computation, 10, 2006, 4, 440-45810.1109/TEVC.2005.859468Search in Google Scholar

[33] Li X., Multimodal function optimization based on fitness-euclidean distance ratio, In: Genetic and Evolutionary Computation Conference, Paper Presented at Genetic and Evolutionary Computation Conference, (Washington, USA), 2007, June 25-29, New York: ACM, 78-85Search in Google Scholar

[34] Zhang J., Zhang J. R., Li K., A sequential niching technique for particle swarm optimization, In: Advances in Intelligent Computing, Paper Presented at Advances in Intelligent Computing, (Hefei, China), 2005, August 23-26, Berlin Heidelberg: Springer-Verlag, 390-39910.1007/11538059_41Search in Google Scholar

[35] García S., Fernández A., Luengo J., Herrera F., Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power, Information Sciences, 180, 2010, 10, 2044-206410.1016/j.ins.2009.12.010Search in Google Scholar

Received: 2018-02-14
Accepted: 2018-08-02
Published Online: 2018-12-31

© 2018 Golzari et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

  1. Regular Articles
  2. Algebraic proofs for shallow water bi–Hamiltonian systems for three cocycle of the semi-direct product of Kac–Moody and Virasoro Lie algebras
  3. On a viscous two-fluid channel flow including evaporation
  4. Generation of pseudo-random numbers with the use of inverse chaotic transformation
  5. Singular Cauchy problem for the general Euler-Poisson-Darboux equation
  6. Ternary and n-ary f-distributive structures
  7. On the fine Simpson moduli spaces of 1-dimensional sheaves supported on plane quartics
  8. Evaluation of integrals with hypergeometric and logarithmic functions
  9. Bounded solutions of self-adjoint second order linear difference equations with periodic coeffients
  10. Oscillation of first order linear differential equations with several non-monotone delays
  11. Existence and regularity of mild solutions in some interpolation spaces for functional partial differential equations with nonlocal initial conditions
  12. The log-concavity of the q-derangement numbers of type B
  13. Generalized state maps and states on pseudo equality algebras
  14. Monotone subsequence via ultrapower
  15. Note on group irregularity strength of disconnected graphs
  16. On the security of the Courtois-Finiasz-Sendrier signature
  17. A further study on ordered regular equivalence relations in ordered semihypergroups
  18. On the structure vector field of a real hypersurface in complex quadric
  19. Rank relations between a {0, 1}-matrix and its complement
  20. Lie n superderivations and generalized Lie n superderivations of superalgebras
  21. Time parallelization scheme with an adaptive time step size for solving stiff initial value problems
  22. Stability problems and numerical integration on the Lie group SO(3) × R3 × R3
  23. On some fixed point results for (s, p, α)-contractive mappings in b-metric-like spaces and applications to integral equations
  24. On algebraic characterization of SSC of the Jahangir’s graph 𝓙n,m
  25. A greedy algorithm for interval greedoids
  26. On nonlinear evolution equation of second order in Banach spaces
  27. A primal-dual approach of weak vector equilibrium problems
  28. On new strong versions of Browder type theorems
  29. A Geršgorin-type eigenvalue localization set with n parameters for stochastic matrices
  30. Restriction conditions on PL(7, 2) codes (3 ≤ |𝓖i| ≤ 7)
  31. Singular integrals with variable kernel and fractional differentiation in homogeneous Morrey-Herz-type Hardy spaces with variable exponents
  32. Introduction to disoriented knot theory
  33. Restricted triangulation on circulant graphs
  34. Boundedness control sets for linear systems on Lie groups
  35. Chen’s inequalities for submanifolds in (κ, μ)-contact space form with a semi-symmetric metric connection
  36. Disjointed sum of products by a novel technique of orthogonalizing ORing
  37. A parametric linearizing approach for quadratically inequality constrained quadratic programs
  38. Generalizations of Steffensen’s inequality via the extension of Montgomery identity
  39. Vector fields satisfying the barycenter property
  40. On the freeness of hypersurface arrangements consisting of hyperplanes and spheres
  41. Biderivations of the higher rank Witt algebra without anti-symmetric condition
  42. Some remarks on spectra of nuclear operators
  43. Recursive interpolating sequences
  44. Involutory biquandles and singular knots and links
  45. Constacyclic codes over 𝔽pm[u1, u2,⋯,uk]/〈 ui2 = ui, uiuj = ujui〉
  46. Topological entropy for positively weak measure expansive shadowable maps
  47. Oscillation and non-oscillation of half-linear differential equations with coeffcients determined by functions having mean values
  48. On 𝓠-regular semigroups
  49. One kind power mean of the hybrid Gauss sums
  50. A reduced space branch and bound algorithm for a class of sum of ratios problems
  51. Some recurrence formulas for the Hermite polynomials and their squares
  52. A relaxed block splitting preconditioner for complex symmetric indefinite linear systems
  53. On f - prime radical in ordered semigroups
  54. Positive solutions of semipositone singular fractional differential systems with a parameter and integral boundary conditions
  55. Disjoint hypercyclicity equals disjoint supercyclicity for families of Taylor-type operators
  56. A stochastic differential game of low carbon technology sharing in collaborative innovation system of superior enterprises and inferior enterprises under uncertain environment
  57. Dynamic behavior analysis of a prey-predator model with ratio-dependent Monod-Haldane functional response
  58. The points and diameters of quantales
  59. Directed colimits of some flatness properties and purity of epimorphisms in S-posets
  60. Super (a, d)-H-antimagic labeling of subdivided graphs
  61. On the power sum problem of Lucas polynomials and its divisible property
  62. Existence of solutions for a shear thickening fluid-particle system with non-Newtonian potential
  63. On generalized P-reducible Finsler manifolds
  64. On Banach and Kuratowski Theorem, K-Lusin sets and strong sequences
  65. On the boundedness of square function generated by the Bessel differential operator in weighted Lebesque Lp,α spaces
  66. On the different kinds of separability of the space of Borel functions
  67. Curves in the Lorentz-Minkowski plane: elasticae, catenaries and grim-reapers
  68. Functional analysis method for the M/G/1 queueing model with single working vacation
  69. Existence of asymptotically periodic solutions for semilinear evolution equations with nonlocal initial conditions
  70. The existence of solutions to certain type of nonlinear difference-differential equations
  71. Domination in 4-regular Knödel graphs
  72. Stepanov-like pseudo almost periodic functions on time scales and applications to dynamic equations with delay
  73. Algebras of right ample semigroups
  74. Random attractors for stochastic retarded reaction-diffusion equations with multiplicative white noise on unbounded domains
  75. Nontrivial periodic solutions to delay difference equations via Morse theory
  76. A note on the three-way generalization of the Jordan canonical form
  77. On some varieties of ai-semirings satisfying xp+1 ≈ x
  78. Abstract-valued Orlicz spaces of range-varying type
  79. On the recursive properties of one kind hybrid power mean involving two-term exponential sums and Gauss sums
  80. Arithmetic of generalized Dedekind sums and their modularity
  81. Multipreconditioned GMRES for simulating stochastic automata networks
  82. Regularization and error estimates for an inverse heat problem under the conformable derivative
  83. Transitivity of the εm-relation on (m-idempotent) hyperrings
  84. Learning Bayesian networks based on bi-velocity discrete particle swarm optimization with mutation operator
  85. Simultaneous prediction in the generalized linear model
  86. Two asymptotic expansions for gamma function developed by Windschitl’s formula
  87. State maps on semihoops
  88. 𝓜𝓝-convergence and lim-inf𝓜-convergence in partially ordered sets
  89. Stability and convergence of a local discontinuous Galerkin finite element method for the general Lax equation
  90. New topology in residuated lattices
  91. Optimality and duality in set-valued optimization utilizing limit sets
  92. An improved Schwarz Lemma at the boundary
  93. Initial layer problem of the Boussinesq system for Rayleigh-Bénard convection with infinite Prandtl number limit
  94. Toeplitz matrices whose elements are coefficients of Bazilevič functions
  95. Epi-mild normality
  96. Nonlinear elastic beam problems with the parameter near resonance
  97. Orlicz difference bodies
  98. The Picard group of Brauer-Severi varieties
  99. Galoisian and qualitative approaches to linear Polyanin-Zaitsev vector fields
  100. Weak group inverse
  101. Infinite growth of solutions of second order complex differential equation
  102. Semi-Hurewicz-Type properties in ditopological texture spaces
  103. Chaos and bifurcation in the controlled chaotic system
  104. Translatability and translatable semigroups
  105. Sharp bounds for partition dimension of generalized Möbius ladders
  106. Uniqueness theorems for L-functions in the extended Selberg class
  107. An effective algorithm for globally solving quadratic programs using parametric linearization technique
  108. Bounds of Strong EMT Strength for certain Subdivision of Star and Bistar
  109. On categorical aspects of S -quantales
  110. On the algebraicity of coefficients of half-integral weight mock modular forms
  111. Dunkl analogue of Szász-mirakjan operators of blending type
  112. Majorization, “useful” Csiszár divergence and “useful” Zipf-Mandelbrot law
  113. Global stability of a distributed delayed viral model with general incidence rate
  114. Analyzing a generalized pest-natural enemy model with nonlinear impulsive control
  115. Boundary value problems of a discrete generalized beam equation via variational methods
  116. Common fixed point theorem of six self-mappings in Menger spaces using (CLRST) property
  117. Periodic and subharmonic solutions for a 2nth-order p-Laplacian difference equation containing both advances and retardations
  118. Spectrum of free-form Sudoku graphs
  119. Regularity of fuzzy convergence spaces
  120. The well-posedness of solution to a compressible non-Newtonian fluid with self-gravitational potential
  121. On further refinements for Young inequalities
  122. Pretty good state transfer on 1-sum of star graphs
  123. On a conjecture about generalized Q-recurrence
  124. Univariate approximating schemes and their non-tensor product generalization
  125. Multi-term fractional differential equations with nonlocal boundary conditions
  126. Homoclinic and heteroclinic solutions to a hepatitis C evolution model
  127. Regularity of one-sided multilinear fractional maximal functions
  128. Galois connections between sets of paths and closure operators in simple graphs
  129. KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy
  130. θ-type Calderón-Zygmund Operators and Commutators in Variable Exponents Herz space
  131. An integral that counts the zeros of a function
  132. On rough sets induced by fuzzy relations approach in semigroups
  133. Computational uncertainty quantification for random non-autonomous second order linear differential equations via adapted gPC: a comparative case study with random Fröbenius method and Monte Carlo simulation
  134. The fourth order strongly noncanonical operators
  135. Topical Issue on Cyber-security Mathematics
  136. Review of Cryptographic Schemes applied to Remote Electronic Voting systems: remaining challenges and the upcoming post-quantum paradigm
  137. Linearity in decimation-based generators: an improved cryptanalysis on the shrinking generator
  138. On dynamic network security: A random decentering algorithm on graphs
https://doi.org/10.1515/math-2018-0132
Keywords for this article
Gravitational Search Algorithm (GSA); multimodal optimization; K-means; niching methods
Creative Commons
BY-NC-ND 4.0

Articles in the same Issue

  1. Regular Articles
  2. Algebraic proofs for shallow water bi–Hamiltonian systems for three cocycle of the semi-direct product of Kac–Moody and Virasoro Lie algebras
  3. On a viscous two-fluid channel flow including evaporation
  4. Generation of pseudo-random numbers with the use of inverse chaotic transformation
  5. Singular Cauchy problem for the general Euler-Poisson-Darboux equation
  6. Ternary and n-ary f-distributive structures
  7. On the fine Simpson moduli spaces of 1-dimensional sheaves supported on plane quartics
  8. Evaluation of integrals with hypergeometric and logarithmic functions
  9. Bounded solutions of self-adjoint second order linear difference equations with periodic coeffients
  10. Oscillation of first order linear differential equations with several non-monotone delays
  11. Existence and regularity of mild solutions in some interpolation spaces for functional partial differential equations with nonlocal initial conditions
  12. The log-concavity of the q-derangement numbers of type B
  13. Generalized state maps and states on pseudo equality algebras
  14. Monotone subsequence via ultrapower
  15. Note on group irregularity strength of disconnected graphs
  16. On the security of the Courtois-Finiasz-Sendrier signature
  17. A further study on ordered regular equivalence relations in ordered semihypergroups
  18. On the structure vector field of a real hypersurface in complex quadric
  19. Rank relations between a {0, 1}-matrix and its complement
  20. Lie n superderivations and generalized Lie n superderivations of superalgebras
  21. Time parallelization scheme with an adaptive time step size for solving stiff initial value problems
  22. Stability problems and numerical integration on the Lie group SO(3) × R3 × R3
  23. On some fixed point results for (s, p, α)-contractive mappings in b-metric-like spaces and applications to integral equations
  24. On algebraic characterization of SSC of the Jahangir’s graph 𝓙n,m
  25. A greedy algorithm for interval greedoids
  26. On nonlinear evolution equation of second order in Banach spaces
  27. A primal-dual approach of weak vector equilibrium problems
  28. On new strong versions of Browder type theorems
  29. A Geršgorin-type eigenvalue localization set with n parameters for stochastic matrices
  30. Restriction conditions on PL(7, 2) codes (3 ≤ |𝓖i| ≤ 7)
  31. Singular integrals with variable kernel and fractional differentiation in homogeneous Morrey-Herz-type Hardy spaces with variable exponents
  32. Introduction to disoriented knot theory
  33. Restricted triangulation on circulant graphs
  34. Boundedness control sets for linear systems on Lie groups
  35. Chen’s inequalities for submanifolds in (κ, μ)-contact space form with a semi-symmetric metric connection
  36. Disjointed sum of products by a novel technique of orthogonalizing ORing
  37. A parametric linearizing approach for quadratically inequality constrained quadratic programs
  38. Generalizations of Steffensen’s inequality via the extension of Montgomery identity
  39. Vector fields satisfying the barycenter property
  40. On the freeness of hypersurface arrangements consisting of hyperplanes and spheres
  41. Biderivations of the higher rank Witt algebra without anti-symmetric condition
  42. Some remarks on spectra of nuclear operators
  43. Recursive interpolating sequences
  44. Involutory biquandles and singular knots and links
  45. Constacyclic codes over 𝔽pm[u1, u2,⋯,uk]/〈 ui2 = ui, uiuj = ujui〉
  46. Topological entropy for positively weak measure expansive shadowable maps
  47. Oscillation and non-oscillation of half-linear differential equations with coeffcients determined by functions having mean values
  48. On 𝓠-regular semigroups
  49. One kind power mean of the hybrid Gauss sums
  50. A reduced space branch and bound algorithm for a class of sum of ratios problems
  51. Some recurrence formulas for the Hermite polynomials and their squares
  52. A relaxed block splitting preconditioner for complex symmetric indefinite linear systems
  53. On f - prime radical in ordered semigroups
  54. Positive solutions of semipositone singular fractional differential systems with a parameter and integral boundary conditions
  55. Disjoint hypercyclicity equals disjoint supercyclicity for families of Taylor-type operators
  56. A stochastic differential game of low carbon technology sharing in collaborative innovation system of superior enterprises and inferior enterprises under uncertain environment
  57. Dynamic behavior analysis of a prey-predator model with ratio-dependent Monod-Haldane functional response
  58. The points and diameters of quantales
  59. Directed colimits of some flatness properties and purity of epimorphisms in S-posets
  60. Super (a, d)-H-antimagic labeling of subdivided graphs
  61. On the power sum problem of Lucas polynomials and its divisible property
  62. Existence of solutions for a shear thickening fluid-particle system with non-Newtonian potential
  63. On generalized P-reducible Finsler manifolds
  64. On Banach and Kuratowski Theorem, K-Lusin sets and strong sequences
  65. On the boundedness of square function generated by the Bessel differential operator in weighted Lebesque Lp,α spaces
  66. On the different kinds of separability of the space of Borel functions
  67. Curves in the Lorentz-Minkowski plane: elasticae, catenaries and grim-reapers
  68. Functional analysis method for the M/G/1 queueing model with single working vacation
  69. Existence of asymptotically periodic solutions for semilinear evolution equations with nonlocal initial conditions
  70. The existence of solutions to certain type of nonlinear difference-differential equations
  71. Domination in 4-regular Knödel graphs
  72. Stepanov-like pseudo almost periodic functions on time scales and applications to dynamic equations with delay
  73. Algebras of right ample semigroups
  74. Random attractors for stochastic retarded reaction-diffusion equations with multiplicative white noise on unbounded domains
  75. Nontrivial periodic solutions to delay difference equations via Morse theory
  76. A note on the three-way generalization of the Jordan canonical form
  77. On some varieties of ai-semirings satisfying xp+1 ≈ x
  78. Abstract-valued Orlicz spaces of range-varying type
  79. On the recursive properties of one kind hybrid power mean involving two-term exponential sums and Gauss sums
  80. Arithmetic of generalized Dedekind sums and their modularity
  81. Multipreconditioned GMRES for simulating stochastic automata networks
  82. Regularization and error estimates for an inverse heat problem under the conformable derivative
  83. Transitivity of the εm-relation on (m-idempotent) hyperrings
  84. Learning Bayesian networks based on bi-velocity discrete particle swarm optimization with mutation operator
  85. Simultaneous prediction in the generalized linear model
  86. Two asymptotic expansions for gamma function developed by Windschitl’s formula
  87. State maps on semihoops
  88. 𝓜𝓝-convergence and lim-inf𝓜-convergence in partially ordered sets
  89. Stability and convergence of a local discontinuous Galerkin finite element method for the general Lax equation
  90. New topology in residuated lattices
  91. Optimality and duality in set-valued optimization utilizing limit sets
  92. An improved Schwarz Lemma at the boundary
  93. Initial layer problem of the Boussinesq system for Rayleigh-Bénard convection with infinite Prandtl number limit
  94. Toeplitz matrices whose elements are coefficients of Bazilevič functions
  95. Epi-mild normality
  96. Nonlinear elastic beam problems with the parameter near resonance
  97. Orlicz difference bodies
  98. The Picard group of Brauer-Severi varieties
  99. Galoisian and qualitative approaches to linear Polyanin-Zaitsev vector fields
  100. Weak group inverse
  101. Infinite growth of solutions of second order complex differential equation
  102. Semi-Hurewicz-Type properties in ditopological texture spaces
  103. Chaos and bifurcation in the controlled chaotic system
  104. Translatability and translatable semigroups
  105. Sharp bounds for partition dimension of generalized Möbius ladders
  106. Uniqueness theorems for L-functions in the extended Selberg class
  107. An effective algorithm for globally solving quadratic programs using parametric linearization technique
  108. Bounds of Strong EMT Strength for certain Subdivision of Star and Bistar
  109. On categorical aspects of S -quantales
  110. On the algebraicity of coefficients of half-integral weight mock modular forms
  111. Dunkl analogue of Szász-mirakjan operators of blending type
  112. Majorization, “useful” Csiszár divergence and “useful” Zipf-Mandelbrot law
  113. Global stability of a distributed delayed viral model with general incidence rate
  114. Analyzing a generalized pest-natural enemy model with nonlinear impulsive control
  115. Boundary value problems of a discrete generalized beam equation via variational methods
  116. Common fixed point theorem of six self-mappings in Menger spaces using (CLRST) property
  117. Periodic and subharmonic solutions for a 2nth-order p-Laplacian difference equation containing both advances and retardations
  118. Spectrum of free-form Sudoku graphs
  119. Regularity of fuzzy convergence spaces
  120. The well-posedness of solution to a compressible non-Newtonian fluid with self-gravitational potential
  121. On further refinements for Young inequalities
  122. Pretty good state transfer on 1-sum of star graphs
  123. On a conjecture about generalized Q-recurrence
  124. Univariate approximating schemes and their non-tensor product generalization
  125. Multi-term fractional differential equations with nonlocal boundary conditions
  126. Homoclinic and heteroclinic solutions to a hepatitis C evolution model
  127. Regularity of one-sided multilinear fractional maximal functions
  128. Galois connections between sets of paths and closure operators in simple graphs
  129. KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy
  130. θ-type Calderón-Zygmund Operators and Commutators in Variable Exponents Herz space
  131. An integral that counts the zeros of a function
  132. On rough sets induced by fuzzy relations approach in semigroups
  133. Computational uncertainty quantification for random non-autonomous second order linear differential equations via adapted gPC: a comparative case study with random Fröbenius method and Monte Carlo simulation
  134. The fourth order strongly noncanonical operators
  135. Topical Issue on Cyber-security Mathematics
  136. Review of Cryptographic Schemes applied to Remote Electronic Voting systems: remaining challenges and the upcoming post-quantum paradigm
  137. Linearity in decimation-based generators: an improved cryptanalysis on the shrinking generator
  138. On dynamic network security: A random decentering algorithm on graphs
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 10.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/math-2018-0132/html
Scroll to top button