Regularization and error estimates for an inverse heat problem under the conformable derivative

Ho Vu; Donal O’Regan; Ngo Van Hoa

doi:10.1515/math-2018-0084

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

Regularization and error estimates for an inverse heat problem under the conformable derivative

Ho Vu , Donal O’Regan and Ngo Van Hoa

Published/Copyright: August 24, 2018

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

$Open Mathematics$

From the journal Open Mathematics Volume 16 Issue 1

Abstract

In this paper we study an inverse time problem for the nonhomogeneous heat equation under the conformable derivative which is a severely ill-posed problem. Using the quasi-boundary value method with two regularization parameters (one related to the error in a measurement process and the other is related to the regularity of the solution) we regularize this problem and obtain a Hölder-type estimation error for the whole time interval. Numerical results are presented to illustrate the accuracy and efficiency of the method.

Keywords: Conformable derivative; Inverse heat problem; Ill-posed problem; Nonhomogeneous heat; Two regularization parameters

MSC 2010: 35R30; 35R35; 58J35

1 Introduction

Partial differential equations (PDEs) arise in the natural sciences, and various boundary value problems for these were widely studied including inverse and ill-posed problems (see, e.g., Tikhonov and Arsenin [1] and Glasko [2]). An example is the backward heat conduction problem (BHCP) and the aim is to detect the previous status of a physical area from present information. The BHCP is a classical ill-posed problem that is difficult to solve since, in general, the solution does not always exist. Furthermore, even if the solution does exist, the continuous dependence of the solution on the data is not guaranteed and numerical calculations are difficult. The BHCP has been considered by many authors using different methods [3], [4], [5], [6], [7], [8], [9], [10]. In [5], Hao, Duc and Lesnic gave an approximation for this problem using a non-local boundary value problem method, Hao and Duc in [6] used the Tikhonov regularization method to give an approximation for this problem in a Banach space, and Trong and Tuan in [11] used the method of integral equations to regularize the BHCP with a nonlinear right hand side.

Fractional calculus arises in many areas in science and engineering such as aerodynamics and control systems, signal processing, bioengineering and biomedical, viscoelasticity, finance and plasma physics, etc. (see [12], [13], [14]). For basic information and results we refer the reader to the monographs of Samko et al. [15], Podlubny [16] and Kilbas et al. [17]. Mathematical modeling of many real world phenomena based on definitions of fractional order integrals and derivatives is regarded as more appropriate than ones depending on integer order operators, so as a result fractional differential equations and fractional partial differential equations are important fields of research [18], [19], [20], [21]. In the above works the definition of the fractional used is either the Riemann-Liouville or the Caputo fractional derivative and most works use an integral form for the fractional derivative. Many researchers are interested in the time-inverse problem for the heat equation where the time-derivative is in the Caputo fractional sense. In particular, they consider the problem

∂αu∂tα−uxx=f(x,t),(x,t)∈(0,π)×(0,T]u(0,t)=u(π,t)=0,t∈[0,T]u(x,T)=g(x),(1)

where α ∈ (0, 1) is the fractional order of derivative and

∂αu∂tα=1Γ(1−α)∫0t(t−s)−αus(x,s)ds.

By a time-inverse problem, we mean that, given information at a specific point of time, say t = T, the goal is to recover the corresponding structure at an earlier time t < T. When α = 1, the problem (1) turns back to the classical ill-posed problem for the well-known heat equation (BCHP). Many researchers have applied different methods to regularize this problem. For example, in [9], [10] the authors successfully applied various methods to stabilize BCHP and obtained many results on the convergent of the regularized solution to the exact one. In [7], [8], the authors consider BCHP where the frequency domain is ℝ. Problem (1) with 0 < α < 1 was studied in [22], [23], [24] where fundamental contributions were made for problem (1) on existence and uniqueness of solution for this problem. In [25], the authors simplified the Tikhonov regularization method to stabilize problem (1). In [26] the authors consider problem (1) where the data is discrete.

However, there are some setbacks in the approaches of the Riemann-Liouville fractional and the Caputo fractional derivative when modeling real world phenomena (see [27] for a discussion). In [27] the authors gave a new well-behaved simple fractional derivative called “the conformable derivative” depending just on the basic limit definition of the derivative and this concept seems to satisfy all the requirements of the standard derivative. For a function u: (0, ∞) → ℝ the conformable derivative of order α ∈ (0, 1) of u at t > 0 is defined by

Dtαu(t)=limh→0⁡u(t+ht1−α)−u(t)h,Dtαu(0)=limt→0+⁡Dtαu(t).(2)

Note that if u is differentiable, then Dtαu (t) = t^1–αu′(t), where u′(t) = lim_{h → 0} [u(t + h) – u(t)]/ h. This concept overcomes the setbacks of the previous concept and this new theory is discussed by Atangana [28] and Abdeljawad [29]. In addition, Anderson and Ulness in [30] provide a potential application of the conformable derivative in quantum mechanics.

For PDEs concerning the conformable derivative there are several studies. In [31], Hammad and Khalil used conformable fourier series to interpret the solution for the conformable heat equation, which is a fundamental equation in mathematical physics. In [32], Chung used the conformable fractional derivative and integral to study fractional Newtonian mechanics, and in addition, the fractional Eule-Lagrange equation was constructed. In [33], Eslami applied the Kudryashov method to obtain the traveling wave solutions to the conformable fractional coupled nonlinear Schrodinger equation. In [34, 35], Çenesiz et al. studied the conformable version of the time-fractional Burgers’ equation, the modified Burgers’s equation, the Burgers-Korteweg-de Vries equation and the solutions of conformable derivative heat equation. Çenesiz, Kurt and Nane in [36] studied stochastic solutions of conformable fractional Cauchy problems where the space operators may correspond to fractional Brownian motion, or a Levy process. Motivated by the above studies, it is natural to consider the time-inverse problem for the heat equation under the conformable derivative. Throughout this paper, we let Ω = [0, a], T is a positive number and Dtα is the conformable derivative of order α with respect to t. We begin with the inverse problem in the conformable heat equation.

1.1 The direct problem

Consider the following conformable heat equation

Dtαu(x,t)−uxx(x,t)=f(x,t),(x,t)∈Ω×(0,T],(3)

u(x,t)=0,(x,t)∈∂Ω×(0,T],(4)

u(x,0)=u0(x),x∈Ω.(5)

Solving this equation with the given information f(x, t) and u₀(x) is called the direct problem.

1.2 The inverse problem

Consider the following conformable heat equation

Dtαu(x,t)−uxx(x,t)=f(x,t),(x,t)∈Ω×(0,T],(6)

u(x,t)=0,(x,t)∈∂Ω×(0,T],(7)

u(x,T)=g(x),x∈Ω,(8)

where f(x, t) ∈ C(0, T;L²(Ω)) and g(x) ∈ L²(Ω). From the information given at final time t = T, the goal of the inverse problem is to recover the information u(x, t) for 0 ≤ t < T. Unfortunately, the inverse problem is usually an ill-posed problem in the sense of Hadamard. An ill-posed problem in the sense of Hadamard is the one which violates at least one of the following conditions:

Existence: There exists a solution of the problem.
Uniqueness: The solution must be unique.
Stability: The solution must depend continuously on the data, i.e., any small error in given data must lead to a corresponding small error in the solution.

Problems which satisfy these conditions are called well-posed problems. We will show that the conformable backward heat problem is an ill-posed problem.

First, let us make clear what a solution of the Problem (6) - (8) is. We call a function u ∈ C^{2, 1}((0, a) × (0, T);L² (Ω)) a solution for Problem (6) - (8) if

Dtαu(⋅,t),w−uxx(⋅,t),w=f(⋅,t),w(9)

for all functions w ∈ L²(Ω). In fact, it is enough to choose w in the orthogonal basis sinnπaxn=1∞ and then (9) reduces to

un(t)=eknTα−tααgn−∫tTsα−1eknsα−tααfn(s)ds,

and as a result, the solution of (6) - (8) can be represented by

u(x,t)=∑n=1∞un(t)sinnπax=∑n=1∞eknTα−tααgn−∫tTsα−1eknsα−tααfn(s)dssinnπax,(10)

where k_n = (n π/a)² and

gn=2a∫0ag(x)sinnπaxdx,fn(t)=2a∫0af(x,t)sinnπaxdx,un(t)=2a∫0au(x,t)sinnπaxdx.(11)

It is noted that the term eknTα−tαα tends to infinity as n tends to infinity. Hence, it causes instability in the solution.

In this paper, we will apply the quasi-boundary value method with a small modification to regularize (6) - (8). In fact, rather than using the original information, we will consider problem (6) - (8) with adjusted information so that the adjusted problem is well-posed and approximates the original one. Consider the following problem

Dtαuε,τ(x,t)−uxxε,τ(x,t)=fε,τ(x,t),(x,t)∈Ω×(0,T],(12)

uε,τ(x,t)=0,(x,t)∈∂Ω×(0,T],(13)

uε,τ(x,T)=gε,τ(x),x∈Ω,(14)

where

fε,τ(x,t)=∑n=1∞e−kn(Tα+τ)αεkn+e−kn(Tα+τ)αfn(t)sinnπax,gε,τ(x)=∑n=1∞e−kn(Tα+τ)αεkn+e−kn(Tα+τ)αgnsinnπax.(15)

Lemma 1.1

Let 0 ≤ t ≤ T, τ > 0, ε ∈ 𝔻:= (0,(Tα+τ)α)and x > 0. Then, for α ∈ (0, 1) the following inequality holds

e−(tα+τ)αxεx+e−(Tα+τ)αx≤(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τ.(16)

Proof

For any ε ∈ 𝔻, x > 0, α ∈ (0, 1] and T > 0, the function

w(x)=1εx+e−(Tα+τ)αx

maximizes at x = ln⁡(Tα+ταε)/(Tα+τα). Therefore,

w(x)=1εx+e−(Tα+τ)αx≤wln⁡(Tα+ταε)/(Tα+τα)=Tα+ταε1+ln⁡(Tα+ταε).(17)

Then, we obtain the following estimation

e−(tα+τ)αxεx+e−(Tα+τ)αx=e−(tα+τ)αxεx+e−(Tα+τ)αxTα−tαTα+τεx+e−(Tα+τ)αxtα+τTα+τ⩽e−(tα+τ)αxe−(tα+τ)αx1εx+e−(Tα+τ)αxTα−tαTα+τ⩽(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τ.

The proof is complete. □

The rest of the paper is organized as follows. In Section 2, we study the well-posedness of problem (12) - (14) and provide an error estimation between solutions of these two problems. Section 3 provides a numerical example to illustrate the efficiency of our method.

2 Well-posedness of the regularized problem (12)-(14)

Theorem 2.1

Let f(x, t) ∈ C(0, T;L²(Ω)) and g(x)∈ L²(Ω). Letτ > 0 and ε ∈ 𝔻 be given. Then, (12)–(14) has a unique solution u^{ε, τ}satisfying

uε,τ(x,t)=∑n=1∞e−kntα+ταεkn+e−knTα+ταgn−e−kntα+ταεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)dssinnπax.(18)

The solution depends continuously on g in L²(Ω).

Proof

First we prove the existence and uniqueness of a solution of the regularized problem (12) - (14).

Existence of solution

For all 0 ≤ t ≤ T, we have

uε,τ(x,t)=∑n=1∞unε,τ(t)sinnπax,

where

unε,τ(t)=e−kntα+ταεkn+e−knTα+ταgn−e−kntα+ταεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)ds.

It follows that

Dtαuε,τ(x,t)=−∑n=1∞kne−kntα+ταεkn+e−knTα+ταgn−e−kntα+ταεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)dssinnπax+∑n=1∞e−knTα+ταεkn+e−knTα+ταfn(t)sinnπax=uxxε,τ(x,t)+∑n=1∞e−knTα+ταεkn+e−knTα+ταfn(t)sinnπax.(19)

On the other hand, we have

uε,τ(x,T)=∑n=1∞e−knTα+ταεkn+e−knTα+ταgnsinnπax.(20)

Hence, u^{ε, τ} is the solution of the regularized problem (12)–(14), so the existence of a solution of the regularized problem (12)–(14) is proved.

Uniqueness of solution

Let u^{ε, τ}(x, t) and v^{ε, τ}(x, t) be two solutions of (12) - (14). We denote w(x, t) = u^{ε, τ}(x, t) - v^{ε, τ}(x, t). It is clear that w(x, T) = 0. We expand w _n(x, t) = ∑n=1∞wn(t)sinnπax with the coefficient

wn(t)=2a∫0aw(x,t)sinnπaxdx,n=1,2,3,....

Multiply both sides of equation (12) by sin nπax and integrate by parts with respect to x, and use the boundary condition to obtain

Dtαwn(t)+knwn(t)=fnε,τ(t),t∈(0,T),(21)

where k_n = (nπ /a)² and

fnε,τ(t)=2a∫0afε,τ(x,t)sinnπaxdx.

The condition w(x, T) = 0 yields w_n(T) = 0. Then, the well-posedness for the fractional differential equation (21) with the boundary condition w _n(T) = 0 yields w_n(t) ≡ 0 in t ∈ [0, T]. This infers that w(x, t) ≡ 0.

Stability of solution

The solution of the problem (12)–(14) depends continuously on g. In fact, let u^{ε, τ} and v^{ε, τ} be two solutions of (12)–(14) corresponding to the final data g^{ε, τ} and h^{ε, τ}, and u^{ε, τ} and v^{ε, τ} are represented by

uε,τ(x,t)=∑n=1∞e−kntα+ταεkn+e−knTα+ταgn−e−kntα+ταεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)dssinnπax,(22)

vε,τ(x,t)=∑n=1∞e−kntα+ταεkn+e−knTα+ταhn−e−kntα+ταεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)dssinnπax,(23)

where

gn=2a∫0agε,τ(x)sinnπaxdx,hn=2a∫0ahε,τ(x)sinnπaxdx.

Direct computation leads us to

uε,τ(x,t)−vε,τ(x,t)=∑n=1∞e−kntα+ταεkn+e−knTα+ταgn−hnsinnπax.

Applying Lemma 1.1 directly, we get

uε,τ(.,t)−vε,τ(.,t)2=a2∑n=1∞e−kntα+ταεkn+e−knTα+ταgn−hn2⩽a2(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τ2∑n=1∞gn−hn2=(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τ2gε,τ−hε,τ2.(24)

Therefore,

uε,τ(⋅,t)−vε,τ(.,t)⩽(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τgε,τ−hε,τ.(25)

The proof is complete. □

We have shown that the regularization problem (12)–(14) is a well-posed problem in the sense of Hadamard. Now, the main goal of the coming theorem is to provide an error estimation between the regularization solution and the exact solution.

Theorem 2.2

Let g, f, u^{ε, τ}as in Theorem 2.1 and assume that problem(6)–(8)has a solution u∈ C^{2, 1}( (0, a)×(0, T); L²(Ω))and∑n=1∞∫0Tknsα−1fn(s)e−knsααds2 < ∞, where k_n = (n π/a)². Suppose that the problem(6)–(8)has uniquely a solution u such that ‖u(⋅, 0) ‖ < ∞. Then the following estimate holds for all 0 < t ≤ T,

u(⋅,t)−uε,τ(⋅,t)⩽C1εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τ,(26)

where

C1=a∑n=1∞kn2un(0)2+∫0Tsα−1fn(s)e−knsααds2,

and u^{ε, τ}is the unique solution of problem(12)–(14).

Proof

The exact solution satisfies

u(x,t)=∑n=1∞eknTα−tααgn−eknTα−tαα∫tTsα−1eknsα−Tααfn(s)dssinnπax.(27)

On the other hand, in terms of u_n(0), we have

u(x,T)=∑n=1∞un(0)e−knTαα+∫0Tsα−1e−knTα−sααfn(s)dssinnπax,(28)

where

un(0)=2au(x,0),sin⁡nπax=2a∫0au(x,0)sinnπaxdx.

It follows that

gn=un(0)e−knTαα+∫0Tsα−1e−knTα−sααfn(s)ds.(29)

Combining (18) and (27), we get

un(t)−unε,τ(t)=εkne−kntααe−knTααεkn+e−knTα+ταgn−εkne−kntααe−knTααεkn+e−knTα+τα∫tTsα−1eknsα−Tααfn(s)ds=εkne−kntααεkn+e−knTα+ταun(0)+εkne−kntααεkn+e−knTα+τα∫0tsα−1eknsααfn(s)ds⩽εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τknun(0)+εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τkn∫0Tsα−1fn(s)e−knsααds.(30)

From the inequality (a + b)² ≤ 2(a² + b²), we have

un(t)−unε,τ(t)2≤2εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τkn2un(0)2+∫0Tsα−1fn(s)e−knsααds2.(31)

From (31) and Parseval’s identity u(⋅,t)−uε,τ(⋅,t)2=a2∑n=1∞un(t)−unε,τ(t)2, we get

un(⋅,t)−uε,τ(⋅,t)2⩽C12εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τ2,(32)

where

C1=a∑n=1∞kn2un(0)2+∫0Tsα−1fn(s)e−knsααds2.(33)

This completes the proof of Theorem 2.2. □

Theorem 2.3

(Error estimates in case of non-exact data) Let f, g as in Theorem 2.1. Let τ ≥ 0 and ε ∈ 𝔻 be given. Assume u is the unique solution of problem(6)–(8)corresponding to the exact data g. Suppose that g^{ε, τ}is measured data such that

|g−gε,τ|≤ε.

Then there exists an approximate solution U^{ε, τ}, which links to the noisy data g^{ε, τ}, satisfying

|Uε,τ(⋅,t)−u(⋅,t)|⩽αtα−TαTα+τ+C1εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τ,∀t∈(0,T).(34)

Proof

Let U^{ε, τ} be the solution of the regularized problem (12)–(14) corresponding to data g^{ε, τ} and let u^{ε, τ} be the solution of the problem (12)–(14) corresponding to the data g. Let u(x, t) be the exact solution, and in view of the triangle inequality, one has

|Uε,τ(x,t)−u(x,t)|≤|Uε,τ(x,t)−uε,τ(x,t)|+|u(x,t)−uε,τ(x,t)|.

Combining the results from Theorem 2.1 (see the proof) and Theorem 2.2, for every t ∈ [0, T], we get

|Uε,τ(x,t)−u(x,t)|≤(αε)tα−TαTα+τTα+τ1+ln⁡(Tα+ταε)Tα−tαTα+τ|gε,τ−g|+C1εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τ ≤αtα−TαTα+τ+C1εtα+τTα+τTα+τα1+ln⁡(Tα+ταε)Tα−tαTα+τ.

The proof is complete. □

3 Numerical illustration

In this section, we illustrate the theoretical results in Section 2 through an example. Consider the space domain Ω = [0, a] in association with the final time T, and our problem is

Dtαu(x,t)−uxx(x,t)=1+πa2etααsinπax,(x,t)∈[0,a]×(0,T],(35)

u(0,t)=u(a,t)=0,t∈(0,T],(36)

u(x,T)=g(x),x∈[0,a],(37)

where g(x) = eTααsinπax. Under the above assumptions, the exact solution of the problem is

uex(x,t)=etααsinπax.(38)

Now, due to the error in the measuring process, the measured data is perturbed by a “noise” with level ε, i.e

gnoise(x)=eTα/αsinπax+∑p=1P0εcpsinpπax,

where P₀ is a natural number and c_p is a finite sequence of random normal numbers with mean 0 and variance A². It follows that the error in the measurement process is bounded by ε, ‖g^noise – g ‖ ≤ R ε where R is some positive number. The error between the measured data and the exact data will tend to 0 as ε tends to 0 . Regarding (18), the regularized solution corresponding to the measured data takes the following form

uε,τ(x,t)=e−k1tα+ταεk1+e−k1Tα+ταeTα/α−1+πa2∫tTsα−1ek1sα−Tααesααdssinπax+∑p=1P0cpεe−kptα+ταεkp+e−kpTα+ταsinpπax.(39)

Let a = 5, P₀ = 1000, A² = 100. Consider the following situation:

In this situation, the regularization parameter ε will be discussed. Fix α = 0.3, τ = 0.5. Consider ε₁ = 10^–1, ε₂ = 10^–3, ε₃ = 10^–5. We have the following figures:

For each point of time we evaluate the “Relative error” between the exact solution and the regularized solution which is defined by

RE(ε,t)=|uε,τ(.,t)−uex(.,t)||uex(.,t)|.(40)

The relative error is a better representation of the difference between the exact and the approximate solution. When the value of the exact solution is large, the difference between the exact and the approximate solution does not tell us much information about the accuracy of the approximation. In this case, the relative error is a better measurement. Figure 3 shows errors for a comparison between the exact solution and the regularized solution at the initial time t₀ = 0 and τ = 1 with various values of ε. In Table 1, we have the error table at time time t_* = 0.1.

Table 1

The error and Relative error at time t_* = 0.1.

∈	‖u^ε(., 0.1) – u^ex(., 0.1)‖	RE(ε, 0.1)
ε1 = 10^–1	2004.6002763324	40.0920055266479
ε2 = 10^–2	93.6668715963709	1.87333743192742
ε3 = 10^–3	11.7191083956268	0.234382i67912537
ε4 = 10^–4	0.333770043724429	0.0666754008744885
ε5 = 10^–5	0.0558155468882481	0.00111631093776496

Remark 3.1

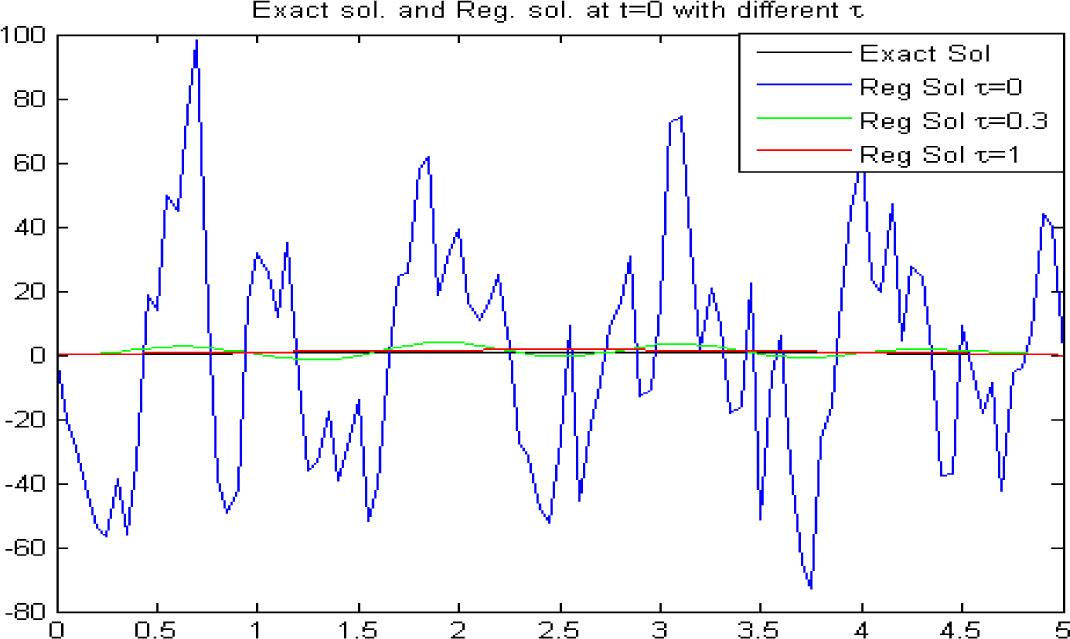
From Figure 1, Figure 2, Figure 3, Figure 4 and Table 1, it is clear that as the mearsuring error ε gets smaller, the regularized solution gets closer and closer to the exact one. It is also noted that in this situation, the noise parameter c_p varies from -249.689 to 242.4461.

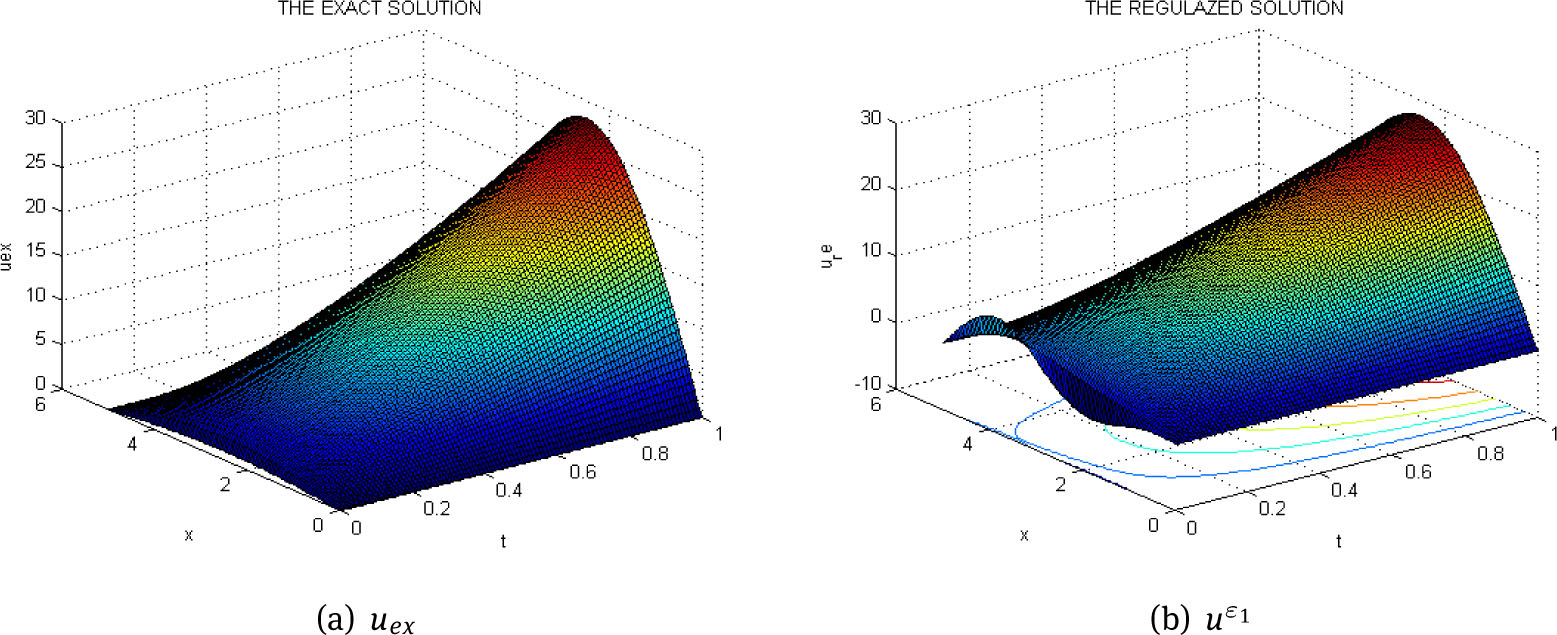
$Fig. 1 The exact solution with α = 0.3 (a) and regularized solution with ε1 = 10–1 (b)$

Fig. 1

The exact solution with α = 0.3 (a) and regularized solution with ε₁ = 10^–1 (b)

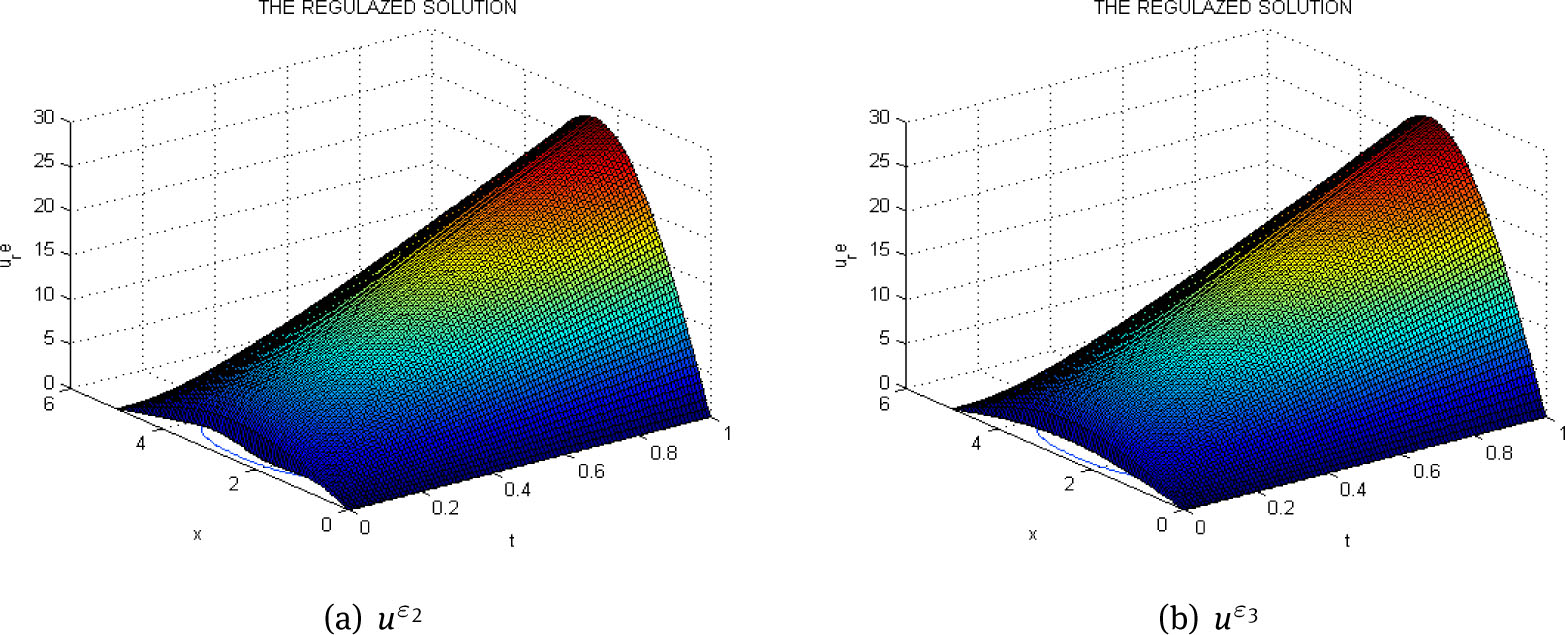
$Fig. 2 The regularized solution with ε2 = 10–3 (a) and with ε3 = 10–5 (b)$

Fig. 2

The regularized solution with ε₂ = 10^–3 (a) and with ε₃ = 10^–5 (b)

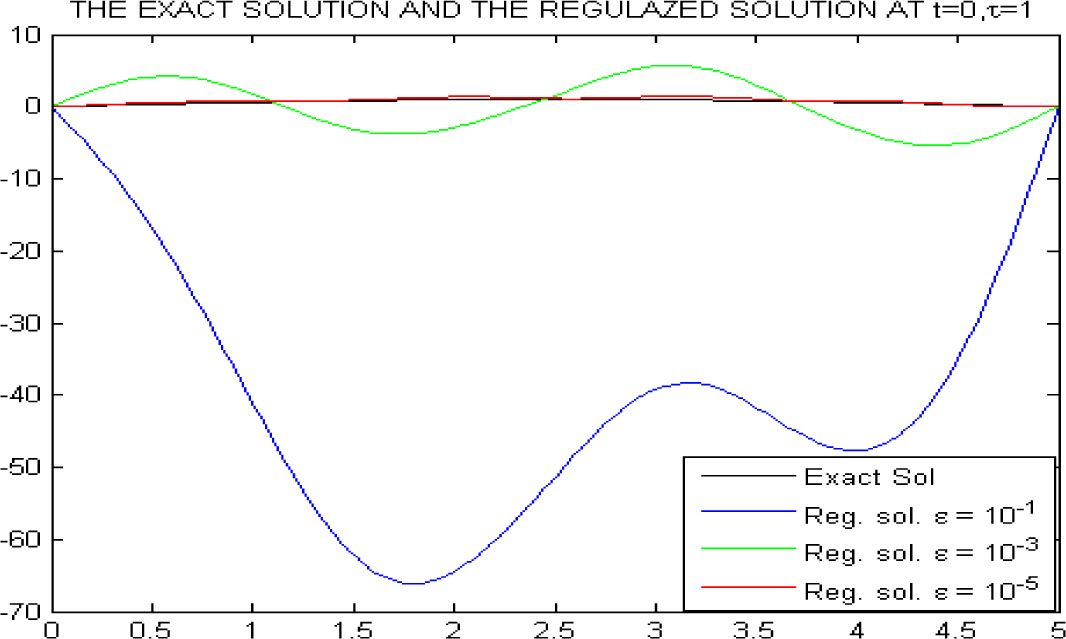
$Fig. 3 At time t0 = 0 and τ = 1: Exact solution with α = 0.9 (black) and Regularized solution with ε1 = 10–1 (blue), ε3 = 10–3 (green), ε5 = 10–5 (red)$

Fig. 3

At time t₀ = 0 and τ = 1: Exact solution with α = 0.9 (black) and Regularized solution with ε₁ = 10^–1 (blue), ε₃ = 10^–3 (green), ε₅ = 10^–5 (red)

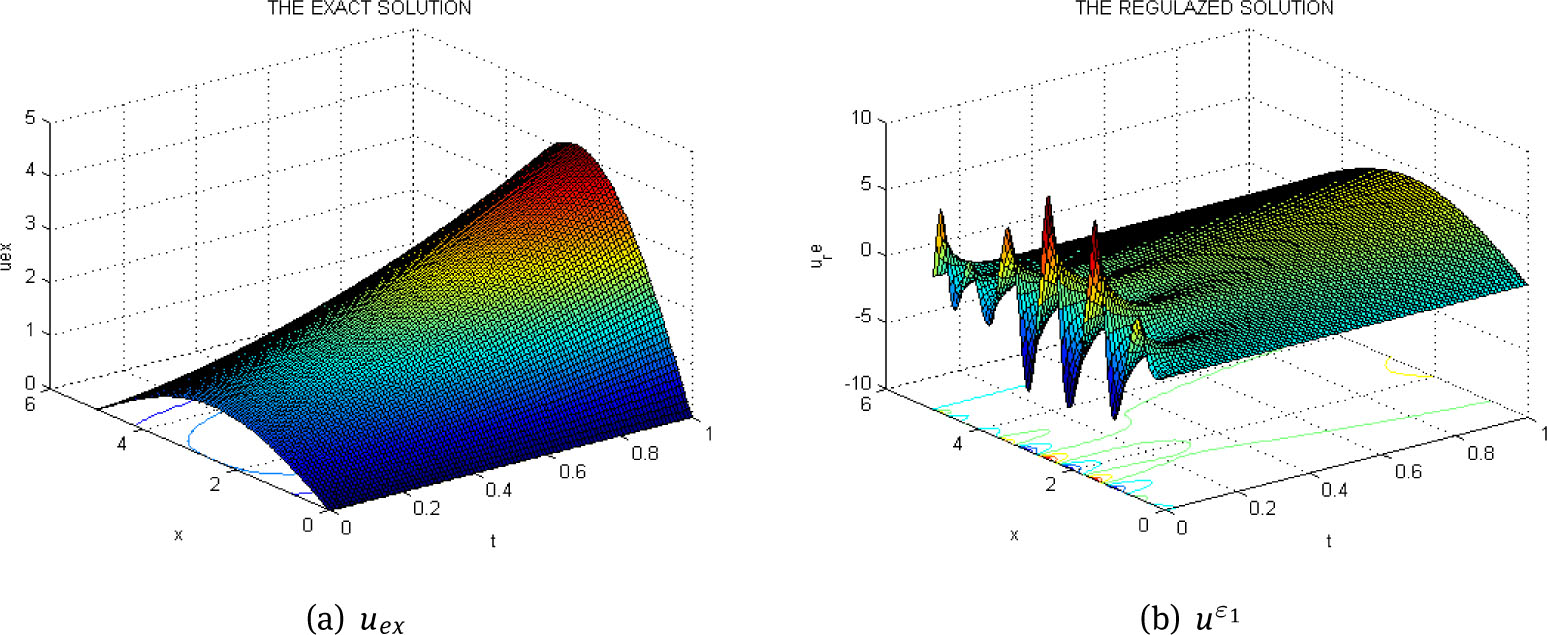
$Fig. 4 The exact solution with α = 0.1 (a) and regularized solution with ε1 = 10–1 (b)$

Fig. 4

The exact solution with α = 0.1 (a) and regularized solution with ε₁ = 10^–1 (b)

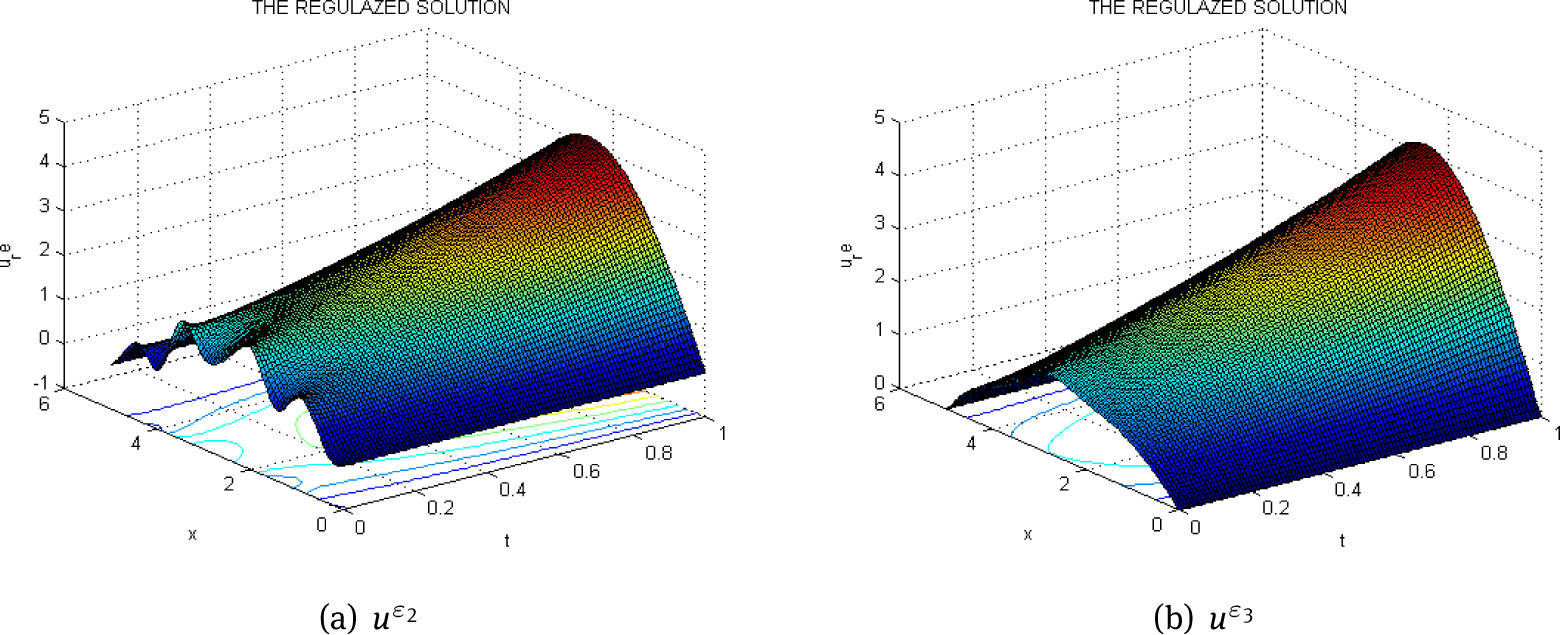
$Fig. 5 The regularized solution with ε2 = 10–3 (a) and with ε3 = 10–5 (b)$

Fig. 5

The regularized solution with ε₂ = 10^–3 (a) and with ε₃ = 10^–5 (b)

In this situation, the focusing parameter is τ. Let α = 0.1 and fix ε = 10^–3. Consider the series of τ: τ₁ = 0.3, τ₂ = 0.5, τ₃ = 1. We have Figure 6 to illustrate our theoretical results. It is also noted that in this situation, the noise parameter c_p varies from -220.5152 to 352.6678.

$Fig. 6 Case α = 0.5, At time t = 0 and ε1 = 10–3: Exact solution (black) and Regularized solution with τ1 = 0 (blue), τ2 = 0.3 (green), τ3 = 1 (red)$

Fig. 6

Case α = 0.5, At time t = 0 and ε₁ = 10^–3: Exact solution (black) and Regularized solution with τ₁ = 0 (blue), τ₂ = 0.3 (green), τ₃ = 1 (red)

Remark 3.2

Figure 6 agrees with the theoretical result: the regularized solution with a higher value of τ is closer to the exact one. The parameter τ is very useful if we want to get a more accurate approximation if the measuring process cannot be improved or if the cost of measuring better is very expensive. In this case, with the appearance of τ, the error can be improved without any extra cost on measuring (as we can see in Figure 6).

4 Conclusion

In this paper, we have stated and discussed the quasi-boundary value regularization method for the inverse problem in the heat equation under the conformable derivative. In addition, we have also established an error estimate between exact and regularized solutions. These estimates are supported by several numerical examples. The estimate is a Hölder-type estimate (ε^t/T) for all values of t in the interval (0, T]. However, at the initial time t = 0, the error estimate is of logarithm type only. In the future, we hope to improve the error estimate as well as to consider the nonlinear case of f.

Competing interests: The authors declare that they have no competing interests.
Authors’ contributions: All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Acknowledgement

The authors are very grateful to the referees for their valuable suggestions, which helped to improve the paper significantly. The third author would like to thank Professor Dang Duc Trong, Associate Professor Nguyen Huy Tuan and Tra Quoc Khanh for their support.

References

[1] Tikhonov A.N., Arsenin V.Y., Solutions of ill-posed problems, Vh Winston, 1977.Search in Google Scholar

[2] Glasko V. B., Inverse problems of mathematical physics, New York: American Institute of Physics, 1984.Search in Google Scholar

[3] Denche M., Bessila K., A modified quasi-boundary value method for ill-posed problems, J. of Math. Anal. and Appl., 2005, 301 419-426.10.1016/j.jmaa.2004.08.001Search in Google Scholar

[4] Hao D.N., Duc N.V., Stability results for the heat equation backward in time, J. of Math. Anal. and Appl., 2009, 353, 627-641.10.1016/j.jmaa.2008.12.018Search in Google Scholar

[5] Hao D.N., Duc N.V., D. Lesnic, Regularization of parabolic equations backward in time by a non-local boundary value problem method, IMA J. of Appl. Math., 2010, 75, 291-315.10.1093/imamat/hxp026Search in Google Scholar

[6] Hao D.N., Duc N.V., Regularization of backward parabolic equations in Banach spaces, J. of Inverse. and Ill-posed Probs., 2012, 20, 745-763.10.1515/jip-2012-0046Search in Google Scholar

[7] Fu C.L., Qian Z., Shi R., A modified method for a backward heat conduction problem, Appl. Math. and Comput., 2007, 185, 564-573.10.1016/j.amc.2006.07.055Search in Google Scholar

[8] Fu C.L., Xiong X.T., Qian Z., Fourier regularization for a backward heat equation, J. Math. Anal. Appl., 2007, 331, 472-480.10.1016/j.jmaa.2006.08.040Search in Google Scholar

[9] Trong D.D., Quan P.H., Khanh T.V., Tuan N.H., A nonlinear case of the 1-D backward heat problem: Regularization and error estimate, Zeitschrift Analysis und ihre Anwendungen, 2007, 26, 231-245.10.4171/ZAA/1321Search in Google Scholar

[10] Trong D.D., Tuan N.H., Regularization and error estimate for the nonlinear backward heat problem using a method of integral equation, Nonlin. Anal.: Theo., Meth. and Appl., 2009, 71, 4167-4176.10.1016/j.na.2009.02.092Search in Google Scholar

[11] Trong D.D., Tuan N.H., Regularization and error estimate for the nonlinear backward heat problem using a method of integral equation, Nonlin. Anal.: Theo., Meth. and Appl., 2009, 71, 4167-4176.10.1016/j.na.2009.02.092Search in Google Scholar

[12] Magin R., Fractional calculus models of complex dynamics in biological tissues, Computers & Mathematics with Applications, 2010, 59, 1586-1593.10.1016/j.camwa.2009.08.039Search in Google Scholar

[13] Magin R., Ortigueira M., Podlubny I., Trujillo J.J., On the fractional signals and systems, Signal Processing, 2011, 91, 350-371.10.1016/j.sigpro.2010.08.003Search in Google Scholar

[14] Merala F.C., Roystona T.J., Magin R., Fractional calculus in viscoelasticity: An experimental study, Communications in Nonlinear Science and Numerical Simulation, 2010, 15, 939-945.10.1016/j.cnsns.2009.05.004Search in Google Scholar

[15] Samko S.G., Kilbas A.A., Marichev O.I., Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach Science Publishers, Switzerland, 1993.Search in Google Scholar

[16] Podlubny I., Fractional differential equation, San Diego: Academic Press, 1999.Search in Google Scholar

[17] Kilbas A.A., Srivastava H.M., Trujillo J.J., Theory and applications of fractional differential equations, Amesterdam: Elsevier Science B.V, 2006.Search in Google Scholar

[18] Atangana A., Baleanu D., New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model, Thermal Science, 2016, 20, 763-769.10.2298/TSCI160111018ASearch in Google Scholar

[19] Atangana A., Koca I., Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order, Chaos, Solitons & Fractals, 2016, 89, 447-454.10.1016/j.chaos.2016.02.012Search in Google Scholar

[20] Atangana A., Alkahtani B.S.T, Modeling the spread of Rubella disease using the concept of with local derivative with fractional parameter, Complexity, 21, 2015, 442-451.10.1002/cplx.21704Search in Google Scholar

[21] Atangana A., Alqahtani R.T., Delling the spread of river blindness disease via the caputo fractional derivative and the beta-derivative, Entropy, 18, 2016, 40. 10.3390/e18020040Search in Google Scholar

[22] Liu J.J., Yamamoto M., A backward problem for the time-fractional diffusion equation, Appl. Anal., 2010, 89, 1769-1788.10.1080/00036810903479731Search in Google Scholar

[23] Kenichi S., Yamamoto M., Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problem, Journal of Mathematical Analysis and Applications, 2011, 382 426-447.10.1016/j.jmaa.2011.04.058Search in Google Scholar

[24] Luchko Y., Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation., Comput. Math. Appl., 2010, 59 1766-1772.10.1016/j.camwa.2009.08.015Search in Google Scholar

[25] Jun-Gang W., Wei T., Zhou Y., Optimal error bound and simplified Tikhonov regularization method for a backward problem for the time-fractional diffusion equation, Journal of Computational and Applied Mathematics, 2015, 279, 277-292.10.1016/j.cam.2014.11.026Search in Google Scholar

[26] Tuan N.H., Nane E., Inverse source problem for time-fractional diffusion with discrete random noise, Statistics and Probability Letters, 2017, 120, 126-134.10.1016/j.spl.2016.09.026Search in Google Scholar

[27] Khalil R., Al Horani M., Yousef A., Sababheh M., A new Definition Of Fractional Derivative, J. Comput. Appl. Math., 2014, 264, 65-7010.1016/j.cam.2014.01.002Search in Google Scholar

[28] Atangana A., Baleanu D., Alsaedi A., New properties of conformable derivative, Open Mathematics, 2015, 13, 889-898.10.1515/math-2015-0081Search in Google Scholar

[29] Abdeljawad T., On conformable fractional calculus, J. Comput. Appl. Math., 2014, 279, 57-66.10.1016/j.cam.2014.10.016Search in Google Scholar

[30] Anderson D.R., Ulness D.J., Properties of the Katugampola fractional derivative with potential application in quantum mechanics, Journal of Mathematical Physics, 2015, 56, 063-50210.1063/1.4922018Search in Google Scholar

[31] Abu Hammad I., Khalil R.. Fractional Fourier Series with Applications, American Journal of Computational and Applied Mathematics, 2014, 4, 187-191.Search in Google Scholar

[32] Chung W.S., Fractional Newton mechanics with conformable fractional derivative, Journal of Computational and Applied Mathematics, 2015, 290, 150-158.10.1016/j.cam.2015.04.049Search in Google Scholar

[33] Eslami M., Exact traveling wave solutions to the fractional coupled nonlinear Schrodinger equations, Applied Mathematics and Computation, 2016, 285, 141-148.10.1016/j.amc.2016.03.032Search in Google Scholar

[34] Çenesiz Y., Baleanu D., Kurt A., Tasbozan O., New exact solutions of Burgers’ type equations with conformable derivative, Waves in Random and Complex Media, 2016, 1-14.10.1080/17455030.2016.1205237Search in Google Scholar

[35] Çenesiz Y., Kurt A., The solutions of time and space conformable fractional heat equations with conformable Fourier transform, Acta Universitatis Sapientiae, Mathematica, 2015, 7, 130-140.10.1515/ausm-2015-0009Search in Google Scholar

[36] Çenesiz Y., Kurt A., Nane E., Stochastic solutions of conformable fractional Cauchy problems, . arXiv preprint arXiv:1606.07010.10.1016/j.spl.2017.01.012Search in Google Scholar

Received: 2017-08-18

Accepted: 2018-07-03

Published Online: 2018-08-24

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

https://doi.org/10.1515/math-2018-0084

Keywords for this article

Conformable derivative; Inverse heat problem; Ill-posed problem; Nonhomogeneous heat; Two regularization parameters

Creative Commons

BY-NC-ND 4.0