On a viscous two-fluid channel flow including evaporation

Jürgen Socolowsky

doi:10.1515/math-2018-0001

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

On a viscous two-fluid channel flow including evaporation

Jürgen Socolowsky

Published/Copyright: January 31, 2018

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

$Open Mathematics$

From the journal Open Mathematics Volume 16 Issue 1

Abstract

In this contribution a particular plane steady-state channel flow including evaporation effects is investigated from analytical point of view. The channel is assumed to be horizontal. The motion of two heavy viscous immiscible fluids is governed by a free boundary value problem for a coupled system of Navier-Stokes and Stephan equations. The flow domain is unbounded in two directions and the free interface separating partially both liquids is semi-infinite, i.e. infinite in one direction. The free interface begins in some point Q where the half-line Σ₁ separating the two parts of the channel in front of Q ends. Existence and uniqueness of a suitable solution in weighted HÖLDER spaces can be proved for small data (i.e. small fluxes) of the problem.

Keywords: Navier-Stokes equations; Stephan equations; Free boundary value problem; Semi-infinite inner channel wall

MSC 2010: 35R35; 35Q30; 76D03; 76D05

1 Introduction

In this paper we are concerned with the investigation of a particular free boundary value problem (= BVP) for a two-fluid non-isothermal channel flow. The infinite channel is assumed to be horizontal and it contains a partial inner wall (cf. the thin red line Σ₁ in Figure 1) which is semi-infinite. The flow problem is assumed to be stationary and 2D. In Figure 1 the blue line denotes the lower channel wall which moves with constant speed R in x₁-direction. The red line Σ₂ denotes the upper channel wall that is at rest. Finally, by the cyan curve Γ we understand the a priori unknown free interface between the two fluid layers. It has the representation x₂ = φ(x₁) where the function φ has to be found as well as the flow fields for velocity v(x), for the pressure p(x) and for the temperature θ(x).

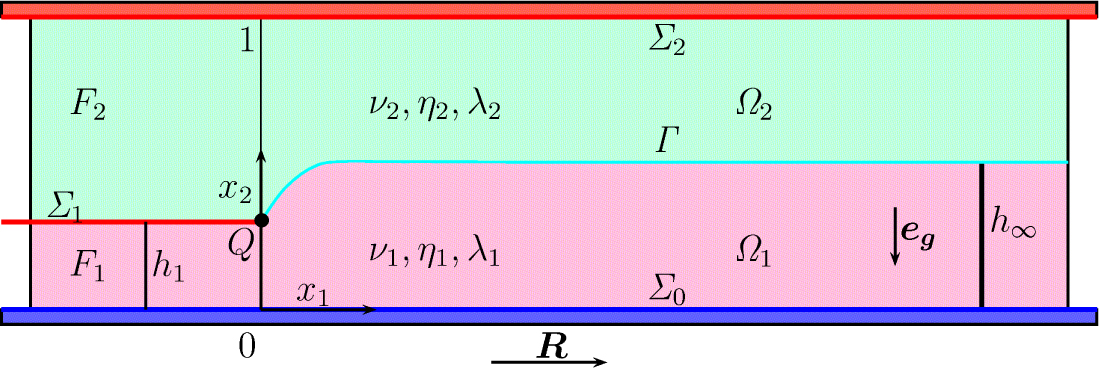
$Fig. 1 Flow domain of a two-fluid channel flow$

Fig. 1

Flow domain of a two-fluid channel flow

Models of the described kind are quite important in many technological and scientific applications. Corresponding examples may be found in the field of materials science, particularly in coating and solidification processes with evaporation or in crystal-growth processes (cf. [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]). The investigations of such problems are performed from technical point of view as well as from analytical and/or numerical point of view. It was our main objective to obtain statements about the existence and/or uniqueness of free BVP for evaporation problems.

The flow describes a coupled heat-and mass transfer (Stephan equations). The (positive) fluxes F_m are prescribed in each fluid layer Ω_m (m = 1,2) (cf. Fig. 1). The lower liquid layer is characterized by red color whereas the upper one is marked by green color. Both liquids are heavy, viscous, heat-conducting, incompressible and immiscible. Therefore, the mathematical model can incorporate evaporation effects. The surface tension σ(θ) is temperature-depending in a known manner.

By ν_m, η_m and λ_m (m = 1,2) we understand the domain-wise (i.e. regional) constant values of the kinematic viscosity, of the density and of the thermal conductivity, respectively, of the m-th fluid. By h_∞ we denote the (asymptotic) position of the free interface Γ when x₁ goes to +∞. By {n, τ, respectively, the unit normal and the unit tangential vectors with respect to Γ are denoted. Their orientation (direction) is the same as for x₁, x₂. By g and e_g we understand the acceleration and the direction of gravity, respectively. Concerning the interface tension σ we suppose the following linear function of temperature θ

σ(θ)=a^−b^θ,(a^,b^>0)

which is frequently used in the literature. This leads to an effect which is called Benard-Marangoni-effect or thermo-capillary convection. Finally, the following symbols and abbreviations have been used throughout this paper: δ_j(t) : = {x₁ = t} ∩ Ω_j, j = 1,2} is some cross section of Ω_j. The frictional stress tensor has the subsequent elements: S_jk = ν η(∂_kv_j + ∂_jv_k) (j,k = 1,2). The symbol [w(x₀)]|_Γ represents the jump of the field w crossing the interface Γ from below to above:

w(x0)|Γ:=limy→x0w(y)−limx→x0w(x),(x0∈Γ,y∈Ω1,x∈Ω2),

2 Mathematical model

The governing equations (Navier - Stokes & Stephan) of the problem which yield in Ω : = Ω₁ ∪ Ω₂ read as follows

(v⋅∇)v−ν∇2v+1η∇p=geg,∇⋅v=0,(v⋅∇)θ−λ∇2θ=0.(1)

They are supplied by the boundary conditions at the lower moving wall Σ₀:

v|Σ0=R,θ|Σ0=θ0=0.(2)

Let us emphasize that the value 0 in Eq. (2) does not represent the absolute temperature but some dimensionless value which is in fact the difference to some reference temperature related to a characteristic temperature difference.

The boundary conditions at the walls at rest Σ_k (k = 1,2) look like:

v|Σk=0,θ|Σk=θk.(3)

Let us explain that the boundary conditions (3) for k = 1 mean both sidesΣ1± of the partial inner wall Σ₁. Finally, the conditions at the free interface Γ are:

[θ]|Γ=0,[v]|Γ=0,v⋅n|Γ−=λ∂θ∂nΓ,[τ⋅S(v)n]|Γ=0,ddx1φ′(x1)1+φ′(x1)2=1σ(θ)[−p+n⋅S(v)n]|Γ,∫δk(t)v⋅ndx2=Fk.(k=1,2)(4)

As a consequence one gets the relation: lim_{x₁ → +∞}φ (x₁) = const. = h_∞.

In order to prove the unique solvability of the BVP in appropriate functional spaces the following two-cycle iteration scheme was applied.

[Γ(0)⟶Ω(0)]⟶(v(0),p(0),θ(0))⟶[Γ(1)⟶Ω(1)]⟶(v(1),p(1),θ(1))⟶⋯⟶[Γ(k)⟶Ω(k)]⟶(v(k),p(k),θ(k))→…(5)

This scheme was introduced by V.V. Pukhnachev and V.A. Solonnikov about 45 years ago (cf. e.g. [13, 14] or [15]). The two-cycle iteration scheme was also applied in the papers [14, 15] and by the author in [9, 16]. In the references [11, 17, 18] other methods are used to handle different free BVP.

The scheme (5) is very senseful in cases where the free boundary is semi-infinite. In a first cycle the three flow fields v, p, θ are computed in a flow domain with fixed boundaries neglecting one of the boundary conditions - mostly the normal stress condition (4)₅, i.e. the 5th equation in (4). This first cycle is then divided into several steps: The linear problem with fixed boundary containing the corresponding estimates for the solution, a model problem at the separation point Q for the determination of the weight functions, the regularity of the solutions at infinity and then the nonlinear problem with fixed boundary.

In a second stage the neglected boundary condition is used in order to compute a new shape of the free boundary (and simultaneously a new shape of the entire flow domain). This equation is usually

K(x1):=1σ(θ)[−p(x)+n⋅S(v)n]|Γ,

where K(x₁) denotes the curvature of Γ in x₁ and it is equal to the left-hand side of Eq. (4)₅. In both cycles a related linear problem is solved and the continuous dependence of the solutions on the boundary data is also proved. Then BANACH‘s fixed point argument related to some contraction operator 𝔅 shows the remaining parts for small data.

3 Function spaces

First of all we define some weighted HÖLDER spaces. Let B be an arbitrary domain in ℝ² and N ⊂ B a manifold of dimension n < 2. Define further ϱ_N(x) : = dist (x,N). By β = (β₁,β₂) we understand a multiindex, and ⌊ r ⌋ is the integer part of r. Then by C^r(B) (r > 0, non-integer) we mean the well-known HÖLDER space with a finite norm |u|B(r). Now we obtain the subsequent weighted HÖLDER space C∘sr(B,N) of functions with the finite norm

|u|C∘sr(B,N)=∑|β|<rsupx∈B∖NϱN|β|−s(x)|Dβu(x)|+∑|β|=⌊r⌋supx∈B∖NϱNr−s(x)sup|x−y|<12ϱN(x)|Dβu(x)−Dβu(y)||x−y|r−⌊r⌋.(6)

Let us remark that the weight functions in (6) represent some kind of power functions with respect to the distance from the singularity points. For (r > s > 0; r,s non-integer) we get the space Csr(B,N) having the norm

|u|Csr(B,N):=|u|B(s)+∑s<|β|<rsupx∈B∖NϱN|β|−s(x)|Dβu(x)|+∑|β|=⌊r⌋supx∈B∖NϱNr−s(x)sup|x−y|<12ϱN(x)|Dβu(x)−Dβu(y)||x−y|r−⌊r⌋.(7)

The spaces Csr(B1∪B2,N) represent the natural generalization of the last ones to the case of two separate subdomains B_k as we have.

Furthermore, C0∞(Ω,Γ) is the set of functions v vanishing for | x | ≫ 1 and satisfying the boundary conditions

v|Σj=0(j=0,1,2),v⋅n|Γ−=0,[v]|Γ=0.

Also, J0∞(Ω,Γ):={v∈C0∞(Ω,Γ), div v=0} and we need the solenoidal spaces with DIRICHLET- norm like D(Ω):=C0∞(Ω,Γ)¯ and H(Ω):=J0∞(Ω,Γ)¯. The DIRICHLET norm is then defined by

∥ux∥Ω2:=∥ux∥L2(Ω)2=∫Ω∑i,j=12∂ui∂xj2dx.

By Cθ,0∞(Ω,Γ) we understand the set of scalar fields θ (x) vanishing for | x | ≫ 1 and θ |_{Σ_j} = 0 (j = 0, 1, 2), [θ]∥_Γ = 0. The symbol D_θ(Ω) is an abbreviation for the set Cθ,0∞(Ω,Γ)¯. The spaces to which the solution belongs are of the subsequent type. First, define some subdomains of the infinite channel (with m = 1,2), i.e. I⁰ = {x₁} ∈ ℝ, 0 < x₁ < 2}, I⁺ = x₁ ∈ ℝ, x₁ > 1}, Ωm0={x∈Ωm,|x1|<2},Ωm+={x∈Ωm,|x1>1},Ωm−={x,|x1<−1}.

Finally, the weighted HÖLDER spaces containing the generalized solutions, are

Cs,zr(Ωm)={u(x),u|Ωm0∈Csr(Ωm0,Q),exp⁡(zx1)u(x)|Ωm+∈Cr(Ωm+),exp⁡(−zx1)u(x)|Ωm−∈Cr(Ωm−)}.

They are essentially used throughout this paper and their norms are given by

∥u∥Ωm,sr,z:=|u|Csr(Ωm0,Q)+|exp⁡(zx1)u|Ωm+(r)+|exp⁡(−zx1)u|Ωm−(r).(8)

The weight functions here in formula (8) are exponential functions and they decay at the infinities. As above, we obtain for our double channel Cs,zr(Ω):=Cs,zr(Ω1∪Ω2,Q).

At the end, for functions of one real variable we deal with the space Cs,zr(R+1) supplied with the norm ∥f∥R+1,sr,z=|f|Csr(I0,0)+|f(x1)exp⁡(zx1)|I+(r).

4 On the Basic Flow for Large x₁

In this section we are interested in getting an approriate starting (or initial) solution for the iteration scheme (5). For this purpose, and under the assumptions

v2≡0,∂v1∂x1≡0,∂θ∂x1≡0,(9)

we calculate for given values F₁, F₂, R, θ₀ = 0, θ₁, θ₂ and associated rheological parameters the flow fields and values v(x), p(x), θ (x), p₀, h_∞, θ_∞. The value θ_∞ which has not been defined before describes the (asymptotic) value of the temperature θ at the free interface when x₁ goes to +∞. Let us emphasize that the assumptions guarantee solution fields that are uniform and unidirectional (not depending on main-stream direction x₁).

Under the assumptions (9) the governing Eqs. (1) take the subsequent reduced form:

−ν∇2v1+1η∂p∂x1=0,∂p∂x2=−ηg,−λ∇2θ=0,

where the second equation replaces the continuity Eq. (1)₂ Now it is possible to divide the original problem into three independent problems for the flow fields. Let us start with the problem for velocities v:

ν1η1d2v1(1)dx22=∂p(1)∂x1,ν2η2d2v1(2)dx22=∂p(2)∂x1,v1(1)(0)=R,v1(2)(1)=0,v1(1)|x2=h∞=v1(2)|x2=h∞,ν1η1dv1(1)dx2x2=h∞=ν2η2dv1(2)dx2x2=h∞,∫0h∞v1(x2)dx2=F1,∫h∞1v1(x2)dx2=F2.(10)

For the pressure p one obtains the following equations

∂p(1)∂x2=−η1g,∂p(2)∂x2=−η2g,p(1)|x2=h∞=p(2)|x2=h∞.(11)

Finally, the problem for temperature θ reads

d2θ(1)dx22=0,d2θ(2)dx22=0,θ(1)|x2=0=θ0=0,θ(2)|x2=1=θ2,θ(1)|x2=h∞=θ(2)|x2=h∞,λ1dθ(1)dx2x2=h∞=λ2dθ(2)dx2x2=h∞,(12)

In Eqs. (10), (11), (12) the superscripts (k), (k = 1, 2) or (+) denote the corresponding fluid layer and the subregion x₁ ⩾ 1. The solutions of these three (independent) problems are of NUSSELT type (cf. also [19]) and allow the representation

v1(+)(x2)=0.5a1x22+b1x2+R,0⩽x2⩽h∞0.5a2(x22−1)+b2(x2−1),h∞⩽x2⩽1,v2(+)(x2)≡0,p0=a1ν1η1=a2ν2η2,r=(ν1η1)/(ν2η2),(13)

The coefficients in (13) are given by

a1=−3F1−Rh∞h∞2−3F2r(1−h∞2),a2=ra1,b1=(2+h∞)F1−Rh∞h∞2+h∞F2r(1−h∞2),b2=rb1.

Note, that the values h_∞ and p₀ are already known for these expressions (see Eq. (16) below). That is why it follows θ_∞ = (λ₂θ₂h_∞)/[λ₁ (1−h_∞) + λ₂h_∞] and for the complete temperature and pressure fields one obtains

θ(+)(x2)=θ∞h∞x2,0⩽x2⩽h∞θ∞+θ2−θ∞1−h∞x2−θ2−θ∞1−h∞h∞,h∞⩽x2⩽1,(14)

p(+)(x)=p0x1−η1gx2+k,p0x1−η2g(x2−h∞)−η1gh∞+k,(15)

Since the associated linear problem is completely decomposed, we got the same polynomial equation for the determination of the value h_∞ as in the former paper [17].

0=r(r−1)Rh∞5+−4r(r−1)R−r(r−1)F1−(r−1)F2h∞4+r(6r−5)R+2r(2r−3)F1−2rF2h∞3+[2r(−2r+1)R+3r(−2r+3)F1+3rF2]h∞2+r2R+4r(r−1)F1h∞−r2F1.(16)

In [17] the subsequent two lemmas were proved.

Lemma 4.1

If F₁F₂ > 0, then Eq. (16)has at least one root h_∞within the open interval ]0, 1[.

Lemma 4.2

If F₁F₂ ⩾ 0, then Eq. (16)has at most three different roots h_∞ ∈]0, 1[.

Note that in the subregion Ω(−):=Ω1(−)∪Ω2(−), i.e. for x₁ ⩽ −1, the corresponding problems are even simpler due to the fact that there is no free boundary. In order not to repeat simple things we restrict the presentation to the basic solution v⁽⁻⁾, p⁽⁻⁾, θ⁽⁻⁾ in the double - channel which can also be determined very simple by straightforward calculations in the left part Ω⁻ of the (double) - channel. The corresponding velocities and temperatures do not depend on x₁. In Ω1− one obtains

v1(−)(x2)=3Rh12−6F1h13x22+−4Rh1+6F1h12x2+R,v2(−)(x)≡0,θ(−)(x2)=x2θ1h1,p(−)(x)=2ν1η13Rh12−6F1h13x1−η1gx2+k1.(17)

In Ω2− one gets, respectively,

v1(−)(x2)=−6F2(1−h1)3x22+6(1+h1)F2(1−h1)3x2−6h1F2(1−h1)3,v2(−)(x)≡0,θ(−)(x2)=θ1+(x2−h1)(1−h1)(θ2−θ1),p(−)(x)=−12ν2η2F2(1−h1)3x1−η2gx2+k2.(18)

It is well-known that the pressure p can be determined only up to an additive constant in channel flows (cf. k₁, k₂ in formulae (17), (18)).

5 The free interface equation

Eq. (16) coincides with equation (A.13) from [17] for horizontal channels. Recall that the final thickness h_∞ is a function of F₁, F₂, R and of the rheological parameters of the fluids. It can have up to three different values in the open interval ]0, 1[ for the same parameter set (cf. [17]). Furthermore, by φ⁽⁺⁾ (x₁) we denote the infinitely differentiable solution of the following free BVP.

ddx1φ′(x1)1+φ′(x1)2−η1−η2a^gφ(x1)=−η1−η2a^gh∞,φ(0)=h1,limx1→+∞φ(x1)=h∞.(19)

which can be obtained from the 5-th condition (4)₅ of (4) by setting v = 0, p = const., θ = 0 as the initial solution for F₁ = F₂ = R = θ₀ = θ₂ = 0. Let ξ = ξ(x₁) be a smooth cut-off function vanishing for |x₁| ⩽ 1 and being equal to 1 for |x₁| ⩾ 2. Finally, assume that η₁ > η₂ is satisfied. This makes physically sense.

Now, the difference function ω (x₁) := (φ (x₁) − φ⁽⁺⁾ (x₁)) is equivalent to exp(−g(η1−η2)/a^x1) as x₁ → + ∞. For the unknown function ω (x₁) we get a two-point BVP like BVP (8.8) from [20] subtracting Eq. (19) from Eq. (4)₅. A difference to BVP (8.8) consists in the following. We have to replace β₁ by g (η₁ − η₂) / â everywhere and, furthermore, we have to introduce the operator 𝔗⁽³⁾ by

T(3)ω:=b^θσ(θ)ω=σ(0)−σ(θ)σ(θ)ω.(20)

The remaining part of the proof of the main theorem is a slightly modified repetition of the proof of Theorem 8.1 in [20]. First of all, one has to study the dependence of the solution to the nonlinear auxiliary problem with fixed boundary on small variations of the boundary. After getting the corresponding estimates one applies BANACH’s fixed point principle to the subsequent operator equation. Instead of the operator Eq. (8.10) from [20] we have to study the following one:

ω=L(T(1)ω+T(2)ω+T(3)ω)=:Bω

with 𝔗⁽³⁾ given in (20) and the other parts taken from [20]. Since 𝔗⁽³⁾ is a contraction operator for small θ, we can conclude as in [20] that 𝔅 is a contraction operator in the ball ∥ω∥R+1,1+s3+s,z<ε. Consequently, we have proved the main result of this paper.

6 Results

Let us formulate the main result of this contribution. A sketch of the proof has been given before. A very detailed application of this method can be found in the thesis [16] as well as in the article [20].

Theorem 6.1

There exist positive real numberss¯,z¯⩽min(z0,1/a^)lsuch that for arbitrary s ∈ ]0,s[, z ∈ ]0,z[ and for sufficiently small values (|F₁|, |F₂|, |R|, |θ₁|,| θ₂|) and for values h_∞fulfilling the condition

|h∞−h1|<2a^g(η1−η2)

the complete mathematical model has a unique solution {v, p, θ, φ} which can be represented in the form

v=ξ(−x1)v(−)+ξ(x1)v(+)+w,φ(x1)=φ(+)(x1)+ω(x1),p=ξ(−x1)p(−)+ξ(x1)p(+)+q;θ=ξ(−x1)θ(−)+ξ(x1)θ(+)+ϑ0,

where ξ is the cut-off function described above, (v⁽⁻⁾, p⁽⁻⁾, θ⁽⁻⁾) is the basic exact solution given by(17), (18)in both channels on left-hand side. The function φ⁽⁺⁾is the solution to the free BVP (19). Moreover, ϑ₀, w ∈ Cs,zs+2(Ω),q∈Cs−1,zs+1(Ω0∪Ω+),∇q∈Cs−2,zs(Ω)andω∈C1+s,z3+s(R+1)hold.

Remark 6.2

If Eq. (16)has more than one real root h_∞between 0 and 1 then the statements of Theorem 6.1 remain true in the neighbourhood of each value.

References

[1] Bänsch, E., Basting, S., Krahl, R., Numerical simulation of two-phase flows with heat and mass transfer, Discrete Contin. Dyn. Syst. 35, (2015) 6, 2325-2347, 10.3934/dcds.2015.35.2325.Search in Google Scholar

[2] Burelbach J.P., Bankhoff, S.G., Davis, S.H., Nonlinear stability of evaporating condensing liquid films, J. Fluid Mech. 195, (1988), 463-494, http://dx.doi.org/10.1017/S0022112088002484.10.1017/S0022112088002484Search in Google Scholar

[3] Denk, R., Geissert, M., Hieber, M., Saal, J., Sawada, O., The spin-coating process: analysis of the free boundary value problem, Commun. Partial Differ. Equations 36, (2011) 7-9, 1145-1192, https://doi.org/10.1080/03605302.2010.546469.10.1080/03605302.2010.546469Search in Google Scholar

[4] Erunova, I.B., Rivkind, V.Ya., Investigation of the problem of liquid evaporation, Vestnik St. Petersburg University - Mathematics 24 (1991), 25-30.Search in Google Scholar

[5] Fontelos, M.A., Hong, S.H., Hwang, H.J., A stable self-similar singularity of evaporating drops: ellipsoidal collapse to a point, Arch. Ration. Mech. Anal. 217, (2015) 2, 373-411, 10.1007/s00205-014-0834-x.Search in Google Scholar

[6] Köhne, M., Prüss, J., Wilke, M., Qualitative behaviour of solutions for the two-phase Navier-Stokes equations with surface tension, Math. Ann. 356, (2013) 2, 737-792, https://doi.org/10.1007/s00208-012-0860-7.10.1007/s00208-012-0860-7Search in Google Scholar

[7] Larina, I.N., Rykov, V.A., Shakov, E.M., Evaporation from a surface and vapor flow through a plane channel into a vacuum, Fluid Dyn. 31, (1996), 127-133, http://dx.doi.org/10.1007/BF02230757.10.1007/BF02230757Search in Google Scholar

[8] Neittaanmäki, P., Rivkind, V.Ya., Mathematical modelling of liquid drops evaporation, Jyväskylä - St. Petersburg Seminar on Partial Differential Equations and Numerical Methods, Ber. Univ. Jyväskylä Math. Inst. 56, (1993), 89-100.Search in Google Scholar

[9] Socolowsky, J., The solvability of a two-layer slot coating flow with evaporation, J. Coupled Syst. Multisc. Dyn. 1, (2013), No. 4, 434-441, 10.1166/jcsmd.2013.1033.Search in Google Scholar

[10] Taylor, Sh.D., Two-Layer Slot Coating: Study of Die Geometry and Interfacial Region (1997). Open Access Dissertations and Theses. Paper 5146. http://digitalcommons.mcmaster.ca/opendissertations/Search in Google Scholar

[11] Xu, L., Zhang, Zh., On the free boundary problem to the two viscous immiscible fluids, J. Differ. Equations 248, (2010) 5, 1044-1111.10.1016/j.jde.2009.11.001Search in Google Scholar

[12] van de Fliert, B.W., A free boundary problem for evaporating layers, Nonlinear Anal., Theory Methods Appl. 47, (2001) 3, 1785-1796, http://dx.doi.org/10.1016/S0362-546X(01)00310-8.10.1016/S0362-546X(01)00310-8Search in Google Scholar

[13] Pukhnachov, V.V., Plane stationary free boundary problem for Navier-Stokes equation, Zh. Prikl. Mekh. i Tekhn. Fiz. 3, (1972), 91-102 (in Russian), English Transl. in J. Appl. Mech. Techn. Phys. 13, (1972).Search in Google Scholar

[14] Solonnikov, V.A., Solvability of a problem on the plane motion of a heavy viscous incompressible capillary liquid partially filling a container, Izv. Akad. Nauk SSSR - Ser. Math. 43, (1979) 1, 203-236 (in Russian), Engl. Transl. in Math. USSR, Izv. 14, (1980), 193-221, http://dx.doi.org/10.1070/IM1980v014n01ABEH001069.10.1070/IM1980v014n01ABEH001069Search in Google Scholar

[15] Solonnikov, V.A., Solvability of a three-dimensional boundary value problem with a free surface for the stationary Navier-Stokes equations, Zapiski Nauchn. Sem. LOMI 84, (1979), 252-285 (in Russian).Search in Google Scholar

[16] Socolowsky, J., Mathematische Untersuchungen freier Randwertaufgaben der Hydrodynamik viskoser Flüssigkeiten, Habilitation thesis, Techn. Hochschule Merseburg, Merseburg (GERMANY), 1989, pp.1-218. (in German)Search in Google Scholar

[17] Pileckas, K., Socolowsky, J., Viscous two-fluid flows in perturbed unbounded domains, Math. Nachrichten 278, (2005) 5, 589-623, http://dx.doi.org/10.1002/mana.200310260.10.1002/mana.200310260Search in Google Scholar

[18] Prüss, J., Simonett, G., On the two-phase Navier-Stokes equations with surface tension, Interfaces Free Bound. 12, (2010) 3, 311-345, 10.4171/IFB/237.Search in Google Scholar

[19] Socolowsky, J., On the Nusselt solution of a non-isothermal two-fluid inclined film flow, International Journal of Mathematics and Mathematical Sciences (IJMMS) (2009), Article ID 981983, 8 pages. [Electronic Journal], 10.1155/2009/981983 (Online and free access Journal)Search in Google Scholar

[20] Socolowsky, J., Solvability of a stationary problem on the plane motion of two viscous incompressible liquids with non-compact free boundaries, Z. Angew. Math. Mech.(ZAMM) 72, (1992) 251-268, 10.1002/zamm.19920720706.Search in Google Scholar

Received: 2016-11-02

Accepted: 2018-01-04

Published Online: 2018-01-31

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

https://doi.org/10.1515/math-2018-0001

Keywords for this article

Navier-Stokes equations; Stephan equations; Free boundary value problem; Semi-infinite inner channel wall

Creative Commons

BY-NC-ND 4.0

On a viscous two-fluid channel flow including evaporation

Article

Abstract

1 Introduction

2 Mathematical model

3 Function spaces

4 On the Basic Flow for Large x1

Lemma 4.1

Lemma 4.2

5 The free interface equation

6 Results

Theorem 6.1

Remark 6.2

References

Articles in the same Issue

Articles in the same Issue

Articles in the same Issue

4 On the Basic Flow for Large x₁