Abstract
The aim of this paper is to study the lattice of subvarieties of the ai-semiring variety defined by the additional identities
where p is a prime. It is shown that this lattice is a distributive lattice of order 179. Also, each member of this lattice is finitely based and finitely generated.
1 Introduction
Semirings (see [9]) abound in the mathematical world around us. The set of natural numbers, the first mathematical structure we encounter, is a semiring. The intensive study of semiring theory was initiated during the late 1960’s when their real and significant applications were found. Nowdays, semiring theory is an enormously broad topic and has advanced on a very broad front. Semirings (S, +, ⋅) occurring in the literature satisfy at least the following axioms: (S, +) and (S, ⋅) are semigroups, and the multiplication distributes over addition from both sides. It is often assumed that (S, +) is idempotent and/or commutative. A semiring S is an additively idempotent semiring, or shortly ai-semiring, if (S, +) is a semilattice (it is also called a semilattice-ordered semigroup in [8, 10, 11]). It is well-known that the endomorphism semiring of a semilattice is an ai-semiring. Also every ai-semiring can be embeded into the endomorphism semiring of some semilattice (see [8, 12]). Important role in mathematics as well as broad applications (in theoretical computer science, optimization theory, quantum physics and many other areas of science [9, 13, 14, 15]) make ai-semirings and, especially, their varieties to be among the favourite subjects for the researchers in the algebraic theory of semirings.
The variety of all ai-semirings is denoted by AI. Let X be a fixed countably infinite set of variables and X+ the free semigroup on X. Then Pf(X+) is free in AI on X (see [8]). An AI-identity means an identity u ≈ v, where u = u1+⋯+uk, v = v1+⋯+ vℓ, ui, vj ∈ X+, i ∈ k, j ∈ ℓ, k = {1, 2, …, k}. Recall that an ai-semiring is called a Burnside ai-semiring if its multiplicative reduct is a Burnside semigroup, i.e., it satisfies the identity xn ≈ xm with m < n (see [16, 17, 18]). The variety of all Burnside ai-semirings (resp., Burnside semigroups) satisfying the identities xn ≈ xm will be denoted by Sr(n, m) (resp., Sg(n, m)). There are many papers in the literature considering Burnside semigroups and Burnside ai-semirings (see [1, 2, 4, 5, 6, 7, 8, 10, 16, 17, 18, 19, 20]). In particular, in 1979, McKenzie and Romanowska [19] studied the lattice of subvarieties of the subvariety Bi of Sr(2, 1) defined by the additional identity xy ≈ yx. They showed that this lattice contains precisely 5 elements: the trivial variety T, the variety D of distributive lattices, the ai-semiring variety M defined by the additional identity x + y ≈ xy, the varieties D ∨ M and Bi (see Figure 1).
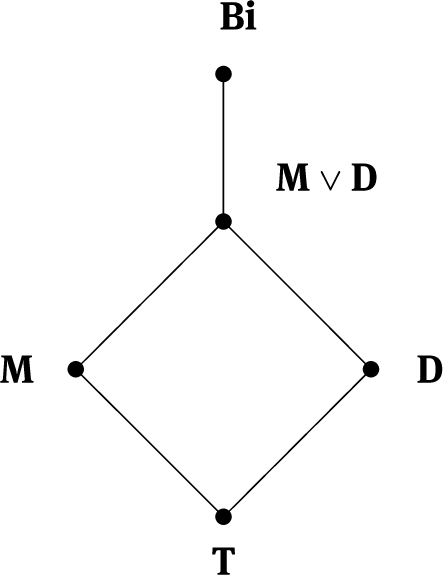
The lattice of subvarieties of Bi
In 2002, Zhao [7] studied the variety Sr(2, 1), which need not satisfy xy ≈ yx. They provided a model of the free object in this variety by introducing the notion of closed subsemigroup of a semigroup. In 2005, Ghosh et al. [1], Pastijn [2] and Pastijn and Zhao [3] studied the lattice of subvarieties of Sr(2, 1). They showed that this lattice is a distributive lattice of order 78 and that every member of this lattice is finitely based and is generated by a finite number of finite ordered bands.
Along this research route, some authors studied the subvarieties of Sr(n, 1). In 2005, Kuřil and Polák generalized the notion of closed subsemigroups introduced by Zhao [7] to that of n-closed subset of a semigroup. They provided a construction of the free object in Sr(n, 1) by using n-closed subset of the free object in Sg(n, 1). Moreover, Gajdoš and Kuřil [10] showed that Sr(n, 1) is locally finite if and only if Sg(n, 1) is locally finite. In 2015, Ren and Zhao [21] introduced the notion of (n, m)-closed subsets of a semigroup and gave a model of the free object in Sr(n, m) by using (n, m)-closed subset of the free object in Sg(n, m). In 2016, Ren, Zhao and Shao [20] proved that the multiplicative semigroup of each member of Sr(n, 1) is a regular orthocryptogroup. As an application, a model of the free object in such a variety is given. In the same year, Ren and Zhao [4] studied the lattice of subvarieties of the subvariety of Sr(3, 1) defined by the additional identity xy ≈ yx. They showed that it is a 9-element distributive lattice. As a continuation of [4], Ren et al. [5] studied the lattice of subvarieties of the subvariety of Sr(n, 1) defined by the additional identity xy ≈ yx. They showed that if n − 1 is square-free, then this lattice is a 2+2r+1+ 3r-element distributive lattice, where r denotes the number of prime divisors of n − 1. They also proved that this lattice is finitely based and finitely generated. In 2017, Ren et al. [6] studied that the lattice of the subvarieties of Sr(3, 1). They showed that this lattice is a 179-element distributive lattice. They also showed that every member of this lattice is finitely based and finitely generated. This paper is another contribution to this line of investigation. We shall characterize the lattice of subvarieties of the subvariety of Sr(p + 1, 1) defined by the additional identities zxyz ≈ (zxzyz)pzyxz(zxzyz)p.
This paper is organized as follows. After this introductory section, in Sect. 2 we shall give some auxiliary results and notations that are needed in the sequel. In Sect. 3 we shall study the subvariety of Sr(p + 1, 1) defined by the additional identity zxyz ≈ (zxzyz)pzyxz(zxzyz)p. We shall show that its lattice of subvarieties is a distributive lattice of order 179. Also, all members of this lattice are finitely based and finitely generated. In particular, Sr(3, 1) is just the case of above variety when p = 2. Thus our main results generalize and extend the main results in [1, 2, 3, 4, 6, 19].
For notation and terminology not given in this paper, the reader is referred to [22, 23, 24, 25].
2 Preliminaries and some notations
Let Ap+1 denote the group variety defined by the identities
For any S ∈ Sr(3, 1), every subgroup of (S, ⋅) satisfies the identity x3 ≈ x. This shows that every subgroup of (S, ⋅) is an abelian group in A3. That is to say, (S, ⋅) is a union of abelian groups which belong to A3.
For any semigroup S ∈ Sg(p + 1, 1), by [22, Proposition II.7.1 and Exercises V.5.8 (V)]), we have
Lemma 2.1
IfSsatisfies the identityzxyz ≈ (zxzyz)pzyxz(zxzyz)p, thenSis a union of abelian groups which belong toAp+1.
We denote by ROBAp+1 the subvariety of Sg(p + 1, 1) defined by the additional identity zxyz ≈ (zxzyz)pzyxz(zxzyz)p. As usual, for a semigroup variety V, we denote by V∘ the semiring variety consisting of all ai-semirings whose multiplicative reduct belongs to V. It is easy to see that
In particular, Sr(3, 1) is equal to
Let SAp+1 denote the semigroup variety defined by the identities (1) and (2), and Sℓ denote the variety of semilattices. By [22, Lemma IV.2.3, Theorem IV. 2.4 and Exercise IV.2.16 (xii(γ))], we have
Lemma 2.2
SAp+1 = Sℓ ∨ Ap+1.
Let ω be an element of X+. The following notions and notation are needed for solving the word problem for SAp+1 and ROBAp+1:
i(ω) denotes the initial part of ω, i.e., the word obtained from ω by retaining only the first occurrence of each variable.
f(ω) denotes the final part of ω, i.e., the word obtained from ω by retaining only the last occurrence of each variable.
c(ω) denotes the content of ω, i.e., the set of all variables occurring in ω.
m(x, ω) denotes the multiplicity of x in ω, i.e., the number of occurrence of x in ω.
ri(ω) denotes the set {x ∈ c(ω) | i ≡ m(x, ω) (mod p)}, where i ∈ {0, 1, …, p − 1}.
rp+1(ω) denotes the set {xk | x ∈ c(ω), x ∈ p − 1, k ≡ m(x, ω) (mod p)}.
ω denotes the word obtaining from ω by deleting all occurrences of variables which belong to r0(ω).
It is easy to check that a semigroup identity u ≈ v is satisfied by Ap+1 if and only if ri(u) = ri(v) for all i ∈ p − 1. Thus, for any semigroup identity u ≈ v,
where ROBAp+1 = ReB ∨ Ap+1 (see [22, Theorem V.5.3]), and ReB the variety of regular bands. Now we have
Lemma 2.3
Proof
By (4), it follows immediately that (5), (6) and (7) hold in
Thus,
Thus,
In a left-right dual way we can show that
Furthermore, we have
Thus,
Lemma 2.4
LetSbe an ai-semiring inSr(p + 1, 1). Then the following is true,
Proof
Suppose that S is an ai-semiring in Sr(p + 1, 1). Then for any a ∈ S, ap+1 = a. Without loss of generality, suppose that i, j ∈ p and i < j. We have
This completes the proof. □
Let u ≈ v be an AI-identity and Σ a set of identities which include the identities determining AI. Under the presence of the identities determining AI, it is easy to verify that u ≈ v gives rise to the identities u ≈ u+vj, v ≈ v+ui, i ∈ k, j ∈ ℓ. Conversely, the latter k + ℓ identities give rise to u ≈ u + v ≈ v. Thus, to show that u ≈ v is derivable from Σ, we only need to show that the simpler identities u ≈ u+vj, v ≈ v+ui, i ∈ k, j ∈ ℓ are derivable from Σ.
3 The lattice 𝓛( R O B A p + 1 ∘ )
In the current section, we shall characterize the lattice 𝓛
Let (Zp, ⋅) be the cyclic group of order p and
Then (
Lemma 3.1
LetSbe an ai-semiring in
Proof
The direct part is obvious. Conversely, suppose that S is an ai-semiring in
Let Mp denote
Lemma 3.2
The interval [T, Mp] consists of the three varietiesT, MandMp. □
Proof
Let V ∈ [T, Mp] and V ≠ T. Then M ⊆ V since M is minimal nontrivial subvariety of Mp. It follows that V ∈ [M, Mp] and so V = M or V = Mp. □
Let u = u1+⋯+uk, where ui ∈ X+, i ∈ k. We put C(u) = ⋃i ∈ kc(ui). To solve the word problem of the ai-semiring
Lemma 3.3
Let u ≈ u+q be anAI-identity, where u = u1+⋯+uk, ui, q ∈ X+, i ∈ k. Then
Lemma 3.4
Let u ≈ u+q be anAI-identity, where u = u1+⋯+uk, ui, q ∈ X+, i ∈ k. If
For a semiring variety V, we denote by 𝓛(V) the lattice of all subvarieties of V. In the following we shall characterize the lattice 𝓛(
Then it is easy to see that φ is subjective. For any V ∈ 𝓛(
then we denote by
Then for any V ∈ [W, Ŵp],
it follows that V ∈ φ−1(W) and so [W, Ŵp] ⊆ φ−1(W). Conversely, if V ∈ φ−1(W), then V ∈ [W, Ŵp]. Otherwise, φ(V) ≠ W, a contradiction. Thus, for any W ∈ 𝓛 (Sr(2, 1)), φ−1(W) is the interval [W,
This implies that φ(⋁i ∈ IVi) = ⋁i ∈ Iφ(Vi) and so φ is a complete ∨-epimorphism. Moreover, it is clear that φ is a complete ∧-epimorphism. It follows that φ is a complete epimorphism. Thus, 𝓛(
Notice that M is the subvariety of Sr (2, 1) determined by the additional identities xy ≈ yx and x+y ≈ xy. Thus
Recall (see [1]) that the lattice 𝓛(Sr (2, 1)) can be divided into five intervals: [T, N ∩ P ∩ Sr (2, 1)], [D, N ∩ Sr (2, 1)], [M, P ∩ Sr (2, 1)], [D ∨ M, K ∩ Sr(2, 1)] and [Bi, Sr(2, 1)], where N ∩ Sr(2, 1) is the subvariety of Sr(2, 1) determined by the identity
P ∩ Sr(2, 1) is the subvariety of Sr(2, 1) determined by the identity
and K ∩ Sr(2, 1) is the subvariety of Sr(2, 1) determined by the identity
Thus we have
Theorem 3.5
LetV ∈ [T, N ∩ P ∩ Sr(2, 1)] ∪ [D, N ∩ Sr(2, 1)]. Then
Proof
From N ∩ Sr(2, 1) ⊨ (11), we have that
Notice that
Assume that V ∈ 𝓛(Sr(2, 1)) and V ⊨ u ≈ u+q, where u = u1+⋯+uk, ui, q ∈ X+, i ∈ k. From
Lemma 3.6
LetV ∈ [M, P ∩ Sr(2, 1)]. ThenV ∨ HSP(
Proof
Since P ∩ Sr(2, 1) ⊨ (12), it follows that
We immediately have that this is the case for
Let u ≈ u+q be an AI-identity which is satisfied in V ∨ HSP(
This derives the identity
In a left-right dual way we have
Therefore the following are satisfied in
Furthermore, we have the following are derivable from the identities which are satisfied in
This shows that u ≈ u+q is satisfied in
By Lemma 3.1 and 3.6, we can establish the following result.
Theorem 3.7
LetV ∈ [M, P ∩ Sr(2, 1)]. Then the interval [V,
For an ai-semiring S we denote by S0 the ai-semiring obtained from S by adding an extra element 0, where a + 0 = a, a0 = 0a = 0 for every a ∈ S. Written Bp as
Lemma 3.8
Let S ∈
if and only if it does not contain a copy of
Proof
Necessary. It is obvious.
Sufficiency. Suppose that S ∈
It is easily verified that c, a+c, a2+c, …, ap+c and a+ap+c are not equal to each other, where c = (a+ap)bp(a+ap). Put S1 = {c, a+c, a2+c, …, ap+c, a+ap+c}. By identities (1) and (10), it is routine to verify that S1 forms a subsemiring of S, which is a copy of
Let u = u1+⋯+um, where ui ∈ X+, i ∈ m, and Z ⊆ ⋃i ∈ mc(ui). If c(ui) ∩ Z ≠ ∅ for every i, then we write DZ(u) = ∅. Otherwise, DZ(u) is the sum of terms ui for which c(ui) ∩ Z = ∅. The proof of the following result is easy and omitted.
Lemma 3.9
Let S ∈
Lemma 3.10
HSP(
Proof
It is obvious that HSP(
Let u ≈ u+q be any identity which is satisfied in HSP(
also is satisfied in
Suppose that S ∈
Lemma 3.11
LetV ∈ [Bi, Sr(2, 1)]. ThenV ∨ HSP(
Proof
Let V ∈ [Bi, Sr(2, 1)]. Since it is easily seen that V ∨ HSP(
Let Z = C(u) ∖ c(q). Since DZ(u+q) ≠ ∅, by Lemma 3.9, DZ(u) ≠ ∅. Assume that DZ(u) = u1+⋯ +uk, k ≤ n. By Lemma 3.9, Bp ⊨ DZ(u) ≈ DZ(u)+q and so ⋃i ∈ kc(ui) = c(q). By Lemma 3.4, there exists q1 in X+ with rp+1(q1) = rp+1(q) (and so ri(q1) = ri(q) for all i ∈ p − 1) and c(q) ⊆ c(q1) ⊆ ⋃i ∈ kc(ui) such that DZ(u) ≈ DZ(u)+q1 is satisfied in
Proof
We only need to show that identity (18) is derivable from (17) and the identities determining
This derives the identity
On the other hand, we also have
This deduces the identity
This shows that the subvariety of
Lemma 3.13
LetV ∈ 𝓛(Sr(2, 1)) such thatD ∨ M ⊆ V. ThenV ∨ HSP(Bp) is the subvariety of [V,
Proof
It is easily seen that V ∨ HSP(Bp) ⊆
Let u ≈ u+q be an AI -identity which is satisfied in V ∨ HSP(Bp), where u = u1+⋯ +un, ui, q ∈ X+, i ∈ n. Since D2 ⊨ u ≈ u+q, there exists ui such that c(ui) ⊆ c(q), where i ∈ n. Since Bp ⊨ u ≈ u+q, by Lemma 3.4 there exists q1 in X+ with rp+1(q1) = rp+1(q) (and so ri(q1) = ri(q) for all i ∈ p − 1) and c(q) ⊆ c(q1) such that u ≈ u+q1 is satisfied in
Similarly,
Thus the following are derivable from identity (18) and the identities which hold in
Hence, u ≈ u+q is derivable from (18) and the identities determining
Theorem 3.14
LetV ∈ [Bi, Sr(2, 1)]. Then the interval [V,
Proof
By Lemma 3.11, V ∨ HSP(
Theorem 3.15
LetV ∈ [D ∨ M, K ∩ Sr(2, 1)]. Then the interval [V,
Proof
Since K ∩ Sr(2, 1) ⊨ (13), it follows immediately that
Notice that
Theorem 3.16
Each member of 𝓛(
Proof
Since each member of 𝓛(Sr(2, 1)) is finitely based and finitely generated, it follows from Lemmas 3.6, 3.11, 3.13, Theorems 3.5, 3.7, 3.14 and 3.15 that this is the case for each member of 𝓛(
Theorem 3.17
𝓛(
Proof
Notice that both [T, N ∩ P ∩ Sr(2, 1)] and [M, P ∩ Sr(2, 1)] have 4 elements, [D, N ∩ Sr(2, 1)] has 9 elements, [D ∨ M, K ∩ Sr(2, 1)] has 25 elements, and [Bi, Sr(2, 1)] has 36 elements (see [2, Section 4]). By Theorems 3.5, 3.7, 3.14 and 3.15, we have that 𝓛(
Assume that V1, V2, V3 ∈ 𝓛(
Acknowledgement
This paper is supported by Natural Science Foundation of China (11571278, 11701449) and Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ1600930).
References
[1] Ghosh S., Pastijn F., Zhao X.Z., Varieties generated by ordered bands I, Order, 2005, 22, 109-12810.1007/s11083-005-9011-zSearch in Google Scholar
[2] Pastijn F., Varieties generated by ordered bands II, Order, 2005, 22, 129-14310.1007/s11083-005-9013-xSearch in Google Scholar PubMed
[3] Pastijn F., Zhao X.Z., Varieties of idempotent semirings with commutative addition, Algebra Universalis, 2005, 54, 301-32110.1007/s00012-005-1947-8Search in Google Scholar
[4] Ren M.M., Zhao X.Z., The variety of semilattice-ordered semigroups satisfying x3 ≈ x and xy ≈ yx, Period Math Hung, 2016, 72, 158-17010.1007/s10998-016-0116-5Search in Google Scholar
[5] Ren M.M., Zhao X.Z., Shao Y., The lattice of ai-semiring varieties satisfying xn ≈ x and xy ≈ yx, Submitted manuscriptSearch in Google Scholar
[6] Ren M.M., Zhao X.Z., Wang A.F., On the varieties of ai-semirings satisfying x3 ≈ x, Algebra Universalis, 2017, 77, 395-40810.1007/s00012-017-0438-zSearch in Google Scholar
[7] Zhao X.Z., Idempotent semirings with a commutative additive reduct, Semigroup Forum, 2002, 64, 289-29610.1007/s002330010048Search in Google Scholar
[8] Kuřil M., Polák L., On varieties of semilattice-ordered semigroups, Semigroup Forum, 2005, 71, 27-4810.1007/s00233-004-0176-3Search in Google Scholar
[9] Golan J.S., The Theory of semirings with Applications in Mathematics and Theoretical Computer Science, Longman Scientific and Technical, Harlow, 1992Search in Google Scholar
[10] Gajdoš P., Kuřil M., On free semilattice-ordered semigroups satisfying xn ≈ x, Semigroup Forum, 2010, 80, 92-10410.1007/s00233-009-9188-3Search in Google Scholar
[11] Pilitowska A., Zamojska-Dzienio A., The lattice of subvarieties of semilattice ordered algebras, Order, 2014, 31(2), 217-23810.1007/s11083-013-9297-1Search in Google Scholar
[12] Dolinka I., The finite basis problem for endomorphism semirings of finite semilattices with zero, Algebra Universalis, 2009, 61(3-4), 441-44810.1007/s00012-009-0024-0Search in Google Scholar
[13] Głazek K., A Guide to the Literature on Semirings and their Applications in Mathematics and Information Science, Kluwer Academic Publishers, Dordrecht, 2001Search in Google Scholar
[14] Hebisch U., Weinert H.J., Semirings. Algebraic Theory and Applications in Computer Science, World Scientific, Singapore, 199810.1142/3903Search in Google Scholar
[15] Kuich W., Salomaa A., Semirings, Automata and Languages, Springer, Berlin, 198610.1007/978-3-642-69959-7Search in Google Scholar
[16] Dershowitz N., Semigroups satisfying xm+n ≈ xn, Lect. Notes Comput. Sci., 1993, 656, 307-31410.1007/3-540-56393-8_23Search in Google Scholar
[17] do Lago A.P., On the Burnside semigroups xn = xn+m, Internat. J. Algebra Comput., 1996, 6(2), 179-22710.1142/S0218196796000106Search in Google Scholar
[18] Plyushchenko A.N., On the word problem for the free Burnside semigroups satisfying x2 = x3, Russian Mathematics Iz VUZ, 2011, 55(11), 76-7910.3103/S1066369X11110119Search in Google Scholar
[19] McKenzie R.N., Romanowska A., Varieties of ⋅-distributive bisemilattices, in: Contributions to General Algebra (Proc. Klagenfurt Conf., Klagenfurt, 1978), Heyn, Klagenfurt, 1979, 213-218Search in Google Scholar
[20] Ren M.M., Zhao X.Z., Shao Y., On a variety of Burnside ai-semirings satisfying xn ≈ x, Semigroup Forum, 2016, 93, 501-51510.1007/s00233-016-9819-4Search in Google Scholar
[21] Ren M.M., Zhao X.Z., On free Burnside ai-semirings, Semigroup Forum, 2015, 90, 174-18310.1007/s00233-014-9606-zSearch in Google Scholar
[22] Petrich M., Reilly N.R., Completely Regular Semigroups, Wiley, New York, 1999Search in Google Scholar
[23] Burris S., Sankappanavar H.P., A Course in Universal Algebra, Springer, New York, 198110.1007/978-1-4613-8130-3Search in Google Scholar
[24] Howie J.M., Fundamentals of Semigroup Theory, Clarendon Press, London, 1995Search in Google Scholar
[25] Shaiq S., Aslam M., On Jordan mappings of inverse semirings, Open Math., 2017, 15, 1123-113110.1515/math-2017-0088Search in Google Scholar
© 2018 Wang and Shao, published by De Gruyter
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.
Articles in the same Issue
- Regular Articles
- Algebraic proofs for shallow water bi–Hamiltonian systems for three cocycle of the semi-direct product of Kac–Moody and Virasoro Lie algebras
- On a viscous two-fluid channel flow including evaporation
- Generation of pseudo-random numbers with the use of inverse chaotic transformation
- Singular Cauchy problem for the general Euler-Poisson-Darboux equation
- Ternary and n-ary f-distributive structures
- On the fine Simpson moduli spaces of 1-dimensional sheaves supported on plane quartics
- Evaluation of integrals with hypergeometric and logarithmic functions
- Bounded solutions of self-adjoint second order linear difference equations with periodic coeffients
- Oscillation of first order linear differential equations with several non-monotone delays
- Existence and regularity of mild solutions in some interpolation spaces for functional partial differential equations with nonlocal initial conditions
- The log-concavity of the q-derangement numbers of type B
- Generalized state maps and states on pseudo equality algebras
- Monotone subsequence via ultrapower
- Note on group irregularity strength of disconnected graphs
- On the security of the Courtois-Finiasz-Sendrier signature
- A further study on ordered regular equivalence relations in ordered semihypergroups
- On the structure vector field of a real hypersurface in complex quadric
- Rank relations between a {0, 1}-matrix and its complement
- Lie n superderivations and generalized Lie n superderivations of superalgebras
- Time parallelization scheme with an adaptive time step size for solving stiff initial value problems
- Stability problems and numerical integration on the Lie group SO(3) × R3 × R3
- On some fixed point results for (s, p, α)-contractive mappings in b-metric-like spaces and applications to integral equations
- On algebraic characterization of SSC of the Jahangir’s graph 𝓙n,m
- A greedy algorithm for interval greedoids
- On nonlinear evolution equation of second order in Banach spaces
- A primal-dual approach of weak vector equilibrium problems
- On new strong versions of Browder type theorems
- A Geršgorin-type eigenvalue localization set with n parameters for stochastic matrices
- Restriction conditions on PL(7, 2) codes (3 ≤ |𝓖i| ≤ 7)
- Singular integrals with variable kernel and fractional differentiation in homogeneous Morrey-Herz-type Hardy spaces with variable exponents
- Introduction to disoriented knot theory
- Restricted triangulation on circulant graphs
- Boundedness control sets for linear systems on Lie groups
- Chen’s inequalities for submanifolds in (κ, μ)-contact space form with a semi-symmetric metric connection
- Disjointed sum of products by a novel technique of orthogonalizing ORing
- A parametric linearizing approach for quadratically inequality constrained quadratic programs
- Generalizations of Steffensen’s inequality via the extension of Montgomery identity
- Vector fields satisfying the barycenter property
- On the freeness of hypersurface arrangements consisting of hyperplanes and spheres
- Biderivations of the higher rank Witt algebra without anti-symmetric condition
- Some remarks on spectra of nuclear operators
- Recursive interpolating sequences
- Involutory biquandles and singular knots and links
- Constacyclic codes over 𝔽pm[u1, u2,⋯,uk]/〈 ui2 = ui, uiuj = ujui〉
- Topological entropy for positively weak measure expansive shadowable maps
- Oscillation and non-oscillation of half-linear differential equations with coeffcients determined by functions having mean values
- On 𝓠-regular semigroups
- One kind power mean of the hybrid Gauss sums
- A reduced space branch and bound algorithm for a class of sum of ratios problems
- Some recurrence formulas for the Hermite polynomials and their squares
- A relaxed block splitting preconditioner for complex symmetric indefinite linear systems
- On f - prime radical in ordered semigroups
- Positive solutions of semipositone singular fractional differential systems with a parameter and integral boundary conditions
- Disjoint hypercyclicity equals disjoint supercyclicity for families of Taylor-type operators
- A stochastic differential game of low carbon technology sharing in collaborative innovation system of superior enterprises and inferior enterprises under uncertain environment
- Dynamic behavior analysis of a prey-predator model with ratio-dependent Monod-Haldane functional response
- The points and diameters of quantales
- Directed colimits of some flatness properties and purity of epimorphisms in S-posets
- Super (a, d)-H-antimagic labeling of subdivided graphs
- On the power sum problem of Lucas polynomials and its divisible property
- Existence of solutions for a shear thickening fluid-particle system with non-Newtonian potential
- On generalized P-reducible Finsler manifolds
- On Banach and Kuratowski Theorem, K-Lusin sets and strong sequences
- On the boundedness of square function generated by the Bessel differential operator in weighted Lebesque Lp,α spaces
- On the different kinds of separability of the space of Borel functions
- Curves in the Lorentz-Minkowski plane: elasticae, catenaries and grim-reapers
- Functional analysis method for the M/G/1 queueing model with single working vacation
- Existence of asymptotically periodic solutions for semilinear evolution equations with nonlocal initial conditions
- The existence of solutions to certain type of nonlinear difference-differential equations
- Domination in 4-regular Knödel graphs
- Stepanov-like pseudo almost periodic functions on time scales and applications to dynamic equations with delay
- Algebras of right ample semigroups
- Random attractors for stochastic retarded reaction-diffusion equations with multiplicative white noise on unbounded domains
- Nontrivial periodic solutions to delay difference equations via Morse theory
- A note on the three-way generalization of the Jordan canonical form
- On some varieties of ai-semirings satisfying xp+1 ≈ x
- Abstract-valued Orlicz spaces of range-varying type
- On the recursive properties of one kind hybrid power mean involving two-term exponential sums and Gauss sums
- Arithmetic of generalized Dedekind sums and their modularity
- Multipreconditioned GMRES for simulating stochastic automata networks
- Regularization and error estimates for an inverse heat problem under the conformable derivative
- Transitivity of the εm-relation on (m-idempotent) hyperrings
- Learning Bayesian networks based on bi-velocity discrete particle swarm optimization with mutation operator
- Simultaneous prediction in the generalized linear model
- Two asymptotic expansions for gamma function developed by Windschitl’s formula
- State maps on semihoops
- 𝓜𝓝-convergence and lim-inf𝓜-convergence in partially ordered sets
- Stability and convergence of a local discontinuous Galerkin finite element method for the general Lax equation
- New topology in residuated lattices
- Optimality and duality in set-valued optimization utilizing limit sets
- An improved Schwarz Lemma at the boundary
- Initial layer problem of the Boussinesq system for Rayleigh-Bénard convection with infinite Prandtl number limit
- Toeplitz matrices whose elements are coefficients of Bazilevič functions
- Epi-mild normality
- Nonlinear elastic beam problems with the parameter near resonance
- Orlicz difference bodies
- The Picard group of Brauer-Severi varieties
- Galoisian and qualitative approaches to linear Polyanin-Zaitsev vector fields
- Weak group inverse
- Infinite growth of solutions of second order complex differential equation
- Semi-Hurewicz-Type properties in ditopological texture spaces
- Chaos and bifurcation in the controlled chaotic system
- Translatability and translatable semigroups
- Sharp bounds for partition dimension of generalized Möbius ladders
- Uniqueness theorems for L-functions in the extended Selberg class
- An effective algorithm for globally solving quadratic programs using parametric linearization technique
- Bounds of Strong EMT Strength for certain Subdivision of Star and Bistar
- On categorical aspects of S -quantales
- On the algebraicity of coefficients of half-integral weight mock modular forms
- Dunkl analogue of Szász-mirakjan operators of blending type
- Majorization, “useful” Csiszár divergence and “useful” Zipf-Mandelbrot law
- Global stability of a distributed delayed viral model with general incidence rate
- Analyzing a generalized pest-natural enemy model with nonlinear impulsive control
- Boundary value problems of a discrete generalized beam equation via variational methods
- Common fixed point theorem of six self-mappings in Menger spaces using (CLRST) property
- Periodic and subharmonic solutions for a 2nth-order p-Laplacian difference equation containing both advances and retardations
- Spectrum of free-form Sudoku graphs
- Regularity of fuzzy convergence spaces
- The well-posedness of solution to a compressible non-Newtonian fluid with self-gravitational potential
- On further refinements for Young inequalities
- Pretty good state transfer on 1-sum of star graphs
- On a conjecture about generalized Q-recurrence
- Univariate approximating schemes and their non-tensor product generalization
- Multi-term fractional differential equations with nonlocal boundary conditions
- Homoclinic and heteroclinic solutions to a hepatitis C evolution model
- Regularity of one-sided multilinear fractional maximal functions
- Galois connections between sets of paths and closure operators in simple graphs
- KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy
- θ-type Calderón-Zygmund Operators and Commutators in Variable Exponents Herz space
- An integral that counts the zeros of a function
- On rough sets induced by fuzzy relations approach in semigroups
- Computational uncertainty quantification for random non-autonomous second order linear differential equations via adapted gPC: a comparative case study with random Fröbenius method and Monte Carlo simulation
- The fourth order strongly noncanonical operators
- Topical Issue on Cyber-security Mathematics
- Review of Cryptographic Schemes applied to Remote Electronic Voting systems: remaining challenges and the upcoming post-quantum paradigm
- Linearity in decimation-based generators: an improved cryptanalysis on the shrinking generator
- On dynamic network security: A random decentering algorithm on graphs
Articles in the same Issue
- Regular Articles
- Algebraic proofs for shallow water bi–Hamiltonian systems for three cocycle of the semi-direct product of Kac–Moody and Virasoro Lie algebras
- On a viscous two-fluid channel flow including evaporation
- Generation of pseudo-random numbers with the use of inverse chaotic transformation
- Singular Cauchy problem for the general Euler-Poisson-Darboux equation
- Ternary and n-ary f-distributive structures
- On the fine Simpson moduli spaces of 1-dimensional sheaves supported on plane quartics
- Evaluation of integrals with hypergeometric and logarithmic functions
- Bounded solutions of self-adjoint second order linear difference equations with periodic coeffients
- Oscillation of first order linear differential equations with several non-monotone delays
- Existence and regularity of mild solutions in some interpolation spaces for functional partial differential equations with nonlocal initial conditions
- The log-concavity of the q-derangement numbers of type B
- Generalized state maps and states on pseudo equality algebras
- Monotone subsequence via ultrapower
- Note on group irregularity strength of disconnected graphs
- On the security of the Courtois-Finiasz-Sendrier signature
- A further study on ordered regular equivalence relations in ordered semihypergroups
- On the structure vector field of a real hypersurface in complex quadric
- Rank relations between a {0, 1}-matrix and its complement
- Lie n superderivations and generalized Lie n superderivations of superalgebras
- Time parallelization scheme with an adaptive time step size for solving stiff initial value problems
- Stability problems and numerical integration on the Lie group SO(3) × R3 × R3
- On some fixed point results for (s, p, α)-contractive mappings in b-metric-like spaces and applications to integral equations
- On algebraic characterization of SSC of the Jahangir’s graph 𝓙n,m
- A greedy algorithm for interval greedoids
- On nonlinear evolution equation of second order in Banach spaces
- A primal-dual approach of weak vector equilibrium problems
- On new strong versions of Browder type theorems
- A Geršgorin-type eigenvalue localization set with n parameters for stochastic matrices
- Restriction conditions on PL(7, 2) codes (3 ≤ |𝓖i| ≤ 7)
- Singular integrals with variable kernel and fractional differentiation in homogeneous Morrey-Herz-type Hardy spaces with variable exponents
- Introduction to disoriented knot theory
- Restricted triangulation on circulant graphs
- Boundedness control sets for linear systems on Lie groups
- Chen’s inequalities for submanifolds in (κ, μ)-contact space form with a semi-symmetric metric connection
- Disjointed sum of products by a novel technique of orthogonalizing ORing
- A parametric linearizing approach for quadratically inequality constrained quadratic programs
- Generalizations of Steffensen’s inequality via the extension of Montgomery identity
- Vector fields satisfying the barycenter property
- On the freeness of hypersurface arrangements consisting of hyperplanes and spheres
- Biderivations of the higher rank Witt algebra without anti-symmetric condition
- Some remarks on spectra of nuclear operators
- Recursive interpolating sequences
- Involutory biquandles and singular knots and links
- Constacyclic codes over 𝔽pm[u1, u2,⋯,uk]/〈 ui2 = ui, uiuj = ujui〉
- Topological entropy for positively weak measure expansive shadowable maps
- Oscillation and non-oscillation of half-linear differential equations with coeffcients determined by functions having mean values
- On 𝓠-regular semigroups
- One kind power mean of the hybrid Gauss sums
- A reduced space branch and bound algorithm for a class of sum of ratios problems
- Some recurrence formulas for the Hermite polynomials and their squares
- A relaxed block splitting preconditioner for complex symmetric indefinite linear systems
- On f - prime radical in ordered semigroups
- Positive solutions of semipositone singular fractional differential systems with a parameter and integral boundary conditions
- Disjoint hypercyclicity equals disjoint supercyclicity for families of Taylor-type operators
- A stochastic differential game of low carbon technology sharing in collaborative innovation system of superior enterprises and inferior enterprises under uncertain environment
- Dynamic behavior analysis of a prey-predator model with ratio-dependent Monod-Haldane functional response
- The points and diameters of quantales
- Directed colimits of some flatness properties and purity of epimorphisms in S-posets
- Super (a, d)-H-antimagic labeling of subdivided graphs
- On the power sum problem of Lucas polynomials and its divisible property
- Existence of solutions for a shear thickening fluid-particle system with non-Newtonian potential
- On generalized P-reducible Finsler manifolds
- On Banach and Kuratowski Theorem, K-Lusin sets and strong sequences
- On the boundedness of square function generated by the Bessel differential operator in weighted Lebesque Lp,α spaces
- On the different kinds of separability of the space of Borel functions
- Curves in the Lorentz-Minkowski plane: elasticae, catenaries and grim-reapers
- Functional analysis method for the M/G/1 queueing model with single working vacation
- Existence of asymptotically periodic solutions for semilinear evolution equations with nonlocal initial conditions
- The existence of solutions to certain type of nonlinear difference-differential equations
- Domination in 4-regular Knödel graphs
- Stepanov-like pseudo almost periodic functions on time scales and applications to dynamic equations with delay
- Algebras of right ample semigroups
- Random attractors for stochastic retarded reaction-diffusion equations with multiplicative white noise on unbounded domains
- Nontrivial periodic solutions to delay difference equations via Morse theory
- A note on the three-way generalization of the Jordan canonical form
- On some varieties of ai-semirings satisfying xp+1 ≈ x
- Abstract-valued Orlicz spaces of range-varying type
- On the recursive properties of one kind hybrid power mean involving two-term exponential sums and Gauss sums
- Arithmetic of generalized Dedekind sums and their modularity
- Multipreconditioned GMRES for simulating stochastic automata networks
- Regularization and error estimates for an inverse heat problem under the conformable derivative
- Transitivity of the εm-relation on (m-idempotent) hyperrings
- Learning Bayesian networks based on bi-velocity discrete particle swarm optimization with mutation operator
- Simultaneous prediction in the generalized linear model
- Two asymptotic expansions for gamma function developed by Windschitl’s formula
- State maps on semihoops
- 𝓜𝓝-convergence and lim-inf𝓜-convergence in partially ordered sets
- Stability and convergence of a local discontinuous Galerkin finite element method for the general Lax equation
- New topology in residuated lattices
- Optimality and duality in set-valued optimization utilizing limit sets
- An improved Schwarz Lemma at the boundary
- Initial layer problem of the Boussinesq system for Rayleigh-Bénard convection with infinite Prandtl number limit
- Toeplitz matrices whose elements are coefficients of Bazilevič functions
- Epi-mild normality
- Nonlinear elastic beam problems with the parameter near resonance
- Orlicz difference bodies
- The Picard group of Brauer-Severi varieties
- Galoisian and qualitative approaches to linear Polyanin-Zaitsev vector fields
- Weak group inverse
- Infinite growth of solutions of second order complex differential equation
- Semi-Hurewicz-Type properties in ditopological texture spaces
- Chaos and bifurcation in the controlled chaotic system
- Translatability and translatable semigroups
- Sharp bounds for partition dimension of generalized Möbius ladders
- Uniqueness theorems for L-functions in the extended Selberg class
- An effective algorithm for globally solving quadratic programs using parametric linearization technique
- Bounds of Strong EMT Strength for certain Subdivision of Star and Bistar
- On categorical aspects of S -quantales
- On the algebraicity of coefficients of half-integral weight mock modular forms
- Dunkl analogue of Szász-mirakjan operators of blending type
- Majorization, “useful” Csiszár divergence and “useful” Zipf-Mandelbrot law
- Global stability of a distributed delayed viral model with general incidence rate
- Analyzing a generalized pest-natural enemy model with nonlinear impulsive control
- Boundary value problems of a discrete generalized beam equation via variational methods
- Common fixed point theorem of six self-mappings in Menger spaces using (CLRST) property
- Periodic and subharmonic solutions for a 2nth-order p-Laplacian difference equation containing both advances and retardations
- Spectrum of free-form Sudoku graphs
- Regularity of fuzzy convergence spaces
- The well-posedness of solution to a compressible non-Newtonian fluid with self-gravitational potential
- On further refinements for Young inequalities
- Pretty good state transfer on 1-sum of star graphs
- On a conjecture about generalized Q-recurrence
- Univariate approximating schemes and their non-tensor product generalization
- Multi-term fractional differential equations with nonlocal boundary conditions
- Homoclinic and heteroclinic solutions to a hepatitis C evolution model
- Regularity of one-sided multilinear fractional maximal functions
- Galois connections between sets of paths and closure operators in simple graphs
- KGSA: A Gravitational Search Algorithm for Multimodal Optimization based on K-Means Niching Technique and a Novel Elitism Strategy
- θ-type Calderón-Zygmund Operators and Commutators in Variable Exponents Herz space
- An integral that counts the zeros of a function
- On rough sets induced by fuzzy relations approach in semigroups
- Computational uncertainty quantification for random non-autonomous second order linear differential equations via adapted gPC: a comparative case study with random Fröbenius method and Monte Carlo simulation
- The fourth order strongly noncanonical operators
- Topical Issue on Cyber-security Mathematics
- Review of Cryptographic Schemes applied to Remote Electronic Voting systems: remaining challenges and the upcoming post-quantum paradigm
- Linearity in decimation-based generators: an improved cryptanalysis on the shrinking generator
- On dynamic network security: A random decentering algorithm on graphs


