Density functional theory study of Mg–Ho intermetallic phases

Yuting Yang; Mengqin He; Yi Luo; Yuhang Gu; Yunfei Ding

doi:10.1515/htmp-2024-0041

Article Open Access

Density functional theory study of Mg–Ho intermetallic phases

Yuting Yang , Mengqin He , Yi Luo , Yuhang Gu and Yunfei Ding

Published/Copyright: December 31, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal High Temperature Materials and Processes Volume 43 Issue 1

Abstract

The present study explores the structural, phase stability, mechanical, and electrical properties of Mg–Ho intermetallic phases, namely Mg₂₄Ho₅, Mg₂Ho, and MgHo. The investigation is conducted using the first-principles plane-wave pseudopotential method within the framework of density functional theory, as implemented in the Vienna Ab initio Simulation Package. The primary objective of this research is to illuminate the phase stability and mechanical behavior of these compounds, which are of paramount importance for their potential applications in magnesium alloys. The study determines the formation enthalpy (ΔH) and elastic constants (C _ij) for each intermetallic phase and calculates the elastic moduli of the corresponding polycrystalline materials. The findings of this study reveal that the MgHo phase exhibits the highest absolute value of formation enthalpy (ΔH = −8.01 kJ·mol⁻¹), indicating its superior stability among the three investigated intermetallic phases. As the concentration of Ho in Mg increases, the G/B ratio for the phases decreases from 1.02 to 0.60 (>0.57), suggesting that the intermetallic phases are stable, albeit brittle. The elastic anisotropy index (A ^U), derived from the elastic constants (C _ij), follows an ascending order of Mg₂₄Ho₅, Mg₂Ho, and MgHo, signifying that MgHo possesses the most favorable elastic anisotropy among the studied phases.

Keywords: Mg alloys; Mg–Ho intermetallic phases; density functional theory; first-principle

1 Introduction

Magnesium and its alloys are the lightest structural materials with advantages including low density, high strength, good machinability, and stable dimensional accuracy. They are widely used in aerospace, automotive, and biomedical applications [1,2]. Nonetheless, at elevated temperatures, the mechanical properties of magnesium alloys degrade, resulting in a substantial reduction in strength and creep resistance as temperature rises. These limitations significantly impede their further advancement and application. Rare earth elements have been used in magnesium alloys to improve their mechanical properties, casting characteristics, and welding attributes [3]. Holmium (Ho) has improved the mechanical properties and corrosion resistance of magnesium alloys [4], making them suitable for a wide range of marine engineering applications. These alloys can be effectively utilized in offshore platform structures, hull structural components, and the casings of detectors. As an added element in magnesium alloy, Ho will combine with magnesium to form alloy phases such as MgHo, Mg₂Ho, and Mg₂₄Ho₅. The distributions, particle sizes, and properties of the intermetallic phases would exhibit significant influence on the corrosion and mechanical properties of Mg alloys. Thus, it is essential to comprehensively investigate the properties of the Mg–Ho phases for the development of new Mg alloys.

Density functional theory (DFT), as a precise computational theory, has gained widespread acceptance for secondary phase calculations and has become a cornerstone technology in materials science computation. Currently, the development of Mg alloys is insufficient on the first-principles methods to predict the properties of Mg alloys. Existing studies have primarily focused on investigating the enthalpy of formation, density of states, and elastic properties of the MgHo phase [5]. This computational approach significantly reduces the time required for scientific research.

In this article, the enthalpy of formation and electronic properties of Mg–Ho intermetallic phases was investigated by DFT. In addition, the DFT was used to calculate the elastic constants and further obtain the bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio. These calculation results allowed for the successful prediction of the mechanical properties of the Mg–Ho alloy phase. The predictive capabilities of DFT offer a significant advantage, furnishing more robust theoretical insights crucial for the prospective design and application of magnesium alloys.

2 Basis for calculation

In this work, based on the DFT, the Vienna Ab-initio Simulation Package based on the plane wave pseudopotential method was used for the first-principles calculation [6]. The Perdew–Burke–Enzerho (PBE) functional form of the generalized gradient approximation (GGA) was employed to specify the exchange-correlation energy [7]. The cut-off of 910.0 eV was implemented, and distinct k-points grids were utilized in the Brillouin zone, specifically 8 × 8 × 8, 5 × 5 × 4, and 4 × 4 × 4. The self-consistent iterative method was employed for total energy calculations with the following convergence criteria: the total energy convergence value for the system was set at 1.0 × 10⁻⁵ eV/atom, the tolerance offset was maintained below 0.001 Å, and the stress deviation was limited to less than 0.05 GPa.

3 Results and discussion

3.1 Crystal structure and formation enthalpy

The crystal structures of the Mg–Ho intermetallic phases are depicted in Figure 1. A summary of the crystal structure parameters and lattice constants can be found in Table 1. The discrepancy between the calculated and experimental values is within 2%, which can be attributed to the fact that the calculations are performed at 0 K and 0 Pa, while the experimental measurements are conducted under different temperature and pressure conditions. Furthermore, the calculated values are slightly higher than their experimental counterpart [8]. This overestimation can be explained by the use of the GGA-PBE functional in the calculations, which is a semi-local functional. The approximation method employed to handle the electron exchange-correlation energy may not adequately capture the many-body effect, potentially leading to an underestimation of the material’s internal pressure. Consequently, this underestimation results in an overestimation of the calculated lattice constant [9].

Figure 1

Crystal structures of Mg–Ho intermetallic phases: (a) MgHo, (b) Mg₂Ho, and (c) Mg₂₄Ho_5.

Table 1

Structural parameters, lattice constant, volume (V) and density (ρ), and formation enthalpy (ΔH) of Mg–Ho intermetallic phases

Phase	Crystal structure	Space group	Lattice constants (Å)		Volume (Å³)	Density (g·cm⁻³)	ΔH (kJ·mol⁻¹)
Phase	Crystal structure	Space group	This work	Experiment	Volume (Å³)	Density (g·cm⁻³)	ΔH (kJ·mol⁻¹)
MgHo	Cubic	PM−3m	a = 3.81	a = 3.77 [10]	55.31	5.68	−8.01
Mg₂Ho	Hexagonal	P63/MMC	a = 6.06	a = 6.02 [11]	311.93	4.55	−7.64
Mg₂Ho	Hexagonal	P63/MMC	c = 9.82	c = 9.75	311.93	4.55	−7.64
Mg₂₄Ho₅	Cubic	I−43m	a = 11.28	a = 11.23 [12]	717.77	3.25	−3.90

In general, the alloying ability can be assessed by considering the value of formation enthalpy. Typically, a negative formation enthalpy indicates a stronger alloying capability [13]. The formation enthalpy for each phase can be determined using the following equation:

(1) Δ H = E tot − N A E solid A − N B E solid B N A + N B ,

where E _tot represents the total energy of each Mg–Ho intermetallic phase, N _A and N _B denote the number of atoms of A and B in the unit cell, and E solid A E solid B signify the per-atom energy of pure elements A and B, respectively. The values of formation enthalpy are compiled in Table 1. From Table 1, it becomes evident that the formation enthalpies of the Mg–Ho intermetallic phases are all negative. This observation suggests that these intermetallic phases can stably exist. Notably, Table 1 reveals that the MgHo phase exhibits the highest absolute values for formation enthalpy. This further underscores its stability among the three intermetallic phases.

3.2 Electronic properties

To gain insight into the electronic properties of Mg–Ho intermetallic phases, an analysis was performed by optimizing the total and partial density of states (DOS) for each phase. As illustrated in Figure 2, the formed intermetallic phases tend to become more stable. The density of states for the three phases exhibited similarities and mainly ranged from −10 to 20 eV; the electron hybridization occurred among Mg-s, p, and Ho-d, f orbitals. The degree of orbital electron hybridization is indicative of the intermetallic phases’ stability, with stronger hybridization indicating greater stability. The partial DOS analysis revealed various degrees of hybridization in the −10–20 eV region for the three phases, affirming their stability. The total DOS increased in the order of Mg₂₄Ho₅ < Mg₂Ho < MgHo, indicating that MgHo exhibited the highest degree of hybridization and superior stability. The pseudogaps were utilized to discern the strength of covalent bonds in the Mg alloys, identified by the width between the peaks on either side of the Fermi level. Generally, a wider pseudogap signifies a stronger covalent bond [14]. Figure 2 shows that the MgHo phase had a slightly larger pseudogap width compared to the Mg₂Ho and Mg₂₄Ho₅ phases, indicating a higher covalent bond strength in the MgHo phase.

Figure 2

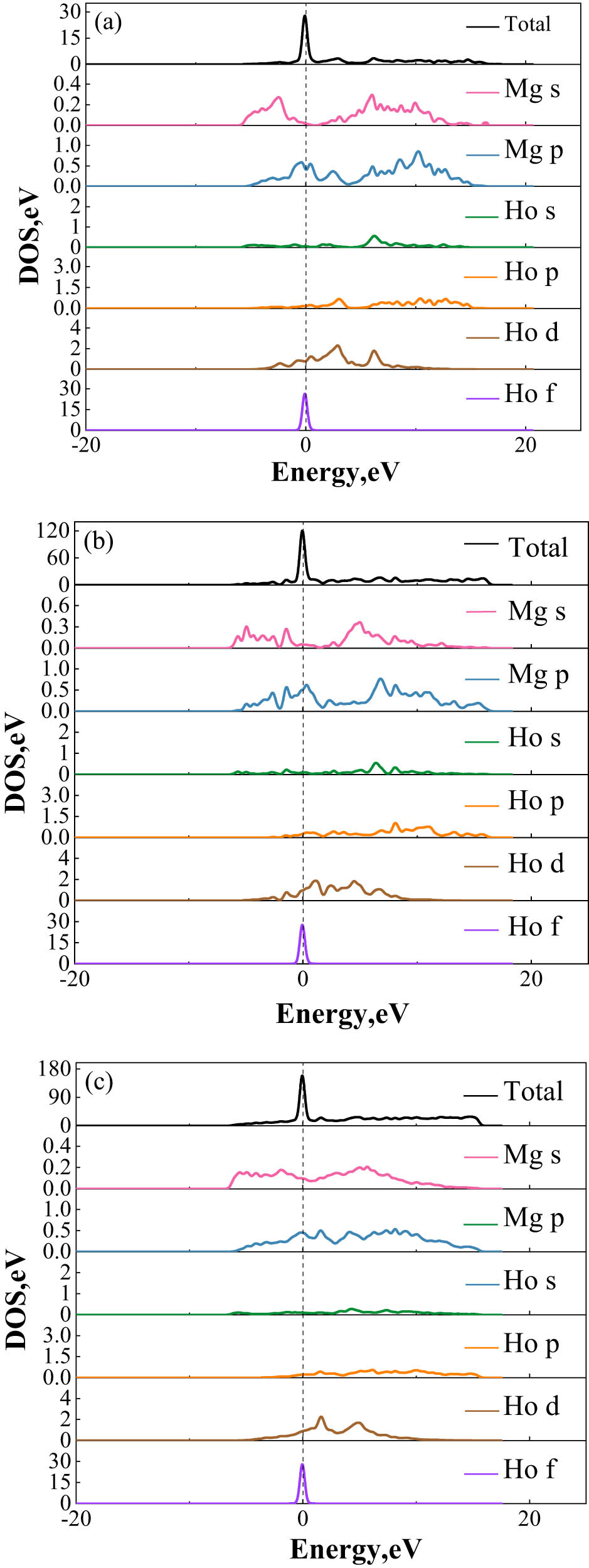
Density of states of MgHo (a), Mg₂Ho (b), and Mg₂₄Ho₅ (c) phases.

3.3 Elastic properties

Elastic constants are commonly employed for characterizing the elastic properties of materials, and they represent the fundamental physical constants of materials. The cubic crystal system has three independent elastic constants: C₁₁, C₁₂, and C₄₄ [14]. To remain stable, their elastic constants must satisfy the following stability conditions: C₁₁ − C₁₂ > 0, C₁₁ > 0, C₄₄ > 0, and C₁₁ + 2C₁₂ > 0. Conversely, the hexagonal system entails five independent elastic constants, namely C₁₁, C₁₂, C₁₃, C₃₃, and C₄₄ [15]. For this system, the mechanical stability criteria involve C₁₁ > 0, C₄₄ > 0, C₁₁ > C₁₂, and (C₁₁ + 2C₁₂) C₃₃ > 2C₁₃ ². Table 2 enumerates the elastic constants (C _ij) for Mg₂₄Ho₅, Mg₂Ho, and MgHo phases. Notably, these intermetallic phases exhibited structural stability and satisfactorily met the mechanical stability criteria.

Table 2

Elastic constants C _ij of Mg–Ho intermetallic phases

Phase	C ₁₁ (GPa)	C ₁₂ (GPa)	C ₁₃ (GPa)	C ₃₃ (GPa)	C ₄₄ (GPa)
MgHo	34.03	21.42	—	—	39.36
Mg₂Ho	57.65	15.45	9.83	80.03	25.42
Mg₂₄Ho₅	64.48	16.80	—	—	17.32

Bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), theoretical hardness (Hv), and universal anisotropic index (A ^U) for each phase, utilizing the following formulas [16,17]:

(2) B = B R + B V 2 ,

(3) G = G R + G V 2 ,

(4) E = 9 B G 3 B + G ,

(5) v = 3 B − 2 G 2 ( 3 B + G ) ,

(6) A U = 5 G V G R + B V B R − 6 .

The calculated results are listed in Table 3. The bulk modulus serves as an indicator of a material’s resistance to volume change caused by external pressure. From Table 3, the bulk modulus of these three phases increased as the Ho concentration decreased. The shear modulus and Young’s modulus offer insights into a material’s hardness to some extent. Generally, higher values of shear modulus and Young’s modulus correspond to greater material hardness. The material’s hardness can be assessed through its theoretical hardness. As shown in Table 3, the shear modulus, Young’s modulus, and theoretical hardness for the three phases follow the sequence of Mg₂₄Ho₅ < Mg₂Ho < MgHo. Based on the comparative analysis, it can be inferred that although the Mg–Ho intermetallic phases exhibit satisfactory mechanical properties, their slightly lower elastic moduli indicate that the Mg₁₇Al₁₂ phase in the AZ91 magnesium alloy possesses superior stiffness and resistance to deformation [18]. This finding holds significant implications for material selection and engineering applications where specific mechanical performance criteria must be satisfied. The insight gained from this study can guide future research and development efforts, which could be directed towards enhancing the elastic properties of Mg–Ho intermetallic phases or optimizing their integration within magnesium alloy systems to achieve the desired balance of properties. Such endeavors would contribute to the development of advanced magnesium alloys with tailored mechanical characteristics, thereby expanding their potential applications in various industries.

Table 3

Bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio (v), theoretical hardness H _v (GPa), and the universal anisotropic index (A ^U) of Mg–Ho intermetallic phases

Phase	B _V	B _R	B	G _V	G _R	G	E	v	G/B	H _V	A ^U
MgHo	25.62	25.62	25.62	26.14	12.71	26.14	58.52	0.12	1.02	6.62	5.289
Mg₂Ho	29.51	29.18	29.35	25.07	24.42	24.74	57.95	0.17	0.85	5.45	0.144
Mg₂₄Ho₅	32.69	32.69	32.69	19.93	19.45	19.69	49.19	0.25	0.60	3.28	0.124

Material brittleness and ductility can be evaluated through the ratio of B/G or Poisson’s ratio. Typically, materials with G/B ＞ 0.5 [19] are classified as brittle. Additionally, Poisson’s ratio is less than 1/3 [19], so the material is considered brittle.

In the Mg–Ho binary alloy system, three distinct phases can form, including MgHo, Mg₂Ho, and Mg₂₄Ho₅. As the concentration of Ho increases, the proportion of the MgHo phase correspondingly rises based on the Mg–Ho phase diagram. According to the data presented in Table 3, the shear modulus (G) and Young’s modulus (E) of the MgHo phase are superior to those of the Mg₂₄Ho₅ and Mg₂Ho phases. This result indicates that in the fabrication of Mg–Ho binary phase alloys, an increment of Ho can effectively improve the mechanical properties of the alloy.

Fang et al. [20] suggest that the incorporation of rare earth elements can significantly influence the elastic anisotropy of magnesium with a hexagonal close-packed crystal structure. Moreover, the nature and concentration of these rare earth elements play a pivotal role in determining the resulting elastic properties. For example, Ho, a rare earth element, has been demonstrated to have a notable impact on the elastic anisotropy of magnesium. To further investigate this phenomenon, the present study calculates the universal anisotropy index (A ^U) for three alloy phases to characterize the elastic anisotropy of each phase. Deviations of the universal anisotropy index (A ^U) from zero are indicative of the degree of elastic anisotropy, with greater deviations corresponding to higher levels of anisotropy. As shown in Table 3, MgHo exhibited the highest A ^U value among the studied phases, signifying its superior anisotropic behavior. This finding underscores the importance of considering the specific rare earth element and its concentration when designing magnesium alloys with tailored elastic properties for various engineering applications (Table 4).

Table 4

Elastic compliance constants Mg–Ho intermetallic phases

Phase	Elastic compliance constants (GPa⁻¹)
Phase	S ₁₁	S ₁₂	S ₁₃	S ₃₃	S ₄₄	S ₆₆
Mg₁Ho₁	0.0572	−0.0220	—	—	0.0254	—
Mg₂Ho₁	0.0189	−0.0048	−0.0017	0.0129	0.0393	0.0474
Mg₂₄Ho₅	0.0175	−0.0037	—	—	0.0595	—

To gain deeper insights into the mechanical anisotropy of the intermetallic phases, three-dimensional (3D) surface profiles of Young’s modulus were generated, as depicted in Figure 3. Therefore, the corresponding reciprocal calculations of Young’s modulus for Mg–Ho intermetallic phases are outlined as follows:

Figure 3

3D surface profiles of Young’s modulus for Mg–Ho intermetallic phases: MgHo (a), Mg₂Ho (b), and Mg₂₄Ho₅ (c).

For cubic crystals:

(7) 1 E = S 11 − 2 S 11 − S 12 − S 44 2 ( l 1 2 l 2 2 + l 2 2 l 3 2 + l 1 1 l 3 2 ) .

For hexagonal crystals:

(8) 1 E = S 11 ( l 1 4 + l 2 4 + 2 l 1 2 l 2 2 ) + S 33 l 3 4 + ( S 44 + 2 S 13 ) ( l 1 2 + l 2 2 ) l 3 2 ,

here, S _ij represents the elastic flexibility constant, and l ₁, l ₂, and l ₃ are the direction cosines in spherical coordinates.

The 3D diagram for MgHo resembles an eight-petal shape, signifying higher anisotropy, consistent with A ^U. In contrast, Mg₂Ho and Mg₂₄Ho₅ exhibit lower anisotropy.

4 Conclusions

In this study, we conducted comprehensive investigations into the stability, elastic properties, and electronic characteristics of Mg–Ho intermetallic phases through DFT calculations. The results can be summarized as follows:

The formation enthalpy (ΔH) of each phase was meticulously computed. The MgHo phase exhibited the highest absolute values, indicating its remarkable stability among the three intermetallic phases.
The result through calculated DOS is in good agreement with the formation enthalpy. Further examination of the DOS affirmed that MgHo displayed the strongest hybridization, underlining its superior stability.
The elastic properties of each intermetallic phase show that these three phases are mechanically stable, brittle, hard, and anisotropic.

Acknowledgement

This work was acknowledged by Jiangsu Ocean University, which provided high-performance computers to perform all first-principles calculations.

Funding information: The work was financially supported by the National Natural Science Foundation of China (Grant No. 51971100), the Lianyungang 521 Scientific Research Project (Grant No. LYG06521202312), and the National Key Research and Development Program of Lianyungang (Grant No. 23CY036).
Author contributions: Yuting Yang: Conceptualization, Methodology, Investigation, Data curation, Formal analysis, Writing – original draft, Writing – review & editing. As the first author, Yuting Yang led the study, performed the DFT calculations, analyzed the results, and wrote the initial draft of the manuscript. Mengqin He: Conceptualization, Methodology, Data curation, Validation. Mengqin He collaborated with Yuting Yang in constructing the paper's framework, processing data, and ensuring the accuracy and quality of the information. Yi Luo: Supervision, Validation, Formal analysis. Yi Luo provided theoretical guidance and expertise in data analysis, contributing to the interpretation of results. Yuhang Gu: Methodology, Software, Validation. Yuhang Gu assisted in the construction of the model and literature review. Yunfei Ding: Supervision, Project administration, Funding acquisition, Writing – review & editing. As the corresponding author, Yunfei Ding provided overall guidance, secured funding for the project, and participated in the review and editing of the manuscript to ensure its scientific rigor.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: Not applicable.

References

[1] Xu, T., Y. Yang, X. Peng, J. Song, and F. Pan. Overview of advancement and development trend on magnesium alloy. Journal of Magnesium and Alloys, Vol. 7, No. 3, 2019, pp. 536–544.10.1016/j.jma.2019.08.001Search in Google Scholar

[2] Gao, Y., C. Wu, W. Feng, H. He, H. He, J. Yang, et al. Effects of the rare earth y on the structural and tensile properties of Mg-based Alloy: A first-principles study. Crystals, Vol. 11, No. 8, 2021, id. 1003.10.3390/cryst11081003Search in Google Scholar

[3] Hu, Z., Q. Hua, H. Yan, X. Jie, and Y. Rao. Effect of trace Sm addition on microstructure and mechanical properties of AZ61 magnesium alloys. Rare Metal Materials and Engineering, Vol. 45, No. 9, 2016, pp. 2275–2281.10.1016/S1875-5372(17)30016-4Search in Google Scholar

[4] Tong, X., D. Zhang, J. Lin, Y. Dai, Y. Luan, Q. Sun, et al. Development of biodegradable Zn–1Mg–0.1 RE (RE = Er, Dy, and Ho) alloys for biomedical applications. Acta Biomaterialia, Vol. 117, 2020, pp. 384–399.10.1016/j.actbio.2020.09.036Search in Google Scholar PubMed

[5] Tao, X., Y. Ouyang, H. Liu, Y. Feng, Y. Du, Y. He, et al. Phase stability of magnesium-rare earth binary systems from first-principles calculations. Journal of Alloys and Compounds, Vol. 509, No. 24, 2011, pp. 6899–6907.10.1016/j.jallcom.2011.03.177Search in Google Scholar

[6] Kresse, G. and J. Furthmüller. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science, Vol. 6, No. 1, 1996, pp. 15–50.10.1016/0927-0256(96)00008-0Search in Google Scholar

[7] Perdew, J. P. and Y. Wang. Accurate and simple analytic representation of the electron-gas correlation energy. Physical Review B, Vol. 45, No. 23, 1992, id. 13244.10.1103/PhysRevB.45.13244Search in Google Scholar

[8] Anua, N. N., R. Ahmed, M. A. Saeed, A. Shaari, and U. H. Bakhtiar. DFT investigations of structural and electronic properties of gallium arsenide (GaAs)[C]. AIP Conference Proceedings, Vol. 1482, No. 1, 2012, pp. 64–68. American Institute of Physics.10.1063/1.4757439Search in Google Scholar

[9] Chen, H. L., L. Lin, P. L. Mao, and Z. Liu. Phase stability, electronic, elastic and thermodynamic properties of Al-RE intermetallics in Mg-Al-RE alloy: A first principles study. Journal of Magnesium and Alloys, Vol. 3, No. 3, 2015, pp. 197–202.10.1016/j.jma.2015.08.003Search in Google Scholar

[10] Iandelli, A. and A. Palenzona. Atomic size of rare earths in intermetallic compounds. MX compounds of CsCl type. Journal of the Less Common Metals, Vol. 9, No. 4, 1965, pp. 1–6.10.1016/0022-5088(65)90028-7Search in Google Scholar

[11] Ebner, M. A. and K. J. Range. Studies on AB2-type intermetallic compounds, III. High-pressure synthesis and single-crystal structure refinement of the Laves-Friauf phases HoMg2, TmMg2 and YbMg2. Journal of Alloys and Compounds, Vol. 236, No. 1–2, 1996, pp. 50–57.10.1016/0925-8388(95)02167-1Search in Google Scholar

[12] Kripyakevich, P. I., V. I. Evdokimenko, and E. I. Gladyshevskii. Compounds with the α-Mn superstructure in the rare earth-magnesium system. Kristallografiya, Vol. 9, No. 3, 1964, pp. 410–411.Search in Google Scholar

[13] Fu, C. L., X. Wang, Y. Y. Ye, and K. M. Ho. Phase stability, bonding mechanism, and elastic constants of Mo5Si3 by first-principles calculation. Intermetallics, Vol. 7, No. 2, 1999, pp. 179–184.10.1016/S0966-9795(98)00018-1Search in Google Scholar

[14] Takagiwa, Y. and K. Kimura. Metallic–covalent bonding conversion and thermoelectric properties of Al-based icosahedral quasicrystals and approximants. Science and Technology of Advanced Materials, Vol. 15, No. 4, 2014, id. 044802.10.1088/1468-6996/15/4/044802Search in Google Scholar PubMed PubMed Central

[15] Panda, K. B. and K. S. R. Chandran. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. Computational Materials Science, Vol. 35, No. 2, 2006, pp. 134–150.10.1016/j.commatsci.2005.03.012Search in Google Scholar

[16] Mian, S. A., M. Muzammil, G. Rahman, and E. Ahmed. The study of structural, elastic, electronic and optical properties of CsY I (Y = F, Cl, Br) using density functional theory. Materials Science-Poland, Vol. 35, No. 1, 2017, pp. 197–210.10.1515/msp-2017-0017Search in Google Scholar

[17] Marmier, A., Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker, and K. E. Evans. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Computer Physics Communications, Vol. 181, No. 12, 2010, pp. 2102–2115.10.1016/j.cpc.2010.08.033Search in Google Scholar

[18] Huang, Z., Y. Zhao, and H. Hou. Structural, thermodynamics and elastic properties of Mg17Al12, Al2Y and Al4Ba phases by first-principles calculations. Journal of Central South University, Vol. 19, No. 6, 2012, pp. 1475–1481.10.1007/s11771-012-1164-5Search in Google Scholar

[19] Vaitheeswaran, G., V. Kanchana, A. Svane, and A. Delin. Elastic properties of MgCNi3 – a superconducting perovskite. Journal of Physics: Condensed Matter, Vol. 19, No. 32, 2007, id. 326214.10.1088/0953-8984/19/32/326214Search in Google Scholar

[20] Fang, C., J. Zhang, Y. Huang, J. L. Xue, and X. Y. Dong. Orientation dependence of elastic properties of Mg binary alloys: A first-principles study. Computational Condensed Matter, Vol. 22, 2020, id. e00447.10.1016/j.cocom.2019.e00447Search in Google Scholar

Received: 2024-04-04

Revised: 2024-06-06

Accepted: 2024-06-10

Published Online: 2024-12-31

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/htmp-2024-0041

Keywords for this article

Mg alloys; Mg–Ho intermetallic phases; density functional theory; first-principle

Creative Commons

BY 4.0