Effect of isothermal transformation temperature on the microstructure, precipitation behavior, and mechanical properties of anti-seismic rebar
-
Junxiang Zhang
Abstract
The synergy between Nb/Ti strengthening and precise isothermal transformation temperatures has resulted in the optimal microstructure and mechanical properties in Nb/Ti anti-seismic rebars. The microstructure, precipitates, and mechanical properties of experimental steels at different isothermal transformation temperatures were characterized using scanning electron microscopy, transmission electron microscopy, electron backscatter diffraction, and universal tensile testing machine. As the isothermal transformation temperature decreased from 700 to 600°C, the ferrite grain size, pearlite interlamellar spacing, and carbon diffusion coefficient of the experimental steel decreased to 6.69 μm, 0.17 μm, and 0.14 cm2·s−1, respectively, while the yield strength and tensile strength increased to 584 and 714 MPa, respectively. At 600°C, the pearlite transformation rate in the experimental steel was the fastest, accompanied by the most rapid precipitation kinetics. The precipitates were (Nb, Ti)C of approximately 50 nm in size, with a mismatch of 14.24% at the matrix/precipitate interface and a screw dislocation angle of 2.07°. The presence of screw dislocation steps may facilitate nucleation of Nb/Ti precipitates, forming semi-coherent interfaces.
1 Introduction
Anti-seismic rebars demonstrate superior strength and ductility in comparison to general steel. This property ensures the structural integrity of buildings during seismic events, preventing sudden collapse. With the continued development of high-rise buildings, the mechanical characteristics of seismic reinforcement bars are subjected to heightened requirements [1]. Among the various enhancement methods, microalloying of steel is widely embraced. Introducing microalloying elements such as Nb, V, and Ti into the steel matrix, along with the thermomechanical control process (TMCP), meticulously regulates the precipitation behaviors of these elements. These measures refine ferrite grains and interlamellar spacing (ILS), suppress dynamic recrystallization, and enhance dislocation density [2–4].
Nb and Ti microalloying represents a commonly employed synergistic strengthening technique. On the one hand, Nb and Ti atoms possess the ability to polarize beneath the dislocation line, forming Kirchhoffer’s gas clusters, which in turn effectively pin dislocations [5]. On the other hand, Nb and Ti are potent carbide–nitride formers, capable to generate rounded or cubic M(C, N) face-centered cubic precipitates [6–8]. These M(C, N) phases play a pivotal role in inhibiting grain boundary migration of new phases and reducing the interfacial mobility between γ and α phases [9–11]. The strengthening efficacy of M(C, N) phases is dependent on various precipitation factors, including size, morphology, orientation relationship (OR), and mismatch [12]. Nb and Ti have the capability to form binary precipitates, which are frequently employed in synergistic strengthening. Ti can create binary precipitates such as (Ti, Nb)(C, N), with TiN and TiC showing preferential precipitation in steel. Their precipitation rate significantly exceeds that of NbC and NbN [12]. The undissolved Ti-rich compounds in steel serve as nucleation sites for Nb-rich compounds [13,14]. Atom probe technique results from Webel et al. [15] revealed that the Nb and Ti composite precipitation phase exhibits a core–shell structure. TiN functions as the core of the precipitates, with Nb encapsulating the TiN, forming the shell of the precipitation phase. Precipitate–temperature–time (PTT) curves serve as a reflection of the precipitation behavior of M(C, N) phases. Yong derived the PTT equation by integrating thermodynamic and Avrami equations [16]. Sun et al. [17] and Zhang et al. [18] utilized the PTT equation to calculate precipitation kinetics curves with varying Ti/V content ratios. Notably, their findings demonstrated excellent alignment between theoretically computed PTT curves and experimental data. M(C, N) phases typically adhere to either the Kurdjumov–Sachs (K–S) relationship or the Baker–Nutting (B–N) relationship. The K–S relationship predominates when larger (Ti, Nb)C phases form, while the B–N relationship prevails with smaller (Ti, Nb)C phases [19]. The isothermal transformation temperature is a pivotal parameter of TMCP. This facilitates the attainment of fine-grain strengthening and precipitation strengthening by regulating both the grain size and precipitation behavior of microalloying elements [20]. Lowering the transformation temperature, while maintaining the same holding time, results in increased pearlite content and reduced ferrite grain size [21]. Tian et al. [22] demonstrated that reducing the isothermal transformation temperature can decrease the diffusion coefficient of carbon atoms, the thickness of cementite, and the ILS. Liu et al. [23] revealed that lowering the final cooling temperature to 450°C, the microstructure transforms into acicular ferrite, and the size of the precipitation is refined to 5–10 nm.
Currently, the majority of research efforts focus on investigating the size, distribution, and orientation of precipitation. These studies often involve thermodynamic or kinetic calculations to elucidate the macroscopic growth patterns of these phases. However, limited attention has been given to examining the interface between Nb and Ti precipitated phases and the matrix, as well as the nucleation mechanisms of these phases. Consequently, this article focuses on scrutinizing the mismatch at the interface of precipitated phases and the matrix. It also involves computing time–temperature–transition (TTT) and precipitate–temperature–time (PTT). Moreover, it employs both growth and kinetic models to investigate the influence of Nb and Ti elements, as well as transition temperatures, on pearlite growth. This research provides theoretical foundations for the development of a new generation of microalloyed anti-seismic rebar.
2 Materials and experimental methods
2.1 Materials prepared
The raw material for the experimental steel consists of 500 MPa grade high-strength anti-seismic rebars. Niobium-iron alloy and titanium-iron alloy were added to the medium-frequency induction heating furnace and melted into 15 kg ingots. The chemical composition of the ingots was analyzed using various instruments including a carbon and sulfur analyzer (CS, LECO CS844, USA), a nitrogen–hydrogen–oxygen analyzer (ONH, LECO ONH836, USA), and an Inductively Coupled Plasma Emission Spectrometer (ICP, PerkinElmer 8300, USA). The results are presented in Table 1.
Chemical composition of HRB500E rebar (wt%)
| Element | C | Si | Mn | P | S | Cr | Nb | Ti | N | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| wt% | 0.22 | 0.59 | 1.43 | 0.029 | 0.002 | 0.061 | 0.022 | 0.014 | 0.0035 | Bal |
2.2 Thermo-mechanical processing
The ingot of steel was processed into rectangular specimens of dimensions 120 mm × 20 mm × 20 mm, and flat compression experiments were conducted on a Gleeble-3800 thermal simulation machine. According to the solubility theory and relevant studies [24–27], a thermal simulation process was designed for the experimental steel: the specimen was heated to 1,200°C at a rate of 20°C·s−1 and held for 10 min to ensure full homogenization of alloying elements. Subsequently, the specimen was cooled to 1,100°C at a rate of 5°C·s−1 for the first deformation stage, with a true strain of 0.3 and a strain rate of 2 s−1. It was then cooled to 1,000°C at the same rate for the second deformation stage, with a true strain of 0.2 and a strain rate of 2 s−1. Finally, it was cooled to 900°C at the same rate for the third deformation stage, with a true strain of 0.2 and a strain rate of 2 s−1. The specimen was then cooled at a rate of 15°C·s−1 to the isothermal transformation temperature and held for 30 s. The isothermal transformation temperatures were 700, 650, and 600°C, respectively, followed by air cooling to room temperature. The thermal simulation process is illustrated in Figure 1.
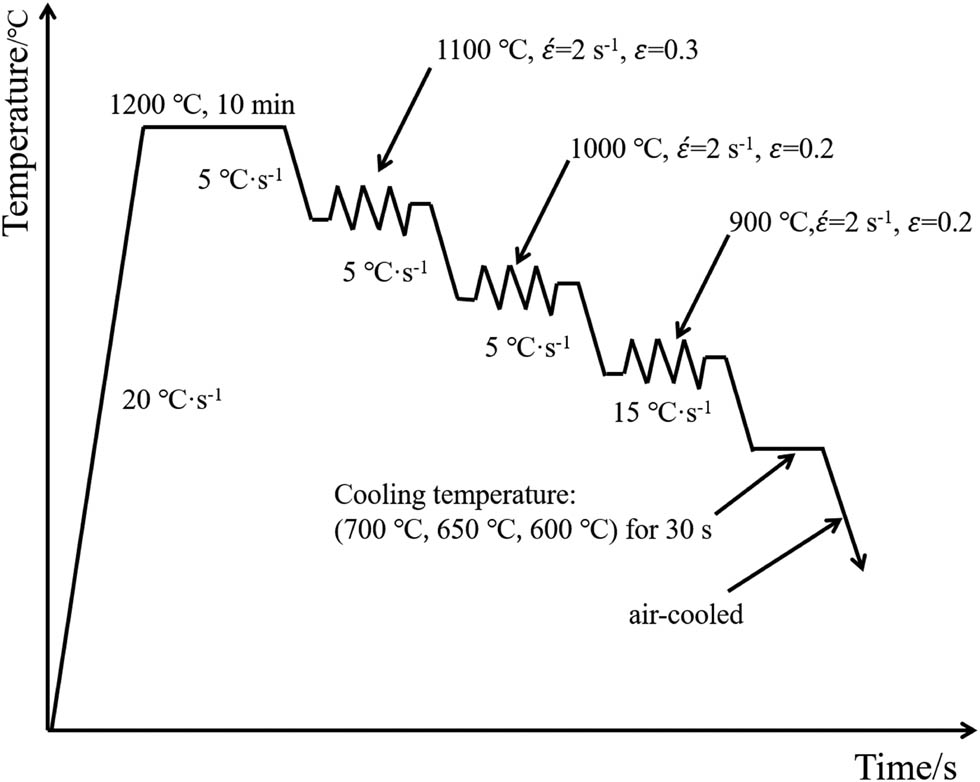
Thermal simulation process of the experimental steel.
2.3 Characterization methods
The microstructure of the experimental steels was characterized using a Z380T metallographic microscope (MM) and a SUPRA40 scanning electron microscope (SEM). The average ferrite grain size, ILS, ferrite content, and pearlite content were determined separately using the linear intercept method. A Tecnai G2 F20 S-TWIN transmission electron microscope (TEM) equipped with an energy spectrometer (EDS) was employed to analyze the structure, morphology, and composition of the precipitates. The original high-resolution images of the precipitates (HRTEM) were processed using the HRTEM filter function of the GMS-3. Electron diffraction spots and lattice stripes of the matrix and precipitates were obtained using the fast Fourier transform (FFT) and inverse fast Fourier transform (IFFT). Electron backscatter diffraction (EBSD) analysis was conducted using Oxford Nordlys max3, with the sample rolling direction aligned with the physical x-axis of the SEM. The EBSD data were analyzed using Channel5. Plate tensile specimens were prepared for the samples under different isothermal transformation temperatures and stretched at a strain rate of 10−2 s−1 using an MTS810 universal tensile tester. Based on the true stress–strain equation, the stage of uniform plastic deformation was identified, and redundant data points were eliminated using the three-strip sample interpolation method. The work hardening indices at different isothermal transformation temperatures were obtained through differentiation and linear fitting, ensuring an R 2 value greater than 0.9.
3 Results and analysis
3.1 Microstructure
Figure 2 shows the microstructure of the experimental steel at different isothermal transformation temperatures.

MM, SEM, and TEM of microstructure under the conditions of different isothermal transformation temperatures: (a1) and (a2) 700°C; (b1) and (b2) 650°C; (c1) and (c2) 600°C (yellow dash line is the interface).
Figure 2 shows the microstructure of the steel at different isothermal transformation temperatures, revealing the presence of polygonal ferrite (PF) and pearlite. The PF appears as the white area, while the black area represents pearlite. The distribution of PF and pearlite is relatively uniform, with a higher proportion of ferrite grains being observed. We observe numerous dislocations between the cementite, with a higher accumulation of dislocations at the boundaries. Additionally, noticeable dislocation entanglements within the ferrite grains form a network that may consist of dislocation cells and walls. Moreover, precipitates with sizes ranging from 3 to 5 nm are present within the lamellae, as depicted in the enlarged image of the red area (a2–c2). Figure 3 illustrates the different isothermal transformation temperatures, along with the inverse pole figure (IPF), grain boundary (GB), and geometric dislocation density (GND) of the experimental steel.

IPF, GB, and GND of simples under the conditions of different isothermal transformation temperatures: (a1)–(a3) 700°C, (b1)–(b3) 650°C, and (c1)–(c3) 600°C.
The analysis of grain boundaries reveals that the content of high angle grain boundary (HAGB) in the experimental steel increases to 82.3%, while the content of low angle grain boundary gradually decreases to 17.7% as the isothermal transformation temperature decreases to 600°C. The GND in the experimental steel gradually diffuses from within the grain interior toward the grain boundaries as the temperature decreases, resulting in a more uniform distribution of GND. Figure 4 presents the orientation distribution function (ODF) and the fiber strengths of 〈110〉//RD, <111>//ND, and 〈011〉//TD in the texture of the experimental steel with a φ 2 angle of 45°.

(a)–(c) ODF at φ 2 = 45° section: (a) 700°C, (b) 650°C, (c) 600°C. (d)–(f) Skeleton plots from at φ 2 = 45° section: (d) α-fiber//RD, (e) γ-fiber//ND, (f) ε-fiber//TD.
In Figure 4(a)–(c), the lines of different colors represent the grain strength (indicating the quantity of grains) for a specific orientation. The red, green, blue, and black lines correspond to values of 2.5, 2.0, 1.5, and 1.0, respectively. Figure 4(a)–(c) shows that there are textures in the experimental steel. Figure 4(e) demonstrates that {111}<110> and {111}<143> exhibit the highest strength in the γ-fiber. In Figure 4(d), as the isothermal transformation temperature decreases, it is evident that the strength of {115}<110>, {111}<110>, and {112}<110> in the experimental steel gradually decreases. It is noteworthy that {112}<110> originates from the Cu-{112}<111> texture in the austenitic parent phase, which significantly reduces the impact toughness of RD [28]. In Figure 4(e), {111}<110> and {111}<143> exhibit the highest strength in the γ-fiber, with {111}<110> component found to enhance elongation and deep drawability. As the isothermal transformation temperature decreased, the strength of {100}<110> gradually decreased, resulting in improved toughness and reduced delamination in the experimental steel. In Figure 4(f), the main components in the ε-fiber was observed to be copper-{121}<111>, {111}<112>, {332}<113>, and Goss-{110}<001>. The static recrystallization of ferrite facilitates the transformation of {111}<110> to {111}<112> and the transformation of brass-{110}<112>γ into {332}<113>α. The transformation of these textures follows: {332}<113>α → {554}<225>α → {111}<112>α. At 600°C, {332}<113>α exhibits the highest strength, while {111}<112>α has the lowest strength. {332}<113> is an ideal texture that can greatly enhance the plasticity and yield strength of the experimental steel [29]. Figure 5 presents the average ferrite grain size, ILS, microstructure content, and GND for the experimental steels.

(a) Grain size, ILS, and GND. (b) Microstructure content.
With the isothermal transformation temperature decreasing from 700 to 600°C, the average ferrite grain size decreased by 4.73 μm, the ILS decreased by 0.08 μm, the proportion of ferrite decreased by 17.14%, the proportion of pearlite increased by 5.85% and the GND increased by 0.19 × 1014 m−2. As the ferrite grain size and the ILS were decreased, the blocking effect on dislocation slip becomes more pronounced, facilitating the accumulation of dislocations between the lamellae and resulting in a higher dislocation density. The existence of a significant angular difference between the HAGB and the slip surface can effectively impede dislocation slip, thereby enhancing dislocation pile-up at the grain boundary. Additionally, TEM observations indicate that a portion of the cementite exhibits continuous curvature. Previous studies [30,31] have shown that the behavior of cementites under shear strain differs depending on their thickness. Specifically, when the thickness of the cementite is reduced below 200 nm, it tends to bend or rotate rather than fracture.
3.2 Precipitates
The Nb/Ti precipitates primary strengthens microalloyed rebars. The composition, size, and interface of the precipitates significantly influence the mechanical properties of microalloyed steels. Figure 6 presents the TEM results of precipitation.

TEM of precipitate: (a) (Nb, Ti)C, (a1) EDS and (b) (Ti, Nb)C, (b1) EDS.
Figure 6 shows that the precipitates appear as circular or rectangular shape, with an average size of ∼50 nm. These precipitates primarily consist of (Nb, Ti)C composite precipitates. Diffusion of solute atoms within the crystal lattice leads to local concentration variations, resulting in the formation of rounded precipitates, whereas solute atom clustering at specific crystal lattice sites leads to the formation of square precipitates [5,16]. NbC predominantly adopts a rounded morphology, while TiC tends to exhibit a square morphology. Research indicates [32,33] that NbC and TiC can make close spatial contact, co-precipitating as a TiC–NbC core–shell structure through epitaxial growth. Depending on the composition of the precipitate shell, precipitates can exhibit either rounded or square shapes. From Figure 6 it can be observed that the precipitates are formed on dislocations. According to the nucleation theory, the formation of precipitated phases requires a certain amount of energy [5]. Due to the significant lattice mismatch between Nb, Ti, and Fe, Nb/Ti is highly prone to biased precipitation at grain or phase boundaries. This effectively reduce the interfacial energy [34,35]. The intense deformation during rolling accelerates the γ → α phase transition, generating a large number of randomly dispersed supersaturated carbide particles within the ferrite matrix [36]. The high-density dislocations within the pearlite lamellae have a remarkable ability to capture carbon atoms, leading to the preferential nucleation of Nb/Ti precipitates at these locations [37,38]. The microstructure exhibits a significant presence of numerous high-density dislocations and subgrain boundaries, serving as nucleation sites for the precipitates [39,40]. Furthermore, the high-density dislocations in the steel synergize with the fine nanoscale Nb/Ti carbides, resulting in a high work hardening capability [41]. During the γ → α phase transformation, the fine precipitates effectively anchor the grain boundaries, thus impeding the migration of austenite along the grain boundaries and refining the ferrite grains. Wang et al. [42] demonstrated that the crystal structure of (Nb, Ti)C precipitated phases in microalloyed steels was a NaCl-type structure, with a specific OR between the crystal structure of the precipitated phase and the ferrite matrix. The precipitated phase tightly binds to the ferrite matrix, nucleating and growing on it. Furthermore, the chemical composition of the precipitates formed at lower austenite temperatures or during the transformation to ferrite is predominantly composed of niobium and carbon [15]. Figure 7 shows the HRTEM of the (Nb, Ti)C precipitates with the FFT and IFFT of the corresponding regions.

HRTEM, FFT, and IFFT of precipitate: (a) (Nb, Ti)C and (b) (Ti, Nb)C (red dash line indicates matrix, the solid blue line indicates precipitates, yellow ⊥ indicates dislocations).
In Figure 7(a), it can be observed that the matrix of the precipitates consists of PF, within crystal planes spacings that are 1.8456 and 2.2197 nm, corresponding to crystal planes of (001) and (011), respectively. The precipitates exhibit a single-crystal structure of (Nb, Ti)C. The crystal zone axis is

HRTEM, FFT, and IFFT of interface of matrix/precipitate: (1) matrix, (2) precipitate, and (3) interface (red dash line indicates matrix, the solid blue line indicates precipitate, yellow dash circle indicates unknown spot, yellow ⊥ denotes dislocation, and red dots denote atoms in the corresponding positions).
Figure 8(b) shows that the matrix is likely α-Fe in the BCC system, with a crystal zone axis of
Mismatch between precipitates and matrix
| d matrix (nm) | d precipation (nm) | θ (°) | d precipation (cos θ) | δ (%) |
|---|---|---|---|---|
| 0.2057 | 0.2528 | 21.62 | 0.2350 | 14.24 |
| 0.2057 | 0.2816 | 51.97 | 0.1735 | 15.65 |
The interface between the precipitates and the matrix exhibited a mismatch of 14.24 and 15.65%, respectively. The two crystal planes were unable to form a co-lattice or semi-coherent interface with the matrix, indicating a non-co-lattice interface (12%). This finding contradicts the experimental observations in this study and is also inconsistent with reports from other researchers [44]. Consequently, the growth of precipitates may not occur directly on the substrate, and the introduction of dislocations becomes necessary to alleviate the interfacial strain energy and promote the formation of a semi-coherent interface. Based on these observations, the following conjectures have been proposed:
The IFFT of the interface of Figure 8 reveals the atomic arrangement with a 2.07° twist, indicating the formation of a spiral dislocation during the deformation process. When a spiral dislocation occurs at a smooth interface, it gives rise to a helical step on the surface perpendicular to the dislocation line. The helical step assists in the nucleation and growth of the Nb/Ti precipitates, as shown in Figure 9.

Nucleation of Nb/Ti precipitates with the help of screw dislocation.
This could explain why the precipitates are able to nucleate and grow despite a matrix/precipitate mismatch of more than 12%. Comparing the positions of diffraction spots in Figure 8 from 1, 2, and 3, besides the diffraction spots originating from the matrix and precipitates, there are a few diffraction spots from unknown crystal planes in the interface FFT (yellow dash circles in the 3-FFT). From the analysis above, it is presumed that the spiral dislocation leads to the deviation of atoms from the original Bravais dot matrix, resulting in the formation of unknown diffraction spots. Wang et al. [45] observed that, owing to the lattice distortion within the ferrite matrix, vanadium (V) forms a co-lattice structure with the ferrite matrix, facilitating the nucleation of V(C, N) on the ferrite matrix. This observation strongly aligns with the hypothesis of this article.
3.3 Mechanical properties
The stress–strain of the experimental steel under different isothermal transformation temperature conditions is shown in Figure 10. The stress–strain data statistics are shown in Table 3.

Stress–strain of the steel under the conditions of different isothermal transformation temperatures (700–600°C).
Stress–strain of the experimental steel
| Isothermal transformation temperature (°C) | R eL (MPa) | R m (MPa) | R m/R eL | A (%) |
|---|---|---|---|---|
| 700 | 516 ± 1 | 614 ± 3 | 1.24 | 27.7 ± 0.2 |
| 650 | 569 ± 3 | 699 ± 2 | 1.25 | 30.6 ± 0.4 |
| 600 | 592 ± 4 | 734 ± 3 | 1.22 | 29.4 ± 0.3 |
Note: R eL is the yield strength, R m is the ultimate tensile strength, R m/R eL is the strength–ductility ratio, and A is the elongation.
When the isothermal transformation temperature is decreased from 700 to 600°C, the yield strength and tensile strength increased by 76 and 120 MPa, respectively. Notably, for an isothermal transformation temperature of 600°C, the steel achieved its highest values for yield strength (592 MPa) and tensile strength (734 MPa). The reduction rates of the work hardening exponent and the work hardening exponent at different stages of the experimental steel are illustrated in Figure 11 and summarized in Table 4, respectively.

Work hardening exponent of experimental steel under the conditions of different isothermal transformation temperatures: (a)–(c) Ln(strain)–Ln(stress) ((a) 600°C, (b) 650°C, (c) 700°C) and (d) work hardening exponent.
Reduction rate of work hardening exponent of experimental steel
| Work hardening stage | 700°C | 650°C | 600°C |
|---|---|---|---|
| Stage I → II | 21.67% | 33.33% | 40.47% |
| Stage II → III | 20.38% | 23.24% | 22.47% |
Figure 11(a)–(c) shows three distinct stages of work hardening in the experimental steel at different isothermal transformation temperatures. The work hardening exponent (n) of the experimental steels decreases from 0.3983 to 0.1838 at 600°C, from 0.3576 to 0.1830 at 650°C, and from 0.2879 to 0.1758 at 700°C. The work hardening exponent of the experimental steel gradually decreases, indicating a reduction in the plastic deformation capability. Figure 11(d) shows that the work hardening exponent of Stage I gradually increases as the isothermal transformation temperature decreases. The work hardening exponent indices of Stages II and III remain similar and show no significant changes. The work hardening exponent is an important parameter to measure the work hardening ability, it is related to the dislocation density in the microstructure. Dislocations undergo slip, intersecting with each other and forming a dislocation network within the microstructure, thereby increasing the dislocation density. The higher the dislocation density, the stronger the work hardening effect becomes. The greater the dislocation density, the more pronounced the work hardening effect becomes. Based on the statistical results presented in Figure 4, the experimental steel at 600°C exhibits the lowest average ferrite grain size and ILS. The microstructure of the experimental steel demonstrates the strongest hindrance to dislocation slip and the highest potential for increasing dislocation density at Stage I, thereby showcasing the greatest work-hardening ability. At Stage II and Stage III, the large number of dislocations undergo cross-slip during Stage I, leading to difficulties in further slip as dislocations intersect with each other. Similar work-hardening behavior in microalloyed steel has also been reported by Ghazani et al. [46]. Table 4 shows that as the isothermal transformation temperature decreases, the reduction rate of the work hardening exponent from Stage I to Stage II gradually increases (21.67% → 40.47%). The reduction rate of the work hardening exponent from Stage II to Stage III gradually decreases. The reduction rate of Stage I → Stage II is consistently greater than Stage II → Stage III.
4 Discussion
4.1 Effect of isothermal transformation temperature on microstructure
Based on the characterization of microstructure and mechanical properties, it is evident that ferrite grain size and ILS both play crucial roles in determining mechanical properties. Moreover, the growth of both ferrite and pearlite is influenced by the diffusion of carbon atoms. By the kinetics of pearlite growth (equation (1)) [47], it becomes possible to establish a relationship between the growth rate of pearlite and the diffusion of carbon:
where D
C is the diffusion coefficient of carbon atoms, λ
α and λ
θ are the thickness of ferrite and cementite, respectively, λ is the interlayer spacing of pearlite, λ
C is the theoretical minimum spacing,
As shown by the pearlite growth kinetics, the pearlite growth rate G is proportional to the carbon atom diffusion rate. According to Fick’s law, it is known that the carbon diffusion rate is related to the carbon diffusion coefficient, and equation (2) is the equation of the carbon diffusion coefficient with temperature [48]:
where D 0 is the carbon diffusion coefficient in austenite, R is the gas constant, and T is the transition temperature. D 0, Q i , and R are 0.23 cm2·s−1, 138 kJ·mol−1, and 8.31 J·(mol−1·K−1) in austenite, respectively [22,49].
Considering that the Nb/Ti atoms in the steel are strongly carbonized elements that can impede the migration of carbon atoms and reduce the diffusion coefficient of carbon atoms. Lee et al. [49] provided the following equation between Nb and carbon diffusion coefficient:
where X
Nb is the molar fraction of Nb and
Since Ti atom is also a strong carbonizing element, X Nb is corrected to X Nb+Ti, and the corrected carbon diffusion coefficient is calculated as a function of temperature. Figure 12 shows TTT and diffusion coefficient of carbon.
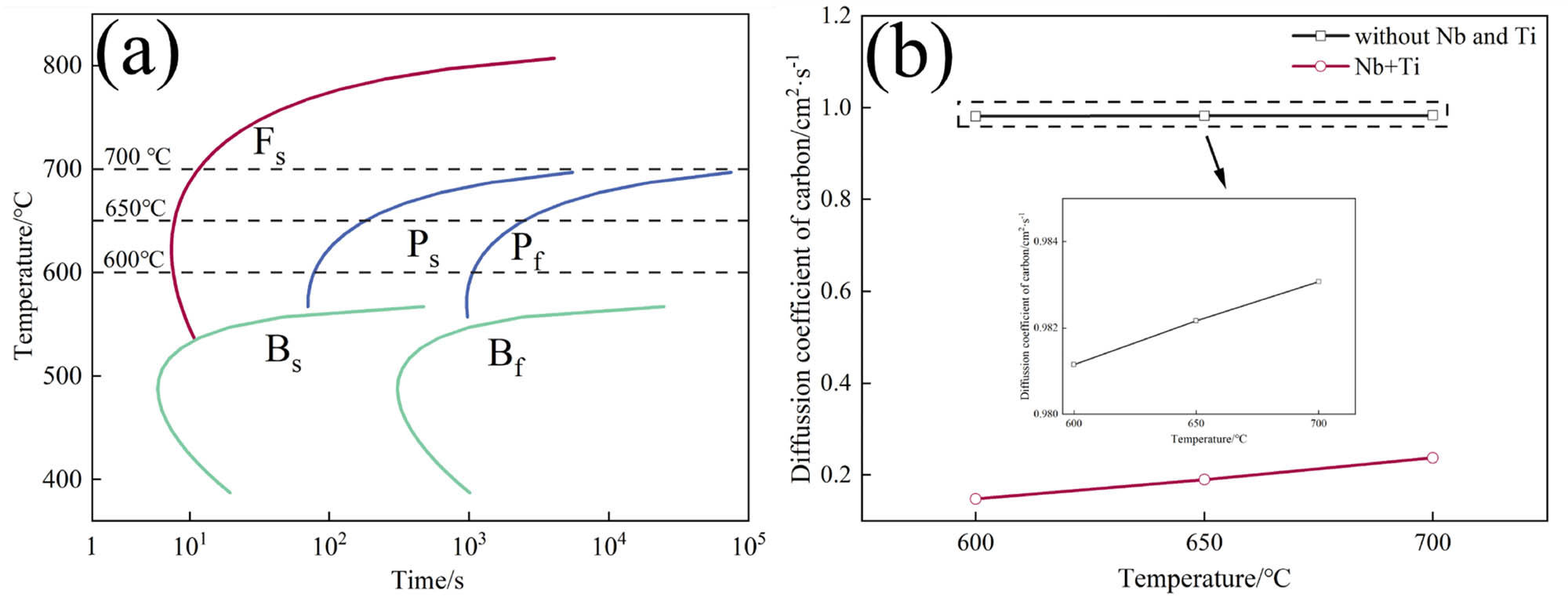
(a) TTT and (b) diffusion coefficient of carbon.
In Figure 12(a), it can be observed that as the isothermal transformation temperature is decreased from 700 to 600°C, the starting time of ferrite transformation in the experimental steel first decreases and then increases, while the starting time of pearlite transformation gradually decreases. However, 600°C is not the fastest transformation time for ferrite, but it is considered the fastest transformation time for pearlite due to the presence of pearlite organization in the steel. As a result, isothermal transformation at 600°C enables an increase in pearlite content while simultaneously controlling the ferrite grain size. The data presented in Figure 4 also confirms that the experimental steel exhibits the highest pearlite content and the smallest ferrite grain size at 600°C. Clearly, in Figure 12(b), the diffusion coefficient of carbon atoms gradually decreases with decreasing temperature, leading to a decrease in diffusion ability. This trend holds true regardless of the presence of the Nb/Ti dragging effect. Adding Nb/Ti elements significantly reduces the diffusion coefficient of carbon atoms compared to that of the rebars without Nb/Ti. Moreover, the reduction rate of the diffusion coefficient of carbon atoms is much higher in the rebars containing Nb/Ti compared to the rebars without the Nb/Ti dragging effect. Since the microstructure of anti-seismic rebars typically consists of ferrite and pearlite, pearlite exhibits a size effect as the strengthening phase. The finer ILS and cementite thickness during deformation hinders effectively dislocations and inhibits the formation of dislocation cells [28]. Moreover, the decreased diffusion coefficient of carbon atoms contributes to a slower growth rate of pearlite and leads to the refinement of cementite.
4.2 Effect of isothermal transformation temperature on the precipitation behavior of Nb/Ti
Based on the analysis of precipitates in Section 3.2, the size of Nb/Ti precipitates is approximately 50 nm. During the γ → α phase transition, the dislocations and fine precipitates at grain boundaries effectively restrict grain boundary migration and inhibit grain growth. Additionally, the high density of dislocations synergizes with the fine nanoscale Nb/Ti carbides, resulting in a high continuous work hardening capability [41]. According to equation (4) [5], the average grain diameter is directly proportional to the size of the precipitated phase when the volume fraction of the precipitated is constant. Consequently, the smaller the size of the precipitated phase, the smaller the ultimate average grain size.
where
Based on the nucleation growth theory and Avrami’s equation [50,51], Yong [16] derived the precipitation kinetic model (equations (5)–(7)) and calculated the difference in Nb/Ti precipitation time as a function of temperature variations:
where t 0a is the temperature-independent parameter (s), t 0.05a is the precipitation fraction of 5% (s), d* is the critical nucleation radius, ΔG* is the critical nucleation work (J), k is the Boltzmann constant, and T is the temperature (K). When the precipitated phase is n 1 = n 2 = 1, α = A 1 for grain boundary nucleation, n 1 = 2/3, n 2 = 2.5, α = (1 + β)3/2 for dislocation nucleation, β is a coefficient associated with dislocation line nucleation, A is the core energy per unit blade dislocation line (J·m−1), ΔG V is the volume free energy (J·m−3), σ is the interface energy between precipitates and matrix (J·m−2), and Q is the atomic activation energy (J·mol−1).
PTT of the precipitates were calculated as shown in Figure 13.
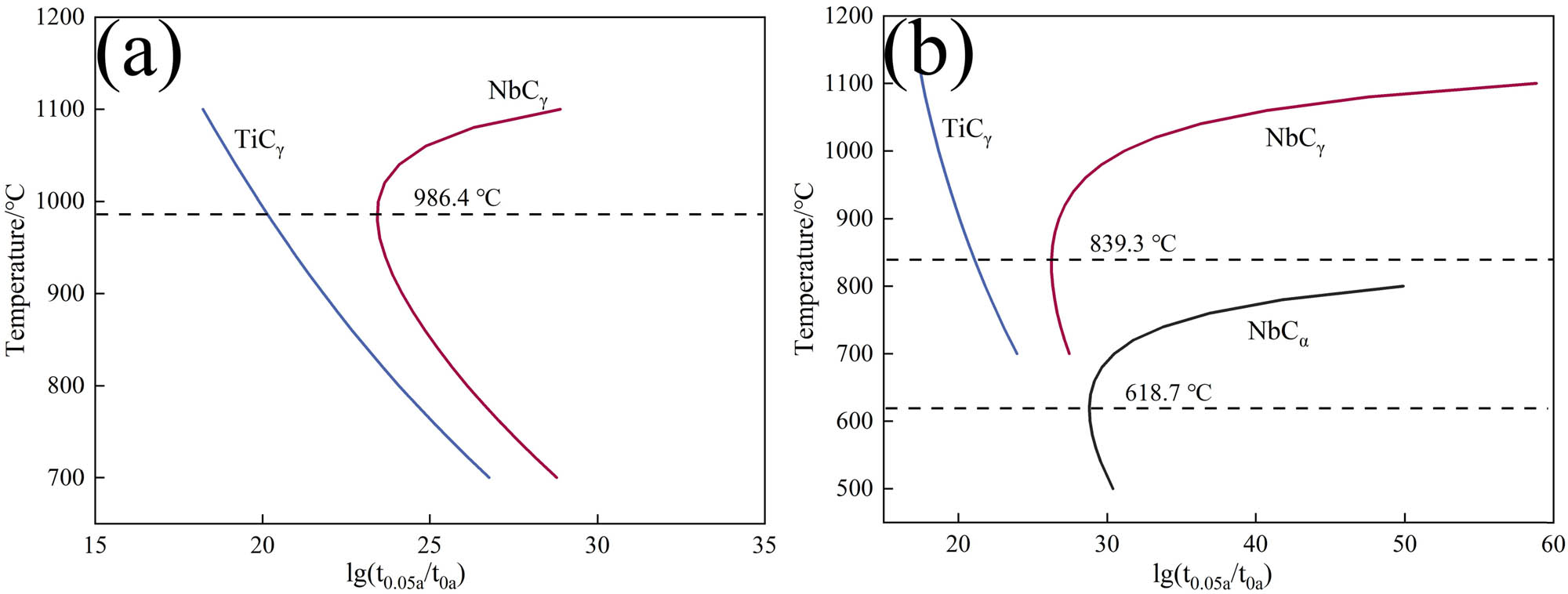
PTT of NbC and TiC: (a) grain boundary nucleation and (b) dislocation nucleation.
Figure 13 shows that TiC precipitates precede NbC in both grain boundary nucleation and dislocation nucleation. Moreover, the temperature for NbC grain boundary nucleation is higher than that for dislocation nucleation. In Figure 13(b), TiC precipitates first at 1,200°C. At 1,100°C, NbC begins to precipitate and combines with TiC to form a composite precipitates, such as (Nb, Ti)C or (Ti, Nb)C. Remaining NbC in the experimental steel continues to precipitate even after the pearlite transformation takes place. As the temperature decreases, the precipitation time also decreases. The isothermal transformation temperature of 600°C is closest to the nasal tip precipitation temperature (618.7°C), with the precipitation rate being the fastest and the precipitate content the highest.
4.3 Strengthening mechanism
Four strengthening mechanisms are known to enhance the performance of steel: solid solution strengthening (σ SS), fine grain strengthening (σ GB), precipitation strengthening (σ PR), and dislocation strengthening (σ Dis). The relationship between yield strength and strengthening mechanism is shown in the following equation:
where σ 0 is the friction stress, which has a value of 53.9 MPa [7]. The four strengthening effects were calculated as follows [16,35,52]:
where [Mn], [Si], [P], and [Cr] are the mass fractions (wt%) of the corresponding elements in the steel. σ f and σ p are the contributions of ferrite and pearlite to strength, V f and V p are the percentages of ferrite and pearlite in the experimental steel [37], d PR is the average precipitate size (∼50 nm), f is the volume fraction of Nb/Ti precipitates in the ferrite (%), α is the constant 0.24 [53], M is the deformation-induced orientation factor of about 2 [37], G is the shear modulus (81,600 MPa for steel) [54], b is the Burgers vector (0.248 nm) [54], and ρ is the dislocation density in the steel.
The strengthening of ferrite and pearlite can be calculated by the following equation [55]:
where k HP is the proportionality constant and takes the value of 17.4 MPa·mm0.5 [56], d is the average ferrite grain size (nm), and ILS (nm).
The volume fraction of (Nb, Ti)C in the ferrite can be calculated by the following equation [57]:
where Mi(Mi = Nb, Ti) is the content of microalloying elements in steel (wt%), [Mi] is the solid solution amount of microalloying elements in ferrite, C is the content of element C in steel (wt%), [C] is the solid solution amount of C in ferrite, ρ Fe and ρ MC are the densities of Fe and MC (MC = (Nb, Ti)C), i.e., ρ Fe=7.8 g·cm−2 and ρ (Nb, Ti)C = 6.385 g·cm−2.
For solid solution strengthening, the solid solution of Nb/Ti elements is almost zero as the temperature decreases [16]. Therefore, the contribution of solid solution strengthening mainly comes from elements such as Mn, Si, and P. Based on the theory of “grain boundary dislocation emission source,” Yong [16] combined the dislocation strengthening and fine-grain strengthening mechanisms by using the root mean square method, considering that grain boundaries can be regarded as dislocations of total length of L. Some researchers also adopted this theory and achieved better results [8]. The following equation shows the modified strengthening mechanism:
Figure 14 illustrates the increment of four strengthening mechanisms on the yield strength.

(a) Strengthen increment of σ YS and (b) strengthen increment of σ PR, σ GB, and σ Dis.
Figure 14(a) shows that the vector superposition of the strengthening mechanism aligns more closely with the experimental yield strength, albeit slightly lower than the theoretical yield strength. This discrepancy may arise from the overestimation of solid solution strengthening and friction stresses in theoretical calculations compared to actual values. Figure 14(b) shows that grain boundary strengthening emerges as the primary contributor to yield strength. As the isothermal transformation temperature decreases, the contributions of precipitation strengthening and dislocation strengthening gradually increase. However, the increase in grain boundary strengthening is the most significant. As discussed in Sections 3.1 and 4.1, the presence of numerous sub-grains and defects within the grains of the rolled experimental steel provides nucleation sites for new grains during the γ → α phase transition [21,58]. Subsequent temperature rise prompts the migration of ferrite grain boundaries and accelerated diffusion of carbon atoms, leading to the coarsening of ferrite grains and cementite. In some cases, abnormal growth may occur, resulting in the diminishing effectiveness of fine grain strengthening. As described in Section 4.2, with increasing temperature, the diffusion rate of Nb/Ti atoms also increases. This leads to the growth of precipitates, causing an increase in precipitates size and a subsequent decrease in the strengthening effect of precipitation [51].
5 Conclusions
The microstructure, precipitates behavior, and mechanical properties of experimental steels treated under different isothermal transformation temperatures were researched using MM, SEM, EBSD, and TEM techniques. The carbon diffusion coefficient, TTT, PTT, and strengthening mechanisms of the experimental steels were calculated. The conclusions are as follows:
When the isothermal transformation temperature decreased from 700°C to 600°C, the average grain size, ILS, and carbon diffusion coefficient of experimental steel are decreased to 9.08 μm, 0.17 μm, and 0.14 cm2·s−1, respectively. Meanwhile, the content of pearlite and dislocation density increased to 15.48% and 1.27 × 1014 m−2, respectively.
The precipitates are primarily Nb/Ti carbides, with an average size of ∼50 nm. The mismatch between the precipitates and the matrix is measured at 14.24%. The Nb/Ti precipitates may be nucleated on the screw dislocations steps, forming a semi-coherent interface. 600°C is closest to the fastest precipitation temperature (618.7°C). During the cooling process, TiC precipitates first, followed by NbC, and finally, (Nb, Ti) C is formed.
When the isothermal transformation temperature decreased from 700 to 600°C, the yield strength and tensile strength of experimental steels are increased to 584 and 714 MPa, respectively. The strength of the {332}<113>α texture is increased. The effect of fine grain, precipitation, and dislocation strengthening are enhanced. The reduction in work hardening rate from Stage II → III is maximum.
Acknowledgement
The authors express their sincere thanks to Mr. Xinqiang Xiong for his help.
-
Funding information: This work was supported by the National Nature Science Foundation of China (grant number 52074095), Guizhou Provincial Department of Science and Technology Qianke Synthetic Fruit [2023] General 100 (grant number QKHCG [2023] YB100), Guizhou Provincial Key Technology R&D Program (grant number QKHZC [2022] YB053).
-
Author contributions: Junxiang Zhang: conducted the rolling processing, mechanical property testing and SEM experiments, conducted the TEM experiments, analyzed the data, wrote the manuscript. Shangjun Gu: analyzed the data. Jie Wang: conducted the rolling processing, mechanical property testing and SEM experiments. Fulong Wei: analyzed the data. Zhiying Li: conducted the TEM experiments. Zeyun Zeng: performed the theoretical analysis. Bin Shen: performed the theoretical analysis. Changrong Li: designed the project and guided the research, wrote the manuscript. All authors contribute to the extensive discussions of the results.
-
Conflict of interest: The authors state no conflict of interest.
-
Data availability statement: All authors can confirm that all data used in this article can be published the Journal “High Temperature Materials and Processes.”
References
[1] Huang, S., C. Li, Z. Li, Z. Zeng, Y. Zhai, and J. Wang. Quantitative analysis of microstructure and mechanical properties of Nb–V microalloyed high-strength seismic reinforcement with different Nb additions. High Temperature Materials and Processes, Vol. 40, 2021, pp. 300–309.10.1515/htmp-2021-0031Search in Google Scholar
[2] Weng, Y. Q. Ultra-fine grain steel-theory and control techniques for the refinement of steel microstructure, Metallurgical Industry Press, Beijing, 2003.Search in Google Scholar
[3] GB/T 1499.2–2018 Steel for the reinforcement of concrete-Part 2: Hot rolled ribbed bars, 2018.Search in Google Scholar
[4] Yong, Q. L., Z. Y. Zhang, X. J. Sun, J. C. Cao, and Z. D. Li. Effect of dissolved niobium on eutectoid transformation behavior. Journal of Iron and Steel Research, International, Vol. 24, 2017, pp. 973–978.10.1016/S1006-706X(17)30141-3Search in Google Scholar
[5] Hu, G. X., X. Cai, and Y. H. Rong. Fundamental of materials science, Shanghai Jiaotong University Press, Shanghai, 2010.Search in Google Scholar
[6] Shanmugam, S., M. Tanniru, R. D. K. Misra, D. Panda, and S. Jansto. Precipitation in V bearing microalloyed steel containing low concentrations of Ti and Nb. Materials Science & Engineering, Vol. 21, No. 8, 2013, pp. 883–892.10.1179/174328405X47564Search in Google Scholar
[7] Zeng, Z. Y., C. R. Li, Z. Y. Li, Y. Q. Zhai, J. Wang, and Z. S. Li. Effect of Nb content and thermal deformation on the microstructure and mechanical properties of high-strength anti-seismic rebar. Materials Science & Engineering A, Vol. 840, 2022, id. 142929.10.1016/j.msea.2022.142929Search in Google Scholar
[8] Liu, G., Y. Li, T. Liao, S. Wang, B. Lv, and H. Guo. Revealing the precipitation kinetics and strengthening mechanisms of a 450 MPa grade Nb-bearing HSLA steel. Materials Science and Engineering: A, Vol. 884, 2023, id. 145506.10.1016/j.msea.2023.145506Search in Google Scholar
[9] Mecozzi, M. G., J. Sietsma, and S. van der Zwaag. Analysis of γ → α transformation in a Nb micro-alloyed C–Mn steel by phase field modelling. Acta Materialia, Vol. 54, No. 5, 2006, pp. 1431–1440.10.1016/j.actamat.2005.11.014Search in Google Scholar
[10] Seo, S. and S. Lee. Effects of Ti and Nb on the grain refinement and mechanical properties of AISI 4145 steel. Transaction of the Indian Institute of Metals, Vol. 71, No. 12, 2018, pp. 3037–3043.10.1007/s12666-018-1405-xSearch in Google Scholar
[11] Hong, S. C., S. H. Lim, H. S. Hong, K. J. Lee, D. H. Shin, and K. S. Lee. Effects of Nb on strain induced ferrite transformation in C–Mn steel. Materials Science and Engineering: A, Vol. 355, No. 1–2, 2003, pp. 241–248.10.1016/S0921-5093(03)00071-6Search in Google Scholar
[12] Li, Z. Y., C. R. Li, Z. Y. Zeng, L. H. Chen, Z. S. Li, and Z. L. Liu. Thermodynamic study of carbide and nitride precipitation of niobiumin 500MPa high-strength anti-seismic rebars. Journal of Iron and Steel Research, Vol. 32, No. 8, 2020, pp. 727–733.Search in Google Scholar
[13] Akhlaghi, S. and D. G. Ivey. Precipitation behaviour of a Grade 100 Structural Steel. Canadian Metallurgical Quarterly, Vol. 41, No. 1, 2002, pp. 111–119.10.1179/000844302794406324Search in Google Scholar
[14] Craven, A. J., K. He, L. A. J. Garvie, and T. N. Baker. Complex heterogeneous precipitation in titanium–niobium microalloyed Al-killed HSLA steels—I. (Ti,Nb)(C,N) particles. Acta Materialia, Vol. 48, No. 15, 2000, pp. 3857–3868.10.1016/S1359-6454(00)00194-4Search in Google Scholar
[15] Webel, J., A. Herges, D. Britz, E. Detemple, V. Flaxa, and H. Mohrbacher. Tracing microalloy precipitation in Nb-Ti HSLA steel during austenite conditioning. Metals (Basel), Vol. 10, No. 2, 2020, id. 243.10.3390/met10020243Search in Google Scholar
[16] Yong, Q. L. Secondary phases in steels, Metallurgical Industry Press, Beijing, 2006.Search in Google Scholar
[17] Sun, X., J. Kang, and Q. Yong. Revealing the difference of precipitation kinetics between TiC and VC in low-carbon tempered martensitic steels. Journal of Materials Science, Vol. 55, No. 33, 2020, pp. 16018–16032.10.1007/s10853-020-05176-3Search in Google Scholar
[18] Zhang, K., X. Sun, Z. Li, K. Xu, T. Jia, and Z. Zhu. Effect of Ti/V ratio on thermodynamics and kinetics of MC in γ/α matrices of Ti–V microalloyed steels. Journal of Iron and Steel Research International, Vol. 28, No. 8, 2021, pp. 1019–1029.10.1007/s42243-020-00539-1Search in Google Scholar
[19] Gan, X., Q. Yuan, G. Zhao, H. Ma, W. Liang, and Z. Xue. Quantitative analysis of microstructures and strength of Nb-Ti microalloyed steel with different Ti additions. Metallurgical and Materials Transactions A, Vol. 51, 2020, pp. 2084–2096.10.1007/s11661-020-05700-9Search in Google Scholar
[20] Zeng, Z. Y., C. R. Li, Z. Y. Li, S. Huang, S. W. Li, and J. T. You. Effect of final temperature of cooling on microstructure and properties of aseismic high-strength steel rebar. Chinese Journal of Materials Research, Vol. 35, No. 11, 2021, pp. 857–865.Search in Google Scholar
[21] Zeng, Z. Y., C. R. Li, Z. Y. Li, Y. Q. Zhai, J. Wang, and Z. L. Liu. Effect of final cooling temperature on the microstructure and mechanical properties of high-strength anti-seismic rebar. Materials Research Express, Vol. 8, No. 9, 2021, id. 96525.10.1088/2053-1591/ac2529Search in Google Scholar
[22] Tian, J., H. Wang, M. Zhu, M. Zhou, Q. Zhang, and X. Su. Improving mechanical properties in high-carbon pearlitic steels by replacing partial V with Nb. Materials Science and Engineering: A, Vol. 834, 2022, id. 142622.10.1016/j.msea.2022.142622Search in Google Scholar
[23] Liu, Y., L. Du, B. Zhang, H. Wu, and R. D. K. Misra. Significance of finish cooling temperature to microstructure and property relationship of low-carbon V–N–Cr microalloyed high-strength steel. Journal of Materials Engineerige and Performange, Vol. 28, No. 10, 2019, pp. 6492–6504.10.1007/s11665-019-04388-2Search in Google Scholar
[24] Dong, J., X. Zhou, Y. Liu, C. Li, C. Liu, and Q. Guo. Carbide precipitation in Nb–V–Ti microalloyed ultra-high strength steel during tempering. Materials Science and Engineering: A, Vol. 683, 2017, pp. 215–226.10.1016/j.msea.2016.12.019Search in Google Scholar
[25] Ghosh, S. and S. Mula. Thermomechanical processing of low carbon Nb–Ti stabilized microalloyed steel: Microstructure and mechanical properties. Materials Science and Engineering: A, Vol. 646, 2015, pp. 218–233.10.1016/j.msea.2015.08.072Search in Google Scholar
[26] Medina, S. F. and J. E. Mancilla. Influence of alloying elements in solution on static recrystalliza. ISIJ International, Vol. 36, No. 8, 1996, pp. 1063–1069.10.2355/isijinternational.36.1063Search in Google Scholar
[27] Pan, H. J., D. Hua, and M. H. Cai. Microstructural evolution and precipitation behavior of the warm-rolled medium Mn steels containing Nb or Nb–Mo during intercritical annealing. Materials Science & Engineering A, Vol. 736, 2018, pp. 375–382.10.1016/j.msea.2018.08.055Search in Google Scholar
[28] Das Bakshi, S., T. Dhande, N. Javed, K. N. Sasidhar, V. Sharma, and M. Mukherjee. Effect of hot deformation and crystallographic texture on toughness anisotropy and fracture behavior of Nb + V microalloyed API X70 steel. International Journal of Pressure Vessels and Pipine, Vol. 171, 2019, pp. 162–172.10.1016/j.ijpvp.2019.02.016Search in Google Scholar
[29] Das Bakshi, S., N. Javed, K. N. Sasidhar, T. Dhande, V. Sharma, and M. Mukherjee. Effect of microstructure and crystallographic texture on mechanical anisotropy of Ti–Nb microalloyed hot rolled 800 MPa HSLA steel. Materials Characterization, Vol. 136, 2018, pp. 346–357.10.1016/j.matchar.2017.12.039Search in Google Scholar
[30] Izotov, V. I., V. A. Pozdnyakov, E. V. Luk Yanenko, O. Y. Usanova, and G. A. Filippov. Influence of the pearlite fineness on the mechanical properties, deformation behavior, and fracture characteristics of carbon steel. The Physics of Metals and Metallography, Vol. 103, 2007, pp. 519–529.10.1134/S0031918X07050122Search in Google Scholar
[31] Mishra, K. and A. Singh. Effect of interlamellar spacing on fracture toughness of nano-structured pearlite. Materials Science and Engineering: A, Vol. 706, 2017, pp. 22–26.10.1016/j.msea.2017.08.115Search in Google Scholar
[32] Hutten, E., S. Liang, E. Bellhouse, S. Sarkar, Y. Lu, and B. Langelier. Mechanical properties and precipitation behavior of high strength hot-rolled ferritic steel containing Nb and V. Journal of Materials Research and Technology, Vol. 14, 2021, pp. 2061–2070.10.1016/j.jmrt.2021.07.107Search in Google Scholar
[33] Ma, X., C. Miao, B. Langelier, and S. Subramanian. Suppression of strain-induced precipitation of NbC by epitaxial growth of NbC on pre-existing TiN in Nb-Ti microalloyed steel. Matetials & Design, Vol. 132, 2017, pp. 244–249.10.1016/j.matdes.2017.07.006Search in Google Scholar
[34] Bansal, G. K., V. C. Srivastava, and S. Ghosh Chowdhury. Role of solute Nb in altering phase transformations during continuous cooling of a low-carbon steel. Materials Science and Engineering: A, Vol. 767, 2019, id. 138416.10.1016/j.msea.2019.138416Search in Google Scholar
[35] Misra, R. D. K., H. Nathani, J. E. Hartmann, and F. Siciliano. Microstructural evolution in a new 770MPa hot rolled Nb–Ti microalloyed steel. Materials Science and Engineering: A, Vol. 394, No. 1–2, 2005, pp. 339–352.10.1016/j.msea.2004.11.041Search in Google Scholar
[36] Chen, C. Y., C. C. Chen, and J. R. Yang. Microstructure characterization of nanometer carbides heterogeneous precipitation in Ti–Nb and Ti–Nb–Mo steel. Materials Characterization, Vol. 88, 2014, pp. 69–79.10.1016/j.matchar.2013.11.016Search in Google Scholar
[37] Feng, H., L. Cai, L. Wang, X. Zhang, and F. Fang. Microstructure and strength in ultrastrong cold-drawn medium carbon steel. Journal of Materials Science & Technology, Vol. 97, 2022, pp. 89–100.10.1016/j.jmst.2021.04.027Search in Google Scholar
[38] Kobayashi, Y., J. Takahashi, and K. Kawakami. Effects of dislocations on the early stage of TiC precipitation kinetics in ferritic steel: a comparative study with and without a pre-deformation. Acta Materialia, Vol. 176, 2019, pp. 145–154.10.1016/j.actamat.2019.06.055Search in Google Scholar
[39] Dey, I., S. K. Ghosh, and R. Saha. Effects of cooling rate and strain rate on phase transformation, microstructure and mechanical behaviour of thermomechanically processed pearlitic steel. Journal of Materials Research and Technology, Vol. 8, No. 3, 2019, pp. 2685–2698.10.1016/j.jmrt.2019.04.006Search in Google Scholar
[40] Huang, S., C. R. Li, Z. Y. Li, C. L. Zhuang, Z. Y. Zeng, and J. Wang. Effect of thermal simulation process on microstructure of seismic steel bars. Materials, Vol. 15, No. 10, 2022, id. 3438.10.3390/ma15103438Search in Google Scholar PubMed PubMed Central
[41] Junkui, L., Y. Zhinan, M. Hua, C. Chen, and Z. Fucheng. A medium-C martensite steel with 2.6 GPa tensile strength and large ductility. Scripta Materialia, Vol. 228, 2023, id. 115327.10.1016/j.scriptamat.2023.115327Search in Google Scholar
[42] Wang, X., Z. Li, S. Zhou, W. Wang, Q. Yong, and Z. Yang. Precipitation behavior of Ti–Nb–V–Mo quaternary microalloyed high strength fire-resistant steel and its influence on mechanical properties. Materials Science and Engineering: A, Vol. 807, 2021, id. 140865.10.1016/j.msea.2021.140865Search in Google Scholar
[43] Bramfitt, B. L. The effect of carbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. Metallurgical Transactions, Vol. 1, 1970, pp. 1987–1995.10.1007/BF02642799Search in Google Scholar
[44] Xiong, X. Q., L. C. Rong, Z. C. Ling, L. Z. Ying, and W. Jie. Effect of NbC on heterogeneous nucleation and grain refinement of HRB500 reinforcement during solidification. Journal of Building Materials, Vol. 25, No. 1, 2022, pp. 68–73.Search in Google Scholar
[45] Wang, H., Y. Li, E. Detemple, and G. Eggeler. Revealing the two-step nucleation and growth mechanism of vanadium carbonitrides in microalloyed steels. Scripta Materialia, Vol. 187, 2020, pp. 350–354.10.1016/j.scriptamat.2020.06.041Search in Google Scholar
[46] Shaban Ghazani, M., H. Irani, and S. H. Mohitfar. Effect of processing by high temperature Ex-ECAP on the microstructure, work hardening behavior and electrochemical properties of Ti-Nb microalloyed steel. Materials Chemistry and Physics, Vol. 271, 2021, id. 124952.10.1016/j.matchemphys.2021.124952Search in Google Scholar
[47] Offerman, S. E., L. J. G. W. van Wilderen, N. H. van Dijk, J. Sietsma, M. T. Rekveldt, and S. van der Zwaag. In-situ study of pearlite nucleation and growth during isothermal austenite decomposition in nearly eutectoid steel. Acta Materialia, Vol. 51, No. 13, 2003, pp. 3927–3938.10.1016/S1359-6454(03)00217-9Search in Google Scholar
[48] Tian, J., G. Xu, L. Wang, M. Zhou, and H. Hu. In situ observation of the lengthening rate of bainite sheaves during continuous cooling process in a Fe–C–Mn–Si superbainitic steel. Transaction of the Indian Institute of Metals, Vol. 71, No. 1, 2018, pp. 185–194.10.1007/s12666-017-1151-5Search in Google Scholar
[49] Lee, K. J. and J. K. Lee. Modelling of γ/α transformation in niobium-containing microalloyed steels. Scripta Materialia, Vol. 40, No. 7, 1999, pp. 831–836.10.1016/S1359-6462(99)00025-1Search in Google Scholar
[50] Avrami, M. Kinetics of phase change. II transformation–time relations for random distribution of nuclei. The Journal of Chemical Physics, Vol. 8, No. 212, 1940, pp. 212–224.10.1063/1.1750631Search in Google Scholar
[51] Karmakar, A., S. Biswas, S. Mukherjee, D. Chakrabarti, and V. Kumar. Effect of composition and thermo-mechanical processing schedule on the microstructure, precipitation and strengthening of Nb-microalloyed steel. Materials Science and Engineering: A, Vol. 690, 2017, pp. 158–169.10.1016/j.msea.2017.02.101Search in Google Scholar
[52] Gladman, T. Precipitation hardening in metals. Materials Science and Technology, Vol. 15, No. 1, 1999, pp. 31–36.10.1179/026708399773002782Search in Google Scholar
[53] Zhang, X., N. Hansen, A. Godfrey, and X. Huang. Dislocation-based plasticity and strengthening mechanisms in sub-20 nm lamellar structures in pearlitic steel wire. Acta Materialia, Vol. 114, 2016, pp. 176–183.10.1016/j.actamat.2016.04.040Search in Google Scholar
[54] Huang, H., G. Yang, G. Zhao, X. Mao, X. Gan, and Q. Yin. Effect of Nb on the microstructure and properties of Ti–Mo microalloyed high-strength ferritic steel. Materials Science and Engineering: A, Vol. 736, 2018, pp. 148–155.10.1016/j.msea.2018.08.092Search in Google Scholar
[55] Singh, P. P., S. Ghosh, and S. Mula. Strengthening behaviour and failure analysis of hot-rolled Nb + V microalloyed steel processed at various coiling temperatures. Materials Science and Engineering: A, Vol. 859, 2022, id. 144210.10.1016/j.msea.2022.144210Search in Google Scholar
[56] Pickering, B. Physical metallurgy and the design of steels, Applied Science Publishers, London, 1978.Search in Google Scholar
[57] Pavlina, E. J., J. G. Speer, and C. J. Van Tyne. Equilibrium solubility products of molybdenum carbide and tungsten carbide in iron. Scripta Materialia, Vol. 66, No. 5, 2012, pp. 243–246.10.1016/j.scriptamat.2011.10.047Search in Google Scholar
[58] Pereloma, E. V., A. G. Kostryzhev, A. AlShahrani, C. Zhu, J. M. Cairney, and C. R. Killmore. Effect of austenite deformation temperature on Nb clustering and precipitation in microalloyed steel. Scripta Materialia, Vol. 75, 2014, pp. 74–77.10.1016/j.scriptamat.2013.11.026Search in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- De-chlorination of poly(vinyl) chloride using Fe2O3 and the improvement of chlorine fixing ratio in FeCl2 by SiO2 addition
- Reductive behavior of nickel and iron metallization in magnesian siliceous nickel laterite ores under the action of sulfur-bearing natural gas
- Study on properties of CaF2–CaO–Al2O3–MgO–B2O3 electroslag remelting slag for rack plate steel
- The origin of {113}<361> grains and their impact on secondary recrystallization in producing ultra-thin grain-oriented electrical steel
- Channel parameter optimization of one-strand slab induction heating tundish with double channels
- Effect of rare-earth Ce on the texture of non-oriented silicon steels
- Performance optimization of PERC solar cells based on laser ablation forming local contact on the rear
- Effect of ladle-lining materials on inclusion evolution in Al-killed steel during LF refining
- Analysis of metallurgical defects in enamel steel castings
- Effect of cooling rate and Nb synergistic strengthening on microstructure and mechanical properties of high-strength rebar
- Effect of grain size on fatigue strength of 304 stainless steel
- Analysis and control of surface cracks in a B-bearing continuous casting blooms
- Application of laser surface detection technology in blast furnace gas flow control and optimization
- Preparation of MoO3 powder by hydrothermal method
- The comparative study of Ti-bearing oxides introduced by different methods
- Application of MgO/ZrO2 coating on 309 stainless steel to increase resistance to corrosion at high temperatures and oxidation by an electrochemical method
- Effect of applying a full oxygen blast furnace on carbon emissions based on a carbon metabolism calculation model
- Characterization of low-damage cutting of alfalfa stalks by self-sharpening cutters made of gradient materials
- Thermo-mechanical effects and microstructural evolution-coupled numerical simulation on the hot forming processes of superalloy turbine disk
- Endpoint prediction of BOF steelmaking based on state-of-the-art machine learning and deep learning algorithms
- Effect of calcium treatment on inclusions in 38CrMoAl high aluminum steel
- Effect of isothermal transformation temperature on the microstructure, precipitation behavior, and mechanical properties of anti-seismic rebar
- Evolution of residual stress and microstructure of 2205 duplex stainless steel welded joints during different post-weld heat treatment
- Effect of heating process on the corrosion resistance of zinc iron alloy coatings
- BOF steelmaking endpoint carbon content and temperature soft sensor model based on supervised weighted local structure preserving projection
- Innovative approaches to enhancing crack repair: Performance optimization of biopolymer-infused CXT
- Structural and electrochromic property control of WO3 films through fine-tuning of film-forming parameters
- Influence of non-linear thermal radiation on the dynamics of homogeneous and heterogeneous chemical reactions between the cone and the disk
- Thermodynamic modeling of stacking fault energy in Fe–Mn–C austenitic steels
- Research on the influence of cemented carbide micro-textured structure on tribological properties
- Performance evaluation of fly ash-lime-gypsum-quarry dust (FALGQ) bricks for sustainable construction
- First-principles study on the interfacial interactions between h-BN and Si3N4
- Analysis of carbon emission reduction capacity of hydrogen-rich oxygen blast furnace based on renewable energy hydrogen production
- Just-in-time updated DBN BOF steel-making soft sensor model based on dense connectivity of key features
- Effect of tempering temperature on the microstructure and mechanical properties of Q125 shale gas casing steel
- Review Articles
- A review of emerging trends in Laves phase research: Bibliometric analysis and visualization
- Effect of bottom stirring on bath mixing and transfer behavior during scrap melting in BOF steelmaking: A review
- High-temperature antioxidant silicate coating of low-density Nb–Ti–Al alloy: A review
- Communications
- Experimental investigation on the deterioration of the physical and mechanical properties of autoclaved aerated concrete at elevated temperatures
- Damage evaluation of the austenitic heat-resistance steel subjected to creep by using Kikuchi pattern parameters
- Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part II
- Synthesis of aluminium (Al) and alumina (Al2O3)-based graded material by gravity casting
- Experimental investigation into machining performance of magnesium alloy AZ91D under dry, minimum quantity lubrication, and nano minimum quantity lubrication environments
- Numerical simulation of temperature distribution and residual stress in TIG welding of stainless-steel single-pass flange butt joint using finite element analysis
- Special Issue on A Deep Dive into Machining and Welding Advancements - Part I
- Electro-thermal performance evaluation of a prismatic battery pack for an electric vehicle
- Experimental analysis and optimization of machining parameters for Nitinol alloy: A Taguchi and multi-attribute decision-making approach
- Experimental and numerical analysis of temperature distributions in SA 387 pressure vessel steel during submerged arc welding
- Optimization of process parameters in plasma arc cutting of commercial-grade aluminium plate
- Multi-response optimization of friction stir welding using fuzzy-grey system
- Mechanical and micro-structural studies of pulsed and constant current TIG weldments of super duplex stainless steels and Austenitic stainless steels
- Stretch-forming characteristics of austenitic material stainless steel 304 at hot working temperatures
- Work hardening and X-ray diffraction studies on ASS 304 at high temperatures
- Study of phase equilibrium of refractory high-entropy alloys using the atomic size difference concept for turbine blade applications
- A novel intelligent tool wear monitoring system in ball end milling of Ti6Al4V alloy using artificial neural network
- A hybrid approach for the machinability analysis of Incoloy 825 using the entropy-MOORA method
- Special Issue on Recent Developments in 3D Printed Carbon Materials - Part II
- Innovations for sustainable chemical manufacturing and waste minimization through green production practices
- Topical Issue on Conference on Materials, Manufacturing Processes and Devices - Part I
- Characterization of Co–Ni–TiO2 coatings prepared by combined sol-enhanced and pulse current electrodeposition methods
- Hot deformation behaviors and microstructure characteristics of Cr–Mo–Ni–V steel with a banded structure
- Effects of normalizing and tempering temperature on the bainite microstructure and properties of low alloy fire-resistant steel bars
- Dynamic evolution of residual stress upon manufacturing Al-based diesel engine diaphragm
- Study on impact resistance of steel fiber reinforced concrete after exposure to fire
- Bonding behaviour between steel fibre and concrete matrix after experiencing elevated temperature at various loading rates
- Diffusion law of sulfate ions in coral aggregate seawater concrete in the marine environment
- Microstructure evolution and grain refinement mechanism of 316LN steel
- Investigation of the interface and physical properties of a Kovar alloy/Cu composite wire processed by multi-pass drawing
- The investigation of peritectic solidification of high nitrogen stainless steels by in-situ observation
- Microstructure and mechanical properties of submerged arc welded medium-thickness Q690qE high-strength steel plate joints
- Experimental study on the effect of the riveting process on the bending resistance of beams composed of galvanized Q235 steel
- Density functional theory study of Mg–Ho intermetallic phases
- Investigation of electrical properties and PTCR effect in double-donor doping BaTiO3 lead-free ceramics
- Special Issue on Thermal Management and Heat Transfer
- On the thermal performance of a three-dimensional cross-ternary hybrid nanofluid over a wedge using a Bayesian regularization neural network approach
- Time dependent model to analyze the magnetic refrigeration performance of gadolinium near the room temperature
- Heat transfer characteristics in a non-Newtonian (Williamson) hybrid nanofluid with Hall and convective boundary effects
- Computational role of homogeneous–heterogeneous chemical reactions and a mixed convective ternary hybrid nanofluid in a vertical porous microchannel
- Thermal conductivity evaluation of magnetized non-Newtonian nanofluid and dusty particles with thermal radiation
Articles in the same Issue
- Research Articles
- De-chlorination of poly(vinyl) chloride using Fe2O3 and the improvement of chlorine fixing ratio in FeCl2 by SiO2 addition
- Reductive behavior of nickel and iron metallization in magnesian siliceous nickel laterite ores under the action of sulfur-bearing natural gas
- Study on properties of CaF2–CaO–Al2O3–MgO–B2O3 electroslag remelting slag for rack plate steel
- The origin of {113}<361> grains and their impact on secondary recrystallization in producing ultra-thin grain-oriented electrical steel
- Channel parameter optimization of one-strand slab induction heating tundish with double channels
- Effect of rare-earth Ce on the texture of non-oriented silicon steels
- Performance optimization of PERC solar cells based on laser ablation forming local contact on the rear
- Effect of ladle-lining materials on inclusion evolution in Al-killed steel during LF refining
- Analysis of metallurgical defects in enamel steel castings
- Effect of cooling rate and Nb synergistic strengthening on microstructure and mechanical properties of high-strength rebar
- Effect of grain size on fatigue strength of 304 stainless steel
- Analysis and control of surface cracks in a B-bearing continuous casting blooms
- Application of laser surface detection technology in blast furnace gas flow control and optimization
- Preparation of MoO3 powder by hydrothermal method
- The comparative study of Ti-bearing oxides introduced by different methods
- Application of MgO/ZrO2 coating on 309 stainless steel to increase resistance to corrosion at high temperatures and oxidation by an electrochemical method
- Effect of applying a full oxygen blast furnace on carbon emissions based on a carbon metabolism calculation model
- Characterization of low-damage cutting of alfalfa stalks by self-sharpening cutters made of gradient materials
- Thermo-mechanical effects and microstructural evolution-coupled numerical simulation on the hot forming processes of superalloy turbine disk
- Endpoint prediction of BOF steelmaking based on state-of-the-art machine learning and deep learning algorithms
- Effect of calcium treatment on inclusions in 38CrMoAl high aluminum steel
- Effect of isothermal transformation temperature on the microstructure, precipitation behavior, and mechanical properties of anti-seismic rebar
- Evolution of residual stress and microstructure of 2205 duplex stainless steel welded joints during different post-weld heat treatment
- Effect of heating process on the corrosion resistance of zinc iron alloy coatings
- BOF steelmaking endpoint carbon content and temperature soft sensor model based on supervised weighted local structure preserving projection
- Innovative approaches to enhancing crack repair: Performance optimization of biopolymer-infused CXT
- Structural and electrochromic property control of WO3 films through fine-tuning of film-forming parameters
- Influence of non-linear thermal radiation on the dynamics of homogeneous and heterogeneous chemical reactions between the cone and the disk
- Thermodynamic modeling of stacking fault energy in Fe–Mn–C austenitic steels
- Research on the influence of cemented carbide micro-textured structure on tribological properties
- Performance evaluation of fly ash-lime-gypsum-quarry dust (FALGQ) bricks for sustainable construction
- First-principles study on the interfacial interactions between h-BN and Si3N4
- Analysis of carbon emission reduction capacity of hydrogen-rich oxygen blast furnace based on renewable energy hydrogen production
- Just-in-time updated DBN BOF steel-making soft sensor model based on dense connectivity of key features
- Effect of tempering temperature on the microstructure and mechanical properties of Q125 shale gas casing steel
- Review Articles
- A review of emerging trends in Laves phase research: Bibliometric analysis and visualization
- Effect of bottom stirring on bath mixing and transfer behavior during scrap melting in BOF steelmaking: A review
- High-temperature antioxidant silicate coating of low-density Nb–Ti–Al alloy: A review
- Communications
- Experimental investigation on the deterioration of the physical and mechanical properties of autoclaved aerated concrete at elevated temperatures
- Damage evaluation of the austenitic heat-resistance steel subjected to creep by using Kikuchi pattern parameters
- Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part II
- Synthesis of aluminium (Al) and alumina (Al2O3)-based graded material by gravity casting
- Experimental investigation into machining performance of magnesium alloy AZ91D under dry, minimum quantity lubrication, and nano minimum quantity lubrication environments
- Numerical simulation of temperature distribution and residual stress in TIG welding of stainless-steel single-pass flange butt joint using finite element analysis
- Special Issue on A Deep Dive into Machining and Welding Advancements - Part I
- Electro-thermal performance evaluation of a prismatic battery pack for an electric vehicle
- Experimental analysis and optimization of machining parameters for Nitinol alloy: A Taguchi and multi-attribute decision-making approach
- Experimental and numerical analysis of temperature distributions in SA 387 pressure vessel steel during submerged arc welding
- Optimization of process parameters in plasma arc cutting of commercial-grade aluminium plate
- Multi-response optimization of friction stir welding using fuzzy-grey system
- Mechanical and micro-structural studies of pulsed and constant current TIG weldments of super duplex stainless steels and Austenitic stainless steels
- Stretch-forming characteristics of austenitic material stainless steel 304 at hot working temperatures
- Work hardening and X-ray diffraction studies on ASS 304 at high temperatures
- Study of phase equilibrium of refractory high-entropy alloys using the atomic size difference concept for turbine blade applications
- A novel intelligent tool wear monitoring system in ball end milling of Ti6Al4V alloy using artificial neural network
- A hybrid approach for the machinability analysis of Incoloy 825 using the entropy-MOORA method
- Special Issue on Recent Developments in 3D Printed Carbon Materials - Part II
- Innovations for sustainable chemical manufacturing and waste minimization through green production practices
- Topical Issue on Conference on Materials, Manufacturing Processes and Devices - Part I
- Characterization of Co–Ni–TiO2 coatings prepared by combined sol-enhanced and pulse current electrodeposition methods
- Hot deformation behaviors and microstructure characteristics of Cr–Mo–Ni–V steel with a banded structure
- Effects of normalizing and tempering temperature on the bainite microstructure and properties of low alloy fire-resistant steel bars
- Dynamic evolution of residual stress upon manufacturing Al-based diesel engine diaphragm
- Study on impact resistance of steel fiber reinforced concrete after exposure to fire
- Bonding behaviour between steel fibre and concrete matrix after experiencing elevated temperature at various loading rates
- Diffusion law of sulfate ions in coral aggregate seawater concrete in the marine environment
- Microstructure evolution and grain refinement mechanism of 316LN steel
- Investigation of the interface and physical properties of a Kovar alloy/Cu composite wire processed by multi-pass drawing
- The investigation of peritectic solidification of high nitrogen stainless steels by in-situ observation
- Microstructure and mechanical properties of submerged arc welded medium-thickness Q690qE high-strength steel plate joints
- Experimental study on the effect of the riveting process on the bending resistance of beams composed of galvanized Q235 steel
- Density functional theory study of Mg–Ho intermetallic phases
- Investigation of electrical properties and PTCR effect in double-donor doping BaTiO3 lead-free ceramics
- Special Issue on Thermal Management and Heat Transfer
- On the thermal performance of a three-dimensional cross-ternary hybrid nanofluid over a wedge using a Bayesian regularization neural network approach
- Time dependent model to analyze the magnetic refrigeration performance of gadolinium near the room temperature
- Heat transfer characteristics in a non-Newtonian (Williamson) hybrid nanofluid with Hall and convective boundary effects
- Computational role of homogeneous–heterogeneous chemical reactions and a mixed convective ternary hybrid nanofluid in a vertical porous microchannel
- Thermal conductivity evaluation of magnetized non-Newtonian nanofluid and dusty particles with thermal radiation

