Home Physical Sciences Influence of the magnetic field on the formation of protostellar disks
Article Open Access

Influence of the magnetic field on the formation of protostellar disks

  • Natalya S. Kargaltseva EMAIL logo , Sergey A. Khaibrakhmanov , Alexander E. Dudorov , Sergey N. Zamozdra and Andrey G. Zhilkin
Published/Copyright: April 25, 2022
Download Article (PDF)
Open Astronomy
From the journal Open Astronomy Volume 31 Issue 1

Abstract

We numerically model the collapse of magnetic rotating protostellar clouds with mass of 10 M ⊙ . The simulations are carried out with the help of 2D MHD code Enlil. The structure of the cloud at the isothermal stage of the collapse is investigated for the cases of weak, moderate, and strong initial magnetic field. Simulations reveal the universal hierarchical structure of collapsing protostellar clouds, consisting of the flattened envelope with the qausi-magnetostatc disk inside and the first core in its center. The size of the primary disk increases with the initial magnetic energy of the cloud. The magnetic braking efficiently transports the angular momentum from the primary disk into the envelope in the case, when the initial magnetic energy of the cloud is more than 20% of its gravitational energy. The intensity of the outflows launched from the region near the boundary of the first core increases with initial magnetic energy. The “dead” zone with small ionization fraction, x < 1 0 − 11 , forms inside the first hydrostatic core and at the base of the outflow. Ohmic dissipation and ambipolar diffusion determine conditions for further formation of the protostellar disk in this region.

Keywords: magnetic fields; magnetic-gas-dynamics; numerical simulation; star formation; interstellar medium

1 Introduction

Observations show that stars form in cold dense cores of filamentary interstellar molecular clouds. This protostellar clouds (PSCs) have typical density n = 1 0 3 – 1 0 6 cm − 3 , temperature T = 10 – 20 K , size R = 0.03 − 0.3 pc, mass M = 0.1 − 30 M ⊙ , velocity dispersion σ ≤ 3 km s − 1 , and angular velocity ω = 1 0 − 12 – 1 0 − 14 s − 1 (see, e.g., Carey et al. 1998, Bergin and Tafalla 2007, Morii et al. 2021 and also review by Dudorov and Khaibrahmanov (2017)).

The distribution of the specific angular momentum inside PSCs was studied only on large scales of 0.1 pc. The energy of rotation of PSCs is of the order of several percent of the gravitational energy (Goodman et al. 1993, Caselli et al. 2002).

Measurements of the Zeeman effect in the OH lines indicates that PSCs have a magnetic field with strength of B = 1 0 − 5 – 1 0 − 4 G. According to polarization mapping of PSCs, the magnetic field has hourglass morphology (Girart et al. 2006, Crutcher 2012, Li 2021).

It is believed that gravitationally unstable PSCs undergo gravitational collapse and evolve into class 0 young stellar objects (YSOs hereafter) observed as the IR sources and interpreted as protostars surrounded by dense flattened envelope of gas and dust (Andre et al. 1993). Bipolar outflows are the characteristic feature of class 0 YSOs (Myers et al. 1988, Andre 1995, Galametz et al. 2020).

Studies in the submillimeter range show that the envelopes of class 0 YSOs have a size of 500–12,000 au. The envelopes are flattened along the axis of rotation and/or the magnetic field direction (Wiseman et al. 2001, Maureira et al. 2020). High angular resolution studies of the central regions around protostars in recent years revealed small disks with signs of Keplerian rotation and sizes of 2–300 au (Ohashi et al. 2014, Dunham et al. 2014, Persson et al. 2016, Pineda et al. 2019, Tobin et al. 2020). These disks can be associated with protostellar accretion disks.

The geometry of the magnetic field is quasi-radial and partially quasi-toroidal inside the envelopes of class 0 YSOs (Lee et al. 2019, Hull and Zhang 2019). The angular momentum distribution changes across disk to envelope transition at radii from 1,000 to 10,000 au (Goodman et al. 1993, Ohashi et al. 1997, Caselli et al. 2002, Belloche 2013).

The transition state between the PSC and class 0 YSO is still not possible to observe. To determine the conditions for the formation of protostellar disks, it is important to perform numerical modeling of the initial stages of the collapse of PSCs and to investigate the formation and evolution of the internal structure of the PSC.

In the simulations of the collapse of magnetic rotating PSCs in the ideal MHD approximation, disks are not formed or very small geometrically thick disks are formed, which does not agree with the observations of protostellar disks (Mellon and Li 2008). This is due to the fact that the frozen-in magnetic field transports the specific angular momentum too quickly from the central part of the cloud. This so-called catastrophic magnetic braking can be weakened due to the action of magnetic ambipolar diffusion, Ohmic dissipation, and/or turbulence allowing for the formation of the protostellar disks (Black and Scott 1982, Mouschovias 1991, Hennebelle and Ciardi 2009, Tsukamoto et al. 2017, Zhao et al. 2020). However, the exact conditions for the formation of protostellar disks are not determined because of large difference between the initial conditions and numerical models of the PSC. Modern simulations are mainly concentrated on the accretion stages of the collapse of solar mass PSC (see, e.g., Hennebelle and Fromang 2008, Zhao et al. 2020). Investigation of the initial stages of collapse will make it possible to more accurately determine the conditions for the formation of protostellar disks and come closer to solution of the problem of magnetic braking catastrophe.

Previously, we numerically simulated the isothermal collapse of rotating magnetic PSCs and found that the hierarchical structure of the cloud forms at this stage (Khaibrakhmanov et al. 2021, Kargaltseva et al. 2021). In this paper, we further develop our approach and analyze the efficiency of the magnetic braking at the isothermal stage of the collapse by simulating the collapse for various initial magnetic energies of the cloud. In Section 2, we describe the problem setup and the code Enlil used for simulations. The general picture of the hierarchical structure of the collapsing PSC is outlined in Section 3.1. Dynamics of the collapse in clouds with different initial magnetic energies is investigated in Section 3.2. Section 3.3 analyzes the role of the Ohmic dissipation and magnetic ambipolar diffusion in the evolution of the magnetic flux of the cloud. Section 4 presents main conclusions and discussion of the results.

2 Problem statement and numerical code

We consider a homogeneous spherically symmetric rotating magnetic PSC with mass M 0 = 10 M ⊙ and radius R 0 = 0.1  pc. The rotation axis coincides with the initial magnetic field direction. We adopt axial symmetry approximation and use the cylindrical coordinates, ( r , 0 , z ) , where r is the radial distance from the cloud’s center and z is the height above its equatorial plane.

The initial state of the cloud is determined by the ratios of thermal, rotational, and magnetic energies of the cloud to the modulus of its gravitational energy: ε t , ε w , and ε m , respectively.

The simulations are carried out using the two-dimensional MHD code Enlil (Dudorov et al. 1999, Dudorov and Zhilkin 1999). To solve the equations of ideal MHD, the code utilizes the quasi-monotone TVD scheme of the third order of approximation in the spatial variable and the first order of approximation in time. Poison’s equation is solved with an implicit alternating direction method. The generalized Lagrange multiplier method is used to clean up the divergence of the magnetic field. An adaptive moving mesh is used with 150 × 150 cells. Ohmic dissipation and ambipolar diffusion are taken into account in the model (see Zhilkin et al. 2009), and the ionization fraction is calculated following Dudorov and Sazonov (1987). Thermal evolution of the cloud is modeled using a variable effective adiabatic index, γ eff , in the same manner as in the study by Kargaltseva et al. (2021). In the process of isothermal collapse, γ eff = 1.001 is used in the equation of state of the ideal gas. When the density reaches ρ c = 1 0 − 13 g cm − 3 , the effective adiabatic index switches to the value of 5/3. This corresponds to the moment of the formation of the first hydrostatic core (Larson 1969). As similar approach was used, for example, by Masunaga and Inutsuka (2000).

3 Results

To investigate the influence of the magnetic field on the collapse, we set the thermal and rotational parameters to ε t = 0.3 and ε w = 0.01 , and varied the magnetic parameter in simulations. Three simulation runs were performed with ε m = 0.01 (run I), 0.2 (run II) and 0.6 (run III). The first case corresponds to highly nonequilibrium cloud, ε t + ε w + ε m ≪ 1 with the weak magnetic field. The cloud with moderate magnetic field strength is considered in the second run. The third run studies the nearly equilibrium cloud, ε t + ε w + ε m ≲ 1 , with strong magnetic field. Adopted values of the magnetic parameter correspond to the following values of nondimensional mass-to-flux ratio: λ = 10.5 (run I), 2.4 (run II) and 1.4 (run III).

In the following, we use the characteristic time of the collapse of the magnetic rotating PSC t fmw = t ff ( 1 − ε m − ε w ) − 1 / 2 as a unit of time, where t ff is the free fall time (see Khaibrakhmanov et al. (2021)).

3.1 Hierarchical structure of the collapsing protostellar cloud

First, let us discuss the general picture of the isothermal collapse of the magnetic rotating PSC using run II as a reference. This run with a moderate magnetic field has been analyzed in detail in our previous paper (Kargaltseva et al. 2021).

In Figure 1, we present the structure of the collapsing PSC at the end of the dynamical collapse, t ∼ 1 t fwm , when typical picture of the collapse is established. Figure 1 shows that hierarchical structure of the cloud is formed. The hierarchy consists of an optically thin geometrically thick flattened envelope, a geometrically and optically thin quasi-magnetostatic, v z ≪ v r , primary disk inside the envelope, and optically thick first core in the center of the primary disk. The boundary of the quasi-magnetostatic primary disk is characterized by a sharp jump in the velocity profile v z ( z ) , when almost free fall of gas along the z -direction turns to magnetostatic equilibrium, v z ≈ 0 . Specifically, we determine the primary disk as a region near the equatorial plane characterized by v z < ( c s 2 + v A 2 ) 1 / 2 , where c s is the sound speed, and v A is the Alfven speed. The first core is a hydrostatic region, at the boundary of which both v r and v z abruptly decrease below the value of local sound speed c s .

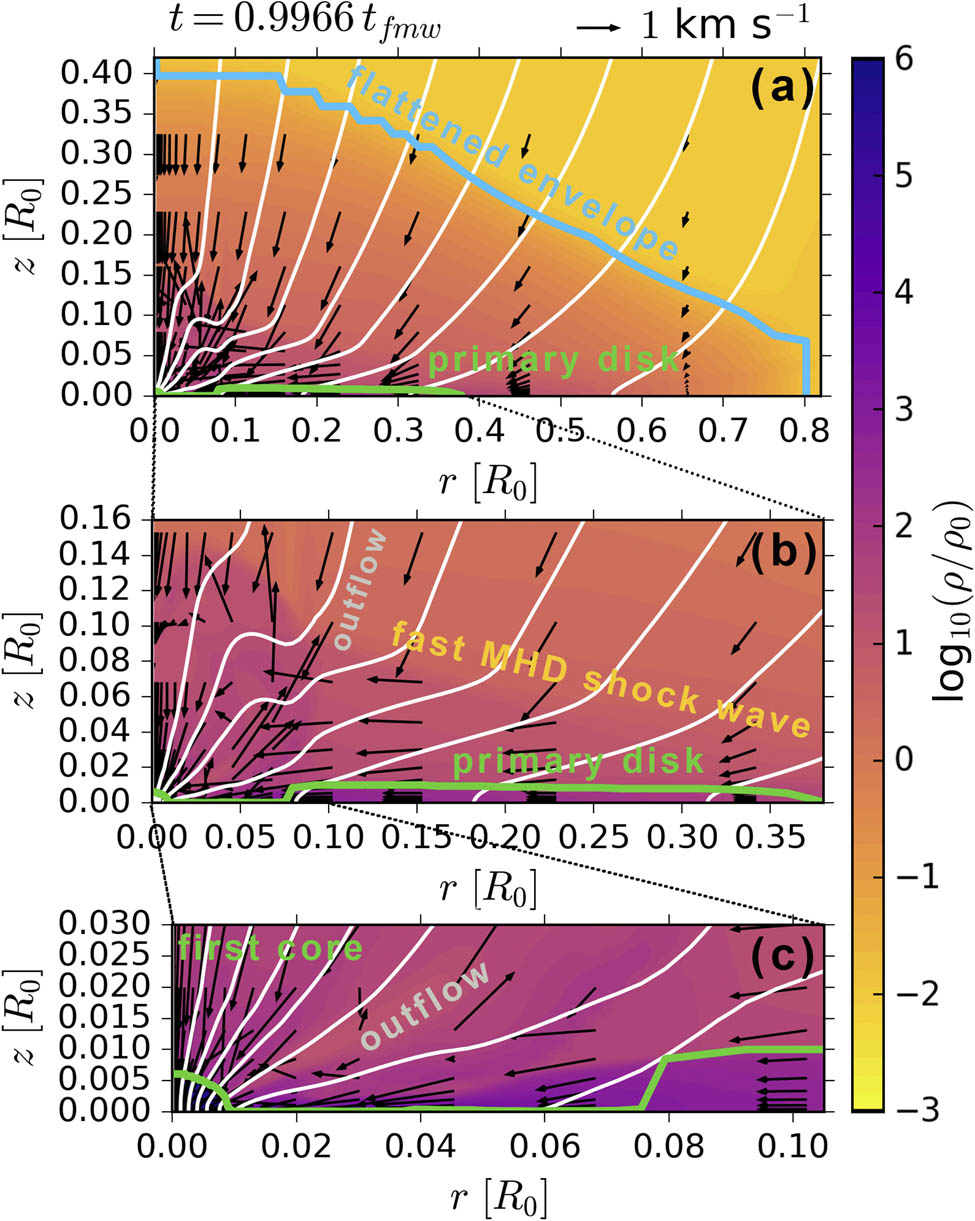
Figure 1 Distribution of density (color filling), velocity field (arrows), and poloidal magnetic field (white lines) in the simulation of the collapse of the magnetic rotating PSC of mass 10 M ⊙ 10\hspace{0.33em}{M}_{\odot } with initial radius R 0 = 0.1 {R}_{0}=0.1 pc, and nondimensional parameters ε t = 0.3 {\varepsilon }_{t}=0.3 , ε m = 0.2 {\varepsilon }_{{\rm{m}}}=0.2 , and ε w = 0.01 {\varepsilon }_{{\rm{w}}}=0.01 (run II) at t ≈ 1.0 t fmw t\approx 1.0\hspace{0.33em}{t}_{{\rm{fmw}}} . Panel (a): Region with r ≤ 0.8 R 0 r\le 0.8\hspace{0.33em}{R}_{0} and z ≤ 0.4 R 0 z\le 0.4\hspace{0.33em}{R}_{0} containing the entire cloud. Blue line corresponds to the border of the cloud. Panel (b): Region near the primary disk. Panel (c): Central part of the cloud. Green line shows the boundary of the quasi-magnetostatic primary disk and the boundary of the first hydrostatic core.
Figure 1

Distribution of density (color filling), velocity field (arrows), and poloidal magnetic field (white lines) in the simulation of the collapse of the magnetic rotating PSC of mass 10 M ⊙ with initial radius R 0 = 0.1 pc, and nondimensional parameters ε t = 0.3 , ε m = 0.2 , and ε w = 0.01 (run II) at t ≈ 1.0 t fmw . Panel (a): Region with r ≤ 0.8 R 0 and z ≤ 0.4 R 0 containing the entire cloud. Blue line corresponds to the border of the cloud. Panel (b): Region near the primary disk. Panel (c): Central part of the cloud. Green line shows the boundary of the quasi-magnetostatic primary disk and the boundary of the first hydrostatic core.

After the formation of the primary disk, a fast MHD shock wave moves from its boundary nearly upwards (see Figure 1(b)). Magnetic field lines are bent and strong toroidal magnetic field is generated behind the shock wave front.

Soon after the formation of the first core, quasi-magnetostatic equilibrium is violated near its boundary, and an outflow arises in this region, propagating along the lines of the magnetic field (see Figure 1(c)).

According to our simulations, the magnetic field geometry changes through the internal hierarchy of the cloud. The magnetic field has a quasi-radial geometry, B r ∼ B z , in the envelope. It remains quasi-uniform, ( B r , B φ ) ≪ B z , inside the primary disk. The magnetic field acquires a quasi-toroidal geometry, B φ ∼ B z , in the region between the boundary of the primary disk and the fast MHD shock wave front. As Kargaltseva et al. (2021) have shown, the specific angular momentum is accumulated near the boundary of the primary disk and then transferred to the envelope by the magnetic braking. The region of efficient magnetic braking lies between the boundary of the primary disk and fast MHD shock wave front.

The picture of the collapse discussed earlier demonstrates the leading role of the primary disks in the evolution of the collapsing PSC at the initial stages of collapse. The primary disk is the main reservoir of mass, angular momentum, and magnetic flux feeding the first core and thus determining the characteristics of the protostellar disk forming during further evolution of the system.

3.2 Influence of the magnetic field on the dynamics of the collapse

Let us analyze the effect of the magnetic field on the dynamics of the collapse of rotating magnetic PSCs, paying special attention to the primary disks.

In Figure 2, we demonstrate the structure of the PSC in runs I (left panels), II (middle panels), and III (right panels) at four different time moments after the formation of the primary disk. We plot two-dimensional distribution of the specific angular momentum to investigate the efficiency of magnetic braking in each run.

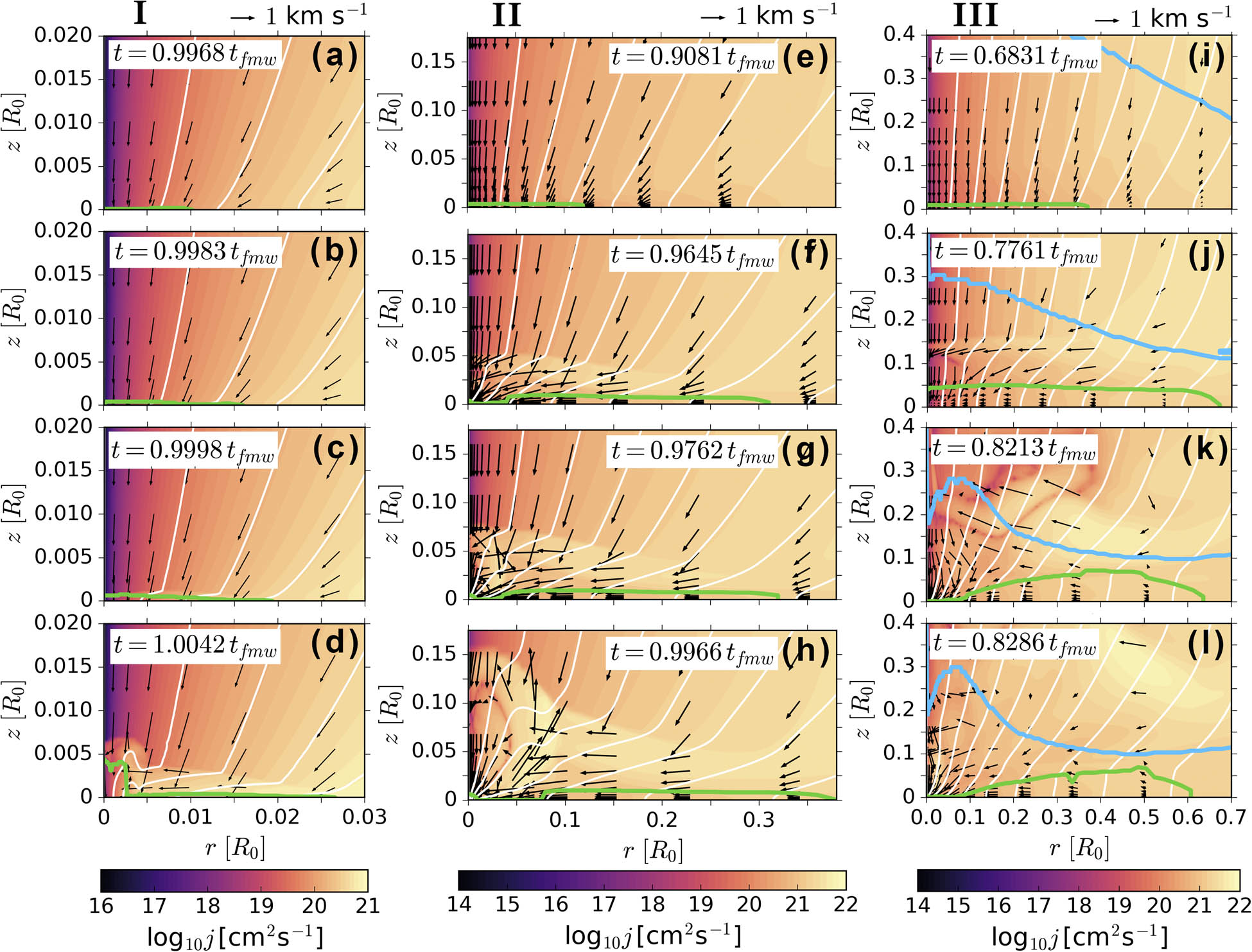
Figure 2 Distribution of the specific angular momentum (color filling), velocity field (arrows), and poloidal magnetic field (white lines) in the simulations with ε m = 0.01 {\varepsilon }_{{\rm{m}}}=0.01 (run I, left panels), ε m = 0.2 {\varepsilon }_{{\rm{m}}}=0.2 (run II, middle panels), ε m = 0.6 {\varepsilon }_{{\rm{m}}}=0.6 (run III, right panels) at different time moments after the primary disk formation (panels from top to bottom). The region near the primary disk is considered. Green line shows the border of the primary disk, and blue line is the border of the cloud.
Figure 2

Distribution of the specific angular momentum (color filling), velocity field (arrows), and poloidal magnetic field (white lines) in the simulations with ε m = 0.01 (run I, left panels), ε m = 0.2 (run II, middle panels), ε m = 0.6 (run III, right panels) at different time moments after the primary disk formation (panels from top to bottom). The region near the primary disk is considered. Green line shows the border of the primary disk, and blue line is the border of the cloud.

Figure 2 shows that the hierarchical structure of the collapsing PSC discussed in Section 3.1 forms in all considered runs. During the collapse, primary disks grow in size. For example, the radius of the primary disk in run I increases from R pd ≈ 0.01 , R 0 ≈ 200 au to ≈ 0.025 R 0 ≈ 500 au (see Figure 2(a–d)). In all cases, the angular momentum firstly accumulates near the surface of the primary disk, and then, it is transferred to the envelope due to the magnetic braking in the region behind the fast MHD shock wave front. Outflow launching from the region near the first core is also a general feature of considered cases. Typical speed of the outflow is of 2 km s − 1 .

The characteristics of primary disks, dynamics of the outflow, and efficiency of the magnetic braking change with ε m . The radius and typical half-thickness of the primary disk increase with ε m . This reflects the increasing role of the electromagnetic force in establishing the magnetostatic equilibrium inside the central part of the cloud. For example, final radius of the primary disk increases from ≈ 0.025 R 0 in run I up to ≈ 0.6 R 0 in run III (compare bottom panels in Figure 2). Therefore, the cloud with strong magnetic field evolves into a state of magnetostatic equilibrium practically as a whole.

The size of the region of efficient magnetic braking bounded by the front of the fast MHD shock wave increases with ε m . Figure 2(d) shows that the shock wave travels small distance of 2 × 1 0 − 3 R 0 along the z -direction within the typical dynamical time t ∼ 1 t fmw in run I, while the shock wave in run III travels a distance of 0.3 – 0.4 R 0 and comes out from the envelope by the time t ∼ 0.83 t fmw (see Figure 2(l)). This is explained by the fact that the speed of fast MHD shock wave increases with ε m , i.e., with initial magnetic field strength of the cloud.

The size of the outflow region by the end of the dynamical collapse also increases with the increasing role of the magnetic field, since the outflow is driven by the electromagnetic force.

To analyze the dynamics of the collapse in more detail, we plot the profiles of the radial and azimuthal velocities along the equatorial plane for runs I, II, and III in Figure 3.

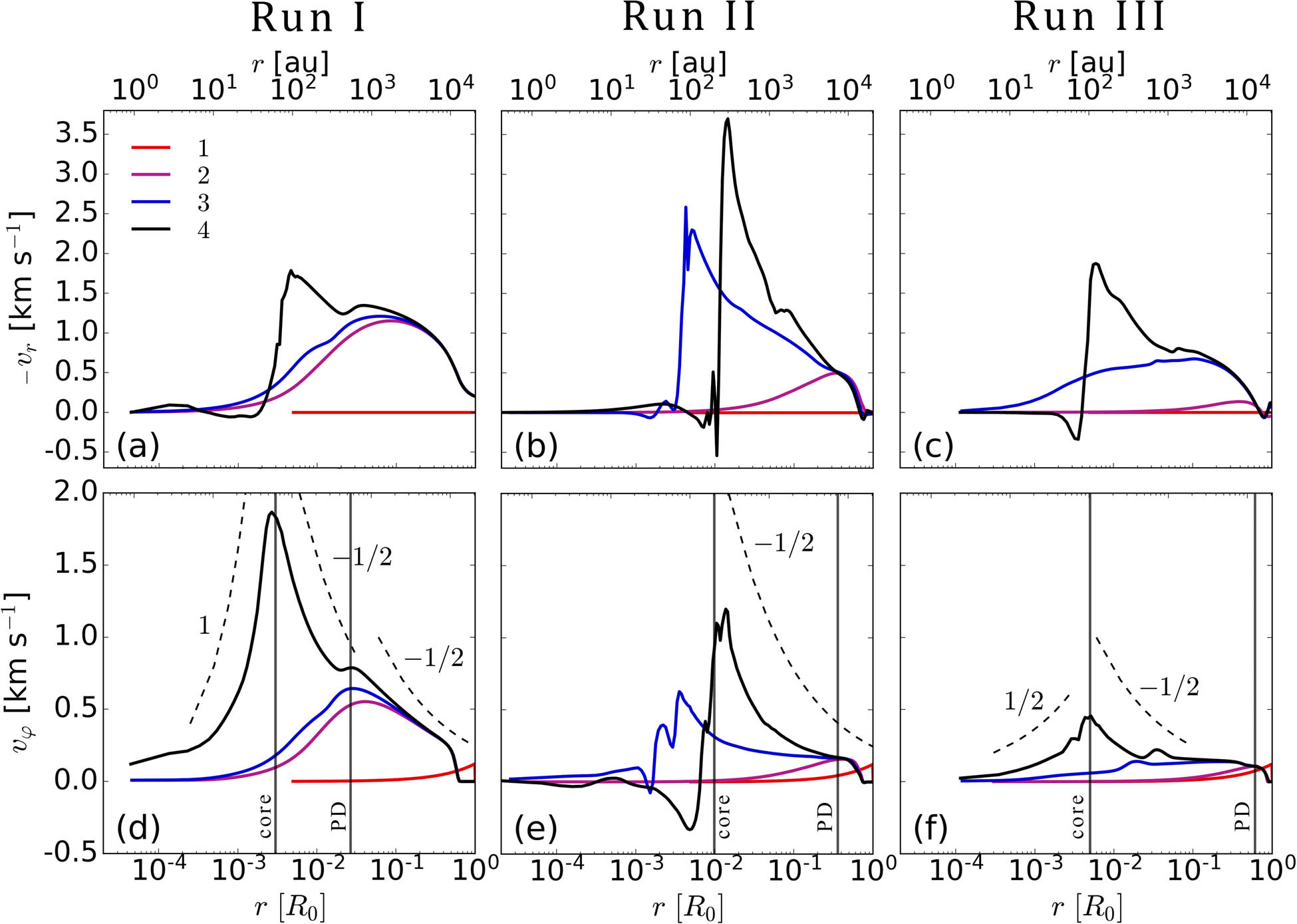
Figure 3 Profiles of radial velocity ( − v r -{v}_{{\rm{r}}} ) and azimuthal velocity v φ {v}_{\varphi } along the equatorial plane for runs with weak (run I, the first column), moderate (run II, the second column), and strong (run III, the third column) magnetic fields at different moments of time. Line 1 (red color): start of the collapse. Line 2 (pink color): the moment of primary disc formation corresponding to Figure 2(a, e, i). Line 3 (blue color): the moment of the first core formation corresponding to the Figure 2(c, f, k). Line 4 (black color): the end of the simulation corresponding to Figure 2(d, h, l). Dashed lines with numbers show characteristic slopes. Vertical lines show the boundaries of the first core and primary disk at the end of the simulation.
Figure 3

Profiles of radial velocity ( − v r ) and azimuthal velocity v φ along the equatorial plane for runs with weak (run I, the first column), moderate (run II, the second column), and strong (run III, the third column) magnetic fields at different moments of time. Line 1 (red color): start of the collapse. Line 2 (pink color): the moment of primary disc formation corresponding to Figure 2(a, e, i). Line 3 (blue color): the moment of the first core formation corresponding to the Figure 2(c, f, k). Line 4 (black color): the end of the simulation corresponding to Figure 2(d, h, l). Dashed lines with numbers show characteristic slopes. Vertical lines show the boundaries of the first core and primary disk at the end of the simulation.

At the initial moment of time (lines 1), the cloud rotates rigidly, so that the azimuthal velocity increases with distance as v φ ∝ r . The cloud is at rest in the radial direction initially, v r = 0 . Consider run I with weak magnetic field (Figure 3a and d). By the time of the formation of the primary disk, differential rotation is established in the region from disk’s boundary, r ≈ 0.02 R 0 , to the periphery of the cloud (line 2). The region of differential rotation increases further in time (line 3). The radial velocity is practically zero inside the first core, v r ≈ 0 , and the entire core rotates rigidly, v φ ∝ r , by the end of the simulation (line 4). The envelope and the primary disk rotate differentially. The azimuthal velocity profile is close to the Keplerian law v φ ∝ r − 1 / 2 in both primary disk and envelope. There is a prominent boundary between the primary disk and the envelope seen in v φ ( r ) profile at r ≈ 0.02 R 0 . Keplerian rotation profile implies that the first core becomes dominant source of the gravity in the system.

The azimuthal velocity becomes comparable to the radial one at the boundary of the first core, v r ≈ v φ ≈ 1.9 km s − 1 .

In runs with the moderate magnetic field (Figure 3(b) and (e)) and the strong magnetic field (Figure 3(d) and (f)), the velocity profiles are different from the velocity profiles in the case of weak magnetic field.

In run II , the first core almost does not rotate by the end of the simulation. The region between the first core and the primary disk, 1 0 − 3 ≲ r ≲ 7 × 1 0 − 3 R 0 , has transient reversed rotation, which is caused by the excitation of the torsional Alfvén wave in this region. As in the case of the weak magnetic field, the primary disk rotates with Keplerian speed, although the speed is smaller than in run I. On the contrary, the radial speed is larger with a maximum value of 3.5 km s − 1 near the surface of the first core, r ≈ 0.02 R 0 .

In run III, the first core rotates differentially, but not in the solid state by the end of the simulation. The inner part of the primary disk rotates with the Keplerian speed, while the outer part has almost constant azimuthal velocity. The rotation speed is minimum compared to runs I and II, which implies very efficient magnetic braking of the disk.

In both runs II and III v r > v φ , that is, the centrifugal barrier has not yet formed. Thus, as the magnetic parameter ε w increases, magnetic braking becomes more efficient.

3.3 Role of dissipative MHD effects

In this section, we analyze the influence of ambipolar diffusion and Ohmic dissipation on the magnetic field strength in the collapsing PSC. We consider run II as a reference one. To investigate the role of the dissipative MHD effects in the evolution of the cloud, we performed runs within the ideal MHD limit, as well as taking into account Ohmic dissipation, magnetic ambipolar diffusion, and both types of diffusion.

The efficiency of magnetic diffusion depends on the level of ionization. In Figure 4, we plot the vertical profiles of the ionization fraction, x , along the z -direction at r = 100 au for run II at the same times, as in panels (e, f, g, h) of Figure 2. Considered radial distance r = 100 au corresponds to the region inside the first core close to its boundary. Figure 4 shows that the ionization fraction increases with z up to a maximum value of 1 0 − 5 at the cloud periphery. This is due to the decrease in gas density and the corresponding increase in the intensity of the interstellar cosmic and X-rays ionization rate. The minimum value of x corresponds to the maximum density in the center of the cloud. Before the formation of the first core at t = 0.9081 t fmw (red line), x ∼ 1 0 − 8 in the central part of the cloud. After the formation of the first core, the degree of ionization drops rapidly down to nearly constant value x ≲ 1 0 − 11 inside the core. Therefore, the first core becomes a “dead” zone with small ionization fraction, in which ambipolar diffusion and Ohmic dissipation weaken the magnetic field. The jumps in the profiles of the degree of ionization in the region z = 1 0 − 3 – 2 × 1 0 − 2 R 0 , correspond to the region of the outflow. Our simulations show that the center of the first core is characterized by smaller ionization fraction of 1 0 − 13 .

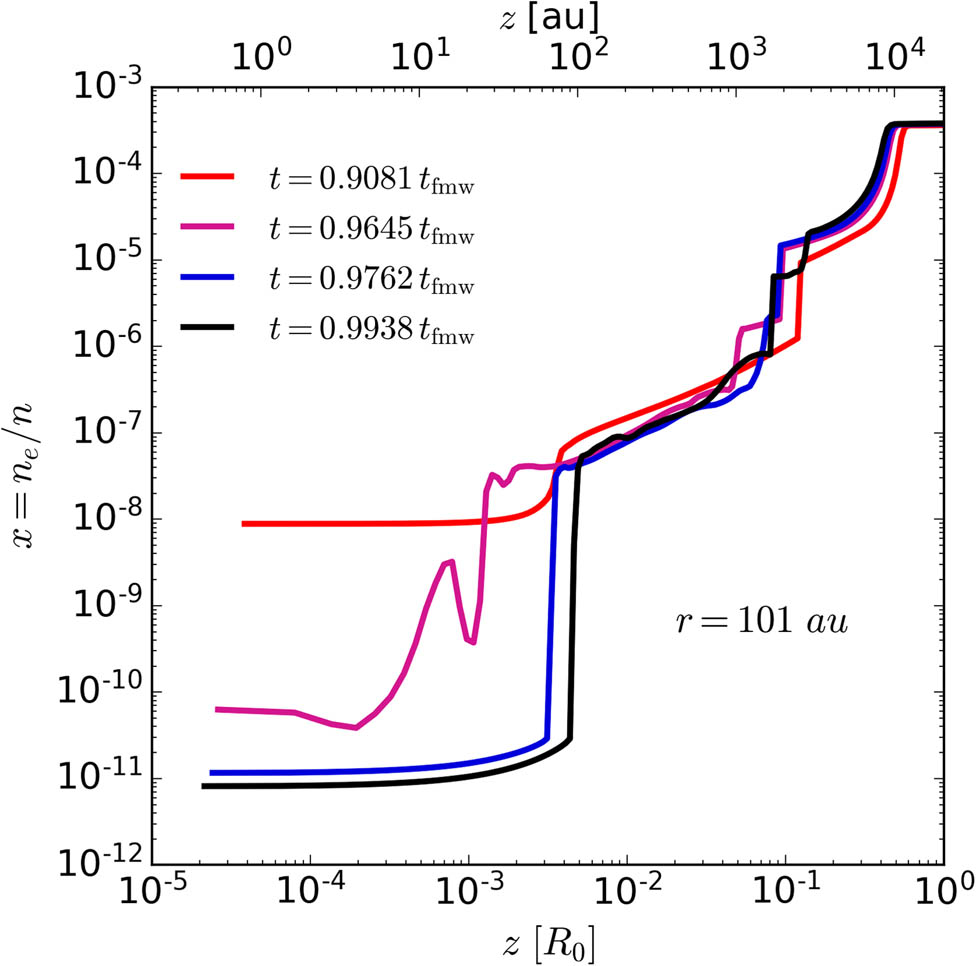
Figure 4 Profiles of the ionization fraction, x x , along the z z -direction at r = 100 r=100 au in run II at several times corresponding to Figure 2(e, f, g, h).
Figure 4

Profiles of the ionization fraction, x , along the z -direction at r = 100 au in run II at several times corresponding to Figure 2(e, f, g, h).

In Figure 5, we plot corresponding vertical profiles of the radial component of the magnetic field B r at r = 100 au inside the first core for runs with different MHD effects included. Figure 5 shows that, in all four cases, B r increases from zero value at the equatorial plane, z = 0 , up to a maximum value of 6 ⋅ 1 0 − 2  G at z ∼ 100  au and then decreases further with z . Maximum in the B r profiles corresponds to the surface of the first hydrostatic core, z ≈ 100  au.

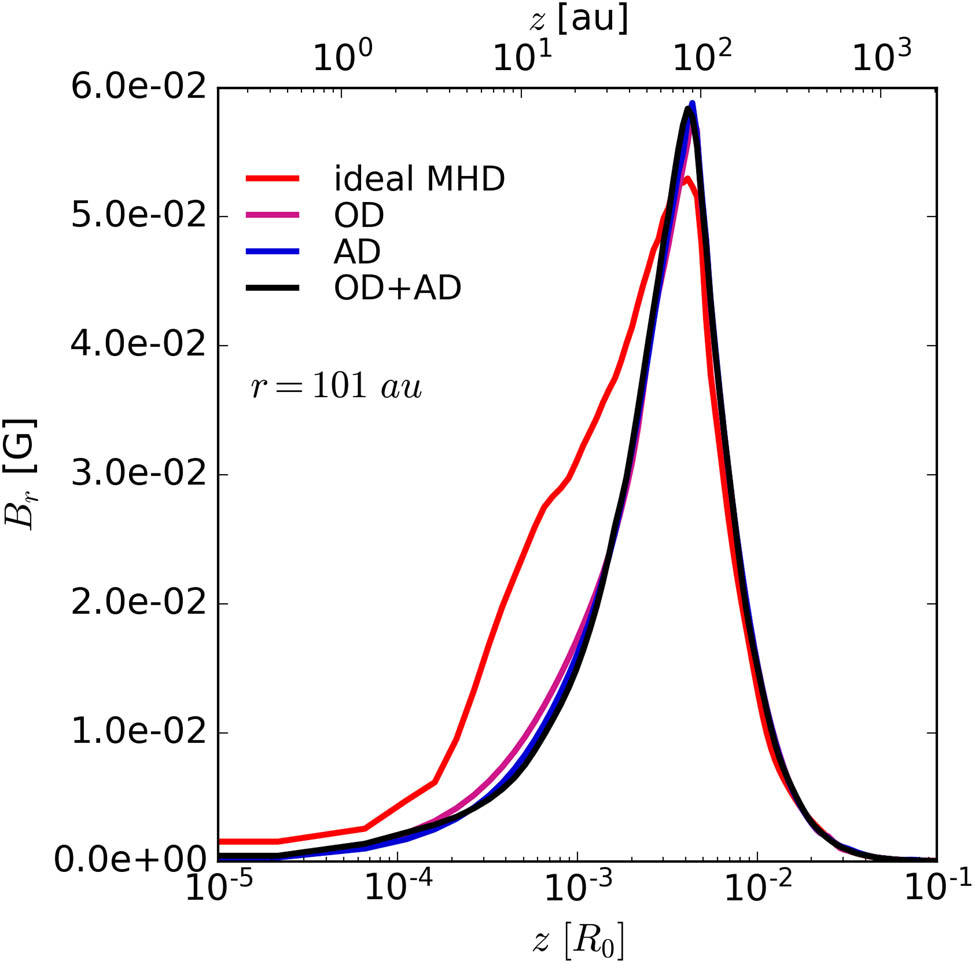
Figure 5 Vertical profiles of the radial component of the magnetic field B r {B}_{r} at 100 au in run with ε t = 0.3 {\varepsilon }_{t}=0.3 , ε m = 0.2 {\varepsilon }_{m}=0.2 , and ε w = 0.01 {\varepsilon }_{w}=0.01 . Different MHD effects are considered: ideal MHD (red line), Ohmic dissipation (pink line), magnetic ambipolar diffusion (blue line) and both types of diffusion (black line).
Figure 5

Vertical profiles of the radial component of the magnetic field B r at 100 au in run with ε t = 0.3 , ε m = 0.2 , and ε w = 0.01 . Different MHD effects are considered: ideal MHD (red line), Ohmic dissipation (pink line), magnetic ambipolar diffusion (blue line) and both types of diffusion (black line).

Inside the first core, the strength of B r is larger in the case of ideal MHD comparing to the runs with nonideal MHD effects. This demonstrates that ambipolar diffusion and Ohmic dissipation weaken the magnetic field in this “dead” zone. This difference will increase with time as the ionization fraction inside the “dead” zone will drop down during further evolution of the system. Above the first core, the profiles B r ( z ) are the same in all runs meaning that the magnetic field is frozen into gas in the envelope.

4 Conclusions and discussion

We performed numerical simulations of the collapse of rotating magnetic PSCs with mass of 10 M ⊙ up to the formation of the first hydrostatic core. The simulations were carried out for the cases with weak, moderate and strong magnetic field to analyze the influence of the magnetic field on the dynamics of the collapse. The effect of Ohmic dissipation and magnetic ambipolar diffusion on the collapse was analyzed.

The simulations have shown that the formation of the hierarchical structure of the PSC found in our previous works (Khaibrakhmanov et al. 2021, Kargaltseva et al. 2021) is the universal property of the collapsing rotating magnetic PSCs. The hierarchy consists of flattened cloud’s envelope with the magnetostatic primary disk inside. The first core forms in the central part of the primary disk. The primary disk acts as a reservoir of mass, angular momentum, and magnetic flux for the protostar and further forming protostellar disk. Therefore, the characteristics of primary disks are of great importance from the point of view of protostellar disks formation.

Properties and evolution of the structures at each level of the hierarchy strongly depends on the initial magnetic energy of the cloud. The radius of the primary disk increases with ε m from 500 au at ε m = 0.01 to 14,000 au at ε w = 0.6 . The thickness of the primary disk also increases with ε m , although the primary disk always remain geometrically thin under considered parameters. The radii of the primary disks are consistent with the observed sizes of flattened envelopes of class 0 YSO (Ohashi et al. 2014, Dunham et al. 2014, Tobin et al. 2020, Maureira et al. 2020).

The efficiency of the magnetic braking increases with the initial magnetic energy of the cloud. The region of magnetic braking lies behind the front of the fast MHD shock wave propagating out of the primary disk’s surface along the initial magnetic field direction. The magnetic field lines are bent behind the shock front and strong toroidal magnetic field is generated, which drives the magnetic braking. This region grows in time as the shock wave travels into the envelope. In the case of weak initial magnetic field, ε m = 0.01 , the fast MHD shock wave travels only small distance of 1 0 − 3 R 0 above the primary disk within the dynamical time scale of the collapse t fmw , i.e., the angular momentum practically does not transferred from the central part of the cloud to its envelope. In the case of moderate initial magnetic field, ε m = 0.2 , the fast MHD shock wave passes the distance of 0.1 R 0 and transfers part of the angular momentum from the primary disk to the envelope within the dynamical time scale. The speed of the fast MHD shock wave is so large in the case of the strong magnetic field, ε m = 0.6 , that its front comes out of the cloud’s envelope at t ∼ 0.8 t fmw , i.e., earlier than the end of the dynamical collapse ( t ∼ 1 t fmw ). A significant part of the angular momentum is transported out from the cloud in this case.

Rotational evolution of the cloud depends significantly on the ε m . In the case of the weak magnetic field, ε m = 0.01 (nondimensional mass-to-flux ratio 10.5), the following picture establishes after the first core formation. The first core rotates rigidly. A centrifugal barrier appears at its boundary with v φ ∼ v r ≈ 1.9 km s − 1 . The primary disk rotates with the Keplerian velocity, as well as the envelope does, which implies that the first core is the dominant source of gravity in the system. In the case of the moderate magnetic field, ε m = 0.2 (mass-to-flux ratio 2.4), the first core is practically nonrotating. The region between the first core and the primary disk is characterized by transient reversed rotation because of torsional Alfvén wave excitation. The primary disk rotates with Keplerian speed, but slower than in the case of the weak magnetic field. In the case of the strong magnetic field, ε m = 0.6 (mass-to-flux ratio 1.4), the first core rotates differentially, but it is not in solid state rotation. The inner part of the primary disk slowly rotates with the Keplerian speed, while its periphery rotates with almost constant azimuthal speed. This is a consequence of efficient magnetic braking of the disk’s rotation.

According to our simulations, the size of the outflow region at the end of the dynamical collapse increases with ε m . In the weak field case, the outflow region occupies only small volume near the core, while in the strong field case, the outflow front propagates practically through the whole cloud by the end of the dynamical collapse. This means that the characteristic time of the outflow development and propagation from the cloud’s center decreases with ε m . This is due to the increasing role of the electromagnetic force driving the outflow.

The “dead” zone with the low ionization fraction, x ≤ 1 0 − 13 – 1 0 − 11 , forms inside the first core and at the base of the outflow region. In this region, Ohmic dissipation and magnetic ambipolar diffusion weaken the magnetic field comparing to the ideal MHD case. This effect is most pronounced for the radial component of the magnetic field. This result is consistent with early studies of the influence of nonideal MHD effects at the initial stages of collapse (e.g., Black and Scott 1982, Dudorov and Sazonov 1987, Mouschovias 1991). Evolution of the first core and primary disk, as well as properties of the further forming protostellar disks in clouds with different initial magnetic energies, will depend on the efficiency of the Ohmic dissipation and magnetic ambipolar diffusion in this region.

In future, we plan to develop our approach and investigate the hierarchy of the collapsing rotating magnetic PSCs in application to more realistic initial configurations of the cloud. Construction of the synthetic continuum emission maps and polarization maps of collapsing PSCs on the basis of our simulations will allow to interpret observations of class 0 YSOs and analyze the conditions for the formation of protostellar disks.

† Deceased.

Acknowledgements

The authors thank anonymous referee for useful comments.

  1. Funding information: This work is financially supported by the Russian Science Foundation (project 19-72-10012).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

Andre P, Ward-Thompson D, Barsony M. 1993. Submillimeter continuum observations of rho Ophiuchi A: The candidate protostar VLA 1623 and prestellar clumps. Astrophys J. 406:122. 10.1086/172425Search in Google Scholar

Andre P. 1995. Low-mass protostars and protostellar stages. Astrophys Space Sci. 224(1–2):29. 10.1007/978-94-011-0147-9_6Search in Google Scholar

Belloche A. 2013. Observation of rotation in star forming regions: clouds, cores, disks, and jets. In: Hennebelle P, Charbonnel C, editors. Role and mechanisms of angular momentum transport during the formation and early evolution of stars, Evry Schatzman School 2012. EAS Publications Series. Vol. 62, p. 25. 10.1051/eas/1362002Search in Google Scholar

Bergin EA, Tafalla M. 2007. Cold dark clouds: the initial conditions for star formation. Annu Rev Astron Astrophys. 45(1):339–396. 10.1146/annurev.astro.45.071206.100404Search in Google Scholar

Black DC, Scott EH. 1982. A numerical study of the effects of ambipolar diffusion on the collapse of magnetic gas clouds. Astrophys J. 263:696–715. 10.1086/160541Search in Google Scholar

Carey SJ, Clark FO, Egan MP, Price SD, Shipman RF, Kuchar TA. 1998. The physical properties of the midcourse space experiment galactic infrared-dark clouds. Astrophys J. 508:721–728. 10.1086/306438Search in Google Scholar

Caselli P, Benson PJ, Myers PC, Tafalla M. 2002. Dense cores in dark clouds. XIV. N2H+ (1-0) maps of dense cloud cores. Astrophys J. 572(1):238–263. 10.1086/340195Search in Google Scholar

Crutcher RM. 2012. Magnetic fields in molecular clouds. Annu Rev Astron Astrophys. 50:29–63. 10.1007/BFb0102095Search in Google Scholar

Dudorov AE, Sazonov YuV. 1987. Hydrodynamical collapse of interstellar clouds. IV. The ionization fraction and ambipolar diffusion. Nauchnye Informatsii. 63:68. Search in Google Scholar

Dudorov AE, Zhilkin AG, Kuznetsov OA. 1999. Numerical simulations of the astrophysical MHD flows. Numer Astrophys Astrophys Space Sci Library. 240:389. 10.1007/978-94-011-4780-4_116Search in Google Scholar

Dudorov AE, Zhilkin AG. 1999. MHD-Collapse of protostellar clouds. Astron Astrophys Trans. 19:91–100. 10.1080/10556799908203040Search in Google Scholar

Dudorov AE, Khaibrahmanov SA. 2017. Hierarchical structure of the interstellar molecular clouds and star formation. Open Astron. 26(1):285–292. 10.1515/astro-2017-0428Search in Google Scholar

Dunham MM, Stutz AM, Allen LE, Evans NJ, Fischer WJ, Megeath ST, et al. 2014. The evolution of protostars: Insights from ten years of infrared surveys with Spitzer and Herschel. In: Beuther H, Klessen RS, Dullemond CP, Henning T, editors. Protostars and Planets VI. Tucson: University of Arizona Press. Vol. 914. p. 195–218. 10.2458/azu_uapress_9780816531240-ch009Search in Google Scholar

Galametz M, Maury A, Girart JM, Rao R, Zhang Q, Gaudel M, et al. 2020. An observational correlation between magnetic field, angular momentum and fragmentation in the envelopes of Class 0 protostars?. Astron Astrophys. 644(A47):19. 10.1051/0004-6361/202038854Search in Google Scholar

Girart JM, Rao R, Marrone DP. 2006. Magnetic fields in the formation of sun-like stars. Science. 313(5788):812–814. 10.1126/science.1129093Search in Google Scholar PubMed

Goodman AA, Benson PJ, Fuller GA, Myers PC. 1993. Dense cores in dark clouds. VIII. Velocity gradients. Astrophys J. 406:528–547. 10.1086/172465Search in Google Scholar

Hennebelle P, Fromang S. 2008. Magnetic processes in a collapsing dense core-I. Astron Astrophys. 477:9–24. 10.1051/0004-6361:20078309Search in Google Scholar

Hennebelle P, Ciardi A. 2009. Disk formation during collapse of magnetized protostellar cores. Astron Astrophys. 506(2):L29–32. 10.1051/0004-6361/200913008Search in Google Scholar

Hull CLH, Zhang Q. 2019. Interferometric observations of magnetic fields in forming stars. Front Astron Space Sci. 6:3. 10.3389/fspas.2019.00003Search in Google Scholar

Kargaltseva NS, Khaibrakhmanov SA, Dudorov AE, Zhilkin AG. 2021. Primary disks and their observational appearance in collapsing magnetic rotating protostellar clouds. Bull Lebedev Phys Inst. 48(9):268. 10.3103/S1068335621090050Search in Google Scholar

Khaibrakhmanov SA, Kargaltseva NS, Dudorov AE, Zhilkin AG. 2021. Simulations of the isothermal collapse of magnetic rotating protostellar clouds. Astron Rep. 65(8):693–704. 10.1134/S1063772921090043Search in Google Scholar

Larson RB. 1969. Numerical calculations of the dynamics of collapsing proto-star. Mon Not R Astron Soc. 145:271. 10.1093/mnras/145.3.271Search in Google Scholar

Li H-B. 2021. Magnetic fields in molecular clouds-observation and interpretation. Galaxies. 9(2):41. 10.3390/galaxies9020041Search in Google Scholar

Lee C-F, Kwon W, Jhan K-S, Hirano N, Hwang H-C, Lai S-P, et al. 2019. A Pseudodisk threaded with a toroidal and pinched poloidal magnetic field morphology in the HH 211 protostellar system. Astrophys J. 879(2):101. 10.3847/1538-4357/ab2458Search in Google Scholar

Maureira MJ, Arce HG, Dunham MM, Mardones D, Guzman AE, Pineda JE, et al. 2020. ALMA observations of envelopes around first hydrostatic core candidates. Mon Not R Astron Soc. 499(3):4394. 10.1093/mnras/staa2894Search in Google Scholar

Masunaga H, Inutsuka Sh-i. 2000. A radiation hydrodynamic model for protostellar collapse. II. The second collapse and the birth of a protostar. Astrophys J. 531:350–365. 10.1086/308439Search in Google Scholar

Mellon RR, Li Z-Y. 2008. Magnetic braking and protostellar disk formation: The ideal MHD limit. Astrophys J. 681:1356. 10.1086/587542Search in Google Scholar

Morii K, Sanhueza P, Nakamura F, Jackson JM, Li S, Beuther H, et al. 2021. The ALMA Survey of 70mum Dark High-mass Clumps in Early Stages (ASHES). IV. Star formation signatures in G023.477. eprint arXiv:2109.01231. 10.3847/1538-4357/ac2365Search in Google Scholar

Mouschovias TCh. 1991. Magnetic braking, ambipolar diffusion, cloud cores, and star formation: natural length scales and protostellar masses. Astrophys J. 373:169. 10.1086/170035Search in Google Scholar

Myers PC, Heyer M, Snell RL, Goldsmith PF. 1988. Dense cores in dark clouds. V. CO Outflow. Astrophys J. 324:907–919. 10.1086/165948Search in Google Scholar

Ohashi N, Hayashi M, Ho PTP, Momose M. 1997. Interferometric imaging of IRAS 04368.2557 in the L1527 molecular cloud core: a dynamically infalling envelope with rotation. Astrophys J. 475:211. 10.1086/303533Search in Google Scholar

Ohashi N, Saigo K, Aso Y, Aikawa Y, Koyamatsu S, Machida MN, et al. 2014. Formation of a Keplerian disk in the infalling envelope around L1527 IRS: transformation from infalling motions to Kepler motions. Astrophys J. 796(2):131. 10.1088/0004-637X/796/2/131Search in Google Scholar

Persson MV, Harsono D, Tobin JJ, van Dishoeck EF, Jorgensen JK, Murillo N, et al. 2016. Constraining the physical structure of the inner few 100 AU scales of deeply embedded low-mass protostars. Astron Astrophys. 590(A33):15. 10.1051/0004-6361/201527666Search in Google Scholar

Pineda JE, Zhao B, Schmiedeke A, Segura-Cox DM, Caselli P, Myers PC, et al. 2019. The specific angular momentum radial profile in dense cores: improved initial conditions for disk formation. Astrophys J. 882(2):103. 10.3847/1538-4357/ab2cd1Search in Google Scholar

Tobin JJ, Sheehan PD, Megeath ST, Diaz-Rodriguez AK, Offner SSR, Murillo NM et al. 2020. The VLA/ALMA nascent disk and multiplicity (VANDAM) survey of orion protostars. II. A statistical characterization of class 0 and class i protostellar disks. Astrophys J. 890(2):130. 10.3847/1538-4357/ab6f64Search in Google Scholar

Tsukamoto Y, Okuzumi S, Iwasaki K, Machida MN, Inutsuka S. 2017. The impact of the Hall effect during cloud core collapse: Implications for circumstellar disk evolution. Publ Astron Soc Jpn. 69(6):95. 10.1093/pasj/psx113Search in Google Scholar

Wiseman J, Wootten A, Zinnecker H, McCaughrean M. 2001. The flattened, rotating molecular gas core of protostellar jet HH 212. Astrophys J. 550(1):L87–L90. 10.1086/319474Search in Google Scholar

Zhao B, Tomida K, Hennebelle P, Tobin JJ, Maury A, Hirota T, et al. 2020. Formation and evolution of disks around young stellar objects. Space Sci Rev. 216(3):43. 10.1007/s11214-020-00664-zSearch in Google Scholar PubMed PubMed Central

Zhilkin AG, Pavlyuchenkov YaN, Zamozdra SN. 2009. Modeling of protostellar clouds and their observational properties. Astron Rep. 53(7):590–604. 10.1134/S1063772909070026Search in Google Scholar
Received: 2021-11-08
Revised: 2022-03-29
Accepted: 2022-04-01
Published Online: 2022-04-25

© 2022 Natalya S. Kargaltseva et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Deep learning application for stellar parameters determination: I-constraining the hyperparameters
  3. Explaining the cuspy dark matter halos by the Landau–Ginzburg theory
  4. The evolution of time-dependent Λ and G in multi-fluid Bianchi type-I cosmological models
  5. Observational data and orbits of the comets discovered at the Vilnius Observatory in 1980–2006 and the case of the comet 322P
  6. Special Issue: Modern Stellar Astronomy
  7. Determination of the degree of star concentration in globular clusters based on space observation data
  8. Can local inhomogeneity of the Universe explain the accelerating expansion?
  9. Processing and visualisation of a series of monochromatic images of regions of the Sun
  10. 11-year dynamics of coronal hole and sunspot areas
  11. Investigation of the mechanism of a solar flare by means of MHD simulations above the active region in real scale of time: The choice of parameters and the appearance of a flare situation
  12. Comparing results of real-scale time MHD modeling with observational data for first flare M 1.9 in AR 10365
  13. Modeling of large-scale disk perturbation eclipses of UX Ori stars with the puffed-up inner disks
  14. A numerical approach to model chemistry of complex organic molecules in a protoplanetary disk
  15. Small-scale sectorial perturbation modes against the background of a pulsating model of disk-like self-gravitating systems
  16. Hα emission from gaseous structures above galactic discs
  17. Parameterization of long-period eclipsing binaries
  18. Chemical composition and ages of four globular clusters in M31 from the analysis of their integrated-light spectra
  19. Dynamics of magnetic flux tubes in accretion disks of Herbig Ae/Be stars
  20. Checking the possibility of determining the relative orbits of stars rotating around the center body of the Galaxy
  21. Photometry and kinematics of extragalactic star-forming complexes
  22. New triple-mode high-amplitude Delta Scuti variables
  23. Bubbles and OB associations
  24. Peculiarities of radio emission from new pulsars at 111 MHz
  25. Influence of the magnetic field on the formation of protostellar disks
  26. The specifics of pulsar radio emission
  27. Wide binary stars with non-coeval components
  28. Special Issue: The Global Space Exploration Conference (GLEX) 2021
  29. ANALOG-1 ISS – The first part of an analogue mission to guide ESA’s robotic moon exploration efforts
  30. Lunar PNT system concept and simulation results
  31. Special Issue: New Progress in Astrodynamics Applications - Part I
  32. Message from the Guest Editor of the Special Issue on New Progress in Astrodynamics Applications
  33. Research on real-time reachability evaluation for reentry vehicles based on fuzzy learning
  34. Application of cloud computing key technology in aerospace TT&C
  35. Improvement of orbit prediction accuracy using extreme gradient boosting and principal component analysis
  36. End-of-discharge prediction for satellite lithium-ion battery based on evidential reasoning rule
  37. High-altitude satellites range scheduling for urgent request utilizing reinforcement learning
  38. Performance of dual one-way measurements and precise orbit determination for BDS via inter-satellite link
  39. Angular acceleration compensation guidance law for passive homing missiles
  40. Research progress on the effects of microgravity and space radiation on astronauts’ health and nursing measures
  41. A micro/nano joint satellite design of high maneuverability for space debris removal
  42. Optimization of satellite resource scheduling under regional target coverage conditions
  43. Research on fault detection and principal component analysis for spacecraft feature extraction based on kernel methods
  44. On-board BDS dynamic filtering ballistic determination and precision evaluation
  45. High-speed inter-satellite link construction technology for navigation constellation oriented to engineering practice
  46. Integrated design of ranging and DOR signal for China's deep space navigation
  47. Close-range leader–follower flight control technology for near-circular low-orbit satellites
  48. Analysis of the equilibrium points and orbits stability for the asteroid 93 Minerva
  49. Access once encountered TT&C mode based on space–air–ground integration network
  50. Cooperative capture trajectory optimization of multi-space robots using an improved multi-objective fruit fly algorithm
https://doi.org/10.1515/astro-2022-0022
Keywords for this article
magnetic fields; magnetic-gas-dynamics; numerical simulation; star formation; interstellar medium
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Deep learning application for stellar parameters determination: I-constraining the hyperparameters
  3. Explaining the cuspy dark matter halos by the Landau–Ginzburg theory
  4. The evolution of time-dependent Λ and G in multi-fluid Bianchi type-I cosmological models
  5. Observational data and orbits of the comets discovered at the Vilnius Observatory in 1980–2006 and the case of the comet 322P
  6. Special Issue: Modern Stellar Astronomy
  7. Determination of the degree of star concentration in globular clusters based on space observation data
  8. Can local inhomogeneity of the Universe explain the accelerating expansion?
  9. Processing and visualisation of a series of monochromatic images of regions of the Sun
  10. 11-year dynamics of coronal hole and sunspot areas
  11. Investigation of the mechanism of a solar flare by means of MHD simulations above the active region in real scale of time: The choice of parameters and the appearance of a flare situation
  12. Comparing results of real-scale time MHD modeling with observational data for first flare M 1.9 in AR 10365
  13. Modeling of large-scale disk perturbation eclipses of UX Ori stars with the puffed-up inner disks
  14. A numerical approach to model chemistry of complex organic molecules in a protoplanetary disk
  15. Small-scale sectorial perturbation modes against the background of a pulsating model of disk-like self-gravitating systems
  16. Hα emission from gaseous structures above galactic discs
  17. Parameterization of long-period eclipsing binaries
  18. Chemical composition and ages of four globular clusters in M31 from the analysis of their integrated-light spectra
  19. Dynamics of magnetic flux tubes in accretion disks of Herbig Ae/Be stars
  20. Checking the possibility of determining the relative orbits of stars rotating around the center body of the Galaxy
  21. Photometry and kinematics of extragalactic star-forming complexes
  22. New triple-mode high-amplitude Delta Scuti variables
  23. Bubbles and OB associations
  24. Peculiarities of radio emission from new pulsars at 111 MHz
  25. Influence of the magnetic field on the formation of protostellar disks
  26. The specifics of pulsar radio emission
  27. Wide binary stars with non-coeval components
  28. Special Issue: The Global Space Exploration Conference (GLEX) 2021
  29. ANALOG-1 ISS – The first part of an analogue mission to guide ESA’s robotic moon exploration efforts
  30. Lunar PNT system concept and simulation results
  31. Special Issue: New Progress in Astrodynamics Applications - Part I
  32. Message from the Guest Editor of the Special Issue on New Progress in Astrodynamics Applications
  33. Research on real-time reachability evaluation for reentry vehicles based on fuzzy learning
  34. Application of cloud computing key technology in aerospace TT&C
  35. Improvement of orbit prediction accuracy using extreme gradient boosting and principal component analysis
  36. End-of-discharge prediction for satellite lithium-ion battery based on evidential reasoning rule
  37. High-altitude satellites range scheduling for urgent request utilizing reinforcement learning
  38. Performance of dual one-way measurements and precise orbit determination for BDS via inter-satellite link
  39. Angular acceleration compensation guidance law for passive homing missiles
  40. Research progress on the effects of microgravity and space radiation on astronauts’ health and nursing measures
  41. A micro/nano joint satellite design of high maneuverability for space debris removal
  42. Optimization of satellite resource scheduling under regional target coverage conditions
  43. Research on fault detection and principal component analysis for spacecraft feature extraction based on kernel methods
  44. On-board BDS dynamic filtering ballistic determination and precision evaluation
  45. High-speed inter-satellite link construction technology for navigation constellation oriented to engineering practice
  46. Integrated design of ranging and DOR signal for China's deep space navigation
  47. Close-range leader–follower flight control technology for near-circular low-orbit satellites
  48. Analysis of the equilibrium points and orbits stability for the asteroid 93 Minerva
  49. Access once encountered TT&C mode based on space–air–ground integration network
  50. Cooperative capture trajectory optimization of multi-space robots using an improved multi-objective fruit fly algorithm
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 29.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/astro-2022-0022/html
Scroll to top button