Home Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method
Article Open Access

Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method

  • Sami M. Ahamed , Sabyasachi Mondal EMAIL logo and Precious Sibanda
Published/Copyright: May 20, 2017
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 15 Issue 1

Abstract

An unsteady, laminar, mixed convective stagnation point nanofluid flow through a permeable stretching flat surface using internal heat source or sink and partial slip is investigated. The effects of thermophoresis and Brownian motion parameters are revised on the traditional model of nanofluid for which nanofluid particle volume fraction is passively controlled on the boundary. Spectral relaxation method is applied here to solve the non-dimensional conservation equations. The results show the illustration of the impact of skin friction coefficient, different physical parameters, and the heat transfer rate. The nanofluid motion is enhanced with increase in the value of the internal heat sink or source. On the other hand, the rate of heat transfer on the stretching sheet and the skin friction coefficient are reduced by an increase in internal heat generation. This study further shows that the velocity slip increases with decrease in the rate of heat transfer. The outcome results are benchmarked with previously published results.

keywords: MHD nanofluid; Slip condition; Internal heat source/sink; Spectral relaxation method; Permeable stretching surface
PACS: 02.60.Cb; 02.60.Lj; 02.70.Hm

1 Introduction

Cooling and heating of liquids are significant in many engineering applications and transportation industries. In general, many common heat transfer fluids such as ethylene glycol, oil and water are not efficient heat transfer fluids for their low thermal conductivities and poor physical and chemical characteristics [1]. In contrast, fluids with added nanometer sized metals such as titanium, aluminum, gold, silver, copper and iron or their oxides and composite materials have significantly higher thermal conductivities than these base fluids. The nanoparticles are commonly made by a high-energy-pulsed process from a conductive material. For these reasons, it is prudent to combine base fluids with nanoparticles to achieve both the characteristics of a base fluid and the physical properties of the nanoparticles [2,3]. Suspending nanoparticles affects the base fluid’s homogeneity and the randomness of molecular motion leading to higher conductive rates and better convective heat transfer performances compared to base fluids [4–7]. There are however mechanisms, which include particle agglomeration, particle shape/surface area, nanoparticle size, temperature and liquid layering on the nanoparticle liquid interface that still need to be fully understood.

Nanofluids have large application in industries, like micro-electro-mechanical or microprocessors electronic systems as well as in the field of biotechnology [8]. Several authors, for instance, [9,10] conducted theoretical and experimental investigations to demonstrate that nanofluids increased the heat transfer properties of base fluid. The numerical solution of the equations that describe the combined effects of thermophoresis and Brownian motion on the nanofluid flow through a flat surface in a saturated porous medium was examined by Nield and Kuznetsov [11]. Kuznetsov and Nield [12] examined a problem on natural convection boundary layer nanofluid flow with showing the effects of thermophoresis and Brownian motion. Buongiorno [13] studied that particle diffusion and thermophoresis play an important role in the flow of a nanofluid. The classical concept of a boundary layer corresponds to a thin region next to a solid surface where viscous forces are important, Blasius [14]. Viscous forces play an essential role in processes such as glass fiber drawing, crystal growing and plastic extrusion. For the case of the Blasius problem, Sakiadis [15] focused on the concept of a boundary layer flow induced by a moving plate in a quiescent ambient fluid. Further studies in this area were made by Schlichting and Gersten [16], Bejan [17], White [18] and Mukhopadhyay [19,20].

The magnetohydrodynamic (MHD) boundary layer flow of a viscous incompressible fluid which is electrically conducted has huge applications in industry and technological sectors, like cooling of nuclear reactors, the extrusion of plastics, textile industry, purification of crude oil, polymer technology, geothermal energy extractions, metallurgy, drug delivery and biological transportation [21, 22]. The application of the magnetic field produces a Lorentz force that increase the mixing processes as an active micro mixing mechanism. The transport system of conductive biological fluids in the micro systems will be benefitted from research [23]. The simultaneous occurrence of buoyancy and magnetic field forces on fluid flow were investigated by many researchers [24–28]. In these investigations, many authors have used a no-slip boundary condition. Recently, some researchers have investigated boundary layer flow assuming a slip condition at the boundary [29–35].

Stagnation point flow, illustrating the fluid motion near a stagnation region, exists near solid bodies in that fluid flow. Chiam [36] studied fluid flow on a steady stagnation-point through an elastic surface with equal free stream and stretching velocities.

The mail focus of this study is to expand the work of Nandy and Mahapatra [37] to unsteady flow over a permeable stretching flat plate with an internal heat source or sink. For the nanoparticles we have used the boundary condition suggested recently by Kuznetsov and Nield [38] where active control of the nanoparticle volume fraction at the surface is not possible. Appropriate similarity transformations reduce the conservation equations to a set of nonlinear ordinary differential equations. These equations are solved by using a spectral relaxation method, numerically (see Motsa et al. [39]).

2 Problem formulations

Consider an unsteady, viscous, incompressible, laminar nanofluid flow past a stretching flat plate. The flow is restricted to the area y ≥ 0, y and x are the coordinate system normal to the stretching flat plate and along the stretching surface, respectively. The concentration and temperature on the surface are ϕw and Tw, respectively, and away from the surface the values are ϕ∞ and T∞, respectively. We assume that at a time t ≥ 0, the plate stretching velocity is uw = bx. The free stream velocity is u∞ = ax. Here, b is constant with b > 0 corresponding to a stretching plate and b < 0 to a shrinking plate. The fluid flow is subjected to a uniform magnetic field of strength B0 which is applied in a normal direction to the plane y = 0 and to the heat source/sink. The fluid is electrically conducting with constant properties, except for the density in the buoyancy term in the momentum equation. With these assumptions, the Oberbeck-Boussinesq and the boundary layer approximations, the unsteady momentum, energy and concentration equations can be described as (see Nandy and Mahapatra [37]);

∂u∂x+∂v∂y=0,(1)
ρf∂u∂t+u∂u∂x+v∂u∂y−u∞du∞dx=μf∂2u∂y2+σB02 (u∞−u)+(1−ϕ∞)ρf∞β(T−T∞)g−(ρp−ρf∞)(ϕ−ϕ∞)g,(2)
∂T∂t+u∂T∂x+v∂T∂y=αf∂2T∂y2+1(ρcp)fq‴+τDB∂ϕ∂y∂T∂y+DTT∞∂T∂y2,(3)
∂ϕ∂t+u∂ϕ∂x+v∂ϕ∂y=DB∂2ϕ∂y2+DTT∞∂2T∂y2,(4)

where t, u and v represent the time, the fluid velocity components along the x and y axis, respectively, νf is the fluid kinematic viscosity, σ is the fluid electrical conductivity, ρf∞ is the density far from the plate surface, g is the acceleration due to gravity, ρf is the fluid density, T is the fluid temperature, β is the coefficient of thermal expansion, ρp is the density of the particles, (ρcp)f is fluid heat capacity, ϕ is nanoparticle volume fraction, αf is thermal diffusivity, q‴ is the rate of internal heat sink (< 0) or heat source (>0) coefficient, The ratio of the effective heat capacity of nanoparticle material with the heat capacity of the fluid is τ, DT denotes the thermophoresis diffusion coefficient and DB is the Brownian diffusion coefficient.

The boundary conditions are (see Kuznetsov and Nield [12], Nandy and Mahapatra [37] and Kuznetsov and Nield [38])

v=Vw,u=uw+L∂u∂y,aty=0,t≥0,T=Tw,DB∂ϕ∂y+DTT∞∂T∂y=0aty=0,t≥0,u→u∞,T→T∞,ϕ→ϕ∞asy→∞,t≥0,(5)

with the initial conditions

u→0,T→T∞,ϕ→ϕ∞att<0,

where L is a proportionality constant. Vw denotes the surface mass flux. Negative values of Vw imply fluid suction and positive values of Vw imply injection. Also, Vw = 0 corresponds to an impermeable plate.

q‴ is defined according as follows, (see [40–42])

q‴=k uwxνf[A∗(Tw−T∞)e−η+B∗(T−T∞)],(6)

where B* and A* are temperature-dependent internal heat source/sink and coefficients of space-dependent, respectively and η is a dimensionless variable defined in Eq. (7). The first term in the Eq. (6) represents the dependence of the internal heat sink or source on the space coordinates while the second term represents its dependence on the temperature. Now, for the case when the case A* < 0 and B* < 0, indicates to internal heat sink while both A* > 0 and B* > 0, indicates to internal heat source.

We introduce non-dimensional variables given by

η=bνfξy,ξ=1−e−τ^,ψ=b νfξxf(η,ξ),θ(η,ξ)=T−T∞Tw−T∞,τ^=bt,Φ(η,ξ)=ϕ−ϕ∞ϕ∞,(7)

where θ(η,ξ) and Φ(η,ξ) are the non-dimensional temperature and concentration, respectively and the stream function ψ is defined as

u=∂ψ∂yand v=−∂ψ∂x.

Substituting (7) into Eqs. (1) - (4) gives

f‴+12(1−ξ)ηf″+ξff″−f′2+Mε−f′+ε2+λ(θ−NrΦ)=ξ(1−ξ)∂f′∂ξ,(8)
θ″+Pr12(1−ξ)ηθ′+ξfθ′+NbΦ′θ′+Ntθ′2+ξA∗e−η+B∗θ=Prξ(1−ξ)∂θ∂ξ,(9)
Φ″+Le12(1−ξ)ηΦ′+ξfΦ′+NtNbθ″=Leξ(1−ξ)∂Φ∂ξ,(10)

with boundary conditions

f(0,ξ)=S,f′(0,ξ)=1+γf″(0,ξ),θ(0,ξ)=1,Φ′(0,ξ)+NtNbθ′(0,ξ)=0,f′(∞,ξ)→ε,θ(∞,ξ)→0,Φ(∞,ξ)→0,(11)

where the differentiation with respect to η is denoted as prime, S is the dimensionless suction/blowing parameter, γ is the dimensionless slip factor, and the stretching parameter is ε where

S=−Vwbνfξ,γ=Lbνfξandε=ab.

In Eqs. (8)-(11) the parameters are the magnetic parameter M, the buoyancy parameter λ, Grx is the local Grashof number, Pr is the Prandtl number, Rex is the local Reynolds number, Nt is the thermophoresis parameter, Nr is the buoyancy ratio parameter, Nb is the Brownian motion parameter, and Le is the Lewis number. These parameters are defined as:

M=σB02ρfb,λ=GrxRex2,Rex=xuwνf,Nb=τDBϕ∞νf,Grx=(1−ϕ∞)ρf∞ρfgβ(Tw−T∞)x3νf2,Nr=(ρp−ρf∞)(1−ϕ∞)ρf∞ϕ∞β(Tw−T∞),Pr=νfαf,Nt=τDT(Tw−T∞)T∞νf,Le=νfDB.(12)

We note that in the case of assisting flow λ > 0, and for opposing flow λ < 0, λ = 0 corresponds to free convection. The skin friction coefficient Cf and the local Nusselt number Nux are defined as

Cf=τwρfuw2,Nux=xqwkfTw−T∞,(13)

where τw is the shear stress along the stretching surface, qw is the wall heat flux, respectively defined as

τw=−μf∂u∂yy=0,qw=−kf∂T∂yy=0.(14)

Hence using Eq.(14) we get

ξRexCf=−f″(0,ξ),ξRexNux=−θ′(0,ξ).(15)

With the revised boundary condition, the Sherwood number which represents the dimensionless mass flux is identically zero (see Kuznetsov and Nield [12], Kuznetsov and Nield [38]).

3 Method of solution

The spectral relaxation method (see [39]) was used to solve the system of non-similar equations (8)–(10) with the boundary conditions (11). In the SRM framework, we obtain the iterative scheme

fr+1′=ur+1(16)
ur+1″+a1,rur+1′+a2,rur+1+a3,r=a4,r∂ur+1∂ξ,(17)
θr+1″+b1,rθr+1′+b2,rθr+1+b3,r=b4,r∂θr+1∂ξ,(18)
Φr+1″+c1,rΦr+1′+c2,r=c3,r∂Φr+1∂ξ,(19)

with boundary conditions

fr+1(0,ξ)=S,ur+1(0,ξ)=1+γf″(0,ξ),θr+1(0,ξ)=1,NbΦr+1′(0,ξ)+Ntθr+1′(0,ξ)=0,ur+1(∞,ξ)→ε,θr+1(∞,ξ)→0,Φr+1(∞,ξ)→0,(20)

where

a1,r=12(1−ξ)η+ξfr,a2,r=−ξM,a3,r=ξε2+Mε−ur2+λ(θr−NrΦr),a4,r=ξ(1−ξ)(21)
b1,r=Pr12(1−ξ)η+ξfr+1+NbΦr′,b2,r=ξB∗b3,r=ξA∗e−η+PrNtθr′2,b4,r=Prξ(1−ξ)(22)
c1,r=Le12(1−ξ)η+ξfr+1,c2,r=NtNbθr+1″,c3,r=Leξ(1−ξ).(23)

In Equations (16)–(23) the indices r and r + 1 denote the previous and current iteration levels, respectively. Starting from initial approximations denoted by f0, u0, θ0, and Φ0, equations (9)–(11) are solved iteratively for fr + 1(η,ξ), ur + 1(η,ξ), θr + 1(η,ξ), and Φr + 1(η,ξ) (r = 0,1,2,…). Equations (8)–(10) were discretized using the Chebyshev spectral collocation method in the η direction while the discretization in the ξ direction uses the implicit finite difference method. This leads to a system of linear equations of the form

A1fr+1n+1=urn,(24)
A2ur+1n+1=B2ur+1n+K2,(25)
A3θr+1n+1=B3θr+1n+K3,(26)
A4Φr+1n+1=B4Φr+1n+K4,(27)

where

A1=D,(28)
A2=12D2+[a1,rn+12]dD+a2,rn+12I−a4,rn+12ΔξI,B2=−12D2+[a1,rn+12]dD+a2,rn+12I−a4,rn+12ΔξI,K2=−a3,rn+12,(29)
A3=12D2+[b1,rn+12]dD+b2,rn+12I−b4,rn+12ΔξI,B3=−12D2+[b1,rn+12]dD+b2,rn+12I−b4,rn+12ΔξI,K3=−b3,rn+12,(30)
A4=12D2+[c1,rn+12]dD−c3,rn+12ΔξI,B4=−12D2+[c1,rn+12]dD−c3,rn+12ΔξI,K4=−c2,rn+12.(31)

Here I is an (N + 1) × (N + 1) identity matrix, and [ . ]d are diagonal matrices of order (N + 1) × (N + 1).

In applying the SRM a computational domain of extent L = 20 was chosen in the η-direction. Through numerical experimentation, this value was found to give accurate results for all the selected physical parameters. Increasing the value of η do not change the results to a significant extent. The number of collocation points is used in the spectral method discretization is Nx = 100 in all cases. The calculations are carried until some desired, tolerance level ε is attained. The tolerance level was defined to be the maximum infinity norm of the difference between the values of the calculated quantities, that is

max∥fr+1n+1−frn+1∥∞,∥θr+1n+1−θrn+1∥∞,∥Φr+1n+1−Φrn+1∥∞<ϵ.

To ensure the accuracy of the results, a sufficiently small step size Δξ was used. The step size was chosen to be small enough such that further reduction in step size did not change the results of the flow properties.

4 Results and discussion

The transformed system of coupled nonlinear ordinary differential equations (8)-(10) including boundary conditions (11) are solved numerically using the spectral relaxation method. The numerical results are presented here to show the velocity, concentration and temperature profiles, the rate of heat transfer and the skin friction coefficient for different physical parameter values. These results are presented both graphically and in tabular form. In the numerical simulations the default parameter values used are, unless otherwise specified; Pr = 6.8, ε = 0.5, λ = 0.5, M = 0.1, Nr = 0.5, A* = 2.0, Nb = 0.5, B* = 1.0, Nt = 0.5, S = 0.1, Le = 10, γ = 0.1 and ξ = 0.5.

To verify the accuracy of our numerical scheme, a comparison of the computed skin friction coefficient is made with earlier results of Anwar et al. [43] in Table 1. Here we observe an excellent agreement validating the accuracy of the current numerical results. The residual error in the numerical simulations against the number of iterations for different values of γ, ε, S and M is shown in Figure 1. These results again confirm that the numerical method used in this study converges.

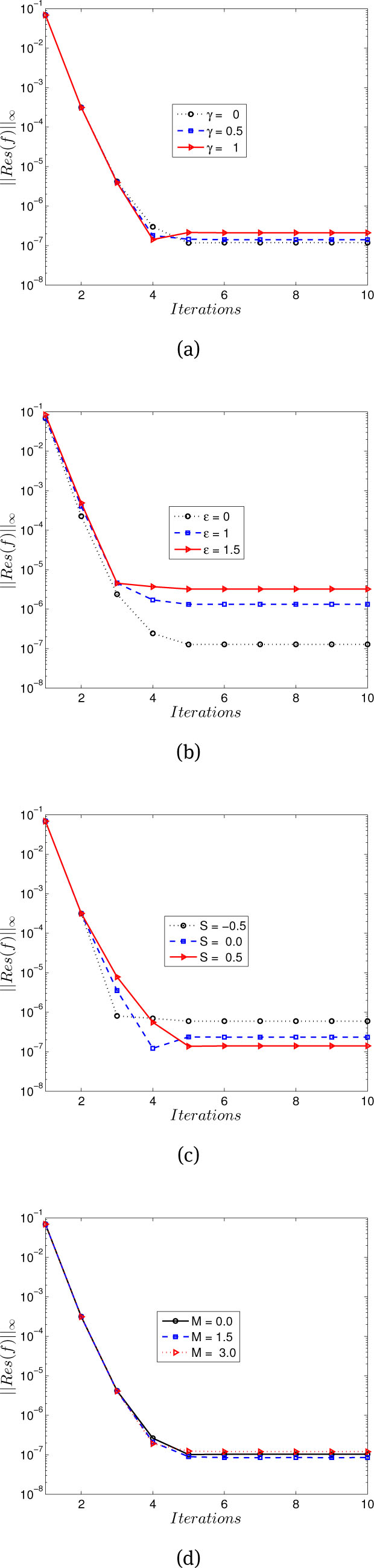
Figure 1 Residual error for different values of (a) dimensionless slip,(b) stretching or shrinking, (c) suction or injection, (d) magnetic field parameters on velocity profile
Figure 1

Residual error for different values of (a) dimensionless slip,(b) stretching or shrinking, (c) suction or injection, (d) magnetic field parameters on velocity profile

Table 1

Comparison of the reduced skin friction coefficient −f″(0,1) when λ = Nr = γ = 0

Anwar et al. [43]Present Results
MεS−f″(0,1)−f″(0,1)
0.10.10.11.05681.056803
2.51.76601.765967
0.10.60.10.59210.592079
1.1−0.1728−0.172795
1.6–−1.165587
2.51.1−0.2328−0.232839
0.10.1−0.50.80500.804972
1.1−0.5–−0.141738
0.10.51.26381.263785
1.10.5−0.1963−0.196310

Figure 2(a) displays the variation of f′ with respect to η for several values of γ when ε < 1, ε = 1 and ε > 1. Here we note that f′ increases with γ when ε > 1 while the opposite is true when ε < 1. An increase in the slip parameter has the effect of reducing the velocity at the wall. The velocity decreases asymptotically to zero at the edge of the boundary layer. The boundary layer thickness decreases as γ increases. We note that when ε = 1, increasing γ gives no further changes in the velocity profiles because at this stage the external stream velocity becomes equal to the stretching velocity. This causes a frictionless Hiemenz flow [44].

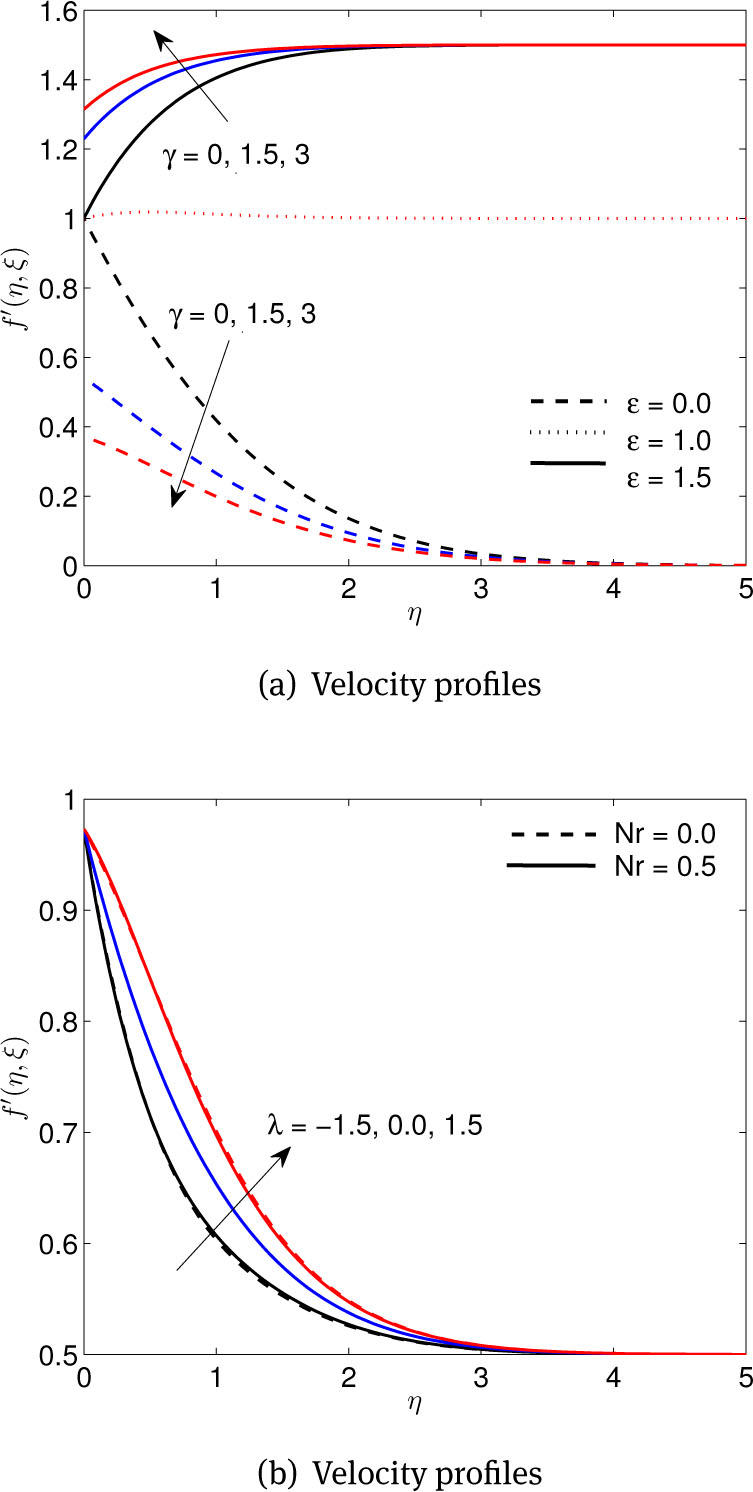
Figure 2 (a) Effects of dimensionless slip factor γ and stretching parameter ε,(b) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, on velocity profiles
Figure 2

(a) Effects of dimensionless slip factor γ and stretching parameter ε,(b) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, on velocity profiles

Figure 2(b) explores the effect of λ and Nr on the velocity profiles. It is seen that the velocity increases as the buoyancy force parameter increases. This is due to the fact that the assisting flow (λ > 0) induces a favorable pressure gradient which enhances the fluid flow in the boundary layer and as a result the momentum boundary layer increases whereas the reverse occurs for the opposing flow when λ < 0.

Figure 3 shows the effects of S and M on f′ with respect to η. Here we note that f′(η, ξ) decreases with increasing values of S and M. This behaviour is due to the fact that M increases the resistive forces on the flat plate which in turn reduces the fluid velocity and hence the motion of the fluid is slowed down. It is known that the wall suction (S > 0) has the tendency to decrease the momentum boundary layer thickness which is the cause of reduction in the velocity. But the the opposite behaviour can be seen for fluid injection (S < 0).

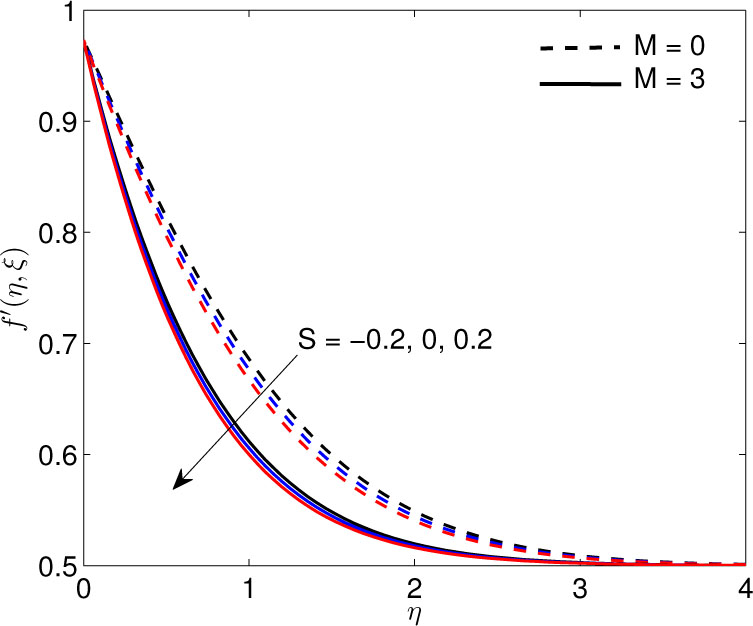
Figure 3 Effects of dimensionless suction/injection S and magnetic M parameters on velocity profiles
Figure 3

Effects of dimensionless suction/injection S and magnetic M parameters on velocity profiles

The internal heat source or sink in the boundary layer has an influence on the temperature fields as illustrated in Figure 4(a). It is clear that increasing A* and B* increases the temperature distribution within the fluid and the thermal boundary layer thickness increases. Figure 4(b) shows the variation of the temperature profiles for various values of the slip and stretching parameters. The temperature profiles increase with increasing γ when ε < 1 but the opposite trend is observed when ε > 1 as the thermal boundary layer thickness decreases.

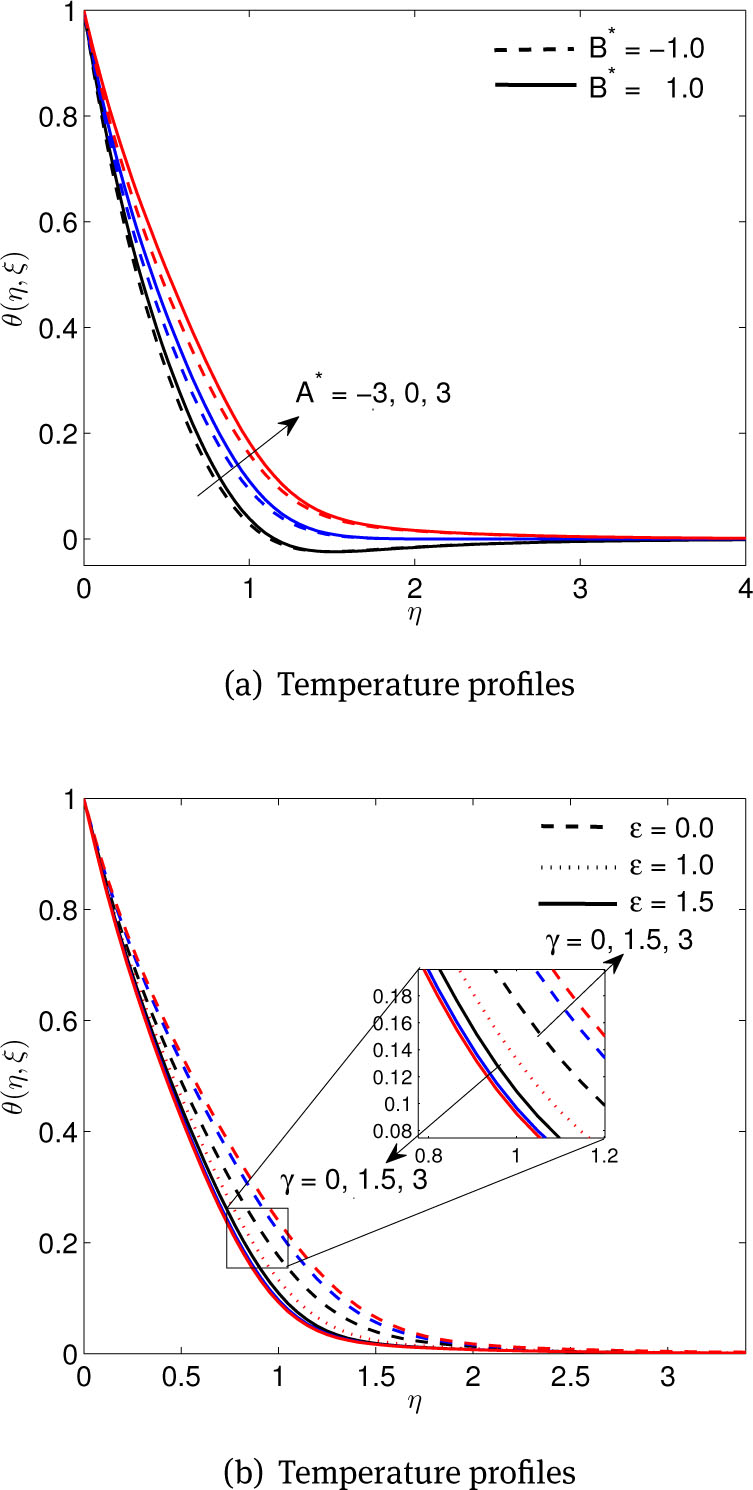
Figure 4 (a) Effects of space-dependant A* and temperature-dependent B* parameters, (b) Effects of dimensionless slip factor γ and stretching parameter ε, on temperature profiles
Figure 4

(a) Effects of space-dependant A* and temperature-dependent B* parameters, (b) Effects of dimensionless slip factor γ and stretching parameter ε, on temperature profiles

Figure 5(a) depicts the effect of λ and Nr on the temperature profiles. We note that with the increasing value of buoyancy force parameter decreases the nanofluid temperature. Moreover, positive λ values induce a favorable pressure gradient that enhances the nanofluid temperature in the boundary layer when Nr increases. Consequently, the thermal boundary layer increases while the opposite is observed for negative λ values. Figure 5(b) demonstrates the influence of Le on the temperature distribution within the boundary layer in the presence of magnetic influence, buoyancy force, heat sink/source, thermophoresis/Brownian motion. It is observed that the temperature profiles including the thickness of the temperature boundary layer increases with increases in the values of Le.

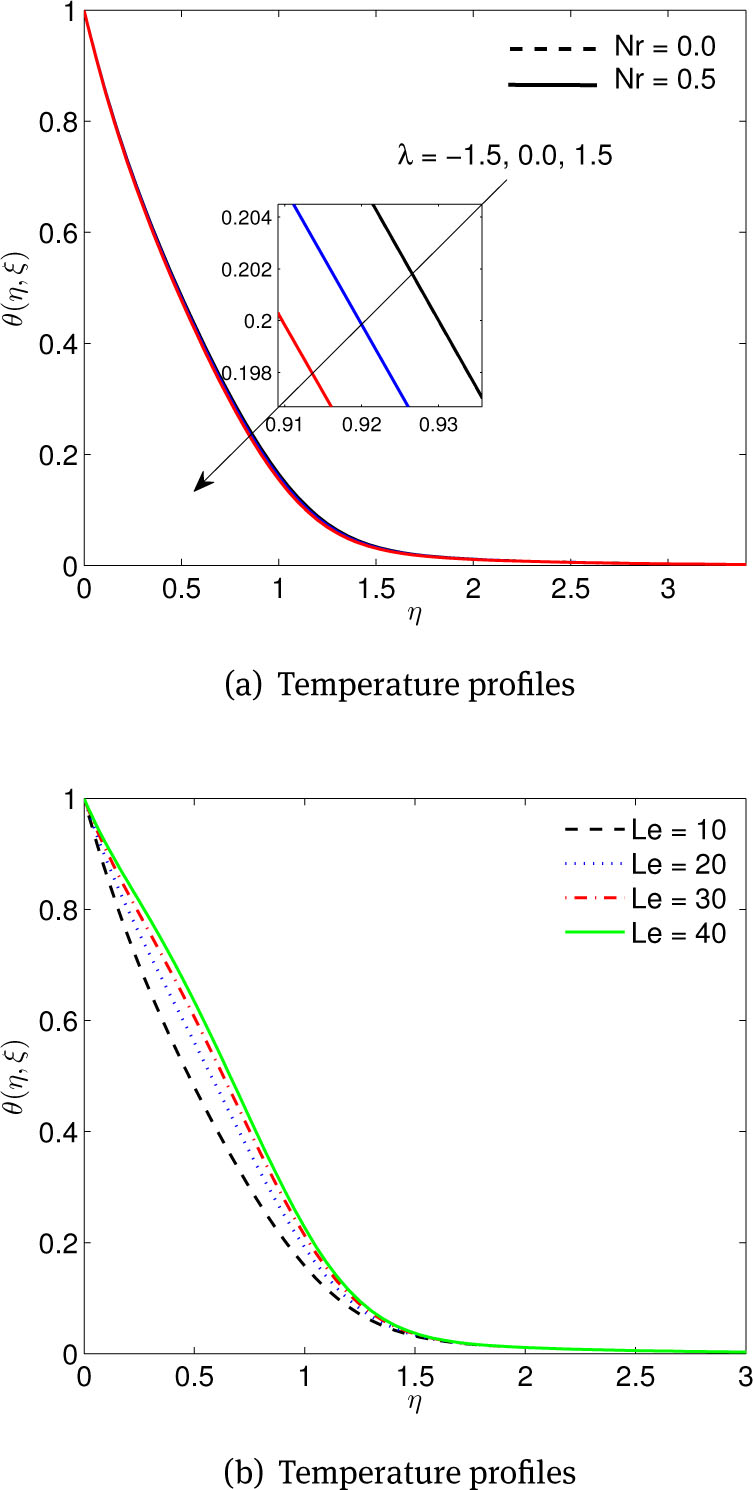
Figure 5 (a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters,(b) Effects of Lewis number Le, on temperature profiles
Figure 5

(a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters,(b) Effects of Lewis number Le, on temperature profiles

Figure 6(a) suggests that, in so far as the boundary layer temperature is concerned, thermophoresis plays the same role as the fluid Brownian motion. Thus, the fluid temperature increases with both Nt and Nb in the boundary layer region. The physical reason for this behaviour is that increased random motion of the nanoparticles increases the fluid temperature which enhances the thickness of the thermal boundary layer profiles. Figure 6(b) depicts the response of the temperature profiles to changing suction and magnetic field parameter values. Moreover, as would be expected, we note that the fluid temperature decreases with increase in suction but is higher in the case of injection.

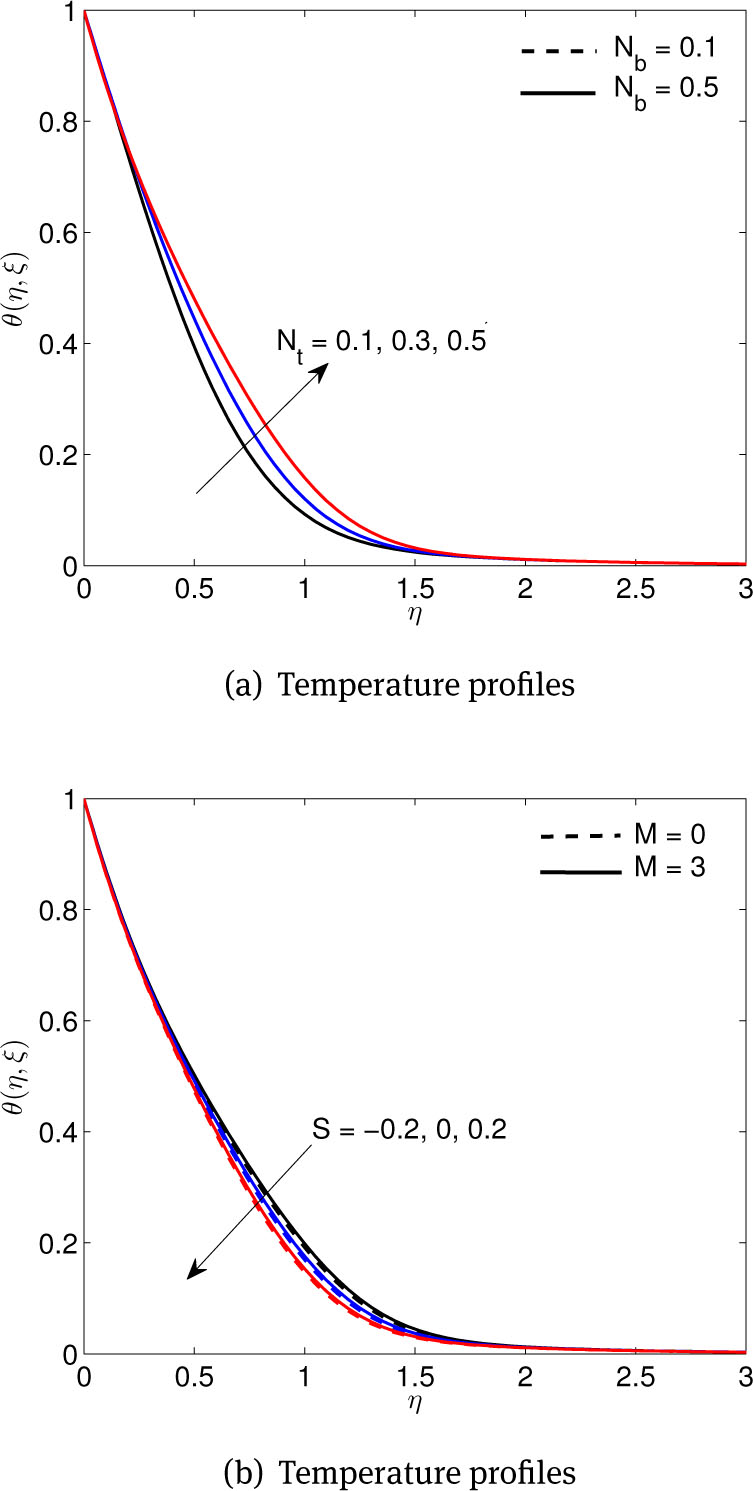
Figure 6 (a) Effects of thermophoresis Nt and Brownian motion Nb parameters, (b) Effects of dimensionless suction/blowing S and magnetic M parameters, on temperature profiles
Figure 6

(a) Effects of thermophoresis Nt and Brownian motion Nb parameters, (b) Effects of dimensionless suction/blowing S and magnetic M parameters, on temperature profiles

The traditional model is revised such that the nanofluid particle volume fraction on the boundary is passively controlled. The effect of this change in boundary conditions can be seen in Figures 7 to 9 for different parameters. The impact of heat sink/source parameters B* and A* on the concentration profiles is presented in Figure 7(a). It can be seen that, away from the boundary, the concentration profiles increase with an increase in the values of A* and B*. The effect of γ and ε on nanoparticle concentration is shown in Figure 7(b). An increase in the value of partial slip parameter value leads to an increase in the nanoparticle concentration when ε < 1 while the opposite trend is observed for ε > 1. In addition, the concentration increases and attains its highest value in the vicinity of the stretching plate near η = 0.9 and then decreases to the zero. Figure 8(a) displays the effect of λ and Nr on the nanoparticle concentration profile distributions. The nanoparticle concentration decreases asymptotically with increasing values of λ. Furthermore, in the case of opposing flow, the nanoparticle concentration decreases with increasing Nr. Figure 8(b) shows the nanoparticle concentration profiles for several values of Le. It is seen that the nanoparticle volume fraction decreases with increases in Le and this manifested through the reduction in the thickness of the concentration boundary layer. Additionally, the nanoparticle concentration profiles decrease asymptotically to zero at the edge of the boundary layer.

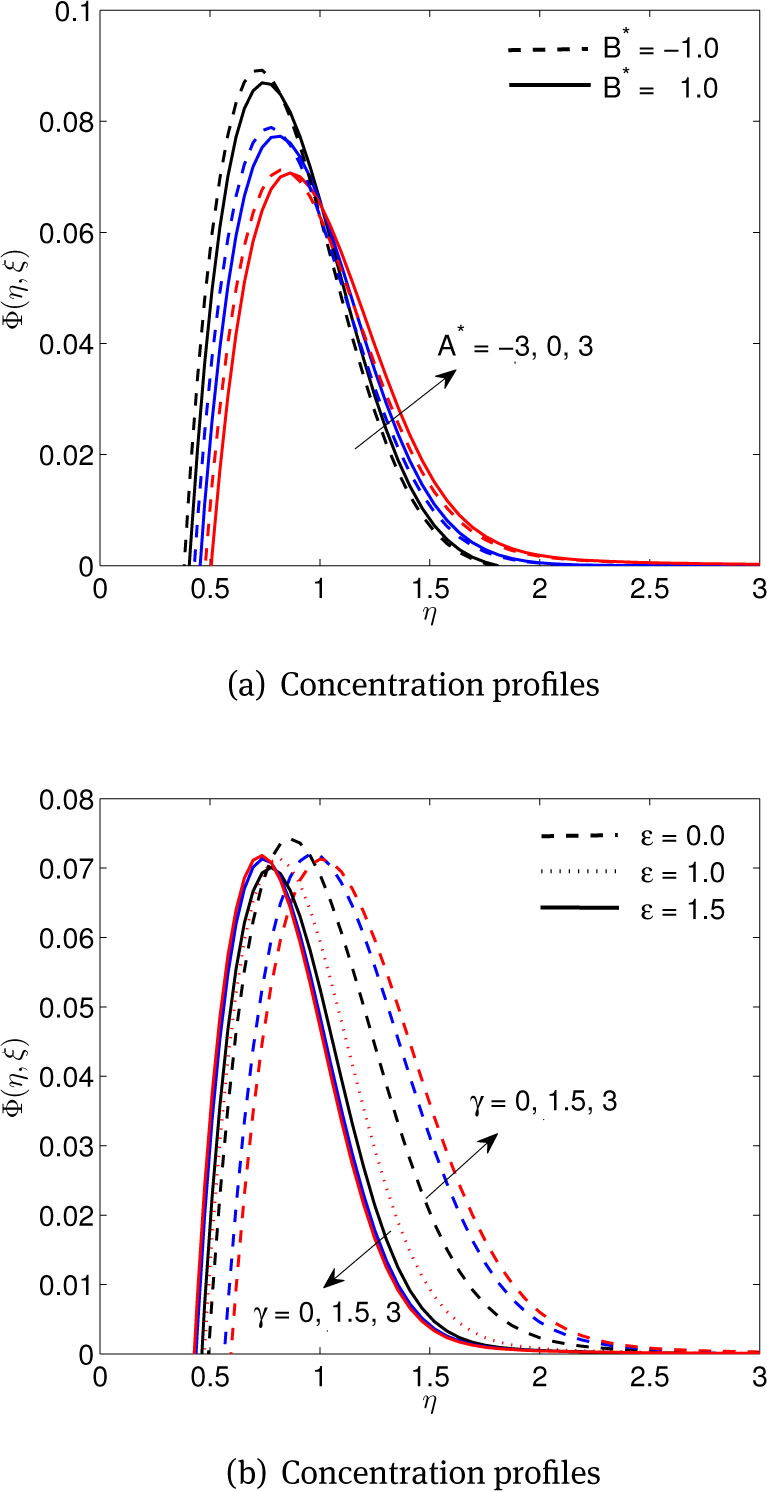
Figure 7 (a) Effects of temperature-dependent B* and space-dependent A* parameters, (b) Effects of dimensionless slip γ and stretching ε parameters, on concentration profiles
Figure 7

(a) Effects of temperature-dependent B* and space-dependent A* parameters, (b) Effects of dimensionless slip γ and stretching ε parameters, on concentration profiles

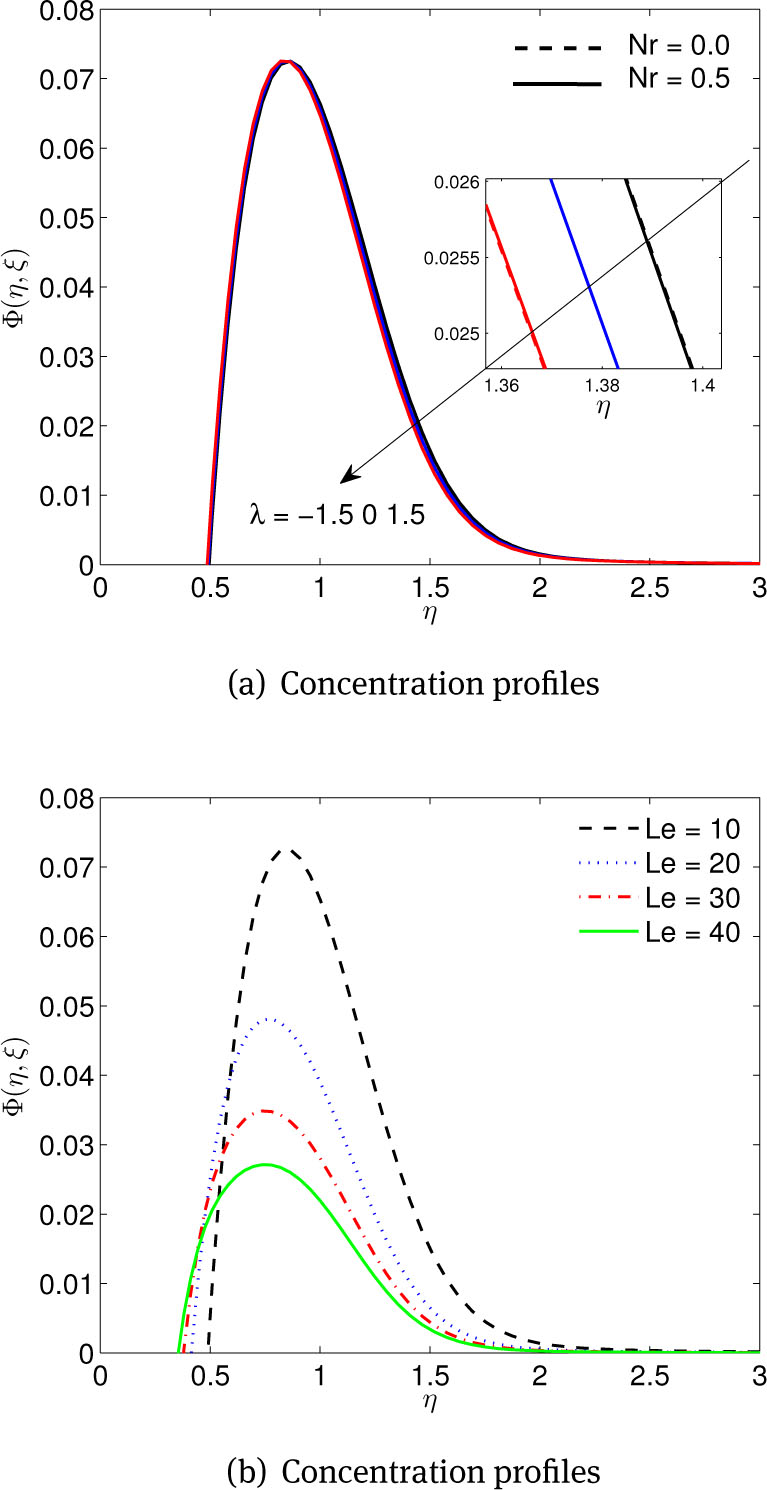
Figure 8 (a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, (b) Effects of Lewis number Le, on concentration profiles
Figure 8

(a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, (b) Effects of Lewis number Le, on concentration profiles

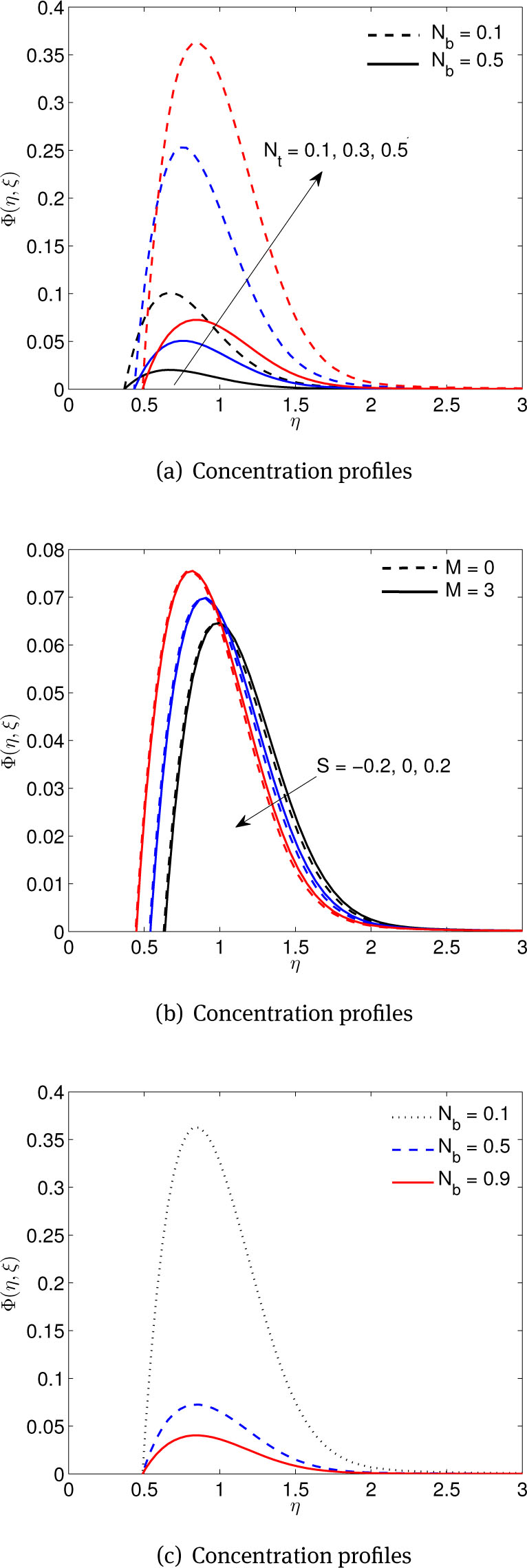
Figure 9 (a) Effects of thermophoresis Nt parameter, (b) Effects of suction/injection S and magnetic M parameters, and (b) Effects of Brownian motion Nb parameters, on concentration profiles
Figure 9

(a) Effects of thermophoresis Nt parameter, (b) Effects of suction/injection S and magnetic M parameters, and (b) Effects of Brownian motion Nb parameters, on concentration profiles

The nanoparticle concentration profiles are presented in Figure 9(a) for various values of the thermophoresis parameter. The results show that the nanoparticle concentration profiles increase with increasing Nt away the boundary layer region. It is interesting to note that the distinctive peaks in the profiles occur in regions adjacent to the surface for higher values of thermophoresis parameter. This means that the nanoparticle concentration profile takes higher value near the plate. Figure 9(b) shows that the nanoparticle concentration profiles increase with increasing M up to a certain value of η, beyond which the opposite trend is observed. It is clear that as S increases the concentration profiles increase to the highest value in the vicinity of the plate and then decreases to zero in the quiescent fluid. As a result, the concentration boundary layer thickness increases close to the plate surface and decreases far from the surface with increasing S. Figure 9(c) shows that the concentration profile for various values of Nb. It is seen that the concentration profiles decrease with increasing Nb. The concentration profiles attain their maximum value near the η = 1.0.

Figure 10(a) shows the variation of the skin friction coefficient with ξ in response to changes in A* and B*. The skin friction coefficient decreases with increases in both A* and B* when ξ increases. This suggests that A* and B* can be useful parameters for reducing the drag coefficient. Variations of the skin friction coefficient as a function of ξ for different values of the slip γ and stretching ε parameters are shown in Figure 10(b). We note that when ε < 1 the skin friction coefficient increases with increasing ξ, and decreases with increasing γ. The highest surface shear stress occurs with the no-slip velocity condition.

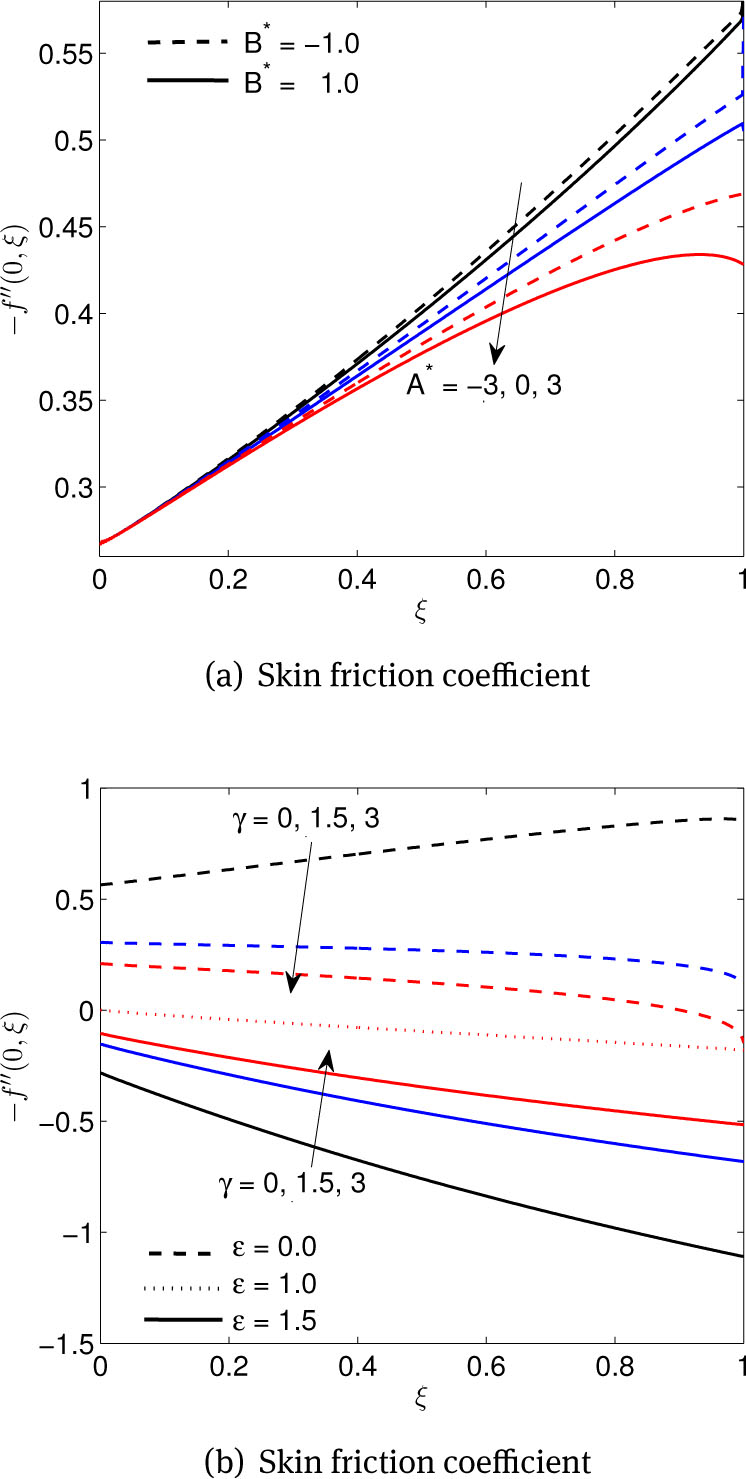
Figure 10 (a) Effects of space-dependent A* and temperature-dependent B* parameters, (b) Effects of dimensionless slip γ and stretching ε parameters, on skin friction coefficient
Figure 10

(a) Effects of space-dependent A* and temperature-dependent B* parameters, (b) Effects of dimensionless slip γ and stretching ε parameters, on skin friction coefficient

The variation of skin friction coefficient with λ and Nr is shown in Figure 11(a). We observe that the skin friction coefficient decreases with increasing λ. In the case of opposing flow, the skin friction coefficient increases with ξ and decreases with an increase in Nr. Figure 11(b) shows that the skin friction coefficient decreases with increasing Lewis numbers but increases with increasing ξ.

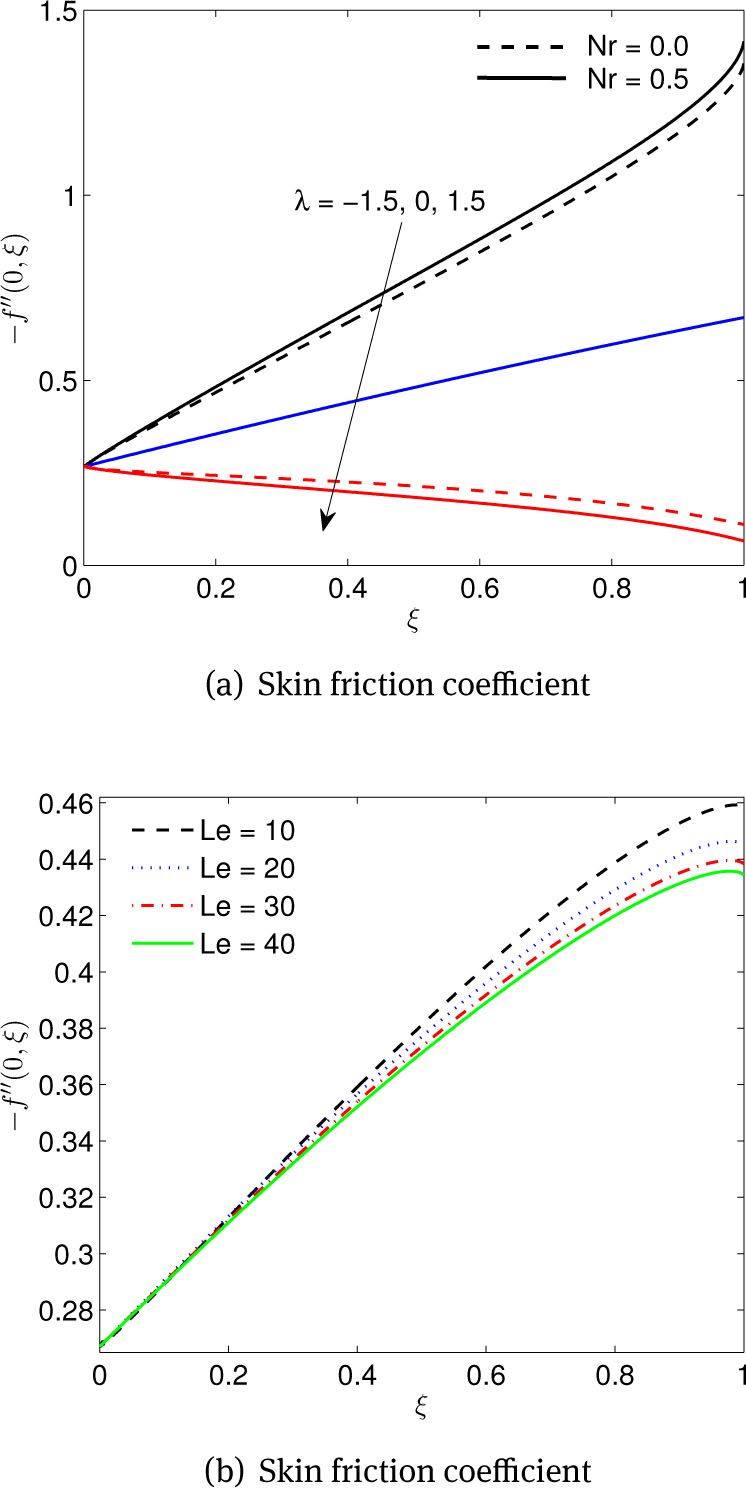
Figure 11 (a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, (b) Effects of Lewis number Le on skin friction coefficient
Figure 11

(a) Effects of buoyancy force λ and buoyancy force ratio Nr parameters, (b) Effects of Lewis number Le on skin friction coefficient

Figure 12(a) shows the variation of the skin friction coefficient with different values of Nt and Nb. The skin friction coefficient decreases as Nt and Nb increase but increases with increasing ξ. Figure 12(b) shows the skin friction coefficient with respect to ξ for different values of M and S. The skin friction coefficient increases with increasing M and S. Figures 13 - 14 show the effect of Pr on temperature and concentration profiles with same values of other parameters where dashed line indicates Nb = 0.1 and solid line for Nb = 0.5. The nature of those figures are similar to the Figures 4(a) and 9(b).

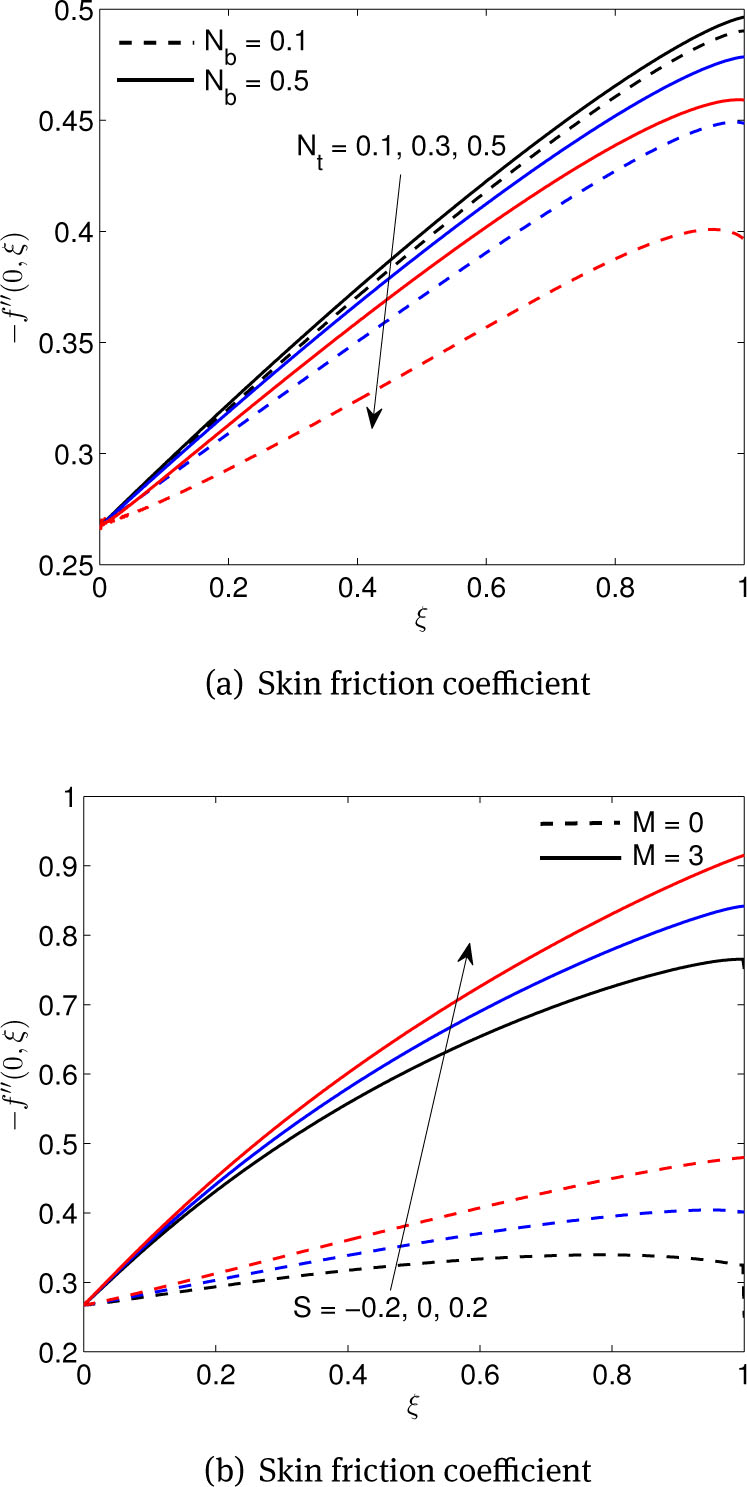
Figure 12 (a) Effects of thermophoresis Nt and Brownian motion Nb parameters, (b) Effects of suction/injection S and magnetic M parameters on skin friction coefficient on skin friction coefficient
Figure 12

(a) Effects of thermophoresis Nt and Brownian motion Nb parameters, (b) Effects of suction/injection S and magnetic M parameters on skin friction coefficient on skin friction coefficient

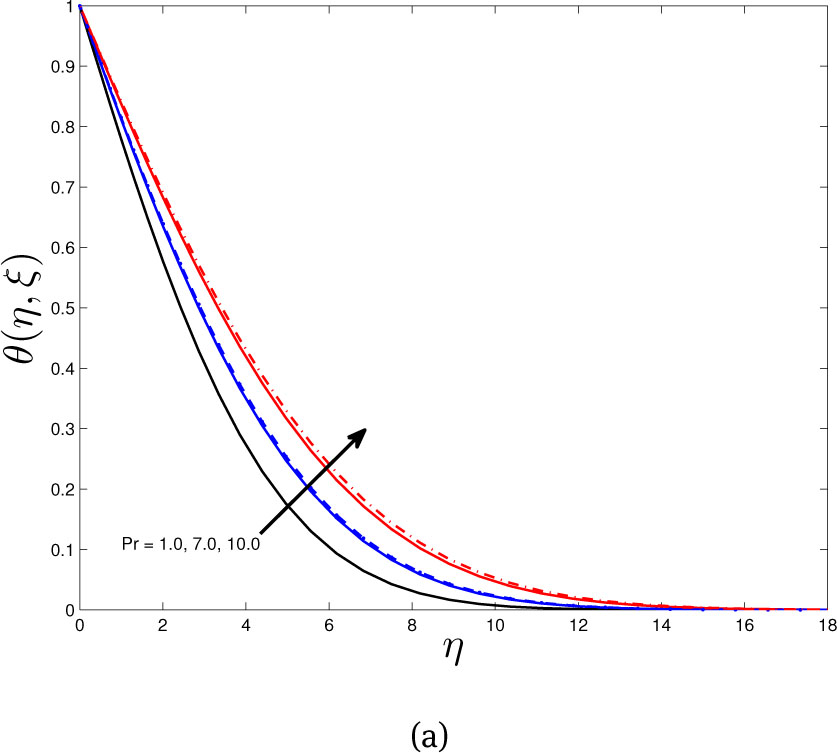
Figure 13 Effect of Pr on temperature profile for with same values of other parameters (dashed line for Nb = 0.1, solid line for Nb = 0.5)
Figure 13

Effect of Pr on temperature profile for with same values of other parameters (dashed line for Nb = 0.1, solid line for Nb = 0.5)

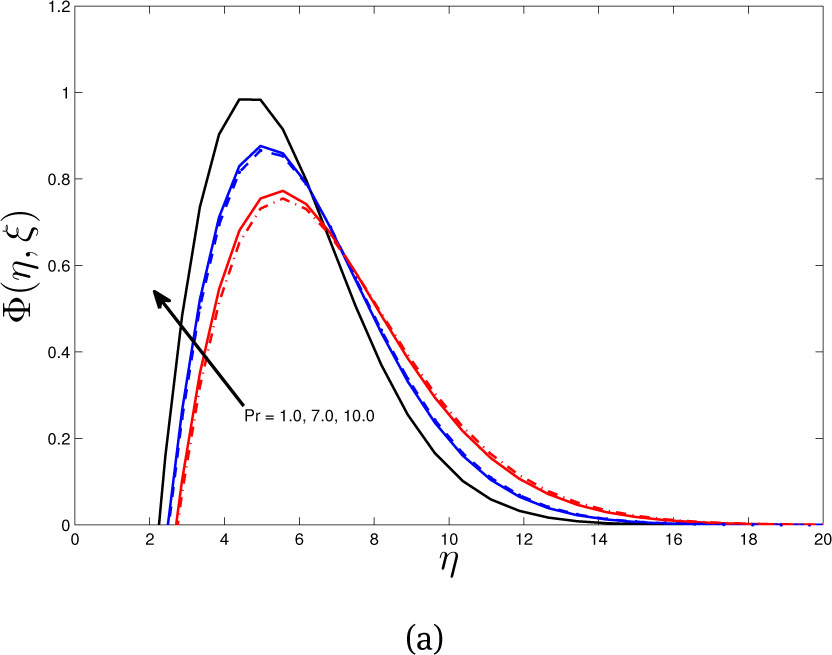
Figure 14 Effect of Pr on concentration profile with same values of other parameters (dashed line for Nb = 0.1, solid line for Nb = 0.5)
Figure 14

Effect of Pr on concentration profile with same values of other parameters (dashed line for Nb = 0.1, solid line for Nb = 0.5)

5 Conclusions

In this work, the unsteady stagnation boundary layer flow of a magnetohydrodynamic nanofluid over a stretching flat plate with velocity slip was investigated. The equations that model the boundary layer equations were solved numerically using the spectral relaxation method. A parametric study was performed to explore the impact of various physical parameters on the flow, and heat and mass transfer characteristics. The internal heat source or sink is shown to enhance the nanofluid motion while reducing the skin friction coefficient and the rate of heat transfer at the stretching surface.

In this study we have shown that increasing the Brownian motion parameter and the Lewis number reduces nanoparticle concentration profiles near the boundary layer region due to increasing mass transfer. The velocity, temperature and concentration profiles and the heat and mass transfer rate on the stretching plate are strongly influenced by the slip parameter. Heat transfer rates decrease with increasing velocity slip parameter values.

Acknowledgement

The authors are grateful to the Claude Leon Foundation and the University of KwaZulu-Natal, South Africa for the financial support.

References

[1] Choi S.U.S., Nanofluids: from vision to reality through research, J. of Heat Transf, 2009, 131, 1 - 9.10.1115/1.3056479Search in Google Scholar

[2] Choi S.U.S., Enhancing thermal conductivity of fluids with nanoparticles, ASME Fluids Eng. Div., 1995, 231, 99 - 105.Search in Google Scholar

[3] Wang X., Xu X., Choi S.U.S., Thermal conductivity of nanoparticle-fluid mixture, J. Therm. Phys. Heat Transfer, 1999, 13, 474 - 480.10.2514/2.6486Search in Google Scholar

[4] Akbarinia A., Abdolzadeh M., Laur R., Critical investigation of heat transfer enhancement using nanofluids in microchannels with slip and non-slip flow regimes, Appl Therm Eng., 2011, 31, 556 - 65.10.1016/j.applthermaleng.2010.10.017Search in Google Scholar

[5] Murshed S.M.S., A review of boiling and convective heat transfer with nanofluids, Renewable and Sustainable Energy Reviews, 2011, 15, 2342 - 2354.10.1016/j.rser.2011.02.016Search in Google Scholar

[6] Yu W., France D.M., Routbort J.L., Choi S.U.S., Review and comparison of nanofluid thermal conductivity and heat transfer enhancements, Heat Transfer Engineering, 2008, 29, 432 - 460.10.1080/01457630701850851Search in Google Scholar

[7] Wong K.V., de Leon O., Applications of nanofluids: current and future, Advances in Mechanical Engineering, 2010, Article ID 519659, 11 pages.10.1201/9781315163574-6Search in Google Scholar

[8] Kiblinski P., Phillpot S.R., Choi S.U.S., Eastman J.A., Mechanism of heat flow is suspensions of nano-sized particles (nanofluids), Int. J. Heat Mass Transfer, 2002, 45, 855 - 863.10.1016/S0017-9310(01)00175-2Search in Google Scholar

[9] Choi S.U.S., Zhang Z.G., Yu W., wood F.E.L., Grulke E.A., Anomalous thermal conductivity enhancement in nanotube suspensions, Applied Physics Letters, 2001, 79, 2252 - 2254.10.1063/1.1408272Search in Google Scholar

[10] Eastman J.A., Choi S.U.S., Li S., Yu W., Thompson L.J., Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles, Applied Physics Letters, 2001, 78, 718 - 720.10.1063/1.1341218Search in Google Scholar

[11] Nield D.A., Kuznetsov A.V., The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid, Int. J. Heat Mass Transfer, 2009, 52, 5792 - 5795.10.1016/j.ijheatmasstransfer.2009.07.024Search in Google Scholar

[12] Kuznetsov A.V., Nield D.A., Natural convective boundary-layer flow of a nanofluid past a vertical plate, Int. J. Therm. Sci., 2010, 49, 243 - 247.10.1016/j.ijthermalsci.2009.07.015Search in Google Scholar

[13] Buongiorno J., Convective transport in nanofluids, ASME J. Heat Transfer, 2006, 128, 240 - 250.10.1115/1.2150834Search in Google Scholar

[14] Blasius H., Grenzschichten in Flü ssigkeiten mit kleiner Reibung, Z. Math. Phys., 1908, 56, 1 - 37.Search in Google Scholar

[15] Sakiadis B.C., Boundary-layer behaviour on continuous solid surfaces. I. Boundary-layer equations for two-dimensional and axisymmetric flow, AIChE, 1961, 7, 1 - 2.10.1002/aic.690070108Search in Google Scholar

[16] Schlichting H., Gersten K., Boundary Layer Theory, Springer Berlin, 2000.10.1007/978-3-642-85829-1Search in Google Scholar

[17] Bejan A., Entropy Generation Minimization, CRC Boca Raton, 1996.Search in Google Scholar

[18] White F.M., Viscous Fluid Flow, McGraw-Hill, New York, 2006.Search in Google Scholar

[19] Mukhopadhyay S., MHD boundary layer flow and heat transfer over an exponentially stretching sheet embedded in a thermally stratified medium, Alex. Eng. J., 2013, 52, 259 - 265.10.1016/j.aej.2013.02.003Search in Google Scholar

[20] Mukhopadhyay S., Analysis of boundary layer flow over a porous nonlinearly stretching sheet with partial slip at the boundary, Alex. Eng. J., 2013, 52, 607 - 613.10.1016/j.aej.2013.07.004Search in Google Scholar

[21] Capretto L., Cheng W., Hill M., Zhang X., Micromixing within microfluidic devices, Top Curr. Chem., 2011, 304, 27 - 68.10.1007/128_2011_150Search in Google Scholar PubMed

[22] Kleinstreuer C., Li J., Koo J., Microfluidics of nano-drug delivery, Int. J. Heat Mass Transfer, 2008, 51, 5590 - 5597.10.1016/j.ijheatmasstransfer.2008.04.043Search in Google Scholar

[23] Yazdi M.H., Abdullah S., Hashim I., Sopian K., Slip MHD liquid flowand heat transfer over non-linear permeable stretching surface with chemical reaction, Int. J. Heat Mass Transfer, 2011, 54, 3214 - 3225.10.1016/j.ijheatmasstransfer.2011.04.009Search in Google Scholar

[24] Singh K.R., Cowling T.G., Effect of magnetic field on free convective flow of electrically conducting fluids past a semiinfinite flat plate, Quarterly Journal of Mechanics and AppliedMathematics, 1963, 16, 1 - 15.10.1093/qjmam/16.1.1Search in Google Scholar

[25] Ahmmed S.F., Sarker A., MHD natural convection flow of viscous incompressible fluid from a vertical flat plate, Journal of Physical Sciences, 2009, 13, 77 - 85.Search in Google Scholar

[26] Devi S.P.A., Kayalvizhi M., Analytical solution of MHDflow with radiation over a stretching sheet embedded in a porous medium, International Journal of Applied Mathematics and Mechanics, 2010, 6, 82 - 106.Search in Google Scholar

[27] Rajesh V., Radiation effects on MHD free convection flow near a vertical plate with ramped wall temperature, International Journal of Applied Mathematics and Mechanics, 2010, 6, 60 - 677.Search in Google Scholar

[28] Reddy M.G., Reddy N.B., Soret and Dufour effects on steady MHD free convection flow past a semi-infinite moving vertical plate in a porous mediumwith viscous dissipation, International Journal of Applied Mathematics and Mechanics, 2010, 6, 1 - 12.Search in Google Scholar

[29] Devi S.P.A., Raj J.W.S., Thermo-diffusion effects on unsteady hydromagnetic free convection flow with heat and mass transfer past a moving vertical plate with time dependent suction and heat source in a slip flow regime, International Journal of Applied Mathematics and Mechanics, 2010, 7, 20 - 51.Search in Google Scholar

[30] Makinde O.D., Computational modelling of MHD unsteady flow and heat transfer toward a flat plate with navier slip and newtonian heating, Brazilian Journal of Chemical Engineering, 2012, 29, 159 - 166.10.1590/S0104-66322012000100017Search in Google Scholar

[31] Mukhopadhyay S., Md Uddin S., Layek G.C., Lie group analysis on MHD boundary layer slip flow past a heated stretching sheet in presence of heat source/sink, International Journal of Applied Mathematics and Mechanic, 2012, 8, 51 - 66.Search in Google Scholar

[32] Eldesoky I.M.I., Influence of slip condition on peristaltic transport of a compressible Maxwell fluid through porous medium in a tube, International Journal of Applied Mathematics and Mechanics, 2012, 8, 99 - 117.Search in Google Scholar

[33] El-Shehawy E.F., El-Dabe N.T., ElDesoky I.M.I., Slip effects on the peristaltic flow of a non-Newtonian Maxwellian fluid, Acta Mechanica, 2006, 186, 141 - 159.10.1007/s00707-006-0343-6Search in Google Scholar

[34] Eldesoky I.M.I., Kamel M.H., Abumandour R. M., Numerical study of slip effect of unsteady MHD pulsatile flow through porous medium in an artery using generalized differential quadrature method (comparative study), Wor. J. Eng. Techno., 2014, 2,131 - 148.10.4236/wjet.2014.22015Search in Google Scholar

[35] Eldesoky I.M.I., Unsteady MHD pulsatile blood flow through porous medium in stenotic channel with slip at permeable walls subjected to time dependent velocity (injection/suction), Walailak J. Sci. Techno., 2014, 11, 901 - 922.10.21608/icmep.2014.29736Search in Google Scholar

[36] Chiam T.C., Stagnation point flow towards a stretching plate, Journal of the Physical Society of Japan., 1994, 63, 2443 - 2444.10.1143/JPSJ.63.2443Search in Google Scholar

[37] Nandy S.K., Mahapatra T.R., Effects of slip and heat generation/ absorption on MHD stagnation flow of nanofluid past a stretching/shrinking surface with convective boundary conditions, International Journal of Heat andMass Transfer, 2013, 64, 1091 - 1100.10.1016/j.ijheatmasstransfer.2013.05.040Search in Google Scholar

[38] Kuznetsov A., Nield D., The Cheng-Minkowycz problem for natural convective boundry layer flow in a porous medium saturated by a nanofluid: A revised model, Int. J. Heat Mass Trans., 2013, 65, 682 - 685.10.1016/j.ijheatmasstransfer.2013.06.054Search in Google Scholar

[39] Motsa S.S., Dlamini P.G., Khumalo M., Spetral relaxation method and spectral quasilinarization method for solving unsteady boundary layer flow problems, Advances inMathematial Physics, 2014, Article ID 341964, 12 pages.10.1155/2014/341964Search in Google Scholar

[40] Cheng P., Minkowycz W.J., Free convection about a vertical flat embedded in a porous mediumwith application to heat transfer from a dike, J. Geophysical Research, 1977, 82, 2040 - 2044.10.1029/JB082i014p02040Search in Google Scholar

[41] Bataller R.C., Viscoelastic fluid flow and heat transfer over a stretchng sheet under the effects of a non-uniform heat source, viscous dissipatio and thermal radiation, Int. J. HeatMass Tran., 2007, 50, 3152 - 3162.10.1016/j.ijheatmasstransfer.2007.01.003Search in Google Scholar

[42] Pal D., Mondal H., Effect of variable viscosity on MHD non-Darcy mixed convective heat transfer over a stretching sheet embedded in a porous medium with non-uniform heat source/sink, Commun. Nonlinear Sci. Numer. Simulat., 2010, 15, 1553 - 1564.10.1016/j.cnsns.2009.07.002Search in Google Scholar

[43] Anwar I., Kasim A.R.M., Ismail Z., Salleh M.Z., Shafie S., Chemical reaction and uniform heat generation or absorption effects on MHD stagnation-point flow of a nanofluid over a porous sheet, World Applied Sciences Journal, 2013, 24, 1390 - 1398.Search in Google Scholar

[44] Sahoo B., Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip, Communications in Nonlinear Science and Numerical Simulation, 2009, 10.1016/j.cnsns.2009.04.032.Search in Google Scholar

Received: 2016-1-30
Accepted: 2016-11-8
Published Online: 2017-5-20

© 2017 Sami M. Ahamed et al.

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 3.0 License.

Articles in the same Issue

  1. Regular Articles
  2. Analysis of a New Fractional Model for Damped Bergers’ Equation
  3. Regular Articles
  4. Optimal homotopy perturbation method for nonlinear differential equations governing MHD Jeffery-Hamel flow with heat transfer problem
  5. Regular Articles
  6. Semi- analytic numerical method for solution of time-space fractional heat and wave type equations with variable coefficients
  7. Regular Articles
  8. Investigation of a curve using Frenet frame in the lightlike cone
  9. Regular Articles
  10. Construction of complex networks from time series based on the cross correlation interval
  11. Regular Articles
  12. Nonlinear Schrödinger approach to European option pricing
  13. Regular Articles
  14. A modified cubic B-spline differential quadrature method for three-dimensional non-linear diffusion equations
  15. Regular Articles
  16. A new miniaturized negative-index meta-atom for tri-band applications
  17. Regular Articles
  18. Seismic stability of the survey areas of potential sites for the deep geological repository of the spent nuclear fuel
  19. Regular Articles
  20. Distributed containment control of heterogeneous fractional-order multi-agent systems with communication delays
  21. Regular Articles
  22. Sensitivity analysis and economic optimization studies of inverted five-spot gas cycling in gas condensate reservoir
  23. Regular Articles
  24. Quantum mechanics with geometric constraints of Friedmann type
  25. Regular Articles
  26. Modeling and Simulation for an 8 kW Three-Phase Grid-Connected Photo-Voltaic Power System
  27. Regular Articles
  28. Application of the optimal homotopy asymptotic method to nonlinear Bingham fluid dampers
  29. Regular Articles
  30. Analysis of Drude model using fractional derivatives without singular kernels
  31. Regular Articles
  32. An unsteady MHD Maxwell nanofluid flow with convective boundary conditions using spectral local linearization method
  33. Regular Articles
  34. New analytical solutions for conformable fractional PDEs arising in mathematical physics by exp-function method
  35. Regular Articles
  36. Quantum mechanical calculation of electron spin
  37. Regular Articles
  38. CO2 capture by polymeric membranes composed of hyper-branched polymers with dense poly(oxyethylene) comb and poly(amidoamine)
  39. Regular Articles
  40. Chain on a cone
  41. Regular Articles
  42. Multi-task feature learning by using trace norm regularization
  43. Regular Articles
  44. Superluminal tunneling of a relativistic half-integer spin particle through a potential barrier
  45. Regular Articles
  46. Neutrosophic triplet normed space
  47. Regular Articles
  48. Lie algebraic discussion for affinity based information diffusion in social networks
  49. Regular Articles
  50. Radiation dose and cancer risk estimates in helical CT for pulmonary tuberculosis infections
  51. Regular Articles
  52. A comparison study of steady-state vibrations with single fractional-order and distributed-order derivatives
  53. Regular Articles
  54. Some new remarks on MHD Jeffery-Hamel fluid flow problem
  55. Regular Articles
  56. Numerical investigation of magnetohydrodynamic slip flow of power-law nanofluid with temperature dependent viscosity and thermal conductivity over a permeable surface
  57. Regular Articles
  58. Charge conservation in a gravitational field in the scalar ether theory
  59. Regular Articles
  60. Measurement problem and local hidden variables with entangled photons
  61. Regular Articles
  62. Compression of hyper-spectral images using an accelerated nonnegative tensor decomposition
  63. Regular Articles
  64. Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes
  65. Regular Articles
  66. Calculating degree-based topological indices of dominating David derived networks
  67. Regular Articles
  68. The structure and conductivity of polyelectrolyte based on MEH-PPV and potassium iodide (KI) for dye-sensitized solar cells
  69. Regular Articles
  70. Chiral symmetry restoration and the critical end point in QCD
  71. Regular Articles
  72. Numerical solution for fractional Bratu’s initial value problem
  73. Regular Articles
  74. Structure and optical properties of TiO2 thin films deposited by ALD method
  75. Regular Articles
  76. Quadruple multi-wavelength conversion for access network scalability based on cross-phase modulation in an SOA-MZI
  77. Regular Articles
  78. Application of ANNs approach for wave-like and heat-like equations
  79. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  80. Study on node importance evaluation of the high-speed passenger traffic complex network based on the Structural Hole Theory
  81. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  82. A mathematical/physics model to measure the role of information and communication technology in some economies: the Chinese case
  83. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  84. Numerical modeling of the thermoelectric cooler with a complementary equation for heat circulation in air gaps
  85. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  86. On the libration collinear points in the restricted three – body problem
  87. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  88. Research on Critical Nodes Algorithm in Social Complex Networks
  89. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  90. A simulation based research on chance constrained programming in robust facility location problem
  91. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  92. A mathematical/physics carbon emission reduction strategy for building supply chain network based on carbon tax policy
  93. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  94. Mathematical analysis of the impact mechanism of information platform on agro-product supply chain and agro-product competitiveness
  95. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  96. A real negative selection algorithm with evolutionary preference for anomaly detection
  97. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  98. A privacy-preserving parallel and homomorphic encryption scheme
  99. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  100. Random walk-based similarity measure method for patterns in complex object
  101. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  102. A Mathematical Study of Accessibility and Cohesion Degree in a High-Speed Rail Station Connected to an Urban Bus Transport Network
  103. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  104. Design and Simulation of the Integrated Navigation System based on Extended Kalman Filter
  105. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  106. Oil exploration oriented multi-sensor image fusion algorithm
  107. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  108. Analysis of Product Distribution Strategy in Digital Publishing Industry Based on Game-Theory
  109. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  110. Expanded Study on the accumulation effect of tourism under the constraint of structure
  111. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  112. Unstructured P2P Network Load Balance Strategy Based on Multilevel Partitioning of Hypergraph
  113. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  114. Research on the method of information system risk state estimation based on clustering particle filter
  115. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  116. Demand forecasting and information platform in tourism
  117. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  118. Physical-chemical properties studying of molecular structures via topological index calculating
  119. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  120. Local kernel nonparametric discriminant analysis for adaptive extraction of complex structures
  121. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  122. City traffic flow breakdown prediction based on fuzzy rough set
  123. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  124. Conservation laws for a strongly damped wave equation
  125. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  126. Blending type approximation by Stancu-Kantorovich operators based on Pólya-Eggenberger distribution
  127. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  128. Computing the Ediz eccentric connectivity index of discrete dynamic structures
  129. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  130. A discrete epidemic model for bovine Babesiosis disease and tick populations
  131. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  132. Study on maintaining formations during satellite formation flying based on SDRE and LQR
  133. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  134. Relationship between solitary pulmonary nodule lung cancer and CT image features based on gradual clustering
  135. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  136. A novel fast target tracking method for UAV aerial image
  137. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  138. Fuzzy comprehensive evaluation model of interuniversity collaborative learning based on network
  139. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  140. Conservation laws, classical symmetries and exact solutions of the generalized KdV-Burgers-Kuramoto equation
  141. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  142. After notes on self-similarity exponent for fractal structures
  143. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  144. Excitation probability and effective temperature in the stationary regime of conductivity for Coulomb Glasses
  145. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  146. Comparisons of feature extraction algorithm based on unmanned aerial vehicle image
  147. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  148. Research on identification method of heavy vehicle rollover based on hidden Markov model
  149. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  150. Classifying BCI signals from novice users with extreme learning machine
  151. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  152. Topics on data transmission problem in software definition network
  153. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  154. Statistical inferences with jointly type-II censored samples from two Pareto distributions
  155. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  156. Estimation for coefficient of variation of an extension of the exponential distribution under type-II censoring scheme
  157. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  158. Analysis on trust influencing factors and trust model from multiple perspectives of online Auction
  159. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  160. Coupling of two-phase flow in fractured-vuggy reservoir with filling medium
  161. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  162. Production decline type curves analysis of a finite conductivity fractured well in coalbed methane reservoirs
  163. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  164. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions
  165. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  166. The size prediction of potential inclusions embedded in the sub-surface of fused silica by damage morphology
  167. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  168. Research on carbonate reservoir interwell connectivity based on a modified diffusivity filter model
  169. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  170. The method of the spatial locating of macroscopic throats based-on the inversion of dynamic interwell connectivity
  171. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  172. Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method
  173. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  174. A volumetric ablation model of EPDM considering complex physicochemical process in porous structure of char layer
  175. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  176. Numerical simulation on ferrofluid flow in fractured porous media based on discrete-fracture model
  177. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  178. Macroscopic lattice Boltzmann model for heat and moisture transfer process with phase transformation in unsaturated porous media during freezing process
  179. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  180. Modelling of intermittent microwave convective drying: parameter sensitivity
  181. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  182. Simulating gas-water relative permeabilities for nanoscale porous media with interfacial effects
  183. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  184. Simulation of counter-current imbibition in water-wet fractured reservoirs based on discrete-fracture model
  185. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  186. Investigation effect of wettability and heterogeneity in water flooding and on microscopic residual oil distribution in tight sandstone cores with NMR technique
  187. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  188. Analytical modeling of coupled flow and geomechanics for vertical fractured well in tight gas reservoirs
  189. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  190. Special Issue: Ever New "Loopholes" in Bell’s Argument and Experimental Tests
  191. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  192. The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  193. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  194. Erratum to: The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  195. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  196. Rhetoric, logic, and experiment in the quantum nonlocality debate
  197. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  198. What If Quantum Theory Violates All Mathematics?
  199. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  200. Relativity, anomalies and objectivity loophole in recent tests of local realism
  201. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  202. The photon identification loophole in EPRB experiments: computer models with single-wing selection
  203. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  204. Bohr against Bell: complementarity versus nonlocality
  205. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  206. Is Einsteinian no-signalling violated in Bell tests?
  207. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  208. Bell’s “Theorem”: loopholes vs. conceptual flaws
  209. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  210. Nonrecurrence and Bell-like inequalities
  211. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  212. Three-dimensional computer models of electrospinning systems
  213. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  214. Electric field computation and measurements in the electroporation of inhomogeneous samples
  215. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  216. Modelling of magnetostriction of transformer magnetic core for vibration analysis
  217. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  218. Comparison of the fractional power motor with cores made of various magnetic materials
  219. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  220. Dynamics of the line-start reluctance motor with rotor made of SMC material
  221. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  222. Inhomogeneous dielectrics: conformal mapping and finite-element models
  223. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  224. Topology optimization of induction heating model using sequential linear programming based on move limit with adaptive relaxation
  225. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  226. Detection of inter-turn short-circuit at start-up of induction machine based on torque analysis
  227. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  228. Current superimposition variable flux reluctance motor with 8 salient poles
  229. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  230. Modelling axial vibration in windings of power transformers
  231. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  232. Field analysis & eddy current losses calculation in five-phase tubular actuator
  233. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  234. Hybrid excited claw pole generator with skewed and non-skewed permanent magnets
  235. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  236. Electromagnetic phenomena analysis in brushless DC motor with speed control using PWM method
  237. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  238. Field-circuit analysis and measurements of a single-phase self-excited induction generator
  239. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  240. A comparative analysis between classical and modified approach of description of the electrical machine windings by means of T0 method
  241. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  242. Field-based optimal-design of an electric motor: a new sensitivity formulation
  243. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  244. Application of the parametric proper generalized decomposition to the frequency-dependent calculation of the impedance of an AC line with rectangular conductors
  245. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  246. Virtual reality as a new trend in mechanical and electrical engineering education
  247. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  248. Holonomicity analysis of electromechanical systems
  249. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  250. An accurate reactive power control study in virtual flux droop control
  251. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  252. Localized probability of improvement for kriging based multi-objective optimization
  253. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  254. Research of influence of open-winding faults on properties of brushless permanent magnets motor
  255. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  256. Optimal design of the rotor geometry of line-start permanent magnet synchronous motor using the bat algorithm
  257. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  258. Model of depositing layer on cylindrical surface produced by induction-assisted laser cladding process
  259. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  260. Detection of inter-turn faults in transformer winding using the capacitor discharge method
  261. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  262. A novel hybrid genetic algorithm for optimal design of IPM machines for electric vehicle
  263. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  264. Lamination effects on a 3D model of the magnetic core of power transformers
  265. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  266. Detection of vertical disparity in three-dimensional visualizations
  267. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  268. Calculations of magnetic field in dynamo sheets taking into account their texture
  269. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  270. 3-dimensional computer model of electrospinning multicapillary unit used for electrostatic field analysis
  271. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  272. Optimization of wearable microwave antenna with simplified electromagnetic model of the human body
  273. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  274. Induction heating process of ferromagnetic filled carbon nanotubes based on 3-D model
  275. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  276. Speed control of an induction motor by 6-switched 3-level inverter
https://doi.org/10.1515/phys-2017-0036
Keywords for this article
MHD nanofluid; Slip condition; Internal heat source/sink; Spectral relaxation method; Permeable stretching surface
Creative Commons
BY-NC-ND 3.0

Articles in the same Issue

  1. Regular Articles
  2. Analysis of a New Fractional Model for Damped Bergers’ Equation
  3. Regular Articles
  4. Optimal homotopy perturbation method for nonlinear differential equations governing MHD Jeffery-Hamel flow with heat transfer problem
  5. Regular Articles
  6. Semi- analytic numerical method for solution of time-space fractional heat and wave type equations with variable coefficients
  7. Regular Articles
  8. Investigation of a curve using Frenet frame in the lightlike cone
  9. Regular Articles
  10. Construction of complex networks from time series based on the cross correlation interval
  11. Regular Articles
  12. Nonlinear Schrödinger approach to European option pricing
  13. Regular Articles
  14. A modified cubic B-spline differential quadrature method for three-dimensional non-linear diffusion equations
  15. Regular Articles
  16. A new miniaturized negative-index meta-atom for tri-band applications
  17. Regular Articles
  18. Seismic stability of the survey areas of potential sites for the deep geological repository of the spent nuclear fuel
  19. Regular Articles
  20. Distributed containment control of heterogeneous fractional-order multi-agent systems with communication delays
  21. Regular Articles
  22. Sensitivity analysis and economic optimization studies of inverted five-spot gas cycling in gas condensate reservoir
  23. Regular Articles
  24. Quantum mechanics with geometric constraints of Friedmann type
  25. Regular Articles
  26. Modeling and Simulation for an 8 kW Three-Phase Grid-Connected Photo-Voltaic Power System
  27. Regular Articles
  28. Application of the optimal homotopy asymptotic method to nonlinear Bingham fluid dampers
  29. Regular Articles
  30. Analysis of Drude model using fractional derivatives without singular kernels
  31. Regular Articles
  32. An unsteady MHD Maxwell nanofluid flow with convective boundary conditions using spectral local linearization method
  33. Regular Articles
  34. New analytical solutions for conformable fractional PDEs arising in mathematical physics by exp-function method
  35. Regular Articles
  36. Quantum mechanical calculation of electron spin
  37. Regular Articles
  38. CO2 capture by polymeric membranes composed of hyper-branched polymers with dense poly(oxyethylene) comb and poly(amidoamine)
  39. Regular Articles
  40. Chain on a cone
  41. Regular Articles
  42. Multi-task feature learning by using trace norm regularization
  43. Regular Articles
  44. Superluminal tunneling of a relativistic half-integer spin particle through a potential barrier
  45. Regular Articles
  46. Neutrosophic triplet normed space
  47. Regular Articles
  48. Lie algebraic discussion for affinity based information diffusion in social networks
  49. Regular Articles
  50. Radiation dose and cancer risk estimates in helical CT for pulmonary tuberculosis infections
  51. Regular Articles
  52. A comparison study of steady-state vibrations with single fractional-order and distributed-order derivatives
  53. Regular Articles
  54. Some new remarks on MHD Jeffery-Hamel fluid flow problem
  55. Regular Articles
  56. Numerical investigation of magnetohydrodynamic slip flow of power-law nanofluid with temperature dependent viscosity and thermal conductivity over a permeable surface
  57. Regular Articles
  58. Charge conservation in a gravitational field in the scalar ether theory
  59. Regular Articles
  60. Measurement problem and local hidden variables with entangled photons
  61. Regular Articles
  62. Compression of hyper-spectral images using an accelerated nonnegative tensor decomposition
  63. Regular Articles
  64. Fabrication and application of coaxial polyvinyl alcohol/chitosan nanofiber membranes
  65. Regular Articles
  66. Calculating degree-based topological indices of dominating David derived networks
  67. Regular Articles
  68. The structure and conductivity of polyelectrolyte based on MEH-PPV and potassium iodide (KI) for dye-sensitized solar cells
  69. Regular Articles
  70. Chiral symmetry restoration and the critical end point in QCD
  71. Regular Articles
  72. Numerical solution for fractional Bratu’s initial value problem
  73. Regular Articles
  74. Structure and optical properties of TiO2 thin films deposited by ALD method
  75. Regular Articles
  76. Quadruple multi-wavelength conversion for access network scalability based on cross-phase modulation in an SOA-MZI
  77. Regular Articles
  78. Application of ANNs approach for wave-like and heat-like equations
  79. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  80. Study on node importance evaluation of the high-speed passenger traffic complex network based on the Structural Hole Theory
  81. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  82. A mathematical/physics model to measure the role of information and communication technology in some economies: the Chinese case
  83. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  84. Numerical modeling of the thermoelectric cooler with a complementary equation for heat circulation in air gaps
  85. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  86. On the libration collinear points in the restricted three – body problem
  87. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  88. Research on Critical Nodes Algorithm in Social Complex Networks
  89. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  90. A simulation based research on chance constrained programming in robust facility location problem
  91. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  92. A mathematical/physics carbon emission reduction strategy for building supply chain network based on carbon tax policy
  93. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  94. Mathematical analysis of the impact mechanism of information platform on agro-product supply chain and agro-product competitiveness
  95. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  96. A real negative selection algorithm with evolutionary preference for anomaly detection
  97. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  98. A privacy-preserving parallel and homomorphic encryption scheme
  99. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  100. Random walk-based similarity measure method for patterns in complex object
  101. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  102. A Mathematical Study of Accessibility and Cohesion Degree in a High-Speed Rail Station Connected to an Urban Bus Transport Network
  103. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  104. Design and Simulation of the Integrated Navigation System based on Extended Kalman Filter
  105. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  106. Oil exploration oriented multi-sensor image fusion algorithm
  107. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  108. Analysis of Product Distribution Strategy in Digital Publishing Industry Based on Game-Theory
  109. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  110. Expanded Study on the accumulation effect of tourism under the constraint of structure
  111. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  112. Unstructured P2P Network Load Balance Strategy Based on Multilevel Partitioning of Hypergraph
  113. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  114. Research on the method of information system risk state estimation based on clustering particle filter
  115. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  116. Demand forecasting and information platform in tourism
  117. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  118. Physical-chemical properties studying of molecular structures via topological index calculating
  119. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  120. Local kernel nonparametric discriminant analysis for adaptive extraction of complex structures
  121. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  122. City traffic flow breakdown prediction based on fuzzy rough set
  123. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  124. Conservation laws for a strongly damped wave equation
  125. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  126. Blending type approximation by Stancu-Kantorovich operators based on Pólya-Eggenberger distribution
  127. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  128. Computing the Ediz eccentric connectivity index of discrete dynamic structures
  129. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  130. A discrete epidemic model for bovine Babesiosis disease and tick populations
  131. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  132. Study on maintaining formations during satellite formation flying based on SDRE and LQR
  133. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  134. Relationship between solitary pulmonary nodule lung cancer and CT image features based on gradual clustering
  135. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  136. A novel fast target tracking method for UAV aerial image
  137. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  138. Fuzzy comprehensive evaluation model of interuniversity collaborative learning based on network
  139. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  140. Conservation laws, classical symmetries and exact solutions of the generalized KdV-Burgers-Kuramoto equation
  141. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  142. After notes on self-similarity exponent for fractal structures
  143. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  144. Excitation probability and effective temperature in the stationary regime of conductivity for Coulomb Glasses
  145. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  146. Comparisons of feature extraction algorithm based on unmanned aerial vehicle image
  147. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  148. Research on identification method of heavy vehicle rollover based on hidden Markov model
  149. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  150. Classifying BCI signals from novice users with extreme learning machine
  151. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  152. Topics on data transmission problem in software definition network
  153. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  154. Statistical inferences with jointly type-II censored samples from two Pareto distributions
  155. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  156. Estimation for coefficient of variation of an extension of the exponential distribution under type-II censoring scheme
  157. Special issue on Nonlinear Dynamics in General and Dynamical Systems in particular
  158. Analysis on trust influencing factors and trust model from multiple perspectives of online Auction
  159. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  160. Coupling of two-phase flow in fractured-vuggy reservoir with filling medium
  161. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  162. Production decline type curves analysis of a finite conductivity fractured well in coalbed methane reservoirs
  163. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  164. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions
  165. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  166. The size prediction of potential inclusions embedded in the sub-surface of fused silica by damage morphology
  167. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  168. Research on carbonate reservoir interwell connectivity based on a modified diffusivity filter model
  169. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  170. The method of the spatial locating of macroscopic throats based-on the inversion of dynamic interwell connectivity
  171. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  172. Unsteady mixed convection flow through a permeable stretching flat surface with partial slip effects through MHD nanofluid using spectral relaxation method
  173. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  174. A volumetric ablation model of EPDM considering complex physicochemical process in porous structure of char layer
  175. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  176. Numerical simulation on ferrofluid flow in fractured porous media based on discrete-fracture model
  177. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  178. Macroscopic lattice Boltzmann model for heat and moisture transfer process with phase transformation in unsaturated porous media during freezing process
  179. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  180. Modelling of intermittent microwave convective drying: parameter sensitivity
  181. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  182. Simulating gas-water relative permeabilities for nanoscale porous media with interfacial effects
  183. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  184. Simulation of counter-current imbibition in water-wet fractured reservoirs based on discrete-fracture model
  185. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  186. Investigation effect of wettability and heterogeneity in water flooding and on microscopic residual oil distribution in tight sandstone cores with NMR technique
  187. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  188. Analytical modeling of coupled flow and geomechanics for vertical fractured well in tight gas reservoirs
  189. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  190. Special Issue: Ever New "Loopholes" in Bell’s Argument and Experimental Tests
  191. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  192. The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  193. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  194. Erratum to: The ultimate loophole in Bell’s theorem: The inequality is identically satisfied by data sets composed of ±1′s assuming merely that they exist
  195. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  196. Rhetoric, logic, and experiment in the quantum nonlocality debate
  197. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  198. What If Quantum Theory Violates All Mathematics?
  199. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  200. Relativity, anomalies and objectivity loophole in recent tests of local realism
  201. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  202. The photon identification loophole in EPRB experiments: computer models with single-wing selection
  203. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  204. Bohr against Bell: complementarity versus nonlocality
  205. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  206. Is Einsteinian no-signalling violated in Bell tests?
  207. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  208. Bell’s “Theorem”: loopholes vs. conceptual flaws
  209. Special Issue on Ever-New "Loopholes" in Bell’s Argument and Experimental Tests
  210. Nonrecurrence and Bell-like inequalities
  211. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  212. Three-dimensional computer models of electrospinning systems
  213. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  214. Electric field computation and measurements in the electroporation of inhomogeneous samples
  215. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  216. Modelling of magnetostriction of transformer magnetic core for vibration analysis
  217. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  218. Comparison of the fractional power motor with cores made of various magnetic materials
  219. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  220. Dynamics of the line-start reluctance motor with rotor made of SMC material
  221. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  222. Inhomogeneous dielectrics: conformal mapping and finite-element models
  223. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  224. Topology optimization of induction heating model using sequential linear programming based on move limit with adaptive relaxation
  225. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  226. Detection of inter-turn short-circuit at start-up of induction machine based on torque analysis
  227. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  228. Current superimposition variable flux reluctance motor with 8 salient poles
  229. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  230. Modelling axial vibration in windings of power transformers
  231. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  232. Field analysis & eddy current losses calculation in five-phase tubular actuator
  233. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  234. Hybrid excited claw pole generator with skewed and non-skewed permanent magnets
  235. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  236. Electromagnetic phenomena analysis in brushless DC motor with speed control using PWM method
  237. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  238. Field-circuit analysis and measurements of a single-phase self-excited induction generator
  239. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  240. A comparative analysis between classical and modified approach of description of the electrical machine windings by means of T0 method
  241. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  242. Field-based optimal-design of an electric motor: a new sensitivity formulation
  243. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  244. Application of the parametric proper generalized decomposition to the frequency-dependent calculation of the impedance of an AC line with rectangular conductors
  245. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  246. Virtual reality as a new trend in mechanical and electrical engineering education
  247. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  248. Holonomicity analysis of electromechanical systems
  249. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  250. An accurate reactive power control study in virtual flux droop control
  251. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  252. Localized probability of improvement for kriging based multi-objective optimization
  253. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  254. Research of influence of open-winding faults on properties of brushless permanent magnets motor
  255. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  256. Optimal design of the rotor geometry of line-start permanent magnet synchronous motor using the bat algorithm
  257. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  258. Model of depositing layer on cylindrical surface produced by induction-assisted laser cladding process
  259. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  260. Detection of inter-turn faults in transformer winding using the capacitor discharge method
  261. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  262. A novel hybrid genetic algorithm for optimal design of IPM machines for electric vehicle
  263. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  264. Lamination effects on a 3D model of the magnetic core of power transformers
  265. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  266. Detection of vertical disparity in three-dimensional visualizations
  267. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  268. Calculations of magnetic field in dynamo sheets taking into account their texture
  269. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  270. 3-dimensional computer model of electrospinning multicapillary unit used for electrostatic field analysis
  271. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  272. Optimization of wearable microwave antenna with simplified electromagnetic model of the human body
  273. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  274. Induction heating process of ferromagnetic filled carbon nanotubes based on 3-D model
  275. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering ISEF 2017
  276. Speed control of an induction motor by 6-switched 3-level inverter
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 16.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2017-0036/html?lang=en
Scroll to top button