Abstract
The influence of acoustic radiation is considered in the prediction of noise attenuation effect of sound barrier, which provides a theoretical reference for further improving the insertion loss of sound barrier. Based on the theory of thin plate vibration, the vibration mode and natural frequencies of sound barrier under arbitrary boundary conditions are established by using two-dimensional beam function method, and the forced vibration response of the sound barrier is calculated based on the modal superposition method. MATLAB software (MathWorks Company, Natick, Massachusetts, USA) is used to calculate the natural frequencies and the radiated sound power level of the sound barrier, which indicated that the sound radiation caused by external excitation would significantly increase the sound pressure level at the received point, which should be considered as one of the influencing factors in the prediction of noise attenuation effect. The influence of diverse structural parameters on the radiated acoustic power is compared, providing an excellent reference for the design of sound barrier with low noise.
1 Introduction
With the mass construction of expressway and high-speed railway elevated road, urban traffic noise has become the main source of environmental noise pollution, which has interfered with people’s life and work, seriously affected their physical and mental health, and also influenced the economic development along the road. Due to the advantages of excellent noise reduction effect, convenient construction, long service life, and elegant appearance, sound barrier is one of the most significant measures of sound environment management [1].
At present, the research on sound barrier is mainly based on its sound absorption and insulation performance. Various sound absorption and insulation structures and diverse calculation methods are proposed and combined with various advanced software [2,3]. All these predictive analysis methods have achieved satisfactory results for the engineering design and further theoretical analysis of sound barrier. However, when external motivation is oversize, such as the sound barriers of highway, high-speed railway vehicles driving through the sound barrier generate large pulsating load of air and noise intensity, and are often considered in the design of the large load of mechanical properties [4,5]. Little consideration has been given to the acoustic radiation performance of sound barriers. The common sound barrier is mainly composed of steel structure columns and sound insulation plate, which is usually made of acrylic plate. Thin plate structure is a common structure in engineering. With advantages of light weight, energy saving, low cost, and environmental protection, thin plate structure has been widely used in various equipment [6]. However, thin plate structure is also an excellent radiation body that generates vibration and radiated noise in response to forced vibration [7]. Therefore, in the design of acoustic barriers, it is necessary to consider the acoustic radiation performance and the corresponding measures to recede the acoustic radiation performance, so as to effectively improve the actual noise reduction effect of sound barriers.
In this article, based on the vibration theory, the dynamic response of forced vibration of the sound barriers is calculated by the two-dimensional beam function. The effects of three structural parameters, such as material, aspect ratio, and thickness, were compared to provide an excellent reference for the low-noise design of sound barriers.
2 Transverse vibration theory of rectangular thin plates
The vibration equation of isotropic and undamped plate is as follows [8]:
where
2.1 Free vibration
When
Set the main vibration mode as
where
Due to the limitation of boundary conditions, all rectangular thin plates with boundary conditions have no analytical solutions except rectangular thin plates with simply supported four sides. By two-dimensional beam function method, the mode of vibration of thin plate can be expressed as the product of two mode functions satisfying quasi-orthogonal and boundary conditions:
By using the orthogonal relation, the natural frequency can be obtained as follows [8]:
where [8]
Simply supported boundary conditions are
Fixed supported boundary conditions are
The mode function satisfying the boundary conditions of the four-sided fixed support is as follows [8]:
where
2.2 Forced vibration
The response w of thin plate is expanded to
where η(t) is the regular coordinate. Its expression is
where q(t) is the regular generalized force, and its expression is
If subjected to the concentrated harmonic force, then
If the harmonic force is uniformly distributed, then
Then take the derivative of time t to obtain the velocity distribution of the plate
3 Acoustic radiation theory of sound barriers
Assuming that the structure is in an infinite baffle plate, each element on the rectangular plate can be regarded as a simple point sound source radiating outward sound, and the radiation sound pressure of the whole rectangular plate can be obtained. The sound pressure can be expressed by velocity with Rayleigh integration [9,10]:
where
Then, ∗ stands for conjugate, the radiated sound power is
The flat plate is divided into N units with equal area
where
Formula (18) is expressed as a matrix:
where the (m, n) unit of matrix R is [9]
If m = n, r
mn
= 0, and
Assuming that the sound point is 5 m away from a sound barrier, the sound pressure level is calculated by using the following formula:
where
4 Numerical calculation
Consider the sound barrier in Figure 1 as an example. The middle transparent plate is acrylic plate, the four sides are fixed by the aluminum alloy profile frame, and the gaps are filled with glass silicone and other sealing materials. Therefore, the middle part can be treated as an ideal isotropic plate with four fixed edges. Since the vibration response is dominated by low-order modes, only the frequencies of first ten modes are calculated, and the natural frequency and acoustic radiation power are obtained by the above formula, so as to discuss the influences of the acoustic radiation power of the sound barrier with its parameters.

Real shot image of a sound barrier.
The thin plate in the middle of the sound barrier has a length of a = 2 m, width of b = 2 m and thickness of
The first ten order natural frequencies of the four-sided fixed supported sound barrier/Hz
| Modal order number | 1(1,1) | 2(2,1) (1,2) | 3(2,2) | 4(3,1) (1,3) | 5(3,2) (2,3) |
|---|---|---|---|---|---|
| MATLAB solution | 7.30 | 14.88 | 21.91 | 26.67 | 33.39 |
| ANSYS simulation results | 7.32 | 14.95 | 22.09 | 26.84 | 33.74 |
| Modal order number | 6(1,4) (4,1) | 7 (3,3) | 8(4,2) (2,4) | 9(4,3) (3,4) | 10(5,1) (1,5) |
| MATLAB solution | 42.68 | 44.46 | 48.99 | 59.83 | 62.62 |
| ANSYS simulation results | 43.03 | 45.13 | 49.64 | 60.95 | 63.30 |
As can be observed from Table 1, the natural frequency calculated by the two-dimensional beam function method is very similar to the ANSYS simulation result, indicating that this method is feasible to calculate the natural frequency of the thin plate. The material is acrylic plate. The sound barrier with other parameters unchanged is denoted as a, and the sound barrier with glass is denoted as b. When the length-to-width ratio is 0.5:1, the sound barrier with other parameters unchanged is denoted as c, and the sound barrier with the length-to-width ratio of 0.5:1 is denoted as d. When the thickness is 20 mm, the sound barrier with other parameters unchanged is denoted as e, and the sound barrier with a thickness of 30 mm is denoted as f. The change in the insertion loss of the sound barrier caused by acoustic radiation is obtained by using the formula, as shown in Figure 2.

Change of insertion loss caused by different forms of sound barrier radiation.
4.1 Influence of flat plate materials on acoustic radiation characteristics of sound barriers
It can be observed from Figure 3 that the excitation frequency has a significant influence on the acoustic radiation power of the sound barrier, especially when it is close to the natural frequency of the acoustic barrier, a peak value will be generated. Moreover, since the external load is assumed to be uniformly distributed, the forced vibration response of the thin plate is only odd–odd terms. Therefore, the suppression of acoustic radiation of the sound barrier is focused on the natural frequency point of odd–odd terms. Due to the neglect of damping, the actual radiated acoustic power is relatively small. Compared with the two materials, the acoustic power radiated by the plate is also diverse. In the frequency range of 0–500 Hz, the radiated sound power of polymethyl methacrylate board with small stiffness is almost all greater than that of ordinary glass, except for a small number of common vibration points. In connection with a and b in Figure 2, the acoustic radiation characteristics of acrylic plate decrease the insertion loss more than that of ordinary glass. It can be concluded that diverse materials have an excellent influence on the radiation characteristics of the sound barrier, and other characteristics such as light transmittance, load resistance and sound insulation should also be considered.
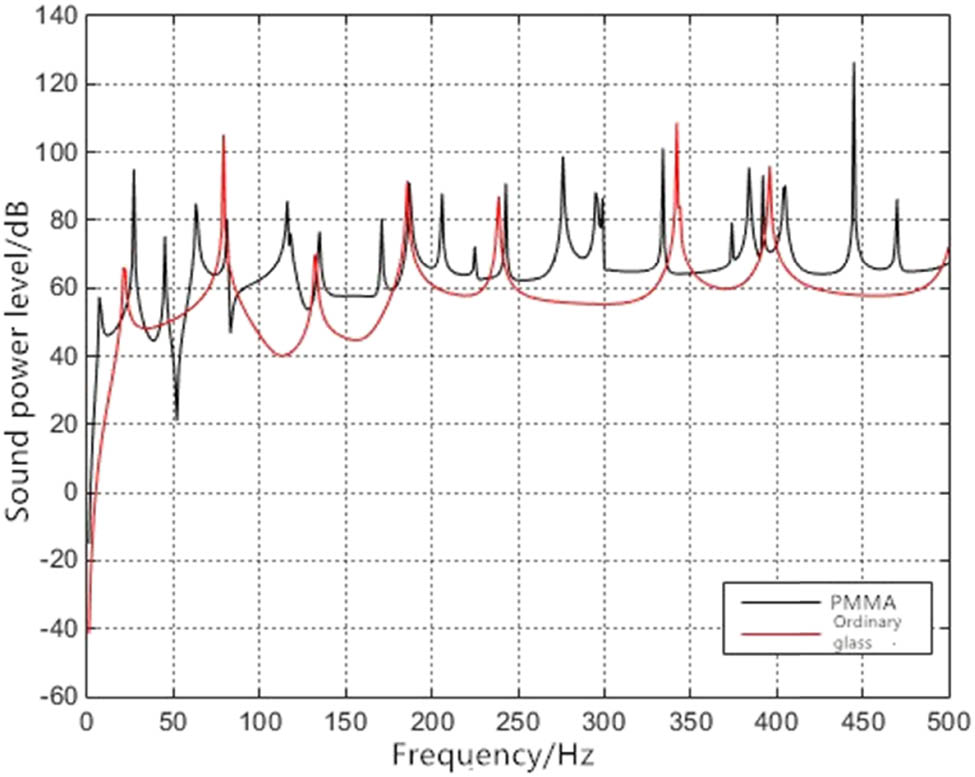
Radiated sound power levels of sound barriers of two materials.
4.2 The influence of the ratio of length to width on the acoustic radiation characteristics of the sound barrier
With other parameters of the plate unchanged, the aspect ratio of the sound insulation board of the sound barrier is 1:1, 0.5:1, and 0.25:1, and the unit length is 2 m. According to the above formula, the natural frequency is calculated by MATLAB programming, as shown in Table 2.
The natural frequency is calculated by MATLAB programming
| Modal order number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Aspect ratio 1:1 | 7.30 | 14.88 | 21.91 | 26.67 | 33.39 |
| Aspect ratio 0.5:1 | 19.88 | 25.60 | 35.89 | 50.73 | 51.78 |
| Aspect ratio 0.25:1 | 73.83 | 77.58 | 84.49 | 95.23 | 110.30 |
| Modal order number | 6 | 7 | 8 | 9 | 10 |
| Aspect ratio 1:1 | 42.68 | 44.46 | 48.99 | 59.83 | 62.62 |
| Aspect ratio 0.5:1 | 57.08 | 66.27 | 69.91 | 79.62 | 93.30 |
| Aspect ratio 0.25:1 | 129.91 | 154.14 | 182.94 | 202.16 | 211.86 |
As can be observed from Table 2 and Figures 2 and 4, when the aspect ratio is 1:1 to 0.5:1 and then 0.5:1, the modal density gradually decreases, and the overall radiated sound power level also reveals a decreasing trend. When the plate shape is square, the modal density is the highest, and the peak value of the radiated sound power level is the highest. When the aspect ratio is away from 1, the peak value of the radiated sound power level decreases, and the overall radiated sound power level is also smaller. It is mainly due to the square thin plate, whose natural frequencies of order (m, n) and order (n, m) are equal, and the actual mode of vibration generated by force has two orders, so the noise radiation capability is relatively strong, as can be observed from Figure 4. When the aspect ratio is 1:1, the radiated sound power of the first peak value (1,1) is less than that of the second peak value (3,1) and that of the second peak value (1,3).

Radiated sound power levels of three aspect ratio of sound barriers.
4.3 Influence of plate thickness on acoustic radiation characteristics of sound barriers
One of the measures to control the acoustic radiation from a sound barrier is how much the acoustic effect can be improved by simply changing the thickness of the board. The first ten natural frequencies and radiated acoustic power of the sound barriers with five thicknesses are compared, as revealed in Table 3 and Figure 5.
The first ten natural frequencies of three thickness barriers/Hz
| Modal order number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| h = 10 mm | 7.30 | 14.88 | 21.91 | 26.67 | 33.39 |
| h = 20 mm | 14.56 | 29.68 | 43.57 | 53.21 | 66.29 |
| h = 30 mm | 21.85 | 44.52 | 65.35 | 79.81 | 99.43 |
| Modal order number | 6 | 7 | 8 | 9 | 10 |
| h = 10 mm | 42.68 | 44.46 | 48.99 | 59.83 | 62.62 |
| h = 20 mm | 85.16 | 87.92 | 97.64 | 118.03 | 125.00 |
| h = 30 mm | 127.74 | 131.88 | 145.80 | 177.05 | 187.49 |

Radiated sound power levels of three thickness barriers.
As can be observed from Table 3 and Figure 5, as the thickness increases, the peak point of radiated sound power within 100 Hz decreases. In other words, the frequency range covered by the same number of peak points increases, and the modal density decreases, thereby affecting the natural frequency. The tenth natural frequency of the plate with h = 10 mm is 62.62 Hz, and the tenth natural frequency of the plate with h = 30 mm is 187.49 Hz. In general, the increase of plate thickness can significantly decrease the radiated sound power, mainly because the bending stiffness D of thin plate is proportional to the cubic of plate thickness. It can also be seen from the comparison of the change value of insertion loss in Figure 2.
5 Conclusion
In the prediction of noise reduction effect of acoustic barriers, the influence of acoustic radiation is analyzed. The sound barrier model is simplified as a four-sided plate with fixed support. The free vibration forced vibration and acoustic radiation characteristics of the sound barrier are analyzed by means of the theory of vibration and acoustic radiation of the plate. The results reveal that when the external excitation is conspicuously large, the acoustic radiation characteristics of the sound barrier have a significant impact on the sound pressure level of the affected sound points, which should be included as one of the influencing factors in the design of noise reduction effect prediction of the sound barrier. The influence of three parameters, namely material, aspect ratio and thickness, on the radiated acoustic power was compared, and the following conclusions were drawn:
1. Diverse materials have diverse radiative capacity.
2. The closer the plate is to the square, the larger the radiation sound power is, mainly because the natural frequency of the square plate of order (m, n) and order (n, m) is the same, the mode of vibration produced by the same order is of two orders, leading to a strong radiation ability.
3. The larger the thickness of the plate, the smaller the radiation sound power, mainly because the bending stiffness D of the plate is proportional to the third square of the plate thickness, the plate surface vibration speed is small, and the radiation capacity is weak.
-
Funding information: This research was supported by the National Natural Science Foundation of China (51175195), Key Scientific Research Projects of Colleges and Universities in Henan Province, China (15A460041), and Guidance Plan of Textile Industry Federation, China (2017053).
-
Authors contribution: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors declare that there are no conflicts of interest regarding the publication of this article.
-
Data availability statement: The data used to support the findings of this study are available from the corresponding author upon request.
References
[1] Zhou JQ , Wu SQ , Wu GQ . Review of new city viaduct noise barrier. Adv Mater Res. 2014;3530(1044):65–8.10.4028/www.scientific.net/AMR.1044-1045.532Suche in Google Scholar
[2] Zhou X , Xiao XB , He B . Influential factors and rules for insertion loss of high-speed railway noise barriers. J Southwest Jiaotong Univ. 2014;49(60):1024–31.Suche in Google Scholar
[3] Chen JH . Study on influence of sound barrier structure on its noise reduction performance with numerical simulation. Noise Vib Control. 2010;19(4):63–6.Suche in Google Scholar
[4] He B , Xiao XB , Zhou X . Numerical study on acoustic performance of high-speed railway noise barriers with different geometric shape. J Mech Eng. 2016;52(2):99–107.10.3901/JME.2016.02.099Suche in Google Scholar
[5] Long LP , Zhao LB , Liu L . Research on the air turbulent force loaded on noise barrier caused by train. Eng Mech. 2010;27(3):246–50.Suche in Google Scholar
[6] Peiró-Torres MP , Redondo J , Bravo JM , Pérez JS . Open noise barriers based on sonic crystals. Advances in noise control in transport infrastructures. Trans Res Proc. 2016;18:392–8.10.1016/j.trpro.2016.12.051Suche in Google Scholar
[7] Zhang YY , Shen HM . Research on the thin plate’s vibration and acoustic radiation based on matlab software. J Chongqing Univ Technol (Nat Sci). 2014;8:34–8.Suche in Google Scholar
[8] Cao ZY . Plate and shell vibration theory. Beijing, China: China Railway Publishing House; 1989.Suche in Google Scholar
[9] Liu C , Jiang Z . Study of radiated sound power and its sensitivity analysis of plate. Noise Vib Control. 2012;4:116–20.Suche in Google Scholar
[10] Zhang B , Shen HM , Zhi W . Sound radiation analysis of variable thickness plate based on FEM and BEM. Sci Technol Eng. 2010;10(36):8963–7.Suche in Google Scholar
© 2021 Jiyong Jin et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge
Artikel in diesem Heft
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge

