Abstract
The aim of this article was to address the lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation with the aid of Hirota bilinear technique. This model concerns in a massive nematic liquid crystal director field. By choosing the function f in Hirota bilinear form, as the general quadratic function, trigonometric function and exponential function along with appropriate set of parameters, we find the lump, lump-one stripe, multiwave and breather solutions successfully. We also interpreted some three-dimensional and contour profiles to anticipate the wave dynamics. These newly obtained solutions have some arbitrary constants and so can be applicable to explain diversity in qualitative features of wave phenomena.
1 Introduction
In waves theory, nonlinear partial differential equations(NPDEs), which explain nonlinear aspects, appear in an extensive diversity of scientific and engineering applications, for example, plasma physics, fluid dynamics, hydrodynamics, acoustics, solid-state physics, hydrodynamics and theory of turbulence, optics, optical fibers, chemical physics, chaos theory and many other applications. The study of NPDEs becomes increasingly significant because of their prominent features. A main attachment of scientific work has been perceived in the last few decades on NPDEs such as efficient integration method [1], improved modified Kudryashov method [2], asymptotic method [3], geometric singular perturbation [4], Lie symmetry analysis [5], Painleve expansion procedure [6],
There are many renowned models, such as Vakhnenko dynamical equation [35], nonlinear Schrodinger equation [36], KdV equation [37], Camassa-Holm equation [38], sine-Gordon equation [39] and Biswas-Milovic equation [40], but here we will obtain the exact solutions of the Hunter–Saxton (HS) equation [41],
This equation is used for propagation of orientation waves in a massive nematic liquid crystal director field. The HS equation can be used as a short wave limit of the Camassa–Holm equation:
The content of this article is organized as follows: in Section 2, we evaluate the lump solutions via some three-dimensional (3D) and contour shapes. In Section 3, we find out lump-one stripe interactional solutions and some physical 3D shapes. In Section 4, the brief discussion of multiwave solutions for the proposed model is given. In Section 5, we find breather solutions. In Section 6, there are results and discussion about our newly obtained solutions and comparison with already published work, and in Section 7, we give concluding remarks.
2 Lump solution
In the direction to find lump solutions of equation (1), we apply the transformation [42],
which transforms equation (1),
Now the function f in equation (5) can be assumed as [36],
where g 2 = a 1 x + a 2 t + a 3, h 2 = a 4 x + a 5 t + a 6. However, a i (1 ≤ i ≤ 7) are all real parameters to be measured. Now, substituting f into equation (5) and associating the coefficients of x and t imply us the subsequent result on parameters:
Set I.
The parameters in equation (6) prevent the lump solutions to equation (1)
Set II.
The parameters in equation (8) imply the lump solutions to equation (1)
3 Lump-one stripe soliton interaction solution
To this aim, f in the bilinear equation can be assumed as [43],
where g 2 = a 1 x + a 2 t + a 3, h 2 = a 4 x + a 5 t + a 6, f 1 = k 1 x + k 2 t. However, a i (1 ≤ i ≤ 7), k 1 and k 2 are all real parameters to be found. Now, inserting f in equation (3) and relating the coefficients of x and t give us:
Set I.
The parameters in equation (11) create the required solutions to equation (1)
where
Set II.
The parameters in equation (13) reveal the required solutions to equation (1)
where
4 Multiwave solutions
For finding multiwave solutions, we use the succeeding transformation in equation (1) [44],
With the help of the above transformation, we obtain:
Now with the aid of the following assumption in equation (16)
we get,
To find the multiwave solutions of equation (18), we apply the subsequent hypothesis [40]:
where a
1, a
2, a
3, a
4, a
5 and a
6 are any constants to be examined. Substituting equation (19) into equation (18) via symbolic computation and collecting the coefficients of all powers of
Set I.
By substituting equation (20) into equation (19), we get
As f solves equation (18), then ψ solves equation (16) via
where
5 Breather solutions
For finding the breathers of equation (18), we assume the successive transformation [45]:
where
Set I.
As f solves equation (18), after that ψ solves equation (16) through applying
where
6 Results and discussion
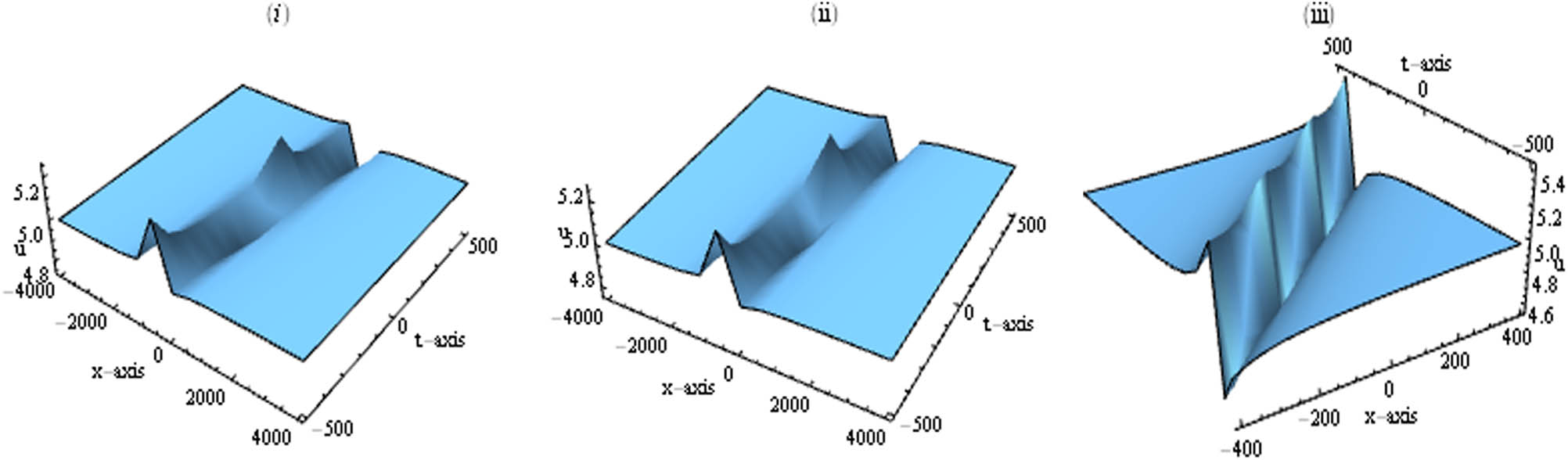
In this section, we have made a detailed comparison of our accomplished results with the earlier literature. Many researchers used various methods for calculating solitary wave solutions of the Hunter–Saxton equation. Particularly, Beals et al. applied inverse scattering technique [46], Alberto et al. used distance functional [47], Lenells applied properties of the Riemannian [48], Lenells et al. applied a geometric approach [49], Bressan et al. utilized Lipschitz metric [50], Zhao et al. applied conservation laws [51], Korpinar used symmetry analysis [51] and Zhao applied conservation laws to obtain the exact solutions for the presented model [52]. But here, in this work we have found the lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation with the aid of Hirota bilinear approach. These types of solutions have been utilized in many fields of science, for example, physics, chemistry, biology, finance, oceanographic engineering, capillary flow and nonlinear optics [42,43, 44,45]. Now we will notice how our obtained results alter their shapes via different values of a 3 from Figure 1(i), and we can see at a 3 = 0.2 that u has a maximum value at some points, expressing 3D shape of u making two bright lump solutions. Similarly, in Figure 1(ii) at a 3 = 0.8 the same features are observed. But at a 3 = 2 in Figure 1(iii), we obtain three bright lump solutions. In the same way, for a 3 = 5 in Figure 2(i) we have achieved seven bright lump solutions and the process was repeated for gradually increasing values of a 3, for instance, a 3 = 8, a 3 = 15 (Figure 2(ii) and (iii)) respectively. Figures 3 and 4 express the relating contour profiles for Figures 1 and 2, respectively. Now we have observed how our obtained solutions change their wave structure via appropriate choices of a 3 from Figure 5(i), and we can notice a lump-one stripe soliton at a 3 = 0.2. Similarly, Figures 5(ii), 5(iii) and 6(i)–(iii) show how a lump-one stripe soliton rises or descends for different values of a 3. Figures 7 and 8 present the associating contour graphs for Figures 5 and 6, respectively. Also, Figures 9(i)–(iii) and 10(i)–(iii) show kink wave and their changes in wave shape via a 3 = −1, a 3 = 0.2, a 3 = 0.5, a 3 = 0.8, a 3 = 2 and a 3 = 5, respectively. Similarly, Figures 11(i)–(iii) and 12(i)–(iii) show solitary wave and the changes in their structure through a 2 = −1, a 2 = 0.2, a 2 = 0.5, a 2 = 0.8, a 2 = 2 and a 2 = 5, respectively. Finally, Figures 13 and 14 present the concerning contour graphs for Figures 11 and 12, respectively.
The graphs of the solution u(x, t) in equation (7) are shown via suitable parameters m = 5, b = −5, a 7 = 7, a 6 = 5. 3D graphs at (i) a 3 = 0.2, (ii) a 3 = 0.8 and (iii) a 3 = 2, respectively.

The profiles of the solution u(x, t) in equation (7) are shown by different choices of parameters m = 5, b = −5, a 7 = 7, a 6 = 5. 3D graphs at (i) a 3 = 5, (ii) a 3 = 8 and (iii) a 3 = 15, respectively.

The corresponding contour profiles for Figure 1.

The associating contour graphs for Figure 2.

The profiles of the solution u(x, t) in equation (14) via various choices of parameters m = 1, b = 5, a 3 = 0.2, a 4 = 1, a 5 = 2, a 6 = 5, b 1 = 2, k 1 = −1, k = 1. Contour profiles at (i) a 3 = 0.2, (ii) a 3 = 0.8 and (iii) a 3 = 2, respectively.

The shapes of the solution u(x, t) in equation (14) are shown by various choices of parameters m = 1, b = 5, a 3 = 0.2, a 4 = 1, a 5 = 2, a 6 = 5, b 1 = 2, k 1 = −1, k = 1. 3D graphs at (i) a 3 = 5, (ii) a 3 = 10 and (iii) a 3 = 15, respectively.

The relating contour graphs for Figure 5.
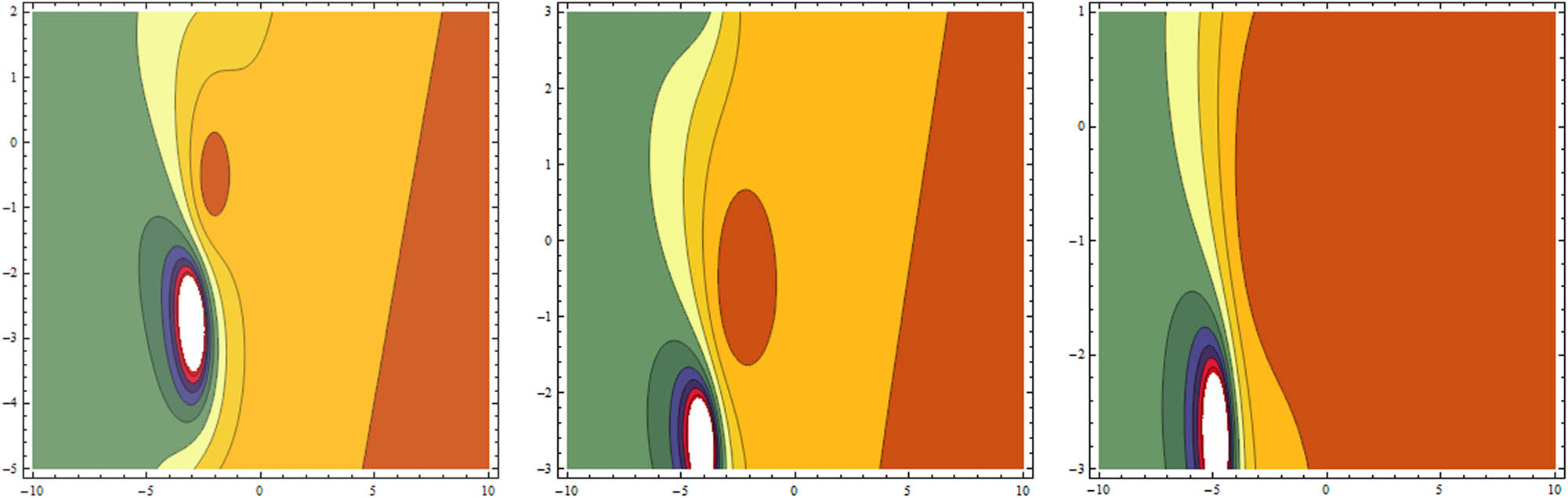
The associating contour profiles for Figure 6.

The profiles of the solution u(x, t) in equation (22) via various choices of parameters m = 1, b = 5, a 4 = 1, a 5 = 2, a 6 = 5, a 7 = 1, b 1 = 2, b 2 = 1, k 1 = −1, k = 1. 3D graphs at (i) a 3 = 0.2, (ii) a 3 = 0.8 and (iii) a 3 = 2, respectively.

The profiles of the solution u(x, t) in equation (22) via various choices of parameters m = 1, b = 5, a 4 = 1, a 5 = 2, a 6 = 5, a 7 = 1, b 1 = 2, b 2 = 1, k 1 = −1, k = 1. 3D graphs at (i) a 3 = 5, (ii) a 3 = 10 and (iii) a 3 = 15, respectively.

The graphs of the solution u(x, t) in equation (25) through different choices of parameters m = 1, p = 5, a 4 = 1, b 0 = 1, b 1 = 2, k 1 = −1, k = 1. 3D graphs at (i) a 2 = −1, (ii) a 2 = 0.2 and (iii) a 2 = 0.4, respectively.
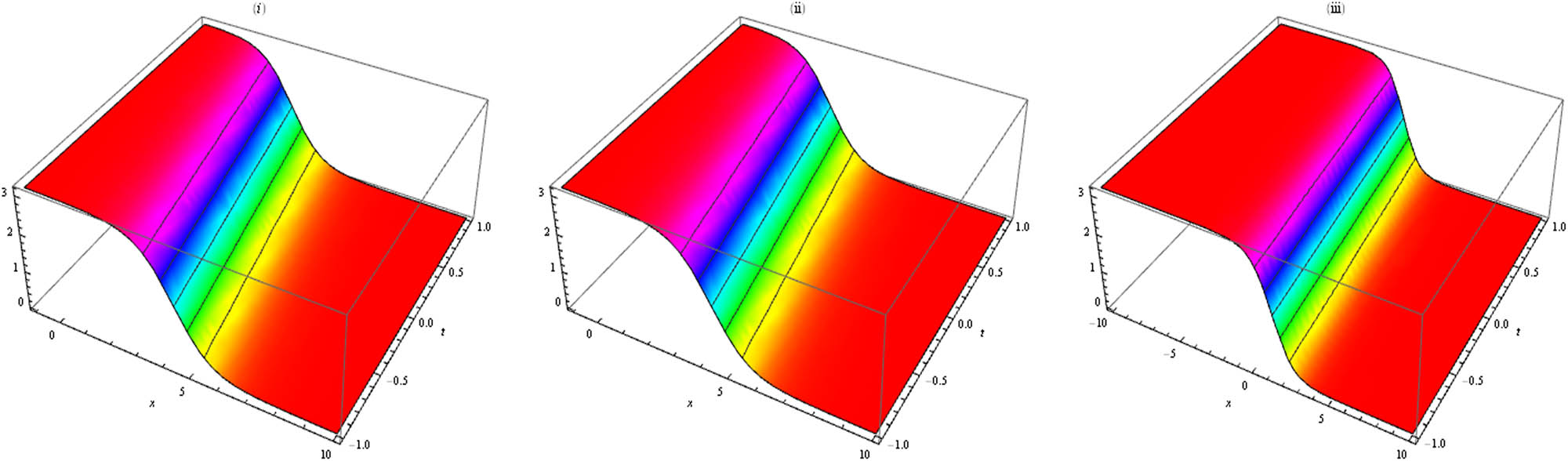
The shapes of the solution u(x, t) in equation (25) via appropriate choices of parameters m = 1, p = 5, a 4 = 1, b 0 = 1, b 1 = 2, k 1 = −1, k = 1. 3D graphs at (i) a 2 = 0.8, (ii) a 2 = 2 and (iii) a 2 = 15, respectively.
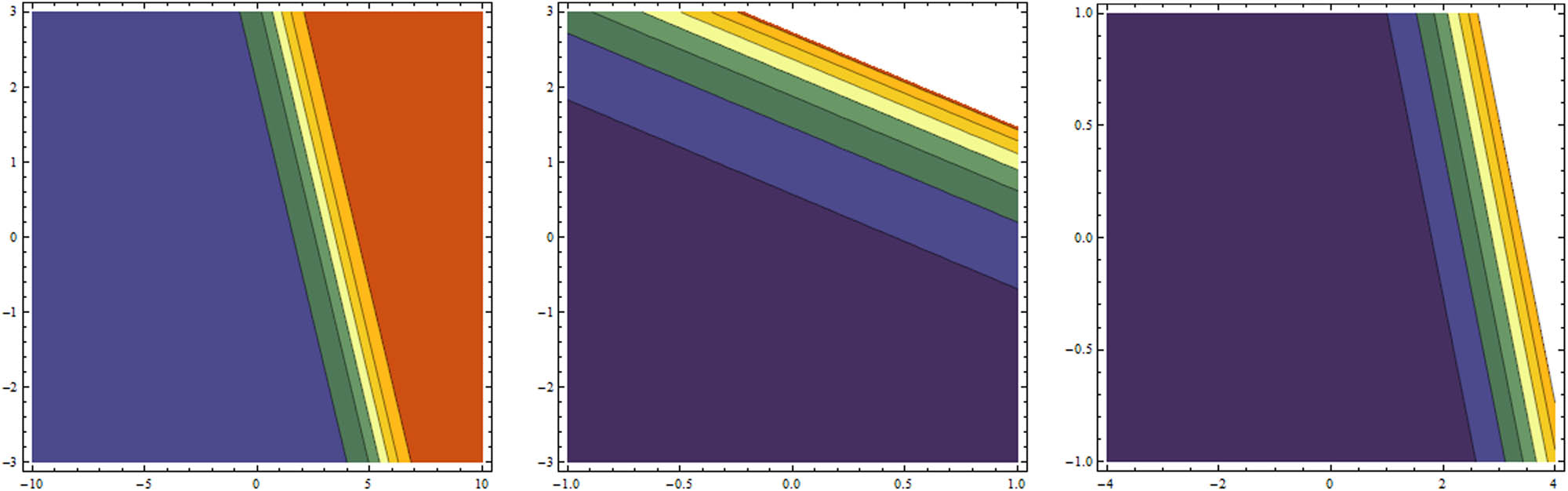
The corresponding contour shapes of Figure 11.

The relating contour profiles of Figure 12.
7 Concluding remarks
The purpose of this article is to accumulate the lump, lump-one stripe, multi wave and breather solutions for the Hunter–Saxton equation by way of Hirota bilinear scheme and through defining appropriate transformations. We have successfully generated some new exact solutions to the concerning model. The 3D and contour graphs mapped different numeric values, to observe the physical behavior of the system. For better understanding and more effectiveness, we have also explained the geometry of the graphs. The attained solutions show that the proposed method is very reliable, aggressive and simple, and so, the recommended idea could be extended for further nonlinear models in mathematical physics.
References
[1] Ghanbari B, Nisar KS, Aldhaifallah M. Abundant solitary wave solutions to an extended nonlinear Schrödingers equation with conformable derivative using an efficient integration method. Adv Diff Equ. 2020;2020(1):1–25.10.1186/s13662-020-02787-7Search in Google Scholar
[2] Hyder AA, Barakat MA. General improved Kudryashov method for exact solutions of nonlinear evolution equations in mathematical physics. Phys Scr. 2020;95(4):045212.10.1088/1402-4896/ab6526Search in Google Scholar
[3] Bildik N, Deniz S. Comparative study between optimal homotopy asymptotic method and perturbation-iteration technique for different types of nonlinear equations. Iran J Sci Technol A. 2018:42(2):647–5410.1007/s40995-016-0039-2Search in Google Scholar
[4] Ge J, Du Z. The solitary wave solutions of the nonlinear perturbed shallow water wave model. Appl Math Lett. 2020;103:106202.10.1016/j.aml.2019.106202Search in Google Scholar
[5] Tian SF. Lie symmetry analysis, conservation laws and solitary wave solutions to a fourth-order nonlinear generalized Boussinesq water wave equation. Appl Math Lett. 2020;100:106056.10.1016/j.aml.2019.106056Search in Google Scholar
[6] Farah N, Seadawy AR, Ahmad S, Rizvi STR, Younis M. Interaction properties of soliton molecules and Painleve analysis for nano bioelectronics transmission model. Opt Quantum Electron. 2020;52(7):1–15.10.1007/s11082-020-02443-0Search in Google Scholar
[7] Seadawy Aly R, El-Rashidy K. Application of the extension exponential rational function method for higher dimensional Broer-Kaup-Kupershmidt dynamical system. Mod Phys Lett A. 2020;35(1):1950345 (14 pages).10.1142/S0217732319503450Search in Google Scholar
[8] Kudryashov NA. Highly dispersive solitary wave solutions of perturbed nonlinear Schrödinger equations. Appl Math Comput. 2020;371:124972.10.1016/j.amc.2019.124972Search in Google Scholar
[9] Younas U, Seadawy Aly R, Younis M, Rizvi STR. Dispersive of propagation wave structures to the Dullin-Gottwald-Holm dynamical equation in a shallow water waves. Chin J Phys. 2020;68:348–64.10.1016/j.cjph.2020.09.021Search in Google Scholar
[10] Younas U, Younis M, Seadawy AR, Rizvi STR. Rizvi, Optical solitons and closed form solutions to (3 + 1)-dimensional resonant Schrodinger equation. Int J Mod Phys B. 2020;34(30):2050291. 10.1142/S0217979220502914.Search in Google Scholar
[11] Bilal M, Seadawy AR, Younis M, Rizvi STR, Zahed Hanadi. Dispersive of propagation wave solutions to unidirectional shallow water wave Dullin-Gottwald-Holm system and modulation instability analysis. Math Methods Appl Sci. 2020. 10.1002/mma.7013.Search in Google Scholar
[12] Kudryashov NA. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik. 2020;312:163550.10.1016/j.ijleo.2019.163550Search in Google Scholar
[13] Zhao Z. Bäcklund transformations, rational solutions and soliton-cnoidal wave solutions of the modified Kadomtsev-Petviashvili equation. Appl Math Lett. 2019;8:103–10.10.1016/j.aml.2018.09.016Search in Google Scholar
[14] Raza Rizvi Syed Tahir, Seadawy AR, Ali Ijaz, Bibi Ishrat, Muhammad Younis. Chirp-free optical dromions for the presence of higher order spatio-temporal dispersions and absence of self-phase modulation in birefringent fibers. Mod Phys Lett B. 2020;34(35):2050399. 10.1142/S0217984920503996.Search in Google Scholar
[15] Liu JG, Yang XJ, Feng YY. On integrability of the time fractional nonlinear heat conduction equation. J Geom Phys. 2019;144:190–8.10.1016/j.geomphys.2019.06.004Search in Google Scholar
[16] Seadawy AR, Cheemaa N. Applications of extended modified auxiliary equation mapping method for high-order dispersive extended nonlinear Schrödinger equation in nonlinear optics. Mod Phys Lett B. 2019;33(18):1950203.10.1142/S0217984919502038Search in Google Scholar
[17] James AJ, Konik RM, Lecheminant P, Robinson NJ, Tsvelik AM. Non-perturbative methodologies for low-dimensional strongly-correlated systems: From non-abelian bosonization to truncated spectrum methods. Rep Prog Phys. 2018;81(4):046002.10.1088/1361-6633/aa91eaSearch in Google Scholar PubMed
[18] Kumar S. A new analytical modelling for fractional telegraph equation via Laplace transform. Appl Math Model. 38(13):3154–63.10.1016/j.apm.2013.11.035Search in Google Scholar
[19] Kumar S, Ghosh S, Samet B, Goufo EFD. An analysis for heat equations arises in diffusion process using new Yang-Abdel-Aty-Cattani fractional operator. Math Methods Appl Sci. 2020;43(9):6062–80.10.1002/mma.6347Search in Google Scholar
[20] Kumar S, Kumar R, Cattani C, Samet B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons Fractals. 2020;135:109811.10.1016/j.chaos.2020.109811Search in Google Scholar
[21] Kumar S, Nisar KS, Kumar R, Cattani C, Samet B. A new Rabotnov fractional-exponential function-based fractional derivative for diffusion equation under external force. 2020;43(7):4460–71.10.1002/mma.6208Search in Google Scholar
[22] Goufo EFD, Kumar S, Mugisha SB. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos, Solitons Fractals. 2019;130:109467.10.1016/j.chaos.2019.109467Search in Google Scholar
[23] Wang KL, Yao SW, Liu YP, Zhang LN. A fractal variational principle for the telegraph equation with fractal derivatives. Fractals. 2020;28(4):2050058.10.1142/S0218348X20500589Search in Google Scholar
[24] Wang KL, Wang KJ. A modification of the reduced differential transform method for fractional calculus. Therm Sci. 2018;22(4):1871–75.10.2298/TSCI1804871WSearch in Google Scholar
[25] Djilali S. Herd behavior in a predator-prey model with spatial diffusion: bifurcation analysis and Turing instability. J Appl Math Compu. 2017;58(1–2):125–49.10.1007/s12190-017-1137-9Search in Google Scholar
[26] Djilali S., Touaoula TM, Miri SEH. A Heroin epidemic model: very general non linear incidence, treat-age, and global stability. Acta Appl Math. 2017;152(1):171–94.10.1007/s10440-017-0117-2Search in Google Scholar
[27] Djilali S. Impact of prey herd shape on the predator-prey interaction. Chaos, Solitons Fractals. 2019;120:139–48.10.1016/j.chaos.2019.01.022Search in Google Scholar
[28] Djilali S., Bentout S. Spatiotemporal patterns in a diffusive predator-prey model with prey social behavior. Acta Appl Math. 2020;169:125–43.10.1007/s10440-019-00291-zSearch in Google Scholar
[29] Djilali S. Pattern formation of a diffusive predator-prey model with herd behavior and nonlocal prey competition. Math Meth Appl Scien. 2020;43(5):2233–50.10.1002/mma.6036Search in Google Scholar
[30] Ahmad H, Seadawy AR, Khan TA, Thounthong P. Analytic approximate solutions Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. J Taibah Univ Sci. 2020;14(1):346–58.10.1080/16583655.2020.1741943Search in Google Scholar
[31] Ozkan YG, Yasar E, Seadawy AR A third-order nonlinear Schrodinger equation: the exact solutions, group-invariant solutions and conservation laws. J Taibah Univ Sci. 2020;14(1):585–97.10.1080/16583655.2020.1760513Search in Google Scholar
[32] Helal MA, Seadawy AR, Zekry MH. Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl Math Comput. 2014;232:1094–103.10.1016/j.amc.2014.01.066Search in Google Scholar
[33] Iqbal M., Seadawy AR, Lu D. Construction of solitary wave solutions to the nonlinear modified Kortewege-de Vries dynamical equation in unmagnetized plasma via mathematical methods. Mod Phys Lett A. 2018;33(32):1850183.10.1142/S0217732318501833Search in Google Scholar
[34] Seadawy AR, Lu D, Yue C. Travelling wave solutions of the generalized nonlinear fifth-order KdV water wave equations and its stability. J Taibah Univ Sci. 2017;11:623–33.10.1016/j.jtusci.2016.06.002Search in Google Scholar
[35] Seadawy AR, Asghar A, Baleanu D. Transmission of high-frequency waves in a tranquil medium with general form of the Vakhnenko dynamical equation. Phys Scr. 2020;95:095208.10.1088/1402-4896/abaa7bSearch in Google Scholar
[36] Islam W, Younis M, Rizvi STR. Optical solitons with time fractional nonlinear Schrödinger equation and competing weakly nonlocal nonlinearity. Optik. 2017;130:562–67.10.1016/j.ijleo.2016.10.090Search in Google Scholar
[37] Wang XB, Tian SF, Xua MJ, Zhang TT. On integrability and quasi-periodic wave solutions to a (3 + 1)-dimensional generalized KdV-like model equation. Appl Math Comput. 2016;283:216–33.10.1016/j.amc.2016.02.028Search in Google Scholar
[38] Dehghan M, Abbaszadeh M, Mohebbi A. An implicit RBF meshless approach for solving the time fractional nonlinear sine-Gordon and Klein-Gordon equations. Eng Anal Bound Elem. 2015;50:412–34.10.1016/j.enganabound.2014.09.008Search in Google Scholar
[39] Ghaffar A, Ali A, Ahmed S, Akram S, Baleanu D, Nisar KS. A novel analytical technique to obtain the solitary solutions for nonlinear evolution equation of fractional order. Adv Differ Equ. 2020;2020(1):1–15.10.1186/s13662-020-02751-5Search in Google Scholar
[40] Rizvi STR, Ali K, Ahmad M. Optical solitons for Biswas-Milovic equation by new extended auxiliary equation method. Optik. 2020;204:164181.10.1016/j.ijleo.2020.164181Search in Google Scholar
[41] Lou S, Feng BF, Yao R. Multi-soliton solution to the two-component Hunter-Saxton equation. Wave Motn. 2016;65:17–28.10.1016/j.wavemoti.2016.04.006Search in Google Scholar
[42] WaZhou Y, Manukure S, Ma WX. Lump and lump-soliton solutions to the Hirota Satsuma equation. Commun Nonlinear Sci Numer Simul. 2019;68:56–62.10.1016/j.cnsns.2018.07.038Search in Google Scholar
[43] Wang H. Lump and interaction solutions to the (2 + 1)-dimensional Burgers equation. Appl Math Lett. 2018;85:27–34.10.1016/j.aml.2018.05.010Search in Google Scholar
[44] Ahmed I, Seadawy AR, Lu D. Kinky breathers, W-shaped and multi-peak solitons interaction in (2 + 1)-dimensional nonlinear Schrödinger equation with Kerr law of nonlinearity. Eur Phys J Plus. 2019;134(3):1–10.10.1140/epjp/i2019-12482-8Search in Google Scholar
[45] Ahmed I, Seadawy AR, Lu D. Mixed lump-solitons, periodic lump and breather soliton solutions for (2 + 1) dimensional extended Kadomtsev Petviashvili dynamical equation. Int J Mod Phys B. 2019;33(05):1950019.10.1142/S021797921950019XSearch in Google Scholar
[46] Beals R, Sattinger DH, Szmigielski J. Inverse scattering solutions of the Hunter-Saxton equation. Appl Anal. 2001;78(3):255–69.10.1080/00036810108840938Search in Google Scholar
[47] Bressan A, Constantin A. Global solutions of the Hunter-Saxton equation. SIAM J Math Anal. 2005;37(3):996–1026.10.1137/050623036Search in Google Scholar
[48] Lenells J. The Hunter-Saxton equation describes the geodesic flow on a sphere. J Geom Phys. 2007;57(10):2049–64.10.1016/j.geomphys.2007.05.003Search in Google Scholar
[49] Lenells J. The Hunter-Saxton equation: a geometric approach. SIAM J Math Anal. 2008;40(1):266–77.10.1137/050647451Search in Google Scholar
[50] Bressan A, Holden H, Raynaud X. Lipschitz metric for the Hunter-Saxton equation. J Math Pures Appl. 2010;94(1):68–92.10.1016/j.matpur.2010.02.005Search in Google Scholar
[51] Korpinar Z. On characterization of invariant and exact solutions of Hunter saxton equation. J Sci Arts. 2018;94(1):18(3):603–10.Search in Google Scholar
[52] Zhao Z. Conservation laws and nonlocally related systems of the Hunter-Saxton equation for liquid crystal. Anal Math Phys. 2019;9(4):2311–27.10.1007/s13324-019-00337-3Search in Google Scholar
© 2021 Aly R. Seadawy et al., published by DeGruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge
Articles in the same Issue
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge

