Optical properties of two-dimensional two-electron quantum dot in parabolic confinement

Menberu Mengesha Woldemariam

doi:10.1515/phys-2021-0067

Artikel Open Access

Optical properties of two-dimensional two-electron quantum dot in parabolic confinement

Menberu Mengesha Woldemariam

Veröffentlicht/Copyright: 1. Oktober 2021

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 19 Heft 1

Abstract

The Hamiltonian and wavefunctions of two-dimensional two-electron quantum dots (2D2eQD) in parabolic confinement are determined. The ground and excited state energies are calculated solving the Schrödinger equation analytically and numerically. To determine the energy eigen-value of the system variational method is employed due to the large coupling constant λ ≈ 1.1 . The trial wavefunctions are developed for both ground and excited states. The ground state wave function is a para state and the excited state wavefunctions belong to both para and ortho states based on the symmetry and antisymmetry of spatial wavefunctions. Using the obtained energy eigen-values at the two states, the first- and third-order nonlinear absorption coefficient and refractive index are analytically obtained with the help of density matrix formalism and iterative procedure.

Keywords: 2D2eQD; parabolic confinement; optical properties

1 Introduction

Zero-dimensional semiconductor systems or quantum dots with one electron are widely used in the nano physics [1,2]. Recently, quantum dots have gained considerable attention due to their wide range of potential applications in optoelectronic devices [3,4]. Few of these applications are single electron transistors [5], quantum lasers, quantum computing [8], optical memories [9], infrared photodetectors [6], and high-speed optical modulators [7]. The advancement of technology leads to the possibility of fabricating quantum dots with two or more electrons where the Coulomb interaction between them must be taken into account [10,11,12]. Due to the localization of the electrons in low-dimensional system the Coulomb interaction can exceed the average kinetic energy of electrons that considerably complicates the analytic solution of the Schrödinger equation [13]. At a temperature smaller than the distance between the ground and excited states, the two-electron quantum dot consists of the para- and ortho-states [13]. These states play a crucial role for quantum information processing [14,15,16]. Due to quantum confinement, engineering the electronic structure of materials by controlling its shape and size leads to the possibility of designing the energy spectrum to produce suitable optical transitions [17]. These characteristics are helpful for developing optoelectronic devices with tunable transmission or emission properties. As the result, nonlinear optical properties of quantum dots have been studied theoretically and experimentally [18,19]. Intraband nonlinear optical properties of G a A s with inversely quadratic Hellman potential have been performed [20]. Simultaneous effects of electric, magnetic, and nonresonant intense laser field on the nonlinear optical properties of G a A s quantum well with an anharmonic potential profile are investigated [21].

In this article, the ground and first excited states of 2D2eQDs with parabolic confinement are considered. Our system is the simplest quantum dot that consists of two electrons confined in a 2D parabolic potential. In this model, the two electrons each with an effective mass m ∗ are at z = 0 in a 2D quantum dot in which the electrons are bounded by the parabolic potential. The following three cases are considered to determine the energy eigenvalues: (1) Two electrons with opposite spin are in the ground state; (2) one electron is in the ground state, the other in the first excited state; and (3) two electrons are in the first excited state. The energy eigenvalues of the ground and excited states are solved using variational techniques. In addition to this, the nonlinear absorption coefficient and refractive index changes are studied as a function of the photon energy and optical intensity, respectively.

2 Statement of the problem

The Hamiltonian of 2D2eQD with soft or parabolic confinement potential is expressed as:

(1) H ˆ = ∑ i = 1 2 − ℏ 2 2 m ∗ d 2 d r i 2 + ∑ i = 1 2 1 2 m ∗ ω 0 2 r i 2 + e 2 ε ∣ r 1 − r 2 ∣ .

In equation (1), the first term indicates the kinetic energy of two electrons, the second term is the parabolic potential for confining electrons and the last term is the electron electron interaction which includes pure Coulombic and exchange correlation part. Using the dimensionless variables ρ 1 and ρ 2 in units of ℏ m ∗ ω 0 , the Hamiltonian can be written as

(2) H ˆ = − ∑ i = 1 2 1 2 ∇ i 2 + ∑ i = 1 2 1 2 ρ i 2 + λ ∣ ρ 1 − ρ 2 ∣ ,

where λ = e 2 ε ℏ ω 0 ℏ m ∗ ω 0 which is equivalent to R y ε 2 ℏ m ∗ m , R y = m e 4 ℏ 2 , is the coupling constant determining the Coulombic interaction between electrons, and ε is the dielectric constant of 2D2e ZnO QD. If we put the Rydberg constant R y = 27.2 eV, m ∗ = 0.21 m e (is the effective mass of ZnO), the confining frequency ω 0 = 1 THz, and the dielectric constant ε = 8.5 , one can obtain λ = 9.33 8.5 ≈ 1.09 . This confirms that the Schrödinger equation corresponding to the Hamiltonian (1) for our system cannot be solved using the perturbation theory. However, it can be solved using either numerical method or variational technique. In this article, the variational technique is employed to obtain the energy eigen values.

3 Ground state energy of 2D2eQD

The energy eigen values of complicated systems are estimated using variational technique. It is based on full minimization of the energy functional with respect to the two-electron wavefunction. In this method, the energy computed from a guessed wavefunction is an upper bound to the true ground state energy. In this section, we are going to determine the ground state energy of 2D2eQD with parabolic confinement. The gaussed wavefunction when two electrons in the ground state may be given as:

(3) ψ 0 ( ρ 1 , ρ 2 ) = α π exp − α 2 ( ρ 1 2 + ρ 2 2 ) .

The total ground state energy is the expectation value of the Hamiltonian and described by,

(4) E 0 = ψ 0 ( ρ 1 , ρ 2 ) 1 2 ∇ ρ 1 2 + 1 2 ∇ ρ 2 2 + 1 2 ρ 1 2 + 1 2 ρ 2 2 + λ ∣ ρ 1 − ρ 2 ∣ ψ 0 ( ρ 1 , ρ 2 ) .

The kinetic energy of the first electron is

(5) T 1 = ∫ 0 ∞ ∫ 0 2 π α π exp − α 2 ρ 1 2 − 1 2 1 ρ 1 ∂ ∂ ρ 1 ρ 1 ∂ ∂ ρ 1 + 1 ρ 1 2 ∂ 2 ∂ θ 1 2 α π exp − α 2 ρ 1 2 ρ 1 d ρ 1 d θ 1 T 1 = α 2 .

The kinetic energy of the second electron is given by,

(6) T 2 = ∫ 0 ∞ ∫ 0 2 π α π exp − α 2 ρ 2 2 − 1 2 1 ρ 2 ∂ ∂ ρ 2 ρ 2 ∂ ∂ ρ 2 + 1 ρ 2 2 ∂ 2 ∂ θ 2 2 α π exp − α 2 ρ 2 2 ρ 2 d ρ 2 d θ 2 T 2 = α 2 .

The expectation value of the potential energies of the two electrons are

(7) V 1 = ∫ 0 ∞ ∫ 0 2 π α π exp − α 2 ρ 1 2 1 2 ρ 1 2 α π × exp − α 2 ρ 1 2 ρ 1 d ρ 1 d θ 1 = 1 2 α ,

(8) V 2 = ∫ 0 ∞ ∫ 0 2 π α π exp − α 2 ρ 2 2 1 2 ρ 2 2 α π × exp − α 2 ρ 2 2 ρ 2 d ρ 2 d θ 2 = 1 2 α .

The Coulombic part is given by,

(9) V 12 = ∫ 0 ∞ ∫ 0 2 π ψ 0 ∗ ( ρ 1 , ρ 2 ) λ ∣ ρ 1 − ρ 2 ∣ ψ 0 ( ρ 1 , ρ 2 ) d 2 ρ 1 d 2 ρ 2 .

After evaluation of equation (9) the Coulombic part becomes

(10) V ˆ 12 = λ α π 2 .

Solving all terms in equation (4) and gathering all values give

(11) E 0 = α + 1 α + λ α π 2 .

The total minimum energy of equation (11) can be obtained from its first derivative with respect to the variational parameter α , d E 0 ( λ , α ) d α = 0 . The calculated values of the variational parameter α and the variational ground state energy of 2D2eQD are demonstrated in Table 1.

Table 1

Ground state energy, E 0 , and variational parameter, α , for different coupling constant, λ

λ	0.0	0.1	0.3	0.5	0.7	0.9	1.1
α	1.00	0.969	0.914	0.865	0.820	0.781	0.746
E 0 ( λ , α )	2.00	2.124	2.367	2.604	2.834	3.058	3.277

4 Excited state energy of 2D2eQD

The wave function of the first excited state in parabolic confinement is given by the symmetrical and anti-symmetrical combination

(12) ψ 0 , 1 ( s , a ) ( ρ 1 , ρ 2 ) = 1 2 { ψ 0 ( ρ 1 ) ψ 1 ( ρ 2 ) ± ψ 0 ( ρ 1 ) ψ 1 ( ρ 2 ) } ,

where

(13) ψ 0 ( ρ 1 ) ψ 1 ( ρ 2 ) = α 1 2 β π exp − 1 2 ( β ρ 1 2 + α ρ 2 2 ) exp [ i θ 1 ] ,

where α is the variational parameter for the ground state and β is the variational parameter for the first excited state. Likewise the gaussed wave function for the state when both noninteracting electrons are in the first excited state is given by

(14) ψ 1 ( ρ 1 , ρ 2 ) = β 2 π ρ 1 ρ 2 exp − β 2 ( ρ 1 2 + ρ 2 2 ) exp [ i ( θ 1 + θ 2 ) ] .

Similarly, the total excited state energy is the expectation value of the Hamiltonian and described by

(15) E 2 = ψ 1 ( ρ 1 , ρ 2 ) 1 2 ∇ ρ 1 2 + 1 2 ∇ ρ 2 2 + 1 2 ρ 1 2 + 1 2 ρ 2 2 + λ ∣ ρ 1 − ρ 2 ∣ ψ 1 ( ρ 1 , ρ 2 ) .

Solving equation (15) yields

(16) E 2 = 2 β + 1 β + 1 16 ( 16 − 7 2 ) π β λ .

The minimum value of the excited state energy in equation (12) can be obtained from the condition

(17) d E 2 ( β , λ ) d β = 0 .

The variational parameter β and the excited state energy of the two electrons for the given value of coupling constant λ are calculated numerically and described in Table 2.

Table 2

Excited state energy, E 2 , and variational parameter, β , for different coupling constant, λ

λ	0.0	0.1	0.3	0.5	0.7	0.9	1.1
β	1.000	0.992	0.975	0.959	0.944	0.929	0.915
E 2 ( λ , β )	4.000	4.067	4.201	4.334	4.466	4.597	4.727

Using the obtained variational parameters α and β for the ground and second excited states, respectively, the symmetrized first excited state wave function of the two electron quantum dot is described by equation (12).

The variational parameters α and β link the ground and the excited state wave functions and are the roots of equations d E 0 ( α ) d α = 0 with E 0 given by equation (4) and d E 2 ( β ) d β = 0 , with E 2 is given by equation (16).

The computation of the average Hamiltonian (2) with respect to the gaussed wavefunction (12) gives

(18) E 1 ( α , β ) = 1 2 α + 1 α + 2 β + 2 β . + J 1 ± A 1 ,

where, J 1 and A 1 are the pure Coulombic electron electron interaction and exchange energies and are given by

(19) J 1 = 1 2 π β 2 1 β 3 2 − 1 ( α + β ) 3 2 + 2 α − 2 α α + β β λ ,

(20) A 1 = π α β 2 [ − 7 + 8 2 + ( − 2 + 4 2 ) α + ( − 2 + 4 2 ) β ] 8 ( α + β ) 3 2 λ .

The first excited state energies: para-state energy with singlet spin and ortho-state energy with triplet spin for different values of coupling constant are described in Table 3.

Table 3

Ground state energy, E 0 , and variational parameter, α , for different coupling constant, λ

λ	α	β	J 1	A 1	E 1 para	E 1 ortho
0.0	1.000	1.000	0.000	0.000	3.000	3.000
0.1	0.969	0.992	0.108	0.030	3.131	3.085
0.3	0.914	0.975	0.316	0.070	3.391	3.251
0.5	0.865	0.959	0.515	0.118	3.645	3.409
0.7	0.820	0.944	0.705	0.167	3.894	3.560
0.9	0.781	0.929	0.886	0.217	4.139	3.705
1.1	0.746	0.915	1.059	0.268	4.378	3.843

Thus, in the first excited state the system of energy levels of 2D2eQD splits into two classes: para- and ortho-state energies. The ortho-state energy lies below the para-state energy. The transition between these two states is very improbable as the spin–spin interaction is too small. If the 2D2eQD is in a state with parallel spins, it is therefore very unlikely that its state will change to one with anti parallel spins in normal situations.

5 Optical properties of two-dimensional two-electron ZnO quantum dots

Zinc oxide is a wide band gap material that has got considerable attention due to its potential application in short wave length optoelectronic devices [22]. This optoelectronic applications include devices such as blue or ultra-violet light emitting diodes and laser. All these interesting applications are based on the nonlinear optical properties such as the optical absorptions and refractive index changes.

In this section, the linear and nonlinear refractive index and absorption coefficients of 2D2eQD can be calculated by employing the density matrix formalism and iterative procedure [23]. It is assumed that 2D2e ZnO QD in parabolic confinement interacts with polarized monochromatic electric field.

(21) E ˆ ( t ) = E → exp ( − i ω t ) + E → exp ( i ω t ) .

The evolution of density matrix ρ = ∣ ψ ⟩ ⟨ ψ ∣ , including the damping constant is

(22) ρ 01 ˙ = ( i ℏ ) − 1 [ H ˆ 0 − e z E ( t ) , ρ ] 01 − δ 01 ( ρ − ρ ( 0 ) ) 01 ,

where H 0 ˆ is the Hamiltonian of the system in the absence of the field, e z is the dipole operator along the z -axis, ρ ( 0 ) is the unperturbed density operator, ρ stands for density, and δ 10 is the relaxation rate, resulting from the electron–electron, electron–phonon, and collision processes. For solving equation (22), we used the perturbation approach by expanding ρ as

(23) ρ ˆ = ∑ n ρ ˆ ( n ) ,

(24) ρ ˙ 01 n + 1 = 1 i ℏ [ [ H ˆ 0 , ρ ˆ ( n + 1 ) ] 01 − [ μ ˆ , ρ ˆ ( n ) ] 01 E → ( t ) − i ℏ δ 01 ρ 01 ( n + 1 ) ] .

The electronic polarization of quantum dot due to the field E → can be expressed as

(25) P ˆ ( t ) = ε 0 χ ω ( 1 ) E ˆ e i ω t + ε 0 χ ω ( 3 ) E ˆ 2 E ˆ e i ω t + c . c ,

where χ ω ( 1 ) and χ ω ( 3 ) are the first- and third-order nonlinear susceptibilities, respectively. Analytical expressions of the linear and nonlinear susceptibilities for a two-level quantum system are given as follows [24,25]:

(26) ε 0 χ ω ( 1 ) = N ∣ μ 01 ∣ 2 Δ E 01 − ℏ ω − i ℏ δ 01 .

For the third-order term,

(27) ε 0 χ ω ( 3 ) = N ∣ μ 01 ∣ 2 ∣ E ∣ 2 Δ E 01 − ℏ ω − i ℏ δ 01 4 ∣ μ 01 ∣ 2 ( E 01 − ℏ ω ) 2 + ( ℏ ω ) 2 − ( μ 11 − μ 00 ) 2 ( Δ E 01 − i ℏ δ 01 ) ( Δ E 01 − ℏ ω − i ℏ δ 01 ) ,

where N is the number of carriers per unit surface. The change in refractive index is related to the susceptibility, where ε 0 is the permittivity of free space.

The linear and nonlinear absorption coefficient and refractive index are related to the imaginary and real parts of the susceptibility (a measure of how much the polarization is built up in the medium by the incident field).

(28) α ( ω ) = ω μ ε R Im [ ε 0 χ ω ( m ) ] , n ( ω ) = Re χ ω ( m ) 2 n r , ( m = 1 , 3 ) ,

where ε R is the real part of the permittivity and n r is the refractive index. Mathematically manipulating these equations

(29) α ( 1 ) ( ω ) = ω μ ε R ∣ μ 01 ∣ 2 ρ v ℏ δ 01 ( E 01 − ℏ ω ) 2 + ( ℏ δ 01 ) 2 ,

(30) α ( 3 ) ( ω ) = − ω μ ε r I 2 ε 0 n r c × ∣ μ 01 ∣ 2 ρ v ℏ δ 01 [ ( E 01 − ℏ ω ) 2 + ( ℏ δ 01 2 ) ] 2 4 ∣ μ 01 ∣ 2 − ∣ μ 11 − μ 00 ∣ 2 [ 3 E 10 2 − 4 E 10 ℏ ω + ℏ 2 ( ω 2 + δ 01 2 ) ] E 10 2 + ( ℏ δ 01 ) 2 ,

where α ( 1 ) ( ω ) and α ( 3 ) ( ω ) are the change in first- and third-order absorption coefficients, respectively. I is the incident optical intensity and defined as I = 2 n r μ c ∣ ε ( ω ) ∣ 2 . The linear and nonlinear refractive indexes are as follows:

(31) n ( 1 ) ( ω ) = 1 2 n r ε 0 ∣ μ 10 ∣ 2 ρ v E 10 − ℏ ω ( E 10 − ℏ ω ) 2 + ( ℏ δ 01 ) 2 ,

(32) n ( 3 ) ( ω ) = − μ c 4 n r 2 ε 0 ∣ μ 01 ∣ 2 ρ I [ ( E 10 − ℏ ω ) 2 + ( ℏ δ 01 ) 2 ] 2 × 4 ( E 10 − ℏ ω ) ∣ μ 21 ∣ 2 − ( μ 11 − μ 00 ) 2 ( E 10 ) 2 + ( ℏ δ 01 ) 2 × { ( E 21 − ℏ ω ) [ E 10 ( E 10 − ℏ ω ) − ( ℏ δ 01 ) 2 ] − ( ℏ δ 01 ) 2 2 ( E 10 − ℏ ω ) } ] .

where ρ v is the carrier concentration, E 10 = E 1 − E 0 = ℏ ω 10 is the energy interval between the ground and excited states [36], and μ i j = ⟨ ψ i j ∣ e r ∣ ψ i j ⟩ , with i , j = 0 , 1 are the matrix elements of the dipole moment, and μ is the permeability of the medium.

The total absorption is the sum of linear and nonlinear absorption coefficients and is approximated by

(33) α ( ω ) = α ( 1 ) ( ω ) + α ( 3 ) ( ω ) .

Similarly, the total refractive index is the sum of linear and nonlinear refractive index and given by

(34) n ( ω ) = n ( 1 ) ( ω ) + n ( 3 ) ( ω ) .

The linear and nonlinear absorption coefficients and changes in refractive index of 2D2eQD are determined in equations (29), (30), (31), and (32), respectively. The parameters used in this calculation are the carrier density ρ v = 3 × 1 0 22 m − 3 , the optical effective mass of ZnO m ∗ = m e ∗ m h ∗ m e ∗ + m h ∗ m 0 = 0.21 m 0 (where m 0 is the electron mass), the static dielectric constant 8.5, the refractive index of the medium n r = 2.92 , and the relaxation rate δ 01 = 0.4 T s − 1 . The linear, third order, and total absorption coefficients and refractive index changes of 2D2eQD as a function of a photon energy with different confining frequencies are shown in Figures 1 and 2.

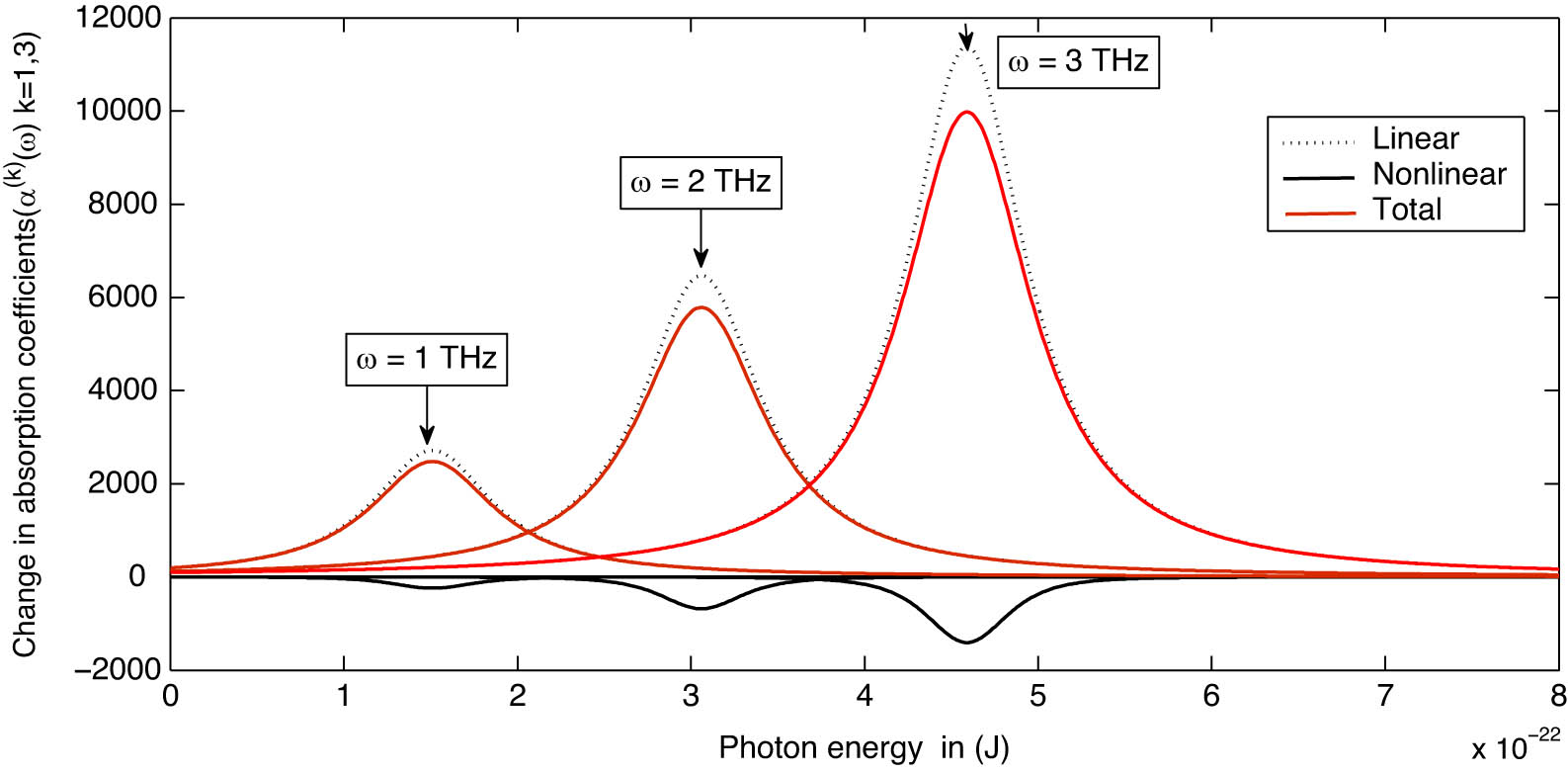
$Figure 1 Absorption coefficients of 2D2eQD for confining frequencies of ω 0 = 1 {\omega }_{0}=1 , 2, and 3 THz.$

Figure 1

Absorption coefficients of 2D2eQD for confining frequencies of ω 0 = 1 , 2, and 3 THz.

$Figure 2 Refractive index changes of 2D2eQD for confining frequencies of ω 0 = 1 {\omega }_{0}=1 , 2, and 3 THz.$

Figure 2

Refractive index changes of 2D2eQD for confining frequencies of ω 0 = 1 , 2, and 3 THz.

As it can be seen from Figure 1, the magnitude of the absorption coefficients (linear, nonlinear, and total) are magnified, as the confining frequency of the 2D2eQD increases from 1 to 3 THz. Moreover the maximas shift toward the high energy or frequency. This property is useful for device application at different frequency regimes.

As it is demonstrated from Figure 2, the magnitude of the refractive index changes (nonlinear and total) are amplified, for the increment of confining frequency from 1 to 3 THz. Moreover blue shift is observed as magnitude of the confining frequency increases. The intensity-dependent nonlinear and total absorption coefficient and refractive index changes are described in Figures 3 and 4, respectively. In Figure 3, it is observed that as the intensity of the source increases, the magnitude of the nonlinear absorption coefficient increases. However, the total absorption coefficient decreases since the linear absorption coefficient does not depend on optical intensity. This nonlinear optical property is a fundamental for developing optical limiting devices. In Figure 4, it is demonstrated that as the intensity of the source increases, the magnitude of the change in nonlinear refractive index increases. But, the total refractive index decreases. The linear refractive index is constant and does not be affected with an increment of optical intensity.

Figure 3

Nonlinear and total absorption coefficients of 2D2eQD for different values of intensity.

$Figure 4 Linear, nonlinear, and total refractive index changes of 2D2eQD for different values of intensity.$

Figure 4

Linear, nonlinear, and total refractive index changes of 2D2eQD for different values of intensity.

6 Conclusion

The ground and excited state energies of 2D2e ZnO QD in parabolic confinement are calculated for different values of coupling constant using variational technique. There are para- and ortho states in 2D2eQD in which quantum transition between them is almost improbable unless electron bombardment is considered. The ortho state of the 2D2eQD with triplet level lies above the ground sate and below the first excited para-state. This state is metastable and the charge carriers stay for long time. The singlet spin wavefunction of the ground state and the triplet spin wavefunction of the lowest ortho state are the states responsible for quantum information processing. Using the calculated energy eigen value, the linear, third order nonlinear, and total absorption coefficient and refractive index changes are studied between the ground state and the first excited para state. The optical study shows that increasing the confining frequency of the 2D2eQD in parabolic confinement alters both the magnitude and position of peak of the linear, third-order nonlinear and total absorption coefficient and refractive index changes. Increasing the confining frequency magnifies the magnitude of the linear, nonlinear, and total absorption coefficient and refractive index changes. Moreover, increasing the confining frequency results in blue shift of the peak for both optical parameters. Increasing the optical intensity of the system while fixing all other parameters constant amplifies the magnitude of the nonlinear absorption and refractive index changes. As the result, the total absorption coefficient and refractive index diminish as the magnitude of the optical intensity increases.

Acknowledgements

The author is thankful to the Department of Physics of Jimma University for material support.

Funding information: The author states no funding involved.
Conflict of interest: The author declares there is no conflict of interest.
Data availability statement: All data relevant to this publication are included in the text and hence available to every one.

References

[1] Rink SS, Miller DAB, Chemla DS. Theory of the linear and nonlinear optical properties of semiconductor microcrystallites. Phys Rev B. 1986;35:8114. 10.1103/PhysRevB.35.8113. Suche in Google Scholar

[2] Bryant GW. Theory for quantum-dot quantum wells: pair correlation and internal quantum confinement in nanoheterostructures. Phys Rev B. 1995;52:R16997. 10.1103/PhysRevB.52.R16997. Suche in Google Scholar PubMed

[3] Harrison P. Quantum wells, wires and dots. Chichester: Wiley; 2005. 10.1002/0470010827Suche in Google Scholar

[4] Sahin M. Photoionization cross section and intersublevel transitions in a one-and two-electron spherical quantum dot with a hydrogenic impurity. Phys Rev B. 2008;77:045317. 10.1103/PhysRevB.77.045317. Suche in Google Scholar

[5] Leobandung E, Guo L, Chou SY. Single hole quantum dot transistors in silicon. Appl Phys Lett. 1995;67:2338. 10.1063/1.114337. Suche in Google Scholar

[6] Likharev KK. Correlated discrete transfer of single electrons in ultrasmall tunnel junctions. IBM J Res Dev. 1998;32:1444. 10.1147/rd.321.0144Suche in Google Scholar

[7] Yuen SY. Fast relaxing absorptive nonlinear refraction in superlattices. Appl Phys Lett. 1983;43:813. 10.1063/1.94518. Suche in Google Scholar

[8] Loss D, DiVincenzo DP. Quantum computation with quantum dots. Phys Rev A. 1998;57:120. 10.1103/PhysRevA.57.120. Suche in Google Scholar

[9] Imamura K, Sugiyama Y, Nakata Y, Murol S, Yokoyama N. New optical memory structure using self assembled InAs quantum dots. Jpn Appl Phys. 1995;11:L1445–47. 10.1143/JJAP34L1445. Suche in Google Scholar

[10] Wei-Ping L, Jing-Lin X, Ji-Wen Y, Yi-Fu Y, Zi-Wu W. The energy levels of a two-electron two-dimensional parabolic quantum dot. Chin Phys B. 2010;19(4):047102. 10.1088/1674-1056/19/4/047102. Suche in Google Scholar

[11] Woldemariam MM. Nonlinear absorption coefficient and refractive index changes of two-dimensional two-electron quantum dot in rigid confinement. Int J Modern Phys B. 2019;33(9):1950078. 10.1142/S0217979219500784. Suche in Google Scholar

[12] Mengesha M, Mal’nev V. Optical properties of two-electron quantum dots in low lying para-and ortho-states. Superlatt Microstruct. 2012;52(1):1–10. 10.1016/j.spmi.2012.04.008. Suche in Google Scholar

[13] Menberu M, Mal’nev VN. Two electron quantum dots with parabolic confinement (Low lying para- and ortho-states). Ukr J Phys. 2011;56(11):ISSN 2071-0194. Suche in Google Scholar

[14] Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev. 1935;47:777. 10.1103/PhysRev.47.777. Suche in Google Scholar

[15] He L, Bester G, Zunger A. Singlet-triplet splitting, correlation, and entanglement of two electrons in quantum dot molecules. Phys Rev B. 2005;72:195307. 10.1103/PhysRevB.72.199903. Suche in Google Scholar

[16] Ferron A, Osenda O, Serra P. Entanglement in resonances of two-electron quantum dots. Phys Rev A. 2009;79:032509. 10.1103/PhysRevA.79.032509. Suche in Google Scholar

[17] Planells J, Rajadel F, Royo M. Dielectric control of spin in semiconductor spherical quantum dots. J Appl Phys. 2008;104:014313. 10.1063/1.2952070. Suche in Google Scholar

[18] Huang LL, Chang HJ, Chou YY, Wang CH, Chen TT, Chen YF, et al. Optical properties of InGaN quantum dots grown by SiNx nanomasks. J Appl Phys. 2007;101:083501. 10.1063/1.2717258. Suche in Google Scholar

[19] Yilmaz S, Şafak H. Oscillator strengths for the intersubband transitions in a CdS-SiO2 quantum dot with hydrogenic impurity. Phys E. 2007;36(1):40–4. 10.1016/j.physe.2006.07.040. Suche in Google Scholar

[20] Turkoglu A, Dakhlaoui H, Durmuslar AS, Mora-Ramos ME, Ungan F. Nonlinear optical properties of a quantum well with inversely quadratic Hellman potential. Eur Phys J B. 2021;94:111. 10.1140/epjb/s10051-021-00129-4. Suche in Google Scholar

[21] Turkoglu A, Aghoutane N, Feddi E, Mora-Ramos ME, Ungan F. Non-resonant intense laser field effect on the nonlinear optical properties associated to the inter-and intra-band transitions in an anharmonic quantum well submitted to electric and magnetic field. Solid State Commun. 2021;334–335:114390. 10.1016/j.ssc.2021.114390. Suche in Google Scholar

[22] Kiliani G, Schneider R, Litvinov D, Gerthsen D, Fonin M, Rüdiger U, et al. Ultraviolet photoluminescence of ZnO quantum dots sputtered at room-temperature. Optics Express. 2011 Jan 17;19(2):1641–7. 10.1364/OE.19.001641. Suche in Google Scholar PubMed

[23] Boyd RW. Nonlinear optics. New York: Rochester; 2007. Suche in Google Scholar

[24] Rezaei G, Vaseghi B, Taghizadh F, Vahdani MRK, Karimi MJ. Intersubband optical absorption coefficient changes and refractive index changes in a two-dimensional quantum pseudodot system. Superlatt Microstruct. 2010;48(5):450–7. 10.1016/j.spmi.2010.08.009. Suche in Google Scholar

[25] Vahdani MR, Rezaei G. Intersubband optical absorption coefficients and refractive index changes in a parabolic cylinder quantum dot. Phys Lett A. 2010 Jan 11;374(4):637–43. 10.1016/j.physleta.2009.06.042. Suche in Google Scholar

Received: 2021-05-01

Revised: 2021-07-18

Accepted: 2021-08-21

Published Online: 2021-10-01

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2021-0067

Schlagwörter für diesen Artikel

2D2eQD; parabolic confinement; optical properties

Creative Commons

BY 4.0