Abstract
This article proposes a metamaterial-based temperature sensor with high sensitivity using the thermally tunable liquid metal of mercury. The response of the metamaterial at different temperatures is theoretically investigated. In the merit of the temperature-sensitive thermal expanding of the embedded mercury resonant structure, different absorption peak frequencies can be observed at different temperatures, which enables the proposed metamaterial capability of temperature sensing. The numerical simulations show that the temperature sensitivity of the proposed sensor can reach up to 27.64 MHz/°C within the range of 0–21.8°C. The calculated electric field and surface current distributions illustrate that the high sensitivity is originated from the dual-dipole mode of the resonant structure. Meanwhile, the dependence of the structural dimensions on temperature sensitivity is discussed to optimize the sensor design. The proposed strategy paves a new way for developing temperature sensors with high sensitivity.
1 Introduction
A metamaterial is an artificial electromagnetic (EM) material with a periodic unit structure [1]. Due to the unique and fabulous ability to manipulate EM waves, the metamaterials have been utilized in several fields such as EM wave transmission modulation, EM shielding, and sensing [2,3,4,5]. By changing the unit cell structure or the dielectric properties of the substrate, one can easily realize the dynamic regulation of EM waves with the metamaterial, which sets a foundation of its application in sensing [6]. In recent years, metamaterial-based biology [7], pressure [8], and chemical [9] sensing has been widely investigated.
Among the sensing technologies, temperature sensing is a key research and has attracted considerable attention [10,11,12,13]. Generally, there are three main methods to realize metamaterial-based temperature sensing. One method is to use temperature-sensitive dielectric materials as the substrate. For example, materials such as liquid crystals [14,15], STO [16], and VO2 [17] were used in thermal tunable metamaterials. It has the advantages of miniaturization and high flexibility. However, the variation of dielectric constant with temperature is usually small, and its nonlinearity is strong, resulting in low resolution/sensitivity of temperature sensing. Moreover, other defects such as small sensing dynamic range further restrict the development of practical applications of this method [18,19]. Another method is to include the nano-scale micro-electro-mechanical system (MEMS) into the metamaterial design. However, the complex preparation processes, low recognition degree, and high costs of the MEMS structures significantly hinder their practical applications [20,21]. Recently, the metamaterial-based temperature sensors have gradually turned to adopt materials with high thermal expansion coefficients. Due to the different thermal expansion coefficients of different materials, the heterogeneous composite structure produces deformation with the change of temperature, changing the equivalent EM parameters of the structure and hence realizing the detection of environmental temperature [12,22,23]. This approach has the advantages of ingenious structural design, continuous adjustability, and repeatability [24]. Meanwhile, the thermal bending will be induced in response to the temperature change by packing two or more materials with different thermal expansion coefficients into a resonant cell, as thermo-mechanical tuning is also an effective way for constructing reconfigurable metamaterials [25]. Thermo-mechanical tuning was first proposed at terahertz frequencies by Tao et al. [26]. Pitchappa et al. experimentally demonstrated thermally reconfigurable metamaterials with a tuning range of 37.5% [23]. However, the defects such as weak deformation and low-temperature sensing resolution for such configurations also hinder their application.
Mercury, as a liquid metal with strong volume expansion capacity with temperature changes, has been utilized in realizing temperature sensors for a long time. For example, the mercury-filled thermometer has been widely used for centuries. Recently, mercury has been used to construct metamaterials. Ma et al. proposed a thermally tunable metamaterial based on the toroidal resonators that could achieve high Q-factor sensing by verifying the temperatures [22]. Wang et al. investigated a temperature-controlled metamaterial absorber based on mercury [27]. By changing the background temperature, the absorption bandwidth can be tuned effectively. However, the method to increase the sensitivity of mercury-based metamaterial is still a focus of the community. In this article, a temperature sensor based on metamaterial design with high sensitivity is proposed. In the merit of high Q-factor resonance of the selected EM metamaterial and the excellent thermal expansion coefficient of mercury material, the temperature sensitivity of the proposed sensor can reach up to 27.64 MHz/°C within the range of 0–21.8°C, with a maximum figure-of-merit (FOM) of 12.5°C. The compact design strategy paves a new way for developing metamaterial-based temperature sensors with high sensitivity.
2 Metamaterial-based sensor design and demonstration
Figure 1 shows the unit cell structure of the proposed mercury-based EM metamaterial. The resonant structure filled with mercury is embedded in the wrapping medium. The resonant structure is divided into upper and lower parts. In the upper part, both ends of the mercury-filled C-shaped pipe are sealed since the electrical length of the mercury bar cannot vary with the change of background temperature. However, since the liquid level can be raised with the increase of temperature, the mercury does not occupy the whole pipe in the initial state in the lower part. Furthermore, a cylindrical tank to store the mercury was placed at the bottom of the pipe. The dielectric constant and the loss tangent of the 4.5 mm-thick wrapping medium are 2.1 and 0.002, respectively. Moreover, the metallic groundsheet was modeled as a continuous copper film with the conductivity σ = 5.88 × 107 S/m.
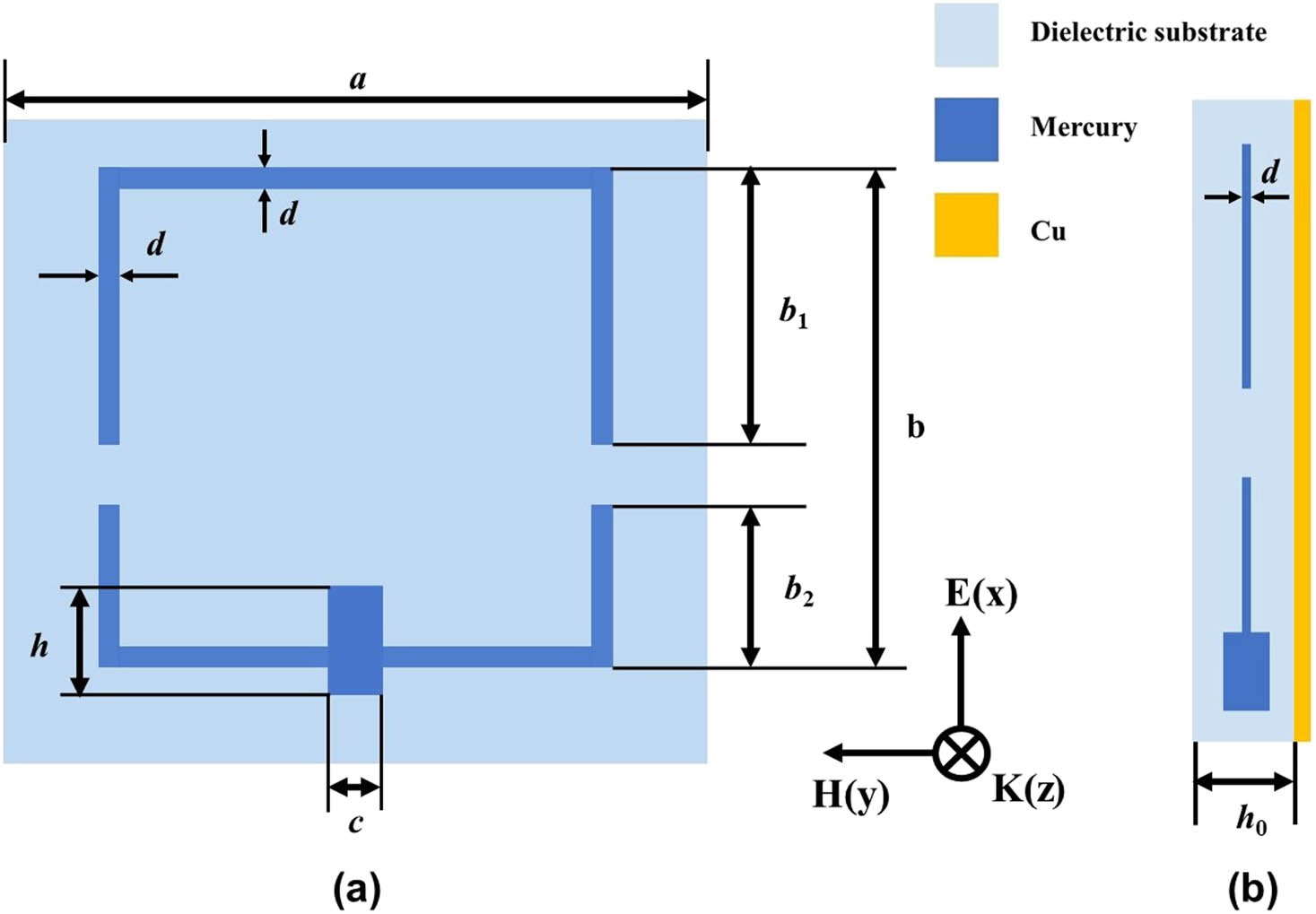
The unit cell of the metamaterial-based temperature sensor: (a) top view and (b) side view.
The thermal expansion of mercury can be described as follows:
where ΔV is the change of volume varied with the change of temperature, V 0 is the initial volume of the material, ΔT is the variation of temperature, and γ is the expansion coefficient.
It can be obtained from equation (1) that V 0 is proportional to ΔV; hence, the larger the initial volume of mercury, the larger the thermal expansion volume per unit temperature change. In this case, a relatively bigger mercury storage tank will lead to a greater change of the electrical length of mercury, which makes a bigger change of resonant frequency and thus a higher sensitivity.
Since the mercury filled in the upper part of the resonant structure is fixed, only the expansion of mercury in the lower part needs to be considered. From Figure 1, the initial volume of mercury filled in the lower part of the structure can be expressed as follows:
Hence, the relationship between the increasing temperature and the thermally expanded volume can be obtained by combining equations (1) and (2). To better show the influence of the temperature on the structural parameter of resonant structure, the change in the height of the liquid level (with the initial value of b 2) versus the change of the temperature can be derived as follows:
For the proposed metamaterial-based sensor, the variable electrical length, e.g., the height of the mercury bar b 2, influences the resonant frequency most. Hence, according to equation (3), Δl should be increased as much as possible to improve the temperature sensitivity. There are two methods to increase Δl for the proposed structure: by increasing the volume of the storage tank V 0 or reducing the section width d of the mercury bar. Therefore, the optimized structural parameters of the proposed unit cell structure are as follows: a = 20, b = 16, b 1 = 8, b 2 = 6, c = 2, d = 0.2, h = 3, and h 0 = 4.5 mm.
The absorption rate of the metamaterial can be calculated by the reflection parameter S 11 and the transmission parameter S 21 with A(w) = 1 − |S 11(w)|2 − |S 21(w)|2. Due to the existence of the ground plate, the transmission is zero and the absorption reads A(w) = 1 − |S 11(w)|2. The simulations were conducted using the finite element method (FEM), where periodic boundary conditions were applied for both x and y directions, and open boundary condition was utilized in the z-direction. In the simulation, the tetrahedral mesh was selected to model the proposed structure, while iterative accuracy of 1 × 10−6 was chosen to ensure the high precision of the simulation. Moreover, the EM response of the proposed structure was assumed to be excited by the plane wave with an electric field parallel to the x-axis. Figure 2 shows the reflection and absorption spectra of the proposed sensor in the initial state with a background temperature of 0°C. Figure 2 shows that there are two resonant peaks f 1 and f 2 located at 7.55 and 9.06 GHz, with absorption rates of 92.3 and 99.9%, respectively. These sharp resonant peaks with high Q-factors set the foundation for temperature sensing.

Reflection and absorption spectra of the metamaterial-based sensor under the initial state with a background temperature of 0°C.
3 Results and discussion
To verify the sensing performance of the proposed structure, EM responses under different background temperatures were simulated. The change in the height of liquid level Δl with temperature was first calculated using equation (3). Then, the lower part structure with a different mercury bar length of b 2 + Δl was simulated to show the resonant frequency variation of the metamaterial at different temperatures. Figure 3(a) shows the relationship between the background temperature and the length of mercury bar b 2 after the thermal expansion. It can be seen from the figure that b 2 increases from 6 to 7 mm, corresponding to the increase in the background temperature from 0 to 21.8°C. Figure 3(b) illustrates the simulated reflection peak frequencies of mode f 2 under different temperatures. The variation of resonant peaks of mode f 1 is also included as a subfigure in Figure 3(b). For mode f 2, the resonant frequency redshifts from 9.06 to 8.47 GHz with the increase in the temperature from 0 to 21.8°C, with a maximum frequency tunability of 6.51%. However, the frequency shifts of mode f 1 in the temperature region of 0–21.8°C are much smaller compared with mode f 2. For example, the calculated frequency tunability of mode f 1 is only 0.5%. A bigger frequency tunability leads to a better sensor resolution as mode f 2 is more suitable for temperature sensing. Moreover, Figure 3(b) shows that the resonant intensity of mode f 1 decreases rapidly with the increase of temperature, which significantly degrades its application in sensing. Hence, mode f 1 will not be further discussed in the following sections. Figure 3(c) shows the absorption spectra of the proposed sensor at different temperatures. It can be seen from the figure that the overall absorption rate maintains above 90% in each case. Hence, the structure can also be used as a temperature-controlled tunable EM wave absorber.
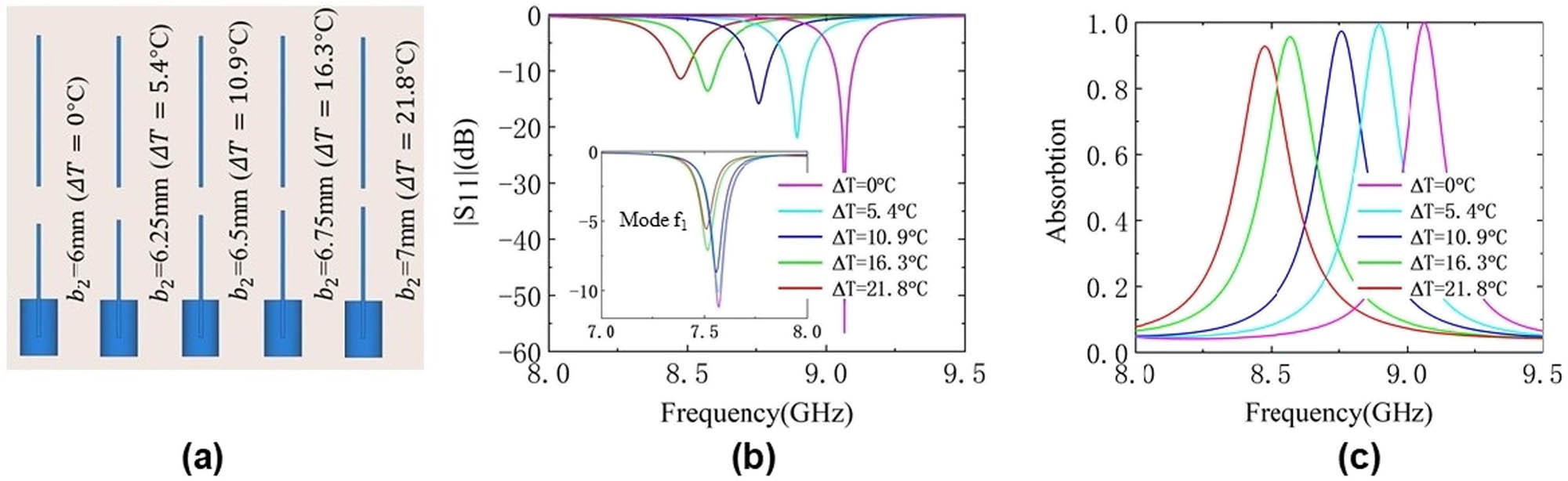
Simulation results for the tunability of mercury-based metamaterial at different temperatures: (a) mercury bar length b 2 and (b) reflection and (c) absorption spectra.
To investigate the physical mechanism of the proposed structure, the electric field distribution and the surface current distribution were simulated on the mercury pattern and the ground plane, respectively. Figure 4(a) and (b) show the electric field and also show the surface current distributions of the metamaterial sensor at the frequency of 9.06 GHz. This figure also shows that there are two electric dipoles located at the bottom of the resonant structure, which excites strong electric resonances. Figure 4(b) further indicates that the currents are mainly concentrated in the lower part of the resonant structure as the resonant frequency is more sensitive to the mercury bar length b 2. Hence, the temperature sensitivity of the proposed structure can be enhanced. The current flow on the ground plate shown in Figure 4(c) is opposite to that on the mercury pattern, which leads to the existence of an equivalent current loop and the excitation of magnetic resonance. Therefore, both the electric and the magnetic resonances are responsible for the strong absorption of the temperature sensor.

Numerical simulation results. (a) Distributions of the electric field and the surface current on (b) mercury pattern layer and (c) metal ground plate. The frequency is 9.06 GHz.
It is well known that the resonance frequency of third-order resonances is approximately three times higher than that of the fundamental mode. However, in the TPA structure, the location of the third-order resonances shows an obvious red shift. To further investigate this phenomenon, we simulated the magnetic field distribution on the surface of some adjacent stacking patches at 27.0 GHz, and the results are shown in Figure 4. As shown in Figure 4b–d, the magnetic field represented as three stripes is originated from the third-order resonances. Furthermore, the distribution of magnetic field is mainly along the diagonal line of the square patch under TE-polarized incidence, which is very different from the circumstances in traditional PA structures. The typical magnetic field distribution of third-order resonance in the nontwisted PA structure is shown in Figure 4e. Compared with the nontwisted PA structure, the M-field spot on TPA’s patch is much larger. Hence, the resonance frequency of the third-order mode in TPA is much lower than that in PA, which enables its coupling with fundamental modes within a broadband region (22.0–35.0 GHz) and finally leads to an extra broadband absorption.
By incorporating the variation of resonant frequency with different temperatures shown in Figure 3(a), the temperature sensitivity of the proposed structure can be calculated. The sensitivity can be defined as S = ∆f/∆T, where ∆f is the change of resonant frequency, while ∆T is the change of the background temperature. Figure 5(a) presents the linear fitting result of the temperature sensitivity. It can be seen from the figure that the calculated temperature sensitivity of the proposed structure is 27.64 MHz/°C within the region of 0–21.8°C. Hence, the sensor can achieve the detection of the background temperature with high sensitivity. Meanwhile, the precision for sensing application was determined using the Q-factor of the sensor, defined as Q = f 0/∆f, where f 0 is the resonant frequency and ∆f represents the 3 dB resonance frequency bandwidth. As shown in Figure 3(a), with the variation of temperature, both the resonant frequency f 0 and the 3 dB bandwidth ∆f change correspondingly. Hence, the Q-factor of the sensor varies in the range of 110–983. The high Q-factor within the overall operation range enables the precision sensing of the proposed temperature sensor.

(a) Relationship between the resonant frequency and background temperature changing ΔT with (a) mercury bar section width d of 0.2 mm and (b) different mercury bar section widths. (c) Calculated temperature sensitivity with different values of section width d.
The influence of structural parameters (e.g., the section width of mercury bar d) on sensing performance is further analyzed. Figure 5(b) shows the change of resonant frequencies with different temperatures under different values of section width d of mercury bar. It is observed that the resonant frequencies redshift with the increase of temperature. However, there is a wider frequency modulation bandwidth for structures with smaller mercury bar section width, which leads to a higher sensitivity. Figure 5(c) shows that the temperature sensitivity of the structure with d of 0.2 mm is 27.64 MHz/°C. When the mercury bar section width increases to 0.6 mm, the sensitivity decreases rapidly to 3.41 MHz/°C. Further decrease of d will lead to a higher sensitivity. However, the sample preparation would be more difficult for such a configuration. It should be noted that the width of the mercury bar d has a strong influence on the sensitivity of the proposed structure. The volume change of the mercury will be enlarged with the increase of the width d, which also leads to an increase of the measurable temperature limit. However, the sensitivity of the absorber will decrease as the resonant frequency shift per temperature is smaller. On the contrary, reducing the width d will enhance the sensitivity at the cost of a lower temperature limit.
The proposed metamaterial-based temperature sensor can be fabricated with the aid of 3D printing technology. In this case, the dielectric material of the substrate should be printable. For instance, the polytetrafluoroethylene (PTFE) can be used as the wrapping medium, which acts as a good mercury container with similar dielectric properties to the design (ε PTFE = 2.1 + 0.001i). To fabricate such a sample, the multi-material hybrid micro-droplets jetting modeling (MHMJM) technology, which enables two-material hybrid printing via two non-contact nozzles, can be utilized to form the PTFE and the mercury layer simultaneously [28,29].
Table 1 compares the performance of the proposed temperature sensor with some reported sensors. It should be noted that the FOM, defined as sensitivity/∆f, was included in the table to show the precision of temperature sensing. It can be observed from Table 1 that the proposed sensor outperforms the recently reported temperature sensors in terms of sensitivity and FOM. Hence, more precision sensing can be achieved with the configuration.
Performance comparison of reported temperature sensors
| Reference | Sensing materials | Dynamic range (°C) | Sensitivity (MHz/°C) | FOM (°C) |
|---|---|---|---|---|
| [6] | Hg | 24–38 | 17.14 | 0.3 |
| [10] | Boron nitride, barium titanate | 20–200 | 0.46 | N/A |
| [11] | BaTiO3 | 20–140 | 7 | N/A |
| [22] | Hg | 0–15 | 11.69 | 10 |
| [24] | Barium titanate | 20–50 | 7.28 | N/A |
| This work | Hg | 0–21.8 | 27.64 | 12.56 |
4 Conclusion
A metamaterial-based temperature sensor using the thermally tunable liquid metal of mercury is proposed in this article. The thermal expansion of mercury leads to a deformation of the metamaterial unit cell structure, hence adjusting the resonant frequency and setting a foundation for temperature sensing. In the merit of the high Q-factor resonance of the selected metamaterial configuration and the excellent thermal expansion coefficient of mercury material, the temperature sensitivity of the proposed sensor can reach up to 27.64 MHz/°C within the range of 0–21.8°C, with the maximum FOM of 12.56. The simulation results demonstrate that the proposed structure can maintain an absorption rate of above 90%. Moreover, the proposed structure can also be treated as a temperature-controlled tunable EM wave absorber with a frequency tunability of 6.51%. Meanwhile, by reducing the mercury bar width, the temperature sensitivity of the proposed structure can be further enhanced. The simulated electric field and surface current distributions show that the high sensitivity of the structure is originated from the excited dual-dipole mode. The proposed metamaterial-based sensor provides an alternative for future applications in high-performance temperature sensing.
-
Funding information: This work was supported by the National Natural Science Foundation of China (No. 61871171), the Aeronautical Science Foundation of China (No. 2020Z0560P4001), and the Fundamental Research Funds for the Central Universities of China (No. JD2020JGPY0012).
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors state no conflict of interest.
References
[1] Zhang Y, Yi Z, Wang X, Chu P, Yao W, Zhou Z, et al. Dual band visible metamaterial absorbers based on four identical ring patches. Phys E Low Dimens Syst Nanostruct. 2021;102(1):114526.10.1016/j.physe.2020.114526Suche in Google Scholar
[2] Kang YQ, Gao P, Liu HM, Gao LS. A polarization-insensitive dual-band plasmonic metamaterial absorber for a sensor application. Phys Scr. 2015;96(6):301358.10.1088/1402-4896/abf007Suche in Google Scholar
[3] Bhardwaj A, Pratap D, Srivastava KV, Ramakrishna SA. Highly sensitive permittivity sensor using an inhomogeneous metamaterial cylindrical waveguide. IEEE Sens J. 2021;21(7):3050778.10.1109/JSEN.2021.3050778Suche in Google Scholar
[4] Tao J, Liang Z, Zeng G, Meng D, Smith DR, Liu QH, et al. Dual functionality metamaterial enables ultra-compact, highly sensitive uncooled infrared sensor. Nanophotonics. 2021;10(4):1337–46.10.1515/nanoph-2020-0607Suche in Google Scholar
[5] Mou N, Liu X, Wei T, Dong H, He Q, Zhou L, et al. Large-scale, low-cost, broadband and tunable perfect optical absorber based on phase-change material. Nanoscale. 2021;12(9):5374–9.10.1039/C9NR07602FSuche in Google Scholar
[6] Liang M, Zheng WX, Li J, Chen DX, Wang WJ, Liu YF, et al. High-Q Hg-anapole resonator with microstrip line coupling for high-precision temperature sensing applications. Results Phys. 2021;24(1):104172.10.1016/j.rinp.2021.104172Suche in Google Scholar
[7] Tamim AM, Faruque MRI, Khandaker MU, Islam MT, Bradley DA. Electromagnetic radiation reduction using novel metamaterial for cellular applications. Radiat Phys Chem. 2021;178:108976.10.1016/j.radphyschem.2020.108976Suche in Google Scholar
[8] Jeong H, Cui YP, Tentzeris MM, Lim S. Hybrid (3D and inkjet) printed electromagnetic pressure sensor using metamaterial absorber. Addit Manuf. 2020;35:101405.10.1016/j.addma.2020.101405Suche in Google Scholar
[9] Qureshi SA, Zainal Abidin Z, Isa Ashyap AY, Majid HA, Kamarudin MR, Yue M, et al. Millimetre-wave metamaterial-based sensor for characterisation of cooking oils. Int J Antennas Propag. 2021;2021:5520268.10.1155/2021/5520268Suche in Google Scholar
[10] Karim H, Delfin D, Chavez LA, Delfin L, Martinez R, Avila J, et al. Metamaterial based passive wireless temperature sensor. Adv Eng Mater. 2017;19(5):1600741.10.1002/adem.201600741Suche in Google Scholar
[11] Zemouli S, Chaabi A, Talbi HS. Design of a compact and high sensitivity temperature sensor using metamaterial. Int J Antennas Propag. 2015;2015:301358.10.1155/2015/301358Suche in Google Scholar
[12] Liu Q, Li SG, Chen HL, Li JS, Fan ZK. High-sensitivity plasmonic temperature sensor based on photonic crystal fiber coated with nanoscale gold film. Appl Phys Express. 2015;8(4):046701.10.7567/APEX.8.046701Suche in Google Scholar
[13] Bie YH, Luo J, Li WJ, Zhang XY, Ji A, Sang HS, et al. Modeling of terahertz metamaterial-sensors for simulation based on effect of resonance induction. In: Tan J, Wen X, editors. 9th International Symposium on Precision Engineering Measurements and Instrumentation; 2014 Aug 8–10. Changsha, China: Proceedings of SPIE; 2015. p. 94460D10.1117/12.2084169Suche in Google Scholar
[14] Kowerdziej R, Olifierczuk M, Parka J. Thermally induced tunability of a terahertz metamaterial by using a specially designed nematic liquid crystal mixture. Opt Express. 2018;26(3):002443.10.1364/OE.26.002443Suche in Google Scholar PubMed
[15] Kowerdziej R, Garbat K, Walczakowski M. Nematic liquid crystal mixtures dedicated to thermally tunable terahertz devices. Liq Cryst. 2017;45(7):1040–6.10.1080/02678292.2017.1404158Suche in Google Scholar
[16] Huang X, He W, Yang F, Ran J, Yang Q, Xie S. Thermally tunable metamaterial absorber based on strontium titanate in the terahertz regime. Opt Mater Express. 2019;9(3):1377–85.10.1364/OME.9.001377Suche in Google Scholar
[17] Zhang GQ, Ma H, Lan CW, Gao R, Zhou J. Microwave tunable metamaterial based on semiconductor-to-metal phase transition. Sci Rep. 2017;7(1):5773.10.1038/s41598-017-06230-ySuche in Google Scholar PubMed PubMed Central
[18] Varadan VV, Ji LM. Temperature dependence of resonances in metamaterials. IEEE Trans Microw Theory Tech. 2010;58(10):2673–81.10.1109/TMTT.2010.2065910Suche in Google Scholar
[19] Mou NL, Liu XL, Wei T, Dong HX, He Q, Zhou L. Large-scale, low-cost, broadband and tunable perfect optical absorber based on phase-change material. Results Phys. 2020;12(9):5374–9.10.1039/C9NR07602FSuche in Google Scholar PubMed
[20] Alves F, Grbovic D, Kearney B, Karunasiri G. High sensitivity metamaterial based bi-material terahertz sensor. In: Sadwick LP, Osullivan CM, editors. Conference on Terahertz, RF, Millimeter, and Submillimeter-Wave Technology and Applications VI; 2013 Feb 5–7. San Francisco, USA: Proceedings of SPIE; 2013. p. 86241110.1117/12.2005272Suche in Google Scholar
[21] Zhang HF, Wang ZL, Hu CX, Liu HB. A tailored broadband terahertz metamaterial absorber based on the thermal expansion feature of liquid metal. Results Phys. 2020;16:102937.10.1016/j.rinp.2020.102937Suche in Google Scholar
[22] Ma L, Chen D, Zheng W, Li J, Wang W, Liu Y, et al. Thermally tunable high-Q metamaterial and sensing application based on liquid metals. Opt Express. 2021;29(4):6069–79.10.1364/OE.418024Suche in Google Scholar PubMed
[23] Pitchappa P, Manjappa M, Krishnamoorthy HNS, Chang YH, Lee C, Singh R. Bidirectional reconfiguration and thermal tuning of microcantilever metamaterial device operating from 77 to 400 K. Appl Phys Lett. 2017;111(26):261101.10.1063/1.5006836Suche in Google Scholar
[24] Karim H, Shuvo MAI, Delfin D, Lin YR, Choudhuri A, Rumpf RC. Development of metamaterial based low cost passive wireless temperature sensor. In: Lynch JP, Wang KW, Sohn H, editors. Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; 2014 Mar 10–13. San Diego, USA: Proceedings of SPIE; 2014. p. 90612K10.1117/12.2045242Suche in Google Scholar
[25] Xiao SY, Wang T, Liu TT, Zhou CB, Jiang XY, Zhang JF. Active metamaterials and metadevices: a review. J Phys D: Appl Phys. 2020;53(50):503002.10.1088/1361-6463/abacedSuche in Google Scholar
[26] Tao H, Strikwerda AC, Fan K, Padilla WJ, Zhang X, Averitt RD. Reconfigurable terahertz metamaterials. Phys Rev Lett. 2009;103(14):147401.10.1103/PhysRevLett.103.147401Suche in Google Scholar PubMed
[27] Wang ZL, Hu CX, Liu HB, Zhang HF. A newfangled terahertz absorber tuned temper by temperature field doped by the liquid metal. Plasmonics. 2020;16(2):425–34.10.1007/s11468-020-01296-3Suche in Google Scholar
[28] Deng G, Sun H, Lv K, Yang J, Yin Z, Li Y, et al. 3D rampart-based dual-band metamaterial absorber with wide-incident-angle stability. Appl Phys Express. 2021;14(2):022005.10.35848/1882-0786/abd9ffSuche in Google Scholar
[29] Deng G, Sun H, Lv K, Yang J, Yin Z, Chi B. 3D-printed multiband absorber based on stereo frequency selective structures. Phys Status Solidi A. 2021;218(7):2000734.10.1002/pssa.202000734Suche in Google Scholar
© 2021 Guangsheng Deng et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge
Artikel in diesem Heft
- Regular Articles
- Circular Rydberg states of helium atoms or helium-like ions in a high-frequency laser field
- Closed-form solutions and conservation laws of a generalized Hirota–Satsuma coupled KdV system of fluid mechanics
- W-Chirped optical solitons and modulation instability analysis of Chen–Lee–Liu equation in optical monomode fibres
- The problem of a hydrogen atom in a cavity: Oscillator representation solution versus analytic solution
- An analytical model for the Maxwell radiation field in an axially symmetric galaxy
- Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application
- Verification of the accommodative responses in viewing an on-axis analog reflection hologram
- Irreversibility as thermodynamic time
- A self-adaptive prescription dose optimization algorithm for radiotherapy
- Algebraic computational methods for solving three nonlinear vital models fractional in mathematical physics
- The diffusion mechanism of the application of intelligent manufacturing in SMEs model based on cellular automata
- Numerical analysis of free convection from a spinning cone with variable wall temperature and pressure work effect using MD-BSQLM
- Numerical simulation of hydrodynamic oscillation of side-by-side double-floating-system with a narrow gap in waves
- Closed-form solutions for the Schrödinger wave equation with non-solvable potentials: A perturbation approach
- Study of dynamic pressure on the packer for deep-water perforation
- Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures
- Crystallization law of karst water in tunnel drainage system based on DBL theory
- Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study
- Application of Fibonacci heap to fast marching method
- An analytical investigation of the mixed convective Casson fluid flow past a yawed cylinder with heat transfer analysis
- Considering the effect of optical attenuation on photon-enhanced thermionic emission converter of the practical structure
- Fractal calculation method of friction parameters: Surface morphology and load of galvanized sheet
- Charge identification of fragments with the emulsion spectrometer of the FOOT experiment
- Quantization of fractional harmonic oscillator using creation and annihilation operators
- Scaling law for velocity of domino toppling motion in curved paths
- Frequency synchronization detection method based on adaptive frequency standard tracking
- Application of common reflection surface (CRS) to velocity variation with azimuth (VVAz) inversion of the relatively narrow azimuth 3D seismic land data
- Study on the adaptability of binary flooding in a certain oil field
- CompVision: An open-source five-compartmental software for biokinetic simulations
- An electrically switchable wideband metamaterial absorber based on graphene at P band
- Effect of annealing temperature on the interface state density of n-ZnO nanorod/p-Si heterojunction diodes
- A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil
- Shannon entropy for Feinberg–Horodecki equation and thermal properties of improved Wei potential model
- Hopf bifurcation analysis for liquid-filled Gyrostat chaotic system and design of a novel technique to control slosh in spacecrafts
- Optical properties of two-dimensional two-electron quantum dot in parabolic confinement
- Optical solitons via the collective variable method for the classical and perturbed Chen–Lee–Liu equations
- Stratified heat transfer of magneto-tangent hyperbolic bio-nanofluid flow with gyrotactic microorganisms: Keller-Box solution technique
- Analysis of the structure and properties of triangular composite light-screen targets
- Magnetic charged particles of optical spherical antiferromagnetic model with fractional system
- Study on acoustic radiation response characteristics of sound barriers
- The tribological properties of single-layer hybrid PTFE/Nomex fabric/phenolic resin composites underwater
- Research on maintenance spare parts requirement prediction based on LSTM recurrent neural network
- Quantum computing simulation of the hydrogen molecular ground-state energies with limited resources
- A DFT study on the molecular properties of synthetic ester under the electric field
- Construction of abundant novel analytical solutions of the space–time fractional nonlinear generalized equal width model via Riemann–Liouville derivative with application of mathematical methods
- Some common and dynamic properties of logarithmic Pareto distribution with applications
- Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model
- Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate
- Liquid metal-based metamaterial with high-temperature sensitivity: Design and computational study
- Biosynthesis and characterization of Saudi propolis-mediated silver nanoparticles and their biological properties
- New trigonometric B-spline approximation for numerical investigation of the regularized long-wave equation
- Modal characteristics of harmonic gear transmission flexspline based on orthogonal design method
- Revisiting the Reynolds-averaged Navier–Stokes equations
- Time-periodic pulse electroosmotic flow of Jeffreys fluids through a microannulus
- Exact wave solutions of the nonlinear Rosenau equation using an analytical method
- Computational examination of Jeffrey nanofluid through a stretchable surface employing Tiwari and Das model
- Numerical analysis of a single-mode microring resonator on a YAG-on-insulator
- Review Articles
- Double-layer coating using MHD flow of third-grade fluid with Hall current and heat source/sink
- Analysis of aeromagnetic filtering techniques in locating the primary target in sedimentary terrain: A review
- Rapid Communications
- Nonlinear fitting of multi-compartmental data using Hooke and Jeeves direct search method
- Effect of buried depth on thermal performance of a vertical U-tube underground heat exchanger
- Knocking characteristics of a high pressure direct injection natural gas engine operating in stratified combustion mode
- What dominates heat transfer performance of a double-pipe heat exchanger
- Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part II
- Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation
- New quantum integral inequalities for some new classes of generalized ψ-convex functions and their scope in physical systems
- Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels
- Gaussian radial basis functions method for linear and nonlinear convection–diffusion models in physical phenomena
- Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model
- On the optical solutions to nonlinear Schrödinger equation with second-order spatiotemporal dispersion
- Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods
- Quantum estimates in two variable forms for Simpson-type inequalities considering generalized Ψ-convex functions with applications
- Series solution to fractional contact problem using Caputo’s derivative
- Solitary wave solutions of the ionic currents along microtubule dynamical equations via analytical mathematical method
- Thermo-viscoelastic orthotropic constraint cylindrical cavity with variable thermal properties heated by laser pulse via the MGT thermoelasticity model
- Theoretical and experimental clues to a flux of Doppler transformation energies during processes with energy conservation
- On solitons: Propagation of shallow water waves for the fifth-order KdV hierarchy integrable equation
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part II
- Numerical study on heat transfer and flow characteristics of nanofluids in a circular tube with trapezoid ribs
- Experimental and numerical study of heat transfer and flow characteristics with different placement of the multi-deck display cabinet in supermarket
- Thermal-hydraulic performance prediction of two new heat exchangers using RBF based on different DOE
- Diesel engine waste heat recovery system comprehensive optimization based on system and heat exchanger simulation
- Load forecasting of refrigerated display cabinet based on CEEMD–IPSO–LSTM combined model
- Investigation on subcooled flow boiling heat transfer characteristics in ICE-like conditions
- Research on materials of solar selective absorption coating based on the first principle
- Experimental study on enhancement characteristics of steam/nitrogen condensation inside horizontal multi-start helical channels
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part I
- Numerical exploration of thin film flow of MHD pseudo-plastic fluid in fractional space: Utilization of fractional calculus approach
- A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation
- Stable novel and accurate solitary wave solutions of an integrable equation: Qiao model
- Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs
- On the oscillation of nonlinear delay differential equations and their applications
- Abundant stable novel solutions of fractional-order epidemic model along with saturated treatment and disease transmission
- Fully Legendre spectral collocation technique for stochastic heat equations
- Special Issue on 5th International Conference on Mechanics, Mathematics and Applied Physics (2021)
- Residual service life of erbium-modified AM50 magnesium alloy under corrosion and stress environment
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part I
- Diverse wave propagation in shallow water waves with the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and Benney–Luke integrable models
- Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge

