Analysis of the structure and properties of triangular composite light-screen targets

Hai Li; Jinping Ni; Xiaodong Yang; Zhichao Wu

doi:10.1515/phys-2021-0070

Article Open Access

Analysis of the structure and properties of triangular composite light-screen targets

Hai Li , Jinping Ni , Xiaodong Yang and Zhichao Wu

Published/Copyright: October 11, 2021

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 19 Issue 1

Abstract

With the development of light-screen targets for ballistic projectiles, not only must accuracy in the measurement of projectiles be assured but also the installation of the system and error compensation in the initial calibrations must be considered. We have designed a triangular composition light-screen target that is easy to install, derived expressions for the speed and direction of ballistic trajectories based on intersecting-CCD vertical targets, and conducted analyses of the points of impact and projectile speed. Results show that errors in the point of impact are affected by the coordinates of the target plane. Positional errors gradually increase with the distance from the origin. The horizontal angle error with the trajectory line does not exceed 0.3°, whereas the vertical angle error does not exceed 0.2°. Errors in the speed of the projectile remain relatively stable when the vertical coordinates are greater. Errors in speed and direction, as well as error fluctuations, are smaller on the x = 0 plane, making it the ideal region for error compensation in initial calibrations.

Keywords: composite light-screen target; point of impact; ballistic trajectory; speed error

1 Introduction

With the rapid development of the arms industry, the precise positioning and testing of weapons and equipment [1] have become an important part of military development, as well as essential links in the process of weapons development [2], production, and acceptance [3,4,5]. As such, it has drawn attention from many researchers. Optoelectronic testing technologies are an effective means for testing equipment [6,7,8]. Due to their advantages of noncontact, high accuracy, and good electromagnetic compatibility, these technologies are often used in ballistic range testing systems [9,10]. Light-screen targets measure the velocity of a bullet using the principles of optoelectronic testing. Due to their simple structures and ease of installation, light-screen targets are not only used in weapons testing systems but are also highly favored in the military training.

In recent years, relevant research have focused mainly on multi-light-screen targets [8,11] in which various technical indicators and data acquisition methods are used to enhance the accuracy in measuring the point of impact and speed. Actual tests in on-site locations are driving the rapid development of light-screen target technologies, for instance, expansion of the testing area from small target planes to large target planes [12,13], reduction in the size of measurable projectiles [14], and generation of optimization technologies for trigger interference signals [15]. Many novel light-screen targets have been developed, including light-screen targets with integrated transmission and receiving functions [16] and intelligent light-screen targets [17]. This diversity in light-screen targets can help to further optimize testing structures and precision.

Intersecting-charge-coupled devices (CCD) vertical target screens [2] are two-dimensional (2D) measurement planes formed from two linear CCD arrays. When a projectile penetrates the measurement plane, it would produce corresponding image points on the CCD arrays. As the primary optical axes of the CCD arrays form fixed angles with the horizontal axis, they allow us to calculate the location of the impact point. Using intersecting-CCD vertical target screens as the base structure, we have designed an easy-to-install and cost-efficient novel composite light-screen target with smaller error magnitudes. This method is a part of early research on the simultaneous measurement of multiple projectiles. We have conducted an error analysis on its structure, providing a theoretical foundation for the development of light-screen target technologies.

2 Methodology

An intersecting-CCD vertical target screen is placed in the z = 0 plane. Two-point light sources, T₁ and S₁, are placed symmetrically in front of the screen. Two linear CCD arrays are placed on the target plane, axisymmetric about the x = 0 plane and forming fixed angles of intersection with the y = 0 plane. These arrays receive signals from the light sources at T₁ and S₁, respectively, to form two spatial planes, the S planes (the red plane) and T planes (the yellow plane), as shown in Figure 1.

Figure 1

Structural schematic of the composite light-screen target.

When a projectile passes through this composite light screen in any arbitrary direction, for instance, the trajectory in Figure 1 marked in blue, it forms two points of intersection, K₂ and K₁, on the two planes in front. This forms a trajectory on the intersecting-CCD target screen that passes through M₁. The intersecting points K₂ and K₁ will respectively project within the T and S planes onto the linear CCD array, with the projected points being M₃ and M₂. The coordinates of M₁ and the 2D coordinates can be expressed as

(1) x = d cos α 0 − arctan h 1 f sin β 0 + arctan h 2 f sin α 0 + β 0 − arctan h 1 f + arctan h 2 f − f sin arctan h 1 f sin α 0 − arctan h 1 f ,

(2) y = d sin α 0 − arctan h 1 f sin β 0 + arctan h 2 f sin α 0 + β 0 − arctan h 1 f + arctan h 2 f ,

where

(3) d = d 0 + sin arctan h 1 f sin α 0 − arctan h 1 f + sin arctan h 2 f sin β 0 + arctan h 2 f ,

h 1 and h 2 are the image heights corresponding to the image heights for the two CCD arrays, α 0 and β 0 are the fixed angles of intersection between the main optical axis of the CCDs and the x-axis, d 0 is the central distance of the CCDs, and f is the shared focal length.

The point of impact will be ( x m , y m , 0 ), the values of which can be measured by the CCD target screen. The coordinates of light source S₁ are defined as ( x 1 , 0 , z 1 ). Two arbitrary reference points, S 2 ( x 1 − 1 , y 1 − 1 , 0 ) and S 3 ( x 1 − 2 , y 1 − 2 , 0 ) , on the linear CCD array in the S plane are chosen. M 2 ( x 3 , y 3 , 0 ) is the point projected by the light source S₁ onto the linear CCD array through the point K₁. Similarly, the coordinates of light source T₁ are defined as ( x 2 , 0 , z 2 ). Two arbitrary reference points, T 2 ( x 2 − 1 , y 2 − 1 , 0 ) and T 3 ( x 2 − 2 , y 2 − 2 , 0 ) , on the linear CCD array in the T plane are chosen. M 3 ( x 4 , y 4 , 0 ) is the point projected by the light source T₁ onto the linear CCD array through the point K₂.

The unit normal vector n 1 for the plane formed by S 1 , M 1 , and M 2 is

(4) n 1 = i j k x 3 − x 1 y 3 − z 1 x 3 − x m y 3 − y m 0 = A i + B j + C k .

The equation of this plane can then be expressed as

(5) A ( x − x 1 ) + B ( y ) + C ( z − z 1 ) = 0 .

The unit normal vector n 2 for the plane formed by T 1 , M 1 , and M 3 is

(6) n 2 = i j k x 4 − x 2 y 4 − z 2 x 4 − x m y 4 − y m 0 = A ′ i + B ′ j + C ′ k .

The equation of this plane can be expressed as

(7) A ′ ( x − x 2 ) + B ′ ( y ) + C ′ ( z − z 2 ) = 0 .

The intersection of the planes described by Eqs. (5) and (7) will be the ballistic trajectory. The direction vector of this trajectory line will be

(8) s = n 1 × n 2 = i j k A B C A ′ B ′ C ′ = A ″ i + B ″ j + C ″ k

The parametric equations for the trajectory line can be expressed as

(9) x = x m + A ″ t y = y m + B ″ t z = C ″ t .

Solving for the parameters of these two normal vectors yields

(10) A = − y 3 z m + z 1 ( y 3 − y m ) B = − z 1 ( x 3 − x m ) C = ( x 3 − x 1 ) ( y 3 − y m ) − y 3 ( x 3 − x m ) ,

(11) A ′ = − y 4 z m + z 2 ( y 4 − y m ) B ′ = − z 2 ( x 4 − x m ) − x 2 z m C ′ = ( x 4 − x 2 ) ( y 4 − y m ) − y 4 ( x 4 − x m ) .

Let the linear vector of the trajectory be m , n , p , in which case

(12) m = B C ′ − B ′ C n = A ′ C − A C ′ p = A B ′ − A ′ B .

Thus, the horizontal angle of intersection between the trajectory line and the z-axis will be

(13) α = arccos × B C ′ − B ′ C ( B C ′ − B ′ C ) 2 + ( A ′ C − A C ′ ) 2 + ( A B ′ − A ′ B ) 2 .

The vertical angle of intersection between the trajectory line and the z-axis will be

(14) β = arccos × A ′ C − A C ′ ( B C ′ − B ′ C ) 2 + ( A ′ C − A C ′ ) 2 + ( A B ′ − A ′ B ) 2 .

The velocity of the projectile can be derived from Eqs. (13) and (14). Unit normal vectors for the planes S and T can be expressed, respectively, in terms of points S 1 , S 2 , S 3 , and T 1 , T 2 , T 3 .

(15) n 3 = i j k x 1 − 1 − x 1 y 1 − 1 − z 1 x 1 − 2 − x 1 y 1 − 2 − z 1 = A ‴ i + B ‴ j + C ‴ k ,

(16) n 4 = i j k x 2 − 1 − x 2 y 2 − 1 − z 2 x 2 − 2 − x 2 y 2 − 2 − z 2 = A ‴ ′ i + B ‴ ′ j + C ‴ ′ k .

The equations of these plans are, respectively:

(17) A ‴ ( x − x 1 ) + B ‴ ( y ) + C ‴ ( z − z 1 ) = 0 ,

(18) A ‴ ′ ( x − x 2 ) + B ‴ ′ ( y ) + C ‴ ′ ( z − z 2 ) = 0 .

Solving Eqs. (15) and (16) yields

(19) A ‴ = − y 1 − 1 z 1 + y 1 − 2 z 1 B ‴ = − z 1 ( x 1 − 2 − x 1 ) + z 1 ( x 1 − 1 − x 1 ) C ‴ = y 1 − 2 ( x 1 − 1 − x 1 ) − y 1 − 1 ( x 1 − 2 − x 1 ) ,

(20) A ‴ ′ = − y 2 − 1 z 2 + y 2 − 2 z 2 B ‴ ′ = − z 2 ( x 2 − 2 − x 2 ) + z 2 ( x 2 − 1 − x 2 ) C ‴ ′ = y 2 − 2 ( x 2 − 1 − x 2 ) − y 2 − 1 ( x 2 − 2 − x 2 ) .

Substituting Eq. (9) into Eq. (17) yields

(21) A ‴ ( x m + A ″ t 2 − x 1 ) + B ‴ ( y m + B ″ t 2 ) + C ‴ ( C ″ t 2 − z 1 ) = 0 .

We can determine that the time taken for the projectile to travel from K 2 to M 1 is

(22) t 2 = A ‴ ( x 1 − x m ) − B ‴ y m + C ‴ z 1 A ‴ A ″ + B ‴ B ″ + C ‴ C ″ .

Similarly, substituting eq. (9) into eq. (18) yields

(23) A ‴ ′ ( x m + A ″ t 1 − x 2 ) + B ‴ ′ ( y m + B ″ t 1 ) + C ‴ ′ ( C ″ t 1 − z 2 ) = 0 .

We can determine that the time taken for the projectile to travel from K 1 to M 1 is

(24) t 1 = A ‴ ′ ( x 2 − x m ) − B ‴ ′ y m + C ‴ ′ z 1 A ‴ ′ A ″ + B ‴ ′ B ″ + C ‴ ′ C ″ .

We can easily use Eqs. (9), (22), and (24) to express the spatial coordinates of K 2 and K 1 as K 2 ( x K 2 , y K 2 , z K 2 ) and K 1 ( x K 1 , y K 1 , z K 1 ) , respectively. The magnitude of the velocity of the projectile can then be expressed as

(25) v = 1 2 ( x K 2 − x m ) 2 + ( y K 2 − y m ) 2 + z K 2 2 t 2 + ( x K 1 − x m ) 2 + ( y K 1 − y m ) 2 + z K 1 2 t 1 .

Here the average value of the two distances, is taken. Alternatively, one can first compare the point distances between K 1 M 1 and K 2 M 1 and solve for velocity using the larger values. Both methods of solution aim to enhance the accuracy of the result.

3 Experimental procedures

Light screens primarily measure a projectile’s point of impact and the speed at which it crosses the plane of the screen. As the point of impact in this system relies directly on the intersecting-CCD vertical target, the system parameters will have a direct impact on the measurement of positions. When the CCDs in the vertical targets are placed 2,000 mm apart, respective front optical lens focal lengths are 14 mm, CCD dimension is 6.4 mm, and baseline angles are 45°, and the horizontal coordinate errors and vertical coordinate errors for the point of impact are affected by the coordinates of the impact point, as shown in Figures 2 and 3.

Figure 2

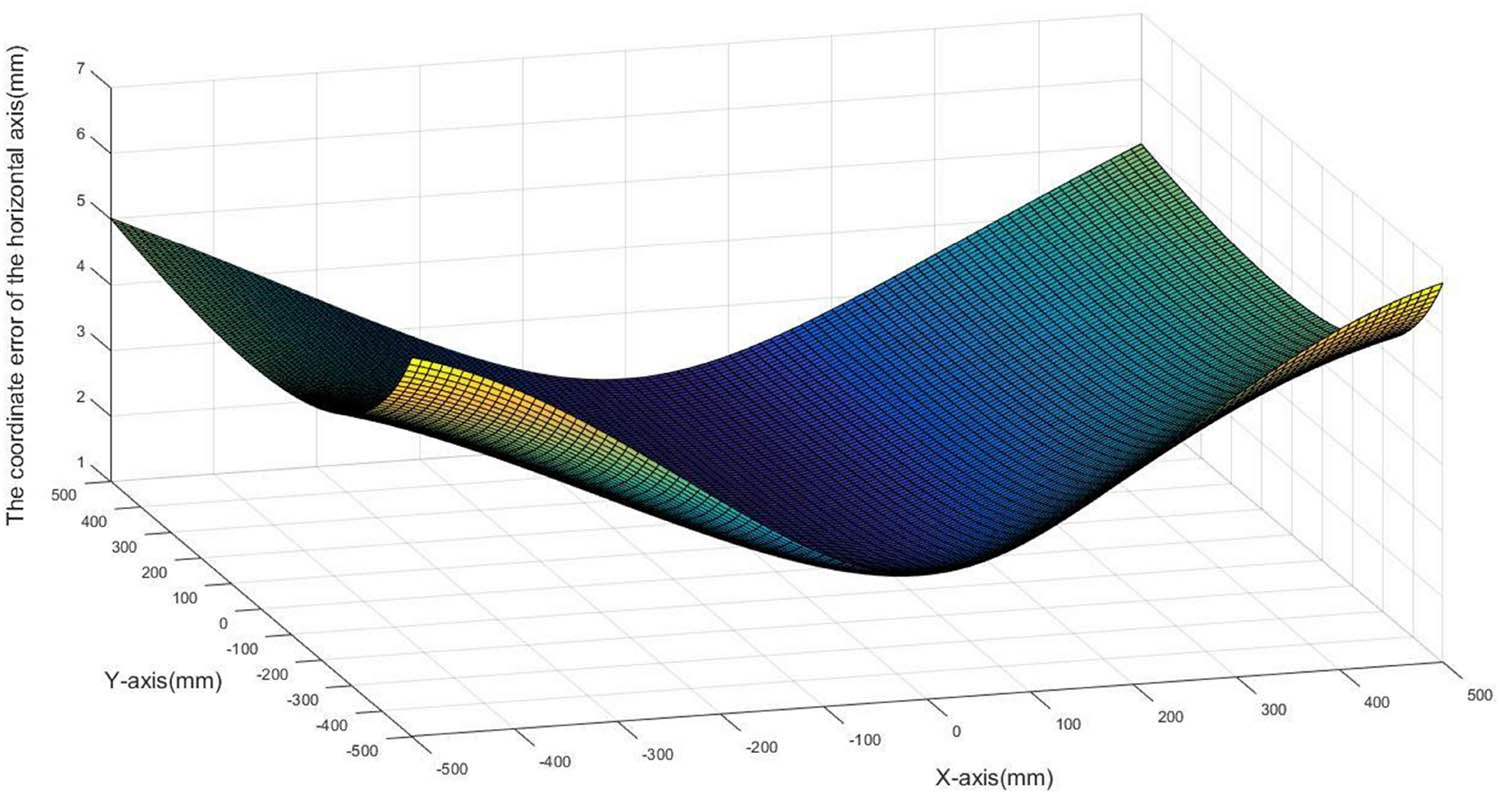
Influence of impact point coordinates on horizontal coordinate errors of the point of impact.

Figure 3

Influence of impact point coordinates on vertical coordinate errors of the point of impact.

As can be seen, the position error is smallest at the origin and increases with the value of the coordinates. The horizontal error increases significantly as the x-coordinate changes, but changes in the y-coordinate can always keep lateral error within 1 mm. Similarly, the vertical error increases significantly as the y-coordinate changes, but changes in the x-coordinate can also keep vertical error within 1 mm. In practical applications, effective detection target surfaces generally have dimensions of ±500 mm × ±500 mm. This can keep position errors within a relatively small range and ensure measurement accuracy.

When the placement distance error of the CCDs in the vertical target screen is 1 mm, the focal length error of the front optical lens is 0.14 mm, and the screen angle error is 0.1°, and the horizontal angle error between the trajectory detection direction and the z-axis is as shown in Figure 4.

Figure 4

Horizontal angle error between the trajectory line and the z-axis.

Horizontal errors within the target plane can be controlled within 0.3°, as shown in Figure 4. Such errors are smaller in regions closer to the x = 0 plane, but increase as the horizontal coordinates of the point of impact take on larger values. However, errors are not symmetrically distributed from left to right on the x = 0 plane. This is because the outward direction of the projectile is random. Projected points M 3 and M 2 on the T and S planes may not be axisymmetric. By contrast, the vertical coordinates of the point of impact have a smaller influence on the horizontal angle errors. Error fluctuations are usually within 0.05°.

Given the same system parameter values, the vertical angle error between the trajectory line and the z-axis is as shown in Figure 5.

Figure 5

Vertical angle error between the trajectory line and the z-axis.

As shown in Figure 5, vertical angle errors in the target screen generally do not exceed 0.2°, smaller than horizontal angle errors. When y-coordinates are smaller, angle errors can be kept within 0.1°, while x-coordinates have a lesser effect on fluctuations in vertical angle errors. As y-coordinates increase, angle errors tend to increase, while x-coordinates will have a larger impact on vertical angle errors. However, peak error values are in the vicinity of 0.2° and can ensure error precision.

When the same values are set for system parameters, errors in the speed of the projectile similarly vary with changes in the coordinates of the target surface, as shown in Figure 6.

Figure 6

Influence of the point of impact on the speed error of the projectile.

As can be seen, changes in the x-coordinate have a greater impact on errors in the speed of the projectile when the y-coordinate is smaller. The impact of the x-coordinate on errors in the speed of the projectile is relatively stable. Even though the horizontal and vertical coordinates will simultaneously have an impact on errors in projectile speed, combined with the measured projectile direction, we can easily find that the speed and the direction errors in the vicinity of the x = 0 plane and are relatively small. Effective measurement target planes are selected symmetrically with the x = 0 plane as the axis. This selection method not only makes installation easier and reduces the time needed for calibration, but can also effectively reduce measurement errors.

4 Conclusion

Based on intersecting-CCD vertical target screens, this study has designed a triangular composite light-screen target and derived the horizontal and vertical angles of intersection between the trajectory line and the z-axis for such light screens. Through parametric equations, we derived an expression for the speed of the projectile. Through error analysis, we discovered that errors in the horizontal and vertical coordinates with respect to the point of impact are affected by the coordinates of impact, with error values increasing with the two orthogonal coordinates. However, x-coordinates have a more significant impact on the horizontal axis error of the point of impact than y-coordinates. Similarly, y-coordinates have a more significant impact on the vertical axis error of the point of impact than x-coordinates. In an effective receiving target screen, points of impact near the origin are more precise. Greater error compensation is required during initial system calibration for regions further from the origin.

Through a simulation analysis of the horizontal and vertical angle errors between the trajectory line and the z-axis, we find that horizontal angle errors can be kept within 0.3°, whereas vertical angle errors generally do not exceed 0.2°. In addition, horizontal coordinates of the point of impact have a more significant influence on the horizontal angle error. Vertical coordinates have a more significant impact on the vertical angle error. Errors in the speed of the projectile are also affected by the orthogonal coordinates. When y-coordinates are larger, fluctuations in speed error are relatively stable. On the whole, errors in speed and direction are smaller in the vicinity of the x = 0 plane. This provides some convenience for the initial system calibration.

In future work, a further analysis on this system and building of experimental platforms in the field to carry out specific analysis by combining simulation data with experimental results, will be conducted. The system with a sound calibration data compensation to make measurements more precise, will be provided.

Funding information: This study is supported by a key laboratory project of Shaanxi provincial department of education (Grant No. 20JS057).
Authors contribution: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Wang LF, Wang H, Jiang HZ, Li LQ, Tuo X, Wan XT, et al. Environmental adaptability test and design of carrier-based aviation ammunition. Ordnance Ind Autom. 2019;38(8):46–8.Search in Google Scholar

[2] Ni JP. Technol application Meas Light screen array. Bei Jing: National Defense Industry Press; 2014. p. 4–22.Search in Google Scholar

[3] Madsen LS, Waleed M, Casacio CA, Terrasson A, Stilgoe AB, Taylor MA, et al. Ultrafast viscosity measurement with ballistic optical tweezers. Nat Photonics. 2021;15(1):386–92.10.1038/s41566-021-00798-8Search in Google Scholar

[4] Salzenstein P, Pavlyuchenko E. Uncertainty evaluation on a 10.52 GHz (5 dBm) optoelectronic oscillator phase noise performance. Micromachines. 2021;12(5):474.10.3390/mi12050474Search in Google Scholar PubMed PubMed Central

[5] Kumru F, Akca T, Acar RS. Performance evaluation of nonlinear filters on impact point prediction of ballistic targets. In: 2017 20th International Conference on Information Fusion (Fusion); 2017. p. 1–7.10.23919/ICIF.2017.8009642Search in Google Scholar

[6] Zong-Min YE, No U. Research on implementation method of infrared imaging guided anti-ship missile. Infrared. 2019;15(2):871–9.Search in Google Scholar

[7] Zheng S, Wang Z, Xu L. Research on the application of photoelectric detection information in air defense missile weapon system. Aerosp Control. 2019;24(1):23–31.Search in Google Scholar

[8] Li H, Zhang X, Zhang X, Lu L. Detection sensitivity correction calculation model and application of photoelectric detection target in four-screen intersection testing system. Measurement. 2021;177(3):109281.10.1016/j.measurement.2021.109281Search in Google Scholar

[9] Liu Y, Jiang M, Zhang Z, Li Y. Study on aerodynamic characteristics of projectile in plateau based on shooting test. J Ordnance Equip Eng. 2019;12(8):557–62.Search in Google Scholar

[10] Wu Z, Zhang X. On-sate calibration method of target distance of the sky screen target velocity measuring system. Optik. 2019;178:483–7.10.1016/j.ijleo.2018.09.150Search in Google Scholar

[11] Chen R, Ni JP, Liu J. Uncertainty analysis of coordinate measurement of six-light-screen array sky screen vertical target based on engineering model. Acta Armamentarii. 2019;46(11):1362–75.Search in Google Scholar

[12] Lu CG, Wang YJ, Yao ZJ, Zhang L, Fan B. Attack angle measurement of projectile with multi-linear array photoelectric vertical target. Transducer Microsyst Technol. 2016;31(2):75–84.Search in Google Scholar

[13] Dong T, Ni JP. Measurement principle of six-light-screen vertical target based on sky screen. J Appl Opt. 2011;32(5):913–6.10.5768/JAO202142.0507001Search in Google Scholar

[14] Kalonia RC, Chhachhia DP, Bajpai PP, Singh M, Biswas I, Yadav MS. Multiple laser-based high-speed digital shadowgraphy system for small caliber projectile-target interaction studies. Optical Eng. 2014;53(3):034104.10.1117/1.OE.53.3.034104Search in Google Scholar

[15] Pan D. Technology of anti-interference of sky screen based on CPLD. Comput Digital Eng. 2017;45(04):655–8.Search in Google Scholar

[16] Shi L. Research on the technology of integrated receiving-transmitting laser screens. Xi’an: Xi’an Technological University; 2010.Search in Google Scholar

[17] Zhang YW, Zhang S, Zhang MY, Zhang HZ Intelligent light screen target coordinate measurement system, CN210570247U; 2020.Search in Google Scholar

Received: 2021-06-17

Revised: 2021-08-05

Accepted: 2021-09-10

Published Online: 2021-10-11

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2021-0070

Keywords for this article

composite light-screen target; point of impact; ballistic trajectory; speed error

Creative Commons

BY 4.0