A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation

Muhammad Ahsan; Shanwei Lin; Masood Ahmad; Muhammad Nisar; Imtiaz Ahmad; Hijaz Ahmed; Xuan Liu

doi:10.1515/phys-2021-0080

Article Open Access

A Haar wavelet-based scheme for finding the control parameter in nonlinear inverse heat conduction equation

Muhammad Ahsan , Shanwei Lin , Masood Ahmad , Muhammad Nisar , Imtiaz Ahmad , Hijaz Ahmed and Xuan Liu

Published/Copyright: November 26, 2021

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 19 Issue 1

Abstract

In this article, a hybrid Haar wavelet collocation method (HWCM) is proposed for the ill-posed inverse problem with unknown source control parameters. Applying numerical techniques to such problems is a challenging task due to the presence of nonlinear terms, unknown control parameter sources along the solution inside the given region. To find the numerical solution, derivatives are discretized adopting implicit finite-difference scheme and Haar wavelets. The computational stability and theoretical rate of convergence of the proposed HWCM are discussed in detail. Two numerical experiments are incorporated to show the well-condition behavior of the matrix obtained from HWCM and hence not required to supplement some regularization procedures. Moreover, the numerical solutions of the considered experiments illustrate the reliability, suitability, and correctness of HWCM.

Keywords: nonlinear ill-posed PDE; Haar wavelets; stability; condition number

1 Introduction

Inverse problems with source control parameters are nonlinear parabolic partial differential equations and are among some of the difficult problems to be handle by numerical methods. Due to the numerous embedded challenges, which are still barriers to get the solution of such inverse heat conduction problems (IHCPs), researchers have concentrated their study on the numerical treatment of these models. Applications of such problems can be witnessed in the modeling of various scientific observable facts like aerospace engineering, metallurgy, nuclear physics, chemical diffusion, optics, nondestructive measurement of stress and strain, control theory, communication theory, computer vision, oceanography, cardiography, thermo-elasticity, and medical imaging.

The general form of a class of IHCPs to be investigated in this article is refs [1,2]:

(1) u t ( x , t ) = u x x ( x , t ) + p ( t ) u ( x , t ) + F ( x , t ) , a ≤ x ≤ b , t > 0 ,

with initial and boundary information:

u ( x , 0 ) = g ( x ) , u ( a , t ) = u o ( t ) , u ( b , t ) = u l ( t ) ,

where p ( t ) and u ( x , t ) are the source control parameter and solution, respectively, which have to be determined numerically. For the determination of these parameters, additional data are presented and is called overdetermination condition:

(2) u ( x ∗ , t ) = q ( t ) , a ≤ x ∗ ≤ b .

Unavailability of these specific parameters, the existence, stability, and uniqueness of the IHCP is usually not guaranteed, and prevention methods of the numerical scheme from these issues are discussed with detail in ref. [1] and the references therein. Inverse problems are generally classified as ill-posed [3,4], and their solutions do not depend on the boundary conditions continuously; therefore, the computational results are affected by the noise intensity available in the input data. In recent literature, many numerical and analytical methods can be found for the complex and challenging problems in refs [5,6,7, 8,9,10, 11,12,13, 14,15,16, 17,18], and the references therein. For the IHCPs, some of the recent attempts include backward euler finite difference scheme [19], finite difference scheme [1,2], methods of fundamental solutions [20], boundary-element method [21], lie-group method [22,23], and the modified polynomial expansion method [24]. Some applicable collocation methods focusing on the numerical results of IHCPs include meshless collocation method [25,26] and Haar wavelets collocation methods [27,28, 29,30]. Mallat has also included a chapter about the inverse problem in his book [31].

The prominence of Haar wavelet for numerical computation for many kinds of scientific and engineering problems can be observed from the recent literature. These scientific and engineering problems include differential and integral equations, which have been solved by several wavelets techniques such as wavelet meshless methods [32], wavelet collocation method [33], wavelet Galerkin method [34], and wavelet-based method [35]. Multi-resolution Haar wavelet collocation procedures have also been used for accurate analysis of time and space-dependent heat sources in IHCPs [28,29]. Haar wavelets have also been utilized to find the approximate solutions of fractional order problems accurately [36]. The employment of Haar wavelet can also be found in other areas such as image compression [37], dose calculation [38], image processing [39], delamination identification [40], detecting and localizing texture defects [41], magnetic resonance imaging [42], identification of software piracy [43], and signal processing [44].

Holding the challenges encountered in the numerical treatment of IHCPs, an easy, suitable, and accurate numerical procedure with the help of Haar wavelets is suggested in this article. This advanced procedure provides stable and efficient results. In this procedure, the Haar wavelets convert the PDE into the well-conditioned system of equations, which has a remarkable impact on the approximate solution. The added beauty of the suggested procedure is that various kinds of given boundary data can be easily utilized in the algorithm to find the solution.

2 Haar wavelets

A Haar wavelet function for x ∈ [ a , b ] can be defined as follows:

(3) h i ( x ) = 1 for x ∈ [ ζ 1 , ζ 2 ) , − 1 for x ∈ [ ζ 2 , ζ 3 ) , 0 o t h e r w i s e ,

where

ζ 1 = a + ( b − a ) k m , ζ 2 = a + ( k + 0.5 ) ( b − a ) m , ζ 3 = a + ( k + 1 ) ( b − a ) m .

In the aforementioned function, m = 2 j , j = 0 , 1 , … , J shows different level of the wavelet and k = 0 , 1 , … , m − 1 shows the translating parameter. The highest level of resolution is represented by J . The index i in equation (3) can be obtained with the help of equation i = m + k + 1 . For smallest values of m = 1 , we can obtain k = 0 and the index i = 2 . The largest value of index i is M = 2 J . Here, we can also present the Haar wavelets scaling function as follows:

h 1 ( x ) = 1 for x ∈ [ a , b ) , 0 o t h e r w i s e .

A function that is finite and can be integrated in the domain [ a , b ] can be approximated as by Haar wavelet series:

f ( x ) = ∑ i = 1 ∞ c i h i ( x ) .

These Haar coefficients

c i = 2 j ∫ a b f ( x ) h i ( x ) d x , i = 1 … 2 j + k + 1

can be calculated following [45] from the minimal condition of the error as follows:

∫ a b E M 2 d x → min , ∣ E M ∣ = ∣ f ( x ) − f M ( x ) ∣ , and f M ( x ) = ∑ i = 1 2 M c i h i ( x ) ,

where f ( x ) and f M ( x ) denote the analytical and estimated functions, respectively. We define the following notations for the integration of the Haar wavelet in equation (3):

P i , 1 ( x ) = ∫ a x h i ( x ′ ) d x ′ P i , 2 ( x ) = ∫ a x P i , 1 ( x ′ ) d x ′ and C i = ∫ a b P i , 1 ( x ′ ) d x ′ .

By using equation (3), we can easily obtain

P i , 1 ( x ) = x − ζ 1 for x ∈ [ ζ 1 , ζ 2 ) , ζ 3 − x for x ∈ [ ζ 2 , ζ 3 ) , 0 o t h e r w i s e , P i , 2 ( x ) = ( x − ζ 1 ) 2 2 for x ∈ [ ζ 1 , ζ 2 ) , ( b − a ) 2 4 m 2 − ( ζ 3 − x ) 2 2 for x ∈ [ ζ 2 , ζ 3 ) , ( b − a ) 2 4 m 2 for x ∈ [ ζ 3 , 1 ) , 0 o t h e r w i s e ,

and

C i = ( b − a ) 2 4 m 2 .

3 Haar wavelets scheme for nonlinear inverse problems

To determine the solution of considered IHCP, we eliminate p ( t ) by putting x = x ∗ in equation (1), and by utilizing the overdetermination data given in equation (2), we get

(4) p ( t ) = q ˙ ( t ) − q x x ( t ) − F ( x ∗ , t ) q ( t ) .

Using equations (4) and (1), we get a nonhomogeneous partial differential equation:

(5) u t ( x , t ) = u x x ( x , t ) + q ˙ ( t ) − q x x ( t ) − F ( x ∗ , t ) q ( t ) u ( x , t ) + F ( x , t ) .

Next we introduce the procedure for approximating the time and spatial derivatives. Starting with construction of Haar wavelet approximation scheme for spatial derivatives in equation (5), we let

(6) u x x ( x , t ) = ∑ i = 1 2 M c i h i ( x ) .

By integrating equation (6) from a to x , we acquire

(7) u x ( x , t ) = u x ( a , t ) + ∑ i = 1 2 M c i P i , 1 ( x ) .

By integrating equation (7) from a to b and then simplifying the result, we have

(8) u x ( a , t ) = B ( t ) b − a − ∑ i = 1 2 M c i C i b − a ,

where B ( t ) = u ( b , t ) − u ( a , t ) . By inserting equation (8) in equation (7), we acquire

(9) u x ( x , t ) = B ( t ) b − a + ∑ i = 1 2 M c i P i , 1 ( x ) − C i b − a .

Finally integrating equation (9) with respect to x , we acquire

(10) u ( x , t ) = A ( t ) + B ( t ) ( x − a ) b − a + ∑ i = 1 2 M c i P i , 2 ( x ) − ( x − a ) C i b − a ,

where A ( t ) = u ( a , t ) . Introducing an implicit scheme for approximating the time derivative, we let t o represent the present time level and t = t o + Δ t be the subsequent time level. Consequently, equation (5) can be revised as follows:

u ( x , t ) − u ( x , t o ) Δ t = u x x ( x , t ) + q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) u ( x , t ) + F ( x , t o ) .

By re-arranging, we acquired

(11) 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) u ( x , t ) − Δ t u x x ( x , t ) = u ( x , t o ) + Δ t F ( x , t o ) .

Inserting equations (10) and (6) into equation (11) and then discretizing at the nodal points x k = a + ( k − 0.5 ) ( b − a ) 2 M , k = 1 , 2 , … , 2 M produces the algebraic equations, which is given as follows:

(12) ∑ i = 1 2 M c i 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) × P i , 2 ( x k ) − ( x k − a ) C i b − a − Δ t h i ( x k ) = u ( x k , t o ) − 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) × A ( t o ) + ( x k − a ) B ( t o ) b − a + Δ t F ( x k , t o ) .

Equation (12) can be presented in matrix form as follows:

(13) 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) P 2 − ( x − a ) C T b − a − Δ t H c = u ( x , t o ) − 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) × A ( t o ) + ( x − a ) B ( t o ) b − a + Δ t F ( x , t o )

where

x = [ x 1 , x 2 , … , x 2 M ] T , C = [ C 1 , C 2 , … , C 2 M ] T , c = [ c 1 , c 2 , … , c 2 M ] T ,

H = h 1 ( x 1 ) h 2 ( x 1 ) … h 2 M ( x 1 ) h 1 ( x 2 ) h 2 ( x 2 ) … h 2 M ( x 2 ) … … … … h 1 ( x 2 M ) h 2 ( x 2 M ) … h 2 M ( x 2 M ) and P 2 = P 1 , 2 ( x 1 ) P 2 , 2 ( x 1 ) … P 2 M , 2 ( x 1 ) P 1 , 2 ( x 2 ) P 2 , 2 ( x 2 ) … P 2 M , 2 ( x 2 ) … … … … P 1 , 2 ( x 2 M ) P 2 , 2 ( x 2 M ) … P 2 M , 2 ( x 2 M ) .

Equation (13) can be written as follows:

(14) Ac = B

where

A = 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) × P 2 − ( x − a ) C T b − a − Δ t H

and

B = u ( x , t o ) − 1 + Δ t q ˙ ( t o ) − q x x ( t o ) − F ( x ∗ , t o ) q ( t o ) × A ( t o ) + ( x − a ) B ( t o ) b − a + Δ t F ( x , t o ) .

We can solve equation (14) for c using any linear solver program in MATLAB and then utilizing these c in equation (10), we can calculate u ( x , t ) . However, p ( t ) can be updated by replacing q x x ( t ) with the new values u x x ( x ∗ , t ) in equation (4):

(15) p ( t ) = q ˙ ( t ) − u x x ( x ∗ , t ) − F ( x ∗ , t ) q ( t ) ,

and we can calculate u x x ( x ∗ , t ) from equation (6) by inserting x = x ∗ for each iteration.

4 Stability and error analysis

In this portation, we study the stability along with the convergence of the HWCM.

4.1 Stability analysis

Following [30] equation (5) can be written as follows:

(16) ∂ u ( x , t ) ∂ t = ∂ 2 ∂ x 2 + q ˙ ( t ) − q x x ( t ) − F ( x ∗ , t ) q ( t ) u ( x , t ) + F ( x , t ) ,

∂ u ( x , t ) ∂ t = ℒ { u ( x , t ) } + F ( x , t ) ,

where ℒ = ∂ 2 ∂ x 2 + q ˙ ( t ) − q x x ( t ) − F ( x ∗ , t ) q ( t ) , is the differential operator. Following the time discretization, we acquire

(17) u ( n + 1 ) = ( I − Δ t ℋ ) − 1 u ( n ) + ( I − Δ t ℋ ) − 1 ( Δ t F ( x , t o ) ) ,

where identity matrix is represented by I and ℋ is the Haar-based matrix for the analogous operator ℒ . If λ denotes the largest eigenvalue of ℋ and the eigenvalue of the identity matrix I is always 1, then from equation (17), we can notice the following stability condition

(18) ( I − Δ t λ ) − 1 ≤ 1 .

Equation (18) will be fulfilled if ( I − Δ t λ ) > 0 , that is only possible when λ ≤ 0 . The computational value of λ ≤ 0 has been observed and found satisfied in Figure 1. The real parts of λ are sketched against t in Figure 1, where the values of λ stay aside from 0 on the left side of the complex-plane. This condition influences us about the satisfactory requirement on the stability of HWCM.

$Figure 1 Verification of stability condition equation (18) on the basis of negative values of λ \lambda for Example 1 and 2 with M = 16 M=16 and Δ t = 0.01 \Delta t=0.01 for different time t = 1 t=1 .$

Figure 1

Verification of stability condition equation (18) on the basis of negative values of λ for Example 1 and 2 with M = 16 and Δ t = 0.01 for different time t = 1 .

4.2 Error analysis

To perform the convergence of HWCM, we take the exact representation of equation (10) as follows:

(19) u ( x , t ) = A ( t ) + B ( t ) ( x − a ) b − a + ∑ i = 1 ∞ c i P i , 2 ( x ) − C i ( x − a ) b − a .

The convergence of HWCM is presented as a theorem. To prove this theorem, we refer the following two lemmas [45,46].

Lemma 1

[46] Assume that u ∈ C 2 ( − ∞ , ∞ ) with ∣ u ′ ∣ ≤ K , ∀ x ∈ ( a , b ) ; K > 0 and u = ∑ i = 0 ∞ λ i h i ( x ) , then ∣ λ i ∣ ≤ K 2 − ( 3 j − 2 ) ∕ 2 .

Lemma 2

[46] Let u ∈ C 2 ( − ∞ , ∞ ) be a continuous on ( a , b ) . Then, the error will be

∣ ∣ E J ∣ ∣ 2 ≤ K 2 12 2 − 2 J ,

where ∣ u ′ ∣ ≤ K , ∀ x ∈ ( a , b ) and K > 0 . The real number M = 2 J > 0 is the wavelet resolution.

Theorem 1

If equation (19) ( u ( x , t ) ) denote the analytical solution and equation (10) ( u 2 M ( x , t ) ) denote the Haar wavelet-based solution of the inverse problem equation (1), the error norm at J th level resolution is given by

∣ ∣ E J ∣ ∣ = ∣ ∣ u − u 2 M ∣ ∣ = O ( 2 − 3 ( 2 J ) ) .

Proof

The error of the proposed method at J th level resolution is given as follows:

(20) ∣ ∣ E J ∣ ∣ = ∣ ∣ u − u 2 M ∣ ∣ = ∑ i = 2 M + 1 ∞ c i P i , 2 ( x ) − C i ( x − a ) b − a ,

which implies

(21) ∣ ∣ E J ∣ ∣ 2 = ∫ − ∞ ∞ ∑ i = 2 M + 1 ∞ c i P i , 2 ( x ) − C i ( x − a ) b − a , ∑ l = 2 M + 1 ∞ c l P l , 2 ( x ) − C l ( x − a ) b − a d x = ∑ i = 2 M + 1 ∞ ∑ l = 2 M + 1 ∞ ∫ a b c i c l P i , 2 ( x ) − C i ( x − a ) b − a P l , 2 ( x ) − C l ( x − a ) b − a d x ≤ ∑ i = 2 M + 1 ∞ ∑ l = 2 M + 1 ∞ c i c l K i , l ,

where K i , l = Sup i , l ∫ a b P i , 2 ( x ) − C i ( x − a ) b − a P l , 2 ( x ) − C l ( x − a ) b − a d x . Now equation (21) can be written as follows:

(22) ∣ ∣ E J ∣ ∣ 2 ≤ ∑ i = 2 M + 1 ∞ ∣ c i ( c 2 M + 1 K i , 2 M + 1 + c 2 M + 2 K i , 2 M + 2 + … ) ∣ ≤ ∑ i = 2 M + 1 ∞ ∣ c i K i ( c 2 M + 1 + c 2 M + 2 + … ) ∣ , where K i = Sup l K i , l ≤ ∑ i = 2 M + 1 ∞ ( ∣ c i K i c 2 M + 1 ∣ + ∣ c i K i c 2 M + 2 ∣ + … ) ≤ ∑ i = 2 M + 1 ∞ ( ∣ c i K i c 2 M + 1 ∣ + ∣ c i K i c 2 M + 2 ∣ + … ) .

Now, using Lemmas 1 and 2, inequality (22) can be written as follows:

∣ ∣ E J ∣ ∣ 2 ≤ K 2 − ( 3 . 2 J + 1 ) 1 − 2 − 3 ∕ 2 ∑ i = 2 M + 1 ∞ ∣ c i K i ∣ ≤ K 1 K 2 − ( 3 . 2 J + 1 ) 1 − 2 − 3 ∕ 2 where K 1 = Sup K i ,

which on further simplification and taking square root, we get

∣ ∣ E J ∣ ∣ ≤ K 1 K 2 − ( 3 . 2 J + 1 ) 1 − 2 − 3 ∕ 2 ≤ O ( 2 − 3 ( 2 J ) ) . □

We can wind up that level of resolution J of the Haar function is inversely related to the error norm, which means that the error of the method can be reduced by increasing J that is

‖ E J ‖ ⟶ 0 a s J ⟶ ∞ , ⇒ ‖ E J ‖ ⟶ 0 a s M ⟶ ∞ .

5 Numerical results

In this portion, we show the results obtained using HWCM by applying it to two different examples in order to demonstrate its robustness. We also insert some noise amount on the overdetermination condition equation (2) as follows:

q ¯ ( t s ) = q ( t s ) + σ r s , s = 1 … N ,

where σ denote noise amount and r s shows the random number obtained by the MATLAB function rand. We utilized the well-known software “MATLAB R2009b” for all our calculations. The computational time (CPU) is presented in seconds for each examples. We have used L ∞ = max ( L a b ) to verify the accuracy of the HWCM, where L a b is defined as follows:

L a b ( u ( x , t ) ) = ∣ u ( x , t ) − u ˆ ( x , t ) ∣ , L a b ( p ( t ) ) = ∣ p ˆ ( t ) − p ( t ) ∣ ,

where u ( x , t ) , p ( t ) are analytical and u ¯ ( x , t ) , p ¯ ( t ) represent the computed solutions.

Example 1

Consider the following IHCP

u t ( x , t ) = u x x ( x , t ) + p ( t ) u ( x , t ) − ( ( cos ( π x ) + sin ( π x ) ) ( π 2 − ( t + 1 ) 2 ) ) e − t 2 , u ( x , 0 ) = sin ( π x ) + cos ( π x ) , u ( 0 , t ) = 1 e t 2 , u ( 1 , t ) = − 1 e t 2 , u ( 0.25 , t ) = 2 e t 2 .

The exact solution is u ( x , t ) = sin ( π x ) + cos ( π x ) e t 2 , and the exact time-dependent coefficient is p ( t ) = t 2 + 1 .

Table 1 shows that the L ∞ error reduces by increasing the nodal points M for different noise levels σ . This table also shows the small condition number of A , which is the key factor to the performance and efficiency of the HWCM. Moreover, the performance of the present scheme in terms of time is also presented in Table 1.

Table 1

L ∞ error norm, CPU time along with condition number of matrix A with different M and σ for Example 1 at t = 1 and Δ t = 0.01

M	σ = 1 %		σ = 5 %		CPU (second)	Condition number of A
	L ∞ ( u )	L ∞ ( p )	L ∞ ( u )	L ∞ ( p )
1	3.4081 × 1 0 − 2	1.8487 × 1 0 − 2	3.4248 × 1 0 − 2	8.9843 × 1 0 − 2	0.58	2.5078
2	1.4800 × 1 0 − 2	1.7376 × 1 0 − 2	1.7562 × 1 0 − 2	8.9137 × 1 0 − 2	0.70	8.2496
4	5.1186 × 1 0 − 3	1.6427 × 1 0 − 2	7.9923 × 1 0 − 3	8.8923 × 1 0 − 2	0.93	17.330
8	2.4010 × 1 0 − 3	1.5876 × 1 0 − 2	5.3277 × 1 0 − 3	8.8138 × 1 0 − 2	2.01	27.879
16	1.7083 × 1 0 − 3	1.4689 × 1 0 − 2	4.6379 × 1 0 − 3	8.8035 × 1 0 − 2	7.30	40.821
32	1.5340 × 1 0 − 3	1.4273 × 1 0 − 2	4.4697 × 1 0 − 3	8.7134 × 1 0 − 2	9.15	58.235
64	1.4904 × 1 0 − 3	1.3859 × 1 0 − 2	4.4274 × 1 0 − 3	8.6732 × 1 0 − 2	12.5	82.545
128	1.4757 × 1 0 − 3	1.3405 × 1 0 − 2	4.4168 × 1 0 − 3	8.6130 × 1 0 − 2	18.7	116.81

The proposed method is also compared with difference scheme [2] in Table 2. It is evident from the table that Haar wavelet approximations for the source control parameter are accurate for a comparatively small number ( M = 32 ) of nodal points at different final times.

Table 2

The comparison of L ∞ error norm for some numerical solutions of p ( t ) for Example 1

Methods	Δ x	Δ t	0.2	0.4	0.6	0.8
HWCM ( σ = 1 % )	1 32	1 80	3.7019 × 1 0 − 3	4.6534 × 1 0 − 3	6.6576 × 1 0 − 3	1.0606 × 1 0 − 2
Difference scheme [2]	1 40	1 80	3.3696 × 1 0 − 2	2.0167 × 1 0 − 2	1.1330 × 1 0 − 2	2.5532 × 1 0 − 2

A graphical view of exact and numerical solutions captured at various noise intensities is shown in Figure 2, where the good agreement of these results at highly polluted data, σ = 10 % strengthens the applicability of the proposed HWCM. Finally, in Figure 3, we present the absolute errors at M = 16 , Δ t = 0.01 with finale time t = 1 for different noise σ . It can be clearly recognized from the figure that the calculated results converge to their exact solutions as the σ reduces from 20% to 1%.

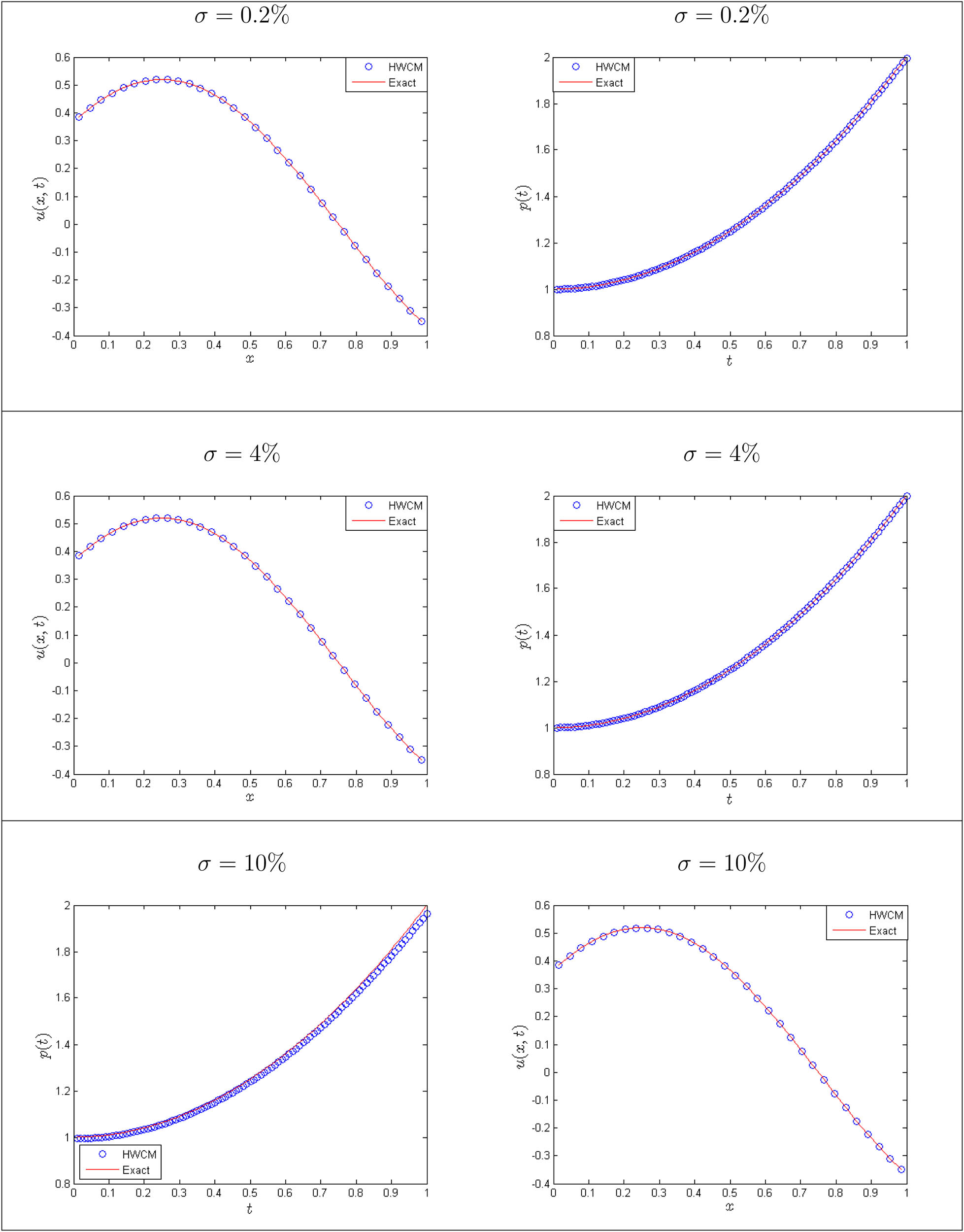
$Figure 2 Comparison of numerical results with different σ \sigma for Example 1 at M = 16 M=16 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 .$

Figure 2

Comparison of numerical results with different σ for Example 1 at M = 16 , Δ t = 0.01 , and t = 1 .

$Figure 3 The absolute values of the errors with different σ \sigma for Example 1 at M = 16 M=16 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 .$

Figure 3

The absolute values of the errors with different σ for Example 1 at M = 16 , Δ t = 0.01 , and t = 1 .

Example 2

Consider the IHCP along with the following input data

u t ( x , t ) = u x x ( x , t ) + p ( t ) u ( x , t ) + 2 x − ( sin ( 2 π x ) + 2 t x + x 2 ) sin ( t ) + 4 π 2 sin ( 2 π x ) − 2 , a ≤ x ≤ b , t > 0 , u ( a , t ) = a 2 + 2 t a + sin ( 2 π a ) , u ( b , t ) = b 2 + 2 t b + sin ( 2 π b ) , u ( x , 0 ) = x 2 + sin ( 2 π x ) , u ( 0.25 , t ) = 1 16 + t 2 + sin π 2 .

The exact solution u ( x , t ) = ( 2 t + x ) x + sin ( 2 π x ) is provided with oscillatory control source parameter p ( t ) = sin ( t ) .

Figure 4 depicts comparison of results of the established method with the analytical solution at M = 16 , σ = 1 % , and Δ t = 0.01 with final time t = 1 for different intervals, which are in good agreement. To observe the performance of the HWCM for increasing the interval and the collocation points, the numerical and exact solutions are shown in Figure 5, where the solutions also match with the peak points of oscillations ( σ = 1 % , Δ t = 0.01 with final time t = 1 and M = 32 ).

$Figure 4 Comparison of numerical results for Example 2 at σ = 1 % \sigma =1 \% , M = 32 M=32 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 in the different intervals.$

Figure 4

Comparison of numerical results for Example 2 at σ = 1 % , M = 32 , Δ t = 0.01 , and t = 1 in the different intervals.

$Figure 5 Comparison of numerical results for Example 2 at σ = 1 % \sigma =1 \% , M = 32 M=32 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 in the interval − π 2 , π 2 \left(-\frac{\pi }{2},\frac{\pi }{2}\right) .$

Figure 5

Comparison of numerical results for Example 2 at σ = 1 % , M = 32 , Δ t = 0.01 , and t = 1 in the interval − π 2 , π 2 .

The flexibility of the proposed HWCM for the oscillatory type numerical solution of p ( t ) in terms of different final times ( t = 1 , 2 , 3 , 5 , 7 , and 10) can also be sighted in Figure 6. Again for this problem, it has been also examined that the calculated results at various collocation points converge to exact solutions as the intensity of noise σ vanish, i.e., from 20 % to 1 % as shown in Figure 7. The 3D plot of the numerical results for both the examples is shown in Figure 8.

$Figure 6 Comparison of exact and numerical results for Example 2 at σ = 1 % \sigma =1 \% , M = 16 M=16 , and Δ t = 0.01 \Delta t=0.01 in the different t t .$

Figure 6

Comparison of exact and numerical results for Example 2 at σ = 1 % , M = 16 , and Δ t = 0.01 in the different t .

$Figure 7 The absolute values of the errors with different σ \sigma for Example 2 at M = 16 M=16 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 .$

Figure 7

The absolute values of the errors with different σ for Example 2 at M = 16 , Δ t = 0.01 , and t = 1 .

$Figure 8 The 3D overview of the numerical solutions at M = 16 M=16 , Δ t = 0.01 \Delta t=0.01 , and t = 1 t=1 .$

Figure 8

The 3D overview of the numerical solutions at M = 16 , Δ t = 0.01 , and t = 1 .

6 Conclusion

In this article, a multi-resolution HWCM is adopted for a time-dependent inverse problem focused on diffusion equation with source control parameter. The propped method is stable and convergent. It is the advantage of the HWCM that convert the ill-posed PDE into a well-condition system of equation and hence no need to introduced any regularization procedure. The numerical results of the examples are in line with the theoretical discussion. The accuracy, stability, and efficiency are due to the well-condition system matrix. The HWCM can also produce stable results for the inverse problem under a large intensity of noise level ( σ = 20 % ). Due to the accurate and reliable performance of the suggested HWCM, the present technique can be applied to two-dimensional and systems of inverse problems.

Funding information: This research was supported by the Project of Guangdong Provincial Department of Education Under No. 2020WQNCX049.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Dehghan M. Finding a control parameter in one-dimensional parabolic equations. Appl Math Comput. 2003;135(2–3):491–503. 10.1016/S0096-3003(02)00063-2Search in Google Scholar

[2] Ye C, Sun Z. On the stability and convergence of a difference scheme for an one-dimensional parabolic inverse problem. Appl Math Comp. 2007;188(1):214–25. 10.1016/j.amc.2006.09.109Search in Google Scholar

[3] Liu C-S. A double optimal descent algorithm for iteratively solving ill-posed linear inverse problems. Inverse Probl Sci Eng. 2015;23(1):38–66. 10.1080/17415977.2014.880905Search in Google Scholar

[4] Liu C-S. A highly accurate LGSM for severely ill-posed BHCP under a large noise on the final time data. Int J Heat Mass Transfer. 2010;53(19–20):4132–40. 10.1016/j.ijheatmasstransfer.2010.05.036Search in Google Scholar

[5] Tariq M, Ahmad H, Sahoo SK. The Hermite-Hadamard type inequality and its estimations via generalized convex functions of Raina type. Math Model Numer Simulat Appl (MMNSA). 2021;1(1):32–43. 10.53391/mmnsa.2021.01.004Search in Google Scholar

[6] Akbar MA, Akinyemi L, Yao S-W, Jhangeer A, Rezazadeh H, Khater MM, et al. Soliton solutions to the boussinesq equation through sine-gordon method and kudryashov method. Results Phys. 2021;25:104228. 10.1016/j.rinp.2021.104228Search in Google Scholar

[7] Ahmad I, Ahsan M, Hussain I, Kumam P, Kumam W. Numerical simulation of PDEs by local meshless differential quadrature collocation method. Symmetry. 2019;11(3):394. 10.3390/sym11030394Search in Google Scholar

[8] Ahmad I, Ahmad H, Inc M, Rezazadeh H, Akbar MA, Khater MM, et al. Solution of fractional-order Korteweg-de Vries and burgers equations utilizing local meshless method. J Ocean Eng Sci. 10.1016/j.joes.2021.08.014. Search in Google Scholar

[9] Ahmad I, Ahsan M, Din Z-u, Masood A, Kumam P. An efficient local formulation for time-dependent PDEs. Mathematics. 2019;7(3):216. 10.3390/math7030216Search in Google Scholar

[10] Wang F, Zhang J, Ahmad I, Farooq A, Ahmad H. A novel meshfree strategy for a viscous wave equation with variable coefficients. Front Phys. 2021;9:359. 10.3389/fphy.2021.701512Search in Google Scholar

[11] Akinyemi L, Rezazadeh H, Yao S-W, Akbar MA, Khater MM, Jhangeer A, et al. Nonlinear dispersion in parabolic law medium and its optical solitons. Results Phys. 2021:104411. 10.1016/j.rinp.2021.104411Search in Google Scholar

[12] Avci D, Yavuz M, Ozdemir N. Fundamental solutions to the Cauchy and Dirichlet problems for a heat conduction equation equipped with the Caputo-Fabrizio differentiation. in: Heat Conduction: Methods, Applications and Research. Hauppauge, New York, USA: NOVA Science Publishers; 2019. p. 95–107. Search in Google Scholar

[13] Yavuz M, Özdemir N. Numerical inverse Laplace homotopy technique for fractional heat equations. Thermal Sci 2018;22(1):85–194. 10.2298/TSCI170804285YSearch in Google Scholar

[14] Akgül EK, Akgül A, Yuvuz M. New illustrative applications of integral transforms to financial models with different fractional derivatives. Chaos Soliton Fractal. 2021;146:110877. 10.1016/j.chaos.2021.110877Search in Google Scholar

[15] Akinyemi L, Rezazadeh H, Shi Q-H, Inc M, Khater MM, Ahmad H, et al. New optical solitons of perturbed nonlinear schrödinger-hirota equation with spatio-temporal dispersion. Results Phys. 2021;29:104656. 10.1016/j.rinp.2021.104656Search in Google Scholar

[16] Yokus A, Yavuz M. Novel comparison of numerical and analytical methods for fractional Burger-Fisher equation. Discrete Contin Dyn Syst-S 2021;14(7):2591. 10.3934/dcdss.2020258Search in Google Scholar

[17] Ahmad H, Khan TA, Ahmad I, Stanimirović PS, Chu Y-M. A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 2020;19:103462. 10.1016/j.rinp.2020.103462Search in Google Scholar

[18] Ahmad I, Ahmad H, Thounthong P, Chu Y-M, Cesarano C. Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry. 2020;12(7):1195. 10.3390/sym12071195Search in Google Scholar

[19] Cannon J, Lin Y, Xu S. Numerical procedures for the determination of an unknown coefficient in semi-linear parabolic differential equations. Inverse Problems. 1994;10(2):227. 10.1088/0266-5611/10/2/004Search in Google Scholar

[20] Yan L, Fu C-L, Yang F-L. The method of fundamental solutions for the inverse heat problem. Eng Anal Bound Elem. 2008;32:216–22. 10.1016/j.enganabound.2007.08.002Search in Google Scholar

[21] Farcas A, Lesnic D. The boundary-element method for the determination of a heat source dependent on one variable. J Eng Math. 2006;54(4):375–88. 10.1007/s10665-005-9023-0Search in Google Scholar

[22] Liu C-S. An iterative algorithm for identifying heat source by using a DQ and a Lie-group method. Inverse Probl Sci Eng. 2015;23(1):67–92. 10.1080/17415977.2014.880907Search in Google Scholar

[23] Liu C-S. Lie-group differential algebraic equations method to recover heat source in a Cauchy problem with analytic continuation data. Int J Heat Mass Transfer. 2014;78:538–47. 10.1016/j.ijheatmasstransfer.2014.07.010Search in Google Scholar

[24] Kuo C-L, Liu C-S, Chang J-R. The modified polynomial expansion method for identifying the time dependent heat source in two-dimensional heat conduction problems. Int J Heat Mass Transfer. 2016;92:658–64. 10.1016/j.ijheatmasstransfer.2015.09.025Search in Google Scholar

[25] NawazKhan M, Ahmad I, Ahmad H. A radial basis function collocation method for space-dependent inverse heat problems. J Appl Comput Mech. 2020;6(Special Issue):1187–99. Search in Google Scholar

[26] Khan MN, Hussain I, Ahmad I, Ahmad H. A local meshless method for the numerical solution of space-dependent inverse heat problems. Math Meth Appl Sci. 2021;44(4):3066–79. 10.1002/mma.6439Search in Google Scholar

[27] Aziz I, Siraj-ul-Islam, Nisar M. An efficient numerical algorithm based on Haar wavelet for solving a class of linear and nonlinear nonlocal boundary-value problems. Calcolo. 2016;53(4):621–33. 10.1007/s10092-015-0165-9Search in Google Scholar

[28] Siraj-ul-Islam, Ahsan M, Hussian I. A multi-resolution collocation procedure for time-dependent inverse heat problems. Int J Therm Sci. 2018;128:160–74. 10.1016/j.ijthermalsci.2018.01.001Search in Google Scholar

[29] Ahsan M, Siraj-ul-Islam, Hussain I. Haar wavelets multi-resolution collocation analysis of unsteady inverse heat problems. Inverse Probl Sci Eng. 2019;27:1498–520. 10.1080/17415977.2018.1481405Search in Google Scholar

[30] Ahsan M, Ahmad I, Ahmad M, Hussian I. A numerical Haar wavelet-finite difference hybrid method for linear and non-linear schrödinger equation. Math Comp Simulat. 2019;165:13–25. 10.1016/j.matcom.2019.02.011Search in Google Scholar

[31] Mallat S. A wavelet tour of signal processing: the sparse way. Burlington, MA: Academic Press; 2008. Search in Google Scholar

[32] Liu Y, Liu Y, Cen Z. Daubechies wavelet meshless method for 2-D elastic problems. Tsinghua Sci Technol. 2008;13(5):605–8. 10.1016/S1007-0214(08)70099-3Search in Google Scholar

[33] Siraj-ul-Islam, Aziz I, Ahmad M. Numerical solution of two-dimensional elliptic PDEs with nonlocal boundary conditions. Comp Math Appl. 2015;69(3):180–205. 10.1016/j.camwa.2014.12.003Search in Google Scholar

[34] Jang G-W, Kim YY, Choi KK. Remesh-free shape optimization using the wavelet-Galerkin method. Int J Solids Struct. 2004;41(22):6465–83. 10.1016/j.ijsolstr.2004.05.010Search in Google Scholar

[35] Díaz LA, Martín MT, Vampa V. Daubechies wavelet beam and plate finite elements. Finite Elem Anal Des. 2009;45(3):200–9. 10.1016/j.finel.2008.09.006Search in Google Scholar

[36] Abdeljawad T, Amin R, Shah K, Al-Mdallal Q, Jarad F. Efficient sustainable algorithm for numerical solutions of systems of fractional order differential equations by Haar wavelet collocation method. Alexandria Eng J. 2020;59(4):2391–400. 10.1016/j.aej.2020.02.035Search in Google Scholar

[37] Rawat S. Quality assessment in image compression by using fast wavelet transformation with 2D Haar wavelets. Int Res J Eng Technol. 2017;4(5):508–18. Search in Google Scholar

[38] Belkadhi K, Elhamdi K, Bhar M, Manai K. Dose calculation using Haar wavelets with buildup correction. Appl Radiat Isotopes. 2017;127:186–94. 10.1016/j.apradiso.2017.06.011Search in Google Scholar PubMed

[39] Fryzlewicz P, Timmermans C. Shah: Shape-Adaptive Haar wavelets for image processing. J Comput Graph Statist. 2016;25(3):879–98. 10.1080/10618600.2015.1048345Search in Google Scholar

[40] Feklistova L, Hein H. Delamination identification using machine learning methods and Haar wavelets. Comp Assist Methods Eng Sci. 2017;19(4):351–60. Search in Google Scholar

[41] Vaidelienė G, Valantinas J. The use of Haar wavelets in detecting and localizing texture defects. Image Anal Stereol. 2016;35(3):195–201. 10.5566/ias.1561Search in Google Scholar

[42] Lefebvre A, Liu J, Mueller E, Nadar MS, Schmidt M, Zenge M, et al. MRI reconstruction with incoherent sampling and redundant Haar wavelets. US Patent No 9,396,562. Jul. 19 2016. Search in Google Scholar

[43] Nazir S, Shahzad S, Wirza R, Amin R, Ahsan M, Mukhtar N, et al. Birthmark based identification of software piracy using haar wavelet. Math Comp Simulat. 2019;166:144–54. 10.1016/j.matcom.2019.04.010Search in Google Scholar

[44] McMorris D, Pearson P, Yurk B. A modified wavelet method for identifying transient features in time signals with applications to bean beetle maturation. Involve J Math. 2016;10(1):21–42. 10.2140/involve.2017.10.21Search in Google Scholar

[45] Majak J, Shvartsman B, Kirs M, Pohlak M, Herranen H. Convergence theorem for the Haar wavelet-based discretization method. Composite Struct. 2015;126:227–32. 10.1016/j.compstruct.2015.02.050Search in Google Scholar

[46] Kumar M, Pandit S. A composite numerical scheme for the numerical simulation of coupled burgers equation. Comp Phys Commun. 2014;185(3):809–17. 10.1016/j.cpc.2013.11.012Search in Google Scholar

Received: 2021-07-05

Revised: 2021-10-08

Accepted: 2021-10-28

Published Online: 2021-11-26

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2021-0080

Keywords for this article

nonlinear ill-posed PDE; Haar wavelets; stability; condition number

Creative Commons

BY 4.0