Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge

Adnan; Umar Khan; Naveed Ahmed; Syed Tauseef Mohyud-Din; El-Sayed M. Sherif; Ilyas Khan

doi:10.1515/phys-2021-0007

Artikel Open Access

Intensification of thermal stratification on dissipative chemically heating fluid with cross-diffusion and magnetic field over a wedge

Adnan , Umar Khan , Naveed Ahmed , Syed Tauseef Mohyud-Din , El-Sayed M. Sherif und Ilyas Khan

Veröffentlicht/Copyright: 31. Dezember 2021

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 19 Heft 1

Abstract

This paper aims to examine the heat and mass characteristics for thermally stratified chemically heated, dissipative flow under the cross-diffusion and imposed Lorentz forces. A self-similar model is obtained employing suitable similarity transformations. Then, the RK technique is used for mathematical analysis. The stimulations of pertinent physical quantities in the flow regimes, shear stresses, and the Nusselt number were examined graphically. It is noted that more radiative flow favors the thermal behavior of the fluid and increases in the Prandtl number causes the decrease in thermal characteristics. Moreover, decreases in mass characteristics were examined by the fluctuating chemical reaction and Schmidt parameters. Lastly, key outcomes of the work are pinpointed.

Keywords: Lorentz force; radiative heat flux; wedge flow; cross-diffusion; shear stresses

1 Introduction

The investigation of boundary layer flow is one of the significant motives and an important part in the field of thermal transportation and fluid dynamics. Currently, regular flow characteristics over a wedge (either flat or porous wedge) are of potential interest.

The earlier work in this direction was examined by Falkner and Snan [1]. They discussed incompressible flow over a stationary wedge and tackled the resulting nonlinear flow model approximately. Later on, Rajagopal et al. [2] extended the study of Falkner and Skan over a stationary wedge situated inside the fluid. Lin and Lin [3] investigated thermal transportation in the convectively heated stationary wedge. They discussed the model for higher values of Prandtl number and found self-similar solutions for the model. Investigation of the characteristics of the Falkner–Skan flow in the presence and absence of convection over a wedge was reported in refs [4,5], respectively. Furthermore, the impacts of radiative heat flux and Lorentz force in the flow regimes are discussed there. Theoretical investigation of fluid under porosity effects and in the presence of mixed convection was carried out by Kumari et al. [6].

Ahmad and Khan [7] discussed the impacts of internally heated viscous dissipative flow over a convectively heated wedge; the wedge is capable of moving. They noted that the thermal field increases in the presence of an internal heat source. In 2014, Khan et al. [8] examined flow characteristics over a wedge. Further, flow along a vertical wedge was reported in Ganapathirao et al. [9]. The colloidal flow over a nonmoving wedge was reported in ref. [10]. The presence of the convection flow condition on the dissipative flow cannot be overlooked because of its direct effect on thermal transportation. The applications of the aforementioned flow with conditions were composed of thermal insulation, rocket engine, cooling of a nuclear reactor, electronic chips, and semiconductor wafers. Keeping the aforementioned applications in mind, Gebhart [11] explored the stimulus of viscous dissipation on flow characteristics. Afterward, the influence of viscous dissipation over a wedge was discussed by Yih [12]. He encountered the effects of the imposed Lorentz force and solved the flow model by employing the Keller-box method.

Recently, Ullah et al. [13] inspected the non-Newtonian model over a wedge. The stimulus of the applied Lorentz force on flow characteristics was part of their discussion. The unsteady Casson model over stretching surfaces was explored in Ullah et al. [14]. Their study contained the novel analysis of radiation, chemical, and mixed convection parameters in the flow regimes. Ahmed et al. [15] reported the study of nanofluids in the rotating system by considering ferromagnetics as nanoparticles. Ishak et al. [16] pointed out the Falkner–Skan flow with the addition of suction or blowing properties. The influence of the magnetohydrodynamic flow with forced convection over a wedge by encountering time-dependent viscosity was discussed by Pal and Mondal [17]. The MHD slip flow over a convectively heated wedge by considering heat generation/absorption was examined by Rahman et al. [18].

Recently, Hussanan et al. [19] examined the unsteady Falkner–Skan flow by encountering the influences of ohmic heating. The impacts of chemical parameters on the porous radiative wedge were reported in ref. [20]. Chambre and Acrivos [21] revealed the boundary layer model by considering the chemical parameters. The Falkner–Skan flow model for the wedge saturated with a colloidal mixture was reflected by Yacob et al. [22]. Recently, Khan et al. [23] investigated a bio-convection dissipative flow model. They highlighted the impacts of Joule heating and applied magnetic field over the flow of gyrotactic microorganisms and studied the model numerically. Furthermore, they analyzed the influence of pertinent flow parameters in flow regimes.

In 1937, Hartree [24] discussed the boundary layer equation approximately. Later on, researchers turned toward the study of wedge flow under different flow conditions. In 1961, Koh and Hartnett [25] explored the shear stresses and Nusselt number for streamline flow by considering the porosity parameter. Lin and Lin [26] discussed the approximate solutions for the wedge flow of any Prandtl number. Analysis of cylindrically shaped nanoparticles in a vertical channel was reported in ref. [27]. Various flow parameters and various channels were investigated in refs [28,29,30,31]. Furthermore, the flow model with a Brinkman-type nanofluid over a vertical plate was discussed by Ali et al. [32]. A natural convection model over a nonlinear sheet surface was studied by Ullah et al. [33]. For the nanofluid flow between Riga plates and second-grade fluid flow between an oblique channel, see refs [34,35], respectively. The analysis of the effective Prandtl model on squeezed flow nanofluids and other fruitful studies in various geometries are given in refs [36,37]. For further studies, one can refer the work presented in refs [38,39,40,41,42,43,44].

The behavior of third-grade fluid by incorporating the Cattaneo–Christov constitutive model, investigation of entropy for a viscoelastic nanofluid, effects of thermal radiation and ohmic heating, cross-flow of mixed convective fluid, and analysis of multiple nanofluids are studied in refs [45,46,47,48,49], respectively. Furthermore, significant studies are found in refs [50,51,52,53,54,55] and references therein.

From the intense science literature survey, it is perceived that the flow of a Newtonian fluid over a flat wedge by incorporating the cross-diffusion gradients and chemical reaction effects is not yet pointed out. For the novelty of the study, the phenomena of Lorentz forces and thermal radiation are taken in the momentum and energy conservation laws. The modeling of the particular flow over a wedge leads to a nonlinear self-similar problem, which is treated numerically. For numerical treatment, the Runge–Kutta technique coupled with the shooting technique is operated. The impacts of various physical dimensionless quantities emerging in the model are perceived via graphical results.

The flow problem and local heat and mass transport rate are modeled in Section 2. Afterward, the particular flow model is treated numerically in Section 3 and the problem is successfully solved over a semi-infinite region. Next, the impacts of the various ingrained flow quantities on the fluid velocity, temperature, concentration trends, shear stresses, and local rate of mass and heat transport are considered in Section 4. Finally, the major results of the presented study are highlighted in the last section.

2 Model formulation

The magnetized streamline flow is considered past a wedge in the presence of radiative heat flux, cross-diffusion, and chemical reaction. The fluid is flowing with the mainstream velocity U ( x ) . The variable temperature at the wedge is denoted by T w ( x ) and C w ( x ) is the concentration. Further, the ambient temperature and concentration are denoted by T and C , respectively. The imposed magnetic field B ( x ) is in the form B ( x ) = B 0 x m − 1 2 , where B 0 is uniform (for instance, see refs [56,57]), and it is supposed that the magnetic Reynolds number and induced magnetic field are almost inconsequential comparative to Lorentz forces. The physical theme of the problem is elucidated in Figure 1.

Figure 1

Flow configuration.

The dimensional wedge flow model is as follows [58]:

(1) ∂ u ∂ x + ∂ v ∂ y = 0 ,

(2) u ∂ u ∂ x + v ∂ u ∂ y = U ( x ) d U ( x ) d x μ ρ ∂ 2 u ∂ y 2 + σ ρ B 2 ( x ) ( U ( x ) − u ) ,

(3) u ∂ T ∂ x + v ∂ T ∂ y = k ρ c p ∂ 2 T ∂ y 2 + D K T ρ c p C s ∂ 2 C ∂ y 2 + 1 ρ c p ∂ u ∂ y 2 − 16 σ ⁎ T ∞ 3 3 k ⁎ ρ c p ∂ 2 T ∂ y 2 ,

(4) u ∂ C ∂ x + v ∂ C ∂ y = D ∂ 2 C ∂ y 2 + D K T T m ∂ 2 T ∂ y 2 − k 1 ( C − C ∞ ) .

Here, the continuity equation satisfies identically. Equation (2) represents the momentum equation with mainstream velocity U ( x ) , imposed magnetic field B ( x ) , dynamic viscosity μ , the density of the fluid ρ , and electrical conductivity σ ; u and v denote the velocities. Equation (3) is the thermal equation with Rd. Here, k is the thermal conductivity, c p is the specific heat capacity, C s is the concentration susceptibility, K T is the thermal diffusion, D is the mass diffusivity, and T is the temperature. In equation (3), C is the fluid concentration, k 1 and T _m are the chemical reaction and mean temperature, respectively.

The feasible conditions are the following [58]:

At y = 0 :

(5) u = 0 , v = 0 , T = T w ( x ) , C = C w ,

At y → ∞ :

(6) u → U ( x ) = u 0 x m , T → T ∞ , C → C ∞ .

The stream functions u = ∂ ψ ∂ y , v = − ∂ ψ ∂ x , and similarity transformations are defined as follows ref. [58]:

(7) ψ = ν u 0 x m + 1 F u 0 x m + 1 ν y x − 1 , η = u 0 x m + 1 ν y x − 1 , β u 0 x m + 1 ν y x − 1 = T − T ∞ T w − T ∞ , ϕ u 0 x m + 1 ν y x − 1 = C − C ∞ C w − C ∞ .

Note that B ( x ) = B 0 x m − 1 2 is the form of an applied magnetic field according to refs [56,57], U ( x ) = u 0 x − m , where 0 ≤ m ≤ 1 . The expression β ⁎ = β ⁎ ( 2 − β ⁎ ) − 1 (where β ⁎ represents the Hartree pressure) corresponds to β ⁎ = Ω π .

After some necessary calculations, the attained dimensionless model is

(8) F ′ ″ − m F ′ 2 − m + 1 2 F F ″ − m + M ( 1 − F ′ ) = 0 ,

(9) ( 1 + Rd ) β ″ + Pr ( m + 1 ) 2 F β ′ + PrEc F ″ 2 + Pr D f ϕ ″ = 0 ,

(10) ϕ ″ + Sc ( m + 1 ) 2 F ϕ ′ + SrSc β ″ − γ Sc ϕ = 0 .

The corresponding boundary conditions for our flow model are the following:

(11) F ( η ↑ η = 0 ) = 0 , F ' ( η ↑ η = 0 ) = 0 , β ( η ↑ η = 0 ) = 1 , ϕ ( η ↑ η = 0 ) = 1 ,

(12) F ' ( η ↑ η = ∞ ) → 1 , β ( η ↑ η = ∞ ) → 0 , ϕ ( η ↑ η = ∞ ) → 0 .

The dimensionless formulas against the involved quantities are

M = σ B 0 2 ρ u 0 , Pr = ν ρ C p k , Rd = − 16 σ ⁎ T ∞ 3 3 k k ⁎ , D f = D k T ( C w − C ∞ ) C s C p ν ( T w − T ∞ ) , Sr = D m k T ( T w − T ∞ ) ν T m ( C w − C ∞ ) , Sc = ν D and γ = ν f k 1 U 2 .

The quantities of physical interest in the dimensional form are described as follows [58]:

(13) C F = μ ρ U 2 ( x ) ∂ u ∂ y ↓ y = 0 ,

(14) Nu x = k x k ( T w − T ∞ ) ∂ T ∂ y ↓ y = 0 ,

(15) Sh x = x C w − C ∞ ∂ C ∂ y ↓ y = 0 .

In self-similar form, these expressions are reduced as follows:

C F Re x = F ″ ( 0 ) ,

Nu x ( Re x ) − 1 2 = − β ′ ( 0 ) ,

Sh ( Re x ) − 1 2 = − ϕ ′ ( 0 ) , where Re x = x U ( x ) ν represents the local Reynold number.

3 Mathematical analysis

The particular model described by equations (8)–(10) with nonhomogenous auxiliary conditions in Equations (11) and (12) does not possess exact solutions due to nonlinearity. Thus, the present flow model can be solved by the numeric technique; we used the RK technique [59,60]. To operate the technique, first, we need to make the following substitutions:

(16) y 1 = F , y 2 = F ′ , y 3 = F ′ , y 4 = β , y 5 = β ′ , y 6 = ϕ , y 7 = ϕ ′ .

Further, the model was reduced to the following version:

(17) F ′ ″ = m F ′ 2 − m + 1 2 F F ″ − m − M ( 1 − F ' ) ,

(18) β ″ = 1 ( 1 + Rd ) − Pr ( m + 1 ) 2 F β ′ − PrEc F ″ 2 − Pr D f ϕ ″ ,

(19) ϕ ″ = − Sc ( m + 1 ) 2 F ϕ ′ − SrSc β ″ + γ Sc ϕ .

Consequently, the following system is attained:

(20) y 1 ′ y 2 ′ y 3 ′ y 4 ′ y 5 ′ y 6 ′ y 7 ′ = y 2 y 3 m y 2 2 − m + 1 2 y 1 y 3 − m − M ( 1 − y 2 ) y 5 1 ( 1 + Rd ) − Pr ( m + 1 ) 2 y 1 y 5 − Pr D f y 7 ′ − PrEc y 3 2 y 7 − Sc ( m + 1 ) 2 y 1 y 7 − SrSc y 5 ′ + γ Sc y 6 .

and the initial conditions are as follows:

(21) y 1 y 2 y 3 y 4 y 5 y 6 y 7 = 0 0 n 1 1 n 2 1 n 3 .

Finally, the solutions of the model are as described in Table 1. This computation is carried out for step size 0.5 .

Table 1

Model solutions over the domain of interest

η	F ′ ( η )	β ( η )	ϕ ( η )
0.0	0.0000000000	1.0000000000	1.0000000000
0.5	0.4575633648	0.8870454597	0.7286054919
1.0	0.7314206224	0.7440129051	0.5164061589
1.5	0.8803175946	0.5933443311	0.3533632878
2.0	0.9526029667	0.4490377056	0.2326710105
2.5	0.9834982230	0.3204734153	0.1471573757
3.0	0.9949960216	0.2133585775	0.0889701955
3.5	0.9986907397	0.1298089980	0.0505958003
4.0	0.9997098593	0.0687575165	0.0258071403
4.5	0.9999508991	0.0269210431	0.0099969650
5.0	1.0000007510	− 6.6748755860 × 10 − 8	2.6103811060 × 10 − 8

4 Graphical results

This section highlights the impact of Eckert number, Prandtl number, thermal radiation, chemical reaction, magnetic number, Schmidt, Dufour, and Soret numbers on the flow characteristics. Here, it is worth mentioning that the wedge flow corresponds to m = 0.5 , while the horizontal plate flow and stagnation point flow correspond to m = 0 and m = 1.0 , respectively. Further, the cross-diffusion in the flow regimes is also under consideration.

Figure 2 shows the alterations in F ′ ( η ) for varied magnetic fields. It is evident that for the stagnation point ( m = 1 ) flow, the velocity field increases rapidly. Maximum variations in the velocity of the fluid F ′ ( η ) are noticed in the area 0.5 ≤ η ≤ 2.5 ., The alterations in F ′ ( η ) are almost similar away from the wedge surface.

$Figure 2 Influence of M M on F ′ ( η ) F^{\prime} (\eta ) . (a) 2D and (b) 3D view.$

Figure 2

Influence of M on F ′ ( η ) . (a) 2D and (b) 3D view.

The behavior of the temperature β ( η ) of the fluid due to varying radiation parameters, Prandtl number, Eckert, and Dufour numbers are shown in Figures 3–5. From Figure 3a, it can be observed that for more thermally stratified fluid, the temperature starts increasing. For a horizontal plate flow, the thermal field increased rapidly. Near η = 5.0 , these variations are maximum. In the region η > 5.0 , β ( η ) increases slowly for the wedge, horizontal plate, and stagnation point flow cases. Beyond the region η ≥ 15.0 , the fluid temperature vanishes asymptotically. For the stagnation point flow, alterations in temperature gradually decrease compared to those in the wedge flow case. Consequently, Figure 3b shows the influences of Pr on β ( η ) . The variable Prandtl number leads to a decrease in β ( η ) . Near the wedge, the decreasing behavior of β ( η ) is almost inconsequential. But, in the region 2.0 ≤ η ≤ 6.0 , these effects are very clear, and maximum decreases in temperature are observed in this area. In the case of a horizontal plate flow, the fluid temperature decreases slowly as compared to the wedge flow and stagnation point flow. The three-dimensional view of the temperature for wedge, stagnation point flow, and horizontal plate flow due to varying Prandtl numbers P r are shown in Figure 4a and b, respectively.

$Figure 3 Stimulus of (a) Rd \text{Rd} and (b) Pr \text{Pr} on β ( η ) \beta (\eta ) .$

Figure 3

Stimulus of (a) Rd and (b) Pr on β ( η ) .

$Figure 4 3D view of β ( η ) \beta (\eta ) for (a) Rd \text{Rd} and (b) Pr \text{Pr} .$

Figure 4

3D view of β ( η ) for (a) Rd and (b) Pr .

$Figure 5 Stimulus of (a) D f {D}_{\text{f}} and (b) Ec \text{Ec} on β ( η ) \beta (\eta ) .$

Figure 5

Stimulus of (a) D f and (b) Ec on β ( η ) .

The stimuli of Dufour and Eckert numbers on the thermal characteristics β ( η ) are shown in Figure 5a and b, respectively. It is noted that increasing Dufour and Eckert numbers lead to an increase in β ( η ) . But, these effects are almost inconsequential for the wedge ( m = 1.0 ), stagnation point flow ( m = 0.5 ), and horizontal plate flow ( m = 0 ). Although, increase in temperature is almost negligible, but, for the horizontal plate flow case, temperature increases quite rapidly compared to the wedge and stagnation point flow case.

Figures 6–8 show the impact of γ , Schmidt number Sc , and Sr on ϕ ( η ) . The decrease in ϕ ( η ) is shown in Figure 6a and b, respectively, for γ and Sc. It is observed that for more chemically heated fluid, decrease in the ϕ ( η ) field is quite slow for the horizontal plate flow. On the contrary, Figure 6b shows a prompt decrease in ϕ ( η ) . This shows that increasing Sc leads to a prompt decrease in the concentration profile. Further, far away from the wedge surface, influences of γ and Sc vanish asymptotically. Fascinating fluctuations in ϕ ( η ) are inspected for varying Sr values in Figure 8a. The concentration field increases due to increasing Soret number. These effects are almost inconsequential for the wedge, stagnation point flow, and horizontal plate flow. Further, 3D scenario of the dimensionless concentration field is shown in Figure 8b.

$Figure 6 Stimulus of (a) γ \gamma and (b) Sc on ϕ ( η ) \phi (\eta ) .$

Figure 6

Stimulus of (a) γ and (b) Sc on ϕ ( η ) .

$Figure 7 3D view of ϕ ( η ) \phi (\eta ) for (a) γ \gamma and (b) Sc.$

Figure 7

3D view of ϕ ( η ) for (a) γ and (b) Sc.

$Figure 8 Influence of Sr on ϕ ( η ) \phi (\eta ) for (a) 2D and (b) 3D view.$

Figure 8

Influence of Sr on ϕ ( η ) for (a) 2D and (b) 3D view.

Influences of M and m on the shear stresses are shown in Figure 9a and b, respectively. For both varying M and m , the skin friction starts increasing. In the case of magnetic parameters, shear stresses increase quite slowly compared to the case of varying m values.

$Figure 9 Stimulus of (a) m m and (b) M M on F ″ ( 0 ) {F}^{^{\prime\prime} }(0) .$

Figure 9

Stimulus of (a) m and (b) M on F ″ ( 0 ) .

The impact of Dufour D f , Rd, and Pr numbers on the local heat transport is shown in Figures 10 and 11, respectively. It can be seen that the local heat transport decreases for D _f and Rd. For the horizontal plate flow, the Nusselt number decreases promptly compared to the wedge and stagnation point flow cases. The reverse behavior of Nu is shown in Figure 11b at varying Prandtl numbers Pr .

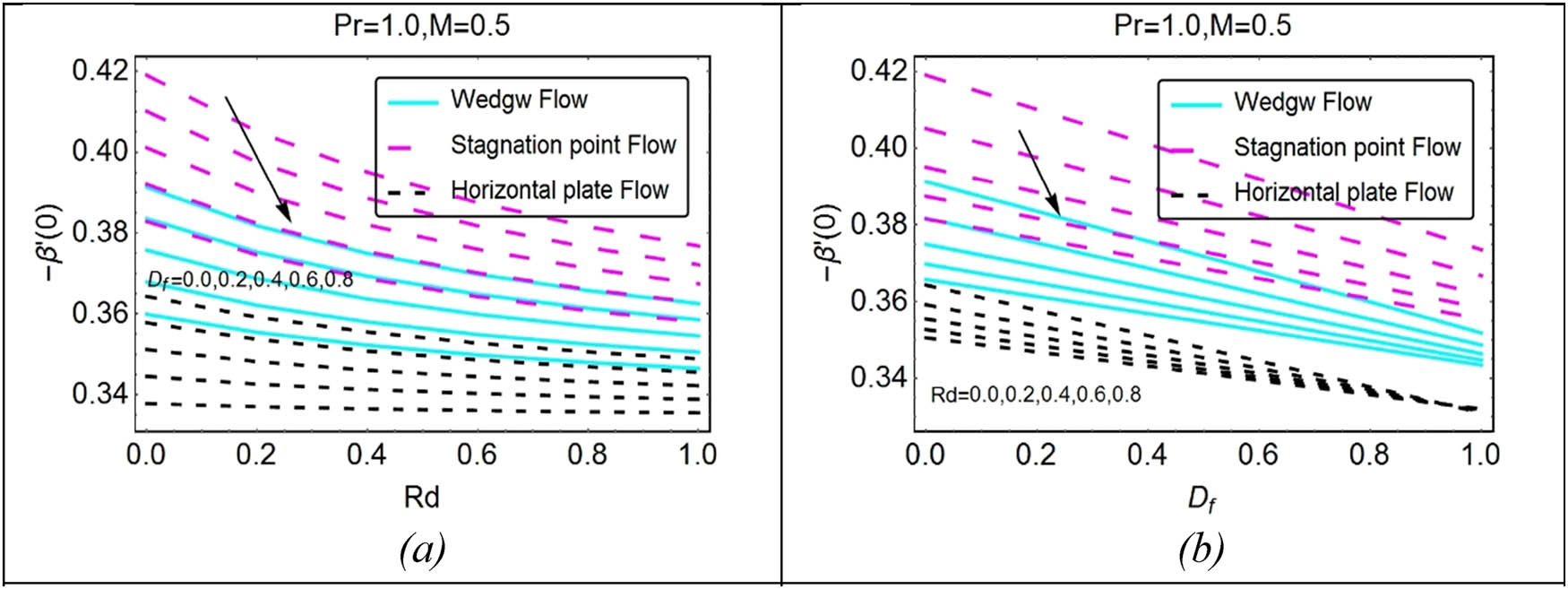
$Figure 10 Stimulus of (a) D f {D}_{\text{f}} and (b) Rd on – β ′ ( 0 ) \mbox{--}{\beta }^{^{\prime} }(0) .$

Figure 10

Stimulus of (a) D f and (b) Rd on – β ′ ( 0 ) .

$Figure 11 Stimulus of (a) D f {D}_{\text{f}} and (b) Pr on – β ′ ( 0 ) \mbox{--}{\beta }^{^{\prime} }(0) .$

Figure 11

Stimulus of (a) D f and (b) Pr on – β ′ ( 0 ) .

Figure 12a and b highlight the variations in the Sherwood number as a function of Sc and γ , respectively. It is noted that at smaller Sc and chemical parameters γ , variations in local mass transfer are quite small. However, for Sc, these effects are prominent as compared to the chemically reacting fluid. A decreasing behavior of the local mass transfer coefficient is observed in Figures 13a and 14a, respectively, for increasing the chemical reaction parameter and the Soret number horizontally. Furthermore, it can be seen from Figures 13b and 14b that the mass transfer coefficient varies linearly.

$Figure 12 Stimulus of (a) Sc and (b) γ \gamma on – ϕ ′ ( 0 ) \mbox{--}{\phi }^{^{\prime} }(0) .$

Figure 12

Stimulus of (a) Sc and (b) γ on – ϕ ′ ( 0 ) .

$Figure 13 Stimulus of (a) Sr and (b) γ \gamma on – ϕ ′ ( 0 ) \mbox{--}{\phi }^{^{\prime} }(0) .$

Figure 13

Stimulus of (a) Sr and (b) γ on – ϕ ′ ( 0 ) .

$Figure 14 Stimulus of (a) Sr and (b) Sc on – ϕ ′ ( 0 ) \mbox{--}{\phi }^{^{\prime} }(0) .$

Figure 14

Stimulus of (a) Sr and (b) Sc on – ϕ ′ ( 0 ) .

5 Conclusion

The fluid flow characteristics over a wedge are reported by incorporating the influences of the imposed magnetic field, thermal radiation, and chemical reactions. From the analysis, it is supposed that the radiative heat flux leads to an increase in the fluid temperature, and decreases in the temperature are noted for the Prandtl number. The temperature β ( η ) increases due to cross-diffusion of gradients and dissipative phenomena. The decrease in the concentration trends is reported for the higher Schmidt number while the Soret number increases the concentration field. Moreover, more surface shear stresses are noted for stronger magnetic effects, and local mass transfer increases for stronger Schmidt effects.

Funding information: This research was supported by Researchers Supporting Project Number (RSP-2021/33), King Saud University, Riyadh, Saudi Arabia.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Falkner VM, Skan SW. Some approximate solutions of the boundary layer equations. London, Edinburgh, Dublin Philos Mag J Sci. 1931;12:865–96.10.1080/14786443109461870Suche in Google Scholar

[2] Rajagopal KR, Gupta AS, Na TY. A note on the Falkner-Skan flows of a non-Newtonian fluid. Int J Non Linear Mech. 1983;18(4):313–20.10.1016/0020-7462(83)90028-8Suche in Google Scholar

[3] Lin HT, Lin LK. Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any Prandtl number. Int J Heat Mass Transf. 1987;30(6):1111–8.10.1016/0017-9310(87)90041-XSuche in Google Scholar

[4] Watanabe T. Thermal boundary layer over wedge with uniform suction or injection in force flow. Acta Mech. 1990;83:119–26.10.1007/BF01172973Suche in Google Scholar

[5] Watanabe T, Pop I. Magnetohydrodynamic free convection flow over a wedge in the presence of a transverse magnetic field. Int Commun Heat Mass Transf. 1993;20(6):871–81.10.1016/0735-1933(93)90040-3Suche in Google Scholar

[6] Kumari M, Takhar HS, Nath G. Mixed convection flow over a vertical wedge embedded in a highly porous medium. Heat Mass Transf. 2001;37:139–46.10.1007/s002310000154Suche in Google Scholar

[7] Ahmad R, Khan WA. Effect of viscous dissipation and internal heat generation/absorption on heat transfer flow over a moving wedge with convective boundary condition. Heat Transf Asian Res. 2013;42(7):589–602.10.1002/htj.21055Suche in Google Scholar

[8] Khan MS, Karim I, Islam MS, Wahiduzzaman M. MHD boundary layer radiative, heat generating and chemical reacting flow past a wedge moving in a nanofluid. Nano Convergence. 2014;1(20). 10.1186/s40580-014-0020-8.Suche in Google Scholar PubMed PubMed Central

[9] Ganapathirao M, Ravindran R, Momoniat E. Effects of chemical reaction, heat and mass transfer on an unsteady mixed convection boundary layer flow over a wedge with heat generation/absorption in the presence of suction or injection. Int J Heat Mass Transf. 2015;51:289–300.10.1007/s00231-014-1414-1Suche in Google Scholar

[10] Kasmani RM, Sivasankaran S, Bhuvaneswari M, Siri Z. Effect of chemical reaction on convective heat transfer of boundary layer in nanofluid over a wedge with heat generation/absorption and suction. J Appl Fluid Mech. 2016;9(1):379–88.10.18869/acadpub.jafm.68.224.24151Suche in Google Scholar

[11] Gebhart B. Effects of viscous dissipation in natural convection. J Fluid Mech. 1962;14(2):225–32.10.1017/S0022112062001196Suche in Google Scholar

[12] Yih KA. MHD forced convection flow adjacent to a non-isothermal wedge. Int Commun Heat Mass Transf. 1999;26(6):819–27.10.1016/S0735-1933(99)00070-6Suche in Google Scholar

[13] Ullah I, Khan I, Shafie S. Hydromagnetic Falkner-Skan flow of Casson fluid past a moving wedge with heat transfer. Alex Eng J. 2016;55(3):2139–48.10.1016/j.aej.2016.06.023Suche in Google Scholar

[14] Ullah I, Bhattacharyya K, Shafie S, Khan I. MHD mixed convection slip flow of Casson fluid over nonlinearly stretching sheet embedded in a porous medium with chemical reaction, thermal radiation, heat generation/absorption and convective boundary conditions. PLoS One. 2016;10(11). 10.1371/journal.pone.0165348.Suche in Google Scholar PubMed PubMed Central

[15] Ahmed N, Abbasi A, Saba F, Khan U, Mohyud-Din ST. Flow of ferro-magnetic nanoparticles in a rotating system: a numerical investigation of particle shapes. Indian J Phys. 2018;92:969–77.10.1007/s12648-018-1186-4Suche in Google Scholar

[16] Ishak A, Nazar R, Pop I. Falkner–Skan equation for flow past a moving wedge with suction or injection. J Appl Math Comput. 2007;25:67–83.10.1007/BF02832339Suche in Google Scholar

[17] Pal D, Mondal H. Influence of temperature-dependent viscosity and thermal radiation on MHD forced convection over a non-isothermal wedge. Appl Math Computation. 2009;212(1):194–208.10.1016/j.amc.2009.02.013Suche in Google Scholar

[18] Rahman MM, Al-Lawatia MA, Eltayeb IA, Al-Salti N. Hydromagnetic slip flow of water based nanofluids past a wedge with convective surface in the presence of heat generation (or) absorption. Int J Therm Sci. 2012;57:172–82.10.1016/j.ijthermalsci.2012.02.016Suche in Google Scholar

[19] Hussanan A, Ismail Z, Khan I, Hussein AG, Shafie S. Unsteady boundary layer MHD free convection flow in a porous medium with constant mass diffusion and Newtonian heating. Eur Phys J Plus. 2014;129(46). 10.1140/epjp/i2014-14046-x.Suche in Google Scholar

[20] Kandasamy R, Raji AWBM, Khamis AB. Effects of chemical reaction, heat and mass transfer on boundary layer flow over a porous wedge with heat radiation in the presence of suction or injection. Theor Appl Mech. 2006;33(2):123–48.10.2298/TAM0602123KSuche in Google Scholar

[21] Chambre PL, Acrivos A. Diffusion of a chemically reactive species in a laminar boundary layer flow. Indian Eng Chem. 1957;49.10.1063/1.1724336Suche in Google Scholar

[22] Yacob NA, Ishak A, Pop I. Falkner-Skan problem for a static or moving wedge in nanofluids. Int J Therm Sci. 2011;50(2):133–9.10.1016/j.ijthermalsci.2010.10.008Suche in Google Scholar

[23] Khan U, Ahmed N, Mohyud-Din ST. Influence of viscous dissipation and Joule heating on MHD bio-convection flow over a porous wedge in the presence of nanoparticles and gyrotactic microorganisms. Springer Plus. 2016;5(1). 10.1186/s40064-016-3718-8.Suche in Google Scholar

[24] Hartree DH. On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer. Math Proc Camb Philos Soc. 1937;33:223–39.10.1017/S0305004100019575Suche in Google Scholar

[25] Koh JCY, Hartnett JP. Skin-friction and heat transfer for incompressible laminar flow over porous wedges with suction and variable wall temperature. Int J Heat Mass Transf. 1961;2:185–98.10.1016/0017-9310(61)90088-6Suche in Google Scholar

[26] Lin HT, Lin LK. Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any Prandtl number. Int J Heat Mass Transf. 1987;30:1111–8.10.1016/0017-9310(87)90041-XSuche in Google Scholar

[27] Khalid A, Khan I, Shafie S. Heat transfer in ferrofluid with cylindrical shape nanoparticles past a vertical plate with ramped wall temperature embedded in a porous medium. J Mol Liq. 2016;221:1175–83.10.1016/j.molliq.2016.06.105Suche in Google Scholar

[28] Ahmed N, Adnan, Khan U, Mohyud-Din ST. Modified heat transfer flow model for SWCNTs-H2O and MWCNTs-H2O over a curved stretchable semi infinite region with thermal jump and velocity slip: A numerical simulation. Phys A: Stat Mech Appl. 2020;545:123431.10.1016/j.physa.2019.123431Suche in Google Scholar

[29] Zin M, Athirah N, Khan I, Shafie S. The impact silver nanoparticles on MHD free convection flow of Jeffery fluid over an oscillating vertical plate embedded in a porous medium. J Mol Liq. 2016;222:138–50.10.1016/j.molliq.2016.06.098Suche in Google Scholar

[30] Ahmed N, Adnan, Khan U, Mohyud-Din ST. A theoretical investigation of unsteady thermally stratified flow of γ-Al2O3–H2O and γ-Al2O3–C2H6O2 nanofluids through a thin slit. J Phys Chem Solids. 2018;119:296–308.10.1016/j.jpcs.2018.01.046Suche in Google Scholar

[31] Ullah I, Shafie S, Khan I. Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium. J King Saud Univ. 2016;29(2). 10.1016/j.jksus.2016.05.003.Suche in Google Scholar

[32] Ahmed N, Adnan, Khan U, Mohyud-Din ST, Khan I, Murtaza R, et al. A novel investigation and hidden effects of MHD and thermal radiations in viscous dissipative nanofluid flow models. Front Phys. 2020. 10.3389/fphy.2020.00075.Suche in Google Scholar

[33] Ullah I, Khan I, Shafie S. MHD natural convection flow of Casson nanofluid over nonlinearly stretching sheet through porous medium with chemical reaction and thermal radiation. Nanoscale Res Lett. 2016;11(527).10.1186/s11671-016-1745-6Suche in Google Scholar PubMed PubMed Central

[34] Khan U, Adnan, Ahmed N, Mohyud-Din ST. Influence of thermal radiation and viscous dissipation on squeezed flow of water between Riga plates saturated with carbon nanotubes. Colloids Surf A: Physicochem Eng Asp. 2017;522:389–98.10.1016/j.colsurfa.2017.02.083Suche in Google Scholar

[35] Adnan, Khan U, Ahmed N, Mohyud-Din ST. Thermo-diffusion and Diffusion-thermo effects on flow of second grade fluid between two inclined plane walls. J Mol Liq. 2016;224:1074–82.10.1016/j.molliq.2016.10.068Suche in Google Scholar

[36] Ahmed N, Adnan, Khan U, Mohyud-Din ST. Influence of an effective Prandtl number model on squeezed flow of γAl2O3–H2O and γAl2O3–C2H6O2 nanofluids. J Mol Liq. 2017;238:447–54.10.1016/j.molliq.2017.05.049Suche in Google Scholar

[37] Adnan, Asadullah M, Khan U, Ahmed N, Mohyud-Din ST. Analytical and numerical investigation of thermal radiation effects on flow of viscous incompressible fluid with stretchable convergent/divergent channels. J Mol Liq. 2016;224:768–75.10.1016/j.molliq.2016.10.073Suche in Google Scholar

[38] Ahmed N, Adnan, Khan U, Mohyud-Din ST. A Bioconvection model for squeezing flow of nanofluid Between parallel plates in the presence gyrotactic microorganisms. Eur Phys J Plus. 2017;132. 10.1140/epjp/i2017-11454-4.Suche in Google Scholar

[39] Khan U, Adnan, Ahmed N, Mohyud-Din ST. Influence of viscous dissipation on copper oxide nanofluid in an oblique channel: implementation of KKL model. Eur Phys J Plus. 2017;132. 10.1140/epjp/i2017-11504-y.Suche in Google Scholar

[40] Sheikholeslami M, Hayat T, Alsaedi A. Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int J Heat Mass Transf. 2017;106:745–55.10.1016/j.ijheatmasstransfer.2016.09.077Suche in Google Scholar

[41] Khan U, Adnan, Ahmed N, Mohyud-Din ST. Soret and Dufour effects on Jeffery–Hamel flow of second-grade fluid between convergent/divergent channel with stretchable walls. Results Phys. 2017;7:361–72.10.1016/j.rinp.2016.12.020Suche in Google Scholar

[42] Sheikholeslami M, Shehzad SA. Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int J Heat Mass Transf. 2017;106:1261–9.10.1016/j.ijheatmasstransfer.2016.10.107Suche in Google Scholar

[43] Ahmed N, Adnan, Khan U, Mohyud-Din ST. Shape effects of nanoparticles on Squeezed flow between two Riga Plates in the presence of thermal radiation. Eur Phys J Plus. 2017;132. 10.1140/epjp/i2017-11576-7.Suche in Google Scholar

[44] Sheikholeslami M, Vajravelu K. Nanofluid flow and heat transfer in a cavity with variable magnetic field. Appl Math Comput. 2017;298:272–82.10.1016/j.amc.2016.11.025Suche in Google Scholar

[45] Adnan, Zaidi SZA, Khan U, Ahmed N, Mohyud-Din ST, Chu YM, et al. Impacts of freezing temperature based thermal conductivity on the heat transfer gradient in nanofluids: applications for a curved Riga surface. Molecules. 2020;25. 10.3390/molecules25092152.Suche in Google Scholar PubMed PubMed Central

[46] Riaz A, Gul A, Khan I, Ramesh K, Khan SU, Baleanu D, et al. Mathematical analysis of entropy generation in the flow of viscoelastic nanofluid through an annular region of two asymmetric annuli having flexible surfaces. Coatings. 2020. 10.3390/coatings10030213.Suche in Google Scholar

[47] Adnan, Khan U, Ahmed N, Mohyud-Din ST. Novel investigation of heat and mass transfer under the effects of thermal radiations. J Nanofluids. 2021;10(2):214–21.10.1166/jon.2021.1785Suche in Google Scholar

[48] Khan U, Zaib A, Khan I, Nisar KS, Baleanu D. Insights into the stability of mixed convective Darcy–forchheimer flows of cross liquids from a vertical plate with consideration of the significant impact of velocity and thermal slip conditions. Math. 2019. 10.3390/math8010031.Suche in Google Scholar

[49] Khan U, Adnan, Ahmed N, Mohyud-Din ST. 3D squeezed flow of γAl2O3–H2O and γAl2O3–C2H6O2 nanofluids: a numerical study. Int J Hydrog Energy. 2017;42(39):24620–33.10.1016/j.ijhydene.2017.07.090Suche in Google Scholar

[50] Ghaffar A, Nisar KS. Numerical analysis of fluid forces for flow past a square rod with detached dual control rods at various gap spacing. Symmetry. 2020. 10.3390/sym12010159.Suche in Google Scholar

[51] Ahmed N, Fatima M, Baleanu D, Nisar KS, Khan I, Rafiq M, et al. Numerical analysis of the susceptible exposed infected quarantined and vaccinated (SEIQV) reaction-diffusion epidemic model. Front Phys. 2020. 10.3389/fphy.2019.00220.Suche in Google Scholar

[52] Baleanu D, Jajarmi A, Mohammadi H, Rezapour S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons & Fractals. 2020;134:109705. 10.1016/j.chaos.2020.109705.Suche in Google Scholar

[53] Jajarmi A, Baleanu D, Sajjadi SS, Asad JH. A new feature of the fractional Euler–Lagrange equations for a coupled oscillator using a nonsingular operator approach. Frontiers in Physics. 2019;7:196. 10.3389/fphy.2019.00196.Suche in Google Scholar

[54] Baleanu D, Asad JH, Jajarmi A. New aspects of the motion of a particle in a circular cavity. Proc Romanian Acad, Ser A. 2018;19(2):361–7.Suche in Google Scholar

[55] Baleanu D, Asad JH, Jajarmi A. The fractional model of spring pendulum: New features within different kernels. Proc Romanian Acad, Ser A. 2018;19(3):447–54.Suche in Google Scholar

[56] Cobble MH. Magneto fluid dynamic flow with a pressure gradient and fluid injection. J Eng Math. 1977;11(2):249–56.10.1007/BF01535969Suche in Google Scholar

[57] Zhang Z, Wang J. Exact self-similar solutions of the magnetohydrodynamic boundary layer system for power-law fluids. Z für Angew Math und Phys. 2007;58:805–17.10.1007/s00033-006-5117-4Suche in Google Scholar

[58] Srinivasacharya D, Mendu U, Venumadhav K. MHD boundary layer flow of a nanofluid past a wedge. Proc Eng. 2015;127:1064–70.10.1016/j.proeng.2015.11.463Suche in Google Scholar

[59] Alqahtani AM, Adnan, Khan U, Ahmed N, Mohyud-Din ST, Khan I. Numerical investigation of heat and mass transport in the flow over a magnetized wedge by incorporating the effects of cross-diffusion gradients: applications in multiple engineering systems. Math Problems Eng. 2020;2020:247583110.1155/2020/2475831Suche in Google Scholar

[60] Mohyud-Din ST, Adnan, Khan U, Ahmed N, Khan I, Abdeljawad T, et al. Thermal transport investigation in magneto-radiative GO-MoS2/H2O-C2H6O2 hybrid nanofluid subject to Cattaneo–Christov model. Materials. 2020;25. 10.3390/molecules25112592.Suche in Google Scholar PubMed PubMed Central

Received: 2020-03-20

Revised: 2020-12-06

Accepted: 2021-02-02

Published Online: 2021-12-31

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2021-0007

Schlagwörter für diesen Artikel

Lorentz force; radiative heat flux; wedge flow; cross-diffusion; shear stresses

Creative Commons

BY 4.0