Abstract
A study on the large amplitude vibration of doubly curved graphene-reinforced composite (GRC) laminated panels is presented in this paper. A doubly curved panel is made of piece-wise GRC layers with functionally graded (FG) arrangement along the thickness direction of the panel. A GRC layer consists of polymer matrix reinforced by aligned graphene sheets. The material properties of the GRC layers are temperature dependent and can be estimated by the extended Halpin-Tsai micromechanical model. The modelling of the large amplitude vibration of the panels is based on the Reddy’s higher order shear deformation theory and the effects of the von Kármán geometric nonlinearity, the panel-foundation interaction and the temperature variation are included in the derivation of the motion equations of the panels. The solutions for the large amplitude vibration of the doubly curved FG-GRC laminated panels are obtained by applying a two-step perturbation approach. A parametric study is carried out to determine the influences of foundation stiffness, temperature variation, FG distribution pattern, in-plane boundary condition and panel curvature ratio on the natural frequencies and the nonlinear to linear frequency ratios of the doubly curved FG-GRC laminated panels.
1 Introduction
Doubly curved panels have many important engineering applications. During their service life, these panels may be subjected to different combinations of loading and environmental conditions which can cause the panels to experience large amplitude vibration with the panel deflection being in the order of the panel thickness. Therefore, it is necessary to fully understand the nonlinear vibration behaviors of doubly curved panels in thermal environments in engineering design and practice. Many studies have been carried out on the nonlinear vibration behavior of isotropic and composite laminated curved panels [1, 2, 3, 4, 5, 6, 7, 8]. It is observed that an acceptable agreement for flat plates can be achieved by different researchers. However, the results for a curved panel exist large discrepancies which may be due to the hardening behavior (i.e. increase in vibration amplitude leads to the increase of the nonlinear frequency) or the softening behavior of the panel (i.e. increase in vibration amplitude leads to the decrease of the nonlinear frequency) [1, 2, 3, 4, 5, 6, 7, 8].
Advanced composite materials possess unique features that many of the conventional materials do not have. We have witnessed the increased use of advanced composite materials, including the functionally graded material (FGM) [9], as key structural members in various engineering applications. Shen [10] first proposed to use FGM concept to nanocomposite structures in order to fully utilize the effect of nano filler reinforcement in composite structures. Shen and his co-authors and other research teams further studied the linear and nonlinear vibration characteristics of FGM curved panels [11, 12, 13, 14, 15, 16, 17] and FG carbon nanotube reinforced composite (CNTRC) curved panels [18, 19, 20, 21, 22] subject to temperature changes and/ or resting on elastic foundations. Since the discovery of graphene by Geim and Novoselov in 2004 [23], extensive studies on graphene have been conducted by many researchers and the extraordinary material properties of graphene have been widely reported [24, 25, 26, 27, 28]. Due to these remarkable properties, graphene has become one of the ideal reinforcement agents in creating advanced polymer composites [29]. For graphene-based nanocomposites, one kind
is graphene platelet reinforced composite (GPLRC) where both the polymer matrix and graphene platelets (GPLs) are assumed to be isotropic and independent of temperature. In essence, GPL reinforced composites belong to particle reinforced composites. The GPLRC model is relatively simple and was adopted by many researchers, for example, the vibration analysis for doubly-curved panels reinforced by GPLs was reported by Wang et al. [30, 31] and Fazelzadeh et al. [32]. It is noted that graphene sheets have anisotropic and temperature dependent material properties [24, 25, 26, 27, 28] and it is possible to align graphene sheets in polymer matrix that can result in better reinforcement effect for the graphene-based composites [33, 34, 35]. Shen et al. [36] first proposed a functionally graded graphene reinforced composite (GRC) model where aligned graphene reinforcements are anisotropic and the material properties of both the polymer matrix and graphene sheets are assumed to be temperature dependent. As reported by Lei et al. [37] the GRC model is more accurate than GPLRC model and was adopted by many researchers [38, 39, 40, 41, 42, 43].
This paper will investigate the nonlinear free vibration behavior of doubly curved GRC laminated panels resting on elastic foundations in thermal environments. The panels with the piece-wise functionally graded GRC laminar layer pattern are considered in the study. The novelty of this study lies in the account of both the functionally graded material configurations and the temperature dependent properties in the nonlinear vibration analyses of FG-GRC laminated doubly curved panels. The extended Halpin-Tsai micromechanical model is applied to estimate the material properties of the GRC layers. The Reddy’s third order shear deformation shell theory is employed to derive the motion equations for the GRC laminated panels. Note that the motion equations of the panels also include the effects of the von Kármán geometric nonlinearity, the foundation support and the temperature variation. The boundary conditions of the panels are assumed to be simply supported. A two-step perturbation approach is employed to determine the nonlinear frequencies of doubly curved GRC laminated panels. The large amplitude vibration behavior of doubly curved FG-GRC laminated panels subject to the influence of foundation support and temperature variation is discussed in detail.
2 Large amplitude vibration of doubly curved GRC laminated panels
A doubly curved GRC laminated panel with two radii of curvature R1 and R2, as shown in Figure 1, is considered in this study. The panel is made of N laminated GRC layers of different graphene volume fractions to form five different functionally graded (FG) patterns, i.e. UD, FG-Λ, FG-V, FG-X and FG-O. The panel with the UD pattern consists of GRC layers of the same graphene volume fraction. The panel with the FG-O pattern has the maximum graphene volume fraction in the GRC layers at the mid-plane and the minimumgraphene volume fraction at the top and bottom GRC layers with a step change of graphene volume fractions between the surface and the mid-plane GRC layers, while the panel with the FG-X pattern has an inverse graphene volume fraction arrangement as that of the FG-O pattern. The FG-V panel consists of graphene-rich top GRC layers and graphene-poor bottom GRC layer, while the FG-Δ panel has an inverse graphene volume fraction arrangement as that of the FG-V panel. The panel has length a, width b and thickness h and is located in a coordinate system (X, Y, Z) as shown in Figure 1. Note that X and Y are in the directions of the curvature lines on the middle surface of the panel and Z is in the direction of the inward normal to the middle surface of the panel. The panel is supported by a Pasternak-type foundation with the panel-foundation pressure being defined by p0 = K̄1W̄ − K̄2∇2W̄, where W̄ is the displacement of the panel in the Z direction, K̄1 is the transverse foundation stiffness (Winkler stiffness) and K̄2 is the shearing layer stiffness of the foundation, and ∇2 = ∂2/∂X2 + ∂2/∂Y2 is the Laplace operator.
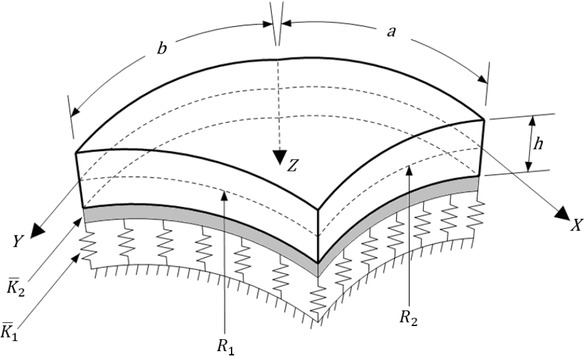
Coordinate system and geometry for a doubly curved panel supported by a Pasternak-type elastic foundation
One of the key issues in structural analysis of graphene reinforced composites is the thermomechanical property evaluation of the composite. The Halpin-Tsai micromechanical model [44] is employed to estimate the effective material properties of the GRC layers in this study as we assume that the graphene sheets are aligned in the polymer matrix to form aligned 2D reinforcement agents. Due to incomplete stress transfer between graphene sheets and polymer matrix resulting from surface effect, strain gradients effect and intermolecular effect, the Halpin-Tsai model needs to be modified to account for these effects [45]. In the present study, the graphene reinforcement is either zigzag (refer to as 0-ply) or armchair (refer to as 90-ply). Based on the extended Halpin-Tsai model, the effective Young’s moduli and the shear modulus of the GRC layer can be expressed as [36]
in which aG, bG and hG are the length, the width and the effective thickness of the graphene sheet, and
where Em and Gm are the elasticity modulus and shear modulus of the polymer matrix. Besides,
Poisson’s ratio v12 and the mass density ρ of the GRC layer may easily be expressed according to the conventional rule of mixtures
where
Note that the material properties of the GRC layers estimated in Eq. (1) are temperature dependent as the material properties of the graphene sheets and the polymer matrix are both temperature dependent. According to Schapery model [47], the thermal expansion coefficients of the GRC layers can be expressed by
in which α11 and α22 are the longitudinal and transverse thermal expansion coefficients of the GRC layers,
The doubly curved GRC laminated panel is subjected to a transverse dynamic load q(X, Y, t̄) in a thermal environment. Within the framework of the Reddy’s third order shear deformation shell theory [48] and considering the effects of the von Kármán geometric nonlinearity, the panel-foundation interaction and the temperature variation, we can derive the motion equations for the doubly curved panel as follows
in which
where a comma denotes partial differentiation with respect to the corresponding coordinates, and W̄ is the transverse displacement,
The panel is assumed to be in a constant temperature field at an isothermal state. The terms associated with the superscript T in Eqs. (5)-(8) contain the effect of temperature variation, N̄T are the thermal forces, M̄T are the thermal moments and P̄T are the higher order thermal moments. The effect of the panel-foundation interaction is included in the terms associated with K̄1 and K̄2 in Eq. (5). The terms Ij,Ȋj and Ĩj as well as N̄T, M̄T and P̄T are given in detail in Appendix A. We can use Eqs. (5)-(8) to analyse the case for GRC laminated cylindrical panels by setting R2 = R and R1 =∝ and for GRC laminated square spherical panels by setting R1 = R2 = R.
Besides the governing equations (5)-(8), it is necessary to deal with different boundary conditions to solve the boundary-value problem. In the current study, the four curved edges of the panel are assumed to be simply supported, and the associate boundary conditions are
where M̄x and M̄y are the bending moments and P̄x and P̄y are the higher order moments as defined in Reddy and Liu [48].
Two in-plane boundary conditions, i.e. movable and immovable, are considered. For movable in-plane boundary conditions, one has
and for immovable in-plane boundary conditions, one has
where Ū and V̄ are the plate displacements in the X and Y directions.
The movable conditions of Eqs. (11c) and (11d) can be imposed in the average sense as
Also, the immovable conditions of Eqs. (11e) and (11f) are fulfilled in the average sense as
or
In the above equations, the reduced stiffness matrices
It should be noticed that, in the current study, either governing equations (5)-(8) or boundary conditions (11a)-(11f) are different from that used in [50]. For nonlinear problems the superposition principle is no longer valid. Hence, each nonlinear boundary value problem with different governing equations or boundary conditions should be solved separately.
3 Solution procedure
The nonlinear vibrations of flat or cylindrical or doubly curved panels are different nonlinear problems. A two-step perturbation approach was developed by Shen [49] and was successfully to solve different kinds of nonlinear problems of beams, plates and shells by many research teams [51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61]. To use this two-step perturbation approach to solve the large amplitude vibration problem of doubly curved FG-GRC laminated panels, the motion equations (5) to (8) can be expressed in dimensionless forms as
with
and the other dimensionless linear operators Lij( ) are given in Shen [49]. In Eqs. (15)-(19), the non-dimensional parameters are defined by
in which E0 and 𝜌0 are the material properties of the polymer matrix Em and m at room temperature (T0=300 K), and the terms
Based on Eq. (20), the boundary conditions of Eqs. (11a) and (11b) can be written in non-dimensional forms as
and the movable in-plane boundary conditions of Eqs. (11c) and (11d) become
and the immovable in-plane boundary conditions of Eqs. (11e) and (11f) become
where ϒijk are defined in Shen [49].
Equations (15) to (18) can be separated into two sets of differential equations which are then solved in sequence. The first set of differential equations is for the nonlinear thermal bending problem and can be solved using the same method as reported in [62], and the second set of differential equations are used to obtain the homogeneous vibration solution on the initial deflected panel. A two-step perturbation technique is applied to determine this homogeneous solution. We assume that the perturbation equations for the displacements and the forces with a small perturbation parameter ε which has no physical meaning in the first step are given by
We introduce τ = ε t to improve the perturbation solution process for solving the large amplitude vibration problem. In order to satisfy the simply supported boundary conditions in the space domain, the first order solution of the panel is assumed to have the form
where (m, n) is the number of waves of vibration mode in the X and Y directions. The initial conditions are assumed to be
Taking into consideration of Eq. (23), a set of perturbation equations are obtained by collecting the terms of the same order of ε in Eqs. (15)-(18). Eq. (24) is then applied as the first step solution to the perturbation equations and following a step by step approach, we can obtain the 4th order asymptotic solutions as
It is worth noting that the perturbation series is a divergent series. Which order solution is closer to the real solution needs to be determined by experimental verification or by comparing with the theoretical exact solution. Contrary to Zhang’s conclusion [63], there is no such thing as a
higher order perturbation solution being more correct than a lower order solution.
In Eqs. (26)-(30), τ is replaced back by t. It is noted that the small perturbation parameter ε is replaced by
in which the terms gij are given in Appendix C. Eq. (31) can be solved to obtain the nonlinear frequency of the panel as follows
where ωL = [g31/g30]1/2 is the dimensionless linear frequency, and
4 Numerical results and discussion
In this section, numerical results for the nonlinear vibration of doubly curved GRC laminated panels resting on elastic foundations and under different thermal environmental conditions are obtained. It is noted that the material properties of graphene sheets are anisotropic [24, 25, 26] and temperature dependent [27]. We select zigzag (refer to as 0-ply) graphene sheets with effective thickness hG = 0.188 nm and ρG = 4118 kg/m3 as reinforcement agents. Lin et al. [46] performed a molecular dynamics simulation to evaluate the material properties of graphene sheets at different temperatures. These material properties at three different temperature levels are provided in Table 1. It must be pointed out that the Young’s modulus of single-layer graphene sheet is not a constant which depends on the value of its effective thickness [64]. For example, it has been reported that Young’s modulus of single-layer graphene sheet is estimated to be about 1 TPa. This is due to the fact that the effective thickness of graphene sheet is taken to be 0.34 nm [65, 66], otherwise the Young’s modulus may reach 2.47 TPa which is significantly larger than that reported in [65, 66], when the effective thickness of graphene sheet is only 0.129 nm [27]. In the MD work of Lin et al. [46], the calculated effective thickness of the graphene sheet is 0.188 nm according to the research findings of Shen et al. [27]. Therefore, the predicted Young’s moduli of the graphene sheet (see in Table 1) reach around 1.8 TPa. The graphene efficiency parameters η1, η2 and η3 used in the extended Halpin-Tsai micromechanical model are given in Table 2 which are obtained by comparing the GRC moduli from the MD simulations and from the Halpin– Tsai model, as previously reported in Shen et al. [36]. We assume that G13 = G23 = 0.5G12. We select Poly (methyl methacrylate), referred to as PMMA, for the matrix. The material properties of PMMA are assumed to be ρm = 1150 kg/m3, vm = 0.34, αm = 45(1+0.0005ΔT)×10−6/K and Em = (3.52-0.0034T) GPa, inwhich T = T0 + and T0 = 300 K (room temperature). Hence, we have αm = 45.0×10−6/K and E m = 2.5 GPa when T = 300 K.
Temperature-dependent material properties of monolayer graphene (aG = 14.76 nm, bG = 14.77 nm, thickness hG = 0.188 nm,
| Temperature (K) | |||||
|---|---|---|---|---|---|
| 300 | 1812 | 1807 | 683 | −0.90 | −0.95 |
| 400 | 1769 | 1763 | 691 | −0.35 | −0.40 |
| 500 | 1748 | 1735 | 700 | −0.08 | −0.08 |
Temperature dependent efficiency parameters of graphene/PMMA nanocomposites [36]
| T (K) | VG | η1 | η2 | η3 |
|---|---|---|---|---|
| 300 | 0.03 | 2.929 | 2.855 | 11.842 |
| 0.05 | 3.068 | 2.962 | 15.944 | |
| 0.07 | 3.013 | 2.966 | 23.575 | |
| 0.09 | 2.647 | 2.609 | 32.816 | |
| 0.11 | 2.311 | 2.260 | 33.125 | |
| 400 | 0.03 | 2.977 | 2.896 | 13.928 |
| 0.05 | 3.128 | 3.023 | 15.229 | |
| 0.07 | 3.060 | 3.027 | 22.588 | |
| 0.09 | 2.701 | 2.603 | 28.869 | |
| 0.11 | 2.405 | 2.337 | 29.527 | |
| 500 | 0.03 | 3.388 | 3.382 | 16.712 |
| 0.05 | 3.544 | 3.414 | 16.018 | |
| 0.07 | 3.462 | 3.339 | 23.428 | |
| 0.09 | 3.058 | 2.936 | 29.754 | |
| 0.11 | 2.736 | 2.665 | 30.773 |
Comparison studies are carried to verify the correctness of the present solution method. The fundamental frequencies from the present method and from Pouresmaeeli and Fazelzadeh [67] using the Galerkin method for CNTRC doubly curved panels with a/b = 1, a/h = 20 and a/R1 = b/R2 = 0.5 are presented in Table 3. Note that Pouresmaeeli and Fazelzadeh [67] employed the first order shear deformation theory with the shear correction factor of 5/6 in their analysis. The dimensionless frequency is defined by
Comparison of linear frequency
| Source | UD | FG-∧ | FG-V | FG-X | FG-O | ||
|---|---|---|---|---|---|---|---|
| 11 | Pouresmaeeli | & | 20.2381 | 18.2514 | 18.5425 | 22.4320 | 17.1397 |
| Fazelzadeh [67] | |||||||
| Present | 20.2587 | 18.8587 | 18.7062 | 24.0664 | 16.9807 | ||
| 14 | Pouresmaeeli | & | 21.6551 | 19.5458 | 19.7789 | 23.9965 | 18.2670 |
| Fazelzadeh [67] | |||||||
| Present | 21.7298 | 20.0403 | 19.9679 | 26.1019 | 18.1251 | ||
| 17 | Pouresmaeeli | & | 25.0512 | 22.6250 | 22.9514 | 27.8527 | 21.2115 |
| Fazelzadeh [67] | |||||||
| Present | 25.1226 | 22.9894 | 23.1790 | 29.8651 | 21.0842 |
Comparisons of fundamental frequencies
| R2/b | N | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1.0 | 2.0 | 5.0 | 10.0 | ||
| 3 | Kiani et al. [11] | 6.2330 | 5.6206 | 5.3523 | 5.1435 | 4.9642 | 4.8300 |
| Kar and Panda [13] | 6.2277 | 5.6191 | 5.3501 | 5.1377 | 4.9540 | 4.8214 | |
| Presenta | 6.2806 | 5.6761 | 5.4091 | 5.1976 | 5.0096 | 4.8711 | |
| Presentb | 6.2806 | 5.5405 | 5.2983 | 5.1156 | 4.9376 | 4.8078 | |
| 5 | Kiani et al. [11] | 5.9412 | 5.3492 | 5.0960 | 4.9077 | 4.7515 | 4.6244 |
| Kar and Panda [13] | 5.9394 | 5.3505 | 5.0963 | 4.9039 | 4.7428 | 4.6174 | |
| Presenta | 5.9585 | 5.3732 | 5.1211 | 4.9302 | 4.7668 | 4.6380 | |
| Presentb | 5.9585 | 5.2455 | 5.0205 | 4.8577 | 4.6999 | 4.5768 | |
| 10 | Kiani et al. [11] | 5.8128 | 5.2310 | 4.9851 | 4.8062 | 4.6599 | 4.5354 |
| Kar and Panda [13] | 5.8127 | 5.2333 | 4.986 | 4.8028 | 4.6515 | 4.5288 | |
| Presenta | 5.8173 | 5.2403 | 4.9946 | 4.8129 | 4.6607 | 4.5360 | |
| Presentb | 5.8173 | 5.1157 | 4.8985 | 4.7448 | 4.5961 | 4.4759 | |
| 20 | Kiani et al. [11] | 5.7802 | 5.2018 | 4.9580 | 4.7816 | 4.6376 | 4.5135 |
| Kar and Panda [13] | 5.7805 | 5.2041 | 4.9589 | 4.7782 | 4.6291 | 4.5068 | |
| Presenta | 5.7815 | 5.2065 | 4.9625 | 4.7831 | 4.6337 | 4.5102 | |
| Presentb | 5.7815 | 5.0826 | 4.8675 | 4.7163 | 4.5700 | 4.4505 | |
| 100 | Kiani et al. [11] | 5.7698 | 5.1932 | 4.9504 | 4.7749 | 4.6315 | 4.5071 |
| Kar and Panda [13] | 5.7701 | 5.1954 | 4.951 | 4.7712 | 4.6227 | 4.5003 | |
| Presenta | 5.7699 | 5.1956 | 4.9522 | 4.7736 | 4.6251 | 4.5019 | |
| Presentb | 5.7699 | 5.0718 | 4.8575 | 4.7073 | 4.5617 | 4.4424 | |
a Voigt model; b Mori-Tanaka model.

Comparisons of frequency-amplitude curves of a (0/90/0) laminated square spherical panel
Tables 5-7 and Figures 3-7 present the numerical results for the large amplitude vibration of doubly curved GRC laminated panels with h = 2 mm, a/b = 1.0, b/h = 10 and 20. Note that GRCs may contain the volume fraction of graphene reinforcement by up to 21%[68] and in this study the maximum graphene volume fraction is 11%. Four FG and one UD GRC laminated doubly curved panels are considered. The UD GRC panel consists of 10 GRC layers with the graphene volume fraction for each layer being identical, i.e.VG = 0.07. The four FG-GRC panels consist of 10 GRC layers with piece-wise graphene volume fractions, i.e. the FG-∧ type with [(0.03)2/(0.05)2/(0.07)2/(0.09)2/(0.11)2], the FG-V with [(0.11)2/(0.09)2/(0.07)2/(0.05)2/(0.03)2], the FG-O type with [0.03/0.05/0.07/0.09/0.11]S and the FG-X type with [0.11/0.09/0.07/0.05/0.03]S. Note that the total graphene volume fraction for all considered GRC laminated panels are the same. The non-dimensional frequency parameter
Natural frequency
| T (K) | Lay-up | (1,1)a | (1,2) | (2,1) | (2,2) | (1,3) | |
|---|---|---|---|---|---|---|---|
| 300 | (0)10 | UD | 48.3014 | 82.6496 | 82.8618 | 118.5889 | 146.2361 |
| FG-V | 45.0530 | 74.4394 | 74.7672 | 106.6529 | 131.3309 | ||
| FG-∧ | 47.0308 | 76.4596 | 76.7165 | 109.7334 | 132.7072 | ||
| FG-X | 49.2661 | 85.4987 | 85.7574 | 123.8480 | 149.7251 | ||
| FG-O | 44.8643 | 71.4763 | 71.7414 | 101.4378 | 124.5773 | ||
| (0/90/0/90/0)S | UD | 48.3017 | 82.7196 | 82.7923 | 118.5891 | 146.4664 | |
| FG-V | 45.0534 | 74.5451 | 74.6625 | 106.6531 | 131.6821 | ||
| FG- | 47.0316 | 76.5387 | 76.6388 | 109.7343 | 133.0248 | ||
| FG-X | 49.2667 | 85.5555 | 85.7016 | 123.8484 | 149.9319 | ||
| FG-O | 44.8650 | 71.6196 | 71.5993 | 101.4382 | 125.0769 | ||
| (0/90)5T | UD | 48.3017 | 82.7651 | 82.7467 | 118.5890 | 146.5894 | |
| FG-V | 45.0534 | 74.6258 | 74.5817 | 106.6530 | 131.8956 | ||
| FG-ρ | 47.0316 | 76.5930 | 76.5844 | 109.7342 | 133.1821 | ||
| FG-X | 49.2666 | 85.6444 | 85.6125 | 123.8482 | 150.1496 | ||
| FG-O | 44.8650 | 71.6066 | 71.6122 | 101.4382 | 125.0617 | ||
| 400 | (0)10 | UD | 34.2138 | 57.5011 | 67.5649 | 94.5042 | 114.5018 |
| FG-V | 36.1359 | 50.9012 | 61.1003 | 85.2160 | 101.3850 | ||
| FG-ρ | 30.5796 | 51.8494 | 62.2123 | 86.4531 | 102.7173 | ||
| FG-X | 36.2822 | 63.0136 | 71.6413 | 101.1963 | 120.8419 | ||
| FG-O | 31.2439 | 45.8868 | 56.8932 | 78.1132 | 92.6827 | ||
| (0/90/0/90/0)S | UD | 34.2140 | 61.7114 | 63.7426 | 94.5043 | 120.2617 | |
| FG-V | 36.1360 | 55.0395 | 57.4023 | 85.2169 | 107.2002 | ||
| FG-ρ | 30.5811 | 56.0494 | 58.4583 | 86.4537 | 108.6451 | ||
| FG-X | 36.2833 | 66.6612 | 68.2621 | 101.1972 | 126.1756 | ||
| FG-O | 31.2451 | 50.7250 | 52.6267 | 78.1138 | 99.4918 | ||
| (0/90)5T | UD | 34.2139 | 62.7425 | 62.7280 | 94.5043 | 121.7073 | |
| FG-V | 36.1360 | 56.2466 | 56.2198 | 85.2167 | 108.9418 | ||
| FG-ρ | 30.5810 | 57.2915 | 57.2412 | 86.4534 | 110.4587 | ||
| FG-X | 36.2833 | 67.4694 | 67.4635 | 101.1972 | 127.3658 | ||
| FG-O | 31.2450 | 51.668 | 51.7008 | 78.1137 | 100.7452 | ||
a vibration mode
Effects of foundation stiffness on the natural frequency
| (k1, k2) | a/R1 | (1,1)a | (1,2) | (2,1) | (2,2) | (1,3) | |
|---|---|---|---|---|---|---|---|
| (0, 0) | 0.2 | UD | 41.1721 | 76.5493 | 81.0143 | 115.8924 | 142.6105 |
| FG-V | 37.8351 | 68.4411 | 72.8904 | 104.1301 | 128.0025 | ||
| FG-ρ | 39.5992 | 69.7487 | 74.7134 | 106.5038 | 128.7642 | ||
| FG-X | 42.4981 | 79.9146 | 84.0718 | 121.3349 | 146.4308 | ||
| FG-O | 37.3048 | 64.7792 | 69.6411 | 98.3588 | 120.8690 | ||
| 0.8 | UD | 64.4642 | 101.4007 | 86.7702 | 125.9762 | 160.0728 | |
| FG-V | 61.3089 | 93.2844 | 78.6432 | 113.8672 | 145.1027 | ||
| FG-ρ | 63.4989 | 96.1479 | 80.8929 | 118.1785 | 147.4119 | ||
| FG-X | 64.8215 | 102.8914 | 89.3618 | 130.7637 | 162.3642 | ||
| FG-O | 61.5448 | 91.6238 | 75.9404 | 109.7616 | 139.7027 | ||
| (1000, 0) | 0.2 | UD | 50.3874 | 81.8504 | 86.0407 | 119.4462 | 145.5074 |
| FG-V | 47.6990 | 74.3210 | 78.4375 | 108.0687 | 131.2189 | ||
| FG-ρ | 49.1102 | 75.5272 | 80.1347 | 110.3581 | 131.9623 | ||
| FG-X | 51.4760 | 85.0073 | 88.9267 | 124.7367 | 149.2571 | ||
| FG-O | 47.2807 | 70.9640 | 75.4283 | 102.5191 | 124.2693 | ||
| 0.8 | UD | 70.7063 | 105.4599 | 91.4809 | 129.2531 | 162.6590 | |
| FG-V | 67.8414 | 97.6801 | 83.8104 | 117.4797 | 147.9477 | ||
| FG- | 69.8272 | 100.4187 | 85.9253 | 121.6637 | 150.2136 | ||
| FG-X | 71.0318 | 106.8950 | 93.9437 | 133.9262 | 164.9176 | ||
| FG-O | 68.0557 | 96.0961 | 81.2803 | 113.5048 | 142.6548 | ||
| (1000, 100) | 0.2 | UD | 64.8411 | 104.1308 | 107.4558 | 144.4679 | 171.4938 |
| FG-V | 62.7740 | 98.3161 | 101.4637 | 135.1959 | 159.5227 | ||
| FG-ρ | 63.8533 | 99.2318 | 102.7823 | 137.0349 | 160.1359 | ||
| FG-X | 65.6898 | 106.6346 | 109.7848 | 148.8911 | 174.7155 | ||
| FG-O | 62.4587 | 95.8065 | 99.1586 | 130.8007 | 153.8491 | ||
| 0.8 | UD | 81.6386 | 123.5538 | 111.8593 | 152.6759 | 186.2677 | |
| FG-V | 79.1696 | 116.9774 | 105.6720 | 142.8296 | 173.5434 | ||
| FG-ρ | 80.8782 | 119.2755 | 107.3585 | 146.2942 | 175.4819 | ||
| FG-X | 81.9200 | 124.7848 | 113.8866 | 156.6703 | 188.2702 | ||
| FG-O | 79.3549 | 115.6610 | 103.6798 | 139.5779 | 169.0476 |
a vibration mode
Effects of end condition on the nonlinear to linear frequency ratios ωNL /ωL for double curved (0/90/0/90/0)S GRC laminated panels in thermal environments (a/b = 1, b/h = 10, h = 2 mm, a/R1 = b/R2 = 0.02)
| T (K) | W̄max/h | ||||||
|---|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |||
| in-plane immovable boundary condition | |||||||
| 300 | UD | 28.0986 | 1.0232 | 1.0898 | 1.1926 | 1.3232 | 1.4742 |
| FG-V | 25.3511 | 1.0258 | 1.0997 | 1.2129 | 1.3556 | 1.5195 | |
| FG-ρ | 25.4331 | 1.0249 | 1.0963 | 1.2059 | 1.3444 | 1.5039 | |
| FG-X | 29.5211 | 1.0191 | 1.0744 | 1.1607 | 1.2717 | 1.4016 | |
| FG-O | 23.5816 | 1.0292 | 1.1122 | 1.2382 | 1.3957 | 1.5752 | |
| 400 | UD | 21.9646 | 1.0333 | 1.1274 | 1.2688 | 1.4437 | 1.6414 |
| FG-V | 19.6591 | 1.0364 | 1.1386 | 1.2910 | 1.4782 | 1.6887 | |
| FG- | 19.6816 | 1.0388 | 1.1475 | 1.3087 | 1.5056 | 1.7262 | |
| FG-X | 23.8171 | 1.0260 | 1.1003 | 1.2141 | 1.3575 | 1.5222 | |
| FG-O | 17.5688 | 1.0455 | 1.1714 | 1.3555 | 1.5775 | 1.8237 | |
| in-plane immovable boundary condition | |||||||
| 300 | UD | 28.0986 | 1.0061 | 1.0242 | 1.0537 | 1.0936 | 1.1429 |
| FG-V | 25.3511 | 1.0068 | 1.0269 | 1.0596 | 1.1037 | 1.1580 | |
| FG-ρ | 25.4331 | 1.0066 | 1.0262 | 1.0580 | 1.1011 | 1.1540 | |
| FG-X | 29.5211 | 1.0050 | 1.0199 | 1.0442 | 1.0773 | 1.1184 | |
| FG-O | 23.5816 | 1.0078 | 1.0308 | 1.0681 | 1.1183 | 1.1796 | |
| 400 | UD | 26.2383 | 1.0063 | 1.0249 | 1.0552 | 1.0963 | 1.1469 |
| FG-V | 23.8420 | 1.0068 | 1.0271 | 1.0600 | 1.1044 | 1.1590 | |
| FG-ρ | 24.0202 | 1.0070 | 1.0278 | 1.0616 | 1.1071 | 1.1631 | |
| FG-X | 27.3880 | 1.0052 | 1.0208 | 1.0462 | 1.0807 | 1.1235 | |
| FG-O | 22.1643 | 1.0080 | 1.0314 | 1.0695 | 1.1205 | 1.1829 | |
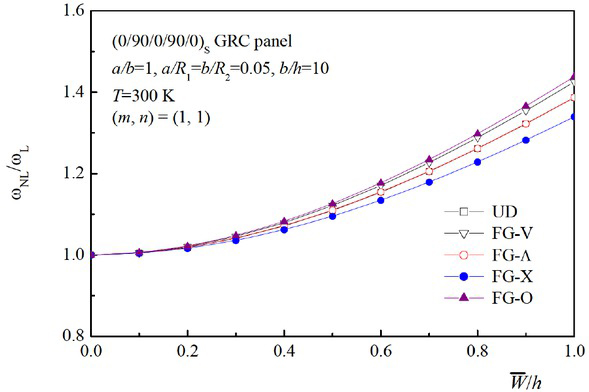
Frequency-amplitude curves for doubly curved (0/90/0/90/0)S GRC laminated panels with different graphene distribution patterns

Influence of temperature variation on the frequency-amplitude curves of doubly curved (0/90/0/90/0)S GRC laminated panels

Influence of panel curvature ratio a/R1 on the frequency-amplitude curves of doubly curved (0/90/0/90/0)S GRC laminated panels

Influence of foundation stiffness on the frequency-amplitude curves of doubly curved (0/90/0/90/0)S GRC laminated panels resting on elastic foundations

Influence of in-plane boundary conditions on the frequency-amplitude curves of doubly curved (0/90/0/90/0)S GRC laminated panels
Table 5 presents the natural frequencies of (0)10, (0/90/0/90/0)S and (0/90)5T doubly curved GRC laminated panels having b/h = 20 and a/R1 = b/R2 = 0.4 with environmental temperature T = 300 and 400 K. It is observed that increasing the environmental temperature will result in the decrease in the natural frequencies of the panels due to the stiffness of the panels being reduced at a higher temperature. Results in Table 5 also reveal that the panel with the FG-X reinforcement pattern has the largest, while the panel with the FG-O pattern has the smallest natural frequencies in the five considered cases. Like in the case of cylindrical panels [50], the doubly curved GRC panels with (0/90/0/90/0)S and (0/90)5T lamination arrangements have the same fundamental frequencies which are slight higher than the ones for the panels with (0)10 lamination arrangement at T = 300 K.
Table 6 presents the effect of foundation stiffness on the natural frequencies of (0/90/0/90/0)S doubly curved GRC laminated panels with b/h = 20, b/R2 = 0.4 and a/R1 = 0.2 and 0.8 under thermal environmental condition T = 300 K. We consider two foundation models which are the Pasternak elastic foundation with (k1, k2) = (1000, 100) and the Winkler elastic foundation with (k1, k2) = (1000, 0). The panel without elastic foundation, i.e. (k1, k2) = (0, 0), is also considered. Like in the case of cylindrical panels [50], the natural frequency is increased when the foundation stiffness is increased at room temperature.
The impact of the in-plane boundary conditions on the nonlinear vibration behavior of the (0/90/0/90/0)S doubly curved GRC laminated panels is investigated and the results are presented in Table 7. The panels have the geometric parameters of b/h = 10 and a/R1 = b/R2 = 0.02 and are subject to environmental temperature of T = 300 and 400 K. The results in Table 7 show that when the panels are subject to room temperature, the fundamental frequencies for the panels with either the movable or the immovable in-plane boundary conditions are the same which is due to the fact that no initial in-plane thermal stresses are present in the panels in this case. However, when the panels are subject to temperature of T = 400 K, in-plane compressive thermal stresses are introduced to the panels with immovable in-plane boundary condition. Like in the case of cylindrical panels [50], the nonlinear-to-linear frequency ratios for the panel with movable in-plane boundary condition are smaller than the one for the panel with immovable in-plane boundary condition.
Figure 3 depicts the frequency-amplitude curves for four FG and one UD doubly curved GRC laminated panels of b/h = 10 and a/R1 = b/R2 = 0.05 at room temperature of T = 300 K. The laminated arrangement of the panels is (0/90/0/90/0)S. It is observed that amongst the five GRC panels, the FG-X panel has the highest fundamental frequency as it has the largest panel stiffness, while the FG-O GRC panel has the lowest fundamental frequency as it has the smallest panel stiffness. It is also observed that the FG-X panel has the lowest and the FG-O has the highest nonlinear to linear frequency ratios in the considered cases. We will focus our analysis on the doubly curved UD and FG-X GRC (0/90/0/90/0)S panels for the subsequent cases.
Figure 4 shows the effect of temperature variation on the large amplitude vibration behavior of doubly curved UD and FG-X laminated panels with b/h = 10 and a/R1 = b/R2 = 0.05. Note that the glass transition temperature of PMMA can be substantially increased when graphene sheets are added in PMMA [69] and in the current study, we will consider the environmental temperature variation from T = 300 to 500K. It can be seen that for the cases of T = 300 and 400K, the frequency-amplitude curve increases with increase in temperature for both UD and FG-X GRC panels, whereas for the case of T = 500 K, the frequency-amplitude curve of the FG-X GRC panel becomes higher than that of the UD GRC panel.
The influence of the curvature ratio a/R1 on the frequency-amplitude curves of the doubly curved UD and FG-X panels of b/h = 10, b/R2 = 0.05 and a/R1 = 0.1, 0.15 and 0.2 at room temperature of T = 300 K is given in Figure 5. As previously reported in [1, 2, 3], the curves of nonlinear frequency as a function of amplitude of curved panels might be hardening or softening type. It is observed that the nonlinear frequency as a function of amplitude of the GRC laminated doubly curved panel is the softening type when a/R1 = 0.2. For other cases, the nonlinear frequency as a function of amplitude of the GRC laminated doubly curved panels is the hardening type.
The impact of foundation stiffness on the frequency-amplitude curves of UD and FG-X doubly curved panels resting on elastic foundations is illustrated in Figure 6. The panel has b/h = 10 and a/R1 = b/R2 = 0.05 at T = 300 K. Two foundation models are considered. The foundation stiffnesses are the same as used in Table 6, i.e., (k1, k2) = (1000, 100) is for the Pasternak elastic foundation, and (k1, k2) = (1000, 0) is for the Winkler elastic foundation. As expected, increasing the foundation stiffness will result in the reduction of the frequency-amplitude curves of the panels.
Figure 7 presents the relationship between the in-plane boundary conditions and the frequency-amplitude curves of the doubly curved UD and FG-X panels with b/h = 10 and a/R1 = b/R2 = 0.05 at T = 300 K. The ‘movable’ and ‘immovable’ in-plane boundary conditions are considered. It is observed that the nonlinear-to-linear frequency ratios for panels with immovable in-plane boundary conditions are larger than the ones for the panels with movable in-plane boundary conditions.
5 Concluding remarks
Applying a multi-scale approach, a large amplitude vibration analysis of doubly curved GRC laminated panels has been carried out. The panels are supported by an elastic foundation and in thermal environments. The piecewise functionally graded (FG) GRC layer arrangement is considered to achieve the UD, FG-X, FG-O, FG-V and FG-ρ laminated panels in this study. The extended Halpin-Tsai model is employed to evaluate the material properties of GRC layers which includes the thermal effect on both the graphene sheets and the polymer matrix. Results for large amplitude vibration of doubly curved UD and FG GRC laminated panels are obtained and discussed in detail. Like in the case of cylindrical panels, the rise of temperature will lead to the decrease of the natural frequencies and the increase of the nonlinear-to-linear frequency ratios for the doubly curved GRC laminated panels. On the other hand, the increase of foundation stiffness will result in the increase of the natural frequencies and the decrease of the nonlinear-to-linear frequency ratios of the panels. We observed that the FG-X panel has the highest fundamental frequency but the lowest nonlinear-to-linear frequency ratios and the FG-O panel has the lowest fundamental frequency but the highest nonlinear-to-linear frequency ratios in the considered cases. Unlike in the case of cylindrical panels where both UD and FG-GRC panels display a hardening nonlinearity, in some cases the frequency-amplitude curves of the doubly curved UD and FG-GRC laminated panels exhibit a softening nonlinear behavior at room temperature.
Acknowledgement
This study was supported by the National Natural Science Foundation of China under Grant 51779138 and the Australian Research Council under Grant DP140104156. The authors are very grateful for these financial supports.
Conflict of Interest
Conflict of Interests: The authors declare that there are no conflicts of interests with publication of this work.
References
[1] Cummings B.E., Large-amplitude vibration and response of curved panels, AIAA J., 1964, 2, 709-716.10.2514/3.2392Suche in Google Scholar
[2] Shin D.K., Large amplitude free vibration behavior of doubly curved shallow open shells with simply-supported edges, Comput. Struct., 1997, 62, 35-49.10.1016/S0045-7949(96)00215-5Suche in Google Scholar
[3] Panda S.K., Singh B.N., Nonlinear free vibration of spherical shell panel using higher order shear deformation theory - A finite element approach, Int. J. Pres. Vess. Pip., 2009, 86, 373-383.10.1016/j.ijpvp.2008.11.023Suche in Google Scholar
[4] Singh V.K., Panda S.K., Nonlinear free vibration analysis of single/doubly curved composite shallow shell panels, Thin-Walled Struct., 2014, 85, 341-349.10.1016/j.tws.2014.09.003Suche in Google Scholar
[5] Mahapatra T.R., Panda S.K., Thermoelastic vibration analysis of laminated doubly curved shallow panels using non-linear FEM, J. Thermal Stress., 2015, 38, 39-68.10.1080/01495739.2014.976125Suche in Google Scholar
[6] Karimiasl M., Ebrahimi F., Vinyas M., Nonlinear vibration analysis of multiscale doubly curved piezoelectric composite shell in hygrothermal environment, J. Intelligent Mater. Systems Struct., 2019, 30, 1594-1609.10.1177/1045389X19835956Suche in Google Scholar
[7] Karimiasl M., Ebrahimi F., Mahesh V., Nonlinear free and forced vibration analysis of multiscale composite doubly curved shell embedded in shape-memory alloy fiber under hygrothermal environment, J. Vib. Control, 2019, 25, 1945-1957.10.1177/1077546319842426Suche in Google Scholar
[8] Karimiasl M., Ebrahimi F., Mahesh V., Nonlinear forced vibration of smart multiscale sandwich composite doubly curved porous shell, Thin-Walled Struct., 2019, 143, 106152.10.1016/j.tws.2019.04.044Suche in Google Scholar
[9] Shen H.-S., Functionally Graded Materials Nonlinear Analysis of Plates and Shells, CRC Press, Boca Raton, 2009.Suche in Google Scholar
[10] Shen H.-S., Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments, Compos. Struct., 2009, 91, 9-19.10.1016/j.compstruct.2009.04.026Suche in Google Scholar
[11] Kiani Y., Shakeri M., Eslami M.R., Thermoelastic free vibration and dynamic behaviour of an FGM doubly curved panel via the analytical hybrid Laplace-Fourier transformation, Acta Mech., 2012, 223, 1199-1218.10.1007/s00707-012-0629-9Suche in Google Scholar
[12] Shen H.-S., Chen X., Guo L., Wu L., Huang X.-L., Nonlinear vibration of FGM doubly curved panels resting on elastic foundations in thermal environments, Aerospace Sci. Technol., 2015, 47, 434-446.10.1016/j.ast.2015.10.011Suche in Google Scholar
[13] Kar V.R., Panda S.K., Large-amplitude vibration of functionally graded doubly-curved panels under heat conduction, AIAA J., 2017, 55, 4376-4386.10.2514/1.J055878Suche in Google Scholar
[14] Fares M.E., Elmarghany M.K., Atta D., Salem M.G., Bending and free vibration of multilayered functionally graded doubly curved shells by an improved layerwise theory, Compos. Part B-Eng., 2018, 154, 272-284.10.1016/j.compositesb.2018.07.038Suche in Google Scholar
[15] Dong D.T., Dung D.V., A third-order shear deformation theory for nonlinear vibration analysis of stiffened functionally graded material sandwich doubly curved shallow shells with four material models, J. Sand. Struct. Mater., 2019, 21, 1316-1356.10.1177/1099636217715609Suche in Google Scholar
[16] Talebitooti R., Anbardan V.S., Haar wavelet discretization approach for frequency analysis of the functionally graded generally doubly-curved shells of revolution, Appl. Math. Modell., 2019, 67, 645-675.10.1016/j.apm.2018.11.044Suche in Google Scholar
[17] Amir M., Talha M., Nonlinear vibration characteristics of shear deformable functionally graded curved panels with porosity including temperature effects, Int. J. Pres. Vess. Pip., 2019, 172, 28-41.10.1016/j.ijpvp.2019.03.008Suche in Google Scholar
[18] Shen, H.-S., He, X.-Q.: Large amplitude free vibration of nanotubereinforced composite doubly curved panels resting on elastic foundations in thermal environments. J. Vib. Control, 2017, 23, 2672-268910.1177/1077546315619280Suche in Google Scholar
[19] Duc N.D., Quan T.Q., Khoa N.D., New approach to investigate nonlinear dynamic response and vibration of imperfect functionally graded carbon nanotube reinforced composite double curved shallow shells subjected to blast load and temperature, Aerospace Sci. Technol., 2017, 71, 360-372.10.1016/j.ast.2017.09.031Suche in Google Scholar
[20] Mehar K., Panda S.K., Thermal free vibration behavior of FG-CNT reinforced sandwich curved panel using finite element method, Poly. Compos., 2018, 39, 2751-2764.10.1002/pc.24266Suche in Google Scholar
[21] Mehar K., Panda S.K., Mahapatra T.R., Nonlinear frequency responses of functionally graded carbon nanotube-reinforced sandwich curved panel under uniform temperature field, Int. J. Appl. Mech., 2018, 10, 1850028.10.1142/S175882511850028XSuche in Google Scholar
[22] Setoodeh A.R., Shojaee M., Malekzadeh P., Vibrational behavior of doubly curved smart sandwich shells with FG-CNTRC face sheets and FG porous core, Compos. Part B-Eng., 2019, 165, 798-822.10.1016/j.compositesb.2019.01.022Suche in Google Scholar
[23] Novoselov K.S., Geim A.K., Morozov S.V., Jiang D., Zhang Y., Dubonos S.V., Grigorieva I.V., Firsov A., Electric filed effect in atomically thin carbon films, Science, 2004, 306, 666-669.10.1126/science.1102896Suche in Google Scholar PubMed
[24] Liu F., Ming P.M., Li J., Ab initio calculation of ideal strength and phonon instability of graphene under tension, Phys. Rev. B, 2007, 76, 064120.10.1103/PhysRevB.76.064120Suche in Google Scholar
[25] Ni Z., Bu H., Zou M., Yi H., Bi K., Chen Y., Anisotropic mechanical properties of graphene sheets from molecular dynamics, Physica B, 2010, 405, 1301-1306.10.1016/j.physb.2009.11.071Suche in Google Scholar
[26] Reddy C.D., Rajendran S., Liew K.M., Equilibrium configuration and elastic properties of finite graphene, Nanotechnol., 2006, 17, 864-870.10.1088/0957-4484/17/3/042Suche in Google Scholar
[27] Shen L., Shen H.-S., Zhang C.-L., Temperature-dependent elastic properties of single layer graphene sheets, Mater. Des., 2010, 31, 4445-4449.10.1016/j.matdes.2010.04.016Suche in Google Scholar
[28] Xu Z., Graphene nano-ribbons under tension, J. Comput. Theor. Nanosci., 2009, 6, 625-628.10.1166/jctn.2009.1082Suche in Google Scholar
[29] Potts J.R., Dreyer D.R., Bielawski C.W., Ruoff R.S., Graphene-based polymer nanocomposites, Polymer, 2011, 52, 5-25.10.1016/j.polymer.2010.11.042Suche in Google Scholar
[30] Wang A., Chen H., Hao Y., Zhang W., Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets, Results Phys., 2018, 9, 550-559.10.1016/j.rinp.2018.02.062Suche in Google Scholar
[31] Wang A., Chen H., ZhangW., Nonlinear transient response of doubly curved shallow shells reinforced with graphene nanoplatelets subjected to blast loads considering thermal effects, Compos. Struct., 2019, 225, 111063.10.1016/j.compstruct.2019.111063Suche in Google Scholar
[32] Fazelzadeh S.A., Rahmani S., Ghavanloo E., Marzocca P., Thermoelastic vibration of doubly-curved nano-composite shells reinforced by graphene nanoplatelets, J. Thermal Stress., 2019, 42, 1-17.10.1080/01495739.2018.1524733Suche in Google Scholar
[33] Zhao X., Zhang Q., Hao Y., Li Y., Fang Y., Chen D., Alternate multilayer films of poly(vinyl alcohol) and exfoliated graphene oxide fabricated via a facial Layer-by-Layer assembly, Macromolecules, 2010, 43, 9411-9416.10.1021/ma101456ySuche in Google Scholar
[34] Liang Q., Yao X., Wang W., Liu Y., Wong C.P., A three-dimensional vertically aligned functionalized multilayer graphene architecture: an approach for graphene-based thermal interfacial materials, ACS Nano, 2011, 5, 2392-2401.10.1021/nn200181eSuche in Google Scholar PubMed
[35] Yousefi N., Sun X., Lin X., Shen X., Jia J., Zhang B., Tang B., Chan M., Kim J.-K., Highly aligned graphene/polymer nanocomposites with excellent dielectric properties for high-performance electromagnetic interference shielding, Adv. Mater., 2014, 26, 5480-5487.10.1002/adma.201305293Suche in Google Scholar PubMed
[36] Shen H.-S., Xiang Y., Lin F., Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments, Comput. Methods Appl. Mech. Eng., 2017, 319, 175-193.10.1016/j.cma.2017.02.029Suche in Google Scholar
[37] Lei Z., Su Q., Zeng H., Zhang Y., Yu C., Parametric studies on buckling behavior of functionally graded graphene-reinforced composites laminated plates in thermal environment, Compos. Struct. 2018, 202, 695-709.10.1016/j.compstruct.2018.03.079Suche in Google Scholar
[38] Kiani Y., Isogeometric large amplitude free vibration of graphene reinforced laminated plates in thermal environment using NURBS formulation, Comput. Methods Appl. Mech. Eng., 2018, 332, 86-101.10.1016/j.cma.2017.12.015Suche in Google Scholar
[39] Kiani Y., NURBS-based isogeometric thermal postbuckling analysis of temperature dependent graphene reinforced composite laminated plates, Thin-Walled Struct., 2018, 125, 211-219.10.1016/j.tws.2018.01.024Suche in Google Scholar
[40] Rout M., Hota S.S., Karrnakar A., Thermoelastic free vibration response of graphene reinforced laminated composite shells, Eng. Struct., 2019, 178, 179-190.10.1016/j.engstruct.2018.10.029Suche in Google Scholar
[41] Wang M., Xu Y.-G., Qiao P., Li Z.M., A two-dimensional elasticity model for bending and free vibration analysis of laminated graphene-reinforced composite beams, Compos. Struct., 2019, 211, 364-375.10.1016/j.compstruct.2018.12.033Suche in Google Scholar
[42] Lei Z.X., Tong L.H., Analytical solution of low-velocity impact of graphene-reinforced composite functionally graded cylindrical shells, J. Brazilian Society Mech. Sci. Eng., 2019, 41, 486.10.1007/s40430-019-1983-5Suche in Google Scholar
[43] Ly L.N., Phuong N.T., Nam V.H., Trung N.T., Duc V.M., An analytical approach of nonlinear thermo-mechanical buckling of functionally graded graphene-reinforced composite laminated cylindrical shells under compressive axial load surrounded by elastic foundation, J. Appl. Comput. Mech., 2020, 6, 357-372.Suche in Google Scholar
[44] Halpin J.C., Kardos J.L., The Halpin-Tsai equations: A review, Polym. Eng. Sci., 1976, 16, 344-352.10.1002/pen.760160512Suche in Google Scholar
[45] Hu K., Kulkarni D.D., Choi I., Tsukruk V.V., Graphene-polymer nanocomposites for structural and functional applications, Progress Polym. Sci., 2014, 39, 1934-1972.10.1016/j.progpolymsci.2014.03.001Suche in Google Scholar
[46] Lin F., Xiang Y., Shen H.-S., Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites - a molecular dynamics simulation, Compos. Part B-Eng., 2017, 111, 261-269.10.1016/j.compositesb.2016.12.004Suche in Google Scholar
[47] Schapery R.A., Thermal expansion coefficients of composite materials based on energy principles, J. Compos. Mater., 1968, 2, 380-404.10.1177/002199836800200308Suche in Google Scholar
[48] Reddy J.N., Liu C.F., A higher-order shear deformation theory of laminated elastic shells, Int. J. Eng. Sci., 1985, 23, 319-330.10.1016/0020-7225(85)90051-5Suche in Google Scholar
[49] Shen H.-S., A Two-Step Perturbation Method in Nonlinear Analysis of Beams, Plates and Shells, John Wiley & Sons Inc., 2013.10.1002/9781118649893Suche in Google Scholar
[50] Shen H.-S., Xiang Y., Fan Y., Hui D., Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical panels resting on elastic foundations in thermal environments, Compos. Part B-Eng., 2018, 136, 177-186.10.1016/j.compositesb.2017.10.032Suche in Google Scholar
[51] Fu Y., Zhong J., Shao X., Chen Y., Thermal postbuckling analysis of functionally graded tubes based on a refined beam model, Int. J. Mech. Sci., 2015, 96-97, 58-64.10.1016/j.ijmecsci.2015.03.019Suche in Google Scholar
[52] Fu Y., Zhong J., Shao X., Tao C., Analysis of nonlinear dynamic stability for carbon nanotube-reinforced composite plates resting on elastic foundations, Mech. Adv. Mater. Struct., 2016, 23, 1284-1289.10.1080/15376494.2015.1068404Suche in Google Scholar
[53] Zhong J., Fu Y., Wan D., Li Y., Nonlinear bending and vibration of functionally graded tubes resting on elastic foundations in thermal environment based on a refined beam model, Appl. Math. Modell., 2016, 40, 7601-7614.10.1016/j.apm.2016.03.031Suche in Google Scholar
[54] Fallah F., Nosier A., Sharifi M., Ghezelbash F., On perturbation method in mechanical, thermal and thermo-mechanical loadings of plates: cylindrical bending of FG plates, ZAMM, 2016, 96, 217-232.10.1002/zamm.201400136Suche in Google Scholar
[55] Najafi F., Shojaeefard M.H., Googarchin H.S., Nonlinear low-velocity impact response of functionally graded plate with nonlinear three-parameter elastic foundation in thermal field, Compos. Part B-Eng., 2016, 107, 123-140.10.1016/j.compositesb.2016.09.070Suche in Google Scholar
[56] Sahmani S., Aghdam M.M., Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams, Compos. Struct., 2017, 179, 77-88.10.1016/j.compstruct.2017.07.064Suche in Google Scholar
[57] Babaei H., Kiani Y., Eslami M.R., Application of two-steps perturbation technique to geometrically nonlinear analysis of long FGM cylindrical panels on elastic foundation under thermal load, J. Thermal Stress., 2018, 41, 847-865.10.1080/01495739.2017.1421054Suche in Google Scholar
[58] Babaei H., Kiani Y., Eslami M.R., Thermally induced large deflection analysis of shear deformable FGM shallow curved tubes using perturbation method, ZAMM, 2019, 99, 201800148.10.1002/zamm.201800148Suche in Google Scholar
[59] Babaei H., Kiani Y., Eslami M.R., Thermomechanical nonlinear in-plane analysis of fix-ended FGM shallow arches on nonlinear elastic foundation using two-step perturbation technique, Int. J. Mech. Mater. Des., 2019, 15, 225-244.10.1007/s10999-018-9420-ySuche in Google Scholar
[60] Gao Y., Xiao W.-S., Zhu H., Free vibration analysis of nano-tubes consisted of functionally graded bi-semi-tubes by a two-steps perturbation method, Latin American J. Solids Struct., 2019, 16, 146.10.1590/1679-78255156Suche in Google Scholar
[61] Gao Y., Xiao W.-S., Zhu H., Nonlinear vibration analysis of different types of functionally graded beams using nonlocal strain gradient theory and a two-step perturbation method, Euro. Phys. J. Plus, 2019, 134, 23.10.1140/epjp/i2019-12446-0Suche in Google Scholar
[62] Shen H.-S., Nonlinear thermal bending of FGM cylindrical panels resting on elastic foundations under heat conduction, Compos. Struct., 2014, 113, 216-224.10.1016/j.compstruct.2014.03.034Suche in Google Scholar
[63] Zhang D., High-order analytical solutions and convergence discussions of the 2-step perturbation method for Euler-Bernoulli beams (in Chinese), Appl. Math. Mech., 2019, 40, 620-629.Suche in Google Scholar
[64] Shi J.-X., Natsuki T., Lei X.-W., Ni Q.-Q., Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models, Appl. Phys. Lett., 2014, 104, 223101.10.1063/1.4880729Suche in Google Scholar
[65] Lee C., Wei X., Kysar J.W., Hone J., Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385-388.10.1126/science.1157996Suche in Google Scholar PubMed
[66] Koenig S.P., Boddeti N.G., Dunn M.L., Bunch J.S., Ultrastrong adhesion of graphene membranes, Nat. Nanotechnol., 2010, 6, 543-546.10.1038/nnano.2011.123Suche in Google Scholar PubMed
[67] Pouresmaeeli S., Fazelzadeh S.A., Frequency analysis of doubly curved functionally graded carbon nanotube-reinforced composite panels, Acta Mech., 2016, 227, 2765-2794.10.1007/s00707-016-1647-9Suche in Google Scholar
[68] Putz K.W., Compton O.C., Palmeri M.J., Nguyen S.T., Brinson L.C., High-nanofiller-content graphene oxide-polymer nanocomposites via vacuum-assisted self-assembly, Adv. Funct. Mater., 2010, 20, 3322-3329.10.1002/adfm.201000723Suche in Google Scholar
[69] Ramanathan T., Abdala A.A., Stankovich S., Dikin D.A., Herrera-Alonso M., Piner R.D., Adamson D.H., Schniepp H.C., Chen X., Ruoff R.S., Nguyen S.T., Aksay I.A., Prud’Homme R.K., Brinson L.C., Functionalized graphene sheets for polymer nanocomposites, Nature Nanotechnol., 2008, 3, 327-331.10.1038/nnano.2008.96Suche in Google Scholar PubMed
[70] Shen H.-S., Kármán-type equations for a higher-order shear deformation plate theory and its use in the thermal postbuckling analysis, Appl. Math. Mech., 1997, 18, 1137-1152.10.1007/BF00713716Suche in Google Scholar
Appendix A
In Eqs. (5)-(8), the thermal forces, moments and higher order moments N̄T, M̄T and P̄T of the shell are evaluated by
and S̄T are defined by
in which T = T − T0 is the change of temperature with respect to a predefined reference temperature T0 at which the panel does no subject to any thermal strains, and
in which α11 and are the thermal expansion coefficients for the kth ply, Q̄ij are the transformed elastic constants for a GRC layer. Note that Q̄ij = Qij as zigzag or armchair graphene sheet is used in the GRC layer and
where E11, E22, G12, are the effective Young’s and shear moduli and ν12 and ν21 are the Poisson’s ratios of the GRC layer, respectively.
The inertias Ii(i = 1, 2, 3, 4, 5, 7) are defined by
in which k is the mass density of the kth ply, and
in which c1 = 4/(3h2).
Appendix B
In Eqs. (14a) and (14
where Aij , Bij, Dij, etc., are the panel stiffnesses defined by
Appendix C
In Eq. (31)
in which
and other symbols are defined as in Shen [49]. Also
where (with m=n=1)
and for the case of in-plane ‘movable’ condition
and for the case of in-plane ‘immovable’ condition
© 2019 H.-S. Shen et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Artikel in diesem Heft
- Research Articles
- Investigation of rare earth upconversion fluorescent nanoparticles in biomedical field
- Carbon Nanotubes Coated Paper as Current Collectors for Secondary Li-ion Batteries
- Insight into the working wavelength of hotspot effects generated by popular nanostructures
- Novel Lead-free biocompatible piezoelectric Hydroxyapatite (HA) – BCZT (Ba0.85Ca0.15Zr0.1Ti0.9O3) nanocrystal composites for bone regeneration
- Effect of defects on the motion of carbon nanotube thermal actuator
- Dynamic mechanical behavior of nano-ZnO reinforced dental composite
- Fabrication of Ag Np-coated wetlace nonwoven fabric based on amino-terminated hyperbranched polymer
- Fractal analysis of pore structures in graphene oxide-carbon nanotube based cementitious pastes under different ultrasonication
- Effect of PVA fiber on durability of cementitious composite containing nano-SiO2
- Cr effects on the electrical contact properties of the Al2O3-Cu/15W composites
- Experimental evaluation of self-expandable metallic tracheobronchial stents
- Experimental study on the existence of nano-scale pores and the evolution of organic matter in organic-rich shale
- Mechanical characterizations of braided composite stents made of helical polyethylene terephthalate strips and NiTi wires
- Mechanical properties of boron nitride sheet with randomly distributed vacancy defects
- Fabrication, mechanical properties and failure mechanism of random and aligned nanofiber membrane with different parameters
- Micro- structure and rheological properties of graphene oxide rubber asphalt
- First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy
- Adsorption performance of hydrophobic/hydrophilic silica aerogel for low concentration organic pollutant in aqueous solution
- Preparation of spherical aminopropyl-functionalized MCM-41 and its application in removal of Pb(II) ion from aqueous solution
- Electrical conductivity anisotropy of copper matrix composites reinforced with SiC whiskers
- Miniature on-fiber extrinsic Fabry-Perot interferometric vibration sensors based on micro-cantilever beam
- Electric-field assisted growth and mechanical bactericidal performance of ZnO nanoarrays with gradient morphologies
- Flexural behavior and mechanical model of aluminum alloy mortise-and-tenon T-joints for electric vehicle
- Synthesis of nano zirconium oxide and its application in dentistry
- Surface modification of nano-sized carbon black for reinforcement of rubber
- Temperature-dependent negative Poisson’s ratio of monolayer graphene: Prediction from molecular dynamics simulations
- Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout
- Preparation of low-permittivity K2O–B2O3–SiO2–Al2O3 composites without the addition of glass
- Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments
- Enhanced flexural properties of aramid fiber/epoxy composites by graphene oxide
- Correlation between electrochemical performance degradation and catalyst structural parameters on polymer electrolyte membrane fuel cell
- Materials characterization of advanced fillers for composites engineering applications
- Humic acid assisted stabilization of dispersed single-walled carbon nanotubes in cementitious composites
- Test on axial compression performance of nano-silica concrete-filled angle steel reinforced GFRP tubular column
- Multi-scale modeling of the lamellar unit of arterial media
- The multiscale enhancement of mechanical properties of 3D MWK composites via poly(oxypropylene) diamines and GO nanoparticles
- Mechanical properties of circular nano-silica concrete filled stainless steel tube stub columns after being exposed to freezing and thawing
- Arc erosion behavior of TiB2/Cu composites with single-scale and dual-scale TiB2 particles
- Yb3+-containing chitosan hydrogels induce B-16 melanoma cell anoikis via a Fak-dependent pathway
- Template-free synthesis of Se-nanorods-rGO nanocomposite for application in supercapacitors
- Effect of graphene oxide on chloride penetration resistance of recycled concrete
- Bending resistance of PVA fiber reinforced cementitious composites containing nano-SiO2
- Review Articles
- Recent development of Supercapacitor Electrode Based on Carbon Materials
- Mechanical contribution of vascular smooth muscle cells in the tunica media of artery
- Applications of polymer-based nanoparticles in vaccine field
- Toxicity of metallic nanoparticles in the central nervous system
- Parameter control and concentration analysis of graphene colloids prepared by electric spark discharge method
- A critique on multi-jet electrospinning: State of the art and future outlook
- Electrospun cellulose acetate nanofibers and Au@AgNPs for antimicrobial activity - A mini review
- Recent progress in supercapacitors based on the advanced carbon electrodes
- Recent progress in shape memory polymer composites: methods, properties, applications and prospects
- In situ capabilities of Small Angle X-ray Scattering
- Review of nano-phase effects in high strength and conductivity copper alloys
- Progress and challenges in p-type oxide-based thin film transistors
- Advanced materials for flexible solar cell applications
- Phenylboronic acid-decorated polymeric nanomaterials for advanced bio-application
- The effect of nano-SiO2 on concrete properties: a review
- A brief review for fluorinated carbon: synthesis, properties and applications
- A review on the mechanical properties for thin film and block structure characterised by using nanoscratch test
- Cotton fibres functionalized with plasmonic nanoparticles to promote the destruction of harmful molecules: an overview
Artikel in diesem Heft
- Research Articles
- Investigation of rare earth upconversion fluorescent nanoparticles in biomedical field
- Carbon Nanotubes Coated Paper as Current Collectors for Secondary Li-ion Batteries
- Insight into the working wavelength of hotspot effects generated by popular nanostructures
- Novel Lead-free biocompatible piezoelectric Hydroxyapatite (HA) – BCZT (Ba0.85Ca0.15Zr0.1Ti0.9O3) nanocrystal composites for bone regeneration
- Effect of defects on the motion of carbon nanotube thermal actuator
- Dynamic mechanical behavior of nano-ZnO reinforced dental composite
- Fabrication of Ag Np-coated wetlace nonwoven fabric based on amino-terminated hyperbranched polymer
- Fractal analysis of pore structures in graphene oxide-carbon nanotube based cementitious pastes under different ultrasonication
- Effect of PVA fiber on durability of cementitious composite containing nano-SiO2
- Cr effects on the electrical contact properties of the Al2O3-Cu/15W composites
- Experimental evaluation of self-expandable metallic tracheobronchial stents
- Experimental study on the existence of nano-scale pores and the evolution of organic matter in organic-rich shale
- Mechanical characterizations of braided composite stents made of helical polyethylene terephthalate strips and NiTi wires
- Mechanical properties of boron nitride sheet with randomly distributed vacancy defects
- Fabrication, mechanical properties and failure mechanism of random and aligned nanofiber membrane with different parameters
- Micro- structure and rheological properties of graphene oxide rubber asphalt
- First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy
- Adsorption performance of hydrophobic/hydrophilic silica aerogel for low concentration organic pollutant in aqueous solution
- Preparation of spherical aminopropyl-functionalized MCM-41 and its application in removal of Pb(II) ion from aqueous solution
- Electrical conductivity anisotropy of copper matrix composites reinforced with SiC whiskers
- Miniature on-fiber extrinsic Fabry-Perot interferometric vibration sensors based on micro-cantilever beam
- Electric-field assisted growth and mechanical bactericidal performance of ZnO nanoarrays with gradient morphologies
- Flexural behavior and mechanical model of aluminum alloy mortise-and-tenon T-joints for electric vehicle
- Synthesis of nano zirconium oxide and its application in dentistry
- Surface modification of nano-sized carbon black for reinforcement of rubber
- Temperature-dependent negative Poisson’s ratio of monolayer graphene: Prediction from molecular dynamics simulations
- Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout
- Preparation of low-permittivity K2O–B2O3–SiO2–Al2O3 composites without the addition of glass
- Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments
- Enhanced flexural properties of aramid fiber/epoxy composites by graphene oxide
- Correlation between electrochemical performance degradation and catalyst structural parameters on polymer electrolyte membrane fuel cell
- Materials characterization of advanced fillers for composites engineering applications
- Humic acid assisted stabilization of dispersed single-walled carbon nanotubes in cementitious composites
- Test on axial compression performance of nano-silica concrete-filled angle steel reinforced GFRP tubular column
- Multi-scale modeling of the lamellar unit of arterial media
- The multiscale enhancement of mechanical properties of 3D MWK composites via poly(oxypropylene) diamines and GO nanoparticles
- Mechanical properties of circular nano-silica concrete filled stainless steel tube stub columns after being exposed to freezing and thawing
- Arc erosion behavior of TiB2/Cu composites with single-scale and dual-scale TiB2 particles
- Yb3+-containing chitosan hydrogels induce B-16 melanoma cell anoikis via a Fak-dependent pathway
- Template-free synthesis of Se-nanorods-rGO nanocomposite for application in supercapacitors
- Effect of graphene oxide on chloride penetration resistance of recycled concrete
- Bending resistance of PVA fiber reinforced cementitious composites containing nano-SiO2
- Review Articles
- Recent development of Supercapacitor Electrode Based on Carbon Materials
- Mechanical contribution of vascular smooth muscle cells in the tunica media of artery
- Applications of polymer-based nanoparticles in vaccine field
- Toxicity of metallic nanoparticles in the central nervous system
- Parameter control and concentration analysis of graphene colloids prepared by electric spark discharge method
- A critique on multi-jet electrospinning: State of the art and future outlook
- Electrospun cellulose acetate nanofibers and Au@AgNPs for antimicrobial activity - A mini review
- Recent progress in supercapacitors based on the advanced carbon electrodes
- Recent progress in shape memory polymer composites: methods, properties, applications and prospects
- In situ capabilities of Small Angle X-ray Scattering
- Review of nano-phase effects in high strength and conductivity copper alloys
- Progress and challenges in p-type oxide-based thin film transistors
- Advanced materials for flexible solar cell applications
- Phenylboronic acid-decorated polymeric nanomaterials for advanced bio-application
- The effect of nano-SiO2 on concrete properties: a review
- A brief review for fluorinated carbon: synthesis, properties and applications
- A review on the mechanical properties for thin film and block structure characterised by using nanoscratch test
- Cotton fibres functionalized with plasmonic nanoparticles to promote the destruction of harmful molecules: an overview

