Home First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy
Article Open Access

First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy

  • Heng Li , Xin Zhang EMAIL logo , Qijun Liu , Yangyang Liu , Haifeng Liu , Xianqu Wang , Jie Huang , Hai Liu , Yuhong Xu , Changjian Tang and Guangjiu Lei
Published/Copyright: November 12, 2019
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanotechnology Reviews
From the journal Nanotechnology Reviews Volume 8 Issue 1

Abstract

The structural, mechanical and thermodynamic properties of tungsten-based alloys, including W0.5Ti0.5,W0.67Zr0.33,W0.666Ti0.1667Zr0.1667,W0.67Hf0.33 and W0.666Ti0.1667Hf0.1667, have been investigated in this paper by first-principles calculations based on density functional theory (DFT). The calculated elastic constants and mechanical stability criteria of cubic crystals indicated that all of these cubic alloys are mechanical stable. The mechanical properties, including bulk modulus (B), shear modulus (G), Young’s modulus(E), ratio B/G, Poisson’s ratio, Cauchy pressure and Vickers hardness are derived from the elastic constants Cij. According to calculated elastic modulus and Vickers hardness, the W0.666Ti0.1667Hf0.1667 alloy has the greatest mechanical strength. The Vickers hardness of these cubic alloys rank as follows: W0.666Ti0.1667Hf0.1667 > W0.67Zr0.33 > W0.666Ti0.1667Zr0.1667 > W0.5Ti0.5 > W0.67Hf0.33. Moreover, calculated ratio B/G, Poisson’s ratio, Cauchy pressure indicated that the ductility of W0.666Ti0.1667Hf0.1667 alloy is the worst among these alloys. The ductility of these cubic alloys rank as follows: W0.67Hf0.33 > W0.5 Ti0.5 > W0.67Zr0.33 > W0.666Ti0.1667Zr0.1667 > W0.666Ti0.1667Hf0.1667. What is noteworthy is that both mechanical strength and ductility of W0.666Ti0.1667Hf0.1667 are greater than pure W. Finally, Debye temperature, melting point and thermal conductivity have been predicted through empirical formulas. All these results will provide scientific data for the study on new product development of electrode materials.

Keywords: Density functional theory; Alloy; Mechanical properties; Thermodynamic properties; Electrode materials

1 Introduction

Tungsten and tungsten-based alloys are widely used in aerospace industries and national defense military project due to their high strength, high melting point, good thermal conductivity, hardness, low thermal expansion coefficient etc. [1, 2, 3, 4]. And they are also applied in nuclear fusion reactors as the potential first wall materials, and the electrode materials applied in NBI system which is the main method used to heat plasma consisting in a beam of high-energy neutral particles that can enter the magnetic confinement field [2, 3, 4, 5, 6]. Recently, in order to improve the low ductility and high ductile-to-brittle transition temperature (DBTT) of tungsten, many experimental and theoretic studies have been reported on the binary W alloy in a wide variety [7].W-Ti alloy is a typical binary W alloy in those studies. The results indicated that the ductility of W-Ti alloy is improved obviously and metallic bonding is strengthened, but the mechanical strength alloy is lower comparing with pure W. The tungsten - titanium system exhibits a completely solid solution in the β phase at the temperatures between the solidus and the critical temperature of the miscibility gap [8].

There were many researches on binary W alloys, but few on ternary alloys. On the basis of previous studies, binary W alloy, especially ternary W alloy has been considered to be the typical representative for studying in this paper. So far, little work has been reported on W-Hf alloy, W-Zr alloy W-Ti-Hf ternary alloy and W-Ti-Zr ternary alloy. Hafnium (Hf) is a chemical element that has a high melting point, high density of physical properties. A series of alloying compounds made of hafnium, such as HfC,which can be used as an additive to hard alloys due to its hardness and high melting point. Another alloy compound of hafnium, 4TaC·HfC, is known to have the highest melting point [9, 10, 11]. Correspondingly, Zirconium is also one of the metals with high melting point. Titanium-zirconium alloy can be used as a kind of biomedical-materials due to its high hardness [12].

In this paper, we investigated the structure, elastic properties, Vicker hardness, Debye temperature, melting point and thermal conductivity of W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667,W0.67Hf0.33,W0.666Ti0.1667Hf0.1667 alloys by first-principles calculations based on density functional theory (DFT). This work will be quite helpful to understanding basic physical properties of these alloys, and these calculated results will provide scientific data for the study on new product development of electrode materials.

2 Calculation methods

The simulation method based on density functional theory (DFT) scheme [13] was carried out to research the mechanical properties, Debye temperature, melting point and minimum thermal conductivity of tungsten-base alloys, and the calculations were performed by using the Cambridge Serial Total Energy Package Code (CASTEP) [14, 15]. The interaction between valence electrons and core ion was described by ultra-soft pseudo-potential plane-wave (UPPW) [16]. Exchange-correlation energy was treated by general gradient approximation (GGA) [17] method, including PBE [18] and PBEsol [19]. For the integral in the first Brillouin zone, Monkhorst-pack method [20] was adopted for k-points sampling, as M×M×M for all of tungsten-base alloys. According to the results of the convergence test, M and plane wave cutoff energy were employed as different value with different kinds of structure, this is shown in Table 1. The atomic structure is fully relaxed in the geometry optimization process, until the forces exerting on all atoms are less than 0.01eV/Å. Geometry optimization results are shown in Table 1.

Table 1

Calculated lattice constants of W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33 and W0.666Ti0.1667Hf0.1667.

PhaseSpace groupk-point mesha (Å)Deviation (%)Energy cutoff (eV)
W0.5Ti0.5This workIm-3m11×11×113.177< 0.22350
ref [7]Im-3m11×11×113.170350
W0.67Zr0.33This workIm-3m8×8×83.258< 2.7350
ref [21]Im-3m-3.172-
W0.666Ti0.1667Zr0.1667This workIm-3m8×8×83.189< 0.73350
ref [21]Im-3m-3.166-
W0.67Hf0.33This workIm-3m15×15×153.186< 0.031000
ref [21]Im-3m-3.185-
W0.666Ti0.1667Hf0.1667This workIm-3m18×18×183.003< 5.451500
ref [21]Im-3m-3.176-

3 Results and discussion

3.1 Structure optimization

The Bravais primitive cell of all the tungsten-base alloys are body-centered cubic, as shown in Figure 1. Before calculated the elastic constant, we tested the convergence. The convergence is good enough when the energy and elastic constants almost no longer change with the increase of cutoff energy and M value. The final determined cutoff energy and M values are shown in Table 1. Compared with the experimental data of references, calculated lattice constants were in good agreement with the former.

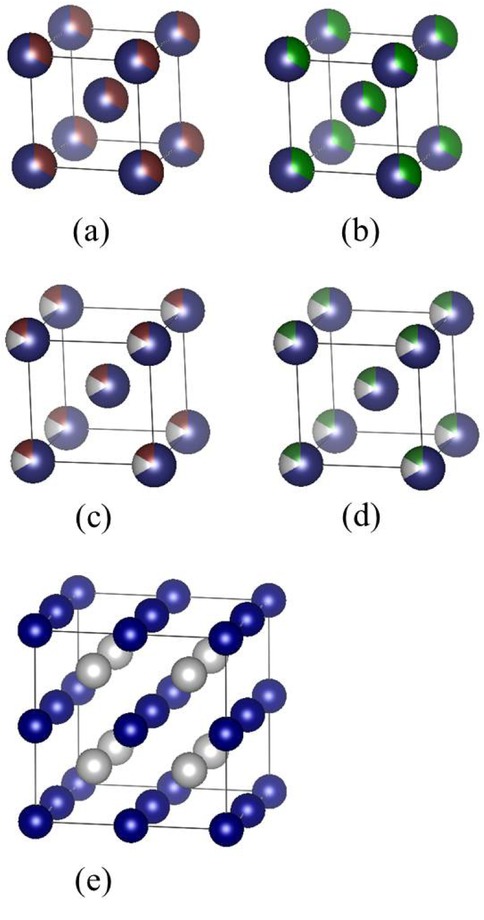
Figure 1 Crystal cell structure of the alloys. (a) W0.67 Hf0.33; (b) W0.67 Zr0.33; (c) W0.666 Ti0.1667 Hf0.1667; (d) W0.666 Ti0.1667 Zr0.1667; (e)W0.5Ti0.5 (2×2×2 supercell). Blue is W atom, white is Ti atom, red is Hf atom, and green is Zr atom.
Figure 1

Crystal cell structure of the alloys. (a) W0.67 Hf0.33; (b) W0.67 Zr0.33; (c) W0.666 Ti0.1667 Hf0.1667; (d) W0.666 Ti0.1667 Zr0.1667; (e)W0.5Ti0.5 (2×2×2 supercell). Blue is W atom, white is Ti atom, red is Hf atom, and green is Zr atom.

3.2 Elastic constants and moduli

Thermodynamic and mechanical properties of crystals, including compressibility, melting point, thermal conductivity and Debye temperature, are related to the elastic constant Cij which determine the ability of crystal to resist external forces. The elastic modulus, including bulk modulus (B), shear modulus (G) and Young’s modulus (E), and ratio B/G, Poisson’s ratio (σ), Cauchy pressure (C’), etc. can be calculated by the elastic constant. Elastic constants Cijcould be calculated by generalized Hooke’s law. For a body-centered cubic system, there are only three independent elastic constants C11, C12, and C44, as shown in Table 2. The elastic constants of ternary W0.666Ti0.1667Hf0.1667 are the greatest. The conditions of mechanical stability of bcc system are [22].

Table 2

The elastic constant (GPa) of W0.5Ti0.5, W0.67Zr0.33, W0.666 Ti0.1667 Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667.

PhaseC11C12C44
W0.5Ti0.5This work238.91165.6845.33
ref [11]248.78174.9439.46
W0.67Zr0.33This work345.63176.4177.29
ref---
W0.666Ti0.1667Zr0.1667This work363.77195.1075.65
ref---
W0.67Hf0.33This work343.72203.132.32
ref---
W0.666Ti0.1667Hf0.1667This work572.58342.58182.58
ref---
(1)C44>0
(2)C11−C12>0
(3)C11+2C12>0

All tungsten-base alloys satisfy equations (1)-(3) indicating that they are mechanically stable. Unfortunately, there were few studies on the mechanical properties of W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667alloys except of W0.5Ti0.5. Cauchy pressure (C’), which characterize the ductility of materials, could be represented by [23].

(4)C′=C12−C442

According to Voigt-Reuss-Hill approximation [24, 25, 26, 27], the bulk moduli (B) and shear modulus (G) could be calculated, as shown in Table 3. Actually, Young’s modulus (E), ratio B/G and Poisson’s ratio, including bulk moduli (B) and shear modulus (G), can be calculated from the known elastic constants [28].

Table 3

Elastic modulus (GPa), ratio B/G and Poisson’s ratio (σ) and Cauchy stress (C ’, GPa) of W, W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667.

PhaseBGVGRGHB/GEσC′
Pure WThis work------
Jiang [7]317.44147.422.15382.960.3035.87
Söderlind [28]314.33--163.401.92417.800.28-
W0.5Ti0.5This work190.0941.8441.3941.624.57116.370.39860.18
Jiang [7]199.56--38.445.19108.370.41067.74
W0.67Zr0.33This work232.8282.2280.0680.143.32215.670.34649.56
ref--------
W0.666Ti0.1667Zr0.1667This work251.3278.9078.1278.013.18212.090.35859.73
ref--------
W0.67Hf0.33This work249.9929.513.7816.6515.0148.870.467100.41
ref--------
W0.666Ti0.1667Hf0.1667This work420.24156.15148.82152.482.76408.080.33880.00
ref--------
(5)B=13(C11+2C12)
(6)GV=15(C11−C12+3C44)
(7)GR=5(C11−C12)C444C44+3(C11−C12)
(8)GH=12(GV+GR)
(9)E=9BGH3B+GH
(10)σ=3B−2GH2(3B+GH)

The tendency of bulk modulus, shear modulus, and Young’s modulus to vary with the alloys as shown in Figure 2. It can be seen that the data of W0.5Ti0.5 in this work is consistent with the data of Jiang’s work.

Figure 2 Trends of Bulk modulus (B), Shear modulus (G) and Young’s modulus (E) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667.
Figure 2

Trends of Bulk modulus (B), Shear modulus (G) and Young’s modulus (E) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667.

The bulk modulus (B) reflects the strength of the material. As can be seen from Figure 2, the bulk modulus (B) of these materials ranks as follows: W0.666Ti0.1667Hf0.1667 > W > W0.666Ti0.1667Zr0.1667 > W0.67Hf0.33 > W0.67Zr0.33 > W0.5Ti0.5. The value of bulk modulus (B) of W0.5Ti0.5 binary alloy is 190.09 GPa, and the value of bulk modulus (B) of W0.666Ti0.1667Hf0.1667 ternary alloy is up to 420.24 GPa. Shear modulus (G) characterizes the material’s resistance to shear strain. The shear modulus value of W0.67Hf0.33 is the minimum, which is 16.65 GPa, and the value of W0.666Ti0.1667Hf0.1667 ternary alloy is still the largest, reached 152.48 GPa. The order is: W0.666Ti0.1667Hf0.1667 > W > W0.67Zr0.33 > W0.666Ti0.1667Zr0.1667 > W0.5Ti0.5 > W0.67Hf0.33. The larger the Young’s modulus (E) is, the stronger the material stiffness is [29]. From Figure 2, it can be seen that the value of Young’s modulus of W0.67Hf0.33 is the smallest.; the value of Young’s modulus of W0.666 Ti0.1667 Hf0.1667 ternary alloy is the largest, which reached 408.08 GPa, the order is: W0.666Ti0.1667Hf0.1667 > W > W0.67Zr0.33 > W0.666Ti0.1667Zr0.1667 > W0.5Ti0.5 > W0.67Hf0.33. In summary, the values of bulk modulus (B), shear modulus (G) and Young’s modulus (E) of W0.666Ti0.1667Hf0.1667 ternary alloy are the largest, even larger than pure W. But the mechanical strength of other alloys are lower than pure W.

According to Pugh’s theory [3], ratio B/G is closely related to the ductility of metallic materials. When the ratio B/G is greater than 1.75, the materials exhibits ductility; conversely, the materials exhibits brittleness. And the larger the ratio B/G is, the better the ductility of the materials is. As can be seen from Table 3, all tungsten-base alloys are plastic materials and W0.67 Hf0.33 has the best ductility.

It can be seen from Figure 3 that the ductility of the two ternary alloys are worse than that of the W0.5Ti0.5 binary alloy, of which W0.666 Ti0.1667 Hf0.1667 is the worst. Be that as it may, the ductility of all tungsten-base alloys we studied are higher than pure W.

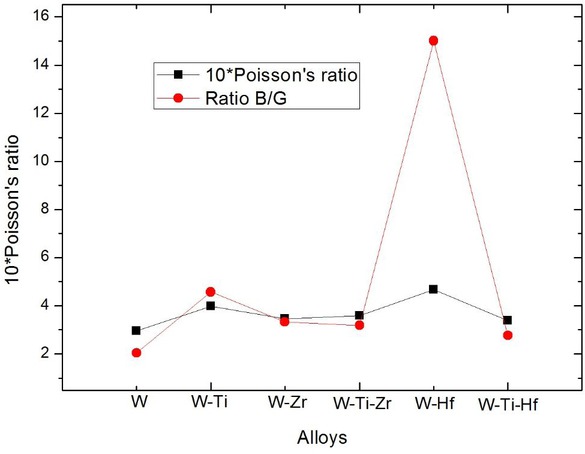
Figure 3 Trends of ratio B/G and Poisson’s ratio (σ) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666 Ti0.1667 Zr0.1667, W0.67Hf0.33, W0.666 Ti0.1667 Hf0.1667.
Figure 3

Trends of ratio B/G and Poisson’s ratio (σ) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666 Ti0.1667 Zr0.1667, W0.67Hf0.33, W0.666 Ti0.1667 Hf0.1667.

Poisson’s ratio (σ) could be used to further analyze the bonding of tungsten-base alloys [31], the greater value of σ is, the better ductility of material is. The conclusions drawn from the ratio B/G could be confirmed by Poisson’s ratio (σ). It can be seen from Figure 3 that the trend of the ratio B/G is consistent with Poisson’s ratio (σ). Poisson’s ratio σ values for different materials range from 0.0 to 0.50. Metallic bonded materials have a big value for σ i.e. ~0.33, for covalent materials the critical value is 0.1 and for ionic materials it is 0.25 [31, 32]. It can be seen that metallic bond take the dominant position in all these crystal materials.

When the Cauchy pressure (C’) is positive, the metal bond predominates in the crystal cell, thereby exhibiting the ductility of the material [33, 34, 35]. and the larger the C’ value is, the stronger the metallic bond of the materials and the better the ductility are. Conversely, if the Cauchy pressure is negative, the material exhibits brittleness. The smaller the negative value is, the stronger the covalent bond and the brittler the material are.

Figure 4 Trend of Cauchy pressure (C’) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667 Zr0.1667, W0.67 Hf0.33, W0.666Ti0.1667 Hf0.1667.
Figure 4

Trend of Cauchy pressure (C’) of pure W, W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667 Zr0.1667, W0.67 Hf0.33, W0.666Ti0.1667 Hf0.1667.

3.3 Vickers hardness

In addition to the elastic modulus which can describe the mechanical properties of materials, hardness is also an important parameter. Table 4 lists the Vickers hardness of five tungsten-base alloys. Among them, the value of HVGis smaller than HVE.As previously analyzed, the alloy material which is of the best mechanical properties is W0.666Ti0.1667Hf0.1667 ternary alloy, and its hardness is much bigger than other binary alloys. Vickers hardness (HV) can be calculated from the elastic modulus. The empirical formula is as follows [36, 37]:

Table 4

Vickers hardness (HV , GPa) of W0.5Ti0.5, W0.67Zr0.33, W0.666 Ti0.1667 Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667 alloys.

W0.5Ti0.5W0.67Zr0.33W0.666Ti0.1667Zr0.1667W0.67Hf0.33W0.666Ti0.1667Hf0.1667
HVG4.4611.2810.900.0524.07
HVE7.0713.1112.902.9724.81
(11)HVG=0.1769G−2.899
(12)HVE=0.0608E

3.4 Thermodynamic property

Thermodynamic property is another important property for materials, such as Debye temperature θD (K), minimum thermal conductivity kmin (W/ (m × K)), and melting point Tm (K). It is known by Solid State Physics that θD is mainly related to the dispersion relation of the lattice wave generated by the lattice vibration. Its relationship in solid state physics is [38]:

(13)θD=ℏωmkB

In the above formula, ℏ is the Planck constant, ωm is the maximum vibration frequency of the lattice wave, and kB is the Boltzmann constant. In some references, we found that the Debye temperature can be estimated by the average elastic wave velocity using a semi-empirical formula. The calculation formulas are as follows [38, 39, 40, 41]:

(14)θD=hkB[3n4π(NAρM)]13 vm
(15)vm=[13(2vt3+1vl3)]−13
(16)vl=(B+43Gρ)12
(17)vt=(Gρ)12

Where ρ is the density; N A is the Avogadro constant; M is the weight of a single cell; n is the number of atoms in the unit cell. Vl and Vt represent the longitudinal sound velocity and the lateral sound velocity, respectively, and Vm is the average sound velocity in units of (m/s).

The minimum thermal conductivity kmin (W/ (m × K)) is an important parameter to characterize the ability of materials to transfer heat. Melting point is an important parameter to characterize the heat resistance of alloy materials. Since the background we assumed is to use these alloys as electrode materials in NBI systems, it must have sufficient high temperature resistance and thermal conductivity. Therefore, the thermal conductivity and melting point of these materials are also estimated in this paper. In the references we found, Cahill and Pohl et al. believe that the minimum thermal conductivity and melting point of the material can be roughly obtained by the following empirical formula [41, 42, 43]:

(18)kmin=kB2.48n23(2vt+vl)
(19)Tm=354+4.52C11+C333

Since for body-centered cubic lattice, C11 is equal to C33. Therefore, the formula for estimating the melting point used in all alloys in this paper uses the following correction formula:

(20)Tm=354+4.5C11

It can be seen from Table 5 that the Debye temperature (θD) of ternary alloy is greater than binary alloy, and the Debye temperature of these alloys ranks as follows: W0.666Ti0.1667Hf0.1667 > W0.666Ti0.1667Zr0.1667 > W0.67Zr0.33 > W0.5Ti0.5 > W0.67Hf0.33. It can be seen that the change of Debye temperature is not obvious when Ti is added to the W-Zr unit cell. On the contrary, when Zr is added to the W-Ti unit cell, the Debye temperature is significantly increase. Similarly, there is an obvious increase for Debye temperature when Ti is introduced into W-Hf unit cell or Hf is introduced into W-Ti unit cell.

Table 5

The thermal parameters of W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667 Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667 alloys.

PhasevlvtvmθDkminTm
W0.5Ti0.54523.861862.342017.62238.150.7291429.10
W0.67Zr0.334805.342348.612638.12303.650.8401909.34
W0.666Ti0.1667Zr0.16674890.452031.752590.59304.640.8391990.97
W0.67Hf0.333815.18943.601077.44126.820.5041900.72
W0.666Ti0.1667Hf0.16675633.172785.643126.97390.480.9902930.61

The minimum thermal conductivity of these alloys ranks as follows: W0.666Ti0.1667Hf0.1667 > W0.67Zr0.33 > W0.666Ti0.1667Zr0.1667 > W0.5Ti0.5 > W0.67Hf0.33. The addition of Ti to the W-Zr unit cell has no significant change in the minimum thermal conductivity. On the contrary, when Zr is added to the W-Ti unit cell, the minimum thermal conductivity significantly improved. Similarly, there is an obvious increase for minimum thermal conductivity when Ti is introduced into W-Hf unit cell or Hf is introduced into W-Ti unit cell.

The melting point of these alloys ranks as follows: W0.666Ti0.1667Hf0.1667 > W0.666Ti0.1667Zr0.1667 > W0.67Zr0.33 > W0.67Hf0.33 > W0.5Ti0.5. The addition of Ti to the W-Zr binary alloy has no obvious change for melting point. The addition of Zr to the W-Ti unit cell has a significantly increase for melting point. There is an obvious increase for melting point when Ti is introduced into W-Hf unit cell or Hf is introduced into W-Ti unit cell.

Unfortunately, there is little previous research on the alloy materials in this paper, so it is difficult to find relevant literature to support our research results.

4 Summary and conclusions

The mechanical properties of tungsten-base alloys, including W0.5Ti0.5, W0.67Zr0.33, W0.666Ti0.1667Zr0.1667, W0.67Hf0.33, W0.666Ti0.1667Hf0.1667, were simulated by first-principles calculations based on density functional theory (DFT). The elastic constant and the elastic modulus combined with the empirical formula calculated the thermodynamic properties:

  1. Comparing with experimental results, the calculated structure parameters are good agreement with it.

  2. All tungsten-base alloys are mechanically stable.

  3. The bulk modulus (B), shear modulus (G) and Young’s modulus (E) of the W0.666Ti0.1667Hf0.1667 ternary alloy are the greatest, even higher than pure W.

  4. All tungsten-base alloys are ductile materials. The ductility of ternary alloys is lower than that of binary alloys, but higher than that of pure tungsten alloys. Further analysis by Poisson’s ratio (σ) and Cauchy pressure (C’) shows that metallic bond take the dominant position in all these crystal materials.

  5. Debye temperature (θD), thermal conductivity and melting point of all alloy materials were predicted and discussed in combination with empirical formulas. These predictions may provide a corresponding reference for the subsequent application of the above alloys.

Acknowledgement

This work was supported by the National Key R&D Program of China (2017YFE0300100).

References

[1] Jiang D.Y., Ouyang C.Y., Liu S.Q., The effect of titanium (Ti) doping on hydrogen incorporation in tungsten(W): First-principles calculations, Fusion Eng. Des., 2017, 121, 227-234.10.1016/j.fusengdes.2017.07.019Search in Google Scholar

[2] Garcia-Rosales C., Erosion processes in plasma-wall interactions, J. Nucl. Mater., 1994, 211(3), 202-214.10.1016/0022-3115(94)90348-4Search in Google Scholar

[3] Chuyanov V.A., ITER EDA project status, J. Nucl. Mater., 1996, 233, 4–8.10.1016/S0022-3115(96)00121-3Search in Google Scholar

[4] Janeschitz G., Plasma-wall interaction issues in ITER, J. Nucl. Mater., 2001, 290(73), 1-11.10.1016/S0022-3115(00)00623-1Search in Google Scholar

[5] Bacal M., Wada M., Negative hydrogen ion production mechanisms, Appl. Phys. Rev., 2015, 2(2), 021305.10.1063/1.4921298Search in Google Scholar

[6] Rieth M., Dudarev S.L., Recent progress in research on tungsten materials for nuclear fusion applications in Europe, J. Nucl. Mater., 2013, 432(1-3), 482-500.10.1016/j.jnucmat.2012.08.018Search in Google Scholar

[7] Jiang D.Y., Ouyang C.Y., Liu S.Q., Mechanical properties of W–Ti alloys from first-principles calculations, Fusion Eng. Des., 2016, 106, 34-39.10.1016/j.fusengdes.2016.03.028Search in Google Scholar

[8] Murray J.L., The Ti-W (Titanium-Tungsten) system, Bull. Alloy Phase Diagrams, 1981, 2(2), 192-196.10.1007/BF02881477Search in Google Scholar

[9] Jiang J., Wang S., Li W., Preparation and Characterization of Ultra High-Temperature Ternary Ceramics Ta 4 HfC 5, J. Am. Ceram. Soc., 2016, 99(10), 3198-3201.10.1111/jace.14436Search in Google Scholar

[10] Lu Y., Sun Y., Zhang T., Polymer-derived Ta4HfC5 nanoscale ultrahigh-temperature ceramics: Synthesis, microstructure and properties, J. Eur. Ceram. Soc., 2019, 39(2-3), 205-211.10.1016/j.jeurceramsoc.2018.10.012Search in Google Scholar

[11] Wen Q., Xu B., Guillon O., Single-source-precursor synthesis of dense SiC/HfC(x)N(1-x)-based ultrahigh-temperature ceramic nanocomposites, Nanoscale, 2014, 6(22), 13678-13689.10.1039/C4NR03376KSearch in Google Scholar PubMed

[12] Kobayashi E., Matsumoto S., Doi H., Mechanical properties of the binary titanium-zirconium alloys and their potential for biomedical materials, J. Biomed. Mater. Res., 1995, 29(8), 943-950.10.1002/jbm.820290805Search in Google Scholar PubMed

[13] Kohn W., Sham L.J., Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133.10.1103/PhysRev.140.A1133Search in Google Scholar

[14] Vanderbilt D., Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B, 1990, 41(11), 7892-7895.10.1103/PhysRevB.41.7892Search in Google Scholar PubMed

[15] Clark S.J., Segall M.D., Pickard C.J., First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567-570.10.1524/zkri.220.5.567.65075Search in Google Scholar

[16] White J.A., Bird D.M., Implementation of gradient-corrected exchange-correlation potentials in Car-Parrinello total-energy calculations, Phys. Rev. B, 1994, 50(7), 4954-4957.10.1103/PhysRevB.50.4954Search in Google Scholar

[17] Perdew J.P., Wang Y., Pair-Distribution Function and its Coupling-Constant Average for the Spin-Polarized Electron gas, Phys. Rev. B, 1992, 46(20), 12947-12954.10.1103/PhysRevB.46.12947Search in Google Scholar

[18] Perdew J.P., Burke K., Ernzerhof M., Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865-3868.10.1103/PhysRevLett.77.3865Search in Google Scholar PubMed

[19] Perdew J.P., Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100(13), 136406.10.1103/PhysRevLett.100.136406Search in Google Scholar PubMed

[20] Monkhorst H.J., Pack J.D., Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13, 5188- 5192.10.1103/PhysRevB.13.5188Search in Google Scholar

[21] Blazina Z., Trojko R., Ban Z., ChemInform Abstract: High-temperature equilibriums in the Zr1−xHfxM2, Zr1−xTixM2 and Hf1−xTixM2 (M=Mo or W) systems, Chem. Informationsdienst, 1982, 13(29).10.1002/chin.198229019Search in Google Scholar

[22] Mouhat F., Coudert F.X., Necessary and suflcient elastic stability conditions in various crystal systems, Phys. Rev. B, 2014, 90(22), 224104.10.1103/PhysRevB.90.224104Search in Google Scholar

[23] Tang B.Y., Yu W.Y., Zeng X.Q., First-principles study of the electronic structure and mechanical properties of CaMg2 Laves phase, Mater. Sci. Eng., A, 2008, 489(1-2), 444-450.10.1016/j.msea.2007.12.025Search in Google Scholar

[24] Boucetta S., Theoretical study of elastic, mechanical and thermodynamic properties of MgRh intermetallic compound, J. Magnesium Alloys, 2014, 2(1), 59-63.10.1016/j.jma.2014.04.001Search in Google Scholar

[25] Voigt W., On the relation between the elasticity constants of isotropic bodies, Ann. Phys. Chem, 1889, 274, 573-587.10.1002/andp.18892741206Search in Google Scholar

[26] Reuss A., Angnew Z., A calculation of the bulk modulus of polycrystalline materials, Math. Meth., 1929, 9, 55-58.Search in Google Scholar

[27] Hill R., The Elastic Behaviour of a Crystalline Aggregate, Proc. Phys. Soc. London, Sect. A, 1952, 65(5), 349-354.10.1088/0370-1298/65/5/307Search in Google Scholar

[28] Söderlind P., Eriksson O., Wills J.M., Theory of elastic constants of cubic transition metals and alloys, Phys. Rev. B, 1993, 48(9), 5844-5851.10.1103/PhysRevB.48.5844Search in Google Scholar

[29] Li H., Chen Y., Wang H., First-principles study of mechanical and thermodynamic properties of Ti-Ga intermetallic compounds, J. Alloys Compd., 2017, 700, 208-214.10.1016/j.jallcom.2017.01.052Search in Google Scholar

[30] Pugh S.F., Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh & Dublin Phil. Mag. J. Sci., 1954, 45(367), 823-843.10.1080/14786440808520496Search in Google Scholar

[31] Murtaza G., Gupta S.K., Seddik T., Structural, electronic, optical and thermodynamic properties of cubic REGa3 (RE = Sc or Lu) compounds: Ab initio study, J. Alloys Compd., 2014, 597, 36-44.10.1016/j.jallcom.2014.01.203Search in Google Scholar

[32] Chen H., Yang L., Long J., First-principles investigation of the elastic, Vickers hardness and thermodynamic properties of Al– Cu intermetallic compounds, Superlattices Microstruct., 2015, 79, 156-165.10.1016/j.spmi.2014.11.005Search in Google Scholar

[33] Kamran S., Chen K., Chen L., Ab initio examination of ductility features of fcc metals. Phys. Rev. B, 2009, 79(2), 024106.10.1103/PhysRevB.79.024106Search in Google Scholar

[34] Rahman M.A., Rahaman M.Z., Rahman M.A., The structural, elastic, electronic and optical properties of MgCu under pressure: A first-principles study, INT J MOD PHYS B, 2016, 30(27), 1650199.10.1142/S021797921650199XSearch in Google Scholar

[35] Lin Y.C., Luo S.C., Chen M.S., Effects of pressure on anisotropic elastic properties and minimum thermal conductivity of DO22- Ni3Nb phase: First-principles calculations, J. Alloys Compd., 2016, 688, 285-293.10.1016/j.jallcom.2016.07.204Search in Google Scholar

[36] Jiang X., Zhao J., Wu A., Mechanical and electronic properties of B12-based ternary crystals of orthorhombic phase, J. Phys.: Condens. Matter, 2010, 22(31), 315503.10.1088/0953-8984/22/31/315503Search in Google Scholar

[37] Reffas M., Bouhemadou A., Khenata R., Ab initio study of structural, elastic, electronic and optical properties of spinel SnMg2O4 Phys. B: Condens. Matter, 2010, 405(18), 4079-4085.10.1016/j.physb.2010.06.058Search in Google Scholar

[38] Kittel C., McEuen P., McEuen P., Introduction to solid state physics, New York: Wiley, 1996.Search in Google Scholar

[39] Chen H., Yang L., Pressure effect on the structural and elastic property of Hf2InC, Phys. B: Condens. Matter, 2011, 406(23), 4489-4493.10.1016/j.physb.2011.09.013Search in Google Scholar

[40] Tani J., Takahashi M., Kido H., Lattice dynamics and elastic properties of Mg3As2 and Mg3Sb2 compounds from first-principles calculations, Phys. B: Condens. Matter, 2010, 405(19), 4219-4225.10.1016/j.physb.2010.07.014Search in Google Scholar

[41] Cahill D.G., Pohl R.O., Heat flow and lattice vibrations in glasses, Solid State Commun., 1989, 70(10), 927-930.10.1016/0038-1098(89)90630-3Search in Google Scholar

[42] Chen Q., Sundman B., Calculation of Debye temperature for crystalline structures—a case study on Ti, Zr, and Hf, Acta Mater., 2001, 49(6), 947-961.10.1016/S1359-6454(01)00002-7Search in Google Scholar

[43] Fine M.E., Brown L.D.,Marcus H.L., Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18(9), 951-956.10.1016/0036-9748(84)90267-9Search in Google Scholar

Received: 2019-03-26
Accepted: 2019-08-27
Published Online: 2019-11-12

© 2019 H. Li et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. Research Articles
  2. Investigation of rare earth upconversion fluorescent nanoparticles in biomedical field
  3. Carbon Nanotubes Coated Paper as Current Collectors for Secondary Li-ion Batteries
  4. Insight into the working wavelength of hotspot effects generated by popular nanostructures
  5. Novel Lead-free biocompatible piezoelectric Hydroxyapatite (HA) – BCZT (Ba0.85Ca0.15Zr0.1Ti0.9O3) nanocrystal composites for bone regeneration
  6. Effect of defects on the motion of carbon nanotube thermal actuator
  7. Dynamic mechanical behavior of nano-ZnO reinforced dental composite
  8. Fabrication of Ag Np-coated wetlace nonwoven fabric based on amino-terminated hyperbranched polymer
  9. Fractal analysis of pore structures in graphene oxide-carbon nanotube based cementitious pastes under different ultrasonication
  10. Effect of PVA fiber on durability of cementitious composite containing nano-SiO2
  11. Cr effects on the electrical contact properties of the Al2O3-Cu/15W composites
  12. Experimental evaluation of self-expandable metallic tracheobronchial stents
  13. Experimental study on the existence of nano-scale pores and the evolution of organic matter in organic-rich shale
  14. Mechanical characterizations of braided composite stents made of helical polyethylene terephthalate strips and NiTi wires
  15. Mechanical properties of boron nitride sheet with randomly distributed vacancy defects
  16. Fabrication, mechanical properties and failure mechanism of random and aligned nanofiber membrane with different parameters
  17. Micro- structure and rheological properties of graphene oxide rubber asphalt
  18. First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy
  19. Adsorption performance of hydrophobic/hydrophilic silica aerogel for low concentration organic pollutant in aqueous solution
  20. Preparation of spherical aminopropyl-functionalized MCM-41 and its application in removal of Pb(II) ion from aqueous solution
  21. Electrical conductivity anisotropy of copper matrix composites reinforced with SiC whiskers
  22. Miniature on-fiber extrinsic Fabry-Perot interferometric vibration sensors based on micro-cantilever beam
  23. Electric-field assisted growth and mechanical bactericidal performance of ZnO nanoarrays with gradient morphologies
  24. Flexural behavior and mechanical model of aluminum alloy mortise-and-tenon T-joints for electric vehicle
  25. Synthesis of nano zirconium oxide and its application in dentistry
  26. Surface modification of nano-sized carbon black for reinforcement of rubber
  27. Temperature-dependent negative Poisson’s ratio of monolayer graphene: Prediction from molecular dynamics simulations
  28. Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout
  29. Preparation of low-permittivity K2O–B2O3–SiO2–Al2O3 composites without the addition of glass
  30. Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments
  31. Enhanced flexural properties of aramid fiber/epoxy composites by graphene oxide
  32. Correlation between electrochemical performance degradation and catalyst structural parameters on polymer electrolyte membrane fuel cell
  33. Materials characterization of advanced fillers for composites engineering applications
  34. Humic acid assisted stabilization of dispersed single-walled carbon nanotubes in cementitious composites
  35. Test on axial compression performance of nano-silica concrete-filled angle steel reinforced GFRP tubular column
  36. Multi-scale modeling of the lamellar unit of arterial media
  37. The multiscale enhancement of mechanical properties of 3D MWK composites via poly(oxypropylene) diamines and GO nanoparticles
  38. Mechanical properties of circular nano-silica concrete filled stainless steel tube stub columns after being exposed to freezing and thawing
  39. Arc erosion behavior of TiB2/Cu composites with single-scale and dual-scale TiB2 particles
  40. Yb3+-containing chitosan hydrogels induce B-16 melanoma cell anoikis via a Fak-dependent pathway
  41. Template-free synthesis of Se-nanorods-rGO nanocomposite for application in supercapacitors
  42. Effect of graphene oxide on chloride penetration resistance of recycled concrete
  43. Bending resistance of PVA fiber reinforced cementitious composites containing nano-SiO2
  44. Review Articles
  45. Recent development of Supercapacitor Electrode Based on Carbon Materials
  46. Mechanical contribution of vascular smooth muscle cells in the tunica media of artery
  47. Applications of polymer-based nanoparticles in vaccine field
  48. Toxicity of metallic nanoparticles in the central nervous system
  49. Parameter control and concentration analysis of graphene colloids prepared by electric spark discharge method
  50. A critique on multi-jet electrospinning: State of the art and future outlook
  51. Electrospun cellulose acetate nanofibers and Au@AgNPs for antimicrobial activity - A mini review
  52. Recent progress in supercapacitors based on the advanced carbon electrodes
  53. Recent progress in shape memory polymer composites: methods, properties, applications and prospects
  54. In situ capabilities of Small Angle X-ray Scattering
  55. Review of nano-phase effects in high strength and conductivity copper alloys
  56. Progress and challenges in p-type oxide-based thin film transistors
  57. Advanced materials for flexible solar cell applications
  58. Phenylboronic acid-decorated polymeric nanomaterials for advanced bio-application
  59. The effect of nano-SiO2 on concrete properties: a review
  60. A brief review for fluorinated carbon: synthesis, properties and applications
  61. A review on the mechanical properties for thin film and block structure characterised by using nanoscratch test
  62. Cotton fibres functionalized with plasmonic nanoparticles to promote the destruction of harmful molecules: an overview
https://doi.org/10.1515/ntrev-2019-0024
Keywords for this article
Density functional theory; Alloy; Mechanical properties; Thermodynamic properties; Electrode materials
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Investigation of rare earth upconversion fluorescent nanoparticles in biomedical field
  3. Carbon Nanotubes Coated Paper as Current Collectors for Secondary Li-ion Batteries
  4. Insight into the working wavelength of hotspot effects generated by popular nanostructures
  5. Novel Lead-free biocompatible piezoelectric Hydroxyapatite (HA) – BCZT (Ba0.85Ca0.15Zr0.1Ti0.9O3) nanocrystal composites for bone regeneration
  6. Effect of defects on the motion of carbon nanotube thermal actuator
  7. Dynamic mechanical behavior of nano-ZnO reinforced dental composite
  8. Fabrication of Ag Np-coated wetlace nonwoven fabric based on amino-terminated hyperbranched polymer
  9. Fractal analysis of pore structures in graphene oxide-carbon nanotube based cementitious pastes under different ultrasonication
  10. Effect of PVA fiber on durability of cementitious composite containing nano-SiO2
  11. Cr effects on the electrical contact properties of the Al2O3-Cu/15W composites
  12. Experimental evaluation of self-expandable metallic tracheobronchial stents
  13. Experimental study on the existence of nano-scale pores and the evolution of organic matter in organic-rich shale
  14. Mechanical characterizations of braided composite stents made of helical polyethylene terephthalate strips and NiTi wires
  15. Mechanical properties of boron nitride sheet with randomly distributed vacancy defects
  16. Fabrication, mechanical properties and failure mechanism of random and aligned nanofiber membrane with different parameters
  17. Micro- structure and rheological properties of graphene oxide rubber asphalt
  18. First-principles calculations of mechanical and thermodynamic properties of tungsten-based alloy
  19. Adsorption performance of hydrophobic/hydrophilic silica aerogel for low concentration organic pollutant in aqueous solution
  20. Preparation of spherical aminopropyl-functionalized MCM-41 and its application in removal of Pb(II) ion from aqueous solution
  21. Electrical conductivity anisotropy of copper matrix composites reinforced with SiC whiskers
  22. Miniature on-fiber extrinsic Fabry-Perot interferometric vibration sensors based on micro-cantilever beam
  23. Electric-field assisted growth and mechanical bactericidal performance of ZnO nanoarrays with gradient morphologies
  24. Flexural behavior and mechanical model of aluminum alloy mortise-and-tenon T-joints for electric vehicle
  25. Synthesis of nano zirconium oxide and its application in dentistry
  26. Surface modification of nano-sized carbon black for reinforcement of rubber
  27. Temperature-dependent negative Poisson’s ratio of monolayer graphene: Prediction from molecular dynamics simulations
  28. Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout
  29. Preparation of low-permittivity K2O–B2O3–SiO2–Al2O3 composites without the addition of glass
  30. Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments
  31. Enhanced flexural properties of aramid fiber/epoxy composites by graphene oxide
  32. Correlation between electrochemical performance degradation and catalyst structural parameters on polymer electrolyte membrane fuel cell
  33. Materials characterization of advanced fillers for composites engineering applications
  34. Humic acid assisted stabilization of dispersed single-walled carbon nanotubes in cementitious composites
  35. Test on axial compression performance of nano-silica concrete-filled angle steel reinforced GFRP tubular column
  36. Multi-scale modeling of the lamellar unit of arterial media
  37. The multiscale enhancement of mechanical properties of 3D MWK composites via poly(oxypropylene) diamines and GO nanoparticles
  38. Mechanical properties of circular nano-silica concrete filled stainless steel tube stub columns after being exposed to freezing and thawing
  39. Arc erosion behavior of TiB2/Cu composites with single-scale and dual-scale TiB2 particles
  40. Yb3+-containing chitosan hydrogels induce B-16 melanoma cell anoikis via a Fak-dependent pathway
  41. Template-free synthesis of Se-nanorods-rGO nanocomposite for application in supercapacitors
  42. Effect of graphene oxide on chloride penetration resistance of recycled concrete
  43. Bending resistance of PVA fiber reinforced cementitious composites containing nano-SiO2
  44. Review Articles
  45. Recent development of Supercapacitor Electrode Based on Carbon Materials
  46. Mechanical contribution of vascular smooth muscle cells in the tunica media of artery
  47. Applications of polymer-based nanoparticles in vaccine field
  48. Toxicity of metallic nanoparticles in the central nervous system
  49. Parameter control and concentration analysis of graphene colloids prepared by electric spark discharge method
  50. A critique on multi-jet electrospinning: State of the art and future outlook
  51. Electrospun cellulose acetate nanofibers and Au@AgNPs for antimicrobial activity - A mini review
  52. Recent progress in supercapacitors based on the advanced carbon electrodes
  53. Recent progress in shape memory polymer composites: methods, properties, applications and prospects
  54. In situ capabilities of Small Angle X-ray Scattering
  55. Review of nano-phase effects in high strength and conductivity copper alloys
  56. Progress and challenges in p-type oxide-based thin film transistors
  57. Advanced materials for flexible solar cell applications
  58. Phenylboronic acid-decorated polymeric nanomaterials for advanced bio-application
  59. The effect of nano-SiO2 on concrete properties: a review
  60. A brief review for fluorinated carbon: synthesis, properties and applications
  61. A review on the mechanical properties for thin film and block structure characterised by using nanoscratch test
  62. Cotton fibres functionalized with plasmonic nanoparticles to promote the destruction of harmful molecules: an overview
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 8.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/ntrev-2019-0024/html
Scroll to top button