Home Semi-analytical approximation of time-fractional telegraph equation via natural transform in Caputo derivative
Article Open Access

Semi-analytical approximation of time-fractional telegraph equation via natural transform in Caputo derivative

  • Mamta Kapoor EMAIL logo and Samanyu Khosla
Published/Copyright: April 28, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 12 Issue 1

Abstract

In the present research study, time-fractional hyperbolic telegraph equations are solved iteratively using natural transform in one, two, and three dimensions. The fractional derivative is considered in the Caputo sense. These equations serve as a model for the wave theory process of signal processing and transmission of electric impulses. To evaluate the validity and effectiveness of the suggested strategy, a graphical comparison of approximated and exact findings is performed. Convergence analysis of the approximations utilising L ∞ has been done using tables. The suggested approach may successfully and without errors solve a wide variety of ordinary differential equations, partial differential equations (PDEs), fractional PDEs, and fractional hyperbolic telegraph equations.

Graphical abstract

Keywords: natural transform; Caputo derivative; fractional telegraph equation; convergence analysis

1 Introduction

Fractional calculus is a branch of mathematics that deals with partial order integrals, derivatives, and their equations. It was initially alluded to in a letter written by L’ Hospital to Leibnitz, essentially asking about a derivative with order ½ [1]. As fractional calculus is further developed, it found its application in many domains, which includes variational calculus [2], random walks [3], optimal control theory [4], image processing [5], etc.

Second-order hyperbolic partial differential equations (PDE) known as telegraph equation, developed by Oliver Heaviside [6], is used to elaborate voltage and current in an electric transmission line. Further generalizing such equations, we come across a particular kind of equation, known as the fractional hyperbolic telegraph equation (FHTE). Being a type of fractional PDE (FPDE), it is quite a challenge to solve such an equation without using advanced numerical and analytical techniques. FPDEs have multiple methods developed by many researchers due to their importance, e.g., Kudryashov method, Bäcklund transformation method based on the Riccati equation, and a new auxiliary ordinary differential equation have been used to obtain obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity [7]. Laplace transform method has been used to solve constructive equations of the fractional second grade fluid [8]. An extension of homotopy analysis method using Laplace transform, called q-homotopy analysis transform method, was used to solve time and space fractional coupled Burgers’ equations [9]. The fractional reduced differential transform method has been used to obtain approximate solutions of time fractional gas dynamics equation [10]. A hybrid method of decomposition method and Elzaki transformation has been used to solve Navier–Stokes equation [11]. Fractional order diffusion equations were solved using natural transform decomposition [12]. Shallow water forced Korteweg–DeVries equation describing free surface critical flow over a hole has been solved using q-homotopy analysis transformed technique [13]. Variable-order time-space fractional KdV–Burgers–Kuramoto equation has been solved using a pseudo-operational collocation scheme [14]. A Vieta-Fibonacci collocation method has been used to solve fractional delay integro-differential equations [15]. A method based on Laplace transform and homotopy analysis method has been used to obtain approximate solutions of time fractional nonlinear water wave equation [16]. The homotopy analysis transform method using Laplace transform has been used to obtain the approximate solution of nonlinear time-fractional Cauchy reaction–diffusion equation [17].

Multiple techniques have been used to solve FHTEs. Khan et al. [18] used a new technique of adomian decomposition method (ADM) to solve fractional order hyperbolic telegraph equations. Sweilam et al. [19] approached time-fractional telegraph equations using the Sinc-Legendre collocation method. Saadatmandi and Mohabbati [20] employed a computational tau technique based on Legendre polynomials to solve time-fractional telegraph equations. A hybrid technique using Sumudu and Fourier transforms has been used to solve time fractional telegraph equation [21]. Shehu transform has been used to obtain series solution of FHTE [22]. For solving linear time-fractional telegraph equations, two-variable Vieta-Fibonacci polynomials have been constructed and coupled with a matrix collocation scheme [23].

1.1 One-dimensional fractional telegraph equation [ 22 ]

D t β φ + ε φ ( γ , t ) + γ φ t = φ γ γ + g ( γ , t ) .

Here, β and γ are arbitrary constants and φ ( γ , t ) is the unknown function. β is the fractional order of the equation.

1.2 Two-dimensional fractional telegraph equation [ 22 ]

D t 2 β φ + 2 μ D t β φ + ε 2 φ = φ γ γ + φ ρ ρ + g ( γ , ρ , t ) ,

where φ ( γ , ρ , 0 ) = f 1 ( γ , ρ ) and φ t ( γ , ρ , 0 ) = f 2 ( γ , ρ ) .

1.3 Three-dimensional fractional telegraph equation [22]

D t 2 β φ + 2 μ D t β φ + ε 2 φ = φ γ γ + φ ρ ρ + φ σ σ + g ( γ , ρ , σ , t ) ,

where φ ( γ , ρ , σ , 0 ) = f 1 ( γ , ρ , σ ) and φ t ( γ , ρ , σ , 0 ) = f 2 ( γ , ρ , σ ) .

There exist different approaches to tackle FHTEs, and one such way is to apply an integral transform on the equation and obtain an iterative solution. Several integral transforms exist, such as Sumudu transform [24], natural transform [25], Shehu transform [26], and Elzaki transform [27]. These transforms can be applied on various techniques, such as homotopy perturbation method [28], ADM [29], reduced differential transform method [30], and generalized differential transform method [31] to obtain solutions to FHTEs. For example, Laplace Transform has been used for solving telegraph equations by implementing q-Homotopy Analysis Transform Method [32]. Natural transform was developed by Khan and Khan [25] in 2008 and was used to solve a certain kind of the fluid flow problem. Since then, it has found its application in many different cases, one such case being natural transform decomposition method (NTDM). NTDM has been used to solve fractional order partial differential equations [33] and Burgers’ equations [34]. In the present article, natural transform would be used to obtain an iterative semi analytical solution to FHTEs. Fractional order has been considered because of it being a more generalized form of hyperbolic telegraph equations, which means the integer order solutions can also be obtained using the appropriate value of fractional order. The approach is based on the one used in solving FHTEs using Shehu transform [22]. When developing the general formula, natural transform is applied on the equation. Linear and nonlinear operators are separated into sum of terms inverse natural transform is applied, which is then used to develop an iterative scheme (Tables 1 and 2).

Table 1

Natural transform of common functions [36]

F ( t ) NT [ F ( t ) ] = Q ( s , v )
1 1 1 s
2 t v s 2
3 t n − 1 Γ ( n ) v n − 1 s n
4 sin at a v s 2 + ( av ) 2
5 e at 1 s − av
6 t n − 1 e at Γ ( n ) v n − 1 ( s − av ) n
7 cos at s s 2 + ( av ) 2
Table 2

Inverse natural transform of common functions [36]

Q ( s , v ) NT − 1 [ Q ( s , v ) ] = F ( t )
1 1 s 1
2 v s 2 t
3 v n − 1 s n t n − 1 Γ ( n )
4 v s 2 + ( av ) 2 sin at a
5 1 s − av e at
6 v n − 1 ( s − av ) n t n − 1 e at Γ ( n )
7 s s 2 + ( av ) 2 cos at

1.4 Basics of natural transform

Definition 1

Natural transform of a function [35].

NT [ φ ( t ) ] = ∫ 0 ∞ e − st φ ( vt ) d t ,

where s , v ∈ ( 0 , ∞ ) .

Definition 2

Natural transform of fractional derivative in Caputo sense [35].

NT [ D t β 0 C φ ( t ) ] = s v β NT [ φ ( t ) ] − 1 s φ ( 0 ) .

Theorem 1

Linearity property of natural transform [25].

NT [ af ( t ) + bf ( t ) ] = aNT [ f ( t ) ] + bNT [ f ( t ) ] ,

where a and b are arbitrary constants and f ( t ) is a function in t .

Theorem 2

Change of scale property of natural transform [36].

NT [ f ( at ) ] = 1 a F s a , v ,

where a is an arbitrary constant, f ( t ) is a function in t , and F ( s , v ) is the natural transform of f ( t ) .

Definition 3

Fractional derivative of a function in Caputo sense [37].

D β 0 C f ( x ) = 1 Γ ( m − β ) ∫ 0 x ( x − t ) m − β − 1 f ( m ) ( t ) d t ,

where m − 1 < β ≤ m , m ∈ N , x > 0 .

2 Development of the formula

2.1 Implementation upon 1D time-fractional telegraph equation

The form of 1D time-fractional telegraph equation is as follows [22]:

D t β φ ( γ , t ) + L [ φ ( γ , t ) ] + N [ φ ( γ , t ) ] = q ( γ , t ) ,

where L is linear operator and N is nonlinear operator. D t β φ ( γ , t ) is Caputo derivative of φ ( γ , t ) . By applying natural transform on the following equation:

NT [ D t β φ ( γ , t ) ] + NT [ L [ φ ( γ , t ) ] + N [ φ ( γ , t ) ] ] = NT [ q ( γ , t ) ]

⇒ s v β NT [ φ ( γ , t ) ] − 1 s φ ( 0 )

= NT [ q ( γ , t ) ] − NT [ L [ φ ( γ , t ) ] ] − NT [ N [ φ ( γ , t ) ] ]

⇒ NT [ φ ( γ , t ) ] = 1 s φ ( 0 ) + v s β NT [ q ( γ , t ) ] − v s β ( NT [ L [ φ ( γ , t ) ] ] + NT [ N [ φ ( γ , t ) ] ] )

⇒ φ ( γ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , t ) ] − NT − 1 v s β ( NT [ L [ φ ( γ , t ) ] ] + NT [ N [ φ ( γ , t ) ] ] ) .

Now,

L [ φ ] = L ∑ r = 0 ∞ φ r ( γ , t ) = L [ φ 0 ( γ , t ) ] + ∑ r = 1 ∞ L ∑ i = 0 r φ i ( γ , t ) − L ∑ i = 0 r − 1 φ i ( γ , t )

N [ φ ] = N ∑ r = 0 ∞ φ r ( γ , t ) = N [ φ 0 ( γ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , t ) − N ∑ i = 0 r − 1 φ i ( γ , t ) .

Therefore,

∑ k = 0 ∞ φ k ( γ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , t ) ]

− NT − 1 v s β NT L [ φ 0 ( γ , t ) ] + N [ φ 0 ( γ , t ) ] + L ∑ r = 1 ∞ φ r ( γ , t ) + N ∑ r = 1 ∞ φ r ( γ , t )

⇒ ∑ k = 0 ∞ φ k ( γ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , t ) ]

− NT − 1 v s β NT ( L [ φ 0 ( γ , t ) ] + N [ φ 0 ( γ , t ) ] )

− NT − 1 v s β NT ∑ r = 1 ∞ L [ φ r ( γ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , t ) − N ∑ i = 0 r − 1 φ i ( γ , t )

⇒ φ 0 ( γ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , t ) ]

⇒ φ 1 ( γ , t ) = − NT − 1 v s β NT ( L [ φ 0 ( γ , t ) ] + N [ φ 0 ( γ , t ) ] )

⇒ φ r + 1 ( γ , t ) = − NT − 1 v s β NT L [ φ r ( γ , t ) ] + N ∑ i = 0 r φ i ( γ , t ) − ∑ i = 0 r − 1 φ i ( γ , t )

r = 1 , 2 , 3 , 4 , 5 , …

2.2 Implementation upon 2D time-fractional telegraph equation

The form of 2D time-fractional telegraph equation is as follows [22]:

D t β φ ( γ , ρ , t ) + L [ φ ( γ , ρ , t ) ] + N [ φ ( γ , ρ , t ) ] = q ( γ , ρ , t ) .

See Appendix A.

2.3 Implementation upon 3D time-fractional telegraph equation

The form of 3D time-fractional telegraph equation is as follows [22]:

D t β φ ( γ , ρ , σ , t ) + L [ φ ( γ , ρ , σ , t ) ] + N [ φ ( γ , ρ , σ , t ) ] = q ( γ , ρ , σ , t ) :

See Appendix B.

3 Examples and calculation

Example 1. Considered following 1D time-fractional telegraph equation [22]:

(1) φ t β = φ − 2 φ t − φ γ γ ,

where φ ( γ , 0 ) = e γ and φ t ( γ , 0 ) = − 2 e γ , 0 < β ≤ 2

φ 0 ( γ , t ) = φ ( γ , 0 ) + t φ t ( γ , 0 ) = e γ − t ( 2 e γ ) = e γ ( 1 − 2 t ) .

By applying natural transform on Eq. (1), we obtain:

NT [ φ t β ] = NT [ φ − 2 φ t − φ γ γ ]

⇒ NT [ D t β φ ( γ , t ) ] = NT [ φ − 2 φ t − φ γ γ ]

⇒ φ ( γ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s β ( NT [ R [ φ ] ] )

(2) ⇒ φ 0 ( γ , t ) = NT − 1 1 s φ ( 0 ) ,

⇒ φ 0 ( γ , t ) = φ ( 0 ) NT − 1 1 s

⇒ φ 0 ( γ , t ) = φ ( 0 ) = e x ( 1 − 2 t )

(3) φ r + 1 ( γ , t ) = NT − 1 v s β ( NT [ R [ φ r ] ] ) ,

r = 0 , 1 , 2 , 3 , …

R [ φ 0 ] = φ 0 − 2 ( φ 0 ) t − ( φ 0 ) γ γ = 4 e γ

By using Eq. (3), we obtain:

φ 1 ( γ , t ) = NT − 1 v s β ( NT [ 4 e γ ] )

⇒ φ 1 ( γ , t ) = 4 e γ NT − 1 v β s β + 1

⇒ φ 1 ( γ , t ) = 4 e γ t β Γ ( β + 1 )

R [ φ 1 ] = φ 1 − 2 ( φ 1 ) t − ( φ 1 ) γ γ = − 8 e γ β t β − 1 Γ ( β + 1 ) .

By using Eq. (3), we obtain:

φ 2 ( γ , t ) = NT − 1 v s β NT − 8 e γ β t β − 1 Γ ( β + 1 )

⇒ φ 2 ( γ , t ) = − 8 e γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v s β NT t β − 1 Γ ( β )

⇒ φ 2 ( γ , t ) = − 8 e γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v 2 β − 1 s 2 β

⇒ φ 2 ( γ , t ) = − 8 e γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β )

R [ φ 2 ] = φ 2 − 2 ( φ 2 ) t − ( φ 2 ) γ γ = 16 e γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β ) .

By using Eq. (3), we obtain:

φ 3 ( γ , t ) = NT − 1 v s β NT 16 e γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β )

⇒ φ 3 ( γ , t ) = 16 e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 × v s β NT t 2 β − 2 Γ ( 2 β − 1 )

⇒ φ 3 ( γ , t ) = 16 e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 v 3 β − 2 s 3 β − 1

⇒ φ 3 ( γ , t ) = 16 e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

R [ φ 3 ] = φ 3 − 2 ( φ 3 ) t − ( φ 3 ) γ γ = − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) .

By using Eq. (3), we obtain:

φ 4 ( γ , t ) = NT − 1 v s β NT − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

⇒ φ 4 ( γ , t ) = − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v s β NT t 3 β − 3 Γ ( 3 β − 2 )

⇒ φ 4 ( γ , t ) = − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v 4 β − 3 s 4 β − 2

⇒ φ 4 ( γ , t ) = − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

R [ φ 4 ] = φ 4 − 2 ( φ 4 ) t − ( φ 4 ) γ γ = 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) .

By using Eq. (3), we obtain:

φ 5 ( γ , t ) = NT − 1 v s β NT 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

⇒ φ 5 ( γ , t ) = 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v s β NT t 4 β − 4 Γ ( 4 β − 3 )

⇒ φ 5 ( γ , t ) = 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v 5 β − 4 s 5 β − 3

⇒ φ 5 ( γ , t ) = 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 )

φ ( γ , t ) = φ 0 ( γ , t ) + φ 1 ( γ , t ) + φ 2 ( γ , t ) + φ 3 ( γ , t ) + φ 4 ( γ , t ) + φ 5 ( γ , t ) + …

⇒ φ ( γ , t ) = e γ ( 1 − 2 t ) + 4 e γ t β Γ ( β + 1 ) − 8 e γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β ) + 16 e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) − 32 e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) + 64 e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 ) − …

By considering α = 2 , the series reduces to:

φ ( γ , t ) = e γ 1 − 2 t 1 ! + ( 2 t ) 2 2 ! − ( 2 t ) 3 3 ! + ( 2 t ) 4 4 ! − ( 2 t ) 5 5 ! + ( 2 t ) 6 6 ! − …

⇒ φ ( x , t ) = e γ − 2 t .

Example 2. Consider the following 1D time-fractional telegraph equation [22]:

(4) φ t β = φ − φ t − φ γ γ ,

where φ ( γ , 0 ) = e γ and φ t ( γ , 0 ) = − e γ , 0 < β ≤ 2 .

φ 0 ( γ , t ) = φ ( γ , 0 ) + t φ t ( γ , 0 ) = e γ − t ( e γ ) = e γ ( 1 − t ) .

By applying natural transform on Eq. (4), we obtain:

NT [ φ t β ] = NT [ φ − 2 φ t − φ γ γ ]

⇒ NT [ D t β φ ( γ , t ) ] = NT [ φ − 2 φ t − φ γ γ ]

⇒ φ ( γ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s β ( NT [ R [ φ ] ] )

(5) ⇒ φ 0 ( γ , t ) = NT − 1 1 s φ ( 0 ) ,

⇒ φ 0 ( γ , t ) = φ ( 0 ) NT − 1 1 s

⇒ φ 0 ( γ , t ) = φ ( 0 ) = e x ( 1 − t )

(6) φ r + 1 ( γ , t ) = NT − 1 v s β ( NT [ R [ φ r ] ] ) ,

r = 0 , 1 , 2 , 3 , …

R [ φ 0 ] = φ 0 − ( φ 0 ) t − ( φ 0 ) γ γ = e γ .

By using Eq. (6):

φ 1 ( γ , t ) = NT − 1 v s β ( NT [ e γ ] )

⇒ φ 1 ( γ , t ) = e γ NT − 1 v β s β + 1

⇒ φ 1 ( γ , t ) = e γ t β Γ ( β + 1 )

R [ φ 1 ] = φ 1 − 2 ( φ 1 ) t − ( φ 1 ) γ γ = − e γ β t β − 1 Γ ( β + 1 ) .

By using Eq. (6):

φ 2 ( γ , t ) = NT − 1 v s β NT − e γ β t β − 1 Γ ( β + 1 )

⇒ φ 2 ( γ , t ) = − e γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v s β NT t β − 1 Γ ( β )

⇒ φ 2 ( γ , t ) = − e γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v 2 β − 1 s 2 β

⇒ φ 2 ( γ , t ) = − e γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β )

R [ φ 2 ] = φ 2 − 2 ( φ 2 ) t − ( φ 2 ) γ γ = e γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β ) .

By using Eq. (6), we obtain:

φ 3 ( γ , t ) = NT − 1 v s β NT e γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β )

⇒ φ 3 ( γ , t ) = e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 × v s β NT t 2 β − 2 Γ ( 2 β − 1 )

⇒ φ 3 ( γ , t ) = e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 v 3 β − 2 s 3 β − 1

⇒ φ 3 ( γ , t ) = e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

R [ φ 3 ] = φ 3 − 2 ( φ 3 ) t − ( φ 3 ) γ = − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) .

By using Eq. (6), we obtain:

φ 4 ( γ , t ) = NT − 1 v s β NT − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

⇒ φ 4 ( γ , t ) = − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v s β NT t 3 β − 3 Γ ( 3 β − 2 )

⇒ φ 4 ( γ , t ) = − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v 4 β − 3 s 4 β − 2

⇒ φ 4 ( γ , t ) = − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

R [ φ 4 ] = φ 4 − 2 ( φ 4 ) t − ( φ 4 ) γ γ = e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) .

By using Eq. (6), we obtain:

φ 5 ( γ , t ) = NT − 1 v s β NT e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

⇒ φ 5 ( γ , t ) = e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v s β NT t 4 β − 4 Γ ( 4 β − 3 )

⇒ φ 5 ( γ , t ) = e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v 5 β − 4 s 5 β − 3

⇒ φ 5 ( γ , t ) = e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 )

φ ( γ , t ) = φ 0 ( γ , t ) + φ 1 ( γ , t ) + φ 2 ( γ , t ) + φ 3 ( γ , t ) + φ 4 ( γ , t ) + φ 5 ( γ , t ) + …

⇒ φ ( γ , t ) = e γ ( 1 − t ) + e γ t β Γ ( β + 1 ) − e γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β ) + e γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) − e γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) + e γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 ) − … .

By substituting α = 2 , the series reduces to:

φ ( γ , t ) = e γ 1 − t 1 ! + t 2 2 ! − t 3 3 ! + t 4 4 ! − t 5 5 ! + t 6 6 ! − …

⇒ φ ( γ , t ) = e γ − t .

Example 3. Considered following nonlinear 1D time-fractional telegraph equation [22]:

(7) D t β φ = φ γ γ + φ t − φ 2 + γ φ φ γ ,

where φ ( γ , 0 ) = γ and φ t ( γ , 0 ) = γ , 0 < β ≤ 2

φ 0 ( γ , t ) = φ ( γ , 0 ) + t φ t ( γ , 0 ) = γ + t γ = γ ( 1 + t )

R [ φ ( γ , t ) ] = φ γ γ + φ t , N [ φ ( γ , t ) ] = − φ 2 + γ φ φ γ .

By applying natural transform on Eq. (7), we obtain:

NT [ D t β φ ( γ , t ) ] = NT [ φ γ γ + φ t − φ 2 + γ φ φ γ ]

⇒ φ ( γ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s β ( NT [ R [ φ ] + N [ φ ] ] )

(8) ⇒ φ 0 ( γ , t ) = NT − 1 1 s φ ( 0 ) ,

(9) φ 1 ( γ , t ) = NT − 1 v s β ( NT [ R [ φ 0 ] + N [ φ 0 ] ] ) ,

(10) φ r + 1 ( γ , t ) = NT − 1 v s β ( NT [ R [ φ r ] + N [ φ r ] ] ) ,

where r = 1 , 2 , 3 , … .

Consider Eq. (8):

φ 0 ( γ , t ) = φ ( 0 ) NT − 1 1 s .

⇒ φ 0 ( γ , t ) = φ ( 0 ) = γ ( 1 + t )

R [ φ 0 ] = ( φ 0 ) γ γ + ( φ 0 ) t = γ

N [ φ 0 ] = − ( φ 0 ) 2 + γ φ 0 ( φ 0 ) γ = 0 .

By using Eq. (9), we obtain:

φ 1 ( γ , t ) = NT − 1 v s β ( NT [ γ ] )

⇒ φ 1 ( γ , t ) = γ NT − 1 v s β ( NT [ 1 ] )

⇒ φ 1 ( γ , t ) = γ NT − 1 v β s β + 1

⇒ φ 1 ( γ , t ) = γ t β Γ ( β + 1 )

R [ φ 1 ] = ( φ 1 ) γ γ + ( φ 1 ) t = γ β t β − 1 Γ ( β + 1 )

N [ φ 1 ] = − ( φ 1 ) 2 + γ φ 1 ( φ 1 ) γ = 0 .

By using Eq. (10), we obtain:

φ 2 ( γ , t ) = NT − 1 v s β NT γ β t β − 1 Γ ( β + 1 )

⇒ φ 2 ( γ , t ) = γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v s β NT t β − 1 Γ ( β )

By using Eq. (10), we obtain:

⇒ φ 2 ( γ , t ) = γ β Γ ( β ) Γ ( β + 1 ) NT − 1 v 2 β − 1 s 2 β

⇒ φ 2 ( γ , t ) = γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β )

R [ φ 2 ] = ( φ 2 ) γ γ + ( φ 2 ) t = γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β )

N [ φ 2 ] = − ( φ 2 ) 2 + γ φ 2 ( φ 2 ) γ = 0 .

By using Eq. (10), we obtain:

φ 3 ( γ , t ) = NT − 1 v s β NT γ β ( 2 β − 1 ) Γ ( β ) t 2 β − 2 Γ ( β + 1 ) Γ ( 2 β )

⇒ φ 3 ( γ , t ) = γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 v s β NT t 2 β − 2 Γ ( 2 β − 1 )

⇒ φ 3 ( γ , t ) = γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( β + 1 ) Γ ( 2 β ) NT − 1 v 3 β − 2 s 3 β − 1

⇒ φ 3 ( γ , t ) = γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

R [ φ 3 ] = ( φ 3 ) γ γ + ( φ 3 ) t = γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

N [ φ 3 ] = − ( φ 3 ) 2 + γ φ 3 ( φ 3 ) γ = 0 .

By using Eq. (10), we obtain:

φ 4 ( γ , t ) = NT − 1 v s β NT γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 )

⇒ φ 4 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v s β NT t 3 β − 3 Γ ( 3 β − 2 )

⇒ φ 4 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) NT − 1 v 4 β − 3 s 4 β − 2

⇒ φ 4 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

R [ φ 4 ] = ( φ 4 ) γ γ + ( φ 4 ) t = γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

N [ φ 4 ] = − ( φ 4 ) 2 + γ φ 4 ( φ 4 ) γ = 0 .

By using Eq. (10), we obtain:

φ 5 ( γ , t ) = NT − 1 v s β NT γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 )

⇒ φ 5 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v s β NT t 4 β − 4 Γ ( 4 β − 3 )

⇒ φ 5 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) NT − 1 v 5 β − 4 s 5 β − 3

⇒ φ 5 ( γ , t ) = γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 )

φ ( γ , t ) = φ 0 ( γ , t ) + φ 1 ( γ , t ) + φ 2 ( γ , t ) + φ 3 ( γ , t ) + φ 4 ( γ , t ) + φ 5 ( γ , t ) + …

⇒ φ ( γ , t ) = γ ( 1 + t ) + γ t β Γ ( β + 1 ) + γ β Γ ( β ) t 2 β − 1 Γ ( β + 1 ) Γ ( 2 β ) + γ β ( 2 β − 1 ) Γ ( β ) Γ ( 2 β − 1 ) t 3 β − 2 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) + γ β ( 2 β − 1 ) ( 3 β − 2 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) t 4 β − 3 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) + γ β ( 2 β − 1 ) ( 3 β − 2 ) ( 4 β − 3 ) Γ ( β ) Γ ( 2 β − 1 ) Γ ( 3 β − 2 ) Γ ( 4 β − 3 ) t 5 β − 4 Γ ( β + 1 ) Γ ( 2 β ) Γ ( 3 β − 1 ) Γ ( 4 β − 2 ) Γ ( 5 β − 3 ) + …

By substituting α = 2 , a series solution is as follows:

φ ( γ , t ) = γ 1 + t 1 ! + t 2 2 ! + t 3 3 ! + t 4 4 ! + t 5 5 ! + t 6 6 ! + …

⇒ φ ( γ , t ) = γ e t .

Example 4. Considered following nonlinear 1D time-fractional telegraph equation [22]:

(11) D t 2 β φ + 2 D t β φ + φ = φ γ γ ,

where φ ( γ , 0 ) = e γ and φ t ( γ , 0 ) = − 2 e γ

φ 0 ( γ , t ) = φ ( γ , 0 ) + t φ t ( γ , 0 ) = e γ − t ( 2 e γ ) = e γ ( 1 − 2 t ) .

Applying natural transform on Eq. (11):

NT [ D t 2 β φ + 2 D t β φ + φ ] = NT [ φ γ γ ]

⇒ NT [ D t 2 β φ ] = NT [ ( φ γ γ − φ ) − 2 D t β φ ]

⇒ NT [ D t 2 β φ ] = NT [ R [ φ ] − 2 D t β φ ]

⇒ φ ( γ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s 2 β ( NT [ R [ φ ] − 2 D t β φ ] )

(12) ⇒ φ 0 ( γ , t ) = NT − 1 1 s φ ( 0 ) ,

⇒ φ 0 ( γ , t ) = φ ( 0 ) NT − 1 1 s

⇒ φ 0 ( γ , t ) = φ ( 0 ) = e x ( 1 − 2 t )

(13) φ r + 1 ( γ , t ) = NT − 1 v s 2 β ( NT [ R [ φ r ] − 2 D t β φ r ] ) ,

r = 0 , 1 , 2 , 3 , …

R [ φ 0 ] = ( φ 0 ) γ γ − φ 0 = 0 .

By using Eq. (13), we obtain:

φ 1 ( γ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 0 ] )

− 2 NT [ D t β φ 0 ] = − 2 s v β NT [ φ 0 ] − 1 s φ 0 ( 0 )

− 2 NT [ D t β φ 0 ] = − 2 s v β NT [ e γ ( 1 − 2 t ) ] − 1 s e γ

− 2 NT [ D t β φ 0 ] = − 2 e γ s v β NT [ 1 ] − 2 NT [ t ] − 1 s

− 2 NT [ D t β φ 0 ] = − 2 e γ s v β 1 s − 2 v s 2 − 1 s

− 2 NT [ D t β φ 0 ] = 4 e γ s β − 2 v β − 1

⇒ φ 1 ( γ , t ) = NT − 1 v s 2 β 4 e γ s β − 2 v β − 1

⇒ φ 1 ( γ , t ) = 4 e γ NT − 1 v β + 1 s β + 2

⇒ φ 1 ( γ , t ) = 4 e γ t β + 1 Γ ( β + 2 )

R [ φ 1 ] = ( φ 1 ) γ γ − φ 1 = 0 .

By using Eq. (13), we obtain:

φ 2 ( γ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 1 ] )

− 2 NT [ D t β φ 1 ] = − 2 s v β NT [ φ 1 ] − 1 s φ 1 ( 0 )

− 2 NT [ D t β φ 1 ] = − 2 s v β NT 4 e γ t β + 1 Γ ( β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 1 ] = − 8 e γ s v β NT t β + 1 Γ ( β + 2 )

− 2 NT [ D t β φ 1 ] = − 8 e γ s v β v β + 1 s β + 2

− 2 NT [ D t β φ 1 ] = − 8 e γ s − 2 v − 1

⇒ φ 2 ( γ , t ) = NT − 1 v s 2 β − 8 e γ s − 2 v − 1

⇒ φ 2 ( γ , t ) = − 8 e γ NT − 1 v 2 β + 1 s 2 β + 2

⇒ φ 2 ( γ , t ) = − 8 e γ t 2 β + 1 Γ ( 2 β + 2 )

R [ φ 2 ] = ( φ 2 ) γ γ − φ 2 = 0 .

By using Eq. (13), we obtain:

φ 3 ( γ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 2 ] )

− 2 NT [ D t β φ 2 ] = − 2 s v β NT [ φ 2 ] − 1 s φ 2 ( 0 )

− 2 NT [ D t β φ 2 ] = − 2 s v β NT − 8 e γ t 2 β + 1 Γ ( 2 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 2 ] = 16 e γ s v β NT t 2 β + 1 Γ ( 2 β + 2 )

− 2 NT [ D t β φ 2 ] = 16 e γ s v β v 2 β + 1 s 2 β + 2

− 2 NT [ D t β φ 2 ] = 16 e γ s − β − 2 v − β − 1

⇒ φ 3 ( γ , t ) = NT − 1 v s 2 β 16 e γ s − β − 2 v − β − 1

⇒ φ 3 ( γ , t ) = 16 e γ NT − 1 v 3 β + 1 s 3 β + 2

⇒ φ 3 ( γ , t ) = 16 e γ t 3 β + 1 Γ ( 3 β + 2 )

R [ φ 3 ] = ( φ 3 ) γ − φ 3 = 0 .

By using Eq. (13), we obtain:

φ 4 ( γ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 3 ] )

− 2 NT [ D t β φ 3 ] = − 2 s v β NT [ φ 3 ] − 1 s φ 3 ( 0 )

− 2 NT [ D t β φ 3 ] = − 2 s v β NT 16 e γ t 3 β + 1 Γ ( 3 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 3 ] = − 32 e γ s v β NT t 3 β + 1 Γ ( 3 β + 2 )

− 2 NT [ D t β φ 3 ] = − 32 e γ s v β v 3 β + 1 s 3 β + 2

− 2 NT [ D t β φ 3 ] = − 32 e γ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , t ) = NT − 1 v s 2 β − 32 e γ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , t ) = − 32 e γ NT − 1 v 4 β + 1 s 4 β + 2

⇒ φ 4 ( γ , t ) = − 32 e γ t 4 β + 1 Γ ( 4 β + 2 )

R [ φ 4 ] = ( φ 4 ) γ γ − φ 4 = 0 .

By using Eq. (13), we obtain:

φ 5 ( γ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 4 ] )

− 2 NT [ D t β φ 4 ] = − 2 s v β NT [ φ 4 ] − 1 s φ 4 ( 0 )

− 2 NT [ D t β φ 4 ] = − 2 s v β NT − 32 e γ t 4 β + 1 Γ ( 4 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 4 ] = 64 e γ s v β NT t 4 β + 1 Γ ( 4 β + 2 )

− 2 NT [ D t β φ 4 ] = 64 e γ s v β v 4 β + 1 s 4 β + 2

− 2 NT [ D t β φ 4 ] = 64 e γ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , t ) = NT − 1 v s 2 β 64 e γ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , t ) = 64 e γ NT − 1 v 5 β + 1 s 5 β + 2

⇒ φ 5 ( γ , t ) = 64 e γ t 5 β + 1 Γ ( 5 β + 2 )

φ ( γ , t ) = φ 0 ( γ , t ) + φ 1 ( γ , t ) + φ 2 ( γ , t ) + φ 3 ( γ , t ) + φ 4 ( γ , t ) + φ 5 ( γ , t ) + …

⇒ φ ( γ , t ) = e γ ( 1 − 2 t ) + 4 e γ t β + 1 Γ ( β + 2 ) − 8 e γ t 2 β + 1 Γ ( 2 β + 2 ) + 16 e γ t 3 β + 1 Γ ( 3 β + 2 ) − 32 e γ t 4 β + 1 Γ ( 4 β + 2 ) + 64 e γ t 5 β + 1 Γ ( 5 β + 2 ) − …

By substituting α = 1 , a series solution is obtained:

φ ( γ , t ) = e γ 1 − 2 t 1 ! + ( 2 t ) 2 2 ! − ( 2 t ) 3 3 ! + ( 2 t ) 4 4 ! − ( 2 t ) 5 5 ! + ( 2 t ) 6 6 ! − …

⇒ φ ( γ , t ) = e γ − 2 t .

Example 5. Considered following nonlinear 2D time-fractional telegraph equation [22]:

(14) D t 2 β φ + 3 D t β φ + 2 φ = φ γ γ + φ ρ ρ ,

where φ ( γ , ρ , 0 ) = e γ + ρ and φ t ( γ , ρ , 0 ) = − 3 e γ + ρ

φ 0 ( γ , ρ , t ) = φ ( γ , ρ , 0 ) + t φ t ( γ , ρ , 0 ) = e γ + ρ − 3 t ( e γ + ρ ) = e γ + ρ ( 1 − 3 t ) .

By applying natural transform on Eq. (14):

NT [ D t 2 β φ + 3 D t β φ + 2 φ ] = NT [ φ γ γ + φ ρ ρ ]

⇒ NT [ D t 2 β φ ] = NT [ ( φ γ γ + φ ρ ρ − 2 φ ) − 3 D t β φ ]

⇒ NT [ D t 2 β φ ] = NT [ R [ φ ] − 3 D t β φ ]

⇒ φ ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s 2 β ( NT [ R [ φ ] − 3 D t β φ ] )

(15) ⇒ φ 0 ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) ,

⇒ φ 0 ( γ , ρ , t ) = φ ( 0 ) NT − 1 1 s

⇒ φ 0 ( γ , ρ , t ) = φ ( 0 ) = e γ + ρ ( 1 − 3 t )

(16) φ r + 1 ( γ , ρ , t ) = NT − 1 v s 2 β ( NT [ R [ φ r ] − 3 D t β φ r ] ) ,

r = 0 , 1 , 2 , 3 , …

R [ φ 0 ] = ( φ 0 ) γ γ + ( φ 0 ) ρ ρ − 2 φ 0 = 0 .

By using Eq. (16), we obtain:

φ 1 ( γ , ρ , t ) = NT − 1 v s 2 β ( − 3 NT [ D t β φ 0 ] )

− 3 NT [ D t β φ 0 ] = − 3 s v β NT [ φ 0 ] − 1 s φ 0 ( 0 )

− 3 NT [ D t β φ 0 ] = − 3 s v β NT [ e γ + ρ ( 1 − 3 t ) ] − 1 s e x + y

− 3 NT [ D t β φ 0 ] = − 3 e γ + ρ s v β NT [ 1 ] − 3 NT [ t ] − 1 s

− 3 NT [ D t β φ 0 ] = − 3 e γ + ρ s v β 1 s − 3 v s 2 − 1 s

− 3 NT [ D t β φ 0 ] = 9 e γ + ρ s β − 2 v β − 1

⇒ φ 1 ( γ , ρ , t ) = NT − 1 v s 2 β 9 e γ + ρ s β − 2 v β − 1

⇒ φ 1 ( γ , ρ , t ) = 9 e γ + ρ NT − 1 v β + 1 s β + 2

⇒ φ 1 ( γ , ρ , t ) = 9 e γ + ρ t β + 1 Γ ( β + 2 )

R [ φ 1 ] = ( φ 1 ) γ γ + ( φ 1 ) ρ ρ − 2 φ 1 = 0 .

By using Eq. (16), we obtain:

φ 2 ( γ , ρ , t ) = NT − 1 v s 2 β ( − 3 NT [ D t β φ 1 ] )

− 3 NT [ D t β φ 1 ] = − 3 s v β NT [ φ 1 ] − 1 s φ 1 ( 0 )

− 3 NT [ D t β φ 1 ] = − 3 s v β NT 9 e γ + ρ t β + 1 Γ ( β + 2 ) − 1 s ( 0 )

− 3 NT [ D t β φ 1 ] = − 27 e γ + ρ s v β NT t β + 1 Γ ( β + 2 )

− 3 NT [ D t β φ 1 ] = − 27 e γ + ρ s v β v β + 1 s β + 2

− 3 NT [ D t β φ 1 ] = − 27 e γ + ρ s − 2 v − 1

⇒ φ 2 ( γ , ρ , t ) = NT − 1 v s 2 β − 27 e γ + ρ s − 2 v − 1

⇒ φ 2 ( γ , ρ , t ) = − 27 e γ + ρ NT − 1 v 2 β + 1 s 2 β + 2

⇒ φ 2 ( γ , ρ , t ) = − 27 e γ + ρ t 2 β + 1 Γ ( 2 β + 2 )

R [ φ 2 ] = ( φ 2 ) γ γ + ( φ 2 ) ρ ρ − 2 φ 2 = 0 .

By using Eq. (16), we obtain:

φ 3 ( γ , ρ , t ) = NT − 1 v s 2 β ( − 3 NT [ D t β φ 2 ] )

− 3 NT [ D t β φ 2 ] = − 3 s v β NT [ φ 2 ] − 1 s φ 2 ( 0 )

− 3 NT [ D t β φ 2 ] = − 3 s v β NT − 27 e γ + ρ t 2 β + 1 Γ ( 2 β + 2 ) − 1 s ( 0 )

− 3 NT [ D t β φ 2 ] = 81 e γ + ρ s v β NT t 2 β + 1 Γ ( 2 β + 2 )

− 3 NT [ D t β φ 2 ] = 81 e γ + ρ s v β v 2 β + 1 s 2 β + 2

− 3 NT [ D t β φ 2 ] = 81 e γ + ρ s − β − 2 v − β − 1

⇒ φ 3 ( γ , ρ , t ) = NT − 1 v s 2 β 81 e γ + ρ s − β − 2 v − β − 1

⇒ φ 3 ( γ , ρ , t ) = 81 e γ + ρ NT − 1 v 3 β + 1 s 3 β + 2

⇒ φ 3 ( γ , ρ , t ) = 81 e γ + ρ t 3 β + 1 Γ ( 3 β + 2 )

R [ φ 3 ] = ( φ 3 ) γ γ + ( φ 3 ) ρ ρ − 2 φ 3 = 0 .

By using Eq. (16), we obtain:

φ 4 ( γ , ρ , t ) = NT − 1 v s 2 β ( − 3 NT [ D t β φ 3 ] )

− 3 NT [ D t β φ 3 ] = − 3 s v β NT [ φ 3 ] − 1 s φ 3 ( 0 )

− 3 NT [ D t β φ 3 ] = − 3 s v β NT 81 e γ + ρ t 3 β + 1 Γ ( 3 β + 2 ) − 1 s ( 0 )

− 3 NT [ D t β φ 3 ] = − 243 e γ + ρ s v β NT t 3 β + 1 Γ ( 3 β + 2 )

− 3 NT [ D t β φ 3 ] = − 243 e γ + ρ s v β v 3 β + 1 s 3 β + 2

− 3 NT [ D t β φ 3 ] = − 243 e γ + ρ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , ρ , t ) = NT − 1 v s 2 β − 243 e γ + ρ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , ρ , t ) = − 243 e γ + ρ NT − 1 v 4 β + 1 s 4 β + 2

⇒ φ 4 ( γ , ρ , t ) = − 243 e γ + ρ t 4 β + 1 Γ ( 4 β + 2 )

R [ φ 4 ] = ( φ 4 ) γ γ + ( φ 4 ) ρ ρ − 2 φ 4 = 0 .

By using Eq. (16), we obtain:

φ 5 ( γ , ρ , t ) = NT − 1 v s 2 β ( − 3 NT [ D t β φ 4 ] )

− 3 NT [ D t β φ 4 ] = − 3 s v β NT [ φ 4 ] − 1 s φ 4 ( 0 )

− 3 NT [ D t β φ 4 ] = − 3 s v β NT − 243 e γ + ρ t 4 β + 1 Γ ( 4 β + 2 ) − 1 s ( 0 )

− 3 NT [ D t β φ 4 ] = 729 e γ + ρ s v β NT t 4 β + 1 Γ ( 4 β + 2 )

− 3 NT [ D t β φ 4 ] = 729 e γ + ρ s v β v 4 β + 1 s 4 β + 2

− 3 NT [ D t β φ 4 ] = 729 e γ + ρ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , ρ , t ) = NT − 1 v s 2 β 729 e γ + ρ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , ρ , t ) = 729 e γ + ρ NT − 1 v 5 β + 1 s 5 β + 2

⇒ φ 5 ( γ , ρ , t ) = 729 e γ + ρ t 5 β + 1 Γ ( 5 β + 2 )

φ ( γ , ρ , t ) = φ 0 ( γ , ρ , t ) + φ 1 ( γ , ρ , t ) + φ 2 ( γ , ρ , t ) + φ 3 ( γ , ρ , t ) + φ 4 ( γ , ρ , t ) + φ 5 ( γ , ρ , t ) + …

⇒ φ ( γ , ρ , t ) = e γ + ρ ( 1 − 2 t ) + 9 e γ + ρ t β + 1 Γ ( β + 2 ) − 27 e γ + ρ t 2 β + 1 Γ ( 2 β + 2 ) + 81 e γ + ρ t 3 β + 1 Γ ( 3 β + 2 ) − 243 e γ + ρ t 4 β + 1 Γ ( 4 β + 2 ) + 729 e γ + ρ t 5 β + 1 Γ ( 5 β + 2 ) − …

By substituting α = 1 , a series solution is obtained:

φ ( γ , ρ , t ) = e γ + ρ 1 − 3 t 1 ! + ( 3 t ) 2 2 ! − ( 3 t ) 3 3 ! + ( 3 t ) 4 4 ! − ( 3 t ) 5 5 ! + ( 3 t ) 6 6 ! − …

⇒ φ ( x , y , t ) = e γ + ρ − 3 t .

Example 6. Considered following nonlinear 3D time-fractional telegraph equation [22]:

(17) D t 2 β φ + 2 D t β φ + 3 φ = φ γ γ + φ ρ ρ + φ σ σ ,

where φ ( γ , ρ , σ , 0 ) = sinh γ sinh ρ sinh σ and φ t ( γ , ρ , σ , 0 ) = − sinh γ sinh ρ sinh σ , 0 < β ≤ 1 .

φ 0 ( γ , ρ , σ , t ) = φ ( γ , ρ , σ , 0 ) + t φ t ( γ , ρ , σ , 0 ) = sinh γ sinh ρ sinh σ − t ( sinh γ sinh ρ sinh σ ) = sinh γ sinh ρ sinh σ ( 1 − t ) .

By applying natural transform on Eq. (17), we obtain:

NT [ D t 2 β φ + 2 D t β φ + 3 φ ] = NT [ φ γ γ + φ ρ ρ + φ σ σ ]

⇒ NT [ D t 2 β φ ] = NT [ ( φ γ γ + φ ρ ρ + φ σ σ − 3 φ ) − 2 D t β φ ]

⇒ NT [ D t 2 β φ ] = NT [ R [ φ ] − 2 D t β φ ]

⇒ φ ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) + NT − 1 v s 2 β ( NT [ R [ φ ] − 2 D t β φ ] )

(18) ⇒ φ 0 ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) ,

⇒ φ 0 ( γ , ρ , σ , t ) = φ ( 0 ) NT − 1 1 s

⇒ φ 0 ( γ , ρ , σ , t ) = φ ( 0 ) = sinh γ sinh ρ sinh σ ( 1 − t )

(19) φ r + 1 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( NT [ R [ φ r ] − 2 D t β φ r ] ) ,

r = 0 , 1 , 2 , 3 , …

R [ φ 0 ] = ( φ 0 ) γ γ + ( φ 0 ) ρ ρ + ( φ 0 ) σ σ − 3 φ 0 = 0 .

By using Eq. (19), we obtain:

φ 1 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 0 ] )

− 2 NT [ D t β φ 0 ] = − 2 s v β NT [ φ 0 ] − 1 s φ 0 ( 0 )

− 2 NT [ D t β φ 0 ] = − 2 s v β NT [ sinh γ sinh ρ sinh σ ( 1 − t ) ] − 1 s sinh γ sinh ρ sinh σ

− 2 NT [ D t β φ 0 ] = − 2 sinh γ sinh ρ sinh σ s v β NT [ 1 ] − NT [ t ] − 1 s

− 2 NT [ D t β φ 0 ] = − 2 sinh γ sinh ρ sinh σ s v β 1 s − 1 v s 2 − 1 s

− 2 NT [ D t β φ 0 ] = 2 sinh γ sinh ρ sinh σ s β − 2 v β − 1

⇒ φ 1 ( γ , ρ , σ , t ) = NT − 1 v s 2 β 2 sinh γ sinh ρ sinh σ s β − 2 v β − 1

⇒ φ 1 ( γ , ρ , σ , t ) = 2 sinh γ sinh ρ sinh σ NT − 1 v β + 1 s β + 2

⇒ φ 1 ( γ , ρ , σ , t ) = 2 sinh γ sinh ρ sinh σ t β + 1 Γ ( β + 2 )

R [ φ 1 ] = ( φ 1 ) γ γ + ( φ 1 ) ρ ρ + ( φ 1 ) σ σ − 3 φ 1 = 0 .

By using Eq. (19), we obtain:

φ 2 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 1 ] )

− 2 NT [ D t β φ 1 ] = − 2 s v β NT [ φ 1 ] − 1 s φ 1 ( 0 )

− 2 NT [ D t β φ 1 ] = − 2 s v β NT 2 sinh γ sinh ρ sinh σ t β + 1 Γ ( β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 1 ] = − 4 sinh γ sinh ρ sinh σ s v β NT t β + 1 Γ ( β + 2 )

− 2 NT [ D t β φ 1 ] = − 4 sinh γ sinh ρ sinh σ s v β v β + 1 s β + 2

− 2 NT [ D t β φ 1 ] = − 4 sinh γ sinh ρ sinh σ s − 2 v − 1

⇒ φ 2 ( γ , ρ , σ , t ) = NT − 1 v s 2 β − 4 sinh γ sinh ρ sinh σ s − 2 v − 1

⇒ φ 2 ( γ , ρ , σ , t ) = − 4 sinh γ sinh ρ sinh σ NT − 1 v 2 β + 1 s 2 β + 2

⇒ φ 2 ( γ , ρ , σ , t ) = − 4 sinh γ sinh ρ sinh σ t 2 β + 1 Γ ( 2 β + 2 )

R [ φ 2 ] = ( φ 2 ) γ γ + ( φ 2 ) ρ ρ + ( φ 2 ) σ σ − 3 φ 2 = 0 .

By using Eq. (19), we obtain:

φ 3 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 2 ] )

− 2 NT [ D t β φ 2 ] = − 2 s v β NT [ φ 2 ] − 1 s φ 2 ( 0 )

− 2 NT [ D t β φ 2 ] = − 2 s v β NT − 4 sinh γ sinh ρ sinh σ t 2 β + 1 Γ ( 2 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 2 ] = 8 sinh γ sinh ρ sinh σ s v β NT t 2 β + 1 Γ ( 2 β + 2 )

− 2 NT [ D t β φ 2 ] = 8 sinh γ sinh ρ sinh σ s v β v 2 β + 1 s 2 β + 2

− 2 NT [ D t β φ 2 ] = 8 sinh γ sinh ρ sinh σ s − β − 2 v − β − 1

⇒ φ 3 ( γ , ρ , σ , t ) = NT − 1 v s 2 β 8 sinh γ sinh ρ sinh σ s − β − 2 v − β − 1

⇒ φ 3 ( γ , ρ , σ , t ) = 8 sinh γ sinh ρ sinh σ NT − 1 v 3 β + 1 s 3 β + 2

⇒ φ 3 ( γ , ρ , σ , t ) = 8 sinh γ sinh ρ sinh σ t 3 β + 1 Γ ( 3 β + 2 )

R [ φ 3 ] = ( φ 3 ) γ γ + ( φ 3 ) ρ ρ + ( φ 3 ) σ σ − 3 φ 3 = 0 .

By using Eq. (19), we obtain:

φ 4 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 3 ] )

− 2 NT [ D t β φ 3 ] = − 2 s v β NT [ φ 3 ] − 1 s φ 3 ( 0 )

− 2 NT [ D t β φ 3 ] = − 2 s v β NT 8 sinh γ sinh ρ sinh σ t 3 β + 1 Γ ( 3 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 3 ] = − 16 sinh γ sinh ρ sinh σ s v β NT t 3 β + 1 Γ ( 3 β + 2 )

− 2 NT [ D t β φ 3 ] = − 16 sinh γ sinh ρ sinh σ s v β v 3 β + 1 s 3 β + 2

− 2 NT [ D t β φ 3 ] = − 16 sinh γ sinh ρ sinh σ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , ρ , σ , t ) = NT − 1 v s 2 β − 16 sinh γ sinh ρ sinh σ s − 2 β − 2 v − 2 β − 1

⇒ φ 4 ( γ , ρ , σ , t ) = − 16 sinh γ sinh ρ sinh σ NT − 1 v 4 β + 1 s 4 β + 2

⇒ φ 4 ( γ , ρ , σ , t ) = − 16 sinh γ sinh ρ sinh σ t 4 β + 1 Γ ( 4 β + 2 )

R [ φ 4 ] = ( φ 4 ) γ γ + ( φ 4 ) ρ ρ + ( φ 4 ) σ σ − 3 φ 4 = 0 .

By using Eq. (19), we obtain:

φ 5 ( γ , ρ , σ , t ) = NT − 1 v s 2 β ( − 2 NT [ D t β φ 4 ] )

− 2 NT [ D t β φ 4 ] = − 2 s v β NT [ φ 4 ] − 1 s φ 4 ( 0 )

− 2 NT [ D t β φ 4 ] = − 2 s v β NT − 16 sinh γ sinh ρ sinh σ t 4 β + 1 Γ ( 4 β + 2 ) − 1 s ( 0 )

− 2 NT [ D t β φ 4 ] = 32 sinh γ sinh ρ sinh σ s v β NT t 4 β + 1 Γ ( 4 β + 2 )

− 2 NT [ D t β φ 4 ] = 32 sinh γ sinh ρ sinh σ s v β v 4 β + 1 s 4 β + 2

− 2 NT [ D t β φ 4 ] = 32 sinh γ sinh ρ sinh σ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , ρ , σ , t ) = NT − 1 v s 2 β 32 sinh γ sinh ρ sinh σ s − 3 β − 2 v − 3 β − 1

⇒ φ 5 ( γ , ρ , σ , t ) = 32 sinh γ sinh ρ sinh σ NT − 1 v 5 β + 1 s 5 β + 2

⇒ φ 5 ( γ , ρ , σ , t ) = 32 sinh γ sinh ρ sinh σ t 5 β + 1 Γ ( 5 β + 2 )

φ ( γ , ρ , σ , t ) = φ 0 ( γ , ρ , σ , t ) + φ 1 ( γ , ρ , σ , t ) + φ 2 ( γ , ρ , σ , t ) + φ 3 ( γ , ρ , σ , t ) + φ 4 ( γ , ρ , σ , t ) + φ 5 ( γ , ρ , σ , t ) + …

⇒ φ ( γ , ρ , σ , t ) = sinh γ sinh ρ sinh σ ( 1 − t ) + 2 sinh γ sinh ρ sinh σ t β + 1 Γ ( β + 2 ) − 4 sinh γ sinh ρ sinh σ t 2 β + 1 Γ ( 2 β + 2 ) + 8 sinh γ sinh ρ sinh σ t 3 β + 1 Γ ( 3 β + 2 ) − 16 sinh γ sinh ρ sinh σ t 4 β + 1 Γ ( 4 β + 2 ) + 32 sinh γ sinh ρ sinh σ t 5 β + 1 Γ ( 5 β + 2 ) − … .

By substituting α = 1 , a series solution is obtained:

φ ( γ , ρ , σ , t ) = sinh γ sinh ρ sinh σ 1 − t 1 ! + 2 t 2 2 ! − 4 t 3 3 ! + 8 t 4 4 ! − 16 t 5 5 ! + 32 t 6 6 ! − …

= sinh γ sinh ρ sinh σ 2 2 − 2 t 1 ! + 4 t 2 2 ! − 8 t 3 3 ! + 16 t 4 4 ! − 32 t 5 5 ! + 64 t 6 6 ! − …

= sinh γ sinh ρ sinh σ 2 1 + 1 − 2 t 1 ! + ( 2 t ) 2 2 ! − ( 2 t ) 3 3 ! + ( 2 t ) 4 4 ! − ( 2 t ) 5 5 ! + ( 2 t ) 6 6 ! − …

⇒ φ ( γ , ρ , σ , t ) = sinh γ sinh ρ sinh σ 2 ( 1 + e − 2 t ) .

4 Graphical and tabular discussion

Figure 1 compares approximate and exact findings for Example 1 at t = 1, 2, and 3. At t = 1, 2, and 3, it is discovered that the approximation and exact graphs are very compatible with one another. In Figure 2, approximate and exact findings for Example 2 are matched for t = 1, 2, and 3. At t = 1, 2, and 3, it is discovered that the approximation and exact graphs are coherent with one another. Figure 3 compares approximate and exact findings for Example 3 at t = 1, 2, and 3. At t = 1, 2, and 3, it is discovered that the approximation and exact graphs are identical with one another. Regarding Example 4, approximate and exact results are matched at t = 1, 2, and 3 in Figure 4. At t = 1, 2, and 3, it is observed that the approximation and exact graphs can coexist peacefully. It is to be noted that Figures 1 and 4 are the same due to same exact and approximate solutions in Examples 1 and 4. Regarding Example 5, the contour graphs of approximate and exact findings at t = 1 are shown in Figure 5. At t = 1, it is determined that the approximated and exact graphs are identical with one another. Figure 6 shows contour graphs of approximate and exact results for Example 5 at t = 2. At t = 2, it is established that the approximate and exact graphs coexist. Regarding Example 5, the contour graphs of approximate and exact findings at t = 3 are shown in Figure 7. At t = 3, it is discovered that the approximation and exact graphs are compatible with one another.

Figure 1 Examining the differences between approximate and exact findings for Example 1 at t t = 1, 2, and 3.
Figure 1

Examining the differences between approximate and exact findings for Example 1 at t = 1, 2, and 3.

Figure 2 Comparison of approximate and exact findings for Example 2 at t t = 1, 2, and 3.
Figure 2

Comparison of approximate and exact findings for Example 2 at t = 1, 2, and 3.

Figure 3 Comparison of approximate and exact findings for Example 3 at t t = 1, 2, and 3.
Figure 3

Comparison of approximate and exact findings for Example 3 at t = 1, 2, and 3.

Figure 4 Comparison of approximate and exact findings for Example 4 at t t = 1, 2, and 3.
Figure 4

Comparison of approximate and exact findings for Example 4 at t = 1, 2, and 3.

Figure 5 Comparison of findings for Example 5 at t t = 1 between approximate and exact outcomes.
Figure 5

Comparison of findings for Example 5 at t = 1 between approximate and exact outcomes.

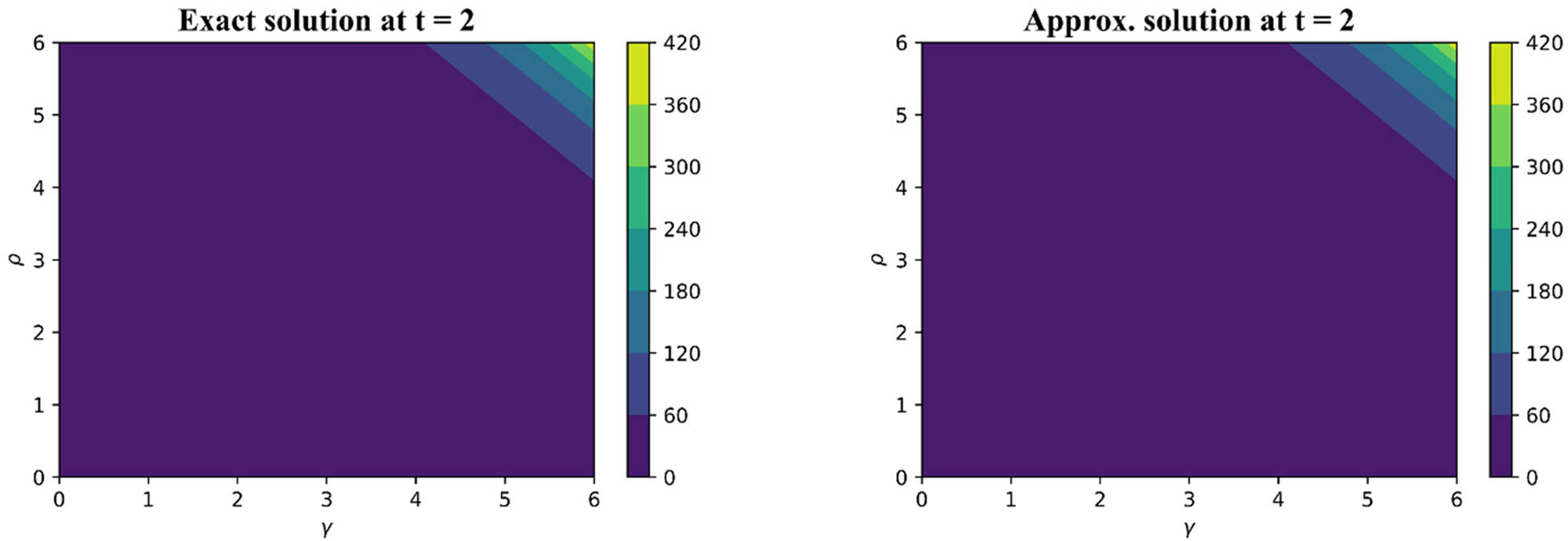
Figure 6 A comparison of roughly and precise outcomes for Example 5 at t t = 2.
Figure 6

A comparison of roughly and precise outcomes for Example 5 at t = 2.

Figure 7 Comparison of findings for Example 5 at t t = 3 between approximate and exact outcomes.
Figure 7

Comparison of findings for Example 5 at t = 3 between approximate and exact outcomes.

We define N as the number of terms in the series solution, thus making it a parameter for convergence. Each graph considers N = 35 , and each table considers the same range for the variables as considered in the graphs of the respective examples. In Table 3, the absolute value of L ∞ error at t = 1.1 , 1.2 , and 1.3 regarding Examples 1 and 4 has been provided. As N is increased, the error reduces up to 10 − 15 . In Table 4, the absolute value of L ∞ error at t = 1.1 , 1.2 , and 1.3 regarding Example 2 has been provided. As N is increased to 30, the error is reduced up to 10 − 16 . In Table 5, the absolute value of L ∞ error at t = 1.1 , 1.2 , and 1.3 regarding Example 3 has been provided. As N is increased to 30, the error is reduced up to 10 − 16 . In Table 6, the absolute value of L ∞ error at t = 0.1 , 0.2 , and 0.3 regarding Example 2 has been provided. As N is increased to 20, the error is reduced up to 10 − 11 . It is confirmed that the suggested approach produces convergent solutions with a respectable order of convergence over a wide variety of time levels.

Table 3

Analysis of the errors in Examples 1 and 4

N L ∞ e rror
t = 1.1 t = 1.2 t = 1.3
10 3 . 35618 × 10 − 4 8 . 6161 × 10 − 4 2 . 049098 × 10 − 3
20 7 . 48457 × 10 − 13 4 . 62771 × 10 − 12 2 . 46437 × 10 − 11
30 1 . 97065 × 10 − 15 3 . 02536 × 10 − 15 2 . 7478 × 10 − 15
↓ ↓ ↓
Up to 10 − 15 Up to 10 − 15 Up to 10 − 15
Table 4

Analysis of the errors in Example 2

N L ∞ e rror
t = 1.1 t = 1.2 t = 1.3
10 1 . 7788 × 10 − 7 4 . 59681 × 10 − 7 1 . 10032 × 10 − 6
20 1 . 11022 × 10 − 15 6 . 66134 × 10 − 16 8 . 88178 × 10 − 16
30 1 . 11022 × 10 − 15 6 . 66134 × 10 − 16 8 . 88178 × 10 − 16
↓ ↓ ↓
Up to 10 − 15 Up to 10 − 16 Up to 10 − 16
Table 5

Analysis of the errors in Example 3

N L ∞ e rror
t = 1.1 t = 1.2 t = 1.3
10 7 . 863 × 10 − 8 2 . 06631 × 10 − 7 5 . 02971 × 10 − 7
20 4 . 44089 × 10 − 16 8 . 88178 × 10 − 16 8 . 88178 × 10 − 16
30 4 . 44089 × 10 − 16 8 . 88178 × 10 − 16 8 . 88178 × 10 − 16
↓ ↓ ↓
Up to 10 − 16 Up to 10 − 16 Up to 10 − 16
Table 6

Analysis of the errors in Example 5

N L ∞ e rror
t = 0.1 t = 0.2 t = 0.3
10 7 . 13044 × 10 − 9 1 . 40856 × 10 − 5 1 . 189793 × 10 − 3
15 7 . 27596 × 10 − 11 5 . 82077 × 10 − 11 1 . 32422 × 10 − 9
20 7 . 27596 × 10 − 11 5 . 82077 × 10 − 11 4 . 36557 × 10 − 11
↓ ↓ ↓
Up to 10 − 11 Up to 10 − 11 Up to 10 − 11

5 Conclusion

In the present article, the approximated and exact solutions of FHTEs in 1D, 2D, and 3D were obtained using an iterative approach using natural transform. Via graphical representation, it was observed that the approximate and exact graphs of Examples 1, 2 3, and 4 each taken at t = 1 , 2 , 3 were found to have good compatibility. Approximate and exact graphs of Example 5 taken at t = 0.1 , 0.2 , 0.3 were found to have good compatibility. Thus, it was claimed that approximate and exact solutions have good compatibility across a wide range of time levels. The absolute values of L ∞ errors were provided in tabular discussion, and convergence to the exact solution was observed. Examples 1 and 4 showed convergence up to 10 − 15 as N was increased. Example 2 showed convergence up to 10 − 16 as N was increased. Example 3 showed convergence up to 10 − 16 as N was increased. Example 5 showed convergence up to 10 − 11 as N was increased. It is thus claimed that the proposed approach is a useful method to tackle FHTEs and fractional differential equations in general.

  1. Funding information: The authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors have no conflict of interest.

  4. Data availability statement: All the data are included within the manuscript.

Appendix A

A.1 Implementation upon 2D time-fractional telegraph equation

The form of 2D time-fractional telegraph equation is as follows [22]:

D t β φ ( γ , ρ , t ) + L [ φ ( γ , ρ , t ) ] + N [ φ ( γ , ρ , t ) ] = q ( γ , ρ , t ) .

where L is linear operator and N is nonlinear operator. D t β φ ( γ , ρ , t ) is Caputo derivative of φ ( γ , ρ , t ) . By applying the natural transform on equation, we obtain:

NT [ D t β φ ( γ , ρ , t ) ] + NT [ L [ φ ( γ , ρ , t ) ] + N [ φ ( γ , ρ , t ) ] ] = NT [ q ( γ , ρ , t ) ]

⇒ s v β NT [ φ ( γ , ρ , t ) ] − 1 s φ ( 0 ) = NT [ q ( γ , ρ , t ) ] − NT [ L [ φ ( γ , ρ , t ) ] ] − NT [ N [ φ ( γ , ρ , t ) ] ]

⇒ NT [ φ ( γ , ρ , t ) ] = 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , t ) ] − v s β ( NT [ L [ φ ( γ , ρ , t ) ] ] + NT [ N [ φ ( γ , ρ , t ) ] ] )

⇒ φ ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , t ) ] − NT − 1 v s β ( NT [ L [ φ ( γ , ρ , t ) ] ] + NT [ N [ φ ( γ , ρ , t ) ] ] ) .

Now,

L [ φ ] = L ∑ r = 0 ∞ φ r ( γ , ρ , t ) = L [ φ 0 ( γ , ρ , t ) ] + ∑ r = 1 ∞ L ∑ i = 0 r φ i ( γ , ρ , t ) − L ∑ i = 0 r − 1 φ i ( γ , ρ , t )

N [ φ ] = N ∑ r = 0 ∞ φ r ( γ , ρ , t ) = N [ φ 0 ( γ , ρ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , ρ , t ) − N ∑ i = 0 r − 1 φ i ( γ , ρ , t ) .

Therefore,

∑ k = 0 ∞ φ k ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , t ) ]

− NT − 1 v s β L [ φ 0 ( γ , ρ , t ) ] + N [ φ 0 ( γ , ρ , t ) ] + L ∑ r = 1 ∞ φ r ( γ , ρ , t ) + N ∑ r = 1 ∞ φ r ( γ , ρ , t )

⇒ ∑ k = 0 ∞ φ k ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , t ) ]

− NT − 1 v s β ( L [ φ 0 ( γ , ρ , t ) ] + N [ φ 0 ( γ , ρ , t ) ] )

− NT − 1 v s β ∑ r = 1 ∞ L [ φ r ( γ , ρ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , ρ , t ) − N ∑ i = 0 r − 1 φ i ( γ , ρ , t )

⇒ φ 0 ( γ , ρ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , t ) ]

⇒ φ 1 ( γ , ρ , t ) = − NT − 1 v s β ( L [ φ 0 ( γ , ρ , t ) ] + N [ φ 0 ( γ , ρ , t ) ] )

⇒ φ r + 1 ( γ , ρ , t ) = − NT − 1 v s β L [ φ r ( γ , ρ , t ) ] + N ∑ i = 0 r φ i ( γ , ρ , t ) − ∑ i = 0 r − 1 φ i ( γ , ρ , t )

r = 1 , 2 , 3 , 4 , 5 , …

Appendix B

A.2 Implementation upon 3D time-fractional telegraph equation

The form of 3D time-fractional telegraph equation is as follows [22]:

D t β φ ( γ , ρ , σ , t ) + L [ φ ( γ , ρ , σ , t ) ] + N [ φ ( γ , ρ , σ , t ) ] = q ( γ , ρ , σ , t ) .

where L is a linear operator and N is a nonlinear operator. D t β φ ( γ , ρ , σ , t ) is Caputo derivative of φ ( x , y , z , t ) . By applying natural transform on the equation:

NT [ D t β φ ( γ , ρ , σ , t ) ] + NT [ L [ φ ( γ , ρ , σ , t ) ] + N [ φ ( γ , ρ , σ , t ) ] ] = NT [ q ( γ , ρ , σ , t ) ]

⇒ s v β NT [ φ ( γ , ρ , σ , t ) ] − 1 s φ ( 0 ) = NT [ q ( γ , ρ , σ , t ) ] − NT [ L [ φ ( γ , ρ , σ , t ) ] ] − NT [ N [ φ ( γ , ρ , σ , t ) ] ]

⇒ NT [ φ ( γ , ρ , σ , t ) ] = 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , σ , t ) ] − v s β ( NT [ L [ φ ( γ , ρ , σ , t ) ] ] + NT [ N [ φ ( γ , ρ , σ , t ) ] ] )

⇒ φ ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , σ , t ) ] − NT − 1 v s β ( NT [ L [ φ ( γ , ρ , σ , t ) ] ] + NT [ N [ φ ( γ , ρ , σ , t ) ] ] ) .

Now,

L [ φ ] = L ∑ r = 0 ∞ φ r ( γ , ρ , σ , t ) = L [ φ 0 ( γ , ρ , σ , t ) ] + ∑ r = 1 ∞ L ∑ i = 0 r φ i ( γ , ρ , σ , t ) − L ∑ i = 0 r − 1 φ i ( γ , ρ , σ , t )

N [ φ ] = N ∑ r = 0 ∞ φ r ( γ , ρ , σ , t ) = N [ φ 0 ( γ , ρ , σ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , ρ , σ , t ) − N ∑ i = 0 r − 1 φ i ( γ , ρ , σ , t ) .

Therefore,

∑ k = 0 ∞ φ k ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , σ , t ) ]

− NT − 1 v s β L [ φ 0 ( γ , ρ , σ , t ) ] + N [ φ 0 ( γ , ρ , σ , t ) ] + L ∑ r = 1 ∞ φ r ( γ , ρ , σ , t ) + N ∑ r = 1 ∞ φ r ( γ , ρ , σ , t )

⇒ ∑ k = 0 ∞ φ k ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , σ , t ) ]

− NT − 1 v s β ( L [ φ 0 ( γ , ρ , σ , t ) ] + N [ φ 0 ( γ , ρ , σ , t ) ] )

− NT − 1 v s β ∑ r = 1 ∞ L [ φ r ( γ , ρ , σ , t ) ] + ∑ r = 1 ∞ N ∑ i = 0 r φ i ( γ , ρ , σ , t ) − N ∑ i = 0 r − 1 φ i ( γ , ρ , σ , t )

⇒ φ 0 ( γ , ρ , σ , t ) = NT − 1 1 s φ ( 0 ) + v s β NT [ q ( γ , ρ , σ , t ) ]

⇒ φ 1 ( γ , ρ , σ , t ) = − NT − 1 v s β ( L [ φ 0 ( γ , ρ , σ , t ) ] + N [ φ 0 ( γ , ρ , σ , t ) ] )

⇒ φ r + 1 ( γ , ρ , σ , t ) = − NT − 1 v s β L [ φ r ( γ , ρ , σ , t ) ] + N ∑ i = 0 r φ i ( γ , ρ , σ , t ) − ∑ i = 0 r − 1 φ i ( γ , ρ , σ , t )

r = 1 , 2 , 3 , 4 , 5 , …

References

[1] Leibniz GW. Letter from Hanover, Germany to GFA L’Hospital, September 30, 1695. Math Schriften. 1849;2:301–2.Search in Google Scholar

[2] El‐Nabulsi RA, Torres DF. Necessary optimality conditions for fractional action‐like integrals of variational calculus with Riemann–Liouville derivatives of order (α, β). Math Methods Appl Sci. 2007;30(15):1931–9.10.1002/mma.879Search in Google Scholar

[3] Hilfer R, Anton L. Fractional master equations and fractal time random walks. Phys Rev E. 1995;51(2):R848.10.1103/PhysRevE.51.R848Search in Google Scholar

[4] Frederico GS, Torres DF. Fractional conservation laws in optimal control theory. Nonlinear Dyn. 2008;53:215–22.10.1007/s11071-007-9309-zSearch in Google Scholar

[5] Yi-Fei PU. Fractional differential analysis for texture of digital image. J Algorithms Comput Technol. 2007;1(3):357–80.10.1260/174830107782424075Search in Google Scholar

[6] Saad A, Brahim N. An efficient algorithm for solving the conformable time-space fractional telegraph equations. Moroccan J Pure Appl Anal. 2021;7(3):413–29.10.2478/mjpaa-2021-0028Search in Google Scholar

[7] Rezazadeh H, Kumar D, Neirameh A, Eslami M, Mirzazadeh M. Applications of three methods for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity. Pramana. 2020;94:1.10.1007/s12043-019-1881-5Search in Google Scholar

[8] Sene N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: analytical investigations via Laplace transforms. Math Model Numer Simul Appl. 2022;2(1):13–25.10.53391/mmnsa.2022.01.002Search in Google Scholar

[9] Singh J, Kumar D, Swroop R. Numerical solution of time-and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex Eng J. 2016;55(2):1753–63.10.1016/j.aej.2016.03.028Search in Google Scholar

[10] Singh BK, Kumar P. Numerical computation for time-fractional gas dynamics equations by fractional reduced differential transforms method. J Math Syst Sci. 2016;6(6):248–59.10.17265/2159-5291/2016.06.004Search in Google Scholar

[11] Khan H, Khan A, Kumam P, Baleanu D, Arif M. An approximate analytical solution of the Navier–Stokes equations within Caputo operator and Elzaki transform decomposition method. Adv Differ Equ. 2020;2020:1–23.10.1186/s13662-020-02839-ySearch in Google Scholar

[12] Shah R, Khan H, Mustafa S, Kumam P, Arif M. Analytical solutions of fractional-order diffusion equations by natural transform decomposition method. Entropy. 2019;21(6):557.10.3390/e21060557Search in Google Scholar PubMed PubMed Central

[13] Veeresha P, Yavuz M, Baishya C. A computational approach for shallow water forced Korteweg–De Vries equation on critical flow over a hole with three fractional operators. An Int J Optim Control Theories Appl (IJOCTA). 2021;11(3):52–67.10.11121/ijocta.2021.1177Search in Google Scholar

[14] Sadri K, Hosseini K, Hinçal E, Baleanu D, Salahshour S. A pseudo‐operational collocation method for variable‐order time‐space fractional KdV–Burgers–Kuramoto equation. Math Methods Appl Sci. 2023.10.1002/mma.9015Search in Google Scholar

[15] Sadri K, Hosseini K, Baleanu D, Salahshour S, Park C. Designing a matrix collocation method for fractional delay integro-differential equations with weakly singular kernels based on Vieta–Fibonacci polynomials. Fractal Fract. 2022;6(1):2.10.3390/fractalfract6010002Search in Google Scholar

[16] Hosseini K, Ilie M, Mirzazadeh M, Yusuf A, Sulaiman TA, Baleanu D, et al. An effective computational method to deal with a time-fractional nonlinear water wave equation in the Caputo sense. Math Comput Simul. 2021;187:248–60.10.1016/j.matcom.2021.02.021Search in Google Scholar

[17] Hosseini K, Ilie M, Mirzazadeh M, Baleanu D. An analytic study on the approximate solution of a nonlinear time‐fractional Cauchy reaction–diffusion equation with the Mittag–Leffler law. Math Methods Appl Sci. 2021;44(8):6247–58.10.1002/mma.7059Search in Google Scholar

[18] Khan H, Khan Q, Kumam P, Tchier F, Singh G, Sitthithakerngkiet K, et al. A new modified technique to study the dynamics of fractional hyperbolic-telegraph equations. Open Phys. 2022;20(1):764–77.10.1515/phys-2022-0072Search in Google Scholar

[19] Sweilam NH, Nagy AM, El-Sayed AA. Solving time-fractional order telegraph equation via Sinc–Legendre collocation method. Mediterr J Math. 2016;13:5119–33.10.1007/s00009-016-0796-3Search in Google Scholar

[20] Saadatmandi A, Mohabbati M. Numerical solution of fractional telegraph equation via the tau method. Math Rep. 2015;17(67):2.Search in Google Scholar

[21] Dubey RS, Goswami P, Belgacem FB. Generalized time-fractional telegraph equation analytical solution by Sumudu and Fourier transforms. J Fract Calculus Appl. 2014;5(2):52–8.Search in Google Scholar

[22] Kapoor M, Shah NA, Saleem S, Weera W. An analytical approach for fractional hyperbolic telegraph equation using Shehu transform in one, two and three dimensions. Mathematics. 2022;10(12):1961.10.3390/math10121961Search in Google Scholar

[23] Sadri K, Hosseini K, Baleanu D, Salahshour S. A high-accuracy Vieta-Fibonacci collocation scheme to solve linear time-fractional telegraph equations. Waves Random Complex Media. 2022;1–24.10.1080/17455030.2022.2135789Search in Google Scholar

[24] Watugala G. Sumudu transform: a new integral transform to solve differential equations and control engineering problems. Integr Educ. 1993 Jan 1;24(1):35–43.10.1080/0020739930240105Search in Google Scholar

[25] Khan ZH, Khan WA. N-transform-properties and applications. NUST J Eng Sci. 2008;1(1):127–33.Search in Google Scholar

[26] Maitama S, Zhao W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv preprint. arXiv:1904.11370; 2019 Apr 19.Search in Google Scholar

[27] Elzaki TM. The new integral transform Elzaki transform. Glob J Pure Appl Math. 2011;7(1):57–64.Search in Google Scholar

[28] Yıldırım A. He’s homotopy perturbation method for solving the space-and time-fractional telegraph equations. Int J Comput Math. 2010;87(13):2998–3006.10.1080/00207160902874653Search in Google Scholar

[29] Garg M, Sharma A. Solution of space-time fractional telegraph equation by Adomian decomposition method. J Inequal Spec Funct. 2011;2(1):1–7.Search in Google Scholar

[30] Srivastava VK, Awasthi MK, Kumar S. Analytical approximations of two and three dimensional time-fractional telegraphic equation by reduced differential transform method. Egypt J Basic Appl Sci. 2014;1(1):60–6.10.1016/j.ejbas.2014.01.002Search in Google Scholar

[31] Garg M, Manohar P, Kalla SL. Generalized differential transform method to space-time fractional telegraph equation. Int J Differ Equ. 2011;2011:548982.10.1155/2011/548982Search in Google Scholar

[32] Prakash A, Veeresha P, Prakasha DG, Goyal M. A homotopy technique for a fractional order multi-dimensional telegraph equation via the Laplace transform. Eur Phys J Plus. 2019;134:1–8.10.1140/epjp/i2019-12411-ySearch in Google Scholar

[33] Eltayeb H, Abdalla YT, Bachar I, Khabir MH. Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry. 2019;11(3):334.10.3390/sym11030334Search in Google Scholar

[34] Aljahdaly NH, Agarwal RP, Shah R, Botmart T. Analysis of the time fractional-order coupled burgers equations with non-singular kernel operators. Mathematics. 2021;9(18):2326.10.3390/math9182326Search in Google Scholar

[35] Zhou MX, Kanth AR, Aruna K, Raghavendar K, Rezazadeh H, Inc M, et al. Numerical solutions of time fractional Zakharov-Kuznetsov equation via natural transform decomposition method with nonsingular kernel derivatives. J Funct Spaces. 2021;2021:1–7.10.1155/2021/9884027Search in Google Scholar

[36] Belgacem FB, Silambarasan R. Theory of natural transform. Math Engg Sci Aeros. 2012;3:99–124.10.1063/1.4765477Search in Google Scholar

[37] Srivastava VK, Awasthi MK, Tamsir M. RDTM solution of Caputo time fractional-order hyperbolic telegraph equation. AIP Adv. 2013;3(3):032142.10.1063/1.4799548Search in Google Scholar
Received: 2023-02-13
Revised: 2023-03-08
Accepted: 2023-03-12
Published Online: 2023-04-28

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. The regularization of spectral methods for hyperbolic Volterra integrodifferential equations with fractional power elliptic operator
  3. Analytical and numerical study for the generalized q-deformed sinh-Gordon equation
  4. Dynamics and attitude control of space-based synthetic aperture radar
  5. A new optimal multistep optimal homotopy asymptotic method to solve nonlinear system of two biological species
  6. Dynamical aspects of transient electro-osmotic flow of Burgers' fluid with zeta potential in cylindrical tube
  7. Self-optimization examination system based on improved particle swarm optimization
  8. Overlapping grid SQLM for third-grade modified nanofluid flow deformed by porous stretchable/shrinkable Riga plate
  9. Research on indoor localization algorithm based on time unsynchronization
  10. Performance evaluation and optimization of fixture adapter for oil drilling top drives
  11. Nonlinear adaptive sliding mode control with application to quadcopters
  12. Numerical simulation of Burgers’ equations via quartic HB-spline DQM
  13. Bond performance between recycled concrete and steel bar after high temperature
  14. Deformable Laplace transform and its applications
  15. A comparative study for the numerical approximation of 1D and 2D hyperbolic telegraph equations with UAT and UAH tension B-spline DQM
  16. Numerical approximations of CNLS equations via UAH tension B-spline DQM
  17. Nonlinear numerical simulation of bond performance between recycled concrete and corroded steel bars
  18. An iterative approach using Sawi transform for fractional telegraph equation in diversified dimensions
  19. Investigation of magnetized convection for second-grade nanofluids via Prabhakar differentiation
  20. Influence of the blade size on the dynamic characteristic damage identification of wind turbine blades
  21. Cilia and electroosmosis induced double diffusive transport of hybrid nanofluids through microchannel and entropy analysis
  22. Semi-analytical approximation of time-fractional telegraph equation via natural transform in Caputo derivative
  23. Analytical solutions of fractional couple stress fluid flow for an engineering problem
  24. Simulations of fractional time-derivative against proportional time-delay for solving and investigating the generalized perturbed-KdV equation
  25. Pricing weather derivatives in an uncertain environment
  26. Variational principles for a double Rayleigh beam system undergoing vibrations and connected by a nonlinear Winkler–Pasternak elastic layer
  27. Novel soliton structures of truncated M-fractional (4+1)-dim Fokas wave model
  28. Safety decision analysis of collapse accident based on “accident tree–analytic hierarchy process”
  29. Derivation of septic B-spline function in n-dimensional to solve n-dimensional partial differential equations
  30. Development of a gray box system identification model to estimate the parameters affecting traffic accidents
  31. Homotopy analysis method for discrete quasi-reversibility mollification method of nonhomogeneous backward heat conduction problem
  32. New kink-periodic and convex–concave-periodic solutions to the modified regularized long wave equation by means of modified rational trigonometric–hyperbolic functions
  33. Explicit Chebyshev Petrov–Galerkin scheme for time-fractional fourth-order uniform Euler–Bernoulli pinned–pinned beam equation
  34. NASA DART mission: A preliminary mathematical dynamical model and its nonlinear circuit emulation
  35. Nonlinear dynamic responses of ballasted railway tracks using concrete sleepers incorporated with reinforced fibres and pre-treated crumb rubber
  36. Two-component excitation governance of giant wave clusters with the partially nonlocal nonlinearity
  37. Bifurcation analysis and control of the valve-controlled hydraulic cylinder system
  38. Engineering fault intelligent monitoring system based on Internet of Things and GIS
  39. Traveling wave solutions of the generalized scale-invariant analog of the KdV equation by tanh–coth method
  40. Electric vehicle wireless charging system for the foreign object detection with the inducted coil with magnetic field variation
  41. Dynamical structures of wave front to the fractional generalized equal width-Burgers model via two analytic schemes: Effects of parameters and fractionality
  42. Theoretical and numerical analysis of nonlinear Boussinesq equation under fractal fractional derivative
  43. Research on the artificial control method of the gas nuclei spectrum in the small-scale experimental pool under atmospheric pressure
  44. Mathematical analysis of the transmission dynamics of viral infection with effective control policies via fractional derivative
  45. On duality principles and related convex dual formulations suitable for local and global non-convex variational optimization
  46. Study on the breaking characteristics of glass-like brittle materials
  47. The construction and development of economic education model in universities based on the spatial Durbin model
  48. Homoclinic breather, periodic wave, lump solution, and M-shaped rational solutions for cold bosonic atoms in a zig-zag optical lattice
  49. Fractional insights into Zika virus transmission: Exploring preventive measures from a dynamical perspective
  50. Rapid Communication
  51. Influence of joint flexibility on buckling analysis of free–free beams
  52. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part II
  53. Research on optimization of crane fault predictive control system based on data mining
  54. Nonlinear computer image scene and target information extraction based on big data technology
  55. Nonlinear analysis and processing of software development data under Internet of things monitoring system
  56. Nonlinear remote monitoring system of manipulator based on network communication technology
  57. Nonlinear bridge deflection monitoring and prediction system based on network communication
  58. Cross-modal multi-label image classification modeling and recognition based on nonlinear
  59. Application of nonlinear clustering optimization algorithm in web data mining of cloud computing
  60. Optimization of information acquisition security of broadband carrier communication based on linear equation
  61. A review of tiger conservation studies using nonlinear trajectory: A telemetry data approach
  62. Multiwireless sensors for electrical measurement based on nonlinear improved data fusion algorithm
  63. Realization of optimization design of electromechanical integration PLC program system based on 3D model
  64. Research on nonlinear tracking and evaluation of sports 3D vision action
  65. Analysis of bridge vibration response for identification of bridge damage using BP neural network
  66. Numerical analysis of vibration response of elastic tube bundle of heat exchanger based on fluid structure coupling analysis
  67. Establishment of nonlinear network security situational awareness model based on random forest under the background of big data
  68. Research and implementation of non-linear management and monitoring system for classified information network
  69. Study of time-fractional delayed differential equations via new integral transform-based variation iteration technique
  70. Exhaustive study on post effect processing of 3D image based on nonlinear digital watermarking algorithm
  71. A versatile dynamic noise control framework based on computer simulation and modeling
  72. A novel hybrid ensemble convolutional neural network for face recognition by optimizing hyperparameters
  73. Numerical analysis of uneven settlement of highway subgrade based on nonlinear algorithm
  74. Experimental design and data analysis and optimization of mechanical condition diagnosis for transformer sets
  75. Special Issue: Reliable and Robust Fuzzy Logic Control System for Industry 4.0
  76. Framework for identifying network attacks through packet inspection using machine learning
  77. Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning
  78. Analysis of multimedia technology and mobile learning in English teaching in colleges and universities
  79. A deep learning-based mathematical modeling strategy for classifying musical genres in musical industry
  80. An effective framework to improve the managerial activities in global software development
  81. Simulation of three-dimensional temperature field in high-frequency welding based on nonlinear finite element method
  82. Multi-objective optimization model of transmission error of nonlinear dynamic load of double helical gears
  83. Fault diagnosis of electrical equipment based on virtual simulation technology
  84. Application of fractional-order nonlinear equations in coordinated control of multi-agent systems
  85. Research on railroad locomotive driving safety assistance technology based on electromechanical coupling analysis
  86. Risk assessment of computer network information using a proposed approach: Fuzzy hierarchical reasoning model based on scientific inversion parallel programming
  87. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part I
  88. The application of iterative hard threshold algorithm based on nonlinear optimal compression sensing and electronic information technology in the field of automatic control
  89. Equilibrium stability of dynamic duopoly Cournot game under heterogeneous strategies, asymmetric information, and one-way R&D spillovers
  90. Mathematical prediction model construction of network packet loss rate and nonlinear mapping user experience under the Internet of Things
  91. Target recognition and detection system based on sensor and nonlinear machine vision fusion
  92. Risk analysis of bridge ship collision based on AIS data model and nonlinear finite element
  93. Video face target detection and tracking algorithm based on nonlinear sequence Monte Carlo filtering technique
  94. Adaptive fuzzy extended state observer for a class of nonlinear systems with output constraint
https://doi.org/10.1515/nleng-2022-0289
Keywords for this article
natural transform; Caputo derivative; fractional telegraph equation; convergence analysis
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. The regularization of spectral methods for hyperbolic Volterra integrodifferential equations with fractional power elliptic operator
  3. Analytical and numerical study for the generalized q-deformed sinh-Gordon equation
  4. Dynamics and attitude control of space-based synthetic aperture radar
  5. A new optimal multistep optimal homotopy asymptotic method to solve nonlinear system of two biological species
  6. Dynamical aspects of transient electro-osmotic flow of Burgers' fluid with zeta potential in cylindrical tube
  7. Self-optimization examination system based on improved particle swarm optimization
  8. Overlapping grid SQLM for third-grade modified nanofluid flow deformed by porous stretchable/shrinkable Riga plate
  9. Research on indoor localization algorithm based on time unsynchronization
  10. Performance evaluation and optimization of fixture adapter for oil drilling top drives
  11. Nonlinear adaptive sliding mode control with application to quadcopters
  12. Numerical simulation of Burgers’ equations via quartic HB-spline DQM
  13. Bond performance between recycled concrete and steel bar after high temperature
  14. Deformable Laplace transform and its applications
  15. A comparative study for the numerical approximation of 1D and 2D hyperbolic telegraph equations with UAT and UAH tension B-spline DQM
  16. Numerical approximations of CNLS equations via UAH tension B-spline DQM
  17. Nonlinear numerical simulation of bond performance between recycled concrete and corroded steel bars
  18. An iterative approach using Sawi transform for fractional telegraph equation in diversified dimensions
  19. Investigation of magnetized convection for second-grade nanofluids via Prabhakar differentiation
  20. Influence of the blade size on the dynamic characteristic damage identification of wind turbine blades
  21. Cilia and electroosmosis induced double diffusive transport of hybrid nanofluids through microchannel and entropy analysis
  22. Semi-analytical approximation of time-fractional telegraph equation via natural transform in Caputo derivative
  23. Analytical solutions of fractional couple stress fluid flow for an engineering problem
  24. Simulations of fractional time-derivative against proportional time-delay for solving and investigating the generalized perturbed-KdV equation
  25. Pricing weather derivatives in an uncertain environment
  26. Variational principles for a double Rayleigh beam system undergoing vibrations and connected by a nonlinear Winkler–Pasternak elastic layer
  27. Novel soliton structures of truncated M-fractional (4+1)-dim Fokas wave model
  28. Safety decision analysis of collapse accident based on “accident tree–analytic hierarchy process”
  29. Derivation of septic B-spline function in n-dimensional to solve n-dimensional partial differential equations
  30. Development of a gray box system identification model to estimate the parameters affecting traffic accidents
  31. Homotopy analysis method for discrete quasi-reversibility mollification method of nonhomogeneous backward heat conduction problem
  32. New kink-periodic and convex–concave-periodic solutions to the modified regularized long wave equation by means of modified rational trigonometric–hyperbolic functions
  33. Explicit Chebyshev Petrov–Galerkin scheme for time-fractional fourth-order uniform Euler–Bernoulli pinned–pinned beam equation
  34. NASA DART mission: A preliminary mathematical dynamical model and its nonlinear circuit emulation
  35. Nonlinear dynamic responses of ballasted railway tracks using concrete sleepers incorporated with reinforced fibres and pre-treated crumb rubber
  36. Two-component excitation governance of giant wave clusters with the partially nonlocal nonlinearity
  37. Bifurcation analysis and control of the valve-controlled hydraulic cylinder system
  38. Engineering fault intelligent monitoring system based on Internet of Things and GIS
  39. Traveling wave solutions of the generalized scale-invariant analog of the KdV equation by tanh–coth method
  40. Electric vehicle wireless charging system for the foreign object detection with the inducted coil with magnetic field variation
  41. Dynamical structures of wave front to the fractional generalized equal width-Burgers model via two analytic schemes: Effects of parameters and fractionality
  42. Theoretical and numerical analysis of nonlinear Boussinesq equation under fractal fractional derivative
  43. Research on the artificial control method of the gas nuclei spectrum in the small-scale experimental pool under atmospheric pressure
  44. Mathematical analysis of the transmission dynamics of viral infection with effective control policies via fractional derivative
  45. On duality principles and related convex dual formulations suitable for local and global non-convex variational optimization
  46. Study on the breaking characteristics of glass-like brittle materials
  47. The construction and development of economic education model in universities based on the spatial Durbin model
  48. Homoclinic breather, periodic wave, lump solution, and M-shaped rational solutions for cold bosonic atoms in a zig-zag optical lattice
  49. Fractional insights into Zika virus transmission: Exploring preventive measures from a dynamical perspective
  50. Rapid Communication
  51. Influence of joint flexibility on buckling analysis of free–free beams
  52. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part II
  53. Research on optimization of crane fault predictive control system based on data mining
  54. Nonlinear computer image scene and target information extraction based on big data technology
  55. Nonlinear analysis and processing of software development data under Internet of things monitoring system
  56. Nonlinear remote monitoring system of manipulator based on network communication technology
  57. Nonlinear bridge deflection monitoring and prediction system based on network communication
  58. Cross-modal multi-label image classification modeling and recognition based on nonlinear
  59. Application of nonlinear clustering optimization algorithm in web data mining of cloud computing
  60. Optimization of information acquisition security of broadband carrier communication based on linear equation
  61. A review of tiger conservation studies using nonlinear trajectory: A telemetry data approach
  62. Multiwireless sensors for electrical measurement based on nonlinear improved data fusion algorithm
  63. Realization of optimization design of electromechanical integration PLC program system based on 3D model
  64. Research on nonlinear tracking and evaluation of sports 3D vision action
  65. Analysis of bridge vibration response for identification of bridge damage using BP neural network
  66. Numerical analysis of vibration response of elastic tube bundle of heat exchanger based on fluid structure coupling analysis
  67. Establishment of nonlinear network security situational awareness model based on random forest under the background of big data
  68. Research and implementation of non-linear management and monitoring system for classified information network
  69. Study of time-fractional delayed differential equations via new integral transform-based variation iteration technique
  70. Exhaustive study on post effect processing of 3D image based on nonlinear digital watermarking algorithm
  71. A versatile dynamic noise control framework based on computer simulation and modeling
  72. A novel hybrid ensemble convolutional neural network for face recognition by optimizing hyperparameters
  73. Numerical analysis of uneven settlement of highway subgrade based on nonlinear algorithm
  74. Experimental design and data analysis and optimization of mechanical condition diagnosis for transformer sets
  75. Special Issue: Reliable and Robust Fuzzy Logic Control System for Industry 4.0
  76. Framework for identifying network attacks through packet inspection using machine learning
  77. Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning
  78. Analysis of multimedia technology and mobile learning in English teaching in colleges and universities
  79. A deep learning-based mathematical modeling strategy for classifying musical genres in musical industry
  80. An effective framework to improve the managerial activities in global software development
  81. Simulation of three-dimensional temperature field in high-frequency welding based on nonlinear finite element method
  82. Multi-objective optimization model of transmission error of nonlinear dynamic load of double helical gears
  83. Fault diagnosis of electrical equipment based on virtual simulation technology
  84. Application of fractional-order nonlinear equations in coordinated control of multi-agent systems
  85. Research on railroad locomotive driving safety assistance technology based on electromechanical coupling analysis
  86. Risk assessment of computer network information using a proposed approach: Fuzzy hierarchical reasoning model based on scientific inversion parallel programming
  87. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part I
  88. The application of iterative hard threshold algorithm based on nonlinear optimal compression sensing and electronic information technology in the field of automatic control
  89. Equilibrium stability of dynamic duopoly Cournot game under heterogeneous strategies, asymmetric information, and one-way R&D spillovers
  90. Mathematical prediction model construction of network packet loss rate and nonlinear mapping user experience under the Internet of Things
  91. Target recognition and detection system based on sensor and nonlinear machine vision fusion
  92. Risk analysis of bridge ship collision based on AIS data model and nonlinear finite element
  93. Video face target detection and tracking algorithm based on nonlinear sequence Monte Carlo filtering technique
  94. Adaptive fuzzy extended state observer for a class of nonlinear systems with output constraint
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 25.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2022-0289/html?lang=en
Scroll to top button