Dynamical aspects of transient electro-osmotic flow of Burgers' fluid with zeta potential in cylindrical tube

Nauman Raza; Ahmad Kamal Khan; Aziz Ullah Awan; Kashif Ali Abro

doi:10.1515/nleng-2022-0256

Artikel Open Access

Dynamical aspects of transient electro-osmotic flow of Burgers' fluid with zeta potential in cylindrical tube

Nauman Raza , Ahmad Kamal Khan , Aziz Ullah Awan und Kashif Ali Abro

Veröffentlicht/Copyright: 21. Februar 2023

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 12 Heft 1

Abstract

In this article, we consider the flow of a Burgers’ fluid of transient electro-osmotic type in a small tube with a circular cross-section. Analytical results are found for the transient velocity and, electric potential profile by solving the Navier–Stokes and the linearized Poisson–Boltzmann equations. Moreover, these equations are solved with the help of the integral transform method. We consider cases in which the velocity of the fluid changes with time and those in which the velocity of the fluid does not change with time. Furthermore, special results for classical fluids such as Newtonian, second grade, Maxwell, and Oldroyd-B fluids are obtained as the particular cases of the outcomes of this work and that these results actually strengthen the results of the solution. This study of the nonlinear problem of Burgers’ fluid in a specified physical model will help us to understand the behavior of blood clotting and the block of any kind of problem in which this type of fluid is used. The solution of the complex velocity profile of Burgers’ fluid will help us in the future to solve the problems in which this transient electro-osmotic type of small tube is involved. At the end, numerical results are shown graphically that can help us to understand the complex behavior of the Burgers’ fluid, and also the analysis of the Burgers’ fluid shows dissimilarity with other fluids that are considered in this work.

Keywords: Burgers’ fluid; integral transform; electro-osmotic; transient flow

Nomenclature
Physical quantity	Symbol	SI units
Velocity vector	V →	m s − 1
Force vector of the external body	F →	N
Cauchy stress tensor	σ	N m − 2
Fluid density	ρ	kg m − 3
Unit tensor	I	—
Extra stress tensor	T	N m − 2
Dynamic viscosity	μ	N sm − 2
Pressure	P	N m − 2
Tensor transpose	τ	—
Relaxation time	λ 1	s
New material parameter	λ 2	1 / s 2
Retardation time	λ 3	s
Circular tube radius	R	m
Time	t	s
Dielectric constant	ε	—
Zeta potential on tube wall	Ψ w	m 2 V − 1 s − 1
Outer electric field	( E 0 )	N C − 1
Component of velocity field	ω	ms − 1
Potential distribution	Ψ	V
Net charge density	ρ e	cm − 3
Valence of ion	z v	—
Fundamental charge	e	C
Boltzmann constant	k B	J K − 1
Absolute temperature	ϒ	K
Electric double layer (EDL) thickness	κ − 1	m
Debye–Hückel parameter	κ = ( 2 z ν 2 e 2 n 0 ε k B T ) 1 / 2	—
Zero order modified bessel function	I 0	—
Bessel function of first kind	J 0	—
Radial coordinate	r	m

1 Introduction

Recently, electro-osmotic flow (EOF) has become a more attractive topic in microfluid because of its operational advantages such as high reliability, better control flow, and low noise, and has found applications in the majority of fields such as biological analyses, chemical, and medical diagnoses. On the basis of the study of EOF, several authors attract our attention to the non-Newtonian fluid [1–3]. Many significant contributions such as articles and books are published in the literature. The first book about electro-osmosis of polymer solutions [4] was published in 2017. Furthermore, many research articles in the literature have been published to discuss electro-osmosis flow. We only discuss and cited those article that is nearly related to our research work.

Many researchers have shown great interest in electrokinetic microflows of non-Newtonian biofluids. The impact of EOF in the field of non-Newtonian fluids was first studied by Das and Chakraborty [5,6]. In their study, the non-Newtonian flow of a fluid in a rectangular small channel is affected by electrokinetic influences. For a similar model of non-Newtonian fluid, Zhao and Yang [7,8] derive the generalized Smoluchowski velocity with zeta random potential over a surface for electro-osmosis. Bandopadhyay and Chakraborty [9] impart the dynamical interchange between consolidated dissipative and elastic conduct of restricted flow by using Fourier transform. They proposed that the variability of EOF is affected by the size of both the ions and the channel. Wang and Zhao [10] introduced the solution of a generalized Maxwell fluid flow of transient electro-osmotic type with fractional derivative in a narrow capillary tube. After the study of this technique, Zhao et al. [11] analyzed the EOF of Oldroyd-B fluid through cylindrical geometry and obtained the solution with the help of an integral transform method. Most research work in EOF is the state of steady flow [12,13]. Berg and Ladipo [14] studied the flow problem with unlimited cylindrical pores in a surface of uniform charge density. Chang [15] studied the flow of transient EOF containing the salt-free medium by a cylindrical microcapillary for both constant potential surface and constant charge surface, and the exact solution of transient EOF velocity field and the potential electric distribution was computed by using the nonlinear Navier–Stokes and the Poisson–Boltzmann equations. The model of EOF flows with the application of a stepwise voltage in a broad capillary, and both aperiodical and periodical flow schemes were inspected by Mishchuk and Gonzlez-Caballero [16]. Some of the authors recently also studied the mass transport process of different fluid flows under magnetic effects [17,18]. We have studied the dynamic aspect of transient electro-osmotic flow with zeta potential combined in the same model, but before this, these models were studied separately as just traveling waves [19,20], dynamic aspects of some biological models [21], or in the thermal conductance of nanofluids [22].

In this article, the non-Newtonian behavior of biofluids is modeled by the Burgers’ constitutive equation, and then we find the analytical results for the electric potential and transient velocity profile by solving the linearized Poisson–Boltzmann and Navier–Stokes equations. Moreover, these equations are solved with the help of the integral transform technique. The motivation behind this work is to find the solution of the unsteady electro-osmotic flow of Burger fluid in a circular cross-sectional tube.

2 Mathematical modeling of the problem

The continuity equation for a fluid of constant density is

(1) ∇ ⋅ V → = 0 ,

and the equation of Cauchy momentum (C.M) in general form is

(2) ρ ( V → ⋅ ∇ ) V → + ρ ∂ V → ∂ t = ∇ ⋅ σ + F → ,

where V → , F → , σ , ρ , and ∇ are the velocity vector, force vector of the extremal body, the Cauchy stress tensor, the fluid density, and gradient operator, respectively. For a Burgers’ fluid, the Cauchy stress tensor σ is

(3) σ = − P I + T ,

(4) 1 + λ 1 D D t + λ 2 D 2 D 2 t T = μ 1 + λ 3 D D t A 1 ,

(5) A 1 = ∇ V → + ( ∇ V → ) τ ,

(6) D T D t = ( V → ⋅ ∇ ) T − ( ∇ V → ) . T − T . ( ∇ V → ) τ + ∂ T ∂ t ,

where I , T , μ , P , and the superscript τ are the unit tensor, extra stress tensor, dynamic viscosity, pressure, and tensor transpose, respectively. Also λ 1 , λ 3 ( < λ 1 ), and λ 2 are generalized relaxation time, retardation times, and the new material parameters of the Burgers’ fluid. The physical parameters mentioned earlier actually build the entire model and allow us to test a variety of different solutions based on parameter changes. Understanding these parameters is far more important than understanding the solution to understanding the use of this model in engineering and biomedical applications.

This model incorporates the Oldroyd-B display (for λ 2 = 0 ), Maxwell model (for λ 2 = λ 3 = 0 ), and the model of Newtonian fluid (when λ 1 = λ 2 = λ 3 = 0 ) as particular cases. In some particular flows, like those considered here, the conditions look like those for second grade fluids (whenever λ 1 = λ 2 = 0 ).

Consider a straight tube with a circular cross-section of radius R . The tube carries the EOF at rest ( t ≤ 0 ) with dielectric constant ε . A zeta potential Ψ w with uniform charge is applied on the wall of tube. As a result of electro-osmosis, when an outer electric field ( E 0 ) is connected along the axial direction, the fluid in the tube begins to move.

We will use polar coordinates ( r , θ , z ) . We consider the distribution of the velocity field as

(7) ( 0 , 0 , ω ( r , t ) ) , 0 ≤ r ≤ R , t > 0 ,

with initial condition

(8) ω ( r , 0 ) = 0 , 0 ≤ r ≤ R ,

and the condition given in Eq. (1) is fulfilled naturally.

As indicated by the theory of electrostatics, the relationship between the potential distribution Ψ and net charge density ρ e , which is stated by the Poison condition, is

(9) ∇ 2 Ψ = 1 r ∂ ∂ r r ∂ Ψ ∂ r + 1 r 2 ∂ 2 Ψ ∂ θ 2 + ∂ 2 Ψ ∂ z 2 = − ρ e ε .

On the tube wall, the boundary condition is the zeta potential Ψ w , which is given as follows:

(10) Ψ ( R , θ ) = Ψ w , ∂ Ψ ∂ r r = 0 = 0 .

In the present investigation, the charge dispersion is not influenced by t in the Debye layer, i.e., the tube divider has constant E 0 . At that point, the equation of motion reduces to

(11) ρ ∂ ω ∂ t = 1 r ∂ ∂ r ( r T r z ) − ρ e E 0 − ∂ P ∂ z ,

where the initial and boundary conditions are as follows:

(12) ω ( r , 0 ) = ∂ ω ( r , t ) ∂ t t = 0 = 0 ,

(13) ω ( r , t ) = 0 , r = R .

3 Exact solution for the model

Considering the limited ionic size, we ignore all nonelectro-static connections between the ions, i.e., here we consider the particles to be point sized. For of Ψ of the EDL, the Debye–Hückel approximation can be utilized effectively. So, we have the linearized ρ (charge density)

(14) ρ = − 2 z ν 2 e 2 n 0 Ψ k B ϒ ,

where z v , e , k B , and ϒ are the valence of ions, fundamental charge, Boltzmann constant, and absolute temperature, respectively.

By using the approximation of the Debye–Hückel, [23,24], Eq. (9) is linearized as follows:

(15) 1 r ∂ ∂ r r ∂ Ψ ∂ r = κ 2 Ψ .

Eq. (11) becomes

(16) ρ ∂ ω ∂ t = 1 r ∂ ∂ r ( r T r z ) − κ 2 ε Ψ E 0 − ∂ P ∂ z ,

here, κ − 1 denotes the EDL thickness and κ = 2 z ν 2 e 2 n 0 ε k B ϒ 1 / 2 denotes the parameter of Debye–Hückel. By picking the ( r , θ , z ) , constitutive condition of the Burgers’ fluid can be written as follows:

(17) 1 + λ 1 ∂ ∂ t + λ 2 ∂ 2 ∂ t 2 T r z = μ 1 + λ 3 ∂ ∂ t ∂ ω ∂ r .

Removing T r z from equations (16) and (17) yields

(18) 1 + λ 1 ∂ ∂ t + λ 2 ∂ 2 ∂ t 2 ρ ∂ ω ∂ t + κ 2 ε E 0 Ψ + ∂ P ∂ z = μ 1 + λ 3 ∂ ∂ t 1 r ∂ ∂ r r ∂ ω ∂ r .

The nondimensional parameters are as follows:

(19) Ψ ∗ = Ψ Ψ w , ω ∗ = ω ω s , r ∗ = r R , t ∗ = μ R 2 ρ t , ω s = ε Ψ w E 0 μ , λ 1 ∗ = λ 1 μ R 2 ρ , λ 2 ∗ = λ 2 μ R 2 ρ 2 , λ 3 ∗ = λ 3 μ R 2 ρ .

By substituting the aforementioned standardized factors into Eqs. (15) and (18) and also the conditions of initial and boundary (10), (12), and (13) results in (for ease of reading, the nondimensional symbol “ ∗ ” is discarded from now on)

(20) 1 r ∂ ∂ r ( r ∂ Ψ ∂ r ) = K 2 Ψ ,

(21) 1 + λ 1 ∂ ∂ t + λ 2 ∂ 2 ∂ t 2 ∂ ω ∂ t − K 2 Ψ + R 2 μ ω s ∂ P ∂ z = 1 + λ 3 ∂ ∂ t 1 r ∂ ∂ r r ∂ ω ∂ r ,

(22) 1 + λ 1 ∂ ∂ t + λ 2 ∂ 2 ∂ t 2 ∂ ω ∂ t − K 2 Ψ + f ( t ) = 1 + λ 3 ∂ ∂ t 1 r ∂ ∂ r r ∂ ω ∂ r ,

where

(23) f ( t ) = R 2 μ ω s ∂ P ∂ z ,

(24) Ψ ( 1 ) = 1 , ∂ Ψ ∂ r r = 0 = 0 ,

(25) ω ( r , 0 ) = ∂ ω ∂ t t = 0 = ∂ 2 ω ∂ t 2 t = 0 = 0 ,

(26) ω ( r , t ) = 0 , at r = 1 ,

and K = κ R is the nondimensional electrokinetic width.

The solution of Eqs. (20) and (24) is

(27) Ψ ( r ) = I 0 ( K r ) I 0 ( K ) .

Here, I 0 is the first kind of modified Bessel function with zero order. To obtain the exact model solution, we use the Laplace and Hankel transforms

(28) ω ¯ ( r , s ) = ∫ 0 ∞ ω ( r , t ) e − s t d t ,

(29) ω ˜ ( β m , t ) = ∫ 0 1 r ω ( r , t ) J 0 ( β m r ) d r ,

and the inverse Laplace and inverse Hakel transforms

(30) ω ( r , t ) = 1 2 π ι ∫ σ − ι ∞ σ + ι ∞ ω ( r , s ) e s t d s ,

(31) ω ( r , t ) = 2 ∑ m = 1 ∞ J 0 ( β m r ) J 1 2 ( β m ) ω ˜ ( β m , t ) ,

where the zero-order J 0 is the Bessel function of the first kind and the positive roots of J 0 ( β m ) = 0 are β m values. By substituting Ψ ( r ) into (22), and utilizing the Laplace and Hankel transforms for t and r , we obtain

(32) ω ¯ ˜ ( β m , s ) = K 2 Ψ ˜ ( β m ) s ( s + λ 1 s 2 + β m 2 + λ 3 s β m 2 + λ 2 s 3 ) − J 1 ( β m ) β m f ¯ ( s ) + λ 1 s f ¯ ( s ) + λ 2 s 2 f ¯ ( s ) − λ 2 f ( 0 ) s − λ 1 f ( 0 ) − λ 2 f ′ ( 0 ) s + λ 1 s 2 + β m 2 + λ 3 s β m 2 + λ 2 s 3 .

Now, we discuss a special case for f ( t ) . When f ( t ) = P 0 e a t , f ( 0 ) = P 0 , and f ¯ ( s ) = P 0 s − a , (where P 0 and a are the constant, for simplification),

Eq. (32) becomes

(33) ω ¯ ˜ ( β m , s ) = K 2 Ψ ˜ ( β m ) s ( s + λ 1 s 2 + β m 2 + λ 3 s β m 2 + λ 2 s 3 ) − J 1 ( β m ) β m P 0 1 + λ 1 a + λ 2 s a ( s − a ) ( s + λ 1 s 2 + β m 2 + λ 3 s β m 2 + λ 2 s 3 ) .

We can find the analytical solution by using inverse Laplace and inverse Hankel transforms:

(34) ω ( r , t ) = 2 ∑ m = 0 ∞ J 0 ( β m r ) J 1 2 ( β m ) K 2 Ψ ˜ ( β m ) β m 2 ( 1 − ω 1 ( β m , t ) ) − J 1 ( β m ) P 0 A ′ β m ( ω 2 ( β m , t ) + e a t ( a 2 λ 2 + a λ 1 + 1 ) ) ,

where

(35) ω 1 ( β m , t ) = ∑ α m = γ λ 2 α m 2 + λ 1 α m + 1 + λ 3 β m 2 1 + 2 λ 1 α m + λ 3 β m 2 + 3 λ 2 α m 2 e α m t ,

(36) ω 2 ( β m , t ) = ∑ α m = γ ( − 1 − a λ 1 + ( − α m 2 a λ 1 − α m a 2 λ 1 − a 3 λ 1 + a α m 2 λ 1 + a β m 2 − α m 2 − a α m − a 2 ) λ 2 − λ 3 β m 2 ( a λ 1 + 1 ) − λ 2 2 a 2 α m ( α m + a ) ) e t α m 3 α m 2 λ 2 + β m 2 λ 3 + 2 α m λ 1 + 1 ,

and

(37) A ′ = 1 a 3 λ 2 + a β m 2 λ 3 + a 2 λ 1 + β m 2 + a ,

where γ is the root of ( λ 2 z 3 + λ 1 z 2 + ( 1 + λ 3 β m 2 ) z + β m 2 ) . This complex type of solution is found very carefully with the help of Mathematica and Maple. Also, these results are verified numerically and shown in graphs. The roots of ( λ 2 z 3 + λ 1 z 2 + ( 1 + λ 3 β m 2 ) z + β m 2 ) can be easily found by using different values of parameters in different conditions, and on the basis of those gamma roots, our solution is validated.

4 Particular cases

4.1 Oldroyd-B fluid

4.1.1 With pressure gradient

Burgers’ fluid becomes Oldroyd-B, when λ 2 = 0 and f ( t ) ≠ 0 . In this form of Oldroyd-B fluid, the pressure gradient f ( t ) = P 0 e a t is included. After substituting these values, Eq. (32) becomes

(38) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ W ( β m , t ) J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) − 2 P 0 ∑ m = 0 ∞ J 0 ( β m r ) L m β m J 1 ( β m ) [ e − a t − U ( β m , t ) ] ,

where

(39) W ( β m , t ) = e − B m t cosh [ A m t ] − 1 + λ 3 β m 2 2 λ 1 1 A m e − B m t sinh [ A m t ] , for A m > 0 , e − B m t cos [ ∣ A m ∣ t ] − 1 + λ 3 β m 2 2 λ 1 1 ∣ A m ∣ e − B m t sin [ ∣ A m ∣ t ] , for A m < 0 ,

also

A m = λ 3 2 β m 4 − 2 ( 2 λ 1 − λ 3 ) β m 2 + 1 4 λ 1 2 , B m = 1 + λ 3 β m 2 2 λ 1 .

(40) U ( β m , t ) = 1 + λ 3 β m 2 λ 1 1 C m e − D m t sinh [ C m t ] , for C m > 0 , 1 + λ 3 β m 2 2 λ 1 1 ∣ C m ∣ e − D m t sin [ ∣ C m ∣ t ] , for C m < 0 ,

and

L m = 1 − a λ 1 a + β m 2 ( a λ 3 − 1 ) − a 2 λ 1 , C m = λ 3 2 β m 4 − 4 ( λ 1 − λ 3 ) β m 2 + 4 2 λ 1 , D m = λ 3 β m 2 + 2 2 λ 1 .

4.1.2 Without pressure gradient

The particular kind of the Burger fluid with λ 2 = 0 and f ( t ) = 0 is Oldroyd-B fluid. From Eq. (32), the exact solution can be written as follows:

(41) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ W ( β m , t ) J 0 ( β m r ) ( β m 2 + K 2 ) β m J 1 ( β m ) ,

where

A m = λ 3 2 β m 4 − 2 ( 2 λ 1 − λ 3 ) β m 2 + 1 4 λ 1 2 , B m = 1 + λ 3 β m 2 2 λ 1 .

4.2 Maxwell fluid

4.2.1 With pressure gradient

The solution for a Maxwell fluid is obtained by introducing λ 1 ≠ 0 , λ 2 = 0 , λ 3 = 0 , and f ( t ) ≠ 0 in Eq. (32), which takes the form

(42) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ W 1 ( β m , t ) J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) − 2 P 0 ∑ m = 0 ∞ J 0 ( β m r ) L 1 m β m 2 J 1 2 ( β m ) [ e − a t − U 1 m ( β m , t ) ] ,

where

(43) W 1 ( β m , t ) = e − B 1 m t cosh [ A 1 m t ] − 1 + λ 3 ¯ β m 2 2 λ 1 ¯ 1 A 1 m e − B 1 m t sinh [ A 1 m t ] , for A 1 m > 0 , e − B 1 m t cos [ ∣ A 1 m ∣ t ] − 1 + λ 3 ¯ β m 2 2 λ 1 ¯ 1 ∣ A 1 m ∣ e − B 1 m t sin [ ∣ A 1 m ∣ t ] , for A 1 m < 0 ,

and

A 1 m = 1 − 4 λ ¯ 1 β m 2 4 λ 1 2 ¯ , B 1 m = 1 2 λ 1 ¯ .

Also,

(44) U ( β m , t ) = e − t / 2 λ 1 λ 1 C 1 m sinh [ C 1 m t ] , for C 1 m > 0 , e − t / 2 λ 1 λ 1 ∣ C 1 m ∣ sin [ ∣ C 1 m ∣ t ] , for C 1 m < 0 ,

and

L 1 m = 1 − a λ 1 a 2 λ 1 + β m 2 − a , C 1 m = 1 − 4 β m 2 λ 1 4 λ 1 2 .

4.2.2 Without pressure gradient

The solution for a Maxwell fluid is obtained by introducing λ 1 ≠ 0 , λ 2 = 0 , λ 3 = 0 , and f ( t ) = 0 in Eq. (32), which takes the form

(45) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ W 1 ( β m , t ) J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) ,

where

A 1 m = 1 − 4 λ 1 β m 2 4 λ 1 2 , B 1 m = 1 2 λ 1 .

4.3 Second grade fluid

4.3.1 With pressure gradient

When λ 3 ≠ 0 , λ 1 = 0 , λ 2 = 0 , and f ( t ) ≠ 0 in Eq. (32), we obtain the second grade fluid solution as follows:

(46) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ exp { − β m 2 t 1 − λ 3 ¯ β m 2 } J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) − 2 P 0 ∑ m = 0 ∞ J 0 ( β m r ) L 2 m β m J 1 ( β m ) [ e − C 2 m t − e − a t ] ,

where

L 2 m = 1 ( a λ 3 − 1 ) β m 2 + a , C 2 m = β m 2 λ 3 β m 2 + 1 .

It is important to mentioned that the value of λ 3 will behave according to the constitutive equation of second grade fluid.

4.3.2 Without pressure gradient

When λ 3 ≠ 0 , λ 1 = 0 , λ 2 = 0 , and f ( t ) = 0 in Eq. (32), we obtain the second grade fluid solution as follows:

(47) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ exp { − β m 2 t 1 − λ 3 ¯ β m 2 } J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) .

4.4 Newtonian fluid

4.4.1 With pressure gradient

By using λ 1 = λ 2 = λ 3 = 0 , and f ( t ) ≠ 0 in Eq. (32), Burgers’ fluid is a Newtonian fluid. From Eq. (32), the exact solution can be written as follows:

(48) ω ( r , t ) = 2 K 2 ∑ m = 0 ∞ [ 1 − e − β m 2 t ] J 0 ( β m r ) β m 2 J 1 2 ( β m ) Ψ ˜ ( β m ) − 2 P 0 ∑ m = 0 ∞ J 0 ( β m r ) ( β m 2 − a ) β m J 1 ( β m ) [ e − a t − e − β m 2 t ] ,

(49) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ e − β m 2 t J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) − 2 P 0 ∑ m = 0 ∞ J 0 ( β m r ) ( β m 2 − a ) β m J 1 ( β m ) [ e − a t − e − β m 2 t ] .

4.4.2 Without pressure gradient

Burgers’ fluid with λ 1 = λ 2 = λ 3 = 0 and f ( t ) = 0 is a Newtonian fluid. From Eq. (32), the exact solution can be written as follows:

(50) ω ( r , t ) = 2 K 2 ∑ m = 0 ∞ [ 1 − e − β m 2 t ] J 0 ( β m r ) β m 2 J 1 2 ( β m ) Ψ ˜ ( β m ) ,

(51) ω ( r , t ) = 1 − I 0 ( K r ) I 0 ( K ) − 2 K 2 ∑ m = 0 ∞ e − β m 2 t J 0 ( β m r ) ( β m 2 + κ 2 ) β m J 1 ( β m ) .

The outcomes of Kang et al. [25] are similar to Eq. (52) by utilizing the technique of Green’s function. In this article the advantage of the solution is the effortlessness of Eq. (52), in which we consider the steady part as follows:

(52) = 1 − I 0 ( K r ) I 0 ( K )

with the outcome given by Rice and Whitehead [26], and the rest is the unsteady one.

5 Numerical results and discussion

To illustrate some physically interesting aspects of the derived results, the normalized velocity ω ( r , t ) as a function of nondimensional time t and dimensionless r / R are shown in plots. We can see the different behaviors (at the center of the pipe) of normalized velocity for the different values of time t and the parameter of interest. For the nonidentical values of electrokinetic width K against t , the graph of normalized velocity along the axial direction of the pipe is shown in Figure 1. Next, Figure 2 shows the behavior of normalized velocity against dimensionless r / R . The plot shows the flow in the pipe between the transient period response from steady state to t = 1.5 . Along the axial part of the pipe, the velocity is maximal when the flow becomes steady. The comparative behavior of Oldroyd-B fluid (with pressure gradient and without pressure gradient) and Burger fluid is shown in Figure 3. It is clear from the figure that the normalized velocity of Oldroyd-B fluid (without pressure gradient) along the axial direction of the pipe is greater than the fluid with pressure gradient. Similarly, the normalized velocity of Oldroyd-B fluid (with pressure gradient) is greater than the Burgers’ fluid. In Figure 4, the comparative behavior of the Maxwell fluid (with pressure gradient and without pressure gradient) and Burgers’ fluid are shown. It is clear from the figure that the normalized velocity of Maxwell fluid (without pressure gradient) along the axial direction of the pipe is greater than that of the fluid with pressure gradient. Similarly, the normalized velocity of the Maxwell fluid (with pressure gradient) is greater than that of the Burgers’ fluid. The comparative behavior of the Newtonian fluid (with pressure gradient and without pressure gradient) and the Burgers’ fluid is shown in Figure 5. It is clear from the figure that the normalized velocity of the Newtonian fluid (without pressure gradient) along the axial direction of the pipe is greater than that of the fluid with pressure gradient. Similarly, the normalized velocity of the Newtonian fluid (with pressure gradient) is greater than that of the Burgers’ fluid. Finally, in Figure 6, the comparative behavior of Oldroyd-B, Maxwell, and Newtonian fluids with Burgers’ fluid is shown. Also, Figure 6 shows the defining properties of these fluids in which the normalized velocity of Newtonian fluid is greater then than that of the Maxwell fluid and the normalized velocity of the Maxwell fluid is greater than the that of the Oldroyd-B fluid. Similarly, the normalized velocity of the Oldroyd-B fluid is greater than that of the Burgers’ fluid. It is also important to mention that the graphical results of the solution are found with the help of Stehfest’s algorithm [27,28], and graphs are illustrated with the help of MathCad.

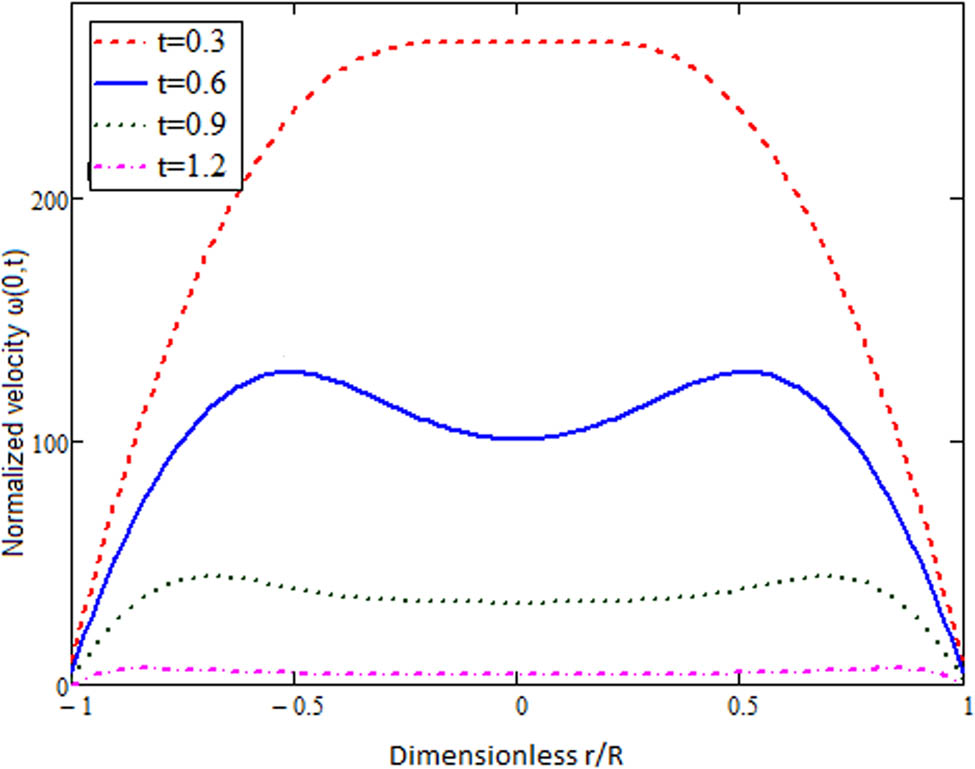
$Figure 1 In the pipe behavior of flow when λ 1 = λ 2 = 1 {\lambda }_{1}={\lambda }_{2}=1 and λ 3 = 0.5 {\lambda }_{3}=0.5 .$

Figure 1

In the pipe behavior of flow when λ 1 = λ 2 = 1 and λ 3 = 0.5 .

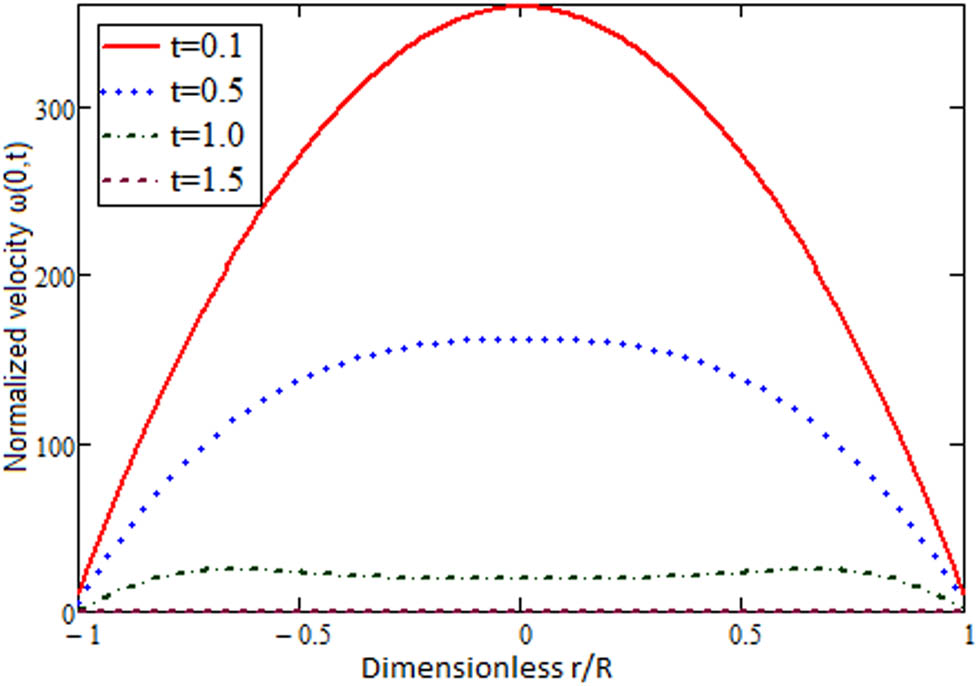
$Figure 2 In the pipe behavior of flow when λ 2 = λ 3 = 1 {\lambda }_{2}={\lambda }_{3}=1 and λ 1 = 1.5 {\lambda }_{1}=1.5 .$

Figure 2

In the pipe behavior of flow when λ 2 = λ 3 = 1 and λ 1 = 1.5 .

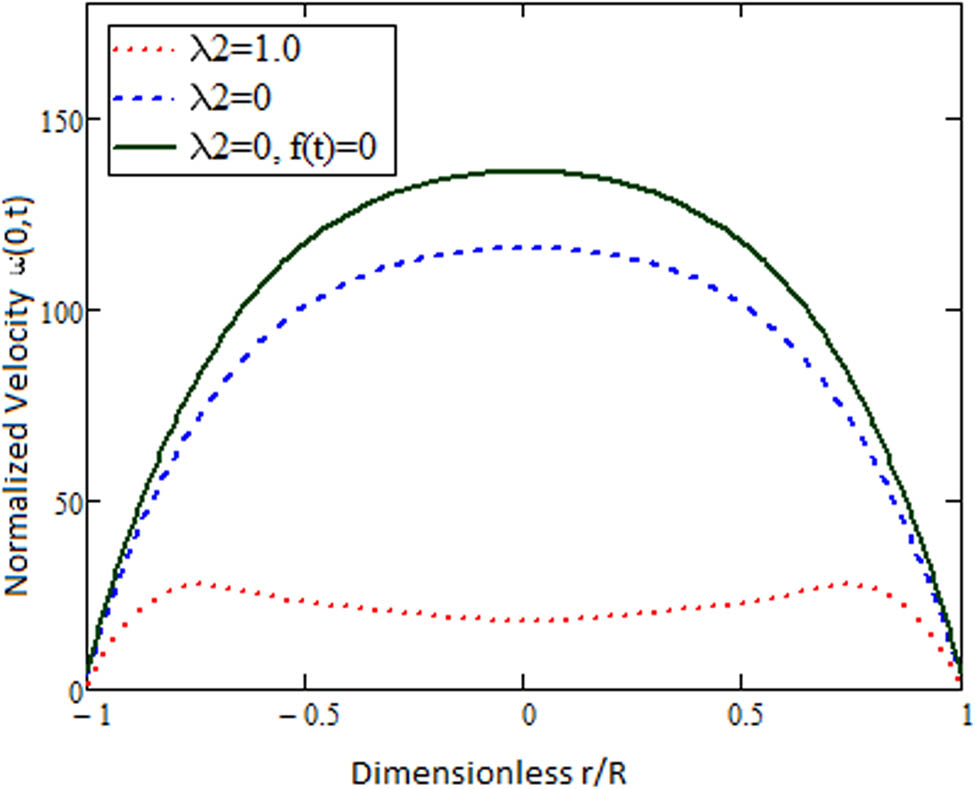
$Figure 3 Comparative behavior of Oldroyd-B fluid (with f ( t ) = 0 f\left(t)=0 and f ( t ) ≠ 0 f\left(t)\ne 0 ) and Burgers’ fluid.$

Figure 3

Comparative behavior of Oldroyd-B fluid (with f ( t ) = 0 and f ( t ) ≠ 0 ) and Burgers’ fluid.

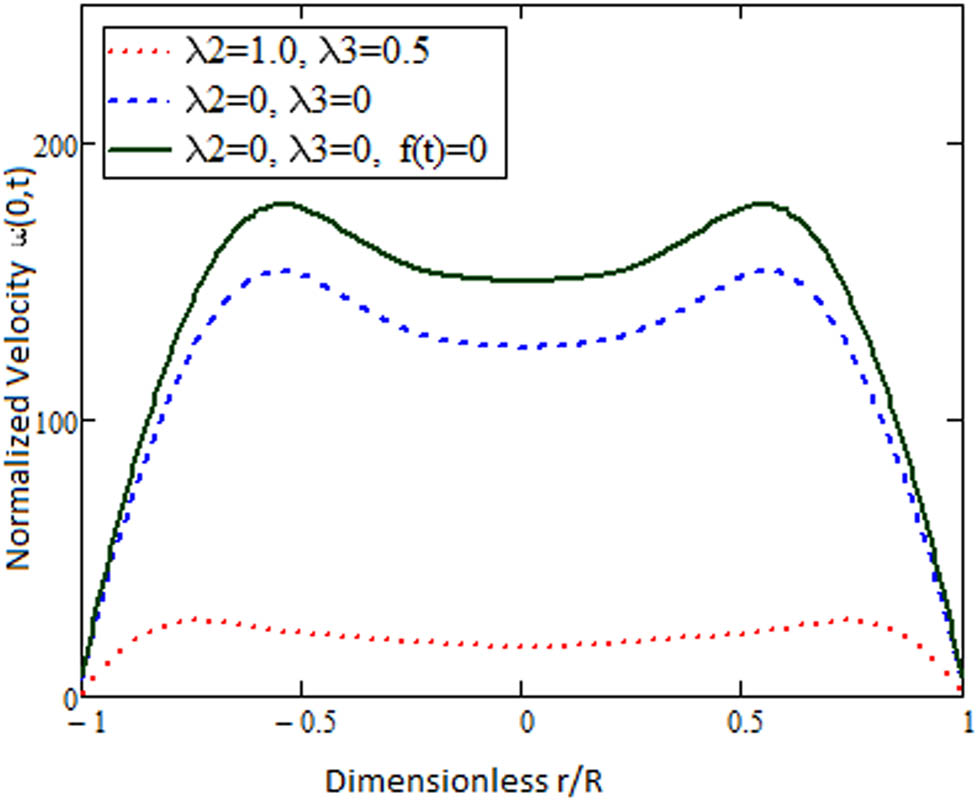
$Figure 4 Comparative behavior of Maxwell fluid (with f ( t ) = 0 f\left(t)=0 and f ( t ) ≠ 0 f\left(t)\ne 0 ) and Burgers’ fluid.$

Figure 4

Comparative behavior of Maxwell fluid (with f ( t ) = 0 and f ( t ) ≠ 0 ) and Burgers’ fluid.

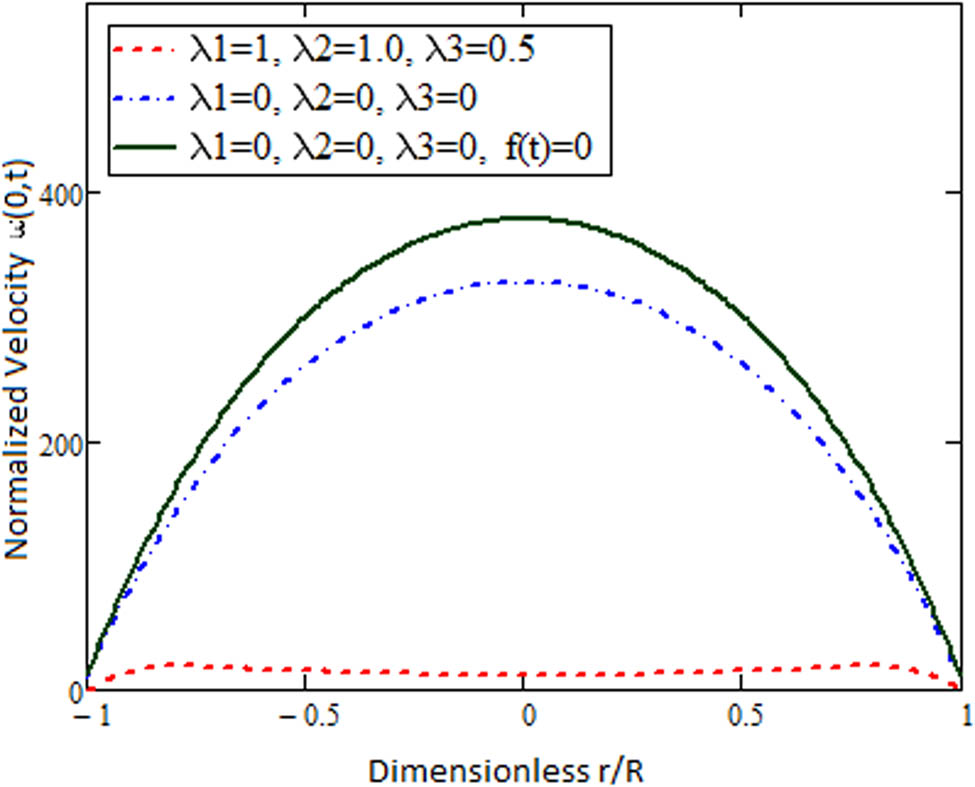
$Figure 5 Comparative behavior of the Newtonian fluid (with f ( t ) = 0 f\left(t)=0 and f ( t ) ≠ 0 f\left(t)\ne 0 ) and Burgers’ fluid.$

Figure 5

Comparative behavior of the Newtonian fluid (with f ( t ) = 0 and f ( t ) ≠ 0 ) and Burgers’ fluid.

Figure 6

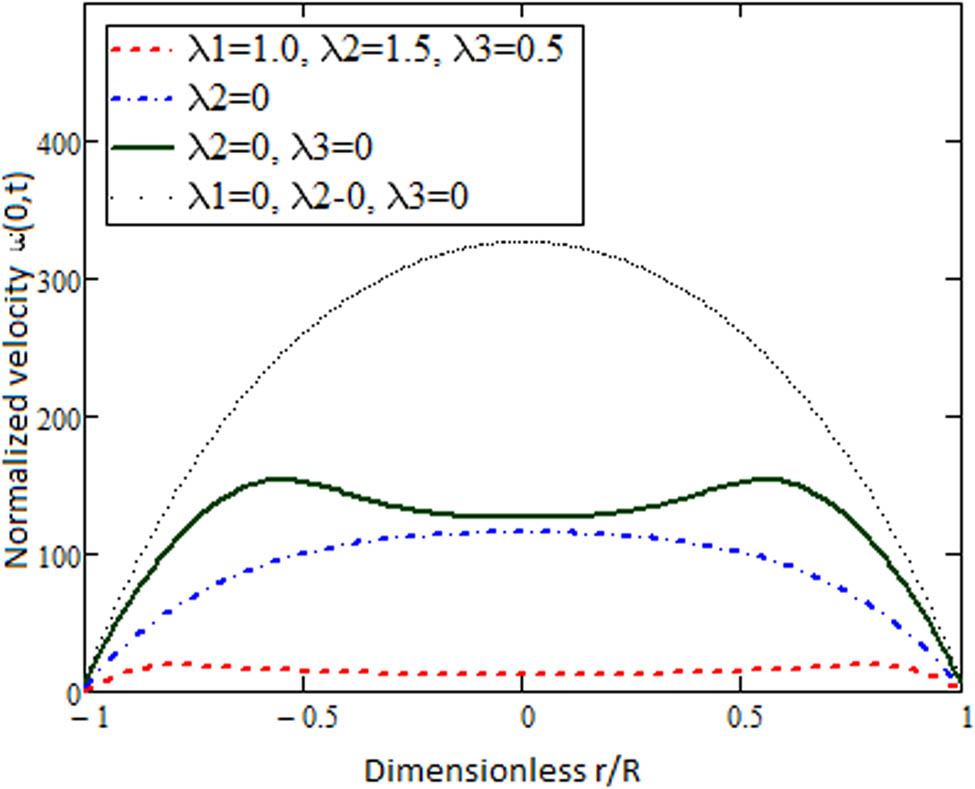
Comparative behavior of Oldroyd-B, Maxwell, Newtonian, and Burgers’ fluids.

6 Conclusion

The analytical solutions for the transient flow of a Burgers’ fluid in a small cross-section tube of electro-osmotic type with Debye–Hückel approximation have obtained in this work. Poisson–Boltzmann and the Navier–Stokes linearized equations are solved to obtain the analytical results for electric potential Ψ and normalized velocity ω profile. These equations are solved with the help of integral transform methods. The velocity can be considered in two parts, the first one in which the velocity of the fluid changes with time t and the second one in which the velocity of fluid does not change with time t . The results for classical fluids such as Oldroyd-B, Maxwell, second grade, and Newtonian fluids have obtained as a special case. After analyzing the analytical results, we noted that the normalized velocity ω ( r , t ) at the center of the tube is decreasing as we increase the time t . From this, it is clear that at the start of the flow in the Burgers’ fluid, the fluid has a steady behavior, but after the passage of time, the normalized velocity of fluid flow gradually decreases. It is also clear from the graph that the comparison of Burgers’ fluid shows high dissimilarity with other fluids in the flow behavior. Also, the different behavior of the velocity profile is obtained by introducing the pressure gradient factor. In the future, we are interested in using this model to solve some exciting problems related to engineering and biomedical research. The velocity profile of Burgers’ fluid under a specified restricted physical model will help us to use these solutions to find the blood clotting and some kinds of sensitive blocking of chemical material in laboratories.

Acknowledgments

Dr. Kashif Ali Abro is highly thankful and grateful to Mehran University of Engineering and Technology, Jamshoro, Pakistan, for generous support and facilities of this research work.

Funding information: The author states no funding involved.
Author contributions: All author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Sadeghi V, Baheri S, Arsalani N. An experimental investigation of the effect of using non-Newtonian nanofluid-graphene oxide/aqueous solution of sodium carboxymethyl cellulose-on the performance of direct absorption solar collector. Sci Iran. 2020;28(3):1284–97. 10.24200/sci.2020.54994.4024Suche in Google Scholar

[2] Rizwan M, Hassan M, Makinde OD, Bhatti MM, Marin M. Rheological modeling of metallic oxide nanoparticles containing non-newtonian nanofluids and potential investigation of heat and mass flow characteristics. Nanomaterials. 2022;12(7):1237. 10.3390/nano12071237Suche in Google Scholar PubMed PubMed Central

[3] Bhatti MM, Zeeshan A, Bashir F, Sait SM, Ellahi R. Sinusoidal motion of small particles through a Darcy-Brinkman-Forchheimer microchannel filled with non-Newtonian fluid under electro-osmotic forces. J Taibah Univ Sci. 2021;15(1):514–29.10.1080/16583655.2021.1991734Suche in Google Scholar

[4] Uematsu Y. Electro-osmosis of polymer solutions: linear and nonlinear behavior. Singapore: Springer; 2017. 10.1007/978-981-10-3424-4Suche in Google Scholar

[5] Das S, Chakraborty S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal Chim Acta. 2006;559(1):15–24. 10.1016/j.aca.2005.11.046Suche in Google Scholar

[6] Chakraborty S. Electro osmotically driven capillary transport of typical non-Newtonian biofluids in rectangular microchannels. Anal Chim Acta. 2007;605(2):175–84. 10.1016/j.aca.2007.10.049Suche in Google Scholar PubMed

[7] Zhao C, Yang C. Exact solutions for electro-osmotic flow of viscoelastic fluids in rectangular micro-channels. Appl Math Comput. 2009;211(2):502–9. 10.1016/j.amc.2009.01.068Suche in Google Scholar

[8] Zhao C, Yang C. Nonlinear Smoluchowski velocity for electroosmosis of Power-law fluids over a surface with arbitrary zeta potentials. Electrophoresis 2010;31(5):973–9. 10.1002/elps.200900564Suche in Google Scholar PubMed

[9] Bandopadhyay A, Chakraborty S. Electro kinetically induced alterations in dynamic response of visco elastic fluids in narrow confinements. Phys Rev E. 2012;85(5):056302. 10.1103/PhysRevE.85.056302Suche in Google Scholar PubMed

[10] Wang S, Zhao M. Analytical solution of the transient electro-osmotic flow of a generalized fractional Maxwell fluid in a straight pipe with a circular cross-section. Eur J Mech B Fluids 2015;54:82–6. 10.1016/j.euromechflu.2015.06.016Suche in Google Scholar

[11] Zhao M, Wang S, Wei S. Transient electro-osmotic flow of Oldroyd-B fluids in a straight pipe of circular cross section. J Non-Newtonian Fluid Mech. 2013;201:135–9. 10.1016/j.jnnfm.2013.09.002Suche in Google Scholar

[12] Dhinakaran S, Afonso AM, Alves MA, Pinho FT. Steady viscoelastic fluid flow between parallel plates under electro-osmotic forces: Phan-Thien-Tanner model. J Colloid Interface Sci. 2010;344(2):513–20. 10.1016/j.jcis.2010.01.025Suche in Google Scholar PubMed

[13] Horiuchi K, Dutta P. Joule heating effects in electroosmotically driven microchannel flows. Int J Heat Mass Transfer. 2004;47(14-16):3085–95. 10.1016/j.ijheatmasstransfer.2004.02.020Suche in Google Scholar

[14] Berg P, Ladipo K. Exact solution of an electro-osmotic flow problem in a cylindrical channel of polymer electrolyte membranes. Proc R Soc A Math Phys Eng Sci. 2009;465(2109):2663–79. 10.1098/rspa.2009.0067Suche in Google Scholar

[15] Chang SH. Transient electro-osmotic flow in cylindrical microcapillaries containing salt-free medium. Biomicrofluidics. 2009;3(1):012802. 10.1063/1.3064113Suche in Google Scholar PubMed PubMed Central

[16] Mishchuk NA, Gonzlez-Caballero F. Nonstationary electro osmotic flow in open cylindrical capillaries. Electrophoresis. 2006;27(3):650–60. 10.1002/elps.200500470Suche in Google Scholar PubMed

[17] Bhatti MM, Jun S, Khalique CM, Shahid A, Fasheng L, Mohamed MS. Lie group analysis and robust computational approach to examine mass transport process using Jeffrey fluid model. Appl Math Comput. 2022;421:126936. 10.1016/j.amc.2022.126936Suche in Google Scholar

[18] Bhatti MM, Zeeshan A, Asif MA, Ellahi R, Sait SM. Non-uniform pumping flow model for the couple stress particle-fluid under magnetic effects. Chem Eng Commun. 2021;209(8):1058–69. 10.1080/00986445.2021.1940156Suche in Google Scholar

[19] Durur H, Yokuş A, Abro KA. Computational and traveling wave analysis of Tzitzéica and Dodd-Bullough-Mikhailov equations: an exact and analytical study. Nonlinear Eng. 2021;10(1):272–81. 10.1515/nleng-2021-0021Suche in Google Scholar

[20] Yokuş A, Durur H, Abro KA. Role of shallow water waves generated by modified Camassa-Holm equation: a comparative analysis for traveling wave solutions. Nonlinear Eng. 2021;10(1):385–94. 10.1515/nleng-2021-0030Suche in Google Scholar

[21] Awan AU, Sharif A, Abro KA, Ozair M, Hussain T. Dynamical aspects of smoking model with cravings to smoke. Nonlinear Eng. 2021;10(1):91–108. 10.1515/nleng-2021-0008Suche in Google Scholar

[22] Panhwer LA, Abro KA, Memon IQ. Thermal deformity and thermolysis of magnetized and fractional Newtonian fluid with rheological investigation. Phys Fluids. 2022;34(5):053115. 10.1063/5.0093699Suche in Google Scholar

[23] Krishnan M, J, Rajagopal KR. Review of the uses and modeling of bitumen from ancient to modern times. Appl Mech Rev. 2003;56(2):149–214. 10.1115/1.1529658Suche in Google Scholar

[24] Masliyah JH, Bhattacharjee S. Electrokinetic and colloid transport phenomena. Hoboken, New Jersey: John Wiley and Sons; 2006. 10.1002/0471799742Suche in Google Scholar

[25] Kang Y, Yang C, Huang X. Dynamic aspects of electroosmotic flow in a cylindrical microcapillary. Int J Eng Sci. 2002;40(20):2203–21. 10.1016/S0020-7225(02)00143-XSuche in Google Scholar

[26] Rice CL, Whitehead R. Electro kinetic flow in a narrow cylindrical capillary. J Phys Chem. 1965;69(11):4017–24. 10.1021/j100895a062Suche in Google Scholar

[27] Stehfest H. Algorithm 368: numerical inversion of Laplace transforms [D5]. Commun ACM. 1970;13(1):47–9. 10.1145/361953.361969Suche in Google Scholar

[28] Awan AU, Riaz S, Abro KA, Siddiqa A, Ali Q. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfestas and Tzouas algorithms. Nonlinear Eng. 2022;11(1):35–46. 10.1515/nleng-2022-0006Suche in Google Scholar

Received: 2022-04-14

Revised: 2022-08-08

Accepted: 2022-09-05

Published Online: 2023-02-21

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2022-0256

Schlagwörter für diesen Artikel

Burgers’ fluid; integral transform; electro-osmotic; transient flow

Creative Commons

BY 4.0