Influence of the blade size on the dynamic characteristic damage identification of wind turbine blades

Peng Chen; Bei Chen

doi:10.1515/nleng-2022-0261

Article Open Access

Influence of the blade size on the dynamic characteristic damage identification of wind turbine blades

Peng Chen and Bei Chen

Published/Copyright: April 6, 2023

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 12 Issue 1

Abstract

In this article, the sensitivity coefficients of dynamic characteristic damage identification of blades with different sizes were investigated. The results show that the first third-order vibration modes of the blade before and after damage are consistent, and the wind turbine blade size has no significant effect on the vibration mode; with the increase of the blade size, the first-, third- and fourth-order natural frequency sensitivity coefficients decrease gradually, while the second-, fifth- and sixth-order natural frequency sensitivity coefficients increase gradually; as the blade size increases, the third-order displacement mode sensitivity coefficient of the blade gradually increases, which indicates that the displacement modes identification effect is better with the increase of the blade size. With the increase of the blade size, the first- and third-order strain modal sensitivity coefficients increase gradually, which indicates that when using first- and third-order strain modes for damage identification, the larger the blade size, the better the identification effect; with the increase of the blade size, the second-order strain modal sensitivity coefficient decreases gradually, which indicates that when using second-order strain mode for damage identification, the larger the blade size, the worse the identification effect. This research could provide a theoretical basis for the application of the dynamic characteristic damage identification method in the damage identification of wind turbine blades of different sizes.

Keywords: wind turbine blade; different blade sizes; blade damage; dynamic characteristics; damage identification

1 Introduction

Sufficient energy is an important guarantee for modern social progress and economic development [1]. The long-term use of petrochemical energy as the main body of the world’s energy has brought a series of problems, such as the exhaustion of petrochemical energy, environmental pollution, ozone layer destruction, the greenhouse effect, etc., and the energy problem has become a major threat to human survival and development. Therefore, renewable energy sources such as solar energy, wind energy, ocean energy, and geothermal energy are gradually being developed and utilized [2]. Wind energy is richer and cleaner than other renewable energy sources, leading to increasing research to make it more efficient [3]. Wind turbines can convert wind energy into electricity, which is the main way to utilize wind energy [4]. Wind turbines have attracted increasing attention due to their advantages of the short infrastructure construction period, flexibly installed capacity, and no environmental pollution [5].

In recent years, with the increasing depletion of fossil fuels and the increasingly prominent environmental problems, investment in wind energy has begun to increase, and the wind power industry has developed rapidly and occupies an important position in renewable energy [6]. Since 2001, the global wind power industry has developed rapidly, and the annual growth rate of the global wind power installed capacity has reached 20–30%. By the end of 2020, the cumulative installed capacity of global wind power reached 733.28 GW.

Blades are the main components of wind turbines, which play an important role in capturing wind energy [7]. Whether the blades can work normally has a very important impact on the entire wind turbine [8]. The working environment of wind turbine blades is harsh, and small debris such as sand and gravel mixed in the wind, as well as wind and snow, lightning, etc., will cause damage to the blades to a varying degree [9]. In addition, the blade is subject to the combined action of alternating load and random load for a long time when it is in a working state, which makes it prone to fatigue damage [10]. Once the blade is damaged in operation, the damage will continue to develop under the action of alternating loads, and when the damage develops to a certain extent, the blade will be broken [11]. This not only affects the normal operation of the wind turbine but also causes damage to the entire unit, which will bring economic losses to the wind farm, and seriously affects the application and promotion of wind power generation.

If the initial blade damage can be timely detected and measures are taken for maintenance, a series of losses caused by the blade breaking can be avoided [12]. However, it is hard to find blade damage in the early stage. The blade is installed at the top of the wind turbine tower, which brings a lot of inconvenience to the detection work. Therefore, effective wind turbine blade damage detection has become a problem worthy of further study.

Wind turbine blade damage identification is to study the response of blade structure under external excitation. Through structural response analysis, various characteristic parameters of the blade structure are obtained and compared with the design data to determine the performance and state of the blade structure. Scholars have systematically studied the damage identification of wind turbine blades and achieved many reliable research results. Ghoshal et al. [13] applied a piezoelectric ceramic actuator (PZT) sensing system to blade damage identification and motivating blade vibration to detect blade damage through PZT. Sundaresan et al. [14] preset the PZT sensing system inside the wind turbine blade to monitor the damage to the blade in real time. In addition, scholars have studied the blade damage identification of wind turbines based on acoustic emission technology [15,16,17,18]. Zhu et al. [19] combined acoustic emission technology with the PZT sensor for damage identification of wind turbine blades. Smith et al. [20] and Beattie and Rumsey [21] identified structural damage according to the temperature change of wind turbine blades. Xiao and Yan [22] applied infrared imaging technology to the nondestructive testing of wind turbine blades.

In recent years, many scholars in China have made some achievements in the detection of blade damage through blade dynamic characteristics [23,24,25]. Compared with static measurement data, dynamic measurement data were more abundant and studied in-depth [26]. Therefore, damage identification methods based on dynamic properties have developed rapidly in recent years and have been widely used in practical engineering [27].

From the dynamic point of view, the general structural system was regarded to be composed of a mass matrix, stiffness matrix, damping matrix, etc. When the structure was damaged, it usually caused changes in the physical parameters of the structure, and the modal parameters were based on the physical parameters of the structure. When the physical parameters of the structure change, the modal parameters (natural frequency, mode shape, etc.) will also change accordingly. Therefore, the damage to the structure could be identified by the change in the modal parameters (natural frequency, mode shape, etc.). When the damage identification of the structure is carried out, the dynamic characteristic analysis of the undamaged structure should be carried out to obtain its modal parameters and the modal parameters should be used as the benchmark. The modal parameters of the damaged structure were then obtained and compared with the benchmark parameters so that the structural damage could be identified [28].

The finite element method could reasonably simplify the complex problem of the structural system, which could solve practical problems more conveniently [29,30]. At present, converting the actual structure into a finite element model and using it as a reference has been used in most structural damage identification methods.

Structural damage identification mainly included damage identification, damage localization, and damage degree assessment [31,32,33]. Generally, the simplest method was used to determine whether the structure was damaged or not, and then a more complex but accurate identification method was used to further identify the structure and then the location of the damage and the degree of damage were judged [34,35,36].

To meet the different needs of society, the power of wind turbines was varied and the blade size was also different. The change in the blade size may have a certain impact on the damage identification effect. At present, several studies have been carried out on the damage detection of wind turbine blades. However, most of the existing studies focus on single-size blades, without considering the effect of blade size on damage identification [37]. In this article, different sizes of blades were selected for modeling, and the finite element analysis software ANSYS was used to analyze the dynamic characteristics of blades in shutdown and running states. The sensitivity coefficients of the dynamic characteristics damage identification of blades with different sizes were investigated, and the results were compared to explore the influence of different blade sizes on the damage identification effect of dynamic characteristics.

2 The wind turbine blade model

2.1 Blade size and material properties

According to the data provided by a wind power equipment company, the blade sizes corresponding to different power wind turbines are shown in Table 1. To study the influence of different blade sizes on the damage identification results of dynamic characteristics, wind turbine blades with lengths of 2.7, 3.2, 3.7, 4.5, and 6.5 m were selected for modeling and analysis. The material properties of wind turbine blades according to Su et al. [37] are shown in Table 2.

Table 1

Blade size of wind turbines with different powers

Wind turbine power (kW)	1	3	5	10	15	20	30	40
Blade size (m)	1.3	1.9	2.7	3.2	3.7	4.5	6.5	12.6

Table 2

Material properties of wind turbine blades

Material type	Span modulus (GPa)	Radial modulus (GPa)	Shear modulus (GPa)	Poisson’s ratio
Glass fiber-reinforced plastic	42.6	16.5	5.5	0.22

2.2 The finite element model of the blade

The finite element model of the blade is shown in Figure 1. The length of the blade was 4.5 m and the widths were 22.5 cm at the tip and 71.0 cm at the widest part of the blade. The blade damage unit in the 4.5 m blade is shown in Figure 2 (the damage unit size is 12.2 cm × 24.3 cm). The damage units at the same position are selected for the analysis of other size blades, and the size of the damage units increased (decreased) in proportion to the increase (decrease) of the blade size. In this article, the initial mesh length of the blade was 40 mm; this was adjusted according to the accuracy requirements of the results and the size of the blade.

Figure 1

Finite element model of the blade.

Figure 2

Damaged area of the blade.

The damage degrees of the blade are 0, 20, 40, 60, and 80%. The different damage degrees of the blade are simulated by adjusting the elastic modulus of the blade ( E is the elastic modulus without damage and E ′ is the elastic modulus with damage) [37], as follows:

(1) λ = E − E ′ E .

3 Recognition of the blade damage

3.1 Mode shape of the blade

The modal analysis of wind turbine blades with different sizes before and after the damage was carried out by ANSYS. The first third-order vibration modes of the blade before and after the damage were consistent: the first-order vibration mode was flapping vibration; the second-order vibration mode was vibration; and the third-order vibration mode was flapping vibration. The size of the wind turbine blade has no significant effect on the vibration mode.

3.2 Sensitivity analysis of damage identification based on the natural frequency

The natural frequency sensitivity coefficient of the blade is as follows ( f i is the natural frequency without damage and f ′ i is the natural frequency with damage) [37]:

(2) Q f = f i − f i ′ f i 4 .

Figures 3 and 4 show the sixth-order natural frequency sensitivity coefficients of blades with different sizes under shutdown and running states, respectively. It can be seen that the sixth-order natural frequency sensitivity coefficient of the blade with different sizes under shutdown and running states (the selected speed rate: 17 rad/s [37]) increased with the increase of the blade damage. With the increase of blade size, the first-, third-, and fourth-order natural frequency sensitivity coefficients decreased gradually, while the second-, fifth-, and sixth-order natural frequency sensitivity coefficients increased gradually. For damage identification based on natural frequency, first-, third-, and fourth-order natural frequencies can be selected when the blade size is small, while second-, fifth-, and sixth-order natural frequency frequencies can be selected when the blade size is large. When the blade size increased from 2.7 to 6.3 m, the maximum change rate of the sixth-order natural frequency sensitivity coefficients under the shutdown state was 28.60%, while it was 27.37% under the running state.

Figure 3

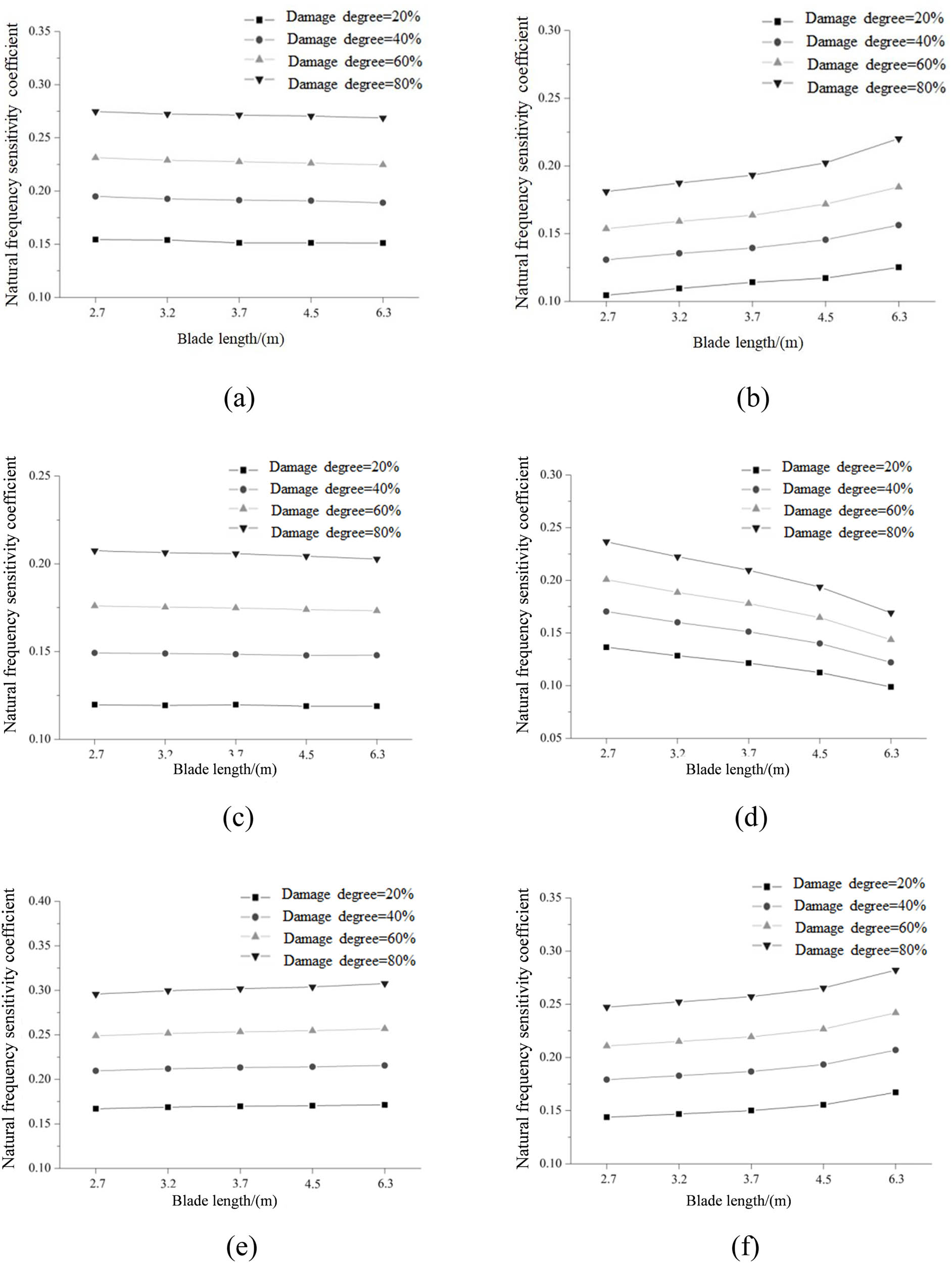
Sensitivity coefficient of natural frequency under the shutdown state: (a) first order, (b) second order, (c) third order, (d) fourth order, (e) fifth order, and (f) sixth order.

Figure 4

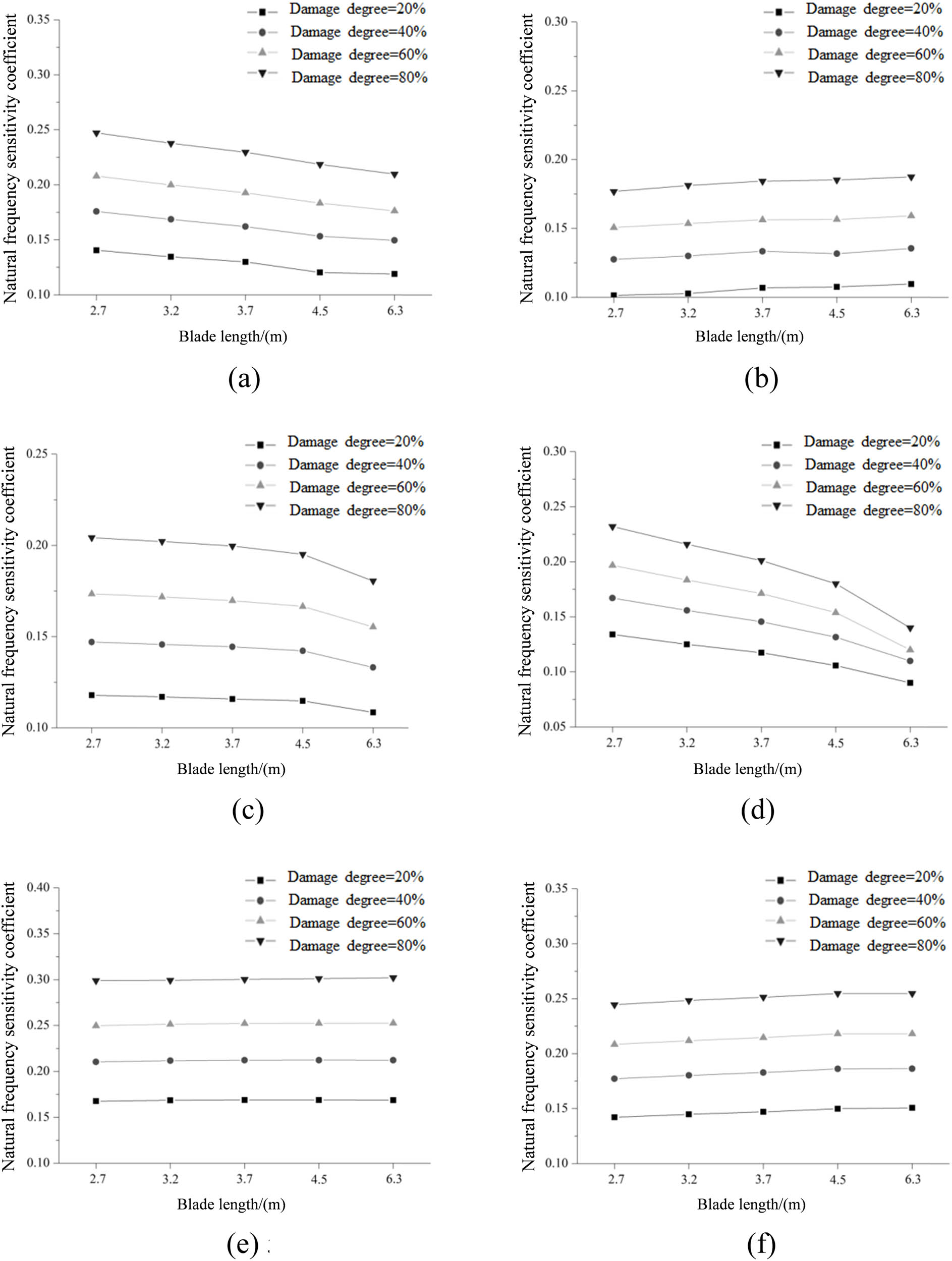
Sensitivity coefficient of natural frequency under the running state: (a) first order, (b) second order, (c) third order, (d) fourth order, (e) fifth order, and (f) sixth order.

3.2.1 Sensitivity analysis of damage identification based on the displacement mode

The displacement mode sensitivity coefficient of the blade is calculated as follows ( φ d is the displacement mode without damage and φ d ′ is the displacement mode with damage) [37]:

(3) Q d = φ d − φ d ′ φ d 4 .

Figures 5 and 6 show the third-order displacement mode sensitivity coefficient of blades with different sizes under shutdown and running states, respectively. It can be seen that the third-order displacement mode sensitivity coefficients of the blade with different sizes under shutdown and running states increased with the increase of the blade damage. It can also be seen that as the blade size increased, the third-order displacement mode sensitivity coefficient of the blade with different sizes gradually increased, which indicated that when using displacement modes for damage identification, the identification effect was better with the increase of blade size. When the blade size increased from 2.7 to 6.3 m, the maximum change rate of the third-order displacement mode sensitivity coefficient under the shutdown state was 18.01%, while it was 15.57% under the running state.

Figure 5

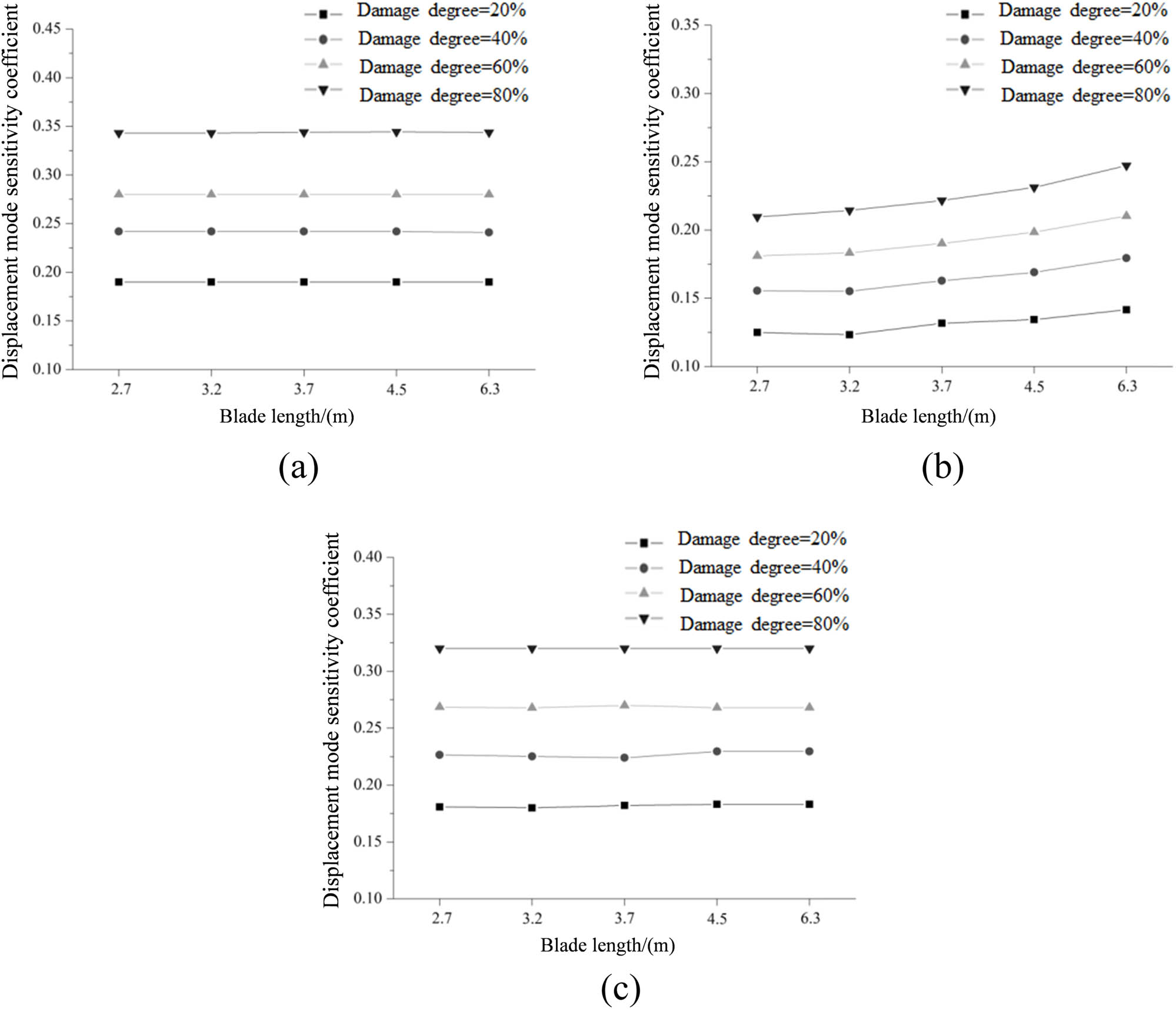
Sensitivity coefficient of the displacement mode under the shutdown state: (a) first order, (b) second order, and (c) third order.

Figure 6

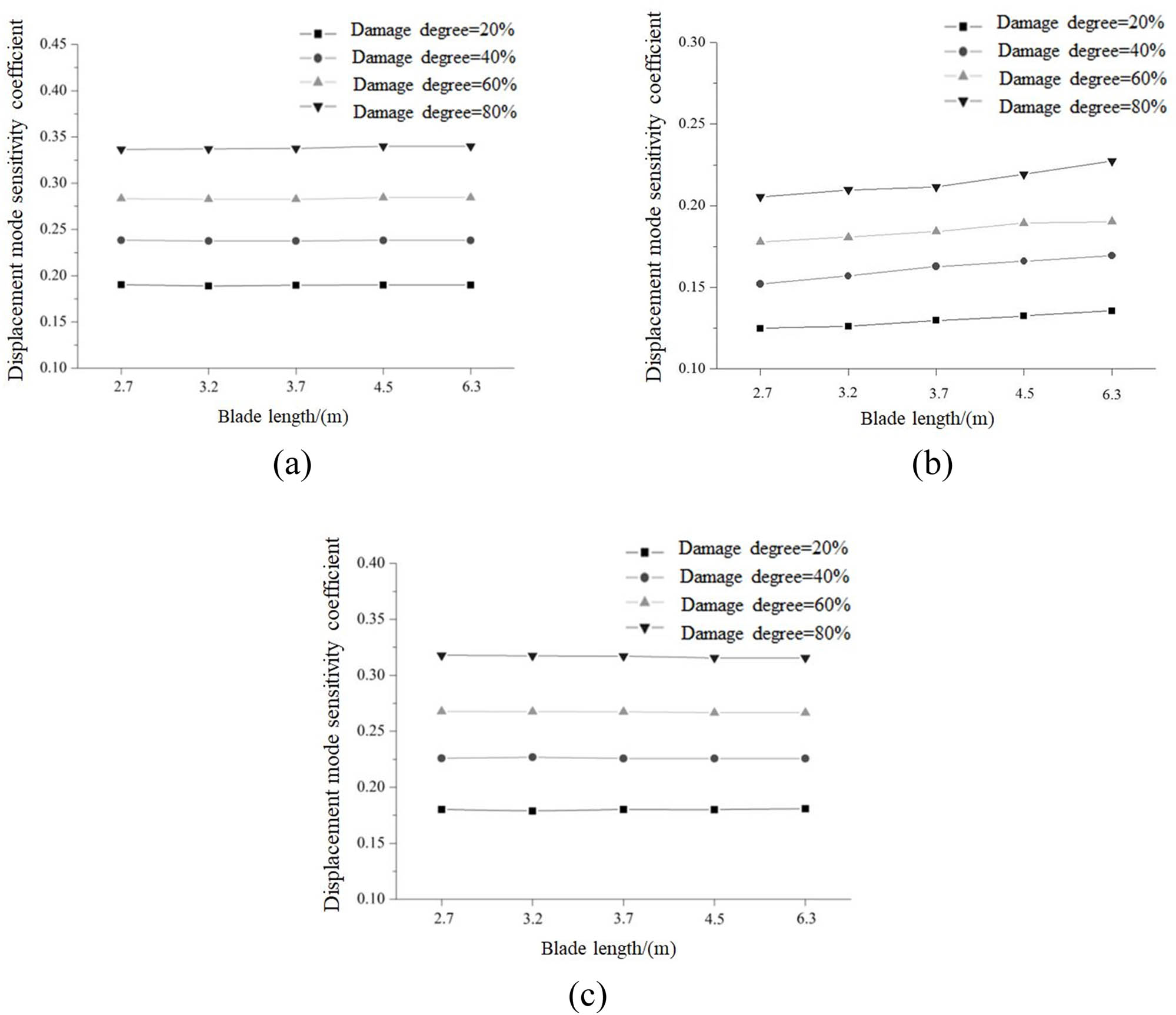
Sensitivity coefficient of the displacement mode under the running state: (a) first order, (b) second order, and (c) third order.

3.2.2 Sensitivity analysis of damage identification based on the strain mode

The strain mode sensitivity coefficient of the blade is calculated as follows ( φ s is the strain mode without damage and φ s ′ is the strain mode with damage) [37]:

(4) Q s = φ s − φ s ′ φ s 4 .

Figures 7 and 8 show the third-order strain mode sensitivity coefficient of blades with different sizes under shutdown and running states, respectively. It can be seen that the third-order strain mode sensitivity coefficient of the blade with different sizes under shutdown and running states increased with the increase of the blade damage. There was no obvious difference in the strain modal sensitivity coefficient of the blade between the running state and the shutdown state. With the increase of the blade size, the first- and third- order strain modal sensitivity coefficient under the shutdown state and running state increased gradually, which indicated that when using first- and third-order strain modes for damage identification, the larger the blade size, the better the identification effect. With the increase of the blade size, the second-order strain modal sensitivity coefficient under the shutdown state and running state decreased gradually, which indicated that when using second-order strain mode for damage identification, the larger the blade size, the worse the identification effect. When the blade size increases from 2.7 to 6.3 m, the maximum change rate of the third-order displacement mode sensitivity coefficient under a shutdown state was 14.26%, while the maximum change rate of the third-order displacement mode sensitivity coefficient under a running state was 15.87%.

Figure 7

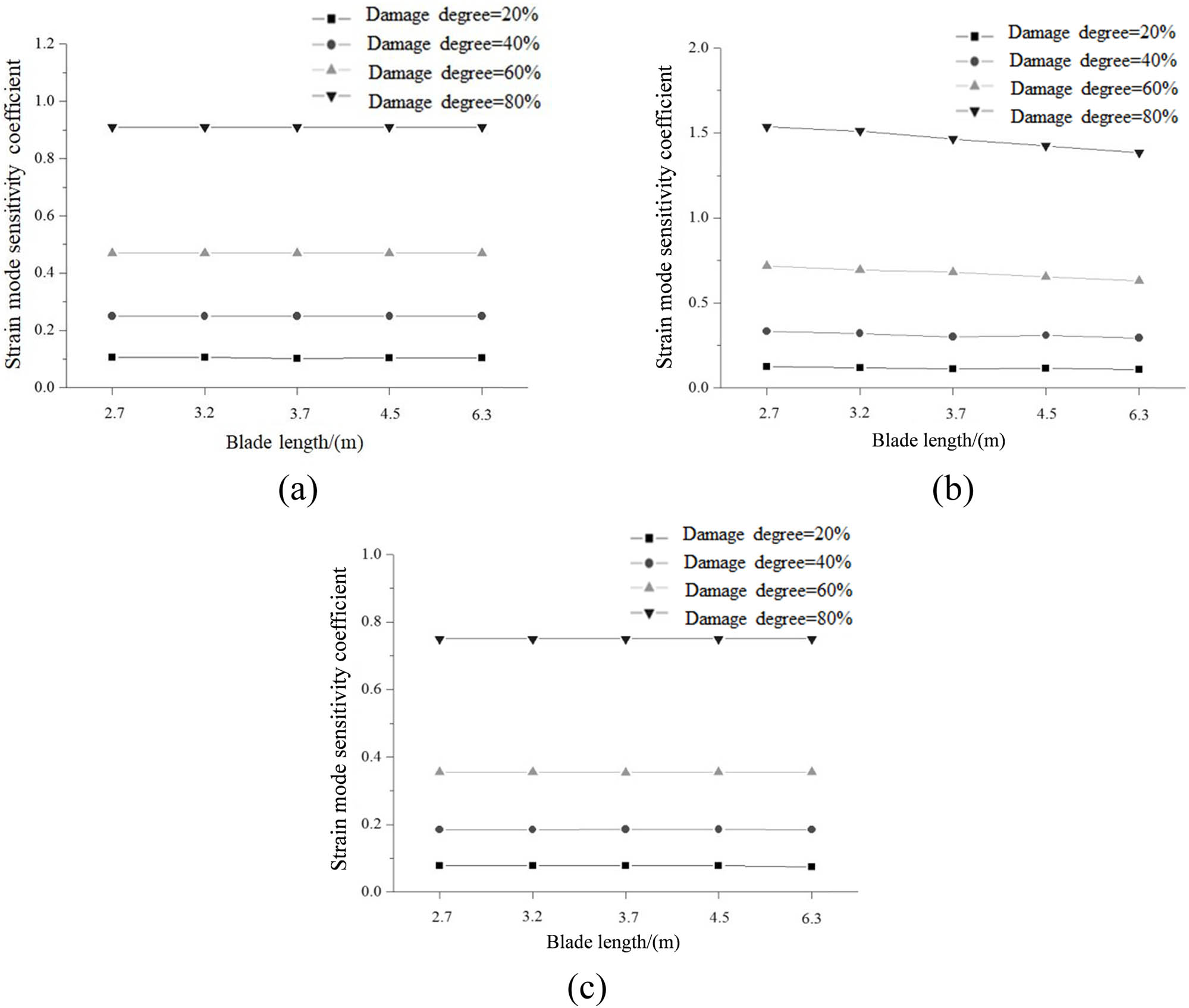
Sensitivity coefficient of the strain mode under a shutdown state: (a) first order, (b) second order, and (c) third order.

Figure 8

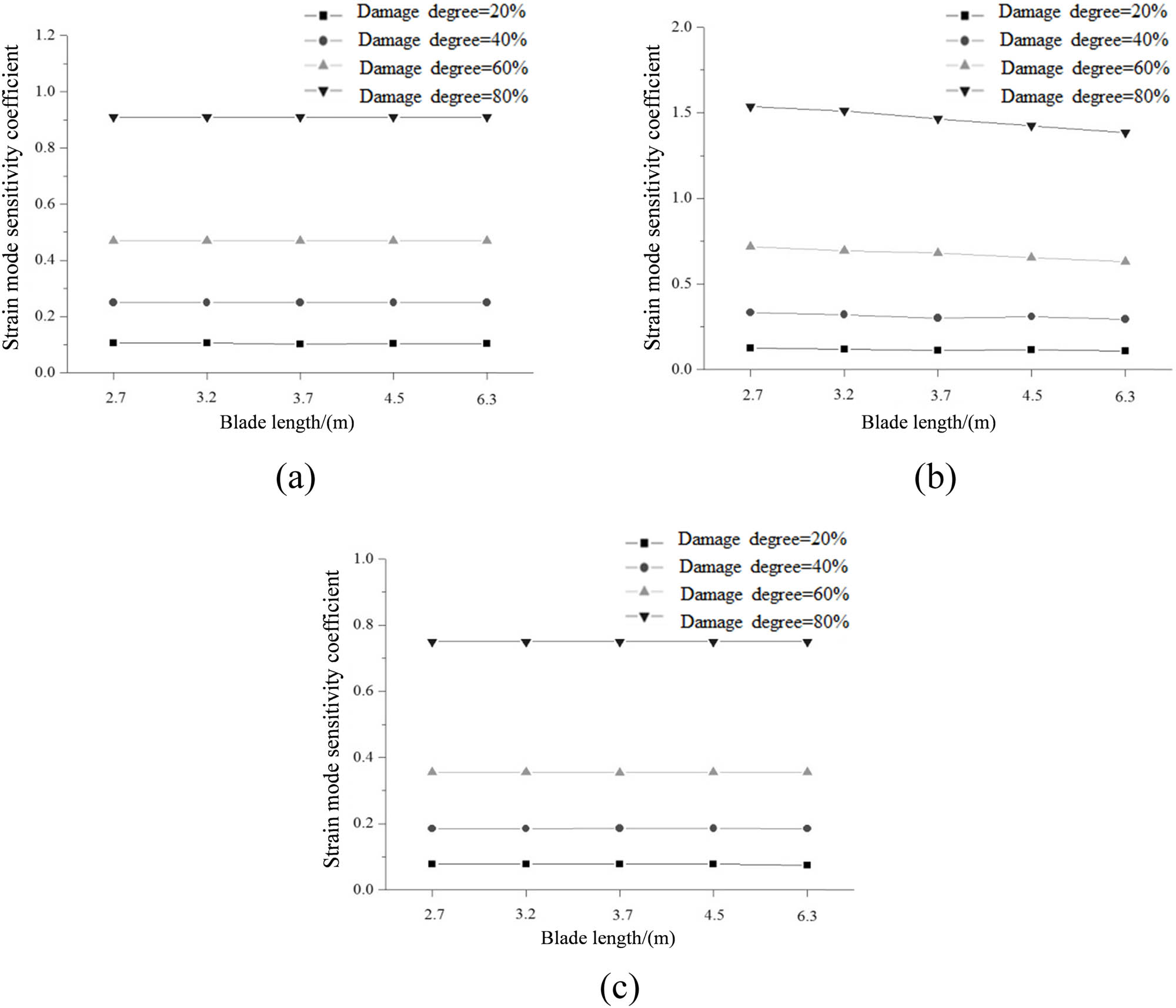
Sensitivity coefficient of the strain mode under a running state: (a) first order, (b) second order, and (c) third order.

4 Conclusions

The first third-order vibration modes of the blade before and after damage were consistent, and the wind turbine blade size had no significant effect on the vibration mode.
With the increase of the blade size, the first-, third-, and fourth-order natural frequency sensitivity coefficients decreased gradually, while the second-, fifth-, and sixth-order natural frequency sensitivity coefficients increased gradually.
With the increase of the blade size, the third-order displacement mode sensitivity coefficient of the blade gradually increased, which indicated that the displacement mode identification effect was better with the increase of the blade size.
With the increase of the blade size, the first- and third-order strain modal sensitivity coefficient increased gradually, while the second-order strain modal sensitivity coefficient decreased gradually.

Funding information: There is no funding to declare for this research article.
Author contributions: Peng Chen: methodology, formal analysis, investigation, and initial draft; Bei Chen: investigation and initial draft. All authors read and approved the final version.
Conflict of interest: The authors state no conflict of interest.

References

[1] Li DS, Ho SM, Song GB, Ren L, Li HN. A review of damage detection methods for wind turbine blades. Smart Mater Struct. 2015;24:033001.10.1088/0964-1726/24/3/033001Search in Google Scholar

[2] Hassan Q. Assessing of renewable energy for electrical household ancillary based on photovoltaics and wind turbines. IOP Conf Ser: Mater Sci Eng. 2021;1076(1):012006.10.1088/1757-899X/1076/1/012006Search in Google Scholar

[3] Michael E, Tjahjana D, Prabowo A. Estimating the potential of wind energy resources using Weibull parameters: A case study of the coastline region of Dar es Salaam, Tanzania. Open Eng. 2021;11(1):1093–104.10.1515/eng-2021-0108Search in Google Scholar

[4] Hameed Z, Hong YS, Cho YM, Ahn SH, Song CK. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew Sustain Energy Rev. 2009;13(1):1–39.10.1016/j.rser.2007.05.008Search in Google Scholar

[5] Adams D, White J, Rumsey M, Farrar C. Structural health monitoring of wind turbines: method and application to a HAWT. Wind Energy. 2011;14(4):603–23.10.1002/we.437Search in Google Scholar

[6] Xu Y, Yang K, Zhao GH. The influencing factors and hierarchical relationships of offshore wind power industry in China. Environ Sci Pollut Res Int. 2021;28(37):1–16.10.1007/s11356-021-14275-wSearch in Google Scholar PubMed PubMed Central

[7] Njiri JG, Beganovic N, Do MH, Söffker D. Consideration of lifetime and fatigue load in wind turbine control. Renew Energy. 2019;131:818–28.10.1016/j.renene.2018.07.109Search in Google Scholar

[8] Blanch MJ, Dutton AG. Acoustic emission monitoring of field tests of an operating wind turbine. Key Eng Mater. 2003;245–246:475–82.10.4028/www.scientific.net/KEM.245-246.475Search in Google Scholar

[9] Larsen JW, Nielsen SRK. Non-linear dynamics of wind turbine wings. Int J Non-Linear Mech. 2006;41(5):629–43.10.1016/j.ijnonlinmec.2006.01.003Search in Google Scholar

[10] Wang CN, Chi TY. Diagnosis of damaged wind turbine blade by noise characteristics. Noise Control Eng J. 2020;68(2):146–56.10.3397/1/376813Search in Google Scholar

[11] Su T, Xue G. Finite element analysis of damage identification of wind turbine blades based on dynamic characteristics. J Inn Mong Univ Sci Technol. 2017;36(1):45–50 + 97. (in Chinese)Search in Google Scholar

[12] Guo JH, Liu C, Cao JF, Jiang DX. Damage identification of wind turbine blades with deep convolutional neural networks. Renew Energy. 2021;174:122–33.10.1016/j.renene.2021.04.040Search in Google Scholar

[13] Ghoshal A, Sundaresan MJ, Schulz MJ, Pai PF. Structural health monitoring techniques for wind turbine blades. J Wind Eng Ind Aerodyn. 2000;85(3):309–24.10.1016/S0167-6105(99)00132-4Search in Google Scholar

[14] Sundaresan MJ, Schulz MJ, Ghoshal A. Structural health monitoring static tests of a wind turbine blade. Subcontractor Report. March: National Renewable Energy Laboratory; 2002 NREL/SR-500-28719.10.2172/15000129Search in Google Scholar

[15] Murtagh PJ, Basu B, Broderick BM. Along-wind response of a wind turbine tower with blade coupling subjected to rotationally sampled wind loading. Eng Struct. 2005;27(8):1209–19.10.1016/j.engstruct.2005.03.004Search in Google Scholar

[16] Yang JB, Jiang LJ, Chen DC. Dynamic modeling and control of a rotating Euler-Bernoulli beam. J Sound Vib. 2004;274:863–75.10.1016/S0022-460X(03)00611-4Search in Google Scholar

[17] Joosse PA, Blanch MJ, Dutton AG, Kouroussis D, Philippidis TP, Vionis P. Acoustic emission monitoring of small wind turbine blades. J Sol Energy Eng. 2002;124(4):401–11.10.1115/1.1509769Search in Google Scholar

[18] Zhao XG. Study on damage identification for the material of blade in large wind turbine based on wavelet and acoustic emission [dissertation]. Shenyang: Shenyang University of Technology; 2009. (in Chinese)Search in Google Scholar

[19] Zhu YK, Pan RQ, Chen SP, Tian GY. Structural health monitoring of wind turbine blade based on sensor array and acoustic emission. Nondestr Test. 2010;32(10):753–61. (in Chinese)Search in Google Scholar

[20] Smith GM, Clayton BR, Dutton AG, Irving AD. Infra-red thermography for condition monitoring of composite wind turbine blade: feasibility studies using cyclic loading tests. In: Pitcher KF, editor. Wind Energy Conversion 1993: Proceedings of the 15th British Wind Energy Association Conference. York, UK; 1993. p. 365–71.Search in Google Scholar

[21] Beattie AG, Rumsey M. Non-destructive evaluation of wind turbine blades using an infrared camera. 37th Aerospace Sciences Meeting and Exhibit; 1999 Jan 11–14; Reno (NV), USA. AIAA, 1999. p. 11–4.10.2514/6.1999-46Search in Google Scholar

[22] Xiao JS, Yan TP. Numerical analysis of NDT of wind turbine blades using infrared imaging. J Beijing Univ Technol. 2006;1(32):48–52. (in Chinese)Search in Google Scholar

[23] Zeng HY. Study on effect of stress stiffening and damage on modal parameters of wind turbine blade [dissertation]. Harbin: Harbin Institute of Technology; 2011. (in Chinese)Search in Google Scholar

[24] Li MM. Research on dynamic methods and technique for detecting mechanical damage of wind turbine blades [dissertation]. Changsha: Changsha University of Science and Technology; 2012. (in Chinese)Search in Google Scholar

[25] Li LP, Li MM, Jin FH, Li HB. Applications of the vibration detection technologies in monitoring the blade crack fault of wind turbines. J Eng Therm Energy Power. 2013;28(2):207–12. (in Chinese)Search in Google Scholar

[26] Mao HJ, Shi KZ. Modal testing and numerical simulation of large wind turbine blade. J Eng Thermophys. 2009;30(4):601–4. (in Chinese)Search in Google Scholar

[27] Xue G, Su T. Damage identification of wind turbine blades based on dynamic characteristics and BP neural network. Acta Energiae Solaris Sin. 2018;39(10):2945–52. (in Chinese)Search in Google Scholar

[28] Zhang X, Gu GM. Simulation for structure damage in dentification of wind turbine blade based on mode strain energy theory. Compos Sci Eng. 2015;11:15–9. (in Chinese)Search in Google Scholar

[29] Gu YQ, Feng JF, Jia BH, Zhang ZW. Numerical simulation and experimental study on natural frequencies of damaged blades. Noise Vib Control. 2021;41(1):103–7. (in Chinese)Search in Google Scholar

[30] Fan T, Zeng CP, Ma K. Damage identification based on strain modal for damage structure. J Guizhou Univ Nat Sci. 2015;32(1):94–7. (in Chinese)Search in Google Scholar

[31] Zhang SH, Han LS, Lou YG. The analysis of grey networks to damage identified in structure. J Dalian Nationalities Univ. 2005;7(5):76–8. (in Chinese)Search in Google Scholar

[32] Sun HY, Dong F. Damage identification of building structural based on neural network. Control Eng China. 2015;22(2):287–90. (in Chinese)Search in Google Scholar

[33] Mu HB. Study on wood defects testing based on BP and RBF neural networks [dissertation]. Harbin: Northeast Forestry University; 2010. (in Chinese)Search in Google Scholar

[34] Chen HP, Sun WL. Dynamic analysis of wind generators blade. Mach Tool Hydraulic. 2010;38(23):101–4. (in Chinese)Search in Google Scholar

[35] Li B, Jiang FJ. The modal analysis of the conical tube tower for wind turbine. J Inn Mong Univ Sci Technol. 2009;28(4):364–8. (in Chinese)Search in Google Scholar

[36] Chang H, Yin CC. Study on structural damage identification based on BP neural network. J Harbin Univ Commer (Nat Sci Ed). 2014;4:474–6. (in Chinese)Search in Google Scholar

[37] Su T, Su W, Du C, Huang Z, Dong J, Hu C. Damage identification of wind turbine blades based on dynamic characteristics. Nonlinear Eng. 2022;11(1):47–57.10.1515/nleng-2022-0007Search in Google Scholar

Received: 2022-09-15

Revised: 2022-10-14

Accepted: 2022-11-02

Published Online: 2023-04-06

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2022-0261

Keywords for this article

wind turbine blade; different blade sizes; blade damage; dynamic characteristics; damage identification

Creative Commons

BY 4.0