Startseite Hyperboloid offset surface in the architecture and construction industry
Artikel Open Access

Hyperboloid offset surface in the architecture and construction industry

  • Edwin Koźniewski und Anna Borowska EMAIL logo
Veröffentlicht/Copyright: 12. August 2019
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Open Engineering
Aus der Zeitschrift Open Engineering Band 9 Heft 1

Abstract

In this paper the issue of approximation of the hyperboloid offset surface off(S(t, v); d) at distance d by the hyperboloid surface S1(ϕ, v) is considered. The problem of determining various surfaces approximating the hyperboloid offset surface off (S(t, v); d) is important due to the applications of the hyperboloid as a mathematical model for miscellaneous objects in the architecture and construction industry. The paper presents the method of determining the angles and coordinates of points of various surfaces approximating the hyperboloid of revolution. A two-sheet hyperboloid offset surface can be used for modelling double-layer domes. A one-sheet hyperboloid offset surface was used to model the reinforced structure of the cooling tower.

Keywords: hyperbola offset curve; one-sheet hyperboloid; two-sheet hyperboloid

1 Introduction

A one-sheet hyperboloid is often used as a model for various objects in the construction industry. It is a doubly ruled surface. Thanks to this, one-sheet hyperboloid shaped constructions can be built with, for example straight steel elements that form a strong structure. Such a clever design guarantees lower costs than other technical solutions. Examples of such constructions are cooling towers (Jaworzno, Cracow in Poland), Kobe Port Tower in Japan, Newcastle International Airport in England, Cathedral of Brasilia in Brazil, the Canton Tower in China and many other structures. A two-sheet hyperboloid can be used to model domes and other roofs which cover stadiums, halls, and shopping centres. Nowadays, lattice domes with elaborate shapes (Golden Terraces in Warsaw) and multilayer (retractable) roofs of large objects (National Stadium in Singapore) are used.

To design structures based on the hyperboloid S(t, v), the coordinates of points of other surfaces that approximate the hyperboloid S(t, v) are necessary. The hyperboloid S(t, v) can be approximated by means of the offset surfaces, a hyperboloid of similar parameters or another surface with the desired properties. The paper provides a convenient methodology for acquiring the angles and coordinates of points of various surfaces that approximate the one-sheet (or two-sheet) hyperboloid surface.

Section 3 suggests the construction of a reinforced hyperboloid-shaped double-layer dome. Section 4 presents a proposal for a reinforced cooling tower structure. Sections 2, 3.1, 3.2 and 4.1 provide mathematical formulas defining the angles and coordinates of points of different surfaces approximating the hyperboloid. The interesting offset surfaces (offset curves) are described in [3, 4, 5]. Section 5 contains examples of the applications of the given geometric method.

2 Mathematical formulas

Let c(t) = (x(t), y(t))(t ∈ [α, β]) be a parametric representation of a planar curve (we write down functions x(t), y(t) as xt, yt). The normal vector to the curve c(t) at the point P(xt , yt) is as follows n=[−yt′,xt′]The unit normal vector at the point P(xt , yt) is of the form (cf. [6], p. 335)

(1)nver=−y′t,x′t/x′t2+y′t2.

For a smooth planar curve c, we define an offset curve cd at distance d in the following way. On each curve normal, we mark the two points that are at distance d from the curve c. The set of all of these points forms the offset cd=(cd′∪cd″)(cf. [6], p. 335). The offset cd(t) at distance d to c(t) is obtained as (cf. [6], p. 335) cd(t) = c(t) ± dnver(t). The curve c and its offset curves cd′andcd″are not always of the same type.

Let us assume that P is any point on the hyperbola ch and l is the normal line to ch at the point P. Points P1 and P2 lie on the normal l at distance d from P. Q1, Q2 are the intersection points of the normal line l with hyperbolas ch1 and ch2 respectively. Non-zero distances dP1Q1=|P1Q1¯|and dP2Q2=|P2Q2¯|mean that hyperbolas ch1 and ch2 do not keep a constant distance d relative to the basic hyperbola ch (cf. Figure 3).

Figure 1 Kobe Port Tower in Japan (cf. [1])
Figure 1

Kobe Port Tower in Japan (cf. [1])

Figure 2 National Stadium in Singapore (cf. [2])
Figure 2

National Stadium in Singapore (cf. [2])

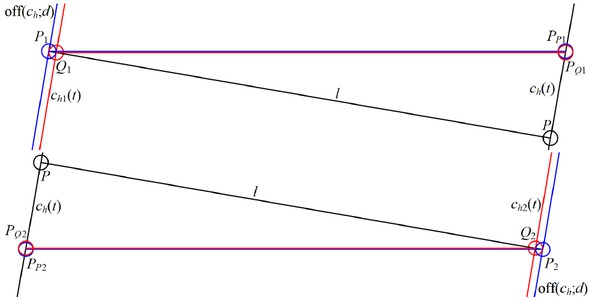
Figure 3 The arrangement of points and curves
Figure 3

The arrangement of points and curves

The ch(t), ch1 (ϕ) and off (ch; d) curves shown in Figure 3 are defined as follows

(2)ch(t):x=acosh⁡(t),z=bsinh⁡(t)

(cf. [7], p. 98),

(3)ch1(ϕ):x=acosh⁡(ϕ)−d,z=bsinh⁡(ϕ),ch2(ϕ):x=acosh⁡(ϕ)+d,z=bsinh⁡(ϕ),off(ch;d)=ch(t)±dnver(t).

Definition 1 (horizontal offset thickness) Let the points P, P1, PP1 (zP1 = zPP1) and curves ch, ch1, off(ch; d) be defined as above (see Figure 3). Horizontal offset thickness measured at height z = zP1 (zP1 is arbitrary but fixed) is defined as the length of the section |P1PP1¯|=dP1PP1≥d

Definition 2 (cf. [7], p. 97)

cosht=et+e−t/2,sinht=et−e−t/2.

3 Double-layer lattice domes

In this section, we suggest the use of the two-sheet rotational hyperboloid surface to form double-layer lattice domes. Such roofs of large buildings (stadiums, halls, shopping centres) made of metal bars can be light constructions with considerable spread. The bar structures of the low-profile single-layer domes are particularly susceptible to stability loss [8]. Therefore, a more advantageous solution is the construction of double-layer structures connected by bars [9].We provide a convenient method for determining the angles and coordinates of points of various surfaces (also the offset surfaces) approximating the two-sheet hyperboloid surface.

3.1 The coordinates of points P1 and P2

Let us take the parametric equations of the hyperbola Ch(t): x = a sinh(t), z = −bcosh(t). We can assume that t ≥ 0, because the graph of the curve Ch(t) is symmetrical about the Z axis. The coordinates of points P1 and P2 lying on the normal l to the hyperbola C h(t) (at the point P(xt, zt)) and distant from P by the length d were determined using the following equation of the offset curves off(Ch(t); d)

(4)off(Ch(t);d):[X,Z]==[xt,zt]±d[bsinh⁡(t),acosh⁡(t)]a2cosh2(t)+b2sinh2(t)

for xt = a sinh(t), zt = −bcosh(t). From here we obtain the coordinates of points P1 and P2

(5)xP1=xt−dbsinh⁡(t)a2cosh2(t)+b2sinh2(t),zP1=zt−dacosh⁡(t)a2cosh2(t)+b2sinh2(t),xP2=xt+dbsinh⁡(t)a2cosh2(t)+b2sinh2(t),zP2=zt+dacosh⁡(t)a2cosh2(t)+b2sinh2(t)

for xt = a sinh(t), zt = −b cosh(t).

3.2 The coordinates of the point Q1

Let us take the parametric equations of the hyperbola Ch1(ϕ) : x = a sinh(ϕ), z = −b cosh(ϕ) − d. The coordinates of the point Q1 (the intersection of the normal line l to the hyperbola Ch(t) at the point P(xt , zt) with the hyperbola Ch1(ϕ)) were determined as follows. We can assume that t, ϕ ≥ 0. The normal vector to the curve Ch(t) at the point P is of the form n = [b sinh(t), a cosh(t)]. The parametric equations of the normal line l to the hyperbola Ch(t) at the point P are as follows (cf. [10], p. 140)

(6)x=sinh⁡(t)(a−kdb),z=−cosh⁡(t)(b+kda).

Let us set the parameter k giving the intersection points of the line l with the hyperbola Ch1(ϕ).

x=sinh⁡(t)(a−kdb)=asinh⁡(ϕ),
z=−cosh⁡(t)(b+kda)=−(bcosh⁡(ϕ)+d).

Let us determine the parameter k from the second equation and put it in the first equation.

k=bdacosh⁡(ϕ)cosh⁡(t)−1+1acosh⁡(t)asinh⁡(t)+b2asinh⁡(t)−b2cosh⁡(ϕ)sinh⁡(t)acosh⁡(t)−bdsinh⁡(t)acosh⁡(t)=
=asinh⁡(ϕ)/∙acosh⁡(t)a2sinh⁡(ϕ)cosh⁡(t)+b2cosh⁡(ϕ)sinh⁡(t)==sinh⁡(t)cosh⁡(t)(a2+b2)−dbsinh⁡(t).

Hence and from definition 2 we have

a2coshteϕ−e−ϕ/2+b2sinhteϕ+e−ϕ/2==sinhtcoshta2+b2−dbsinht

Hence

Ae2ϕ+Beϕ+C=0,

where

A = a2 cosh(t) + b2 sinh(t),

B = −2 sinh(t)(cosh(t)(a2 + b2)− db),

C = b2 sinh(t) − a2 cosh(t).

Let us denote E = eϕ. Then for Δ = B2 − 4AC = 0 we have E1=−B+Δ/2Aand E2=−B−Δ/2A.Hence ϕ 1 = ln E1 and ϕ2 = ln E2. Finally we obtain the parameter k for the point Q1

(7)k=k1=bdacosh⁡(ϕ1)cosh⁡(t)−1+1acosh⁡(t),ϕ1=ln⁡E1=arsinhsinh⁡(t)1−k1dba.

Lemma 1 (cf. [5], Lemma 3, p. 46)

Let us denote kP1=1/b2sinh2t+a2cosh2t.

  1. The coordinates of the points P, P1 and Q1 can be determined using the parametric equations (6) of the normal line l to the hyperbola C h(t) at the point P(xt , zt) (we also write down P(xP, zP)) for the parameter k equal respectively k = 0, k = kP1 (cf. (5)) and k = k1 (cf. (7)).

  2. dPQ1 ≤ d iff k1 ≤ kP1.

The property (b) results from the fact that points P, P1 and Q1 lie on the normal l.

Figure 4 shows the two-sheet rotational hyperboloid S h(t, v) (the red surface), the two-sheet rotational hyperboloid Sh1(ϕ, v) (the bright blue surface) and the hyperboloid offset surface off(Sh; d) at distance d (the dark blue surface).

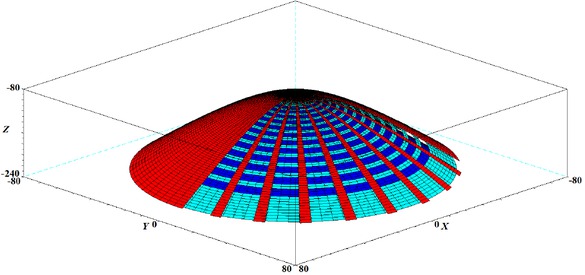
Figure 4 Fragment of the (red) two-sheet hyperboloid Sh(t, v), the (bright blue) two-sheet hyperboloid Sh1(ϕ, v) and the (blue) hyperboloid offset surface off(Sh; d)
Figure 4

Fragment of the (red) two-sheet hyperboloid Sh(t, v), the (bright blue) two-sheet hyperboloid Sh1(ϕ, v) and the (blue) hyperboloid offset surface off(Sh; d)

Sh(t, v) : x = (a sinh(t)) cos(v),

y = (a sinh(t)) sin(v), z = −b cosh(t),

Sh1(ϕ, v) : x = (a sinh(ϕ)) cos(v),

y = (a sinh(ϕ)) sin(v), z = −b cosh(ϕ) − d,

off(Sh; d) : x = sinh(t)(a − dbkP1) cos(v),

y = sinh(t)(a − dbkP1) sin(v),

z = − cosh(t)(b + dakP1),

where kP1=1/b2sinh2t+a2cosh2t.

Figure 5 shows a fragment of the double-layer lattice dome of the shape based on the two-sheet rotational hyperboloid. The black lattice is shaped by the hyperboloid Sh(t, v) (a = 30, b = 40), the blue lattice is formed by the offset surface off(Sh; d) (d = 6) and the pink lattice is a part

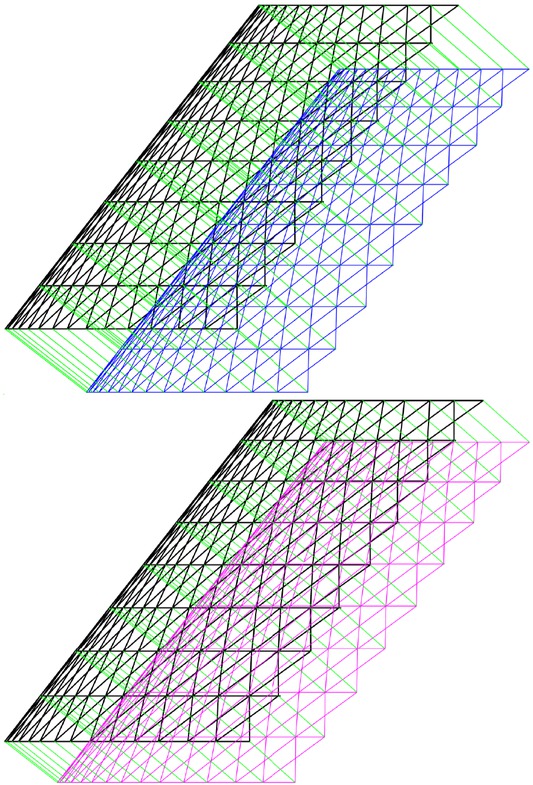
Figure 5 Fragment of the double-layer lattice dome of the shape based on the two-sheet rotational hyperboloid
Figure 5

Fragment of the double-layer lattice dome of the shape based on the two-sheet rotational hyperboloid

Figure 6 Fragment of the double-layer lattice dome of the shape based on the two-sheet rotational hyperboloid
Figure 6

Fragment of the double-layer lattice dome of the shape based on the two-sheet rotational hyperboloid

of the hyperboloid Sh1(ϕ, v). The bars connecting the two lattice surfaces are perpendicular to the outer surface. The given formulas allow designers to use any lattice pattern.

4 Cooling towers

A cooling tower is a device used to cool industrial water in those energy and industrial plants that do not have the possibility to make use of water from a river, lake or sea. Cooling towers are equipped with a very high (usually) reinforced concrete chimney. The chimney wall is a thin shell in the shape (from outside and inside) of the one-sheet rotational hyperboloid. This chimney construction is rigid and resistant to bending. Such a design guarantees the possibility of obtaining a large diameter and height. Thanks to the high chimney and the heated water, the so-called chimney effect is obtained.

Figure 7 shows the model of the chimney wall. The one-sheet hyperboloid surface sh(t, v) modelling the outer part of the chimney wall is coloured bright blue. The one-sheet hyperboloid surface sh1(ϕ, v) modelling the inner part of the chimney wall is coloured red. The offset surface off(sh; d) at distance d to the outer part of the chimney wall is coloured dark blue. The use of the offset surface (i.e. horizontal offset thickness) could reinforce the structure of the chimney wall. The wall would be more resistant to wind force. The surfaces sh(t, v) and sh1(ϕ, v) were cut out to show the next layer (see Figure 7).

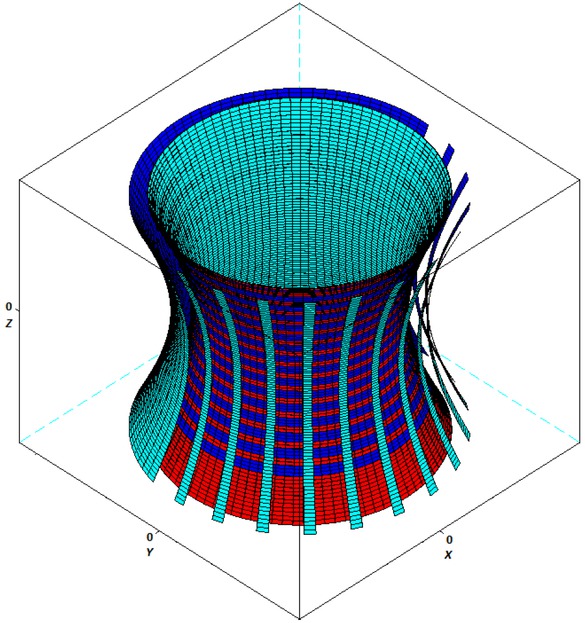
Figure 7 Wall model of a cooling tower
Figure 7

Wall model of a cooling tower

sh(t, v) : x = a cosh(t) cos(v),

y = a cosh(t) sin(v), z = b sinh(t),

sh1(ϕ, v) : x = (a cosh(ϕ) − d) cos(v),

y = (a cosh(ϕ) − d) sin(v), z = b sinh(ϕ),

off(sh; d) = sh(t, v) + dnver(t, v),

where nver(t, v) is the unit normal vector to the surface sh(t, v) at any point.

4.1 The coordinates of points P1, P2, Q1 and Q2

Let the points P, P1, P2, Q1, Q2 and curves (hyperbolas) ch(t), ch1(ϕ), ch2(ϕ) be defined as in section 2 (see Figure 3, (2), (3)).We can assume that t, ϕ ≥ 0, because the graph of the curve ch(t) (also ch1(ϕ), ch2(ϕ)) is symmetrical about the X axis. By conducting analogous calculations as in 3.1 we get the coordinates of points P1 and P2 lying on the normal l to the hyperbola ch(t) (at the point P(xt , zt)) and distant from P by the length d.

(8)xP1=xt−dbcosh⁡(t)a2sinh2(t)+b2cosh2(t),zP1=zt+dasinh⁡(t)a2sinh2(t)+b2cosh2(t),xP2=xt+dbcosh⁡(t)a2sinh2(t)+b2cosh2(t),zP2=zt−dasinh⁡(t)a2sinh2(t)+b2cosh2(t)

for xt = a cosh(t), zt = b sinh(t).

By conducting analogous calculations as in 3.2 we get the coordinates of the point Q1 (and the point Q2) (the intersection of the normal line l to the hyperbola ch(t) at the point P(xt , zt) with the hyperbola ch1(ϕ) (with the hyperbola ch2(ϕ))).

Lemma 2 (a) The coordinates of the point Q1 can be determined using the parametric equations

(9)x=cosh⁡(t)(a−kdb),z=sinh⁡(t)(b+kda)

of the normal line l to the hyperbola ch(t) at the point P(xt , zt) for the following parameter k

(10)k=k1=adb1−cosh⁡(ϕ1)cosh⁡(t)+1bcosh⁡(t)ϕ1=ln⁡E1=arsinhsinh⁡(t)1+k1dab,

where E1=(−B+Δ)/2A for

A = a2 sinh(t) + b2 cosh(t),

B = −2 sinh(t)(cosh(t)(a2 + b2) + da),

C = a2 sinh(t) − b2 cosh(t), Δ = B2 − 4AC.

(b) The coordinates of the point Q2 can be determined using the parametric equations

(11)x=cosh⁡(t)(a+kdb),z=sinh⁡(t)(b−kda)

of the normal line l to the hyperbola ch(t) at the point P(xt , zt) for the following parameter k

(12)k=k1=adbcosh⁡(ϕ1)cosh⁡(t)−1+1bcosh⁡(t)ϕ1=ln⁡E1=arsinhsinh⁡(t)1−k1dab,

where E1=(−B+Δ)/2Afor

A = a2 sinh(t) + b2 cosh(t),

B = −2 sinh(t)(cosh(t)(a2 + b2)− da),

C = a2 sinh(t) − b2 cosh(t), Δ = B2 − 4AC.

4.2 Variability of the thickness of the cooling tower shell

The deviation of the chimney wall thickness from the horizontal offset thickness has been analyzed. The structure under investigation was the chimney of the Rybnik cooling tower. The outer side of the chimney of the Rybnik cooling tower has the shape of the hyperboloid SRh(t, v). Parameters of the Rybnik chimney are shown in Figure 8 (a = 26m, b = 60.83m, constant shell thickness d = 0.14m, radius of the bottom base R2 = 47.5m, radius of the upper base R1 = 27.4m, chimney height z = 93 + 20m). Figure 8 also shows the variability of the chimney shell thickness. The first ring from the bottom is 0.6m thick. Next, on the 13 metres section, the thickness of the shell decreases to 0.18m according to the hyperbolic function. On the next 36 metres section the thickness decreases linearly to 0.14m. At the next stage (59m) the thickness is constant, equal to 0.14m. Over the last 5m the thickness increases linearly to 0.25m. We assume that the inside of the chimney (on the 59 metres section) has the shape of the hyperboloid SRh1(ϕ, v).

Figure 8 Diagram of the Rybnik chimney (cf. [11, 12])
Figure 8

Diagram of the Rybnik chimney (cf. [11, 12])

SRh(t, v) : x = 26 cosh(t) cos(v),

y = 26 cosh(t) sin(v), z = 60.83 sinh(t),

SRh1(ϕ, v) : x = (26 cosh(ϕ) − d) cos(v),

y = (26 cosh(ϕ) − d) sin(v),

z = 60.83 sinh(ϕ).

The measurements of the shape of the outer surface of the Rybnik chimney made in 1991 and 2010 showed the execution of the object with numerous deviations from the ideal geometry of the one-sheet rotational hyperboloid. The results obtained in 2010 gave extreme deviation values (to the interior of the shell −1.124m, outside the shell +0.788m) (cf. [11]).

The measurements made in the last 19 years have shown a very disturbing increment of displacements in extreme cases reaching values of 0.3-0.4m (with a tendency to move towards the interior in the lower part of the shell and outside in the upper one). The tests showed a clear threat to the load-bearing capacity and stability of the object (cf. [11]).

The method for determining the wall thickness of the cooling tower has been given. The thickness of the chimney wall is measured along the normal line l to the external surface of the chimney passing through the point P. More specifically, it was assumed that the external surface (the inner surface) of the chimney was shaped as the hyperboloid surface SRh(t, v) (respectively as the hyperboloid surface SRh1(ϕ, v)). The formula specifying distance dPQ1=|PQ1|¯(measured along the normal l to the surface SRh(t, v), between the point P and the point Q1 (the intersection of the normal l with the hyperboloid surface SRh1(ϕ, v))) was given. Because both hyperboloids are surfaces of revolution, they were replaced with hyperbolas ch(t) and ch1(ϕ) on the XZ plane. Because the hyperbolas graphs are symmetrical about the X axis, it was assumed that t, ϕ ≥ 0. Points and curves are defined as in Figure 3.

Test 1 A numerical analysis was carried out for the problem described above (see Table 1).

Table 1

Coordinates of points P and Q1, the angle t (for the point P) and ϕ (for the point Q1), coefficient k and distance dPQ1 measured at successive heights of the Rybnik chimney

xP / zPt / ϕk / dPQ1xQ1 / zQ1
xP=26t=0∘k=0.016439xQ1=25.86
zP=0ϕ=0∘dPQ1=0.14(100%)zQ1=0
xP=26.3490t=9∘22’37"k=0.016144xQ1=26.2096
zP=10ϕ=9∘23’10"dPQ1=0.1397(99.8%)zQ1=10.0097
xP=27.3692t=18∘30’51"k=0.015343xQ1=27.2317
zP=20ϕ=18∘31’50"dPQ1=0.1388(99.1%)zQ1=20.0184
xP=28.9900t=27∘13’17"k=0.014235xQ1=28.8548
zP=30ϕ=27∘14’34"dPQ1=0.1376(98.3%)zQ1=30.0255
xP=31.1175t=35∘23’1"k=0.013017xQ1=30.9849
zP=40ϕ=35∘24’29"dPQ1=0.1363(97.3%)zQ1=40.0311
xP=33.6559t=42∘57’22"k=0.011828xQ1=33.5255
zP=50ϕ=42∘58’55"dPQ1=0.1351(96.5%)zQ1=50.0354
xP=36.5196t=49∘56’39"k=0.010736xQ1=36.3911
zP=60ϕ=49∘58’12"dPQ1=0.1341(95.8%)zQ1=60.0385
xP=39.6380t=56∘22’56"k=0.009766xQ1=39.5112
zP=70ϕ=56∘24’27"dPQ1=0.1332(95.1%)zQ1=70.0409
xP=42.9559t=62∘19’4"k=0.008918xQ1=42.8304
zP=80ϕ=62∘20’31"dPQ1=0.1325(94.6%)zQ1=80.0427
xP=46.4303t=67∘48’5"k=0.008180xQ1=46.3059
zP=90ϕ=67∘49’28"dPQ1=0.1320(94.3%)zQ1=90.0440
xP=50.0288t=72∘52’56"k=0.007538xQ1=49.9053
zP=100ϕ=72∘54’16"dPQ1=0.1315(93.9%)zQ1=100.0451

The distances dPQ1 were measured for points P(xP, zP), where zP = 0, 10, ..., 100m. The distance dPQ1 decreases with the increase of zP and at the height zP = 100m dPQ1 = 0.939d.

In order to strengthen the chimney wall (at the design stage) in the part where the thickness of the shell is smallest, it is proposed to design a wall with the horizontal offset thickness. Such a construction will be more resistant to wind force. For this purpose, it is enough to shape the inside of the chimney using the hyperboloid offset surface off(SRh; d)

off(SRh; d) : x = cosh(t)(a − dbkP1) cos(v),

y = cosh(t)(a − dbkP1) sin(v),

z = sinh(t)(b + dakP1),

where kP1=1/a2sinh2t+b2cosh2t.

Test 2 A numerical analysis was carried out for the following problem. At the following heights zPP1 = 0, 10, ..., 100m of the chimney (see the point PP1(xPP1, zPP1) in Figure 3) the horizontal offset thickness of the chimney wall was determined. I.e. for consecutive values zP1 = zPP1 the coordinates of points P1, PP1 and distance dP1PP1=|P1PP1|¯were calculated. Because the hyperboloid SRh(t, v) and the offset off(SRh; d) are surfaces of revolution, they were replaced with hyperbola ch(t) and offset off(ch; d) on the XZ plane. Because the graphs of both these curves are symmetrical about the X axis, it was assumed that t, ϕ ≥ 0. Points and curves are defined as in Figure 3.

Method. For each value i = 0, 10, ..., 100 such an angle t was determined that zP1(t) = i. Because zP1(t) = zPP1(t), the coordinates of the point PP1 can be determined as follows xPP1 = a cosh(α), zPP1 = b sinh(α), where α = arsinh(zP1/b). Additionally, the point Q1(xQ1, zQ1) was determined for the angle ϕ (cf. (10)). Table 2 also gives the distance dPQ1 ≤ d (when the inner wall is shaped as the surface SRh1) and the horizontal offset thickness dP1PP1 ≥ d (when the inner wall is shaped as the offset surface off(SRh; d)). The distance dP1PP1 increases with increasing zP1.

Table 2

Coordinates of points P, PP1, P1 and Q1, the angle t (for the point P), ϕ (for the point Q1), α (for the point PP1) and distances dPQ1 and dP1PP1 measured at successive heights of the Rybnik chimney

xP/xPP1/xP1/xQ1zP/zPP1/zP1/zQ1t / ϕ / αdPQ1 / dP1PP1
xP=26zP=0t=0∘dPQ1=0.14
xPP1=26zPP1=0ϕ=0∘(100%)
xP1=25.86zP1=0α=0∘dP1PP1=0.14
xQ1=25.86zQ1=0
xP=27.3668zP=19.9815t=18∘29’51"dPQ1=0.1388
xPP1=27.3692zPP1=20ϕ=18∘30’50"(99.1%)
xP1=27.2280zP1=20α=18∘30’51"dP1PP1=0.1412
xQ1=27.2292zQ1=19.9998
xP=31.1100zP=39.9680t=35∘21’30"dPQ1=0.1363
xPP1=31.1175zPP1=40ϕ=35∘22’58"(97.3%)
xP1=30.9737zP1=40α=35∘23’1"dP1PP1=0.1438
xQ1=30.9773zQ1=39.9991
xP=36.5075zP=59.9598t=49∘55’2"dPQ1=0.1341
xPP1=36.5196zPP1=60ϕ=49∘56’35"(95.8%)
xP1=36.3734zP1=60α=49∘56’39"dP1PP1=0.1462
xQ1=36.3790zQ1=59.9983
xP=42.9405zP=79.9549t=62∘17’31"dPQ1=0.1325
xPP1=42.9559zPP1=80ϕ=62∘18’59"(94.6%)
xP1=42.8080zP1=80α=62∘19’4"dP1PP1=0.1479
xQ1=42.8150zQ1=79.9976
xP=50.0113zP=99.9520t=72∘51’32"dPQ1=0.1315
xPP1=50.0288zPP1=100ϕ=72∘52’51"(93.9%)
xP1=49.8798zP1=100α=72∘52’56"dP1PP1=0.1490
xQ1=49.8878zQ1=99.9971

5 Applications of the given method

The given geometric method can be used, among other things, for modelling hyperboloid objects in architecture and civil engineering design. Its advantages will be presented using examples of domes and elevations designed with a hyperboloid shape.

The geometry of the base surface of the dome (roof) has a decisive influence on the majority of its construction features: load-bearing capacity, rigidity, simplicity of execution, aesthetics. Therefore, at present mainly geodesic lattice domes are used (low dead weight of the structure with relatively high load capacity [13]) (cf. [14]). Since the offset surfaces of the sphere are spheres, it is easy to obtain surfaces approximating the base sphere. However, for more representative architectural objects, designers propose more glamorous roofs (Sydney Opera House, Wanda Metropolitano (Madrit), Yas Island Marina Hotel

(Abu Dhabi),Mercedes Benz Stadium (Atlanta), Khalifa International Stadium (Qatar).

In order to shape a lattice dome (or a roof) it is necessary to define (in a mathematical way) the surface on which the coating will be stretched. The proposed method provides simple mathematical formulas for angles and coordinates of points of various surfaces approximating the hyperboloid of revolution. Additionally, it allows the designer to adjust the height of the dome in order to ensure its stability. The given method can be used in CAD (Computer-Aided Design). (A) Thanks to the given formulas, any element (e.g. a dome, its fragment) of hyperboloid shape can be designed in any programming language (e.g. Cpp) and saved in DXF format. The DXF file can be imported into AutoCAD to get a DWG file (a standard file format for CAD). In this way, the designer can obtain (cf. [15]) in a very short time (at very little cost) a set of complicated digital models (for different parameters). If the object consists of many hyperboloid fragments, in order to make a digital mock-up of the whole object, the designer can "assemble" created digital submodels (fragments) instead of scanning a three-dimensional mock-up made by the artist. There are a lot of programs (Digital Project, Rhino-Grasshopper, CA-TIA, Pro / ENGINEER) that contain parametric design tools and offer designers tools for creating parametric scripts (cf. [16, 17]). Mainly thanks to them, it was possible to design objects such as Sagrada Familia (Barcelona), Beijing National Stadium (China) (cf. [16]). The reader can see the parametric script for positioning hyperbolas and their placement on a given substrate written (by Burry M.) in Python programming language (cf. [16, 18]). (B) The possibility of (easy) precise dimensioning of individual elements of a structure with complex geometry can be used for prefabrication using CNC machine (Computerized Numerical Control). More precisely, for a 3D model designed in CAD a designer can obtain (using CAM software (Computer Aided Manufacturing)) instructions for a CNC machine [19]. CNC machining allows fast, precise and repeatable execution of elements with a complex shape. Hence, more and more architectural companies are interested in designing objects with a curvilinear geometry. The advantages of assembling prefabricated structures are precise execution, easier transport and assembly. The hyperboloid surface ensures repeatability of elements (e.g. triangular panels) at the same height of the coating.

The given method simplifies the analysis of the approximation of the hyperboloid offset surface off(S(t, v); d) by the hyperboloid surface S1(ϕ, v). For illustration, the wall thickness of the cooling tower formed by two one-sheet rotational hyperboloids SRh(t, v) and SRh1(ϕ, v) was analyzed (cf. section 4.2). The distance between the two hyperboloid surfaces was measured (along the normal line to the surface SRh(t, v)). It was shown that the deviation from the constant thickness d = 0.14m increases with the increase of the coordinate zP. For the cooling tower Rybnik, the largest deviation is 3% (dPQ1 = 0.1358m) and takes place for zP = 44m (=59m-15m (cf. Figure 8)).

In a similar way, the thickness of the dome formed by the two-sheet rotational hyperboloids S h(t, v) and Sh1(ϕ, v) (cf. 3.2) was tested (for the parameter values a = 30, b = 40, d = 0.4m). The maximum deviation from the intended thickness d = 0.4m (for the dome with a base diameter equal to 30m (40m, 50m, 60m) and a height equal to 4.7214m (8.0740m, 12.0684m, 16.5686m)) is 14.00% (19.50%, 23.86%, 27.18%). The test was repeated for b = 50. Then the maximum deviation from the intended thickness d (of the dome with a base diameter equal to 30m (40m, 50m, 60m) and a height equal to 5.9017m (10.0925m, 15.0854m, 20.7107m)) was 19.67% (26.45%, 31.53%, 35.24%).

Similar calculations can help a designer decide whether to use the offset surface and assemble the object from the CNC prefabricates or accept the deviation (or change the values of the hyperboloid parameters).

6 Summary

In order to design objects in the shape of the hyperboloid S(t, v), different surfaces approximating this hyperboloid are needed. It is necessary to ensure that the construction has the appropriate thickness (stability). The paper presents the method of determining the angles and coordinates of points of various surfaces approximating the hyperboloid of revolution. Thanks to this method, the designer can easily calculate the distance between the hyperboloid S(t, v) and the surface approximating it along the normal line l passing through the point P.

The one-sheet hyperboloid is a doubly ruled surface. It means that hyperboloid shaped constructions can be built with straight steel beams that form a strong structure. The surface approximating the hyperboloid was used to strengthen the wall of the cooling tower (at the design stage). The new mathematical models have been tested and proven in real cases, such as the Rybnik cooling tower chimney, providing real parameters.

A double-layer hyperboloid-shaped lattice dome was proposed as a roof for a large object (e.g. shopping centre). The connection by means of bars of two layers with an approximate shape is intended to strengthen the roof structure. The bar structures of the low-profile single-layer domes are particularly susceptible to stability loss (cf. [8]).

The main advantage of the given method is the simplification of the design process as well as time and cost saving. To design any hyperboloid shaped dome, a student needs a compiler for a programming language (cost=0) and AutoCAD (for students).

Acknowledgement

The research presented in this paper was founded by the BST S/WI/1/2014 and WZ/WBiIŚ/6/2019.

References

[1] Figure 1 https://commons.wikimedia.org/wiki/File:Kobe_Kobe_Port_Tower_%26_Maritime_Museum_1.jpg.Suche in Google Scholar

[2] Figure 2 http://chodor-projekt.net/encyclopedia/najwiekszekopuly.Suche in Google Scholar

[3] Koźniewski E., Offsets in geometric creation of roof skeletons with varying slope and cut-and-fill problems in topographic projection, The Journal Biuletyn of Polish Society for Geometry and Engineering Graphics, 2010, vol. 21, 29-35.Suche in Google Scholar

[4] Koźniewski M., Thickness analysis of a saddle, The Journal Biuletyn of Polish Society for Geometry and Engineering Graphics, 2016, vol. 28, 25-32.Suche in Google Scholar

[5] Borowska A., Approximation of the ellipse offset curves in turbo roundabouts design, The Journal Biuletyn of Polish Society for Geometry and Engineering Graphics, 2018, vol. 31, 43-51.Suche in Google Scholar

[6] Pottmann H., Asperl A., Hofer M., Kilian A., Architectural Geometry, 2007, Pennsylvania USA: Bentley Institute Press. Exton.Suche in Google Scholar

[7] Leja F., Rachunek różniczkowy i całkowy [Differential and integral calculus], 1973, Warsaw: PWN.Suche in Google Scholar

[8] Bysiec D., The investigation of stability of double-layer octahedron-based geodesic domes, Structure and Environment, 2011, vol. 3, No. 3, 30-41.Suche in Google Scholar

[9] Mirski J., The investigation of the geometric stability of the selected group of the double-layer bar domes. The 6th Scientific-Technical Conference "Current Scientific and Exploratory Problems in Civil Engineering", The University of Warmia and Mazury, (Olsztyn-Kortowo, Poland), 2003, 225-234.Suche in Google Scholar

[10] Grzegorczyk J., Mathematics, 1978, Warsaw: Wydawnictwa Politechniki Warszawskiej.Suche in Google Scholar

[11] Mazur J., Zastosowanie nowoczesnych technologii wzmacniania obiektów przemysłwych na przykładzie wzmocnienia płaszcza żelbetowego chłodni kominowej nr 1 w EDF Rybnik SA (Elektrownia Rybnik SA) [Application of modern reinforcement technologies for industrial structures shown in exemplary reinforced concrete lining repair at cooling tower no. 1 in EDF Rybnik SA (Rybnik Power Plant SA)]. XXVI Konferencja Naukowo-Techniczna Awarie Budowlane, (Międzyzdroje, Poland), 2013, May 21-24, 1023-1032.Suche in Google Scholar

[12] Owczarzy J., Kossowski J., Nieklasyczne zachowanie się modelu hiperboloidalnej chłodni kominowej pod obciążeniem osiowo symetrycznym [A nonclasic behaviour model of hyperbolic shell of cooling tower under axisymmetric loading], Journal of Theoretical and Applied Mechanics, 1981, 2, 19, 225-238.Suche in Google Scholar

[13] Radoń U., Zastosowanie metody FORM w analizie niezawodności konstrukcji kratowych podatnych na przeskok [Application method FORM in reliability analysis of node snapping truss structures], Monografie Studia Rozprawy nr M27, 2012, Kielce: Wydawnictwo Politechniki Świętokrzyskiej.Suche in Google Scholar

[14] Gayakwad B.R., Hiriyur A., Patil V.V., Arjun K., Lakshmi S., Design considerations for a geodesic dome – a critical review, International Journal of Advances in Science Engineering and Technology, 2018, vol. 6, Iss. 1, 8-13.Suche in Google Scholar

[15] Koźniewski E., Geometria odwzorowań inżynierskich powierzchni 05A, Scriptiones Geometrica, 2014, vol. 1, No. 5A, 1-17. https://docplayer.pl/14511873-Geometria-odwzorowaninzynierskich-powierzchnie-05a.htmlSuche in Google Scholar

[16] Januszkiewicz K., Projektowanie parametryczne oraz parametryczne narzędzia cyfrowe w projektowaniu architektonicznym [Parametric design and parametric digital tools in architectural design], Architecture et Artibus, 2016, vol. 8, No. 3, 43-60.Suche in Google Scholar

[17] Stavrić M., Stokić D., Ilić M., Architectural Scale Model in Digital Age – Design Process, Representation and Manufacturing, ECAADE Conference, (Prague, Czech Republic), 2012, September 12, Prague: Faculty of Architecture, 33-41.Suche in Google Scholar

[18] Burry M., Scripting Cultures, 2013, Chichester: JohnWiley & Sons Ltd.10.1002/9781118670538Suche in Google Scholar

[19] Czech-Dudek K., Zastosowanie systemów CAD/CAM w przygotowaniu produkcji [Application systems CAD/CAM in the preparation of production], Mechanik, 2015, 7, 149-158.Suche in Google Scholar

Received: 2019-05-21
Accepted: 2019-07-02
Published Online: 2019-08-12

© 2019 E. Koźniewski and A. Borowska, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Regular Article
  2. Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
  3. A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
  4. Identification of geodetic risk factors occurring at the construction project preparation stage
  5. Multicriteria comparative analysis of pillars strengthening of the historic building
  6. Methods of habitat reports’ evaluation
  7. Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
  8. Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
  9. On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
  10. Dynamic safety system for collaboration of operators and industrial robots
  11. Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
  12. Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
  13. EFQM model implementation in a Portuguese Higher Education Institution
  14. Assessment of direct and indirect effects of building developments on the environment
  15. Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
  16. Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
  17. Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
  18. Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
  19. Synthesis Conditions for LPV Controller with Input Covariance Constraints
  20. Procurement management in construction: study of Czech municipalities
  21. Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
  22. Control of construction projects using the Earned Value Method - case study
  23. Model supporting decisions on renovation and modernization of public utility buildings
  24. Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
  25. Failure Analysis of Super Hard End Mill HSS-Co
  26. Simulation model for resource-constrained construction project
  27. Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
  28. Analysis of renewable energy use in single-family housing
  29. Modeling of the harmonization method for executing a multi-unit construction project
  30. Effect of foam glass granules fillers modification of lime-sand products on their microstructure
  31. Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
  32. Analysis of occupational accidents in the construction industry with regards to selected time parameters
  33. Bill of quantities and quantity survey of construction works of renovated buildings - case study
  34. Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
  35. Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
  36. Quartz bentonite sandmix in sand-lime products
  37. The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
  38. Analysis of workplace injuries in Slovakian state forestry enterprises
  39. Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
  40. Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
  41. Hyperboloid offset surface in the architecture and construction industry
  42. Analysis of the preparatory phase of a construction investment in the area covered by revitalization
  43. The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
  44. Impact of high temperature drying process on beech wood containing tension wood
  45. Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
  46. Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
  47. The feasibility of using a low-cost depth camera for 3D scanning in mass customization
  48. Urban Water Infrastructure Asset Management Plan: Case Study
  49. Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
  50. Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
  51. IoT Applications in Wind Energy Conversion Systems
  52. A new method for graph stream summarization based on both the structure and concepts
  53. “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
  54. Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
  55. Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
  56. Statistical model used to assessment the sulphate resistance of mortars with fly ashes
  57. Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
  58. Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
  59. Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
  60. Optimization of shape memory alloy braces for concentrically braced steel braced frames
  61. Topical Issue Modern Manufacturing Technologies
  62. Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
  63. Topical Issue: Progress in area of the flow machines and devices
  64. Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
  65. Investigations of drilled and multi-piped impellers cavitation performance
  66. The novel solution of ball valve with replaceable orifice. Numerical and field tests
  67. The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
  68. Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
  69. A new solution of the semi-metallic gasket increasing tightness level
  70. Design and analysis of the flange-bolted joint with respect to required tightness and strength
  71. Special Issue: Actual trends in logistics and industrial engineering
  72. Intelligent programming of robotic flange production by means of CAM programming
  73. Static testing evaluation of pipe conveyor belt for different tensioning forces
  74. Design of clamping structure for material flow monitor of pipe conveyors
  75. Risk Minimisation in Integrated Supply Chains
  76. Use of simulation model for measurement of MilkRun system performance
  77. A simulation model for the need for intra-plant transport operation planning by AGV
  78. Operative production planning utilising quantitative forecasting and Monte Carlo simulations
  79. Monitoring bulk material pressure on bottom of storage using DEM
  80. Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
  81. Design of evaluation tool used to improve the production process
  82. Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
  83. Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
  84. The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
  85. Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
  86. Current options in the life cycle assessment of additive manufacturing products
  87. Ideal mathematical model of shock compression and shock expansion
  88. Use of simulation by modelling of conveyor belt contact forces
https://doi.org/10.1515/eng-2019-0051
Schlagwörter für diesen Artikel
hyperbola offset curve; one-sheet hyperboloid; two-sheet hyperboloid
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Regular Article
  2. Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
  3. A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
  4. Identification of geodetic risk factors occurring at the construction project preparation stage
  5. Multicriteria comparative analysis of pillars strengthening of the historic building
  6. Methods of habitat reports’ evaluation
  7. Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
  8. Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
  9. On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
  10. Dynamic safety system for collaboration of operators and industrial robots
  11. Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
  12. Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
  13. EFQM model implementation in a Portuguese Higher Education Institution
  14. Assessment of direct and indirect effects of building developments on the environment
  15. Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
  16. Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
  17. Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
  18. Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
  19. Synthesis Conditions for LPV Controller with Input Covariance Constraints
  20. Procurement management in construction: study of Czech municipalities
  21. Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
  22. Control of construction projects using the Earned Value Method - case study
  23. Model supporting decisions on renovation and modernization of public utility buildings
  24. Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
  25. Failure Analysis of Super Hard End Mill HSS-Co
  26. Simulation model for resource-constrained construction project
  27. Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
  28. Analysis of renewable energy use in single-family housing
  29. Modeling of the harmonization method for executing a multi-unit construction project
  30. Effect of foam glass granules fillers modification of lime-sand products on their microstructure
  31. Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
  32. Analysis of occupational accidents in the construction industry with regards to selected time parameters
  33. Bill of quantities and quantity survey of construction works of renovated buildings - case study
  34. Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
  35. Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
  36. Quartz bentonite sandmix in sand-lime products
  37. The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
  38. Analysis of workplace injuries in Slovakian state forestry enterprises
  39. Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
  40. Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
  41. Hyperboloid offset surface in the architecture and construction industry
  42. Analysis of the preparatory phase of a construction investment in the area covered by revitalization
  43. The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
  44. Impact of high temperature drying process on beech wood containing tension wood
  45. Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
  46. Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
  47. The feasibility of using a low-cost depth camera for 3D scanning in mass customization
  48. Urban Water Infrastructure Asset Management Plan: Case Study
  49. Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
  50. Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
  51. IoT Applications in Wind Energy Conversion Systems
  52. A new method for graph stream summarization based on both the structure and concepts
  53. “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
  54. Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
  55. Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
  56. Statistical model used to assessment the sulphate resistance of mortars with fly ashes
  57. Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
  58. Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
  59. Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
  60. Optimization of shape memory alloy braces for concentrically braced steel braced frames
  61. Topical Issue Modern Manufacturing Technologies
  62. Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
  63. Topical Issue: Progress in area of the flow machines and devices
  64. Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
  65. Investigations of drilled and multi-piped impellers cavitation performance
  66. The novel solution of ball valve with replaceable orifice. Numerical and field tests
  67. The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
  68. Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
  69. A new solution of the semi-metallic gasket increasing tightness level
  70. Design and analysis of the flange-bolted joint with respect to required tightness and strength
  71. Special Issue: Actual trends in logistics and industrial engineering
  72. Intelligent programming of robotic flange production by means of CAM programming
  73. Static testing evaluation of pipe conveyor belt for different tensioning forces
  74. Design of clamping structure for material flow monitor of pipe conveyors
  75. Risk Minimisation in Integrated Supply Chains
  76. Use of simulation model for measurement of MilkRun system performance
  77. A simulation model for the need for intra-plant transport operation planning by AGV
  78. Operative production planning utilising quantitative forecasting and Monte Carlo simulations
  79. Monitoring bulk material pressure on bottom of storage using DEM
  80. Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
  81. Design of evaluation tool used to improve the production process
  82. Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
  83. Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
  84. The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
  85. Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
  86. Current options in the life cycle assessment of additive manufacturing products
  87. Ideal mathematical model of shock compression and shock expansion
  88. Use of simulation by modelling of conveyor belt contact forces
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 18.10.2025 von https://www.degruyterbrill.com/document/doi/10.1515/eng-2019-0051/html
Button zum nach oben scrollen