Abstract
Expanding the use of smart braced frames to govern the seismic response of structures by providing ductility and elasticity has been hampered and delayed by cost indexes. The braces in frames comprise two segments of expensive shape memory alloys (SMAs) and high-strength steel with high stiffness. These smart materials can reduce seismic damage by providing stiffness, yielding, and phase shifting. In this study, the length of the SMA segments in three- and six-story frames (applied either at all floors or as part of a dual system) was increased to determine the optimal length at a constant period. Performance levels and fragility curves were obtained to evaluate the seismic behavior of the optimized frame. The response modification factor determined based on the static pushover, incremental nonlinear dynamic analysis, and linear dynamic analysis suggests the ductility and over-strength of the optimized frame. The probability of being in or exceeding each damage state was determined with a Monte Carlo analysis and was acceptable and in accordance with previous deterministic analysis results.
1 Introduction
The aspiration of a design must always be balanced by safety and cost. Increased observations, new inventions, and a progressive shift in design philosophy have tended to challenge the creativity and approach of engineers. Earlier seismic designs, for example, were determined only by the ductility and energy dissipation of the beam–column connections of the moment-resisting frames, which gradually enhanced the stiffness of the steel braced frames to preclude massive sections and decrease displacements. However, the introduction of performance-based seismic design approaches, which determine failures through residual roof and interstory drifts, necessitates significantly more ductility in nonlinear regions and stiffness in linear regions of the design compared to conventional design. Buckling-restrained brace (BRB) frames that are used to respond to these requirements can provide stiffness by restraining buckling. However, the accumulation of displacements owing to large ground motions and inappropriate eccentricity may still result in destruction.
Remarkable breakthroughs in material engineering and the emergence of shape memory alloys (SMAs) with promising material characteristics such as super-elasticity, high damping capacity, high fatigue and corrosion resistance, and less maintenance allow for the possibility of alternative load-resisting systems [1]. An SMA can provide stiffness in linear regions and ductility and energy dissipation in nonlinear regions by exhibiting two macroscopic behaviors through a flag-shaped stress–strain hysteresis diagram: super-elasticity (SE) and a shape memory effect (SME).
A phase transformation alternating between two crystalline structures makes these characteristics possible. One crystalline structure, austenite, is a symmetric stable cubic structure, which occurs at high temperature and low stress; the other crystalline structure, martensite, is a less ordered structure, which is stable at low temperature and high stress. The transformations between these structures may be activated by stress, tension, temperature, electrical and magnetic fields, or even light [2].
Super-elasticity eliminates severe strain during cyclic loading. In this regard, the material exposed to a load above the austenite finish temperature shifts from full-austenite (A) to de-twinned martensite (B). This deformation reverts upon unloading (A). SME is a property which can recover residual plastic deformation upon heating. While the ambient temperature is less than the austenite start temperature after loading and unloading, the remaining de-twinned martensite returns to its original state (austenite) after heating through loss of strain [3].
The ability of an element to recover its shape without any additional load owing to its SE properties paves a path for cost-efficient passive control systems to mitigate residual drifts, which impose geometric nonlinearity and unwelcome moments for the stability. The flag-shaped stress– strain relationship also dissipates large amounts of energy during cyclic hysteresis loading through the SME. As a result, new applications have been found in fields such as medicine [4], aerospace, mechanical engineering, and structural engineering.
Following the Memory Alloys for New Seismic Isolation DEvices (MANSIDE) project [5], the functionality of SMA for seismic control was demonstrated by Dolce [6]. Subsequent researchers including DesRoches investigated the effects of changing parameters such as the intensity, loading amount, and geometry of SMA equipment [7].SMA has been used in dampers [8, 9, 10], springs, smart connections [11, 12, 13], 14, isolations, and concrete reinforcement bars [15, 16]. McCormick et al. compared SMA frames to conventional steel frames using an analytical model [17], and then assessed a micro-scale sample using a shaking table [18]. Smaller residual interstory drifts were established in comparison with the BRB frame [19, 20], and a dual system was introduced consisting of both BRB and SMA braces in the height [21]. Cost-effective hybrid dampers consisting of lower amounts of SMA were proposed [22], while another study proposed a damper utilizing not only SMA, but also BRB components at one brace element [23]. Some studies have calculated the overstrength and response modification factor for frames enhanced by smart braces [24, 25, 26].
Despite the introduction of new SMAs and manufacturing developments [27, 28], there are still challenges with the manufacturing and weaker performance of many SMAs. Thus, the expensive nickel–titanium (NiTi) is one of the most commonly used SMA materials [2]. Bruno and Valente performed a cost-induced study by considering direct (structural and non-structural) and indirect (health and injury) effects, which was one of the pioneering projects comparing conventional systems with SMA [29]. The self-centering property for mitigating drifts has made cost-effective passive control more acquirable by reducing financial loss and minimizing human risk.
Inasmuch as the whole brace cannot utilize the costly SMA while the size of civil engineering structures is large owing to surrounding forces [30], engineers equip one segment of the brace with an SMA welded to a high-strength steel comprising the rest of the brace, and thus the strains will only be observed in the SMA portion. However, questions persist about what the optimized length should be, and how any change in that length may affect the structural behavior.
To this end, SMA segments in three- and six-story concentrically braced frames with a constant stiffness at the braces were varied and analyzed using the Open System for Earthquake Engineering System (OpenSEES) [31]. The results were compared in Matlab based on the maximum interstory and residual roof drifts along with the construction costs. Dual bracing systems containing SMA braces at the lower floors and steel braces at the upper stories were also assessed, which presented the number of stories minus one, optimized frames.
Then, performance of the three-story optimized frame was broadly assessed when subjected to 40 ground motions. Response modification factors were then suggested through an incremental dynamic analysis (IDA) of 22 far field records. The fragility curve for each damage state of the optimized frame, along with the probability of being in or exceeding each damage state, were estimated with a Monte Carlo probabilistic analysis.
This time-wise method was found to be effective in reducing the seismic response and limiting the structural cost, as a large number of frames were generated and compared with the obtained optimum one. The probabilistic and deterministic results combined with the performance level showed that a small amount of SMA can improve the seismic response. Optimum dual-braced frames in this regard were found to be suitable representatives of the lateral load system.
2 Analytical model
Three- and six-story concentrically braced frames proposed by McCormick and derived from the investigation conducted by Sabelli on broadening the assessment of braced frames complementary to a FEMA/ SAC project [32] in Los Angeles, USA were used in this assessment for consistency. The structural designs were governed by the 1994 Uniform Building Code and 1997 National Earthquake Hazard Reduction Program; Recommended Provisions for Seismic Regulations for New Buildings and Other Structures. The lateral load resistance of the structures has been provided with the traditional chevron braced bays along the perimeter. There are eight bays of bracing, four in each direction, placed in non-adjacent bays for both buildings. Further details concerning the building design are provided in these previous studies [17, 33, 34].
The frames have a span 9.144 m (30 ft) in width, and the height of each story is 3.962 m(13 ft), excluding the first floor of the six-story frame, which has a height of 5.486 m (18 ft). The base connections are rigid. The periods of the three- and six-story frames are 0.46 and 0.74 s, respectively. A plan view of buildings, braced bay dimensions, and the member sizes of the steel braced frames are presented in Figure 1 and Figure 2.
![Figure 1 Plan and elevated view of the three-story frames (mm), the penthouse indicated with a dashed line [35].](/document/doi/10.1515/eng-2019-0084/asset/graphic/j_eng-2019-0084_fig_001.jpg)
Plan and elevated view of the three-story frames (mm), the penthouse indicated with a dashed line [35].
![Figure 2 Plan and elevated view of the six-story frame (mm), the penthouse indicated with a dashed line [35].](/document/doi/10.1515/eng-2019-0084/asset/graphic/j_eng-2019-0084_fig_002.jpg)
Plan and elevated view of the six-story frame (mm), the penthouse indicated with a dashed line [35].
Because the whole structure is symmetric, only one braced bay is modeled in two dimensions. As the braces are the only systems resisting the lateral load, the masses in each floor are derived by dividing the total mass of each floor by the number of braces for each horizontal direction. A typical Rayleigh damping of 5% for the frames and the P-delta effect are also considered in the analysis.
The sections were input in OpenSEES using the fiber-section command. Except for the roof, all beam–column connections are rigid. The Steel01 bilinear command described the steel behavior in the beams and columns, while the steel in the braces was input with a uniaxial hysteric command describing the strength and stiffness degradation along with the pinching behavior.
The smart frames have the same beams and columns as the steel frames, and only the braces are replaced. For rational comparison, both the steel and smart frames have the same natural period, and the material at both braces should yield at the same strength.
The whole brace in the smart frame is not fabricated from SMA; rather, a rigid segment connected to the specific length of SMA is used to construct the brace (see Figure 3). This rigid segment causes all the deformation to occur in the SMA portion. In a constant-period section of SMA, segments with different lengths are equal to the stiffness of the brace multiplied by the length of the SMA segment and divided by the modulus of elasticity of the SMA.
![Figure 3 Detail of the SMA brace installed in the three-story frame [35].](/document/doi/10.1515/eng-2019-0084/asset/graphic/j_eng-2019-0084_fig_003.jpg)
Detail of the SMA brace installed in the three-story frame [35].
The SMA was implemented with the self-centering command in OpenSEES. Five integral points were considered for each element defined by the nonlinear beam column command. Segments of the braces were connected with zero-length elements having high stiffness at the SMA–steel connections. Material properties adopted for numerical simulations are presented in Table 1.
Material Properties Adopted for the Numerical Simulations [35].
| Young’s modulus (MPa) | Steel yielding stress (MPa) | Transformation stress level (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| Austenite-martensite | Martensite-austenite | |||||||
| Steel | SMA | Brace | Beam | Column | Start | Finish | Start | Finish |
| 200000 | 27579 | 250 | 345 | 345 | 414 | 550 | 390 | 200 |
3 Optimizing smart frames
As the advantages of SMA-braced frames over conventional steel frames have previously been established, determining the optimum length of the SMA segments based on the roof and interstory driftswhile limiting the construction cost is necessary. To this end, the SMA length of each brace is increased sequentially to create a series of frames, each of which can be analyzed to determine the optimal configuration.
In this type of an analysis, time is essential, particularly for a high-rise structure. If each of the runs requires a unit of time, T, then for an M-story frame with N divisions of the brace, the whole run will require a time equal to N^M×T.
On the other hand, as the need for SMA lies in the lower stories of the frames, frames with varying lengths of SMA in the first floor and the lowest possible length of SMA in the upper stories are first analyzed to determine the optimum length of SMA for the first floor. Then, once the optimal length for the SMA segments in the first floor braces is established, the length of SMA in the second floor will be changed to determine the optimum length for that floor. This procedure is then repeated for the other stories until optimum SMA segment lengths have been determined for the braces in all floors. This method can reduce the total required analysis time to M×N×T. For example, in a three-story frame with 16 divisions for each brace, the total time required to complete the analysis is 0.117 times that required with the previous method, while for a six-story frame, the total time required is 0.0000057 times that required previously.
Meta-heuristic methods with the ability to escape from local extrema could also be utilized; the predefined path, as it is limited on the first floor, is not only immune to becoming trapped in local extrema, but it is also time-efficient. Although extremely time-efficient, there could be a non-analyzed frame which has a better result than all the analyzed combinations. Therefore, a series of frames with different divisions for each brace were produced to verify the result.
3.1 Cost analysis of the steel–SMA structure
The SMA used in the design can reduce the seismic response. It would nonetheless increase the structural cost. Thus, this increase in the cost of the optimum frame should be compared with the cost of conventional steel frame or frames with a smaller amount of SMA. Therefore, a series of frames has been introduced and analyzed to evaluate the effectiveness of the method in response reduction as well as to portray the relation between response reduction and cost.
Cost assessments of possible candidates were performed for thewhole structure by considering the steel and SMA costs,while neglecting other costs such as fabrication and erection. SMA and steel costs can be calculated easily based on the information provided by the suppliers of these materials [36, 37]. For steel, multiplying the steel cost per unit weight by the weight of steel in the building was used to evaluate the cost.
In this calculation, Csteel is the steel cost; i is the number of members; Csi is cost per unit weight,which ranged from 1.7 to 2.2 USD/ kg depending on the sections [38]; and Wi is the weight, which is equal to ρiliai, where ρi is the steel density (equal to 7.85 g/cm3), li is the length, and ai is the section area of the elements.
SMA bars with symmetrical behavior under tension and compression are commonly assumed to be trapped in a buckle-resistant hollow tube [25] with diameters ranging from 12mm to 30 mm[17]; members with similar section areas have very similar cost.
In this calculation, CSMA is the SMA cost; Csm is the cost per unit volume, which is equal to 5150 USD/m3 [39]; j is the number of SMA elements; and Vj is volume, which is equal to ljaj, where lj is the length, and aj is the section area of the SMA elements.
3.2 Seismic behavior of the optimized frames
3.2.1 Performance-based analysis
Performance-based criteria include imposed damage and remaining occupancy and can be obtained from either force or deformation control approaches. Joint rotation, residual and maximum drift of elements with respect to the seismic design level, lateral load resistance systems, and the height of the structure are common deformation control approaches proposed in the relevant guidelines. The Hazus [40] recommendations for low- and mid-rise steel brace frames are presented in Table 2.
Structural Performance Levels for Steel Braced Frame [40].
| Steel braced frame | Interstory drift at threshold of damage state | |||
|---|---|---|---|---|
| Slight | Moderate | Extensive | Complete | |
| Low- rise | 0.005 | 0.01 | 0.03 | 0.08 |
| Mid- rise | 0.0033 | 0.0067 | 0.02 | 0.0533 |
3.2.2 Response modification factor
Traditional simple linear analyses, although reducing the analysis time and cost, may significantly increase the base shear responses. Excluding the energy dissipation of non-linear regions leads to this elevated response. The force reduction or response modification factor considers the over-strength and ductility to relate the nonlinear response to the linear response. Response modification factors for the optimized frames were calculated using the proposed ATC-19 procedure [41]. Thus, the response modification factor is a combination of the overstrength factor
![Figure 4 lateral load-roof displacement relationship [42].](/document/doi/10.1515/eng-2019-0084/asset/graphic/j_eng-2019-0084_fig_004.jpg)
lateral load-roof displacement relationship [42].
3.2.3 Possibility of destruction
While a deterministic analysis can effectively determine structural behaviors, the random essence of the solution space inhibits the principle of exactly defining decisive variables such as the strength, member section area, and ambient loading. In fact, mathematically engaging the uncertainty associated with the variables in the solution method is a decent step toward estimating the reliability of the structure. As a result, the lower the reliability of the structure is, the more the chance of failure will increase. A probabilistic analysis using a Monte Carlo method considering the mean and standard deviations of variables produces and analyzes random samples to determine the average response.
To this end, after establishing the mean and standard deviation for the elements representing the frame, a series of frames are produced and analyzed using the IDA. The peak ground acceleration scaling factors corresponding to each damage state for each sample can then be obtained. Finally, the probability of damage for each record and performance level can be determined from the extent of overlapping in the lognormal diagram of the Peak Ground Acceleration (PGA) scaling factors and the seismic loads.
4 Results and Discussion
4.1 Optimized smart frame
In the analysis procedure, the parametric code in OpenSEES used two for-loops. The lower ran the analysis using the time history of the 1994 Rinaldi receiving station Northridge ground motion (LA16) for varying lengths of the SMA segments in the selected story. The results were transferred as a text file to the Matlab software. The M-file in Matlab determined the optimum length of the braces for that floor considering the interstory and roof drifts. The number indicating the optimum length was written in another text file that was used to generate the analysis of the upper floors. Data transfer between the two programs stopped when the last loop finished the uppermost brace, and the optimized braced frame was output.
Three-story frames with varying SMA lengths in the braces of the first floor, ranging from 1 to 64 portions of the entire 64 divisions of the brace, exhibit nearly the same residual interstory drift (less than 0.8 mm). However, when 12 SMA portions are subjected to the LA16 seismic record, the maximum interstory drift is decreased to 57.7 mm(1.457% of the story height) (see Figure 5), while utilizing more SMA than that would only serve to increase the price with no impact on the result.
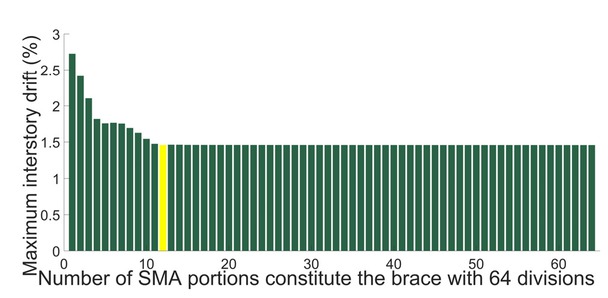
Maximum interstory drift of the three- story frames.
Initially, the upper floors previously included only one SMA element in the 64 divisions of the brace; utilizing 5 SMA elements in the second floor segment and 6 in the roof comprise the optimum combination. This combination eventually reduces the maximum interstory drift to 43.1 mm (1.087% of the story height).
Meanwhile, to verify this procedure and consider possible alternatives, a large number of frames were produced and subjected to the time history of the LA16 seismic record. Because the optimum frame has braces including up to 12 SMA portions of the entire 64 divisions in the segment, 8000 frames comprising SMA segments of 1 to 20 portions of the entire 64 divisions were introduced. The interstory drift of the frames with varying length of the SMA segments used in the frame is shown in Figure 6(a). The previously defined optimum frame is also shown here to be a suitable representative for decreasing drifts. The construction cost of the three-story steel and SMA structures of these frames is also shown in Figure 6(b). In a constant period, the SMA volume used in the frame is related to the square of the length. Thus, in this objective optimization of the interstory drifts, the optimum frame may not be a cost-effective example in the solution space.
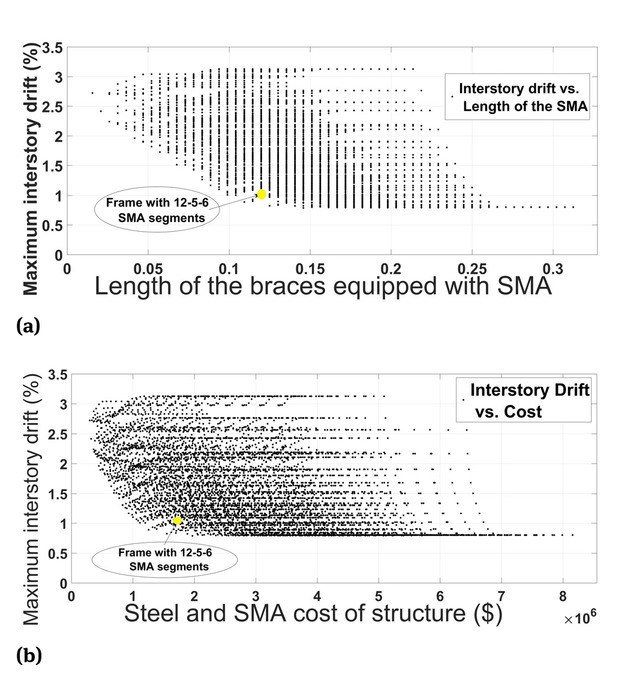
Maximum interstory drift of the produced frames; (a). Length of the SMA segments; (b). Steel and SMA construction cost.
4.1.1 Dual-braced frame behavior
To examine another possible brace ordering, with SMA braces in the lower floors and steel braces at the upper floors of the frame, all of the above procedures were followed. However, in this case, at the upper stories, instead of braces with the lowest segments, conventional steel braces are used and will be replaced with SMA braces at the end of each inner loop. Therefore, the source code includes both steel and SMA braces. At the end of each inner loop, based on the optimal length calculated in Matlab, the optimized brace is analyzed with the time history analysis in the next loop before varying the length of the SMA at the upper floor. The number of optimized dual-braced frames were equal to the number of stories minus one.
Using six elements in the SMA segment of the braces in the first floor, along with steel braces at the upper floors, produced the optimum result. The other optimum frame among the 64 frames analyzed also involved six elements in the first floor, with four elements in the second story, and steel braces at the roof floor. The maximum interstory drifts for all the three-story optimized frames and the conventional steel frame subjected to the Palos Verdes simulated ground motion (LA40) are compared in the bar chart shown in Figure 7. The maximum interstory drift of the frames decreased from 4.26 of the story height for the conventional steel frame to 2.79, 2.2, and 0.8, respectively, of the story height for the optimized frames. Figure 7 shows the demands for column rotation with respect to the story. The frame with SMA at all floors experienced the lowest maximum interstory drift and a negligible residual drift.
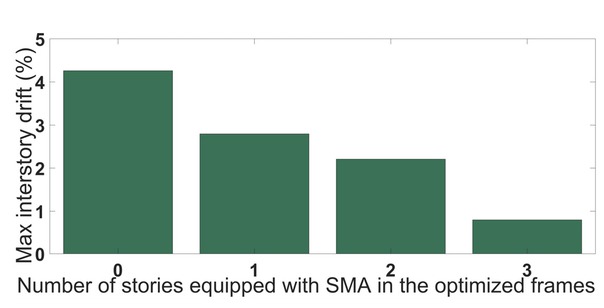
Maximum interstory drift of three-story frames regarding the number of stories equipped with SMA braces.
The maximum interstory drift for all six-story optimized frames and the conventional steel frame has been compared in the bar chart shown in Figure 9. Optimized frames with one to six stories of SMA braces recorded maximum interstory drift values of 4.05, 2.98, 3.25, 2.71, 1.8 and 0.58 of the story height, respectively. The demand for column rotation with respect to the story, presented in Figure 10, was smaller for the dual-braced frames that had more stories equipped with SMA.
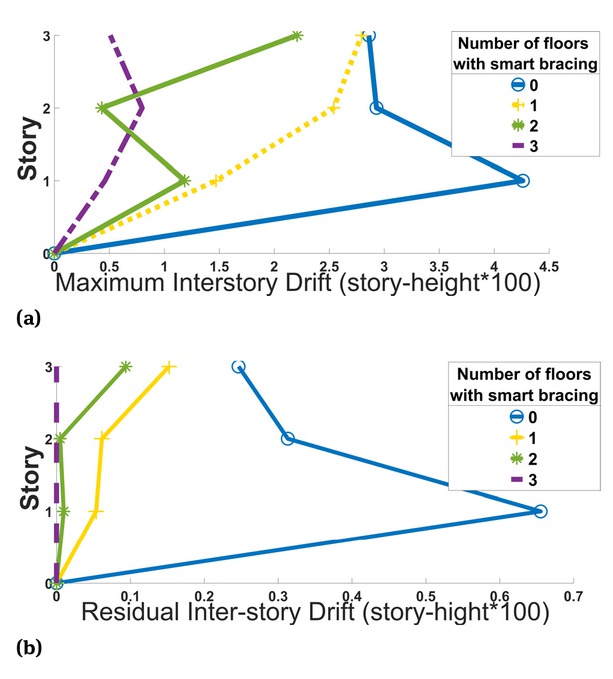
Maximum interstory drift regarding the number of floors equipped with SMA braces along the height; (b) Maximum residual interstory drift regarding the number of floors equipped with SMA braces along the height.
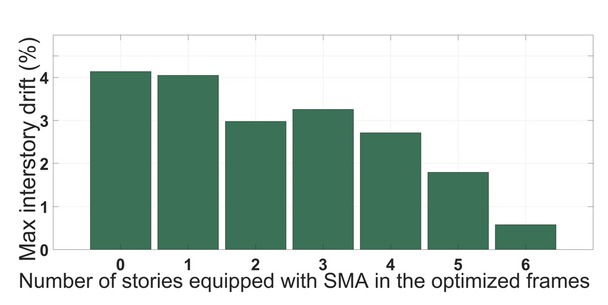
Maximum interstory drift of six-story optimized frame considering the number of floors equipped with SMA braces.
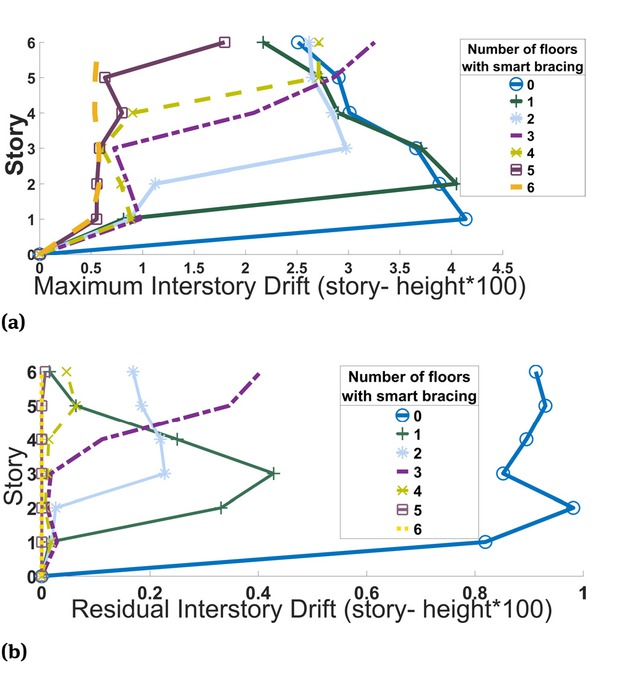
a) maximum interstory drift regarding the number of floors equipped with SMA braces along the height; (b) maximum residual interstory drift regarding the number of floors equipped with SMA braces along the height.
Based on Figure 8 and Figure 10, the ability of SMA to reduce the maximum interstory drift is evident. Local buckling at the lower floors of three- and six-story steel frames resulted in severe rotation of the columns and strain in the braces. The resulting bending trigger higher mode responses and generate large interstory drifts, posing safety concerns. On the other hand, frames with SMA braces at all floors enhance the super-elasticity and increase in stiffness after SMA yields, and thus exhibited uniform deformation through the height and negligible residual drifts.
Dual-braced frames utilizing SMA segments at the lower floors shift the maximum interstory drift to the steel braces at the upper floors. However, a three-story frame with just one SMA floor and a six-story frame with two SMA floors satisfy the safety requirements by producing a 25% reduction in the interstory drift compared to the conventional steel frame (see Figure 7 and Figure 9).
4.2 Performance level of the three-story optimized frame
With the three-story optimized frame previously introduced, for a rigorous assessment, 40 records taken from the FEMA/SAC project [43] were used, corresponding to a hazard level of 2 and a 10% probability of exceedances in 50 y. The performance level of the frame with respect to the interstory drift is presented in Figure 11(a). The smart braced frame subjected to records with 10% and 2% probabilities of exceedance, by allowing the SMA segments to bear 5.61% and 10.16% of the strain along with 1.18% and 2.267% of the maximum interstory drifts, respectively, exhibited very few instances with an extensive damage state. The maximum elongation of SMA segments corresponding to each record are also presented in Figure 11(b).
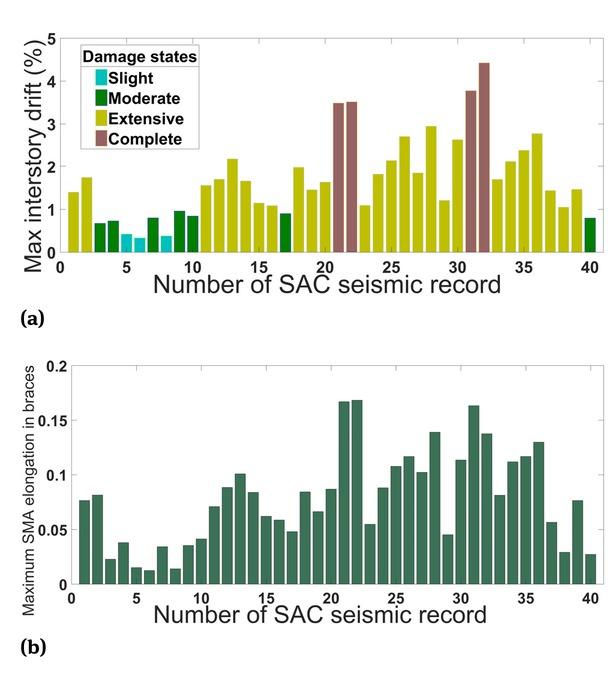
(a) Performance level of three-story optimized frame subjected to 40 ground motions; (b) Maximum elongation of SMA segments of three-story optimized frame subjected to 40 ground motions.
4.3 Response modification factor and fragility curve of the optimized frame
As previously defined, the response modification factor depends on the overstrength, ductility, and redundancy factor. Accordingly, Vd is the design base shear and Vs is the base shear representing the formation of the first plastic hinge when the frame was subjected to a static pushover analysis proportional to the predominant mode shape. Vy is the base shear corresponding to the maximum interstory drift of the extensive damage state performance level (0.03 of the story height) calculated through IDA of 22 far field records [44] in both vertical directions.
Figure 12(a) shows the maximum roof drift and base shear in the IDA results for three records (Hector Mine, Loma Prieta, and Chi-Chi), along with the pushover corresponding to the first mode. The initial stiffness up to the first plastic hinge for all records and the pushover analyses are the same, while after yielding of the SMA segments in the lateral load resistance system, the base shear tends to increase in the IDA results. This stiffness resurgence may be deduced from Figure 12(b) that shows the maximum interstory drift and scaling factors for 22 records in the x-direction.
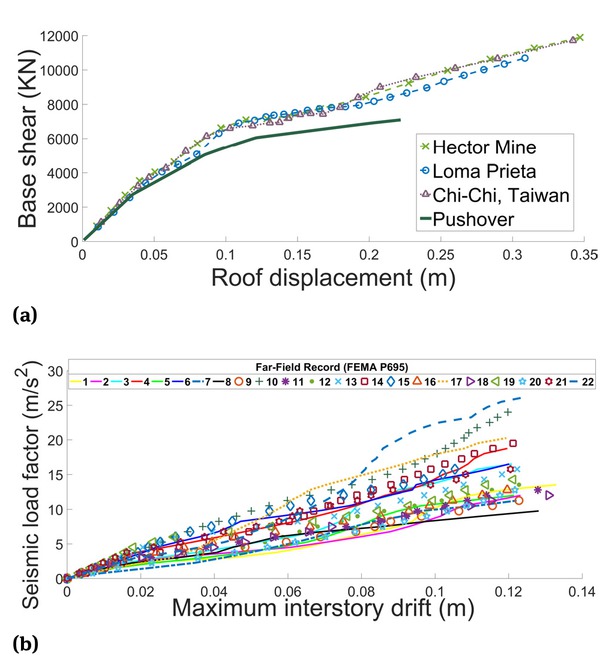
(a) Comparison of IDA and static pushover roof displacement–base shear curve for three-story optimized frame; (b) response of three-story optimized frame.
The maximum linear base shear, Ve, is then obtained from a linear time history analysis considering the maximum scaling factor of the IDA step. The base shear values for four records are listed in Table 3. The Ve and Vy results are different for the 22 records, implying that the response modification factor is record-dependent. The average response modification for the 22 records is 14.76.
Base Shear Related to Initial Yielding and Final Yielding of Structure, and Elastic Behavior.
| Seismic record | Vs (kN) | Vy(kN) | Ve (kN) |
|---|---|---|---|
| Hector Mine, 1999, Hector | 2657 | 11265 | 15303 |
| Loma Prieta, 1989, Gilroy Array #3 | 2657 | 10342 | 22956 |
| Manjil, Iran, 1990, Abbar | 2657 | 7755 | 14332 |
| Chi-Chi, Taiwan, 1999, CHY101 | 2657 | 10656 | 23518 |
Fragility curves for the three-story smart frame considering the interstory drift with 22 records are shown in Figure 13 In this lognormal diagram, the slight damage state may be reached when the average peak ground acceleration of the record exceeds 0.27 times the acceleration of gravity (g). The average peak acceleration threshold for the moderate and extensive damage states are 0.47 and 1.43 g, respectively.
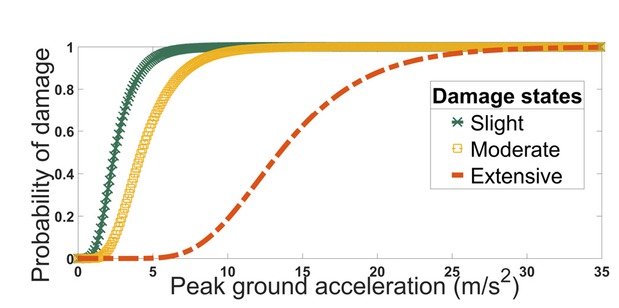
Fragility curves for slight, moderate and extensive damage state.
4.4 Probability of exceeding damage states for the three-story optimized frame
To examine the seismic behavior of the three-story frame in a probabilistic environment, after determining the mean and standard deviations of variables such as the section area of the members and yield strain of the steel and SMA, numerous series for the frame with lognormal distributions were produced in Matlab. Then, distinctive frames formed from these series were analyzed in OpenSEES with IDA using the time history of the 1989 Gilroy Loma Prieta (LA12) and simulated Elysian Park (LA36) ground motions containing 70 steps with intervals of 0.1g. Eventually, by determining the peak ground acceleration scaling factors at the threshold of each damage state for each series, the mean and standard deviations of the scaling factors for those damage states could be calculated. Although 1000 sample frames were produced, the mean and standard deviation were converged using fewer samples.
The mean and standard deviation of the seismic records, scaling factor of the PGA at the threshold of the damage states and probability of meeting or exceeding the damage states are shown in Figure 14 and Table 4. The means and standard deviations of the seismic records are equal to the PGA corresponding to each record (9.509 m/s2 for LA12 and 10.793 m/s2 for LA36) and IDA steps interval (1 m/s2), respectively.
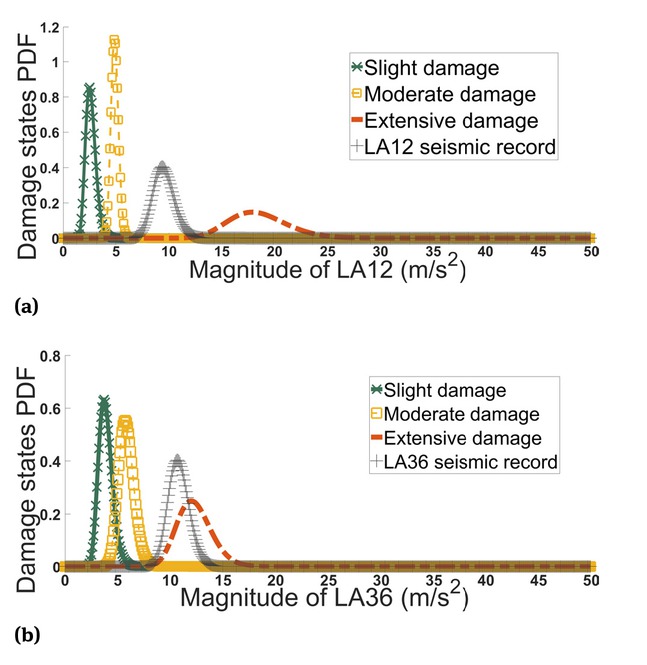
Probability of being in or exceeding damage states of the three-story optimized frame subjected to, (a). LA12 and (b) LA36 seismic record.
Mean and standard deviation of the seismic records, scaling factor of the PGA at the threshold of the damage states and probability of meeting or exceeding the damage states.
| Seismic record | Damage states | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LA12 | Slight | Moderate | Extensive | |||||||
| M | SD | M | SD | PE | M | SD | PE | M | SD | PE |
| 9.509 | 1.0 | 2.614 | 0.236 | 0.998 | 4.874 | 0.126 | 0.998 | 18.489 | 7.754 | 0.011 |
| LA36 | ||||||||||
| 10.793 | 1.0 | 3.853 | 0.427 | 0.997 | 5.829 | 0.541 | 0.995 | 12.299 | 2.674 | 0.55 |
M: mean (m/s2), SD: standard deviation (m/s2), PE: Probability of exceedance.
According to Figure 14, the probability of being in or exceeding the slight or moderate damage states for both records is greater than 99% (see Table 4). Exceeding the extensive damage state, however, is least probable for the LA12 record at 1%, while the LA36 record, through apparent overlapping with the extensive damage response, has a 55% chance to reach this damage state. These results agree with the deterministic analysis results in Figure 11 showing the interstory drifts and damage states.
The probability of being in or exceeding the extensive damage state for all three-story optimized frames subjected to the LA12 seismic record are shown in Figure 15. The frame with SMA braces on all floors was able to sustain a greater load intensity (18.49 m/s2) before reaching the extensive damage state in comparison with the dual-braced frames (11.33 m/s2 and 15.38 m/s2). Uniform deformation through the height and the super-elasticity of the SMA used in all floors made the performance of this frame more reliable, as was predicted by prior deterministic analysis results.
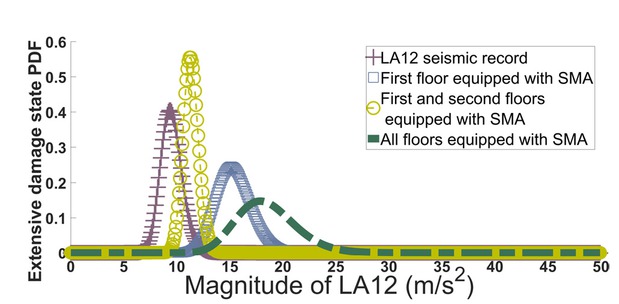
Probability of being in or exceeding extensive damage state for three-story optimized frames.
5 Conclusions
Special properties of SMAs such as super-elasticity and a high damping capacity, along with its significant disadvantage of high material cost, were assessed in low- and mid-rise concentrically braced frames. Smart braced frames and dual-braced frames were optimized by considering the amount of SMA in the braces of each floor and were subjected to both deterministic and probabilistic analyses.
Although the optimum length of the SMA segments is record-dependent, longer segments are often needed in the lower floors of both three- and six-story frames. Despite compensating for the cost by accepting greater drifts with dual bracing, the difference in the interstory drift between stories equipped with SMA braces and those with steel braces were perceptible.
Frames with SMA braces at all floors subjected to two ground motion series exhibited a reliable performance level owing to uniform deformation along the height. One series of 20 records with a 10% probability and 20 records with a 2% probability of exceedance in 50 y resulted in 5.61% and 10.16% of the strain being endured at the SMA segments, and did not reach the extensive damage state except for in a few cases. In another series comprising 22 records, a peak ground acceleration of greater than 1.43 g could induce the extensive damage state.
Stiffness resurgence of the SMA after the initial yielding enhances the base shear in the IDA compared to the pushover analysis. This property and the super-elasticity significantly increase the response modification factor of the optimized frame to 14.67.
A Monte Carlo analysis estimating the probability of being in or exceeding each damage state indicates that the slight and moderate damage states are inevitable, while the extensive damage state was only reached for a record with a 2% probability of exceedance in 50 y.
Funding This research received no external funding.
Conflict of Interest
Conflict of Interest: The authors declare that they have no conflicts of interest regarding the publication of this paper.
References
[1] C. Menna, F. Auricchio, and D. Asprone, Chapter 13 - Applications of Shape Memory Alloys in Structural Engineering, in Shape Memory Alloy Engineering, L. Lecce and A. Concilio, Eds. Boston: Butterworth-Heinemann, 2015, pp. 369-403.10.1016/B978-0-08-099920-3.00013-9Search in Google Scholar
[2] C. Lexcellent, Shape-memory Alloys Handbook. 2013.10.1002/9781118577776Search in Google Scholar
[3] M. Taheri Andani, Constitutive Modeling of Superelastic Shape Memory Alloys Considering Rate Dependent Non-Mises Tension-torsion Behavior, 53, The University of Toledo, 2013.Search in Google Scholar
[4] J. Tu and N. Reeves, Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser, in Open Engineering vol. 9, ed, 2019, p. 167.10.1515/eng-2019-0023Search in Google Scholar
[5] M. Dolce and R. Marnetto, Seismic devices based on shape memory alloys. Proceedings of Final workshop on the BRITE-MANSIDE (Memory Alloys for New Seismic Isolation and Energy Dissipation Devices) project. Rome, Italy: Servizio sismico nazionale, 1999.Search in Google Scholar
[6] M. Dolce, D. Cardone, and R. Marnetto, Implementation and testing of passive control devices based on Shape Memory Alloys, Earthquake Engineering & Structural Dynamics, vol. 29, no. 7, pp. 945-968, 2000/07/01 2000.10.1002/1096-9845(200007)29:7<945::AID-EQE958>3.0.CO;2-#Search in Google Scholar
[7] R. DesRoches, J. McCormick, and M. Delemont, Cyclic Properties of Superelastic Shape Memory Alloy Wires and Bars, vol. 130, no. 1, pp. 38-46, 2004.10.1061/(ASCE)0733-9445(2004)130:1(38)Search in Google Scholar
[8] B. Asgarian, N. Salari, and B. Saadati, Application of Intelligent Passive Devices Based on Shape Memory Alloys in Seismic Control of Structures, Structures, vol. 5, pp. 161-169, 2016/02/01/ 2016.10.1016/j.istruc.2015.10.013Search in Google Scholar
[9] B. Silwal, O. E. Ozbulut, and R. J. Michael, Seismic collapse evaluation of steel moment resisting frames with superelastic viscousdamper, Journal of Constructional Steel Research, vol. 126, pp. 26-36, 2016/11/01/ 2016.10.1016/j.jcsr.2016.07.002Search in Google Scholar
[10] L. Tian, G.Gao, C. Qiu, and K. Rong, Effect of hysteresis properties of shape memory alloy-tuned mass damper on seismic control of power transmission tower, Advances in Structural Engineering, vol. 22, no. 4, pp. 1007-1017, 2019/03/01 2018.10.1177/1369433218791606Search in Google Scholar
[11] X. Xu, Y. Zhang, and Y. Luo, Self-centering eccentrically braced frames using shape memory alloy bolts and post-tensioned tendons, Journal of Constructional Steel Research, vol. 125, pp. 190-204, 2016/10/01/ 2016.10.1016/j.jcsr.2016.06.017Search in Google Scholar
[12] P. Sultana and M. A. Youssef, Seismic performance of steel moment resisting frames utilizing superelastic shape memory alloys, Journal of Constructional Steel Research, vol. 125, pp. 239-251, 2016/10/01/ 2016.10.1016/j.jcsr.2016.06.019Search in Google Scholar
[13] M. S. Speicher, R. DesRoches, and R. T. Leon, Investigation of an articulated quadrilateral bracing system utilizing shape memory alloys, Journal of Constructional Steel Research, vol. 130, pp. 65-78, 2017/03/01/ 2017.10.1016/j.jcsr.2016.11.022Search in Google Scholar
[14] W. Wang, T.-M. Chan, and H. Shao, Seismic performance of beam– column joints with SMA tendons strengthened by steel angles, Journal of Constructional Steel Research, vol. 109, pp. 61-71, 2015/06/01/ 2015.10.1016/j.jcsr.2015.02.011Search in Google Scholar
[15] C. S. Cai, W. WU, S. Chen, and G. Voyiadjis, Applications of Smart Materials in Structural Engineering, in Components, Louisiana State University, Baton RougeLRTC Project No. 02-4TIRE, State PN 736-99-1055, 2003.Search in Google Scholar
[16] A. Zafar and B. Andrawes, Seismic behavior of SMA–FRP reinforced concrete frames under sequential seismic hazard, Engineering Structures, vol. 98, pp. 163-173, 2015/09/01/ 2015.10.1016/j.engstruct.2015.03.045Search in Google Scholar
[17] J. McCormick, R. DesRoches, D. Fugazza, and F. Auricchio, Seismic Assessment of Concentrically Braced Steel Frames with Shape Memory Alloy Braces, Journal of Structural Engineering, vol. 133, no. 6, pp. 862-870, 2007/06/01 2007.10.1061/(ASCE)0733-9445(2007)133:6(862)Search in Google Scholar
[18] J. McCormick, R. DesRoches, D. Fugazza, and F. Auricchio, Seismic Vibration Control Using Superelastic Shape Memory Alloys, Journal of Engineering Materials and Technology, vol. 128, no. 3, pp. 294-301, 2006.10.1115/1.2203109Search in Google Scholar
[19] S. A. Motahari, M. Ghassemieh, and S. A. Abolmaali, Implementation of shape memory alloy dampers for passive control of structures subjected to seismic excitations, Journal of Constructional Steel Research, vol. 63, no. 12, pp. 1570-1579, 2007/12/01/ 2007.10.1016/j.jcsr.2007.02.001Search in Google Scholar
[20] B. Asgarian and S. Moradi, Seismic response of steel braced frames with shape memory alloy braces, Journal of Constructional Steel Research, vol. 67, no. 1, pp. 65-74, 2011/01/01/ 2011.10.1016/j.jcsr.2010.06.006Search in Google Scholar
[21] A. Kari, M. Ghassemieh, and S. A. Abolmaali, A new dual bracing system for improving the seismic behavior of steel structures, Smart Materials and Structures, vol. 20, no. 12, p. 125020, 2011/11/28 2011.10.1088/0964-1726/20/12/125020Search in Google Scholar
[22] C.-S. Walter Yang, R. DesRoches, and R. T. Leon, Design and analysis of braced frames with shape memory alloy and energy-absorbing hybrid devices, Engineering Structures, vol. 32, no. 2, pp. 498-507, 2010/02/01/ 2010.10.1016/j.engstruct.2009.10.011Search in Google Scholar
[23] D. J. Miller, L. A. Fahnestock, and M. R. Eatherton, Development and experimental validation of a nickel–titanium shape memory alloy self-centering buckling-restrained brace, Engineering Structures, vol. 40, pp. 288-298, 2012/07/01/ 2012.10.1016/j.engstruct.2012.02.037Search in Google Scholar
[24] H. Ghaffarzadeh and A. Mansouri, Investigation of the Behavior Factor in SMA Braced Frames, presented at the The 14th World Conference on Earthquake Engineering, Beijing, China 2008.Search in Google Scholar
[25] M. Ghassemieh and R. Kargarmoakhar, Response modification factor of steel frames utilizing shape memory alloys, Journal of Intelligent Material Systems and Structures, vol. 24, no. 10, pp. 1213-1225, 2013/07/01 2013.10.1177/1045389X12471869Search in Google Scholar
[26] M. Mahmoudi and A. Havaran, SEISMIC BEHAVIOUR OF X-BRACED FRAMES WITH SHAPE MEMORY ALLOYS, Advances in Civil and Environmental Engineering, vol. 01, no. 3, pp. 124-135, 2013.Search in Google Scholar
[27] C.-x. Qiu and S. Zhu, Characterization of cyclic properties of superelastic monocrystalline Cu–Al–Be SMA wires for seismic applications, Construction and Building Materials, vol. 72, pp. 219-230, 2014/12/15/ 2014.10.1016/j.conbuildmat.2014.08.065Search in Google Scholar
[28] E. Kaya and B. Akyüz, Effects of cutting parameters on machin-ability characteristics of Ni-based superalloys: a review, in Open Engineering vol. 7, ed, 2017, p. 330.10.1515/eng-2017-0037Search in Google Scholar
[29] S. Bruno and C. Valente, Comparative response analysis of conventional and innovative seismic protection strategies, Earthquake Engineering& Structural Dynamics, vol. 31, no. 5, pp. 1067-1092, 2002/05/01 2002.10.1002/eqe.138Search in Google Scholar
[30] M. S. Alam, M. A. Youssef, and M. Nehdi, Utilizing shape memory alloys to enhance the performance and safety of civil infrastructure: a review, Canadian Journal of Civil Engineering, vol. 34, no. 9, pp. 1075-1086, 2007/09/01 2007.10.1139/l07-038Search in Google Scholar
[31] F. McKenna and G. L. Fenves, OpenSEES command language manual, ed: Pacific Earthquake Engineering Research Center.Search in Google Scholar
[32] G. A. MacRae, Parametric Study on the Effect of Ground Motion Intensity and Dynamic Characteristics on Seismic Demands in Steel Moment Resisting Frames, SAC Background Document SAC/BD-99/01, Sacramento, CA.1999.Search in Google Scholar
[33] R. Sabelli, Research on improving the design and analysis of earthquake-resistant steel-braced frames, NEHRP Professional Fellowship Report. EERI2001.Search in Google Scholar
[34] R. Sabelli, S. Mahin, and C. Chang, Seismic demands on steel braced frame buildings with buckling-restrained braces, Engineering Structures, vol. 25, no. 5, pp. 655-666, 2003/04/01/ 2003.10.1016/S0141-0296(02)00175-XSearch in Google Scholar
[35] D. Fugazza, Use of Shape-Memory Alloy Devices in Earthquake Engineering: Mechanical Properties, Advanced Constitutive Modelling and Structural Applications, 2005.Search in Google Scholar
[36] N. Bel Hadj Ali, M. Sellami, A.-F. Cutting-Decelle, and J.-C. Mangin, Multi-stage production cost optimization of semi-rigid steel frames using genetic algorithms, Engineering Structures, vol. 31, no. 11, pp. 2766-2778, 2009/11/01/ 2009.10.1016/j.engstruct.2009.07.004Search in Google Scholar
[37] S.-W. Jin, H. Ohmori, and S.-J. Lee, Optimal design of steel structures considering welding cost and constructability of beam-column connections, Journal of Constructional Steel Research, vol. 135, pp. 292-301, 2017/08/01/ 2017.10.1016/j.jcsr.2017.03.020Search in Google Scholar
[38] (2018). MetalsDepot. Available: https://www.metalsdepot.com/steel-products/steel-beamsSearch in Google Scholar
[39] (2018). Kellogg’s Research Labs. Available: https://www.kelloggsresearchlabs.com/NitinolSearch in Google Scholar
[40] D. o. H. Security, E. P. Fema, D. Response, and D. C. Mitigation Division Washington,Multi-hazard Loss Estimation Methodology Earthquake Model HAZUS®MH MR4 Technical Manual. 2003.Search in Google Scholar
[41] C. Applied Technology, ATC-19 Structural Response Modification Factors, Redwood City, California1995.Search in Google Scholar
[42] J. Kim and H. Choi, Response modification factors of chevron-braced frames, Engineering Structures, vol. 27, no. 2, pp. 285-300, 2005/01/01/ 2005.10.1016/j.engstruct.2004.10.009Search in Google Scholar
[43] P. G. Somerville, N. Smith, S. Punyamurthula, and J. Sun, Development of Ground Motion Time Histories for Phase 2 of the FEMA/SAC Steel Project, SACBD-97/04, Sacramento, CA1997.Search in Google Scholar
[44] J. R. Harris et al., Quantification of Building Seismic Performance Factors, no. June, 2009.Search in Google Scholar
© 2019 S. Babaei and P. Zarfam, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Article
- Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
- A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
- Identification of geodetic risk factors occurring at the construction project preparation stage
- Multicriteria comparative analysis of pillars strengthening of the historic building
- Methods of habitat reports’ evaluation
- Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
- Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
- On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
- Dynamic safety system for collaboration of operators and industrial robots
- Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
- Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
- EFQM model implementation in a Portuguese Higher Education Institution
- Assessment of direct and indirect effects of building developments on the environment
- Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
- Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
- Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
- Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
- Synthesis Conditions for LPV Controller with Input Covariance Constraints
- Procurement management in construction: study of Czech municipalities
- Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
- Control of construction projects using the Earned Value Method - case study
- Model supporting decisions on renovation and modernization of public utility buildings
- Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
- Failure Analysis of Super Hard End Mill HSS-Co
- Simulation model for resource-constrained construction project
- Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
- Analysis of renewable energy use in single-family housing
- Modeling of the harmonization method for executing a multi-unit construction project
- Effect of foam glass granules fillers modification of lime-sand products on their microstructure
- Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
- Analysis of occupational accidents in the construction industry with regards to selected time parameters
- Bill of quantities and quantity survey of construction works of renovated buildings - case study
- Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
- Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
- Quartz bentonite sandmix in sand-lime products
- The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
- Analysis of workplace injuries in Slovakian state forestry enterprises
- Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
- Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
- Hyperboloid offset surface in the architecture and construction industry
- Analysis of the preparatory phase of a construction investment in the area covered by revitalization
- The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
- Impact of high temperature drying process on beech wood containing tension wood
- Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
- Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
- The feasibility of using a low-cost depth camera for 3D scanning in mass customization
- Urban Water Infrastructure Asset Management Plan: Case Study
- Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
- Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
- IoT Applications in Wind Energy Conversion Systems
- A new method for graph stream summarization based on both the structure and concepts
- “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
- Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
- Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
- Statistical model used to assessment the sulphate resistance of mortars with fly ashes
- Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
- Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
- Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
- Optimization of shape memory alloy braces for concentrically braced steel braced frames
- Topical Issue Modern Manufacturing Technologies
- Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
- Topical Issue: Progress in area of the flow machines and devices
- Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
- Investigations of drilled and multi-piped impellers cavitation performance
- The novel solution of ball valve with replaceable orifice. Numerical and field tests
- The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
- Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
- A new solution of the semi-metallic gasket increasing tightness level
- Design and analysis of the flange-bolted joint with respect to required tightness and strength
- Special Issue: Actual trends in logistics and industrial engineering
- Intelligent programming of robotic flange production by means of CAM programming
- Static testing evaluation of pipe conveyor belt for different tensioning forces
- Design of clamping structure for material flow monitor of pipe conveyors
- Risk Minimisation in Integrated Supply Chains
- Use of simulation model for measurement of MilkRun system performance
- A simulation model for the need for intra-plant transport operation planning by AGV
- Operative production planning utilising quantitative forecasting and Monte Carlo simulations
- Monitoring bulk material pressure on bottom of storage using DEM
- Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
- Design of evaluation tool used to improve the production process
- Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
- Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
- The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
- Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
- Current options in the life cycle assessment of additive manufacturing products
- Ideal mathematical model of shock compression and shock expansion
- Use of simulation by modelling of conveyor belt contact forces
Articles in the same Issue
- Regular Article
- Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
- A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
- Identification of geodetic risk factors occurring at the construction project preparation stage
- Multicriteria comparative analysis of pillars strengthening of the historic building
- Methods of habitat reports’ evaluation
- Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
- Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
- On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
- Dynamic safety system for collaboration of operators and industrial robots
- Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
- Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
- EFQM model implementation in a Portuguese Higher Education Institution
- Assessment of direct and indirect effects of building developments on the environment
- Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
- Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
- Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
- Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
- Synthesis Conditions for LPV Controller with Input Covariance Constraints
- Procurement management in construction: study of Czech municipalities
- Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
- Control of construction projects using the Earned Value Method - case study
- Model supporting decisions on renovation and modernization of public utility buildings
- Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
- Failure Analysis of Super Hard End Mill HSS-Co
- Simulation model for resource-constrained construction project
- Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
- Analysis of renewable energy use in single-family housing
- Modeling of the harmonization method for executing a multi-unit construction project
- Effect of foam glass granules fillers modification of lime-sand products on their microstructure
- Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
- Analysis of occupational accidents in the construction industry with regards to selected time parameters
- Bill of quantities and quantity survey of construction works of renovated buildings - case study
- Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
- Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
- Quartz bentonite sandmix in sand-lime products
- The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
- Analysis of workplace injuries in Slovakian state forestry enterprises
- Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
- Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
- Hyperboloid offset surface in the architecture and construction industry
- Analysis of the preparatory phase of a construction investment in the area covered by revitalization
- The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
- Impact of high temperature drying process on beech wood containing tension wood
- Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
- Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
- The feasibility of using a low-cost depth camera for 3D scanning in mass customization
- Urban Water Infrastructure Asset Management Plan: Case Study
- Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
- Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
- IoT Applications in Wind Energy Conversion Systems
- A new method for graph stream summarization based on both the structure and concepts
- “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
- Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
- Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
- Statistical model used to assessment the sulphate resistance of mortars with fly ashes
- Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
- Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
- Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
- Optimization of shape memory alloy braces for concentrically braced steel braced frames
- Topical Issue Modern Manufacturing Technologies
- Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
- Topical Issue: Progress in area of the flow machines and devices
- Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
- Investigations of drilled and multi-piped impellers cavitation performance
- The novel solution of ball valve with replaceable orifice. Numerical and field tests
- The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
- Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
- A new solution of the semi-metallic gasket increasing tightness level
- Design and analysis of the flange-bolted joint with respect to required tightness and strength
- Special Issue: Actual trends in logistics and industrial engineering
- Intelligent programming of robotic flange production by means of CAM programming
- Static testing evaluation of pipe conveyor belt for different tensioning forces
- Design of clamping structure for material flow monitor of pipe conveyors
- Risk Minimisation in Integrated Supply Chains
- Use of simulation model for measurement of MilkRun system performance
- A simulation model for the need for intra-plant transport operation planning by AGV
- Operative production planning utilising quantitative forecasting and Monte Carlo simulations
- Monitoring bulk material pressure on bottom of storage using DEM
- Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
- Design of evaluation tool used to improve the production process
- Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
- Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
- The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
- Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
- Current options in the life cycle assessment of additive manufacturing products
- Ideal mathematical model of shock compression and shock expansion
- Use of simulation by modelling of conveyor belt contact forces

