Abstract
Practical problems in construction can be easily qualified as NP-hard (non-deterministic, polynomial-time hard) problems. The time needed for solving these problems grows exponentially with the increase of the problem’s size – this is why mathematical and heuristic methods do not enable finding solutions to complicated construction problems within an acceptable period of time. In the view of many authors, metaheuristic algorithms seem to be the most appropriate measures for scheduling and task sequencing. However even metaheuristic approach does not guarantee finding the optimal solution and algorithms tend to get stuck around local optima of objective functions. This is why authors considered improving the metaheuristic approach by the use of neural networks. In the article, authors analyse possible benefits of using a hybrid approach with the use of metaheuristics and neural networks for solving the multi-mode, resource-constrained, project-scheduling problem (MRCPSP). The suggested approach is described and tested on a model construction project schedule. The results are promising for construction practitioners, the hybrid approach improved results in 87% of tests. Based on the research outcomes, authors suggest future research ideas.
1 Introduction
The resource-constrained, project-scheduling problem (RCPSP) is commonly known in scientific literature [1, 2]. In its classic form, RCPSP aims to minimize the makespan or total duration of a project subject to precedence relations between the activities and the limited renewable resource availabilities. The problem is known to be NP-hard (non-deterministic, polynomial-time hard) [1].
The multi-mode, resource-constrained, project-scheduling problem (MRCPSP, sometimes also known as MMRCPSP) is a generalized version of RCPSP. The term multi-mode means that the schedule activities can be performed in different modes (ways). Each mode has a specific duration and specific resource requirements [2]. Due to such an approach, it is possible to take into account situations in which, for example, additional resources can be allocated to a task in order to shorten its duration. However, with the introduction of the additional decision variables, the amount of time required to solve the problem increases (it grows exponentially with the increase of the problem’s size). As a result, the computational time required for solving a MRCPS problem instance is longer than that of a similar RCPS problem instance without multiple modes. The problem can be even harder if one introduces probabilistic/fuzzy data [3, 4]. For this reason, it is of utmost importance to create efficient computational algorithms/ approaches for solving MRCPS class problems.
Mathematical methods do not enable finding acceptable solutions to complicated, practical construction problems within an acceptable period of time. That is why, in the view of many authors, metaheuristic algorithms seem to be the most appropriate measures for scheduling and task sequencing [1, 4]. Among the approaches for solving MRCPSP with the use of metaheuristics, several algorithms were proposed and tested by various authors: genetic algorithms (GA) [2, 5]; simulated annealing (SA) [6]; tabu search (TS) [7, 8]; particle swarm optimization (PSO) [9]; ant colony optimization (ACO) [10], or hybrid algorithms/approaches [11]. Recent research shows that tabu search is one of the most efficient metaheuristics for such combinatorial problems [4, 7, 8]. A summary of the methods used for solving MRCPS instances in construction can be found in [1].
Unfortunately, in particularly complicated cases, even metaheuristic approach does not guarantee finding the optimal solution and algorithms tend to get stuck around local optima of objective functions (especially while MR-CPS problems which are more complicated than corresponding RCPS problems). That is why alternative approaches to solving scheduling problems are being constantly developed, some include hybrid or multi-stage algorithms, other artificial neural networks (ANN) (such approach was developed by the authors of the manuscript).
Colak et al. [12] proposed adaptive metaheuristic procedure based on neural networks: for the first iteration, the weights for all the activities are the same (the first iteration solution is identical to the single-pass heuristic solution). In the subsequent iterations, the weights are modified and weighted processing times recalculated and later the same heuristic is applied. Rondon et al. [13] analyzed the scheduling process on single machine supported by neural networks. The operating variables studied included e.g. processing time, setup time, deadline time, duedate time, priority. Adeli with other contributors [14, 15] used Neural Dynamics Model (developed by Adeli and Park) for different types of construction projects to minimize total project cost by creating functions for direct cost calculations on the base of resource assignment to the given task. Jaberi & Jaberi [16] proposed Potts mean field annealing neural network based heuristic. In all these works, neural networks components were used simultaneously with the metaheuristic algorithms. More information on neural networks for construction schedules optimization can be found in [17].
Unfortunately, the above mentioned methods have some shortcomings. For example, they are restricted to 1-5 modes (while in reality construction companies are facing much more possible options/modes). Also most of them are focused on makespan optimization, excluding crucial, financial aspects of construction projects. Even when tackling time cost trade-off, authors are only minimizing project total cost, omitting other practical aspects and indicators important for contractors like NPV or maximum monthly cash demand. Such indicators are crucial for the efficient management of a construction company [1, 4, 7, 8]. To make up for these shortcomings, new hybrid approach for solving multi-mode resource-constrained project scheduling was developed by the authors of this manuscript.
2 Methods
In the considered model MRCPSP can be formulated as follows: a project network G (N, A) (in AON format) has N set of activities numbered from 0 (the start dummy node) to n+1 (the end dummy node), A is the set of activity pairs between which exists a finish-start precedence relationship (with a time lag ≥ 0). A schedule S is defined by a vector of activity start si and its corresponding finish fi times. T is a deadline given by the client.
In the literature authors generally focus on renewable resources (e.g. workers, machinery) [1, 12]. In presented model authors considered non-renewable resources (money). Rv is a set of such resources, its availability can be stated as alv, l є Rv. This allows for a greater flexibility for the contractor, i.e. there are more modes for activities, each representing the possibility of change not only in employment, but also materials, technology, machinery or possibility of hiring subcontractors.
The decision variables were limited to the mode of activity omitting task sequencing. That is why the researched method is dedicated to the projects in which predecessor-successor relationships between activities are set. It focuses on economic aspects of scheduling. Each activity i є N can be performed in mi different execution modes, mi є Mi = {1,..., |Mi|}. The duration of the activity i performed in the mode mi is dimi. Each mode mi requires rivmil non-renewable resources. The schedule is feasible if all precedence and resource constraints are satisfied:
where:
(1) the start dummy node time = 0, construction begins in assumed zero time,
(2) all time data is integer and positive (for all activities except for start dummy node),
(3) predecessors / successor rule for activities, no task can start before finishing of its predecessors,
(4) the resource usage constraint,
(5) the project cannot finish later than on deadline (agreed with the client).
The main optimization criterion was selected: reducing (minimizing) maximum monthly demand for cash (CD-max):
where:
k is a given month and k є K = {1,..., ⌈sn+1/ 21⌉} (21 workdays a month),
CDk is a demand for cash for a month k,
IFk is a contractor’s cash income for a month k,
OFk is a contractor’s cash outcome (including direct and indirect costs) for a month k.
This criterion is rather rarely used in the literature, nevertheless it is a very important factor for construction contractors as it limits their operational capability and is strictly connected to the cash flow [8].
In the cited literature neural networks components were used simultaneously with the metaheuristic algorithms. In the proposed approach, neural networks are used once, to limit variables range therefore allowing for simplification of the problem instance. The proposed approach (approach for MRCPSP transformation with the use of artificial neural networks – AMTANN) consists of the 5 following steps:
In the first step software calculates problem instance to obtain single-pass metaheuristic solution, at the same time saving interim results. These results are later used as a training sample for the neural network.
The second step includes neural network processing to establish the weights for each variable.
The next step includes studying of profiles in order to determine relationships between predictors (variables) and the response (output), and interactions between predictors. Several profiles are studied in order to find certain unfavorable combinations.
Basing on the findings from the previous step, some combinations are excluded resulting in the decrease in the range of the chosen variables values. The limited range means that some modes are excluded and the initial problem instance is transformed into instance that is easier to solve (has less possible variants).
In the final step software repeats single-pass metaheuristic calculation, this time optimizing simplified problem instance.
3 Numerical Example
In the presented example, contractor builds an object with a defined list of summary tasks (work packages) such as ground works, foundation works, shell, roofing, finishing works etc. The original network diagram is presented in Figure 1, schedule data is presented in Table 1.
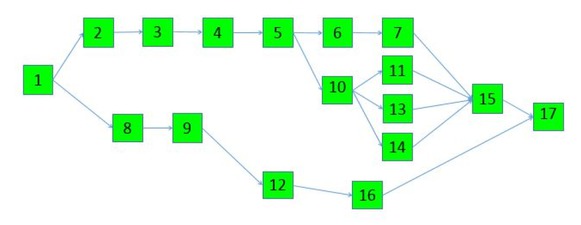
Network diagram of the example construction Project
The example project schedule - initial data
| Id. | Description | Minimum duration [days] | Maximum duration [days] | Maximum cost [USD] | Minimum cost [USD] |
|---|---|---|---|---|---|
| 1 | Start | - | - | - | - |
| 2 | Excavation | 6 | 10 | 514800 | 269096 |
| 3 | Foundations | 3 | 6 | 848353 | 406276 |
| 4 | Cellars | 3 | 4 | 256740 | 117468 |
| 5 | Structure | 11 | 18 | 593632 | 120298 |
| 6 | Roof structure | 3 | 5 | 199000 | 185001 |
| 7 | Roof covering | 2 | 3 | 366950 | 336950 |
| 8 | External Installations | 220 | 250 | 423500 | 353500 |
| 9 | Foundation covering | 6 | 9 | 661513 | 369966 |
| 10 | Partition walls | 10 | 14 | 888850 | 588885 |
| 11 | Internal plasters | 10 | 17 | 531383 | 135383 |
| 12 | Facade | 22 | 24 | 564386 | 554881 |
| 13 | Electrical installations | 183 | 255 | 59946 | 29289 |
| 14 | Sanitary installations | 3 | 5 | 38567 | 26233 |
| 15 | Painting | 70 | 81 | 229100 | 200291 |
| 16 | Terrain architecture | 4 | 6 | 73450 | 66592 |
| 17 | Finish | - | - | - | - |
Financing assumption: invoices are issued every month with payments after 14 days, discount rate is 10%, indirect costs 8 900 USD/day; penalty of each day of overrun 5 000 USD. Due-to-time – 23 months = 483 workdays (21 workdays a month). Initially assumed profit at the level of 14%.
Initial version of the schedule included 15 variables: X1-X15 (parameters), each representing selection of a mode for one of the 15 activities (activities 2-16). In this scenario there were up to 73 (activity 13) modes per activity. In total there were 2.3 × 1011 combinations possible.
First, authors calculated initial solutions, to this end authors used tabu search algorithm – TS. It was developed by Fred Glover in 1980s [18]. The basic idea behind this algorithm is to search the solution space by a sequence of moves. In this sequence, some moves are considered tabu moves – they are forbidden. The TS algorithm avoids getting stuck in local optima by storing the information about previously checked solutions in form of tabu lists. The list is growing as the algorithm proceeds. However, when it reaches its maximum capacity, the oldest entries of tabu list are being overwritten be the new ones [18].
Interim results of single-pass metaheuristic TS solutions were saved for neural network processing. In this stage weights were established for each variable. Authors analyzed multiple networks to find the best suitable parameters.
Final calculations were done with a feedforward neural network for 15 inputs (representing each variable), 1 hidden layer (with 4 neurons), and 1 output (Figure 2). Several options were tried in terms of training and validation sets. Final training set included 2000 records, 10% of the records were randomly chosen for validation.
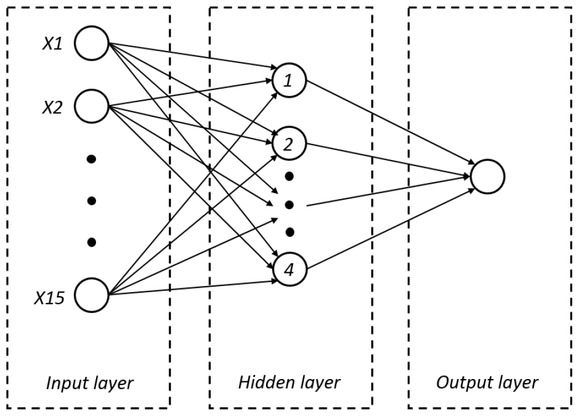
The best performing topological structure (architecture) of the Multilayer Perceptron used in numerical example.
Profiles obtained by the use of ANNs were studied. At this stage 6 predictors’ intervals were decreased. Studies showed that no matter which combinations were set for other variables, the outcome (CDmax) was getting better with the increase (or decrease) of a given parameter. As a result, the ranges of the said 6 parameters were cut in half leaving higher values (or lower values in case of decrease). The change of the variables range allowed for simplification of the example to 6.5 × 109 possible results. The new, limited data for scheduling is presented in Table 2. Finally, the simplified problem instance was calculated by the TS metaheuristic algorithm.
The example project schedule data – limited range
| Id. | Description | Minimum duration [days] | Maximum duration [days] | Maximum cost [USD] | Minimum cost [USD] |
|---|---|---|---|---|---|
| 1 | Start | - | - | - | - |
| 2 | Excavation | 8 | 10 | 391948 | 269096 |
| 3 | Foundations | 4 | 6 | 700994 | 406276 |
| 4 | Cellars | 4 | 4 | 117468 | 117468 |
| 5 | Structure | 15 | 18 | 323156 | 120298 |
| 6 | Roof structure | 3 | 5 | 199000 | 185001 |
| 7 | Roof covering | 3 | 3 | 336950 | 336950 |
| 8 | External Installations | 235 | 250 | 388500 | 353500 |
| 9 | Foundation covering | 6 | 9 | 661513 | 369966 |
| 10 | Partition walls | 10 | 14 | 888850 | 588885 |
| 11 | Internal plasters | 10 | 17 | 531383 | 135383 |
| 12 | Facade | 22 | 24 | 564386 | 554881 |
| 13 | Electrical installations | 183 | 255 | 59946 | 29289 |
| 14 | Sanitary installations | 3 | 5 | 38567 | 26233 |
| 15 | Painting | 70 | 81 | 229100 | 200291 |
| 16 | Terrain architecture | 4 | 6 | 73450 | 66592 |
| 17 | Finish | - | - | - | - |
4 Results
To test the efficiency of artificial neural networks in terms of problem instance simplification authors carried out tests. Metaheuristic algorithm was used for calculations using different settings to compare results achieved for the initial and simplified problem instance. 30 different settings were tested. Results of CDmax optimization are presented in Table 3.
Results comparison.
| Test no. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| TS | 1008622 | 1008470 | 1010047 | 1010965 | 1009578 | 1010662 | 1010965 | 1007383 | 1010965 | 1010965 |
| AMTANN | 1007533 | 1006694 | 1008002 | 1008002 | 1007852 | 1010965 | 1008173 | 1008497 | 1009559 | 1009559 |
| Difference | 1089,000 | 1776,411 | 2045,021 | 2962,908 | 1726,432 | -302,213 | 2791,571 | -1113,37 | 1405,264 | 1405,264 |
| Test no. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| TS | 1006749 | 1006749 | 1006749 | 1008622 | 1006749 | 1006749 | 1005647 | 1006749 | 1007065 | 1008154 |
| AMTANN | 1007065 | 1004992 | 1004992 | 1007533 | 1006170 | 1006749 | 1004992 | 1005647 | 1006749 | 1006749 |
| Difference | -316,040 | 1756,579 | 1756,579 | 1089,223 | 578,638 | 0 | 654,412 | 1102,167 | 316,04 | 1405,263 |
| Test no. | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| TS | 1008622 | 1010047 | 1010965 | 1006749 | 1006749 | 1010047 | 1010965 | 1010047 | 1010965 | 1006749 |
| AMTANN | 1007533 | 1008002 | 1008002 | 1004992 | 1004992 | 1008002 | 1008002 | 1008002 | 1008002 | 1004992 |
| Difference | 1089,223 | 2045,021 | 2962,908 | 1756,579 | 1756,579 | 2045,021 | 2962,908 | 2045,021 | 2962,908 | 1756,579 |
| Summary | Minimum | Maximum | Mean | |||||||
| TS | 1005647 | 1010965 | 1008683 | |||||||
| AMTANN | 1004992 | 1010965 | 1007233 | |||||||
| Difference | 654,412 | 0 | 1450,397 | all values for rows TS, AMTANN and difference are given in USD | ||||||
In 26 cases AMTANN provided results better than classic single-pass metaheuristic calculation – TS (87% success rate: that is the percentage of success among a number of attempts), in one case the results were equal (test no. 16), in 3 cases slightly worse (tests 6, 8, 11). The mean of the improved results was almost 3 times greater (absolute value) than the mean of worsened results. Although the absolute improvement of the results is not large, it proves that AMTANN can be used for MRCPSP simplification.
The cash flow for respective periods and project schedule for the best calculated case are presented in Figure 3 and 4.
![Figure 3 The cash flow for respective periods - the best result [USD]](/document/doi/10.1515/eng-2019-0006/asset/graphic/j_eng-2019-0006_fig_003.jpg)
The cash flow for respective periods - the best result [USD]
5 Discussion
The results are promising for construction practitioners. Although AMTANN did not achieve 100% success rate (87% success rate was obtained) in the preliminary tests, its first step include single-pass metaheuristic calculation. So even if the proposed approach cannot find better solution in the final step, the user already has the best solution (can be sub-optimal) stored (result of the first step). It means that the user does not risk worsening of the classic metaheuristic solution, at the same time having a great chance for its improvement.
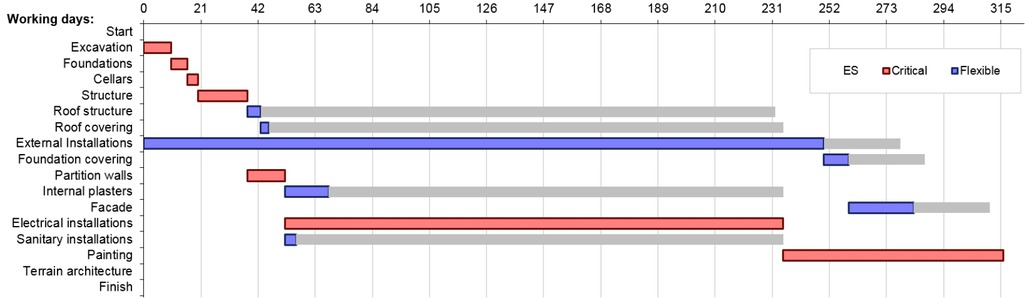
The project schedule - the best result
AMTANN proves that metaheuristic algorithms can be supported by artificial neural networks (in terms of problem instances simplification) in order to improve schedule optimization results for MRCPSP in construction. In the future authors plan to research further the described topic. In particular: test more instances, additional variables reduction options and other machine learning approaches. Should the future tests be also successful, authors will consider developing automatic tool (software). Such tool would significantly reduce the time needed for AMTANN performance, increasing its value for the construction industry.
At the same time authors would like to underline that metaheuristic approach does never guarantee finding the optimal solution, however it seems perfect for solving complicated, NP-hard class problems because it allows for computing sub-optimal, acceptable solutions within an acceptable time frame.
Acknowledgement
Authors would like to thank Faculty of Civil Engineering, Warsaw University of Technology for providing software and hardware necessary for the research.
References
[1] Rosłon J., The multi-mode, resource-constrained project scheduling problem in construction: state of art review and research challenges, Technical Transactions, 2017, 10.4467/2353737XCT.17.070.6427Search in Google Scholar
[2] Van Peteghem V., Vanhoucke M., A genetic algorithm for the preemptive and non-preemptive multi-mode resource-constrained project scheduling problem. European Journal of Operational Research, 2010, 201(2), 409-41810.1016/j.ejor.2009.03.034Search in Google Scholar
[3] Ibadov N., Fuzzy estimation of activities duration in construction projects, Archives of Civil Engineering, 2015, 61, 23–34, 10.1515/ace-2015-0012Search in Google Scholar
[4] Rosłon J., Zawistowski J., Construction projects’ indicators improvement using selected metaheuristic algorithms, Procedia Engineering, 2016, 153, 595-598, https://doi.org/10.1016/j.proeng.2016.08.19810.1016/j.proeng.2016.08.198Search in Google Scholar
[5] Magalhães-Mendes J., A two-level genetic algorithm for the multi-mode resource-constrained project scheduling problem, International Journal of Systems Applications, Engineering & Development, 2011, Issue 3, Volume 5Search in Google Scholar
[6] Józefowska J., Mika M., Różycki R., Waligóra G., Weglarz J., Simulated annealing for multi-mode resource-constrained project scheduling, Annals of Operations Research, 2001, 102(1-4), 137-15510.1023/A:1010954031930Search in Google Scholar
[7] Kulejewski J., Zawistowski J., Metoda symulacyjna wyznaczania wielkosci buforów stabilizujacych harmonogramy budowlane, Budownictwo i Inzynieria Srodowiska 2: 2011, 563-572Search in Google Scholar
[8] Rosłon J., Porównanie algorytmów genetycznego i przeszukiwania tabu wykorzystanych do szeregowania zadan w budownictwie. Materiały Budowlane, 2016, 10.15199/33.2016.06.18Search in Google Scholar
[9] Zhang H., Tam C. M., Li H., Multimode project scheduling based on particle swarm optimization, Computer-Aided Civil and Infrastructure Engineering, 2006, 21(2), 93-10310.1111/j.1467-8667.2005.00420.xSearch in Google Scholar
[10] Urbaniak M., Zastosowanie algorytmu mrówkowego do optymalizacji czasowo-kosztowej projektów informatycznych, Ekonometria, 2012 (38), 343-355Search in Google Scholar
[11] Ranjbar M., De Reyck B., Kianfar F., A hybrid scatter search for the discrete time/resource trade-off problem in project scheduling, European Journal of Operational Research, 2009, 193(1), 35-4810.1016/j.ejor.2007.10.042Search in Google Scholar
[12] Colak S., Agarwal A., Erenguc S., Multi-mode resource-constrained project-scheduling problem with renewable resources: new solution approaches. Journal of Business & Economics Research (Online), 2013, 11(11), 45510.19030/jber.v11i11.8193Search in Google Scholar
[13] Rondon R. L. A., da Carvalho A. S., Hernández G. I., Neural network modelling and simulation of the scheduling, In Innovation in Manufacturing Networks, 2008, 231-238, Springer, Boston, MA10.1007/978-0-387-09492-2_25Search in Google Scholar
[14] Adeli H., Karim A., Scheduling/cost optimization and neural dynamics model for construction, Journal of Construction Engineering and Management, 1997, 123(4), 450-45810.1061/(ASCE)0733-9364(1997)123:4(450)Search in Google Scholar
[15] Senouci A. B., Adeli H., Resource scheduling using neural dynamics model of Adeli and Park. Journal of Construction Engineering and Management, 2001, 127(1), 28-3410.1061/(ASCE)0733-9364(2001)127:1(28)Search in Google Scholar
[16] Jaberi M., Jaberi M., A multi-objective resource-constrained project-scheduling problem using mean field annealing neural networks, J Math Comput Sci, 2014, 9, 228-23910.22436/jmcs.09.03.07Search in Google Scholar
[17] Adeli, H., Karim A., Construction scheduling, cost optimization and management, 2014, CRC Press.Search in Google Scholar
[18] Fridgeirsson T.V., Rosłon J., Optimisation of construction processes, 2017 Civil Engineering Faculty of Warsaw University.Search in Google Scholar
© 2019 J.H. Rosłon and J.E. Kulejewski, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Article
- Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
- A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
- Identification of geodetic risk factors occurring at the construction project preparation stage
- Multicriteria comparative analysis of pillars strengthening of the historic building
- Methods of habitat reports’ evaluation
- Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
- Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
- On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
- Dynamic safety system for collaboration of operators and industrial robots
- Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
- Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
- EFQM model implementation in a Portuguese Higher Education Institution
- Assessment of direct and indirect effects of building developments on the environment
- Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
- Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
- Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
- Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
- Synthesis Conditions for LPV Controller with Input Covariance Constraints
- Procurement management in construction: study of Czech municipalities
- Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
- Control of construction projects using the Earned Value Method - case study
- Model supporting decisions on renovation and modernization of public utility buildings
- Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
- Failure Analysis of Super Hard End Mill HSS-Co
- Simulation model for resource-constrained construction project
- Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
- Analysis of renewable energy use in single-family housing
- Modeling of the harmonization method for executing a multi-unit construction project
- Effect of foam glass granules fillers modification of lime-sand products on their microstructure
- Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
- Analysis of occupational accidents in the construction industry with regards to selected time parameters
- Bill of quantities and quantity survey of construction works of renovated buildings - case study
- Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
- Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
- Quartz bentonite sandmix in sand-lime products
- The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
- Analysis of workplace injuries in Slovakian state forestry enterprises
- Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
- Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
- Hyperboloid offset surface in the architecture and construction industry
- Analysis of the preparatory phase of a construction investment in the area covered by revitalization
- The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
- Impact of high temperature drying process on beech wood containing tension wood
- Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
- Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
- The feasibility of using a low-cost depth camera for 3D scanning in mass customization
- Urban Water Infrastructure Asset Management Plan: Case Study
- Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
- Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
- IoT Applications in Wind Energy Conversion Systems
- A new method for graph stream summarization based on both the structure and concepts
- “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
- Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
- Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
- Statistical model used to assessment the sulphate resistance of mortars with fly ashes
- Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
- Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
- Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
- Optimization of shape memory alloy braces for concentrically braced steel braced frames
- Topical Issue Modern Manufacturing Technologies
- Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
- Topical Issue: Progress in area of the flow machines and devices
- Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
- Investigations of drilled and multi-piped impellers cavitation performance
- The novel solution of ball valve with replaceable orifice. Numerical and field tests
- The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
- Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
- A new solution of the semi-metallic gasket increasing tightness level
- Design and analysis of the flange-bolted joint with respect to required tightness and strength
- Special Issue: Actual trends in logistics and industrial engineering
- Intelligent programming of robotic flange production by means of CAM programming
- Static testing evaluation of pipe conveyor belt for different tensioning forces
- Design of clamping structure for material flow monitor of pipe conveyors
- Risk Minimisation in Integrated Supply Chains
- Use of simulation model for measurement of MilkRun system performance
- A simulation model for the need for intra-plant transport operation planning by AGV
- Operative production planning utilising quantitative forecasting and Monte Carlo simulations
- Monitoring bulk material pressure on bottom of storage using DEM
- Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
- Design of evaluation tool used to improve the production process
- Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
- Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
- The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
- Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
- Current options in the life cycle assessment of additive manufacturing products
- Ideal mathematical model of shock compression and shock expansion
- Use of simulation by modelling of conveyor belt contact forces
Articles in the same Issue
- Regular Article
- Exploring conditions and usefulness of UAVs in the BRAIN Massive Inspections Protocol
- A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction
- Identification of geodetic risk factors occurring at the construction project preparation stage
- Multicriteria comparative analysis of pillars strengthening of the historic building
- Methods of habitat reports’ evaluation
- Effect of material and technological factors on the properties of cement-lime mortars and mortars with plasticizing admixture
- Management of Innovation Ecosystems Based on Six Sigma Business Scorecard
- On a Stochastic Regularization Technique for Ill-Conditioned Linear Systems
- Dynamic safety system for collaboration of operators and industrial robots
- Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria
- Seasonal evaluation of surface water quality at the Tamanduá stream watershed (Aparecida de Goiânia, Goiás, Brazil) using the Water Quality Index
- EFQM model implementation in a Portuguese Higher Education Institution
- Assessment of direct and indirect effects of building developments on the environment
- Accelerated Aging of WPCs Based on Polypropylene and Plywood Production Residues
- Analysis of the Cost of a Building’s Life Cycle in a Probabilistic Approach
- Implementation of Web Services for Data Integration to Improve Performance in The Processing Loan Approval
- Rehabilitation of buildings as an alternative to sustainability in Brazilian constructions
- Synthesis Conditions for LPV Controller with Input Covariance Constraints
- Procurement management in construction: study of Czech municipalities
- Contractor’s bid pricing strategy: a model with correlation among competitors’ prices
- Control of construction projects using the Earned Value Method - case study
- Model supporting decisions on renovation and modernization of public utility buildings
- Cements with calcareous fly ash as component of low clinker eco-self compacting concrete
- Failure Analysis of Super Hard End Mill HSS-Co
- Simulation model for resource-constrained construction project
- Getting efficient choices in buildings by using Genetic Algorithms: Assessment & validation
- Analysis of renewable energy use in single-family housing
- Modeling of the harmonization method for executing a multi-unit construction project
- Effect of foam glass granules fillers modification of lime-sand products on their microstructure
- Volume Optimization of Solid Waste Landfill Using Voronoi Diagram Geometry
- Analysis of occupational accidents in the construction industry with regards to selected time parameters
- Bill of quantities and quantity survey of construction works of renovated buildings - case study
- Cooperation of the PTFE sealing ring with the steel ball of the valve subjected to durability test
- Analytical model assessing the effect of increased traffic flow intensities on the road administration, maintenance and lifetime
- Quartz bentonite sandmix in sand-lime products
- The Issue of a Transport Mode Choice from the Perspective of Enterprise Logistics
- Analysis of workplace injuries in Slovakian state forestry enterprises
- Research into Customer Preferences of Potential Buyers of Simple Wood-based Houses for the Purpose of Using the Target Costing
- Proposal of the Inventory Management Automatic Identification System in the Manufacturing Enterprise Applying the Multi-criteria Analysis Methods
- Hyperboloid offset surface in the architecture and construction industry
- Analysis of the preparatory phase of a construction investment in the area covered by revitalization
- The selection of sealing technologies of the subsoil and hydrotechnical structures and quality assurance
- Impact of high temperature drying process on beech wood containing tension wood
- Prediction of Strength of Remixed Concrete by Application of Orthogonal Decomposition, Neural Analysis and Regression Analysis
- Modelling a production process using a Sankey diagram and Computerized Relative Allocation of Facilities Technique (CRAFT)
- The feasibility of using a low-cost depth camera for 3D scanning in mass customization
- Urban Water Infrastructure Asset Management Plan: Case Study
- Evaluation the effect of lime on the plastic and hardened properties of cement mortar and quantified using Vipulanandan model
- Uplift and Settlement Prediction Model of Marine Clay Soil e Integrated with Polyurethane Foam
- IoT Applications in Wind Energy Conversion Systems
- A new method for graph stream summarization based on both the structure and concepts
- “Zhores” — Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology
- Economic Disposal Quantity of Leftovers kept in storage: a Monte Carlo simulation method
- Computer technology of the thermal stress state and fatigue life analysis of turbine engine exhaust support frames
- Statistical model used to assessment the sulphate resistance of mortars with fly ashes
- Application of organization goal-oriented requirement engineering (OGORE) methods in erp-based company business processes
- Influence of Sand Size on Mechanical Properties of Fiber Reinforced Polymer Concrete
- Architecture For Automation System Metrics Collection, Visualization and Data Engineering – HAMK Sheet Metal Center Building Automation Case Study
- Optimization of shape memory alloy braces for concentrically braced steel braced frames
- Topical Issue Modern Manufacturing Technologies
- Feasibility Study of Microneedle Fabrication from a thin Nitinol Wire Using a CW Single-Mode Fiber Laser
- Topical Issue: Progress in area of the flow machines and devices
- Analysis of the influence of a stator type modification on the performance of a pump with a hole impeller
- Investigations of drilled and multi-piped impellers cavitation performance
- The novel solution of ball valve with replaceable orifice. Numerical and field tests
- The flow deteriorations in course of the partial load operation of the middle specific speed Francis turbine
- Numerical analysis of temperature distribution in a brush seal with thermo-regulating bimetal elements
- A new solution of the semi-metallic gasket increasing tightness level
- Design and analysis of the flange-bolted joint with respect to required tightness and strength
- Special Issue: Actual trends in logistics and industrial engineering
- Intelligent programming of robotic flange production by means of CAM programming
- Static testing evaluation of pipe conveyor belt for different tensioning forces
- Design of clamping structure for material flow monitor of pipe conveyors
- Risk Minimisation in Integrated Supply Chains
- Use of simulation model for measurement of MilkRun system performance
- A simulation model for the need for intra-plant transport operation planning by AGV
- Operative production planning utilising quantitative forecasting and Monte Carlo simulations
- Monitoring bulk material pressure on bottom of storage using DEM
- Calibration of Transducers and of a Coil Compression Spring Constant on the Testing Equipment Simulating the Process of a Pallet Positioning in a Rack Cell
- Design of evaluation tool used to improve the production process
- Planning of Optimal Capacity for the Middle-Sized Storage Using a Mathematical Model
- Experimental assessment of the static stiffness of machine parts and structures by changing the magnitude of the hysteresis as a function of loading
- The evaluation of the production of the shaped part using the workshop programming method on the two-spindle multi-axis CTX alpha 500 lathe
- Numerical Modeling of p-v-T Rheological Equation Coefficients for Polypropylene with Variable Chalk Content
- Current options in the life cycle assessment of additive manufacturing products
- Ideal mathematical model of shock compression and shock expansion
- Use of simulation by modelling of conveyor belt contact forces

