‘Hardcastle Hollows’ in loess landforms: Closed depressions in aeolian landscapes – in a geoheritage context

Roger Fagg; Ian Smalley

doi:10.1515/geo-2018-0005

Artikel Open Access

‘Hardcastle Hollows’ in loess landforms: Closed depressions in aeolian landscapes – in a geoheritage context

Roger Fagg und Ian Smalley

Veröffentlicht/Copyright: 18. April 2018

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Open Geosciences Band 10 Heft 1

Abstract

Loess landscapes sometimes contain isolated depressed areas, which often appear as lakes. The outline shape (and distribution) of these depressions could be controlled by random processes, particularly if the depressions are caused by loess hydroconsolidation and ground subsidence. By applying the Zingg system of shape classification it is possible to propose a mean random shape for the closed depressions. A Zingg rectangle with a side ratio of about 2:1 is produced by a very simple Monte Carlo method, which had been used previously to calculate the mean random shape of a loess particle. The Zingg rectangle indicates the basic shape of the mean closed depression. A simple four stage process for the formation of the depressions is proposed. They might be called ‘Hardcastle Hollows’ in honour of John Hardcastle who first reported them, in New Zealand. Studies on Ukrainian deposits suggest that there might be some stratigraphic value in the observation of closed depressions; they are often not superimposed in successive depositions of loess. Hydroconsolidation is important in landscape processes. The hollows provide interesting habitats and enlarge the ecological interest of loess deposits; the geoheritage scene is enhanced.

Keywords: Loess landforms; closed depressions; random shapes; Zingg rectangle; Monte Carlo methods

“Peculiar features of the Timaru loess are the numerous shallow hollows in the surface, the larger of which, half an acre or an acre or two in extent, in their natural state retained water enough to allow peat and sedges to flourish in them. The origin of these depressions must be sought in the conditions under which the loess was built up as a dust heap.”
John Hardcastle 1908

1 Introduction

Loess on top; loess is a surficial deposit, a superficial deposit. Loess forms the landscape, it is the initial encounter, the dust on the crust. It is initially unimpressive and perhaps unappealing-but, armed with some knowledge, it becomes interesting, it presents interesting aspects. Some are quite well known but some are not. Little attention has been directed to the closed depressions, which we tentatively propose to call ‘Hardcastle Hollows’. The name would be useful in that it would demarcate a particular type of landform depression. They were first noted by John Hardcastle in the 1880s, and discussed in his 1908 book [1].

Loess is a remarkable deposit; an aeolian, landscapedraping sediment, notable particularly for the silt particle size mode and the internal structural collapsibility, and the ability to preserve climatic signals from all of the Quaternary record. Many formation aspects have been investigated and reported on, and many property aspects. It is a unique material with many interesting macro-and microproperties. It has an open structure and this allows one of the most interesting properties to be observed. The soil structure of loess can collapse to form a more compact structure; this is usually accomplished via the process of hydroconsolidation. In this paper we consider the process of hydroconsolidation in a basic loess landscape – which causes the formation of a set of hollows or depressions. Some consideration is given to the shape of these hollows and this allows us to deploy the very simple Monte Carlo methods which have been used in investigations of the mode particle shape of loess, as well as model building for loess structures [2, 3].

Rogers and Smalley [4] calculated the mean shape of a loess particle using a very simple Monte Carlo method. This turned out to be a very blade shaped particle with axial ratios of 8:5:2-a surprisingly flat particle, although Krinsley and Smalley [5], from observation, had proposed that the mode particle would be a flat blade shape. Calculating shapes depends initially on accepting the basic Zingg classification for particle description, this allows for quantitative methods to be applied. The Zingg approach [6, 7, 8] defines four particle types; type I a=b>c disc, II a=b=c cube/sphere, III a>b>c blade, and IV a=b<c rod. With carefully chosen (and acceptable) numerical values in use this approach allows a quantitative exploration of shape expectations. Simple probability predicts 72% of class III particles in an ideal silt [6, 9]; simple Monte Carlo methods suggest that the mode silt particle is a class III particle with axial ratios 8:5:2; in effect an 8:5:2 box just contains the typical particle.

2 Two-dimensional random shapes

These three dimensional 3d results appear to be satisfactory and have not been seriously questioned, however there remains some doubt about the randomness of the system; rigorous randomness is difficult to maintain. In a regression from the 3d case it is possible to look at random shapes and manipulations in two dimensions 2d, and perhaps test the general idea.

The idea of a random variation of properties in a planar geo-deposit worked quite well for drumlins [10] and very well for a cooling basalt flow [11]; it might be valid for some aspects of self-weight collapse in a loess deposit, and for the random plan shapes of the collapsed regions. The work of Kolodynska-Gawrysiak and co-workers in Poland [12, 13] is now focussing attention on ‘closed depressions’ in loess deposits, and this suggests another application of the basic Monte Carlo approach to shape. Do these depressions have random plan shapes? What does a random plan shape look like? Can we generate random rectangles?

2.1 Simple Monte Carlo methods

In Zingg world there are only two 2d shapes; squares and rectangles. Our random rectangles are generated in the same manner as the Rogers-Smalley random particles. A sequence of random numbers is generated, between 1 and 10, so ten possible lengths (using Kendall & Babington-Smith random numbers [14]; Figure 1). These are taken in succeeding pairs, and each pair of numbers defines a Zingg rectangle. These are tabulated with large sides in one column and short sides in another. Total each column and the l/s ratio gives the random rectangle-which we find to be about 2:1. So a random depression just fits into a 2:1 Zingg rectangle. 2:1 seems like an absurdly neat ratio; the actual tests give a range from about 1.7 to about 2.3, but if an integer result was wanted it would be 2:1. (Figure 2).

Figure 1

A page of random numbers from Kendall & Babington-Smith [14]. These numbers have been tested for randomness and it is this that makes printed numbers still useful in a computer age. The line of numbers indicated would give a 1.87:1 Zingg rectangle.

Figure 2

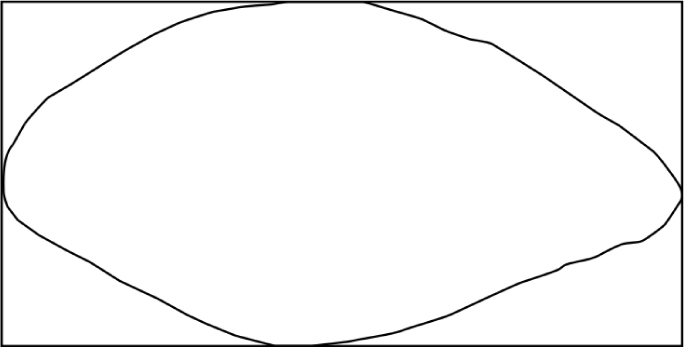
The Zingg rectangle. This is the mode random Zingg rectangle. The Monte Carlo approach gives a rectangle with a side ratio of 2:1, this is the truly random rectangle with ten possible size units defined.

A test row is shown in Figure 1. This yields 20 rectangles and a side ratio of 1.87. In the KBS numbers zero is read as 10; this gives a range of sizes from 1 to 10. This was the range used in the initial shape distribution calculations [8] and appears satisfactory; but it must be acknowledged that a choice of length parameters has been made. Sarmah & Chakrabarty [15], aware of the need for high quality random numbers, have tested the randomness of the KBS numbers and found satisfactory randomness.

2.2 Ground observations

Zeeden et al. [16] have examined these closed depressions on the Titel Plateau in Serbia, and given a good insight into their shape and distribution, and suggested some mechanisms for formation – in very general terms. Hardcastle [1,17] was the first to describe these closed depressions, in the Timaru loess in New Zealand; no illustrations but size descriptions in terms of tens and hundreds of metres. If these are manifestations of randomness in loess land-forms and a modelling approach is taken a large amount of randomness will have to be accounted for (Figure 3). It was relatively simple to model drumlins in a random field because it could be assumed initially that all the drumlins were the same size and had the same orientation [10]. The closed depressions can have random shapes (mean Zingg rectangle 2:1), and random orientations, maybe random density and perhaps random size. If these depressions are the result of hydroconsolidation and self-weight soil structure collapse, as seems likely from the soil mechanics point of view [18], then it might be expected that all of these random conditions would operate- and the mean shape would be defined by a Zingg rectangle with 2:1 side ratio. If this 2:1 ratio proves to be correct, then the Rogers-Smalley approach is to some extent justified and the 3d results can be viewed with more confidence.

Figure 3

The closed depression in an ideal loess landscape. Much randomness is involved; shape, size, density of packing, orientation. The ideal landscape is a closed space, as in Smalley & Unwin [10], the opposite sides of the square are identified, so the space is effectively infinite.

The most detailed studies of the loess depressions appear to be those of Grecu et al. [19]. They produced many measurements, and it appears that the idea of the default 2:1 rectangle may be supported. But this was a complex study and more analysis may be required.

3 Discussion (mechanism)

The closed depressions were discussed by Różycki [20] (Figures 4, 5). In his ‘Caspian-Black Sea Aeolian Province’ he described these ‘Pody’. The elementary forms, he reported, are small sinking basins (prosadochnye bludtsa) with circular or oval outlines and an area of a few hectares to a few tens of hectares; fusing together, the basins form larger and irregular forms 0.5 – 2m deep (see also Popov [21]).

Figure 4

The Romanian landscape described; the loess landscape in southern Romania from Grecu et al. [21]. In the loess regions random hydroconsolidation occurs leading to hardcastle hollow formation. They report 2:1 as a rectangle ratio. 1- collapsible loess, maximum collapsibility, 2- 4 collapsible loess with diminishing collapsibility, 5- rivers, 6-localities.

Figure 5

South Ukrainian ‘podes [21]: 1- loess, 2- sandy loess, 3- active podes, 4- dead podes.

Figure 6

Pode migration and their relation to fossil soils in South Ukraine [20, 21]. 1- loess in situ, 2- loess hydroconsolidated into podes, 3- palaeosols.

Several stages can be described in the formation of a closed depression landscape:

The formation of the initial loess deposit; a substantial planar deposit of default loess; open structure, metastable nature; a substantial uniform deposit.
This deposit becomes thick enough and wet enough for self-weight collapse to occur. Selective hydroconsolidation is observed. At this point first stage randomness is observed. Although the loess deposit appears to be uniform there is no possibility for total uniformity to be produced. So there are small variations in the properties of the planar system. The subsidence activity begins at random points.
The subsiding regions themselves have a second aspect of randomness; the shape of the depression has a random aspect. In a perfect system a round depression might be expected because the ground properties would be the same in each direction. However there are small variations so there will be departures from circularity. However no great deviation should be expected; there is no reason to expect very elongated features, there is a certain uniformity of ground property.
The depressions develop; they are best described in plan by a two-dimensional Zingg shape, they are Zingg rectangles but without too great a range in side ratio. The suggested side range of 1-10 seems to fit with observation. This yields 2:1 structures, and this agrees, more or less, with observation.
The depressions can merge and this will introduce a new range of shapes. They may become lakes; a fairly complex landscape may develop. The ‘Pode’ landscape described by Różycki is a fairly complex landscape.

Examination of Figure 5 from the Popov studies cited by Różycki [20] shows several loess layers each of which contains a region where hydrocollapse has allowed a closed depossion to develop. This sequence of collapse systems allows a possible stratigraphy to be developed. A planar randomness allows some overlap of collapsed regions but also some independent collapsed regions in individual layers.

4 Discussion (Geoheritage)

Loess is a remarkable geo-material, but the question has to be raised as to whether its fascinating intrinsic properties have any interest or value in a geoheritage situation. There is a logical approach; the loess museum of the future will probably feature the role of loess as what Hardcastle called ‘a climate register’ [1]. A loess museum will be built where it can exploit a thick loess deposit, a long loess section covering as much of the Pleistocene as possible. A vertical museum at Stari Slankamen or Timaru or on the Loess Plateau in China is an attractive prospect, and can show the changing of the climate and the environment for the last several million years. This is the simple direct view of loess in a geoheritage situation. Alternatively perhaps an interest can be cultivated in the stuff of loess, perhaps a loess ‘enthusiasm’ will develop. Leonard Horner [24] has been credited with his pioneering efforts in promoting loess enthusiasm; he was certainly a pioneer of loess geoheritage endeavours. The value of the hardcastle hollows lies in the fact that they demonstrate the most fascinating properties of loess in a fairly direct way. The open structured loess can collapse and subsidence can occur. This manifests itself as a hardcastle hollow and causes and consequences can be discussed. The close-to-ideal basalt flow, e.g. the Giants Causeway [11] demonstrates interesting properties of molten rock; the hardcastle hollows in Central Europe or New Zealand can demonstrate interesting properties of an airfall silt. It may be that the more modest an unassuming geo-features may come to be more appreciated. They may not compete with the Grand Canyon but the loess plains may be seen as regions of interest, as Geoheritage matures. As Thomas Hardy said in The Return of the Native:

“A new Vale of Tempe may be a gaunt waste in Thule; human souls may find themselves in closer and closer harmony with external things wearing a sombreness distasteful to out race when it was young.”

5 Commentary

The formation of the open aeolian structure, the development of collapsibility and then structure collapse and hydroconsolicdation – these are the most loessic of activities. By chance most of the attention to hydroconsolidation has been in the field of geotechnology (see Rogers et al. [18]) because of the continuing problems of subsidence leading to damage to buildings and other structures. But the most interesting manifestation could be in the field of geomorphology; this is where hydroconsolidation might best be studied. In the case of the hardcastle hollows there is a boundary situation. The hollows form by self weight collapse of the open structure; in the landscape there are collapsed regions and uncollapsed regions. This is pure collapse, not collapse brought about by oedometer testing in a soil mechanics laboratory but collapse caused by a coming together of the critical factors in nature: an open aeolian structure, the bond adjustment to allow collapsibility, the right amount of overburden pressure, the correct moisture content. The regions around the hollows lack one or more of these key factors.

There is a growing awareness of the relevance of hydroconsolidation in landscape processes and the most obvious of the processes considered is the formation of fragipan horizons within loess deposits. The most scientific explanation of fragipan formation is the Bryant process which directly involves hydroconsolidation (see Smalley et al. [22, 23]). The right combination of factors allows collapse in the soil system and the dense fragipan horizon is formed.

Acknowledgement

We thank members of the University of Novi Sad, in particular Slobodan Markovic and Nemanja Tomic, for facilitating our access to the Titel Plateau. The idea of the mean random Zingg rectangle emerged at the ‘Loess 2M Modelling & Mapping’ conference in Novi Sad in August 2016. Further discussions at the GeoHeritage 2 conference in 2017.

References

[1] Hardcastle, J. 1908. Notes on the Geology of South Canterbury. Timaru Herald Timaru 62p. (reprinted by Loess Letter June 2014).Suche in Google Scholar

[2] Assallay, A.M., Rogers, C.D.F., Smalley, I.J. 1997. Formation and collapse of metastable particle packings and open structures in loess deposits. Engineering Geology 48, 101-115.10.1016/S0013-7952(97)81916-3Suche in Google Scholar

[3] Dibben, S.C., Jefferson, I.F., Smalley, I.J. 1998. The Loughborough Loess Monte Carlo model of soil structure. Computers & Geosciences 24, 345-352.10.1016/S0098-3004(97)00118-0Suche in Google Scholar

[4] Rogers, C.D.F., Smalley, I.J. 1973. The shape of loess particles. Naturwissenschaften 80, 461-463.10.1007/BF01136036Suche in Google Scholar

[5] Krinsley, D.H., Smalley, I.J. 1973. Shape and nature of small sedimentary quartz particles. Science 180, 1277-1279.10.1126/science.180.4092.1277Suche in Google Scholar PubMed

[6] Domokos, G., Sipos, A., Szabo, T., Varkonyi, P. 2010. Pebbles, shapes and equilibria. Mathematical Geosciences 42, 29-47.10.1007/s11004-009-9250-4Suche in Google Scholar

[7] Szabo, T; Domokos, G. 2010. A new classification system for pebble and crystal shapes based on static equilibrium points. Central European Geology 53, 1-19.10.1556/CEuGeol.53.2010.1.1Suche in Google Scholar

[8] Smalley, I.J. 1966a. The expected shapes of blocks and grains. Journal of Sedimentary Research 36, 626-629.Suche in Google Scholar

[9] Howarth, J. 2010. The shape of loess particles reviewed. Open Geosciences 2, 41-44.10.2478/v10085-009-0039-ySuche in Google Scholar

[10] Smalley, I.J., Unwin, D.J. 1968. The formation and shape of drumlins and their distribution and orientation in drumlin fields. Journal of Glaciology 7, 377-390.10.1017/S0022143000020591Suche in Google Scholar

[11] Smalley, I.J. 1966b. Contraction crack networks in basalt flows. Geological Magazine 103, 110-11410.1017/S0016756800050482Suche in Google Scholar

[12] Kolodynska-Gawrysiak, R., Mroczek, P., Chabudzinski, L. 2013. Closed depressions in the prehistoric loess landscape and their influence on settlement location, in the light of selected examples from the Naleczow Plateau (Lublin Upland, E.Poland). Archaeologia Polona 49, 37-54.Suche in Google Scholar

[13] Kolodynska-Gawrysiak, R., Poesen, J. 2017. Closed depressions in the European loess belt-natural or anthropogenic origin? Geomorphology http://dx.doi/10.1016/j.geomorph.207.02.004.10.1016/j.geomorph.2017.02.004Suche in Google Scholar

[14] Kendall, M.G., Babington Smith, B. 1971. Tables of Random Sampling Numbers (Tracts for Computers 24). Cambridge University Press Cambridge 60p.Suche in Google Scholar

[15] Sarmah, B.K., Chakrabarty, D. 2015. Examination of proper randomness of numbers of M.G. Kendall and B. Babington Smith’s random numbers table: run test. International Journal of Multidisciplinary Research and Modern Education. 1, 223-226.Suche in Google Scholar

[16] Zeeden, C., Hark, M., Hambach, U., Markovic, S.B., Zoeller, L. 2007. Depressions on the Titel loess plateau: form-patterngenesis. Geographica Pannonica 11, 4-8.10.5937/GeoPan0711004ZSuche in Google Scholar

[17] Hardcastle, J. 1899. Origin of the loess deposits on the Timaru Plateau. Transactions and Proceedings of the New Zealand Institute 22, 406-414.(reprinted in Loess Letter 71, www.loessletter.msu.edu).Suche in Google Scholar

[18] Rogers, C.D.F., Dijkstra, T.A., Smalley, I.J. 1994. Hydroconsolidation and subsidence of loess: Studies from China, Russia, North America and Europe. Engineering Geology 37, 83-113.10.1016/0013-7952(94)90045-0Suche in Google Scholar

[19] Grecu, F., Eftene, A., Ghita, C., Benabbas, C. 2015. The loess micro-depressions within the Romanian plain; Morphometric and morphodynamic analysis. Revista de geomorfologie 17, 5-18.Suche in Google Scholar

[20] Różycki, S.Z. 1991. Loess and loess-like deposits. Ossolineum Wroclaw 187p.Suche in Google Scholar

[21] Popov, I.V. 1965. Engineering Geology of the USSR. Moscow University Press, Moscow (in Russian).Suche in Google Scholar

[22] Smalley, I.J., Bentley, S.P., Markovic, S.B. 2016. Loess and fragipans: Development of polygonal-crack-network structures in fragipan horizons in loess ground. Quaternary International 399, 218-223.10.1016/j.quaint.2015.01.034Suche in Google Scholar

[23] Smalley, I.J., Markovic, S.B. 2014. Loessification and hydroconsolidation; there is a connection. Catena 117, 94-99.10.1016/j.catena.2013.07.006Suche in Google Scholar

[24] Smalley, I.J. Kels, H. 2017. Leonard Horner and an enthusiasm for loess. Aeolioan Research in press.10.1016/j.aeolia.2017.03.004Suche in Google Scholar

Received: 2018-01-12

Accepted: 2018-03-13

Published Online: 2018-04-18

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Artikel in diesem Heft

https://doi.org/10.1515/geo-2018-0005

Schlagwörter für diesen Artikel

Loess landforms; closed depressions; random shapes; Zingg rectangle; Monte Carlo methods

Creative Commons

BY-NC-ND 4.0