Theoretical analysis of piezoceramic ultrasonic energy harvester applicable in biomedical implanted devices

Aboozar Dezhara; Alfio Dario Grasso; Andrea Ballo

doi:10.1515/ehs-2023-0085

Article Open Access

Theoretical analysis of piezoceramic ultrasonic energy harvester applicable in biomedical implanted devices

Aboozar Dezhara , Alfio Dario Grasso and Andrea Ballo

Published/Copyright: December 18, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Energy Harvesting and Systems Volume 11 Issue 1

Abstract

In this article, we theoretically analyze the one-dimensional model of a piezoceramic energy harvester that uses piezoelectric transduction in the 3-3 mode to convert ultrasonic pressure waves into electrical energy. Our approach to this problem is new because we did not use impedance approach which is a common method in many other articles. Nonetheless, our solution accounts for loss of acoustic environment. Our goal here is to extract maximum power from output load. Based on our simulations, the frequencies that the acoustic strength peaks are as same as frequencies that the pressure at receiver side peaks, and between these frequencies, the resonance occurs at a frequency that the pressure at the receiver side has a maximum peak. We propose two boundary conditions for radiating acoustical waves. In this article for a square shape transducer with a thickness of 2.1 mm and length of 1.46 cm, the resistive output load gave the most power, in which its value for free-fixed and free-free boundary conditions are 13.75 W and 17.37 W respectively, and at output resistances of 8.51 Ω and 13.11 Ω respectively. The required acoustic strengths to produce these powers for free-fixed and free-free boundary conditions are 424.944 × 1 0 7 m 3 s 2 and 129.977 × 1 0 8 m 3 s 2 . The resonance frequencies are 9.13545 MHz and 14.3617 MHz respectively, and the pressures at receiver side in the distance of 5 cm from transmitter transducer are 623.968 MPa and 1382.39 MPa respectively.

Keywords: ultrasonic waves; piezoceramic square element transmitter and receiver; energy harvesting; biomedical implanted devices

1 Introduction

Over the past few decades, the demand for wireless sensors, implantable electronics, and other low-power consumption devices has been growing rapidly. In many cases, these sensors or devices are used in places where supplying power through wires is difficult or inappropriate. As a result, their lifetime is greatly limited by the energy autonomy of the batteries usually embedded as power sources. As a substitute for traditional power supply, harvesting ambient energy (Dezhara 2024, Dezhara 2022) or transmitting energy wirelessly (Wang et al. 2007 Apr, Taalla et al. 2019, Tseng et al. 2020, Wu et al. 2020) is an effective way to power them. In comparison to the other methods of wireless transfer, such as inductive coupling, energy transfer based on the propagation of acoustic waves at ultrasonic frequencies is a recently explored alternative that offers increased transmitter–receiver distance, reduced loss, and the elimination of electromagnetic fields (Shahab 2014). As this research area receives growing attention, there is an increased need for fully coupled model development to quantify the energy transfer characteristics, with a focus on the transmitter, receiver, medium, geometric, and material parameters (Shahab 2014). Acoustic waves are one kind of common environmental energy. Acoustic waves include longitudinal, transverse bending, hydrostatic and shear waves with frequencies ranging from less than 1 Hz to more than 10 kHz (Sherrit 2008). In comparison with transversal waves, longitudinal waves have the advantage of propagating in fluids (Roes et al. 2013) and their transmission ability through biological tissues has been widely used in medical treatments, such as high intensity focused ultrasound therapy (Roes et al. 2013, Humphrey 2007). The idea of using acoustic waves to transmit and harvest energy was proposed as early as 1958 by Ozeri and Shmilovitz (2010). Harvesting certain longitudinal ultrasonic energy to power implantable devices is a preferred technology due to its power transfer efficiency, compactness, and electromagnetic immunity (Ozeri and Shmilovitz 2010, Yang et al. 2013). Recently, ultrasonic wireless energy-harvesting technologies have been proposed (Piech et al. 2020). Compared to electromagnetic waves, ultrasound can realize a longer travel depth and a better spatial resolution in the tissues (Jiang et al. 2020). Furthermore, according to the U.S. Food and Drug Administration’s regulation, the safety threshold of ultrasound waves in the human body is 720 mW cm 2 (Pritchard and Carey 1997), which is dozens of times greater than that of radio waves ( 10 mW cm 2 ) (Lin 2006). These two factors enable ultrasonic wireless energy-harvesting technology’s unique advantages in biomedical applications in contrast to other wireless power transmission technologies, such as electromagnetic. The goal of this article is to quantify the electrical power delivered to the load (connected to the receiver) in terms of the source strength. In this article, we first derive the electric field and displacement of a rectangular piezoceramic element using one-dimensional piezoelectricity constitutive law. Here we neglect the displacement in the x or y direction just because of the low aspect ratio; thus, the transverse displacement is calculated. After an introduction to the piezoelectric behavior of piezoceramic rectangular elements, we open the discussion of ultrasonic wave propagation in the nonlinear form in viscous fluid with a known shear and bulk viscosity as a prototype medium of body tissue of humans. Then we discuss the coupling between the mechanical and electrical parts of piezoelectric (piezoceramic) and derive the electrical damping as well as energy injection lock coefficient (the coefficient that is responsible for reactive power (Dezhara 2022)) and calculate the output power versus frequency in MATLAB. In summary, the article is structured as follows: Section 2 introduces analytical bases on ultrasonic piezoelectric energy harvesters. Section 3 gives the formulas to describe the ultrasonic link between sender and receiver transducers. Section 4 gathers output solutions for three load cases, namely, resistive, inductive and capacitive loads. Section 5 discusses about efficiency. Finally, a numerical example and conclusions close the work. As useful support for the reading of the manuscript, two appendixes are also provided.

2 Basics of ultrasonic piezoelectric energy harvesters

In this section, we analyze the constitutive laws of piezoceramic using a one-dimensional model of piezoelectricity, and also the ultrasonic wave propagation in viscous fluid will be analyzed.

2.1 Piezoceramic (piezoelectric) constitutive laws

This subsection reports the constitutive laws governing the piezoceramic element shown in Figure 1. The analysis is done using the one-dimensional model for law aspect ratio (less than 0.1) and the result of the analysis, i.e., displacement and electric potential, is applied to the boundary conditions in the following subsection, which deals with sound waves in a viscous fluid. The constitutive laws are as follow (Yang et al. 2015, Erturk and Inman 2008, Safaei et al. 2019):

(1a) T i j = c i j k l S k l − e k i j E k ,

(1b) D i = e i k l S k l + ε i k E k ,

where T is the mechanical stress, S is the mechanical strain, D is the electric flux density, E is the electric field intensity, e is the matrix for indirect piezoelectric effect, c E is the stiffness matrix at constant electric field, and ε S : permittivity at constant strain.

Figure 1

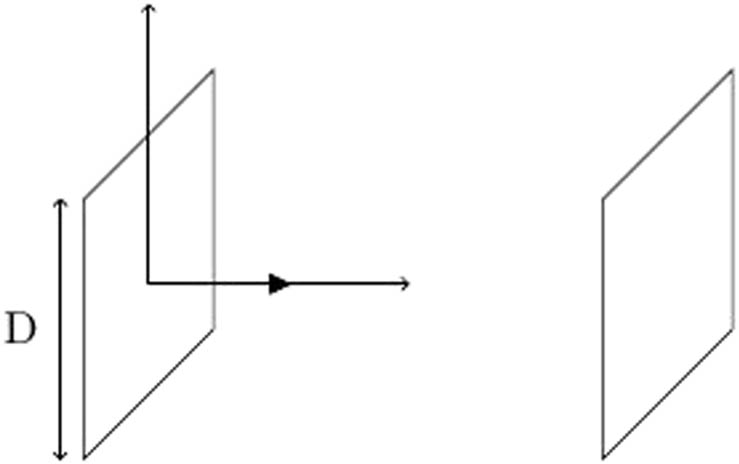
Model of square piezoceramic elements. The distance between two mid-plane of transducers is L + 2 h (not shown), where L is the distance between transducers and h is half of the thickness of transducers.

The Newton second law in mechanic and third law of Maxwell (electric Guess law) in electromagnetic for charge free medium are expressed, respectively, as follows:

(1c) T i j , j = ρ u ¨ i , D i , i = 0 ,

where u i is displacement in specific direction, and ρ is density of piezoceramic disk, and “,” sign is derivative with respect to displacement. We now introduce compact matrix notation. This notation consists of replacing pairs of tensor indices i , j or k , l by single matrix indices p or q , where i , j , k , l take the values 1 , 2 , 3 and p and q take the values of 1 , 2 , 3 , 4 , 5 , 6 according to:

i , j or k , l : 11 22 33 23 31 12 ( 1 d ) p or q : 1 2 3 4 5 6 ( 1 e )

Thus,

(1f) c i j k l → c p q , e i k l → e i p , T i j → T p .

Note that the matrices are symmetrical, and therefore, values for index 32 are the same as 23 and that for 13 are the same as 31. So we obtain:

(1g) T p = c p q E S q − e k p E k ,

(1h) D i = e i q S q + ε i k S E k .

According to equation of (1e). For the strain tensor, we introduce S p as follows:

(1i) S 1 = S 11 , S 2 = S 22 , S 3 = S 33 ,

(1j) S 4 = 2 S 23 , S 5 = 2 S 31 , S 6 = 2 S 12 .

In th following analysis for simplicity, we dropped the superscript of E in c p q E and that of S in ε i k S .

2.2 Displacement and electric potential of transmitter

Here, the AC voltage is applied to the electrodes of the piezoceramic disk. We will derive the acceleration of the vibrating disk and relate the pressure at the receiver transducer to this acceleration (in the next section).

The nonvanishing strain and electric field components are as follows:

(2a) S 33 = u ¯ 3 , 3 , E 3 = − ϕ ¯ , 3 ,

where the time-harmonic factor has been dropped and the comma means derivative with respect to displacement. If we assume sinusoidal function for u 3 and ϕ such as u 3 = u ¯ 3 cos ( ω t ) = ℜ ( u ¯ 3 exp ( j ω t ) ) and ϕ = ϕ ¯ cos ( ω t ) = ℜ ( ϕ ¯ exp ( j ω t ) ) . The nontrivial stress and electric displacement components are as follows:

(2b) T 11 = T 22 = e 13 u ¯ 3 , 3 + e 31 ϕ ¯ , 3 T 33 = c 33 u ¯ 3 , 3 + e 33 ϕ ¯ , 3 D 3 = e 33 u ¯ 3 , 3 − ε 33 ϕ ¯ , 3 .

By substituting equation (2b) into equation (1c), we obtain:

(2c) c 33 u ¯ 3 , 3 + e 33 ϕ ¯ , 3 = − ρ ω 2 u ¯ 3 ,

(2d) e 33 u ¯ 3 , 3 − ε 33 ϕ ¯ , 3 = 0 .

Equation (2d) can be integrated to yield:

(2e) ϕ ¯ = e 33 ε 33 u ¯ 3 + C 1 z + C 2 ,

where C 1 and C 2 are integration constants. By substituting equation (2e) into second and third equation (2b), we obtain

(2f) T 33 = c ¯ 33 u ¯ 3 , 3 + e 33 C 1 ,

(2g) D 3 = − ε 33 C 1 ,

(2h) c ¯ 33 u ¯ 3 , 3 + ρ ω 2 u ¯ 3 = 0 ,

where

(2i) c ¯ 33 = c 33 ( 1 + k 33 2 ) ,

(2j) k 33 2 = e 33 2 ε 33 c 33 ,

where k 33 is the electro-mechanical coupling factor of the piezoelectric material. The general solution to the displacement equation (2h) and the corresponding expression for the potential are as follows:

(2k) u ¯ 3 = B 1 sin ( ζ z ) + B 2 cos ( ζ z ) ,

(2l) ϕ ¯ = e 33 ε 33 ( B 1 sin ( ζ z ) + B 2 cos ( ζ z ) ) + C 1 z + C 2 ,

where − h ≤ z ≤ h and B 1 and B 2 are integration constant, and also we have:

(2m) ζ 2 = ρ c ¯ 33 ω 2 .

As mentioned earlier, the time harmonic factor is dropped and u ¯ 3 and ϕ ¯ are in the phasor form. The expression for the stress is as follows:

(2n) T 33 = c ¯ 33 ( B 1 ζ cos ( ζ z ) − B 2 ζ sin ( ζ z ) ) + e 33 C 1 ,

(2o) S 33 = B 1 ζ cos ( ζ z ) − B 2 ζ sin ( ζ z ) ,

(2p) S 33 = d u ¯ 3 d z = T 33 c ¯ 33 − e 33 C 1 c ¯ 33 .

2.2.1 Boundary conditions (transmitter, free at both sides)

Here, we assumed that the both sides of transmitter piezoceramic square element is free to touch fluid, i.e., the stress at both sides is zero. The boundary conditions between the piezoceramic transmitter disk and the acoustic environment are as follows:

(2q) T 33 ∣ z = − h = T 33 ∣ z = + h = 0 ,

(2r) ϕ ¯ ∣ z = + h − ϕ ¯ ∣ z = − h = V 0 ,

(2s) ϕ ¯ ∣ z = 0 = 0 ,

where 2 h is the thickness of the piezoceramic disk. By applying boundary conditions in equations (2k) and (2l):

(2t) c ¯ 33 ( B 1 ζ cos ( ζ h ) − B 2 ζ sin ( ζ h ) ) + e 33 C 1 = 0 ,

(2u) c ¯ 33 ( B 1 ζ cos ( ζ h ) + B 2 ζ sin ( ζ h ) ) + e 33 C 1 = 0 ,

(2v) 2 e 33 ε 33 B 1 sin ( ζ h ) + 2 C 1 h = V 0 .

To solve the aforementioned equations, add and also subtract the first two equations from each other. The third equation will remain intact.

(2w) c ¯ 33 B 1 ζ cos ( ζ h ) + e 33 C 1 = 0 ,

(2x) c ¯ 33 B 2 ζ sin ( ζ h ) = 0 ,

(2y) 2 e 33 ε 33 B 1 sin ( ζ h ) + 2 C 1 h = V 0 ,

(2z) e 33 ε 33 B 2 + C 2 = 0 .

Thus, the aforementioned constants are as follows:

(3a) B 1 = − e 33 V 0 2 c ¯ 33 ζ h cos ( ζ h ) − 2 e 33 2 ε 33 sin ( ζ h ) ,

(3b) B 2 = 0 ,

(3c) C 1 = V 0 c ¯ 33 ζ cos ( ζ h ) 2 c ¯ 33 ζ h cos ( ζ h ) − 2 e 33 2 ε 33 sin ( ζ h ) ,

(3d) C 2 = − e 33 ε 33 B 2 = 0 .

By knowing these constants, we can express the boundary conditions in the sound wave equation in terms of the velocity of the piezoceramic solid–fluid interface, which is the topic of the next section. The acoustic strength of the transmitter transducer normalized to acoustic volume velocity is calculated as follows:

(3e) J 1 = Q 1 c A = A u ¨ 3 ∣ z = + h c A ,

(3f) J 1 ¯ = ω 2 ∣ B 1 sin ( ζ h ) ∣ c ,

where A is the area of the transducers and Q 1 is acoustic strength with dimension of [ L 3 T 2 ] , where L is length and T is time dimension. Note that J in this case is J 1 and J 1 = J 1 ¯ cos ( ω t ) . We use absolute value since J 1 ¯ should be positive. It should be noted that the value of J 1 ¯ is maximum exactly when sin ( ζ h ) = 1 because in this case cos ( ζ h ) = 0 and the B 1 will also be maximum (the denominator of B 1 becomes minimum). Thus, the resonance frequency can be derived as follows:

(3g) sin ( ζ h ) = 1 ,

(3h) ζ h = n + 1 2 π ,

(3i) ζ = ρ c ¯ 33 ω ,

(3j) f = n + 1 2 ρ c ¯ 33 t , n = 0 , 1 , 2 , … ,

where ρ is the mechanical density of piezoceramic and t is thickness of it ( t = 2 h ). As mentioned previously, the frequencies that acoustic strength peaks are as same as frequencies that pressure at receiver side peaks and resonance occurs at frequency that the pressure has maximum peak. The antiresonance frequency for this case of boundary conditions occurs when sin ( ζ h ) = 0 . As a result, we have:

(3k) ζ h = n π ,

(3l) f = n ρ c ¯ 33 t , n = 1 , 2 , 3 , … .

2.2.2 Boundary conditions (transmitter, free at front side and fixed at back side)

Here, we assumed that the right sides of transmitter in direction of receiver, piezoceramic square element is free to touch fluid, i.e., the stress at right side is zero; however, the left side is fixed (no strain condition) and there is a back layer with suitable thickness at the left side that suppresses the acoustic pressure. The boundary conditions between the piezoceramic transmitter disk and the acoustic environment are as follows:

(3m) S 33 ∣ z = − h = 0 ,

(3n) T 33 ∣ z = + h = 0 ,

(3o) ϕ ¯ ∣ z = + h − ϕ ¯ ∣ z = − h = V 0 ,

(3p) ϕ ¯ ∣ z = 0 = 0 ,

where S 33 = u 3 , 3 . By applying boundary conditions in equations (2k) and (2l):

(3q) B 1 ζ cos ( ζ h ) − B 2 ζ sin ( ζ h ) = 0 ,

(3r) c ¯ 33 ( B 1 ζ cos ( ζ h ) + B 2 ζ sin ( ζ h ) ) + e 33 C 1 = 0 ,

(3s) 2 e 33 ε 33 B 1 sin ( ζ h ) + 2 C 1 h = V 0 .

Derive B 1 from the first equation and plug it into the second equation, then derive C 1 and now we have B 1 and C 1 in terms of B 2 . We can plug the aforementioned parameters into third equation and derive B 2 . Note that these algebraic manipulation is admissible only if cos ( ζ h ) ≠ 0 :

(3t) B 1 = B 2 tan ( ζ h ) ,

(3u) C 1 = − 2 c ¯ 33 e 33 B 2 ζ sin ( ζ h ) ,

(3v) 2 e 33 ε 33 B 2 tan ( ζ h ) sin ( ζ h ) − 2 2 c ¯ 33 e 33 B 2 ζ sin ( ζ h ) h = V 0 ,

(3w) e 33 ε 33 B 2 + C 2 = 0 .

Thus, the aforementioned constants are as follows:

(4a) B 1 = V 0 2 e 33 ε 33 sin ( ζ h ) − 4 c ¯ 33 e 33 ζ h cos ( ζ h ) ,

(4b) B 2 = V 0 2 e 33 ε 33 tan ( ζ h ) sin ( ζ h ) − 4 c ¯ 33 e 33 ζ h sin ( ζ h ) ,

(4c) C 1 = − 2 c ¯ 33 e 33 V 0 ζ 2 e 33 ε 33 tan ( ζ h ) − 4 c ¯ 33 e 33 ζ h ,

(4d) C 2 = − e 33 ε 33 B 2 .

The normalized acoustic strength of the transmitter transducer is calculated as follows:

(4e) J 2 = A u ¨ 3 ∣ z = + h c A → J 2 ¯ = ω 2 ∣ B 1 sin ( ζ h ) + B 2 cos ( ζ h ) ∣ c .

Note that J in this case is J 2 and J 2 = J 2 ¯ cos ( ω t ) . Finding the maximum value of the J 2 ¯ is more complex than J 1 ¯ ; thus, we will introduce a general method based on energy to find the resonance frequency.

2.3 Resonance frequency of transmitter

We can consider thickness as a constant and sweep the acoustic strength vs frequency to find the resonance, and in this case, we use analytical approach as a verification method for the optimum frequency we fined from graphical method, i.e., sweeping. In this approach, we find the extremum (minimum in this case) of the average Lagrangian with respect to frequency.

2.3.1 Potential energy

The strain energy per unit volume stored in the piezoceramic due to deformation is expressed as follows:

(5a) U 0 = ∫ T 33 d S 33 = ∫ T 33 d T 33 c ¯ 33 − e 33 C 1 c ¯ 33 ,

(5b) U 0 = ∫ − h + h T 33 d T 33 c ¯ 33 = 1 2 c ¯ 33 T 33 2 ,

(5c) U ¯ = ∫ − h + h U 0 A d z = A 2 c ¯ 33 ∫ − h + h T 33 2 d z = A 2 c ¯ 33 I 1 ,

where I 1 = ∫ − h + h T 33 2 d z and U ¯ is energy stored in the piezoceramic due to deformation. From (2n), we have

(5d) I 1 = c ¯ 33 2 B 1 2 N 1 + c ¯ 33 2 B 2 2 N 2 + e 33 2 C 1 2 N 3 ,

(5e) − 2 ( c ¯ 33 2 B 1 B 2 N 4 + c ¯ 33 e 33 C 1 B 2 N 5 − c ¯ 33 B 1 C 1 e 33 N 6 ) ,

where

(5f) N 1 = ∫ ζ 2 cos ( ζ z ) d z ,

(5g) N 2 = ∫ ζ 2 sin ( ζ z ) d z ,

(5h) N 3 = ∫ d z ,

(5i) N 4 = ∫ ζ cos ( ζ z ) d z ,

(5j) N 5 = ∫ ζ 2 cos ( ζ z ) sin ( ζ z ) d z ,

(5k) N 6 = ∫ ζ sin ( ζ z ) d z .

These integrals easily can be solved by changing the variable, assume u = ζ z , and solve the aforementioned integrals^[1]:

(5l) N 1 = ζ 2 h + ζ 2 sin ( 2 ζ h ) ,

(5m) N 2 = ζ 2 h − ζ 2 sin ( 2 ζ h ) ,

(5n) N 3 = 2 h ,

(5o) N 4 = 2 sin ( ζ h ) ,

(5p) N 5 = 0 ,

(5q) N 6 = 0 .

After substitution of these integral solutions into I 1 , we have

(6a) U ¯ = 1 2 ζ 2 h A c ¯ 33 ( B 1 2 + B 2 2 ) + A c ¯ 33 ζ 2 ( B 1 2 − B 2 2 ) sin ( ζ h ) + 2 A e 33 2 C 1 2 h c ¯ 33 − 4 A c ¯ 33 B 1 B 2 sin ( ζ h ) ,

It should be noted that we had dropped the sinusoidal term in stress and strain, but we should consider it for calculating the average value of potential energy. We have U = U ¯ sin 2 ( ω t ) = U ¯ sin 2 ( θ ) . The average value of U is:

(6b) U av = 1 ω T ∫ 0 ω T U ¯ 1 − cos ( 2 θ ) 2 d θ ,

(6c) U av = U ¯ 2 ω T ∫ 0 ω T ( 1 − cos ( 2 θ ) ) d θ ,

(6d) U av = U ¯ 2 .

2.3.2 Kinetic energy

In contrast to potential energy, which is internal to the system, the kinetic energy is due to a external agent, for obtaining this energy, the newton second law for the transmitter should be solved. Here, we just use the result of section efficiency (section 5). According to this (efficiency) section, velocity is: x ˙ = − A 1 ω sin ( ω t ) + A 2 ω cos ( ω t ) , where A 1 and A 2 are as the same constants as derived in section efficiency. The kinetic energy is expressed as follows:

(7a) T = 1 2 m x ˙ 2 = 1 2 m A 1 2 ω 2 2 + A 2 2 ω 2 2 − A 1 2 ω 2 2 − A 2 2 ω 2 2 cos ( 2 ω t ) − A 1 A 2 ω 2 sin ( 2 ω t ) ) ,

Similarly, the average value of kinetic energy is as follows:

(7b) T av = m 2 A 1 2 ω 2 2 + A 2 2 ω 2 2 .

2.3.3 External force work as a potential

The mechanical work done on transmitter piezoceramic is caused by piezoelectric force K v in which is denoted by V and is assumed to be stored as a potential energy.

(8a) V = − ∫ K v d x = − K v x ,

(8b) V = − K V 0 sin ( ω t ) × ( A 1 cos ( ω t ) + A 2 sin ( ω t ) ) ,

(8c) V = − K V 0 A 2 2 − K V 0 A 1 2 sin ( 2 ω t ) + K V 0 A 2 2 cos ( 2 ω t ) ,

(8d) V av = − K V 0 A 2 2 .

Note that K v is constant and comes out of the integration.

2.3.4 Resonance frequency

We will find optimum excitation frequency and thickness at constant excitation voltage. For doing this, we should first take the average of the Lagrangian.

(9a) L av = T av − π av = T av − ( U av + V av ) ,

where π is total potential of the system. Now we should extremetize the Lagrangian as follows:

(10a) ∂ L av ∂ ω = 0 , ∂ L av ∂ h = 0 .

As mentioned earlier, the analytical method can be used as a verification of the frequency derived from sweeping the acoustic strength (at given thickness). By solving the aforementioned nonlinear equations numerically in MATLAB, we can find the optimum resonance frequency and even optimum thickness at which we have maximum pressure at a receiver side.

3 Propagation of acoustic waves between transducers

The most exact simplified sound wave equation in viscous fluid without considering compressibility, which can be considered as a model of human body tissue can be described as follows^[2] (Kino 1987):

(11a) 1 + μ ′ ρ 0 c 2 ∂ ∂ t ∇ 2 Φ − 1 c 2 ∂ 2 Φ ∂ t 2 = J ,

where Φ is the velocity potential, J is the the ratio of acoustic source strength at the transmitter-fluid interface to acoustic volume velocity, i.e., Q c A , Q is the acoustic source strength, μ ′ = μ v + 4 3 μ , μ v is the bulk viscosity, μ is the shear viscosity, ρ 0 is the acoustic environment density (i.e., humane body tissue density), and c is the sound velocity in the viscous fluid.

Note that the dimension of Q is [ L 3 T 2 ] . The shear viscosity dissipates energy by friction between adjacent layers of fluid, while the bulk viscosity dissipates energy with the dilatational-compressional motion of the fluid. By solving this nonlinear wave equation, one can obtain the velocity as a derivative of the potential function Φ so that we will be able to calculate the pressure at any distance from the source (sender transducer). This pressure is sinusoidal and has an amplitude with exponential decay with distance from the source.

By knowing the velocity potential, one can derive the pressure according to the following differential equation (Kino 1987):

(11b) 1 + μ ′ ρ 0 c 2 ∂ ∂ t p + ρ 0 ∂ Φ ∂ t = μ ′ J .

Assume a one-dimensional model^[3]. We assume the response of equation (11a) as follows:

(11c) Φ h = D 1 ℜ ( exp ( − j K 1 z ) exp ( j ω t ) ) ,

where K 1 and ℜ are the complex wave number and real part of the time exponential term, respectively. D 1 is the amplitude of velocity potential. Equation (11c) in frequency domain is given as follows:

(11d) Φ ¯ h = D 1 exp ( − j K 1 z ) ∠ 0 ,

where the bar-sign means frequency domain. By substituting equation (11c) or (11d) into homogenized equation (11a) and drop time harmonic real part terms, we obtain:

(11e) − K 1 2 D 1 + − μ ′ ρ 0 c 2 ( − K 1 2 D 1 j ω ) + ω 2 c 2 D 1 = 0 .

Note that we drop the exponential terms.

(11f) K 1 = ω c ( a 2 + b 2 ) ( a − j b ) = k 1 − j k 2 k 1 = ω a c ( a 2 + b 2 ) k 2 = ω b c ( a 2 + b 2 ) ,

where a and b are given as follows:

(11g) a = ρ 0 2 + ( μ ′ ω c 2 ) 2 + ρ 0 2 ρ 0 b = ρ 0 2 + ( μ ′ ω c 2 ) 2 − ρ 0 2 ρ 0 .

Note that k 2 and not k 1 is attenuation constant, and k 1 is wave number. The nonhomogeneous solution of the differential equation (11a) in the time domain is given as follows:

(11h) Φ non- h = c 2 J 1 ¯ ω 2 ℜ ( exp ( j ω t ) ) .

And the phasor form is:

(11i) Φ ¯ non- h = c 2 J 1 ¯ ω 2 ∠ 0 .

Thus, the homogeneous plus nonhomogeneous solution in the frequency domain becomes as follows:

(11j) Φ ¯ = Φ ¯ h + Φ ¯ non- h .

By applying boundary condition, we obtain

(11k) − d Φ ¯ d z z = + h = u ˙ 3 ∣ z = + h ,

(11l) u ˙ 3 ∣ z = + h = j ω ( B 1 sin ( ζ h ) + B 2 cos ( ζ h ) ) = j R 1 ,

where we introduced R 1 in which is arbitrary constant for simplicity. Note that we dropped the cosine term in the equation (11l). We can write equation (11l) as follows:

(11m) − j K D 1 = j R 1 → D 1 = − ∣ D 1 ∣ ∠ tan − 1 k 2 k 1 ,

where ∣ D 1 ∣ = R 1 ∣ K 1 ∣ 2 . By knowing the velocity potential, we can calculate the pressure at any distance ( x ) from the transmitter transducer. According to equation (11b), we have (in time domain) the following:

(12a) d p d t + ρ 0 c 2 μ ′ p = ρ 0 c 2 J 1 ¯ c o s ( ω t ) + ρ 0 2 c 2 ω ∣ D 1 ∣ μ ′ × e − k 2 x cos ( ω t − k 1 x + ϕ 1 ) + ρ 0 c 4 J 1 ¯ μ ′ ω sin ( ω t ) ,

where ϕ 1 = π 2 + tan − 1 k 2 k 1 and the third term on the right-hand side is due to nonhomogeneous solution of velocity potential. We assume the steady state solution as follows:

(13a) p = C 3 cos ( ω t ) + C 4 sin ( ω t ) + C 5 e − k 2 x cos ( ω t − k 1 x + ϕ 1 ) + C 6 e − k 2 x sin ( ω t − k 1 x + ϕ 1 ) ,

where x is distance from transmitter transducer. Note that the transient solution is p 0 e − ( μ ′ ρ 0 c 2 t ) in which we neglect our calculations. By using superposition method and substituting equation (13a) into the differential equation (12a), we can solve for constants C 3 , C 4 , C 5 , C 6 :

(13b) − C 3 ω + C 4 ρ 0 c 2 μ ′ = ρ 0 c 4 J 1 ¯ μ ′ ω ,

(13c) C 4 ω + C 3 ρ 0 c 2 μ ′ = ρ 0 c 2 J 1 ¯ ,

(13d) ω C 6 + ρ 0 c 2 μ ′ C 5 = ρ 0 2 c 2 ω ∣ D 1 ∣ μ ′ ,

(13e) − ω C 5 + ρ 0 c 2 μ ′ C 6 = 0 .

Note that the dominance of each term in the aforementioned function determines near-field or far-field pressure in acoustic domain. By solving the aforementioned equations, we obtain:

(13f) C 6 = ρ 0 2 c 2 ω 2 μ ′ ∣ D 1 ∣ ( μ ′ ω ) 2 + ( ρ 0 c 2 ) 2 ,

(13g) C 5 = ρ 0 c 2 μ ′ ω C 6 ,

(13h) C 4 = ρ 0 c 4 ω + μ ′ 2 ω ρ 0 c 2 J 1 ¯ ( μ ′ ω ) 2 + ( ρ 0 c 2 ) 2 ,

(13i) C 3 = ρ 0 c 2 μ ′ ω C 4 − ρ 0 c 4 μ ′ ω 2 J 1 ¯ .

Note that for free-fixed boundary conditions, we should use J 2 ¯ instead of J 1 ¯ . The steady-state response in phasor form at distance L became^[4]:

(14a) p ¯ = C 3 − j C 4 + C 5 exp ( − k 2 L ) ∠ ( ϕ 1 − k 1 L ) + C 6 exp ( − k 2 L ) ∠ ϕ 1 − k 1 L − π 2 = ( C 3 + C 5 exp ( − k 2 L ) cos ( Y ) + C 6 exp ( − k 2 L ) sin ( Y ) ) + j ( − C 4 + C 5 exp ( − k 2 L ) sin ( Y ) − C 6 exp ( − k 2 L ) cos ( Y ) ) ,

where Y = ϕ 1 − k 1 L .

(14b) θ = tan − 1 − C 4 + C 5 exp ( − k 2 L ) sin ( Y ) − C 6 exp ( − k 2 L ) cos ( Y ) C 3 + C 5 exp ( − k 2 L ) cos ( Y ) + C 6 exp ( − k 2 L ) sin ( Y ) .

3.1 Reynolds number

We can define Reynolds number as follows:

(15) Re = ρ 0 c 2 μ ′ ω .

This can be interpreted as inertia force (acceleration) to viscous force (friction). Note that it is a nondimensional number. If this term became small, then the pressure decreases substantially with distance from transmitter and the decaying term became dominant with respect to steady terms in pressure function. We will calculate this number in the numerical example section.

4 Receiver transducer

In this section, we express the mechanical and electrical differential equations for resistive, capacitive, and inductive loads and decouple them in the frequency domain so that the electrical damping and output power can be calculated. Figure 2 depicts the general circuit of the equivalent electrical part of the receiver transducer, where C 0 and I 0 are internal capacitance of piezoceramic transducer and the generated current, respectively, due to the deformation of piezoceramic disk.

Figure 2

The equivalent electrical part of receiver transducer.

4.1 Resistive load

The second Newton law on the mechanical side and the Kirchhoff current law on the electrical side with X = 0 are as follows:

(16) m x ¨ + C m x ˙ + k s x + K v = F e x c C 0 d v d t + v R − K x ˙ = 0 .

Note that I 0 is equal to K x ˙ and K v is the piezoelectric force, where v and x ˙ are velocity and load voltage, respectively. C 0 is ε A t , where A is area of transducer and t is thickness of it. In frequency domain, equation (16) can be written as follows:

(17) ( − m ω 2 + j ω C m + k s ) x ¯ + K v ¯ = F ¯ 1 R + j ω C 0 v ¯ = j K ω x ¯ ,

where the bar sign means frequency domain. And F ¯ = p ¯ A . By simplifying the aforementioned equations and after substitution, we have:

(18) v ¯ = j K ω 1 R + j ω C 0 x ¯ × − m ω 2 + j ω C m + k s + j K 2 ω 1 R + j ω C 0 x ¯ ( ω ) = F ¯ .

Therefore, the transfer function is given as follows:

(19) x ¯ F ¯ = 1 ω k s ω − m ω + K 2 ω C 0 1 R 2 + ω 2 C 0 2 + j ω C m + K 2 R 1 R 2 + ω 2 C 0 2 ,

Now we calculate the input electrical power into the electrical domain. Note that only the work of piezoelectric force, i.e., K v , contributes to electrical input power into electrical domain.

(20a) P ( t ) = − d d t ∫ K v d x ,

(20b) P ( ω ) = − j ω K ∫ v ¯ d x ¯ ,

(20c) P ( ω ) = − j ω K ∫ j ω K x ¯ 1 R + j ω C 0 d x ¯ = 1 2 ω 2 K 2 1 R + j ω C 0 x ¯ x ¯ ∗ .

After simplifying and transforming the aforementioned equation into standard form, we obtain:

(20d) P ( ω ) = 1 2 K 2 R 1 R 2 + ω 2 C 0 2 − j K 2 ω C 0 1 R 2 + ω 2 C 0 2 ∣ x ˙ ∣ 2 ,

(20e) P = 1 2 ( c e − j c e ′ ) ∣ x ˙ ∣ 2 ,

(20f) P = 1 2 C e ∣ x ˙ ∣ 2 ,

(20g) C e = c e − j c e ′ ,

(20h) c e = K 2 R 1 R 2 + ω 2 C 0 2 ,

(20i) c e ′ = K 2 ω C 0 1 R 2 + ω 2 C 0 2 ,

(20j) v ¯ x ¯ = j ω K j ω C 0 + 1 R ,

(20k) v x 2 = K 2 ω 2 C 0 2 ω 2 + 1 R 2 ,

(20l) P = v 2 R = K 2 x 2 ω 2 C 0 2 ω 2 R + 1 R ,

(20m) P RMS = P 2 ,

where RMS stands for the root mean square. Note that the P in equation (20m) is P of equation (20l). Note that the x can be replaced by the transfer function, i.e., equation (19). c e is the electrical damping coefficient and c e ′ is the energy injection lock coefficient or simply lock coefficient (Dezhara 2022). The former is responsible for active power, and the latter is responsible for the reactive power. It should be noted that the flow of reactive power is always from the electrical domain into the mechanical domain even if the sign of c e ′ is negative.^[5] Finally, we can put the transfer function into the form

(21) x ¯ F ¯ = 1 k s − m ω 2 + ω c e ′ + j ω ( C m + c e ) .

And the resonance condition in which we can calculate the resonance frequency of the receiver transducer from is given as follows:

(22) k s − m ω 2 + K 2 ω 2 C 0 1 R 2 + ω 2 C 0 2 = 0 → c e ′ = m ω − k s ω .

It is worth noting that this condition guarantees that the mechanical displacement amplitude is maximum, and the frequency that derived from it is also called natural frequency of the receiver piezoceramic element. The active electrical power in the resistor is given as follows:

(23) P = ω 2 2 c e x 2 → ∂ P ∂ c e = 0 .

By applying the resonance condition

(24) x ¯ = F ¯ j ω ( C m + c e ) → ∣ x ¯ ∣ = ∣ F ¯ ∣ w ( C m + c e ) .

And, finally, plugging (24) into (23), the following is obtained

(25) P = ∣ F ¯ ∣ 2 2 c e ( C m + c e ) 2 .

It should be observed that

(26) ∂ P ∂ c e = 0 → ( C m + c e ) 2 − 2 ( C m + c e ) c e = 0 → c e = C m .

This condition states that, at resonance, input electrical power in the electrical domain is maximized, i.e., maximum peak when the electrical damping coefficient equals the mechanical damping coefficient.

4.2 Capacitive load

When the load reactance in Figure 2 has a negative value (capacitive load), an analysis approach similar to those for resistive load can be used, which yields to the following equations:

(27a) C 0 R d i d t + 1 + C 0 C i = K x ˙ ,

(28a) − m ω 2 + C m j ω + k s + K 2 j ω ( R + 1 j ω C ) 1 + C 0 C + j ω C 0 R x ¯ = F ¯ ,

(28b) c e = K 2 R 1 + C 0 C 2 + ω 2 R 2 C 0 2 ,

(28c) c e ′ = K 2 1 + C 0 C C ω + R 2 ω C 0 1 + C 0 C 2 + R 2 ω 2 C 0 2 ,

where v is the load voltage and x is the displacement.

(29a) i ¯ x ¯ = j ω K R C 0 ω j + 1 + C 0 C ,

(29b) i x 2 = K 2 ω 2 R 2 C 0 2 ω 2 + 1 + C 0 C 2 ,

(29c) P = i 2 R = K 2 x 2 R ω 2 R 2 C 0 2 ω 2 + 1 + C 0 C 2 ,

(29d) P RMS = P 2 .

4.3 Inductive load

The analysis can be done in the case of an inductive load. The electrical side equations are given as follows:

(30) K x ˙ = C 0 R d i d t + C 0 L d 2 i d t 2 + i ,

which, in the frequency domain, becomes

(31) j ω K x ¯ ( ω ) = ( j ω C 0 R + 1 − C 0 L ω 2 ) i ¯ ( ω ) .

The load voltage in the frequency domain is given as follows:

(32) v ¯ = ( R + j ω L ) i ¯ ( ω ) .

So, the transfer function is

(33) x ¯ F ¯ = 1 − m ω 2 + k s + j ω C m + j ω K 2 ( R + j ω L ) ( 1 − C 0 L ω 2 ) + j ω R C 0 .

On the basis of the real and imaginary parts of the transfer function denumerator, we obtain

(34) c e = K 2 R ( 1 − C 0 ω 2 L ) 2 + ( R C 0 ω ) 2 ,

(35) c e ′ = K 2 R 2 ω C 0 − K 2 ω L ( 1 − C 0 L ω 2 ) ( 1 − C 0 ω 2 L ) 2 + ( R C 0 ω ) 2 ,

and, finally, according to (31), the output power is

(36a) i ¯ x ¯ = j ω K ( 1 − C 0 L ω 2 ) + R C 0 ω j ,

(36b) i x 2 = K 2 ω 2 R 2 C 0 2 ω 2 + ( 1 − C 0 ω 2 L ) 2 ,

(36c) P = i 2 R = K 2 ω 2 R x 2 R 2 C 0 2 ω 2 + ( 1 − C 0 ω 2 L ) 2 ,

(36d) P RMS = P 2 .

5 Efficiency

In this section, we derive a formula for efficiency of transmitter and receiver. However, before that, we should define efficiency as output electrical power to input power due to deformation. In other words, we can define efficiency just for direct piezoelectric effect (energy harvesting effect) and not indirect effect. Whenever we have indirect effect such as in transmitter, we should reverse the result and define the efficiency as input electric power to output mechanical power due to velocity and deformation. Otherwise it is value became larger than one.

5.1 Transmitter

The differential equation governing the vibration of transmitter transducer is as follows:

(37a) m x ¨ + C m x ˙ + k s x = K V 0 sin ( ω t ) ,

where V 0 is peak excitation voltage and the excitation term in the aforementioned differential equation is piezoelectric force induced on transmitter transducer. If we assume a sinusoidal solution of x = A 1 cos ( ω t ) + A 2 sin ( ω t ) , then by substituting this solution into the differential equation, we can derive constant of A 1 and A 2 . The result is:

(37b) A 1 = − K V 0 C m ω ( k s − m ω 2 ) ( k s − m ω 2 ) 2 + ( C m ω ) 2 ,

(37c) A 2 = K V 0 ( k s − m ω 2 ) ( k s − m ω 2 ) 2 + ( C m ω ) 2 .

Now consider the electrical peak input power to transmitter:

(37d) P ( t ) = − v ( t ) × K x ˙ ( t ) ,

(37e) x ˙ ( t ) = − A 1 ω sin ( ω t ) + A 2 ω cos ( ω t ) ,

(37f) v ( t ) = V 0 sin ( ω t ) .

Note that the minus sign in power equation is due to the reverse direction of current into transmitter. After substitution, we have

(37g) P ( t ) = K ω V 0 A 1 sin 2 ( ω t ) − K ω V 0 A 2 sin ( ω t ) cos ( ω t ) .

After simplification, we have

(37h) P ( t ) = K ω V 0 A 1 2 − 1 2 K ω V 0 ( A 1 cos ( 2 ω t ) + A 2 sin ( 2 ω t ) ) .

The RMS input value of the power is given as follows:

(37i) ( P RMS ) in = K ω V 0 3 A 1 2 8 + A 2 2 8 .

For deriving the output power of transmitter, it should be noted that the electrical input power to transmitter is converted to mechanical one. In other words, the electrical input power causes the transmitter piezoceramic to have displacement and velocity. Thus, we first should calculate the sum of potential and kinetic energy function (the total energy) with respect to time and take a derivative of it and at the end take the R M S of the output power. From Section 2.3, we can obtain the total mechanical energy of the transmitter.

(37j) E = U + T E ( t ) = U ¯ sin 2 ( ω t ) + m 2 ω 2 A 1 2 2 + A 2 2 2 − A 1 2 2 − A 2 2 2 cos ( 2 ω t ) − A 1 A 2 sin ( ω t ) .

After simplification and some algebraic manipulation:

(37k) E ( t ) = U ¯ 2 + m 2 ω 2 A 1 2 2 + A 2 2 2 − m 2 ω 2 A 1 2 2 − A 2 2 2 − U ¯ 2 cos ( 2 ω t ) − A 1 A 2 sin ( 2 ω t ) ,

Now we can take the derivative of equation (37k) to find the output power of the transmitter transducer.

(37l) P out ( t ) = d E ( t ) d t P out ( t ) = 2 ω A 1 A 2 cos ( 2 ω t ) + m ω 3 A 1 2 2 − A 2 2 2 − ω U ¯ sin ( 2 ω t ) .

By taking the RMS of equation (37l), we have:

(37m) ( P out ) RMS = Z 1 2 4 + Z 2 2 4 ,

where

(37n) Z 1 = 2 ω A 1 A 2 ,

(37o) Z 2 = m ω 3 A 1 2 2 − A 2 2 2 − ω U ¯ .

The efficiency is:

(37p) η = ( P in ) RMS ( P out ) RMS ,

(37q) η = K ω V 0 2 3 A 1 2 + A 2 2 Z 1 2 + Z 2 2 .

Note that according to the definition of efficiency for indirect piezoelectric effect we should reverse the the ratio of output mechanical power to the input electrical power for transmitter transducer.

5.2 Receiver

We define the efficiency for receiver transducer as the ratio of the output power in load resistor to the input power deliver by pressure imposed on transducer by ultrasonic waves. It should be noted that the input power to the receiver energy harvester is equal to the power consumed in the mechanical and electrical dampers (refer to similar article about efficiency from the first author (Dezhara 2023)). We have calculated the electrical damping coefficient for each load and also output power. Thus, we define the efficiency in this case as follows:

(38a) η = P R L ( C m + c e ) ∣ x ˙ ∣ 2 = ( P R L ) RMS 1 2 ( C m + c e ) ∣ x ˙ ∣ 2 ,

where P R L is the load resistor output power for each kind of load we considered in Section 4. Note that square of velocity in the denumerator is peak value and can be written as ω 2 x 0 2 , where x 0 is amplitude of displacement, the parameter of x 0 2 from denominator cross out with x 0 2 of numerator, and as a result, there is no need to calculate it or substitute it by transfer function derived in Section 4. For instance, for resistive load, the efficiency for receiver energy harvester is given as follows:

(38b) η = K 2 ω 2 x 0 2 C 0 2 ω 2 R + 1 R ( C m + c e ) ω 2 x 0 2 = K 2 C 0 2 ω 2 R + 1 R C m + K 2 R 1 R 2 + ω 2 C 0 2 ,

(38c) η = 1 C m K 2 C 0 2 ω 2 R + 1 R + 1 .

In this simple case (resistive load), the maximum efficiency for receiver energy harvester can be easily derived:

(38d) ∂ η ∂ R = 0 ,

(38e) ∂ η ∂ R = − C m K 2 C 0 2 ω 2 − 1 R 2 C m K 2 C 0 2 ω 2 R + 1 R + 1 2 = 0 → R = 1 ω C 0 .

We conclude that for resistive load, the maximum efficiency of receiver transducer occurs when the load resistance is equal to internal impedance (reactance) of piezoceramic transducer. Note that this resistance is not the optimum resistance for maximum power because generally for energy harvesters, maximum efficiency does not occurs at load that maximize power (Dezhara 2023). The maximum efficiency is obtained by substitution of (38e) into efficiency formula:

(38f) η max = 1 2 C m C 0 ω K 2 + 1 .

6 Design method

Here, we introduce an example to find excitation frequency at constant excitation voltage and thickness by designing maximum acoustic strength parameter to produce maximum pressure at receiver side. It should be noted that both of pressure and acoustic strength peak at same frequencies. The resonance frequency is defined as a frequency that the pressure has a maximum peak at receiver side. Note that the output power depends on area of the transducer, and the more the area, the more the power at constant pressure we have. The pressure varies with time through sinusoidal function; however, for receiver, the phase difference between pressure (excitation force) and load voltage (i.e., Kv which is piezoelectric force) is always π 2 (In other words, at maximum pressure, we have zero displacement, and at maximum displacement, we have zero pressure.).

6.1 Numerical example

Let us assume to know the mechanical damping coefficient, as well as the piezoelectric coupling factor between the mechanical and electrical side of receiver transducer and also mass of the transducer^[6]. Furthermore, assume other parameters for a commercial piezoceramic transducer and the acoustic environment as listed in Tables 1, 2, and 3.

Table 1

Material properties of PIC155 and geometric constants

Symbol	Parameter	Value	Unit
ρ	Density	7,800	kg m 3
ε 33 T ε 0	Relative permittivity	1,450	—
c 33 D	Elastic constant	11.1 × 1 0 10	N m 2
Coupling factor	k 33	0.69	—
Distance	L	5	cm
Square length	D	1.46	cm
Half of the thickness	h	2.1 2	mm
Peak excitation voltage	V 0	10	V
Coupling factor	K	2.16	N m

Table 2

Properties of acoustic environment (distilled water at 2 5 ∘ C )

Symbol	Parameter	Value	Unit (SI)
c	Sound velocity	1,498	m s
μ v	Bulk viscosity	2.47 × 1 0 ‒ 2	Pa s
μ	Shear viscosity	0.888 × 1 0 ‒ 3	Pa s
ρ 0	Density of fluid	997	kg m 3

Table 3

Mechanical parameters of transducers

Symbol	Parameter	Value	Unit (SI)
m	Mass (2.1 mm thickness)	3.49	g
k s	Mechanical stiffness (2.1 mm thickness)	259,893,847	N m
C m	Mechanical damping	0.31	N s m

Note that the value of K is calculated by equation (A14) that will be derived in the appendix. In the afore-mentioned equation, the parameters of open circuit voltage are obtained from the experiment and other parameters are known by calculations. The known input data are arranged in Tables 1 and 2. Note that the value of K should be calculated through open circuit voltage experiment (Figures 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).

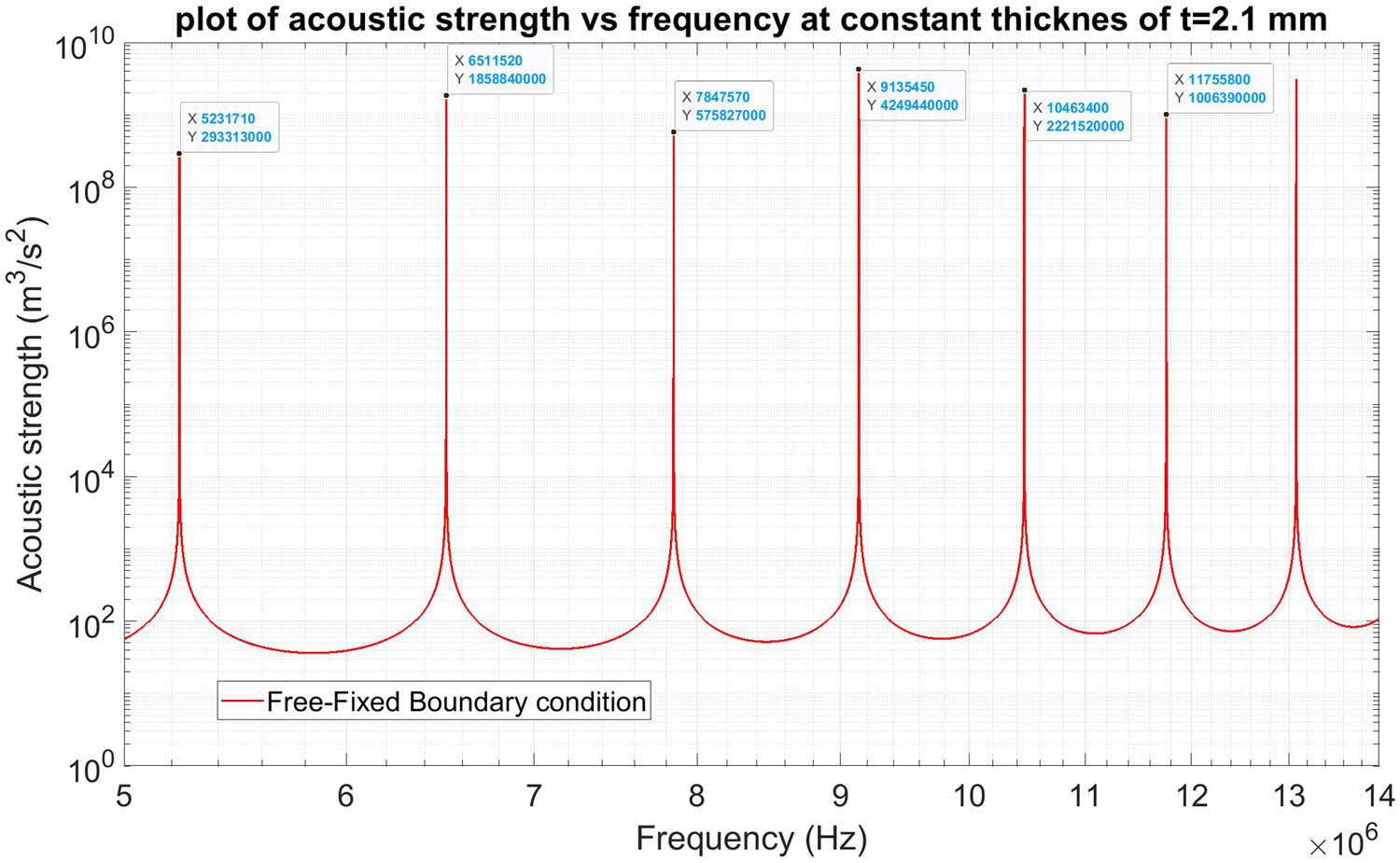
Figure 3

Plot of acoustic strength vs frequency.

$Figure 4 Plot of pressure vs frequency at constant distance between transducers, the resonance frequency is 9.13545 MHz, L = 5 cm L=5\hspace{0.33em}{\rm{cm}} .$

Figure 4

Plot of pressure vs frequency at constant distance between transducers, the resonance frequency is 9.13545 MHz, L = 5 cm .

Figure 5

Plot of output power vs resistive load for free-fixed boundary condition.

Figure 6

Plot of output power vs capacitive load for free-fixed boundary condition.

Figure 7

Plot of output power vs inductive load for free-fixed boundary condition.

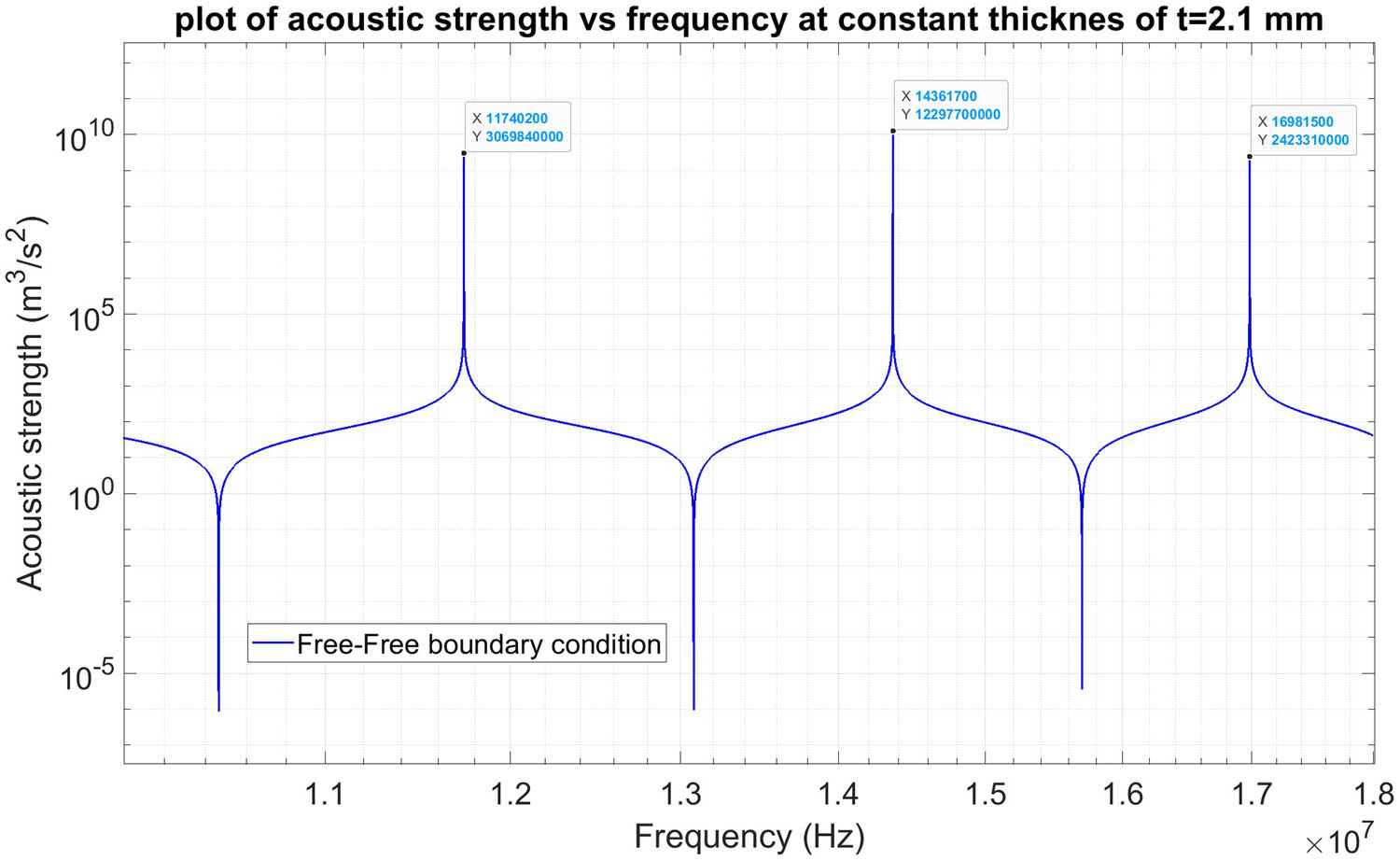
Figure 8

Plot of acoustic strength vs frequency.

Figure 9

Plot of pressure vs frequency at constant distance between transducers, the resonance frequency is 11.7402 MHz, L = 5 cm.

Figure 10

Plot of output power vs resistive load for free-free boundary condition.

Figure 11

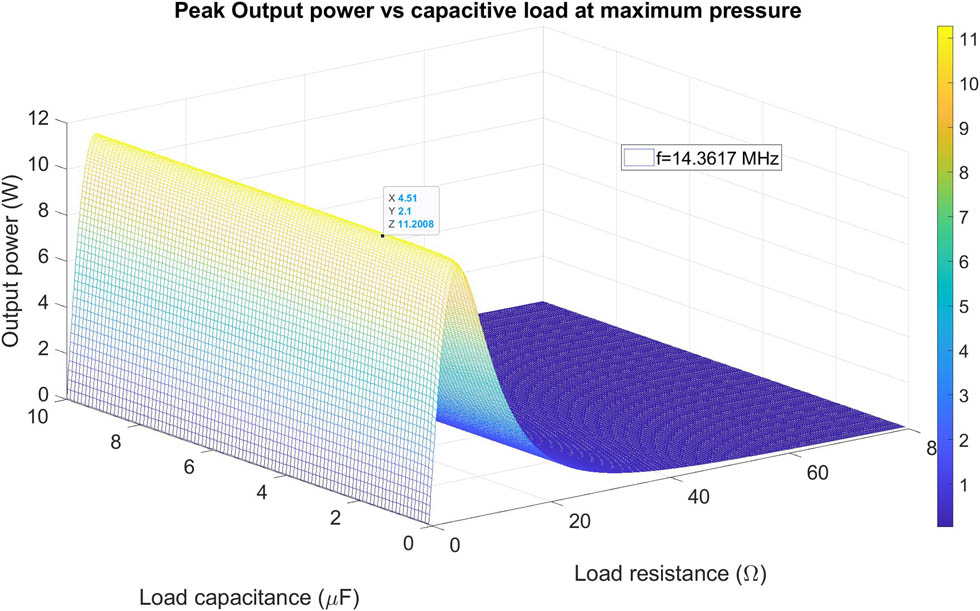
Plot of output power vs capacitive load for free-free boundary condition.

Figure 12

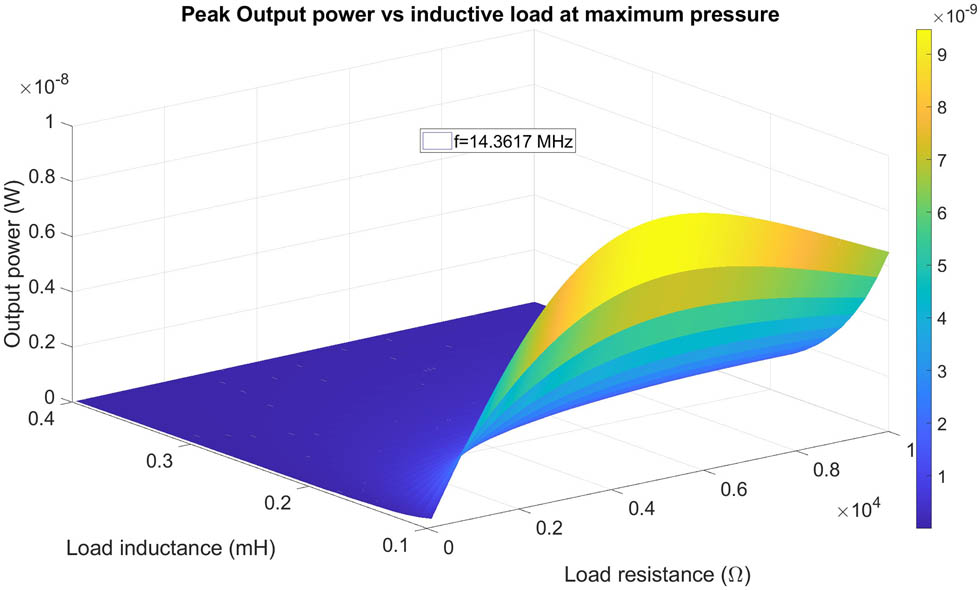
Plot of output power vs inductive load for free-free boundary condition.

We also include the mechanical parameters (Table 3) such as the stiffness of the transducers, which have importance in our calculations. It should be noted that the value of stiffness is calculated using a structural model in MATLAB.

According to Figure 13, we can calculate the stiffness (the ratio of force due to pressure over displacement), as 259 , 893 , 847 N m for the thickness of 2.1 mm. Note that based on our finite element simulation in MATLAB, the displacement of center of receiver transducer for the an arbitrary^[7] imposed pressure of 1.2 MPa is 1.5764 × 1 0 − 5 mm .

Figure 13

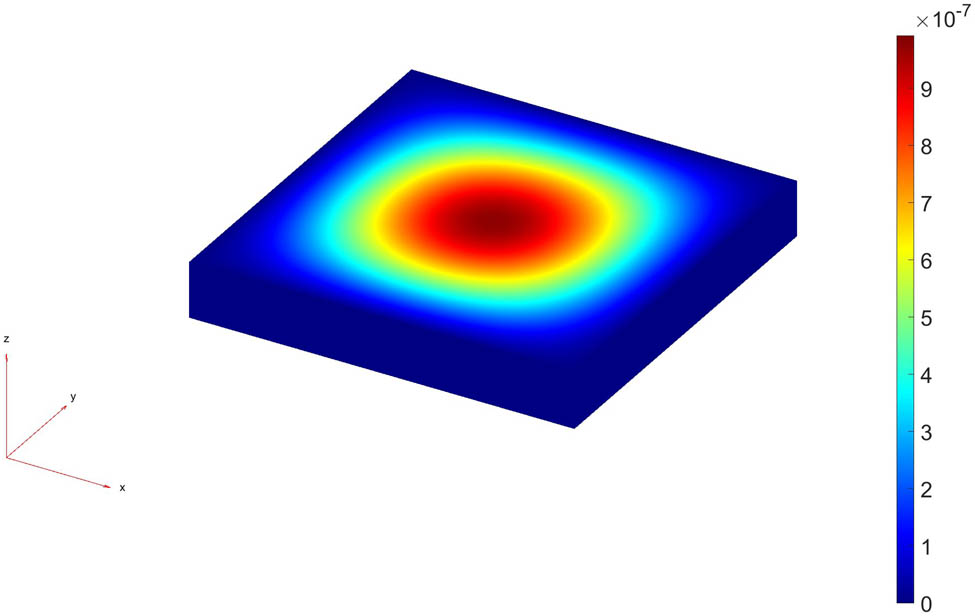
Deflection of receiver transducer (with 2.1 mm thickness) due to imposed pressure of 1.19448 MPa on it vs displacement (in meter) by finite element method in MATLAB.

6.1.1 Calculation of efficiency

Note that the maximum efficiency for resistive load based on equation (38f) and for free-fixed transmitter (Table 4) radiation ( t = 2.1 mm ) is η max = 99.3 % that occur at R = 18.93 Ω . It should be noted that for receiver, based on Tables 5 and 7, the free-fixed boundary conditions shows higher efficiency than free-free one. At the end, based on Tables 4 and 6 the efficiency of transmitter at free-free boundary condition is higher than free-fixed case.

Table 4

Transmitter efficiency (free-fixed boundary conditions)

Parameter	Value
( P in ) RMS	0.5748 mW
( P out ) RMS	4.014 × 1 0 8 W
η	1.432 × 1 0 ‒ 10 %

Table 5

Receiver efficiency (free-fixed boundary conditions)

Resistive load	Capacitive load	Inductive load
R = 15.2 Ω	R = 8.71 Ω	R = 4 × 1 0 3 Ω
—	C = 2.1 μ F	L = 0.1 mH
η = 99.29%	η = 59.38%	η = 2.26 × 1 0 ‒ 4 %

Table 6

Transmitter efficiency (free-free boundary conditions)

Parameter	Value
( P in ) RMS	0.8235 mW
( P out ) RMS	1.151 W
η	7.16 × 1 0 ‒ 2 %

Table 7

Receiver efficiency (free-free boundary conditions)

Resistive load	Capacitive load	Inductive load
R = 15.2 Ω	R = 8.71 Ω	R = 4 × 1 0 3 Ω
—	C = 2.1 μ F	L = 0.1 mH
η = 98.81%	η = 34.97%	η = 3.78 × 1 0 ‒ 5 %

6.1.2 Calculation of resonance frequency

Here, we plot the average Lagrangian for free-fixed boundary condition, and as seen from the plot, it has a minimum at frequency of 9.13545 MHz at constant thickness of 2.1 mm. The reveres is also true, i.e., it also has minimum at thickness of 2.1 mm and constant frequency of 9.13545 MHz (Figures 14 and 15).

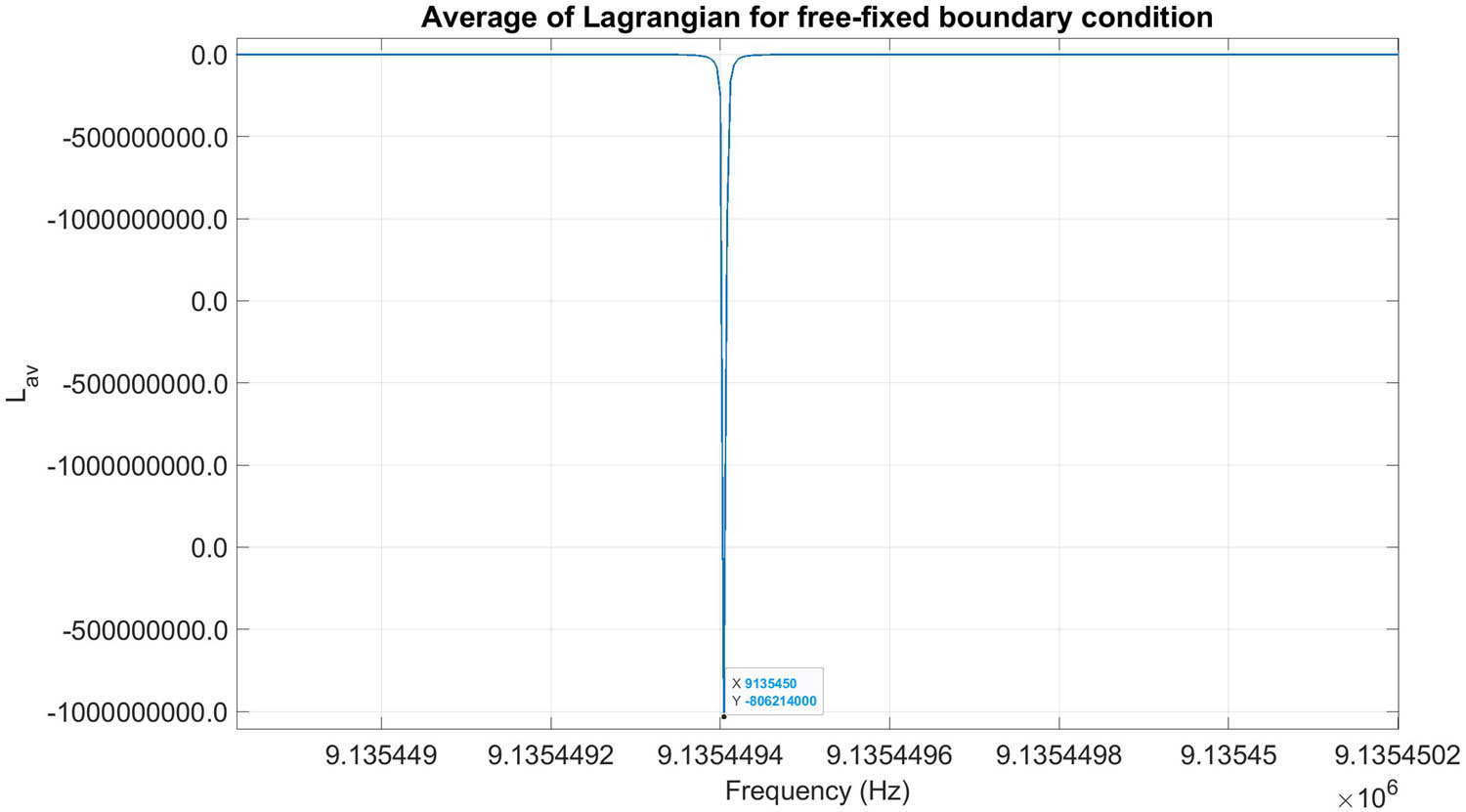
$Figure 14 Extremum (minimum) of the Lagrangian with respect to frequency at thickness of t = 2.1 mm t=2.1\hspace{0.33em}{\rm{mm}} .$

Figure 14

Extremum (minimum) of the Lagrangian with respect to frequency at thickness of t = 2.1 mm .

$Figure 15 Extremum (minimum) of the Lagrangian with respect to thickness at frequency of f = 9.13545 MHz f=9.13545\hspace{0.33em}{\rm{MHz}} .$

Figure 15

Extremum (minimum) of the Lagrangian with respect to thickness at frequency of f = 9.13545 MHz .

The Reynolds number for free-fixed boundary conditions is: Re = 997 × 149 8 2 ( 24.7 + 0.888 ) × 1 0 − 3 × 2 × π × 9 , 135 , 450 = 1523.25 . As a result, the Reynolds number is very large, and hence, the the viscous force is a bit fraction of inertia force and the steady terms in pressure are dominant. Thus, the pressure does not decay in the near field.

7 Discussion

From the plot of acoustic strength vs thickness (Figure 3), we see that the fixed-free boundary condition leads to multi-resonance at different acoustic strengths. On the other hand, the free-free boundary condition leads to resonance and antiresonance. Now a question may arises here is that where these two different behaviors come from?. The answer to this curiosity is that the behavior of transmitter under the free-free boundary condition is due to constructive and destructive interference. These interferences stems from forward and backward traveling wave from transmitter which causes constructive interference and resonance and destructive interference and antiresonance. However, the transmitter behavior under free-fixed boundary condition experience just radiation of forward traveling acoustic wave and its backward radiation suppressed by a layer with suitable thickness and that is why we do not see any antiresonance under this boundary condition. From mechanical design point of view, we should ask ourselves that does the pressure at resonance frequency cause mechanical failure in receiver transducer?. If you multiply the pressure by area of the receiver transducer, it leads to a large force in the order of several hundreds kilograms on small area of receiver especially for the case of free-free boundary conditions. Calculation of stress and strain due to this force is beyond the topic and scope of our article; however, we are free to choose a less excitation frequency and as a result less pressure peak for the safety reasons.

8 Conclusion

We conclude that by the resistive load, we can extract more power with even better efficiency with compared to capacitive and inductive loads. We also conclude that in the case of free-fixed boundary conditions in addition to graphical method, the resonance frequency can be calculated by energy methods, i.e., Lagrangian.

Funding information: None declared.
Author contributions: Conceptualization, Alfio Dario Grasso and Aboozar Dezhara; methodology, Aboozar Dezhara; data curation, Aboozar Dezhara and Andrea Ballo; writing – original draft preparation, Aboozar Dezhara; writing – review and editing, Aboozar Dezhara and Alfio Dario Grasso; visualization, Aboozar Dezhara; supervision, Alfio Dario Grasso and Andrea Ballo. All authors have accepted responsibility for the entire content of the manuscript and agreed to the published version.
Conflict of interest: The authors declare no conflicts of interest regarding this article.
Data availability statement: Reported data in this manuscript are available upon request to the corresponding author.

Appendixes

Here, we consider impedance matching for the receiver side and also deriving some parameters analytically.

A.1 Impedance matching (receiver side)

The mobility similarity, rather than the impedance similarity, of spring-mass system with electrical circuits as according to Dezhara (2022), Beeby et al. (2006), Ottman et al. (2002), Priya et al. (2017) is used in this article.

(A1) m → C , 1 C m → R , 1 k s → L ,

Figure A1 depicts the equivalent circuit of the PZT at the receiver side. The term p A is an ac current source. The Thévénin equivalent impedance can be calculated using short circuit current and open circuit voltage (Figures A2 and A3, respectively) (Kim et al. 2007, Liang and Liao 2012, Chen et al. 2018, Wang et al. 2011, Wang et al. 2022).

Figure A1

Receiver side transducer circuit.

Figure A2

Open circuit voltage.

Figure A3

Short circuit current.

(A2a) V o.c = 1 C 0 ∫ i 2 d t = K C 0 ∫ V 1 d t ,

(A2b) V o.c = K V 1 j C 0 ω ,

(A2c) i 1 = K V 2 = K V o.c = K 2 V 1 j C 0 ω ,

(A2d) p A = V 1 1 C m + V 1 j ω k s + V 1 1 j ω m + i 1 ,

(A2e) V 1 = p A C m + X 1 − K 2 C 0 ω j ,

(A2f) V o.c = K p A C 0 ω j C m − X 1 − K 2 C 0 ω .

In regarding to Figure A3, we have:

(A3a) I s.c + 0 = i 2 = K V 1 ,

(A3b) V 1 = p A C m + ( m ω − k s ω ) j ,

(A3c) I s.c = p K A C m + X 1 j ,

(A4a) Z th = V o.c I s.c = C m + j X 1 j C 0 ω C m − C 0 ω X 1 − K 2 C 0 ω ,

(A4b) Z th = R th + j X th ,

(A4c) R th = K 2 C m C 0 2 ω 2 X 1 − K 2 C 0 ω 2 + ( C 0 ω C m ) 2 ,

(A4d) X th = − X 1 C 0 ω X 1 − K 2 C 0 ω + C m 2 C 0 ω C 0 2 ω 2 X 1 − K 2 C 0 ω 2 + ( C 0 ω C m ) 2 ,

where X 1 = m ω − k s ω . For maximum power transfer:

(A5a) R = R th ,

(A5b) X = − X th .

Note that the optimum resistance and reactance does not depend on the pressure imposed on receiver transducer.

A.2 Mechanical damping coefficient and short circuit piezoelectric element

The mechanical damping coefficient can be calculated from logarithmic reduction law by measuring the consecutive peaks of transient response of piezoelectric shorted circuit in a oscilloscope.

(A6a) exp ( α t 1 ) = I 1 ,

(A6b) exp ( α t 2 ) = I 2 ,

(A6c) ( I 2 − I 1 ) = exp ( α t 2 ) − exp ( α t 1 ) ,

(A6d) Ln I 2 I 1 = α ( t 2 − t 1 ) = α T ,

(A6e) α = 1 T Ln I 2 I 1 .

To calculate the value of α , we proceed as follows:

(A7) m x ¨ + C m x ˙ + k s x = 0 x ( 0 ) = x 0 x ˙ ( 0 ) = 0 .

If you solve the differential equation (A7), we have:

(A8) x ( t ) = x 0 e − C m 2 m t cos 4 k s m − C m m 2 t ,

we assumed that we have under damped oscillation, i.e., C m 2 k s m < 1 . So the value of α , which is the attenuation constant is expressed as follows:

(A9) α = − C m 2 m .

If you equate the relations of (A6e) and (A9), we can calculate the values of C m as follows:

(A10) − C m 2 m = 1 T Ln I 2 I 1 .

Thus, we obtain:

(A11) C m = 2 m T Ln I 1 I 2

Note that the velocity is also decayed as e − C m 2 m t , and consequently, the current decaying factor is the same as the displacement decaying factor.

A.3 Piezoelectric Coupling Factor

Here, we propose two methods for deriving a formula for calculating the value of the coupling factor between the mechanical and electrical sides of piezoceramic transducers.

A.3.1 Method 1 (analytical method)

The value of K can be found by the open circuit transient response of the piezoelectric transducer. In other words, we just give the transducer a initial conditions and solve the transient equation of motion.

(A12a) m x ¨ + C m x ˙ + k s x + K v = 0 ,

(A12b) x ( 0 ) = x 0 v ( 0 ) = v 0 x ˙ ( 0 ) = 0 ,

(A12c) K x ˙ − C 0 v ˙ = 0 → K x − C 0 v = K x 0 − C 0 v 0 ,

(A12d) v = K C 0 Δ x + v 0 .

By substituting (A12d) into (A12a), we have:

(A12e) m x ¨ + C m x ˙ + k s + K 2 C 0 x = K 2 C 0 x 0 − K v 0 .

By solving the aforementioned differential equation and obtaining the nonhomogeneous and homogeneous solution, we have:

(A12f) x ( t ) = K 2 C 0 x 0 − K v 0 k s + K 2 C 0 1 − e − C m 2 m t cos ( ω d t ) + x 0 e − C m 2 m t cos ( ω d t ) ,

where ω d = 4 k s + K 2 C 0 m − C m m 2 is called natural damped frequency of receiver piezoceramic. Note that with regard to large value of k s with compared to C m , we have under-damped solution and the overdamped solution is not our target. We seek the finial value of load voltage, which is its DC value as times goes to infinity. We name the final value of load voltage as v ∞ . By solving equation (A12c) or by using equation equation (A12d), we can find v ∞ :

(A12g) v ∞ = K C 0 ( x ∞ − x 0 ) + v 0 ,

where x ∞ = K 2 C 0 x 0 − K v 0 k s + K 2 C 0 . Now we resort to piezoelectric constitutive laws of equation (1h) at the time of infinity:

(A12h) T 3 = c 33 E S 3 − e 33 E 3 = c 33 E S 3 − e 33 − v ∞ t ,

(A12i) D 3 = e 33 S 3 + ε 33 S E 3 = e 33 S 3 + ε 33 S − v ∞ t .

From equation (A12i), we can write guess law as follows:

(A12j) − ∫ D 3 d A = q → D 3 = − C 0 v ∞ A ,

(A12k) e 33 S 3 + ε 33 S − v ∞ t = − C 0 v ∞ A ,

(A12l) C 0 = ε 33 S A t ,

After substituting relation of (A12k) into (26), we can find strain along the (33) direction.

(A12m) e 33 S 3 + ε 33 S − v ∞ t = − ε 33 S v ∞ t → S 3 = 0 .

By knowing the the value of strain, we can find stress in (33) direction from equation (A12h).

(A12n) T 3 = − e 33 E 3 = e 33 v ∞ t ,

Now we should relate the stress force to piezoelectric force ( K v ∞ ).

(A12o) T 3 = K v ∞ A = e 33 v ∞ t ,

From equation (A12o), we can find a formula for K .

(A12p) K = e 33 ε 33 S C 0 = c 33 E d 33 ε 33 S C 0 .

If we calculate the value of K based on the numerical example parameters, we have:

(A12q) c 33 E = 11.1 × 1 0 10 ,

(A12r) d 33 = 360 × 1 0 − 12 for PIC 155 ,

(A12s) ε 33 S = 1,450 ε 0 = 1,450 × 8.855 × 1 0 − 12 ,

(A12t) C 0 = 1,450 × 8.855 × 1 0 − 12 × ( 1.46 × 1 0 − 2 ) 2 3.9519 × 1 0 − 3 ,

(A12u) K = 2.16 A.s m .

A.3.2 Method 2 (experimental method)

In the second method, we use equation (A2f). Note that everything is known except the parameter K . The magnitude is expressed as follows:

(A13) V o.c 2 = K 2 A 2 p 2 ( C m C 0 ω ) 2 + C 0 2 ω 2 X 1 − K 2 C 0 ω 2 .

We can put the aforementioned equation in the following form:

(A14) K 4 − p 2 A 2 V o.c 2 + 2 C 0 ω X 1 K 2 + C 0 2 ω 2 ( X 1 2 + C m 2 ) = 0 .

By solving the aforementioned equation symbolically in MATLAB, we can find the acceptable values of K .

References

Beeby S. P., Tudor M. J., and White N. M. (2006). “Energy harvesting vibration sources for microsystems applications,” Measurement Science and Technology, vol. 17, no. 12, R175. 10.1088/0957-0233/17/12/R01Search in Google Scholar

Chen N., Wei T., Ha D. S., Jung H. J., and Lee S. (2018). “Alternating resistive impedance matching for an impact-type microwind piezoelectric energy harvester,” IEEE Transactions on Industrial Electronics, vol. 65, no. 9, pp. 7374–7382. 10.1109/TIE.2018.2793269Search in Google Scholar

Dezhara A. (2022). “Frequency response locking of electromagnetic vibration-based energy harvesters using a switch with tuned duty cycle,” Energy Harvesting and Systems, vol. 9, no. 1, pp. 83–96. 10.1515/ehs-2021-0057Search in Google Scholar

Dezhara A. (2023). “The efficiency of linear electromagnetic vibration-based energy harvester at resistive, capacitive and inductive loads,” Energy Harvesting and Systems, vol. 10, no. 1, pp. 93–104. 10.1515/ehs-2022-0028Search in Google Scholar

Dezhara A. (2024). “Non-transient optimum design of nonlinear electromagnetic vibration-based energy harvester using homotopy perturbation method,” Energy Harvesting and Systems, vol. 11, no. 1, p. 20220101. 10.1515/ehs-2022-0101Search in Google Scholar

Erturk A. and Inman D. J. (2008). “Issues in mathematical modeling of piezoelectric energy harvesters,” Smart Materials and Structures, vol. 17, no. 6, pp. 065016. 10.1088/0964-1726/17/6/065016Search in Google Scholar

Humphrey V. F. (2007). “Ultrasound and matter-physical interactions,” Progress in Biophysics and Molecular Biology, vol. 93, no. 1, pp. 195–211. Effects of ultrasound and infrasound relevant to human health. 10.1016/j.pbiomolbio.2006.07.024Search in Google Scholar PubMed

Jiang L., Yang Y., Chen Y., and Zhou Q. (2020). “Ultrasound-induced wireless energy harvesting: From materials strategies to functional applications,” Nano Energy, vol. 77, p. 105131. 10.1016/j.nanoen.2020.105131Search in Google Scholar PubMed PubMed Central

Kim H., Priya S., Stephanou H., and Uchino K. (2007). “Consideration of impedance matching techniques for efficient piezoelectric energy harvesting,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 54, no. 9, pp. 1851–1859. 10.1109/TUFFC.2007.469Search in Google Scholar PubMed

Kino G. S. (January 1, 1987). Acoustic waves: Devices, imaging, and analog signal processing, Prentice Hall. Search in Google Scholar

Liang J. and Liao W.-H. (2012). “Impedance modeling and analysis for piezoelectric energy harvesting systems,” IEEE/ASME Transactions on Mechatronics, vol. 17, no. 6, pp. 1145–1157. 10.1109/TMECH.2011.2160275Search in Google Scholar

Lin J. (2006). “A new ieee standard for safety levels with respect to human exposure to radio-frequency radiation,” IEEE Antennas and Propagation Magazine, vol. 48, no. 1, pp. 157–159. 10.1109/MAP.2006.1645601Search in Google Scholar

Ottman G., Hofmann H., Bhatt A., and Lesieutre G. (2002). “Adaptive piezoelectric energy harvesting circuit for wireless remote power supply,” IEEE Transactions on Power Electronics, vol. 17, no. 5, pp. 669–676. 10.1109/TPEL.2002.802194Search in Google Scholar

Ozeri S. and Shmilovitz D. (2010). “Ultrasonic transcutaneous energy transfer for powering implanted devices,” Ultrasonics, vol. 50, no. 6, pp. 556–566. Search in Google Scholar

Ozeri S. and Shmilovitz D. (2010 May). “Ultrasonic transcutaneous energy transfer for powering implanted devices,” Ultrasonics, vol. 50, no. 6, pp. 556–66. 10.1016/j.ultras.2009.11.004Search in Google Scholar PubMed

Piech D. K., Johnson B. C., Shen K., Ghanbari M. M., Li K. Y., Neely R. M., et al. (2020). “A wireless millimetre-scale implantable neural stimulator with ultrasonically powered bidirectional communication,” Nature Biomedical Engineering, vol. 4, pp. 207–222. 10.1038/s41551-020-0518-9Search in Google Scholar PubMed

Pritchard W. F., and Carey R. F. (1997). “Food and drug administration and regulation of medical devices in radiology,” Radiology, vol. 205, no. 1, pp. 27–36. 10.1148/radiology.205.1.9314955Search in Google Scholar PubMed

Priya S., Song H.-C., Zhou Y., Varghese R., Chopra A., Kim S.-G., et al. (2017). “A review on piezoelectric energy harvesting: Materials, methods, and circuits,” Energy Harvesting and Systems, vol. 4, no. 1, pp. 3–39. 10.1515/ehs-2016-0028Search in Google Scholar

Roes M. G. L., Duarte J. L., Hendrix M. A. M., and Lomonova E. A. (2013). “Acoustic energy transfer: A review,” IEEE Transactions on Industrial Electronics, vol. 60, no. 1, pp. 242–248. 10.1109/TIE.2012.2202362Search in Google Scholar

Safaei M., Sodano H. A., and Anton S. R. (2019). “A review of energy harvesting using piezoelectric materials: state-of-the-art a decade later (2008-2018),” Smart Materials and Structures, vol. 28, no. 11, pp. 113001. 10.1088/1361-665X/ab36e4Search in Google Scholar

Shahab S. (2014). “Contactless ultrasonic energy transfer: Acoustic-piezoelectric structure interaction modeling and performance enhancement,” Smart Materials and Structures, vol. 23, pp. 125032. 10.1088/0964-1726/23/12/125032Search in Google Scholar

Sherrit S. (2008). “The physical acoustics of energy harvesting,” Proceedings - IEEE Ultrasonics Symposium. 10.1109/ULTSYM.2008.0253Search in Google Scholar

Taalla R. V., Arefin M. S., Kaynak A., and Kouzani A. Z. (2019). “A review on miniaturized ultrasonic wireless power transfer to implantable medical devices,” IEEE Access, vol. 7, pp. 2092–2106. 10.1109/ACCESS.2018.2886780Search in Google Scholar

Tseng V. F.-G., Bedair S. S., Radice J. J., Drummond T. E., and Lazarus N. (2020). “Ultrasonic lamb waves for wireless power transfer,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 67, no. 3, pp. 664–670. 10.1109/TUFFC.2019.2949467Search in Google Scholar PubMed

Wang H., Shan X., Xie T., and Fang M. (2011). “Analyses of impedance matching for piezoelectric energy harvester with a resistive circuit,” In: Proceedings of 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, vol. 4, pp. 1679–1683. 10.1109/EMEIT.2011.6023423Search in Google Scholar

Wang J., Chen Z., Li Z., Jiang J., Liang J., and Zeng X. (2022). “Piezoelectric energy harvesters: An overview on design strategies and topologies,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 7, pp. 3057–3063. 10.1109/TCSII.2022.3173966Search in Google Scholar

Wang X., Song J., Liu J., Wang Z. L. (2007 Apr 6). “Direct-current nanogenerator driven by ultrasonic waves,” Science, vol. 316, no. 5821, pp. 102–5. 10.1126/science.1139366Search in Google Scholar PubMed

Wu M., Chen X., Qi C., and Mu X. (2020). “Considering losses to enhance circuit model accuracy of ultrasonic wireless power transfer system,” IEEE Transactions on Industrial Electronics, vol. 67, no. 10, pp. 8788–8798. 10.1109/TIE.2019.2947802Search in Google Scholar

Yang Z., Zeng D., Wang H., Zhao C., and Tan J. (2015). “Harvesting ultrasonic energy using 1-3 piezoelectric composites,” Smart Materials and Structures, vol. 24, no. 7, pp. 075029. 10.1088/0964-1726/24/7/075029Search in Google Scholar

Yang Z., Zeng D., Zhao C., Li F., and Wang H. (2013). “Wireless energy transmission using ultrasound for implantable devices,” In 2013 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (pp. 1–4). IEEE. 10.1109/SPAWDA.2013.6841073Search in Google Scholar

Received: 2023-07-11

Revised: 2024-07-05

Accepted: 2024-09-21

Published Online: 2024-12-18

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/ehs-2023-0085

Keywords for this article

ultrasonic waves; piezoceramic square element transmitter and receiver; energy harvesting; biomedical implanted devices

Creative Commons

BY 4.0