Home Influence of coupling effects on analytical solutions of functionally graded (FG) spherical shells of revolution
Article Open Access

Influence of coupling effects on analytical solutions of functionally graded (FG) spherical shells of revolution

  • Justyna Flis and Aleksander Muc EMAIL logo
Published/Copyright: October 19, 2021
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 60 Issue 1

Abstract

Due to the lack of commercially available finite elements packages allowing us to analyse the behaviour of porous functionally graded (FG) structures in this paper, axisymmetric deformations of coupled FG spherical shells are studied. The analytical solution is presented by using complex hypergeometric polynomial series. The results presented agree closely with the reference results for isotropic spherical shells of revolution. The influence of the effects of material properties is characterized by a multiplier characterizing an unsymmetric shell wall construction (stiffness coupling). The results can be easily adopted in design procedures. The present results can be treated as the benchmark for finite element investigations.

Keywords: spherical shells; analytical solutions; porous functionally graded materials; construction of material properties

1 Introduction

The analytical description of axisymmetric isotropic shells of revolution is demonstrated in monographs [1,2,3]. Galletly and Muc [4,5] and Muc [6] studied buckling and deformations of laminated shells of revolution considering only laminated unidirectional symmetric configurations. Due to coupling effects between the membrane and bending stress resultants, the analysis of arbitrarily laminated shells was usually carried out using numerical methods, e.g. Czebyshev expansions [7].

Considering the structural deformations in only the elastic range, the analysis of composite constructions can be divided into three categories:

  1. Unidirectional laminates – the potential abrupt variation of mechanical properties between laminae.

  2. Porous functionally graded materials (FGM) – a smooth variation of the properties from the bottom to the top surface.

  3. Nanostructures reinforcing isotropic matrix – they are made of a polymer matrix reinforced with nanoplatelets or carbon nanotubes; the material properties are derived with the use of homogenization theories, e.g. the Mori–Tanaka method.

Due to the possible variations of material characteristics along the spatial coordinates (x, y, z – the thickness direction), it is rather difficult or impossible to find analytical solutions characterizing structural deformations even for the simplest shells as, e.g. cylindrical, conical, spherical, etc. The variations along the thickness direction z can be eliminated by the 2D approximations (power series, Legendre, Czebyshev polynomials – Muc [8], Fantuzzi et al. [9]). Considering two geometrical variables (x = Rφ, y = Rθ, where R is the radius of the sphere, φ the meridional coordinate, and θ the circumferential coordinate) defining the variations along the shell reference midsurface for axisymmetric shell constructions, it is possible to formulate and solve three independent problems: (1) shells closed at the vertex, (2) shells opened at the vertex and (3) shell panels (Figure 1).

Figure 1 Geometry of the spherical shells: (a) hemispherical shells 0 ≤ φ ≤ π/2, 0 ≤ θ ≤ 2π, (b) shells opened at the vertex 0 < φ 1 ≤ φ ≤ φ 2 < π/2, 0 ≤ θ ≤ 2π, and (c) shell panels 0 < φ 1 ≤ φ ≤ φ 2 < π/2, 0 < θ 1 ≤ θ ≤ θ 2 < 2π.
Figure 1

Geometry of the spherical shells: (a) hemispherical shells 0 ≤ φ ≤ π/2, 0 ≤ θ ≤ 2π, (b) shells opened at the vertex 0 < φ 1 ≤ φ ≤ φ 2 < π/2, 0 ≤ θ ≤ 2π, and (c) shell panels 0 < φ 1 ≤ φ ≤ φ 2 < π/2, 0 < θ 1 ≤ θ ≤ θ 2 < 2π.

For the 2D Love–Kirchhoff kinematical hypothesis, the stress–strain relations can be expressed in the following way: N i = A ij ε j + B ij κ j , M i = B ij ε j + D ij κ j , where N denotes the membrane forces, M the bending moments, ε the membrane strains and κ the changes in curvatures. Each of the above values has three components. A, B and D denotes the matrices [3 × 3], and their explicit form will be presented in the next section.

For anisotropic shell structures (unidirectional laminates, nanoplates and nanotubes embedded in a matrix), the terms of the stiffness matrices A, B and D are functions of two global coordinates x and y and define the structural configuration along the thickness coordinate z. Considering porous FGM, the variability of the terms of the matrices A, B and D depends on the definition of the thickness distributions t(x, y, z) (assuming that the Young modulus E is a function of the z coordinate). If the shell thickness t is the function of the z coordinate only, the B terms are not equal to zero for unsymmetric configurations of pores (Figure 2).

Figure 2 Shell wall construction for the uniform thickness t(x, y, z) = t: (a) uniform distribution of pores, (b) symmetric distribution, and (c) unsymmetric distribution.
Figure 2

Shell wall construction for the uniform thickness t(x, y, z) = t: (a) uniform distribution of pores, (b) symmetric distribution, and (c) unsymmetric distribution.

Note that in the literature a variety of papers exists solving different problems for 2D axisymmetric shell constructions (anisotropic or porous FGM); see Table 1. In general, these problems can be divided into two classes:

  1. Solutions are functions of two geometrical variables x and y for shells with unsymmetric loading and boundary conditions and shell panels (Figure 1) and shells having unsymmetric wall configurations; see Muc and Muc-Wierzgoń [10]. This class deals also with buckling and free vibrations problems where the expansion along the circumferential direction is required.

  2. Solutions are functions of one meridional variable only for symmetric shell wall configurations, axisymmetric boundary and loading conditions for constructions plotted in Figures 1a and b; the above condition is also satisfied for unsymmetric shell wall constructions made of FG materials (Figure 1c).

Table 1

Classification of approaches used in the analysis of spherical shells

Material characteristics of the shell wall Forms of a shell geometry
Closed shell at the vertex (two regular singular points: φ = 0, φ = π/2) Open shell at the vertex (without singular points) Shell panel (without singular points)
Unidirectional laminates [13,14,15,20,28,29,33,39,46,47,48,49,54,70] [7,24,30,51] [26,31,32,38,52]
Nanostructures [50,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69] [53,74,75,76,77]
Porous functionally graded materials (FGM) [12,23,35,37,40,45] [25,27,41,42,43,44] [34,36,71,72,73]

Although a great number of studies have been done for static, buckling and free vibration analysis of axisymmetric shells using isotropic and laminated materials, as pointed out in Table 1, a general lack of information for axisymmetric structures made of FGM is observed since the problems were solved with the use of numerical methods only (finite element [11,12] or finite difference methods [13,14,15] including also the generalized differential quadrature method GDQ [16,17,18,19]). Note that the applied method of solutions is directly connected with the used numerical method – for instance, the problems with singular points are solved with the use of finite difference methods [13,14,15], whereas the GDQ method was adopted to the discussion of problems without singular points only (see e.g. Sayyad and Ghugal [20]).

The aim of the present article is to extend the analytical solutions for axisymmetric spherical shells made of FGM and subject to the normal uniform pressure. The solutions are obtained with the use of hypergeometric functions and compared with the available published results for isotropic shells. Since such a class of problems has not been considered and discussed in the literature, to the best of our knowledge, the demonstrated herein solutions are the novelty in the existing literature and in addition they can constitute and can be easily adopted to the design codes of composite spherical shells. It has been proved analytically that for FGM shells the influence of the unsymmetric shell wall construction (the non-zero terms of the stiffness matrix B, Figure 1c) can be described by only one parameter (function – multiplier) and is independent of the form of boundary value problems.

2 Formulation of the problem

The shells of revolution can be defined in the curvilinear orthogonal coordinates φ and θ of a point on the shell midsurface. It is convenient to take the spherical coordinates, where the angle φ defines the location of a point along the meridian, and θ describes the location of a point along the parallel circle – the circumferential coordinate (see Figure 3). R 1 = R 1(φ) is the principal radius of the meridian and R 2 = R 2(φ)is the principal radius of the parallel circle. Note that r = R 2 sin(φ) and the Lame parameters are defined as follows: A = R 1, B = r.

Figure 3 Cross-section of an axisymmetric shell of revolution.
Figure 3

Cross-section of an axisymmetric shell of revolution.

When an arbitrary shell of revolution is subjected to rotationally symmetrical loads, its deformations and stress resultants and couples do not depend upon the circumferential variable θ. The axisymmetric deformations of shells of revolution are described by two displacement components of the shell midsurface u and w in the meridional and normal directions to the shell cross-section, respectively (Figure 3).

For shells of revolution under axisymmetrical loads, the strain displacement relations take the following form:

(1) ε 1 = 1 R 1 d u d φ + w , ε 2 = 1 R 2 ( u cot φ + w ) ,

(2) κ 1 = 1 R 1 d β d φ , κ 2 = 1 R 2 β cot φ , β = 1 R 1 u − d w d φ ,

where ε denotes the membrane strain, κ the change in curvature, and 1, 2 correspond to the meridional φ and circumferential directions θ, respectively. The constitutive equations are written in the following way:

(3) N r = A r s ε s + B r s κ s , M r = B r s ε s + D r s κ s , r , s = 1 , 2 ,

where

(4) A r s = ∫ − t / 2 t / 2 Q r s d z , B r s = ∫ − t / 2 t / 2 Q r s z d z , D r s = ∫ − t / 2 t / 2 Q r s z 2 d z , r , s = 1 , 2 ,

Q 11 = Q 22 = E ( z ) 1 − ν 2 , Q 12 = Q 21 = ν Q 11 ,

where N r are the stress resultants and M r the moment resultants. The elastic modulus E variation characterizes the distribution of porosity along the thickness direction z and is defined as

(5) E ( z ) / E b = [ ( E t / E b − 1 ) f ( z ) + 1 ] , f ( z ) = z t + 1 2 n ,

where t and b refer to the material properties on top and bottom surfaces, n is the power index and ν is Poisson’s ratio.

To complete the set of fundamental relations, we add the equilibrium equations derived using the principle of virtual work [1,2,3]:

(6) d d φ ( r N 1 ) − N 2 R 1 cos φ + r T = 0 , d d φ ( r T ) − N 1 R 1 + N 2 R 2 r R 1 − r R 1 q = 0 , d d φ ( r M 1 ) − M 2 R 1 cos φ − r R 1 T = 0 .

where T denotes the transverse shear force and q is the normal pressure to the shell midsurface.

Note that the present formulation (the Love–Kirchhoff hypothesis) is valid for thin FG plates or shells, i.e. for t/R < 0.05. For thicker structures, it is necessary to adopt more complicated forms of kinematical approximations taking into account possible deformations of the normal to a shell/plate midsurface, e.g. in the form proposed by Vlasov [21]. A broader discussion of these problems is presented by Muc and Flis [22]. In the buckling, free vibration analysis the use of geometrically nonlinear relations is required, e.g. in the form proposed by Muc [8,15].

Both for complex kinematical hypotheses and nonlinear relations, the stress–strain relations (3) become more complex as defined in refs [8,9,15].

3 Solution of governing relation for axisymmetric spherical shells

Let us examine deformations of spherical shells (R 1 = R 2 = R) having constant thickness, i.e. t(φ) = const. Using the classical approach [1,2,3] for isotropic shells, the system of equations is reduced to the following form:

(7) L ( T ) + ν T = ( B + R A ) β / R + Φ ( φ ) / R ,

(8) L ( β ) − ν β = R ( B + R A ) B 2 − A D T ,

(9) L = d 2 d φ 2 + cot φ d d φ − cot 2 φ , A = A 11 , B = B 11 , D = D 11 ,

(10) Φ ( φ ) = ( 1 + ν ) cot φ F ( φ ) sin 2 φ − q ( 1 + ν ) R 2 cot φ − d d φ ( 1 + ν ) F ( φ ) sin 2 φ − q R 2 F ( φ ) = R 2 ∫ φ e φ q sin φ ¯ cos φ ¯ d φ ¯ + C ,

φ e is a coordinate of the shell edge and the constant C characterizes an axial coordinate of the external load applied at the top edge.

By inserting B = 0, relations (7) and (8) are reduced to the classical Meissner equations for isotropic shells. Elimination of each variable (T or β) in equations (7) and (8) leads to fourth-order differential equations, i.e.

(11) L L ( β ) − ν 2 β − ( B + R A ) 2 B 2 − A D β − ( B + R A ) B 2 − A D Φ ( φ ) = 0 ,

(12) L L ( T ) − ν 2 T − ( B + R A ) 2 B 2 − A D T + 1 R [ ν Φ ( φ ) ] − L [ Φ ( φ ) ] = 0 .

Each of equations (11) and (12) can be solved for one of the dependent variables. The solutions can be represented as

(13) β = β c + β p , T = T c + T p ,

where superscripts c and p denote the complementary (Φ = 0) and particular (Φ ≠ 0) solutions, respectively. The complementary solutions satisfy the relation

(14) [ L ( β c ) + i μ 2 β c ] [ L ( β c ) − i μ 2 β c ] = 0 , μ 2 = ( B + R A ) 2 A D − B 2 − ν 2 .

Each of the equations has complex solutions (AD > B 2). The hypergeometric equation (14) has three regular singular points: 0 (φ = 0), 1 (φ = π/2) and ∞. Usually, for spherical shells, the analytical solutions of complementary equations are formulated for two regions corresponding to singularity. Using the Mathematica package, the solutions of the fourth-order differential equations for complementary variables can be derived analytically with the aid of one command DSolve ; see the general formulation presented by Polyanin and Zaitsev [78]. The general solution is represented by the complex hypergeometric functions and have the following form:

(15a) T c ( or β c ) = C 1 Z 1 + C 2 Z 2 + C 3 Z 3 + C 4 Z 4 ,

the regular singular point at φ = 0

(15b) Z 1 = F 1 2 [ 0.25 ( 3 − α 1 ) , 0.25 ( 3 + α 1 ) , 0.5 , cos 2 φ ] sin φ , Z 2 = F 1 2 [ 0.25 ( 3 − α 2 ) , 0.25 ( 3 + α 2 ) , 0.5 , cos 2 φ ] sin φ , Z 3 = F 1 2 [ 0.25 ( 5 − α 1 ) , 0.25 ( 5 + α 1 ) , 1.5 , cos φ ] sin φ cos φ , Z 4 = F 1 2 [ 0.25 ( 5 − α 2 ) , 0.25 ( 5 + α 2 ) , 1.5 , cos φ ] sin φ cos φ ,

the regular singular point at φ = π/2

(15c) Z 1 = F 1 2 [ 0.25 ( 3 − α 1 ) , 0.25 ( 3 + α 1 ) , 2 , cos 2 φ ] sin φ , Z 2 = F 1 2 [ 0.25 ( 3 − α 2 ) , 0.25 ( 3 + α 2 ) , 2 , cos 2 φ ] sin φ , Z 3 = F 1 2 [ 0.5 + 0.25 ( 5 − α 1 ) , 0.5 + 0.25 ( 5 + α 1 ) , 2 , cos 2 φ ] sin φ cos φ , Z 4 = F 1 2 [ 0.5 + 0.25 ( 5 − α 2 ) , 0.5 + 0.25 ( 5 + α 2 ) , 2 , cos 2 φ ] sin φ cos φ , α 1 = 5 − 4 μ 2 − 1 , α 2 = 5 + 4 μ 2 − 1 ,

where C 1…C 4 are the complex constants of integration. Since Re(Z 1) = Re(Z 2), Im(Z 1) = −Im(Z 2), Re(Z 3) = Re(Z 4), and Im(Z 3) = −Im(Z 4), the solutions of equation (15a) can be represented as real variables with real constants of integration C ˜ 1 , . . . , C ˜ 4 . For FGM spherical shells, the deformation functions are controlled by the value of the parameter μ 2 (equation (14)). For isotropic shells, this value is the function of the ratio R/t:

(16) μ isotr 2 = ( B + R A ) 2 A D − B 2 − ν 2 = 12 R 2 t 2 − ν 2 ≈ 2 3 R t ,

but for FGM shells, it is also the function of the coupling effects expressed by the term B (equation (14)). Figure 4 illustrates the influence of the coupling effects on the variations of the parameter μ 2. It is represented by two values: the ratio E t/E b and the porosity index n (equation (5)).

Figure 4 Variations of the dimensionless controlling parameter μ 2 / μ isotr 2 {\mu }^{2}/{\mu }_{\text{isotr}}^{2} (1 – isotropy; 2 – E t/E b = 1; 3 – E t/E b = 10).
Figure 4

Variations of the dimensionless controlling parameter μ 2 / μ isotr 2 (1 – isotropy; 2 – E t/E b = 1; 3 – E t/E b = 10).

The evaluation of T c and β c variables is identical and therefore the value of the parameter μ affects the solutions of the complementary equation (14) in a similar way. The results are presented in Figure 5 for a spherical segment where 0 < φ 1 ≤ φ ≤ φ 2 < π/2. In such a case, the solutions (equation (15b)) have no singular points and demonstrate only the coupling effects. For isotropic and porous FG structures, the difference in the complementary solution Re[Z 1], Im[Z 1] (equation (15b)) can reach even almost 10%; however, for the solution, Im[Z 1] is almost negligible. The identical plots can be drawn for equation (15c), which are the solutions for φ 1 ≤ φ ≤ π/2 < φ 2 (the singular point at π/2; Figure 6).

Figure 5 Solution functions for the FGM spherical shell segment 0 < φ 1 ≤ φ ≤ φ 2 < π/2 (1– isotropy; 2 – E b/E t = 10, n = 2; 3 – E b/E t = 10, n = 10).
Figure 5

Solution functions for the FGM spherical shell segment 0 < φ 1 ≤ φ ≤ φ 2 < π/2 (1– isotropy; 2 – E b/E t = 10, n = 2; 3 – E b/E t = 10, n = 10).

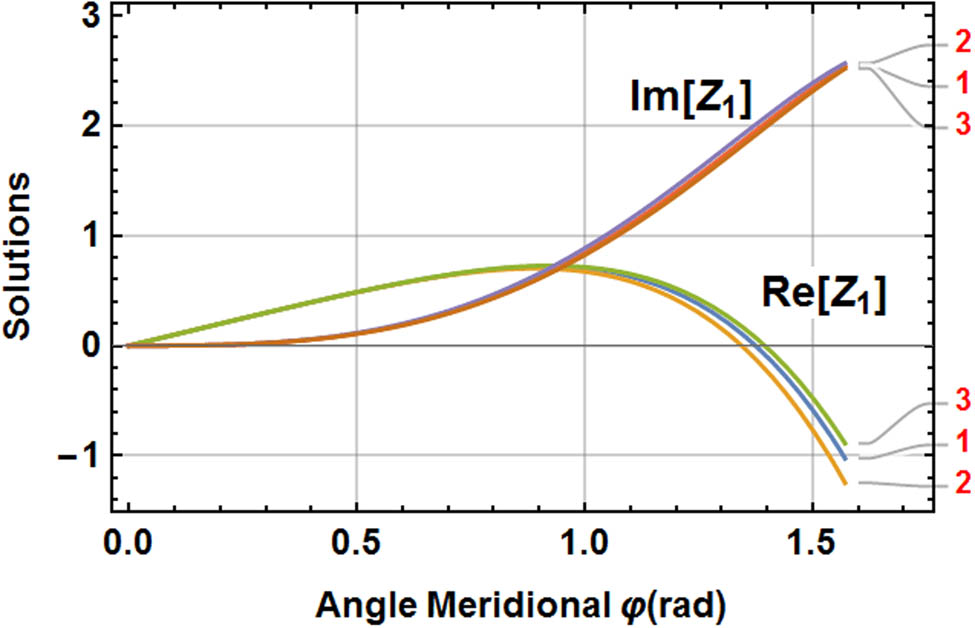
Figure 6 Solution functions for FGM hemispherical shells (1 – isotropy; 2 – E b/E t = 10, n = 2; 3 – E b/E t = 10, n = 10).
Figure 6

Solution functions for FGM hemispherical shells (1 – isotropy; 2 – E b/E t = 10, n = 2; 3 – E b/E t = 10, n = 10).

Comparing the complementary solutions for isotropic and FGM shells (Figures 5 and 6), one can observe the effects of the μ 2 / μ isotr 2 ratio. Both the changes in the index parameter n and of the E b/E t ratio affect the solutions expressed by the solution functions. In general, the results illustrate the localized effects at the lower boundary (i.e. φ = φ 2, φ = π/2).

From the equilibrium equation (17), one can obtain the analytical form of the stress resultants N φ c , N θ c :

(17) R N θ c = 1 sin ( φ ) d d φ ( r T c ) − r N φ c , N φ c = T c cot ( φ ) .

Finally, the kinematic complementary displacements u c, w c can be derived in the closed analytical way with the use of the relations (17), the fundamental definitions (1) and (2) and the constitutive relations (3):

u c = A u sin φ + sin φ ∫ φ e φ d ψ R ( ε φ c − ε θ c ) sin ψ , w c = R ε θ c − u c cot ( φ ) ,

(18) ε φ c = − B A R d β c d φ + N φ c − ν N θ c A ( 1 − ν 2 ) , ε θ c = − B A R β c cot φ + N θ c − ν N φ c A ( 1 − ν 2 ) .

A u denotes a real constant of integration. The computations can be made easily applying the symbolic packages, e.g. Mathematica.

It is convenient and necessary to distinguish two classes of problems that should be introduced independently, referring directly to the convenience and simplicity of analytical solutions given for two types of singular points (equation (15b) and (15c)).

4 Spherical shells under a uniform internal pressure

Let us consider the case of the spherical shell loaded by the uniform external pressure q. For particular solutions, the appropriate differential equations (11) and (12) are homogeneous and

(19) T p = β p = w p = u p = N i p = M i p = 0 .

Now, we consider two solutions.

4.1 Clamped spherical segment 0 < φ 1 ≤ φ ≤ φ 2 < π/2

The clamped edge conditions are the following:

(20) u = w = d w d φ = 0 at φ = φ 1 and φ = φ 2 .

Conditions (20) correspond to β c = 0 at the edges (equation (2)).

Using the equilibrium equation (6) and taking into account the form of particular solutions (20), one can find that

(21) N 1 = − d T c d φ + R q 4 cos 2 φ − cos 2 φ 1 sin 2 φ − R q , N 2 = − T c c t g φ − R q 4 cos 2 φ − cos 2 φ 1 sin 2 φ .

The bending moments can be derived from the constitutive relations (3):

(22) M 1 = B ( ε 1 + ν ε 2 ) + D ( κ 1 + ν κ 2 ) , M 2 = B ( ε 2 + ν ε 1 ) + D ( κ 2 + ν κ 1 ) .

For clamped spherical shells, it is convenient to express the boundary conditions (20) in the equivalent form

(23) β = β c = 0 , ε 2 = 0 at φ = φ 1 , φ = φ 2 .

The solution of equation (11) has four real constants of integration C ˜ 1 , . . . , C ˜ 4 . They are evaluated from equation (23). T c is represented by β c in equation (8), and ε 2 is computed from equations (3), (21), and (22), where all unknown functions are expressed by functions β c.

Figure 7 illustrates the distributions of circumferential membrane forces N 2 for spherical segments. These results are similar to those presented by Muc [70] for shallow shell segments. The maximal difference between isotropic and porous FG spherical shell segments occurs at the lower φ 1 boundary and corresponds to the results of complementary solutions plotted in Figure 5.

Figure 7 Distributions of the dimensionless circumferential forces N 2 (t/R = 0.02).
Figure 7

Distributions of the dimensionless circumferential forces N 2 (t/R = 0.02).

4.2 Clamped hemispherical shell 0 ≤ φ ≤ π/2

For the structure, the boundary conditions can be written in the following way:

(24) u = d w d φ = κ 1 = 0 at φ = 0 and β = β c = 0 , ε 2 = 0 at φ = π / 2 .

Two solutions (equation (15c) Z 3, Z 4 are singular at the shell apex and they would have to be suppressed [2] and one can find that

(25) T c = A 1 S 1 + A 2 S 2 and S 1 = Re[ Z 1 ] , S 2 = Im[ Z 1 ] ,

and clamped at the edge φ = π/2:

(26) w = w c + w p = 0 , β = β c + β p = 0 .

The value of the particular solutions:

(27) T p = β p = 0 .

Since equations (11) and (12) are homogeneous. However, the effects of the distributed load q are brought by the equilibrium equation (6), i.e.

(28) N φ p = N θ 2 = q R 2 .

The stress resultants can be derived from the equilibrium conditions (6) and the relations (24) and (26)–(28):

(29) N φ = q R 2 [ ( P 1 S 1 + P 2 S 2 ) cot φ + 1 ] ,

(30) N θ = q R 2 P 1 d S 1 d φ + P 2 d S 2 d φ + 1 .

Using the above relations and the definitions (2) and (3) and the relation (7), the stress couples can be written in the following way:

(31) M φ = q R 2 μ 4 ( ν P 1 + 2 μ 2 P 2 ) d S 1 d φ + ν S 1 cot φ + ( ν P 2 − 2 μ 2 P 1 ) d S 2 d φ + ν S 2 cot φ + B R A N φ ,

(32) M θ = q R 2 μ 4 ( ν P 1 + 2 μ 2 P 2 ) ν d S 1 d φ + S 1 cot φ + ( ν P 2 − 2 μ 2 P 1 ) ν d S 2 d φ + S 2 cot φ + B R A N φ .

Inserting the coupling stiffness B = 0, one can find the relations (29)–(32) for isotropic shells [2,3]. The symbols P1, P2 are integration constants and, for the boundary conditions (26), they are equal to

(33) P i = 2 C i q R 2 , P 1 = P 2 2 μ 2 J 1 + v J 2 2 μ 2 J 2 − v J 1 , P 2 = − ( 1 − v ) ( 2 μ 2 J 2 − v J 1 ) J 1 ′ ( 2 μ 2 J 1 + v J 2 ) + J 2 ′ ( 2 μ 2 J 2 − v J 2 ) , J 1 = S 1 ( φ = π / 2 ) , J 2 = S 2 ( φ = π / 2 ) , J 1 ′ = d S 1 ( φ = π / 2 ) d φ , J 2 ′ = d S 2 ( φ = π / 2 ) d φ .

Figure 8 demonstrates the distributions of the dimensionless circumferential forces N 2/(qt) along the shell meridian. The results demonstrate that the localized effects at the clamped edge increase with the decrease of the thickness ratio. The coupling effects expressed by the controlling parameter μ 2 (14) have a significant influence on the values of the circumferential forces at the clamped edge – the growth of this value results in the increase of bending effects.

Figure 8 Distributions of the dimensionless circumferential forces N 2 (t/R = 0.02).
Figure 8

Distributions of the dimensionless circumferential forces N 2 (t/R = 0.02).

The distributions of the stress resultants N 2 show that these values are almost equal to 0.5qR (the membrane state).

5 Concluding remarks

The analytical solutions presented herein demonstrate evidently the significant influence of the coupling terms B illustrating the unsymmetry in the construction of shell walls of porous FGM. These effects are characterized by the controlling parameter μ. It is worth mentioning that a similar controlling parameter is proposed and introduced in the description of flutter problems for structures made of porous FGM or plates reinforced by nanostructures (nanoplates or nanotubes)(see Muc et al. [10,22]).

It is very important to formulate precisely the assumptions of the analysis, particularly in view of the used approaches. In our opinion, the classification presented in Table 1 can be useful in understanding the limitations (or generality) of the results and not only for spherical shells.

Let us note that the distributions of the stress resultants and bending moments are sensitive to the variations of the thickness ratio t/R. In the present work, the classical Love–Kirchhoff hypothesis is employed but, for thicker structures (t/R > 0.1), the higher-order 2D shell theories should be used, e.g. in the form proposed in the Appendix of ref. [22].

The present results are derived for spherical shells; however, the identical analysis can be easily extended to the analysis of shells or pressure vessels having various forms: paraboloidal, hyperbolical, elliptical, and torispherical discussed from the numerical and optimization point of view, e.g. in ref. [79,80].

The results presented demonstrate that the analytical results can be treated as a benchmark for finite element analysis.

  1. Funding information: The paper publication has received funding from Cracow University of Technology.

  2. Authors contribution: Flis J.: Conceptualization, methodology, visualization, formal analysis, writing – original draft, review and editing. Muc A.: conceptualization, methodology.

  3. Conflict of interest: Authors state no conflict of interest.

References

[1] Flügge, W. Stresses in shells, Springer-Verlag, Berlin-Heidelberg, 1962.Search in Google Scholar

[2] Kraus, H. Thin elastic shells, John Wiley and Sons, New York, 1967.Search in Google Scholar

[3] Mazurkiewicz, Z. E. and R. T. Nagórski. Shells of revolution, Elsevier Amsterdam, PWN Warszawa, 1991.Search in Google Scholar

[4] Galletly, G. D. and A. Muc. Buckling of fibre-reinforced plastic-steel torispherical shells under external pressure. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 202, No. 6, 1988, pp. 409–420.10.1243/PIME_PROC_1988_202_143_02Search in Google Scholar

[5] Galletly, G. D. and A. Muc. Buckling of externally pressurized composite torispherical domes. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, Vol. 203, No. 1, 1989, pp. 41–56.10.1243/PIME_PROC_1989_203_187_02Search in Google Scholar

[6] Muc, A. On the buckling of composite shells of revolution under external pressure. Composite Structures, Vol. 21, No. 2, 1992, pp. 107–119.10.1016/0263-8223(92)90046-FSearch in Google Scholar

[7] El-Nady, A. O. and H. M. Negm. Analysis of arbitrarily laminated composite spherical shells by Chebyshev series. Journal of Engineering and Applied Science, Vol. 51, No. 4, 2004, pp. 777–794.Search in Google Scholar

[8] Muc, A. Mechanics of fibrous composites, Wydawnictwo “Księgarnia Akademicka”, Kraków, 2003 (in Polish).Search in Google Scholar

[9] Fantuzzi, N., S. Brischetto, F. Tornabene, and E. Viola. 2D and 3D shell models for the free vibration investigation of functionally graded cylindrical and spherical panels. Composite Structures, Vol. 154, 2016, pp. 573–590.10.1016/j.compstruct.2016.07.076Search in Google Scholar

[10] Muc, A. and M. Muc-Wierzgoń. Effects of material constructions on supersonic flutter characteristics for composite rectangular plates reinforced with carbon nano-structures. Science and Engineering of Composite Materials, Vol. 28, 2021, pp. 107–115.10.1515/secm-2021-0010Search in Google Scholar

[11] Panda, S. K. and B. N. Singh. Nonlinear free vibration of spherical shell panel using higher order shear deformation theory – a finite element approach. International Journal of Pressure Vessels and Piping, Vol. 86, 2009, pp. 373–383.10.1016/j.ijpvp.2008.11.023Search in Google Scholar

[12] Moita, J. S., C. M. Mota Soares, C. A. Mota Soares, and A. J. M. Ferreira. Elastoplastic and nonlinear analysis of functionally graded axisymmetric shell structures under thermal environment, using a conical frustum finite element model. Composite Structures, Vol. 226, 2019, id. 111186.10.1016/j.compstruct.2019.111186Search in Google Scholar

[13] Bushnell, D. Panda – Interactive program for minimum weight design of stiffened cylindrical panels and shells. Computers & structures, Vol. 16, No. 1–4, 1983, pp. 167–185.10.1016/0045-7949(83)90158-XSearch in Google Scholar

[14] Bushnell, D. B0S0R5 – program for buckling of elastic-plastic complex shells of revolution including large deflections and creep. Computers & Structures, Vol. 6, No. 3, 1976, pp. 221–239.10.1016/0045-7949(76)90034-1Search in Google Scholar

[15] Muc, A. Buckling and deformation analysis of composite domed ends of pressure vessels, Politechnika Krakowska, Kraków, 1992 (in Polish).Search in Google Scholar

[16] Tornabene, F. and E. Viola. Vibration analysis of spherical structural elements using the GDQ method. Computers & mathematics with applications (Oxford, England : 1987), Vol. 53, 2007, pp. 1538–1560.10.1016/j.camwa.2006.03.039Search in Google Scholar

[17] Tornabene, F. 2-D GDQ solution for free vibrations of anisotropic doubly – curved shells and panels of revolution. Composite Structures, Vol. 93, 2011, pp. 1854–1876.10.1016/j.compstruct.2011.02.006Search in Google Scholar

[18] Viola, E., L. Rossetti, and N. Fantuzzi. Numerical investigation of functionally graded cylindrical shells and panels using the generalized unconstrained third order theory coupled with the stress recovery. Composite Structures, Vol. 94, 2012, pp. 3736–3758.10.1016/j.compstruct.2012.05.034Search in Google Scholar

[19] Viola, E., L. Rossetti, N. Fantuzzi, and F. Tornabene. Static analysis of functionally graded conical shells and panels using the generalized unconstrained third order theory coupled with the stress recovery. Composite Structures, Vol. 112, 2014, pp. 44–65.10.1016/j.compstruct.2014.01.039Search in Google Scholar

[20] Sayyad, A. S. and Y. M. Ghugal. Static and free vibration analysis of laminated composite and sandwich spherical shells using a generalized higher-order shell theory. Composite Structures, Vol. 219, 2019, pp. 129–146.10.1016/j.compstruct.2019.03.054Search in Google Scholar

[21] Vlasov, V. Z. General theory of shells – the applications in engineering, Moscow, Gostechizdat, 1949 (in Russian).Search in Google Scholar

[22] Muc, A. and J. Flis. Flutter characteristics and free vibrations of rectangular functionally graded porous plates. Composite Structures, Vol. 261, 2021, id. 113301.10.1016/j.compstruct.2020.113301Search in Google Scholar

[23] Bagheri, H., Y. Kiani, and M. R. Eslami. Free vibration of FGM conical–spherical shells. Thin-Walled Structures, Vol. 160, 2021, id. 107387.10.1016/j.tws.2020.107387Search in Google Scholar

[24] Liu, J., B. Yu, Y. Zhou, Y. Zhang, and M. Duan. The buckling of spherical-cylindrical composite shells by external pressure. Composite Structures, Vol. 265, 2021, id. 113773.10.1016/j.compstruct.2021.113773Search in Google Scholar

[25] Gong, Q., H. Li, H. Chen, Y. Teng, and N. Wang. Application of Ritz method for vibration analysis of stepped functionally graded spherical torus shell with general boundary conditions. Composite Structures, Vol. 243, 2020, id. 112215.10.1016/j.compstruct.2020.112215Search in Google Scholar

[26] Hosseini-Hashemi, Sh. and M. Fadaee. On the free vibration of moderately thick spherical shell panel – A new exact closed-form procedure. Journal of Sound and Vibration, Vol. 330, No. 17, 2011, pp. 4352–4367.10.1016/j.jsv.2011.04.011Search in Google Scholar

[27] Li, H., F. Pang, Y. Ren, X. Miao, and K. Ye. Free vibration characteristics of functionally graded porous spherical shell with general boundary conditions by using first-order shear deformation theory. Thin-Walled Structures, Vol. 144, 2019, id. 106331.10.1016/j.tws.2019.106331Search in Google Scholar

[28] Evkin, A. Y. Composite spherical shells at large deflections. Asymptotic analysis and applications. Composite Structures, Vol. 233, 2020, id. 111577.10.1016/j.compstruct.2019.111577Search in Google Scholar

[29] Li, H., F. Pang, X. Miao, S. Gao, and F. Liu. A semi analytical method for free vibration analysis of composite laminated cylindrical and spherical shells with complex boundary conditions. Thin Walled Structures, Vol. 136, 2019, pp. 200–220.10.1016/j.tws.2018.12.009Search in Google Scholar

[30] Juhász, Z. and A. Szekrényes. An analytical solution for buckling and vibration of delaminated composite spherical shells. Thin Walled Structures, Vol. 148, 2020, id. 106563.10.1016/j.tws.2019.106563Search in Google Scholar

[31] Biswal, D. K. and S. C. Mohanty. Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers. Composites, Part B: Engineering, Vol. 159, 2019, pp. 72–85.10.1016/j.compositesb.2018.09.075Search in Google Scholar

[32] Kareem, M. G. and W. I. Majeed. Transient dynamic analysis of laminated shallow spherical shell under low-velocity impact. Journal of Materials Research and Technology, Vol. 8, No. 6, 2019, pp. 5283–5300.10.1016/j.jmrt.2019.08.050Search in Google Scholar

[33] Şahan, M. F. Dynamic analysis of linear viscoelastic cross-ply laminated shallow spherical shells. Composite Structures, Vol. 149, 2016, pp. 261–270.10.1016/j.compstruct.2016.04.045Search in Google Scholar

[34] Fadaee, M., S. R. Atashipour, and Sh. Hosseini-Hashemi. Free vibration analysis of Lévy-type functionally graded spherical shell panel using a new exact closed-form solution. International Journal of Mechanical Science, Vol. 77, 2013, pp. 227–238.10.1016/j.ijmecsci.2013.10.008Search in Google Scholar

[35] Ganapathi, M. Dynamic stability characteristics of functionally graded materials shallow spherical shells. Composite Structures, Vol. 79, No. 3, 2007, pp. 338–343.10.1016/j.compstruct.2006.01.012Search in Google Scholar

[36] Viola, E., L. Rossetti, N. Fantuzzi, and F. Tornabene. Generalized stress–strain recovery formulation applied to functionally graded spherical shells and panels under static loading. Composite Structures, Vol. 156, 2016, pp. 145–164.10.1016/j.compstruct.2015.12.060Search in Google Scholar

[37] Mao, Y. Q., Y. M. Fu, C. P. Chen, and Y. L. Li. Nonlinear dynamic response for functionally graded shallow spherical shell under low velocity impact in thermal environment. Applied Mathematical Modelling, Vol. 35, No. 6, 2011, pp. 2887–2900.10.1016/j.apm.2010.12.012Search in Google Scholar

[38] Lal, A., B. N. Singh, and S. Anand. Nonlinear bending response of laminated composite spherical shell panel with system randomness subjected to hygro-thermo mechanical loading. International Journal of Mechanical Sciences, Vol. 53, 2011, pp. 855–866.10.1016/j.ijmecsci.2011.07.008Search in Google Scholar

[39] Yiming, F., M. Yiqi, and T. Yanping. Damage analysis and dynamic response of elasto-plastic laminated composite shallow spherical shell under low velocity impact. International Journal of Solids and Structures, Vol. 47, 2010, pp. 126–137.10.1016/j.ijsolstr.2009.09.017Search in Google Scholar

[40] Yiming, F., H. Sumin, and M. Yiqi. Nonlinear transient response of functionally graded shallow spherical shells subjected to mechanical load and unsteady temperature field. Acta Mechanica Solida Sinica, Vol. 27, No. 5, 2014, pp. 496–508.10.1016/S0894-9166(14)60058-6Search in Google Scholar

[41] Nguyen, D. D., H. B. Dao, and T. T. A. Vu. On the nonlinear stability of eccentrically stiffened functionally graded annular spherical segment shells. Thin-Walled Structures, Vol. 106, 2016, pp. 258–267.10.1016/j.tws.2016.05.006Search in Google Scholar

[42] Xie, X., H. Zheng, and G. Jin. Free vibration of four-parameter functionally graded spherical and parabolic shells of revolution with arbitrary boundary conditions. Composites, Part B: Engineering, Vol. 77, 2015, pp. 59–73.10.1016/j.compositesb.2015.03.016Search in Google Scholar

[43] Su, Z., G. Jin, S. Shi, and T. Ye. A unified accurate solution for vibration analysis of arbitrary functionally graded spherical shell segments with general end restraints. Composite Structures, Vol. 111, 2014, pp. 271–284.10.1016/j.compstruct.2014.01.006Search in Google Scholar

[44] Wu, C.-P. and Y.-H. Tsai. Asymptotic DQ solutions of functionally graded annular spherical shells. European Journal of Mechanics A/Solids, Vol. 23, 2004, pp. 283–299.10.1016/j.euromechsol.2003.11.002Search in Google Scholar

[45] Mao, Y., Y. Fu, S. Ai, and D. Fang. Interfacial damage analysis of shallow spherical shell with FGM coating under low velocity impact. International Journal of Mechanical Sciences, Vol. 71, 2013, pp. 30–40.10.1016/j.ijmecsci.2013.03.004Search in Google Scholar

[46] Civalek, Ö. Geometrically nonlinear dynamic and static analysis of shallow spherical shell resting on two-parameters elastic foundations. International Journal of Pressure Vessels and Piping, Vol. 113, 2014, pp. 1–9.10.1016/j.ijpvp.2013.10.014Search in Google Scholar

[47] Semenyuk, N. P., V. M. Trach, and V. V. Ostapchuk. Nonlinear axisymmetric deformation of anisotropic spherical shells. International Applied Mechanics, Vol. 45, 2009, pp. 1101–1111.10.1007/s10778-010-0251-2Search in Google Scholar

[48] Nath, Y. and K. Sandeep. Effect of transverse shear on static and dynamic buckling of antisymmetrically laminated polar orthotropic shallow spherical shells. Composite Structures, Vol. 40, No. 1, 1998, pp. 67–72.10.1016/S0263-8223(97)00153-0Search in Google Scholar

[49] Krizhevsky, G. and Y. Stavsky. Refined theory for non-linear buckling of heated composite shallow spherical shells. Computers & Structures, Vol. 55, No. 6, 1995, pp. 1007–1014.10.1016/0045-7949(94)00512-2Search in Google Scholar

[50] Lugovoi, P. Z., V. F. Meish, and S. P. Orlenko. Numerical simulation of the dynamics of spherical sandwich shells reinforced with discrete ribs under a shockwave. International Applied Mechanics, Vol. 56, No. 5, 2020, pp. 590–598.10.1007/s10778-020-01037-3Search in Google Scholar

[51] Kar, A. and M. Kanoria. Generalized thermo-visco-elastic problem of a spherical shell with three-phase-lag effect. Applied Mathematical Modelling, Vol. 33, No. 8, 2009, pp. 3287–3298.10.1016/j.apm.2008.10.036Search in Google Scholar

[52] Krysko, V., J. Awrejcewicz, and T. Shchekaturova. Chaotic vibrations of spherical and conical axially symmetric shells. Archive of Applied Mechanics, Vol. 74, 2005, pp. 338–358.10.1007/s00419-004-0356-3Search in Google Scholar

[53] Birman, V., S. Griffin, and G. Knowles. Axisymmetric dynamics of composite spherical shells with active piezoelectric/composite stiffeners. Acta Mechanica, Vol. 141, 2000, pp. 71–83.10.1007/BF01176808Search in Google Scholar

[54] Han, P., K. Ri, K. Choe, and Y. Han. Vibration analysis of rotating cross-ply laminated cylindrical, conical and spherical shells by using weak-form differential quadrature method. Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 42, 2020, id. 352.10.1007/s40430-020-02434-ySearch in Google Scholar

[55] Ghavanloo, E. and S. A. Fazelzadeh. Nonlocal shell model for predicting axisymmetric vibration of spherical shell-like nanostructures. Mechanics of Advanced Materials and Structures, Vol. 22, 2015, pp. 597–603.10.1080/15376494.2013.828816Search in Google Scholar

[56] Zaera, R., J. Fernández-Sáez, and J. A. Loya. Axisymmetric free vibration of closed thin spherical nano-shell. Composite Structures, Vol. 104, 2013, pp. 154–161.10.1016/j.compstruct.2013.04.022Search in Google Scholar

[57] Fazelzadeh, S. A. and E. Ghavanloo. Coupled axisymmetric vibration of nonlocal fluid-filled closed spherical membrane shell. Acta Mechanica, Vol. 223, 2012, pp. 2011–2020.10.1007/s00707-012-0692-2Search in Google Scholar

[58] Ghavanloo, E., S. A. Fazelzadeh, T. Murmu, and S. Adhikari. Radial breathing-mode frequency of elastically confined spherical nanoparticles subjected to circumferential magnetic field. Physica E, Vol. 66, 2015, pp. 228–233.10.1016/j.physe.2014.10.003Search in Google Scholar

[59] Ghavanloo, E. and S. A. Fazelzadeh. Nonlocal elasticity theory for radial vibration of nanoscale spherical shells. European Journal of Mechanics – A/Solids, Vol. 41, 2013, pp. 37–42.10.1016/j.euromechsol.2013.02.003Search in Google Scholar

[60] Hu, J., Z. Qiu, and T. C. Su. Axisymmetric vibrations of a viscous-fluid-filled piezoelectric spherical shell and the associated radiation of sound. Journal of Sound and Vibration, Vol. 330, 2011, pp. 5982–6005.10.1016/j.jsv.2011.07.030Search in Google Scholar

[61] Vila, J., R. Zaera, and J. Fernández-Sáez. Axisymmetric free vibration of closed thin spherical nanoshells with bending effects. Journal of Vibration and Control,Vol. 22, No. 18, pp. 3789–3806. 10.1177/1077546314565808.Search in Google Scholar

[62] Murray, D. B. and L. Saviot. Acoustic vibrations of embedded spherical nanoparticles. Physica E, Vol. 26, 2005, pp. 417–421.10.1016/j.physe.2004.08.091Search in Google Scholar

[63] Fazelzadeh, S. A. and E. Ghavanloo. Radial vibration characteristics of spherical nanoparticles immersed in fluid medium. Modern Physics Letters B, Vol. 27, 2013, id. 1350186.10.1142/S0217984913501868Search in Google Scholar

[64] Ansari, R., F. Sadeghi, and B. Motevalli. A comprehensive study on the oscillation frequency of spherical fullerenes in carbon nanotubes under different system parameters. Communications in Nonlinear Science and Numerical Simulation, Vol. 18, 2013, pp. 769–784.10.1016/j.cnsns.2012.08.011Search in Google Scholar

[65] Liu, D., Y. Zhou, and J. Zhu. On the free vibration and bending analysis of functionally graded nanocomposite spherical shells reinforced with graphene nanoplatelets: Three-dimensional elasticity solutions. Engineering Structures, Vol. 226, 2021, id. 111376.10.1016/j.engstruct.2020.111376Search in Google Scholar

[66] Hosseini-Hashemi, Sh., F. Sharifpour, and M. R. Ilkhani. On the free vibrations of size-dependent closed micro/nano-spherical shell based on the modified couple stress theory. International Journal of Mechanical Sciences, Vol. 115–116, 2016, pp. 501–515.10.1016/j.ijmecsci.2016.07.007Search in Google Scholar

[67] Baowan, D., N. Thamwattana, and J. M. Hill. Continuum modelling of spherical and spheroidal carbon onions. European Physical Journal D: Atomic, Molecular, Optical and Plasma Physics, Vol. 44, 2007, pp. 117–123.10.1140/epjd/e2007-00159-8Search in Google Scholar

[68] Ghavanloo, E. and S. A. Fazelzadeh. Continuum modeling of breathing-like modes of spherical carbon onions. Physics Letters A, Vol. 379, 2015, pp. 1600–1606.10.1016/j.physleta.2015.04.006Search in Google Scholar

[69] Wang, B. C., H. W. Wang, J. C. Chang, H. C. Tso, and Y. M. Chou. More spherical large fullerenes and multi-layer fullerene cages. Journal of Molecular Structure, Vol. 540, 2001, pp. 171–176.10.1016/S0166-1280(00)00739-9Search in Google Scholar

[70] Muc, A. Buckling and post-buckling behaviour of laminated shallow spherical shells subjected to external pressure. International Journal of Non-Linear Mechanics, Vol. 27, No. 3, 1992, pp. 465–476.10.1016/0020-7462(92)90013-WSearch in Google Scholar

[71] Sofiyev, A. H., F. Turan, and Z. Zerin. Large-amplitude vibration of functionally graded orthotropic double-curved shallow spherical and hyperbolic paraboloidal shells. International Journal of Pressure Vessels and Piping, Vol. 188, 2020, id. 104235.10.1016/j.ijpvp.2020.104235Search in Google Scholar

[72] Sofiyev, A. H. and F. Turan. On the nonlinear vibration of heterogenous orthotropic shallow shells in the framework of the shear deformation shell theory. Thin-Walled Structures, Vol. 161, 2021, id. 107181.10.1016/j.tws.2020.107181Search in Google Scholar

[73] Sofiyev, A. H. and P. Ozyigit. Thermal buckling analysis of non-homogenous shallow spherical shells. Journal of the Faculty of Engineering and Architecture of Gazi University, Vol. 27, 2012, pp. 397–405.Search in Google Scholar

[74] Duc, N. D., H. Hadavinia, T. Q. Quan, and N. D. Khoa. Free vibration and nonlinear dynamic response of imperfect nanocomposite FG-CNTRC double curved shallow shells in thermal environment. European Journal of Mechanics/A Solids, Vol. 75, 2019, pp. 355–366.10.1016/j.euromechsol.2019.01.024Search in Google Scholar

[75] Duc, N. D., T. Q. Quan, and N. D. Khoa. New approach to investigate nonlinear dynamic response and vibration of imperfect functionally graded carbon nanotube reinforced composite double curved shallow shells subjected to blast load and temperature. Aerospace Science and Technology, Vol. 71, 2017, pp. 360–372.10.1016/j.ast.2017.09.031Search in Google Scholar

[76] Al-Furjan, M. S. H., M. A. Oyarhossein, M. Habibi, H. Safarpourf, D. W. Jung, and A. Tounsi. On the wave propagation of the multi-scale hybrid nanocomposite doubly curved viscoelastic panel. Composite Structures, Vol. 255, 2021, id. 112947.10.1016/j.compstruct.2020.112947Search in Google Scholar

[77] Wang, A., H. Chen, Y. Hao, and W. Zhang. Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results in Physics, Vol. 9, 2018, pp. 550–559.10.1016/j.rinp.2018.02.062Search in Google Scholar

[78] Polyanin, A. D., V. F. Zaitsev. Handbook of exact solutions for ordinary differential equations, Chapman & Hall CRC, Boca Raton, 2003.Search in Google Scholar

[79] Muc, A. Evolutionary design of engineering constructions. Latin American Journal of Solids and Structures, Vol. 15, No. 4, 2018, id. e87.10.1590/1679-78254947Search in Google Scholar

[80] Muc, A. Choice of design variables in the stacking sequence optimization for laminated structures. Mechanics of Composite Materials, Vol. 52, No. 2, 2016, pp. 211–224.10.1007/s11029-016-9574-3Search in Google Scholar
Received: 2021-05-05
Revised: 2021-08-07
Accepted: 2021-08-17
Published Online: 2021-10-19

© 2021 Justyna Flis and Aleksander Muc, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. A review on filler materials for brazing of carbon-carbon composites
  3. Nanotechnology-based materials as emerging trends for dental applications
  4. A review on allotropes of carbon and natural filler-reinforced thermomechanical properties of upgraded epoxy hybrid composite
  5. High-temperature tribological properties of diamond-like carbon films: A review
  6. A review of current physical techniques for dispersion of cellulose nanomaterials in polymer matrices
  7. Review on structural damage rehabilitation and performance assessment of asphalt pavements
  8. Recent development in graphene-reinforced aluminium matrix composite: A review
  9. Mechanical behaviour of precast prestressed reinforced concrete beam–column joints in elevated station platforms subjected to vertical cyclic loading
  10. Effect of polythiophene thickness on hybrid sensor sensitivity
  11. Investigation on the relationship between CT numbers and marble failure under different confining pressures
  12. Finite element analysis on the bond behavior of steel bar in salt–frost-damaged recycled coarse aggregate concrete
  13. From passive to active sorting in microfluidics: A review
  14. Research Articles
  15. Revealing grain coarsening and detwinning in bimodal Cu under tension
  16. Mesoporous silica nanoparticles functionalized with folic acid for targeted release Cis-Pt to glioblastoma cells
  17. Magnetic behavior of Fe-doped of multicomponent bismuth niobate pyrochlore
  18. Study of surfaces, produced with the use of granite and titanium, for applications with solar thermal collectors
  19. Magnetic moment centers in titanium dioxide photocatalysts loaded on reduced graphene oxide flakes
  20. Mechanical model and contact properties of double row slewing ball bearing for wind turbine
  21. Sandwich panel with in-plane honeycombs in different Poisson's ratio under low to medium impact loads
  22. Effects of load types and critical molar ratios on strength properties and geopolymerization mechanism
  23. Nanoparticles in enhancing microwave imaging and microwave Hyperthermia effect for liver cancer treatment
  24. FEM micromechanical modeling of nanocomposites with carbon nanotubes
  25. Effect of fiber breakage position on the mechanical performance of unidirectional carbon fiber/epoxy composites
  26. Removal of cadmium and lead from aqueous solutions using iron phosphate-modified pollen microspheres as adsorbents
  27. Load identification and fatigue evaluation via wind-induced attitude decoupling of railway catenary
  28. Residual compression property and response of honeycomb sandwich structures subjected to single and repeated quasi-static indentation
  29. Experimental and modeling investigations of the behaviors of syntactic foam sandwich panels with lattice webs under crushing loads
  30. Effect of storage time and temperature on dissolved state of cellulose in TBAH-based solvents and mechanical property of regenerated films
  31. Thermal analysis of postcured aramid fiber/epoxy composites
  32. The energy absorption behavior of novel composite sandwich structures reinforced with trapezoidal latticed webs
  33. Experimental study on square hollow stainless steel tube trusses with three joint types and different brace widths under vertical loads
  34. Thermally stimulated artificial muscles: Bio-inspired approach to reduce thermal deformation of ball screws based on inner-embedded CFRP
  35. Abnormal structure and properties of copper–silver bar billet by cold casting
  36. Dynamic characteristics of tailings dam with geotextile tubes under seismic load
  37. Study on impact resistance of composite rocket launcher
  38. Effects of TVSR process on the dimensional stability and residual stress of 7075 aluminum alloy parts
  39. Dynamics of a rotating hollow FGM beam in the temperature field
  40. Development and characterization of bioglass incorporated plasma electrolytic oxidation layer on titanium substrate for biomedical application
  41. Effect of laser-assisted ultrasonic vibration dressing parameters of a cubic boron nitride grinding wheel on grinding force, surface quality, and particle morphology
  42. Vibration characteristics analysis of composite floating rafts for marine structure based on modal superposition theory
  43. Trajectory planning of the nursing robot based on the center of gravity for aluminum alloy structure
  44. Effect of scan speed on grain and microstructural morphology for laser additive manufacturing of 304 stainless steel
  45. Influence of coupling effects on analytical solutions of functionally graded (FG) spherical shells of revolution
  46. Improving the precision of micro-EDM for blind holes in titanium alloy by fixed reference axial compensation
  47. Electrolytic production and characterization of nickel–rhenium alloy coatings
  48. DC magnetization of titania supported on reduced graphene oxide flakes
  49. Analytical bond behavior of cold drawn SMA crimped fibers considering embedded length and fiber wave depth
  50. Structural and hydrogen storage characterization of nanocrystalline magnesium synthesized by ECAP and catalyzed by different nanotube additives
  51. Mechanical property of octahedron Ti6Al4V fabricated by selective laser melting
  52. Physical analysis of TiO2 and bentonite nanocomposite as adsorbent materials
  53. The optimization of friction disc gear-shaping process aiming at residual stress and machining deformation
  54. Optimization of EI961 steel spheroidization process for subsequent use in additive manufacturing: Effect of plasma treatment on the properties of EI961 powder
  55. Effect of ultrasonic field on the microstructure and mechanical properties of sand-casting AlSi7Mg0.3 alloy
  56. Influence of different material parameters on nonlinear vibration of the cylindrical skeleton supported prestressed fabric composite membrane
  57. Investigations of polyamide nano-composites containing bentonite and organo-modified clays: Mechanical, thermal, structural and processing performances
  58. Conductive thermoplastic vulcanizates based on carbon black-filled bromo-isobutylene-isoprene rubber (BIIR)/polypropylene (PP)
  59. Effect of bonding time on the microstructure and mechanical properties of graphite/Cu-bonded joints
  60. Study on underwater vibro-acoustic characteristics of carbon/glass hybrid composite laminates
  61. A numerical study on the low-velocity impact behavior of the Twaron® fabric subjected to oblique impact
  62. Erratum
  63. Erratum to “Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete”
  64. Topical Issue on Advances in Infrastructure or Construction Materials – Recycled Materials, Wood, and Concrete
  65. Structural performance of textile reinforced concrete sandwich panels under axial and transverse load
  66. An overview of bond behavior of recycled coarse aggregate concrete with steel bar
  67. Development of an innovative composite sandwich matting with GFRP facesheets and wood core
  68. Relationship between percolation mechanism and pore characteristics of recycled permeable bricks based on X-ray computed tomography
  69. Feasibility study of cement-stabilized materials using 100% mixed recycled aggregates from perspectives of mechanical properties and microstructure
  70. Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete
  71. Research on nano-concrete-filled steel tubular columns with end plates after lateral impact
  72. Dynamic analysis of multilayer-reinforced concrete frame structures based on NewMark-β method
  73. Experimental study on mechanical properties and microstructures of steel fiber-reinforced fly ash-metakaolin geopolymer-recycled concrete
  74. Fractal characteristic of recycled aggregate and its influence on physical property of recycled aggregate concrete
  75. Properties of wood-based composites manufactured from densified beech wood in viscoelastic and plastic region of the force-deflection diagram (FDD)
  76. Durability of geopolymers and geopolymer concretes: A review
  77. Research progress on mechanical properties of geopolymer recycled aggregate concrete
https://doi.org/10.1515/rams-2021-0064
Keywords for this article
spherical shells; analytical solutions; porous functionally graded materials; construction of material properties
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. A review on filler materials for brazing of carbon-carbon composites
  3. Nanotechnology-based materials as emerging trends for dental applications
  4. A review on allotropes of carbon and natural filler-reinforced thermomechanical properties of upgraded epoxy hybrid composite
  5. High-temperature tribological properties of diamond-like carbon films: A review
  6. A review of current physical techniques for dispersion of cellulose nanomaterials in polymer matrices
  7. Review on structural damage rehabilitation and performance assessment of asphalt pavements
  8. Recent development in graphene-reinforced aluminium matrix composite: A review
  9. Mechanical behaviour of precast prestressed reinforced concrete beam–column joints in elevated station platforms subjected to vertical cyclic loading
  10. Effect of polythiophene thickness on hybrid sensor sensitivity
  11. Investigation on the relationship between CT numbers and marble failure under different confining pressures
  12. Finite element analysis on the bond behavior of steel bar in salt–frost-damaged recycled coarse aggregate concrete
  13. From passive to active sorting in microfluidics: A review
  14. Research Articles
  15. Revealing grain coarsening and detwinning in bimodal Cu under tension
  16. Mesoporous silica nanoparticles functionalized with folic acid for targeted release Cis-Pt to glioblastoma cells
  17. Magnetic behavior of Fe-doped of multicomponent bismuth niobate pyrochlore
  18. Study of surfaces, produced with the use of granite and titanium, for applications with solar thermal collectors
  19. Magnetic moment centers in titanium dioxide photocatalysts loaded on reduced graphene oxide flakes
  20. Mechanical model and contact properties of double row slewing ball bearing for wind turbine
  21. Sandwich panel with in-plane honeycombs in different Poisson's ratio under low to medium impact loads
  22. Effects of load types and critical molar ratios on strength properties and geopolymerization mechanism
  23. Nanoparticles in enhancing microwave imaging and microwave Hyperthermia effect for liver cancer treatment
  24. FEM micromechanical modeling of nanocomposites with carbon nanotubes
  25. Effect of fiber breakage position on the mechanical performance of unidirectional carbon fiber/epoxy composites
  26. Removal of cadmium and lead from aqueous solutions using iron phosphate-modified pollen microspheres as adsorbents
  27. Load identification and fatigue evaluation via wind-induced attitude decoupling of railway catenary
  28. Residual compression property and response of honeycomb sandwich structures subjected to single and repeated quasi-static indentation
  29. Experimental and modeling investigations of the behaviors of syntactic foam sandwich panels with lattice webs under crushing loads
  30. Effect of storage time and temperature on dissolved state of cellulose in TBAH-based solvents and mechanical property of regenerated films
  31. Thermal analysis of postcured aramid fiber/epoxy composites
  32. The energy absorption behavior of novel composite sandwich structures reinforced with trapezoidal latticed webs
  33. Experimental study on square hollow stainless steel tube trusses with three joint types and different brace widths under vertical loads
  34. Thermally stimulated artificial muscles: Bio-inspired approach to reduce thermal deformation of ball screws based on inner-embedded CFRP
  35. Abnormal structure and properties of copper–silver bar billet by cold casting
  36. Dynamic characteristics of tailings dam with geotextile tubes under seismic load
  37. Study on impact resistance of composite rocket launcher
  38. Effects of TVSR process on the dimensional stability and residual stress of 7075 aluminum alloy parts
  39. Dynamics of a rotating hollow FGM beam in the temperature field
  40. Development and characterization of bioglass incorporated plasma electrolytic oxidation layer on titanium substrate for biomedical application
  41. Effect of laser-assisted ultrasonic vibration dressing parameters of a cubic boron nitride grinding wheel on grinding force, surface quality, and particle morphology
  42. Vibration characteristics analysis of composite floating rafts for marine structure based on modal superposition theory
  43. Trajectory planning of the nursing robot based on the center of gravity for aluminum alloy structure
  44. Effect of scan speed on grain and microstructural morphology for laser additive manufacturing of 304 stainless steel
  45. Influence of coupling effects on analytical solutions of functionally graded (FG) spherical shells of revolution
  46. Improving the precision of micro-EDM for blind holes in titanium alloy by fixed reference axial compensation
  47. Electrolytic production and characterization of nickel–rhenium alloy coatings
  48. DC magnetization of titania supported on reduced graphene oxide flakes
  49. Analytical bond behavior of cold drawn SMA crimped fibers considering embedded length and fiber wave depth
  50. Structural and hydrogen storage characterization of nanocrystalline magnesium synthesized by ECAP and catalyzed by different nanotube additives
  51. Mechanical property of octahedron Ti6Al4V fabricated by selective laser melting
  52. Physical analysis of TiO2 and bentonite nanocomposite as adsorbent materials
  53. The optimization of friction disc gear-shaping process aiming at residual stress and machining deformation
  54. Optimization of EI961 steel spheroidization process for subsequent use in additive manufacturing: Effect of plasma treatment on the properties of EI961 powder
  55. Effect of ultrasonic field on the microstructure and mechanical properties of sand-casting AlSi7Mg0.3 alloy
  56. Influence of different material parameters on nonlinear vibration of the cylindrical skeleton supported prestressed fabric composite membrane
  57. Investigations of polyamide nano-composites containing bentonite and organo-modified clays: Mechanical, thermal, structural and processing performances
  58. Conductive thermoplastic vulcanizates based on carbon black-filled bromo-isobutylene-isoprene rubber (BIIR)/polypropylene (PP)
  59. Effect of bonding time on the microstructure and mechanical properties of graphite/Cu-bonded joints
  60. Study on underwater vibro-acoustic characteristics of carbon/glass hybrid composite laminates
  61. A numerical study on the low-velocity impact behavior of the Twaron® fabric subjected to oblique impact
  62. Erratum
  63. Erratum to “Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete”
  64. Topical Issue on Advances in Infrastructure or Construction Materials – Recycled Materials, Wood, and Concrete
  65. Structural performance of textile reinforced concrete sandwich panels under axial and transverse load
  66. An overview of bond behavior of recycled coarse aggregate concrete with steel bar
  67. Development of an innovative composite sandwich matting with GFRP facesheets and wood core
  68. Relationship between percolation mechanism and pore characteristics of recycled permeable bricks based on X-ray computed tomography
  69. Feasibility study of cement-stabilized materials using 100% mixed recycled aggregates from perspectives of mechanical properties and microstructure
  70. Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete
  71. Research on nano-concrete-filled steel tubular columns with end plates after lateral impact
  72. Dynamic analysis of multilayer-reinforced concrete frame structures based on NewMark-β method
  73. Experimental study on mechanical properties and microstructures of steel fiber-reinforced fly ash-metakaolin geopolymer-recycled concrete
  74. Fractal characteristic of recycled aggregate and its influence on physical property of recycled aggregate concrete
  75. Properties of wood-based composites manufactured from densified beech wood in viscoelastic and plastic region of the force-deflection diagram (FDD)
  76. Durability of geopolymers and geopolymer concretes: A review
  77. Research progress on mechanical properties of geopolymer recycled aggregate concrete
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2021-0064/html
Scroll to top button