Abstract
Three novel three-dimensional orthorhombic carbon phases are proposed based on first-principles calculations in this work. These phases possess dynamic stability and mechanical stability and are theoretically more favorable in energy compared to most other carbon allotropes. The hardness levels of oP-C16, oP-C20, and oP-C24 are 47.5, 49.6, and 55.3 GPa, respectively, which are greater than those of T10, T18, and O12 carbon. In addition, although oP-C16, oP-C20, and oP-C24 are metals, their ideal shear strengths are also greater than those of common metals such as Cu, Fe, and Al. Due to p y electrons crossing the Fermi level, oP-C16, oP-C20, and oP-C24 show metallicity, and their charge densities of the band decomposition suggest that all the conductive directions of oP-C16, oP-C20, and oP-C24 are exhibited along the a- and b-axis, similar to C5.
Graphical abstract
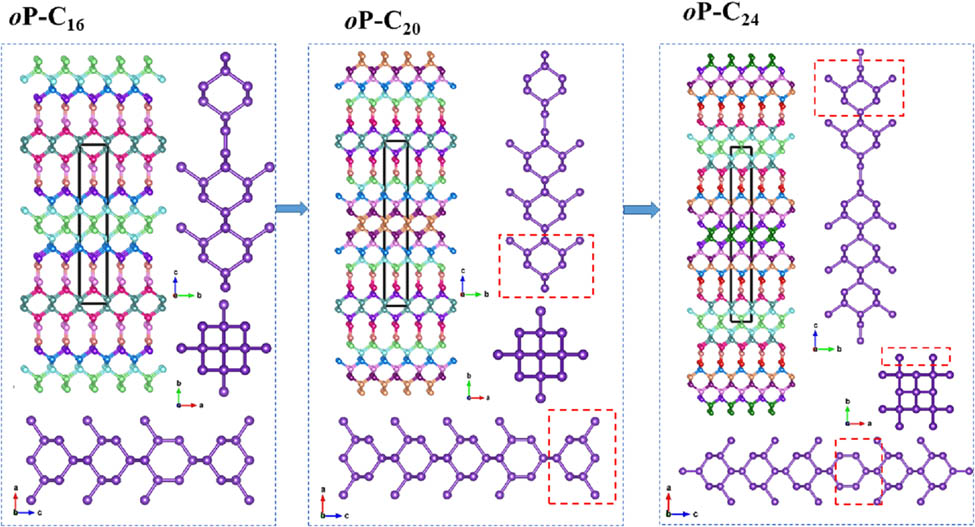
The crystal structures of oP-C16, oP-C20, and oP-C24.
1 Introduction
The rapid growth of computer performance and the abundance of various experimental data have led to the intensified exploration of new energy materials [1] and novel electronic information materials. The use of computers for scientific calculations is already the third scientific method for mankind to understand and conquer nature after theoretical science and experimental science. Due to the extensive role and important influence of metal superhard carbon materials in the fields of industry, machinery, and aerospace, there is an urgent need for metal superhard carbon materials with excellent mechanical and electronic properties. However, despite theoretical predictions that carbon allotropes emerge in an endless stream, there are not many carbon materials that simultaneously exhibit metallic and superhard properties and enjoy favorable physical properties. Obviously, there is still a long way to go in designing and discovering breakthrough carbon materials with remarkable features. In this work, three superhard metal carbon materials are theoretically predicted and the results obtained show that these three carbon phases all have superhard metal characteristics and many advantageous properties, which are of great significance for enriching the gene pool of excellent materials and providing a solid theoretical basis for future experiments. More importantly, owing to their metallic and superhard properties, oP-C16, oP-C20, and oP-C24 may possess the opportunity to play applications in industrial and electronic fields.
In recent years, a considerable number of carbon allotropes and carbon-based materials have been identified. For instance, five carbon allotropes, tP12, tP16, tP24, oP12, and oP18, with nanotubes and cage types were proposed recently [2]. There are two-dimensional (2D) TPH-I carbon and TPH-II carbon obtained from pentagraphene through Stone-Wales conversion [3]. The electronic and mechanical properties of the new superhard indirect semiconductor oP8 carbon have also been predicted [4]. Li and Xing designed a superhard semiconductor material, P2/m C 54, which is a new type of semiconductor material that can be applied to frequency-hopping absorption filters [5]. TiO2/graphite carbon nanocomposite materials, which can improve photocatalytic efficiency, are synthesized under certain temperatures and conditions [6]. In light of the synthesis of graphene with benzene as the precursor, a novel all-sp 2 hybridized 2D carbon allotrope with poly-butadiene–cyclooctatetraene framework is proposed [7]. By means of molecular dynamics simulation, the interface characteristics of carbon nanotube–polyimide nanocomposites have been systematically analyzed [8].
In particular, metallic carbon has attracted much attention due to its usefulness in electronic devices, superconductivity applications, and high-performance anode materials. By cross-linking graphene sheet with sp 3-hybridized carbon chains, Wang et al. established a new type of porous asymmetric carbon honeycomb (CHC), namely bco-C24 [9]. Using the self-assembled C8 skeleton of pentene as a building block, a series of 3D carbon allotropes (superpentalene-n family) were constructed [10]. A new type of orthogonal metal carbon phase o-C12 with high stability and hardness has been proposed, which is expected to be applied to actual electronic and mechanical equipment [11]. Zhang et al. proposed a metal superhard carbon allotrope C10, which has an sp 2 + sp 3 hybrid carbon network in the orthorhombic unit cell and has a hardness of 58.70 GPa [12]. Liu et al. proposed two carbon polymorphs Orth-C10 and Orth-C10’ with excellent superhard and conductive properties through first-principles calculations, which are more energetically stable than fullerene C60 at 0 GPa [13]. There are also paper carbon nanotubes that can replace aluminum foil as a current collector [14].
Recently, Wu et al. [15] reported a novel three-dimensional orthorhombic phase utilizing first-principles calculations. The novel three-dimensional orthorhombic phase, namely, C14-diamond, which was assembled with nanolayered sp 3 carbon in a diamond structure, was bonded with ethene-type –C═C– links and so C14-diamond is a superhard material and metallic carbon allotrope. In addition, the conductive direction of C14-diamond is also exhibited along these sp 2 carbon atoms. Additionally, Liu et al. [16] designed O-type and T-type carbon allotropes. The diamond nanostripes in O-type and T-type carbon allotropes are similar to C14-diamond and are also bonded with ethene-type –C═C– links. All the O-type and T-type carbon allotropes exhibited metallic properties, and the bulk modulus (B) and shear modulus (E) of O-type and T-type carbon allotropes exceeded 357 and 223 GPa, respectively.
In recent years, the focus of development has been to predict the properties of new materials and to design novel structures or some details in the new phases with function-oriented reverse design. However, compared with the huge demand in various fields such as modern industry, manufacturing, and aviation, carbon materials that are harder, more conductive, and lighter are still waiting for scientists to explore.
From ancient times to the present, carbon materials have been playing an increasingly important role in industrial applications, from initial heating materials to electronic materials and other functional materials. For example, supercapacitors based on carbon materials [17] have the same excellent characteristics as all-paper-based supercapacitor devices [18], such as fast charge and discharge speed, high power density, and long-term cycle stability. Complementary carbon nanotube transistors can even be used to build modern microprocessors [19]. Carbon nanomaterial-reinforced cement-based composites, which are stronger than traditional cement materials, smarter, and more durable, are also attracting attention [20]. Novel carbon materials and composite carbon materials [21] with excellent performance are closely related to modern engineering. The material gene bank is equivalent to the guiding light for the synthesis of new materials, so the theoretical importance of the exploration of new carbon structure is self-evident.
In this work, the three novel superhard metallic carbon allotropes (according to the number of carbon atoms in the conventional cell, denoted oP-C16, oP-C20, and oP-C24 below) are proposed in this work and these novel metallic carbon allotropes from the space group and graph theory (RG2) code [22]. The crystal structures of oP-C16, oP-C20, and oP-C24 are similar to C14-diamond, O-type, and T-type carbon allotropes. The process is shown in graphical abstract. It can be seen that the structures of these three carbon allotropes are related and similar, and they are all composed of six-membered rings and ten-membered rings. From the ab plane, the structure of oP-C16 is exactly identical to that of oP-C20. The difference exists in bc and ac planes, as shown in the red wireframe in graphical abstract, that is the structure of oP-C20 possesses one more six-membered ring than that of oP-C16. Interestingly, the addition of a six-membered ring to the structure of oP-C20 along the bc and ac planes converts it to the structure of oP-C24. The hardness level of oP-C24 is higher than those of C14-diamond, O12 carbon, O20 carbon, T10 carbon, T18 carbon, and T26 carbon. Additionally, the conductive directions of oP-C16, oP-C20, and oP-C24 are also investigated in this work.
2 Computational method
The crystal structures of oP-C16, oP-C20, and oP-C24 are obtained from the random sampling strategy combining space group and graph theory (RG2) [22]. For geometry optimization, ultrasoft pseudopotentials [23] are adopted in the interactions of the core electrons, and norm-conserving pseudopotentials [24] are employed for electronic band structure calculations. A generalized gradient approximation (GGA) proposed by Perdew et al. [25] and local density approximations (LDA), as developed by Ceperley and Alder and parameterized by Perdew and Zunger (CA-PZ) [26,27], is performed by utilizing the Cambridge Serial Total Energy Package [28] by means of density functional theory [29,30] calculations. The Broyden–Fletcher–Goldfarb–Shenno (BFGS) [31] minimization technique is used for geometry optimization. A plane wave basis set with an energy cut-off of 400 eV is used for oP-C16, oP-C20, and oP-C24. A high-accuracy grid spacing of lower than 2π × 0.025/Å is selected utilizing the Monkhorst–Pack scheme [32] (for oP-C16: 16 × 15 × 3, oP-C20: 16 × 16 × 2, and oP-C20: 16 × 16 × 2).
For other carbon materials (C14-diamond [15], T10 carbon, T18 carbon, T26 carbon, O12 carbon, O20 carbon, O26 carbon [16], and C14 carbon [33]) for comparison, the cutoff energy of 400 eV is also used, and the k-points of the other carbon materials (T10 carbon: 16 × 16 × 4, T18 carbon: 16 × 16 × 2, T26 carbon: 16 × 16 × 2, O12 carbon: 4 × 16 × 15, O20 carbon: 2 × 16 × 16, O26 carbon: 2 × 16 × 16, C14-diamond: 2 × 16 × 16, and C14 carbon: 16 × 4 × 11) are also used for the high-accuracy grid spacing of lower than 2π × 0.025/Å. The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional [34] is adopted to estimate the electronic properties of oP-C16, oP-C20, and oP-C24. The density functional perturbation theory [35] is employed to investigate the phonon spectra for oP-C16, oP-C20, and oP-C24. First-principles calculations are favored by many researchers in the fields of condensed matter physics and computational materials science. Regarding the study of the physical properties of metallic carbon, some references [13,15,16,33] use first-principles calculations. Thus, in this work, first-principles calculations are adopted to study the physical properties of the three proposed carbon allotropes.
3 Results and discussion
The designed constructions of oP-C16, oP-C20, and oP-C24, and their crystal structures are shown in graphical abstract. There are four sp 2 hybridization carbon atoms in all three structures, that is, there are two –C═C– bonds in the oP-C16, oP-C20, and oP-C24 crystal structures. The oP-C16, oP-C20, and oP-C24 carbon phases are established by the sp 2 + sp 3 hybrid bonding network in a three-dimensional formation. These three structures also contain different numbers of inequivalent atomic positions. oP-C16 has eight different inequivalent atomic positions, oP-C20 has ten different inequivalent atomic positions, and oP-C24 has twelve different inequivalent atomic positions. The optimal lattice parameters of oP-C16, oP-C20, and oP-C24 are presented in Table 1. Furthermore, the theoretical and experimental values of the lattice parameters for diamond are displayed in Table 1 for comparison. The estimated results obtained by using the GGA method are closer to the experimental values than those obtained by using LDA. Thus, all theoretical calculations in our article are performed at the GGA level.
Obtained lattice constants (Å), cell volume/atom V (Å3), and density (g/cm3) for oP-C16, oP-C20, oP-C24, c-BN, and diamond
| Materials | Method | a | b | c | V | ρ |
|---|---|---|---|---|---|---|
| oP-C16 | GGA | 2.515 | 2.597 | 14.901 | 6.085 | 3.278 |
| LDA | 2.488 | 2.563 | 14.742 | 5.877 | 3.394 | |
| oP-C20 | GGA | 2.517 | 2.580 | 18.464 | 5.994 | 3.327 |
| LDA | 2.489 | 2.547 | 18.265 | 5.791 | 3.444 | |
| oP-C24 | GGA | 2.518 | 2.569 | 22.028 | 5.936 | 3.360 |
| LDA | 2.490 | 2.537 | 21.789 | 5.736 | 3.477 | |
| c-BN | GGA | 3.623 | 5.945 | 3.466 | ||
| LDA | 3.577 | 5.721 | 3.602 | |||
| Exp.a | 3.620 | 5.930 | 3.475 | |||
| Diamond | GGA | 3.566 | 5.668 | 3.519 | ||
| LDA | 3.527 | 5.484 | 3.637 | |||
| Exp.b | 3.567 | 5.673 | 3.516 |
The dynamic stability for oP-C16, oP-C20, and oP-C24 can be checked using phonon spectra. The phonon spectra of oP-C16, oP-C20, and oP-C24 are shown in Figure 1(a–c). As described in ref. [15], the phonon modes greater than 40 THz chiefly originate from the vibration of sp 2 hybridization connected with the –C═C– bond, and the vibration frequency of sp 3 hybridization carbon atoms is mainly below 40 THz. In addition, most importantly, no hypothetical frequency is found in the whole Brillouin zone, demonstrating that the three predicted carbon allotropes are dynamically stable. Figure 1(d) shows the enthalpy per atom of oP-C16, oP-C20, and oP-C24, including C14-diamond [15], T26 carbon, T10 carbon, T18 carbon, O18 carbon, O12 carbon, and O20 carbon [16] in the sp 2 + sp 3 bonding network and C14 carbon [33] in all sp 3 bonding networks compared with other carbon phases reported theoretically. As shown in Figure 1(d), oP-C24 is more stable than T10 carbon, T18 carbon, O12 carbon, O20 carbon, and C14 carbon in thermodynamics; oP-C20 is thermodynamically more stable than those of T10, O12, O20, and C14 carbon; and oP-C16 is thermodynamically more stable than those of T10 carbon and O12 carbon.
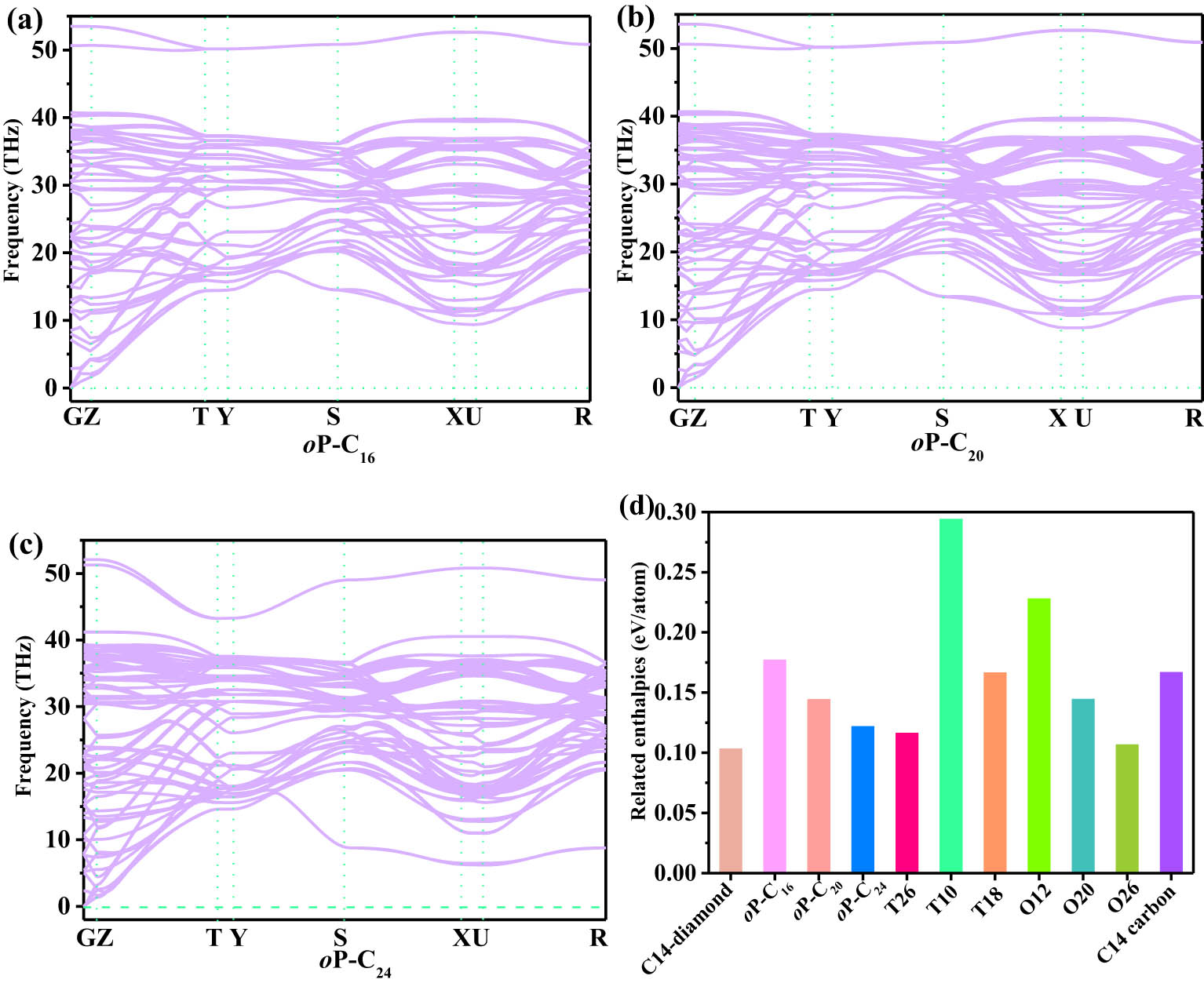
Phonon spectra of oP-C16 (a), oP-C20 (b), and oP-C24 (c), and the related enthalpies of other metallic carbon allotropes (d).
For the structure of a stable orthorhombic crystal system, the elastic constants C
ij
should meet the mechanical elasticity criteria [36]: C
11 > 0, C
11
C
22 >
The elastic constants (GPa), elastic modulus (GPa), and hardness (GPa) of metallic carbon allotropes, c-BN, and diamond
| Materials | Method | C 11 | C 22 | C 33 | C 44 | C 55 | C 66 | C 12 | C 13 | C 23 | B | G | E | H Chen | H M-O | H L-O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| oP-C16 | GGA | 1,138 | 848 | 1,092 | 132 | 540 | 269 | 19 | 136 | 62 | 385 | 333 | 775 | 47.5 | 52.5 | 71.8 |
| LDA | 1,206 | 912 | 1,151 | 103 | 568 | 273 | 20 | 156 | 76 | 414 | 325 | 773 | 41.4 | |||
| oP-C20 | GGA | 1,141 | 908 | 1,087 | 136 | 545 | 307 | 20 | 131 | 73 | 395 | 347 | 805 | 49.6 | 55.6 | 69.3 |
| LDA | 1,210 | 974 | 1,140 | 113 | 574 | 312 | 21 | 152 | 88 | 424 | 343 | 810 | 44.5 | |||
| oP-C24 | GGA | 1,143 | 948 | 1,083 | 170 | 548 | 332 | 21 | 130 | 80 | 402 | 372 | 853 | 55.3 | 63.2 | 66.7 |
| LDA | 1,212 | 1,014 | 1,139 | 155 | 578 | 339 | 22 | 150 | 96 | 431 | 377 | 876 | 52.0 | |||
| Diamond | GGA | 1,053 | 563 | 120 | 431 | 522 | 1,116 | 94.3 | ||||||||
| LDA | 1,104 | 598 | 140 | 461 | 549 | 1,179 | 95.3 | |||||||||
| Exp.a | 1,076 | 577 | 125 | 442 |
aRef. [47].
Using Chen’s model [38] to estimate hardness, the related results of their carbon materials within the GGA level are also shown in Table 2. From Table 2, the hardness values of oP-C16, oP-C20, and oP-C24 are estimated to be 47.5, 49.6, and 55.3 GPa, respectively. The hardness value of C14-diamond determined in the same way is 53.1 GPa, which is close to the previously reported hardness value (55.8 GPa [15]). In this work, the hardness values of oP-C16, oP-C20, and oP-C24 are greater than those of O12 carbon (39.9 GPa), T10 carbon (25.6 GPa), T18 carbon (34.8 GPa), and T26 carbon (43.8 GPa). Furthermore, the hardness value of oP-C20 is also higher than that of O20 carbon (48.8 GPa), and the hardness value of oP-C24 is also higher than those of C14-diamond and O28 carbon (54.3 GPa). In order to verify the superhardness of the three proposed carbon allotropes, H M-O [39] and H L-O model [40] are employed. Here, H M-O can be obtained based on Poisson’s ratio and Young’s modulus using the following equation [39]: H M-O = 0.096 E (1–8.5v + 19.5v 2)(1–7.5v + 12.2v 2 + 19.6v 3)−1. The calculated hardness levels of oP-C16, oP-C20, and oP-C24 are 52–64 and 66–72 GPa, respectively, which are all greater than 40 GPa. All these three methods prove the fact that oP-C16, oP-C20, and oP-C24 have superhard characteristics.
To have a better understanding of the potential application of these carbons structures with superhard and metal properties, the stress–strain curves of the three carbon phases proposed by us under the tensile and shear strains in the low-index directions are calculated. The shear strength and tensile strength of oP-C16, oP-C20, and oP-C24 as functions of shear strain and tensile strain within the GGA functional are plotted in Figure 2. The turning point on the stress–strain curve indicates the ideal tensile strength or the ideal shear strength. The ideal shear strengths along the different shear directions of oP-C16/oP-C20/oP-C24 are listed in Table 3. For oP-C16/oP-C20/oP-C24, the peak shear stresses are 12.0/12.5/11.5, 12.2/12.6/11.6, 16.6/17.2/16.2, 17.0/17.9/16.1, and 17.5/18.1/16.2 GPa along the (010)[001], (010)[101], (110)[001], (110)[1–11], and (111)[1–10] directions, respectively. The possible cause is also the fracture of sp 2 –C═C– bonds, similar to C14-diamond, O12 carbon, O20 carbon, O28 carbon, T10 carbon, T18 carbon, and T26 carbon. As discussed in Reference [16], although the three proposed carbon allotropes in this work are metals, their ideal shear strengths are also greater than those of common metals such as Cu (4.0 GPa) [41], Al (3.4 GPa) [41], and Fe (6.40 GPa) [42]. In addition, the three kinds of carbon allotropes proposed by us can only break when the shear strain along these directions is above 0.07, while T18 carbon and T26 carbon break when the shear strain is 0.06 and 0.04, respectively. The minimum peak shear stresses along the (001)[100], (010)[100], (100)[010], (110)[1–10], and (111) [1–12] directions of oP-C16/oP-C20/oP-C24 are 94.4 GPa, which is slightly larger than that of O28 carbon along the (100)[010] direction.
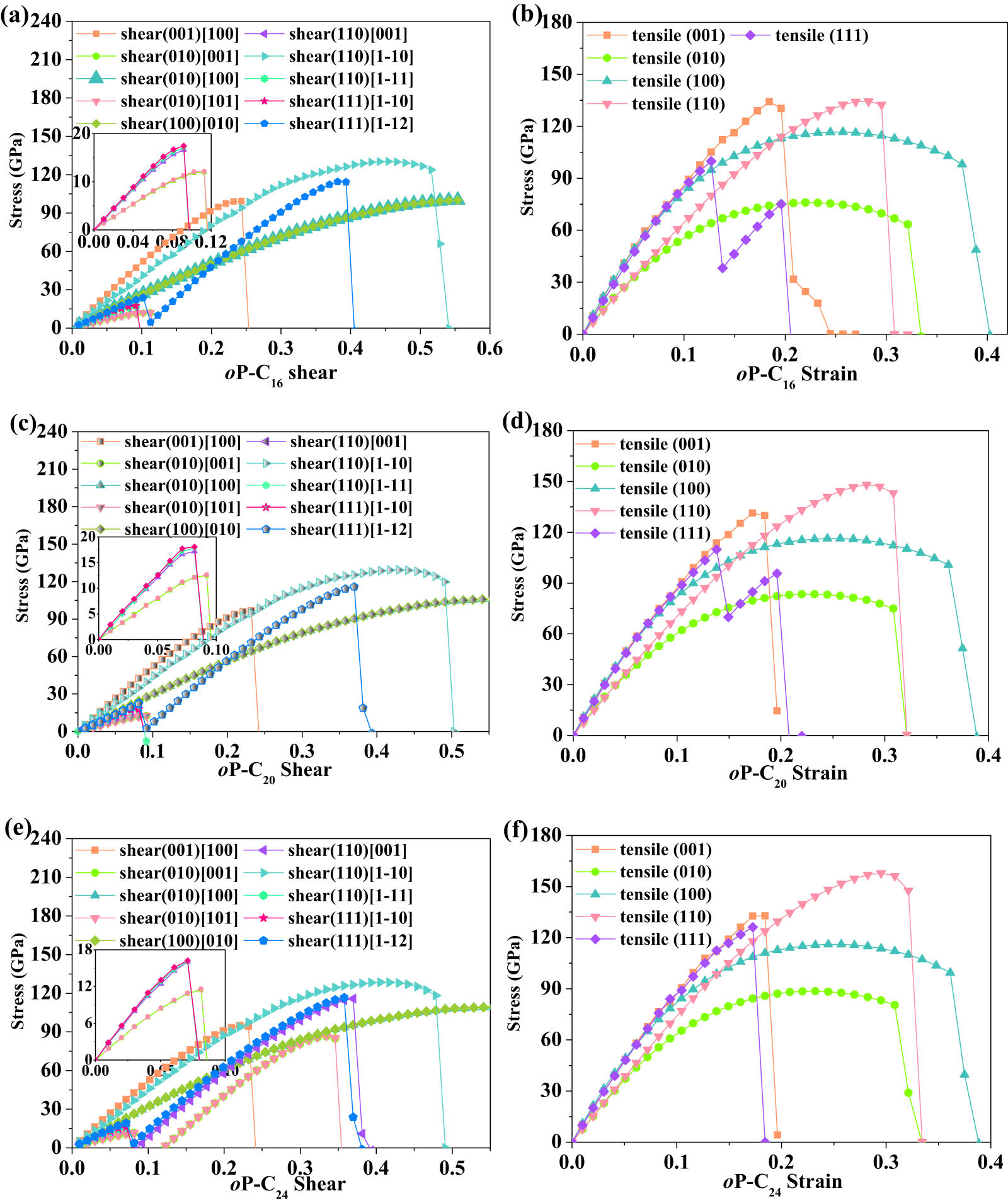
Calculated stress vs shear strain and the stress versus tensile strain for oP-C16 (a and b), oP-C20 (c and d), and oP-C24 (e and f) in principal symmetry directions.
Obtained ideal shear strengths for oP-C16, oP-C20, and oP-C24 with the corresponding strains that produce the maximum stress (GPa)
| (001)[100] | (010)[001] | (010)[100] | (010)[101] | (100)[010] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | |
| oP-C16 | 0.2431 | 99.2 | 0.1128 | 12.0 | 0.5537 | 100.2 | 0.1128 | 12.2 | 0.5537 | 100.2 |
| oP-C20 | 0.2319 | 96.6 | 0.0918 | 12.5 | 0.5410 | 105.9 | 0.0918 | 12.6 | 0.5537 | 105.9 |
| oP-C24 | 0.2319 | 94.4 | 0.0814 | 11.5 | 0.5537 | 109.4 | 0.0814 | 11.6 | 0.5537 | 109.4 |
| (110)[001] | (110)[1–10] | (110)[1–11] | (111)[1–10] | (111)[1–12] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | |
| oP-C16 | 0.0918 | 16.6 | 0.4538 | 130.3 | 0.0918 | 17.0 | 0.0918 | 17.5 | 0.3815 | 114.4 |
| oP-C20 | 0.0814 | 17.2 | 0.4294 | 129.3 | 0.0814 | 17.9 | 0.0814 | 18.1 | 0.3696 | 115.8 |
| oP-C24 | 0.0711 | 16.2 | 0.4053 | 128.5 | 0.0711 | 16.1 | 0.0711 | 16.2 | 0.3578 | 116.5 |
The tensile strengths of oP-C16, oP-C20, and oP-C24 as functions of tensile strain within the GGA functional are displayed in Figure 2(b), (d), and (e), respectively. The ideal tensile strengths along the different tensile directions of oP-C16/oP-C20/oP-C24 are presented in Table 4. From Figure 2(b), (d), and (e), it can be seen that the tensile stress–strain curve of oP-C16/oP-C20/oP-C24 shows a plastic deformation relationship along the [010] and [100] directions, a relationship similar to that of O20 carbon. For the [001], [100], [110], and [111] directions, the ideal tensile strength is basically greater than 100 GPa, and the maximum is 157.9 GPa, which is the [110] direction of oP-C24. Although for the [010] direction, the ideal tension strengths of oP-C16, oP-C20, and oP-C24 are the worst, reaching 75.9, 83.4, and 88.6 GPa, respectively. For the [111] direction, the ideal tensile strengths of oP-C16, oP-C20, and oP-C24 are 99.8, 109.8, and 126.2 GPa, respectively. The smallest ideal tension strength of the three carbon materials along the [111] direction is nearly 18 GPa greater than that of diamond, 30 GPa greater than that of O28 carbon, and 60 GPa larger than that of T10 carbon. The high values of B modulus, hardness, and ideal strength provide these new materials broad application prospects in wear-resistant metal coatings and cutting tools.
Calculated ideal tensile strengths for oP-C16, oP-C20, oP-C24 with the corresponding strains that produce the maximum stress (GPa)
| [001] | [010] | [100] | [110] | [111] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | Strain | Stress | |
| oP-C16 | 0.1843 | 134.2 | 0.2202 | 75.9 | 0.2572 | 116.6 | 0.2824 | 134.4 | 0.1268 | 99.8 |
| oP-C20 | 0.1726 | 131.4 | 0.2202 | 83.4 | 0.2447 | 116.3 | 0.2821 | 148.1 | 0.1381 | 109.8 |
| oP-C24 | 0.1726 | 132.7 | 0.2324 | 88.6 | 0.2447 | 116.1 | 0.2953 | 157.9 | 0.1726 | 126.2 |
To analyze the electronic band structures of oP-C16, oP-C20, and oP-C24, the projected weights of each kind of orbital of oP-C16, oP-C20, and oP-C24 using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional are plotted in Figure 3. By showing the weights of the electrons in different orbits, it is found that the conduction band minimum between the S and X points and the valence band maximum at the Γ point both cross the Fermi surface. Similar to T10 carbon, T18 carbon, T26 carbon, O12 carbon, O20 carbon, O20 carbon, and C14-diamond, oP-C16, oP-C20, and oP-C24 all have metallic properties. In addition, the Fermi level is chiefly provided by the p y electrons. In the Brillouin zone, the coordinates for oP-C16, oP-C20, and oP-C24 are taken Γ (0.0, 0.0, 0.0), Z (0.0, 0.0, 0.5), T (−0.5, 0.0, 0.5), Y (−0.5, 0.0, 0.0), S (−0.5, 0.5, 0.0), X (0.0, 0.5, 0.0), U (0.0, 0.5, 0.5), and R (−0.5, 0.5, 0.5) of the high symmetry points. To visualize the chemical bonding in oP-C16, oP-C20, and oP-C24, the electron localization function (ELF) [43,44] using an isosurface value of 0.75 is demonstrated in Figure 4(a–c). The calculated ELF of oP-C16, oP-C20, and oP-C24 further indicates the strong covalent C–C bonding feature; at the same time, it can be clearly seen that the σ bond is formed by the sp 2 hybrid carbon atom. To further analyze in which direction the three metal carbon materials conduct electricity, the charge density of the band decomposition observed along the a-axis and b-axis of oP-C16, oP-C20, and oP-C24 are shown in Figure 5(a–f), which suggests that the conductive directions of oP-C16, oP-C20, and oP-C24 are all exhibited along the a- and b-axis.
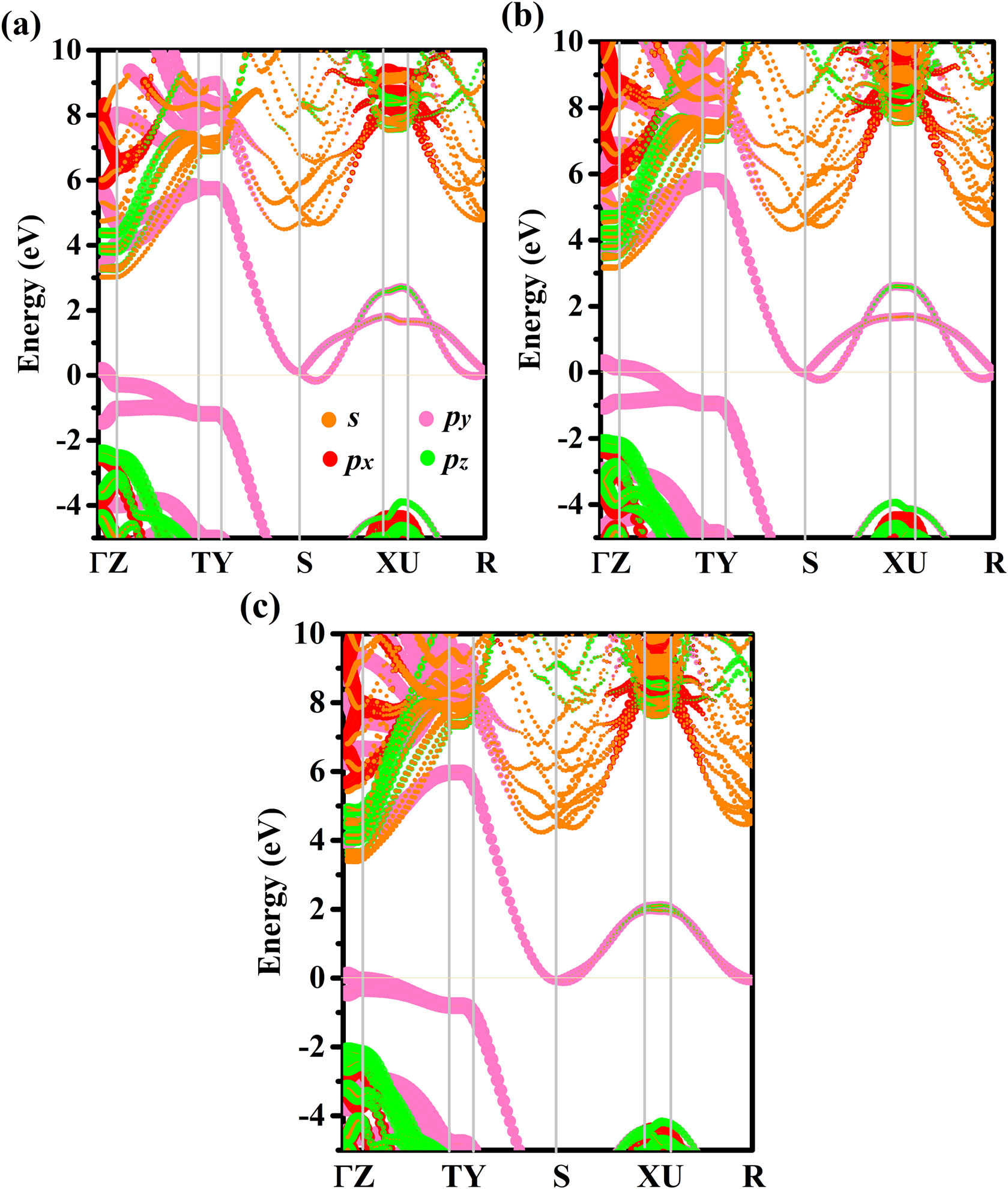
Band structures of oP-C16 (a), oP-C20 (b), and oP-C24 (c).
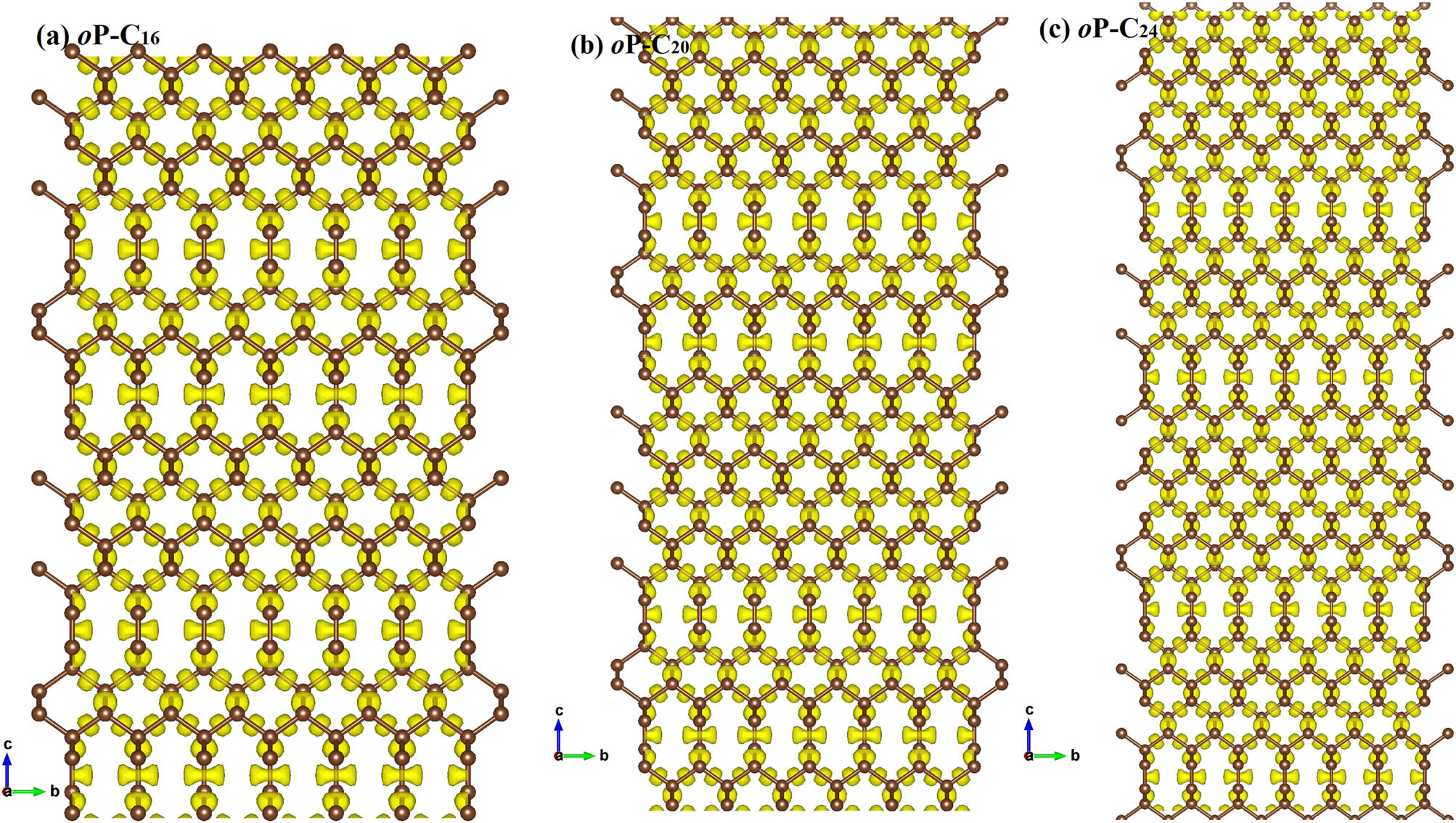
The electron localization function (ELF) of oP-C16 (a), oP-C20 (b), and oP-C24 (c) with an isosurface level set to 0.75.
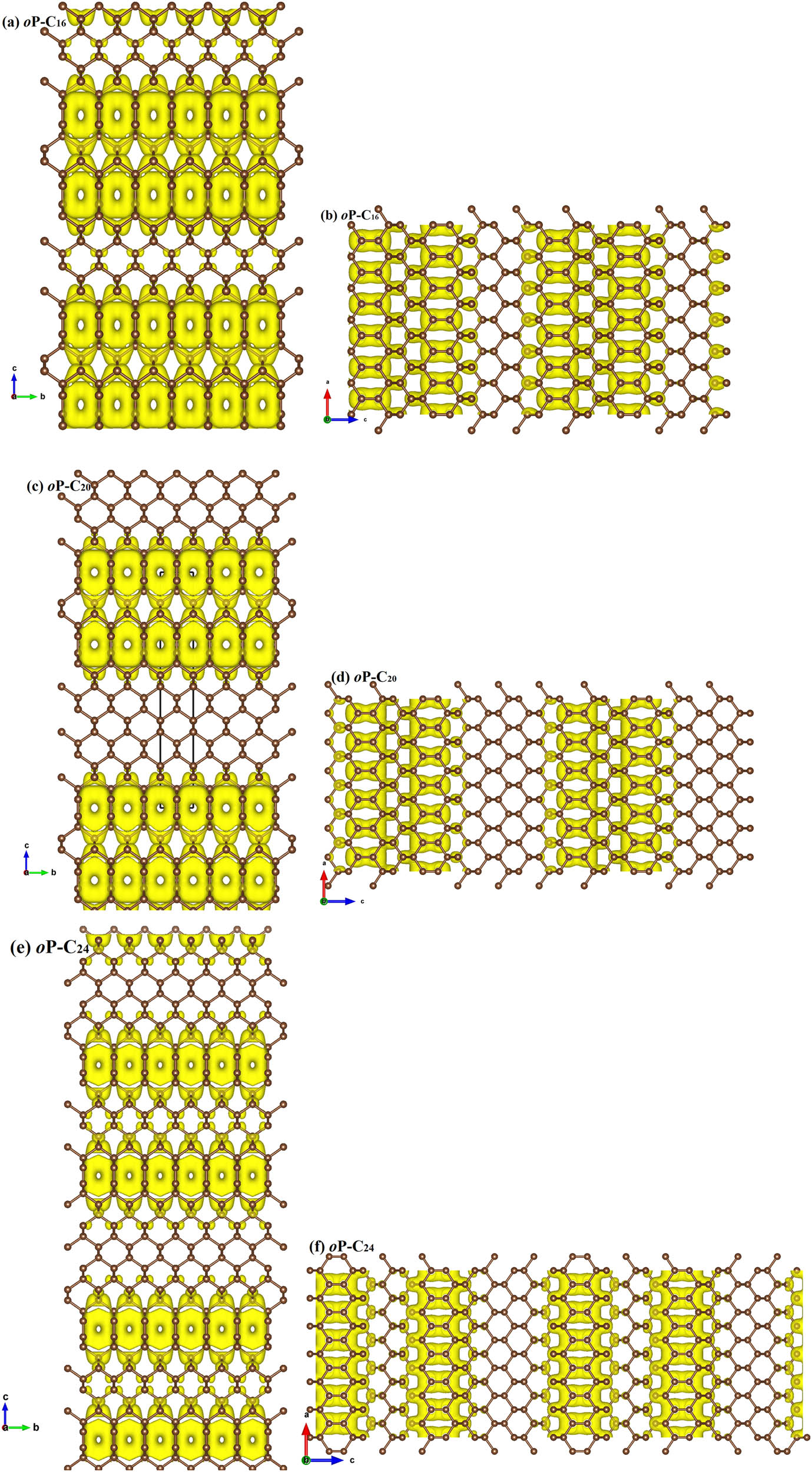
The calculated band decomposed charge density in the energy range of E F – 1 ∼ E F + 1 eV for oP-C16 (a and b), oP-C20 (c and d), and oP-C24 (e and f) along the a and b axes with an isovalue level set to 0.005.
To achieve additional information for probable future experimental examination, the simulation of x-ray diffraction (XRD) patterns for oP-C16, oP-C20, and oP-C24 along with that of diamond are shown in Figure 6. Diamond possesses two diffraction peaks, which appear at 43.93 and 75.29° of (111) and (220), respectively, and in the present work, they are in good agreement with the experimental XRD spectra of 43.9 and 75.2° for (111) and (220) of diamond [45], indicating that the performed simulation method is reliable. Because of the same space groups of oP-C16, oP-C20, and oP-C24, their XRD spectra are also very close, which is reflected in the fact that all their three strong peaks appear between 35° and 48°. The peak intensities in the XRD patterns of oP-C16, oP-C20, and oP-C24 are not equivalent. The strongest peaks are (104), (105), and (106), which are located around 43.97, 43.48, and 43.55° for oP-C16, oP-C20, and oP-C24, respectively. For oP-C16 and oP-C20, their stronger peaks both contain the two peaks (013) and (105), while the stronger peaks of oP-C24 are (015), (106), and (017). Apart from these major diffraction peaks, several other weak diffraction peaks appeared in the XRD spectrum, such as, for (101) peaks, the diffraction angles are 36.19, 35.99, and 35.87° for oP-C16, oP-C20, and oP-C24, respectively; for (111) peaks, the diffraction angles are 50.86, 50.89, and 50.91° for oP-C16, oP-C20, and oP-C24, respectively. These XRD features have important significance and guidance for identifying the structures of oP-C16, oP-C20, and oP-C24 in future experiments.
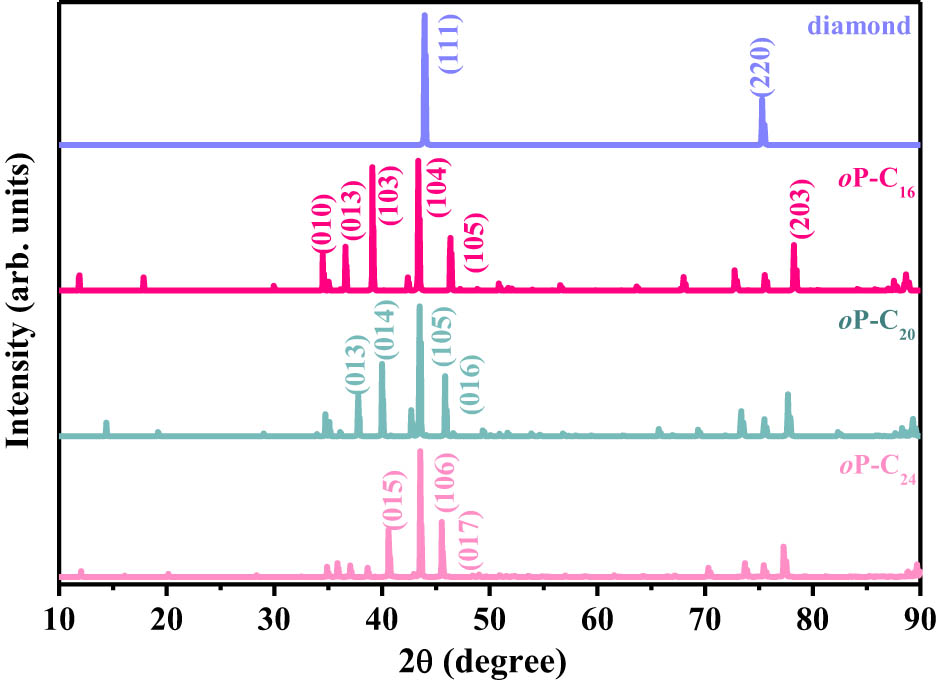
Simulated XRD patterns of oP-C16, oP-C20, oP-C24, and diamond, using an x-ray wavelength (1.5406 Å) with a copper source for simulation in this work.
4 Conclusion
In summary, three new carbon allotropes, oP-C16, oP-C20, and oP-C24, with metallic and superhard properties are proposed theoretically through first-principles calculations. These three new types of carbon structures possess many outstanding characteristics. oP-C16 is energetically more favorable than T10 and O12 carbon, while oP-C20 and oP-C24 are more favorable in energy than T18, O12, and O20 carbon. More importantly, oP-C16, oP-C20, and oP-C24 enjoy hardness levels of 47.5, 49.6, and 55.3 GPa, respectively. For oP-C16/oP-C20/oP-C24, the peak shear stresses are 11.5–18.1 GPa along the (010)[001], (010)[101], (110)[001], (110)[1–11], and (111)[1–10] directions, respectively. Although the three carbon allotropes proposed in this work are metals, their ideal shear strengths are also greater than those of common metals such as Cu, Fe, and Al. The p y electrons cross the Fermi level, revealing that oP-C16, oP-C20, and oP-C24 exhibit metallicity. Superhard, conductive, and other excellent physical properties make oP-C16, oP-C20, and oP-C24 have great application potential in multifunctional devices under extreme conditions, and they are also potential materials for electronic devices and mechanical tools. The theoretical research in this article is of great significance for enriching the gene pool of excellent materials and providing a solid theoretical basis for future experiments.
-
Funding information: This work was supported by the National Natural Science Foundation of China (Nos. 61804120, 61803294, and 61901162); the China Postdoctoral Science Foundation (Nos. 2019TQ0243 and 2019M663646); key scientific research plan of Education Department of Shaanxi Provincial Government (Key Laboratory Project) (No. 20JS066); the Young Talent fund of University Association for Science and Technology in Shaanxi, China (No. 20190110); and the National Key R&D Program of China (No. 2018YFB1502902); and Key Program for International S&T Cooperation Projects of Shaanxi Province (No. 2019KWZ-03).
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors state no conflict of interest.
References
[1] Takeo O. Crystal structures of perovskite halide compounds used for solar cells. Rev Adv Mater Sci. 2020;59(1):264–305.10.1515/rams-2020-0015Search in Google Scholar
[2] Fan Q, Wang H, Song Y, Zhang W, Yun S. Five carbon allotropes from Squaroglitter structures. Comput Mater Sci. 2020;178:109634.10.1016/j.commatsci.2020.109634Search in Google Scholar
[3] Zhang W, Chai C, Fan Q, Song Y, Yang Y. Two-dimensional carbon allotropes with tunable direct band gaps and high carrier mobility. Appl Surf Sci. 2021;537:147885.10.1016/j.apsusc.2020.147885Search in Google Scholar
[4] Fan Q, Li C, Yang R, Yu X, Zhang W, Yun S. Stability, mechanical, anisotropic and electronic properties of oP8 carbon: a superhard carbon allotrope in orthorhombic phase. J Solid State Chem. 2021;294:121894.10.1016/j.jssc.2020.121894Search in Google Scholar
[5] Li XZ, Xing MJ. Prediction of a novel carbon allotrope from first-principle calculations: a potential superhard material in monoclinic symmetry. Mater Chem Phys. 2020;242:122480.10.1016/j.matchemphys.2019.122480Search in Google Scholar
[6] Janusz T, Niko G, Grzegorz Z, Malwina P, Aleksander G, Ewelina KN, et al. Magnetic properties of TiO2/graphitic carbon nanocomposites. Rev Adv Mater Sci. 2019;58(1):107–22.10.1515/rams-2019-0009Search in Google Scholar
[7] Zhang W, Chai C, Fan Q, Song Y, Yang Y. PBCF-graphene: a 2D Sp2 hybridized honeycomb carbon allotrope with a direct band gap. ChemNanoMat. 2020;6:139–47.10.1002/cnma.201900645Search in Google Scholar
[8] Jiang Q, Tallury SS, Qiu Y, Pasquinelli MA. Interfacial characteristics of a carbon nanotube-polyimide nanocomposite by molecular dynamics simulation. Nanotechnol Rev. 2020;9(1):136–45.10.1515/ntrev-2020-0012Search in Google Scholar
[9] Wang S, Yang B, Ruckenstein E, Chen H. Bco-C24: a new 3D Dirac nodal line semi-metallic carbon honeycomb for high performance metal-ion battery anodes. Carbon. 2020;159:542–8.10.1016/j.carbon.2019.12.069Search in Google Scholar
[10] Zhang W, Chai C, Fan Q, Song Y, Yang Y. Metallic and semiconducting carbon allotropes comprising of pentalene skeletons. Diam Relat Mater. 2020;109:108063.10.1016/j.diamond.2020.108063Search in Google Scholar
[11] Zhou Y, Liu Z, Gan LH. o-C12: a novel orthorhombic metallic superhard carbon phase. Solid State Sci. 2021;119:106607.10.1016/j.solidstatesciences.2021.106607Search in Google Scholar
[12] Zhang W, Chai C, Fan Q, Song Y, Yang Y. Superhard three-dimensional carbon with one-dimensional conducting channels. New J Chem. 2020;44(45):19789–95.10.1039/D0NJ04104ASearch in Google Scholar
[13] Liu L, Hu M, Zhao Z, Pan Y, Dong H. Superhard conductive orthorhombic carbon polymorphs. Carbon. 2020;158:546–52.10.1016/j.carbon.2019.11.024Search in Google Scholar
[14] Ventrapragada LK, Creager SE, Rao AM, Podila R. Carbon nanotubes coated paper as current collectors for secondary Li-ion batteries. Nanotechnol Rev. 2019;8(1):18–23.10.1515/ntrev-2019-0002Search in Google Scholar
[15] Wu X, Shi X, Yao M, Liu S, Yang X, Zhu L, et al. Superhard three-dimensional carbon with metallic conductivity. Carbon. 2017;123:311–7.10.1016/j.carbon.2017.07.034Search in Google Scholar
[16] Liu Y, Jiang X, Fu J, Zhao J. New metallic carbon: Three dimensionally carbon allotropes comprising ultrathin diamond nanostripes. Carbon. 2018;126:601–10.10.1016/j.carbon.2017.10.066Search in Google Scholar
[17] Jiang Q, Tallury SS, Qiu Y, Pasquinelli MA. Recent development of supercapacitor electrode based on carbon materials. Nanotechnol Rev. 2019;8(1):35–49.10.1515/ntrev-2019-0004Search in Google Scholar
[18] Xiong C, Li M, Han Q, Zhao W, Dai L, Ni Y. Screen printing fabricating patterned and customized full paper-based energy storage devices with excellent photothermal, self-healing, high energy density and good electromagnetic shielding performances. J Mater Sci Technol. 2022;97:190–200.10.1016/j.jmst.2021.04.054Search in Google Scholar
[19] Hills G, Lau C, Wright A, Fuller S, Bishop MD, Srimani T, et al. Modern microprocessor built from complementary carbon nanotube transistors. Nature. 2019;572(7771):595–602.10.1038/s41586-019-1493-8Search in Google Scholar PubMed
[20] Du M, Jing H, Gao Y, Su H, Fang H. Carbon nanomaterials enhanced cement-based composites: advances and challenges. Nanotechnol Rev. 2020;9(1):115–35.10.1515/ntrev-2020-0011Search in Google Scholar
[21] Xiong C, Li B, Duan C, Dai L, Nie S, Qin C, et al. Supercapacitor, strain sensing and moisture-electric generation applications. Chem Eng J. 2021;418:129518.10.1016/j.cej.2021.129518Search in Google Scholar
[22] Shi X, He C, Pickard CJ, Tang C, Zhong J. Stochastic generation of complex crystal structures combining group and graph theory with application to carbon. Phys Rev B. 2018;97(1):014104.10.1103/PhysRevB.97.014104Search in Google Scholar
[23] Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys Rev B. 1990;41(11):7892–5.10.1103/PhysRevB.41.7892Search in Google Scholar PubMed
[24] Hamann DR, Schluter M, Chiang C. Norm-conserving pseudopotentials. Phys Rev Lett. 1979;43(20):1494–7.10.1103/PhysRevLett.43.1494Search in Google Scholar
[25] Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;78(7):1396.10.1103/PhysRevLett.77.3865Search in Google Scholar PubMed
[26] Ceperley DM, Alder BJ. Ground state of the electron gas by a stochastic method. Phys Rev Lett. 1980;45(7):566.10.2172/5208790Search in Google Scholar
[27] Perdew JP, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B. 1981;23(10):5048–79.10.1103/PhysRevB.23.5048Search in Google Scholar
[28] Clark SJ, Segall MD, Pickard CJ, Hasnip PJ, Probert MIJ, Refson K, et al. First principles methods using CASTEP. Z Kristallogr. 2005;220:567–70.10.1524/zkri.220.5.567.65075Search in Google Scholar
[29] Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. 1964;136(3):B864.10.1103/PhysRev.136.B864Search in Google Scholar
[30] Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965;140(4A):A1133.10.1103/PhysRev.140.A1133Search in Google Scholar
[31] Pfrommer BG, Côté M, Louie SG, Cohen ML. Relaxation of crystals with the quasi-Newton method. J Comput Phys. 1997;131(1):233–40.10.1006/jcph.1996.5612Search in Google Scholar
[32] Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys Rev B. 1976;13(12):5188.10.1103/PhysRevB.13.5188Search in Google Scholar
[33] Yang X, Lv C, Liu S, Zang J, Qin J, Du M, et al. Orthorhombic C14 carbon: a novel superhard sp3 carbon allotrope. Carbon. 2020;156:309–12.10.1016/j.carbon.2019.09.049Search in Google Scholar
[34] Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened coulomb potential. J Chem Phys. 2003;118(18):8207–15.10.1063/1.1564060Search in Google Scholar
[35] Baroni S, de Gironcoli S, dal Corso A, Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev Mod Phys. 2001;73(2):515.10.1103/RevModPhys.73.515Search in Google Scholar
[36] Mouhat F, Coudert FX. Necessary and sufficient elastic stability conditions in various crystal systems. Phys Rev B. 2014;90(22):224104.10.1103/PhysRevB.90.224104Search in Google Scholar
[37] Wu ZJ, Zhao EJ, Xiang HP, Hao XF, Liu XJ, Meng J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys Rev B. 2007;76(5):054115.10.1103/PhysRevB.76.054115Search in Google Scholar
[38] Chen XQ, Niu H, Li D, Li Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics. 2011;19(9):1275–81.10.1016/j.intermet.2011.03.026Search in Google Scholar
[39] Mazhnik E, Oganov AR. A model of hardness and fracture toughness of solids. J Appl Phys. 2019;126(12):125109.10.1063/1.5113622Search in Google Scholar
[40] Lyakhov AO, Oganov AR. Evolutionary search for superhard materials: methodology and applications to forms of carbon and TiO2. Phys Rev B. 2019;84(9):92103.10.1103/PhysRevB.84.092103Search in Google Scholar
[41] Roundy D, Krenn CR, Cohen ML, Morris JW. Ideal shear strengths of fcc aluminum and copper. Phys Rev Lett. 1999;82(13):2713–6.10.1103/PhysRevLett.82.2713Search in Google Scholar
[42] Krenn CR, Roundy D, Morris JW, Cohen ML. Ideal strengths of bcc metals. Mater Sci Eng A. 2001;319:111–4.10.1016/S0921-5093(01)00998-4Search in Google Scholar
[43] Silvi B, Savin A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature. 1994;371(6499):683–6.10.1038/371683a0Search in Google Scholar
[44] Becke AD, Edgecombe KE. A simple measure of electron localization in atomic and molecular systems. J Chem Phys. 1990;92:5397–403.10.1063/1.458517Search in Google Scholar
[45] Mao WL, Mao HK, Eng P, Trainor T. Bonding changes in compressed superhard graphite. Science. 2003;302(5644):425–7.10.1126/science.1089713Search in Google Scholar PubMed
[46] Petrescu ML. Boron nitride theoretical hardness compared to carbon polymorphs. Diam Relat Mater. 2004;13(10):1848–53.10.1016/j.diamond.2004.05.004Search in Google Scholar
[47] Grimsditch M, Zouboulis ES, Polian A. Elastic constants of boron nitride. J Appl Phys. 1994;76:832.10.1063/1.357757Search in Google Scholar
© 2021 Qingyang Fan et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Improved impedance matching by multi-componential metal-hybridized rGO toward high performance of microwave absorption
- Pure-silk fibroin hydrogel with stable aligned micropattern toward peripheral nerve regeneration
- Effective ion pathways and 3D conductive carbon networks in bentonite host enable stable and high-rate lithium–sulfur batteries
- Fabrication and characterization of 3D-printed gellan gum/starch composite scaffold for Schwann cells growth
- Synergistic strengthening mechanism of copper matrix composite reinforced with nano-Al2O3 particles and micro-SiC whiskers
- Deformation mechanisms and plasticity of ultrafine-grained Al under complex stress state revealed by digital image correlation technique
- On the deformation-induced grain rotations in gradient nano-grained copper based on molecular dynamics simulations
- Removal of sulfate from aqueous solution using Mg–Al nano-layered double hydroxides synthesized under different dual solvent systems
- Microwave-assisted sol–gel synthesis of TiO2-mixed metal oxide nanocatalyst for degradation of organic pollutant
- Electrophoretic deposition of graphene on basalt fiber for composite applications
- Polyphenylene sulfide-coated wrench composites by nanopinning effect
- Thermal conductivity and thermoelectric properties in 3D macroscopic pure carbon nanotube materials
- An effective thermal conductivity and thermomechanical homogenization scheme for a multiscale Nb3Sn filaments
- Friction stir spot welding of AA5052 with additional carbon fiber-reinforced polymer composite interlayer
- Improvement of long-term cycling performance of high-nickel cathode materials by ZnO coating
- Quantum effects of gas flow in nanochannels
- An approach to effectively improve the interfacial bonding of nano-perfused composites by in situ growth of CNTs
- Effects of nano-modified polymer cement-based materials on the bending behavior of repaired concrete beams
- Effects of the combined usage of nanomaterials and steel fibres on the workability, compressive strength, and microstructure of ultra-high performance concrete
- One-pot solvothermal synthesis and characterization of highly stable nickel nanoparticles
- Comparative study on mechanisms for improving mechanical properties and microstructure of cement paste modified by different types of nanomaterials
- Effect of in situ graphene-doped nano-CeO2 on microstructure and electrical contact properties of Cu30Cr10W contacts
- The experimental study of CFRP interlayer of dissimilar joint AA7075-T651/Ti-6Al-4V alloys by friction stir spot welding on mechanical and microstructural properties
- Vibration analysis of a sandwich cylindrical shell in hygrothermal environment
- Water barrier and mechanical properties of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch (TPS)/poly(lactic acid) (PLA) blend bionanocomposites
- Strong quadratic acousto-optic coupling in 1D multilayer phoxonic crystal cavity
- Three-dimensional shape analysis of peripapillary retinal pigment epithelium-basement membrane layer based on OCT radial images
- Solvent regulation synthesis of single-component white emission carbon quantum dots for white light-emitting diodes
- Xanthate-modified nanoTiO2 as a novel vulcanization accelerator enhancing mechanical and antibacterial properties of natural rubber
- Effect of steel fiber on impact resistance and durability of concrete containing nano-SiO2
- Ultrasound-enhanced biosynthesis of uniform ZnO nanorice using Swietenia macrophylla seed extract and its in vitro anticancer activity
- Temperature dependence of hardness prediction for high-temperature structural ceramics and their composites
- Study on the frequency of acoustic emission signal during crystal growth of salicylic acid
- Controllable modification of helical carbon nanotubes for high-performance microwave absorption
- Role of dry ozonization of basalt fibers on interfacial properties and fracture toughness of epoxy matrix composites
- Nanosystem’s density functional theory study of the chlorine adsorption on the Fe(100) surface
- A rapid nanobiosensing platform based on herceptin-conjugated graphene for ultrasensitive detection of circulating tumor cells in early breast cancer
- Improving flexural strength of UHPC with sustainably synthesized graphene oxide
- The role of graphene/graphene oxide in cement hydration
- Structural characterization of microcrystalline and nanocrystalline cellulose from Ananas comosus L. leaves: Cytocompatibility and molecular docking studies
- Evaluation of the nanostructure of calcium silicate hydrate based on atomic force microscopy-infrared spectroscopy experiments
- Combined effects of nano-silica and silica fume on the mechanical behavior of recycled aggregate concrete
- Safety study of malapposition of the bio-corrodible nitrided iron stent in vivo
- Triethanolamine interface modification of crystallized ZnO nanospheres enabling fast photocatalytic hazard-free treatment of Cr(vi) ions
- Novel electrodes for precise and accurate droplet dispensing and splitting in digital microfluidics
- Construction of Chi(Zn/BMP2)/HA composite coating on AZ31B magnesium alloy surface to improve the corrosion resistance and biocompatibility
- Experimental and multiscale numerical investigations on low-velocity impact responses of syntactic foam composites reinforced with modified MWCNTs
- Comprehensive performance analysis and optimal design of smart light pole for cooperative vehicle infrastructure system
- Room temperature growth of ZnO with highly active exposed facets for photocatalytic application
- Influences of poling temperature and elongation ratio on PVDF-HFP piezoelectric films
- Large strain hardening of magnesium containing in situ nanoparticles
- Super stable water-based magnetic fluid as a dual-mode contrast agent
- Photocatalytic activity of biogenic zinc oxide nanoparticles: In vitro antimicrobial, biocompatibility, and molecular docking studies
- Hygrothermal environment effect on the critical buckling load of FGP microbeams with initial curvature integrated by CNT-reinforced skins considering the influence of thickness stretching
- Thermal aging behavior characteristics of asphalt binder modified by nano-stabilizer based on DSR and AFM
- Building effective core/shell polymer nanoparticles for epoxy composite toughening based on Hansen solubility parameters
- Structural characterization and nanoscale strain field analysis of α/β interface layer of a near α titanium alloy
- Optimization of thermal and hydrophobic properties of GO-doped epoxy nanocomposite coatings
- The properties of nano-CaCO3/nano-ZnO/SBR composite-modified asphalt
- Three-dimensional metallic carbon allotropes with superhardness
- Physical stability and rheological behavior of Pickering emulsions stabilized by protein–polysaccharide hybrid nanoconjugates
- Optimization of volume fraction and microstructure evolution during thermal deformation of nano-SiCp/Al–7Si composites
- Phase analysis and corrosion behavior of brazing Cu/Al dissimilar metal joint with BAl88Si filler metal
- High-efficiency nano polishing of steel materials
- On the rheological properties of multi-walled carbon nano-polyvinylpyrrolidone/silicon-based shear thickening fluid
- Fabrication of Ag/ZnO hollow nanospheres and cubic TiO2/ZnO heterojunction photocatalysts for RhB degradation
- Fabrication and properties of PLA/nano-HA composite scaffolds with balanced mechanical properties and biological functions for bone tissue engineering application
- Investigation of the early-age performance and microstructure of nano-C–S–H blended cement-based materials
- Reduced graphene oxide coating on basalt fabric using electrophoretic deposition and its role in the mechanical and tribological performance of epoxy/basalt fiber composites
- Effect of nano-silica as cementitious materials-reducing admixtures on the workability, mechanical properties and durability of concrete
- Machine-learning-assisted microstructure–property linkages of carbon nanotube-reinforced aluminum matrix nanocomposites produced by laser powder bed fusion
- Physical, thermal, and mechanical properties of highly porous polylactic acid/cellulose nanofibre scaffolds prepared by salt leaching technique
- A comparative study on characterizations and synthesis of pure lead sulfide (PbS) and Ag-doped PbS for photovoltaic applications
- Clean preparation of washable antibacterial polyester fibers by high temperature and high pressure hydrothermal self-assembly
- Al 5251-based hybrid nanocomposite by FSP reinforced with graphene nanoplates and boron nitride nanoparticles: Microstructure, wear, and mechanical characterization
- Interlaminar fracture toughness properties of hybrid glass fiber-reinforced composite interlayered with carbon nanotube using electrospray deposition
- Microstructure and life prediction model of steel slag concrete under freezing-thawing environment
- Synthesis of biogenic silver nanoparticles from the seed coat waste of pistachio (Pistacia vera) and their effect on the growth of eggplant
- Study on adaptability of rheological index of nano-PUA-modified asphalt based on geometric parameters of parallel plate
- Preparation and adsorption properties of nano-graphene oxide/tourmaline composites
- A study on interfacial behaviors of epoxy/graphene oxide derived from pitch-based graphite fibers
- Multiresponsive carboxylated graphene oxide-grafted aptamer as a multifunctional nanocarrier for targeted delivery of chemotherapeutics and bioactive compounds in cancer therapy
- Piezoresistive/piezoelectric intrinsic sensing properties of carbon nanotube cement-based smart composite and its electromechanical sensing mechanisms: A review
- Smart stimuli-responsive biofunctionalized niosomal nanocarriers for programmed release of bioactive compounds into cancer cells in vitro and in vivo
- Photoremediation of methylene blue by biosynthesized ZnO/Fe3O4 nanocomposites using Callistemon viminalis leaves aqueous extract: A comparative study
- Study of gold nanoparticles’ preparation through ultrasonic spray pyrolysis and lyophilisation for possible use as markers in LFIA tests
- Review Articles
- Advance on the dispersion treatment of graphene oxide and the graphene oxide modified cement-based materials
- Development of ionic liquid-based electroactive polymer composites using nanotechnology
- Nanostructured multifunctional electrocatalysts for efficient energy conversion systems: Recent perspectives
- Recent advances on the fabrication methods of nanocomposite yarn-based strain sensor
- Review on nanocomposites based on aerospace applications
- Overview of nanocellulose as additives in paper processing and paper products
- The frontiers of functionalized graphene-based nanocomposites as chemical sensors
- Material advancement in tissue-engineered nerve conduit
- Carbon nanostructure-based superhydrophobic surfaces and coatings
- Functionalized graphene-based nanocomposites for smart optoelectronic applications
- Interfacial technology for enhancement in steel fiber reinforced cementitious composite from nano to macroscale
- Metal nanoparticles and biomaterials: The multipronged approach for potential diabetic wound therapy
- Review on resistive switching mechanisms of bio-organic thin film for non-volatile memory application
- Nanotechnology-enabled biomedical engineering: Current trends, future scopes, and perspectives
- Research progress on key problems of nanomaterials-modified geopolymer concrete
- Smart stimuli-responsive nanocarriers for the cancer therapy – nanomedicine
- An overview of methods for production and detection of silver nanoparticles, with emphasis on their fate and toxicological effects on human, soil, and aquatic environment
- Effects of chemical modification and nanotechnology on wood properties
- Mechanisms, influencing factors, and applications of electrohydrodynamic jet printing
- Application of antiviral materials in textiles: A review
- Phase transformation and strengthening mechanisms of nanostructured high-entropy alloys
- Research progress on individual effect of graphene oxide in cement-based materials and its synergistic effect with other nanomaterials
- Catalytic defense against fungal pathogens using nanozymes
- A mini-review of three-dimensional network topological structure nanocomposites: Preparation and mechanical properties
- Mechanical properties and structural health monitoring performance of carbon nanotube-modified FRP composites: A review
- Nano-scale delivery: A comprehensive review of nano-structured devices, preparative techniques, site-specificity designs, biomedical applications, commercial products, and references to safety, cellular uptake, and organ toxicity
- Effects of alloying, heat treatment and nanoreinforcement on mechanical properties and damping performances of Cu–Al-based alloys: A review
- Recent progress in the synthesis and applications of vertically aligned carbon nanotube materials
- Thermal conductivity and dynamic viscosity of mono and hybrid organic- and synthetic-based nanofluids: A critical review
- Recent advances in waste-recycled nanomaterials for biomedical applications: Waste-to-wealth
- Layup sequence and interfacial bonding of additively manufactured polymeric composite: A brief review
- Quantum dots synthetization and future prospect applications
- Approved and marketed nanoparticles for disease targeting and applications in COVID-19
- Strategies for improving rechargeable lithium-ion batteries: From active materials to CO2 emissions
Articles in the same Issue
- Research Articles
- Improved impedance matching by multi-componential metal-hybridized rGO toward high performance of microwave absorption
- Pure-silk fibroin hydrogel with stable aligned micropattern toward peripheral nerve regeneration
- Effective ion pathways and 3D conductive carbon networks in bentonite host enable stable and high-rate lithium–sulfur batteries
- Fabrication and characterization of 3D-printed gellan gum/starch composite scaffold for Schwann cells growth
- Synergistic strengthening mechanism of copper matrix composite reinforced with nano-Al2O3 particles and micro-SiC whiskers
- Deformation mechanisms and plasticity of ultrafine-grained Al under complex stress state revealed by digital image correlation technique
- On the deformation-induced grain rotations in gradient nano-grained copper based on molecular dynamics simulations
- Removal of sulfate from aqueous solution using Mg–Al nano-layered double hydroxides synthesized under different dual solvent systems
- Microwave-assisted sol–gel synthesis of TiO2-mixed metal oxide nanocatalyst for degradation of organic pollutant
- Electrophoretic deposition of graphene on basalt fiber for composite applications
- Polyphenylene sulfide-coated wrench composites by nanopinning effect
- Thermal conductivity and thermoelectric properties in 3D macroscopic pure carbon nanotube materials
- An effective thermal conductivity and thermomechanical homogenization scheme for a multiscale Nb3Sn filaments
- Friction stir spot welding of AA5052 with additional carbon fiber-reinforced polymer composite interlayer
- Improvement of long-term cycling performance of high-nickel cathode materials by ZnO coating
- Quantum effects of gas flow in nanochannels
- An approach to effectively improve the interfacial bonding of nano-perfused composites by in situ growth of CNTs
- Effects of nano-modified polymer cement-based materials on the bending behavior of repaired concrete beams
- Effects of the combined usage of nanomaterials and steel fibres on the workability, compressive strength, and microstructure of ultra-high performance concrete
- One-pot solvothermal synthesis and characterization of highly stable nickel nanoparticles
- Comparative study on mechanisms for improving mechanical properties and microstructure of cement paste modified by different types of nanomaterials
- Effect of in situ graphene-doped nano-CeO2 on microstructure and electrical contact properties of Cu30Cr10W contacts
- The experimental study of CFRP interlayer of dissimilar joint AA7075-T651/Ti-6Al-4V alloys by friction stir spot welding on mechanical and microstructural properties
- Vibration analysis of a sandwich cylindrical shell in hygrothermal environment
- Water barrier and mechanical properties of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch (TPS)/poly(lactic acid) (PLA) blend bionanocomposites
- Strong quadratic acousto-optic coupling in 1D multilayer phoxonic crystal cavity
- Three-dimensional shape analysis of peripapillary retinal pigment epithelium-basement membrane layer based on OCT radial images
- Solvent regulation synthesis of single-component white emission carbon quantum dots for white light-emitting diodes
- Xanthate-modified nanoTiO2 as a novel vulcanization accelerator enhancing mechanical and antibacterial properties of natural rubber
- Effect of steel fiber on impact resistance and durability of concrete containing nano-SiO2
- Ultrasound-enhanced biosynthesis of uniform ZnO nanorice using Swietenia macrophylla seed extract and its in vitro anticancer activity
- Temperature dependence of hardness prediction for high-temperature structural ceramics and their composites
- Study on the frequency of acoustic emission signal during crystal growth of salicylic acid
- Controllable modification of helical carbon nanotubes for high-performance microwave absorption
- Role of dry ozonization of basalt fibers on interfacial properties and fracture toughness of epoxy matrix composites
- Nanosystem’s density functional theory study of the chlorine adsorption on the Fe(100) surface
- A rapid nanobiosensing platform based on herceptin-conjugated graphene for ultrasensitive detection of circulating tumor cells in early breast cancer
- Improving flexural strength of UHPC with sustainably synthesized graphene oxide
- The role of graphene/graphene oxide in cement hydration
- Structural characterization of microcrystalline and nanocrystalline cellulose from Ananas comosus L. leaves: Cytocompatibility and molecular docking studies
- Evaluation of the nanostructure of calcium silicate hydrate based on atomic force microscopy-infrared spectroscopy experiments
- Combined effects of nano-silica and silica fume on the mechanical behavior of recycled aggregate concrete
- Safety study of malapposition of the bio-corrodible nitrided iron stent in vivo
- Triethanolamine interface modification of crystallized ZnO nanospheres enabling fast photocatalytic hazard-free treatment of Cr(vi) ions
- Novel electrodes for precise and accurate droplet dispensing and splitting in digital microfluidics
- Construction of Chi(Zn/BMP2)/HA composite coating on AZ31B magnesium alloy surface to improve the corrosion resistance and biocompatibility
- Experimental and multiscale numerical investigations on low-velocity impact responses of syntactic foam composites reinforced with modified MWCNTs
- Comprehensive performance analysis and optimal design of smart light pole for cooperative vehicle infrastructure system
- Room temperature growth of ZnO with highly active exposed facets for photocatalytic application
- Influences of poling temperature and elongation ratio on PVDF-HFP piezoelectric films
- Large strain hardening of magnesium containing in situ nanoparticles
- Super stable water-based magnetic fluid as a dual-mode contrast agent
- Photocatalytic activity of biogenic zinc oxide nanoparticles: In vitro antimicrobial, biocompatibility, and molecular docking studies
- Hygrothermal environment effect on the critical buckling load of FGP microbeams with initial curvature integrated by CNT-reinforced skins considering the influence of thickness stretching
- Thermal aging behavior characteristics of asphalt binder modified by nano-stabilizer based on DSR and AFM
- Building effective core/shell polymer nanoparticles for epoxy composite toughening based on Hansen solubility parameters
- Structural characterization and nanoscale strain field analysis of α/β interface layer of a near α titanium alloy
- Optimization of thermal and hydrophobic properties of GO-doped epoxy nanocomposite coatings
- The properties of nano-CaCO3/nano-ZnO/SBR composite-modified asphalt
- Three-dimensional metallic carbon allotropes with superhardness
- Physical stability and rheological behavior of Pickering emulsions stabilized by protein–polysaccharide hybrid nanoconjugates
- Optimization of volume fraction and microstructure evolution during thermal deformation of nano-SiCp/Al–7Si composites
- Phase analysis and corrosion behavior of brazing Cu/Al dissimilar metal joint with BAl88Si filler metal
- High-efficiency nano polishing of steel materials
- On the rheological properties of multi-walled carbon nano-polyvinylpyrrolidone/silicon-based shear thickening fluid
- Fabrication of Ag/ZnO hollow nanospheres and cubic TiO2/ZnO heterojunction photocatalysts for RhB degradation
- Fabrication and properties of PLA/nano-HA composite scaffolds with balanced mechanical properties and biological functions for bone tissue engineering application
- Investigation of the early-age performance and microstructure of nano-C–S–H blended cement-based materials
- Reduced graphene oxide coating on basalt fabric using electrophoretic deposition and its role in the mechanical and tribological performance of epoxy/basalt fiber composites
- Effect of nano-silica as cementitious materials-reducing admixtures on the workability, mechanical properties and durability of concrete
- Machine-learning-assisted microstructure–property linkages of carbon nanotube-reinforced aluminum matrix nanocomposites produced by laser powder bed fusion
- Physical, thermal, and mechanical properties of highly porous polylactic acid/cellulose nanofibre scaffolds prepared by salt leaching technique
- A comparative study on characterizations and synthesis of pure lead sulfide (PbS) and Ag-doped PbS for photovoltaic applications
- Clean preparation of washable antibacterial polyester fibers by high temperature and high pressure hydrothermal self-assembly
- Al 5251-based hybrid nanocomposite by FSP reinforced with graphene nanoplates and boron nitride nanoparticles: Microstructure, wear, and mechanical characterization
- Interlaminar fracture toughness properties of hybrid glass fiber-reinforced composite interlayered with carbon nanotube using electrospray deposition
- Microstructure and life prediction model of steel slag concrete under freezing-thawing environment
- Synthesis of biogenic silver nanoparticles from the seed coat waste of pistachio (Pistacia vera) and their effect on the growth of eggplant
- Study on adaptability of rheological index of nano-PUA-modified asphalt based on geometric parameters of parallel plate
- Preparation and adsorption properties of nano-graphene oxide/tourmaline composites
- A study on interfacial behaviors of epoxy/graphene oxide derived from pitch-based graphite fibers
- Multiresponsive carboxylated graphene oxide-grafted aptamer as a multifunctional nanocarrier for targeted delivery of chemotherapeutics and bioactive compounds in cancer therapy
- Piezoresistive/piezoelectric intrinsic sensing properties of carbon nanotube cement-based smart composite and its electromechanical sensing mechanisms: A review
- Smart stimuli-responsive biofunctionalized niosomal nanocarriers for programmed release of bioactive compounds into cancer cells in vitro and in vivo
- Photoremediation of methylene blue by biosynthesized ZnO/Fe3O4 nanocomposites using Callistemon viminalis leaves aqueous extract: A comparative study
- Study of gold nanoparticles’ preparation through ultrasonic spray pyrolysis and lyophilisation for possible use as markers in LFIA tests
- Review Articles
- Advance on the dispersion treatment of graphene oxide and the graphene oxide modified cement-based materials
- Development of ionic liquid-based electroactive polymer composites using nanotechnology
- Nanostructured multifunctional electrocatalysts for efficient energy conversion systems: Recent perspectives
- Recent advances on the fabrication methods of nanocomposite yarn-based strain sensor
- Review on nanocomposites based on aerospace applications
- Overview of nanocellulose as additives in paper processing and paper products
- The frontiers of functionalized graphene-based nanocomposites as chemical sensors
- Material advancement in tissue-engineered nerve conduit
- Carbon nanostructure-based superhydrophobic surfaces and coatings
- Functionalized graphene-based nanocomposites for smart optoelectronic applications
- Interfacial technology for enhancement in steel fiber reinforced cementitious composite from nano to macroscale
- Metal nanoparticles and biomaterials: The multipronged approach for potential diabetic wound therapy
- Review on resistive switching mechanisms of bio-organic thin film for non-volatile memory application
- Nanotechnology-enabled biomedical engineering: Current trends, future scopes, and perspectives
- Research progress on key problems of nanomaterials-modified geopolymer concrete
- Smart stimuli-responsive nanocarriers for the cancer therapy – nanomedicine
- An overview of methods for production and detection of silver nanoparticles, with emphasis on their fate and toxicological effects on human, soil, and aquatic environment
- Effects of chemical modification and nanotechnology on wood properties
- Mechanisms, influencing factors, and applications of electrohydrodynamic jet printing
- Application of antiviral materials in textiles: A review
- Phase transformation and strengthening mechanisms of nanostructured high-entropy alloys
- Research progress on individual effect of graphene oxide in cement-based materials and its synergistic effect with other nanomaterials
- Catalytic defense against fungal pathogens using nanozymes
- A mini-review of three-dimensional network topological structure nanocomposites: Preparation and mechanical properties
- Mechanical properties and structural health monitoring performance of carbon nanotube-modified FRP composites: A review
- Nano-scale delivery: A comprehensive review of nano-structured devices, preparative techniques, site-specificity designs, biomedical applications, commercial products, and references to safety, cellular uptake, and organ toxicity
- Effects of alloying, heat treatment and nanoreinforcement on mechanical properties and damping performances of Cu–Al-based alloys: A review
- Recent progress in the synthesis and applications of vertically aligned carbon nanotube materials
- Thermal conductivity and dynamic viscosity of mono and hybrid organic- and synthetic-based nanofluids: A critical review
- Recent advances in waste-recycled nanomaterials for biomedical applications: Waste-to-wealth
- Layup sequence and interfacial bonding of additively manufactured polymeric composite: A brief review
- Quantum dots synthetization and future prospect applications
- Approved and marketed nanoparticles for disease targeting and applications in COVID-19
- Strategies for improving rechargeable lithium-ion batteries: From active materials to CO2 emissions

