Strong quadratic acousto-optic coupling in 1D multilayer phoxonic crystal cavity

Jun Jin; Xiaohong Wang; Lamin Zhan; Hongping Hu

doi:10.1515/ntrev-2021-0034

Article Open Access

Strong quadratic acousto-optic coupling in 1D multilayer phoxonic crystal cavity

Jun Jin , Xiaohong Wang , Lamin Zhan and Hongping Hu

Published/Copyright: June 9, 2021

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nanotechnology Reviews Volume 10 Issue 1

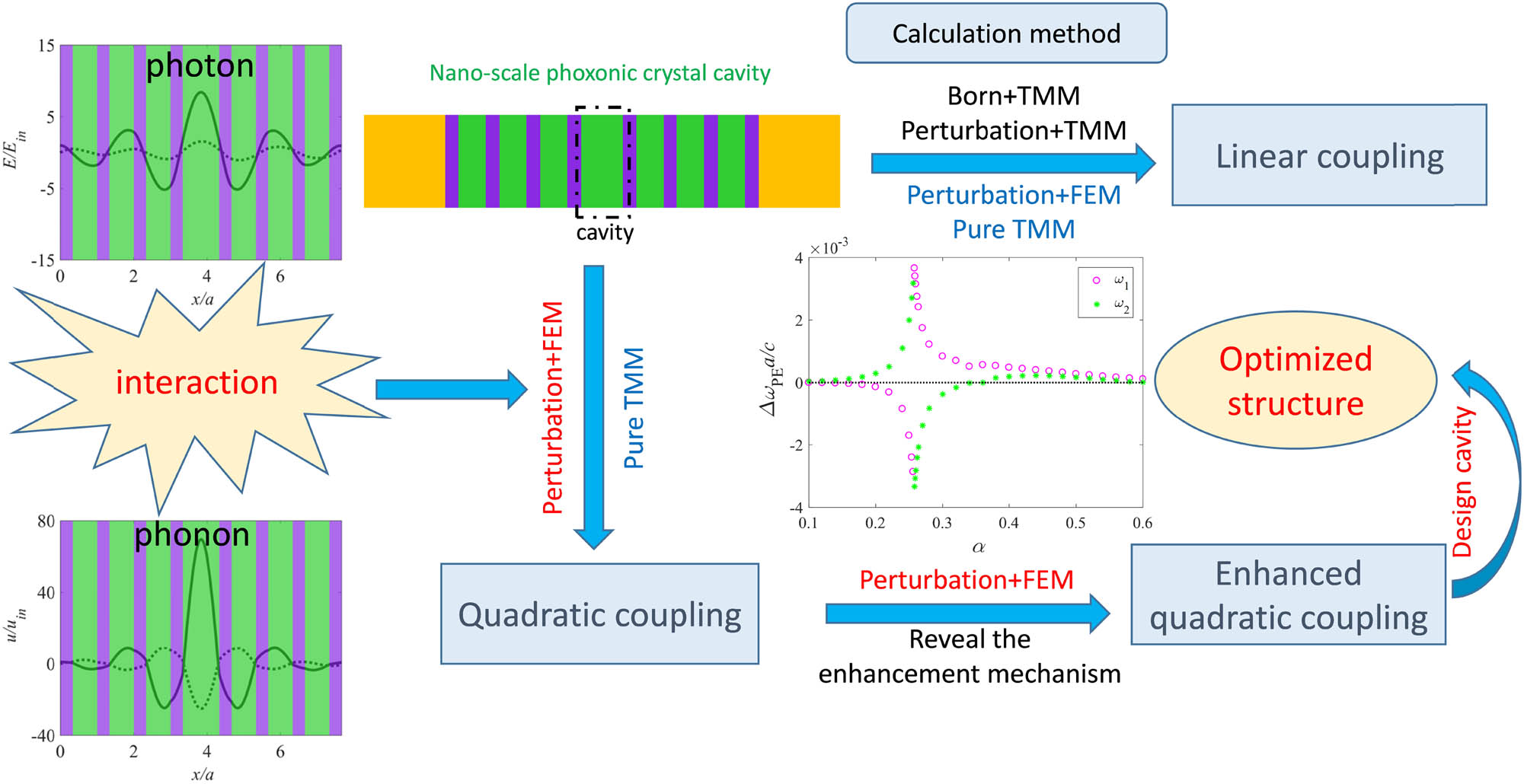
Abstract

Four methods are applied to calculate the acousto-optic (AO) coupling in one-dimensional (1D) phoxonic crystal (PXC) cavity: transfer matrix method (TMM), finite element method (FEM), perturbation theory, and Born approximation. Two types of mechanisms, the photoelastic effect (PE) and the moving interface effect (MI), are investigated. Whether the AO coupling belongs to linear or quadratic, the results obtained by the perturbation theory are in good agreement with the numerical results. We show that the combination method of FEM and perturbation theory has some advantages over Born approximation. The dependence of linear and quadratic couplings on the symmetry of acoustic and optical modes has been discussed in detail. The linear coupling will vanish if the defect acoustic mode is even symmetry, but the quadratic effect may be enhanced. Based on second-order perturbation theory, the contribution of each optical eigenfrequency to quadratic coupling is clarified. Finally, the quadratic coupling is greatly enhanced by tuning the thickness of the defect layer, which is an order of magnitude larger than that of normal defect thickness. The enhancement mechanism of quadratic coupling is illustrated. The symmetry of the acoustic defect mode is transformed from odd to even, and two optical defect modes are modulated to be quasi-degenerated modes. This study opens up a possibility to achieve tunable phoxonic crystals on the basis of nonlinear AO effects.

Graphical abstract

Keywords: acousto-optic coupling; phoxonic crystals; photoelastic effect; transfer matrix method; finite elements method; moving interface effect

1 Introduction

The acousto-optic (AO) effect, also known as optomechanics interaction, has been widely used to process light signals in homogeneous materials in recent years [1,2,3,4,5,6], for example, gravitational wave detection [2], tunable photonic crystals [3], and the optical bandpass switching [4]. The study concerning the AO effect begins with the opening of dual phononic and photonic band gaps [7]. Such simultaneous band gaps have been demonstrated and optimized in various PXCs [8,9,10,11,12,13,14,15,16,17]. Square, hexagonal (honeycomb), and triangular arrays are included, and large bandgaps can be obtained in square and hexagonal arrays but not for triangular arrays [9]. By introducing a defect into perfect periodic PXC, the PXC cavity can be obtained. In such a cavity, both mechanical energy and electromagnetic energy are localized [18]. From a quantum perspective, phonon and photon are highly confined in a very small volume, and interaction between phonon and photon can be boosted. Large per-photon force is realized in a nanometer-scale photonic crystal, making it possible for the exploration of cavity optomechanical regimes [19]. The experimental demonstration of optomechanical interaction between 200 THz photon and several GHz phonon provides new methods for stimulating optomechanical interactions in a chip-scale platform [20]. Etching air holes array into thin film of silicon, electromagnetically induced transparency and tunable optical delays are both demonstrated with optomechanics [21,22,23]. By utilizing optical radiation pressure, the nanomechanical mode of several GHz with the bath temperature of 20 K is cooled into its quantum mechanical ground state [24]. This enables the control of mesoscale mechanical oscillators in the quantum regime. The interaction of the acoustic wave and the optical wave in cavities has attracted strong attention. The design for quasi-2D PXC cavities is proposed in detail [25]. The AO coupling in L ₁ cavity, including optical frequency modulation and the coupling rate, was studied by FEM [26,27,28,29]. Both slow photon and phonon modes are induced in nanobeam waveguide, and the AO couplings are significantly enhanced due to the slow group velocities [30]. The symmetry of the modes was found to play a dominant role in AO coupling [31,32,33,34]. The phononic and photonic modes highly overlap near the slot within a 2D air-slot PXC cavity, which greatly enhances the interface effect [35]. Considering the plasmonic behavior, AO coupling was studied in 2D PXC cavities with a line defect [36,37]. The development of AO coupling in recent years was studied [38]. A recent research showed an efficient AO modulation realized in an on-chip piezo-optomechanical transducer and addressed several challenges such as low optical quality factor [39]. Quadratic AO coupling has attracted more interests [40,41]. As we know earlier, quadratic AO coupling is proportional to the square of input displacement. Because the quadratic coupling is generally weak, its enhancement is very important for a PXC. Up to now, the quadratic coupling has just been enhanced in a 2D PXC by adjusting its cavity slot width approaching cavity mode linewidth [40,42].

Almost all of these studies were carried out by FEM. Although FEM is very convenient to calculate the AO coupling, it cannot provide intrinsic physical interpretation due to its purely numerical calculation. The analytical results of the AO coupling in 1D PXC cavity can be obtained by solving the wave equations of the low-dimensional system. Moreover, due to the similarity between the Maxwell equation and the Schrodinger equation, the solution method of the nonlinear Schrodinger equation can also be used to solve the nonlinear Maxwell equation. As an analytical method, Born approximation was first applied to analyze the reflection and transmission of light in multilayer media perturbed by acoustic waves, and the expression of reflection coefficient was derived by means of Green’s function [43]. In this method, the complex reflection coefficient perturbed by the acoustic wave was evaluated, and then, the perturbed optical frequency was obtained in the reflectivity spectrum. The linear and nonlinear AO couplings were analyzed by Born approximation [44,45]. Elastodynamic and electrodynamic layer multiple-scattering method was used for the calculation [46,47,48]. For linear coupling, the results obtained by the first-order Born approximation are consistent with numerical results when the input displacement is at the low level. Nevertheless, as the incident displacement increases, the results start to deviate from the numerical results. For its calculation on quadratic coupling, it has not been verified by the numerical method.

In this study, four methods are compared to find the most effective and accurate method. We combine the perturbation theory with TMM or FEM to analyze AO coupling. The strength of AO coupling is evaluated by the normalized optical frequency shift. The normalized frequency shift obtained by the perturbation theory, especially combined with FEM, is highly consistent with the numerical result, whether linear or quadratic coupling, even for large input displacement levels. Besides, we can also predict the direction of optical frequency drift from equations of the perturbation theory for both PE and MI contributions, which cannot be realized directly by Born approximation. Furthermore, the quadratic coupling is enhanced by adjusting the thickness of the defect layer. We focus on the enhancement mechanism of the quadratic coupling. The study provides an efficient method to evaluate AO coupling and the theoretical basis to design strong AO coupling devices, especially for quadratic AO coupling.

This study is organized as follows. In Section 2, we review the perturbation theory briefly and introduce the 1D PXC structure. In Section 3, four kinds of methods are applied to the calculation of linear and quadratic coupling, and the advantages and disadvantages of each method are then analyzed. In addition, some coupling laws are drawn for linear coupling and quadratic coupling. In Section 4, the enhancement mechanism of the quadratic coupling is further revealed. The structure with an optimal cavity is designed. The graphical abstract is also presented.

2 Perturbation theory

A 1D PXC has a multilayer structure of periodically arranging materials with different acoustic and optical properties as shown in Figure 1. The PXC cavity is formed by the introduction of a defect into the perfect periodic structure. Defect acoustic modes and optical modes are highly confined in a small volume. The interactions between these two modes are enhanced. When a resonant acoustic wave propagates in the structure, a strain field is induced, and the interfaces between different materials are also moved. The perturbation by the acoustic wave results in redistribution of the permittivity of the structure. Two mechanisms are responsible for the interactions between acoustic modes and optical modes: (1) photoelastic effect (PE), permittivity variation induced by the strain field; (2) moving interface effect (MI), permittivity variation caused by the moving of the interface. The variation of permittivity can be regarded as a quasi-static behavior since the speed of the light is several orders of magnitude larger than that of the sound. The permittivity variation is related to the amplitude of the acoustic wave. In the following, the displacement amplitude of the PXC is named as input displacement u _in, which is a perfect candidate as the perturbation parameter. The permittivity variations caused by two effects in the 1D structure are reduced as follows:

(1) Δ ε PE ( z ) = − p 12 ( z ) ε ( z ) S ( z ) Δ ε MI = ( ε i − ε i − 1 ) u i ∣ u i ∣ ,

where p ₁₂(z) and S(z) denote the photoelastic coefficient and strain field of the material at point z, respectively. ε _i the relative permittivity in the ith layer of the multilayer structure and u _i is the displacement of ith interface.

Figure 1

Schematic diagram of 1D multilayer PXC cavity.

The perturbation theory is a classic method to evaluate the effect of small variation in parameters on solutions to the equations. It is widely used in astrophysics, solid mechanics, and other disciplines. The Maxwell equations are written in a Dirac notation form:

(2) ∇ × ∇ × ∣ E 〉 = ω c 2 ε ∣ E 〉 ,

where E and c denote electric field and velocity of light, respectively. Based on perturbation theory, and the orthogonality of the modes for the generalized Hermitian eigenproblem, the first-order correction is obtained as follows [49]:

(3) Δ ω ( 1 ) = − ω ( 0 ) 2 〈 E ( 0 ) ∣ Δ ε ∣ E ( 0 ) 〉〈 E ( 0 ) ∣ ε ( 0 ) ∣ E ( 0 ) 〉 ,

where E ⁽⁰⁾ and ω ⁽⁰⁾ denote the unperturbed eigensolutions.

(4) 〈 E ( 0 ) ∣ ε ( 0 ) ∣ E ( 0 ) 〉 = ∫ L ε ( z ) ∣ E ( z ) ∣ 2 d z ,

where L denotes the length of the structure. The term 〈 E ( 0 ) ∣ Δ ε ∣ E ( 0 ) 〉 has different forms for different effects. For the PE effect,

(5) 〈 E ( 0 ) ∣ Δ ε ∣ E ( 0 ) 〉 = − ∫ L p 12 ( z ) ε 2 ( z ) S ( z ) ∣ E ( z ) ∣ 2 d z .

If the structure is symmetric and the integrand is odd, linear coupling of the PE effect will vanish. For MI effect,

(6) 〈 E ( 0 ) ∣ Δ ε ∣ E ( 0 ) 〉 = − ∑ i N ( ε i + 1 − ε i ) u i ∣ E i ∣ 2 ,

where N denotes the total number of interfaces between adjacent layers. The second-order correction is expressed as follows [50]:

(7) Δ ω i ( 2 ) = 3 8 ω i ( 0 ) 〈 E i ( 0 ) ∣ Δ ε ∣ E i ( 0 ) 〉〈 E i ( 0 ) ∣ ε ( 0 ) ∣ E i ( 0 ) 〉 2 − 1 2 ∑ j ≠ i ∑ k = 1 d j ω i ( 0 ) 3 ω j ( 0 ) 2 − ω i ( 0 ) 2 × ∣ 〈 E j , k ( 0 ) ∣ Δ ε ∣ E i ( 0 ) 〉 ∣ 2 〈 E j , k ( 0 ) ∣ ε ( 0 ) ∣ E j , k ( 0 ) 〉〈 E i ( 0 ) ∣ ε ( 0 ) ∣ E i ( 0 ) 〉 ,

where d _j denotes the degree of the degeneracy mode.

3 Calculation methods on linear and quadratic couplings

We apply the perturbation theory to the same structure as previously investigated by Born approximation [44]. As shown in Figure 1, each lattice of the multilayer structure consists of As₂Se₃(a/3)/PES(2a/3) with the lattice constant a = 440 nm. As a resonant cavity, the defect layer is made of PES whose thickness is denoted by a _d. a _d is equal to a unless otherwise stated. The whole structure is embedded in a silica (SiO₂) matrix. The structure can be formed in silicon-on-insulator (SOI). The acoustic and optical parameters of three kinds of materials are listed in Table 1.

Table 1

Acoustic and optical physical parameters of As₂Se₃, PES, and SiO₂

	Refractive index n	Photoelastic coefficient p ₁₂	Density ρ (kg/m³)	Longitudinal sound velocity c _l (m/s)
As₂Se₃	2.83	0.27	4,640	2,250
PES	1.55	0.30	1,370	2,260
SiO₂	1.44	0.27	2,200	5,965

The calculations on the unperturbed structure are carried out by TMM [51,52]. Figure 2(a) and (d) displays the dispersion curve of PTC and PNC, respectively. After the introduction of a defect into the perfect periodic PXC, two defect PTC modes and two defect PNC modes are localized in the defect of the PXC. Their dispersion curves appear in the green and yellow shadow regions of PTC and PNC band gaps, respectively. Normalized frequencies of the defect PNC modes are Ω 1 a / c l ; SiO 2 = 1.25492 (2.70 GHz) and Ω 2 a / c l ; SiO 2 = 2.31323 (4.99 GHz). The corresponding Q factors of these two PNC modes are 1,550 and 2,811, respectively. The Q factors certainly can be magnified by increasing the number of the layer. Figure 2(b) and (c) displays the localized electric fields, i.e., PTC defect modes, of two normalized optical resonant frequencies of ω ₁ and ω ₂ at 1.61176 and 1.77056, respectively. The AO coupling of the second PTC defect mode (ω ₂ a/c = 1.77056, 192 THz) is emphasized to compare different calculation methods. Figure 2(e) and (f) displays the localized displacement fields, i.e., PNC defect modes, of two acoustic resonance frequencies Ω ₁ and Ω ₂, respectively. The defect modes have either odd or even symmetry due to the even symmetric structure. Specifically, the second PTC defect mode ω ₂ has even symmetry. As for symmetry of the first PTC defect mode ω ₁, the real part is even, whereas the imaginary part is odd. The first PNC defect mode Ω ₁ has even symmetry. As the gradient of displacement, the strain field has an opposite symmetry, i.e., odd symmetry. However, the second PNC defect mode Ω ₂ is just the opposite.

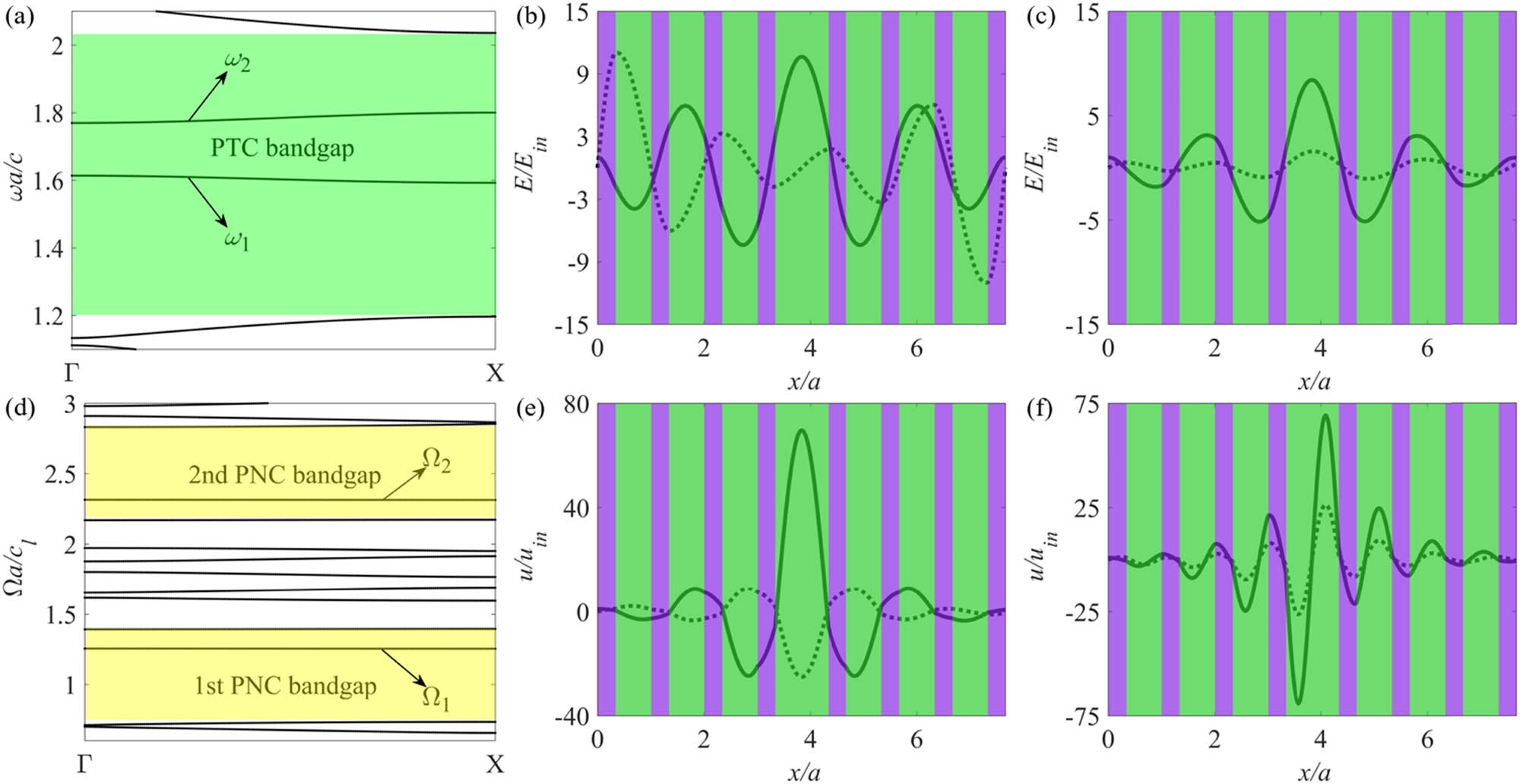
$Figure 2 (a) Dispersion curve of PTC. Electric distribution of the defect PTC modes (b) ω 1 a/c = 1.61176 (because the imaginary part is much bigger than real part at this frequency, the imaginary is multiplied with 0.1 to show the real part), and (c) ω 2 a/c = 1.77056. (d) Dispersion curve of PNC. Displacement distribution of the defect PNC modes (e) Ω 1 a / c l ; SiO 2 = 1.25492 {\Omega }_{1}a/{c}_{\text{l};{\text{SiO}}_{\text{2}}}=1.25492 , and (f) Ω 2 a / c l ; SiO 2 = 2.31323 {\Omega }_{2}a/{c}_{\text{l};{\text{SiO}}_{\text{2}}}=2.31323 (solid line: real part, dotted line: imaginary part). The thickness of the defect layer a d = a.$

Figure 2

(a) Dispersion curve of PTC. Electric distribution of the defect PTC modes (b) ω ₁ a/c = 1.61176 (because the imaginary part is much bigger than real part at this frequency, the imaginary is multiplied with 0.1 to show the real part), and (c) ω ₂ a/c = 1.77056. (d) Dispersion curve of PNC. Displacement distribution of the defect PNC modes (e) Ω 1 a / c l ; SiO 2 = 1.25492 , and (f) Ω 2 a / c l ; SiO 2 = 2.31323 (solid line: real part, dotted line: imaginary part). The thickness of the defect layer a _d = a.

With four methods, the linear AO coupling is studied. The normal incident acoustic wave perturbation is applied to the cavity. We know the first-order correction for PE effect from equation (5), and the terms p ₁₂(z), ε ²(z), and |E(z)|² of the line integral all have even symmetry. The linear AO coupling, measured by the first-order correction Δω ⁽¹⁾, will vanish if the strain field of the acoustic mode has odd symmetry, namely, displacement field has even symmetry, such as Ω ₁ shown in Figure 2(e). The same conclusion can be drawn for MI contribution. Hence, we turn to Ω ₂. For comparison, input displacement u _in = 0.022 nm, which is similar to that mentioned in ref. [44]. Computed by four methods, the AO couplings between optical mode ω ₂ and acoustic mode Ω ₂ are listed in Table 2. Two analytical methods, the first-order Born approximation and the first-order perturbation theory, are carried out by TMM, which are denoted by “Born + TMM” and “Perturbation + TMM,” respectively. “Perturbation + FEM” means FEM based on the perturbation theory. “Pure FEM” represents numerical calculation by FEM. The results obtained by the first-order perturbation theory are highly consistent with the numerical results and are more accurate than that by the first-order Born approximation for both PE effect and MI effect.

Table 2

Normalized frequency shift of optical mode ω ₂ is continuously perturbed by the acoustic wave at the resonance frequency Ω 2 a / c l ; SiO 2 = 2.31323 . The input displacement u _in = 0.022 nm

Methods	ω ( 0 ) a / c	Δ ω PE a / c (×10⁻³)	Δ ω MI a / c (×10⁻³)	Δ ω PE&MI a / c (×10⁻³)
1st Born + TMM	1.77056	2.13	1.05	2.93
1st Perturbation + TMM	1.77056	2.31	1.10	3.41
1st Perturbation + FEM	1.77056	2.366	1.09	3.456
Pure FEM	1.77056	2.367	1.09	3.457

Figure 3 illustrates the variation of the normalized frequency shift of the optical modes ω ₂ with the input displacement at Ω 2 a / c l ; SiO 2 = 2.31323 . For the sake of simplicity, only the PE effect is taken into account here since the same conclusions can also be drawn for the MI effect. The results obtained by the “Born + TMM” agree with the numerical results of “Pure FEM” only in relative low input displacement. As the input displacement increases, the results deviate from the numerical results gradually. What is worse is when the input displacement u _in is greater than 0.132 nm, the reflectivity obtained by “Born + TMM” exceeds 1 at some certain optical frequency, which is against the principle of conservation of energy. Under these circumstances, the method fails to evaluate AO coupling. Both “Perturbation + TMM” and “Perturbation + FEM” agree well with numerical calculation even when the input displacement is at relatively high level. Because of the mode shape solved by FEM in “FEM + perturbation,” the results obtained by “FEM + perturbation” are a little more consistent with “pure FEM” than that obtained by “TMM + perturbation.” Certainly, to calculate the AO coupling higher than the second order, we need to further study the higher order perturbation theory. Table 3 lists the advantages and shortcomings of these four methods.

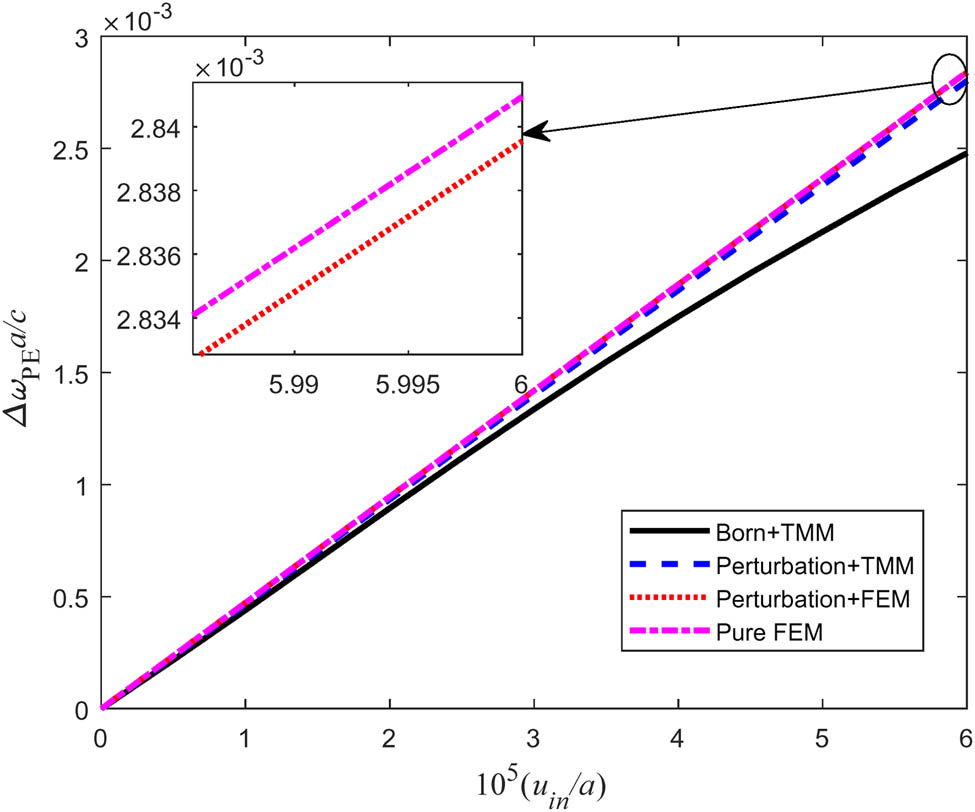
$Figure 3 Normalized frequency shift of the optical modes ω 2 versus the input displacement at the acoustic normalized frequency of Ω 2 a / c l ; SiO 2 = 2.31323 {\Omega }_{2}a/{c}_{\text{l};{\text{SiO}}_{\text{2}}}=2.31323 , where four methods are applied.$

Figure 3

Normalized frequency shift of the optical modes ω ₂ versus the input displacement at the acoustic normalized frequency of Ω 2 a / c l ; SiO 2 = 2.31323 , where four methods are applied.

Table 3

Advantages and shortcomings of these four methods for evaluating AO coupling

Methods	Advantages	Shortcomings
Born + TMM	Good physical interpretation	Only 1D structure
		Low accuracy on nonlinear effect
		Limit on small acoustic perturbation
Perturbation + TMM	High accuracy	Only 1D structure
Perturbation + TMM	Best physical interpretation	Only linear and quadratic effects
Perturbation + FEM	Highest accuracy	Only linear and quadratic effects
Perturbation + FEM	Best physical interpretation	Only linear and quadratic effects
Pure FEM	Highest accuracy	Weak physical interpretation

From equation (3), a positive frequency correction sign means an increase in the optical frequency, and a negative sign means the opposite. The frequency correction sign of the PE effect is further analyzed. From equation (5), ε ²(z) and |E(z)|² are always positive. For the given materials, the sign of p ₁₂(z) is known. Thus, only the strain field is unknown. The sign of the PE effect can be transformed by redistributing the photoelastic coefficient and strain field of the materials. As for the MI effect, the same methods can be applied as well.

Quadratic coupling is then investigated. The PNC defect mode Ω ₂ has an odd symmetry, and the quadratic coupling is suppressed since the linear coupling is much stronger. Hence, we turn to the first PNC defect mode with the normalized frequency of Ω 1 a / c l ; SiO 2 = 1.25492 . From equations (5) and (6), the linear coupling vanishes because of the even symmetry of the displacement field and the odd symmetry of the strain field as shown in Figure 2(e). Therefore, based on equation (7), the second-order perturbation theory is applied to study the quadratic coupling. Figure 4 illustrates that the normalized frequency shift is proportional to the square of acoustic input displacement (u _in/a)², where the PE effect is only taken into account. This indicates that quadratic coupling is dominant in AO coupling. Only “Perturbation + FEM” and “Pure FEM” are carried out in the calculation owing to their good performance. The results obtained by these two methods show a high consistency even when the input displacement increases close to u _in = 0.132 nm (a displacement limit is set to ensure structural safety). It should be pointed out that the convergence is reached by only taking the first 30 eigenfrequencies into account although infinite terms are included in equation (7). Therefore, the combination method of “Perturbation + FEM” has great advantages in the AO coupling analysis since the perturbation theory can give the physical interpretation and only the unperturbed electric field solutions are required, while FEM provides a high-precision solution and integration. The first term in equation (7) vanishes since it depends on the first-order correction. Thus, the sign of the second-order correction depends on 1 / [ ω j ( 0 ) 2 − ω i ( 0 ) 2 ] in the last term. As a result, the second-order correction from the lower eigenfrequencies than ω _i ⁽⁰⁾ has a positive sign, while that from higher eigenfrequencies has a negative sign.

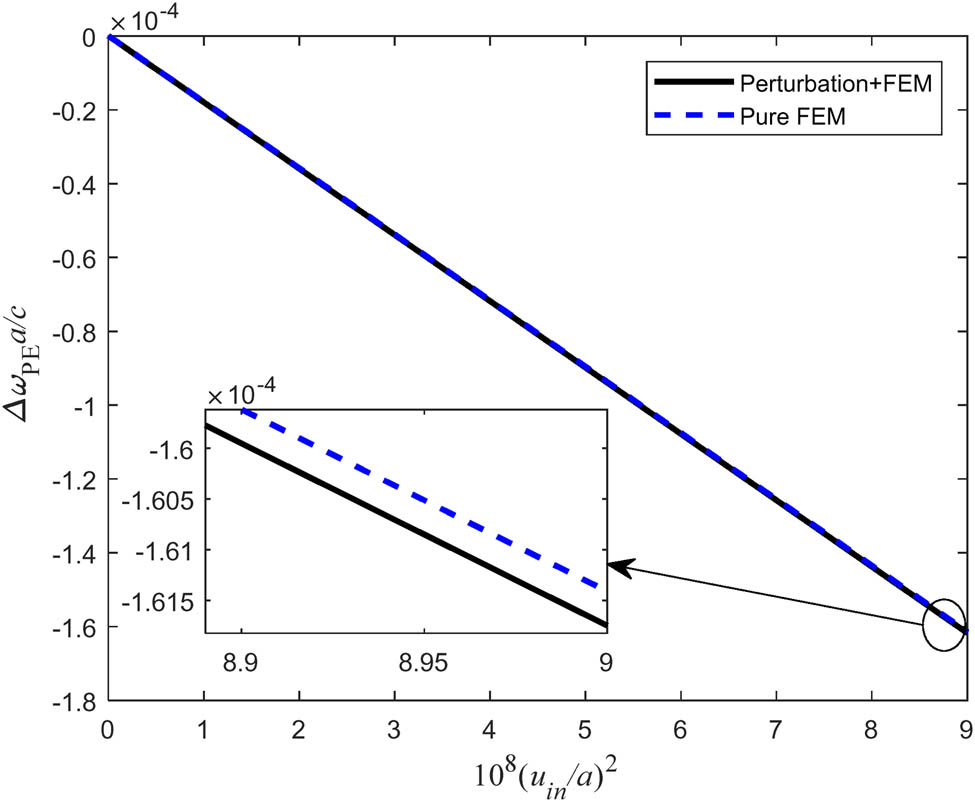
$Figure 4 Normalized frequency shift of the optical modes ω 1 as a function of the acoustic input displacement level (u in/a)2 at the acoustic normalized frequency of Ω 1 a / c l ; SiO 2 = 1.25492 {\Omega }_{1}a/{c}_{\text{l};{\text{SiO}}_{\text{2}}}=1.25492 , which is calculated by two methods.$

Figure 4

Normalized frequency shift of the optical modes ω ₁ as a function of the acoustic input displacement level (u _in/a)² at the acoustic normalized frequency of Ω 1 a / c l ; SiO 2 = 1.25492 , which is calculated by two methods.

It is noteworthy that quadratic coupling is not only affected by the symmetry of the acoustic mode but also determined by the symmetry of the optical mode of the eigenfrequency. Its contribution to quadratic coupling will vanish if the optical mode of one eigenfrequency has the same symmetry as the defect mode. Furthermore, the quadratic coupling will also be weakened if these eigenfrequencies are too far away from the defect optical resonance frequency, even if their modes and defect mode have different symmetries. Table 4 lists the linear and quadratic couplings depending on the symmetry of the PNC defect mode, the defect PTC mode, and the other PTC modes. It can be inferred that the quartic coupling will be dominant in the AO coupling if both linear and quadratic couplings vanish. In our case, the relatively large contribution on the quadratic coupling is −0.10, −0.21, −0.42, −0.60, and −0.20 (×10⁻⁴), which comes from the optical eigenfrequencies of 231, 272, 315, 356, and 401 THz, respectively. Finally, with the input displacement similar to that of ref. [44], the PE contribution is −1.6 × 10⁻⁴ and MI contribution is −3.0 × 10⁻⁵, which can be obtained by TMM or FEM. The superposition of both effects is −8.9 × 10⁻⁵, which is calculated by FEM. However, the superposition of both effects is about −0.001 in ref. [44]. It should be noted that for quadratic coupling, these two effects cannot be added linearly as their superposition.

Table 4

Linear and quadratic couplings depend on symmetry of the defect PNC mode, the defect PTC mode, and the other PTC modes

Defect PNC mode	Linear effect	Defect PTC mode	Other PTC mode	Quadratic effect
Odd	Strong	—	—	Suppressed
Even	Vanish	Even	Even	Vanish
Even	Vanish	Odd	Odd	Vanish

4 Enhanced quadratic AO coupling

We further study the dependence of the symmetry of the PNC defect mode on the thickness a _d of the defect layer. The symmetry remains the same when the thickness a _d is an integer multiple of the lattice constant a, i.e., a _d = ma (m is an arbitrary integer). However, the symmetry of these defect modes can be transformed if the thickness a _d ≠ ma. Figure 5 displays the second PNC defect mode Ω′₂ and two PTC defect modes when a _d = 5a/4. The symmetry of the PNC defect mode transforms from odd (Figure 2(f)) to even (Figure 5(a)), while the PTC defect mode remains even symmetric. Certainly, when thickness a _d increases from a to 5a/4, the normalized frequency of the second PNC mode increases from 2.3132 to 2.6522, but the normalized unperturbed frequency of the second PTC defect mode decreases from 1.77056 to 1.61596, while that of the first PTC defect mode remains unchanged. The mode profile of ω ₂ and ω′ ₂ has little difference. However, the normalized imaginary parts of ω ₁ and ω′ ₁ are significantly different, whose amplitude varies from 110 to 0.51.

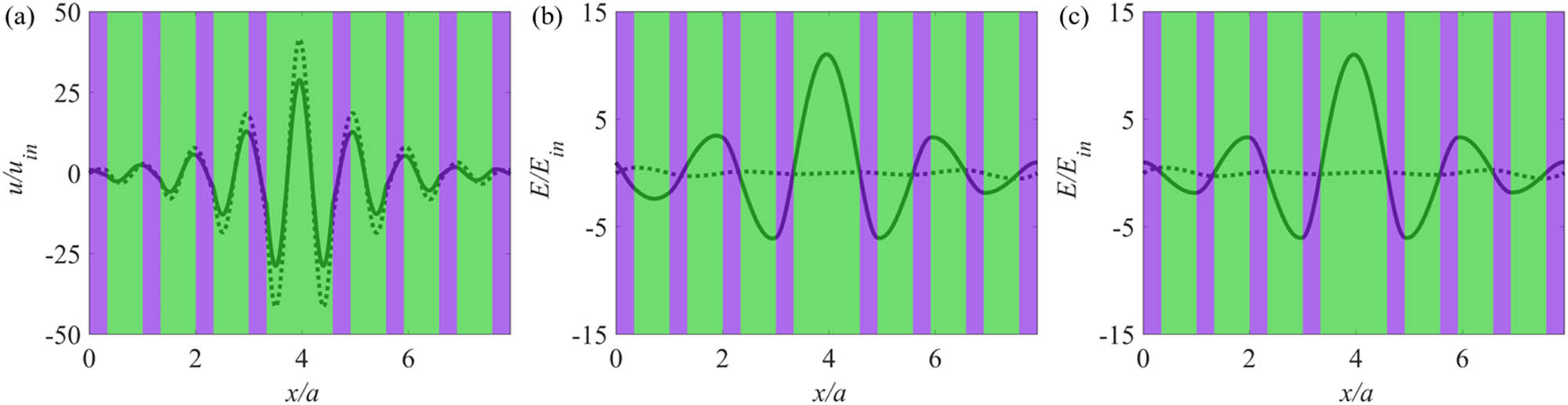
$Figure 5 (a) Displacement field distribution of the defect PNC mode Ω ′ 2 a / c l ; SiO 2 = 2.65520 {\Omega ^{\prime} }_{2}a/{c}_{\text{l};{\text{SiO}}_{\text{2}}}=2.65520 . Electric field distribution of the defect PTC modes (b) ω ′ 1 a / c = 1.61164 {\omega ^{\prime} }_{1}a/c=1.61164 and (c) ω ′ 2 a / c = 1.61596 {\omega ^{\prime} }_{2}a/c=1.61596 . The thickness of the defect layer a d = 5a/4.$

Figure 5

(a) Displacement field distribution of the defect PNC mode Ω ′ 2 a / c l ; SiO 2 = 2.65520 . Electric field distribution of the defect PTC modes (b) ω ′ 1 a / c = 1.61164 and (c) ω ′ 2 a / c = 1.61596 . The thickness of the defect layer a _d = 5a/4.

We then focus on the dependence of the symmetry of the second PNC defect mode on the thickness of the defect layer. The relative thickness increment of the defect layer is defined as α = (a _d – a)/a _d. Results show that the symmetry of the PNC defect mode Ω ₂ can be transformed from odd to even as long as 0 < α < 0.6. Nevertheless, when α is less than 0.1, the frequency of the defect mode moves toward the band gap edge and the corresponding displacement field is no longer localized in the cavity. Thus, the quadratic coupling is studied by setting α between 0.1 and 0.6, as shown in Figure 6(a). The input displacement is set as u _in = 0.132 nm. The normalized frequency shift of the quadratic coupling is obtained by “pure FEM” and “Perturbation + FEM,” respectively, where only the PE effect is taken into consideration. The result obtained by “Perturbation + FEM” agrees well with that done by “pure FEM” unless the frequencies of these two PTC defect modes are too close. Hence, it is still reasonable to reveal the enhancement mechanism of the quadratic coupling by the perturbation theory. The absolute values of the normalized frequency shift of these two PTC defect modes increase first and then decrease as α increases. The normalized frequency shift reaches its maximum value when α approaches 0.258 and then undergoes a leapfrog change. From Figure 6(b), as α increases, the frequency ω ₁ remains the same, whereas the frequency ω ₂ decreases all the time. The curves of ω ₂ and ω ₁ intersect when α is equal to 0.258, and these two PTC defect modes become quasi-degenerate modes. The AO coupling becomes stronger, which is not only quadratic but also contains higher-order nonlinear contributions. Here, the term 1 / [ ω j ( 0 ) 2 − ω i ( 0 ) 2 ] in equation (7) increases rapidly as the frequencies of these two modes approach, and the dominant contribution for quadratic coupling comes from each other; hence, the strongest coupling is achieved. At that time, the normalized frequency shift jumps as shown in Figure 6(a). The normalized optical frequency shift for PE contribution was obtained as 3.6 × 10⁻³, which is an order of magnitude larger than the structure of α = 0 under the same input displacement. Besides, Figure 6(c) depicts the relationship between quadratic coupling and wavenumber in the first irreducible Brillouin zone for different α values. With the increase of the wavenumber, a sharp dip of the quadratic coupling can be seen near Γ point, especially for α = 0.256. The quadratic coupling is strong because the two frequencies ω ₂ and ω ₁ are closest to each other at Γ point, which is shown in Figure 2(a). For weak coupling, in other words, when ω ₂ is not so close to ω ₁, the quadratic coupling is almost independent of the wavenumber.

Figure 6

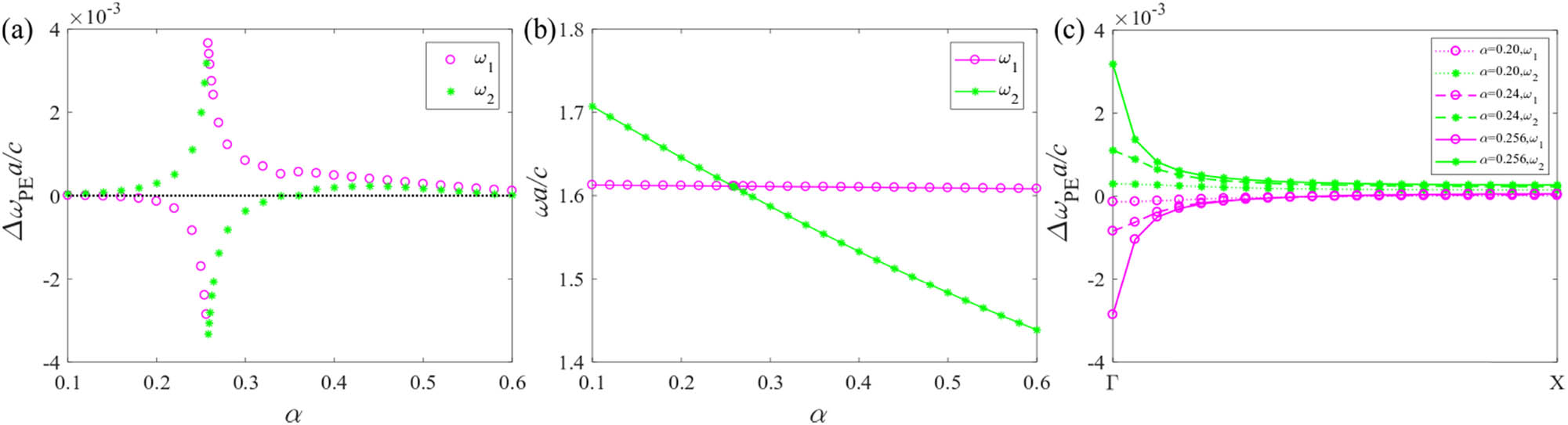
When two PTC defect modes are coupled with the second PNC defect mode, (a) their normalized frequency shift and (b) their unperturbed frequencies versus the relative increment α of the defect layer thickness, and (c) their normalized frequency shift versus the wavenumber in first irreducible Brillouin zone for different α.

5 Conclusions

We applied the perturbation theory to the calculation of the AO coupling in a multilayer PXC cavity. In the calculation of linear AO coupling, four methods were compared. We further focus on the quadratic coupling to find the coupling mechanism, especially for enhancing the coupling. The following conclusions can be drawn:

Among these four methods, “Perturbation + FEM” is the best choice for the AO coupling analysis, the physical interpretation, high-speed computing, and high precision.
As listed in Table 4, the linear, quadratic, or quartic coupling is dominant under specific acoustic and optical mode symmetry. Besides, these modes of symmetry can be changed by adjusting the thickness of the defect layer. Thus, the linear coupling can be transformed to quadratic coupling and vice versa.
Quadratic coupling is enhanced by tuning two defect photonic modes to be quasi-degenerate modes. When the two defect photonic modes become quasi-degenerate modes, the coupling strength is wavenumber dependent and reaches the maximum value in Γ point of the first irreducible Brillouin zone.

Funding information: The authors gratefully acknowledge the financial support of the National Natural Science Foundation of China (NSFC; 11872186) and Fundamental Research Funds for the Central Universities (HUST: 2016JCTD114).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Yariv A, Yeh P. Optical waves in crystals. New York: Wiley; 1984.Search in Google Scholar

[2] Kippenberg TJ, Vahala KJ. Cavity opto-mechanics. Opt Express. 2007;15(25):17172–205.10.1364/OE.15.017172Search in Google Scholar PubMed

[3] Ma H, Qu S, Xu Z. Photonic crystals based on acousto-optic effects. J Appl Phys. 2008;103(10):104904.10.1063/1.2924432Search in Google Scholar

[4] Berstermann T, Brüggemann C, Bombeck M, Akimov A, Yakovlev D, Kruse C, et al. Optical bandpass switching by modulating a microcavity using ultrafast acoustics. Phys Rev B Condens Matter Microelectron Eng. 2010;81(8):085316.10.1103/PhysRevB.81.085316Search in Google Scholar

[5] Sun Y, Peng Y, Zhou T, Liu H, Gao P. Study of the mechanical-electrical-magnetic properties and the microstructure of three-layered cement-based absorbing boards. Rev Adv Mater Sci. 2020;59(1):160–9.10.1515/rams-2020-0014Search in Google Scholar

[6] Lofy J, Gasparian V, Gevorkian Z, Jódar E. Faraday and Kerr effects in right and left-handed films and layered materials. Rev Adv Mater Sci. 2020;59(1):243–51.10.1515/rams-2020-0032Search in Google Scholar

[7] Bian Z, Yang S, Zhou X, Hui D. Band gap manipulation of viscoelastic functionally graded phononic crystal. Nanotechnol Rev. 2020;9(1):515–23.10.1515/ntrev-2020-0042Search in Google Scholar

[8] Maldovan M, Thomas EL. Simultaneous localization of photons and phonons in two-dimensional periodic structures. Appl Phys Lett. 2006;88(25):251907.10.1063/1.2216885Search in Google Scholar

[9] Mohammadi S, Eftekhar AA, Khelif A, Adibi A. Simultaneous two-dimensional phononic and photonic band gaps in opto-mechanical crystal slabs. Opt Express. 2010;18(9):9164–72.10.1364/OE.18.009164Search in Google Scholar PubMed

[10] Bria D, Assouar M, Oudich M, Pennec Y, Vasseur J, Djafari-Rouhani B. Opening of simultaneous photonic and phononic band gap in two-dimensional square lattice periodic structure. J Appl Phys. 2011;109(1):014507.10.1063/1.3530682Search in Google Scholar

[11] Pennec Y, Djafari-Rouhani B, El Boudouti E, Li C, El Hassouani Y, Vasseur J, et al. Simultaneous existence of phononic and photonic band gaps in periodic crystal slabs. Opt Express. 2010;18(13):14301–10.10.1364/OE.18.014301Search in Google Scholar PubMed

[12] Safavi-Naeini AH, Hill JT, Meenehan S, Chan J, Gröblacher S, Painter O. Two-dimensional phononic-photonic band gap optomechanical crystal cavity. Phys Rev Lett. 2014;112(15):153603.10.1103/PhysRevLett.112.153603Search in Google Scholar PubMed

[13] Dong HW, Wang YS, Ma TX, Su XX. Topology optimization of simultaneous photonic and phononic bandgaps and highly effective phoxonic cavity. J Optical Soc Am B. 2014;31(12):2946–55.10.1364/JOSAB.31.002946Search in Google Scholar

[14] Dong HW, Wang YS, Zhang C. Topology optimization of chiral phoxonic crystals with simultaneously large phononic and photonic bandgaps. IEEE Photonics J. 2017;9(2):1–16.10.1109/JPHOT.2017.2665700Search in Google Scholar

[15] Sadat-Saleh S, Benchabane S, Baida FI, Bernal M-P, Laude V. Tailoring simultaneous photonic and phononic band gaps. J Appl Phys. 2009;106(7):074912.10.1063/1.3243276Search in Google Scholar

[16] Tang Z, Jiang Z, Chen T, Lei D, Yan W, Qiu F, et al. Simultaneous microwave photonic and phononic band gaps in piezoelectric–piezomagnetic superlattices with three types of domains in a unit cell. Phys Lett B. 2016;380(20):1757–62.10.1016/j.physleta.2016.02.037Search in Google Scholar

[17] Laude V, Beugnot J-C, Benchabane S, Pennec Y, Djafari-Rouhani B, Papanikolaou N, et al. Simultaneous guidance of slow photons and slow acoustic phonons in silicon phoxonic crystal slabs. Opt Express. 2011;19(10):9690–8.10.1364/OE.19.009690Search in Google Scholar PubMed

[18] Hasan T. Mechanical properties of nanomaterials: a review. Nanotechnol Rev. 2020;9(1):259–73.10.1515/ntrev-2020-0021Search in Google Scholar

[19] Eichenfield M, Camacho R, Chan J, Vahala KJ, Painter O. A picogram-and nanometre-scale photonic-crystal optomechanical cavity. Nature. 2009;459(7246):550–5.10.1038/nature08061Search in Google Scholar PubMed

[20] Eichenfield M, Chan J, Camacho RM, Vahala KJ, Painter O. Optomechanical crystals. Nature. 2009;462(7269):78.10.1038/nature08524Search in Google Scholar PubMed

[21] Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, et al. Optomechanically induced transparency. Science. 2010;330(6010):1520–3.10.1126/science.1195596Search in Google Scholar PubMed

[22] Safavi-Naeini AH, Alegre TM, Chan J, Eichenfield M, Winger M, Lin Q, et al. Electromagnetically induced transparency and slow light with optomechanics. Nature. 2011;472(7341):69–73.10.1038/nature09933Search in Google Scholar PubMed

[23] Chang D, Safavi-Naeini AH, Hafezi M, Painter O. Slowing and stopping light using an optomechanical crystal array. N J Phys. 2011;13(2):023003.10.1088/1367-2630/13/2/023003Search in Google Scholar

[24] Chan J, Alegre TM, Safavi-Naeini AH, Hill JT, Krause A, Gröblacher S, et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature. 2011;478(7367):89–92.10.1038/nature10461Search in Google Scholar PubMed

[25] Safavi-Naeini AH, Painter O. Design of optomechanical cavities and waveguides on a simultaneous bandgap phononic-photonic crystal slab. Opt Express. 2010;18(14):14926–43.10.1364/OE.18.014926Search in Google Scholar PubMed

[26] El-Jallal S, Oudich M, Pennec Y, Djafari-Rouhani B, Makhoute A, Rolland Q, et al. Optomechanical interactions in two-dimensional Si and GaAs phoXonic cavities. J Phys Condens Matter. 2013;26(1):015005.10.1088/0953-8984/26/1/015005Search in Google Scholar PubMed

[27] Rolland Q, Oudich M, El-Jallal S, Dupont S, Pennec Y, Gazalet J, et al. Acousto-optic couplings in two-dimensional phoxonic crystal cavities. Appl Phys Lett. 2012;101(6):061109.10.1063/1.4744539Search in Google Scholar

[28] Djafari-Rouhani B, El-Jallal S, Pennec Y. Phoxonic crystals and cavity optomechanics. CR Phys. 2016;17(5):555–64.10.1016/j.crhy.2016.02.001Search in Google Scholar

[29] El-Jallal S, Oudich M, Pennec Y, Djafari-Rouhani B, Laude V, Beugnot J, et al. Analysis of optomechanical coupling in two-dimensional square lattice phoxonic crystal slab cavities. Phys Rev B. 2013;88(20):205410.10.1103/PhysRevB.88.205410Search in Google Scholar

[30] Hsiao FL, Hsieh HY, Hsieh CY, Chiu CC. Acousto–optical interaction in fishbone-like one-dimensional phoxonic crystal nanobeam. Appl Phys A. 2014;116(3):873–8.10.1007/s00339-014-8456-6Search in Google Scholar

[31] Chiu CC, Chen WM, Sung KW, Hsiao FL. High-efficiency acousto-optic coupling in phoxonic resonator based on silicon fishbone nanobeam cavity. Opt Express. 2017;25(6):6076–91.10.1364/OE.25.006076Search in Google Scholar PubMed

[32] Hsiao FL, Hsieh CY, Hsieh HY, Chiu CC. High-efficiency acousto-optical interaction in phoxonic nanobeam waveguide. Appl Phys Lett. 2012;100(17):171103.10.1063/1.4705295Search in Google Scholar

[33] Eichenfield M, Chan J, Safavi-Naeini AH, Vahala KJ, Painter O. Modeling dispersive coupling and losses of localized optical and mechanical modes in optomechanical crystals. Opt Express. 2009;17(22):20078–98.10.1364/OE.17.020078Search in Google Scholar PubMed

[34] Chandel VS, Wang G, Talha M. Advances in modelling and analysis of nano structures: a review. Nanotechnol Rev. 2020;9(1):230–58.10.1515/ntrev-2020-0020Search in Google Scholar

[35] Ma TX, Wang YS, Zhang C. Enhancement of acousto-optical coupling in two-dimensional air-slot phoxonic crystal cavities by utilizing surface acoustic waves. Phys Lett B. 2017;381(4):323–9.10.1016/j.physleta.2016.10.052Search in Google Scholar

[36] Lin TR, Lin CH, Hsu JC. Enhanced acousto-optic interaction in two-dimensional phoxonic crystals with a line defect. J Appl Phys. 2013;113(5):053508.10.1063/1.4790288Search in Google Scholar

[37] Hsu JC, Lu TY, Lin TR. Acousto-optic coupling in phoxonic crystal nanobeam cavities with plasmonic behavior. Opt Express. 2015;23(20):25814–26.10.1364/OE.23.025814Search in Google Scholar PubMed

[38] Pennec Y, Laude V, Papanikolaou N, Djafari-Rouhani B, Oudich M, El Jallal S, et al. Modeling light-sound interaction in nanoscale cavities and waveguides. Nanophotonics. 2014;3(6):413–40.10.1515/nanoph-2014-0004Search in Google Scholar

[39] Jiang W, Sarabalis CJ, Dahmani YD, Patel RN, Mayor FM, McKenna TP, et al. Efficient bidirectional piezo-optomechanical transduction between microwave and optical frequency. Nat Commun. 2020;11(1):1–7.10.1364/CLEO_AT.2020.AF3K.4Search in Google Scholar

[40] Kalaee M, Paraiso TK, Pfeifer H, Painter O. Design of a quasi-2D photonic crystal optomechanical cavity with tunable, large x 2-coupling. Opt Express. 2016;24(19):21308–28.10.1364/OE.24.021308Search in Google Scholar PubMed

[41] Kaviani H, Healey C, Wu M, Ghobadi R, Hryciw A, Barclay PE. Nonlinear optomechanical paddle nanocavities. Optica. 2015;2(3):271–4.10.1109/PN.2015.7292526Search in Google Scholar

[42] Paraïso TK, Kalaee M, Zang L, Pfeifer H, Marquardt F, Painter O. Position-squared coupling in a tunable photonic crystal optomechanical cavity. Phys Rev X. 2015;5(4):041024.10.1103/PhysRevX.5.041024Search in Google Scholar

[43] Matsuda O, Wright O. Reflection and transmission of light in multilayers perturbed by picosecond strain pulse propagation. J Opt Soc Am B. 2002;19(12):3028–41.10.1364/JOSAB.19.003028Search in Google Scholar

[44] Almpanis E, Papanikolaou N, Stefanou N. Breakdown of the linear acousto-optic interaction regime in phoxonic cavities. Opt Express. 2014;22(26):31595–607.10.1364/OE.22.031595Search in Google Scholar

[45] Psarobas IE, Papanikolaou N, Stefanou N, Djafari-Rouhani B, Bonello B, Laude V. Enhanced acousto-optic interactions in a one-dimensional phoxonic cavity. Phys Rev B. 2010;82(17):174303.10.1103/PhysRevB.82.174303Search in Google Scholar

[46] Stefanou N, Yannopapas V, Modinos A. Heterostructures of photonic crystals: frequency bands and transmission coefficients. Comput Phys Commun. 1998;113(1):49–77.10.1016/S0010-4655(98)00060-5Search in Google Scholar

[47] Stefanou N, Yannopapas V, Modinos A. MULTEM 2: a new version of the program for transmission and band-structure calculations of photonic crystals. Comput Phys Commun. 2000;132(1–2):189–96.10.1016/S0010-4655(00)00131-4Search in Google Scholar

[48] Sainidou R, Stefanou N, Psarobas I, Modinos A. A layer-multiple-scattering method for phononic crystals and heterostructures of such. Comput Phys Commun. 2005;166(3):197–240.10.1016/j.cpc.2004.11.004Search in Google Scholar

[49] Johnson SG, Ibanescu M, Skorobogatiy M, Weisberg O, Joannopoulos J, Fink Y. Perturbation theory for Maxwell’s equations with shifting material boundaries. Phys Rev E. 2002;65(6):066611.10.1103/PhysRevE.65.066611Search in Google Scholar PubMed

[50] El-Soussi A, Gazalet J, Dupont S, Kastelik J. Evaluation of second order optomechanical coupling strength in photonic crystal cavities including the case of degenerated modes. J Opt. 2019;21(4):045103.10.1088/2040-8986/ab0400Search in Google Scholar

[51] Mizuno S, Tamura S. Theory of acoustic-phonon transmission in finite-size superlattice systems. Phys Rev B. 1992;45(2):734.10.1103/PhysRevB.45.734Search in Google Scholar

[52] Yariv A, Yeh P. Photonics: optical electronics in modern communications. New York: Oxford university press; 2007.Search in Google Scholar

Received: 2021-03-15

Revised: 2021-05-01

Accepted: 2021-05-24

Published Online: 2021-06-09

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/ntrev-2021-0034

Keywords for this article

acousto-optic coupling; phoxonic crystals; photoelastic effect; transfer matrix method; finite elements method; moving interface effect

Creative Commons

BY 4.0