Shrinking the surface plasmon

Fan Yang; Kun Ding; John Brian Pendry

doi:10.1515/nanoph-2020-0361

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Shrinking the surface plasmon

Fan Yang , Kun Ding und John Brian Pendry

Veröffentlicht/Copyright: 31. Juli 2020

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nanophotonics Band 10 Heft 1

Abstract

Surface plasmons at an interface between dielectric and metal regions can in theory be made arbitrarily compact normal to the interface by introducing extreme anisotropy in the material parameters. We propose a metamaterial structure comprising a square array of gold cylinders and tune the filling factor to achieve the material parameters we seek. Theory is compared to a simulation wherein the unit cell dimensions of the metamaterial are shown to be the limiting factor in the degree of localisation achieved.

Keywords: metamaterials; surface plasmons; transformation optics

Surface plasmons exist at an interface between a metal, ε_m < 0, and dielectric, ε_d > 0 [1], [2], [3]. If these surface states have in-plane wave vectors k_x, they are confined normal to the surface by imaginary wave vectors,

(1)kz=+ikx2−εd(ωsp)c0−2ωsp2 , z>0 ,kz=−ikx2−εm(ωsp)c0−2ωsp2, z<0 ,

where we assume that the dielectric occupies the space z > 0, ω_sp is the surface plasmon frequency and c₀ is the velocity of light in free space. We have assumed isotropic media: ε_d, ε_m are the permittivities of the dielectric and metal, respectively. They are in general dependent on frequency. At lower values of k_x, the surface plasmon is rather diffuse in extent, but at large values of k, the surface plasmon becomes compact and increasingly electrostatic in nature: kz→±ikx and is confined to the surface region. This compact nature results in a high density of states in the immediate vicinity of the surface, which is exploited in many applications. In this letter, we show how by exploiting transformation optics theory, surface plasmons can in principle be made arbitrarily compact, depending only on the availability of suitable materials. We propose a new metamaterial designed to address the latter issue.

Transformation optics [4], [5], [6], [7] is a theory that relates distortions of geometry to redefined values of permittivity and permeability. For example, in our case, we seek to compress the surface plasmon normal to the surface. In the study by Kundtz et al. [7], we learn that if we compress the wave fields by a factor β (β < 1) so that the new imaginary wave vectors increase by a factor β⁻¹, in order that the compressed wave fields continue to obey Maxwell’s equations, we must introduce new values of permittivity as follows,

(2)εd‖=β−1εd, εm‖=β−1εm ,εdz=βεd, εmz=βεm ,

with analogous formulas for the permeability. This formula solves our problem at a stroke, always provided of course that we can find suitably anisotropic materials. It is also possible to expand the surface plasmon by choosing β > 1 [8].

To solve the problem of finding permittivities tunable in the fashion required, we turn to metamaterials [9], [10], [11], [12], [13]. These are composite materials structured on a scale much less than the relevant wavelengths in the problem, whose properties owe more to their structure than to their chemical composition. Tuning the magnetic response is more of a problem because even metamaterials struggle with magnetism at optical frequencies. However, here, we appeal to the mainly electrostatic nature of the surface plasmon at higher values of k_x and show that a high degree of compression can be achieved by tuning the electrical response alone.

Our target metamaterial structure is shown in Figure 1. In the first instance, we use a simple approximation to find the effective medium parameters of our structure, which we then check against COMSOL simulations. The Maxwell Garnett theory gives the following formula for the metamaterial parameters [14], [15],

(3)ε∥=εd(1+fm)εm+(1−fm)εd(1+fm)εd+(1−fm)εm, εz=fmεm+(1−fm)εd ,

where f_m is the metal volume filling fraction of the cylinders. We model the metal with a Drude permittivity and the dielectric as vacuum,

(4)εm=1−ωp2ω(ω+iγ), ωp=8.95eV, γ=0.329eV, εd=1 ,

with the metal parameters chosen to model gold. In the first instance, we shall neglect losses, γ = 0, but later when comparing to COMSOL simulations, loss is taken into account.

$Figure 1: A two-dimensional square array of metallic cylinders much smaller than the relevant wavelengths, embedded in a dielectric. In the plane z = 0, there is an interface between two sets of cylinders. This is where the interface plasmon forms. We tune the volume fraction to achieve the desired properties of an effective medium shown on the right.$

Figure 1:

A two-dimensional square array of metallic cylinders much smaller than the relevant wavelengths, embedded in a dielectric. In the plane z = 0, there is an interface between two sets of cylinders. This is where the interface plasmon forms. We tune the volume fraction to achieve the desired properties of an effective medium shown on the right.

Although (3) is an approximation, it can be shown to be highly accurate [16]. Figure 2 compares a COMSOL simulation of transmission and reflection coefficients for the structure shown in Figure 1, with an effective medium calculation using the parameters given by the Maxwell Garnet formula.

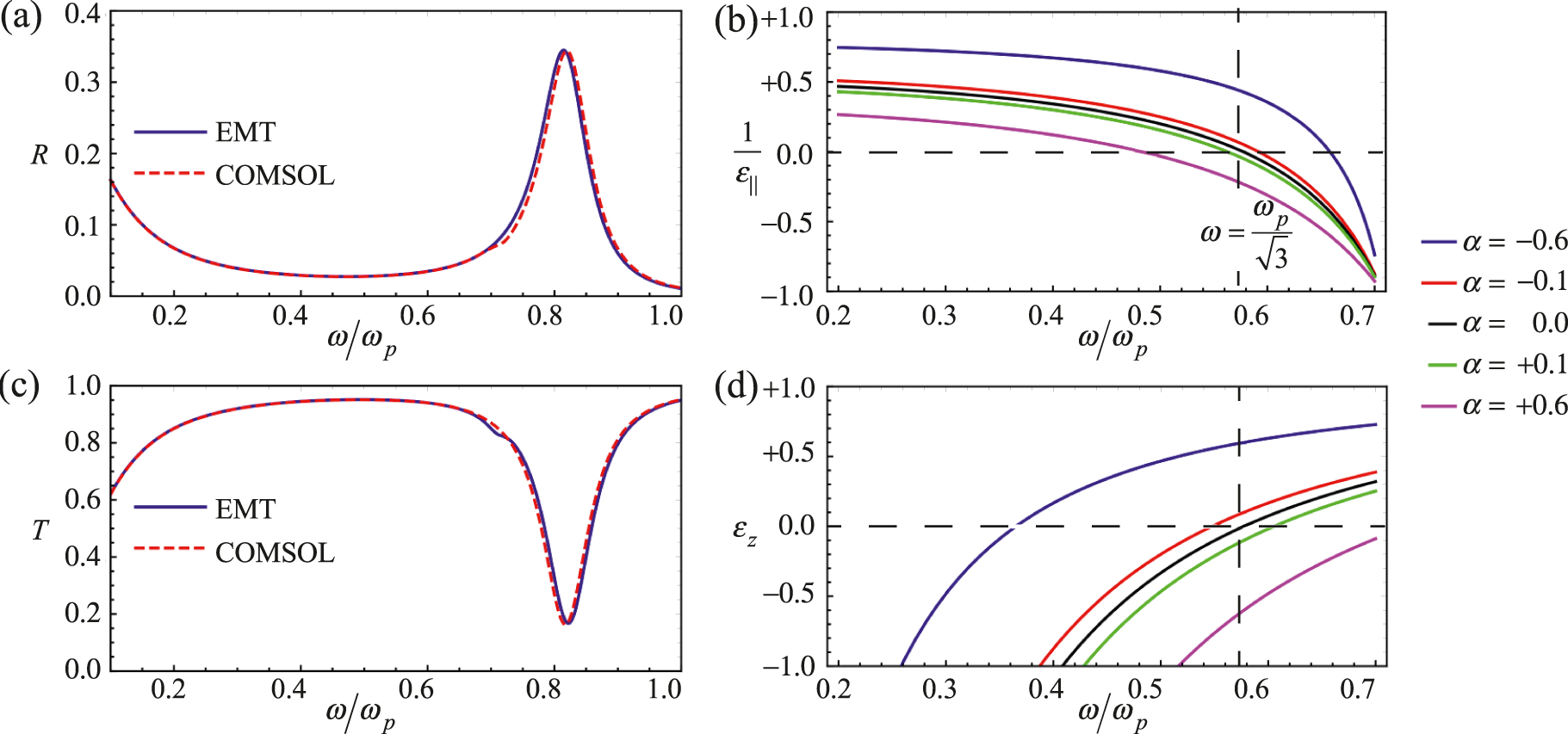
$Figure 2: (a) Reflection from and (c) transmission through one unit cell of a nanowire metamaterial with period 10 nm and filling ratio fm = 1/3, calculated with effective medium theory (EMT) theory and COMSOL. The incident angle is at 45° to the z-axis, and the electric field has both Ez and Ex components. The magnetic field has only a Hy component. (b) 1/ε∥$1/{\varepsilon }_{\parallel }$ for various −0.6 < α < 0.6, plotted against ω/ωp. (d) εz for various −0.6 < α < 0.6.$

Figure 2:

(a) Reflection from and (c) transmission through one unit cell of a nanowire metamaterial with period 10 nm and filling ratio f_m = 1/3, calculated with effective medium theory (EMT) theory and COMSOL. The incident angle is at 45° to the z-axis, and the electric field has both E_z and E_x components. The magnetic field has only a H_y component. (b) 1/ε∥ for various −0.6 < α < 0.6, plotted against ω/ω_p. (d) ε_z for various −0.6 < α < 0.6.

The challenge is to design two metamaterials each with huge anisotropies, but one pair taking negative values and the other taking positive values. This will realize our requirements for compression of a surface plasmon at the interface between the two.

Recognizing that ε_d, ε_m have opposite signs, inspection of (3) shows that we can make the real part of ε_z very small by choice of fm=εd/(εd+|εm|). The imaginary part of ε_m will be a limiting factor in how close we can come to our ideal. Having chosen f_m, we can solve for,

(5)ε∥=−εd|εm|(εd+|εm|)2|εd|2+|εm|εd−|εm|2 ,

where we have recognized that ε_m < 0. We can arrange that the denominator takes a very small value by adjusting |εm|/εd=2 and hence f_m = 1/3. Thus, by exploiting the properties of a plasmonic material, we can achieve our goal of extreme anisotropy. Furthermore, if we vary f_m about the singular point,

(6)fm=(1+α)/3 ,

we find that for α > 0, we have an extremely anisotropic metal, and for α < 0, we have an extremely anisotropic dielectric.

In Figure 2b and d, we plot the Maxwell Garnett formula for the metallic and dielectric metamaterial anisotropic permittivities for several values of α. When α = 0, the curves intersect at zero and a frequency of ω/ωp=1/3=0.5774. Somewhere in the range where the α > 0 parameters are both negative and the α < 0 parameters are both positive, we expect to find a surface plasmon.

Next, we present some calculations to demonstrate the feasibility of our theory.

We also need to recognize that the metamaterial concept only holds good on length scales greater than the metamaterial structure, which we take to be 10 nm.

Figure 3 shows dispersion of the surface plasmon trapped between the metametal and the metadielectric calculated for an effective medium corresponding to two media with filling factors defined by ±α. Shown on the same plot is the light line for the metadielectric. Dispersion curves to the right of this line represent surface plasmons trapped at the surface; to the left of this line, dispersion curves represent waves that are perfectly transmitted across the interface in the manner of a Brewster condition. This is a typical behaviour when a surface plasmon dispersion curve appears to cross the light line. For example, the α = ±0.1 surface plasmon exists between 0.56268 < ω/ω_p < 0.57765. The pure metal-vacuum surface plasmon is shown for comparison. It disperses much more rapidly with frequency than the compressed surface plasmon and therefore has a much lower density of states. All dispersion curves are degenerate at ω=ωp/3; increasing α lowers the frequency at k_x = 0 while increasing the limiting frequency at kx→∞.

Figure 3:

Dispersion of the surface plasmons for α = 0.1 and α = 0.6 together with dispersion of the pure metal-vacuum surface plasmon plotted against k_x in units of m⁻¹. The dotted lines show the associated light lines in the dielectric.

Figure 4a shows an interface surface state plotted as a function of distance from the interface calculated in the effective medium approximation. Compared to the surface plasmon existing between a pure metal and pure vacuum, we can see very large compression by a factor of about 20 when α = ±0.1. Furthermore, as noted in Figure 3, the density of states is greatly enhanced by the flattened dispersion of the interface surface plasmon.

Figure 4:

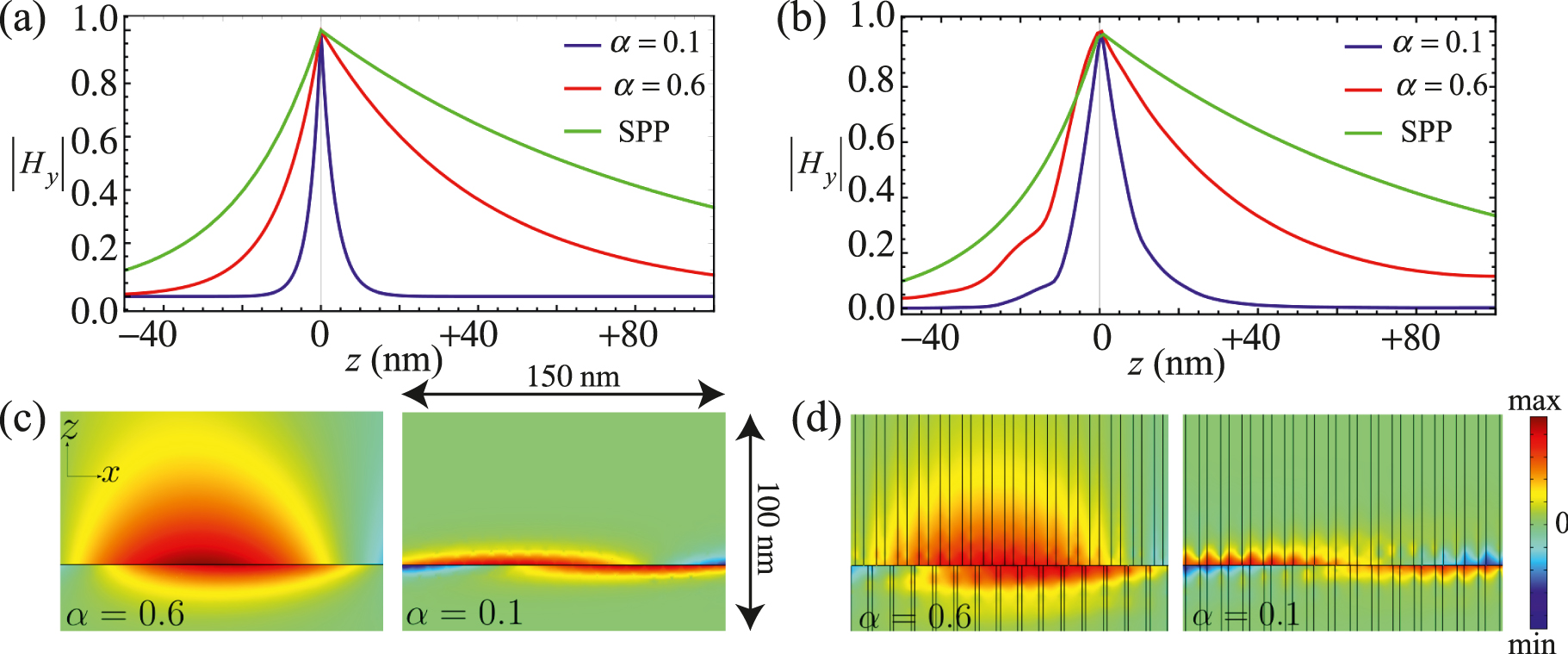
(a) Modulus of the magnetic field for the interface plasmon calculated in the effective medium approximation at k_x = 2.26 × 10⁷ m⁻¹ compared to a surface plasmon that exists between a pure metal and pure vacuum at the same frequency. (b) The same calculation but now deploying COMSOL on the metamaterial structure, lattice spacing a = 10 nm. (c) An effective medium calculation of the magnetic field distribution plotted in the vicinity of the interface. (d) The same calculation but now deploying COMSOL on the metamaterial structure and plotted in a plane taken through the centre of the cylinders. The surface mode is excited by a surface current along the x-direction at the interface, which makes the magnetic field discontinuous.

So far, we have worked in the effective medium approximation, but now, we make a more realistic test by including the microstructure of the metamaterial and the loss parameter γ = 0.329 eV, which so far, we have taken to be zero. Loss is also included in the effective medium calculation in Figure 4. Figure 4b presents a COMSOL simulation of a metamaterial structure in which the metal permittivity includes loss as described in (4), and the lattice period is 10 nm. At the interface, the two sets of cylinders on either side are coaxial with one other and touch at the interface. The pure metal/dielectric SPP is unchanged of course, but we see spreading of the metamaterial interface plasmon. This is mainly due to the finite dimensions of the metamaterial unit cell: on length scales <10 nm, the effective medium approximation breaks down. Nevertheless, our model metamaterial still shows substantial compression of the surface plasmon by about a factor of 7.

In conclusion, we have shown that in theory, interface surface plasmons can be arbitrarily compressed provided that the specified anisotropic material parameters can be realized. We proposed a metamaterial structure based on a square array of gold cylinders and showed how the design parameters can be tuned to approach the ideal anisotropic parameters for the metamaterials on each side of the interface. In practice, although substantial compression of the interface surface plasmon can be achieved, the extreme values predicted by an ideal theory are limited first by the finite unit cell of the metamaterial, which limits compression to no less than the unit cell dimensions, and secondly by metallic losses, which limit the compression of the density of states and hence also of the local density of states.

Corresponding author: John Brian Pendry, The Blackett Laboratory, Imperial College London, London, SW7 2AZ, UK, E-mail: j.pendry@imperial.ac.uk

Funding source: Gordon and Betty Moore Foundation

Acknowledgements

F.Y. acknowledges the Gordon and Betty Moore Foundation. J.B.P. and K.D. acknowledge funding from the Gordon and Betty Moore Foundation.

Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: Funding from the Gordon and Betty Moore Foundation.
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.

References

[1] R. H. Ritchie, “Plasma losses by fast electrons in thin films,” Phys. Rev., vol. 106, pp. 874–881, 1957. https://doi.org/10.1103/physrev.106.874.Suche in Google Scholar

[2] W. L. Barnes, A. Dereux, and T. W. Ebbesen, “Surface plasmon subwavelength optics,” Nature, vol. 424, pp. 824–830, 2003. https://doi.org/10.1038/nature01937.Suche in Google Scholar PubMed

[3] S. A. Maier, Plasmonics: Fundamentals and Applications, New York, Springer Science & Business Media, 2007.10.1007/0-387-37825-1Suche in Google Scholar

[4] A. Ward and J. B. Pendry, “Refraction and geometry in Maxwell’s equations,” J. Mod. Opt., vol. 43, pp. 773–793, 1996. https://doi.org/10.1080/09500349608232782.Suche in Google Scholar

[5] J. B. Pendry, D. Schurig, and D. R. Smith, “Controlling electromagnetic fields,” Science, vol. 312, pp. 1780–1782, 2006. https://doi.org/10.1126/science.1125907.Suche in Google Scholar PubMed

[6] U. Leonhardt, “Optical conformal mapping,” Science, vol. 312, pp. 1777–1780, 2006. https://doi.org/10.1126/science.1126493.Suche in Google Scholar PubMed

[7] N. B. Kundtz, D. R. Smith, and J. B. Pendry, “Electromagnetic design with transformation optics,” Proc. IEEE, vol. 99, pp. 1622–1633, 2011. https://doi.org/10.1109/jproc.2010.2089664.Suche in Google Scholar

[8] F. Yang, S. Ma, K. Ding, S. Zhang, and J. B. Pendry, “Continuous topological transition from metal to dielectric,” Proc. Natl. Acad. Sci., 2020, to appear. https://doi.org/10.1073/pnas.2003171117.Suche in Google Scholar PubMed PubMed Central

[9] J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, “Magnetism from conductors and enhanced non-linear phenomena,” IEEE Trans. Microw. Theor. Tech., vol. 47, pp. 2075–2084, 1999. https://doi.org/10.1109/22.798002.Suche in Google Scholar

[10] D. R. Smith, J. B. Pendry, and M. C. K. Wiltshire, “Metamaterials and negative refractive index,” Science, vol. 305, pp. 788–792, 2004. https://doi.org/10.1126/science.1096796.Suche in Google Scholar PubMed

[11] J. B. Pendry, “Metamaterials and the control of electromagnetic fields”, in Coherence and Quantum Optics IX, N. P. Bigelow, J. H. Eberly and C. R. StroudJr., Eds., Washington, DC, OSA Publications, 2009, 2008, pp. 42–52.10.1364/CQO.2007.CMB2Suche in Google Scholar

[12] W. Cai and V. M. Shalaev, Optical Metamaterials, New York, Springer, 2010.10.1007/978-1-4419-1151-3Suche in Google Scholar

[13] A. Poddubny, I. Iorsh, P. Belov, and Y. Kivshar, “Hyperbolic metamaterials,” Nat. Photonics, vol. 7, pp. 948–957, 2013. https://doi.org/10.1038/nphoton.2013.243.Suche in Google Scholar

[14] S. I. Bozhevolnyi, L. Martin-Moreno, and F. Garcia-Vidal, Quantum Plasmonics, New York, NY, Springer, 2017.10.1007/978-3-319-45820-5Suche in Google Scholar

[15] J. Elser, R. Wangberg, V. A. Podolskiy, and E. E. Narimanov, “Nanowire metamaterials with extreme optical anisotropy,” Appl. Phys. Lett., vol. 89, p. 261102, 2006. https://doi.org/10.1063/1.2422893.Suche in Google Scholar

[16] D. R. Smith, S. Schultz, P. Markos, and C. M. Soukoulis, “Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients,” Phys. Rev. B, vol. 65, p. 195104, 2002. https://doi.org/10.1103/physrevb.65.195104.Suche in Google Scholar

Received: 2020-07-02

Accepted: 2020-07-16

Published Online: 2020-07-31

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nanoph-2020-0361

Schlagwörter für diesen Artikel

metamaterials; surface plasmons; transformation optics

Creative Commons

BY 4.0