Abstract
Broadband, quantum-engineered, quantum cascade lasers (QCLs) are the most powerful chip-scale sources of optical frequency combs (FCs) across the mid-infrared and the terahertz (THz) frequency range. The inherently short intersubband upper state lifetime spontaneously allows mode proliferation, with large quantum efficiencies, as a result of the intracavity four-wave mixing. QCLs can be easily integrated with external elements or engineered for intracavity embedding of nonlinear optical components and can inherently operate as quantum detectors, providing an intriguing technological platform for on-chip quantum investigations at the nanoscale. The research field of THz FCs is extremely vibrant and promises major impacts in several application domains crossing dual-comb spectroscopy, hyperspectral imaging, time-domain nanoimaging, quantum science and technology, metrology and nonlinear optics in a miniaturized and compact architecture. Here, we discuss the fundamental physical properties and the technological performances of THz QCL FCs, highlighting the future perspectives of this frontier research field.
1 Introduction
Frequency comb (FC) synthesizers [1] revolutionized the field of optical metrology and spectroscopy, emerging as one of the main photonic tools of the third millennium. The peculiar characteristic, which makes a FC a unique optical device, is the multifrequency coherent state of its emission, which is composed, in the frequency domain, by a series of evenly spaced optical modes, all locked in phase. They inherently generate a precise frequency ruler, capable of providing a direct link between optical and microwave/radio frequencies. Due to the tight phase relation among all optical modes, FC emission can be described by two key parameters: the carrier frequency offset and the spectral frequency spacing [2], [3].
Traditionally generated by frequency-stabilized and controlled femtosecond mode-locked lasers, FCs quickly conquered the visible and near-infrared (IR) domain, where different generation techniques were successfully demonstrated, tested and commercialized, such as Ti:Sa [4], fiber-based lasers [5], optical microresonators [6], upconversion of low frequency sources [7] or downconversion of high-frequency combs [8]. High optical powers, outstanding long-term stability, broad spectral coverage and frequency tunability have been demonstrated so far [9]. Despite such impressive performances, most of these systems have a relatively large footprint, even in a fiber-based configuration.
In the mid-infrared domain, FCs are conventionally generated via difference frequency generation (DFG) [10], [11], [12] by continuous-wave (CW) or pulsed lasers and have been widely exploited for high-resolution sensing of molecular fingerprints. Mid-IR FCs also include optically pumped microresonators [13] or electrically pumped sources as interband cascade lasers (ICL–FCs) [14] and quantum cascade lasers (QCLs) (QCL–FCs) [15], [16], [17], [18]. A common characteristic of these latter sources is the high third-order (Kerr) nonlinearity, which allows comb generation via degenerate and nondegenerate four-wave mixing (FWM) [15], [19] (Figure 1).

Schematic representation of frequency comb formation mechanisms through degenerate and nondegenerate four-wave mixing (FWM).
At THz frequencies, supercontinuum generation, recently recognized as FC emission [20], has been conventionally obtained by optical rectification of pulsed lasers. A few microwatts power output has been achieved in a configuration relying on bulky mode-locked lasers. This limits a broader use of these sources in application fields like optical communications, in-situ molecular spectroscopy, gas sensing, homeland security, quantum optics, where chip-scale configurations are highly desirable.
The advent of miniaturized THz QCL frequency combs [21], [22], [23] revolutionized the field, opening new avenues in unexplored domains. In a THz QCL, FC operation occurs spontaneously owing to intracavity third-order nonlinear optical processes, stemming from a large nonlinear χ(3) susceptibility (7 × 1016 (m/V)2) [24] in the GaAs/AlGaAs active material. Specifically, the resonant third-order nonlinearity inherently induces self-phase locking by FWM. FWM tends to homogenize the mode spacing and, consequently, acts as the main mode proliferation and comb generation mechanism in a free running QCL.
In this opinionated article, we will review QCL FCs emitting at THz frequencies, discussing their performances, present techniques to assess their coherence properties, applications, and with a final outlook on future perspectives of this rapidly progressing research field.
2 Quantum cascade laser frequency combs at THz frequencies: architectures and performances
Electrically pumped QCLs, in either standard [21], [22], [23] or DFG configurations [25], are the most compact on-chip sources of FCs at THz frequencies. QCLs have indeed some peculiar features that make them unique for devising FCs: the broad optical bandwidth (OB) (up to an octave) [22], the inherently high optical power levels (hundred mW in CW, W- in pulsed mode) [26], [27], [28] and the high spectral purity (intrinsic linewidths of ∼100 Hz) [29]. Such a combination of specs recently allowed designing THz QCL FCs covering an OB ≤ 1.2 THz [22], [23] delivering CW optical powers of 4–8 mW [23], [30] with a THz power/comb tooth in the 3 µW [31] to 6 µW [21] range in standard double-metal configurations and hundred nW in the DFG configuration [25].
THz QCL FCs can be quantum engineered with either homogeneous [21], [32] or heterogeneous designs [22], [23], [31]. The latter configuration relies on multistacked active regions (ARs) that ideally should display common threshold currents [23] and that are conventionally exploited to target a broad spectral coverage; conversely, homogenous ARs usually display much narrower gain profiles (≤600 GHz) [21], [32], [33], but are in principle easier to be injection locked in the laser operation regime in which dispersion is not compensated.
In a free-running multimode QCL, the modes are not uniformly spaced owing to chromatic dispersion. As result of the frequency-dependent refractive index, the laser free spectral range is index dependent, producing an unevenly spaced spectrum. The interplay between FWM and group velocity dispersion (GVD) in the laser cavity therefore has a major role in determining the QCL comb degradation mechanism. Figure 2a and b show the gain profile and the corresponding group delay dispersion (GDD) in the case of a hererogeneous (Figure 2a) and homogeneous (Figure 2b) THz QCL, respectively.
![Figure 2: Gain of the QCL (black), plotted as a function of frequency, together with the corresponding group delay dispersion (red), in the case of a (a) heterogeneous (Reproduced from the study by Garrasi et al. [23]) or (b) homogeneous THz QCL. QCLs, quantum cascade lasers.](/document/doi/10.1515/nanoph-2020-0429/asset/graphic/j_nanoph-2020-0429_fig_002.jpg)
Gain of the QCL (black), plotted as a function of frequency, together with the corresponding group delay dispersion (red), in the case of a (a) heterogeneous (Reproduced from the study by Garrasi et al. [23]) or (b) homogeneous THz QCL. QCLs, quantum cascade lasers.
Gain medium engineering inherently leads to a flat top gain implemented only at the desired bias point, meaning that the nature of that gain media itself entangles the dispersion dynamics at other biases. As a result, FC operation usually occurs over less than 25% of the lasing bias range [21], [22], [23], [31].
Handling such a bias-dependent dispersion compensation, at small far-infrared photon energies (10 meV), is a very challenging task. Present attempts include passive or active schemes. In the first case, the laser bar can be shaped with an integrated dispersion compensator [21] providing a negative GVD to cancel the positive cavity dispersion but allows achieving FC operation over only 29% of the QCL operational regime. Alternative configurations include tunable Gires–Tournois interferometers (GTIs), comprising a movable gold mirror backcoupled with the QCL (Figure 3a) defining an external cavity, which leads to a further 15% increase of the regime where the THz QCL operates as a FC [34], as a result of a partial compensation of the total GDD.
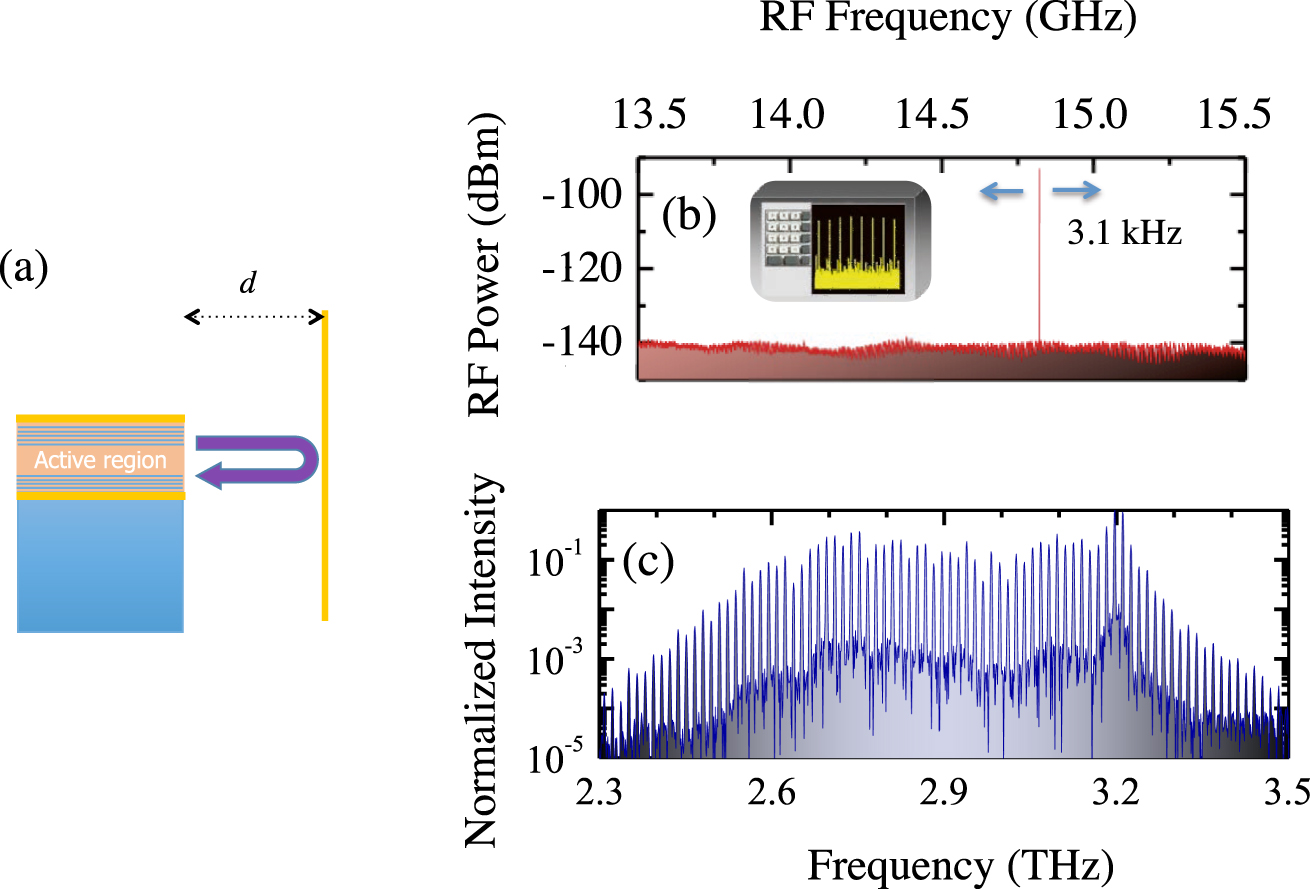
(a) Chip-scale Gires–Tournois interferometer (GTI): Part of the light emitted from the QCL back facet is reflected back into the waveguide mode. (b) Intermode beatnote frequency measured in a heterogenorus THz quantum cascade laser while driving it in continuous wave (CW) at a fixed current density J = 0.67 Jmax and at a heat sink temperature TH = 18 K. The IBN linewidth is 3.1 kHz. (c) Fourier-transform infrared spectra collected under vacuum in rapid-scan mode, with a 0.075 cm−1 resolution, while driving the QCL at 18 K in CW and at J = 0.67 Jmax. QCL, quantum cascade laser; IBN, intermodal beatnote.
Active approaches rely on the use of external cavities, as coupled dc-biased sections [35] or GTIs [36], allowing either a full coverage of the bias range, at the price of a reduced OB (average OB = 400 GHz) [34] and negligible (µW) optical power outputs [35] or only at a specific operational point [36].
A summary of present-day performances of THz QCL FCs is shown in Table 1.
Summary of the actual performances of the THz QCL comb in terms of power per mode, number of modes, single IBN regime and optical bandwidth in this latter regime.
| References | Power per mode | # modes | Single IBN regime (% operational range) | OB of single IBN regime (THz) |
|---|---|---|---|---|
| Ref. [21] | 60 uW | ∼62 | 29% | 0.6 |
| Ref. [22] | 1.2 uW | ∼34 | 20% | 0.58 |
| Ref. [23] | 15 uW | ∼50 | 16% | 1.05 |
| Ref. [31] | 1.6 uW | ∼50 | 20% | 1.1 |
| Ref. [32] | (Not available) | ∼24 | 29% | 1 |
| Ref. [34] | 20 uW | ∼52 | 23% | 1.12 |
| Ref. [35] | (Not available) | ∼22 | 100% | 0.4 |
| Ref. [30] | 90 uW | ∼90 | 55% | 1.2 |
| Ref. [33] | 42 uW | ∼98 | 35% | 1 |
*: with active modulation. QCL, quantum cascade laser; OB, optical bandwidth; IBN, intermodal beatnote.
Extending FC operation in THz QCLs over most of the laser operational range and particularly at the operation point (Jmax) of high power emission, with a broad (>1 THz) spectral coverage and without any spectral gap, is a very demanding task. Novel architectures exploiting more exotic device technologies and/or physical phenomena have been very recently proposed. One option is to use single-layer graphene grating–gated modulators acting as passive dispersion compensators. After proper integration with THz QCLs, the QCL emission can be amplitude modulated. This scheme enables FC operation over 35% of the laser operational range [33]. Another option relies on GTIs comprising an ultrafast (fs switching time) intersubband polaritonic mirror [37] backcoupled with a THz QCL. The THz electric field–induced bleaching of the intersubband polariton causes a reflectivity change in the polaritonic mirror. Once properly matched with the QCL gain bandwidth, compensation of GDD over a wide spectral portion of the QCL emission (35% of the laser operational range in the FC regime) is enabled. Finally, solution processed THz graphene saturable absorbers [38] can be embedded on the back facet of a THz QCL FC; the fast intraband-driven graphene saturable absorption can then reshape the intracavity mode dynamics leading to FC operation over 55% of the QCL driving regime [30].
3 Characterization techniques
The total complex field of a FC can be written as follows:
where En is the amplitude of the nth comb mode, fs is the mode spacing, fo is the frequency offset and φn is the Fourier phase of the nth comb mode. Ultimately, the most important characteristic of a FC, which makes it different from a standard multimode laser, is the fixed (i.e., constant over time) phase relation between the emitted optical modes that translates into fixed Fourier phases for all the emitted modes. In a traditional passive mode-locked comb source, the presence of sharp pulses corresponds to a linear phase relation among the modes [39], but this specific trend is not guaranteed under different circumstances.
A preliminary analysis of FC operation in a THz QCL is usually done through a characterization of the driving current-dependent intermodal beatnote (IBN). The latter is easily extracted either by means of a bias tee in the driving current line or using a resonating antenna placed closed to the device. The presence of a single and sharp (linewidths in the kHz range) IBN may indicate that at least some of the modes emitted by the device are fairly well equally spaced in frequency, thus representing a good precursor for a genuine comb operation. However, such a technique lacks to provide information about the stability of the Fourier phases that can be extracted via alternative optical techniques. Figure 3b and c show the IBN and the Fourier infrared spectrum retrieved while driving a heterogeneous THz QCL at a current density value J = 0.67 Jmax being Jmax the maximum current density value at which the QCL shows laser action.
One option to assess the phases is the shifted wave interference Fourier-transform (SWIFT) spectroscopy [40], [41] that gives access to the phase domain by measuring the phase difference between adjacent FC modes. Such a procedure allows retrieving the phase relation of continuous portions of the FC spectrum by a cumulative sum on the phases. In SWIFT spectroscopy, the need for a mechanical scan does not allow for a simultaneous analysis of the phases but, provided that all the measurement frequency chain is properly calibrated, this technique can assess if the phases are stable during the measurement time.
A more recent technique relies on extracting the modal phases of the THz QCL comb through a Fourier analysis of the comb emission (FACE) [39], [42]. Relying on a multiheterodyne detection scheme (see Figure 4), this technique is capable of real-time tracing the phases of the modes emitted by the FC, thus working even if the comb presents spectral gaps. A phase-stable reference comb overlapping with the sample comb under analysis is required for FACE taking to a more complicated setup but providing a more general and accurate assessment of FC operation.
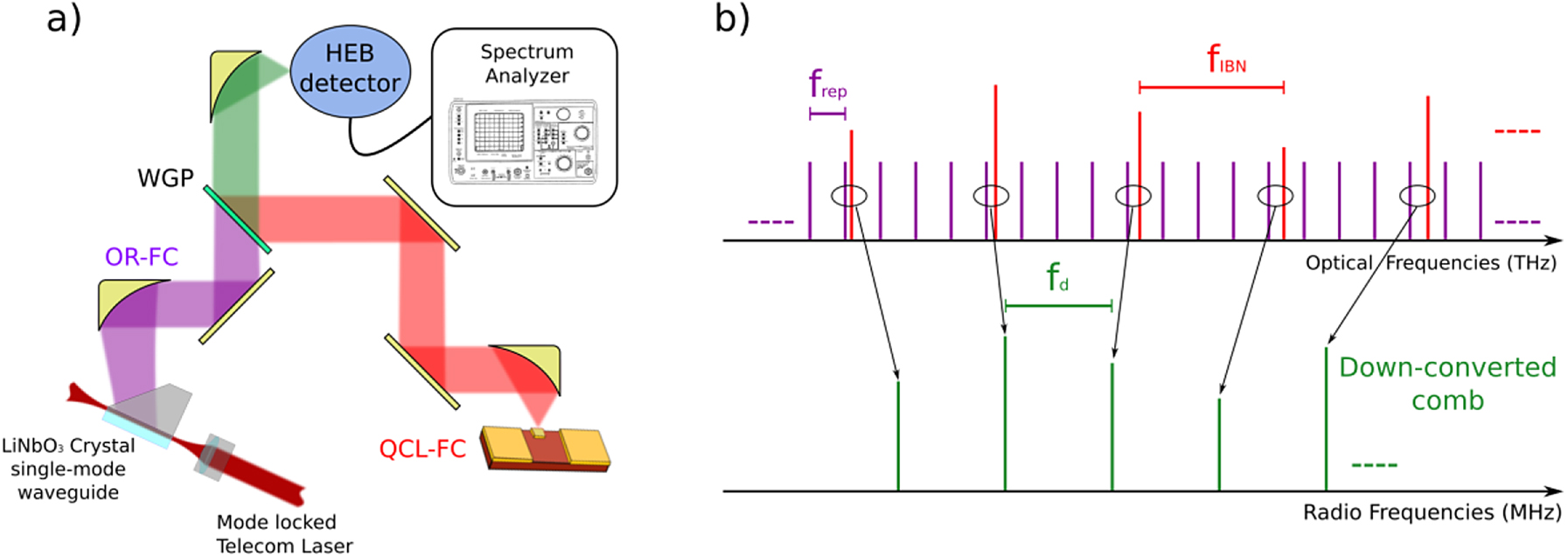
(a) Representation of the multiheterodyne detection scheme: the optically rectified (OR) and quantum cascade laser (QCL) frequency comb (FC) beams are superimposed by means of a wire grip polarizer (WGP) and mixed on a fast hot-electron bolometer (HEB) detector. (b) Sketch of the downconversion process: the two combs, with different modes spacing (frep: repetition rate of the OR FC and fIBN, frequency of the QCL’s intermodal beatnote), close to an integer ratio, are downconverted into a radio frequency comb.
Phase measurements on THz QCLs to assess a genuine FC operation regime, performed with both SWIFT spectroscopy and FACE, proved that FWM establishes a tight phase relation among the modes emitted by the analyzed devices, resulting in stable Fourier modal phases [39], [40], [41], [42]. The retrieved phase relations among the modes are never trivial (i.e., not linear, like in pulsed operation combs), leading to a frequency and amplitude modulated laser emission, different from that obtained by passive mode-locking pulsed operation. Nevertheless, these measurements confirm that FWM-based mode-locking is ensured at least in a limited operation range, usually very close to the laser threshold, and that QCL-based FCs are definitely well suited for most metrological-grade applications.
3.1 Applications and perspectives
The assessment of stable FC operation in a THz QCL enabled the quest for novel applications, aiming to exploit the large optical power per comb tooth (with respect to optically rectified [OR] THz combs) and intrinsic spectral purity of these devices.
One of the most straightforward applications of FCs is certainly dual-comb spectroscopy (DCS), which allows retrieving Fourier spectra without the need of moving interferometric components, therefore resulting in a fast and spectrally resolved acquisition procedure. However, while QCL–FC–based DCS setups have been successfully adopted in the mid-IR [43], [44], the THz region is lagging behind. After the first attempts of a proof-of-principle acquisition of an etalon signal simulating a molecular absorption [45], or of a low resolution spectrum of ammonia gas, dual-comb THz setups have been developed for pioneering hyperspectral imaging [46], self-detection schemes [47] and time resolved spectroscopy on molecular gas mixtures [48]. At the same time, a hybrid dual-comb spectrometer based on a OR– and a QCL–FC has been recently demonstrated [49], merging the sensitivity allowed by a 4 mW [23] THz QCL, with the accuracy of the absolute frequency scale, provided by the referenced OR–FC. Such a technique leads to a state-of-the-art accuracy, of the order of 10−8, in the determination of molecular transition line centers.
However, it is worth mentioning that although, in the described experiments, THz QCLs are driven by low-noise current drivers and their operational temperature is stabilized, they are always free running. This means that their full metrological-grade potential, proven by the SWIFT and FACE measurements, has never been exploited, so far, for spectroscopy. Indeed, this can only be done by tight phase referencing both the QCL-FC modes spacing and the frequency offset to a precise frequency standard. These two degrees of freedom usually require two different orthogonal actuators to be stabilized, while, to date, the only available fast actuator, acting simultaneously on spacing and offset, is the QCL driving current. Recently, these difficulties have been overcome by exploiting the driving current actuator in two very different frequency ranges [42] (Figure 5). This technique allows full phase stabilization of a QCL–FC, the emission linewidth of each comb mode being narrowed down to ∼2 Hz in 1 s, and a metrological-grade tuning of their individual modes frequencies. Currently, the use of visible light as an additional actuator on QCL–FC degrees of freedom is under investigation and has already taken to demonstration of phase stabilization of the QCL comb mode spacing [50].
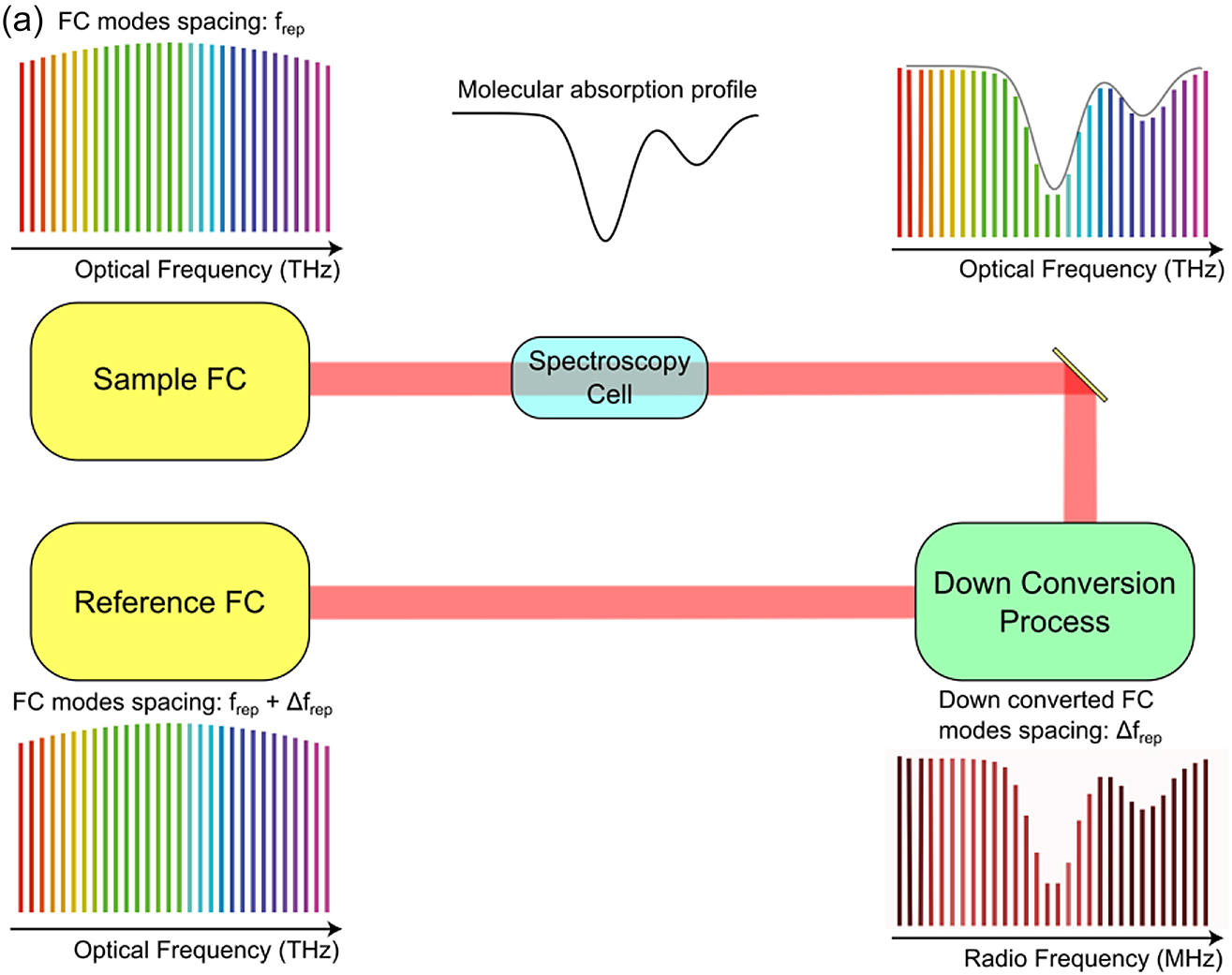
(a) Schematic representation of a generic dual-comb spectroscopy setup. A sample frequency comb (FC) with repetition rate frep interrogates a molecular sample inside a spectroscopy cell. The molecular information is encoded in the sample FC and is downconverted to radio frequencies, thanks to multiheterodyne mixing with a reference FC with slightly different repetition rate frep + Δfrep.
Full control of FCs, i.e., of linewidth and phase of teeth and spacing between them, as well as of their shape, that means getting control on the overall number and on the intensity pattern of the manifold [51] is the key challenge to widen the application spectrum of FCs. In particular, phase control and a significant increase of the intensity of each tooth (e.g., hundreds µW power range), together with the assessment of a stable FC operation over the entire operational range of the QCL, will make it easier to access the nonlinear interaction regime [52]. Saturation of gas-phase molecular lines is a straightforward example of application that could be accompanied by cavity-enhanced setups, although the cavity finesse reported to date, at THz frequencies, is very limited [53], [54]. Nonetheless, progress in this direction could take to THz development of much more sophisticated spectroscopic setups, similar to those working, till now, not beyond the mid-IR [55]. They could be used, e.g., to interrogate molecules prepared in unprecedented thermodynamic states, like ultracold molecules obtained by buffer-gas cooling schemes [56]. Such perspectives could fully exploit the parallelism between mid-IR, that is, the well-assessed “fingerprint region”, and the THz frequency range that could have an even higher potential, due to the similar molecular line strengths of polar molecules but with up to two orders of magnitude narrower molecular linewidths, similarly improving line discrimination [57], [58].
Chip-scale THz QCL FCs can allow developing new instruments, as compact time-domain THz spectrometers, mimicking previous experiments in the mid-IR [59] and pioneering new application areas as multicolor coherent THz tomography, with major implications for cultural heritage, quality and process control and biomedical inspections [60].
Also, near-field microscopy could benefit of powerful QCL FCs for pioneering fundamental investigations at the nanoscale, as inspecting charge carrier density [61], plasmon–polariton [62], [63] and phonon–polariton [64], [65] modes with an unprecedented spatial resolution and over a broad bandwidth, overcoming the present limitations of time domain spectroscopy combined with scatterning near field optical microscopy (TDS s-SNOM) apparatuses. FC-based near-field microscopy can allow mapping the spatial variation and the bias dependence of local currents induced by light illumination, therefore tracking the photocarrier transport and the electronic band bending in a plethora of electronic and photonic nanodevices, unveiling fundamental physical phenomena in semiconductors, superconductors or more exotic bidimensional materials as graphene, phosphorene or transition metal dichalcogenides.
Quantum technologies represent another key area of development for THz QCL FCs. Indeed, QCLs are “quantum lasers” by design, with a relatively simple quantum well–based architecture, which is now the subject of analog simulation by Bose–Einstein condensate platforms to fully exploit their quantum properties that cannot be tailored by classical designs [66]. This could be a really disruptive area of application for THz FCs, including novel quantum sensors, quantum imaging devices and, in principle, q-bits made by entangled teeth for photonic-based quantum computation. Of course, most of these quantum applications need preliminary demonstration of subshot-noise operation of THz QCLs, hitherto impossible to achieve due to the technological gap of THz components, as compared to other spectral regions, as well as to the strong background thermal noise typical at these frequencies, generally requiring cryogenic detectors.
Funding source: ERC
Award Identifier / Grant number: 681379
Funding source: FET Flagship on Quantum Technologies
Award Identifier / Grant number: 820419
Acknowledgments
The authors acknowledge financial support from the ERC Project 681379 (SPRINT) and FET Flagship on Quantum Technologies Project 820419 (QOMBS).
Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: The authors acknowledge financial support from the ERC Project 681379 (SPRINT) and FET Flagship on Quantum Technologies Project 820419 (QOMBS).
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
[1] T. W. Hänsch, “Nobel lecture: passion for precision,” Rev. Mod. Phys., vol. 78, no. 4, pp. 1297–1309, 2006. https://doi.org/10.1103/revmodphys.78.1297.Search in Google Scholar
[2] R. Holzwarth, T. Udem, T. W. Hänsch, J. C. Knight, W. J. Wadsworth, and P. S. J. Russell, “Optical frequency synthesizer for precision spectroscopy,” Phys. Rev. Lett., vol. 85, no. 11, pp. 2264–2267, 2000. https://doi.org/10.1103/physrevlett.85.2264.Search in Google Scholar
[3] D. J. Jones, S. A. Diddams, J. K. Ranka, et al., “Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis,” Science, vol. 288, pp. 635–639, 2000. https://doi.org/10.1126/science.288.5466.635.Search in Google Scholar
[4] R. Ell, U. Morgner, F. X. Kärtner, et al., “Generation of 5-fs pulses and octave-spanning spectra directly from a Ti:sapphire laser,” Opt. Lett., vol. 26, no. 6, p. 373, 2001. https://doi.org/10.1364/ol.26.000373.Search in Google Scholar
[5] I. Hartl, G. Imeshev, M. E. Fermann, C. Langrock, and M. M. Fejer, “Integrated self-referenced frequency-comb laser based on a combination of fiber and waveguide technology,” Opt. Express, vol. 13, no. 17, p. 6490, 2005. https://doi.org/10.1364/opex.13.006490.Search in Google Scholar
[6] I. S. Grudinin, A. B. Matsko, A. A. Savchenkov, D. Strekalov, V. S. Ilchenko, and L. Maleki, “Ultra high Q crystalline microcavities,” Opt. Commun., vol. 265, no. 1, pp. 33–38, 2006. https://doi.org/10.1016/j.optcom.2006.03.028.Search in Google Scholar
[7] K.-L. Yeh, M. C. Hoffmann, J. Hebling, and K. A. Nelson, “Generation of 10 mJ ultrashort terahertz pulses by optical rectification,” Appl. Phys. Lett., vol. 90, p. 171121, 2007. https://doi.org/10.1063/1.2734374.Search in Google Scholar
[8] J. C. Pearson, B. J. Drouin, A. Maestrini, et al., “Demonstration of a room temperature 2.48–2.75 THz coherent spectroscopy source,” Rev. Sci. Instrum., vol. 82, p. 093105, 2011. https://doi.org/10.1063/1.3617420.Search in Google Scholar
[9] T. Fortier and E. Baumann, “20 Years of developments in optical frequency comb technology and applications,” Commun. Phys., vol. 2, no. 1, p. 153, 2019. https://doi.org/10.1038/s42005-019-0249-y.Search in Google Scholar
[10] P. Maddaloni, P. Malara, G. Gagliardi, and P. De Natale, “Mid-infrared fiber-based optical comb,” New J. Phys., vol. 8, p. 262, 2006. https://doi.org/10.1088/1367-2630/8/11/262.Search in Google Scholar
[11] I. Galli, F. Cappelli, P. Cancio, et al., “High-coherence mid-infrared frequency comb,” Opt. Express, vol. 21, no. 23, p. 28877, 2013. https://doi.org/10.1364/oe.21.028877.Search in Google Scholar
[12] A. Gambetta, N. Coluccelli, M. Cassinerio, et al., “Milliwatt-level frequency combs in the 8–14 μm range via difference frequency generation from an Er:fiber oscillator,” Opt. Lett., vol. 38, no. 7, p. 1155, 2013. https://doi.org/10.1364/ol.38.001155.Search in Google Scholar
[13] T. J. Kippenberg, R. Holzwarth, and S. A. Diddams, “Microresonator-based optical frequency combs,” Science (80-,) vol. 332, no. 6029, pp. 555–559, 2011. https://doi.org/10.1126/science.1193968.Search in Google Scholar
[14] B. Schwarz, J. Hillbrand, M. Beiser, et al., “Monolithic frequency comb platform based on interband cascade lasers and detectors,” Optica, vol. 6, no. 7, p. 890, 2019. https://doi.org/10.1364/optica.6.000890.Search in Google Scholar
[15] A. Hugi, G. Villares, S. Blaser, H. C. Liu, and J. Faist, “Mid-infrared frequency comb based on a quantum cascade laser,” Nature, vol. 492, no. 7428, pp. 229–233, 2012. https://doi.org/10.1038/nature11620.Search in Google Scholar
[16] C. Y. Wang, L. Kuznetsova, V. M. Gkortsas, et al., “Mode-locked pulses from mid-infrared quantum cascade lasers,” Opt. Express, vol. 17, no. 15, p. 12929, 2009. https://doi.org/10.1364/oe.17.012929.Search in Google Scholar
[17] A. K. Wójcik, P. Malara, R. Blanchard, T. S. Mansuripur, F. Capasso, and A. Belyanin, “Generation of picosecond pulses and frequency combs in actively mode locked external ring cavity quantum cascade lasers,” Appl. Phys. Lett., vol. 103, no. 23, p. 231102, 2013. https://doi.org/10.1063/1.4838275.Search in Google Scholar
[18] M. Piccardo, B. Schwarz, D. Kazakov, et al., “Frequency combs induced by phase turbulence,” Nature, vol. 582, no. 7812, pp. 360–364, 2020. https://doi.org/10.1038/s41586-020-2386-6360.Search in Google Scholar
[19] J. Khurgin, Y. Dikmelik, A. Hugi, and J. Faist, “Coherent frequency combs produced by self frequency modulation in quantum cascade lasers,” Appl. Phys. Lett., vol. 104, p. 081118, 2014. https://doi.org/10.1063/1.4866868.Search in Google Scholar
[20] S. Bartalini, L. Consolino, P. Cancio, et al., “Frequency-comb-assisted terahertz quantum cascade laser spectroscopy,” Phys. Rev. X, vol. 4, p. 021006, 2014. https://doi.org/10.1103/physrevx.4.021006.Search in Google Scholar
[21] D. Burghoff, T.-Y. Y. Kao, N. Han, et al., “Terahertz laser frequency combs,” Nat. Photonics, vol. 8, no. 6, pp. 462–467, 2014. https://doi.org/10.1038/nphoton.2014.85.Search in Google Scholar
[22] M. Rösch, G. Scalari, M. Beck, and J. Faist, “Octave-spanning semiconductor laser,” Nat. Photonics, vol. 9, no. 1, pp. 42–47, 2014. https://doi.org/10.1038/nphoton.2014.279.Search in Google Scholar
[23] K. Garrasi, F. P. Mezzapesa, L. Salemi, et al., “High dynamic range, heterogeneous, terahertz quantum cascade lasers featuring thermally tunable frequency comb operation over a broad current range,” ACS Photonics, vol. 6, no. 1, pp. 73–78, 2019. https://doi.org/10.1021/acsphotonics.8b01483.Search in Google Scholar
[24] P. Cavalié, J. Freeman, K. Maussang, et al., “High order sideband generation in terahertz quantum cascade lasers,” Appl. Phys. Lett., vol. 102, p. 221101, 2013. https://doi.org/10.1063/1.4808385.Search in Google Scholar
[25] Q. Lu, F. Wang, D. Wu, S. Slivken, and M. Razeghi, “Room temperature terahertz semiconductor frequency comb,” Nat. Commun., vol. 10, p. 2403, 2019. https://doi.org/10.1038/s41467-019-10395-7.Search in Google Scholar
[26] L. H. Li, K. Garrasi, I. Kundu, et al., “Broadband heterogeneous terahertz frequency quantum cascade laser,” Electron. Lett., vol. 54, no. 21, pp. 1229–1231, 2018. https://doi.org/10.1049/el.2018.6062.Search in Google Scholar
[27] M. Brandstetter, C. Deutsch, M. Krall, et al., “High power terahertz quantum cascade lasers with symmetric wafer bonded active regions,” Appl. Phys. Lett., vol. 103, no. 17, p. 171113, 2013. https://doi.org/10.1063/1.4826943.Search in Google Scholar
[28] M. Wienold, B. Röben, L. Schrottke, et al., “High-temperature, continuous-wave operation of terahertz quantum-cascade lasers with metal-metal waveguides and third-order distributed feedback,” Opt. Express, vol. 22, pp. 3334–3348, 2014. https://doi.org/10.1364/oe.22.003334.Search in Google Scholar
[29] M. S. Vitiello, L. Consolino, S. Bartalini, et al., “Quantum limited fluctuations in a THz lasers,” Nat. Photonics, vol. 6, pp. 525–528, 2012. https://doi.org/10.1038/nphoton.2012.145.Search in Google Scholar
[30] F. P. Mezzapesa, K. Garrasi, J. Schmidt, et al., submitted (2020).Search in Google Scholar
[31] M. Rösch, M. Beck, M. J. Süess, et al., “Heterogeneous terahertz quantum cascade lasers exceeding 1.9 THz spectral bandwidth and featuring dual comb operation,” Nanophotonics, vol. 7, no. 1, pp. 237–242, 2018. https://doi.org/10.1515/nanoph-2017-0024.Search in Google Scholar
[32] A. Forrer, M. Franckié, D. Stark, et al., “Photon-driven broadband emission and frequency comb RF injection locking in THz quantum cascade lasers,” ACS Photonics, vol. 7, no. 3, pp. 784–791, 2020. https://doi.org/10.1021/acsphotonics.9b01629.Search in Google Scholar
[33] A. Di Gaspare, E. A. A. Pogna, L. Salemi et al., submitted (2020).Search in Google Scholar
[34] F. P. Mezzapesa, V. Pistore, K. Garrasi, et al., “Tunable and compact dispersion compensation of broadband THz quantum cascade laser frequency combs,” Opt. Express, vol. 27, no. 15, pp. 20231–20240, 2019. https://doi.org/10.1364/oe.27.020231.Search in Google Scholar
[35] Y. Yang, D. Burghoff, J. Reno, and Q. Hu, “Achieving comb formation over the entire lasing range of quantum cascade lasers,” Opt. Lett., vol. 42, no. 19, pp. 3888–3891, 2017. https://doi.org/10.1364/ol.42.003888.Search in Google Scholar
[36] F. Wang, H. Nong, T. Fobbe, et al., “Short terahertz pulse generation from a dispersion compensated modelocked semiconductor laser,” Laser Photonics Rev., vol. 11, no. 4, pp. 1–9, 2017. https://doi.org/10.1002/lpor.201770042.Search in Google Scholar
[37] J. Raab, F. P. Mezzapesa, L. Viti, et al., “Ultrafast terahertz saturable absorbers using tailored intersubband polaritons,” Nat. Commun., vol. 11, pp. 1–8, 2020. https://doi.org/10.1038/s41467-020-18004-8.Search in Google Scholar
[38] V. Bianchi, T. Carey, L. Viti, et al., “Terahertz saturable absorbers from liquid phase exfoliation of graphite,” Nat. Commun., vol. 8, p. 15763, 2017. https://doi.org/10.1038/ncomms15763.Search in Google Scholar
[39] F. Cappelli, L. Consolino, G. Campo, et al., “Retrieval of phase relation and emission profile of quantum cascade laser frequency combs,” Nat. Photonics, vol. 13, pp. 562–568, 2019. https://doi.org/10.1038/s41566-019-0451-1.Search in Google Scholar
[40] D. Burghoff, Y. Yang, D. J. Hayton, J.-R. Gao, J. L. Reno, and Q. Hu, “Evaluating the coherence and time-domain profile of quantum cascade laser frequency combs,” Opt. Express, vol. 23, no. 2, p. 1190, 2015. https://doi.org/10.1364/oe.23.001190.Search in Google Scholar
[41] Z. Han, D. Ren, and D. Burghoff, “Sensitivity of SWIFT spectroscopy,” Opt. Express, vol. 28, no. 5, p. 6002, 2020. https://doi.org/10.1364/oe.382243.Search in Google Scholar
[42] L. Consolino, M. Nafa, F. Cappelli, et al., “Fully phase-stabilized quantum cascade laser frequency comb,” Nat. Commun., vol. 10, no. 1, 2019. https://doi.org/10.1038/s41467-019-10913-7.Search in Google Scholar
[43] G. Villares, A. Hugi, S. Blaser, and J. Faist, “Dual-comb spectroscopy based on quantum-cascade-laser frequency combs,” Nat. Commun., vol. 5, p. 5192, 2014. https://doi.org/10.1038/ncomms6192.Search in Google Scholar
[44] M. Gianella, A. Nataraj, B. Tuzson, et al., “High-resolution and gapless dual comb spectroscopy with current-tuned quantum cascade lasers,” Opt. Express, vol. 28, no. 5, p. 6197, 2020. https://doi.org/10.1364/oe.379790.Search in Google Scholar
[45] Y. Yang, D. Burghoff, D. J. Hayton, J.-R. Gao, J. L. Reno, and Q. Hu, “Terahertz multiheterodyne spectroscopy using laser frequency combs,” Optica, vol. 3, no. 5, pp. 499–502, 2016. https://doi.org/10.1364/optica.3.000499.Search in Google Scholar
[46] L. A. Sterczewski, J. Westberg, Y. Yang, et al., “Terahertz hyperspectral imaging with dual chip-scale combs,” Optica, vol. 6, no. 6, p. 766, 2019. https://doi.org/10.1364/optica.6.000766.Search in Google Scholar
[47] H. Li, Z. Li, W. Wan, et al., “Toward compact and real-time terahertz dual-comb spectroscopy employing a self-detection scheme,” ACS Photonics, vol. 7, no. 1, pp. 49–56, 2020. https://doi.org/10.1021/acsphotonics.9b01427.Search in Google Scholar
[48] L. A. Sterczewski, J. Westberg, Y. Yang, et al., “Terahertz spectroscopy of gas mixtures with dual quantum cascade laser frequency combs,” ACS Photonics, vol. 7, no. 5, pp. 1082–1087, 2020. https://doi.org/10.1021/acsphotonics.9b01758.Search in Google Scholar
[49] L. Consolino, M. Nafa, M. De Regis, et al., “Quantum cascade laser based hybrid dual comb spectrometer,” Commun. Phys., vol. 3, p. 69, 2020. https://doi.org/10.1038/s42005-020-0344-0.Search in Google Scholar
[50] L. Consolino, A. Campa, M. De Regis, et al., Controlling and Phase-Locking a THz Quantum Cascade Laser Frequency Comb by Small Optical Frequency Tuning, 2020. Arxiv arXiv:2006.10.1002/lpor.202000417Search in Google Scholar
[51] G. Campo, A. Leshem, F. Cappelli, et al., “Shaping the spectrum of a down-converted mid-infrared frequency comb,” J. Opt. Soc. Am. B, vol. 34, no. 11, p. 2287, 2017. https://doi.org/10.1364/josab.34.002287.Search in Google Scholar
[52] M. Wienold, T. Alam, L. Schrottke, H. T. Grahn, and H.-W. Hübers, “Doppler-free spectroscopy with a terahertz quantum-cascade laser,” Opt. Express, vol. 26, pp. 6692–6699, 2018. https://doi.org/10.1364/oe.26.006692.Search in Google Scholar
[53] A. Campa, L. Consolino, M. Ravaro, et al., “High-Q resonant cavities for terahertz quantum cascade lasers,” Opt. Express, vol. 23, no. 3, p. 3751, 2015. https://doi.org/10.1364/oe.23.003751.Search in Google Scholar
[54] L. Consolino, A. Campa, D. Mazzotti, M. S. Vitiello, P. De Natale, and S. Bartalini, “Bow-tie cavity for terahertz radiation,” Photonics, vol. 6, no. 1, p. 1, 2018. https://doi.org/10.3390/photonics6010001.Search in Google Scholar
[55] G. Giusfredi, S. Bartalini, S. Borri, et al., “Saturated-absorption cavity ring-down spectroscopy,” Phys. Rev. Lett., vol. 104, no. 11, 2010. https://doi.org/10.1103/physrevlett.104.110801.Search in Google Scholar
[56] V. Di Sarno, R. Aiello, M. De Rosa, et al., “Lamb-dip spectroscopy of buffer-gas-cooled molecules,” Optica, vol. 6, no. 4, p. 436, 2019. https://doi.org/10.1364/optica.6.000436.Search in Google Scholar
[57] L. Consolino, F. Cappelli, M. Siciliani de Cumis, and P. De Natale, “QCL-based frequency metrology from the mid-infrared to the THz range: a review,” Nanophotonics, vol. 8, pp. 181–204, 2018. https://doi.org/10.1515/nanoph-2018-0076.Search in Google Scholar
[58] L. Consolino, S. Bartalini, P. De Natale, J. Infrared, and Millimeter, “Terahertz frequency metrology for spectroscopic applications: a review,” Terahertz Waves, vol. 38, no. 11, pp. 1289–1315, 2017. https://doi.org/10.1007/s10762-017-0406-x.Search in Google Scholar
[59] F. Keilmann, C. Gohle, and R. Holzwarth, “Time-domain mid-infrared frequency- comb spectrometer,” Opt. Lett., vol. 29, pp. 1542–1544, 2004. https://doi.org/10.1364/ol.29.001542.Search in Google Scholar
[60] A. W. M. Lee, T.-Y. Kao, D. Burghoff, Q. Hu, and J. L. Reno, “Terahertz tomography using quantum-cascade lasers,” Opt. Lett., vol. 37, pp. 217–219, 2012. https://doi.org/10.1364/OL.37.000217.Search in Google Scholar
[61] A. J. Huber, F. Keilmann, J. Wittborn, J. Aizpurua, and R. Hillenbrand, “Terahertz near-field nanoscopy of mobile carriers in single semiconductor nanodevices,” Nano Lett., vol. 8, pp. 3766–3770, 2008. https://doi.org/10.1021/nl802086x.Search in Google Scholar
[62] J. Chen, M. Badioli, P. Alonso-González, et al., “Optical nano-imaging of gate-tunable graphene plasmons,” Nature, vol. 487, pp. 77–81, 2012. https://doi.org/10.1038/nature11254.Search in Google Scholar
[63] Z. Fei, A. S. Rodin, G. O. Andreev, et al., “Gate-tuning of graphene plasmons revealed by infrared nano-imaging,” Nature, vol. 486, pp. 82–85, 2012. https://doi.org/10.1038/nature11253.Search in Google Scholar
[64] P. Li, M. Lewin, A. V. Kretinin, et al., “Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing,” Nat. Commun., vol. 6, p. 7507, 2015. https://doi.org/10.1038/ncomms8507.Search in Google Scholar
[65] T. Low, A. Chaves, J. D. Caldwell, et al., “Polaritons in layered two-dimensional materials,” Nat. Mater., vol. 16, p. 182, 2017. https://doi.org/10.1038/nmat4792.Search in Google Scholar
[66] F. Scazza, et al., submitted.Search in Google Scholar
© 2020 Miriam S. Vitiello et al., published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Editorial
- Editorial
- Optoelectronics and Integrated Photonics
- Disorder effects in nitride semiconductors: impact on fundamental and device properties
- Ultralow threshold blue quantum dot lasers: what’s the true recipe for success?
- Waiting for Act 2: what lies beyond organic light-emitting diode (OLED) displays for organic electronics?
- Waveguide combiners for mixed reality headsets: a nanophotonics design perspective
- On-chip broadband nonreciprocal light storage
- High-Q nanophotonics: sculpting wavefronts with slow light
- Thermoelectric graphene photodetectors with sub-nanosecond response times at terahertz frequencies
- High-performance integrated graphene electro-optic modulator at cryogenic temperature
- Asymmetric photoelectric effect: Auger-assisted hot hole photocurrents in transition metal dichalcogenides
- Seeing the light in energy use
- Lasers, Active optical devices and Spectroscopy
- A high-repetition rate attosecond light source for time-resolved coincidence spectroscopy
- Fast laser speckle suppression with an intracavity diffuser
- Active optics with silk
- Nanolaser arrays: toward application-driven dense integration
- Two-dimensional spectroscopy on a THz quantum cascade structure
- Homogeneous quantum cascade lasers operating as terahertz frequency combs over their entire operational regime
- Toward new frontiers for terahertz quantum cascade laser frequency combs
- Soliton dynamics of ring quantum cascade lasers with injected signal
- Fiber Optics and Optical Communications
- Propagation stability in optical fibers: role of path memory and angular momentum
- Perspective on using multiple orbital-angular-momentum beams for enhanced capacity in free-space optical communication links
- Biomedical Photonics
- A fiber optic–nanophotonic approach to the detection of antibodies and viral particles of COVID-19
- Plasmonic control of drug release efficiency in agarose gel loaded with gold nanoparticle assemblies
- Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective
- Hyperbolic dispersion metasurfaces for molecular biosensing
- Fundamentals of Optics
- A Tutorial on the Classical Theories of Electromagnetic Scattering and Diffraction
- Reflectionless excitation of arbitrary photonic structures: a general theory
- Optimization Methods
- Multiobjective and categorical global optimization of photonic structures based on ResNet generative neural networks
- Machine learning–assisted global optimization of photonic devices
- Artificial neural networks for inverse design of resonant nanophotonic components with oscillatory loss landscapes
- Adjoint-optimized nanoscale light extractor for nitrogen-vacancy centers in diamond
- Topological Photonics
- Non-Hermitian and topological photonics: optics at an exceptional point
- Topological photonics: Where do we go from here?
- Topological nanophotonics for photoluminescence control
- Anomalous Anderson localization behavior in gain-loss balanced non-Hermitian systems
- Quantum computing, Quantum Optics, and QED
- Quantum computing and simulation
- NIST-certified secure key generation via deep learning of physical unclonable functions in silica aerogels
- Thomas–Reiche–Kuhn (TRK) sum rule for interacting photons
- Macroscopic QED for quantum nanophotonics: emitter-centered modes as a minimal basis for multiemitter problems
- Generation and dynamics of entangled fermion–photon–phonon states in nanocavities
- Polaritonic Tamm states induced by cavity photons
- Recent progress in engineering the Casimir effect – applications to nanophotonics, nanomechanics, and chemistry
- Enhancement of rotational vacuum friction by surface photon tunneling
- Plasmonics and Polaritonics
- Shrinking the surface plasmon
- Polariton panorama
- Scattering of a single plasmon polariton by multiple atoms for in-plane control of light
- A metasurface-based diamond frequency converter using plasmonic nanogap resonators
- Selective excitation of individual nanoantennas by pure spectral phase control in the ultrafast coherent regime
- Semiconductor quantum plasmons for high frequency thermal emission
- Origin of dispersive line shapes in plasmon-enhanced stimulated Raman scattering microscopy
- Epitaxial aluminum plasmonics covering full visible spectrum
- Metaoptics
- Metamaterials with high degrees of freedom: space, time, and more
- The road to atomically thin metasurface optics
- Active nonlocal metasurfaces
- Giant midinfrared nonlinearity based on multiple quantum well polaritonic metasurfaces
- Near-field plates and the near zone of metasurfaces
- High-efficiency metadevices for bifunctional generations of vectorial optical fields
- Printing polarization and phase at the optical diffraction limit: near- and far-field optical encryption
- Optical response of jammed rectangular nanostructures
- Dynamic phase-change metafilm absorber for strong designer modulation of visible light
- Arbitrary polarization conversion for pure vortex generation with a single metasurface
- Enhanced harmonic generation in gases using an all-dielectric metasurface
- Monolithic metasurface spatial differentiator enabled by asymmetric photonic spin-orbit interactions
Articles in the same Issue
- Editorial
- Editorial
- Optoelectronics and Integrated Photonics
- Disorder effects in nitride semiconductors: impact on fundamental and device properties
- Ultralow threshold blue quantum dot lasers: what’s the true recipe for success?
- Waiting for Act 2: what lies beyond organic light-emitting diode (OLED) displays for organic electronics?
- Waveguide combiners for mixed reality headsets: a nanophotonics design perspective
- On-chip broadband nonreciprocal light storage
- High-Q nanophotonics: sculpting wavefronts with slow light
- Thermoelectric graphene photodetectors with sub-nanosecond response times at terahertz frequencies
- High-performance integrated graphene electro-optic modulator at cryogenic temperature
- Asymmetric photoelectric effect: Auger-assisted hot hole photocurrents in transition metal dichalcogenides
- Seeing the light in energy use
- Lasers, Active optical devices and Spectroscopy
- A high-repetition rate attosecond light source for time-resolved coincidence spectroscopy
- Fast laser speckle suppression with an intracavity diffuser
- Active optics with silk
- Nanolaser arrays: toward application-driven dense integration
- Two-dimensional spectroscopy on a THz quantum cascade structure
- Homogeneous quantum cascade lasers operating as terahertz frequency combs over their entire operational regime
- Toward new frontiers for terahertz quantum cascade laser frequency combs
- Soliton dynamics of ring quantum cascade lasers with injected signal
- Fiber Optics and Optical Communications
- Propagation stability in optical fibers: role of path memory and angular momentum
- Perspective on using multiple orbital-angular-momentum beams for enhanced capacity in free-space optical communication links
- Biomedical Photonics
- A fiber optic–nanophotonic approach to the detection of antibodies and viral particles of COVID-19
- Plasmonic control of drug release efficiency in agarose gel loaded with gold nanoparticle assemblies
- Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective
- Hyperbolic dispersion metasurfaces for molecular biosensing
- Fundamentals of Optics
- A Tutorial on the Classical Theories of Electromagnetic Scattering and Diffraction
- Reflectionless excitation of arbitrary photonic structures: a general theory
- Optimization Methods
- Multiobjective and categorical global optimization of photonic structures based on ResNet generative neural networks
- Machine learning–assisted global optimization of photonic devices
- Artificial neural networks for inverse design of resonant nanophotonic components with oscillatory loss landscapes
- Adjoint-optimized nanoscale light extractor for nitrogen-vacancy centers in diamond
- Topological Photonics
- Non-Hermitian and topological photonics: optics at an exceptional point
- Topological photonics: Where do we go from here?
- Topological nanophotonics for photoluminescence control
- Anomalous Anderson localization behavior in gain-loss balanced non-Hermitian systems
- Quantum computing, Quantum Optics, and QED
- Quantum computing and simulation
- NIST-certified secure key generation via deep learning of physical unclonable functions in silica aerogels
- Thomas–Reiche–Kuhn (TRK) sum rule for interacting photons
- Macroscopic QED for quantum nanophotonics: emitter-centered modes as a minimal basis for multiemitter problems
- Generation and dynamics of entangled fermion–photon–phonon states in nanocavities
- Polaritonic Tamm states induced by cavity photons
- Recent progress in engineering the Casimir effect – applications to nanophotonics, nanomechanics, and chemistry
- Enhancement of rotational vacuum friction by surface photon tunneling
- Plasmonics and Polaritonics
- Shrinking the surface plasmon
- Polariton panorama
- Scattering of a single plasmon polariton by multiple atoms for in-plane control of light
- A metasurface-based diamond frequency converter using plasmonic nanogap resonators
- Selective excitation of individual nanoantennas by pure spectral phase control in the ultrafast coherent regime
- Semiconductor quantum plasmons for high frequency thermal emission
- Origin of dispersive line shapes in plasmon-enhanced stimulated Raman scattering microscopy
- Epitaxial aluminum plasmonics covering full visible spectrum
- Metaoptics
- Metamaterials with high degrees of freedom: space, time, and more
- The road to atomically thin metasurface optics
- Active nonlocal metasurfaces
- Giant midinfrared nonlinearity based on multiple quantum well polaritonic metasurfaces
- Near-field plates and the near zone of metasurfaces
- High-efficiency metadevices for bifunctional generations of vectorial optical fields
- Printing polarization and phase at the optical diffraction limit: near- and far-field optical encryption
- Optical response of jammed rectangular nanostructures
- Dynamic phase-change metafilm absorber for strong designer modulation of visible light
- Arbitrary polarization conversion for pure vortex generation with a single metasurface
- Enhanced harmonic generation in gases using an all-dielectric metasurface
- Monolithic metasurface spatial differentiator enabled by asymmetric photonic spin-orbit interactions


