Multiobjective and categorical global optimization of photonic structures based on ResNet generative neural networks

1 Introduction

Inverse algorithms are among the most effective methods for designing efficient, multifunctional photonic devices [1], [2], [3]. It remains an open question how to select and implement a design algorithm, and over the last few years, much research has been focused on deep neural networks as inverse design tools [4], [5], [6]. Many of these demonstrations are based on the generation of a training set, consisting of device geometries and their optical responses, and modeling these data using discriminative [7], [8] or generative [9], [10], [11], [12] neural networks. These methods have proven to be capable of producing high-speed surrogate solvers and can perform inference-type tasks with training data. When the training data are curated using advanced gradient-based optimization methods, such as the adjoint variables [13], [14], [15], [16], [17] or objective-first methods [18], the networks can learn to generate high-performing, free-form photonic structures.

To perform global optimization, alternative approaches are required that do not depend on interpolation from a training set. The reason is because the design space is nonconvex and contains multiple local optima, and even devices based on advanced gradient-based optimization methods cannot help a neural network search for the global optimum. In this vein, global optimization networks (GLOnets) have been developed to perform the nonconvex global optimization of free-form photonic devices [19], [20]. GLOnets are gradient-based optimizers that do not use a training set but instead combine a generative neural network with an electromagnetic simulator to perform population-based optimization. The evolution of the generated device distribution is driven by both figure-of-merit values (i.e., efficiencies) and gradients for devices sampled from the generative network. Initial implementations of GLOnets were configured for single-objective problems with binary design variables, such as the maximization of deflection efficiency for a normally incident beam in a metagrating comprising silicon nanostructures. “Single-objective” refers to the optimization of a system operating with one conditional parameter, in this case a system with fixed incidence beam angle, and “binary” refers to silicon and air as our design materials.

A more general formulation of the problem that captures the design space of many photonic technologies is multiobjective, categorical optimization with more than two design materials. “Multiobjective” refers to the optimization of a system operating involving more than one objective function to be optimized simultaneously, such as a metagrating operating over a range of incident beam angles, and “categorical” refers to design variables that have two or more categories without intrinsic ordering, such as multiple material types. In this study, we show that GLOnets can be configured as a multiobjective, categorical global optimizer, and we adapt GLOnets to optimize thin-film stacks to demonstrate the capabilities of our algorithms. Thin-film stacks are an ideal model system for multiple reasons. First, the design problem is multiobjective as devices are typically configured for a range of incident wavelengths, angles, and polarizations. Second, the design problem is categorical as individual layer materials are chosen from a library of materials. Third, thin-film stacks are a well-established technology, and there are a number of pre-existing studies that enable proper benchmarking of algorithm performance [21], [22], [23].

Thin-film stacks have been widely used in many optical systems including passive radiative coolers [24], efficient solar cells [25], [26], broadband spectral filtering [27], [28], thermal emitters [29], and spatial multiplexing filters [30]. The materials and thicknesses of thin-film layers have to be carefully optimized to achieve the desired transmission and reflection proprieties across a broad wavelength and angular bandwidth. Design methods based on physical intuition result in limited performance, and they are generally difficult to scale to aperiodic thin-film stacks comprising many layers. To address these limitations, various global optimization approaches have been explored, including the Monte Carlo approach [31], particle swarm optimization [32], needle optimization [33], [34], [35], and the memetic algorithm [21]. These methods are all derivative-free global optimization algorithms that search the design space through the evaluation of a batch of samples without any gradient calculations, limiting their ability to reliably solve for the global optimum.

2 Method

We consider the design of N-layer thin-film stacks each comprising an isotropic material specified from a material library (Figure 1). The refractive indices of the total stack are denoted as a vector n(λ)=(n1(λ),n2(λ),⋯,nN(λ))T, where each index term is a function of wavelength to account for dispersion, and the values can be real or complex valued without loss of generality. The thin-film stack thicknesses are t=(t1,t2,⋯,tN)T. The material library consists of M material types, and their refractive indices are represented as {m1(λ),m2(λ),⋯,mM(λ)}.

Figure 1:

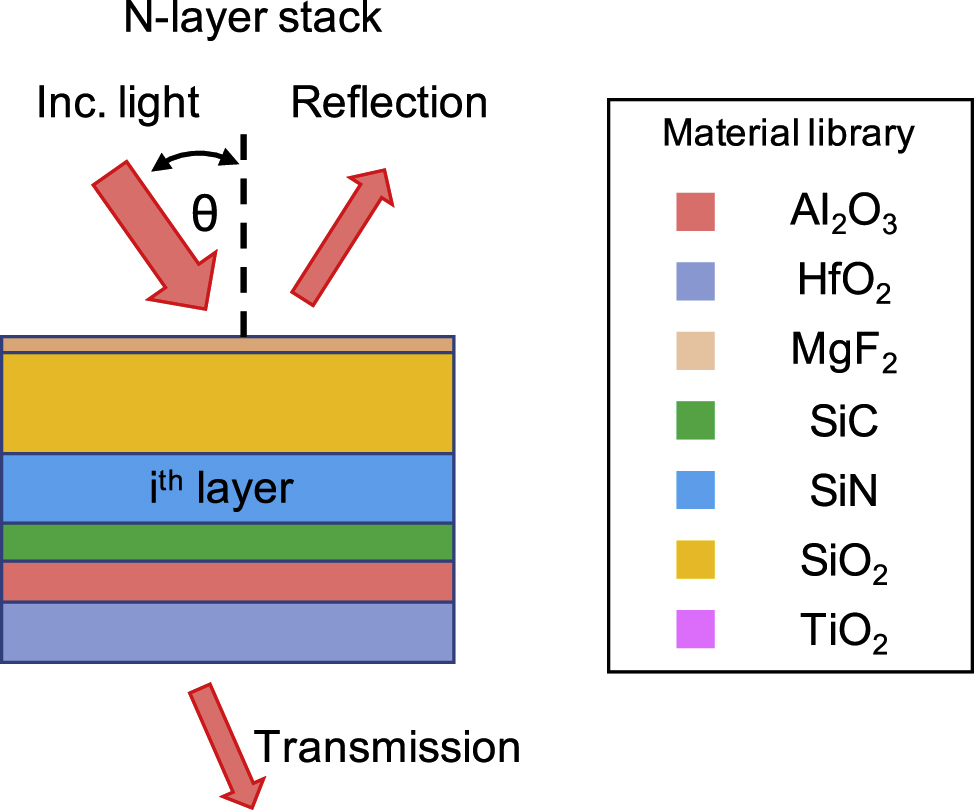
Schematic of the N-layer thin-film stack system. The refractive index and thickness of each layer are optimized to produce a desired reflection profile, and the composition of each layer is constrained to index values specified in a material library.

The optimization problem is posed as finding the proper n and t that produces the desired reflection characteristics over a given wavelength bandwidth, incident angle range, and incident polarization:

The desired reflection spectrum is denoted as ℛ*(λ,θ,pol), and {n*,t*} are the corresponding global optimal refractive indices and thicknesses. This optimization problem can be readily cast as the minimization of the objective function: O(n,t)=∑λ,θ,pol(ℛ(n,t|λ,θ,pol)−ℛ*(λ,θ,pol))2. n are categorical variables because the index values are chosen from a material database, while t can span a continuous set of values and is a continuous variable.

2.2 Res-GLOnet algorithm

A schematic of GLOnets configured for our thin-film stack system is outlined in Figure 2a. We term this GLOnet variant as Res-GLOnets because the generator has a residual network architecture that includes skip connections between layers (blue box inset), which will be discussed in a later section. First, a generative neural network G with trainable weights ϕ produces a distribution of thin-film stack configurations. The input to the generator is a uniformly distributed random vector z∼U(0,1), so that the generator can be regarded as a function that maps the uniform distribution to a complex distribution of thin-film stack configurations, Gϕ:U(0,1)→Pϕ(n,t). Different samplings of the input random variable z(k) map onto different device refractive index and thickness configurations within Pϕ(n,t), denoted as {n(k),t(k)}=Gϕ(z(k)). The generated n from the network do not take categorical values from the material library but are relaxed to be continuous variables, to stabilize the optimization process. These n are further processed using a probability matrix to enforce the categorical value constraint, which is discussed in the next section. After processing, the reflection spectra of the generated devices, ℛ(n(k),t(k)|λ,θ,pol), are calculated using the TMM solver.

Figure 2:

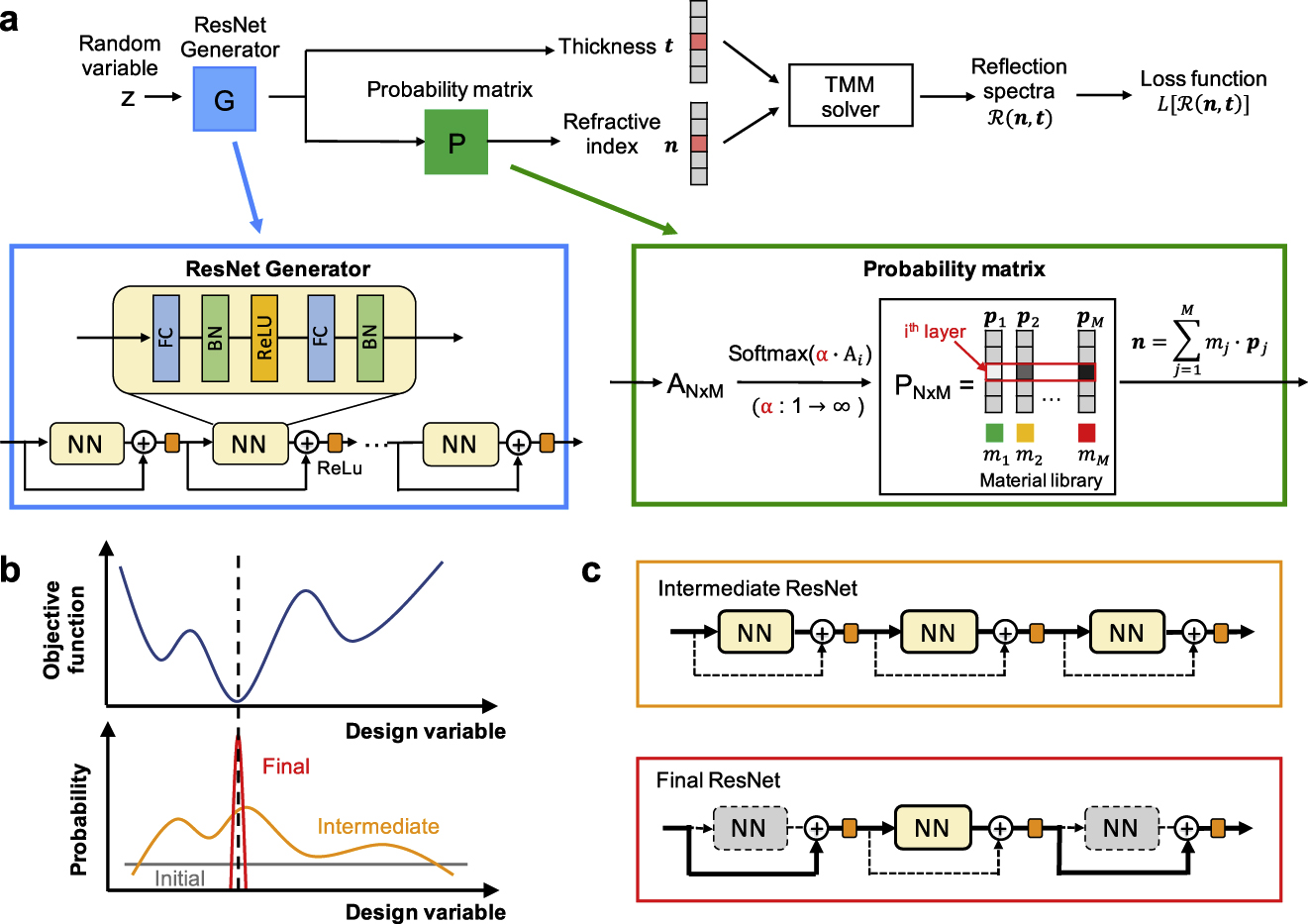
Thin-film global optimization with the Res-GLOnet. (a) Schematic of the Res-GLOnet. A ResNet generator maps a uniformly distributed random variable to a distribution of devices, which are then evaluated using a transfer matrix method solver and used to evaluate the loss function. A probability matrix pushes the continuous generated device indices n to discrete values. (b) Evolution of the generated device distribution over the course of network training. The network initially samples the full design space and converges to a narrow distribution centered around the global minimum of the objective function. (c) During training, the network operates as a deep architecture with little impact from the skip connections (Intermediate ResNet). Near training completion, the network evolves to a shallow architecture with large impact from the skip connections (Final ResNet). Bold and dashed lines indicate large and small contributions to the network architecture, respectively. TMM, transfer matrix method; GLOnet, global optimization network.

The optimization objective, or the loss function, for GLOnet is defined as:

(2)L=E[exp (−O(n,t)σ)]

(3)=∫exp (−O(n,t)σ)Pϕ(n,t)dndt

(4)=∫exp (−O(Gϕ(z))σ)P(z)dz

(5)≈∑k=1Kexp(−O(n(k),t(k))σ)

σ is a hyperparameter. These equations follow the derivation of the GLOnet formalism described in the study by Jiang and Fan [20]. To train the generative network and update its weights in a manner that improves the mapping of z to devices, the gradient of the loss function with respect to the neuron weights, ∇ϕL, is calculated by backpropagation.

A schematic of the evolution of the generative network over the course of network training is outlined in Figure 2b. Initially, the generator has no knowledge about the design space and outputs a broad distribution of devices spanning the full design space. Over the course of network training, the distribution of generated devices narrows and gets biased toward design space regions that feature relatively small objective function values. Upon the completion of network training, the distribution of generated thin-film stack configurations converges to a narrow distribution centered around the global optimum.

3 Optimization of an antireflection coating

We first apply our Res-GLOnet algorithm to the design of a three-layer antireflection (AR) coating for a silicon solar cell. The thin-film AR stack is designed to minimize the average reflection at an air-silicon interface over the incident angle range [0°, 60°] and wavelength range [400, 1100] nanometer for both transverse magnetic (TM) and transverse electric (TE) polarization. As a benchmark, we compare our results with those from the study by Azunre et al. [22], which provides a guaranteed global optimum solution using a parallel branch-and-bound method. The algorithm requires extensive searching through the full design space and utilizes over 19 days of CPU computation to solve for the global optimum. To be consistent with the study by Azunre et al. [22], the refractive indices of the layers in our design implementation do not take discrete categorical values from a material library but are dispersionless and continuously varying in the interval [1.09, 2.60]. The thicknesses of each layer are also continuous variables within the interval [5, 200] nm.

To accommodate the continuous variable nature of the refractive index values in this problem, we modify our categorical optimization scheme by setting the hyperparameter α = 1 as a constant and specifying the material library to contain only two materials with constant refractive indices {mL,mU}. mL=1.09 is the lower bound of the refractive index, while mU=2.60 is the upper bound. The constraint on thickness can be satisfied by a transformation: t=tL+Sigmoid(t˜)⋅(tU−tL). Here, the thickness directly outputted by the generator, t˜, is normalized to [0, 1] and then linearly transformed to the interval [t^L, t^U], where t^L = 5 and t^U = 200 are the lower and upper thickness bound, respectively.

As a reference, we first optimize devices using local gradient-based optimization, by replacing the ResNet generator in our Res-GLOnet algorithm with an individual device layout. The optimizations are performed with 100 different devices, initialized using random thickness and refractive index values within the limits of [1.09, 2.60] and [5, 200] nm, respectively. Each optimization is performed over 200 iterations, so that a total of 20,000 sets of calculations are performed for the entire set of optimizations. A histogram of the results (Figure 3a) shows that the optimized devices have average reflectivities that span a wide range of values, from approximately 2 to 10%, demonstrating the highly nonconvex nature of the design space. Average reflectivity is calculated as the reflectivity averaged over the wavelengths, incident angles, and polarizations covered in the design specifications. A fraction of devices are near the global optimum, and the best device has an efficiency of 1.82%.

Figure 3:

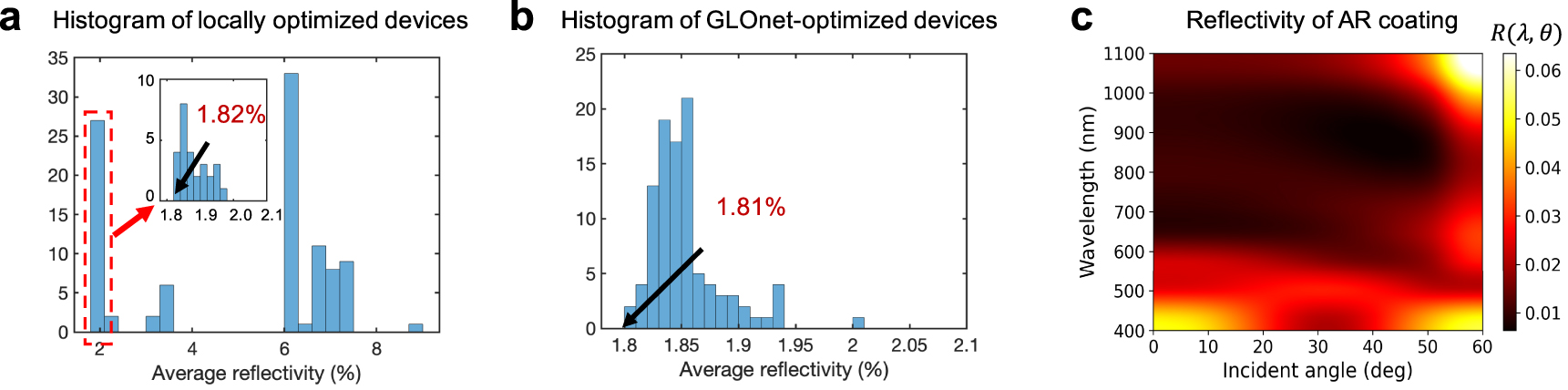
Optimization of a third-layer thin film antireflection (AR) coating on silicon. (a) Histogram of the average reflectivity from 100 AR coatings designed using local gradient-based optimization. The best device has an average reflectivity of 1.82%. (b) Histogram of the average reflectivity from 100 AR coatings designed using a single Res-GLOnet. The best device has an average reflectivity of 1.81%. (c) Contour plot of reflectivity from the best Res-GLOnet–designed AR coating in (b) as a function of the incidence angle and wavelength, averaged for both TE- and TM-polarized waves. GLOnet, global optimization network.

A histogram of devices sampled from a single trained Res-GLOnet is summarized in Figure 3a. A total of 200 iterations is used together with a batch size of 20 devices, so that a total of 4000 sets of calculations are performed. The total time that Res-GLOnet requires for training is 7 s with a single GPU. All of the devices sampled from the Res-GLOnet are near the global optimum, showing the ability for the generative network to produce a narrow distribution of devices centered at the global optimum. The best device has an efficiency of 1.81%, and its reflectivity for differing incident wavelengths and angles is plotted in Figure 3c. The design of this best device is summarized in Table 1 and is consistent with the result reported in the study by Azunre et al. [22].

4 Optimization of the incandescent light bulb filter

To explore the applicability of Res-GLOnets to more complex problems, we apply our algorithm to optimize incandescent light bulb filters that transmit visible light and reflect infrared light (Figure 4a). In this scheme, the emitter filament heats to a relatively higher temperature using recycled infrared light, thereby enhancing the emission efficiency in the visible range [29].

Figure 4:

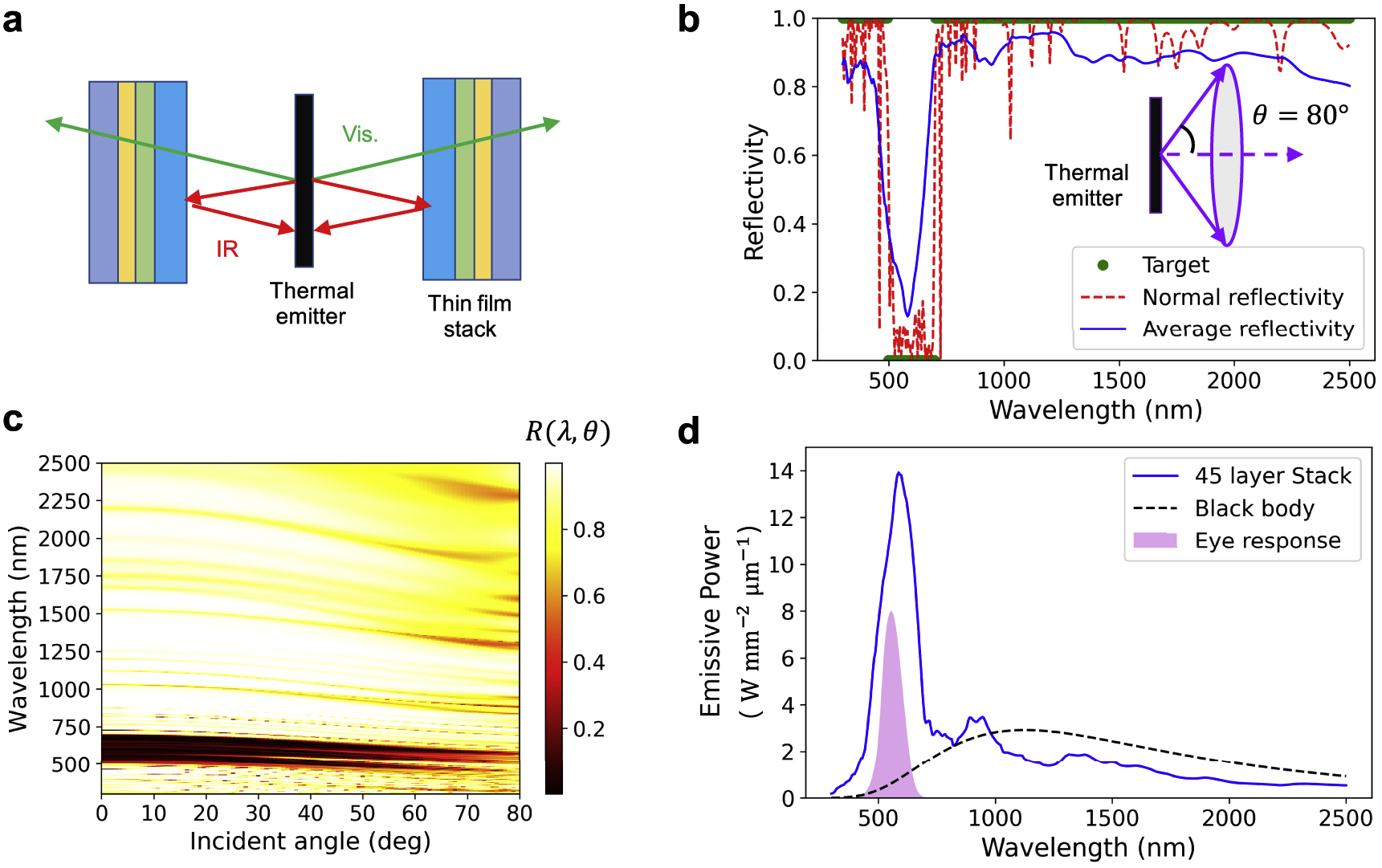
Thin-film stacks for incandescent light bulb filtering. (a) Schematic of an incandescent light bulb filter that transmits visible light and reflects infrared and ultraviolet light. (b) Reflection spectra of a 45-layer Res-GLOnet–optimized device, for normally incidence waves and waves averaged over a large incident solid angle, shown in the inset. (c) Reflection spectra of the device featured in (b) as a function of the incident angle, averaged for TE- and TM-polarized incident waves. (d) Emissive power of a blackbody incandescent source and an equivalent source sandwiched by the filter featured in (b). Also shown is the spectral response of the eye. GLOnet, global topology optimization network.

A range of design methods have been previously applied to this problem. In the initial demonstration of the concept, binary thin-film stacks were designed using a combination of local gradient-based optimization, used to tune the thickness of each layer, and needle optimization, which determined whether an existing layer should be removed or a new layer should be introduced [29]. A memetic algorithm was subsequently applied in which crossover, mutation, and downselecting operations were iteratively performed on a population of thin-film stacks to evolve the quality of devices [21]. Gradient-based local optimizations of device thicknesses were also periodically performed to refine the structures and accelerate algorithm convergence. In a third study, reinforcement learning (RL) was used in which an autoregressive recurrent neural network generated thin-film stacks layer by layer as a sequence [23]. Unlike the GLOnet generator, the probability distribution of the thin-film stack was explicitly outputted by the autoregressive generator. The distribution evolved by optimizing a reward function, and the gradient of the reward function with respect to the neural network weights was calculated using proximal policy optimization.

In our demonstration, we benchmark Res-GLOnets with the memetic and RL studies, which consider a material library comprising seven dielectric material types: Al₂O₃, HfO₂, MgF₂, SiC, SiN, SiO₂, and TiO₂. The superstrate and substrate are both set to be air. The complete wavelength range under consideration is [300, 2500] nm, and the target reflection is set to be 0% for the wavelength range [500, 700] nm and 100% for all other wavelengths. The incident angles span [0, 72] degrees, and both TE and TM polarizations are considered.

We train a Res-GLOnet comprising 16 residue blocks for 1000 iterations with a batch size of 1000. The network is optimized using gradient decent with the momentum algorithm ADAM [42], and a learning rate of 1 × 10⁻³ is used. The broadband reflection characteristics of a 45-layer device show that the device operates with nearly ideal transmission in the [500, 700] nm interval and nearly ideal reflection at ultraviolet and near-infrared wavelengths, for both normal incidence and for incidence angles averaged over all solid angles within [0, 80] degrees (Figures 4b and 4c). The emission intensity spectrum of the light bulb with and without the thin-film filter is shown in Figure 4d. The input power is fixed at 100 W, and the surface area of the emitter is 20 mm².

To evaluate the enhancement of visible light emission due to the filter, we compute the emissivity enhancement factor, χ, as a function of the number of thin-film layers:

Figure 5:

Plot of emissivity enhancement as a function of the number of thin-film layers, for devices optimized using Res-GLOnets and FC-GLOnets. Reference points are also plotted for devices designed using the reinforcement learning (RL) [23] and memetic [21] algorithm. GLOnet, global optimization network.

5 Conclusion

In summary, we show that Res-GLOnets are effective and efficient global optimizers for the multiobjective, categorical design of thin-film stacks. Categorical optimization is performed through the use of a probability matrix, which is fully differentiable and compatible with our neural network training framework. The incorporation of skip connections in our generative neural network helps it evolve from a deep to shallow architecture, which fits with our training objective and improves our search for the global optimum. Benchmarks of our algorithm with a known AR coating and incandescent light filter systems indicate that the Res-GLOnet is effective at searching for global optima, is computationally efficient, and outperforms a number of alternative design algorithms.

We anticipate that concepts developed within Res-GLOnets, particularly those in categorical optimization, can directly apply to the design of other photonics systems, such as lens design where the material type is selected from a material database. We also expect that the implementation of application-specific electromagnetic solvers, in conjunction with automatic differentiation packages, will serve as a foundational concept for many high-speed optimization algorithms beyond those for thin-film stacks. Generalizing the GLOnet algorithm to 3D photonic structures is challenging owing to the requirement of computational expensive simulations. We envision that this roadblock can be overcome by using neural networks as fast surrogate solvers, for which much progress has been made [43], [44]. Looking ahead, we see opportunities for Res-GLOnets to apply to other fields in the physical science, ranging from material science and chemistry to mechanical engineering, where devices and systems are designed using combinations of discrete material types.