Homogeneous quantum cascade lasers operating as terahertz frequency combs over their entire operational regime

1 Introduction

The terahertz (THz) region of the electromagnetic spectrum, loosely defined in the frequency range between 0.1 and 10 THz [1], attracted a renewed attention, in recent years, for targeting far-infrared applications requiring a tight control of the frequency and phase jitter of the laser modes, such as high-resolution and high-sensitivity spectroscopy [2], [3], telecommunications [4], [5], and quantum metrology [6], amongst many others.

Although relevant models for gigahertz–terahertz generation exploiting nonlinearity in semiconductor superlattices have been recently proposed [7], electrically pumped quantum cascade lasers (QCLs) are the most efficient on-chip sources of optical frequency comb (FC) synthesizers at THz frequencies [8], [9], [10], [11], thanks to the wide frequency coverage [10], [12] and the inherently high optical power levels [13], [14], which allow continuous-wave (CW) emitting powers per comb tooth in the 3 μW [12] to 60 μW [8] range and the high spectral purity (intrinsic linewidths of ∼100 Hz) [15]. Such a combination of performances makes THz QCL FCs the most suitable choice for the aforementioned applications.

In a THz QCL, the inherently high optical nonlinearity of the quantum engineered gain medium allows locking in phase the laser modes, passively [8], [16]. Specifically, the resonant third-order active material susceptibility inherently induces self-phase locking through the four-wave mixing (FWM) process. FWM tends to homogenize the mode spacing and consequently promotes the spontaneous proliferation of phase-locked equispaced optical modes.

However, to achieve a stable comb regime, the total chromatic dispersion has to be minimized over the laser operational bandwidth [8] so that the phase mismatch from the material, the laser waveguide, and the active region gain approaches zero in the QCL cavity. This has been achieved either by integrating a dispersion compensator in a homogeneous QCL active region [8] providing a negative group velocity dispersion (GVD) to cancel the positive cavity dispersion or by gain medium engineering of heterogeneous multistacked active regions (ARs) [10], [17], [18] or of individual homogeneous ARs [19], in both cases designed to have a relatively flat gain top, within which the intrinsic dispersion is small enough to preserve comb formation. Heterogeneous designs are ideal for achieving a broad spectral coverage, but they also come with some inherent disadvantages, such as the design-related difficulties associated with a proper matching of the threshold currents between the different AR modules, which can prevent the simultaneous mode proliferation over the full operation range of the QCL. On the other hand, homogenous ARs are usually engineered with a narrower gain profile but are in principle easier to be injection locked in the laser operation regime in which dispersion is not compensated.

Although a broad spectral coverage (0.7–1.1 THz) [8], [10], [12], [19] has been demonstrated using both a dispersion compensator [8] or through heterogeneous [10], [12] or homogeneous [8], [19] gain medium engineering, both approaches are ineffective in handling the bias-dependent cavity dispersion, meaning that spontaneous comb operation has been demonstrated to occur only over a limited driving current dynamic range, usually <20–29% of the QCL operational regime [8], [9], [10], [12], [19]. To date, external approaches such as coupled dc-biased cavities [20] or Gires–Tournois interferometers [21] proved to be the only way to increase the operational dynamic range of THz FC synthesizers, although with poor spectral coverage [20], optical power outputs [20], or with only a moderate increase of the current dynamic range [21].

In this work, we quantum engineer and devise a broadband homogeneous QCL FC covering a bandwidth of 0.6 THz (3.05–3.65 THz), with a dynamic range J_dr = J_max/J_th = 1.53 (J_th is the threshold current density and J_max the maximum current density value) and a maximum CW output power of 7 mW. Remarkably, the collected electrical intermode beatnote map reveals spontaneous FC operation over the entire operational range of the laser, classifying the proposed device as a unique frequency-tunable metrological tool across the far-infrared.

2 Results and discussion

The active region design of the homogeneous gain medium is a slightly modified version [22], [23] of the four quantum well bound-to-continuum structures described in Ref. [24]. The highly diagonal laser transition ensures gain recovery times much larger (>35 ps) [25] than those usually achieved in THz QCLs (5–10 ps), together with shorter upper state lifetimes, above threshold. This is an ideal condition for amplitude modulations up to tens of GHz, ideal for FC operation [19]. Indeed, a GHz modulation envelope, possibly synchronized to the THz field in the time domain, could also help stabilizing the laser in a fashion reminiscent of active mode-locking, supporting the formation of an amplitude-modulated comb. The GaAs/AlGaAs hetoerostructure used in this work is grown by molecular beam epitaxy (MBE) on a semi-insulating GaAs substrate. The final gain medium includes a sequence of 160 periods of a four-well quantum cascade design centered at 3.3 THz. The 10-μm thick final structure consists of a 250 nm undoped GaAs buffer layer, an undoped 250 nm Al_0.5Ga_0.5As etch-stop layer, a 700 nm Si-doped (2 × 10¹⁸ cm⁻³) GaAs layer, the AR (doped at 3 × 10¹⁶ cm⁻³), and a 80 nm heavily Si-doped (5 × 10¹⁸ cm⁻³) GaAs top contact layer.

Device fabrication is based on a standard metal–metal processing technique that relies on Au–Au thermocompression wafer bonding of the MBE sample onto a highly doped GaAs substrate. A Cr/Au (10 nm/150 nm) top contact is lithographically patterned on the top laser surface, leaving uncoated the two sides of the ridge along two lateral stripes, whose width ranges between 3 and 5 μm, depending on the ridge width [10]. Laser bars are then realized via deep inductively coupled plasma reactive ion etching (ICP-RIE) with vertical sidewalls to allow uniform current injection and ridge widths in the 50–90 μm range. A 5-nm thick Ni layer is then deposited on the uncoated top lateral stripes to define lossy side absorbers needed to suppress undesired high-order lateral modes. Laser bars 50–70 μm wide and 2.75 mm long were then In soldered on a copper plate, wire bonded, and mounted on the cold head of a helium flow cryostat.

The voltage–current density (V–J) and the light–current density (L–J) characteristics, measured while driving the QCL in CW, as a function of the heat sink temperature (T_H), show laser action up to a maximum heat sink temperature T_H = 88 K. Figure 1A shows the V–J–L collected in the T_H = 15–75 K interval. At T_H = 27 K, the CW threshold current density is J_th = (428 A cm⁻²), the maximum current density J_max = 653 A cm⁻², the operational dynamic range is J_dr = J_max/J_th = 1.53, and the maximum peak optical power is 7 mW.

Figure 1:

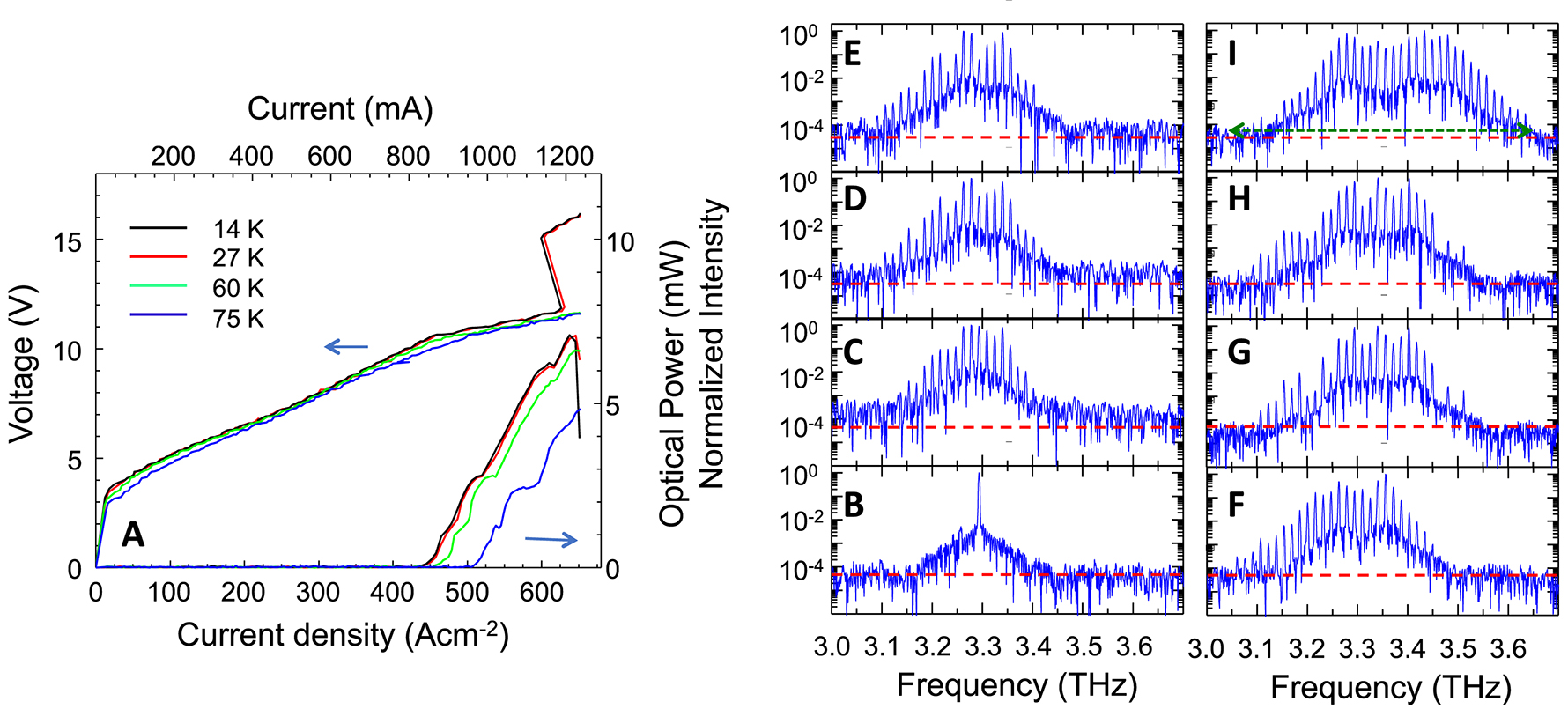
(A) Voltage–current density (V–J) and light–current density (L–J) characteristics, measured in continuous wave, as a function of the heat sink temperature in the 15–75 K range. (B–I) Fourier transform infrared spectra measured at T_H = 27 K, in rapid scan mode, under vacuum with a 0.075 cm⁻¹ spectral resolution, while driving the quantum cascade laser (QCL) in continuous wave at (B) 445 A cm⁻², (C) 465 A cm⁻², (D) 470 A cm⁻², (E) 480 A cm⁻², (F) 512 A cm⁻², (G) 550 A cm⁻², (H) 583 A cm⁻², and (I) 645 A cm⁻². The red dashed lines indicate, roughly, the noise floor of the measurements. The green arrow in panel I marks the laser bandwidth.

CW Fourier transform infrared spectra (FTIR), acquired under vacuum (Bruker vertex 80) with a 0.075 cm⁻¹ spectral resolution (Figure 1B–I), while progressively increasing the driving current, show that the laser is initially emitting a single frequency mode (∼3.3 THz) at threshold (J = 445 A cm⁻², Figure 1B) and then turns multimode with a progressively richer (Figure 1C–I) sequence of equidistant optical modes, spaced by the cavity round-trip frequency. The overall spectral coverage reaches 600 GHz (Figure 1I), and differently from the very first demonstration [8], does not show any spectral dip; at a current density of 645 A cm⁻² (Figure 1I), corresponding to 7 mW peak optical power, 36 optically active laser modes are retrieved. Under this condition, the CW optical power per optical mode is ∼200 µW, significantly larger than that of any previous THz QCL FC, demonstrated so far [8], [9], [10], [11], [12], [19].

To investigate the coherence properties of the devised THz QCL, we then trace the intermode beatnote radio frequency (RF) as a function of the driving current (Figure 2A). The QCL is driven in CW by a low-noise power supply (Wavelength Electronics QCL2000 LAB), and the RF signal is recorded using a bias tee (Tektronix AM60434) connecting the QCL and an RF spectrum analyzer (Rohde and Schwarz FSW43). Remarkably, the intermode beatnote map shows a single narrow beatnote over the entire dynamic range of the QCL. An idividual beatnote appears at a current density just above threshold and persists, continuously, upon entering in the negative differential resistance (NDR) region.

Figure 2:

(A) Intermode beatnote map as a function of the driving current density measured at 27 K in a 2.75-mm-long, 70-µm-wide laser bar, operating in continuous wave (CW). The beatnote signal is extracted from the laser bias line using a bias tee and is recorded with a radio frequency (RF) spectrum analyzer (Rohde & Schwarz FSW; resolution bandwidth [RBW]: 500 Hz, video bandwidth [VBW]: 500 Hz, root mean square (RMS) acquisition mode). The vertical dashed lines identify four relevant transport regimes: (I) from onset for conduction to band alignment ; II (band alignment); III (peak optical power); IV (NDR). NDR, negative differential resistance.

The analysis of the beatnote linewithds (LWs) (Figure 2B) shows that the LW is initially varying in the range of ∼2–5 kHz (Figure 3A) for J up to 558 A cm⁻² (region I in the beatnote map in Figure 2A and B), then it becomes narrower (∼500 Hz, Figure 3B) for current densities up to 616 A cm⁻², (region II). This is followed by a limited current density region, around the peak optical power (J = 632 A cm⁻²) (region III), in which the LW increases progressively from 500 Hz up to 2 kHz. Interestingly, when the QCL is then driven beyond the roll-off current (region IV), the beatnote is still narrow (2–7 kHz, Figure 3C), but weaker (∼15 dBm), due to the electric field instabilities, associated with the bias fluctuations, occurring in this regime. Surprisingly, the laser does not show any high phase noise regime [8], [9], [10], [11], [12], [19], [21].

Figure 3:

(A–C) Intermode beatnote linewidth measured at T_H = 27 K, while driving the quantum cascade laser (QCL) in continuous wave at (A) 480 A cm⁻², (B) 570 A cm⁻², (C) 645 A cm⁻² with a radio frequency (RF) spectrum analyzer (resolution bandwidth [RBW]: 500 Hz, video bandwidth [VBW]: 500 Hz).

The analysis of the electrical frequency tuning of the intermode beatnote reflects the different dynamics along the distinctive operational bias regimes. Indeed, by varying the driving current at a fixed operating temperature T_H = 27 K, the beatnote initially blue shifts across region I, spanning a 70 MHz range with a tuning coefficient of +0.47 MHz mA⁻¹, then the beatnote jumps at a lower value at the onset of region II and the tuning coefficient then decreases to +0.2 MHz mA⁻¹. The beatnote then jumps again at a lower value (13.315 GHz) at the onset of region III and remains almost constant over the entire NDR regime. The overall tuning behavior clearly reflects the lack of Joule heating–related effects that would led to a negative tuning coefficient with a monotonic decrease of the beatnote frequency with respect to the driving current. The observed trend is instead ascribed to the intracavity dynamics of the AR, specifically to the chromatic dispersion affecting the frequency, and thus the spacing of the cavity modes owing to the variation in the effective refractive index of the gain medium.

To get a deeper insight on the intracavity dynamics, we perform numerical simulations of the group delay dispersion (GDD). The dispersion profile is retrieved including the contributions from the material, the waveguide and the gain of the QCL [9], [21]. The first two terms are computed considering a Drude–Lorentz model for the frequency-dependent refractive index of the material; we then compute the QCL gain from the experimental emission spectra and evaluate the refractive index deviation as a consequence of the gain by applying the Kramers–Kronig equations. Finally, the dispersion provided by the whole structure is computed from the second derivative of the phase. Figure 4 shows the individual GDD contributions, calculated at J = 645 A cm⁻², i.e. in the high voltage regime, in which the laser spectrum is particularly rich of optical modes.

Figure 4:

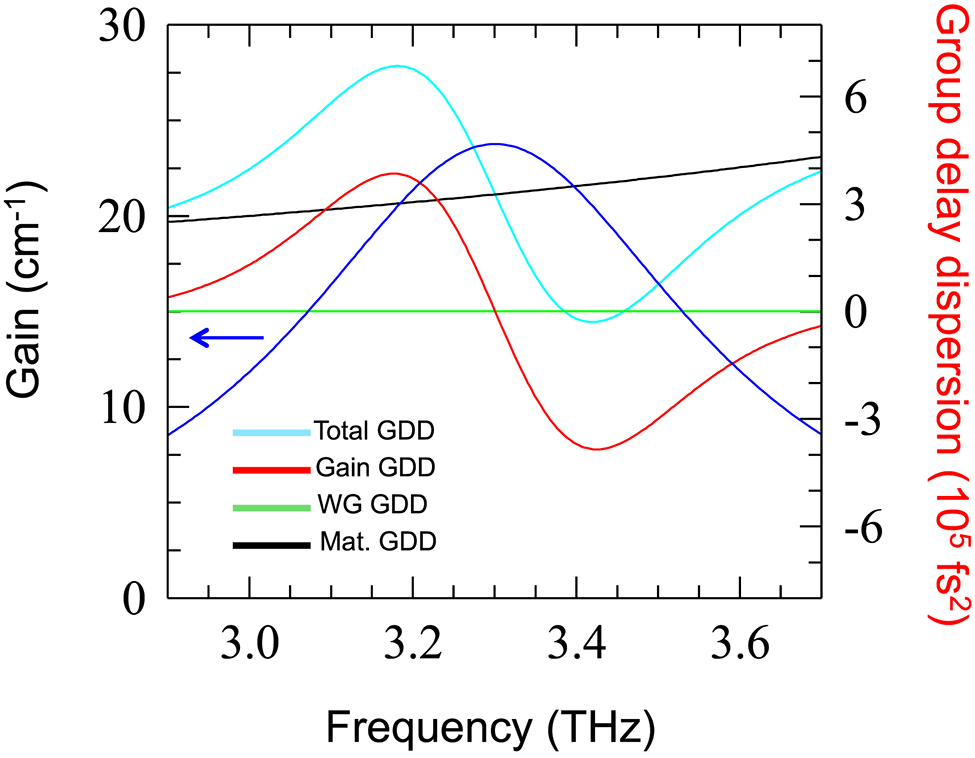
Simulations of the group delay dispersion including contributions from the material (GaAs), waveguide and gain, performed at J = 645 A cm⁻². The estimated gain curve (blue) is plotted on the left vertical axis of the graph and marked with an arrow.

In the spectral region where the QCL shows laser action, the waveguide shows a low dispersive refractive index; therefore, the waveguide-related contribution to the dispersion is negligible (<10⁵ fs²) with respect to the other terms. The gain profile (Figure 4), centered at 3.3 THz is extracted from the emission spectra of Figure 1I and it is then normalized considering the cavity length, the light intensity ratio between the center of the bandwidth and the peripheral lasing modes and adding up the total losses from the waveguide (∼7.3 cm⁻¹), the material (∼3.0 cm⁻¹) [9] and the QCL facets (∼1.6 cm⁻¹). The total GDD shows a visible oscillating behavior at the center of the laser gain bandwidth; in the operational range of the QCL, its value ranges between 3 × 10⁵ fs² and 2.5 × 10⁵ fs², reaching a maximum of 6.5 × 10⁵ fs² at 3.2 THz and approaches zero over a range of about 200 GHz. On average, even in such a high-voltage regime, the GDD is equivalent to the values reported in heterogeneous FCs, just above threshold, i.e. in the regime in which the QCL clearly behaves as a comb [9], [26].

We then investigate the frequency locking characteristics of the laser structure at the onset of the NDR range. Injection locking maps are acquired by using an RF synthesizer (Rohde and Schwarz SMA100B) connected to the laser driver line, for the simultaneous supply of both the CW dc bias and the RF injection signal over a bias tee. The RF and dc biases are fed to the QCL through 18 GHz-cutoff sub-miniature type A (SMA) cables and connectors up to the cryostat input ports. The simultaneous monitoring of the injection signal and of the beatnote was performed positioning a RF antenna in close proximity (∼3 cm) of the QCL and recording the antenna signal through the spectrum analyzer.

The injection-locking map, acquired with a RF injection power of 25 dBm while the QCL is driven at the onset of the NDR region (J = 635 A cm⁻²), is reported in Figure 5A. Under these conditions, the emission spectrum of the QCL, under injection locking, comprises more than 36 optically active modes. The collected map discloses the typical injection-locking behavior, with the initial pulling and then locking of the beatnote to the injection signal, with the simultaneous appearance of multiple sidebands.

Figure 5:

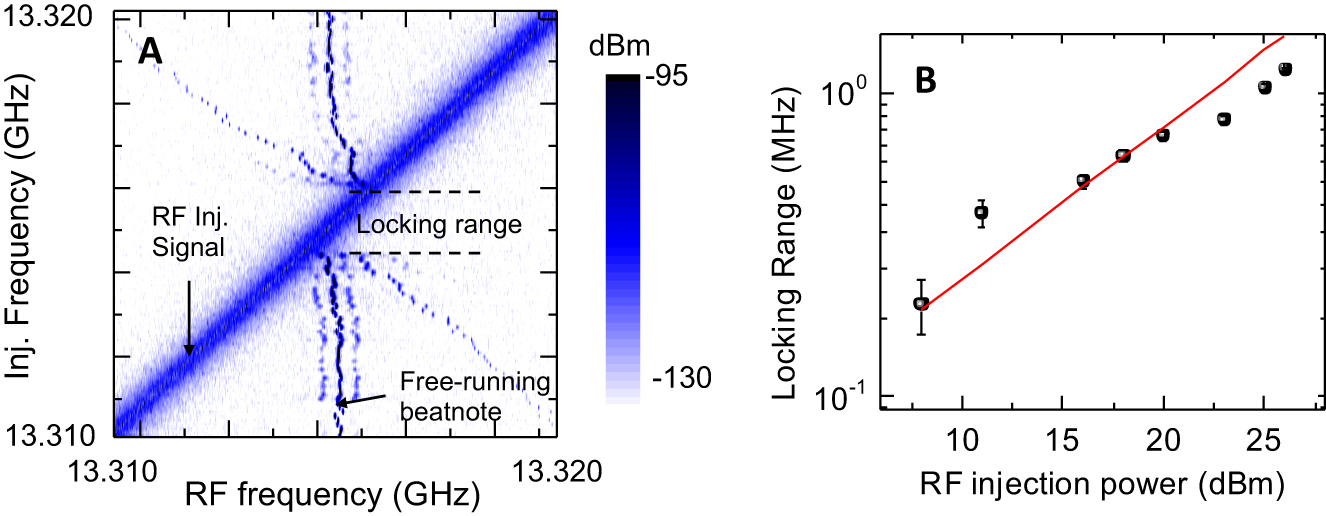
(A) Injection locking map for an injected radio frequency (RF) power of +25 dBm. The map is recorded by sweeping the RF injection signal (diagonal line across the panel) toward the free running beatnote and then locking it. The quantum cascade laser (QCL) is 2.7 mm long and 70 µm wide. (B) Locking range extracted from the QCL injection locking at different RF injection power (black squares), following a 0.5-slope dependence in log–log scale (red line).

In Figure 5B, we report the locking range as a function of the injection power. The plot shows a good agreement with the 0.5-slope dependence in log–log scale foreseen in the Adler’s equation [27] particularly in the lowest power region. We observed a maximum locking range of 1.2 MHz with an RF power of 25 dBm. The locking range values are slightly lower than that recently reported for homogeneus QCL FCs [19], [28], around the peak optical power. Conversely, the injection locking power is significantly higher than the typical values reported to date [19], [28], [29], while the actual power injected to the QCL is much lower. This can be understood by considering the total RF losses from cables, connectors, Au pads and bonding wires; by directly measuring the RF power transmitted to the laser chip, we estimate a total RF attenuation of ∼35 dB. This latter value is extracted from a direct measurement of the RF power transmitted to the cold finger.

3 Conclusions

In conclusion, we demonstrate a THz QCL based on a homogenous active region design with an emission bandwidth of 600 GHz, a CW optical output power of 7 mW, operating as a FC synthesizer over the entire laser operation range, including the NDR regime. The electrical intermode beatnote map unveils stable comb operation over the entire dynamic range J_max/J_th = 1.53, with a single narrow beatnote reaching minimum linewidth = 500 Hz under free running operation. The laser shows more than 36 optically active, equally spaced, modes delivering 200 µW of optical power per comb tooth, the largest value reported to date in any THz QCL FC. We furthermore prove the RF injection locking capability of the devised laser bars in a regime conventionally characterized by electric field instabilities. The achieved results provide a concrete route for the development of miniaturized homogeneous chip-scale FC spectroscopic setups for addressing metrological-grade applications in the far-infrared, addressing absorption line strengths comparable or even stronger than fundamental, mid-infrared vibration transitions, but with much narrower Doppler-limited LWs, ruled by inverse linear relationship with the wavelength [3].