Abstract
The liquidus temperature and temperature drop coefficients of medium manganese steel were systematically studied using Factsage and differential scanning calorimetry (DSC) experiments. The results indicated that the temperature drop coefficients of C, Mn, Cr, Si, and Al were complex, while the coefficients of Mo, V, and Nb were of a constant value. Based on the temperature drop coefficients, the empirical formula for calculating the liquidus temperature of medium manganese steel was established. The liquidus temperature calculated using the empirical formula was 1422.7°C, while that obtained by the DSC experiment was 1422.9°C. By comparison with different calculation formulas, the liquidus temperature obtained from the formula that was constructed in this study was much closer to the experiment one, indicating the high accuracy of the empirical formula in predicting the liquidus temperature of medium manganese steel.
1 Introduction
Medium manganese steel, with excellent wear resistance, has been widely used in mining machinery of wear-resistant lining boards [1,2,3]. However, serious shrinkage cavity and shrinkage porosity defects occur frequently in the production process of the steel [4] when high C [5,6] and high Mn [7] contents are present in the steel. In addition, other alloying elements such as Cr [8] are also added. Therefore, the liquidus temperature of medium manganese steel must be quite different from that of conventional steel. Significant progress has been achieved in the research of the microscopic structure [9,10], heat treatment process [11,12,13], rolling process [14], and wear performance [15,16] of medium manganese steel; however, the study on liquidus temperature is rarely reported.
Liquidus temperature plays a vital role during the solidification process of steel, which is closely related to the microstructure evolution and solidification quality [17]. In the steelmaking process, the confirmation of tapping temperature is based on the liquidus temperature. An appropriate liquidus temperature can not only ensure the running of the pouring process but also can improve the quality of the billet significantly [18]. At present, experimental methods including the differential thermal analysis (DTA) [19,20,21,22], differential scanning calorimetry (DSC) [23,24,25,26], thermodynamic software calculation method [22], and empirical formula method [27,28,29,30] are often adopted to determine the liquidus temperature of steel. Hamada and Karjalainen [20] investigated the liquidus temperature of Fe–22Mn–0.6C high manganese TWIP steel by DTA measurement and found that the liquidus temperature was 1378°C. Zinke et al. [21] also used DTA and reported the liquidus temperature of Fe–17.8Mn–0.59C–1.33Al–0.22Si steel to be 1,416°C. In order to reduce the experimental errors caused by Mn volatilization during the test and improve the reliability of the results, Zhuang et al. [19] found that the liquidus temperatures of Fe–20Mn–0.75C–1.5Al–0.05Si and Fe–10Mn–0.5C–1.5Al steels were 1406.5 and 1,466°C, respectively, by using the improved DTA equipment. The results obtained by DTA or DSC experiments are accurate; however, the experimental process is expensive and time-consuming, which is not suitable for industrial field production. In addition, some thermodynamic software such as Factsage and Thermo-calc [26,31] can also be used to calculate the liquidus temperature. Pierer et al. [31] pointed out that the liquidus temperature of Fe–25Mn–0.5C–1Al steel calculated with Thermo-calc was 1,411°C, which was lower than that of conventional steel. Because of convenience, the empirical formula method [27,28,29] was widely adopted during the production process. In this method, the temperature drop coefficients of the composition need to be calculated and then the liquidus temperature can be obtained by the linear sum of the temperature drop coefficients [30]. It should be noted that the temperature drop coefficients of different elements vary, and even the temperature drop coefficients of the same element also varied greatly under different steel components. It was reported that in some steels, the temperature drop coefficients are not independent but shared.
During the past few decades, some formulas have been constructed to predict the liquidus temperature. However, the vast majority of them were applicable to infinitely dilute solutions. But, high alloy content steel such as medium manganese steel does not belong to the category of dilute solution. Thus, these formulas cannot predict the liquidus temperature of high alloy content steels effectively.
Fast and accurate prediction of the liquidus temperature of high alloy content steels is of great significance to the casting temperature of ingot casting and continuous casting, which will eventually affect the quality and yield of the casting billet. Therefore, in the current study, the empirical formula that can effectively determine the liquidus temperature of medium manganese steel was constructed. The results obtained by the formula were in good agreement with the DTA/DSC experiment results. Compared with other formulae, the empirical formulae in this study can effectively predict the liquidus temperature of medium manganese steel. The present study provides theoretical guidance for industrial production, especially for the development of a continuous casting process of medium manganese. Besides, it also provides experience and reference for the accurate prediction of liquidus temperature of other high alloy steels.
2 Materials and methods
2.1 Materials
The ingot of medium manganese steel was fabricated in the ZGJ0.05–100–25 50 kg capacity vacuum induction furnace where the maximum temperature can reach 1,700°C, and the limit vacuum degree is 6.67 × 10−3 Pa. In addition, the ingot was manufactured from commercial pure materials and cast using a cast-iron mold in a vacuum. After the solidification was completed, the riser was removed from the ingot, and the specimens used in ICP and DSC experiments were cut longitudinally at the same position as the ingot. The chip samples of about 5 g were drilled from the specimens for the ICP test. The chemical composition of the experimental steel is given in Table 1.
Composition of high-carbon medium manganese steel (wt%)
| Element | C | Si | Mn | Cr | Mo | Nb | V | Alt |
|---|---|---|---|---|---|---|---|---|
| Content | 0.95 | 0.20 | 8.5 | 2.1 | 0.32 | 0.035 | 0.065 | 0.01 |
2.2 DSC test
The liquidus temperature can be determined accurately using DSC. It shows exothermic and endothermic peaks according to the phase transformation of the sample during heating or cooling. The size of the samples in DSC was 3 mm × 2 mm and the weight was approximately 10 mg. The equipment used in this study was NETZSCH STA 449 F5, where the maximum heating temperature can reach 1,800°C, and the range of heating rates can be controlled from 0.001 to 50°C·min−1. Besides, the measurements were conducted in an inert atmosphere of pure argon with the flow rate maintained at 50 ml·min−1. In order to shorten the duration of measurement, the samples were first heated from room temperature to 1,200°C at a heating rate of 50 K·min−1. Then, after 30 min of preservation, the samples were continued to be heated above the liquidus temperature to 1,550°C with heating rates of 5, 10, and 15°C·min−1, respectively. Finally, the temperature was reduced to room temperature at a rate of 50°C·min−1. The liquidus temperature can be obtained according to the characteristic exothermic peak in the heating process of the steel.
2.3 Calculation using Factsage
The empirical formula method is based on the Fe–I phase diagram. The general formula is shown as follows [32]:
where T
liq is the liquidus temperature (°C), M
Fe is the melting point of pure iron, which is usually selected as 1,536–1,539°C, ω
i
is the mass fraction of the alloying element, and
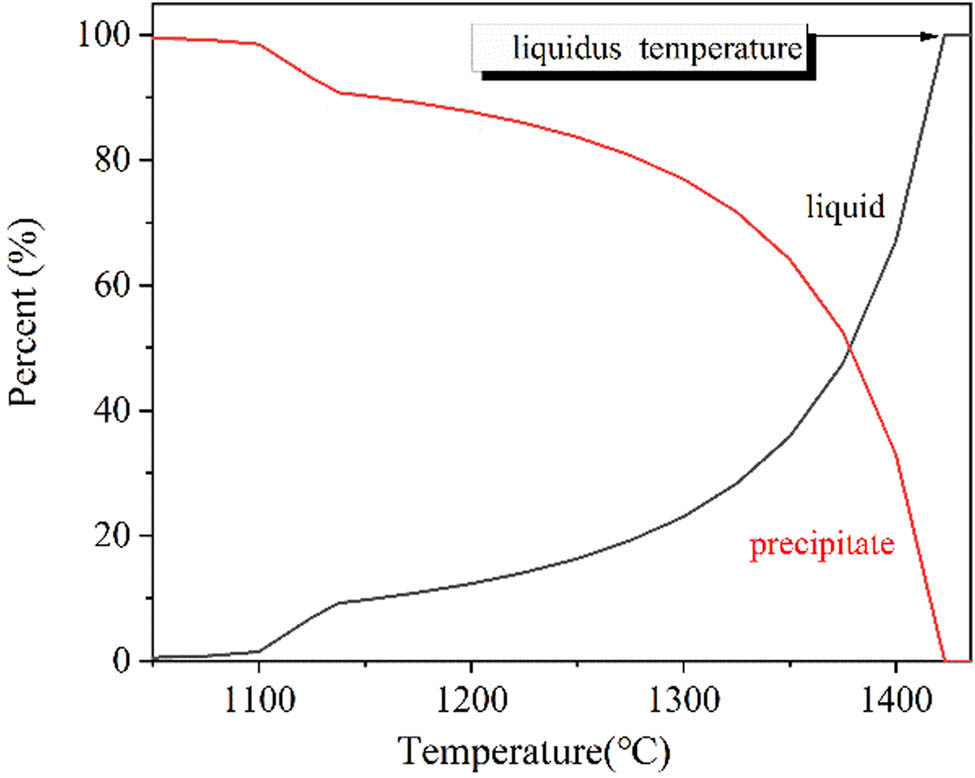
The precipitates during the solidification process of Fe–0.95C–8.5Mn–2.1Cr–0.32Mo–0.035Nb–0.065V–0.01Al steel.
3 Results
3.1 Effect of C on the liquidus temperature
Generally, the increase of C will significantly decrease the liquidus temperature of steel [28]. In this study, the influence of C on the liquidus temperature of medium manganese steel was studied with Factsage8.0. In order to ensure the accuracy and adaptability of the calculation results, the calculation was carried out in a wider range of C content. The results are shown in Table 2. It can be seen that when the content of C increased from 0 to 1.1%, the liquidus temperature of the medium manganese steel decreased from 1478.62 to 1413.12°C. In addition, the temperature drop coefficients also dropped from 91 to 67.82. Other scholars [28,29,33] pointed out the relationship between the liquidus temperature and the C content was linear, which was quite different from the results in this study. The traditional empirical formula was not applicable to predict the liquidus temperature of the medium manganese steel. The temperature drop coefficients of C were fitted, as shown in Figure 2. The relationship between coefficients and content conforms to the quadratic distribution, and the fitting degree R 2 = 0.989, indicating that the results are reliable. The formula is shown in equation (2):
The liquidus temperature and temperature drop coefficients with different C contents of the medium manganese steel
| ω C (wt%) | Fe–(0–1.1)C–8.5Mn–0.2Si–2.1Cr–0.01Al0.035Nb–0.065V–0.32Mo | ω C (wt%) | Fe–(0–1.1)C–8.5Mn–0.2Si–2.1Cr–0.01Al0.035Nb–0.065V–0.32Mo | ||
|---|---|---|---|---|---|
| T liq (°C) |
|
T liq (°C) |
|
||
| 0.1 | 1478.62 | 91 | 0.9 | 1426.15 | 68.41 |
| 0.2 | 1470.06 | 88.3 | 0.92 | 1424.87 | 68.32 |
| 0.3 | 1463.12 | 82 | 0.94 | 1423.58 | 68.23 |
| 0.4 | 1457.13 | 76.48 | 0.95 | 1422.93 | 68.2 |
| 0.5 | 1451.09 | 73.26 | 0.96 | 1422.29 | 68.16 |
| 0.6 | 1444.98 | 71.23 | 0.98 | 1420.99 | 68.09 |
| 0.7 | 1438.8 | 69.89 | 1.00 | 1419.69 | 68.03 |
| 0.8 | 1432.52 | 69 | 1.02 | 1418.38 | 67.98 |
| 0.82 | 1431.26 | 68.85 | 1.04 | 1417.07 | 67.93 |
| 0.84 | 1429.99 | 68.73 | 1.06 | 1415.76 | 67.89 |
| 0.86 | 1428.71 | 68.62 | 1.08 | 1414.44 | 67.85 |
| 0.88 | 1427.44 | 68.5 | 1.1 | 1413.12 | 67.82 |
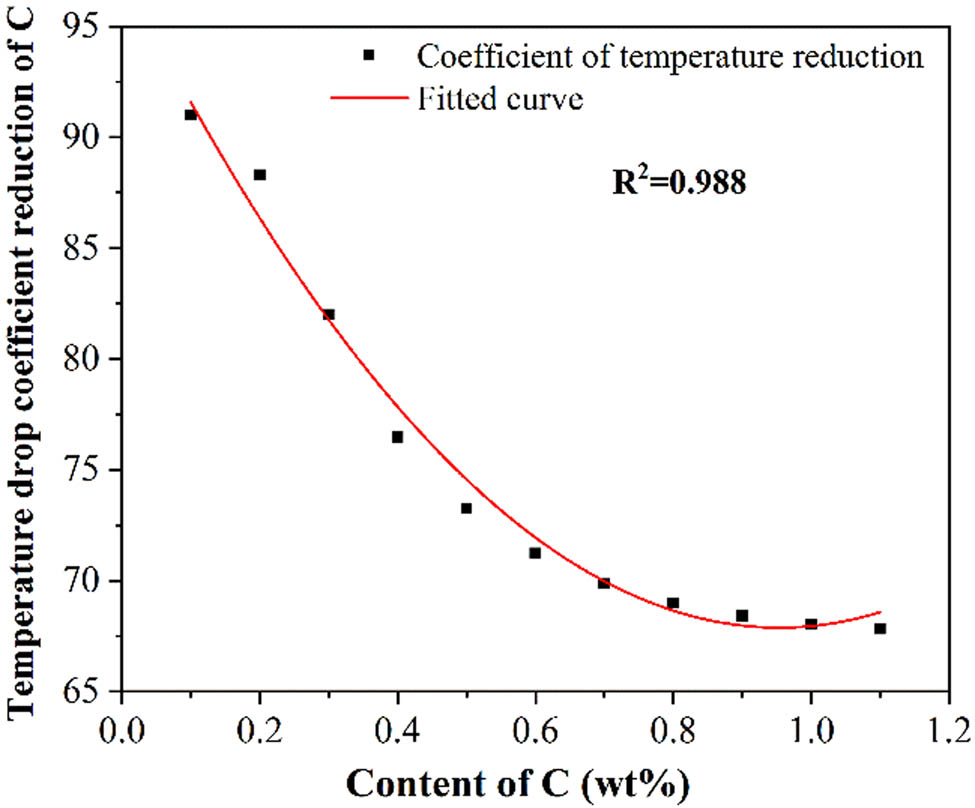
Relationship between the temperature drop coefficients and the C content.
3.2 Effect of Mn on the liquidus temperature
To date, studies on the influence of Mn on the liquidus temperature are rare. The content of Mn in medium manganese steel is much higher than that of conventional steel [34]. Therefore, it is of significance to study the effect of Mn on the liquidus temperature. Figure 3 shows the liquidus temperature and temperature drop coefficients with different contents of Mn. It was found that when the Mn content Mn increased from 7 to 10 wt%, the liquidus temperature decreased almost linearly from 1428.49 to 1417.35°C. Besides, the temperature drop coefficients of Mn were almost constant at around 3.67 (Table 3).
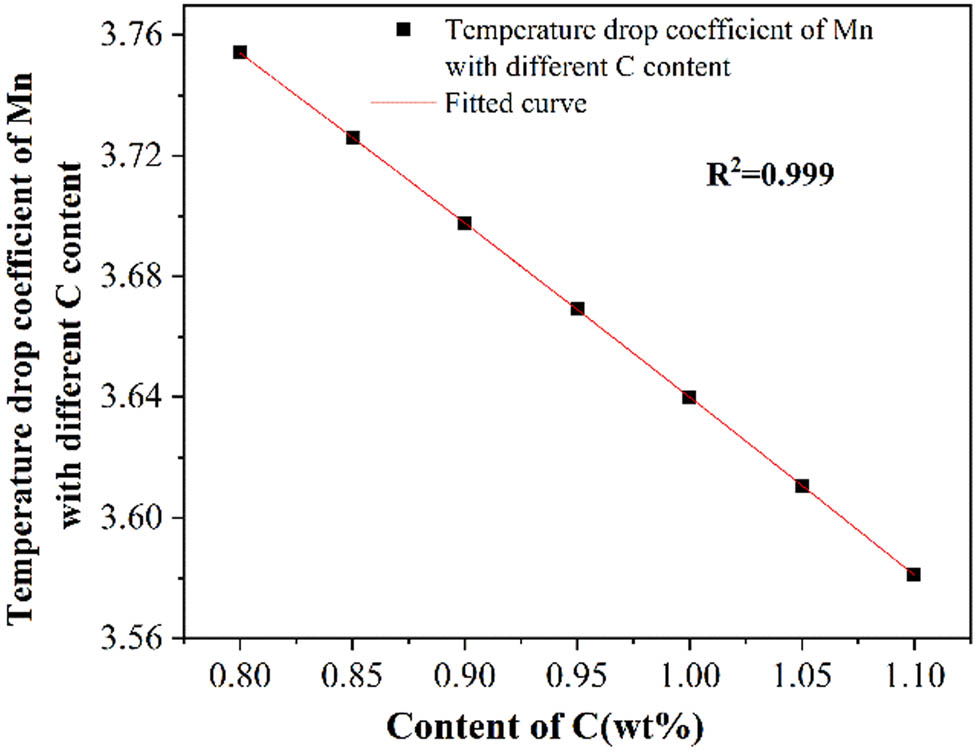
Relationship between the temperature drop coefficients of Mn with different C contents.
The liquidus temperature and temperature drop coefficients with different Mn contents of the medium manganese steel
| ω Mn (wt%) | Fe–0.95C–(7–10)Mn–0.2Si–2.1Cr–0.035Nb–0.065V–0.32Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 7 | 1428.49 | 3.66 |
| 7.25 | 1427.57 | 3.66 |
| 7.5 | 1426.64 | 3.66 |
| 7.75 | 1425.72 | 3.66 |
| 8 | 1424.79 | 3.67 |
| 8.25 | 1423.86 | 3.67 |
| 8.5 | 1422.93 | 3.67 |
| 8.75 | 1422.00 | 3.67 |
| 9 | 1421.08 | 3.67 |
| 9.25 | 1420.15 | 3.67 |
| 9.5 | 1419.22 | 3.67 |
| 10 | 1417.35 | 3.68 |
Liu et al. [35] investigated the liquidus temperature of Fe–Mn–C–Al TWIP steels and found that the influence of Mn on the liquidus temperature was closely related to the C content. Whether a similar phenomenon existed in the medium manganese steel needs to be verified. Therefore, the influence of Mn on the liquidus temperature and temperature drop coefficients with different C contents was investigated. The results are shown in Table 4. It was found that when the C content increased from 0.8 to 1.1 wt%, the coefficients decreased from 3.75 to 3.58. Although the temperature drop coefficients of Mn were lower than that of C, considering the Mn content in the medium manganese steel was much higher than C, the influence of Mn on the liquidus temperature cannot be ignored.
The liquidus temperature and temperature drop coefficients of Mn with different C contents of the medium manganese steel
| ω C (wt%) | T liq (°C) |
|
|
|---|---|---|---|
| Fe–(0.8–1.1)C–0.2Si–2.1Cr–0.035Nb–0.065V–0.32Mo–0.01Al | Fe–(0.8–1.1)C–8.5Mn–0.2Si–2.1Cr–0.035Nb–0.065V–0.32Mo–0.01Al | ||
| 0.8 | 1464.43 | 1432.52 | 3.75 |
| 0.85 | 1461.02 | 1429.35 | 3.73 |
| 0.9 | 1457.58 | 1426.15 | 3.70 |
| 0.95 | 1454.12 | 1422.93 | 3.67 |
| 1.00 | 1450.63 | 1419.69 | 3.64 |
| 1.05 | 1447.11 | 1416.42 | 3.61 |
| 1.10 | 1443.56 | 1413.12 | 3.58 |
The coefficients of Mn with different C contents were fitted. As shown in Figure 3, the variation of the curve is in agreement with the binary polynomial, as shown in equation (3):
The fitting degree R 2 = 0.999, indicating the reliability of the results.
3.3 Effect of Cr on the liquidus temperature
An appropriate amount of Cr element added to the steel can improve the mechanical properties of steel effectively [8]. The content of Cr in the medium manganese steel was about 2%, which was lower than that of Mn and much higher than that of C. Therefore, it is of great significance to systematically study the effect of Cr on the liquidus temperature of the medium manganese steel. The liquidus temperature and temperature drop coefficients with different Cr contents were calculated. As shown in Table 5, when the Cr increased from 1 to 3%, the liquidus temperature decreased from 1487.7 to 1422.3°C. Besides, the coefficients of Cr were not constant and it increased from 1.56 to 1.69; although the degree is small, it cannot be neglected. The coefficients of Cr were fitted, as shown in Figure 4. The results demonstrated that the relationship between coefficient and content of Cr is in agreement with linear changes; the fitting degree R 2 = 0.999, indicating that the fitting degree was reliable.
The liquidus temperature and temperature drop coefficients with different Cr contents of the medium manganese steel
| ω Cr (wt%) | Fe–0.95C–8.5Mn–(1–3)Cr–0.035Nb–0.065V–0.2Si–0.32Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 0 | 1426.36 | |
| 1.0 | 1424.8 | 1.56 |
| 1.2 | 1424.47 | 1.57 |
| 1.4 | 1424.14 | 1.59 |
| 1.6 | 1423.8 | 1.60 |
| 1.8 | 1423.46 | 1.61 |
| 2.0 | 1423.11 | 1.63 |
| 2.2 | 1422.76 | 1.64 |
| 2.4 | 1422.4 | 1.65 |
| 2.6 | 1422.04 | 1.66 |
| 2.8 | 1421.67 | 1.67 |
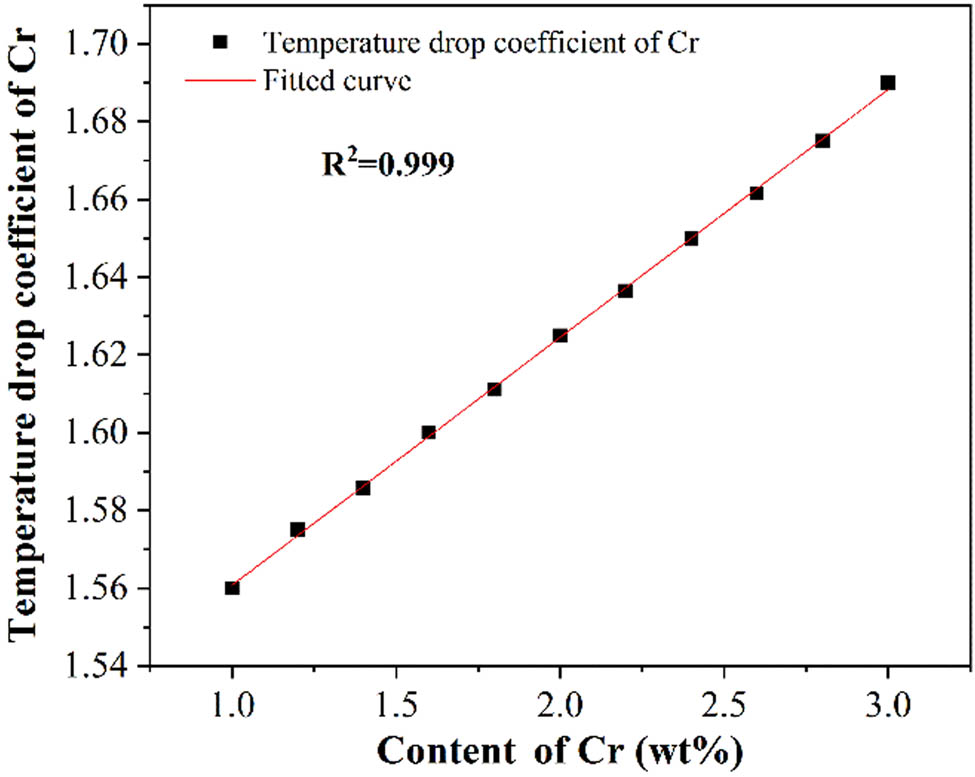
Relationship between the temperature drop coefficients and the Cr content.
3.4 Effect of Al on the liquidus temperature
The addition of Al can stabilize and expand the volume fraction of the α phase [8]. However, excessive Al will generate work hardening and deteriorate the strength and ductility of the steel [36,37]. The content of Al in medium manganese steel is lower than 0.01%; therefore, in order to ensure the applicability of the calculation results, the liquidus temperature and temperature drop coefficients with different Al contents were investigated in a wider range. The calculation results are shown in Table 6. It was found that the effect of Al on the liquidus temperature was complex. When the content of Al increased from 0.01 to 0.5%, the liquidus temperature increased from 1422.93 to 1423.29°C. However, as the Al continued to increase to 1.7%, the liquidus temperature decreased to 1421.71°C. When the Al further increased to 4%, the liquidus temperature again increased to 1428.2°C. It can be seen that when the Al content was lower than 1.7%, the coefficients increased with the increase in Al. However, when the Al content was between 1.8 and 3.5%, the coefficients decreased with an increase in Al. When the content of Al exceeded 4.0%, the coefficients showed again an increasing tendency. Generally speaking, the liquidus temperature increased with the increase in the Al content in conventional steel [30]. However, the calculation results proved that this relationship did not apply to medium manganese steel. The reason that caused this phenomenon is not clear at present. It was speculated that it may be related to the transformation of the structure in medium manganese steel, which still needs to be further confirmed. To reveal the effect of Al on the liquidus temperature of the medium manganese steel, the temperature drop coefficients with various Al contents were fitted, and the results are shown in Figure 5 and equations (5) and (6):
The liquidus temperature and temperature drop coefficients with different Al contents of the medium manganese steel
| ω Al (wt%) | Fe–(0–1.1)C–8.5Mn–0.2Si–2.1Cr–0.01Al0.035Nb–0.065V–0.32Mo | ω Al (wt%) | Fe–(0–1.1)C–8.5Mn–0.2Si–2.1Cr–0.01Al0.035Nb–0.065V–0.32Mo | ||
|---|---|---|---|---|---|
| T liq (°C) |
|
T liq (°C) |
|
||
| 0.01 | 1422.93 | −1.00 | 0.9 | 1423.09 | −0.19 |
| 0.02 | 1422.95 | −1.50 | 1.0 | 1422.98 | −0.06 |
| 0.03 | 1422.96 | −1.33 | 1.1 | 1422.84 | 0.07 |
| 0.04 | 1422.98 | −1.50 | 1.2 | 1422.68 | 0.20 |
| 0.05 | 1422.99 | −1.40 | 1.3 | 1422.51 | 0.32 |
| 0.06 | 1423.01 | −1.50 | 1.4 | 1422.31 | 0.44 |
| 0.07 | 1423.02 | −1.43 | 1.5 | 1422.1 | 0.55 |
| 0.08 | 1423.03 | −1.38 | 1.6 | 1421.86 | 0.66 |
| 0.09 | 1423.05 | −1.44 | 1.7 | 1421.71 | 0.71 |
| 0.1 | 1423.06 | −1.40 | 1.8 | 1422.25 | 0.37 |
| 0.12 | 1423.08 | −1.33 | 1.9 | 1422.77 | 0.08 |
| 0.14 | 1423.1 | −1.29 | 2.0 | 1423.25 | −0.17 |
| 0.16 | 1423.13 | −1.31 | 2.1 | 1423.71 | −0.38 |
| 0.18 | 1423.15 | −1.28 | 2.2 | 1424.13 | −0.55 |
| 0.2 | 1423.16 | −1.20 | 2.3 | 1424.54 | −0.70 |
| 0.3 | 1423.24 | −1.07 | 2.4 | 1424.91 | −0.83 |
| 0.4 | 1423.28 | −0.90 | 2.5 | 1425.27 | −0.94 |
| 0.5 | 1423.29 | −0.74 | 3.0 | 1426.7 | −1.26 |
| 0.6 | 1423.28 | −0.60 | 3.5 | 1427.66 | −1.35 |
| 0.7 | 1423.24 | −0.46 | 4.0 | 1428.2 | −1.32 |
| 0.8 | 1423.18 | −0.33 | |||
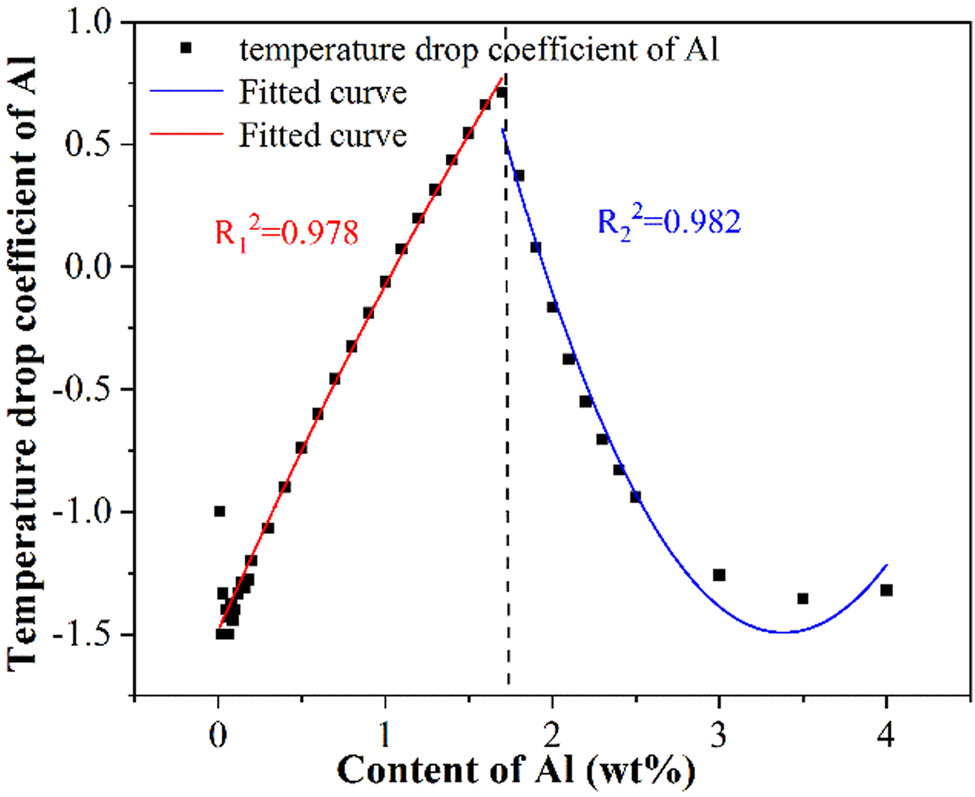
Relationship between the temperature drop coefficients and the Al content.
The fitting degree R 2 = 0.978 and 0.982, indicating the reliability of the results.
3.5 Effect of Si on the liquidus temperature
The effect of Si added to the medium manganese steel is similar to that of Al [8]. Si is also one of the ferrite-stable elements. The formation of carbides will be inhibited when appropriate Si is added to the medium manganese steel [38]. The liquidus temperature and temperature drop coefficients were calculated with the Si content ranging from 0 to 4.0%. The results are shown in Table 7. It can be seen that the liquidus temperature decreased from 1429.01 to 1352.26°C and the coefficients decreased from 30.8 to 19.2. The temperature drop coefficients of Si were fitted. As shown in Figure 6 and equation (7), the relationship between the coefficients and the Si content was in accordance with the univariate quadratic distribution:
Theliquidus temperature and the temperature drop coefficients with different Si contents of the medium manganese steel
| ω Si (wt%) | Fe–0.95C–8.5Mn–(0–1)Si–2.1Cr–0.035Nb–0.065V–0.32Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 0 | 1429.01 | — |
| 0.1 | 1425.93 | 30.80 |
| 0.2 | 1422.93 | 30.40 |
| 0.3 | 1420.05 | 29.87 |
| 0.4 | 1417.26 | 29.38 |
| 0.5 | 1414.59 | 28.84 |
| 06 | 1412.02 | 28.32 |
| 0.7 | 1409.55 | 27.80 |
| 0.8 | 1407.17 | 27.30 |
| 0.9 | 1404.88 | 26.81 |
| 1.0 | 1402.67 | 26.34 |
| 1.5 | 1392.64 | 24.25 |
| 2.0 | 1383.81 | 22.6 |
| 2.5 | 1375.66 | 21.34 |
| 3.0 | 1367.84 | 20.39 |
| 3.5 | 1360.09 | 19.69 |
| 4.0 | 1352.26 | 19.19 |
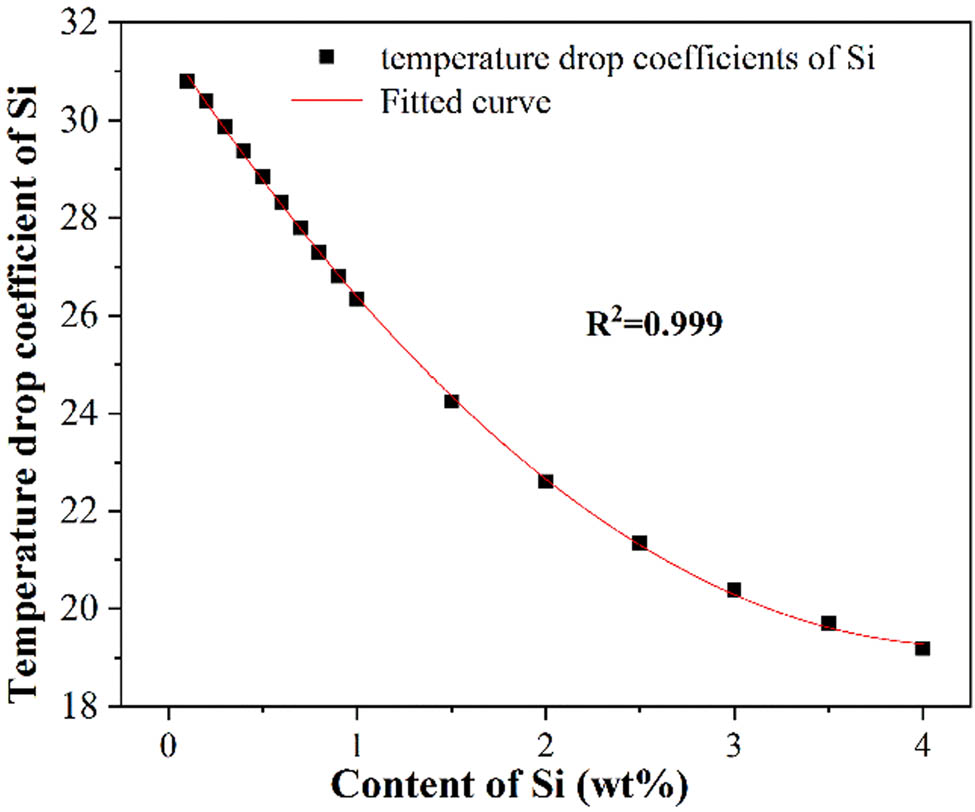
Relationship between the temperature drop coefficients and the content of Si.
3.6 Effect of other elements on the liquidus temperature
Other alloying elements such as Mo, V, and Nb were also added to the medium manganese steel [39,40], which can combine with other elements to form nano-scale precipitates and strengthen the second phase of steel, thus refining the grain, and finally, the strength of the steel can be improved by maintaining certain plasticity [41,42]. Considering that the contents of Mo, V, and Nb were less, the liquidus temperature and temperature drop coefficients were investigated in the range of 0–1, 0–0.1, and 0–0.1%, respectively. As shown in Tables 8–10, when the Mo, V, and Nb contents increased, the liquidus temperature decreased almost linearly. However, the temperature drop coefficients have no obvious changes. Because of the low content of Mo, V, and Nb in medium manganese steel, the coefficients were regarded to be constant and were equal to 4, 4, and 6, respectively.
Theliquidus temperature and temperature drop coefficients with different Mo contents of the medium manganese steel
| ω Mo (wt%) | Fe–0.95C–8.5Mn–0.2Si–2.1Cr–0.035Nb–0.065V–(0–1)Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 0 | 1424.2 | — |
| 0.1 | 1423.81 | 3.90 |
| 0.2 | 1423.41 | 3.95 |
| 0.3 | 1423.01 | 3.97 |
| 0.4 | 1422.62 | 3.95 |
| 0.5 | 1422.22 | 3.96 |
| 0.6 | 1421.82 | 3.97 |
| 0.7 | 1421.42 | 3.97 |
| 0.8 | 1421.02 | 3.98 |
| 0.9 | 1420.61 | 3.99 |
| 1.0 | 1420.21 | 3.99 |
The liquidus temperature and temperature drop coefficients with different V contents of the medium manganese steel
| ω V (wt%) | Fe–0.95C–8.5Mn–0.2Si–2.1Cr–0.035Nb–(0–0.1)V–0.32Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 0 | 1423.19 | — |
| 0.01 | 1423.15 | 4 |
| 0.02 | 1423.11 | 4 |
| 0.03 | 1423.07 | 4 |
| 0.04 | 1423.03 | 4 |
| 0.05 | 1422.99 | 4 |
| 0.06 | 1422.95 | 4 |
| 0.07 | 1422.91 | 4 |
| 0.08 | 1422.87 | 4 |
| 0.09 | 1422.84 | 3.89 |
| 0.1 | 1422.8 | 3.90 |
The liquidus temperature and temperature drop coefficients with different Nb contents of the medium manganese steel
| ω Nb (wt%) | Fe–0.95C–8.5Mn–0.2Si–2.1Cr–(0–0.1)Nb–0.065V–0.32Mo–0.01Al | |
|---|---|---|
| T liq (°C) |
|
|
| 0 | 1423.15 | — |
| 0.01 | 1423.09 | 6.0 |
| 0.02 | 1423.03 | 6.0 |
| 0.03 | 1422.97 | 6.0 |
| 0.04 | 1422.9 | 6.25 |
| 0.05 | 1422.84 | 6.20 |
| 0.06 | 1422.78 | 6.17 |
| 0.07 | 1422.71 | 6.29 |
| 0.08 | 1422.65 | 6.25 |
| 0.09 | 1422.59 | 6.22 |
| 0.1 | 1422.52 | 6.30 |
3.7 The empirical formula of the liquidus temperature of medium manganese steel
The influence of C, Mn, Cr, Al, Si, Mo, V, and Nb on the liquidus temperature and temperature drop coefficients are calculated in Sections 3.1–3.6. Then, the formula to calculate the liquidus temperature of the medium manganese steel can be obtained by the linear sum of these coefficients. It should be noted that the formula can be obtained in the sections according to the Al content. When the Al content ranged from 0 to 1.7%, the liquidus temperature can be obtained as follows:
Similarly, when the Al content was 1.7–4.0%, the liquidus temperature can be obtained as follows:
4 Discussion
4.1 Verification of the results calculated with Factsage
Figure 7 shows the DSC curves during the heating process of the medium manganese steel at heating rates of 5, 10, and 15 K·min−1. The exothermic peak on the DSC curves is considered to be the liquidus temperature of the steel. Therefore, the liquidus temperatures at different heating rates were 1428.4, 1426.6, and 1424.6°C, respectively. That is, the liquidus temperature increased when the heating rates increased. It should be noted that there was a linear relationship between the liquidus temperature and heating rate. Thus, the liquidus temperature of medium manganese steel at a heating rate of 0 K·min−1 was 1422.7°C, which can be seen in Figure 8. It should be noted that the liquidus temperature calculated with Factsage was 1422.9°C. The error between the DSC experimental results and the calculated results was within 1%, indicating the accuracy and reliability of the calculated results using Factsage.
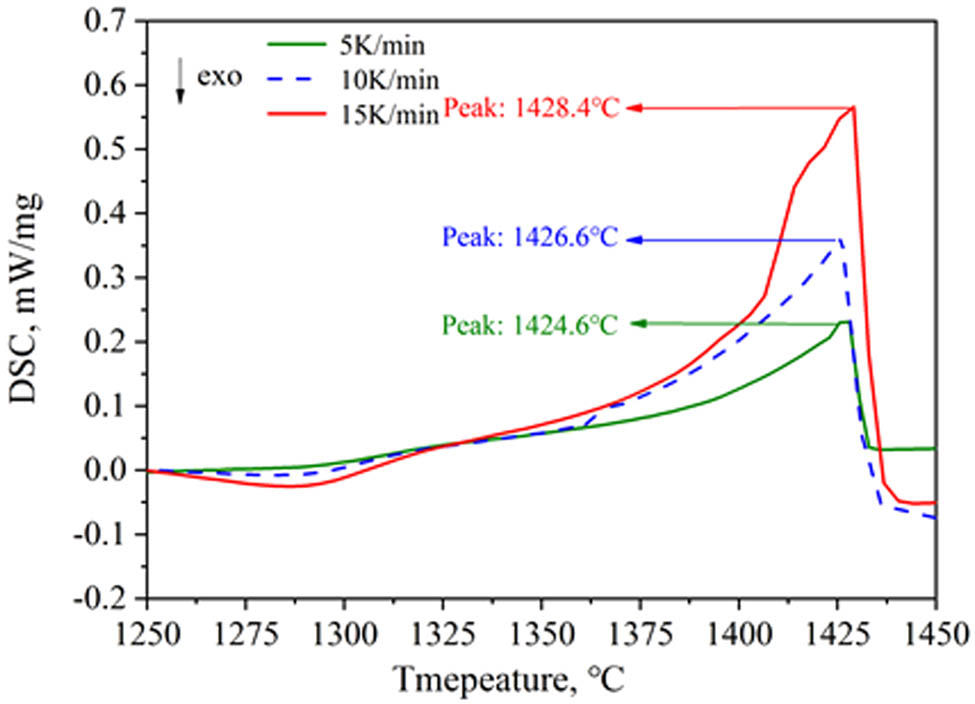
Liquidus temperatures at different heating rates.
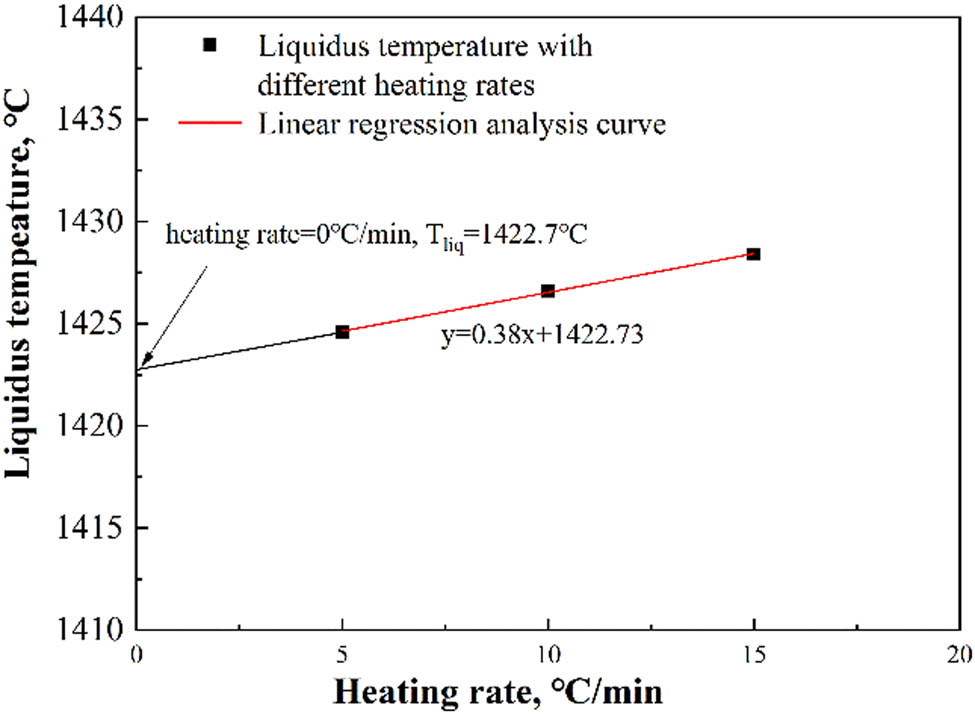
Linear regression analysis of liquidus temperatures.
4.2 Verification of the empirical formula
The liquidus temperatures of the medium manganese steel obtained by DTA or DSC experiments [19,21,43] were investigated, and the results are shown in Table 11. It can be found that the liquidus temperatures calculated by the empirical formula were close to experiment results, and all of the errors were within 8°C. Besides, the different empirical formulas for calculating liquidus temperatures of steel are also given in Table 12. Figure 9 shows the liquidus temperatures obtained by different empirical formulas. On the whole, except for a few examples, most of the results obtained using the empirical formula in the current study were much closer to experiment results, indicating the accuracy and reliability of the formula to predict the liquidus temperature of the medium manganese steel. It should be noted that the composition in the table is only to verify the accuracy and adaptability of the empirical formula. Therefore, although the content of some elements exceeds the limited range of the empirical formula in this study, the calculation results still have reference value.
Liquidus temperatures obtained by experiments and the empirical formula
| Sample | Composition (wt%) | Liquidus temperature (°C) | Errors | ||||
|---|---|---|---|---|---|---|---|
| C | Mn | Al | Si | Results by DTA/DSC | Results by empirical formula | ||
| 1 | 0.59 | 17.8 | 1.33 | 0.22 | 1,416 | 1412.41 | −3.59 |
| 2 | 0.75 | 20 | 1.5 | 0.05 | 1406.49 | 1401.04 | −5.45. |
| 3 | 0.79 | 13.62 | — | 0.39 | 1,419 | 1414.02 | −4.98 |
| 4 | 0.8 | 12.95 | — | 0.34 | 1,422 | 1417.38 | −4.62 |
| 5 | 0.05 | 19.64 | 3.47 | 2.44 | 1402.68 | 1397.65 | −5.03 |
| 6 | 0.38 | 25.64 | 4.12 | 2.11 | 1354.9 | 1356.2 | 1.30 |
| 7 | 0.38 | 25.1 | 3.53 | 2.78 | 1346.5 | 1348.76 | 2.26 |
| 8 | 0.4 | 22 | — | — | 1,405 | 1412.55 | 7.55 |
Different empirical formulae for calculating liquidus temperatures
| Number | Empirical formulae |
|---|---|
| 1 [44] |
|
| 2 [28] |
|
| 3 [44] |
|
| 4 [44] |
|
| 5 [33] |
|
| 6 [27] |
|
| 7 [29] |
|
| 8 [44] |
|
| 9 [44] |
|
| 10[44] |
|
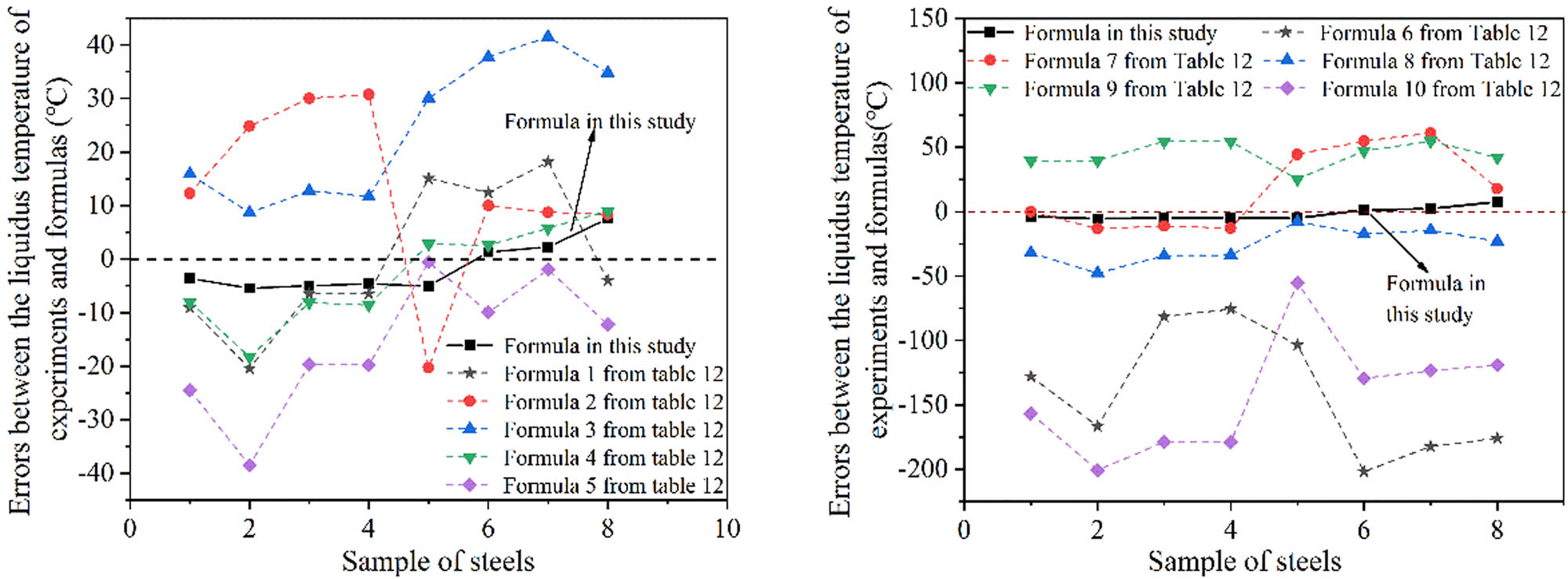
Errors between the liquidus temperature of experiments and formulae.
5 Conclusions
The temperature drop coefficients of the medium manganese steel were calculated using Factsage. When the content of C,、Mn,、Cr, and、Si increased, the coefficients of C and Mn increased nonlinearly, and the coefficients of Cr increased linearly, while the coefficient of Si decreased. However, the coefficients of Al were complex when the Al content was lower than 1.7% and the coefficient increased with an increase in Al. When the Al content was between 1.8 and 3.5%, the coefficient decreased with an increase in Al. When the content of Al exceeded 4.0%, the coefficient showed an increasing trend again. Considering the lower contents of Mo, V, and Nb in the medium manganese steel, the temperature drop coefficients were constant and equal to 4, 4, and 6, respectively.
The empirical formulae for calculating the liquidus temperature of the medium manganese steel were established by the linear sum of the corresponding temperature drop coefficients. In the current study, when the Al content ranged from 0 to 1.7%, the liquidus temperature can be obtained as
When the content of Al was 1.7–4.0%, the liquidus temperature can be calculated as by
The reliability of the empirical formulae to predict the liquidus temperature was verified. The liquidus temperature of the medium manganese steel found by the DSC experiment was 1422.7°C, which was closer to that obtained using the empirical formula. By comparison with different empirical formulas, the results calculated by the formula in this study were closer to the experimental results, indicating the reliability of the empirical formula in determining the liquidus temperature of the medium manganese steel.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the Natural Science Foundation of Hebei Province (No. E2021318004) and the Central and Local Science and Technology Development Fund Project (No. 216Z1009G).
-
Funding information: This research was supported by: Natural Science Foundation of Hebei Province (No. E2021318004) as well as Central and Local Science and Technology Development Fund Project (No. 216Z1009G).
-
Author contributions: Conceptualization, L.Y.; methodology, L.M. and C.X.R.; validation, X.R.Y.; formal analysis, Z.C.D.; investigation, T.Z.Q.; writing – original draft preparation, L.M.; writing – review and editing – L.H.B and L.M.; Supervision, X.H.
-
Conflict of interest: The authors state no conflict of interest.
-
Data availability statement: The data presented in this study are available on request from the corresponding author.
References
[1] Song, Y. P., J. P. Xie, Y. M. Zhu, and A. Q. Wang. Effect of RE-modifier on microstructure and mechanical property of high-carbon medium-manganese steel. Journal of Iron and Steel Research International, Vol. 9, No. 1, 2002, pp. 36–39.Search in Google Scholar
[2] Sun, R. M., W. H. Xu, C. Y. Wang, J. B. Qiu, and W. Q. Cao. Wear resistant of new type medium manganese high strength martensite steel. Iron and Steel, Vol. 12, 2012, pp. 64–70.Search in Google Scholar
[3] Ge, S. R., J. X. Wang, Q. L. Wang, and H. Chen. Self-strengthening wear resistant mechanism and application of medium manganese steel applied for the chute of scraper conveyor. Journal of China Coal Society, Vol. 41, No. 9, 2016, pp. 2373–2379.Search in Google Scholar
[4] Wang, D., J. Liu, H. Luo, L. Guo, and H. Zhang. Delaminating defects analysis of continuous casting mid-manganese wear-resistant steel slab. Baosteel Technology, 2016, Vol. 7, No. 3, pp. 36–40.Search in Google Scholar
[5] Dou, C., S. Wei, S. I. Anheng, Z. Shen, and S. Liao. Effect of carbon content and heat treatment on microstructure and properties of medium manganese wear-resistant steel. Foundry Technology, Vol. 2, 2018, pp. 289–294.Search in Google Scholar
[6] Grajcar, A., E. Kalinowska-Ozgowicz, M. Opiela, B. Grzegorczyk, and K. Golombek. Effects of Mn and Nb on the macro-and microsegregation in high-Mn high-Al content TRIP steels. Archives of Materials Science and Engineering, Vol. 49, No. 1, 2011, pp. 5–14.Search in Google Scholar
[7] Chen, J., J. J. Wang, H. Zhang, W. G. Zhang, and C. M. Liu. Evolution of deformation twins with strain rate in a medium-manganese wear-resistant steel Fe–8Mn–1C–1.2Cr–0.2V]. Journal of Iron and Steel Research International, Vol. 26, 2019, pp. 983–990.10.1007/s42243-018-00225-3Search in Google Scholar
[8] Ren-bo, S. O., H. U. Wei-feng, Z. H. Nai-peng, L. I. Jia-jia, Z. H. Zhe-rui, and W. A. Yong-jin. Research progress and prospect of Fe− Mn− Al− C medium Mn steels. Chinese Journal of Engineering, Vol. 42, No. 7, 2020, pp. 814–828.Search in Google Scholar
[9] Cai, Z. H., H. Ding, X. Xue, J. Jiang, Q. B. Xin, and R. D. K. Misra. Significance of control of austenite stability and three-stage work-hardening behavior of an ultrahigh strength–high ductility combination transformation-induced plasticity steel. Scripta Materialia, Vol. 11, 2013, pp. 865–868.10.1016/j.scriptamat.2013.02.010Search in Google Scholar
[10] Lee, S., K. Lee, and B. C. De Cooman. Observation of the TWIP + TRIP plasticity-enhancement mechanism in Al-added 6 wt pct medium Mn steel. Metallurgical and Materials Transactions A, Vol. 6, 2015, pp. 2356–2363.10.1007/s11661-015-2854-zSearch in Google Scholar
[11] Hu, J., W. Cao, C. Wang, H. Dong, and J. Li. Phase transformation behavior of cold rolled 0.1 C–5Mn steel during heating process studied by differential scanning calorimetry. Materials Science and Engineering: A, Vol. 636, 2015, pp. 108–116.10.1016/j.msea.2015.03.080Search in Google Scholar
[12] Luo, L., W. Li, L. Wang, S. Zhou, and X. Jin. Tensile behaviors and deformation mechanism of a medium Mn-TRIP steel at different temperatures. Materials Science and Engineering: A, Vol. 682, 2017, pp. 698–703.10.1016/j.msea.2016.11.017Search in Google Scholar
[13] Speer, J. G., D. V. Edmonds, F. C. Rizzo, and D. K. Matlock. Partitioning of carbon from supersaturated plates of ferrite, with application to steel processing and fundamentals of the bainite transformation. Current Opinion in Solid State and Materials Science, Vol. 8, No. 3–4, 2004, pp. 219–237.10.1016/j.cossms.2004.09.003Search in Google Scholar
[14] Wang, J., Q. Wang, X. Zhang, and D. Zhang. Impact and rolling abrasive wear behavior and hardening mechanism for hot-rolled medium-manganese steel. Journal of Tribology, Vol. 140, No. 3, 2018, id. 031608.10.1115/1.4038414Search in Google Scholar
[15] Luo, K. and B. Bai. Microstructure, mechanical properties and high stress abrasive wear behavior of air-cooled MnCrB cast steels. Materials & Design (1980-2015), Vol. 31, No. 5, 2010, pp. 2510–2516.10.1016/j.matdes.2009.11.040Search in Google Scholar
[16] Yan, X., J. Hu, H. Yu, C. Wang, and W. Xu. Unraveling the significant role of retained austenite on the dry sliding wear behavior of medium manganese steel. Wear, Vol. 476, 2021, id. 203745.10.1016/j.wear.2021.203745Search in Google Scholar
[17] Schaffnit, P., C. Stallybrass, J. Konrad, F. Stein, and M. Weinberg. A Scheil–Gulliver model dedicated to the solidification of steel. Calphad, Vol. 48, 2015, pp. 184–188.10.1016/j.calphad.2015.01.002Search in Google Scholar
[18] Howe, A. A. Estimation of liquids temperatures for steels. Ironmaking & Steelmaking, Vol. 3, 1988, pp. 134–142.Search in Google Scholar
[19] Zhuang, C., J. Liu, C. Bernhard, and P. Presoly. Analysis of solidification of high manganese steels using improved differential thermal analysis method. Journal of Iron and Steel Research, International, Vol. 22, No. 8, 2015, pp. 709–714.10.1016/S1006-706X(15)30061-3Search in Google Scholar
[20] Hamada, A. S. and L. Karjalainen. Hot ductility behaviour of high-Mn TWIP steels. Materials Science & Engineering A, Vol. 3, 2011, pp. 1819–1827.10.1016/j.msea.2010.11.030Search in Google Scholar
[21] Keil, D., M. Zinke, and H. Pries. Investigations on hot cracking of novel high manganese TWIP-steels[M]//Hot Cracking Phenomena in Welds III, Berlin, Heidelberg: Springer: 2011, pp. 209–223.10.1007/978-3-642-16864-2_12Search in Google Scholar
[22] Martiník, O., B. Smetana, J. Dobrovská, S. Zlá, M. Kawuloková, K. Gryc, et al. Experimental and theoretical assessment of liquidus, peritectic transformation, and solidus temperatures of laboratory and commercial steel grades. Journal of Phase Equilibria and Diffusion, Vol. 40, 2019, pp. 93–103.10.1007/s11669-019-00707-1Search in Google Scholar
[23] Han, Z. B., J. H. Liu, Y. He, K. W. Li, Y. L. Ji, and J. Liu. Determination of the liquidus and solidus temperatures of FeCrAl stainless steel. International Journal of Minerals Metallurgy & Materials, Vol. 22, 2015, pp. 1141–1148.10.1007/s12613-015-1178-8Search in Google Scholar
[24] Kousksou, T., A. Jamil, Y. Zeraouli, and J. P. Dumas. Equilibrium liquidus temperatures of binary mixtures from differential scanning calorimetry. Chemical Engineering Science, Vol. 62, No. 23, 2007, pp. 6516–6523.10.1016/j.ces.2007.07.008Search in Google Scholar
[25] Steiner Petrovič, D., G. Klančnik, M. Pirnat, and J. Medved. Differential scanning calorimetry study of the solidification sequence of austenitic stainless steel. Journal of Thermal Analysis and Calorimetry, Vol. 1, 2011, pp. 251–257.10.1007/s10973-011-1375-2Search in Google Scholar
[26] Shen, Y., J. Liu, and H. Xu. Investigation of solidification modes of high Manganese steels. Materials Science and Technology, Vol. 4, 2021, pp. 446–457.10.1080/02670836.2021.1911444Search in Google Scholar
[27] Mathew, J. and H. Brody. Solidification and Casting of Metals[C]. Sheffield Conference, 1979.Search in Google Scholar
[28] Kagawa, A. and T. Okamoto. Influence of alloying elements on temperature and composition for peritectic reaction in plain carbon steels. Metal Science Journal, Vol. 10, 1986, pp. 997–1008.10.1179/mst.1986.2.10.997Search in Google Scholar
[29] Wang, X., X. Wang, B. Wang, B. Wang, and Q. Liu. Differential calculation model for liquidus temperature of steel. Steel Research International, Vol. 823, 2011, pp. 164–168.10.1002/srin.201000080Search in Google Scholar
[30] Wu, Y. J., Z. H. Jiang, L. K. Liang, M. Jiang, and Y. Li. Calculation on liquidus temperature of steel. Gangtie Yanjiu Xuebao (Journal of Iron and Steel Research) (China), Vol. 14, 2002, pp. 6–9.Search in Google Scholar
[31] Gigacher, G., R. Pierer, J. Wiener, and C. Bernhard. Metallurgical aspects of casting high‐manganese steel grades. Advanced Engineering Materials, Vol. 8, No. 11, 2010, pp. 1096–1100.10.1002/adem.200600152Search in Google Scholar
[32] Won, Y.-M. and B. G. Thomas. Simple model of microsegregation during solidification of steels. Metallurgical and Materials Transactions A, Vol. 32, 2001, pp. 1755–1767.10.1007/s11661-001-0152-4Search in Google Scholar
[33] Choudhary, S. K. and A. Ghosh. Mathematical model for prediction of composition of inclusions formed during solidification of liquid steel. ISIJ International, Vol. 49, No. 12, 2009, pp. 1819–1827.10.2355/isijinternational.49.1819Search in Google Scholar
[34] Sun, B., H. Aydin, F. Fazeli, and S. Yue. Microstructure evolution of a medium manganese steel during thermomechanical processing. Metallurgical and Materials Transactions A, Vol. 47, 2016, pp. 1782–1791.10.1007/s11661-016-3338-5Search in Google Scholar
[35] Liu, H., J. Liu, B. Wu, Y. Shen, Y. He, H. Ding, et al. Effect of Mn and Al contents on hot ductility of high alloy Fe-xMn-C-yAl austenite TWIP steels. Materials Science and Engineering: A, Vol. 708, 2017, pp. 360–374.10.1016/j.msea.2017.10.001Search in Google Scholar
[36] Cai, Z. H., B. Cai, H. Ding, Y. Chen, and R. D. Misra. Microstructure and deformation behavior of the hot-rolled medium manganese steels with varying aluminum-content. Materials Science and Engineering: A, Vol. 676, 2016, pp. 263–270.10.1016/j.msea.2016.08.119Search in Google Scholar
[37] Lehnhoff, G., K. Findley, and B. De Cooman. The influence of silicon and aluminum alloying on the lattice parameter and stacking fault energy of austenitic steel. Scripta Materialia, Vol. 92, 2014, pp. 19–22.10.1016/j.scriptamat.2014.07.019Search in Google Scholar
[38] Heo, Y.-U., Y.-Y. Song, S.-J. Park, H. K. D. H. Bhadeshia, and D. W. Suh. Influence of silicon in low density Fe-C-Mn-Al steel. Metallurgical and Materials Transactions A, Vol. 6, 2012, pp. 1731–1735.10.1007/s11661-012-1149-xSearch in Google Scholar
[39] Cai, M., Z. Li, Q. Chao, and P. D. Hodgson. A novel Mo and Nb microalloyed medium Mn TRIP steel with maximal ultimate strength and moderate ductility. Metallurgical and Materials Transactions A, Vol. 12, 2014, pp. 5624–5634.10.1007/s11661-014-2504-xSearch in Google Scholar
[40] Lee, D., J. K. Kim, S. Lee, K. Lee, and B. C. De Cooman. Microstructures and mechanical properties of Ti and Mo micro-alloyed medium Mn steel. Materials Science and Engineering: A, Vol. 706, 2017, pp. 1–14.10.1016/j.msea.2017.08.110Search in Google Scholar
[41] Lee, S. and B. C. De Cooman. Tensile Behavior of Intercritically Annealed Ultra‐Fine Grained 8% Mn Multi‐Phase Steel. Steel Research International, Vol. 10, 2015, pp. 1170–1178.10.1002/srin.201500038Search in Google Scholar
[42] Cai, Z. H., H. Ding, H. Kamoutsi, G. N. Haidemenopoulos, and R. D. Misra. Interplay between deformation behavior and mechanical properties of intercritically annealed and tempered medium-manganese transformation-induced plasticity steel. Materials Science and Engineering: A, Vol. 654, 2016, pp. 359–367.10.1016/j.msea.2015.12.057Search in Google Scholar
[43] Zhung, C. L. Research on metallurgical fundamental and solidification of low carbon TWIP steels abstract[D]. 2014Search in Google Scholar
[44] Liu, H. B. Analysis of Metallurgical Fundamental and Solidification Characteristics of Fe-Mn-C (-Al) TWIP Steel[D]. 2018.Search in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying
- Improvement and prediction on high temperature melting characteristics of coal ash
- First-principles calculations to investigate the thermal response of the ZrC(1−x)Nx ceramics at extreme conditions
- Study on the cladding path during the solidification process of multi-layer cladding of large steel ingots
- Thermodynamic analysis of vanadium distribution behavior in blast furnaces and basic oxygen furnaces
- Comparison of data-driven prediction methods for comprehensive coke ratio of blast furnace
- Effect of different isothermal times on the microstructure and mechanical properties of high-strength rebar
- Analysis of the evolution law of oxide inclusions in U75V heavy rail steel during the LF–RH refining process
- Simultaneous extraction of uranium and niobium from a low-grade natural betafite ore
- Transfer and transformation mechanism of chromium in stainless steel slag in pedosphere
- Effect of tool traverse speed on joint line remnant and mechanical properties of friction stir welded 2195-T8 Al–Li alloy joints
- Technology and analysis of 08Cr9W3Co3VNbCuBN steel large diameter thick wall pipe welding process
- Influence of shielding gas on machining and wear aspects of AISI 310–AISI 2205 dissimilar stainless steel joints
- Effect of post-weld heat treatment on 6156 aluminum alloy joint formed by electron beam welding
- Ash melting behavior and mechanism of high-calcium bituminous coal in the process of blast furnace pulverized coal injection
- Effect of high temperature tempering on the phase composition and structure of steelmaking slag
- Numerical simulation of shrinkage porosity defect in billet continuous casting
- Influence of submerged entry nozzle on funnel mold surface velocity
- Effect of cold-rolling deformation and rare earth yttrium on microstructure and texture of oriented silicon steel
- Investigation of microstructure, machinability, and mechanical properties of new-generation hybrid lead-free brass alloys
- Soft sensor method of multimode BOF steelmaking endpoint carbon content and temperature based on vMF-WSAE dynamic deep learning
- Mechanical properties and nugget evolution in resistance spot welding of Zn–Al–Mg galvanized DC51D steel
- Research on the behaviour and mechanism of void welding based on multiple scales
- Preparation of CaO–SiO2–Al2O3 inorganic fibers from melting-separated red mud
- Study on diffusion kinetics of chromium and nickel electrochemical co-deposition in a NaCl–KCl–NaF–Cr2O3–NiO molten salt
- Enhancing the efficiency of polytetrafluoroethylene-modified silica hydrosols coated solar panels by using artificial neural network and response surface methodology
- High-temperature corrosion behaviours of nickel–iron-based alloys with different molybdenum and tungsten contents in a coal ash/flue gas environment
- Characteristics and purification of Himalayan salt by high temperature melting
- Temperature uniformity optimization with power-frequency coordinated variation in multi-source microwave based on sequential quadratic programming
- A novel method for CO2 injection direct smelting vanadium steel: Dephosphorization and vanadium retention
- A study of the void surface healing mechanism in 316LN steel
- Effect of chemical composition and heat treatment on intergranular corrosion and strength of AlMgSiCu alloys
- Soft sensor method for endpoint carbon content and temperature of BOF based on multi-cluster dynamic adaptive selection ensemble learning
- Evaluating thermal properties and activation energy of phthalonitrile using sulfur-containing curing agents
- Investigation of the liquidus temperature calculation method for medium manganese steel
- High-temperature corrosion model of Incoloy 800H alloy connected with Ni-201 in MgCl2–KCl heat transfer fluid
- Investigation of the microstructure and mechanical properties of Mg–Al–Zn alloy joints formed by different laser welding processes
- Effect of refining slag compositions on its melting property and desulphurization
- Effect of P and Ti on the agglomeration behavior of Al2O3 inclusions in Fe–P–Ti alloys
- Cation-doping effects on the conductivities of the mayenite Ca12Al14O33
- Modification of Al2O3 inclusions in SWRH82B steel by La/Y rare-earth element treatment
- Possibility of metallic cobalt formation in the oxide scale during high-temperature oxidation of Co-27Cr-6Mo alloy in air
- Multi-source microwave heating temperature uniformity study based on adaptive dynamic programming
- Round-robin measurement of surface tension of high-temperature liquid platinum free of oxygen adsorption by oscillating droplet method using levitation techniques
- High-temperature production of AlN in Mg alloys with ammonia gas
- Review Article
- Advances in ultrasonic welding of lightweight alloys: A review
- Topical Issue on High-temperature Phase Change Materials for Energy Storage
- Compositional and thermophysical study of Al–Si- and Zn–Al–Mg-based eutectic alloys for latent heat storage
- Corrosion behavior of a Co−Cr−Mo−Si alloy in pure Al and Al−Si melt
- Al–Si–Fe alloy-based phase change material for high-temperature thermal energy storage
- Density and surface tension measurements of molten Al–Si based alloys
- Graphite crucible interaction with Fe–Si–B phase change material in pilot-scale experiments
- Topical Issue on Nuclear Energy Application Materials
- Dry synthesis of brannerite (UTi2O6) by mechanochemical treatment
- Special Issue on Polymer and Composite Materials (PCM) and Graphene and Novel Nanomaterials - Part I
- Heat management of LED-based Cu2O deposits on the optimal structure of heat sink
- Special Issue on Recent Developments in 3D Printed Carbon Materials - Part I
- Porous metal foam flow field and heat evaluation in PEMFC: A review
- Special Issue on Advancements in Solar Energy Technologies and Systems
- Research on electric energy measurement system based on intelligent sensor data in artificial intelligence environment
- Study of photovoltaic integrated prefabricated components for assembled buildings based on sensing technology supported by solar energy
- Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part I
- Performance optimization and investigation of metal-cored filler wires for high-strength steel during gas metal arc welding
- Three-dimensional transient heat transfer analysis of micro-plasma arc welding process using volumetric heat source models
Articles in the same Issue
- Research Articles
- First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying
- Improvement and prediction on high temperature melting characteristics of coal ash
- First-principles calculations to investigate the thermal response of the ZrC(1−x)Nx ceramics at extreme conditions
- Study on the cladding path during the solidification process of multi-layer cladding of large steel ingots
- Thermodynamic analysis of vanadium distribution behavior in blast furnaces and basic oxygen furnaces
- Comparison of data-driven prediction methods for comprehensive coke ratio of blast furnace
- Effect of different isothermal times on the microstructure and mechanical properties of high-strength rebar
- Analysis of the evolution law of oxide inclusions in U75V heavy rail steel during the LF–RH refining process
- Simultaneous extraction of uranium and niobium from a low-grade natural betafite ore
- Transfer and transformation mechanism of chromium in stainless steel slag in pedosphere
- Effect of tool traverse speed on joint line remnant and mechanical properties of friction stir welded 2195-T8 Al–Li alloy joints
- Technology and analysis of 08Cr9W3Co3VNbCuBN steel large diameter thick wall pipe welding process
- Influence of shielding gas on machining and wear aspects of AISI 310–AISI 2205 dissimilar stainless steel joints
- Effect of post-weld heat treatment on 6156 aluminum alloy joint formed by electron beam welding
- Ash melting behavior and mechanism of high-calcium bituminous coal in the process of blast furnace pulverized coal injection
- Effect of high temperature tempering on the phase composition and structure of steelmaking slag
- Numerical simulation of shrinkage porosity defect in billet continuous casting
- Influence of submerged entry nozzle on funnel mold surface velocity
- Effect of cold-rolling deformation and rare earth yttrium on microstructure and texture of oriented silicon steel
- Investigation of microstructure, machinability, and mechanical properties of new-generation hybrid lead-free brass alloys
- Soft sensor method of multimode BOF steelmaking endpoint carbon content and temperature based on vMF-WSAE dynamic deep learning
- Mechanical properties and nugget evolution in resistance spot welding of Zn–Al–Mg galvanized DC51D steel
- Research on the behaviour and mechanism of void welding based on multiple scales
- Preparation of CaO–SiO2–Al2O3 inorganic fibers from melting-separated red mud
- Study on diffusion kinetics of chromium and nickel electrochemical co-deposition in a NaCl–KCl–NaF–Cr2O3–NiO molten salt
- Enhancing the efficiency of polytetrafluoroethylene-modified silica hydrosols coated solar panels by using artificial neural network and response surface methodology
- High-temperature corrosion behaviours of nickel–iron-based alloys with different molybdenum and tungsten contents in a coal ash/flue gas environment
- Characteristics and purification of Himalayan salt by high temperature melting
- Temperature uniformity optimization with power-frequency coordinated variation in multi-source microwave based on sequential quadratic programming
- A novel method for CO2 injection direct smelting vanadium steel: Dephosphorization and vanadium retention
- A study of the void surface healing mechanism in 316LN steel
- Effect of chemical composition and heat treatment on intergranular corrosion and strength of AlMgSiCu alloys
- Soft sensor method for endpoint carbon content and temperature of BOF based on multi-cluster dynamic adaptive selection ensemble learning
- Evaluating thermal properties and activation energy of phthalonitrile using sulfur-containing curing agents
- Investigation of the liquidus temperature calculation method for medium manganese steel
- High-temperature corrosion model of Incoloy 800H alloy connected with Ni-201 in MgCl2–KCl heat transfer fluid
- Investigation of the microstructure and mechanical properties of Mg–Al–Zn alloy joints formed by different laser welding processes
- Effect of refining slag compositions on its melting property and desulphurization
- Effect of P and Ti on the agglomeration behavior of Al2O3 inclusions in Fe–P–Ti alloys
- Cation-doping effects on the conductivities of the mayenite Ca12Al14O33
- Modification of Al2O3 inclusions in SWRH82B steel by La/Y rare-earth element treatment
- Possibility of metallic cobalt formation in the oxide scale during high-temperature oxidation of Co-27Cr-6Mo alloy in air
- Multi-source microwave heating temperature uniformity study based on adaptive dynamic programming
- Round-robin measurement of surface tension of high-temperature liquid platinum free of oxygen adsorption by oscillating droplet method using levitation techniques
- High-temperature production of AlN in Mg alloys with ammonia gas
- Review Article
- Advances in ultrasonic welding of lightweight alloys: A review
- Topical Issue on High-temperature Phase Change Materials for Energy Storage
- Compositional and thermophysical study of Al–Si- and Zn–Al–Mg-based eutectic alloys for latent heat storage
- Corrosion behavior of a Co−Cr−Mo−Si alloy in pure Al and Al−Si melt
- Al–Si–Fe alloy-based phase change material for high-temperature thermal energy storage
- Density and surface tension measurements of molten Al–Si based alloys
- Graphite crucible interaction with Fe–Si–B phase change material in pilot-scale experiments
- Topical Issue on Nuclear Energy Application Materials
- Dry synthesis of brannerite (UTi2O6) by mechanochemical treatment
- Special Issue on Polymer and Composite Materials (PCM) and Graphene and Novel Nanomaterials - Part I
- Heat management of LED-based Cu2O deposits on the optimal structure of heat sink
- Special Issue on Recent Developments in 3D Printed Carbon Materials - Part I
- Porous metal foam flow field and heat evaluation in PEMFC: A review
- Special Issue on Advancements in Solar Energy Technologies and Systems
- Research on electric energy measurement system based on intelligent sensor data in artificial intelligence environment
- Study of photovoltaic integrated prefabricated components for assembled buildings based on sensing technology supported by solar energy
- Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part I
- Performance optimization and investigation of metal-cored filler wires for high-strength steel during gas metal arc welding
- Three-dimensional transient heat transfer analysis of micro-plasma arc welding process using volumetric heat source models

