Home First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying
Article Open Access

First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying

  • Shishi Wei , Xuan Xiao EMAIL logo , Kai Zhou , Jing Yao and Dezhi Chen
Published/Copyright: January 10, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
High Temperature Materials and Processes
From the journal High Temperature Materials and Processes Volume 42 Issue 1

Abstract

Based on the first-principles method of density functional theory, the microscopic mechanism of the effect of addition of alloying element Ru content on the stability and elastic properties of Laves phase TaCr2 was investigated by parameters such as formation enthalpy, electronic structure, and elastic constants. The addition of Ru atoms tends to preferentially occupy the lattice sites of Cr. With the increase in the Ru content, the alloying ability of Ta8Cr16−n Ru n (n = 0–6) becomes progressively weaker, the stability gradually decreases, whereas the Poisson’s ratio grows. The bonding peak appears to drop and widen, weakening the bonding strength of Ta–Cr atoms, rendering the shear deformation to be performed easily, thereby improving toughness. When the Ru content rises to 20.83 at%, the bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio of the alloy attain the maximum value, the brittleness diminishes to the most extent, the resistance to elastic deformation is the strongest, as well at the optimum fracture toughness.

Keywords: ruthenium alloying; Laves phase TaCr2 ; phase stability; elastic properties; first-principles

1 Introduction

Laves phase TaCr2 alloy with high melting point (2,020°C), moderate density (10.7 g·cm−3), a combination of good high-temperature strength, and creep resistance, is a new high temperature structural material with promising applications [1,2,3,4,5,6,7,8]. Nevertheless, the room temperature brittleness of Laves phase TaCr2 alloys severely limits their practical applications [9,10]. Doping alloying elements is an essential strategy to improve the room temperature brittleness of Laves Phase alloys [11,12,13,14,15,16,17,18,19]. The first-principles calculations can reveal the microscopic mechanisms by which element types and varying atomic percentages of concentrations affect the mechanical properties of the alloys [20,21,22,23,24,25,26,27,28,29,30]. Huang et al. [31] investigated the impact of nickel alloying on the fracture toughness of NbCr2 based on first-principles calculations method. It was found that Ni tended to occupy the Cr site, and the fracture toughness values of NbCr2 alloys were significantly improved with the addition of Ni atomic percentage content of 4.17 at%, reaching 1.45, 1.51, and 1.74 MPa·m1/2 in the direction of (100), (110), and (111) Miller indices, respectively. Nickel alloying significantly enhanced the fracture toughness of Laves phase NbCr2. Liu et al. [32] studied the occupation mode, generalized stacking layer dislocation energy, and surface energy of the doped elements M (V, Zr, Mo) in NbCr2 alloy and M (V, Ta, W) in HfCr2 according to the first-principles calculation method. When Mo took up the Nb sites in NbCr2 and Ta or W occupied Hf sites in HfCr2, the toughness of NbCr2 and HfCr2 was improved. The doping of alloying elements can alter the electron concentration, elastic modulus, lattice constant, and stacking layer dislocation energy of Laves phase intermetallic compounds, and form vacancy defects and trigger lattice distortion, thus the bonding characteristics are modified and the resistance to dislocation movement is lessened, which will result in the improvement of plastic deformation capacity and in the enhancement of toughness of Laves phase intermetallic compounds.

The ideal atomic ratio R A/R B of AB2 intermetallic compound is 1.225. If another ternary atom X is incorporated to cause R A > R x > R B, the ideal atomic ratio will be transformed and the free volume in the topologically dense crystal structure will be expanded, thus contributing to the occurrence of shear deformation and eventually toughening. The atomic radius of elements Ta, Cr, and Ru are 1.48, 1.27, and 1.32 Å, respectively, which meet the atomic size relationship R Ta > R Ru > R Cr. In accordance with the atomic size theory, it is concluded that the alloying of element Ru can enhance the toughness of TaCr2. Tien et al. [11] investigated the effect of alloying element Ru on the mechanical properties of hot-pressed Ta–12.5Cr alloy and found that the addition of Ru increased the hardness; however, the addition of Ru did not effectively improve the fracture toughness, and further studies on the mechanical properties of Cr–Ta–Ru alloys with lower Ta content are desirable to clarify the effect of Ru in Cr-based two-phase alloys. Among the C36, C14, and C15 structures of Laves phase TaCr2, the highest structural stability is C15–TaCr2 [33]. Consequently, the effect of adding different contents of the element Ru on the phase stability and elastic properties of the C15-TaCr2 will be illuminated in this study by means of first- principles calculation method.

2 Computational models and methods

2.1 Computational models

C15-TaCr2 has a face-centered cubic structure with space group Fd3̄m (227) and cell parameters a = b = c = 6.9850 Å, α = β = γ = 90°, with 24 atoms in the supercell, Ta atoms occupying the location of 8a (0, 0, 0) and Cr atoms occupying the position of 6d (0.625, 0.625 0.625). The doping element Ru is assigned to substitute the Ta or Cr atom in the cell of Ta8Cr16 with an atomic concentration ratio of 4.17 at%, the molecular formulas are Ta7RuCr16 and Ta8Cr15Ru, and the structural models are as presented in Figure 1(a) and (b), respectively. In order to achieve Ru alloying, Ta or Cr atoms with varying amounts of n are substituted in the supercell Ta8Cr16, the molecular formulas are Ta8−n Ru n Cr16 and Ta8Cr16−n Ru n (n = 0, 1, 2, 3, 4, 5, and 6), where the Ru content (at%) is 0, 4.17, 8.33, 12.50, 16.67, 20.83, and 25.00, respectively.

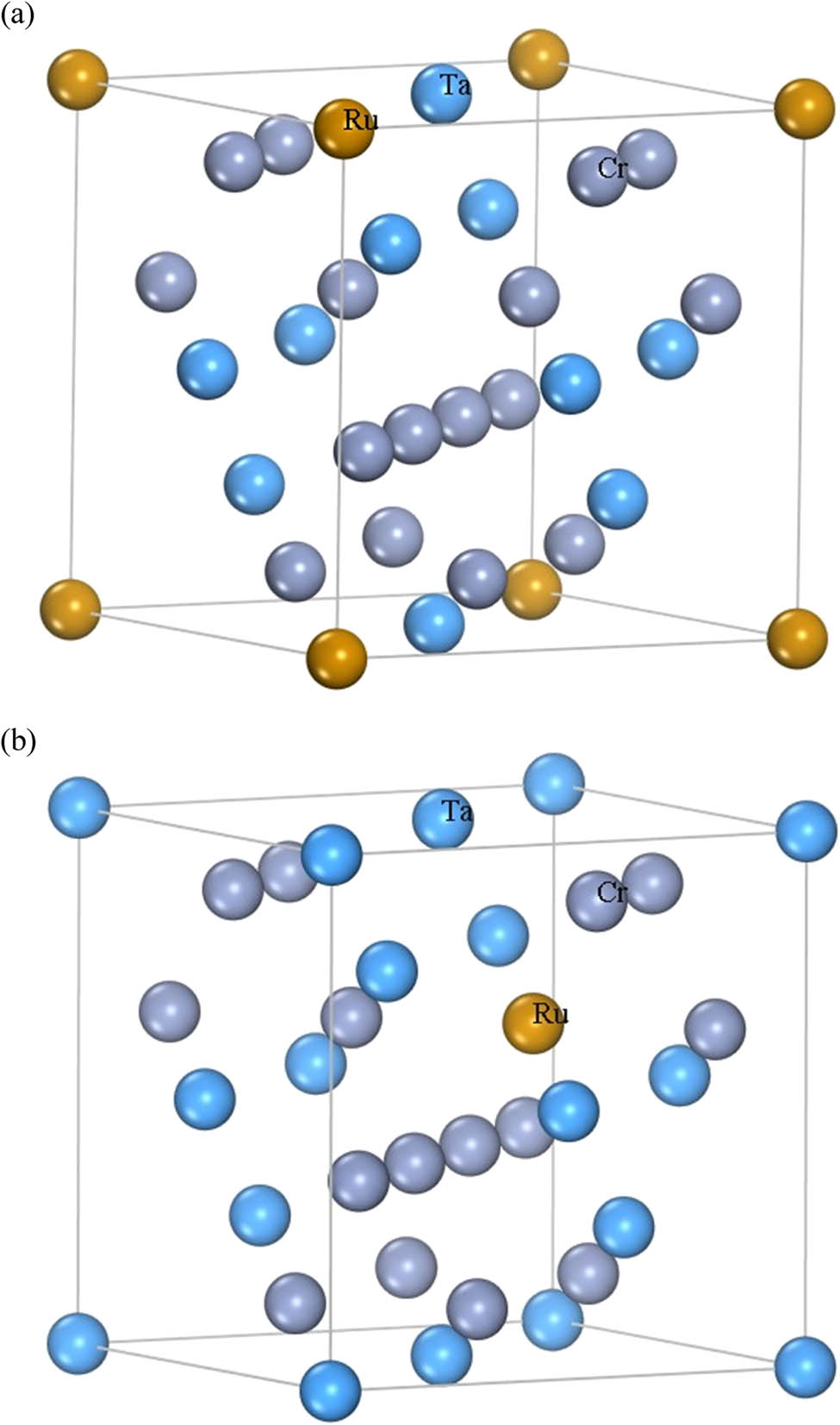
Figure 1 (a) Supercell model of Ta7RuCr16 and (b) supercell model of Ta8Cr15Ru.
Figure 1

(a) Supercell model of Ta7RuCr16 and (b) supercell model of Ta8Cr15Ru.

2.2 Computational methods

The Cambridge serial total energy package software based on density functional theory was used to calculate the potential function using an ultrasoft pseudopotential expressed in inverse space [34], and generalized gradient approximation in the Perdew–Burke–Ernzerhof method [35] to calculate the exchange correlation energy. The cutoff energy of the plane wave after convergence tests were taken as 450 eV, and the number of K-point grids by the Monkhorst-Pack method [36] was 4 × 4 × 4. The geometric structures were optimized through the Broyden–Fletcher–Goldfarb–Shannon algorithm [37], the total energy E of the self-consistent calculation system was 1.0 × 10−5 eV·atom−1, the maximum force F max on each atom was 0.03 eV·Å−1, the stress deviation S max was 0.05 GPa, and the tolerance shift D max was 1.0 × 10−3 Å. The calculated TaCr2 for the C15 structure lattice constant is a = b = c = 6.9779 Å, which is in close match with the experimental values in the literature listed in Table 1.

Table 1

Cell parameters for Ta atom and C15–TaCr2 alloy

Ta C15–TaCr2
Crystal structure BCC FCC
Space group Im3̄m(229) Fd3̄m(227)
Lattice parameters (experimental) a = b = c = 3.0600 Å [35] a = b = c = 6.9850 Å [38]
Lattice parameters (this study) a = b = c = 2.9165 Å a = b = c = 6.9779 Å

3 Results and analysis of the calculation

3.1 Formation enthalpy and lattice constants

The lattice occupancy of the doped atoms in the C15-TaCr2 is determined by the occupancy energy. In purpose of identifying the reasonable lattice occupancy of the doped Ru elements in TaCr2 at Ta or Cr sites, the occupancy energy is figured out by the following equation:

(1) E site = H A – H B ,

where H A and H B are the formation enthalpies of Ta7RuCr16 and Ta8Cr15Ru, respectively. When E site > 0, it refers to the tendency of Ru to occupy the lattice position of Cr atoms in the C15-TaCr2 cell, and the larger the value of E site , the stronger the tendency to preferentially take up the lattice site of Cr atoms. On the contrary, if the value of E site < 0, it indicates that Ru tends to occupy the lattice position of Ta atoms, and the smaller the value of E site , the more obvious the tendency to preferentially occupy the lattice location of Ta atoms. The formulas for calculating the formation enthalpy H A and H B of Ta7RuCr16 and Ta8Cr15Ru are

(2) H A = E total Ta 7 Ru Cr 16 − 7 E solid Ta − E solid Ru − 16 E solid Cr 24 ,

(3) H B = E total Ta 8 Cr 15 Ru − 8 E solid Ta − 15 E solid Cr − E solid Ru 24 ,

where E total Ta 7 Ru Cr 16 and E total Ta 8 Cr 15 Ru are the total energy of Ta7RuCr16 and Ta8Cr15Ru, E solid Ta , E solid Cr , and E solid Ru represents the average energy of each Ta, Cr, and Ru atom in the ground state, respectively. Table 2 illustrates the ground state energies E solid for individual atoms of Ta, Cr, and Ru. The enthalpies of formation H A and H B for Ta7RuCr16 and Ta8Cr15Ru are −3.3554 and −4.2424 eV, respectively, and the lattice occupation energy E site is greater than 0. It can be concluded that Ru atoms tend to preferentially occupy the sites of Cr atoms. The calculated results are consistent with the experimental results [11].

Table 2

Ground state and freedom energy for Ta, Cr, and Ru atoms

Atom E solid ( eV)
Ta −137.1187
Cr −2467.6458
Ru −2602.2481

The geometrical optimization of the ternary phase after doping with Ru elements of different atomic percentage concentrations is conducted from the spatial position of the doped Ru elements occupying the C15-TaCr2, and the formation enthalpy and lattice constant changes are calculated and analyzed. The formation enthalpy H n of Ta8Cr16−n Ru n is formulated as

(4) H n = E total Ta 8 Cr 16 − n Ru n − 8 E solid Ta − ( 16 − n ) E solid Cr − n E solid Ru 24 .

The formation enthalpy H n and the lattice constants of Laves phase Ta8Cr16−n Ru n doped with varying concentrations of Ru elements following geometric optimization are exhibited in Table 3. With the increase in the doping concentration from 4.17 at% to 16.67 at%, the absolute values of formation enthalpy H n of Ta8Cr16−n Ru n (n = 1 → 4) gradually decline, which reflects that the alloying ability of forming ternary alloy gradually weakens as the doping concentration of Ru increases. When the Ru concentration continues to improve to 20.83 at% (n = 5), the absolute value of the formation enthalpy enlarges slightly. With further addition of Ru concentration to 25 at% (n = 6), the absolute value of the enthalpy of generation is 4.0150 eV at the minimum. According to Table 3 and the above lattice occupation calculations, it appears that the lattice constant of C15-TaCr2 is 6.9779 Å. The lattice constant of the ternary Laves phase formed by adding Ru exhibits a significant increase. As the Ru concentration goes from 0 to 25 at%, the lattice constant of the corresponding Ta8Cr16−n Ru n ternary phase progressively rises to a maximum of 7.1002 Å. With the radius of Ru atoms larger than that of Cr atoms, the substitution of Ru elements for Cr atoms will contribute to an enlargement of the volume of the cell system. When relaxation is undertaken for specific positions occupied by more atoms in a volume-optimized supercell, it will push up the volume of the entire cell system even further.

Table 3

Formation enthalpy H n and lattice constants of Ta8Cr16−n Ru n by doping Ru with different atomic percent concentrations

Crystalline cell H n (eV) Lattice constants (Å)
Ta8Cr15Ru1 −4.2424 6.9945
Ta8Cr14Ru2 −4.1807 7.0159
Ta8Cr13Ru3 −4.1023 7.0299
Ta8Cr12Ru4 −4.0415 7.0466
Ta8Cr11Ru5 −4.0450 7.0745
Ta8Cr10Ru6 −4.0150 7.1002

3.2 Density of states (DOS)

To comprehend the effect of Ru alloying on the electronic structure of TaCr2, the DOS before and after alloying are computed. The total DOS and the fractional wave DOS of TaCr2 are demonstrated in Figure 2. It can be noticed that the total DOS of TaCr2 is mainly contributed by d electron orbitals, and the percentage of s and p electron orbitals rarely contributes to DOS. The external valence electrons of Ta and Cr are 6s25d34f14 and 4s13d5, respectively, so the total DOS of TaCr2 is mainly contributed by 5d electrons of states of Ta and 3d electrons of states of Cr, indicating that the d electron orbitals have a significant impact on the Laves phase TaCr2 alloying. Electrons near the Fermi energy level play a dominant role in the formation of chemical bonds, so only the electronic structure near the Fermi energy level is analyzed. The shape of the bond peaking near the Fermi energy level can reveal the strength of the electronic hybridization reactions and the bonding intensity of the chemical bonds [39].

Figure 2 Total DOS and partial DOS of TaCr2.
Figure 2

Total DOS and partial DOS of TaCr2.

The electronic DOS of Ta8Cr16−n Ru n (x = 1–6) crystals in the −5–4.5 eV energy level region is depicted in Figure 3, and the dashed lines in the figure are the Fermi energy levels. With the improvement in Ru atom concentration, the bonding peaks in the Ta8Cr16−n Ru n exhibit declining and broadening. Moreover, with the Ru content greater than or equal to 12.50 at%, new bonding peaks appear near the −5 to −3 eV energy level (as shown by the arrows in Figure 3), which indicates that Ru atoms have formed bonding interactions with Ta and Cr atoms in the cell, and the replacement solid solution of Ru weakens the bonding strength of the Ta–Cr bond in TaCr2. When Ru is enlarged up to 25 at% (n = 6), the new bonding peaks tend to vanish.

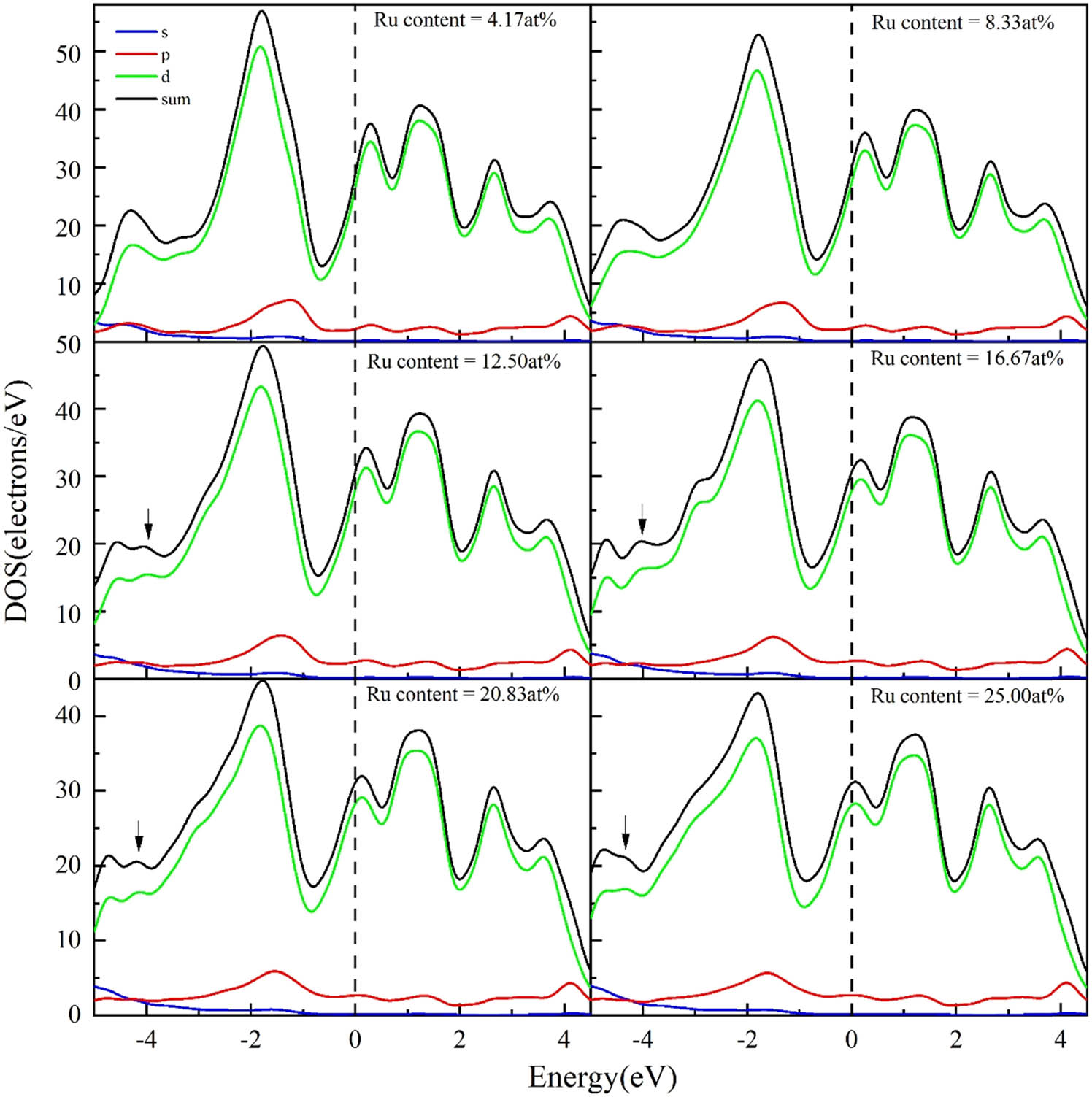
Figure 3 DOS of Ta8Cr16−n Ru n (x = 1–6) alloys.
Figure 3

DOS of Ta8Cr16−n Ru n (x = 1–6) alloys.

DOS of TaCr2 alloys doped with various atomic percentage concentrations of Ru elements in the −3 to 2 eV energy level regions are illustrated in Figure 4. The energy of DOS of the initial Laves phase TaCr2 and the Ru-doped alloy do not obviously change, and the bond peak DOS of Ta8Cr16−n Ru n (n = 0 → 6) are measured to be 61.60, 56.53, 52.52, 49.05, 47.01, 44.43, and 42.76 electron·eV−1. The significant reduction in the density of bonding peaks before and after doping indicates that the doping of Ru atoms weakens the hybridization reaction between the d electron orbitals of Ta and Cr, which in turn also leads to a reduction in the bonding strength of the chemical bond. It can also be viewed from Figure 4 that there are two more apparent spikes on both sides of the Fermi energy level, and the distance between the spikes is the pseudo-energy gap. In general, the wider the pseudo-energy gap, the stronger the bonding of the atoms of the alloy or compound and the more stable the structure. As the Ru doping concentration progressively proceeds from 4.17 to 25.00 at%, the pseudo-energy gap of Ta8Cr16−n Ru n (n = 1 → 6) falls gradually from 2.10 eV to 1.85 eV, which implies that as the Ru content increases, the pseudo-energy gap increasingly becomes narrower and the alloy turns more unstable.

Figure 4 Total DOS of TaCr2 alloys doped with different atomic percentages of Ru element in the energy level range of −3 to 2 eV.
Figure 4

Total DOS of TaCr2 alloys doped with different atomic percentages of Ru element in the energy level range of −3 to 2 eV.

3.3 Elastic properties

The elastic constants are essential for a comprehension of the structural stability and bonding properties between adjacent atoms. Crystals of distinct crystal systems have different numbers of independent elastic constants. The C15 structure of Laves phase TaCr2 has cubic symmetry and only three independent elastic constants, C11, C12, and C44. The mechanical stability of cubic crystals has to be met [40]: C11 – C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0. The elastic constants of C15-TaCr2 and Ta8Cr15Ru are described as shown in Table 4. It is obvious that the elastic constants of Ta8Cr15Ru and C15-TaCr2 satisfy all the above inequalities, which suggests that they are stable in the ground state. The bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, and anisotropy constant A of the cubic structure can be directly calculated from the elastic constants, where the shear modulus G is the value of Hill model and the value of Hill model is the arithmetic average of Voigt model value G V and Reuss value G R [41], that is Voigt-Reuss-Hill approximation. The computational equation is as follows:

(5) B = 1 3 ( C 11 + 2 C 12 ) ,

(6) G V = 1 5 ( C 11 – C 12 + 3 C 44 ) ,

(7) G R = 5 C 44 ( C 11 – C 12 ) 4 C 44 + 3 ( C 11 – C 12 ) ,

(8) G = 1 2 ( G V + G R ) ,

(9) E = 9 GB G + 3 B ,

(10) ν = 3 B − 2 G 6 B + 2 G ,

(11) A = 2 C 44 C 11 − C 12 .

Table 4

Elastic constants for C15-TaCr2 and Ta8Cr15Ru

Crystals C11 (GPa) C12 (GPa) C44 (GPa) B (GPa) G (GPa) E (GPa) V B/G A
C15-TaCr2 341 192 89 241 83 223 0.34 2.90 1.19
Ta8Cr15Ru 332 202 90 245 79 214 0.35 3.10 1.38
TaCr2 Theo. [33] 347 218 88 261 78.6 214 0.363 3.32 1.36
TaCr2 Theo. [44] 360 220 94 267 83 226 0.359 3.22 1.35
TaCr2 Expt. [44] 281 173 73 209 64 175 0.360 3.26 1.34

The bulk modulus B reflects the ability of the material to resist strain and the difficulty of deformation. The greater the value of B, the more difficult the material is for compression and deformation. After doping with alloying element Ru, the modulus of elasticity B increases from 241 to 245 GPa, and Ta8Cr15Ru is more resistant to compression and deformation. The shear modulus G reflects the material’s ability to resist shear strain, and the shear modulus G value of Ta8Cr15Ru is lower than that of C15-TaCr2, and the ability to resist shear strain of Ta8Cr15Ru is lessened. Young’s modulus E is commonly applied to embody the material’s ability to resist elastic deformation. In a certain stress, the larger the E value, the smaller the elastic deformation, compared with the undoped system, the doping of Ru makes the Young’s modulus E value of TaCr2 decrease by 9 GPa, indicating that Ru doping makes the elastic deformation occur to a greater extent. The higher the value of Poisson’s ratio ν, the better the plasticity of the material, and the value is between −1 and 0.5. The results demonstrate that the plasticity of Ta8Cr15Ru is better than that of C15-TaCr2. The anisotropy constant A is adopted to quantify the degree of anisotropy of a solid. When A is equal to 1, the material is elastically isotropic, otherwise it is elastically anisotropic. The more the deviation of the A value from 1, the more pronounced the elastic anisotropy is. The A value of Ta8Cr15Ru is more than that of C15-TaCr2, which represents that the elastic anisotropy of the Ru-doped system is more obvious.

In accordance with the Pugh criterion [42], when the B/G ratio > 1.75, the alloy is ductile in character, otherwise it shows brittleness. All theoretical and experimental results were found to be greater than 1.75 on the basis of the B/G ratio in Table 4, illustrating that the Laves phase TaCr2 has favorable plasticity. However, a multitude of experimental results reveal that TaCr2 is a brittle intermetallic compound at room temperature with a minor fracture toughness value of about 1.0 MPa·m1/2. The B/G criterion of Pugh was proposed based on pure metals rather than compounds, and the mechanical properties of the C15-NbCr2 Laves phase and other Laves phases and some compounds exceed the B/G criterion of Pugh [43], and the brittleness and ductility of the compounds are more sophisticated, which rely on several factors such as crystal structure, electronic structure, chemical bonding, and deformation mechanisms.

The elastic constants of the ternary phase Ta8Cr16−n Ru n with varying percentage concentrations of Ru-doped elements are shown in Figure 5. The bulk modulus B changes slightly between 0 and 16.67 at% of Ru content, and the shear modulus G and Young’s modulus E tend to decrease, and at the time of Ru content of 16.67 at%, the values of B, G, and E are all minimal, and meanwhile the hardness of Ta8Cr16−n Ru n is the smallest and the degree of elastic deformation is the largest. The Poisson’s ratio ν tends to rise with the increase in Ru concentration, and ν reaches the maximum value of 0.371 at the Ru content of 20.83 at%, the brittleness reduces to a greater extent, and the B, G, and E values are obviously increasing, and the elastic deformation resistance is enhanced at this occasion. From the DOS in Figure 3, it can be noticed that with Ru content of 25 at%, the new bonding peak disappears and the difficulty of breaking the Ta–Cr chemical bond is enhanced relative to that with Ru content of 20.83 at% (n = 5), and the Poisson’s ratio ν declines slightly compared to the previous one at a Ru atomic percentage concentration of 20.83 at%, the improvement in brittleness is satisfactory and the enhancement of hardness is greater.

Figure 5 Elastic constants of ternary phases with different percentage concentrations of ruthenium alloying.
Figure 5

Elastic constants of ternary phases with different percentage concentrations of ruthenium alloying.

4 Conclusion

The lattice occupation energy calculations of Ta–Ru–Cr ternary alloys illustrate that Ru atoms tend to preferentially occupy the lattice positions of Cr atoms in C15-TaCr2, and their alloying ability decreases with the increase in the Ru element content, while the absolute value of the generation enthalpy rises slightly when the Ru concentration is 20.83 at%. The atomic radius of Ru is larger than that of Cr, accounting for the continuous growth of the lattice constant of the alloy as Ru content rises. Ru alloying reduces the stability of TaCr2, the pseudo-energy gap narrows and the stability decreases gradually. The elastic constants indicate that Ru alloying can reduce the brittleness of TaCr2, and the bonding peaks are both decreased and broadened, which weakens the bonding strength of Ta–Cr atoms and improves the deformability of the material. When the Ru content is 16.67 at%, Ta8Cr16−n Ru n has the smallest hardness and the largest elastic deformation degree, and when the Ru concentration is 20.83 at%, the brittleness improvement effect is more obvious and the hardness is larger.

Acknowledgements

The authors gratefully acknowledge the fundamental support from the National Natural Science Foundation of China (Grant no. 52161021 and 51964034), the S&T plan projects of Jiangxi Provincial Department of Education (DA202101175), and Graduate Innovative Special Fund Projects of Jiangxi Province (YC2021-S676).

  1. Funding information: National Natural Science Foundation of China (Grant no. 52161021 and 51964034), the S&T plan projects of Jiangxi Provincial Department of Education (DA202101175), and Graduate Innovative Special Fund Projects of Jiangxi Province (YC2021-S676).

  2. Author contributions: Shishi Wei: data calculation and analyses, and wrote the manuscript; Xuan Xiao: methodology and supervision; Kai Zhou: conception of the study and manuscript preparation; Jing Yao: analysis; Dezhi Chen: manuscript preparation.

  3. Conflict of interest: Authors state no conflict of interest.

References

[1] Guénolé, J., F. Z. Mouhib, L. Huber, B. Grabowski, and S. Korte-Kerzel. Basal slip in Laves phases: the synchroshear dislocation. Scripta Materialia, Vol. 166, 2019, pp. 134–138.10.1016/j.scriptamat.2019.03.016Search in Google Scholar

[2] Sun, F., J. Zhang, S. Mao, and X. Han. First-principles studies of the structural and electronic properties of the C14 Laves phase XCr2 (X = Ti, Zr, Nb, Hf and Ta). Philosophical Magazine, Vol. 9319, 2013, pp. 2563–2575.10.1080/14786435.2013.778427Search in Google Scholar

[3] Xian, Y., H. Zheng, Q. Zhai, and Z. Luo. A two-dimensional structure map for prediction of the transition-metal Laves phases. Computational Materials Science, Vol. 125, 2016, pp. 1–7.10.1016/j.commatsci.2016.08.023Search in Google Scholar

[4] Wilson, A. S., E. J. Pickering, C. N. Jones, C. M. F. Rae, and H. J. Stone. Addition of Ge to Cr-Ta-Si laves phase-based alloys. Intermetallics, Vol. 138, 2021, id. 107311.10.1016/j.intermet.2021.107311Search in Google Scholar

[5] Zubair, M., S. Sandlöbes, M. A. Wollenweber, C. F. Kusche, W. Hildebrandt, C. Broeckmann, et al. On the role of Laves phases on the mechanical properties of Mg-Al-Ca alloys. Materials Science and Engineering: A, Vol. 756, 2019, pp. 272–283.10.1016/j.msea.2019.04.048Search in Google Scholar

[6] Rabadia, C. D., Y. J. Liu, L. Y. Chen, S. F. Jawed, L. Q. Wang, H. Sun, et al. Deformation and strength characteristics of Laves phases in titanium alloys. Materials & Design, Vol. 179, 2019, id. 107891.10.1016/j.matdes.2019.107891Search in Google Scholar

[7] Xue, Y., N. Takata, H. Li, M. Kobashi, and L. Yuan. Critical resolved shear stress of activated slips measured by micropillar compression tests for single-crystals of Cr-based Laves phases. Materials Science and Engineering: A, Vol. 806, 2021, id. 140861.10.1016/j.msea.2021.140861Search in Google Scholar

[8] Yan, X., X. Q. Chen, A. Grytsiv, P. Rogl, R. Podloucky, V. Pomjakushin, et al. Crystal structure, phase stability and elastic properties of the Laves phase ZrTiCu2. Intermetallics, Vol. 16, No. 5, 2008, pp. 651–657.10.1016/j.intermet.2008.01.015Search in Google Scholar

[9] Vedmedenko, O., F. Rösch, and C. Elsässer. First-principles density functional theory study of phase transformations in NbCr2 and TaCr2. Acta materialia, Vol. 5618, 2008, pp. 4984–4992.10.1016/j.actamat.2008.06.014Search in Google Scholar

[10] Bhowmik, A., C. N. Jones, I. M. Edmonds, and H. J. Stone. Effect of Mo, Al and Si on the microstructure and mechanical properties of Cr-Cr2Ta based alloys. Journal of Alloys and Compounds, Vol. 530, 2012, pp. 169–177.10.1016/j.jallcom.2012.03.070Search in Google Scholar

[11] Tien, R. H., J. H. Zhu, C. T. Liu, and L. R. Walker. Effect of Ru additions on microstructure and mechanical properties of Cr-TaCr2 alloys. Intermetallics, Vol. 13, No. 3–4, 2005, pp. 361–366.10.1016/j.intermet.2004.07.017Search in Google Scholar

[12] Bhowmik, A., S. Neumeier, J. S. Barnard, C. H. Zenk, M. Göken, C. M. Rae, et al. Microstructure and mechanical properties of Cr-Ta-Si Laves phase-based alloys at elevated temperatures. Philosophical Magazine, Vol. 9434, 2014, pp. 3914–3944.10.1080/14786435.2014.971086Search in Google Scholar

[13] Brady, M. P., C. T. Liu, J. H. Zhu, P. F. Tortorelli, and L. R. Walker. Effects of Fe additions on the mechanical properties and oxidation behavior of Cr2Ta Laves phase reinforced Cr. Scripta Materialia, Vol. 52, No. 9, 2005, pp. 815–819.10.1016/j.scriptamat.2005.01.016Search in Google Scholar

[14] Fujita, M., Y. Kaneno, and T. Takasugi. Phase field and room-temperature mechanical properties of C15 Laves phase in Nb-Hf-Cr and Nb-Ta-Cr alloy systems. Journal of alloys and compounds, Vol. 424, No. 1–2, 2006, pp. 283–288.10.1016/j.jallcom.2005.11.087Search in Google Scholar

[15] Xue, Y., S. Li, Y. Wu, C. Liu, H. Liu, and L. Yuan. Strengthening and toughening effects in Laves phase Cr2Ta/Cr in situ composites by Si additions. Vacuum, Vol. 174, 2020, id. 109202.10.1016/j.vacuum.2020.109202Search in Google Scholar

[16] Yao, Q., J. Sun, Y. Zhang, and B. Jiang. First-principles studies of ternary site occupancy in the C15 NbCr2 Laves phase. Acta materialia, Vol. 5413, 2006, pp. 3585–3591.10.1016/j.actamat.2006.03.039Search in Google Scholar

[17] Ran, J. Q., M. W. Fu, and W. L. Chan. The influence of size effect on the ductile fracture in micro-scaled plastic deformation. International Journal of Plasticity, Vol. 41, 2013, pp. 65–81.10.1016/j.ijplas.2012.09.002Search in Google Scholar

[18] Lu, S., H. Zheng, L. Deng, and J. Yao. Effect of silicon on the fracture toughness and oxidation behavior of hot pressed NbCr2 alloys. Materials & Design, Vol. 51, 2013, pp. 432–437.10.1016/j.matdes.2013.04.033Search in Google Scholar

[19] Takasugi, T., M. Yoshida, and S. Hanada. Deformability improvement in C15 NbCr2 intermetallics by addition of ternary elements. Acta materialia, Vol. 44, No. 2, 1996, pp. 669–674.10.1016/1359-6454(95)00174-3Search in Google Scholar

[20] Peng, L., S. Takizawa, K. I. Ikeda, T. Horiuchi, and S. Miura. Effect of Si on the stability of NbCr2 Laves phase in Cr-Mo-Nb system. Intermetallics, Vol. 110, 2019, id. 106457.10.1016/j.intermet.2019.03.020Search in Google Scholar

[21] Tang, H., W. Xing, X. Li, B. Chen, P. Zhao, L. Shu, et al. Insights into the gradient-characteristic precipitation behaviors of Laves phase induced by Fe/W/Mo addition in Ti42Al5Mn alloy. Intermetallics, Vol. 128, 2021, id. 107022.10.1016/j.intermet.2020.107022Search in Google Scholar

[22] Chen, S., Y. Sun, Y. H. Duan, B. Huang, and M. J. Peng. Phase stability, structural and elastic properties of C15-type Laves transition-metal compounds MCo2 from first-principles calculations. Journal of Alloys and Compounds, Vol. 630, 2015, pp. 202–208.10.1016/j.jallcom.2015.01.038Search in Google Scholar

[23] Nong, Z. S., J. C. Zhu, Y. Cao, X. W. Yang, Z. H. Lai, and Y. Liu. A first-principles study on the structural, elastic and electronic properties of the C14 Laves phase compounds TiX2 (X = Cr, Mn, Fe). Physica B: Condensed Matter, Vol. 419, 2013, pp. 11–18.10.1016/j.physb.2013.03.012Search in Google Scholar

[24] Rabahi, L., B. Alili, D. Bradai, T. Grosdidier, and A. Kellou. DFT calculations of structural, magnetic and thermal properties of C15, C14 and C36 Laves phases in Fe-Nb-Zr. Intermetallics, Vol. 83, 2017, pp. 92–100.10.1016/j.intermet.2016.12.011Search in Google Scholar

[25] Du, J., A. Zhang, Z. Guo, M. Yang, M. Li, and S. Xiong. Atomic cluster structures, phase stability and physicochemical properties of binary Mg-X (X = Ag, Al, Ba, Ca, Gd, Sn, Y and Zn) alloys from ab-initio calculations. Intermetallics, Vol. 95, 2018, pp. 119–129.10.1016/j.intermet.2018.02.005Search in Google Scholar

[26] Kazantzis, A. V., M. Aindow, I. P. Jones, G. K. Triantafyllidis, and J. T. M. De. Hosson. The mechanical properties and the deformation microstructures of the C15 Laves phase Cr2Nb at high temperatures. Acta Materialia, Vol. 55, No. 6, 2007, pp. 1873–1884.10.1016/j.actamat.2006.10.048Search in Google Scholar

[27] Li, C., K. Zhang, and J. G. Ru. Pressure dependence of structural, elastic and electronic of Mg2Y: A first principles study. Journal of Alloys and Compounds, Vol. 647, 2015, pp. 573–577.10.1016/j.jallcom.2015.05.132Search in Google Scholar

[28] Pluengphon, P., T. Bovornratanaraks, and U. Pinsook. Structural, electronic, optical and mechanical properties of InP alloyed with Zn, Si, Sn and S under pressure: First-principles calculation. Journal of Alloys and Compounds, Vol. 700, 2017, pp. 98–105.10.1016/j.jallcom.2017.01.063Search in Google Scholar

[29] Hu, Y. L., L. H. Bai, Y. G. Tong, D. Y. Deng, X. B. Liang, J. Zhang, et al. First-principle calculation investigation of NbMoTaW based refractory high entropy alloys. Journal of Alloys and Compounds, Vol. 827, 2020, id. 153963.10.1016/j.jallcom.2020.153963Search in Google Scholar

[30] Li, C., J. Kuo, B. Wang, and R. Wang. Effects of X (V, W, Mo, Hf, Ta, Zr) additions on the ideal cleavage fracture of Cr2Nb: First-principles determination. Intermetallics, Vol. 18, No. 1, 2010, pp. 65–69.10.1016/j.intermet.2009.06.007Search in Google Scholar

[31] Huang, H., G. Li, X. Xiao, S. Lu, and P. Peng. Micromechanism in fracture toughness of NbCr2 Laves phase improved by nickel alloying: first-principles calculation. Journal of Alloys and Compounds, Vol. 857, 2021, id. 158040.10.1016/j.jallcom.2020.158040Search in Google Scholar

[32] Liu, L., P. Shen, X. Wu, R. Wang, W. Li, and Q. Liu. First-principles calculations on the stacking fault energy, surface energy and dislocation properties of NbCr2 and HfCr2. Computational Materials Science, Vol. 140, 2017, pp. 334–343.10.1016/j.commatsci.2017.08.030Search in Google Scholar

[33] Nie, X. W., Y. Du, and H. H. Xu. First-principles studies on structural and electronic properties of TaCr2 Laves phase. Physica B: Condensed Matter, Vol. 40520, 2010, pp. 4279–4282.10.1016/j.physb.2010.07.025Search in Google Scholar

[34] Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Physical Review B, Vol. 4111, 1990, id. 7892.10.1103/PhysRevB.41.7892Search in Google Scholar

[35] Perdew, J. P., K. Burke, and M. Ernzerhof. Generalized gradient approximation made simple. Physical Review Letters, Vol. 7718, 1996, id. 3865.10.1103/PhysRevLett.77.3865Search in Google Scholar PubMed

[36] Monkhorst, H. J. and J. D. Pack. Special points for Brillouin-zone integrations. Physical Review B, Vol. 1312, 1976, id. 5188.10.1103/PhysRevB.13.5188Search in Google Scholar

[37] Fischer, T. H. and J. Almlof. General methods for geometry and wave function optimization. The Journal of Physical Chemistry, Vol. 9624, 1992, pp. 9768–9774.10.1021/j100203a036Search in Google Scholar

[38] Kumar, K. S., L. Pang, C. T. Liu, J. Horton, and E. A. Kenik. Structural stability of the Laves phase Cr2Ta in a two-phase Cr-Cr2Ta alloy. Acta Materialia, Vol. 48, No. 4, 2000, pp. 911–923.10.1016/S1359-6454(99)00377-8Search in Google Scholar

[39] Li, G. F., S. Q. Lu, X. J. Dong, and P. Peng. Microcosmic mechanism of carbon influencing on NiTiNb9 alloy. Journal of alloys and compounds, Vol. 542, 2012, pp. 170–176.10.1016/j.jallcom.2012.07.043Search in Google Scholar

[40] Wang, J., S. Yip, S. R. Phillpot, and D. Wolf. Crystal instabilities at finite strain. Physical Review Letters, Vol. 7125, 1993, id. 4182.10.1103/PhysRevLett.71.4182Search in Google Scholar PubMed

[41] Thoma, D. J., F. Chu, P. Peralta, P. G. Kotula, K. C. Chen, and T. E. Mitchell. Elastic and mechanical properties of Nb(Cr, V)2 C15 Laves phases. Materials Science and Engineering: A, Vol. 239, 1997, pp. 251–259.10.1016/S0921-5093(97)00589-3Search in Google Scholar

[42] Pugh, S. F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Vol. 45367, 1954, pp. 823–843.10.1080/14786440808520496Search in Google Scholar

[43] Long, Q., X. Nie, S. L. Shang, J. Wang, Y. Du, Z. Jin, et al. C15 NbCr2 Laves phase with mechanical properties beyond Pugh’s criterion. Computational Materials Science, Vol. 121, 2016, pp. 167–173.10.1016/j.commatsci.2016.04.042Search in Google Scholar

[44] Hong, S., C. L. Fu, and M. H. Yoo. Elastic properties and stacking fault energies of Cr2Ta. Intermetallics, Vol. 7, No. 10, 1999, pp. 1169–1172.10.1016/S0966-9795(99)00039-4Search in Google Scholar
Received: 2022-09-26
Accepted: 2022-11-08
Published Online: 2023-01-10

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying
  3. Improvement and prediction on high temperature melting characteristics of coal ash
  4. First-principles calculations to investigate the thermal response of the ZrC(1−x)Nx ceramics at extreme conditions
  5. Study on the cladding path during the solidification process of multi-layer cladding of large steel ingots
  6. Thermodynamic analysis of vanadium distribution behavior in blast furnaces and basic oxygen furnaces
  7. Comparison of data-driven prediction methods for comprehensive coke ratio of blast furnace
  8. Effect of different isothermal times on the microstructure and mechanical properties of high-strength rebar
  9. Analysis of the evolution law of oxide inclusions in U75V heavy rail steel during the LF–RH refining process
  10. Simultaneous extraction of uranium and niobium from a low-grade natural betafite ore
  11. Transfer and transformation mechanism of chromium in stainless steel slag in pedosphere
  12. Effect of tool traverse speed on joint line remnant and mechanical properties of friction stir welded 2195-T8 Al–Li alloy joints
  13. Technology and analysis of 08Cr9W3Co3VNbCuBN steel large diameter thick wall pipe welding process
  14. Influence of shielding gas on machining and wear aspects of AISI 310–AISI 2205 dissimilar stainless steel joints
  15. Effect of post-weld heat treatment on 6156 aluminum alloy joint formed by electron beam welding
  16. Ash melting behavior and mechanism of high-calcium bituminous coal in the process of blast furnace pulverized coal injection
  17. Effect of high temperature tempering on the phase composition and structure of steelmaking slag
  18. Numerical simulation of shrinkage porosity defect in billet continuous casting
  19. Influence of submerged entry nozzle on funnel mold surface velocity
  20. Effect of cold-rolling deformation and rare earth yttrium on microstructure and texture of oriented silicon steel
  21. Investigation of microstructure, machinability, and mechanical properties of new-generation hybrid lead-free brass alloys
  22. Soft sensor method of multimode BOF steelmaking endpoint carbon content and temperature based on vMF-WSAE dynamic deep learning
  23. Mechanical properties and nugget evolution in resistance spot welding of Zn–Al–Mg galvanized DC51D steel
  24. Research on the behaviour and mechanism of void welding based on multiple scales
  25. Preparation of CaO–SiO2–Al2O3 inorganic fibers from melting-separated red mud
  26. Study on diffusion kinetics of chromium and nickel electrochemical co-deposition in a NaCl–KCl–NaF–Cr2O3–NiO molten salt
  27. Enhancing the efficiency of polytetrafluoroethylene-modified silica hydrosols coated solar panels by using artificial neural network and response surface methodology
  28. High-temperature corrosion behaviours of nickel–iron-based alloys with different molybdenum and tungsten contents in a coal ash/flue gas environment
  29. Characteristics and purification of Himalayan salt by high temperature melting
  30. Temperature uniformity optimization with power-frequency coordinated variation in multi-source microwave based on sequential quadratic programming
  31. A novel method for CO2 injection direct smelting vanadium steel: Dephosphorization and vanadium retention
  32. A study of the void surface healing mechanism in 316LN steel
  33. Effect of chemical composition and heat treatment on intergranular corrosion and strength of AlMgSiCu alloys
  34. Soft sensor method for endpoint carbon content and temperature of BOF based on multi-cluster dynamic adaptive selection ensemble learning
  35. Evaluating thermal properties and activation energy of phthalonitrile using sulfur-containing curing agents
  36. Investigation of the liquidus temperature calculation method for medium manganese steel
  37. High-temperature corrosion model of Incoloy 800H alloy connected with Ni-201 in MgCl2–KCl heat transfer fluid
  38. Investigation of the microstructure and mechanical properties of Mg–Al–Zn alloy joints formed by different laser welding processes
  39. Effect of refining slag compositions on its melting property and desulphurization
  40. Effect of P and Ti on the agglomeration behavior of Al2O3 inclusions in Fe–P–Ti alloys
  41. Cation-doping effects on the conductivities of the mayenite Ca12Al14O33
  42. Modification of Al2O3 inclusions in SWRH82B steel by La/Y rare-earth element treatment
  43. Possibility of metallic cobalt formation in the oxide scale during high-temperature oxidation of Co-27Cr-6Mo alloy in air
  44. Multi-source microwave heating temperature uniformity study based on adaptive dynamic programming
  45. Round-robin measurement of surface tension of high-temperature liquid platinum free of oxygen adsorption by oscillating droplet method using levitation techniques
  46. High-temperature production of AlN in Mg alloys with ammonia gas
  47. Review Article
  48. Advances in ultrasonic welding of lightweight alloys: A review
  49. Topical Issue on High-temperature Phase Change Materials for Energy Storage
  50. Compositional and thermophysical study of Al–Si- and Zn–Al–Mg-based eutectic alloys for latent heat storage
  51. Corrosion behavior of a Co−Cr−Mo−Si alloy in pure Al and Al−Si melt
  52. Al–Si–Fe alloy-based phase change material for high-temperature thermal energy storage
  53. Density and surface tension measurements of molten Al–Si based alloys
  54. Graphite crucible interaction with Fe–Si–B phase change material in pilot-scale experiments
  55. Topical Issue on Nuclear Energy Application Materials
  56. Dry synthesis of brannerite (UTi2O6) by mechanochemical treatment
  57. Special Issue on Polymer and Composite Materials (PCM) and Graphene and Novel Nanomaterials - Part I
  58. Heat management of LED-based Cu2O deposits on the optimal structure of heat sink
  59. Special Issue on Recent Developments in 3D Printed Carbon Materials - Part I
  60. Porous metal foam flow field and heat evaluation in PEMFC: A review
  61. Special Issue on Advancements in Solar Energy Technologies and Systems
  62. Research on electric energy measurement system based on intelligent sensor data in artificial intelligence environment
  63. Study of photovoltaic integrated prefabricated components for assembled buildings based on sensing technology supported by solar energy
  64. Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part I
  65. Performance optimization and investigation of metal-cored filler wires for high-strength steel during gas metal arc welding
  66. Three-dimensional transient heat transfer analysis of micro-plasma arc welding process using volumetric heat source models
https://doi.org/10.1515/htmp-2022-0255
Keywords for this article
ruthenium alloying; Laves phase TaCr2; phase stability; elastic properties; first-principles
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. First-principles investigation of phase stability and elastic properties of Laves phase TaCr2 by ruthenium alloying
  3. Improvement and prediction on high temperature melting characteristics of coal ash
  4. First-principles calculations to investigate the thermal response of the ZrC(1−x)Nx ceramics at extreme conditions
  5. Study on the cladding path during the solidification process of multi-layer cladding of large steel ingots
  6. Thermodynamic analysis of vanadium distribution behavior in blast furnaces and basic oxygen furnaces
  7. Comparison of data-driven prediction methods for comprehensive coke ratio of blast furnace
  8. Effect of different isothermal times on the microstructure and mechanical properties of high-strength rebar
  9. Analysis of the evolution law of oxide inclusions in U75V heavy rail steel during the LF–RH refining process
  10. Simultaneous extraction of uranium and niobium from a low-grade natural betafite ore
  11. Transfer and transformation mechanism of chromium in stainless steel slag in pedosphere
  12. Effect of tool traverse speed on joint line remnant and mechanical properties of friction stir welded 2195-T8 Al–Li alloy joints
  13. Technology and analysis of 08Cr9W3Co3VNbCuBN steel large diameter thick wall pipe welding process
  14. Influence of shielding gas on machining and wear aspects of AISI 310–AISI 2205 dissimilar stainless steel joints
  15. Effect of post-weld heat treatment on 6156 aluminum alloy joint formed by electron beam welding
  16. Ash melting behavior and mechanism of high-calcium bituminous coal in the process of blast furnace pulverized coal injection
  17. Effect of high temperature tempering on the phase composition and structure of steelmaking slag
  18. Numerical simulation of shrinkage porosity defect in billet continuous casting
  19. Influence of submerged entry nozzle on funnel mold surface velocity
  20. Effect of cold-rolling deformation and rare earth yttrium on microstructure and texture of oriented silicon steel
  21. Investigation of microstructure, machinability, and mechanical properties of new-generation hybrid lead-free brass alloys
  22. Soft sensor method of multimode BOF steelmaking endpoint carbon content and temperature based on vMF-WSAE dynamic deep learning
  23. Mechanical properties and nugget evolution in resistance spot welding of Zn–Al–Mg galvanized DC51D steel
  24. Research on the behaviour and mechanism of void welding based on multiple scales
  25. Preparation of CaO–SiO2–Al2O3 inorganic fibers from melting-separated red mud
  26. Study on diffusion kinetics of chromium and nickel electrochemical co-deposition in a NaCl–KCl–NaF–Cr2O3–NiO molten salt
  27. Enhancing the efficiency of polytetrafluoroethylene-modified silica hydrosols coated solar panels by using artificial neural network and response surface methodology
  28. High-temperature corrosion behaviours of nickel–iron-based alloys with different molybdenum and tungsten contents in a coal ash/flue gas environment
  29. Characteristics and purification of Himalayan salt by high temperature melting
  30. Temperature uniformity optimization with power-frequency coordinated variation in multi-source microwave based on sequential quadratic programming
  31. A novel method for CO2 injection direct smelting vanadium steel: Dephosphorization and vanadium retention
  32. A study of the void surface healing mechanism in 316LN steel
  33. Effect of chemical composition and heat treatment on intergranular corrosion and strength of AlMgSiCu alloys
  34. Soft sensor method for endpoint carbon content and temperature of BOF based on multi-cluster dynamic adaptive selection ensemble learning
  35. Evaluating thermal properties and activation energy of phthalonitrile using sulfur-containing curing agents
  36. Investigation of the liquidus temperature calculation method for medium manganese steel
  37. High-temperature corrosion model of Incoloy 800H alloy connected with Ni-201 in MgCl2–KCl heat transfer fluid
  38. Investigation of the microstructure and mechanical properties of Mg–Al–Zn alloy joints formed by different laser welding processes
  39. Effect of refining slag compositions on its melting property and desulphurization
  40. Effect of P and Ti on the agglomeration behavior of Al2O3 inclusions in Fe–P–Ti alloys
  41. Cation-doping effects on the conductivities of the mayenite Ca12Al14O33
  42. Modification of Al2O3 inclusions in SWRH82B steel by La/Y rare-earth element treatment
  43. Possibility of metallic cobalt formation in the oxide scale during high-temperature oxidation of Co-27Cr-6Mo alloy in air
  44. Multi-source microwave heating temperature uniformity study based on adaptive dynamic programming
  45. Round-robin measurement of surface tension of high-temperature liquid platinum free of oxygen adsorption by oscillating droplet method using levitation techniques
  46. High-temperature production of AlN in Mg alloys with ammonia gas
  47. Review Article
  48. Advances in ultrasonic welding of lightweight alloys: A review
  49. Topical Issue on High-temperature Phase Change Materials for Energy Storage
  50. Compositional and thermophysical study of Al–Si- and Zn–Al–Mg-based eutectic alloys for latent heat storage
  51. Corrosion behavior of a Co−Cr−Mo−Si alloy in pure Al and Al−Si melt
  52. Al–Si–Fe alloy-based phase change material for high-temperature thermal energy storage
  53. Density and surface tension measurements of molten Al–Si based alloys
  54. Graphite crucible interaction with Fe–Si–B phase change material in pilot-scale experiments
  55. Topical Issue on Nuclear Energy Application Materials
  56. Dry synthesis of brannerite (UTi2O6) by mechanochemical treatment
  57. Special Issue on Polymer and Composite Materials (PCM) and Graphene and Novel Nanomaterials - Part I
  58. Heat management of LED-based Cu2O deposits on the optimal structure of heat sink
  59. Special Issue on Recent Developments in 3D Printed Carbon Materials - Part I
  60. Porous metal foam flow field and heat evaluation in PEMFC: A review
  61. Special Issue on Advancements in Solar Energy Technologies and Systems
  62. Research on electric energy measurement system based on intelligent sensor data in artificial intelligence environment
  63. Study of photovoltaic integrated prefabricated components for assembled buildings based on sensing technology supported by solar energy
  64. Topical Issue on Focus of Hot Deformation of Metaland High Entropy Alloys - Part I
  65. Performance optimization and investigation of metal-cored filler wires for high-strength steel during gas metal arc welding
  66. Three-dimensional transient heat transfer analysis of micro-plasma arc welding process using volumetric heat source models
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/htmp-2022-0255/html
Scroll to top button