Temperature uniformity optimization with power-frequency coordinated variation in multi-source microwave based on sequential quadratic programming

3.1 Frequency shifting strategy with hot spot alternation

The heating UI is introduced to evaluate the volume uniformity of the heated material [29]; the smaller the UI is, the better the heating uniformity, UI = 0 is considered completely uniform. The UI is defined as follows:

where V vol denotes the volume of the material being heated, T denotes the instantaneous temperature of the material, T av denotes the average temperature, and T 0 denotes the initial temperature.

The material exists in a completely homogeneous state before heating. After heating, the material develops cold and hot spots. With fixed-frequency heating, the hot and cold areas do not change as the heating time increases. Additionally, if the frequency is changed, the material develops a different temperature distribution, indicating that each frequency results in fixed hot and cold regions for a given material. According to these theories, a regional hot spot alternation method is proposed in this work to study the microwave heating of both single-material systems and multi-material systems.

The two studies considered here are as follows. Single-material study: A single SiC material was divided into four regions, and each region was numbered as shown in Figure 2(a). Multi-material study: The aforementioned SiC block was increased to four SiC blocks of equal size, and the four materials were numbered as shown in Figure 2(b).

Figure 2

Zoning of SiC materials: (a) single-material zoning and (b) multi-material zoning (unit: mm).

The flow chart of the regional hot spot alternation algorithm is shown in Figure 3. The input power is fixed at P = 200 W, and 2.41 GHz, 2.42 GHz, and so on till 2.50 GHz are used as the input frequency values. These ten frequencies are used to heat the SiC for 30 s each, and the numbering of the temperature regions is recorded in ascending order as L _n (n = 2.41, 2.42…,2.50). The index “n” in L _n represents the frequency; for example, L _2.41 represents the temperatures of the four numbers in ascending order after heating at a fixed frequency of 2.41 GHz. If L_2.41 = [3 1 4 2], it means that the temperature of region 2 is the highest, followed by region 4, then region 1, and finally region 3, after heating at a fixed frequency of 2.41 GHz. We start by using the common frequency of 2.45 GHz as the initial frequency f ₁, with a heating time step of t _s = 2 s. After heating for 2 s at frequency f ₁, we record the temperatures of the four zones of the material in ascending order and denote the result as L ₁ (index 1 in L ₁ represents the first frequency). If L ₁ = [4 2 3 1], L ₁ is assigned to L _next, and the descending order of L _next is L _d = [1 3 2 4]. Then, the similarity matching factor J between L _d and the ten sequences of L _2.41, L _2.42,…,L _2.50 is calculated, and the frequency f _m corresponding to the sequence with the highest similarity matching rate is determined as the next heating frequency f _next. Assuming that L _2.42 = [1 3 2 4], and its similarity matching rate J is 100%, if this is the only sequence with the highest matching rate, then f _next = f _m = 2.42 GHz (if there are multiple sequences that share the highest matching rate, then the frequency with the smallest UI is selected as the next heating frequency). Then, 2.42 GHz is used as the second heating frequency to heat for 2 s (f ₂ = 2.42 GHz), and the temperatures obtained for the regions in ascending order are assigned to L _next. The above steps are repeated, and the best frequency change order can be selected.

Figure 3

Hot spot alternation frequency flow chart.

3.2 SQP algorithm

While the hot spot alternation algorithm determines the order of frequency shifting, different frequencies correspond to different microwave absorption efficiencies. To improve the microwave heating efficiency, the power needs to be accordingly reallocated. Additionally, the power is proportional to the UI, and to guarantee the uniformity of heating, the relative UI loss power is used as a constraint. The expression of the objective function to be optimized is as follows:

where X i denotes the power; η i denotes the absorption efficiency; m ( X i ) denotes the UI function expression power; UI_i denotes the UI value of each frequency under constant power; δ i denotes the weight; and a i , b i , and c i denote the coefficients.

Furthermore, to ensure that the total power does not change during frequency shifting, the following constraints are imposed:

The SQP algorithm is widely used to solve nonlinear constrained optimization problems because of its superlinear convergence characteristics. For convenience, the above power optimization problems are henceforth converted into the following nonlinear constrained problems:

where f ( X ) is the objective function, g u ( X ) and h v ( X ) are the inequality constraint function and the equation constraint function, and u and v are the numbers of inequalities and equations, respectively [30].

where d k is the iterative search direction and B k is the Hessian matrix ∇ x 2 L ( X , μ , λ ) of the Lagrange function, whose Lagrange function is as follows:

where μ and λ are Lagrange multipliers.

A line search is used to determine the step size, which satisfies the strong Wolfe condition [31].

After determining α k , X k + 1 satisfies the following conditions:

The Hessian matrix of the Lagrange function is calculated using the BGFS update formula (Newton-like method) as follows:

where S k = X k + 1 − X k ; y k = ∇ x L ( X k + 1 , μ , λ ) − ∇ x L ( X k , μ , λ ) . The iteration is stopped when X k + 1 satisfies the accuracy requirement.

4.1 Model parameters and boundary conditions

The initial temperature of the system T ₀ = 20°C, the heated material is a SiC block, the rest of the interior area of the cavity is set up as an air domain, the mat and support column are made of polycrystalline mullite, the heating time is 30 s, and the reaction cavity and WR340 waveguide are copper media. The microwave frequency change order is the order of the frequencies arranged as determined by the hot spot alternation algorithm (the time step for frequency changes t _s = 2 s). The parameters in the model are set as shown in Table 1, and the expressions for the temperature change parameters in SiC are as follows:

The cavity wall and the metallic waveguide wall are considered ideal electrical conductors with the electromagnetic boundary conditions shown below [5,10]:

where n → denotes the unit normal vector of the corresponding surface.

The SiC heating material exchanges heat with the surrounding air through convection, and its heat conduction boundary conditions are as follows [8,33,34]:

where ∂ T / ∂ n is expressed as the temperature gradient perpendicular to the temperature field, T air is the temperature of air, and h is the heat transfer coefficient of air. Since the polycrystalline mullite heat mat has a heat transfer coefficient close to that of air, the bottom of the heating material and the mat can also be represented by equation (18).

The grid size has an important impact on the computational accuracy and computational time of the method. Meshing too coarsely leads to inaccurate calculation accuracy, yet meshing too finely leads to a long calculation time. The selection of the appropriate number of grid cells is thus a critical step in the numerical simulation process. In this study, the normalized absorption rate (NPA) is used to establish the number of grid cells [5,10,34], which is expressed as follows:

where Q e ( τ ) is the electromagnetic power loss density at time τ , P ( τ ) is the total input power, and t is the heating time. The effects of grid size division on the NPA and computational time are shown in Figure 4. As shown, the NPA gradually stabilizes as the number of grid elements increases, but the computational time continues to increase. To balance the NPA with the computational time, the numerical simulation in this work declares a maximum mesh size of 6 mm for the heated material.

Figure 4

Mesh independence study.

4.2 Numerical calculation results and analysis

4.2.1 Model validation

To verify the accuracy of the numerical model, we compared the actual experimental heating results with the numerical calculation model. Heating material: 50 mm × 50 mm × 20 mm SiC, the experimental equipment is as shown in Figure 5(a), top view of SiC block and location of sampling points are as shown in Figure 5(b).

Figure 5

Microwave reactor and heated specimen: (a) microwave reactor and (b) SiC specimen.

We input a fixed power to heat SiC, and the experiment compared the center temperature variation curve with time and the temperature of nine sampling points at 30 s. Five sets of replicate experiments were conducted with arithmetic means as measurements and using standard deviation as the error line variable. A comparison of the experimental results with the numerical calculation results is shown in Figure 6, and the center point in Figure 6(a) is the sampling point 5.

Figure 6

Experimental comparison results: (a) central temperature variation and (b) temperature of each sampling point.

As shown in Figure 6, the experimental results deviated slightly from the numerical calculation, but the overall trend was the same. The reasons for the deviations are: (1) the parameters and conditions of the numerical simulation model are idealized, and there are differences between the actual experiment (including material purity, characteristic parameters, insulation conditions, heat transfer conditions, etc.). (2) The temperature measurement using infrared thermometer requires opening of the cavity, which leads to heat loss. (3) Measurement and instrumentation errors. The results show that the numerical model results are reliable within a certain error tolerance.

4.2.2 Single-material numerical calculation results and analysis

A single 50 mm × 50 mm × 20 mm SiC block is heated, and the frequency conversion sequence of the single material is obtained using the regional hot spot alternation method presented in Section 3.1, as shown in Figure 7(a). Simultaneously, the values of a i , b i , c i , and UI _i within the objective function are brought into equations (8)–(15) with the coefficients shown in Table 2. Redistributed power values are thus obtained, as shown in Figure 7(b).

Figure 7

Single material power–frequency synergy curves: (a) frequency variation curve and (b) power variation curve.

Table 2

Single material factor

Factor	Frequency (GHz)
	2.42	2.43	2.44	2.45	2.47	2.49	2.50
a i	−4.02 × 10−9	−6.31 × 10−9	−4.59 × 10−9	−9.74 × 10−9	−9.27 × 10−9	−7.28 × 10−9	−1.17 × 10−9
b i	1.11 × 10−5	1.63 × 10−5	1.22 × 10−5	3.89 × 10−5	2.42 × 10−5	3.79 × 10−5	2.40 × 10−5
c i	2.61 × 10−3	3.45 × 10−3	1.92 × 10−3	5.97 × 10−3	3.42 × 10−3	6.76 × 10−3	2.94 × 10−3
UI i	4.60 × 10−3	6.40 × 10−3	4.10 × 10−3	1.39 × 10−3	8.00 × 10−3	1.38 × 10−3	7.10 × 10−3

Under these conditions, frequency and power form a one-to-one correspondence, where a specific time corresponds to specific frequency and power values. Power and frequency controls together improve the distribution of the temperature field in the material and the cavity. To qualitatively compare the effects of the three main heating methods (fixed frequency, hot spot alternating frequency, and power–frequency synergistic variation), the silicon carbide block is simulated with COMSOL software using the three heating methods for a heating duration of 30 s. The resulting temperature distributions are shown in Figure 8.

Figure 8

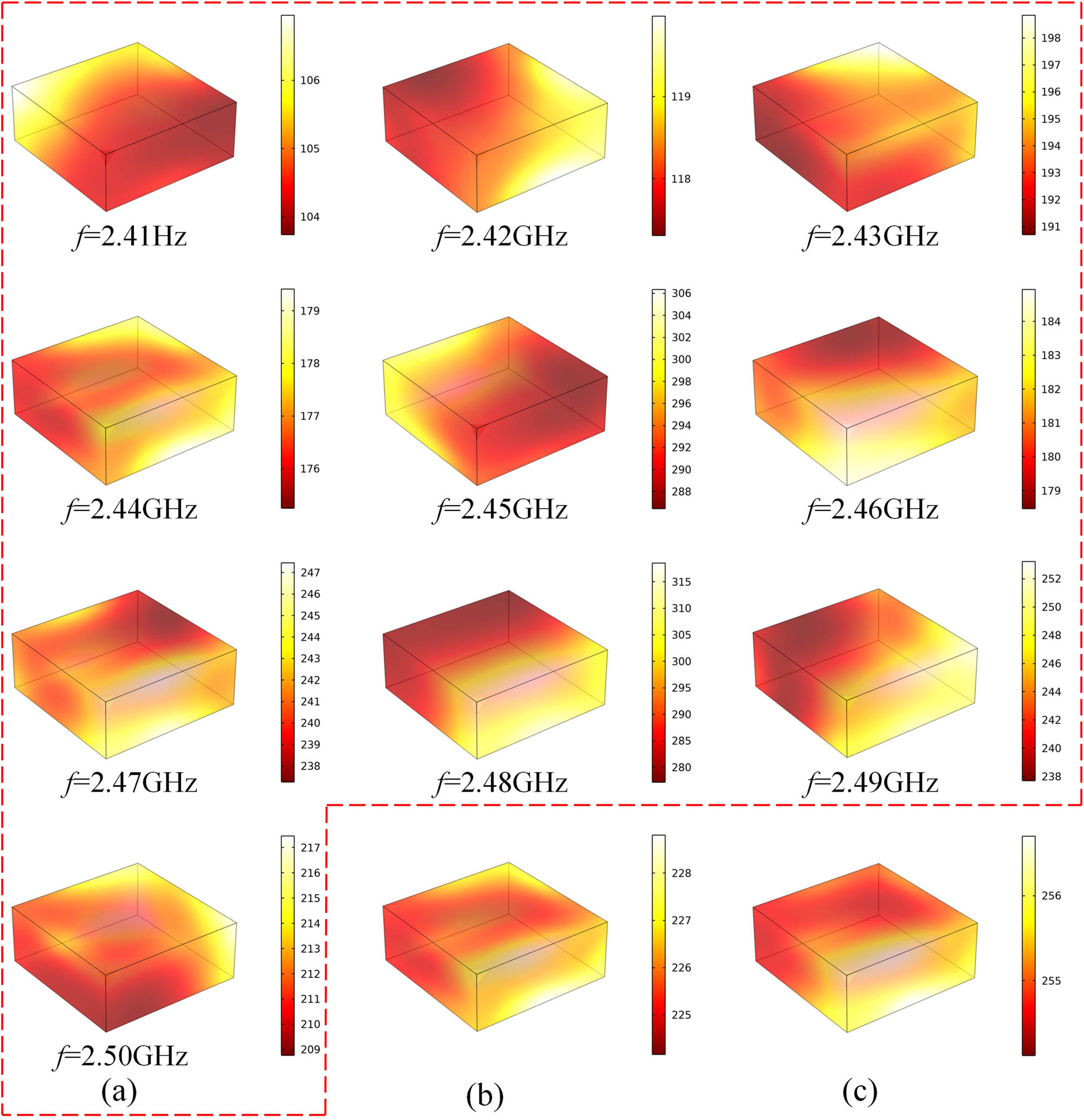
Single material temperature distribution: (a) fixed-frequency heating; (b) hot spot alternating frequency heating; and (c) power–frequency synergistic heating (unit: °C).

As shown in Figure 8, the temperature distributions of SiC under different heating frequencies are different, and frequency shift heating based on hot spot alternation can significantly improve the temperature uniformity of the material compared with fixed-frequency heating. However, the hot spot alternation method affects the heating efficiency when compared with some fixed frequencies. Yet considering the power conversion efficiency, power–frequency cooperative heating produces not only a more uniform temperature but also an improved heating efficiency level. To quantitatively analyze the three heating modes, the UI is used to measure the uniformity of each heating strategy, and the average temperature (T _av) is used to measure the heating efficiency. A data comparison is shown in Table 3.

Table 3

Single material heating performance index

Heating strategy	Frequency (GHz)	T av (°C)	UI
Fixed frequency	2.41	104.66	0.0061
	2.42	118.25	0.0050
	2.43	193.16	0.0067
	2.44	176.60	0.0044
	2.45	291.97	0.0130
	2.46	180.80	0.0083
	2.47	240.45	0.0079
	2.48	289.46	0.0332
	2.49	242.66	0.0144
	2.50	211.42	0.0075
Hot spot alternation frequency	—	225.57	0.0035
Power–frequency synergy	—	254.92	0.0019

As seen from the data in Table 3, hot spot alternating frequency conversion obtains UI data that are better than those of fixed-frequency heating (2.41–2.50 GHz), and the uniformity improves by 20.5–89.5% compared with that of fixed-frequency heating, which proves that hot spot alternation-based frequency conversion helps achieve improved heating uniformity. However, the heating temperature produced under the hot spot alternation method is still reduced compared with that of the fixed-frequency method possessing the best heating efficiency. The proposed multisource microwave power–frequency cooperative heating approach based on SQP not only improves the heating uniformity by 58.5% compared with the optimal value of UI at a fixed frequency but also increases the average heating temperature by 29.35°C compared with the hot spot alternating frequency, which proves that the proposed method can improve the heating uniformity more effectively without considerably affecting the heating efficiency.

Therefore, cooperatively heating multiple microwave sources using power-frequency controls based on SQP, as proposed in this study, can effectively improve heating uniformity. In addition, the hot spot alternation frequency conversion method can neutralize the hot and cold regions while benefitting from the self-organizing property of temperature. Power changes accelerate the conduction of temperature from high-temperature regions to relatively low-temperature regions, and the temperature distribution within the material constantly converges under the influence of both forces. As a result, the temperature differences between the regions decrease, and the uniformity of the heated material is enhanced. The SQP algorithm is used to allocate as much power as possible to the frequencies with high heating efficiency levels under the conditions of constant total power and no uniformity compromise, resulting in a heating temperature increase.

4.2.3 Multi-material numerical calculation results and analysis

To further investigate the effectiveness of the method of this study, it is applied to multi-material heating by simultaneously heating four 50 mm × 50 mm × 20 mm SiC blocks with spacing intervals of 10 mm. The multi-material frequency conversion sequence is obtained according to the hot spot alternation algorithm, as shown in Figure 9(a). The unknown coefficients in the SQP algorithm are shown in Table 4, and redistributed power values are obtained, as shown in Figure 9(b).

Figure 9

Multi material power–frequency synergy curve: (a) frequency variation curve and (b) power variation curve.

Table 4

Multi material factor

Factor	Frequency (GHz)
	2.42	2.43	2.44	2.45	2.47	2.48	2.49	2.50
a i	−6.22 × 10−9	−7.31 × 10−9	−1.04 × 10−9	−6.83 × 10−9	−8.82 × 10−9	−6.64 × 10−9	−4.50 × 10−9	−8.42 × 10−9
b i	1.62 × 10−5	1.42 × 10−5	1.82 × 10−5	1.44 × 10−5	2.27 × 10−5	1.63 × 10−5	1.19 × 10−5	2.28 × 10−5
c i	5.18 × 10−3	4.30 × 10−3	4.54 × 10−3	3.56 × 10−3	4.45 × 10−3	4.65 × 10−3	2.28 × 10−3	6.39 × 10−3
UI i	8.20 × 10−3	6.90 × 10−3	7.80 × 10−3	6.20 × 10−3	8.60 × 10−3	7.70 × 10−3	4.50 × 10−3	1.07 × 10−2

COMSOL software is used to simulate the heating of multi-material using three heating methods: fixed-frequency heating, hot spot alternating frequency-based heating and power–frequency cooperative heating, with a heating time of 30 s. A comparison among the heating effects of the three methods is shown in Figure 10. As shown, the temperature differences between the four materials are very significant after heating them with a fixed frequency. The use of hot spot alternation frequency-based heating effectively improves the temperature distribution of each material and reduces the temperature difference range across the four materials, which better serves the integrity demands of multi-material heating. Power–frequency synergistic heating not only further improves the uniformity but also increases the overall heating temperature. In the quantitative multi-material analysis, the average UI (UI_av) and the maximum mean temperature difference (MTD_max) among the four materials are used to measure the overall uniformity, and their average temperature (T _av) is used to measure the overall heating efficiency. A data comparison is shown in Table 5.

Figure 10

Multi material temperature distribution: (a) fixed-frequency heating; (b) hot spot alternation frequency heating; and (c) power–frequency synergistic heating (unit: °C).

Table 5

Multi material heating performance indicators

Heating strategy	Frequency (GHz)	T av (°C)	UIav	MTDmax (°C)
Fixed frequency	2.41	107.08	0.0096	17.22
	2.42	106.94	0.0082	16.61
	2.43	129.91	0.0069	35.72
	2.44	144.01	0.0078	16.11
	2.45	144.04	0.0062	50.98
	2.46	125.52	0.0058	19.98
	2.47	143.11	0.0086	17.51
	2.48	122.18	0.0077	38.31
	2.49	138.99	0.0045	28.79
	2.50	150.31	0.0107	32.70
Hot spot alternation frequency	—	142.03	0.0043	1.88
Power–frequency synergy	—	146.68	0.0025	2.29

Table 5 shows that the method proposed in this work achieves the minimum average UI and the maximum mean temperature difference data in comparison with fixed-frequency heating. The average UI is improved by 44.4–76.6% over that of fixed-frequency heating, which indicates that the method in this study can continue to improve heating uniformity even when applied to multi-material heating. In particular, considering the maximum mean temperature difference, hot spot alternating frequency conversion and power–frequency synergy achieve values of 1.88 and 2.29°C, respectively, which proves that these two methods can allow the average temperature difference among the four materials to remain in a low range after the heating process completes; this enables the heating system to satisfy the demand of consistent heating temperature across multiple materials. Furthermore, the power–frequency cooperative heating method improves the temperature uniformity of each material (the average UI of the four materials improves by 41.9%) and enhances the heating efficiency (the average temperature of the four materials is raised by 4.65°C) on the basis of alternate hot spot frequency conversion, which fully verifies the feasibility of the method proposed in this work.