Home Ultrasensitive analysis of SW-BNNT with an extra attached mass
Article Open Access

Ultrasensitive analysis of SW-BNNT with an extra attached mass

  • JinRu Zhong EMAIL logo
Published/Copyright: July 23, 2021
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Science and Engineering of Composite Materials
From the journal Science and Engineering of Composite Materials Volume 28 Issue 1

Abstract

In this article, the ultrasensitive analysis of single-walled boron nitride nanotubes (SW-BNNTs) with an extra attached mass is studied by employing atomistic analysis technique. Numerical examples are carried out for vibration characteristic of SW-BNNT with an extra attached mass. Our results show that the vibration frequencies and magnitudes of SW-BNNT are very sensitive to the extra attached mass. In addition, the influence of length and chirality of SW-BNNT on the vibration frequencies and magnitudes of SW-BNNT with an extra attached mass are also examined in detail. This investigation indicates that SW-BNNTs have a great potential in the field of sensor technology.

Keywords: ultrasensitive analysis; vibration; atomistic simulation; SW-BNNT

1 Introduction

Pure boron nitride nanotubes (BNNTs) were first synthesized in 1994 by Chopra et al. [1]. In recent years, many investigations related to BNNTs have already been carried out [2,3,4,5,6,7,8,9,10,11,12]. The atomic structure of BNNTs is similar to that of the carbon nanotubes (CNTs), and can be regarded as replacements of carbon atoms in CNT by boron and nitrogen atoms. The elastic material properties of multiwalled BNNTs were determined experimentally by Chen et al. [13] in 2004. They also presented that due to the effect of nitrogen and boron atoms, the oxidation resistance of BNNTs is stronger than that of CNTs. Furthermore, boron nitride structures have high chemical and thermal stability. Therefore, the material superiorities of BNNT make it a potential candidate for many applications.

In the past years, much attention has been paid to the BNNTs’ mechanical properties. It is reported that the axial Young’s modulus of an individual multiwalled BNNT was about 1.22 ± 0.24 [14]. Li et al. [15] examined the mechanical properties of both single-walled (SW)-BNNTs and CNTs. Serhan et al. [9] presented the impact of electronic properties of defected boron nitride nanotubes with different chiralities. They also found that near the Stone-Wales defect area, the bond angles and lengths of all BNNTs vary significantly. Salavati et al. [16] predicted the piezoelectric coefficients and elastic modulus of BNNTs. Vaccarini et al. [17] investigated axial stiffness, bending, and torsion dynamic behaviors of both BNNTs and CNTs. Ansari et al. [18] studied the buckling properties of SW-BNNTs with different boundary conditions and geometries by using a 3-D FEM model. Jiang and Guo [19] studied the elastic material properties of SW-BNNTs by using a small-scale molecular model. Patra and Batra [20] studied the axial stress wave propagation in BNNTs with different lengths and chiralities under adiabatic conditions. Song et al. [21] examined the stress–strain curves, Young’s modulus, and nonlinear bifurcation in BNNTs. They discovered that the diameter and length of the BNNTs have little effect on the mechanical behavior of the BNNTs, but the mechanical behavior of BNNTs is strongly dependent on the helicity. Rezania and Aghaiimanesh [22] studied the influence of a transverse magnetic field on the electronic properties of both boron nitride monolayer and zigzag nanotubes with Hubbard model at the antiferromagnetic sector.

One potential application of BNNT is serving as highly sensitive nanomechanical resonators and sensors. When there is additional mass attached onto the surface of BNNT, the resonance frequency or surface stress changes of BNNT can be used for defining the sensitivity of BNNT [23,24]. Yan et al. [4] studied the free vibration behaviors of SW-BNNTs using a multiscale simulation approach. They indicated that there is a critical radius for the vibration fundamental frequency of BNNTs. Based on nonlocal piezoelasticity cylindrical shell theory, Ghorbanpour Arani et al. [25] investigated the nonlinear vibration and instability of the embedded double-walled BNNTs conveying viscous fluid. Aydin [26] calculated IR, non-resonance Raman spectra, and vertical electronic transitions of the zigzag single-walled and double-walled BNNTs. Using continuum plate model and molecular dynamics simulation, Yi et al. [27] studied the vibrational behaviors of the single-layered hexagonal boron nitride. Fakrach et al. [28] calculated the Raman spectra of SW-BNNTs based on the force constants model. They discovered that the change in the diameter of the SW-BNNTs will significantly change the modes in the low-frequency region.

It is noteworthy that the generalized continuum mechanics such as nonlocal elasticity theory are suggested to replace the classical continuum mechanics when studying the nanomaterials since scale effect has to be considered. Nevertheless, how to exactly determine the scale parameter is still quite difficult and many literatures are focused on the study of the variation of scale parameter on the mechanical behaviors of nanomaterials [29]. Based on the above literature review, there is little investigation for the ultrasensitive analysis of SW-BNNTs with an extra attached mass. In this work, an atomistic simulation is employed for studying the vibration frequency shifts of cantilevered SW-BNNT with an extra mass attached on the surface at different positions. Different numerical cases are provided to investigate the influence of length and chirality on the vibration frequencies and magnitudes of SW-BNNT.

2 Atomistic simulation for BNNTs

In this investigation, we employ an atomistic simulation for analysis of vibration frequency changes of SW-BNNT with an extra mass attached to the surface at different positions. For the atomic finite element method (AFEM), a system that contains a number of NN boron and nitrogen atoms is considered. In BNNT, there is only covalent bond between B and N atoms, and the energy stored in the B–N bonds is a function of all atoms’ positions, which can be expressed as:

(1) U nb = U nb ( q 1 , q 2 , ⋯ , q N ) = ∑ I < J NA V IJ ( q J − q I ) ,

where V I J ( q J − q I ) and q I are the empirical potential and atom positions, respectively. To describe the atomic interaction, here we use the Tersoff-Brenner multi-body interatomic potential, where the atomic bond energy V I J ( q J − q I ) is related to the atoms outside the bond.

The atomic system potential energy is given as:

(2) E tot ( q ) = U nb ( q ) − ∑ I = 1 NA F ¯ I ⋅ q I ,

where F ¯ I denotes the external force on the atom I . The state of the equilibrium configuration is presented as:

(3) ∂ E tot ( q ) ∂ q = 0 .

By taking the Taylor expansion of E tot ( q ) around an initial guess of q 0 = ( q 1 0 , q 2 0 , … , q NA 0 ) T for the equilibrium state, we can obtain the following equation:

(4) E tot ( q ) ≈ E tot ( q 0 ) + ∂ E tot ( q ) ∂ q q = q 0 ⋅ ( q − q 0 ) + 1 2 ( q − q 0 ) T ⋅ ∂ 2 E tot ( q ) ∂ q ∂ q q = q 0 ⋅ ( q − q 0 ) .

Substituting equation (4) in equation (3), we can obtain the following equation for Δ q = ( q − q 0 ) as:

(5) K A Δ q = P ,

where

(6) K A = ∂ 2 E tot ∂ q ∂ q = ∂ 2 U nb ∂ q ∂ q ,

(7) P = − ∂ E tot ∂ q = F ¯ − ∂ U nb ∂ q ,

where the external force vector is described by F ¯ = ( F ¯ 1 , F ¯ 2 , … , F ¯ NA ) T . By iteratively solving equation (5) using Newton–Raphson method until the nonequilibrium force vector P reaches zero and the hexagonal boron nitride (h-BN) sheet equilibrium configurations under external loading are achieved. In this model, the atomic-scale finite elements are dependent not only on the atomic structure but also on the atomic interactions.

Here the nonequilibrium force vector and the element stiffness matrix are given by the following equations:

(8) P element = F ¯ 1 − ∂ U tot ∂ x 1 3 × 1 ( 0 ) 27 × 1 ,

(9) K element = ∂ 2 U tot ∂ x 1 ∂ x 1 3 × 3 1 2 ∂ 2 U tot ∂ x 1 ∂ x i 3 × 27 1 2 ∂ 2 U tot ∂ x i ∂ x 1 3 × 27 ( 0 ) 27 × 27 ,

where the external force imposed on the central atom is denoted by F ¯ 1 , and i ranges from 2 to 10 in ∂ 2 U tot ∂ x i ∂ x 1 and ∂ 2 U tot ∂ x 1 ∂ x i .

The stored atomic bond energy is a combination of attractive and repulsive pairs, which is described by the widely used Tersoff-Brenner multi-body potential [30]

(10) V B ( r I J ) = V R ( r I J ) − B I J V A ( r I J ) ,

(11) V R ( r I J ) = D ( e ) S − 1 e − 2 S β ( r I J − R ( e ) ) f c ( r I J ) ,

(12) V A ( r I J ) = D ( e ) S S − 1 e − 2 / S β ( r I J − R ( e ) ) f c ( r I J ) ,

(13) B I J = 1 + ∑ K ≠ I , J G ( θ I J K ) f c ( r I K ) − δ ,

where r IJ is the bond length between atoms I and J and V R and V A denote the repulsive and attractive potentials, respectively. Due to atoms I and J located in different environments, Brenner suggested an average value to replace B IJ (a coupling multi-body parameter):

(14) B ¯ I J = 1 2 ( B I J + B J I ) .

The angle function G ( θ I J K ) is given as:

(15) G ( θ I J K ) = a 0 1 + c 0 2 d 0 2 − c 0 2 d 0 2 + ( 1 + cos ( θ I J K ) ) 2 ,

where θ I J K denotes the angle between bonds I–K and I–J.

The cutoff function f c is presented as:

(16) f c ( r ) = 1 , r ≤ R ( 1 ) 1 2 1 + cos π ( r − R ( 1 ) ) R ( 2 ) − R ( 1 ) , R ( 1 ) ≤ r ≤ R ( 2 ) 0 , r ≥ R ( 2 ) ,

in which the valid ranges of the cutoff function are R (1) and R (2). In the present study, the revised values of parameters related to h-BN nanosheets for the Tersoff-Brenner potential are selected from the literature [31].

Based on the AFEM, the governing equation of vibration of SW-BNNT with an extra mass attached on the surface at different positions is given as:

(17) ∑ i = 1 N N ( m i q ̈ i + K A q ) = 0 . ,

in which m i is the mass per atom.

Considering the field function q ( t ) = A exp ( i ω t ) , the dynamic equation is given as:

(18) ∑ i = 1 N N ( K A ∣ x 0 − ω 2 m i ) q = 0 .

The vibration frequency of SW-BNNTs can be obtained from the solution of equation (18).

3 Numerical results and discussion

An atomistic simulation is presented to investigate the resonant frequency of cantilevered SW-BNNT with an extra mass attached on the surface at different positions. The AFEM has been used to study the free vibration behaviors of BNNTs by Yan et al. [4]. They also developed a novel multiscale atomistic-continuum approach under the same empirical potential of the present AFEM to fast predict the vibrational behaviors with high consistency, which can be observed from the results shown in Table 1. As the tubular length and radius increasing, the edge dangling bonds and the curvature effect of the BNNTs become smaller and smaller, and the average potential per atom becomes close to that of the semi-analytical result, −6.4979 eV [31,32].

Table 1

The average potential per atom for the three kinds of BNNTs with different lengths

BNNT (nm) Potential per atom (eV)
(3,3) (6,6) (9,9)
4.05 −6.02086 −6.33045 −6.38814
6.09 −6.03835 −6.35017 −6.40842
8.13 −6.04722 −6.36018 −6.41871

In this investigation, (3,3), (6,6), and (9,9) SW-BNNTs with lengths of 4.05, 6.09, and 8.13 are considered. Figure 1 shows the geometric figure of cantilevered SW-BNNT with an extra mass attached on the surface at the free end. The BNNT atomic structure can be regarded as replacing the carbon atoms by boron and nitrogen atoms, as shown in Figure 2.

Figure 1 The geometric diagram of cantilevered SW-BNNT with an extra mass attached on the surface at the free end.
Figure 1

The geometric diagram of cantilevered SW-BNNT with an extra mass attached on the surface at the free end.

Figure 2 The atomic structure of BNNTs by replacing carbon atoms of CNT by boron and nitrogen atoms.
Figure 2

The atomic structure of BNNTs by replacing carbon atoms of CNT by boron and nitrogen atoms.

Figure 3 depicts the frequency-attached mass curves for cantilevered (3,3), (6,6), and (9,9) SW-BNNTs with the extra mass attached on the surface at the free end. The length of SW-BNNT is 4.05 nm. It can be seen that when the extra mass attached on the surface at the free end is larger than 10−21 g, an obvious variation of resonant frequency is observed, which implies that the mass sensitivity for SW-BNNT is at the level of 10−21 g. Figure 4 shows the variation of frequency shifts for cantilevered (3,3), (6,6), and (9,9) SW-BNNTs with the extra mass attached on the surface at the free end. The frequency shift for a cantilevered (3,3) SW-BNNT with the extra mass of 10−21 g attached on the surface at the free end is 71.0684 GHz, and those for the (6,6) and (9,9) SW-BNNTs are 157.9924 and 230.7156 GHz, respectively. Since it is easier to detect large frequency change, (9,9) SW-BNNT is more sensitive than (3,3) and (6,6) SW-BNNT. When we change the extra mass attached on the surface at the free end from 10−20 to 10−21 g, the frequency changes for the (3,3), (6,6), and (9,9) SW-BNNT are 125.1134, 81.5113, and 40.6197 GHz, respectively. Furthermore, when we change the extra mass attached on the surface at the free end from 10−21 to 10−22 g, the frequency changes for the (3,3), (6,6), and (9,9) SW-BNNT are 36.6987, 30.2546, and 23.711 GHz, respectively. Therefore, it can be concluded that the mass sensitivity for the (9,9) cantilevered SW-BNNT is at the level of 10−22 g.

Figure 3 Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 4.05 nm for different attached masses.
Figure 3

Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 4.05 nm for different attached masses.

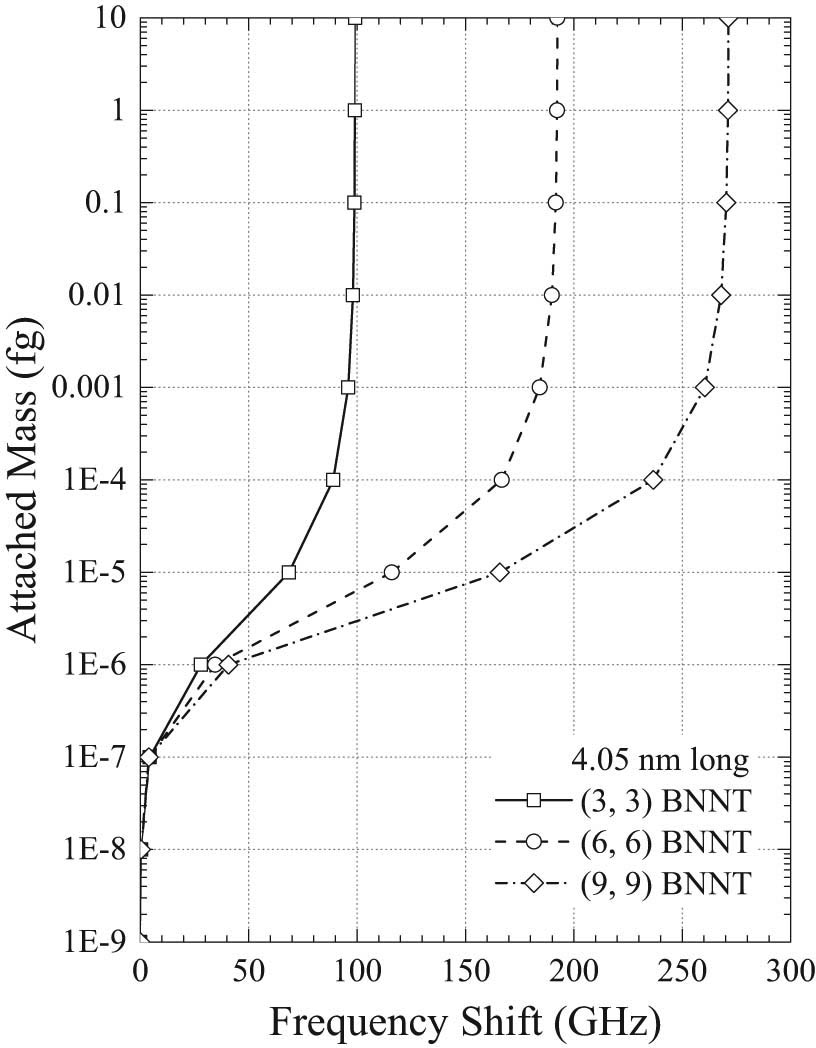
Figure 4 Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 4.05 nm for different attached masses.
Figure 4

Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 4.05 nm for different attached masses.

Figures 5 and 6 present the resonant frequencies and frequency changes for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with the extra mass attached on the surface at the free end for length 6.09. It can be seen that the chirality of SW-BNNT has a significant effect on the resonant frequencies. From Figure 6, it can be seen that when the extra mass attached on the surface at the free end is larger than 10−20 g, the three frequency change curves are almost parallel. It means that the mass sensitivities of (3,3), (6,6), and (9,9) cantilevered SW-BNNT are the same in this case. Also, it can be found that an increase in the size of the SW-BNNT leads to a slight reduction in the accuracy.

Figure 5 Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 6.09 nm for different attached masses.
Figure 5

Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 6.09 nm for different attached masses.

Figure 6 Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 6.09 nm for different attached masses.
Figure 6

Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 6.09 nm for different attached masses.

Figures 7 and 8 present the resonant frequencies and frequency changes for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with the extra mass attached on the surface at the free end for length 8.13 nm. Compared with the results of Figures 1–4, similar conclusions can be obtained. For this case, we further studied the high performance of (3,3), (6,6), and (9,9) SW-BNNT in mass detection with the extra mass attached at arbitrary places on the surface. Here we use symbol a to denote the distance between the attached point and the free end in axial direction, and an additional geometrical parameter ξ = a L is introduced, where L is the total length of SW-BNNT. Figures 9 and 10 present the resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with the extra masses of 10−20 and 10−21 g attached at different locations. Figures 11 and 12 show the frequency changes for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with the extra masses of 10−20 and 10−21 g attached at different locations. From Figures 11 and 12, it can be seen that the frequency shifts for cantilevered (3,3), (6,6), and (9,9) SW-BNNT-based mass resonators decrease significantly as the value of ξ increases, which reveals that the mass detection sensitivity significantly depend on the location of the extra attached masses. From the frequency change curves for (3,3), (6,6), and (9,9) cantilevered SW-BNNT, we can also conclude that the most sensitive location is the free end of SW-BNNT. Finally, it can also be seen that when the value of additional geometrical parameter ξ = a L is more than 0.6, the differences of frequency shift for (3,3), (6,6), and (9,9) SW-BNNT become smaller and smaller.

Figure 7 Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm for different attached masses.
Figure 7

Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm for different attached masses.

Figure 8 Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm for different attached masses.
Figure 8

Frequency shifts for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm for different attached masses.

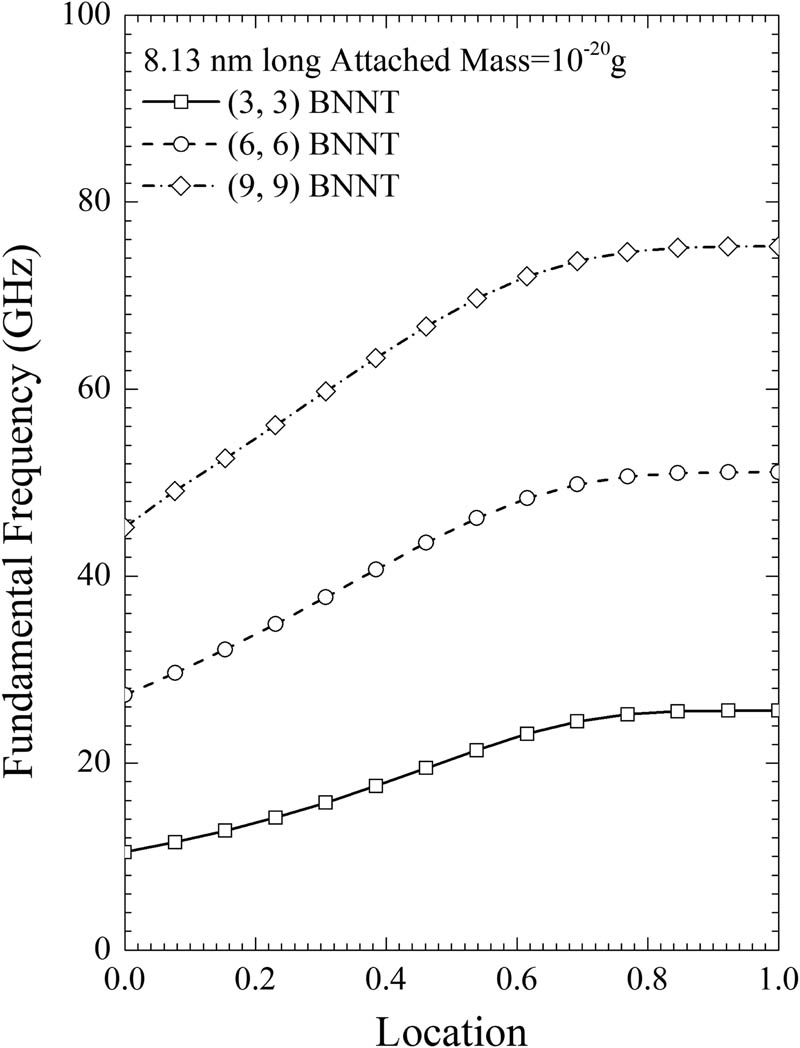
Figure 9 Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with mass of 10−20 g attached at different locations.
Figure 9

Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with mass of 10−20 g attached at different locations.

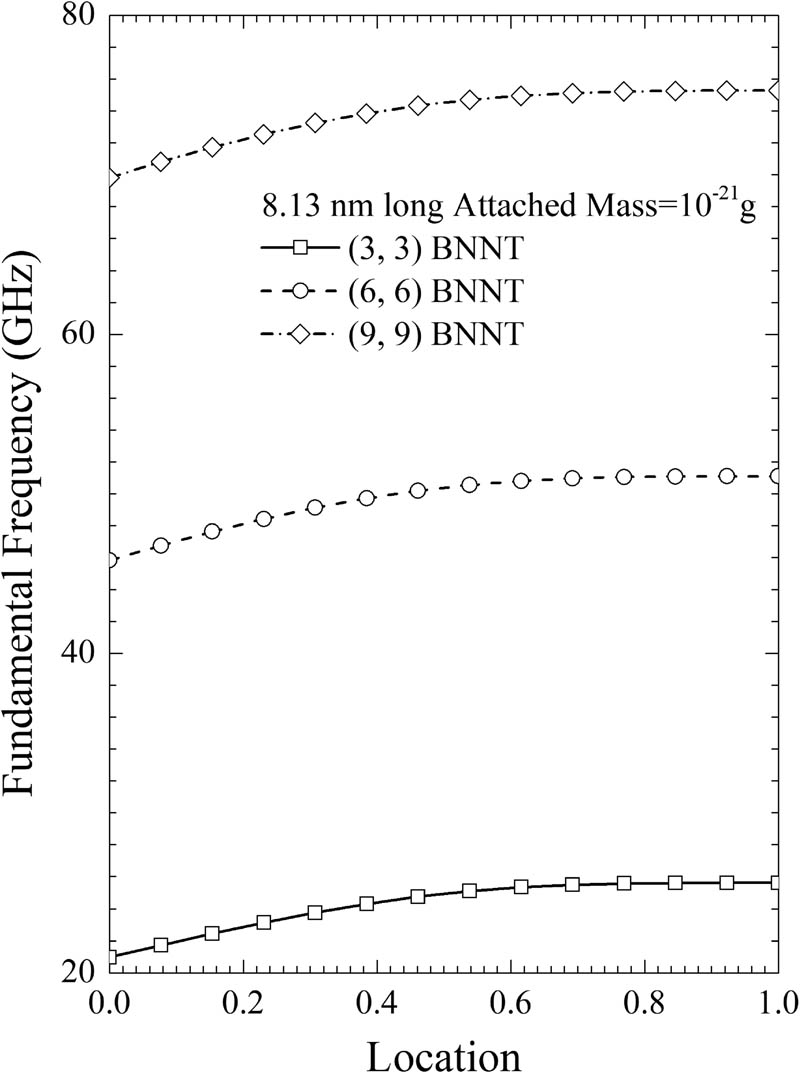
Figure 10 Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with mass of 10−21 g attached at different locations.
Figure 10

Resonant frequencies for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with mass of 10−21 g attached at different locations.

Figure 11 The variations of resonant frequency shift for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with an extra mass of 10−20 g versus different attached positions on the surface.
Figure 11

The variations of resonant frequency shift for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with an extra mass of 10−20 g versus different attached positions on the surface.

Figure 12 The variations of resonant frequency shift for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with an extra mass of 10−21 g versus different attached positions on the surface.
Figure 12

The variations of resonant frequency shift for (3,3), (6,6), and (9,9) cantilevered SW-BNNT with length 8.13 nm with an extra mass of 10−21 g versus different attached positions on the surface.

4 Conclusion

In this article, the potential application of cantilevered SW-BNNT for mass detection was studied based on an atomistic simulation. Results show that the frequencies of SW-BNNT with the extra mass attached on the surface are at extremely high level, and when the lengths of SW-BNNT increase, the frequencies decrease quickly. We also found that the effect of length, of SW-BNNT with the extra mass attached on the surface, on the frequency changes proves that the mass sensitivity of SW-BNNT depends on the tube length. The effect of the attached mass position on the frequency shift is also investigated. Our investigation indicates that the most sensitive location is the free end of SW-BNNT.

  1. Conflict of interest: Author states no conflict of interest.

References

[1] Chopra NG, Luyken RJ, Cherrey K, Crespi VH, Cohen ML, Louie SG, et al. Boron nitride nanotubes. Science. 1995;269(5226):966.10.1126/science.269.5226.966Search in Google Scholar PubMed

[2] Mirhaji E, Afshar M, Rezvani S, Yoosefian M. Boron nitride nanotubes as a nanotransporter for anti-cancer docetaxel drug in water/ethanol solution. J Mol Liq. 2018;271:151–6.10.1016/j.molliq.2018.08.142Search in Google Scholar

[3] Yamakov V, Park C, Kang JH, Chen X, Ke C, Fay C. Piezoelectric and elastic properties of multiwall boron-nitride nanotubes and their fibers: a molecular dynamics study. Comput Mater Sci. 2017;135:29–42.10.1016/j.commatsci.2017.03.050Search in Google Scholar

[4] Yan JW, Tong LH, Xiang P. Free vibration analysis of single-walled boron nitride nanotubes based on a computational mechanics framework. Superlattice Microst. 2017;112:230–48.10.1016/j.spmi.2017.09.028Search in Google Scholar

[5] Giannopoulos GI, Kontoni DPN, Georgantzinos SK. Efficient FEM simulation of static and free vibration behavior of single walled boron nitride nanotubes. Superlattice Microst. 2016;96:111–20.10.1016/j.spmi.2016.05.016Search in Google Scholar

[6] Zhang J, Wang C. Beat vibration of hybrid boron nitride-carbon nanotubes – a new avenue to atomic-scale mass sensing. Comput Mater Sci. 2017;127:270–6.10.1016/j.commatsci.2016.11.014Search in Google Scholar

[7] Wildoer JWG, Venema LC, Rinzler AG, Smalley RE, Dekker C. Electronic structure of atomically resolved carbon nanotubes. Nature. 1998;391(6662):59–62.10.1038/34139Search in Google Scholar

[8] Rubio A, Miyamoto Y, Blase X, Cohen ML, Louie SG. Theoretical study of one-dimensional chains of metal atoms in nanotubes. Phys Rev B. 1996;53(7):4023–6.10.1103/PhysRevB.53.4023Search in Google Scholar PubMed

[9] Serhan M, Abusini M, Almahmoud E, Omari R, Al-Khaza’leh K, Abu-Farsakh H, et al. The electronic properties of different chiralities of defected boron nitride nanotubes: theoretical study. Comput Condens Matter. 2020;22:e00439.10.1016/j.cocom.2019.e00439Search in Google Scholar

[10] Kim M, Lee YH, Oh J-H, Hong S-H, Min B-I, Kim T-H, et al. Synthesis of boron nitride nanotubes using triple DC thermal plasma reactor with hydrogen injection. Chem Eng J. 2020;395:125148.10.1016/j.cej.2020.125148Search in Google Scholar

[11] Zarifi A, Razavizadeh Y, Sadeghi E. Interband faraday rotation in boron nitride nanotubes. Superlattice Microst. 2019;130:297–307.10.1016/j.spmi.2019.05.001Search in Google Scholar

[12] Yoosefian M, Etminan N, Moghani MZ, Mirzaei S, Abbasi S. The role of boron nitride nanotube as a new chemical sensor and potential reservoir for hydrogen halides environmental pollutants. Superlattice Microst. 2016;98:325–31.10.1016/j.spmi.2016.08.049Search in Google Scholar

[13] Chen Y, Zou J, Campbell SJ, Le Caer G. Boron nitride nanotubes: pronounced resistance to oxidation. Appl Phys Lett. 2004;84(13):2430–2.10.1063/1.1667278Search in Google Scholar

[14] Chopra NG, Zettl A. Measurement of the elastic modulus of a multi-wall boron nitride nanotube. Solid State Commun. 1998;105(5):297–300.10.1016/S0038-1098(97)10125-9Search in Google Scholar

[15] Li T, Tang Z, Huang Z, Yu J. A comparison between the mechanical and thermal properties of single-walled carbon nanotubes and boron nitride nanotubes. Phys E Low Dimens Syst Nanostruct. 2017;85:137–42.10.1016/j.physe.2016.08.012Search in Google Scholar

[16] Salavati M, Ghasemi H, Rabczuk T. Electromechanical properties of boron nitride nanotube: atomistic bond potential and equivalent mechanical energy approach. Comput Mater Sci. 2018;149:460–5.10.1016/j.commatsci.2018.03.037Search in Google Scholar

[17] Vaccarini L, Goze C, Henrard L, Hernández E, Bernier P, Rubio A. Mechanical and electronic properties of carbon and boron–nitride nanotubes. Carbon. 2000;38(11):1681–90.10.1016/S0008-6223(99)00293-6Search in Google Scholar

[18] Ansari R, Rouhi S, Mirnezhad M, Aryayi M. Stability characteristics of single-walled boron nitride nanotubes. Arch Civ Mech Eng. 2015;15(1):162–70.10.1016/j.acme.2014.01.008Search in Google Scholar

[19] Jiang L, Guo W. A molecular mechanics study on size-dependent elastic properties of single-walled boron nitride nanotubes. J Mech Phys Solids. 2011;59(6):1204–13.10.1016/j.jmps.2011.03.008Search in Google Scholar

[20] Patra PK, Batra RC. Stress wave propagation in boron-nitride nanotubes. Comput Mater Sci. 2017;130:144–51.10.1016/j.commatsci.2017.01.008Search in Google Scholar

[21] Song J, Huang Y, Jiang H, Hwang KC, Yu MF. Deformation and bifurcation analysis of boron-nitride nanotubes. Int J Mech Sci. 2006;48(11):1197–207.10.1016/j.ijmecsci.2006.06.006Search in Google Scholar

[22] Rezania H, Aghaiimanesh Z. Electronic properties of boron nitride sheet and nanotube in the presence of transverse magnetic field. Phys E Low Dimens Syst Nanostruct. 2015;73:100–4.10.1016/j.physe.2015.05.022Search in Google Scholar

[23] Li C, Chou T-W. Mass detection using carbon nanotube-based nanomechanical resonators. Appl Phys Lett. 2004;84(25):5246–8.10.1063/1.1764933Search in Google Scholar

[24] Ren Q, Zhao YP. Influence of surface stress on frequency of microcantilever-based biosensors. Microsyst Technol. 2005;11(6):456.10.1007/s00542-004-0464-6Search in Google Scholar

[25] Ghorbanpour Arani A, Kolahchi R, Khoddami Maraghi Z. Nonlinear vibration and instability of embedded double-walled boron nitride nanotubes based on nonlocal cylindrical shell theory. Appl Math Model. 2013;37(14):7685–707.10.1016/j.apm.2013.03.020Search in Google Scholar

[26] Aydin M. Vibrational and electronic properties of single-walled and double-walled boron nitride nanotubes. Vib Spectrosc. 2013;66:30–42.10.1016/j.vibspec.2013.01.011Search in Google Scholar

[27] Yi J, Wang L, Zhang Y. Vibration of two-dimensional hexagonal boron nitride. Theor Appl Mech Lett. 2018;8(6):408–14.10.1016/j.taml.2018.06.003Search in Google Scholar

[28] Fakrach B, Rahmani A, Chadli H, Sbai K, Sauvajol JL. Raman spectrum of single-walled boron nitride nanotube. Phys E Low Dimens Syst Nanostruct. 2009;41(10):1800–5.10.1016/j.physe.2009.07.002Search in Google Scholar

[29] Selvamani R, Jayan MMS, Dimitri R, Tornabene F, Ebrahimi F. Nonlinear magneto-thermo-elastic vibration of mass sensor armchair carbon nanotube resting on an elastic substrate. Curved Layer Struct. 2020;7(1):153–65.10.1515/cls-2020-0012Search in Google Scholar

[30] Tersoff J. New empirical approach for the structure and energy of covalent systems. Phys Rev B. 1988;37(12):6991–7000.10.1103/PhysRevB.37.6991Search in Google Scholar PubMed

[31] Oh ES. Elastic properties of boron-nitride nanotubes through the continuum lattice approach. Mater Lett. 2010;64(7):859–62.10.1016/j.matlet.2010.01.041Search in Google Scholar

[32] Yan JW, Liew KM. Predicting elastic properties of single-walled boron nitride nanotubes and nanocones using an atomistic-continuum approach. Compos Struct. 2015;125:489–98.10.1016/j.compstruct.2015.02.043Search in Google Scholar
Received: 2021-04-19
Revised: 2021-06-16
Accepted: 2021-07-05
Published Online: 2021-07-23

© 2021 JinRu Zhong, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Effects of Material Constructions on Supersonic Flutter Characteristics for Composite Rectangular Plates Reinforced with Carbon Nano-structures
  2. Processing of Hollow Glass Microspheres (HGM) filled Epoxy Syntactic Foam Composites with improved Structural Characteristics
  3. Investigation on the anti-penetration performance of the steel/nylon sandwich plate
  4. Flexural bearing capacity and failure mechanism of CFRP-aluminum laminate beam with double-channel cross-section
  5. In-Plane Permeability Measurement of Biaxial Woven Fabrics by 2D-Radial Flow Method
  6. Regular Articles
  7. Real time defect detection during composite layup via Tactile Shape Sensing
  8. Mechanical and durability properties of GFRP bars exposed to aggressive solution environments
  9. Cushioning energy absorption of paper corrugation tubes with regular polygonal cross-section under axial static compression
  10. An investigation on the degradation behaviors of Mg wires/PLA composite for bone fixation implants: influence of wire content and load mode
  11. Compressive bearing capacity and failure mechanism of CFRP–aluminum laminate column with single-channel cross section
  12. Self-Fibers Compacting Concrete Properties Reinforced with Propylene Fibers
  13. Study on the fabrication of in-situ TiB2/Al composite by electroslag melting
  14. Characterization and Comparison Research on Composite of Alluvial Clayey Soil Modified with Fine Aggregates of Construction Waste and Fly Ash
  15. Axial and lateral stiffness of spherical self-balancing fiber reinforced rubber pipes under internal pressure
  16. Influence of technical parameters on the structure of annular axis braided preforms
  17. Nano titanium oxide for modifying water physical property and acid-resistance of alluvial soil in Yangtze River estuary
  18. Modified Halpin–Tsai equation for predicting interfacial effect in water diffusion process
  19. Experimental research on effect of opening configuration and reinforcement method on buckling and strength analyses of spar web made of composite material
  20. Photoluminescence characteristics and energy transfer phenomena in Ce3+-doped YVO4 single crystal
  21. Influence of fiber type on mechanical properties of lightweight cement-based composites
  22. Mechanical and fracture properties of steel fiber-reinforced geopolymer concrete
  23. Handcrafted digital light processing apparatus for additively manufacturing oral-prosthesis targeted nano-ceramic resin composites
  24. 3D printing path planning algorithm for thin walled and complex devices
  25. Material-removing machining wastes as a filler of a polymer concrete (industrial chips as a filler of a polymer concrete)
  26. The electrochemical performance and modification mechanism of the corrosion inhibitor on concrete
  27. Evaluation of the applicability of different viscoelasticity constitutive models in bamboo scrimber short-term tensile creep property research
  28. Experimental and microstructure analysis of the penetration resistance of composite structures
  29. Ultrasensitive analysis of SW-BNNT with an extra attached mass
  30. Active vibration suppression of wind turbine blades integrated with piezoelectric sensors
  31. Delamination properties and in situ damage monitoring of z-pinned carbon fiber/epoxy composites
  32. Analysis of the influence of asymmetric geological conditions on stability of high arch dam
  33. Measurement and simulation validation of numerical model parameters of fresh concrete
  34. Tuning the through-thickness orientation of 1D nanocarbons to enhance the electrical conductivity and ILSS of hierarchical CFRP composites
  35. Performance improvements of a short glass fiber-reinforced PA66 composite
  36. Investigation on the acoustic properties of structural gradient 316L stainless steel hollow spheres composites
  37. Experimental studies on the dynamic viscoelastic properties of basalt fiber-reinforced asphalt mixtures
  38. Hot deformation behavior of nano-Al2O3-dispersion-strengthened Cu20W composite
  39. Synthesize and characterization of conductive nano silver/graphene oxide composites
  40. Analysis and optimization of mechanical properties of recycled concrete based on aggregate characteristics
  41. Synthesis and characterization of polyurethane–polysiloxane block copolymers modified by α,ω-hydroxyalkyl polysiloxanes with methacrylate side chain
  42. Buckling analysis of thin-walled metal liner of cylindrical composite overwrapped pressure vessels with depressions after autofrettage processing
  43. Use of polypropylene fibres to increase the resistance of reinforcement to chloride corrosion in concretes
  44. Oblique penetration mechanism of hybrid composite laminates
  45. Comparative study between dry and wet properties of thermoplastic PA6/PP novel matrix-based carbon fibre composites
  46. Experimental study on the low-velocity impact failure mechanism of foam core sandwich panels with shape memory alloy hybrid face-sheets
  47. Preparation, optical properties, and thermal stability of polyvinyl butyral composite films containing core (lanthanum hexaboride)–shell (titanium dioxide)-structured nanoparticles
  48. Research on the size effect of roughness on rock uniaxial compressive strength and characteristic strength
  49. Research on the mechanical model of cord-reinforced air spring with winding formation
  50. Experimental study on the influence of mixing time on concrete performance under different mixing modes
  51. A continuum damage model for fatigue life prediction of 2.5D woven composites
  52. Investigation of the influence of recyclate content on Poisson number of composites
  53. A hard-core soft-shell model for vibration condition of fresh concrete based on low water-cement ratio concrete
  54. Retraction
  55. Thermal and mechanical characteristics of cement nanocomposites
  56. Influence of class F fly ash and silica nano-micro powder on water permeability and thermal properties of high performance cementitious composites
  57. Effects of fly ash and cement content on rheological, mechanical, and transport properties of high-performance self-compacting concrete
  58. Erratum
  59. Inverse analysis of concrete meso-constitutive model parameters considering aggregate size effect
  60. Special Issue: MDA 2020
  61. Comparison of the shear behavior in graphite-epoxy composites evaluated by means of biaxial test and off-axis tension test
  62. Photosynthetic textile biocomposites: Using laboratory testing and digital fabrication to develop flexible living building materials
  63. Study of gypsum composites with fine solid aggregates at elevated temperatures
  64. Optimization for drilling process of metal-composite aeronautical structures
  65. Engineering of composite materials made of epoxy resins modified with recycled fine aggregate
  66. Evaluation of carbon fiber reinforced polymer – CFRP – machining by applying industrial robots
  67. Experimental and analytical study of bio-based epoxy composite materials for strengthening reinforced concrete structures
  68. Environmental effects on mode II fracture toughness of unidirectional E-glass/vinyl ester laminated composites
  69. Special Issue: NCM4EA
  70. Effect and mechanism of different excitation modes on the activities of the recycled brick micropowder
https://doi.org/10.1515/secm-2021-0038
Keywords for this article
ultrasensitive analysis; vibration; atomistic simulation; SW-BNNT
Creative Commons
BY 4.0

Articles in the same Issue

  1. Effects of Material Constructions on Supersonic Flutter Characteristics for Composite Rectangular Plates Reinforced with Carbon Nano-structures
  2. Processing of Hollow Glass Microspheres (HGM) filled Epoxy Syntactic Foam Composites with improved Structural Characteristics
  3. Investigation on the anti-penetration performance of the steel/nylon sandwich plate
  4. Flexural bearing capacity and failure mechanism of CFRP-aluminum laminate beam with double-channel cross-section
  5. In-Plane Permeability Measurement of Biaxial Woven Fabrics by 2D-Radial Flow Method
  6. Regular Articles
  7. Real time defect detection during composite layup via Tactile Shape Sensing
  8. Mechanical and durability properties of GFRP bars exposed to aggressive solution environments
  9. Cushioning energy absorption of paper corrugation tubes with regular polygonal cross-section under axial static compression
  10. An investigation on the degradation behaviors of Mg wires/PLA composite for bone fixation implants: influence of wire content and load mode
  11. Compressive bearing capacity and failure mechanism of CFRP–aluminum laminate column with single-channel cross section
  12. Self-Fibers Compacting Concrete Properties Reinforced with Propylene Fibers
  13. Study on the fabrication of in-situ TiB2/Al composite by electroslag melting
  14. Characterization and Comparison Research on Composite of Alluvial Clayey Soil Modified with Fine Aggregates of Construction Waste and Fly Ash
  15. Axial and lateral stiffness of spherical self-balancing fiber reinforced rubber pipes under internal pressure
  16. Influence of technical parameters on the structure of annular axis braided preforms
  17. Nano titanium oxide for modifying water physical property and acid-resistance of alluvial soil in Yangtze River estuary
  18. Modified Halpin–Tsai equation for predicting interfacial effect in water diffusion process
  19. Experimental research on effect of opening configuration and reinforcement method on buckling and strength analyses of spar web made of composite material
  20. Photoluminescence characteristics and energy transfer phenomena in Ce3+-doped YVO4 single crystal
  21. Influence of fiber type on mechanical properties of lightweight cement-based composites
  22. Mechanical and fracture properties of steel fiber-reinforced geopolymer concrete
  23. Handcrafted digital light processing apparatus for additively manufacturing oral-prosthesis targeted nano-ceramic resin composites
  24. 3D printing path planning algorithm for thin walled and complex devices
  25. Material-removing machining wastes as a filler of a polymer concrete (industrial chips as a filler of a polymer concrete)
  26. The electrochemical performance and modification mechanism of the corrosion inhibitor on concrete
  27. Evaluation of the applicability of different viscoelasticity constitutive models in bamboo scrimber short-term tensile creep property research
  28. Experimental and microstructure analysis of the penetration resistance of composite structures
  29. Ultrasensitive analysis of SW-BNNT with an extra attached mass
  30. Active vibration suppression of wind turbine blades integrated with piezoelectric sensors
  31. Delamination properties and in situ damage monitoring of z-pinned carbon fiber/epoxy composites
  32. Analysis of the influence of asymmetric geological conditions on stability of high arch dam
  33. Measurement and simulation validation of numerical model parameters of fresh concrete
  34. Tuning the through-thickness orientation of 1D nanocarbons to enhance the electrical conductivity and ILSS of hierarchical CFRP composites
  35. Performance improvements of a short glass fiber-reinforced PA66 composite
  36. Investigation on the acoustic properties of structural gradient 316L stainless steel hollow spheres composites
  37. Experimental studies on the dynamic viscoelastic properties of basalt fiber-reinforced asphalt mixtures
  38. Hot deformation behavior of nano-Al2O3-dispersion-strengthened Cu20W composite
  39. Synthesize and characterization of conductive nano silver/graphene oxide composites
  40. Analysis and optimization of mechanical properties of recycled concrete based on aggregate characteristics
  41. Synthesis and characterization of polyurethane–polysiloxane block copolymers modified by α,ω-hydroxyalkyl polysiloxanes with methacrylate side chain
  42. Buckling analysis of thin-walled metal liner of cylindrical composite overwrapped pressure vessels with depressions after autofrettage processing
  43. Use of polypropylene fibres to increase the resistance of reinforcement to chloride corrosion in concretes
  44. Oblique penetration mechanism of hybrid composite laminates
  45. Comparative study between dry and wet properties of thermoplastic PA6/PP novel matrix-based carbon fibre composites
  46. Experimental study on the low-velocity impact failure mechanism of foam core sandwich panels with shape memory alloy hybrid face-sheets
  47. Preparation, optical properties, and thermal stability of polyvinyl butyral composite films containing core (lanthanum hexaboride)–shell (titanium dioxide)-structured nanoparticles
  48. Research on the size effect of roughness on rock uniaxial compressive strength and characteristic strength
  49. Research on the mechanical model of cord-reinforced air spring with winding formation
  50. Experimental study on the influence of mixing time on concrete performance under different mixing modes
  51. A continuum damage model for fatigue life prediction of 2.5D woven composites
  52. Investigation of the influence of recyclate content on Poisson number of composites
  53. A hard-core soft-shell model for vibration condition of fresh concrete based on low water-cement ratio concrete
  54. Retraction
  55. Thermal and mechanical characteristics of cement nanocomposites
  56. Influence of class F fly ash and silica nano-micro powder on water permeability and thermal properties of high performance cementitious composites
  57. Effects of fly ash and cement content on rheological, mechanical, and transport properties of high-performance self-compacting concrete
  58. Erratum
  59. Inverse analysis of concrete meso-constitutive model parameters considering aggregate size effect
  60. Special Issue: MDA 2020
  61. Comparison of the shear behavior in graphite-epoxy composites evaluated by means of biaxial test and off-axis tension test
  62. Photosynthetic textile biocomposites: Using laboratory testing and digital fabrication to develop flexible living building materials
  63. Study of gypsum composites with fine solid aggregates at elevated temperatures
  64. Optimization for drilling process of metal-composite aeronautical structures
  65. Engineering of composite materials made of epoxy resins modified with recycled fine aggregate
  66. Evaluation of carbon fiber reinforced polymer – CFRP – machining by applying industrial robots
  67. Experimental and analytical study of bio-based epoxy composite materials for strengthening reinforced concrete structures
  68. Environmental effects on mode II fracture toughness of unidirectional E-glass/vinyl ester laminated composites
  69. Special Issue: NCM4EA
  70. Effect and mechanism of different excitation modes on the activities of the recycled brick micropowder
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/secm-2021-0038/html
Scroll to top button