Abstract
New generation non-crimp fabric (NCF) offers an attractive thin and lightweight building block alternative in the design of composite materials and structures. Pre-assembly of multiple plies of parallel fibers, each laying in a different orientation would not require crimping of the fibers and would enable one-axis lay-up that can substantially reduce the labor, scrap, and manufacturing costs. A state-of-the-art tow-spreading technique enables ply thickness to be reduced to as low as one-third of the typical commercial high quality pre-preg ply thickness. The thin-ply NCF stacks result in well-dispersed plies of different fiber orientations and creates the so-called homogenized laminates without ply clustering. As an option, bi-angle thin-ply NCF offers two different fiber orientations with one being off-axis, e.g. at ϕ°, along with an on-axis 0° forming (0/ϕ) assembly. This allows to design in anisotropic properties within the NCF building block. An overview of several aspects of the thin-ply bi-angle NCF composites is provided to address associated benefits and opportunities in the lightweight structural composites design process.
- Nomenclature
- 1−2
material coordinate system for a given ply
- x−y
general coordinate system for sub-laminate/laminate
- ϕ
fiber orientation angle in a given ply with respect to x-axis
- E1, E2, ν12,, G12
UD ply material properties
- Ex (GPa)
sub-laminate (homogenized/equivalent) stiffness in x
- Ey (GPa)
sub-laminate (homogenized/equivalent) stiffness in y
- Gxy (GPa)
sub-laminate (homogenized/equivalent) shear stiffness in x−y system
- νxy
sub-laminate (homogenized/equivalent) Poisson’s Ratio in x−y system
- X (MPa)
sub-laminate (homogenized/equivalent) tensile strength in x
- Xʹ (MPa)
sub-laminate (homogenized/equivalent) compressive strength in x
- Y (MPa)
sub-laminate (homogenized/equivalent) tensile strength in y
- Yʹ (MPa)
sub-laminate (homogenized/equivalent) compressive strength in y
- S, Sʹ (MPa)
sub-laminate (homogenized/equivalent) shear strength in x−y system
- εx
extensional (on-axis) strain component in x−y system
- γxy
in-plane shear strain component in x−y system
- σx, σy, σxy
in-plane stress state in x−y system
- px (N/mm)
distributed axial load
- pz (N/mm)
distributed lateral load
- mx (N)
distributed twisting moment
- my (N)
distributed bending moment
- dtip (mm)
lateral tip displacement
1 Introduction
Among the variety of reinforcement architectures in structural composite materials, non-crimp fabric (NCF) has become an attractive building block for versatile composite design in many engineering challenges. As an assembly strategy for non-crimped unidirectional (UD) plies, NCF reduces labor by enabling one-axis lay-up, in addition to reducing scrap and manufacturing costs [1]. However, the process may yield distinct fiber bundles that have ellipsoid-like cross-section and separated by resin-rich pockets (Figure 1A). Substantial work evaluating the structure and mechanical properties of NCF-based structural composites has already been reported using multi-scale modeling and experimentation [2], [3], [4], [5], [6], [7], [8].
![Figure 1: Image of laminate cross sections.Note the scale and relative size of resin-rich pockets: (A) ordinary NCFs; (B) Thin-ply NCFs (Courtesy of ADVAERO Technologies and Prof. Stephen W. Tsai, Stanford University Composite Design Workshop lecture notes [35]).](/document/doi/10.1515/secm-2015-0386/asset/graphic/j_secm-2015-0386_fig_001.jpg)
Image of laminate cross sections.
Note the scale and relative size of resin-rich pockets: (A) ordinary NCFs; (B) Thin-ply NCFs (Courtesy of ADVAERO Technologies and Prof. Stephen W. Tsai, Stanford University Composite Design Workshop lecture notes [35]).
As Edgren et al. [9] had suggested, typical areal weight and corresponding ply thickness of NCFs are already higher than conventional high-performance pre-preg plies. A new generation of NCF with thin plies are realized by tow spreading technology (Figure 2), yielding for instance thin plies of NCF with half the thickness of a typical high-performance UD ply (75 g/m2 vs. 150 g/m2, respectively). During production of the thin-plied NCF-based composites, the problem of large ellipsoid tow bundles separated by resin pockets can be eliminated to a larger extent (see Figure 1B). Their stack forms a fine through-the-thickness dispersion of the plies of different fiber orientations and creates the so-called herein homogenized laminates without ply clustering. Table 1 summarizes the potential consequences of manufacturing NCFs as of thin plies, while providing a list of the advantages and disadvantages of the structural NCF composites. The objective of this article is to provide an overview of the thin-ply NCF and a perspective on the design of the NCF building block itself, along with its effective implementation in the analysis and design of the structural composites.
![Figure 2: (A) Tow-spreading technique [15]; (B) Bi-angle thin-ply NCF pre-preg C-ply™ with Aldila’s AR2527 resin: (−45/0) (left) and its flipped-over look as (0/45) (right).](/document/doi/10.1515/secm-2015-0386/asset/graphic/j_secm-2015-0386_fig_002.jpg)
(A) Tow-spreading technique [15]; (B) Bi-angle thin-ply NCF pre-preg C-ply™ with Aldila’s AR2527 resin: (−45/0) (left) and its flipped-over look as (0/45) (right).
Overview of pros and cons associated with the use of NCF building block and potential improvements by the thin-ply feature.
| Pros | Cons | Potent against the cons |
|---|---|---|
| Homogenized laminates are practical | Limited fiber orientations | Customized NCF building block for efficient design is possible |
| One axis lay-ups reduce the materials scrap and labor cost | Handling of a thick material block, draping | Thin-ply NCFs by tow-spreading |
| NCF tapes can be adapted into automated tape laying | Fiber discontinuities on the off-axis plies | Efficient and smart staggering schemes may be explored |
| Customized building block or sub-laminate can be readily available | Typical available NCFs are 0/90, 45/−45 and quasi-isotropic | [0/ϕ] anisotropic bi-angle and [0/ϕ/−ϕ] three-angle thin-ply NCFs are also possible |
| Easy to characterize: testing of homogenized building block for strength. | Depending on the number of fiber orientations, flipping over or rotating does not provide symmetry if needed | With the thin plies and homogenized layups, symmetry constraint becomes less critical. Building block or sub-laminate stacking is also inherent |
| Accurate failure envelopes can be readily available for design | Properties for ply-by-ply analysis may be lacking | Basic testing scheme for back calculation of the ply data |
2 Why a thin-ply NCF building block?
Because microscopic damage accumulation in UD fiber composites is sensitive to the thickness of fiber orientation in a continuous stack [10], [11], the thin-ply concept was originally introduced as individual UD plies [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22]. By incorporating a technique called tow-spreading, Sasayama et al. [12] at Fukui Technology Center were able to spread the carbon fiber tows (see Figure 2) without inducing any stress to the individual fibers, eliminating the risk of fiber damage. The process involved blowing air across a 12 k or 24 k tow to create thin plies down to about 1/6 of the conventional 0.12 mm (5 mil) ply thickness [12], [13], [14], [15]. Experimental results in support of the benefit from tow-spread thin-plies have been reported. For instance, Yamaguchi and Hahn [16] investigated and reported increased resistance to the matrix crack accumulation and improved the fatigue life of thin-ply carbon fiber reinforced polymer laminates in tension. Sihn et al. [15] also studied damage resistance against static and fatigue tensile loading and demonstrated the improvement associated with the use of thin-ply UD pre-preg materials. The thin-ply pre-pregs were also shown to be useful for enhancing the compressive strength and impact resistance [17]. More recently Yokozeki et al. [18] reported that the standard ply laminates subject to out-of-plane transverse loadings by indentation exhibited increased delamination and matrix cracks, whereas thin-ply laminates ultimately failed by sudden fiber fractures. Saito et al. [19] evaluated the thin-plied quasi-isotropic laminates with regard to damage accumulation and progression. They followed an experimental procedure focused on compression after impact and incorporated ultrasonic scanning and sectional fractography for their assessments. They reported a strength increase of 23% with significantly reduced transverse crack density. The group also extended their assessments by computational stress analysis [20]. The simulations showed that stresses leading to crack progression were smaller within the thin plies in the vicinity of the adjacent layers. In another recent work, Amacher et al. [21] elaborated on the effect of ply thickness by covering a range of pre-pregs of 30–300 gsm (g/m2) fiber areal density by North Thin Ply Technology (Renens, Switzerland). They reported experimental findings on tension, open-hole compression, and open-hole tensile fatigue tests on quasi-isotropic laminates. The results also suggest that decreasing the ply thickness can improve the strength and on-set of damage characteristics significantly. Wisnom [22] indicated that there may be a trade-off between the damage mode and strength in some cases, and dispersion of the fiber orientations may alter the ultimate strength, e.g. [0/45/90/–45]4s vs. [02/452/902/–452]2s vs. [04/454/904/–454]s. This is attributed to the fact that well-dispersed plies (an equivalent effect of the thin-ply concept) eliminate the delamination and the failure mode is dominated by the fiber failure. The delamination, however, may serve to blunt the stress concentrated states and increase the ultimate strength in the existence of stress-raisers. In other words, it is imperative to discuss and assess the effect of the spatial dispersion of the ply orientations in terms of the applied driving loads, material discontinuities, and the associated stress-state characteristics. This can be noted also by the work of Shin et al. [15]. The experimental findings [15], [18], [22] suggested that the thin-ply is to delay, if not to eliminate, the microcracks-driven failure modes and free-edge delamination.
With the technology of the tow-spreading (Figure 2) integrated into multi-axial dry reinforcement production lines (e.g. Chomarat, Le Cheylard, France and Metyx Composites, Istanbul, Turkey), the thin-ply NCF choices have been available. Figure 1 shows a comparison of a traditional NCF vs. a thin-ply NCF laminate. Note that the size of the resin-rich pockets between the spread tows is one order of magnitude smaller than with the regular ellipsoid-like bundle NCFs. With the availability of the commercial materials, thin-plied NCF studies emerged in recent years [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33]. Artiero et al. [28], for instance, demonstrated the suppression of the damage mechanisms and increase in strength due to the choice of thin-plied NCF. More recently, Guillamet et al. [29] contributed to the understanding of the benefit by making the NCF thinner plied as they focused particularly on the onset of damage mechanisms at the free-edges.
In addition to the thinner plies, another intriguing feature can be realized by making the building block NCF as the unbalanced bi-angle, i.e. composed of on- and off-axis fiber orientations [23], [24]. The commercial bi-angle NCF, the so-called C-ply™ (by Chomarat) delivers a sub-laminate of (0/45) or (–45/0) in about 0.125 mm cured thickness. The consequence is that one can actually achieve reinforcement in two distinct orientations within a typical UD ply thickness, and can take several significant advantages of fiber orientations being well dispersed in making laminates, such as the:
suppressed microcracks ( see later in Figure 7),
availability of customized anisotropic building blocks arguably for more efficient design, and
possibility for one axis lay-up, reducing the lay-up time and materials scrap.
3 Designing the NCF building block
The fixed building block or sub-laminate-based design has been a somewhat constrained option, as the ply-orientations are typically 0°, 90°, 45°, −45° combinations, despite the fact that many other ply combinations are possible for NCFs. One of the ideas that has not been considered sufficiently in the open literature is the possibility of a custom-selected NCF building block by design. The building block may be of two types: a conventional balanced (and/or orthotropic) design and an “unconventional” anisotropic design.
3.1 Conventional NCF building block
The typical and conventional NCF building block choices seem to be angle-ply, cross-ply, and/or combinations thereof, which all result in a balanced and/or orthotropic building block [e.g. (45/−45), (0/90), and (0/45/90/−45), respectively]. The balanced/orthotropic designs to start with are also useful for implementing the general design of an NCF building block. It is because one requires nominal ply data for the NCF design process, such as in CLT-based (classical lamination theory [34]) calculations/predictions on the mechanical behavior of the NCF building block. And the ply properties can be back-calculated from the data of a baseline, somewhat more traditional NCF configuration, which enables arguably more reliable coupon test data.
A UD ply may also be produced with the NCF machines by laying the fiber tows in parallel and stitching for the planar stability of the tows. This procedure, for instance, was reported for a carbon/epoxy material [25]. Although it was a direct method for obtaining the single ply data, the stitching and tow placement are not necessarily the best representation of an optimized multi-angle NCF production that may be the primary goal. Stabilizing a UD ply of the tows may require a nonwoven mat and/or somewhat heavier stitching than what may be the optimal and minimally intrusive stitching of a multi-angle/layer NCFs. Unlike in a single UD NCF ply, multi-angle plies assist each other in stabilizing the tows within themselves. Therefore, multi-angle NCFs, for instance an angle-ply balanced NCF of (±ϕ) fiber orientations and preferably with a shallow angle ϕ, may be used to make test coupons and back-calculate the UD equivalent ply data, as the associated stitching would be more representative.
The following approach for the back-calculation of the nominal ply properties can be incorporated: (i) prepare NCF-made laminates and characterize them for the laminate mechanical properties (ExEy, νxy, Gxy); (ii) suggest ranges for nominal UD ply parameters (E1, E2, ν12,, G12) and calculate the laminate stiffness parameters for the tested lay-ups using CLT; and (iii) compare with the available test data to determine the ply properties which result in the best correlated predictions. Figure 3 shows an illustration of the procedure. For the selected ranges of E1 and E2, predicted contour bands of different laminate properties capturing the associated experimental findings on the tested laminates can be overlapped. This enables one to zoom-in to the nominal ply property settings which can correlate all the test data reasonably well. This approach can also be adopted for the strength parameters by incorporating failure predictions, for instance by the Tsai-Wu failure criterion.
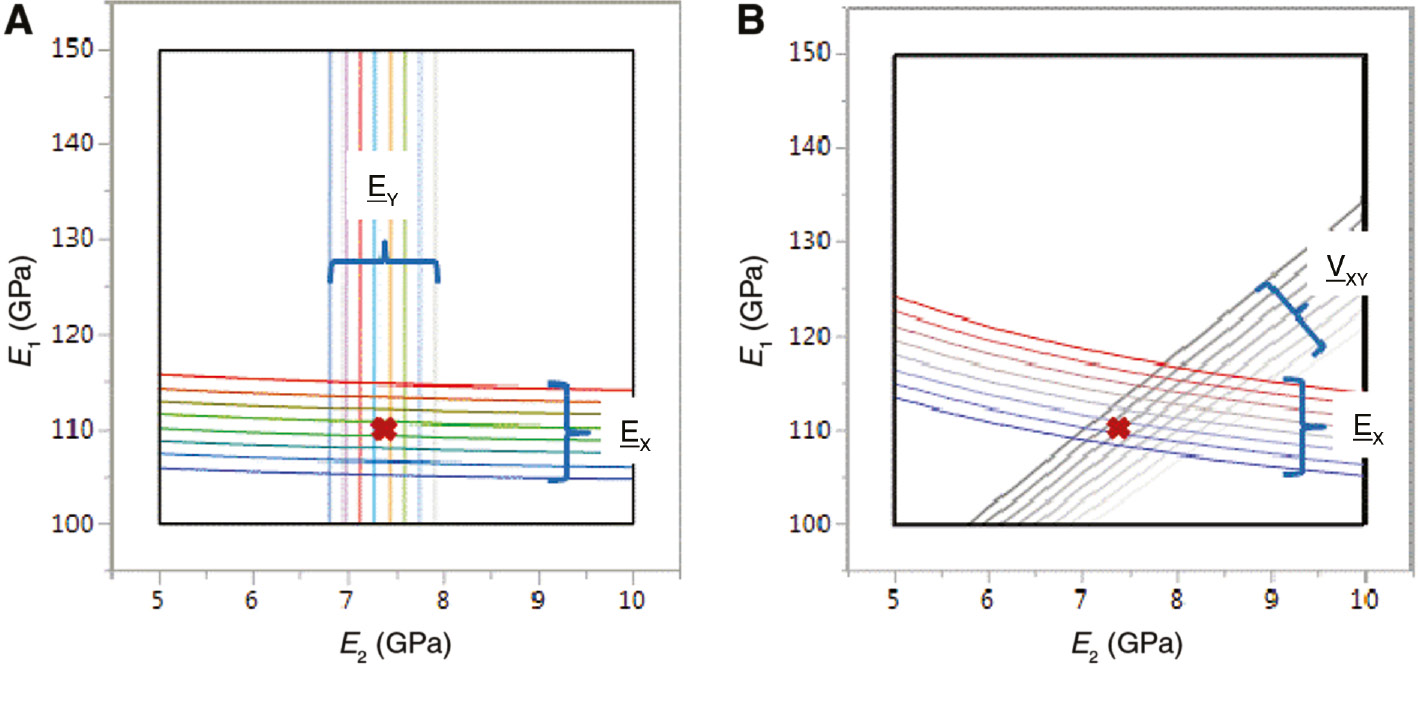
Illustration of the approach to back-calculate nominal UD ply data due to available NCF-made laminate mechanical properties.
Contours represent estimated range of laminate longitudinal modulus, Ex transverse modulus Ey and Poisson’s ratio νxy as function of the ply moduli covering the experimental data of the laminates, say (A) laminate (±ϕ1), and (B) laminate (0/±ϕ2/0). Red cross indicates the selected ply moduli, E1 and E2 which best predicts the available test data of the laminates.
In the work of the Stanford Composite Design Group focusing on the thin-ply NCF, test coupons of C-ply™/epoxy were made available by using various manufacturing techniques [25], [26], [27]. The laminates tested were of (±12.5), (±22.5), (0/±25/0), and (0/±45/0) thin-ply NCF building blocks. Back-calculated nominal carbon fiber (0)-ply stiffness and strength parameters were reported in Refs. [28], [31], which are also included in the second column of Table 2.
T700/epoxy C-ply™ NCF’s ply [28], [31] and sub-laminate (homogenized laminate) properties (Vf=0.50).
| [0]a | [0/25] | [0/25]b | [0/±25/0] | [0/±25/0]b | [0/±45/90] | [0/±45/90]b | |
|---|---|---|---|---|---|---|---|
| Ex (GPa) | 110 | 70.3 | 63.5 | 85.2 | 74.8 | 42.6 | 38.1 |
| Ey (GPa) | 7.4 | 8.0 | 5.0 | 8.6 | 2.9 | 42.6 | 39.2 |
| νxy | 0.30 | 0.47 | 0.60 | 0.98 | 2.2 | 0.31 | 0.30 |
| Gxy (GPa) | 4.2 | 8.0 | 6.6 | 11.3 | 8.9 | 16.3 | 15.3 |
| X (MPa) | 2300 | 718 | 862 | 1293 | 1293 | 393 | 797 |
| Xʹ (MPa) | 1500 | 666 | 745 | 641 | 641 | 609 | 609 |
| Y (MPa) | 66 | 71 | 71 | 78 | 93 | 393 | 797 |
| Yʹ (MPa) | 220 | 221 | 221 | 230 | 230 | 609 | 332 |
| S (MPa) | 93 | 209 | 209 | 188 | 248 | 255 | 255 |
| Sʹ (MPa) | 93 | 101 | 112 | 188 | 248 | 255 | 255 |
ax–y (Global) and 1–2 (material) coordinate systems are identical.
bCorresponds to LPF parameters.
With these nominal ply properties incorporated, the stiffness and strength parameters of two NCF sub-laminate families, namely (±ϕ) and (0/±ϕ/0), were predicted as a function of the off-axis fiber orientation angle ϕ via classical lamination theory and the micromechanics-based MicMac toolset [34], [35]. This exercise is simply equivalent to the design of the NCF building block. Figure 4 presents typical balanced/orthotropic-like (no extension-shear coupling) NCF design curves for sub-laminate stiffness and strength. They also include the test data from four coupons: sub-laminates by (±12.5), (±22.5), (0/±25/0), and (0/±45/0) NCFs [27].
3.2 Anisotropy in NCF building block: unconventional and intriguing for design
One of the features in NCFs, deserving emphasis is that the building block NCF can be designed to introduce anisotropy inherently [23], [24]. That is, a choice of the ply orientations can make a highly anisotropic building block NCF, such as (0/25), (0/45) orientations (shown in Figure 2B). Their stacks or repeats then translate into an anisotropic, homogenized laminate (as discussed in the next section). The anisotropy is typically due to the unbalanced off-axis fiber orientation ϕ along with the 0-degree ply forming the (0/ϕ) NCF. This building block results in shear-extension coupling. Figure 5 shows how shear-extension coupling is induced on homogenized laminates of an anisotropic (0/ϕ) NCF as opposed to a (0/ϕ/–ϕ) NCF building block, subject to the plane stress state of combined normal and shear stresses. When the applied stress state is uniaxial (σx≠0, σxy/σx=0), no shear, but an extensional normal strain, γxy/εx=0 results for the balanced NCF building block regardless of the off-axis ply angle ϕ (Figure 5A). In contrast, when the sub-laminate is unbalanced, the γxy/εx ratio is nonzero and depends on the off-axis ply angle ϕ due to the nonzero shear-extension stiffness coupling (Figure 5B). Figure 5B also indicates the stress ratio being positive or negative will result in differences in the absolute magnitude of the strain ratio, unlike in the sub-laminate of balanced off-axis plies. The in-plane extension-shear coupling due to anisotropy and associated strain dependence can be tailored by the design of the NCF that can translate into the laminate design for deformation, as discussed in the upcoming sections.

Ratio of γxy : in-plane shear strain component and εx: extensional (on-axis) strain component as a result of applied shear-normal stresses.
Shear-extensional strain ratio for (A) (0/ϕ/−ϕ) balanced, orthotropic-like NCF; (B) (0/ϕ) anisotropic NCF.
One can also exemplify the potential benefit of the custom design NCF building block by comparing the most traditional quasi-isotropic [π/4=(0/45/90/−45)] design against shallow off-axis angle (ϕ) NCF configurations. Figure 6 provides Tsai-Wu failure surfaces under combined stress states. The contour plot was tailored so that the stress-states stand out, where the shallow angle designs are safer than the π/4 design. Considering the stress-ratios on the plot, these colored regions (corresponding to the failure surface towers) suggest that the shallow angle NCF designs are likely to outperform the π/4 design for highly slender structural problems.

Comparison of Tsai-Wu failure surfaces for laminates of QI: (0/45/90/−45), (0/±25/0), and (0/25) stacks.
4 Homogenization at the laminate level: well-dispersed fiber orientations by NCF sub-laminate stacking
The homogenization at the laminate level can be better discussed by normalizing the laminate stiffness matrices. Tsai [34] suggested normalization so that laminate normalized stiffness components have the same unit (in Pa for instance):
where h is the total laminate thickness, A, B and D are the laminate’s extensional, extension-bending coupling and bending stiffness matrices, respectively.
As the use of NCF inherently suggests, fixed building block or sub-laminate of several fiber orientations, typically two to four angles, are stacked repeatedly in the construction of composite structures. The number of repeats of the sub-laminate and the thickness associated with each of the distinct orientations are two determining factors in the definition of the homogenization through the thickness, or at the laminate level. The homogenized laminates are expected to provide a dispersion of the distinct fiber orientations. Figure 7 schematically describes how the plies of distinct orientations can be dispersed, such that the laminates become homogenized through the thickness. Repeat index ‘r’ increases the dispersion of the distinct ply orientations or building blocks relative to the total thickness. The laminate becomes more of an equivalent homogenized material at the laminate level, for which normalized extensional and bending stiffness matrices are equal, [A*]=[D*] [34]. The homogenized laminates can thus be easier to produce at a reduced total thickness, giving rise to the salient characteristic of a thin-ply NCF.

Representation of homogenized laminates and the dispersion of distinct fiber orientations as the repeat ‘r’ increases, red curves for anticipated crack stopping characteristics (top).
Description of building block approach and homogenized laminate thickness (bottom).
Homogenization at the laminate level leads to various benefits for composite design not readily possible with the traditional heterogeneous approach. Because bi-angle thin-ply NCF enables facile realization of substantial weight and cost savings, [24], [25], [26], [27], [28], [29], [30], [31], [32], [33] it has been suggested that (0/25)- or (0/45)-like bi-angle, anisotropic, sub-laminate stacks as the basic building block can replace more traditional, but constraining designs of family [0p/±45q/90r]S where ‘p’, ‘q’, and ‘r’ represent repeat numbers. With 16 or more repeated thin-ply NCF sub-laminates the resultant laminate becomes homogenized. So, the laminate can be stacked without mid-plane symmetry; another advantage for the ease of manufacturing practices.
4.1 Asymmetry associated with the fixed sub-laminates of NCF
While symmetrical stacking sequences are often preferred in laminated composites, as noted in Table 1, not all NCF building blocks are suitable for creating overall symmetric laminates, unless their matching alternates for symmetry are also made available [e.g. (0/45) and (45/0) both to be available]. An NCF building block may not necessarily provide its own mirror image alone by simple lamination practices, such as flipping over and/or rotating by an angle unless the ply orientations are of cross-ply family, (0/90) or (45/−45), and π/4-quasi-isotropic (0/45/−45/90) (Table 3). A consequence of this intrinsic asymmetry is the nonzero extension-bending coupling matrix [B]. However, the effect of the asymmetry is also reduced as homogenization at the laminate level is increased by a sufficiently high number of repeats of the building block or sub-laminate. Figure 8A shows how the entities of the normalized extension-bending coupling stiffness matrix [B*] vanish as the number of repeats increase for sub-laminate π/4, suggesting the minimized effect of the asymmetry of the whole laminate.
Examples of NCF configurations in the view of mirror image possibilities by basic lay-up practices.
| Original NCF | Mirror image by flip-over? | Mirror image by rotation angle? |
|---|---|---|
| 0/90 | 90/0→no | 90→90/0→yes |
| 45/−45 | 45/−45→no | 90→−45/45→yes |
| 0/45/−45/90 | 90/45/−45/0→no | 90→90/−45/45/0→yes |
| 0/45/90/−45 | 45/90/−45/0→no | 90→90/−45/0/45→no |
| 0/60/−60 | 60/−60/0→no | (Flip and then) 90→−60/60/90→no |
| 0/ϕ | −ϕ/0→no | ϕ→ϕ/2ϕ→no |
| 0/ϕ/−ϕ | ϕ/−ϕ/0→no | (Flip and then) 90→−ϕ/ϕ/90→no |
![Figure 8: (A) Normalized extension-bending coupling stiffness matrix for π/4 sub-laminate repeated r times, [0/45/90/−45]r.(B) Diminishing effect of asymmetry on flexural strain to axial strain ratio under simple uni-axial stress, σx.](/document/doi/10.1515/secm-2015-0386/asset/graphic/j_secm-2015-0386_fig_008.jpg)
(A) Normalized extension-bending coupling stiffness matrix for π/4 sub-laminate repeated r times, [0/45/90/−45]r.
(B) Diminishing effect of asymmetry on flexural strain to axial strain ratio under simple uni-axial stress, σx.
The number of the distinct fiber orientations within the NCF sub-laminate is also a factor in the homogenization at the laminate level. Among the bi-, tri- and quad-angle sub-laminates, a lower repeat of the building block or sub-laminate will be sufficient, when fewer angles or orientations are used within a building block. This can be demonstrated by the diminishing ratio of resulting bending/flexural (εflex) to in-plane (εin-plane) strains for the asymmetric stacks of bi-, tri-, and quad-angle sub-laminates, when the loading is extensional only (Figure 8B). That is, the symmetry and asymmetry of the lay-up may converge to the same overall deformation as the number of repeats ‘r’ is increased. This also suggests that simplicity of the basic building block results in minimized errors due to use of the homogenized or equivalent properties instead of the ply-by-ply values, the topic to be discussed in the next section.
4.2 Homogenized properties of thin-ply NCF building block and failure envelopes
The NCF building block or sub-laminate design curves in Figure 4 also represent fully homogenized laminate properties before the first ply failure (FPF). For general and multi-angle NCF sub-laminates, on the other hand, progressive failure may occur, calling attention to the last ply failure (LPF), as well as the FPF. Therefore, the prediction procedure of FPF is also followed for the homogenized LPF predictions, but incorporating an additional degradation scheme [34], which traditionally imposes an empirical degradation factor, d in the range of 0.1–0.2. For this present study, a factor d=0.2 was used on the matrix material properties and reflected here onto the matrix-dominating ply properties by using micromechanics relations [34], [35]. In contrast, the longitudinal-ply modulus was maintained at its “intact value”. The laminate strength parameters can be computed by applying the ply-by-ply Tsai-Wu criterion based analyses. Specifically, six basic uni-mode loading/stress state scenarios are considered, namely (σx, σy, σxy)=(1, 0, 0), (−1, 0, 0), (0, 1, 0), (0, −1, 0), (0, 0, 1), and (0, 0, −1) corresponding to the laminate strength parameters X, Xʹ, Y, Yʹ, S and Sʹ, respectively. The representative stiffness and strength predictions for several thin-ply NCF building block designs of C-ply™/epoxy are given both for FPF and LPF in consecutive columns of Table 2. Such predictions shall be the essential data/parameters in designing NCF laminates and structures by analyses within the most commercial finite element software in which Tsai-Wu criterion is typicaly built-in.
4.3 Homogenized FPF and LPF envelopes
Another direct graphical way to assess the performance of the NCF designs is to study the failure surfaces or envelopes, which were also considered for the homogenized laminates. Following a common practice in the design cycle of laminated composites, the FPF and LPF envelope predictions can be performed using the ply-by-ply analyses. Alternatively, the use of homogenized equivalent strength parameters in LPF along with the FPF predictions is discussed here. The envelopes based on traditional Tsai-Wu criterion [34] are referred to as the homogenized envelopes [32]. If the repeat of a sub-laminate increases, the laminate characteristics normalized with respect to its thickness converge to those of a symmetric laminate. For instance, a quadratic failure envelope for a sub-laminate, say (ϕ1/ϕ2), and a homogenized laminate with its sufficiently large repeat ‘r’, [ϕ1/ϕ2]r can be considered to be equivalent to the envelope of a simple symmetric laminate of [ϕ1/ϕ2]s.
In order to compare the homogenized laminate failure envelopes with the ply-by-ply envelopes, the results for several sub-laminates of bi-, tri-, and quad- ply orientations are shown in Figure 9. The choice of the sub-laminates for comparison are: quasi-isotropic, orthotropic-like, and anisotropic building-blocks. Recalling the discussion in Figure 4, focus was specifically on the σx−σxy plane, where the bi-angle NCF can make the utmost impact. This is the stress plane, where highly loaded slender structures such as wind turbine blades and wing designs, can be improved for reduced weight, but increased strength. It should be noted that although homogenized envelopes require ply-by-ply analyses along with the anchor points, X, Xʹ, Y, Yʹ, S and Sʹ as in Table 2, once they are formed, the implementation in the design cycle can be performed as if a homogenous material [31] was used.

Sub-laminate first ply (FPF) and last ply (LPF) failure envelopes (in MPa): ply-by-ply (-P) vs. homogenized (-H) (A) quasi-isotropic, (B) balanced and orthotropic-like (C) anisotropic.
The failure envelopes presented in Figure 9 suggest the following: (i) the degree of anisotropy does not adversely affect the accuracy of equivalent or homogenized laminate failure envelopes: they are all in very good agreement with the ply-by-ply analyses; (ii) the ply-by-ply LPF envelopes with discontinuity-like abrupt shape changes may be hard to implement in automated design cycles (in the case of equivalent or homogenized LPF envelopes, these models are also ellipsoids, similar to the FPF envelopes and well-behaved quadratic functions. They can easily be incorporated parametrically as constraints to avoid failure in the design optimization process.); and (iii) bi-angle NCF homogenized laminates with shallow off-axis plies do not have a significant FPF and LPF distinction, i.e. FPF (without an assumed/empirical degradation scheme) predominantly drives the design cycle.
5 NCF sub-laminate based analysis for structural design
The aim of the previous section was to introduce the NCFs within the context of a building block or sub-laminate approach, and provide ways of assessment and characterization for designing the NCF building-block itself. In this section the focus is shifted to discussing about a couple of aspects on design of laminates based on the NCF building-blocks.
In order to demonstrate application of the laminate analysis as a basis of homogenized laminate design approach, an example problem is a laminated flat plate of aspect ratio 3 (300×900 mm2), as schematically represented in Figure 10. MSC.Patran software incorporating MSC.Nastran solvers was used in modeling and solving the problem [36]. The finite element model contains 2D four nodes QUAD4 shell elements formed via a 30 by 30 uniform mesh. Boundary conditions are to simulate a clamped end at the x=0 edge and free ends at y=0 and 300 mm edges, and at x=900 mm where the additional distributed forces/moments are also imposed (the basic in-plane axial load by distributed force px, lateral distributed force pz, distributed twisting and bending moments mxand my, respectively). Linear solver SOL 101 was typically utilized, but SOL 105 and SOL 200 were also employed for buckling and structural optimization, respectively. Note the demonstrations herein can also be perceived as examples of how one can customize the NCF building block by laminated structural design and optimization, provided that the application problem is well defined and the NCF design is feasible by the material providers. The C-ply based NCFs by Chomarat in epoxy matrix (with 0.0625 mm nominal individual ply thickness) were considered in the examples for consistency (material properties from Table 2).

Description of the clamped-free ended flat-plate problem.
5.1 Design for deformation
As any NCF ply arrangement is virtually possible, the sub-laminates are not necessarily orthotropic, but may also be anisotropic. For instance, a building block, bi-angle thin-ply NCF may reunite composite designers and practitioners with the anisotropy and associated benefits complemented by the one-axis lay-up advantage. One can homogenize the laminates and reduce the normalized in-plane/bending coupling to a great extent by the bi-angle thin-ply NCFs, while taking advantage of the bending-twisting coupling for the out-of-plane deflection control.
Slender load-bearing structures such as wings and wind turbine blades are subject to inevitable combined bending and twisting type loading and deformations. Unlike traditional quasi-isotropic laminates, anisotropic lay-ups under either one of the loadings result in the both types of deformation simultaneously due to the bending-twisting coupling.
The bending-twisting coupling due to anisotropy has been long recognized for its potential of controlling or designing the deformation counter effects on the loading types, usually referred to as passive aeroelastic tailoring in the field of aerostructures. The potential of the bi-angle NCF for such a tailoring approach can be shown on the simple laminated plate design (Figure 10) for suppressing one of the deformation modes despite combined loading. Figure 11A (left column) and Figure 11B (right column) show how an off-axis angle ϕ can be determined for zero tip deflection and zero tip rotation, respectively, when the anisotropic laminate [0/ϕ]8S is subject to combined loading.
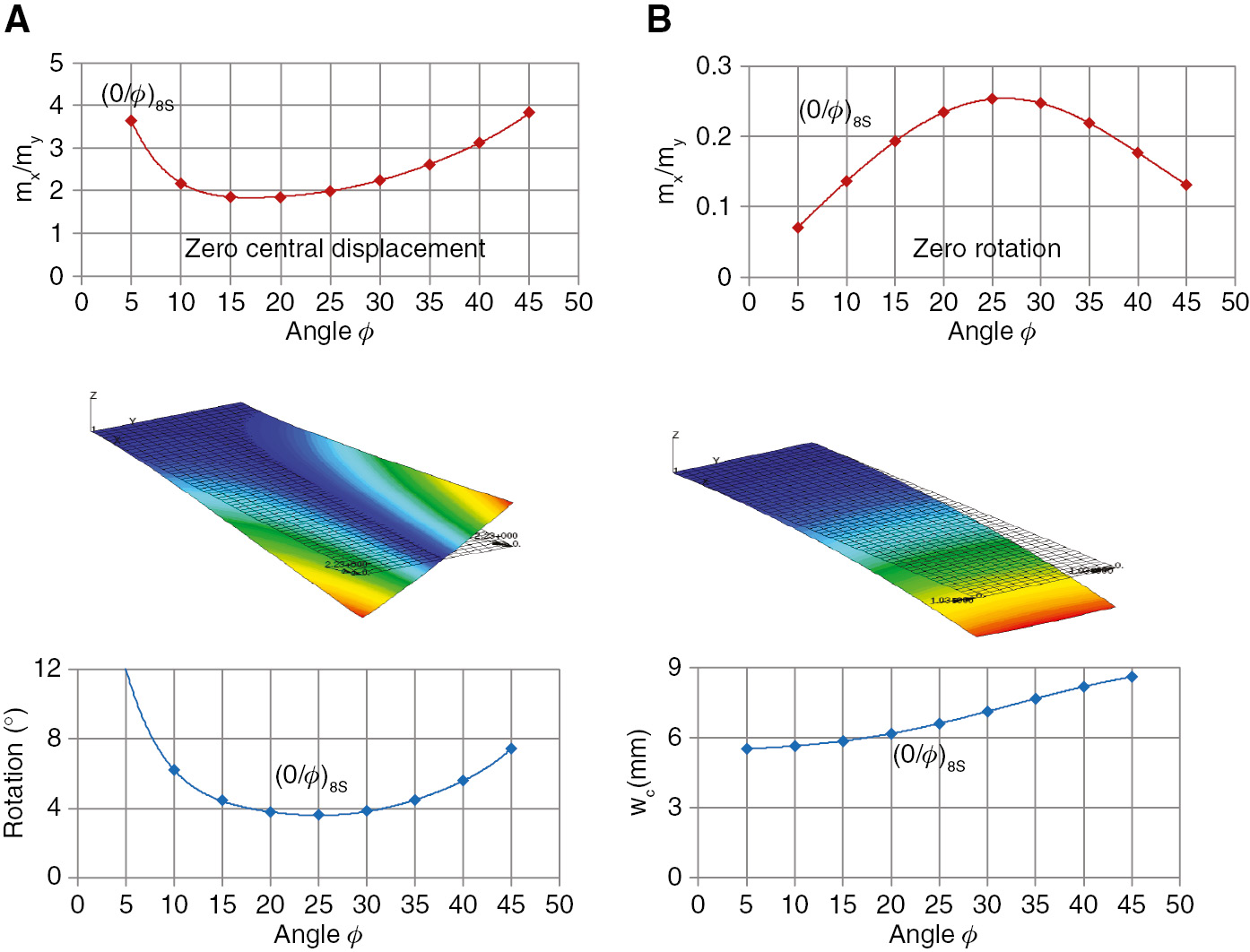
Design of deflection and twisting of a cantilever flat anisotropic panel subject to combined twisting and bending moments, mx and my, respectively.
Design vs. loading ratio (A) for zero central deflection with tip rotation; (B) for zero tip rotation with tip central deflection wc.
5.2 Design optimization using homogenized laminate properties
Although design optimization of composite structures is a well-established field [37], [38], [39], [40], [41], [42], associated research continuously progresses. Novel strategies are demonstrated such as the use of lamination parameters as design variables while adapting the evolving manufacturing capabilities and practicability into the design [40], [41].
The form of the materials used in the composite structures may also be a decisive factor regarding the strategies. One supplementary aspect herein, for instance, is to tailor the design framework to the distinct and descriptive characteristics of NCF. Homogenized or dispersed collections of fiber orientations in the form of sub-laminates, which are intrinsic to NCF in composites, offer several advantages. Analyses for preliminary design can be carried out by adjusting to a building block approach which relies on the homogenized material properties and failure envelopes. Preliminary composite design may implement simplified analyses by replacing the composite laminates in the structural model as if they were constructed of equivalent homogenized material [40], [43]. Parnell and Tsai [33] reported use of the equivalent properties in finite element analyses of a typical stiffened panel problem. The approach can provide a design optimization framework five times faster, due to overall solution and memory reductions. In addressing the use of sub-laminates and their equivalent properties in the design of composite structures, Venkataraman et al. [44] have demonstrated that error due to equivalent properties may be as high as 20%, but can be reduced to 6% if the repeat of the sub-laminate is increased. They have also cautioned that their findings may not be applicable, when the lay-up is asymmetric, which is typically the case in this article.
One simplifying difference here, yet specific to NCF practices in analysis and design, is that the sub-laminate is formed from a single unit basic building block. This approach reduces the error in the bending stiffness matrix [D] and enables even an asymmetric overall lay-up, provided that the number of repeats is sufficient. Recall Figure 8B which showed how the ratio of bending to in-plane strains converges to zero, for asymmetric stacks of bi-, tri- and quad-angle sub-laminates, when the loading is extensional in nature only.
The process of sub-laminate-based analysis and design herein can be represented by Figure 7. The NCF sub-laminate is treated as a homogenous material with the associated homogenized/equivalent properties. Then homogenous thickness variables are assigned to the spatial domain(s) of the structure so that they can be optimized for the given problem. Once the optimal homogenized thickness profile is found for the structure, it can then be converted back to the sub-laminate stack.
Several isolated unit-load cases were first evaluated for deformation and stress fields computed from finite element analyses, using individual ply-data and NCF building block/sub-laminate properties within the ply-by-ply and homogenized laminate analyses, respectively. The lay-up was made-up of a stack of (0/25) sub-laminates with a repeat of 16, resulting in a total laminate thickness of 2 mm (32 thin plies of C-ply material). Table 4 summarizes the comparisons for the load cases and associated percentage errors due to use of the homogenized properties. In addition, Figure 12 shows how the tip displacement due to axial (in-plane) unit load deviates from the ply-by-ply analysis result (A), and when the homogenized properties are utilized (B). The latter results in zero lateral tip displacement, as the coupling stiffness matrix [B] is not incorporated, despite the asymmetry of the lay-up. The difference is negligible – 0.2 mm (as opposed to 900 mm length of the plate) for the unit load case, although it is directly proportional to the applied load. For the same problem, a stress field comparison is also presented in Figure 12. As reported in Table 4, the three in-plane stress components σx, σy, σxy were underestimated by 5%, 17% and 27%, respectively. However, it should be noted that the latter two stress components are the minor ones and an order of magnitude smaller than the axial stress. Furthermore, the Tsai-Wu failure criterion based strength ratio predictions differ by about 10%.
Clamped-free [0/25]16T thin-ply NCF (C-ply/epoxy) flat laminate example: percent errors due to the use of homogenized laminate properties relative to ply-by-ply analyses.
| Tip displacement | Max σx | Max σy | Max σxy | Strength ratio | |
|---|---|---|---|---|---|
| px only | 100a | 5 | 17 | 27 | 10 |
| pz only | <1 | <1 | 3 | 2 | 1 |
| my only | <1 | <1 | 3 | 2 | 1 |
| mxonly | <1 | 1 | 3 | 2 | 6 |
| px and mx | 2 | 1 | 4 | 4 | 7 |
| Buckling load, mode 1 | Buckling load, mode 2 | Buckling load, mode 3 | Buckling load, mode 4 | Buckling load, mode 5 | |
| px, cl-ssb | <1 | <1 | <1 | <1 | <1 |
| px, cl-freec | <1 | <1 | <1 | <1 | <1 |
aMaximum tip displacement, 0 vs. 0.2 mm at a span of 900 mm.
bClamped simply supported ends, at x=0 and 900 mm, respectively.
cClamped free ends, at x=0 and 900 mm, respectively.
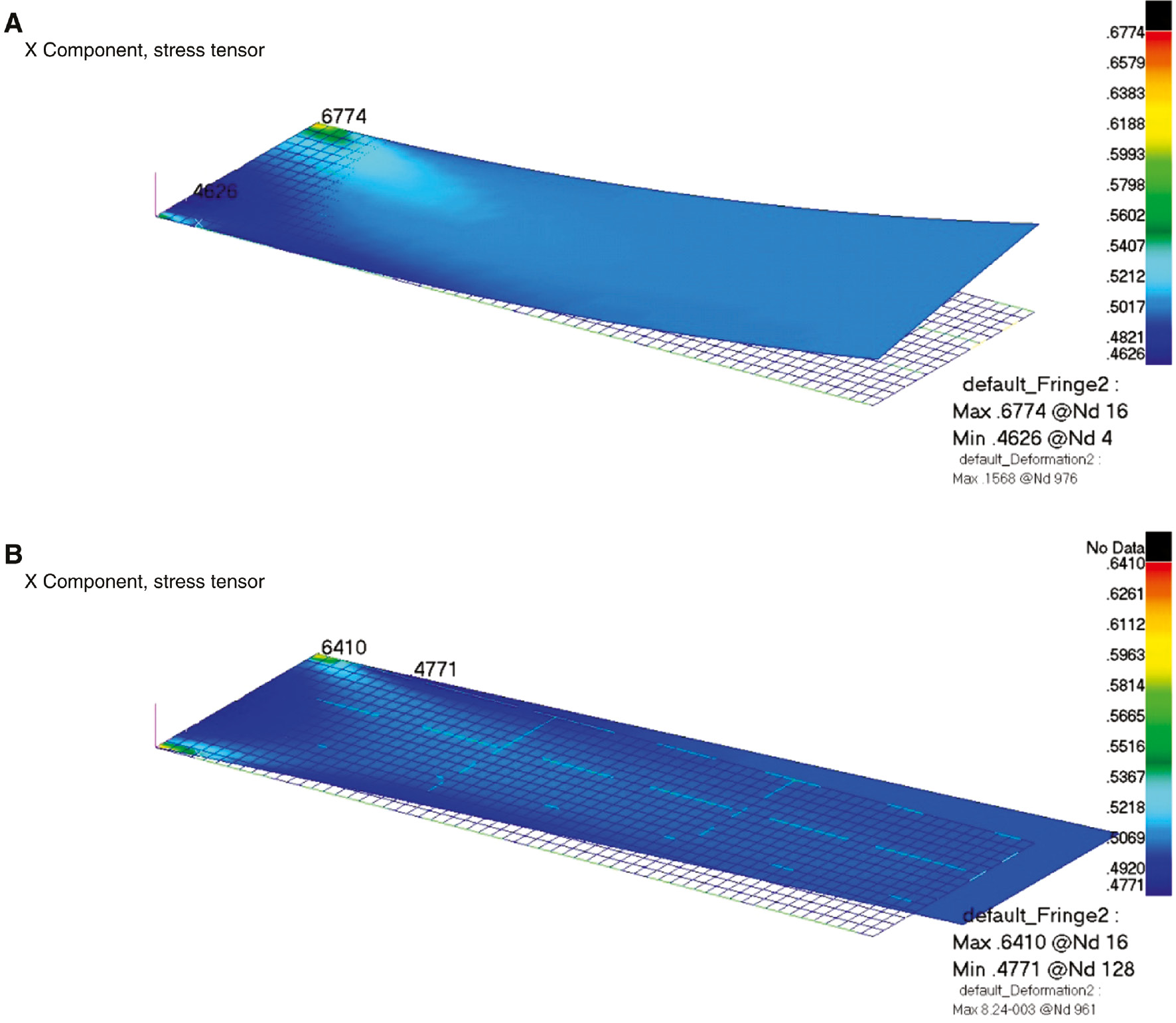
Lay-up, (0/25)16T – total 16 repeats of (0/25) NCF, Load case: px=1 N/mm, deformed shape and stress contours, σx.
(A) Ply-by-ply analysis; (B) homogenized laminate analysis (displacements are not scaled).
As for the distributed lateral (out-of-plane) load case, the tip displacements predicted by the two approaches are almost the same, where the difference is about 0.1%. The three in-plane stress components (σx, σy, σxy) are different by, 0.7%, 2.5% and 2.1%, respectively (Table 4).
Twisting and bending moment unit load cases were also studied, and their results are presented in Table 4. Deformed shape and the stress contours for the bending moment load case are presented in Figure 13. Furthermore, as an example of the combined loading, analysis by the homogenized laminate approach under axial load and twisting moment results in stresses and deformation, to within 5% of the results by the conventional ply-by-ply analysis. Comparisons of the displacement, stress fields, buckling loads, and strength ratio in Table 4 suggest that the homogenized (equivalent or effective) laminate properties within the course of the NCF sub-laminate/building block approach can be utilized for preliminary analysis and design efficiency.
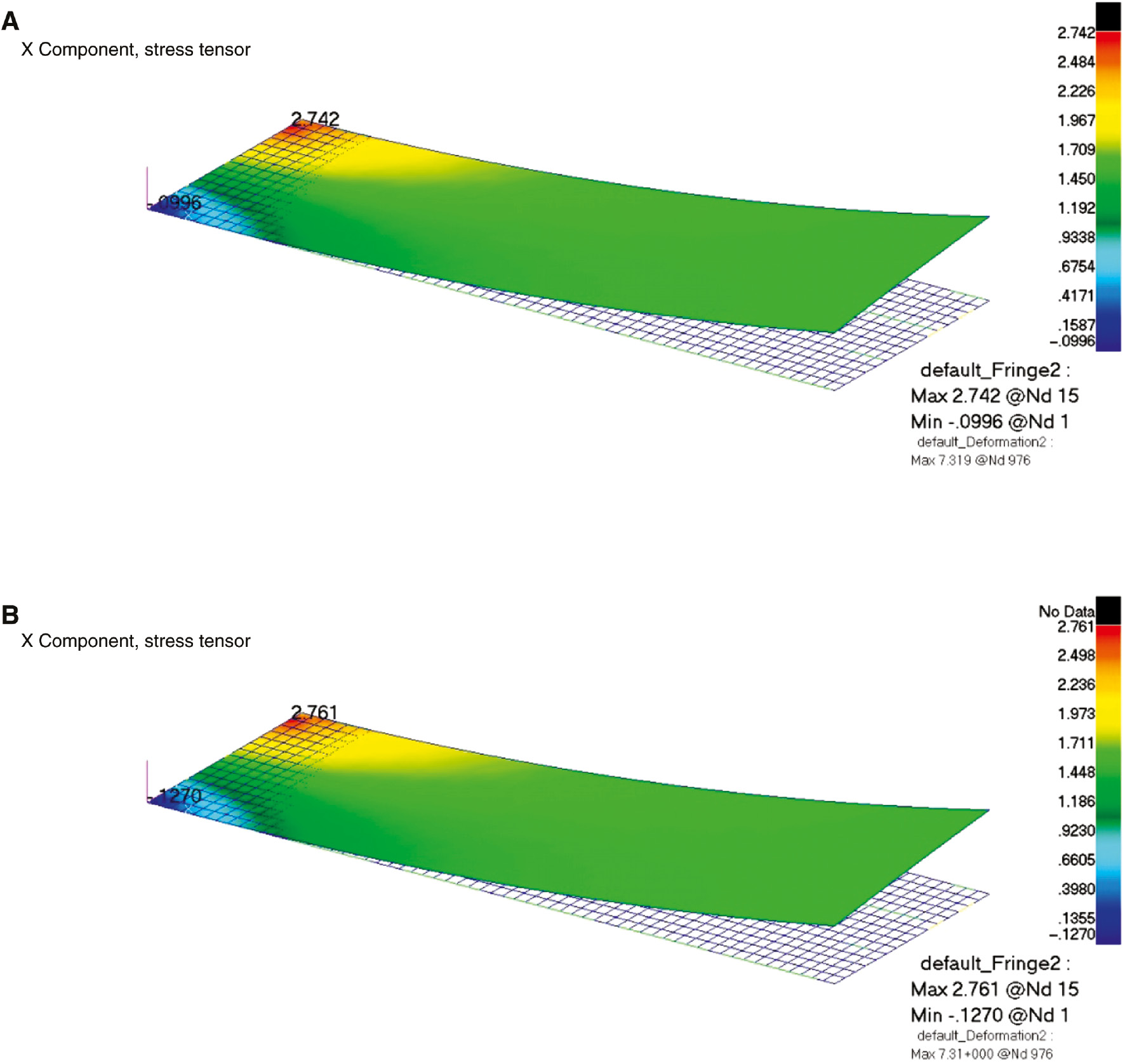
Lay-up, (0/25)16T – total 16 repeats of (0/25) NCF, Load case: my=1 N, deformed shape and stress contours, σx.
(A) Ply-by-ply analysis; (B) homogenized laminate analysis (displacements are not scaled).
In order to demonstrate the expected accuracy along with the simplicity of sub-laminate building block/homogenized laminate based design optimization as summarized in Figure 7, the same flat plate problem subject to distributed transverse load pz and twisting moment mx was considered. Finite elements of the model were grouped as 15 longitudinal (along the x-axis) regions, each assigned to a homogenized thickness resulting in a total of 15 continuous design variables. The sub-laminate building block for the homogenized laminates was chosen as [0/25]. The minimum weight optimization problem was solved for a constrained maximum tip displacement, dtip. Figure 14 shows the initial design and the optimal thickness profiles for two different load cases while the tip displacement constraint was fixed to 30 mm. The results are based on the homogenized laminate approach and require verification by the ply-by-ply analysis. Figure 15 presents the comparisons for the combined load case of pz=1 N/mm and mx=10 N, such that dtip≤30 mm. The ply-by-ply analysis on the optimal thickness profile results in the tip displacement dtip=32 mm, as opposed to 30 mm in the homogenized laminate analysis; an error of about 8%. The stress distributions were well captured, but the error may be as high as 6%. Note that the stress constraints were found to be inactive for this problem. The optimal solution of the homogenized laminate was driven by the tip displacement constraint. Despite the error in the tip displacement for this example problem, the homogenized laminate or sub-laminate building block based optimization approach is in general proposed to be an efficient and accurate preliminary sizing strategy.

Optimization of clamped-free flat plate problem (Figure 10) subject to distributed lateral force pz and distributed twisting moment, mx for constrained tip displacement dtip≤30 mm.
Minimum weight laminate thickness profiles by (0/25) sub-laminate: distribution of 15 discrete thickness variable zones and nominal smoothing fit.

Deformation of the optimal laminate design subject to pz=1 N/mm mx=10 N.
(A) homogenized laminate analysis of the design optimization cycle; (B) posterior ply-by-ply analysis of the optimal profile due to Figure 14.
6 Conclusions
Incorporating tow-spreading technology, an innovative bi-angle thin-ply NCF offers an attractive alternative for laminate production. With prior assessments on laminate stiffness and strength, a customized building block or sub-laminate can be easily designed and serve as a replacement for the traditional choices, such as quasi-isotropic NCFs. Anisotropic NCF building blocks may also be considered, which may facilitate isolation of the deformation modes under combined loading. Several thin-ply NCF building-block design curves were presented as examples. The advantages associated with the thin plies were also discussed, in particular the opportunity for making homogenized laminates a practicality. Repeat of the NCF building block/sub-laminates is the basis of the homogenized laminates. As the repeat increases, one can treat the laminate as if it was made of a homogenous material, for which equivalent material properties can easily be predicted for further use. These properties are also referred to as homogenized laminate properties: stiffness and strength. Homogenized FPF and LPF envelopes, based on the Tsai-Wu criterion, were demonstrated to compare well with the ply-by-ply analyses of the failure by the same criterion. Finally, a flat plate problem subject to several load cases was considered. The results of finite element analyses using ply-by-ply and homogenized laminate representations were shown to be consistent. It is concluded that accuracy of the homogenized laminate or sub-laminate based analyses is sufficient for enabling the incorporation of continuous homogenized laminate thickness variables into the design optimization of structures made of thin-ply NCF.
Acknowledgments
The author acknowledges the support of the European Commission under the Marie Curie International Outgoing Fellowship (IOF) Programme, grant FP7-PEOPLE-2010-IOF-274737. And very special thanks to Prof. Stephen W. Tsai for his insight and guidance during the outgoing phase of the fellowship at Stanford University. Also thanks to Prof. Ali Rana Atılgan for his support and invaluable comments for the incoming phase of the IOF at Sabancı University.
References
[1] Biboa GA, Hogga PJ, Backhouse R, Mills A. Compos. Sci. Technol. 1998, 58, 129–143.10.1016/S0266-3538(97)00106-1Search in Google Scholar
[2] Mattsson D. Mechanical Performance of NCF Composites, PhD Dissertation, Luleå University of Technology, 2005.Search in Google Scholar
[3] Edgren F. Physically Based Engineering Models for NCF Composites, PhD Dissertation, Stockholm, Kungliga Tekniska Högskolan, 2006.Search in Google Scholar
[4] Edgren F, Asp LE. Compos. Part A Appl. Sci. Manuf. 2005, 36, 173–181.10.1016/S1359-835X(04)00155-1Search in Google Scholar
[5] Greve L, Pickett AK. Compos. Part A: Appl. Sci. Manuf. 2006, 37, 1983–2001.10.1016/j.compositesa.2005.12.012Search in Google Scholar
[6] Zhao LG, Warrior NA, Long AC. Compos. Sci. Technol. 2006, 66, 36–50.10.1016/j.compscitech.2005.06.002Search in Google Scholar
[7] Tserpes KI, Labeas GN. Compos. Struct. 2009, 87, 358–369.10.1016/j.compstruct.2008.02.006Search in Google Scholar
[8] Lomov SV (editor). Non-Crimp Fabric Composites: Manufacturing, Properties and Applications. Woodhead Publishing, Cambridge, UK, 2011.10.1533/9780857092533Search in Google Scholar
[9] Edgren F, Asp LE, Joffe R. Compos. Sci. Technol. 2006, 66, 2865–2877.10.1016/j.compscitech.2006.02.021Search in Google Scholar
[10] Flaggs D, Kural M. J. Compos. Mater. 1982, 16, 103–116.10.1177/002199838201600203Search in Google Scholar
[11] Nairn JA. Matrix microcracking in composites, In Polymer Matrix Composites, Talreja, R, Manson JAE, Eds.,, Elsevier: Amsterdam, 2000, p. 403–432.10.1016/B0-08-042993-9/00069-3Search in Google Scholar
[12] Sasayama H, Kawabe K, Tomoda S, Ohsawa I, Kageyama K, Ogata N. Effect of Lamina Thickness on First Ply Failure in Multi-Directionally Laminated Composites. Proceedings of the 8th Japan International SAMPE Symposium & Exhibition (JISSE-8), Tokyo, Japan, pp. 18–21, 2003.Search in Google Scholar
[13] Tsai SW, Kawabe K. Thin Ply Laminates, US20060093802 A1, 2006.Search in Google Scholar
[14] Tsai SW. JEC Compos. Mag. 2005, 18. Available at: http://www.jeccomposites.com/knowledge/international-composites-news/thin-ply-composites.10.2514/6.2005-2005Search in Google Scholar
[15] Sihn S, Kim RY, Kawabe K, Tsai SW. Compos. Sci. Technol. 2007, 67, 996–1008.10.1016/j.compscitech.2006.06.008Search in Google Scholar
[16] Yamaguchi K, Hahn TH. The Improved Ply Cracking Resistance of Thin-Ply Laminates. Proceedings of the 15th International Conference on Composite Materials (ICCM-15). CD-ROM, Durban, South Africa, 2005.Search in Google Scholar
[17] Yokozeki T, Aoki Y, Ogasawara T. Compos. Struct. 2008, 82, 382–389.10.1016/j.compstruct.2007.01.015Search in Google Scholar
[18] Yokozeki T, Kuroda A, Yoshimura A, Ogasawara A, Aoki T. Compos. Struct. 2010, 93, 49–57.10.1016/j.compstruct.2010.06.016Search in Google Scholar
[19] Saito H, Morita M, Kawabe K, Kanesaki M, Takeuchi H, Tanaka M, Kimpara I. J. Reinforced Plast. Compos. 2011, 30, 1097–1106.10.1177/0731684411416532Search in Google Scholar
[20] Saito H, Takeuchi H, Kimpara I. J. Compos. Mater. 2014, 48, 2085–2096.10.1177/0021998313494430Search in Google Scholar
[21] Amacher R, Cugnoni J, Botsis J, Sorensen L, Smith W, Dransfeld C. Compos. Sci. Technol. 2014, 101, 121–132.10.1016/j.compscitech.2014.06.027Search in Google Scholar
[22] Wisnom MR. In Trade-Off Between Damage and Strength: Why Weaker May Mean Stronger, Shankar BV, Waas AM, Eds., DEStech Pub, Lancaster, PA, 2013.Search in Google Scholar
[23] Tsai SW, Cognet M, Sanial P. Composite Laminated Structures and Methods for Manufacturing and Using the Same, WO2012096696 A1, 2012.Search in Google Scholar
[24] Tsai SW, Cognet M. JEC Compos. Mag. 2011, 68, 51–52.10.1080/09674845.2011.11978205Search in Google Scholar
[25] Massard T, Harry R, Sanial P, Lorriot T. JEC Compos. Mag. 2011, 68, 55–56.Search in Google Scholar
[26] Saremi FF. JEC Compos. Mag. 2011, 68, 57–58.10.1365/s35128-011-0229-8Search in Google Scholar
[27] Tsai SW, Nettles A. JEC Compos. Mag. 2011, 68, 62–63.10.1063/1.3592014Search in Google Scholar
[28] Arteiro A, Catalanotti G, Xavier J, Camanho PP. Compos. Sci. Technol. 2013, 79, 97–114.10.1016/j.compscitech.2013.02.001Search in Google Scholar
[29] Guillamet G, Turon A, Costa J, Renart J, Linde P, Mayugo JA. Compos. Sci. Technol. 2014, 98, 44–50.10.1016/j.compscitech.2014.04.014Search in Google Scholar
[30] Tsai SW, Papila M. JEC Compos. Mag. 2011, 68, 66–67.Search in Google Scholar
[31] Tsai SW, Papila M. JEC Compos. Mag. 2011, 68, 70–71.10.1111/pcn.12363Search in Google Scholar
[32] Tsai SW, Papila M. JEC Compos. Mag. 2011, 68, 72–73.10.1016/j.ando.2011.03.006Search in Google Scholar
[33] Parnell TK, Tsai SW. JEC Compos. Mag. 2011, 68, 74–75.10.1111/j.1747-0080.2010.01491.xSearch in Google Scholar
[34] Tsai SW. Theory of Composites Design. e-book, Stanford University, 2008.Search in Google Scholar
[35] MicMac 4.3, Composites Design Workshop, Stanford University, Department of Aeronautics & Astrounatics, Available at: http://www.stanford.edu/group/composites/, 2011.Search in Google Scholar
[36] MSC.Patran User’s guide, 2012.Search in Google Scholar
[37] Gürdal Z, Haftka RT, Prabhat H. Design and Optimization of Laminated Composite Materials, John Wiley & Sons, New York, 1999.Search in Google Scholar
[38] Venkataraman S, Haftka RT. Composite Panel Optimization: Review. Proceedings of the American Society of Composites—14th Annual Technical Conference, Fairborn, OH, pp. 479–488, 1999.Search in Google Scholar
[39] Papila M, Haftka RT. J. Int. Soc. Struct. Multidiscip. O. 2003, 25, 327–338.10.1007/s00158-003-0329-0Search in Google Scholar
[40] Glenn AA, Thuwis RD, Abdalla MA, Gürdal Z. Struct. Multidiscip. O. 2010, 41, 637–646.10.1007/s00158-009-0437-6Search in Google Scholar
[41] Khani A, IJsselmuiden ST, Abdalla MM, Gürdal Z. Compos. Part B Eng. 2011, 42, 546–552.10.1016/j.compositesb.2010.11.005Search in Google Scholar
[42] Schmit LA, Farshi B. Int. J. Numer. Methods Eng. 1977, 11, 623–640.10.1002/nme.1620110403Search in Google Scholar
[43] Ainsworth J, Collie C, Yarrington P, Lucking R, Locke J. Airframe Wingbox Preliminary Design and Weight Prediction. SAWE, Society of Allied Weight Engineers: Virginia Beach, VA, 2010.Search in Google Scholar
[44] Venkataraman S, Haftka RT, Johnson TF. AIAA J. 2001, 39, 296–302.10.2514/2.1304Search in Google Scholar
©2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- Original articles
- Review of the mechanical performance of variable stiffness design fiber-reinforced composites
- Exact solution for bending analysis of functionally graded micro-plates based on strain gradient theory
- Synthesis, microstructure, and mechanical properties of in situ TiB2/Al-4.5Cu composites
- Microstructure and properties of W-Cu/1Cr18Ni9 steel brazed joint with different Ni-based filler metals
- Drilling studies on the prepared aluminum metal matrix composite from wet grinder stone dust particles
- Studies on mechanical properties of thermoplastic composites prepared from flax-polypropylene needle punched nonwovens
- Design of and with thin-ply non-crimp fabric as building blocks for composites
- Effect of coir fiber reinforcement on mechanical properties of vulcanized natural rubber composites
- Investigation and analysis of glass fabric/PVC composite laminates processing parameters
- Abrasive wear behavior of silane treated nanoalumina filled dental composite under food slurry and distilled water condition
- Finite element study into the effects of fiber orientations and stacking sequence on drilling induced delamination in CFRP/Al stack
- Preparation of PAA/WO3 composite films with enhanced electrochromism via layer-by-layer method
- Effect of alkali treatment on hair fiber as reinforcement of HDPE composites: mechanical properties and water absorption behavior
- Integration of nano-Al with one-step synthesis of MoO3 nanobelts to realize high exothermic nanothermite
- A time-of-flight revising approach to improve the image quality of Lamb wave tomography for the detection of defects in composite panels
- The simulation of the warpage rule of the thin-walled part of polypropylene composite based on the coupling effect of mold deformation and injection molding process
- Novel preparation method and the characterization of polyurethane-acrylate/ nano-SiO2 emulsions
- Microwave properties of natural rubber based composites containing carbon black-magnetite hybrid fillers
- Simulation on impact response of FMLs: effect of fiber stacking sequence, thickness, and incident angle
Articles in the same Issue
- Frontmatter
- Original articles
- Review of the mechanical performance of variable stiffness design fiber-reinforced composites
- Exact solution for bending analysis of functionally graded micro-plates based on strain gradient theory
- Synthesis, microstructure, and mechanical properties of in situ TiB2/Al-4.5Cu composites
- Microstructure and properties of W-Cu/1Cr18Ni9 steel brazed joint with different Ni-based filler metals
- Drilling studies on the prepared aluminum metal matrix composite from wet grinder stone dust particles
- Studies on mechanical properties of thermoplastic composites prepared from flax-polypropylene needle punched nonwovens
- Design of and with thin-ply non-crimp fabric as building blocks for composites
- Effect of coir fiber reinforcement on mechanical properties of vulcanized natural rubber composites
- Investigation and analysis of glass fabric/PVC composite laminates processing parameters
- Abrasive wear behavior of silane treated nanoalumina filled dental composite under food slurry and distilled water condition
- Finite element study into the effects of fiber orientations and stacking sequence on drilling induced delamination in CFRP/Al stack
- Preparation of PAA/WO3 composite films with enhanced electrochromism via layer-by-layer method
- Effect of alkali treatment on hair fiber as reinforcement of HDPE composites: mechanical properties and water absorption behavior
- Integration of nano-Al with one-step synthesis of MoO3 nanobelts to realize high exothermic nanothermite
- A time-of-flight revising approach to improve the image quality of Lamb wave tomography for the detection of defects in composite panels
- The simulation of the warpage rule of the thin-walled part of polypropylene composite based on the coupling effect of mold deformation and injection molding process
- Novel preparation method and the characterization of polyurethane-acrylate/ nano-SiO2 emulsions
- Microwave properties of natural rubber based composites containing carbon black-magnetite hybrid fillers
- Simulation on impact response of FMLs: effect of fiber stacking sequence, thickness, and incident angle

![Figure 4: Basic stiffness and strength predictions for T700/Epoxy (±ϕ) and (0/±ϕ/0) C-ply™ laminates.Test data from (±12.5), (±22.5), (0/±25/0), and (0/±45/0) type laminates [25], [26], [27].](/document/doi/10.1515/secm-2015-0386/asset/graphic/j_secm-2015-0386_fig_004.jpg)
