Temperature dependence of hardness prediction for high-temperature structural ceramics and their composites

1 Introduction

High-temperature structural ceramics including oxide structural ceramics and non-oxide structural ceramics are widely used in various industrial fields such as aerospace due to their excellent mechanical and thermal properties [1,2,3,4]. Furthermore, the ceramics are used as substrates or reinforcing materials to prepare composite materials, to improve performance and stability, such as ceramic–ceramic composites, diamond–ceramic composites, and ceramic-based cermet [5,6,7,8,9,10].

Because of the material’s high-temperature applications, the characterization of mechanical properties of the material at different temperatures is very important. Considering that hardness is one of the important mechanical properties of the materials, the temperature dependence of hardness is a critical point, and the hardness at different temperatures has also been a hot topic [11,12,13,14,15,16]. Wang and Hon tested the hardness of Al₂O₃, mullite, and SiC ceramics at different temperatures and discussed the factors influencing the hardness [11]. Gibson et al. tested the hardness and Young’s modulus of Cr₂AlC ceramic up to 980°C [12]. Niihara et al. measured the temperature-dependent hardness of an Al₂O₃–5% SiC composite up to about 1100°C and analyzed the effect of SiC particles on the hardness [13]. Cygan et al. investigated the hardness of the diamond–ceramic composites at elevated temperatures [14]. Milman et al. reported the temperature dependence of hardness of porous SiC ceramics with porosity of 5, 16, and 20% up to 900°C and discussed the effects of porosity on the mechanical properties of the materials [15]. Zunega tested the high-temperature hardness of the WC–6% Co and WC–10% Co composites [16]. All of the above-mentioned experimental measurements reported that the hardness of the ceramics and their composites are highly temperature-dependent. However, there is still scant knowledge on the predictive models for the temperature dependence of the hardness of the ceramics and their composites in the available literature. The quantitative relationships of the hardness with temperature and material parameters are barely known. As a result, the underlying mechanisms of the changing trends of the hardness with temperature are largely unclear, thus limiting the further design of the materials for the high-temperature applications.

In our previous work [17], based on the concept of the maximum energy storage limit of a ceramic associated with the material yielding, a simple temperature-dependent model of the hardness of ceramics without considering the damage factor was expressed by Young’s modulus and melting points. In this work, to further fill these research gaps, we developed a novel and highly efficient theoretical method that can be used to predict the temperature dependence of the hardness of different types of ceramics and their composites by using some basic material parameters, Young’s modulus, the melting point, and the critical damage size. The proposed models are verified by the excellent agreements between the predictions and the experimental measurements.

2 Theoretical models

The hardness of the ceramic materials corresponds to the yield stress under indentation. The hardness and the yield stress are showed to have the following simple relation [18]:

where H is the hardness of materials, σ P is the yield stress of materials, and c is a constant that is assumed to be temperature independent.

Assuming that the hardness and the yield stress of the materials at a reference temperature T ₀ and a certain temperature T are known, one can obtain the following [17]:

In equations (2a) and (2b), H ( T 0 ) and H ( T ) are the hardness of the materials at temperatures of T ₀ and T, respectively. σ P ( T 0 ) and σ P ( T ) are the yield stress of the materials at temperatures of T ₀ and T, respectively.

Under indentation, there is an energy balance between the energy for the creation of new solid surfaces W S and the energy for the plastic deformation W Y [7,19]. In this critical case, the following relations exist [7,19]:

In equations (3a) and (3b), W Y ( T 0 ) and W Y ( T ) are the energy for the plastic deformation at temperatures of T ₀ and T, respectively. W S ( T 0 ) and W S ( T ) are the energy for the creation of new solid surfaces at temperatures of T ₀ and T, respectively. E ( T 0 ) and E ( T ) are the Young’s moduli of the materials at temperatures of T ₀ and T, respectively. R ( T 0 ) and R ( T ) are the critical damage sizes of the materials corresponding to the plastic deformation at temperatures of T ₀ and T, respectively, just like the temperature-dependent critical flaw size of the fracture strength of the ceramics proposed by Neuman et al. [5]. G ( T 0 ) and G ( T ) are the crack propagation energy at temperatures of T ₀ and T, respectively.

The increase in temperature can lead to the material yielding. The study showed that there exists maximum storage of energy associated with the onset of material yielding [17,20], which should include the energy for the plastic deformation and the corresponding heat energy, i.e., molecular kinetic energy,

where W M is the maximum storage of energy, E K ( T ) is the kinetic energy, and k is the ratio coefficient between W Y ( T ) and E K ( T ) .

E K ( T ) can be expressed as follows [17,19]:

where N represents the corresponding total number of molecules and β is the Boltzmann constant.

Then, W M has the form:

At the melting temperature T _m, W Y ( T ) = 0 . Then,

k can be given as

Then, combining equations (5), (6), and (8), a novel and quite simple theoretical model for the temperature dependence of the hardness of the ceramic materials can be proposed as follows:

It can be observed that the used parameters are not created when this model is developed. The Young’s modulus of the materials at a high temperature can be obtained by the experimental measurements or the existing empirical formula. The melting point of the materials can be obtained just from the material handbook. The critical damage size of the materials can be obtained through microscopic measurements [7,19]. Compared with the simple temperature-dependent hardness model of the ceramics reported by Wang et al. [17], the critical damage size is considered in this model (equation (9)), which can thus better analyze the main mechanisms of controlling hardness at different temperatures.

For the ceramic composites, the expression of the hardness of the materials in equation (9) can also be given by the simple rule of mixtures as follows:

where E m ( T 0 ) and E m ( T ) are the Young’s moduli of matrix at temperatures of T ₀ and T, respectively; E p ( T 0 ) and E p ( T ) are the Young’s moduli of reinforcing material at temperatures of T ₀ and T, respectively; and V m and V p are the volume fractions of matrix and reinforcing materials, respectively.

A simple relationship between the pore volume fraction P and the Young’s modulus of the ceramics E can be expressed as follows [15]:

where E 0 is Young’s modulus of the pore-free materials and ν 0 is the Poisson’s ratio of the pore-free materials.

Then, by considering the sensitivities of the thermophysical properties of the materials to temperature, a simple theoretical model for depicting the temperature dependence of the hardness of the porous ceramic materials (equation (12)) can be developed by using equations (9) and (11):

where E 0 ( T 0 ) and E 0 ( T ) are the Young’s moduli of the pore-free materials at temperatures of T ₀ and T, respectively; ν 0 ( T 0 ) and ν 0 ( T ) are the Poisson’s ratio of the pore-free materials at temperatures of T ₀ and T, respectively; P ( T 0 ) and P ( T ) are the porosity at temperatures of T ₀ and T, respectively; R ( T 0 , P ( T 0 ) ) is the critical damage size corresponding to T ₀ and P ( T 0 ) ; and R ( T , P ( T ) ) is the critical damage size corresponding to T and P ( T ) .

It should be noted that all the developed models (equations (9)–(12)) have no fitting parameters, which could be simple to implement in engineering applications. No such hardness model of the ceramics, composites, or porous materials considering the combined effects of temperature and damage factors and without any fitting parameters has previously been reported.

3 Results and discussion

In this part, the hardness of some oxide and non-oxide ceramics, composite materials, and porous materials with respect to temperature are predicted and compared with the experimental measurements. During calculation, Young’s modulus of each material is obtained from the experiment or just used the existing empirical formula. The melting points of the materials are mainly sourced from the material handbook [21]. The melting point of a ceramic composite is simply taken as the melting point of the matrix.

Figure 1 shows the comparisons between measured and predicted hardness of some ceramics at high temperature by equation (9). During prediction, the experimental Young’s moduli of the Cr₂AlC and mullite ceramics are used [12,22]. The Young’s moduli of the WC and B₄C ceramics are calculated by equations (13) and (14) [23]:

Figure 1

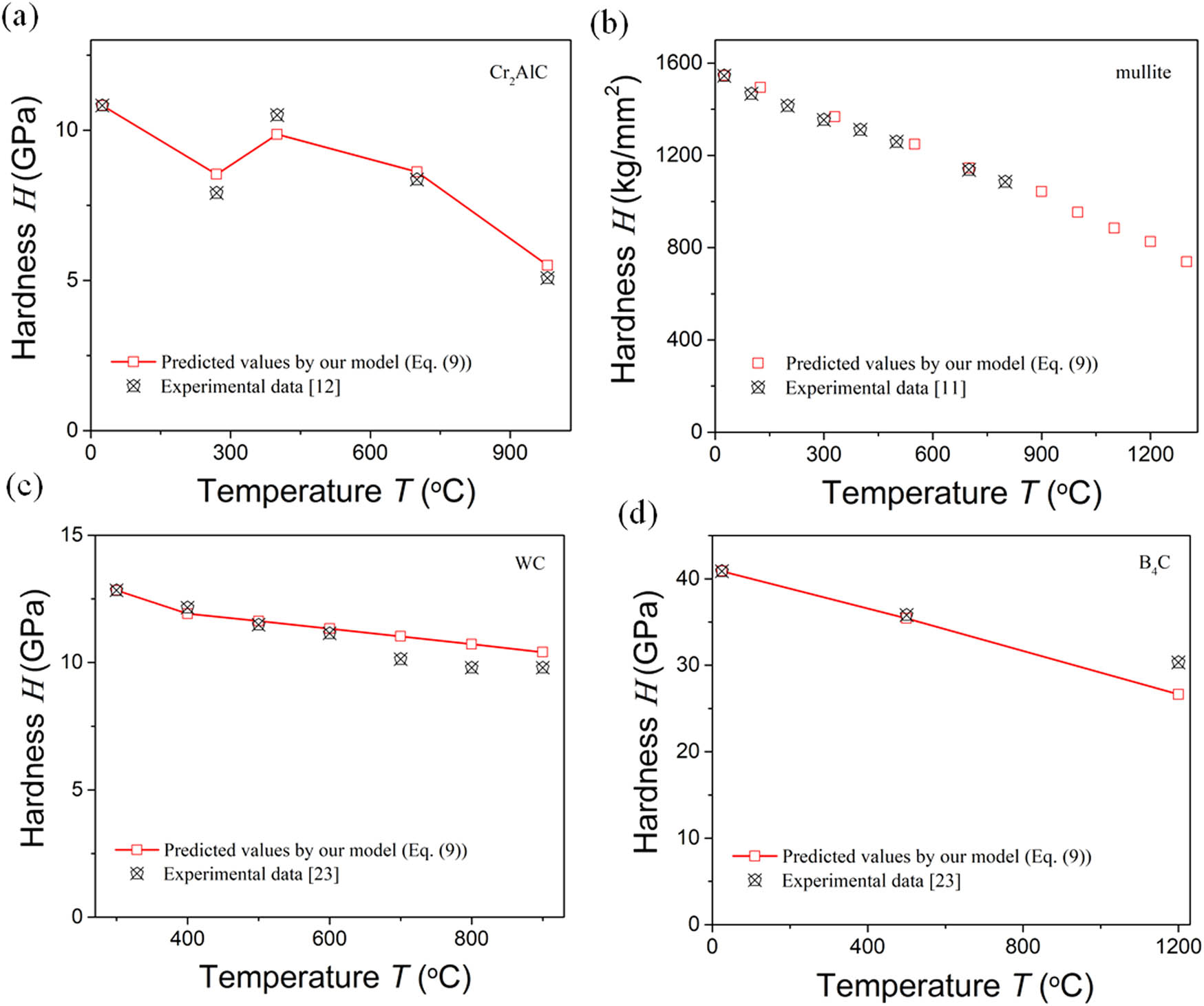
Comparison between the model-predicted and measured hardness of some ceramics at high temperature: (a) Cr₂AlC, (b) mullite, (c) WC, and (d) B₄C.

The melting point of the Cr₂AlC ceramic is sourced from ref. [24]. For all the above-mentioned predicted ceramics, the ratio of R(T ₀)/R(T) is assumed to be 1 based on the measured temperature dependence of the hardness of the ceramic [11,12,23]. The model predictions are shown to agree very well with data from experiments, thereby confirming that the critical damage size R of each ceramic in the studied temperature range is nearly temperature independent. Under such circumstances, the developed temperature-dependent hardness model of the materials (equation (9)) can be simplified to equation (15), just as the model developed in our previous work [17]. Then, the hardness of the materials at high temperatures can be calculated just by using Young’s modulus and the melting point [17].

Figure 2 shows the model predictions and experimental data of the temperature-dependent hardness of an Al₂O₃ ceramic. During prediction, Young’s modulus of the Al₂O₃ ceramic is calculated by equation (16) [25]:

Figure 2

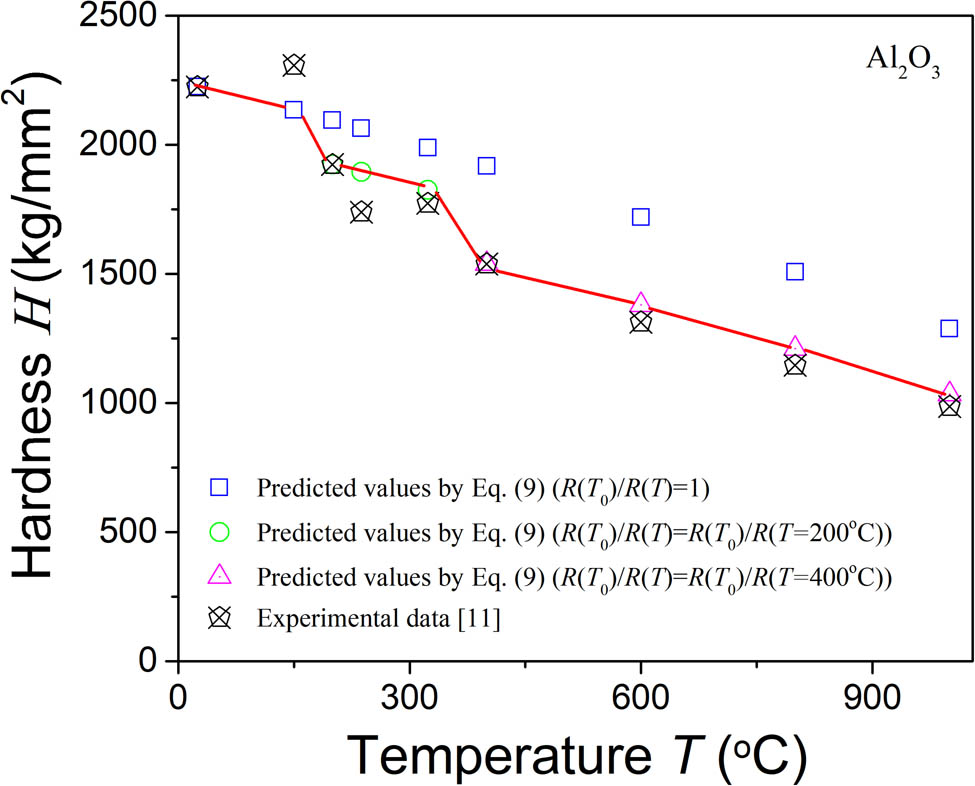
Comparison between the model-predicted and measured hardness of an Al₂O₃ ceramic at high temperature.

When defining R(T ₀)/R(T) as 1, the predicted value of the hardness of the ceramic at 150°C agrees very well with the experimental data. However, at and above 200°C, the predicted values are much bigger than the tested values, especially above 400°C. According to the experimental obtainment of the temperature dependence of the hardness of the ceramic [11], two obvious turning points (sharp decline) occurred at 200 and 400°C. Some experimental findings showed that the grain-boundary degradation at a certain temperature could cause a rapid decline in the yield stress at this temperature [26,27], and this can be reflected by the change in the critical damage size [20]. In this work, it is considered that at 200 and 400°C, the effects of temperature such as grain-boundary degradation cause the change of the critical damage size of this ceramic [11]. We thus calculate the R(T ₀)/R(T) at 200 and 400°C by using the model (equation (9)) and the tested hardness at the two temperature points, which are used to predict the hardness of this ceramic at higher temperatures. Figure 2 indicates the surprising agreements between the model-predicted and tested values in the temperature ranges of 200–400°C and 400–1000°C (see the red line). It can be observed that our model predictions reveal the reason for the rapid decline of the hardness of the material at 200 and 400°C. And more importantly, the model is capable of giving the temperature range where the material hardness is significantly affected by this reason. Additionally, apart from the model prediction, clearly, our proposed model could also become an experimental design tool for the selection of temperature points.

Figure 3 shows the comparison between the model-predicted and measured hardness of a SiC ceramic. During prediction, Young’s modulus of the SiC ceramic is calculated by equation (17) [6].

Figure 3

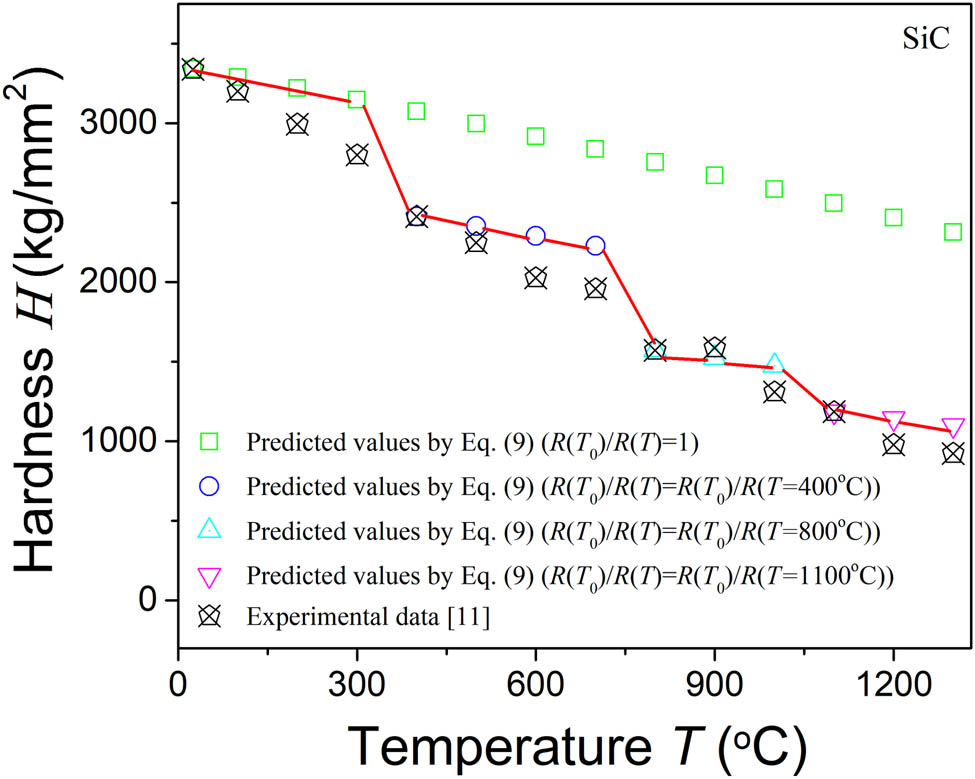
Comparison between the model-predicted and measured hardness of a SiC ceramic at high temperature.

Similarly, as the temperature increases, the temperature points at which the hardness of the material drops sharply can be observed from the figure. The model cannot make a good quantitative characterization at the temperature point if the underlying effect of this phenomenon is not included. We consider that the changes in microstructures such as weak grain boundary with temperature cause changes in critical damage sizes corresponding to the yield stress at thoee temperatures. We thus calculate the R(T ₀)/R(T) at 400, 800, and 1100°C by using the model (equation (9)) and the corresponding measured hardness of the materials, which are used to predict the hardness of this ceramic at higher temperatures. This indicates the excellent agreements between model predictions and measurements of the hardness of the material at different temperatures (see the red line), thereby providing the validation of the authors’ definition of the critical damage size at some certain temperature and showing its applicable temperature range.

Figure 4 shows the comparison between the measured and model-predicted temperature dependence of hardness of the Al₂O₃–SiC, diamond–TiC, and diamond–TiB₂ composites by equation (10). During prediction, the used Young’s moduli of Al₂O₃ [25], SiC [6], diamond [28], TiC [29], and TiB₂ [30] are given by equations (16)–(20):

Figure 4

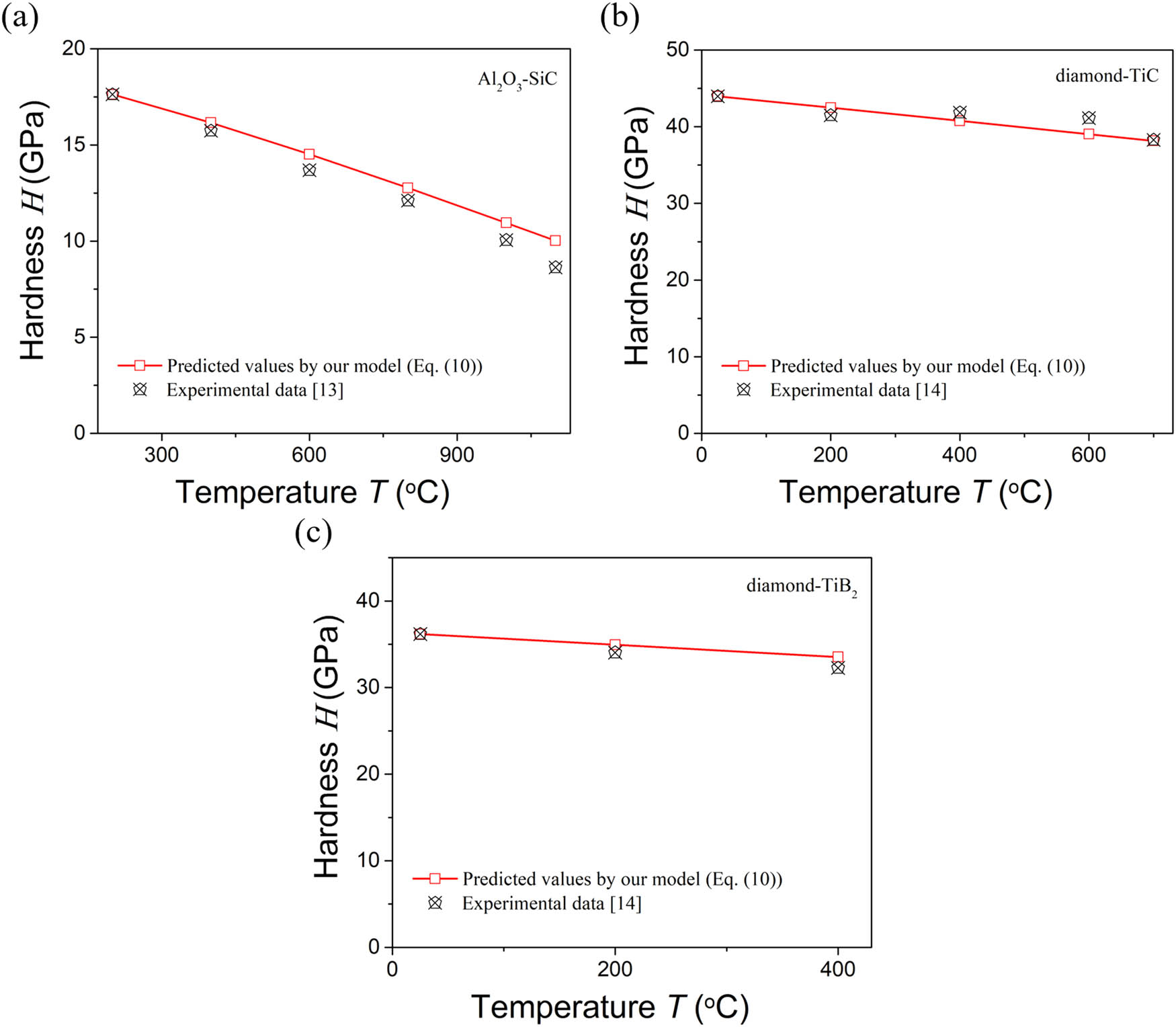
Comparison between the model-predicted and measured hardness of some ceramic composites at high temperature: (a) Al₂O₃–SiC, (b) diamond–TiC, (c) diamond–TiB₂.

As there are no temperature points at which the hardness of the materials decreases sharply [13,14], the ratio of R(T ₀)/R(T) of the materials is set to be 1 in the studied temperature range. Under such circumstances, the model predictions for the hardness of the composite materials are all in surprising agreement with the measured values.

Taken together, the model to tested data comparisons reveal that when the sharp declines of the hardness of the materials occur at some temperature points, the change of critical damage size corresponding to the yielding of the materials should be considered. Figure 5 shows the comparisons between theory (equation (12)) and experiments of the temperature dependence of the hardness of the porous SiC ceramics with different porosities. During calculation, the expression of equation (17) of Young’s modulus of SiC is used [6]. The Poisson’s ratio of the material is considered to be temperature independent [6]. According to the changing trend of the measured hardness of the material with temperature [15], the ratios of R(T ₀)/R(T) of the material with a porosity of 5% at 400 and 600°C, the material with a porosity of 16% at 800°C, and the material with a porosity of 20% at 800°C are calculated by using the proposed model (equation (12)) and the measured hardness at the corresponding temperature. Then, the obtained ratios are used to predict the hardness of the materials at the higher temperatures. Figure 5 indicates the excellent agreements between the model predictions and experimental measurements, thus verifying our assumption of the effect of critical damage size with respect to temperature on the hardness of the porous ceramic materials at high temperatures. Furthermore, this reflects the thermal stability of the different porous materials. For example, the thermal stability of the material with a porosity of 5% is lower than the materials a with porosity of 16 and 20%, which showed the obvious reduction of hardness at a lower temperature [15]. Finally, the comparisons reveal that the model is capable of predicting the hardness of the porous materials at high temperatures and showing the temperature dependence of the stability of different pore materials.

Figure 5

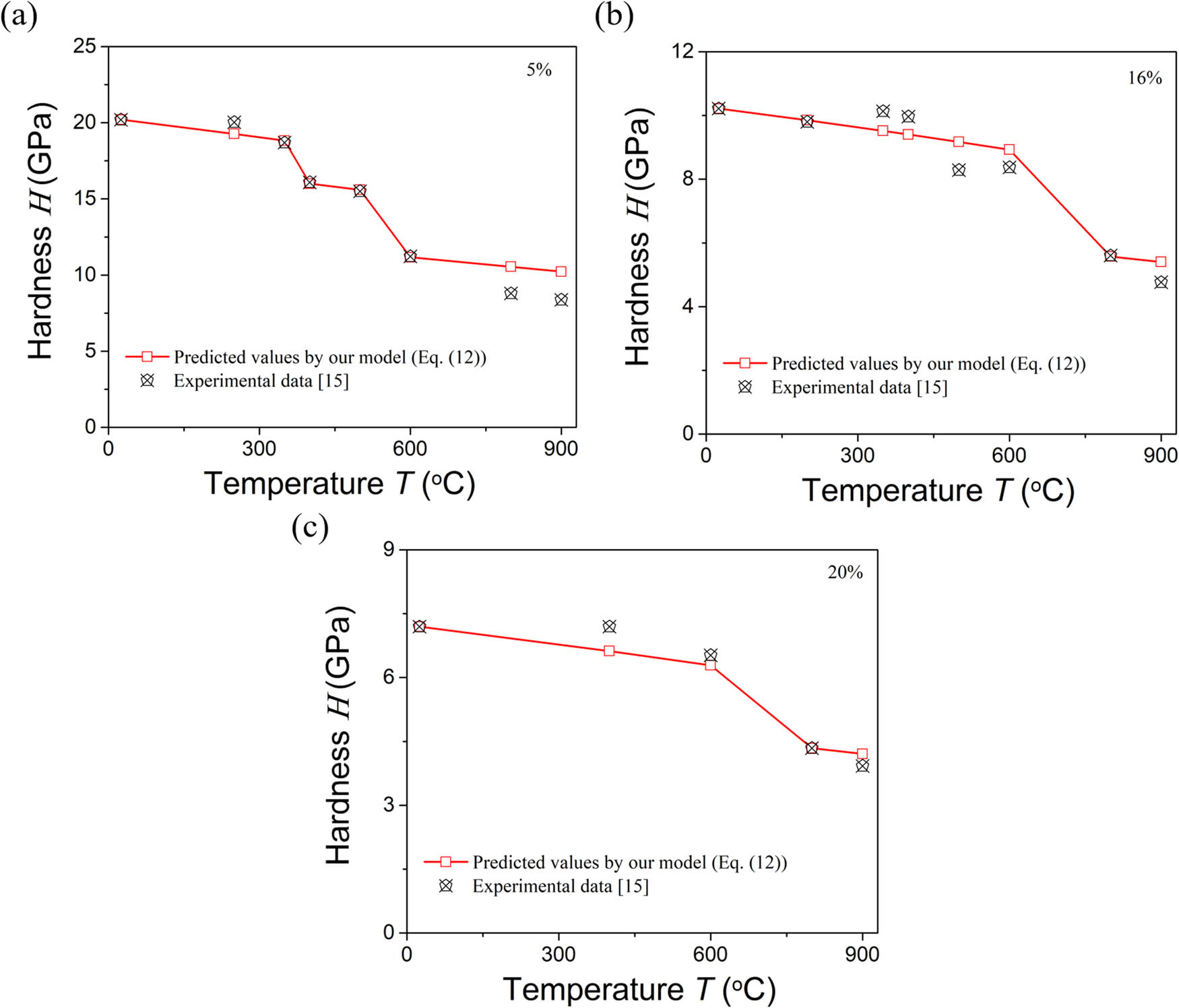
Comparison between the model-predicted and measured hardness of the porous SiC ceramics with different porosity at high temperature: (a) 5%, (b) 16%, (c) 20%.

We also use the developed temperature-dependent hardness model to predict the hardness of WC-based cermet (also known as the cemented carbides). Figure 6 compares the model predictions for the hardness of WC–6% Co and tested values. During prediction, the used Young’s moduli of materials are sauced from Ref. [31]. The ratio of R(T ₀)/R(T) of the material in Figure 6(a) is assumed to be 1. The ratios of R(T ₀)/R(T) of the materials in Figure 6(b) and (c) are equal to 1 lower than 300°C, equal to the value of R(T ₀)/R(T = 300°C) in the temperature range of 300–500°C and equal to the value of R(T ₀)/R(T = 500°C) higher than 500°C. These definitions are based on the changing trends of the hardness of the materials with respect to temperature [16]. The ratios of R(T ₀)/R(T) of the materials in Figure 6(b) and (c) at 300 and 500°C are calculated by using the proposed model and the measured hardness. Figure 6 shows the excellent agreements between the measured and predicted values.

Figure 6

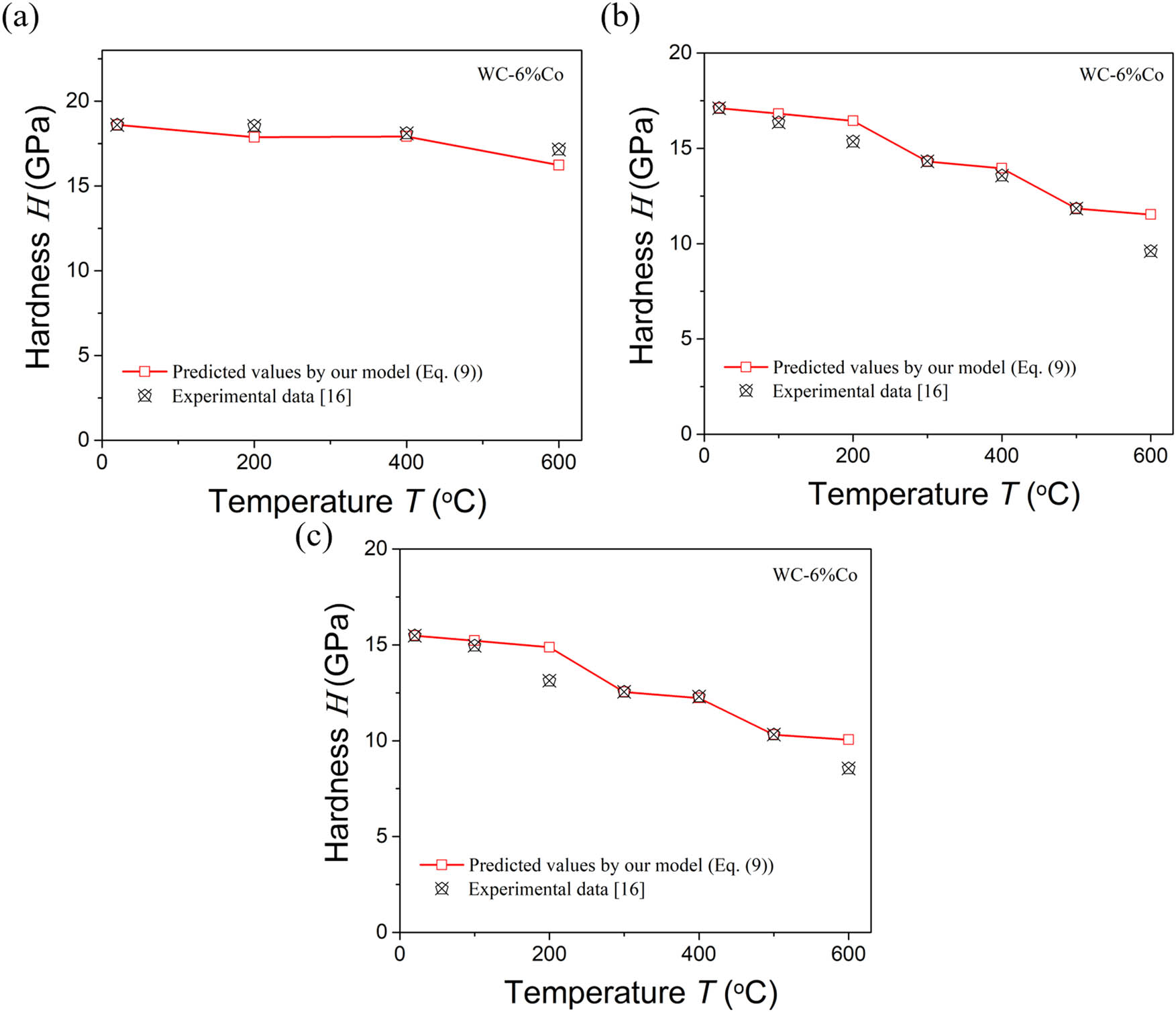
Comparison between the model-predicted and measured hardness of the WC–6% Co composites at high temperature: (a) WC–6% Co composite, (b) 0.87 WC–6% Co composite, (c) 0.87 WC–6% Co composite with pile-up.

Figure 7 compares the model predictions for the temperature-dependent hardness of WC–10% Co and tested values. During prediction, the used Young’s moduli of the materials are sauced from ref. [30]. Based on the measured temperature dependence of the hardness of the materials [16], the ratios of R(T ₀)/R(T) of the materials in Figure 7(a) and (b) are set to be 1 lower than 500°C and which are assumed to equal to R(T ₀)/R(T = 500°C) higher than 500°C. The ratio R(T ₀)/R(T = 500°C) is calculated by using the proposed model and the measured hardness at 500°C. As observed from Figure 7, the surprising excellent agreements are obtained between the model predictions and measured values, thereby showing the model’s capable of predicting the hardness of the ceramic-based cermet at high temperatures.

Figure 7

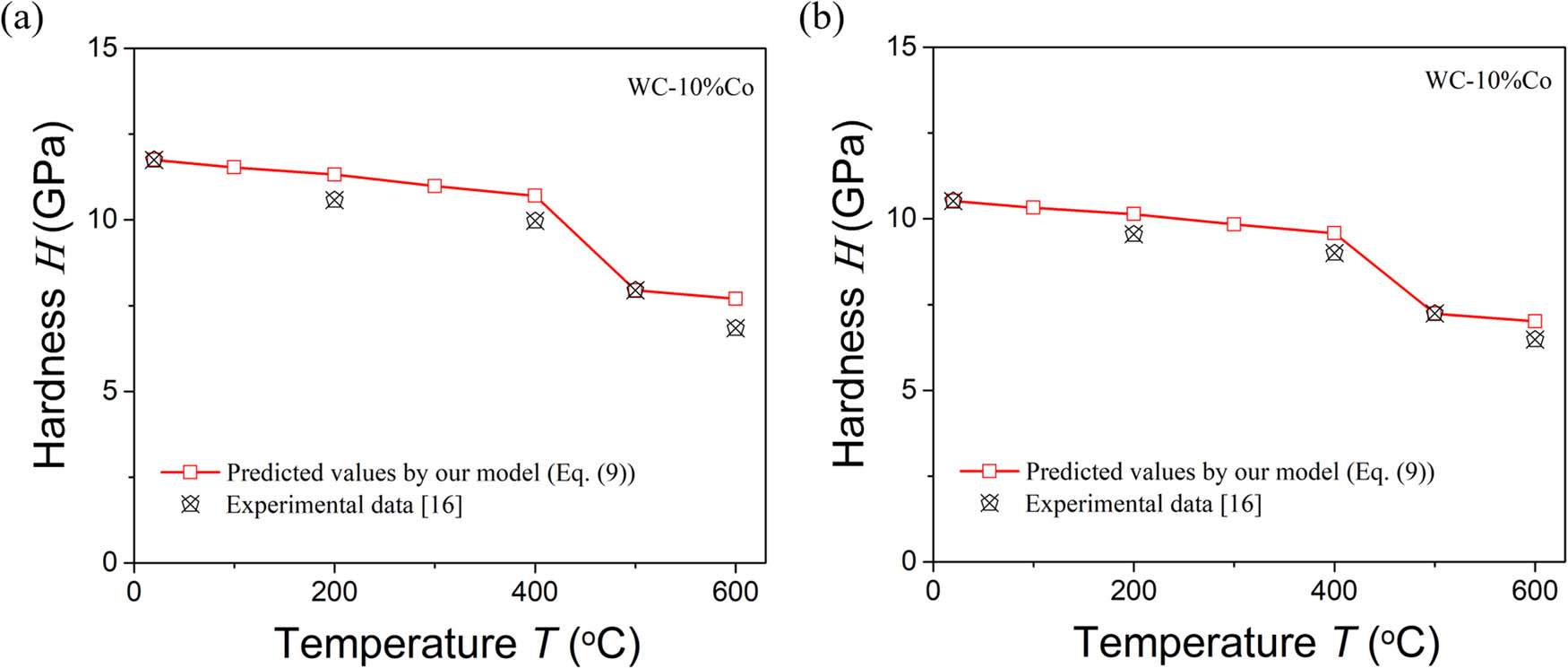
Comparison between the model-predicted and measured hardness of the WC–10% Co composites at high temperature: (a) 0.87 WC–10% Co composite, (b) 0.87 WC–10% Co composite with pile-up.

In summary, the comparisons between the model-predicted and measured values of the hardness of oxide ceramics, non-oxide ceramics, ceramic–ceramic composites, diamond–ceramic composites, porous ceramics, and ceramic-based cermet in different temperature ranges, as described earlier, illustrate the capacity of the model to predict the temperature dependence of the hardness of ceramics and their composites. When the critical damage size of the materials is nearly temperature independent in a certain temperature range, one can just use the values of Young’s modulus and melting points to obtain the temperature dependence of the hardness of the materials.

While for the materials for which the critical damage size changes with the increase of the temperature, the effect of temperature on the critical damage size should be considered. However, owing to the lack of a theoretical model that can quantitatively characterize the temperature dependence of hardness of the materials, the researchers give the many possible influencing factors while without the determined key control mechanisms. No researchers realize and propose the influence of the critical damage size and its change with the temperature on the hardness of the materials at high temperatures. Even for the fracture strength of the ceramics at high temperature, it is found that only the experimental work of Neuman et al. [5] proposed the concept of the temperature-dependent critical flaw size. The determination of the critical flaw size of the materials leads them to found the key control mechanisms (the certain microstructure) of the strength at different temperatures [5]. Therefore, with the help of the developed temperature-dependent hardness model in this work, the future work should be devoted to characterizing the effect of certain microstructures on the hardness of the materials at high temperatures, as to determine the key control mechanisms of the hardness of the materials, which can be used directly in the design of materials for the high-temperature applications.

4 Conclusion

In this work, the novel and simple theoretical models for predicting temperature dependence of the hardness of the high-temperature structural ceramics and their composites are presented. The developed temperature-dependent models are just expressed in terms of Young’s modulus, melting points, and critical damage size, which are simple for engineering applications. Several examples of oxide ceramics, non-oxide ceramics, ceramic–ceramic composites, diamond–ceramic composites, porous ceramics, and ceramic-based cermet are presented and analyzed to show that the model-predicted value agrees very well with the measured data. The authors believe that the novel models proposed in this study could provide practical and simple tools for guidelines to materials scientists and engineers in the design of high-temperature structural ceramics in critical applications. By using the developed novel model, the future work would be devoted to characterizing the effects of certain microstructures on the hardness of the materials at high temperatures, as to determine the key control mechanisms of the hardness of the materials at different temperatures. This could become a new entry point for the temperature dependence of the hardness of the materials. This can also further verify the applicability and rationality of this modeling idea.