Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations

1 Introduction

Early works of material scientists [1, 2, 3, 4] shown that carbon nanotubes (CNTs) possess unprecedentedly extraordinary mechanical, electrical and thermal properties which no previous material has displayed. In addition to these superior properties is extremely large aspect ratio of CNTs. Accordingly, CNTs are usually used as advanced filler into polymer matrix to constitute carbon nanotube reinforced composite (CNTRC), a new class of nanocomposite. In addition, structural components made of the CNTRC are widely used in advanced engineering and are expected to have promising applications in aerospace science [5]. Motivated by first work of Shen [6], subsequent studies relating to response of functionally graded carbon nanotube reinforced composite (FG-CNTRC) structures have been performed. Linear and nonlinear bending behaviors and free vibration of FG-CNTRC plates have been investigated in works [7, 8, 9, 10] based on shear deformation theories and numerical approaches. Using theory of elasticity, Alibeigloo and co-worker [11, 12] have presented results for bending problem of FG-CNTRC plates with and without piezoelectric layers. Fantuzzi et al. [13] used generalized differential quadrature method to analyze free vibration of arbitrarily shaped functionally graded carbon nanotube-reinforced plates. Basing on a higher order shear deformation theory and finite element method, Mehar et al. [14, 15] studied nonlinear vibration of FG-CNTRC single layer and sandwich plates. Nonlinear bending analysis of thick FG-CNTRC plates under the combined thermo-mechanical load has been carried out in work of Mehar and Panda [16].

Liew and collaborators [17, 18, 19, 20] made use of numerical methods and first order shear deformation theory (FSDT) to analyze linear buckling of FG-CNTRC rectangular and skew plates with and without the support of elastic foundations under compressive loads. Linear buckling and free vibration responses for FG-CNTRC plates has been analyzed by Wang et al. [21] employing semi-analytical solutions and classical plate theory (CPT). Thermal buckling and postbuckling behaviors of FG-CNTRC plates have been dealt with in works of Shen and Zhang [22] utilizing two-step iteration technique, Tung [23] using Galerkin method and Kiani [24] making use of Ritz method. Investigations on postbucking and large deflection behavior for FG-CNTRC plates under mechanical loads have been performed by Zhang and Liew [25] and Lei et al. [26], respectively, using an element-free approach.

Static and dynamic responses of FG-CNTRC cylindrical panels have been investigated in works of Zhang et al. [27] basing on a numerical approach, Alibeigloo [28, 29, 30], Pourasghar and Chen [31] using an analytical approach and Mirzaei and Kiani [32] making use of Ritz method. Kiani [33] also used Ritz method with Gram-Schmidt shape functions for free vibration analysis of FG-CNTRC spherical panels. Linear buckling of FG-CNTRC cylindrical panels subjected to mechanical loads has been treated in works of Nasihatgozar et al. [34] based on an analytical approach accounting for effects of piezoelectric layers and Garcia et al. [35] utilizing a numerical approach. Nonlinear response and postbuckling of FG-CNTRC cylindrical panels subjected to lateral pressure in thermal environments have been analyzed by Shen and Xiang [36] and Shen [37] making use of a semi-analytical approach with a two-step perturbation technique. Based on a similar approach, Shen and Xiang have presented results of post-buckling analysis for FG-CNTRC cylindrical panels resting on elastic foundations in thermal environments and subjected to axial compression [38], uniform thermal loading [39] and combined mechanical loads [40]. Basing on meshless methods, Liew and co-workers [41, 42] examined the geometrically nonlinear response and postbuckling of FG-CNTRC cylindrical panels without elastic foundation under transverse mechanical loading and uniform axial compression, respectively.

Based on several higher order shear deformation theories and generalized differential quadrature method, Tornabene and co-workers [43, 44, 45] analyzed the static and free vibration responses of laminated composite plates and doubly curved shells reinforced by agglomerated CNTs. Using finite element method and a higher order shear deformation theory, nonlinear vibration and flexural behaviors of composite single layer and sandwich doubly curved shell panels reinforced by CNTs under mechanical and thermal loads have been investigated by Mehar and co-authors [46, 47, 48, 49, 50, 51, 52]. There is a limited number of investigations on the nonlinear stability of FG-CNTRC doubly curved panels. Recently, employing a two-step perturbation technique, Shen and Xiang [53] studied the postbuckling of pressure-loaded FG-CNTRC doubly curved panels resting on elastic foundation in thermal environments. More recently, an investigation on nonlinear thermomechanical response of FG-CNTRC doubly curved panels without elastic foundations under different mechanical loads has been given by Mehar and Pandar [54] using nonlinear finite element method. It is observed that, although research subject is quite similar, nonlinear pressure-deflection equilibrium paths in the works [53] and [54] are substantially different. Specifically, pressure-loaded FG-CNTRC doubly curved panels exhibit an extremum type buckling response and relatively intense snap-through phenomenon in the work [53], whereas these panels have no buckling response and pressure-deflection paths are benignly developed in the work [54]. Previous studies on ceramic-metal FGM structures [55, 56, 57] indicated that buckling response of pressure-loaded curved panels with tangentially restrained edges may change from extremum type at room temperature to bifurcation type at elevated temperature. Very recently, thermomechanical nonlinear stability of FG-CNTRC cylindrical panels with tangentially restrained edges under external pressure and axial compression has been analyzed by Tung and Trang [58, 59].

Motivated by previous works [55, 56, 57, 58, 59] and questions relating to type of buckling response of CNTRC doubly curved panels under thermomechanical load, the present paper uses an analytical approach and Galerkin method to investigate the nonlinear stability of CNTRC doubly curved panels resting on elastic foundations and subjected to uniform external pressure in thermal environments. Basic equations for CNTRC doubly curved panels are based on the classical shell theory accounting for Von Karman-Donnell nonlinear terms, initial geometrical imperfection and Pasternak type foundation interaction. Novel findings of the present study are that buckling type of pressure-loaded curved panels may be changed due to pre-existent thermal stresses at immovable edges and efficiency of CNT distribution is influenced by panel curvature and in-plane behavior of boundary edges. Moreover, separate and combined effects of CNT volume fraction, elastic foundations, imperfection size and thermal environments on the buckling pressures and load carrying capacity of CNTRC curved panels are analyzed in detail.

2 CNT-reinforced composite doubly curved panel on an elastic foundation

Fig. 1 shows a doubly curved nanocomposite shell panel resting on a two-parameter elastic foundation and defined in a coordinate system xyz origin of which is located at a corner and on the middle surface of shell panel, x and y are in-plane coordinates and z is perpendicular to the middle surface of the panel such that z = −h/2 and z = h/2 represent the top and bottom surfaces of the panel, respectively. The plan-form dimensions in x, y directions and uniform thickness of the panel are denoted by a, b and h, respectively, and principal radii of curvature in x, y directions are denoted by R_x, R_y, respectively. The panel is reinforced by single-walled carbon nanotubes (SWCNTs) in such a way that x axis is the aligned direction of CNTs. In this study, the SWCNTs are reinforced into isotropic polymer matrix according to uniform distribution (UD) or four types of functionally graded (FG) distribution, referred to as FG−Λ, FG-V, FG-O and FG-X, and volume fraction V_CNT of CNTs corresponding to these types of distribution are defined as

Fig. 1

Configuration and coordinate system of a doubly curved panel on an elastic foundation.

where

in which w_CNT is the mass fraction of CNTs in the CN-TRC panel, ρ_CNT and ρ_m are the densities of the CNTs and matrix, respectively. Based on a micromechanical model, the overall mechanical properties of CNT-reinforced structures can be evaluated through Eshelby-Mori-Tanaka approach or theory of mixture. As shown in works of Tornabene and co-authors [43, 44, 45], the Eshelby-Mori-Tanaka approach allows to calculate the effective properties of an elastic medium with inclusions and is appropriate for CNT-reinforced structures with agglomerated carbon nanotubes, whereas the rule of mixture is simple to estimate overall properties of two-phase composites. An excellent agreement between results based on the Eshelby-Mori-Tanaka approach and those calculated according to the rule of mixture for buckling analysis of FG-CNTRC cylindrical panels is demonstrated in work of Garcia et al. [35]. In the present study, the effective Young’s moduli E₁₁, E₂₂ and shear modulus G₁₂ of the CNTRC panel are determined according to the extended rule of mixture [6]

where E11CNT,E22CNTand G12CNTare the Young’s moduli and shear modulus, respectively, of the CNT, and E^m,G^m, V_m = 1 − V_CNT are Young’s modulus, shear modulus, volume fraction of the isotropic matrix, respectively. In addition, CNT efficiency parameters η_j (j = 1, 2, 3), specific values of which are given later, are inserted into Eqs. (3) to account for the size-dependent material properties.

Similarly, effective Poisson’s ratio depending weakly on position can be estimated by

where ν12CNTand v^m are Poisson’s ratios of the CNT and matrix, respectively.

The effective coefficients of thermal expansion of the CNTRC in the longitudinal and transverse directions have the form as [6, 22]

where α11CNT,α22CNTand α^m are thermal expansion coefficients, respectively, of the CNT and isotropic matrix and, evidently, α₁₁ and α₂₂ are also graded in the thickness direction.

3 Basic equations

Based on the classical shell theory (CST), the strains across the panel thickness are expressed as

where strains of the middle surface ε_x0,ε_y0, _yxy0 and curvature changes k_x, k_y, k_xy are related to displacement components u,v and w in the coordinate directions x, y and z, respectively, as

and herein subscript prime indicates the partial derivative, e.g. u,_x = ∂u/∂x.

Stress-strain relations for a CNTRC panel in a thermal environment are expressed as

where

and ΔT is uniform temperature rise in comparison with thermal stress free state. The force and moment intensities of a CNTRC panel are related to the stress components by the equations

Through Eqs. (3), (6), (8) and (10), the constitutive relations are written in the form

where e_ij (i, j = 1 ÷ 3) and e_klT (k, l = 1 ÷ 2) are defined as in works [58, 59].

Based on the CST, the nonlinear equilibrium equations of a geometrically imperfect doubly curved panel resting on an elastic foundation are

where w^*(x, y) is a known function representing initial geometrical imperfection of the panel, q is external pressure uniformly distributed on the top surface of the panel and q_f is panel-foundation interactive pressure represented through Pasternak model as

in which Δ denotes Laplace’s operator, k₁ and k₂ are modulus of Winkler springs and the stiffness of Pasternak shear layer, respectively.

Introduction of Eqs. (7) and (11) into Eqs. (12) gives the nonlinear equilibrium equation of a CNTRC doubly curved panel as

where coefficients a_i1 (i = 1 ÷ 4) have been defined in the works [58, 59] and f (x, y) is a stress function defined as

Next, the strain compatibility equation of a geometrically imperfect doubly curved panel is [56]

From Eqs. (7), (11) and (15), the compatibility equation of a geometrically imperfect CNTRC doubly curved panel is rewritten in the form

where coefficients a_j2 (j = 1 ÷ 6) have their definitions the same as in works [58, 59].

In this study, edges of CNTRC doubly curved panels are assumed to be simply supported. Depending on in-plane behavior at the edges, the following two cases of boundary conditions are considered.

Case 1: All edges of panel are simply supported and freely movable. The associated boundary conditions are expressed as

Case 2: All edges of panel are simply supported and immovable. In this case, boundary conditions are

where N_x0, N_y0 are compressive force intensities in the x and y directions, respectively, in the Case 1 and are fictitious compressive loads at immovable edges in the Case 2.

4 Formulations

One-term solution of deflection satisfying out-of-plane boundary conditions (18) is assumed as

where W is maximum deflection and β_m = mπ/a, δ_n = nπ/b with m, n are positive integers representing numbers of half waves in the x and y directions, respectively. Similarly, the initial imperfection is assumed to be in the form of the deflection function

where μ denotes imperfection size. The stress function is assumed in the form

where A₁,A₂,A₃ are constant coefficients and these coefficients are determined by placing Eqs. (19), (20) into the compatibility equation (17) as

Now, the solutions (19a,b) and (20) are substituted into the equilibrium equation (14) and applying Galerkin method for the resulting equation yield

where coefficients a_i3 (i = 1 ÷ 4) are displayed in Eq. (34) in Appendix A and

5 Results and discussion

This section presents numerical results of the nonlinear stability analysis for CNTRC doubly curved panels made of Poly (methyl methacrylate), referred to as PMMA,as matrix material and reinforced by (10,10) SWCNTs. The temperature independent properties of the PMMA are v^m = 0.34, α^m = 45 × 10⁻⁶/K and E^m = 2.5 GPa, and those of the (10,10) SWCNTs are [22] E11CNT=5.6466TPa,E22CNT=7.0800TPa,G12CNT=1.9445TPa,α11CNT=3.4584×10−6/K,α22CNT=5.1682×10−6/K. The CNT efficiency parameters η_j (j = 1 ÷ 3) are determined by matching Young’s moduli obtained from the rule of mixture to those obtained from molecular dynamics (MD) simulations [60] and given in works [22, 38] as follows: η₁ = 0.137, η₂ = 1.022 for case of VCNT∗=0.12;η₁ = 0.142, η₂ = 1.626 for case of VCNT∗=0.17, and η₁ = 0.141, η₂ = 1.585 for case of VCNT∗=0.28. Due to lack of MD results in the work [60] for shear modulus G₁₂, it is assumed that η₃ : η₂ = 0.7 : 1 in the present study.

First, the nonlinear response of a simply supported CNTRC cylindrical panel with movable edges resting on elastic foundations and under uniform external pressure is considered as verification part of the proposed approach. Load-deflection curves corresponding to two different types of CNT distribution are depicted by using closed-form expression (24) and are shown in Fig. 2 in comparison with results of Shen and Xiang [36] using a two-step perturbation technique. As can be seen, a good agreement is achieved in this comparison.

Fig. 2

Comparison of load-deflection response for CNTRC cylindrical panels with movable edges under uniform external pressure, (m, n) = (1, 1).

The remainder of this section presents results of buckling and nonlinear response analyses for CNTRC cylindrical and spherical panels of square plan-form (a = b), side-to-thickness ratio b/h = 40 and mode shape (m, n) = (1, 1). Figs. 3 – 11 consider the CNTRC panels only subjected to uniform external pressure, whereas the nonlinear thermomechanical response of pressure-loaded CN-TRC

Fig. 3

Comparison of nonlinear response of FG-CNTRC cylindrical and spherical panels under uniform external pressure.

Fig. 4

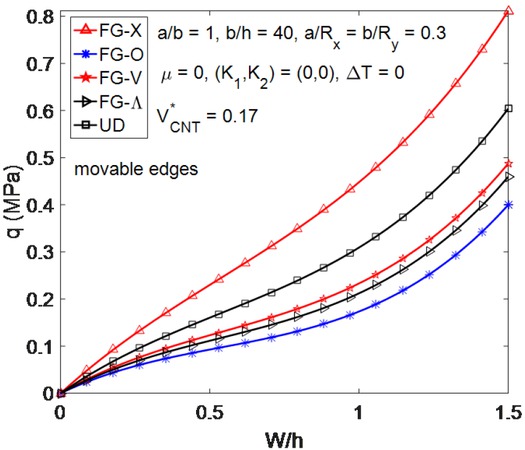
Effects of CNT distribution types on the nonlinear response of CNTRC spherical panels under uniform external pressure with movable edges.

Fig. 5

Effects of CNT distribution types on the nonlinear response of CNTRC spherical panels under uniform external pressure with immovable edges.

Fig. 6

Effects of CNT volume fraction on the nonlinear response of CNTRC spherical panels under uniform external pressure.

Fig. 7

Effects of curvature and CNT distribution on the extremum type buckling pressures of CNTRC spherical panels with immovable edges.

Fig. 8

Effects of imperfection and CNT volume fraction on the extremum type buckling pressures of CNTRC spherical panels with immovable edges.

Fig. 9

Effects of curvature on the nonlinear response of FG-CNTRC spherical panels under uniform external pressure with immovable edges.

Fig. 10

Effects of geometrical imperfection on the nonlinear response of FG-CNTRC spherical panels under uniform external pressure.

Fig. 11

Effects of elastic foundations on the nonlinear response of FG-CNTRC spherical panels under uniform external pressure with immovable edges.

panels with immovable edges in thermal environments is analyzed in Figs. 12 – 16. In addition, for the sake of brevity, the panels are assumed to be geometrically perfect and without foundation interaction, unless otherwise specified. A comparison of the nonlinear response of CN-TRC spherical and cylindrical panels under external pressure is carried out in Fig. 3. This figure indicates that load-deflection path of cylindrical panel is higher than that of spherical panel as edges are movable, and load carrying capacity of spherical panel is better than that of cylindrical panel in the small region of deflection as edges are immovable. Figs. 4 and 5 examine the effects of five different patterns of CNT distribution on the nonlinear re-

Fig. 12

Effects of CNT distribution types on the nonlinear thermomechanical response of FG-CNTRC spherical panels with immovable edges.

Fig. 13

Comparisons of the nonlinear thermomechanical response of CNTRC cylindrical and spherical panels with immovable edges.

Fig. 14

Effects of curvature and temperature on the nonlinear response of FG-CNTRC spherical panels on elastic foundation with immovable edges.

Fig. 15

Effects of CNT volume fraction and elastic foundation on the nonlinear thermomechanical response of FG-CNTRC spherical panels with immovable edges.

Fig. 16

Effects of imperfection and curvature parameters on the nonlinear thermomechanical response of FG-CNTRC spherical panels with immovable edges.

sponse of CNTRC spherical panels under uniform external pressure with movable and immovable edges, respectively. When all edges are movable, the load-deflection paths corresponding to FG-X and FG-O types of CNT distribution are the highest and lowest, respectively, and uniform distribution (UD) of CNTs results in higher load-deflection paths of CNTRC panels in comparison with those corresponding to the remaining three types of FG distribution (i.e. FG-V,FG − Λ and FG-O). It should be emphasized that the load bearing capability of FG-X panel is remarkably higher than that of UD, FG-V,FG − Λ and FG-O panels, and load-deflection curve of FG-V panel is slightly higher than that of FG − Λ panel as all edges are movable as demon-

strated in the Fig. 4. In a very alternative tendency, FG-V and FG−Λ types of CNT distribution give the highest and lowest pressure-deflection curves of CNTRC panels, respectively, when the deflection is small, and FG-X type yields the most beneficial nonlinear response of the panels in the deep region of deflection in the immovable case of in-plane restraint, as illustrated in the Fig. 5. This figure also indicates that intensity of snap-through response, measured by difference between upper and lower buckling pressures, of FG-V and FG-X CNTRC panels are very severe and benign, respectively. Next, Fig. 6 proves that load-deflection paths are considerably enhanced as CNT

volume fraction VCNT∗ is increased from 0.12 to 0.28. In addition, snap-through phenomenon may occur for CNTRC panels with higher percentage of CNT volume and immovable edges. As shown in Figs. 3 – 6, pressure-deflection paths of CNTRC panels with movable edges are low and quite stable, whereas these paths are much higher and snap-through instability can occur for CNTRC panels with immovable edges.

Subsequently, Fig. 7 indicates that the upper buckling pressures of FG-V and FG − Λ CNTRC panels are the highest and lowest, respectively, and difference between upper buckling pressures corresponding to these types of FG dis-

tribution is increased as the panel is more curved. Fig. 8 assesses the effects of CNT volume fraction and imperfection size μ on the buckling pressures, in which positive and negative values of μ describe initial perturbation of panel surfaces towards concave and convex sides (i.e. positive and negative directions of deflection) of the panel, respectively. As can be seen, the upper buckling pressures are continuously decreased when the imperfection size μ is increased from −0.2 to 0.2 for CNTRC panels with and without foundation interaction. Furthermore, the rate of reduction of buckling pressures is faster for higher value of CNT volume fraction. Next, the nonlinear response of FG-X and FG-V CNTRC spherical panels with immovable edges and

different values of curvature is compared in Fig. 9. It is evident that load-deflection path corresponding to FG-X type is pronouncedly higher than that corresponding to FG-V type for relatively shallow panel (a/R_x = b/R_y = 0.1 in this example). Conversely, load carrying capability of FG-V panel is higher than that of FG-X panel as the panel is relatively more curved (a/R_x = b/R_y = 0.5 in this example). Fig. 10 shows the effects of initial geometrical imperfection on the nonlinear response of pressure-loaded CN-TRC spherical panels with movable and immovable edges. When edges are movable, initial imperfection has mild effect on the nonlinear response of the panel and load-deflection curve is enhanced due to increase in imperfection size μ as the deflection exceeds a definite value. In contrast, buckling point pressure, load bearing capacity and intensity of snap-through of the panels are considerably decreased as μ increases from −0.1 to 0.1 and edges are immovable. Overall, initial geometrical imperfection may change the curvature of panel and, as a result, has significant influence on the nonlinear response of the panel, especially for case of immovable edges. As final example for mechanical response analysis, Fig. 11 demonstrates an expected fact that buckling loads and nonlinear equilibrium paths of CNTRC panels are pronouncedly improved due to increase in CNT volume percentage and/or the support of elastic foundations. In addition, severity of snap-through phenomenon of CNTRC curved panels may be reduced, even prevented, because of elastic foundations, especially Pasternak type foundations.

The nonlinear thermomechanical response of pressure-loaded CNTRC doubly curved panels with immovable edges in thermal environments is analyzed in Figs. 12 – 16. Fig. 12 examines the effects of five different types of CNT distribution on the nonlinear thermomechanical stability of CNTRC spherical panels. As predicted in previous section, CNTRC curved panels exposed to a thermal environment and mechanically loaded by external pressure will experience a bifurcation type buckling response the nature of which may be explained as follows. Pre-existent thermal stress developed at immovable edges make the curved panel deflected outwards (i.e. negative direction of deflection) and external pressure must reach a definite value equaling bifurcation point pressure in order for the panel returns reference state. It is interesting to note that bifurcation buckling pressure of UD CNTRC panel is the highest and bifurcation buckling pressures corresponding to four types of FG distribution are almost the same. Another important remark is that CNTRC curved panels under thermomechanical load exhibit an unstable postbuckling response and intensity of snap-through instability is the weakest and strongest for FG-X and FG-V panels, respectively. Next, the nonlinear thermomechanical response of CNTRC spherical and cylindrical panels is compared in Fig. 13. It is observed that both bifurcation buckling load and postbuckling load capacity of CNTRC cylindrical panel is very much lower than those of CNTRC spherical panel. In other words, the CNTRC cylindrical panel is easily deteriorated under thermomechanical load, whereas the CNTRC spherical panel can withstand the harmful action of thermomechanical loading efficiently. Fig. 14 considers the effects played by curvature parameters a/R_x , b/R_yon the nonlinear response of pressure-loaded CNTRC spherical panels with immovable edges in thermal environments. In general, bifurcation type buckling pressure and postbuckling load bearing capability of CNTRC spherical panels are remarkably enhanced when the curvature of panel is increased. Specifically, the panel is buckled later and postbuckling strength is higher for larger value of curvature parameters. Next illustration relating to the effects of CNT volume fraction and elastic foundation on the nonlinear thermomechanical response of CNTRC spherical panels is displayed in Fig. 15. It is clear that bifurcation buckling pressures and initial postbuckling strength of the panels are significantly increased when the panels are enriched by CNTs. In particular, CNT-richer panels may experience a more intense snap-through phenomenon in deep region of postbuckling response. It is very interesting to note that bifurcation buckling pressures are not depended on elastic foundations, although these foundations have beneficial influences on load carrying capability of CNTRC spherical panels as the deflection is sufficiently large. Finally, the combined effects of the curvature and initial imperfection parameters on the nonlinear thermomechanical response of FG-CNTRC spherical panels on Pasternak foundation are given in Fig. 16. Evidently, both bifurcation point pressure and initial postbuckling strength (in small region of deflection) of the panels are basically decreased as the imperfection size μ is increased from −0.1 to 0.1. A worth note is gained is that more shallow CNTRC panel will exhibit an immediate snap-through response, whereas more curved CNTRC panel (a/R_x = b/R_y = 0.3 in this illustration) will experience a delayed snap-through response. More specifically, pressure-deflection curves are immediately dropped after bifurcation type buckling for small values of curvature, whereas pressure-deflection curves are increased in initial region of postbuckling deflection for larger values of curvature.

6 Concluding remarks

The geometrically nonlinear, buckling and postbuckling responses of pressure-loaded CNTRC doubly curved panels resting on elastic foundations in thermal environments have been presented. The results show that buckling loads and load carrying capability of CNTRC panels are enhanced when CNT volume fraction and/or stiffness parameters of elastic foundations are increased. In addition to this expected conclusion, the following remarks are reached:

1. Load-deflection paths of CNTRC doubly curved panel are lower and monotonically developed as edges are movable, whereas these paths are considerably higher and the panel may experience an extremum type buckling response followed by snap-through instability as edges are immovable.

2. Generally, the FG-X type of CNT distribution results in the best effects on the nonlinear response of doubly curved panels because the FG-X CNTRC panels have basically higher capabilities of buckling resistance and load bearing, and more benign snap-through response. Particularly, the FG-V type leads to the highest buckling pressure and the best capacity of load carrying among five types of CNT distribution for relatively curved panel with immovable edges.

3. Pressure-loaded CNTRC doubly curved panels with immovable edges exposed to elevated temperature may exhibit a bifurcation type buckling response. Bifurcation point pressure and thermomechanical postbuckling load capacity are remarkably enhanced when temperature and/or curvature of panel are elevated.

4. Initial geometrical imperfection can cause a change in the curvature and, as a result, significantly influences the nonlinear stability of the panel, especially for thermomechanically loaded CNTRC panels with immovable edges.

A Appendix

The coefficients a_i3 (i = 1 ÷ 4)in Eqs. (22) are defined as

in which

B Appendix

The details of coefficients b_ij (i = 1 ÷ 3, j = 1 ÷ 2) in the Eqs. (27) are

in which

The details of coefficients b _k3 (k = 1 ÷ 6) in the Eq. (28) are