Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating

1 Introduction

Coating hydrodynamics has been an area of considerable interest since the monumental paper by Landau and Levich (1942) in which an elegant formulation was developed for the thickness of the film of a fluid which is deposited on a plate withdrawn vertically from a bath at constant velocity. This work was however confined to Newtonian viscous fluids. In many modern industries non-Newtonian fluids are encountered e.g. in polymer coating processes (Lawrence and Zhou, 1991). Numerous researchers have therefore investigated coating dynamics of different stationary or rotating geometrical bodies (plates, cones, spheres, cylinders) with non-Newtonian liquids and have employed a range of mathematical constitutive equations. Jenekhe and Schuldt (1984) studied coating flows of power-law and Carreau fluids on spinning disks. Campanella et al. (1986) investigated dip coating of a circular cylinder in non-Newtonian power-law fluids. Zevallos et al. (2005) presented a finite element simulation of forward roll coating flows of viscoelastic liquids using both Oldroyd-B and FENE-P models. These studies however ignored heat transfer which may be critical in certain coating systems (Mitsoulis, 1986). The diffusion of heat can modify polymer properties significantly (Mark, 1996). Several authors have therefore studied thermofluid transport in non-Newtonian external coating flows. Cao and Cui (2015) examined Ostwald-DeWaele pseudo-plastic fluids in free convection flow in porous media. Choudhury and Das (2016) employed the Reiner-Rivlin second order differential viscoelastic model for reactive magnetized thermosolutal convection in porous media. Thirumurugan and Vasanthakumari (2016) utilized the Walters B viscoelastic model to investigate the thermosolutal convection in two-phase porous media transport. Prasad et al. (2013) and Subba Rao et al. (2016) investigated computationally the momentum and heat transfer characteristics in external boundary layer slip flow of a viscoplastic fluid from a cylinder.

The classical Navier–Stokes theory does not describe sufficiently the flow properties of polymeric fluids, colloidal suspensions, and fluids having certain additives. Eringen (1966) proposed therefore the theory of micropolar fluids which exhibit micro-rotation effects as well as micro-inertia. Micropolar fluids are fluids with microstructure. They belong to a class of fluids with non-symmetric stress tensor also known as polar fluids. Micropolar fluids include as a special case the conventional Navier-Stokes model of classical viscous fluids that we shall call ordinary fluids. Physically micropolar fluids consist of arbitrarily oriented particles suspended in a viscous medium. The formulation for micropolar fluid theory allows their implementation in boundary layer flows, of relevance to materials processing, and has resulted in considerable activity among researchers. Yacob et al., (2011) proposed a mathematical model to characterise the melting heat transfer in both stretching and shrinking sheet flows of a micropolar fluid. Prakash and Sinha (1976) applied micropolar fluid theory to simulate lubrication squeeze films for circular disks, deriving analytical expressions for film characteristics. Papautsky et al. (1999) employed micropolar fluid theory to study low speed flows in micro-machined rectangular metallic pipette arrays. Bhargava et al. (2016) analyzed the thermo-solutal convection in a cavity containing micro polar fluid with a variation finite element method. Latiff et al. (2015) used Maple software to analyse the multiple slip effects on transient forced bio convection flow of a micro polar nanofluid from a stretching/shrinking sheet with applications in materials fabrication. Alam et al. (2015) used Eringen’s micropolar model to study transient Falkner-Skan magnetic convection flows. Transport from external surfaces of curved bodies e.g. vertical cones has also stimulated some interest in recent years. Such flows are of relevance to chemical engineering systems and also materials synthesis. Cheng (2015) studied the free convection heat transfer from a non-isothermal permeable cone with suction and temperature-dependent viscosity. Solchana et al. (2016) analysed the momentum, heat and mass transfer behaviour of magneto hydrodynamic flow towards a vertical rotating cone in porous medium with thermophoresis and Brownian motion effects. Cheng (2015) examined the natural convection heat transfer about a vertical cone embedded in a porous medium with isothermal wall conditions. Yih (1999) studied the effect of thermal radiation flux on free convection about a truncated cone. Gorla et al. (1986) investigated the micro polar convection boundary layer flow from a cone.

An interesting model in non-Newtonian fluid mechanics is the viscoelastic Jeffrey fluid model. This model degenerates to a Newtonian fluid at a very high wall shear stress. This fluid model also approximates reasonably well the rheological behaviour of a wide range of industrial liquids including biotechnological detergents, physiological suspensions, dense foams, geological sediments, cosmetic creams, syrups, etc. Many researchers have explored a range of industrial and biological flow problems using the Jeffery model. Prasad et al. (2014) and Subba Rao et al. (2015) studied external Jeffery viscoelastic boundary layer flow from a circular cylinder using an implicit finite difference code and showed that with increasing Deborah numbers there is a fall in Nusselt number (heat transfer rate) and the skin-friction coefficient. Tripathi and Bég (2013) analysed peristaltic propulsion with thermal diffusion using the Jeffery model. Hayat et al. (2015) simulated the polymeric thermal flow from a stretching cylinder in Jeffery viscoelastic liquid. Further studies of viscoelastic transport phenomena with the Jeffery’s model include, Kodandapani et al. (2008), Nadeem et al. (2009), Hayat et al. (2012). The Jeffery model quite accurately describes the characteristics of relaxation and retardation times which arise in certain polymeric flows. Furthermore, this model utilizes time derivatives rather than converted derivatives, which facilitates numerical solutions in boundary value problems.

Relatively few studies have considered polymeric external boundary layer flows from curved bodies where the fluid possesses both microstructural and viscoelastic characteristics. Prasad et al. (2015) have studied nanoscale micropolar convection from a cylinder. However they did not consider viscoelastic effects. Thus, the objective of the current study is to examine the viscoelastic micropolar heat transfer in external boundary layer flow from a cone using the Jeffery non-Newtonian (2005) and Eringen micropolar models (2001). This is the novelty of this article.

2 Mathematical Model

The regime under investigation is natural convection boundary layer flows of incompressible viscoelastic micropolar fluid (polymeric liquid) from a vertical isothermal solid cone, as shown in Fig. 1. Both cone and liquid are maintained initially at the same temperature. Fourier’s law is assumed for heat conduction i.e. thermal relaxation effects are negated. Thermal stratification and dispersion are also neglected as is viscous heating. The flow is laminar, steady-state and the cone surface isothermal. These conditions correspond to steady polymeric convection in external boundary layer flow development on an axisymmetric cone geometry. Instantaneously the cone surface is raised to a temperature T_w> T_∞, where the latter (ambient) temperature of the polymeric fluid is maintained as constant. The x-coordinate is measured along the slant surface of the cone from the origin (at the vertex) and the y - coordinate is directed normal to the cone surface. The cone has a semi-vertex angle of A.

Fig. 1

Physical model and coordinate system

With the Boussinesq buoyancy and boundary layer approximations, the governing equations for the conservation of mass, momentum, micro-rotation and energy can be written in two-dimensional Cartesian coordinates (x, y) as follows:

Here r is the local radius of the truncated cone, and v are the velocity components in x and y directions, Tand are the temperature and angular velocity of the viscoelastic micropolar fluid, k and j are the vortex viscosity and micro inertia density, y^* = (μ + 0.5k) j is the spin gradient viscosity, υ=μρis the kinematic viscosity of the viscoelastic micropolar fluid, μ is the dynamic viscosity of the viscoelastic micropolar fluid and ρ is the fluid density. Furthermore, α is the thermal diffusivity, β is the coefficient for thermal expansion and g^* is the gravitational acceleration. With regard to the viscoelasticity in the polymeric liquid considered, this is simulated via the λ parameter i.e. the ratio of relaxation to retardation times, and λ₁ parameter i.e. the retardation time. The following boundary conditions are imposed:

Here T_∞ is the free steam temperature. We introduce a stream function defined by the Cauchy-Riemannequations, ru=∂ψ∂yandrv=−∂ψ∂xand therefore, the mass conservation eqn. (1) is automatically satisfied. Furthermore, the following dimensionless variables are introduced into eqns. (2) – (4):

Here all parameters are defined in the notation at the end of the article. The following non-dimensional partial differential equations for momentum and energy conservation therefore emerge:

The eight corresponding dimensionless boundary conditions emerge as:

Here primes denote the differentiation with respect to non-dimensional transverse co-ordinateηHere we also define the micropolar material parameters:

The local Nusselt number of the inverted cone can be written as

In equation (12),

Here h is the local heat transfer coefficient and k is the thermal conductivity of the micropolar viscoelastic fluid.

3 Numerical Solution With Keller Box Implict Method

In this study the Keller-box implicit difference method is implemented to solve the non-linear eight order system of coupled boundary layer eqns. (7) – (9) subject to the boundary conditions (10). This method continues to be popular in boundary layer flows. Recent works employing Keller’s box scheme include Cheng (2008) for micropolar non-isothermal flow from a truncated cone, Bég et al. (2016) for micro polar wall plume dynamics in permeable systems, Malik et al. (2015) and Subba Rao et al. (2017) for magnetic polymeric flows and Gaffar et al. (2015) and Subba Rao et al. (2017, 2018) for viscoelastic heat transfer from curved bodies. Very few of these papers however have provided guidance for researchers as to customization of the Keller-box scheme to heat transfer problems. We have included details of the discretization procedure below. Implementation of Keller’s scheme involves the following four stages:

1. Reduction of the N^th order partial differential equation system to N first order equations

2. Finite Difference Discretization

3. Quasilinearization of Non-Linear Keller Algebraic Equations

4. Block-tridiagonal Elimination of Linear Keller Algebraic Equations

4 Keller Box Method (KBM) Numerical Results and Discussion

Moreover, in order to verify the accuracy of present method, the analytical results obtained in the present work were compared with those available in the literature, obtaining an excellent agreement with those given in Alam et al. [19] for particular values of ξ. The table presents the influence of increasing the tangential coordinate ξ on the skinfriction and local nussult number results. Increaseing ξ, is found to decrease skinfriction and increse heat transfer rate. There is a vast change in skin friction and heat transfer rate when taking the larger values of ξ.

Comprehensive solutions have been obtained and are presented in Figs. 2 – 19. We examine the influence of several key parameters, namely Deborah number (De), ratio of relaxation to retardation times (λ), Prandtl number (Pr), micropolar parameter (R) i.e. vortex to dynamic viscosity ratio and micro-inertia density parameter (B). The effect of

Fig. 2

Influence of De on velocity.

Fig. 3

Influence of De on the temperature.

Fig. 4

Influence of De on the angular velocity.

Fig. 5

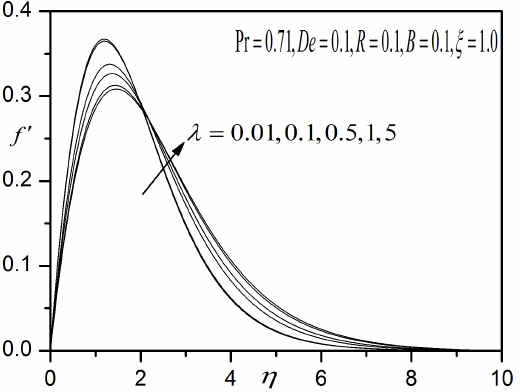
Influence of λ on the velocity.

Fig. 6

Influence of λ on the temperature.

Fig. 7

Influence of λ on the angular velocity.

Fig. 8

Influence of R on the velocity.

Fig. 9

Influence of R on the temperature.

Fig. 10

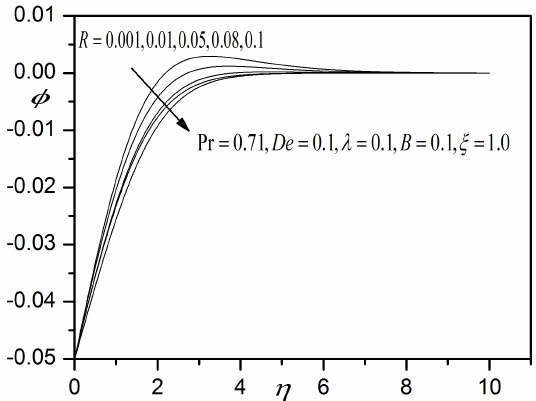
Influence of R on the angular velocity.

Fig. 11

Influence of B on the velocity.

Fig. 12

Influence of B on the temperature.

Fig. 13

Influence of B on the angular velocity.

Fig. 14

Influence of Pr on the velocity.

Fig. 15

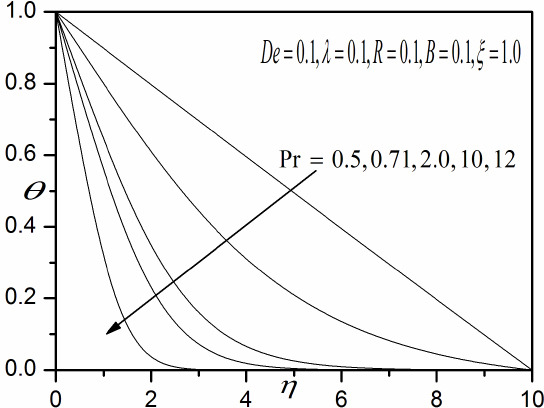
Influence of Pr on the temperature.

Fig. 16

Influence of Pr on the angular velocity.

Fig. 17

Influence of De on Nusselt number.

Fig. 18

Influence of R on the Nusselt number.

Fig. 19

Influence of Pr on the Nusselt number result.

the stream wise coordinate (ξ) is not explicitly examined. Default parameter values prescribed are: De = 0.1, λ = 0.1, Pr = 0.71, R = 0.1, B = 0.1, ξ = 1.0. In the graphs the angular velocity (g) is denoted asφ.

Figures 2 – 4, illustrate the influence of Deborah number on velocity (f^′), temperature (θ) and angular velocity (Ø). Dimensionless velocity component (Fig. 2) is considerably reduced with increasing De values. De arises in connection with some higher order derivatives in the momentum boundary layer equations, (7), i.e., −De1+λ2f′f‴−(f″)2+7ffiv+4ξfivand also ξ−De1+λf′∂f‴∂ξ−f‴∂f′∂ξ+f″∂f″∂ξ−fiv∂f∂ξ. This parameter therefore exerts a significant influence on shearing characteristics of the polymer flow. Deborah number is defined as the ratio of the characteristic time to the time scale of deformation. For a fixed value of the characteristic time, there may be different values of the time scale of deformation and hence there can be many different Deborah number values for the same polymer. If De > 1.0, elastic effects are dominant while if De < 0.5, viscous effects prevail. For any values other than these two extremes, the material would depict viscoelastic behaviour. For polymers i.e., for non-Newtonian fluids, higher De values correspond to the polymer becoming highly oriented in one direction and stretched. For very high De values, the fluid movement is too fast for elastic forced to relax and the material acts as a purely elastic fluid. For small De values, the time scale of fluid moment is much greater than the relaxation time of elastic forces in the polymer. In Fig. 3 an increase in Debroah number enhance temperature throughout the boundary layer regime. This has also been observed by Hayat et al. (2012). In Fig. 4 with increasing De values, there is a substantial decrease in angular velocity i.e. microelement rotary motion is inhibited. The heat transfer rate is substantially decreased with increasing De values. There is a progressive decay in heat transfer rate with incresing the tangential coordinate. Adecrease in heat transfer rate at the wall imply less heat is convected from the fluid regime to the cone, thereby heating the boundary layer

Figures 5 – 7 present the effect of the ratio of relaxation ()to retardation times i.e., λ on velocity (f^′), temperature (θ) and angular velocity (Ø) distributions throughout the boundary layer regime. A significant increase in velocity is observed with increasing λ values. Conversely, temperature is markedly reduced with increasing values of λ. Also increasing λ is seen to increase the angular velocity significantly i.e. encourage spin of the micro-elements.

Velocity is significantly incresed with increasing λ. The polymer flow is therefore considerbly accelarated with an increase in relaxation time (or decrease in retardation time).

The mathematical model reduces to the Newtonian viscous flow model as λ → 0and De → 0, since this negates relaxation, retadation and elasticity effects.The momentum boundary layer equation in theese cases contracts to the familiar equation for Newtonian mixed convection from the cone:

Effectively with greater relaxation time of the polymer the thermal boundary layer thickness is reduced.

Figures 8 – 10 depicts the effect of the vortex viscosity parameter (R) on velocity, f′temperature (θ) and angular velocity (Ø). For R = 1, the micropolar and Newtonian dynamic viscosity are equivalent. For R = 0, micropolarity is neglected and the equations reduce to the non-polar case. Although relatively simple in definition, R, has a prominent influence on all the flow variables. We observe in Fig. 8 that an increase in R strongly decelerates the flow i.e. damps linear velocity. Fig. 9 demonstrates that with stronger micro-polarity i.e. greater R value, the temperatures are elevated in the boundary layer. The regime is significantly heated and thermal boundary layer thickness is increased. The increased vortex viscosity encourages thermal diffusion i.e. energizes the flow. This increases the efficiency of thermal convection within the body of the fluid from the microscopic to the macroscopic scale and effectively transports heat with greater intensity from the cone surface into the fluid regime. Fig. 11 depicts that strong reversal of micro-element rotation is induced very close to the wall (cone surface) with increasing R values.

Figures 11 – 13 depict the influence of velocity f′, temperature (θ) and angular velocity for different values of material parameter B. It is observed that an increase of B significantly decelerates the flow, i.e. depresses velocity throughout the boundary layer regime. The temperature is also decreased with increasing B values. Conversely with increasing material parameter, B, the angular velocity (micro-rotation) is increased, indicating that faster gyratory motions of micro-elements are induced.

Figures 14 – 16 represent typical profiles for (f^′), temperature (θ) and angular velocity (Ø) for various values of Pr. It is observed that an increase in Pr decreases in velocity. The most prominent variation in profiles arises at intermediate distances from the cone surface. Furthermore, increasing Pr generates a substantial reduction in the fluid temperature and the thermal boundary layer thickness. At large Pr, the thermal boundary layer is thinner than at a smaller Pr. This is associated with the fact that for small Prandtl numbers the fluid has very high thermal conductivity. An increase in Pr from 0.5 through 0.71, 2.0, 10, 12 as shown in Fig. 14, substantially decelerates the flow i.e. reduces hydrodynamic boundary layer thickness. Similarly higher Prandtl number, which corresponds to lower thermal conductivity of the polymer results in a marked depression in temperatures (fig. 16). The lower thermal conductivity of denser polymers inhibits thermal diffusion via conduction heat transfer. Less heat is therefore conveyed from the cone surface (wall) into the boundary layer and thermal boundary layer thickness is decreased.

Increasing Pr as observed in Fig. 16, reduces angular velocity i.e stifles micro-element spin (angular deceleration).

Figures 17 – 19 presents the Nusselt Number comparisons for different values of De, R and Pr respectively: Increasing Deborah number, decrease the Nusselt number i.e reduces heat transfer from the viscoelastic micropolar fluid to the cone wall. Increasing vortex viscosity parameter, R is also seen to decrease the Nusselt number. Increasing Prandtl number, Pr is observed to enhance the Nusselt number since temperatures are reduced in the fluid and greater heat is convected to the cone surface. This inevitably has implications for cooling of thin film coatings.

5 Conclusions

A mathematical model has been developed for the buoyancy-driven, natural convection boundary layer flow of a viscoelastic micropolar fluid from a vertical isothermal cone. The Jeffery non-Newtonian and Eringen microstructural models have been used to simulate different rheological characteristics. The transformed boundary layer conservation equations have been solved with prescribed boundary conditions using the finite difference implicit Keller–box method which has second order accuracy. A comprehensive assessment of the effects of Deborah number De, ratio of retardation to relaxation timeλ, vortex viscosity parameter, Prandtl number Pr, micro-inertia density parameter B. Excellent convergence and stability characteristics are demonstrated by the Keller box scheme which is capable of solving very strongly nonlinear rheological problems.

The present simulations have shown that:

1. (i) Increasing Deborah number, De reduces velocity and Nusselt number whereas it increases temperature and angular velocity (micro-rotation of micro-elements).

2. (ii) Increasing ratio of retardation to relaxation time, λ increases the velocity and angular velocity whereas it reduces the temperature (and thermal boundary layer thickness).

3. (iii) Increasing Eringen vortex viscosity parameter, R decreases the velocity and angular velocity whereas it elevates temperature.

4. (iv) Increasing micro-inertia density parameter, B, reduces velocity and temperature whereas it enhances angular velocity.

5. (v) Increasing Prandtl number, Pr decreases velocity, temperature and angular velocity.

6. (vi) Increasing Deborah number and vortex viscosity parameter both depress Nusselt numberwhereas an increase in Prandtl number enhances the Nusselt number (heat transfer rate at the cone surface).

The current study has neglected rotation of the cone and therefore Coriolis body force effects, which are also relevant in polymer chemical processing operations, for example in spin coating processes. These will be considered in the near future.