Abstract
The separately excited Direct Current (DC) motor is widely used in many industrial sectors. During the operation of the DC motor, the load torque and the voltage of the network can cause a destabilization of the actual speed and actual current. Thus, the need to regulate the speed and current of the DC motor is a very important research problem. In this paper, a control strategy of separately excited DC motor using a series multi-cells chopper is described. The proposed control is based on Proportional-Integral (PI) and Petri nets controllers. Specifically, the conventional PI controller is used to control the speed of DC motor. The Petri nets controller ensures the regulation of the armature current and to maintain the capacitor voltage of the multi-cells converter to its reference. The Petri nets controller also generates binary control switches. The proposed control system has been implemented using MATLAB Sim Power. Simulation results demonstrate that a series multi-cells chopper and the proposed control give a good performance and high robustness in load disturbance for the separately excited DC motor.
1 Introduction
Many industrial sectors such as robotics, steel rolling mills, electric cranes, and grinding, electrical vehicles use the DC motor [1, 2, 3, 4, 5, 6]. Some important advantages in using the DC motor can be listed as follows:
A DC motor is controllable for a wide range and it can be easily used for constant torque and speed.
A DC motor can be rapidly accelerated or decelerated, and can respond to feedback control, low cost and less complex control structure.
There are several ways to vary the speed of the DC motor such as field flux control and rheostatic armature control. The rheostatic armature control method is just used in the case of low power. The speed of the DC motor can also be varied by varying the armature voltage. In this case, a portion of the energy is consumed by the feeding device. For this reason, it is preferable to feed the DC motor discontinuously with a controlled rectifier or with a buck chopper. The traditional buck chopper is used in many works as in [7, 8, 9, 10, 11, 12].
In this work, a series multi-cells chopper structure is used to control the separately excited DC motor. The series multi-cells chopper structure is based on the series association of elementary switching cells [13, 14, 15, 16]. This structure, which appeared at the beginning of the 1990s, allows the sharing of voltage constraints by all commutation series connected cells and flying capacitors, where the flying capacitor voltages determine the output waveform quality and the safe converter operation. The multi-cells converter is used in different applications such as harmonics filtering, renewable energy systems, and voltage dynamic restoration.
During the operation of the DC motor, the load torque and the voltage of the network can cause a destabilization of the actual speed and actual current, which is not desired. Thus, it is important to regulate the speed and the current of the DC motor. The regulation works on two sides: (i) on the speed of the DC motor and (ii) the armature current to keep it within acceptable limits in the situations such as rapid start, sudden change in the resistive torque, sudden braking or very rapid increase in the set point of the speed.
The structure of the DC motor controller of the speed generally consists of two loops. The first loop compares the actual speed with the speed reference, and the second loop controls the armature current.
Proportional-Integral (PI) controller is often to control the motor speed of the DC motor. The major features of the PI controller are its simplicity and ability to maintain a zero steady-state error to a step change in reference. Instead of using another PI or hysteresis controller to regulate the armature current as used in [4, 5, 6, 17, 18, 19, 20], we propose the use of the Petri nets controller.
The role of the Petri nets controller is to achieve both the armature current tracking and a good balance of the capacitor voltage of 2-cells chopper with respect to the tolerance errors of armature current and capacitor voltage .The outputs of the Petri nets controller generate binary control switches which boot up the IGBTs of the two cells chopper. A control based on Petri nets is proposed in [26] to control a three multi-cells chopper connected to R, L load. The experimental results have shown the performance of the proposed controller.
The Petri nets controller minimizes the number of the commutations compared to the PWM control (see [21, 22, 23, 24, 25, 26]).It is important to improve the content of the output energy and the efficiency of the system by the reduction of the switching losses.
This paper is organized as follow: The modeling of separately excited DC motor is presented in Section 2.The modeling of the driving system based on series multi-cells chopper is given in Section 3.The proposed control strategy is presented in Section 4. The simulation results are tested and analyzed in Section 5. Finally, a conclusion is drawn in Section 6.
2 Modeling of Separately Excited DC Motor
The separately excited DC motor has two windings and each one of them is powered by a separate power supply voltage. Figure 1 shows the equivalent circuit of separately excited motor, where Ra and La represent the resistance and the inductance of the armature winding, respectively. The resistance and the inductance of the field winding are denoted by Rf and Lf, respectively. Also, Ea is the emf induced in the armature circuit, ω the motor speed, kb is the back emf constant, Te,TL are the motor and the load torque, respectively, B is the viscous friction coefficient and J is the total inertia of motor.
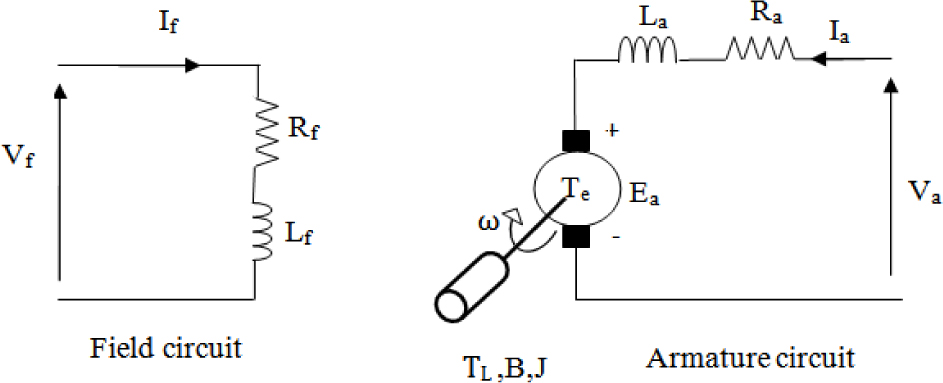
Separately excited DC motor
The mathematical model of the DC motor consists of electrical and mechanical equations. These two groups of equations allow us to understand better the DC motor in its real operation. This model is governed by the following equations:
3 Series Multi-cells Chopper Model
Figure 2 represents a p–cells chopper connected to the DC motor. It is based on the association of p commutation cells where each one is composed of pairs of complementary switches [27]. We insert flying capacitors between these complimentary switches later. Each cell is controlled by a binary function uk(t) ∈ {0,1},k = 1,2,…, n, where uk = 1 indicates that the upper switch is closed, and thelower switch is open.
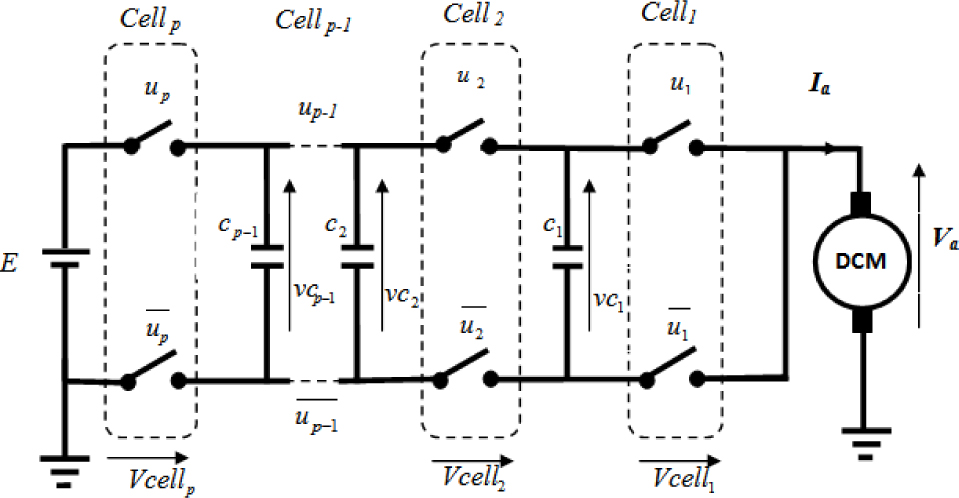
p–cells chopper structure
The instantaneous model of a multicellular chopper with a p–cells connected to DC motor is described by the system of equations (5).
where
In our application, the two cells chopper is used. Thus, the system (5) becomes:
In Eq. (8), Vc1 is the capacitor voltage, and u1,u2 are the binary switches.
To ensure normal operations, it is necessary to guarantee a balanced distribution of the floating voltages, i.e.
The hybrid model of the two cells chopper is given as follows.
where
Also, u is the vector of interconnection
Table 1 represents the different configurations of the two cells chopper, depending on the position of switches. In this case, we have 22 = 4 discrete modes.
Operating modes of the 2-cells chopper
| U2 | Ul | VC1 | Va |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | –VC1 | E/2 |
| 1 | 0 | –VC1 | E/2 |
| 1 | 1 | 0 | E |
4 Control Strategy
The control model scheme of a PI - Petri nets controller of the separately excited DC motor is shown in Figure 4.The control scheme consists of two parts: (i) a continuous part and (ii) a discrete part. The first part is based on the PI controller. The inputs of the PI controller are the reference speed and the actual speed. The output is the armature current reference, which is compared with actual armature current. The second part is based on the Petri nets controller to regulate the armature current and the capacitor voltage. The control strategy consists to regulate the capacitor voltage VC1 to the reference value VC1ref and to regulate the armature Ia current to the reference value Iaref.
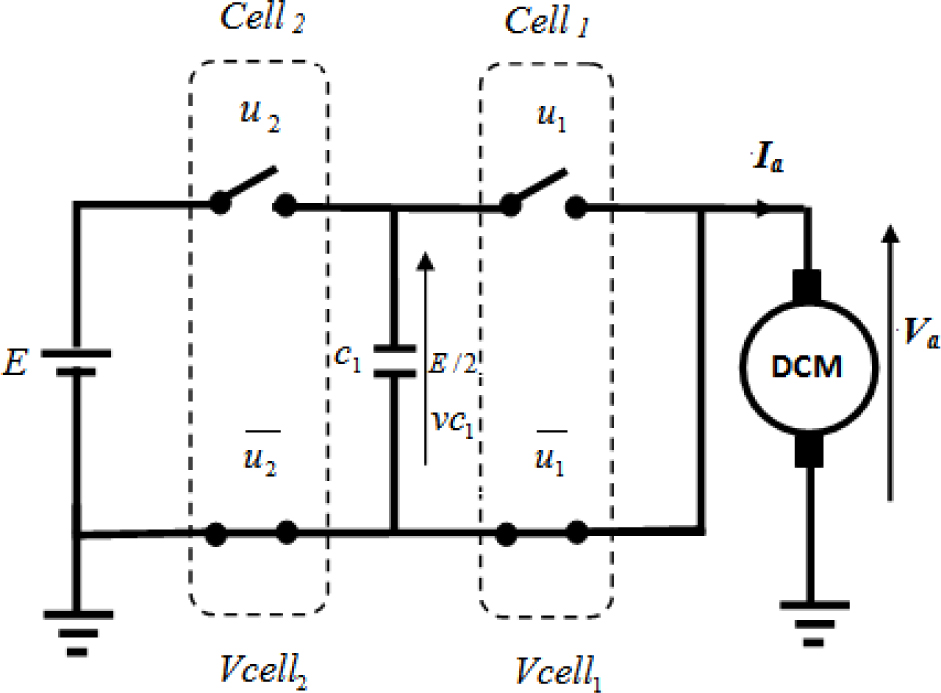
Two cells chopper connected to DC motor
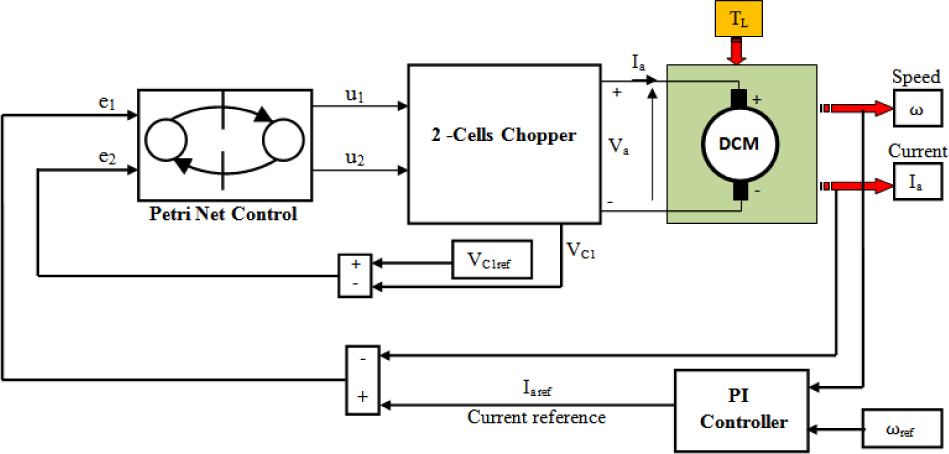
Design of PI-Petri nets Controller for a SEDCM
To ensure this regulation, a hysteresis methodology is used [25, 26].
An operating band (tolerance errors) is provided such that the load current and capacitor voltage rest inside:
where δ1 and δ2are the tolerance errors of load current and capacitor voltage, respectively. The states of the binary switches of cell1 and cell2 are denoted by u1,u2, respectively, which are modeled by the two places P1 and P2 (Figure 5).The converter is allowed to configure by two possible configurations. In the first configuration, only one switch is allowed to be passing. In the second configuration, two switches are allowed to be passing.
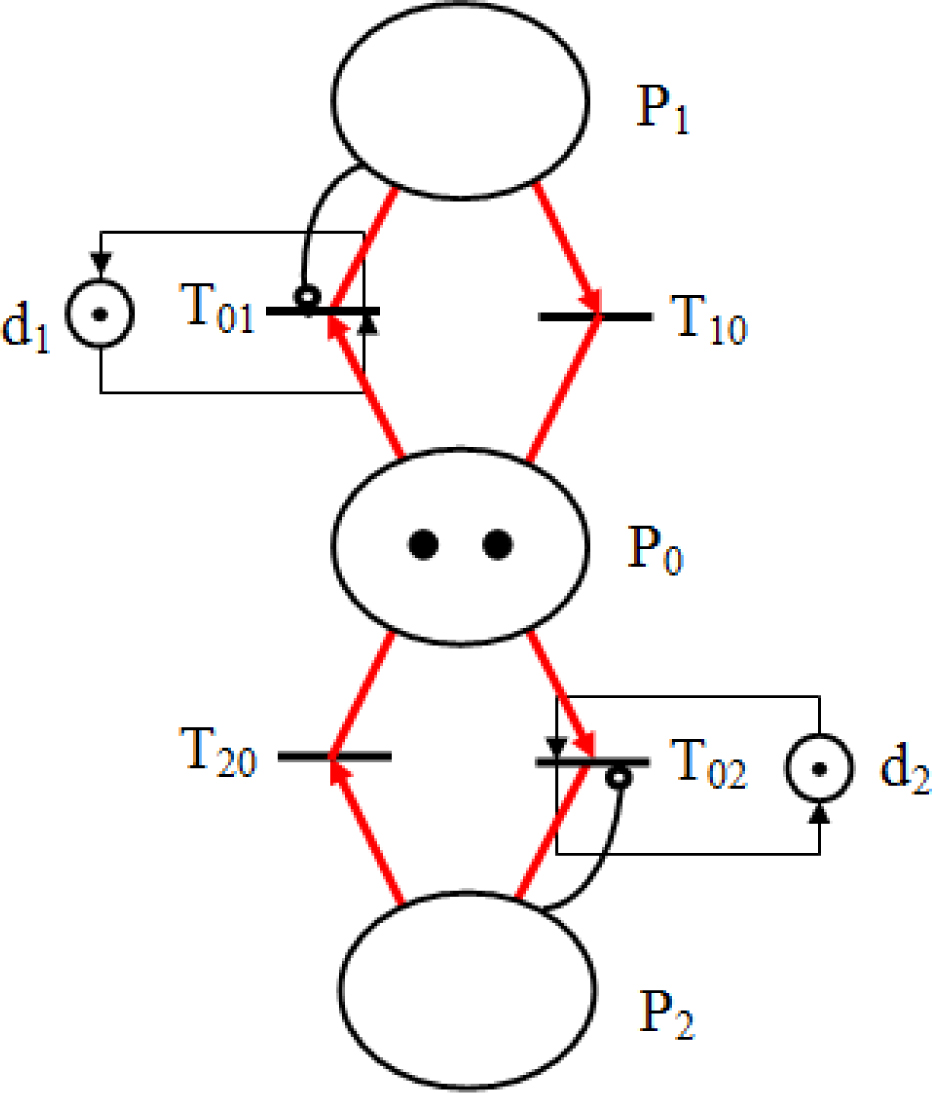
Petri net graph for a control switches of 2-cells chopper
The significance of all places and transitions are shown in Table 2.The closure of the switch of the cell (Celli) depends on the validation of the transition ti0 and the elapsed delay di, i = 1,2 (d1 of P1 for the switching Cell1 and d2 of P2 for the switching Cell2). It is noted that the time allowed between two successive commutations is modeled by the delay di. In this work, the delays of P1 and P2 places are considered as the same d1 = d2 = 2E – 5s). Finally, the presence of two arcs inhibitors in the proposed Petri net control leads to prevent the presence of more than one token in places P1 and P2.
Signification of Places
| Places | Designations |
|---|---|
| P0 | The initial state of the commutation switches |
| P1 | The state of the switch of the first cell |
| P2 | The state of the switch of the second cell |
Transitions from one place to another depend on the admissible errors of output current andcapacitor voltage as shown in Table 3.
Transitions
| Transitions | Designations |
|---|---|
| T01 | (e1 ≥ δ1 or -δ1 < e1 < δ1)and e2 < – δ2 |
| T02 | (e1 ≥ δ1 or – δ1 < e1 < δ1)and e2 > δ2 |
| T10 | (e1 ≥ – δ1 or – δ1 < e1 < δ1) and e2 > δ2 |
| T20 | (e1 ≥ – δ1 or and e2 < – δ2 |
In Table 3, δ1 is the load current tolerance error and δ2 is the capacitor voltage tolerance error. After many tests to define the safe values of the load current and the capacitor voltage tolerance errors, we found that for the values of δ1 and δ2 chosen as δ1 = 0.01A and δ2 = 0.2V we get the optimum functioning of our system.
For the two cells chopper, four transitions are possible. For example, the T01 transition is firing if the armature current error is superior or equal to the positive tolerance of the output current, i.e. e1 ≥ δ1. In this case, the current must increase. Thus, the u1 switch is committed to open and hence T01=1. If the armature current is inside the hysteresis band, i.e. the T01 transitionis depending on the capacitor voltage. If the capacitor voltage is less than the negative tolerance error of the voltage capacitor, i.e. the capacitor should be unloaded, and the transition T01 is reached.
5 Simulations and Results
The parameters used in this work are the parameters of the available separately excited DC motor in the LATAGE laboratory. After carrying out several tests of identification of the parameters, the Separately excited DC motor and multicellular chopper characteristics are given in Table 4.
The separately excited DC motor and the two cells chopper parameters
| Nominal motor speed ω | 157rad/s |
| Power | 3 Kw |
| Nominal armature voltage Va | 300 V |
| Nominal Field voltage Vf | 110 V |
| Armature resistance Ra | 1.35 Ω |
| Field resistance Rf | 65,15 Ω |
| Armature inductance La | 0.0059 H |
| Field inductance Lf | 8.35 H |
| Field-armature mutual inductance | 1.07 H |
| Back Emf constant kb | 1.41 V/rd/s |
| Viscous friction coefficient B | 0.0045 N.m.s |
| Total inertia J | 0.036 kg.m^2 |
| Capacitance C1 | 33 μF |
| Voltage source E | 300 V |
| VClref = E/2 | 150V |
The PI-Petri Nets controller was simulated using Matlab-Simpower System software and the speed controller of the separately excited motor was successfully tested. Three performance testing are made as follows:
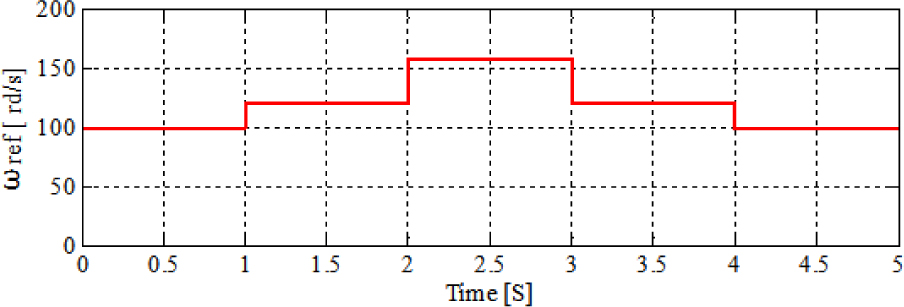
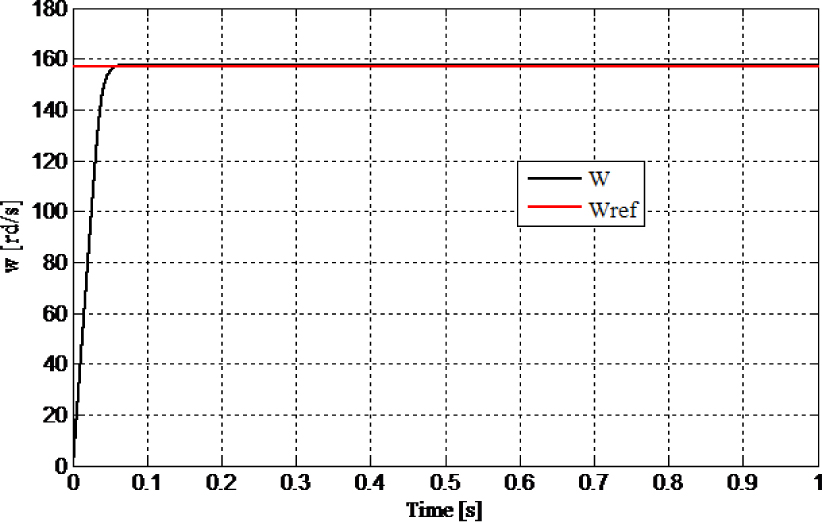
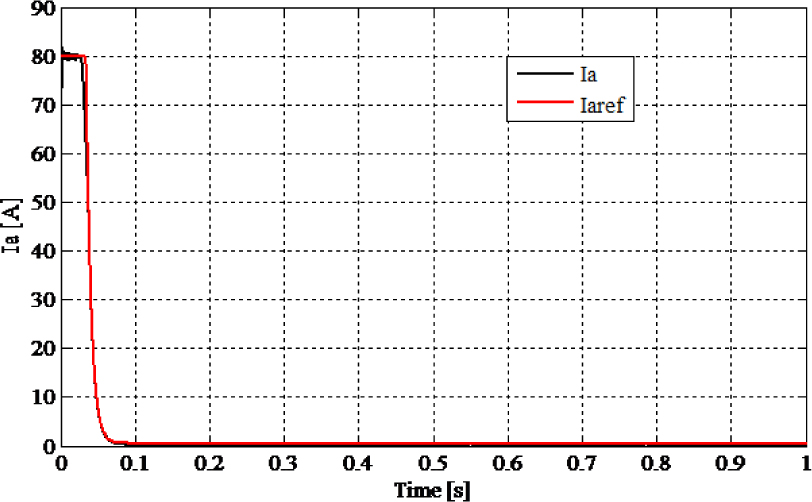
The reference speed change according to the protocol shown in Figure 6 with the load conditions (5 Nm). Figures 9 and 10 show the corresponding simulation results.
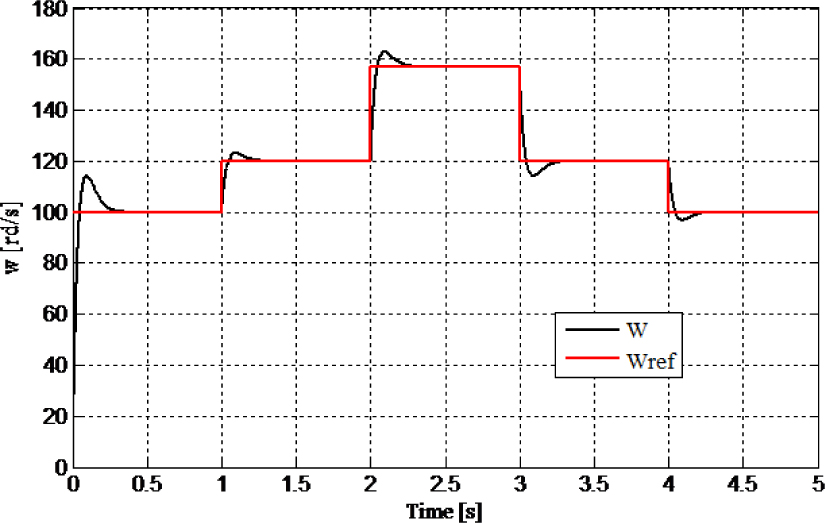 Fig. 9
Fig. 9Rotor speed of the motor (variation of the speed reference)
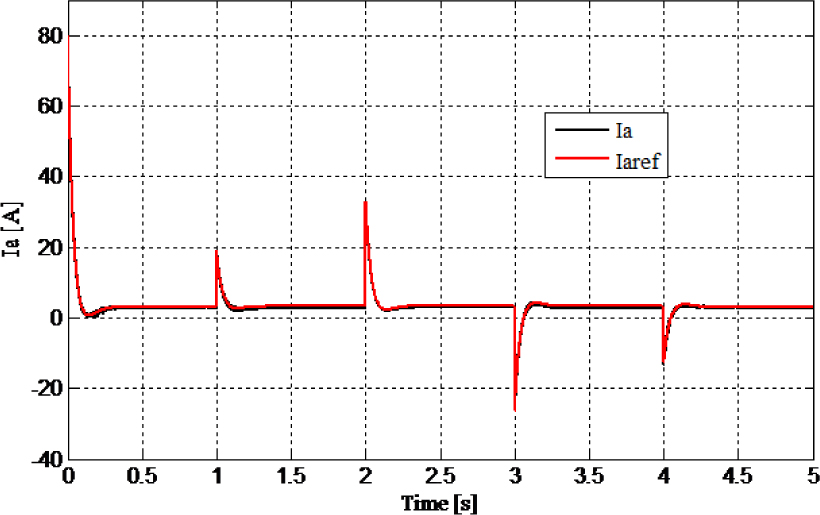 Fig. 10
Fig. 10Armature current and its reference (variation of the speed reference)
The load torque change at t=2.5 s from 5 Nm to 15 Nm and the corresponding simulation results are shown in Figures 11 and 12.
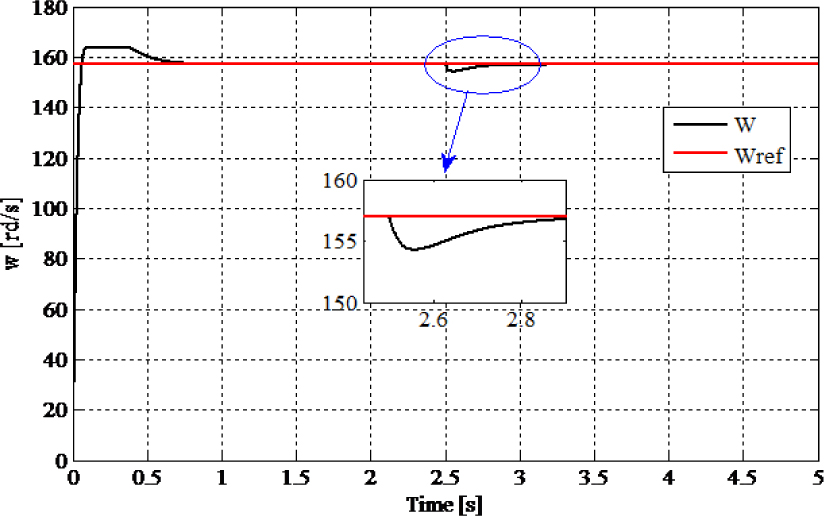
Rotor speed of the motor (speed reference fixed and the torque is changed from 5 Nm to 10 Nm at t = 2.5 s)
The simulation results confirm that using the multicellular chopper in the proposed control scheme gives good results in the closed-loop control scheme. It is clear that the proposed PI-Petri nets controller permits to regulate the motor speed to its reference in a short time. The Petri nets controller shows a good tracking of armature current in a short time and is perfectly maintained between the desired bands. It also showed that the floating voltage reach its desired value in a short time and is well balanced around the reference value (Figure 13) with respect to the predefined tolerance error.
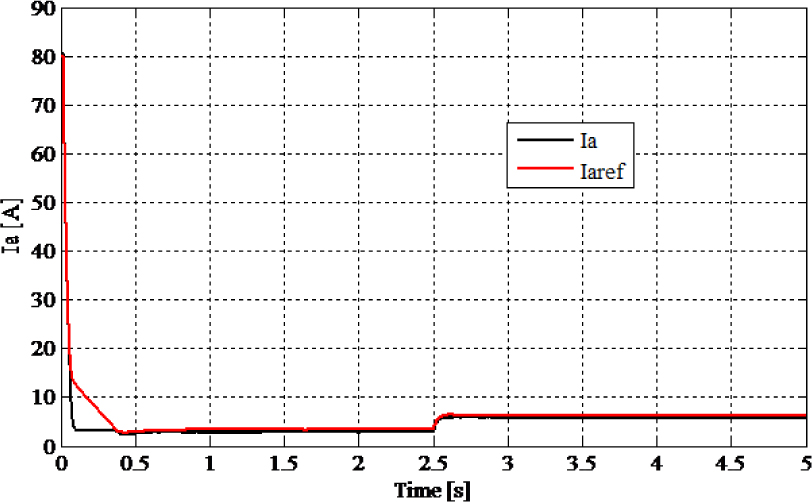
Armature current and its reference (speed reference fixed and the torque is changed from 5 Nm to 10 Nm at t = 2.5 s)
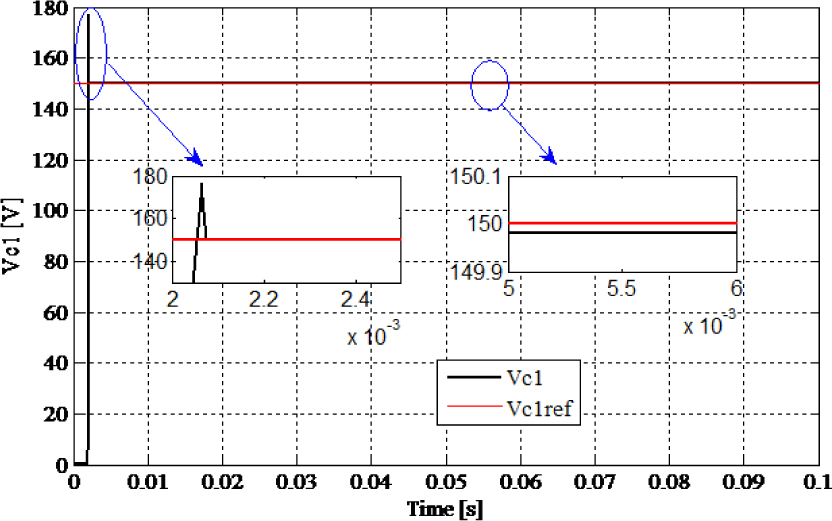
Capacitor voltage
6 Conclusion
The PI-Petri nets controller proposed in this paper regulates successfully the speed and the armature current of the separately excited DC motor. We use the multi-cells chopper converter to feed the separately excited DC motor, and the combination of the PI and Petri nets controllers. Explicitly, the use Petri nets controller instead of just a PI controller in our control strategy gives interesting results. On one hand, the armature current tracks perfectly its reference, and on the other hand the capacitor voltage is perfectly regulated, which ensures a safe converter operation and minimizes the losses in the system. This improves the quality of output energy and the lifetime of the DC motor. It is also noted that the proposed controller can be readily implemented in practice. As a future work, we are working to develop our control method with a multi-cells chopper model more than two cells, which further improves the quality of the output energy.
References
[1] A.Z. Ahmad and M.N. Taib, “A study on the DC motor speed control by using back-EMF voltage”, Asian Conference on Sensors (AsiaSense 2003), pp. 359-364, 2003.10.1109/ASENSE.2003.1225047Search in Google Scholar
[2] M. Zeraoulia, M.E.H. Benbouzid and D. Diallo, “Electric motor drive selection issues for HEV propulsion systems: A comparative study,”IEEE Transactions on Vehicular Technology, vol. 55, no. 6, pp. 1756-1764, 2006.10.1109/VPPC.2005.1554571Search in Google Scholar
[3] S. Tharani, P. Palpandian and N. Gowthaman, “Speed control of a separately excited dc motor using optimization techniques,” International Journal of Innovative Research in Computer and Communication Engineering, vol. 2, pp. 3924-3934, 2014.Search in Google Scholar
[4] N. Jeddi, N. Ouasli, L. El Amraoui and F. Tadeo, “Speed control of a separately-excited DC motor powered by photovoltaic energy,” IREC2015 - The Sixth International Renewable Energy Congress, pp. 1-6, 2015.10.1109/IREC.2015.7110895Search in Google Scholar
[5] R. Nagarajan, S. Sathishkumar, K. Balasubramani, C. Boobalan, S. Naveen and N. Sridhar, “Chopper fed speed control of DC motor using PI controller,” IOSR Journal of Electrical and Electronics Engineering, vol.11, pp. 65-69, 2016.Search in Google Scholar
[6] K. Shantanu and U. Chand bind, “Performance analysis of separately excited DC motor using PI and fuzzy logic controller,” International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, vol.6, pp. 4109- 4019, 2017.Search in Google Scholar
[7] M. George “Speed control of separately excited DC motor,” American Journal of Applied Science, vol.5, pp. 1546-9239, 2008.10.3844/ajassp.2008.227.233Search in Google Scholar
[8] R. Abhinav and S. Sheel, “An adaptive, robust control of DC motor using fuzzy-PID controller,”2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, pp. 1-5, 2012.10.1109/PEDES.2012.6484325Search in Google Scholar
[9] V.R. Vadapalli, H.K. Kella, T.R. Sekhar, Y.D. Samson and N. Avinash, “Speed control of DCmotor using chopper”, International Journal of Electrical and Electronics Research, vol. 3, pp. 289-295, 2015.Search in Google Scholar
[10] R. Nagarajan, S. Sathishkumar, S. Deepika, G. Keerthana, J.K. Kiruthika and R. Nandhini, “Implementation of chopper fed speed control of separately excited DC motor using PI controller”, International Journal of Engineering and Computer Science, vol. 6, pp. 20631-20633, 2017.10.18535/ijecs/v6i3.42Search in Google Scholar
[11] K.S. Deshmukh and R.S. Hiware, “Speed control of separately excited DC motor using chopper,” International Research Journal of Engineering and Technology, vol. 4, pp. 799-803, 2017.Search in Google Scholar
[12] A. Harrouz, H. Becheri, I. Colak and K. Kayisli, “Backstepping control of a separately excited DC motor,” Electrical Engineering, https://doi.org/10.1007/s00202-017-0592-5, 2017.10.1007/s00202-017-0592-5Search in Google Scholar
[13] G. Gateau, Contribution à la commande des convertisseurs statiques multicellulaires: Commande non linéaire et commande floue, Ph.D. dissertation, INPT, French, 1997.Search in Google Scholar
[14] O. Tachon, Commande découplante linéaire des convertisseurs multicellulaires série, Ph.D. dissertation, INPT, French, 1998.Search in Google Scholar
[15] T.A. Meynard, H. Foch, P. Thomas, J. Courault, R. Jakob and M. Nahrstaedt, “Multicell converters: basic concepts and industry applications”, IEEE Transactions on Industrial Electronics, vol.49, pp. 955-964, 2002.10.1109/TIE.2002.803174Search in Google Scholar
[16] S. Ben Said, K. Ben Saad and M. Benrejeb, “HIL simulation approach for a multicellular converter controlled by sliding mode,” International Journal of Hydrogen Energy, vol. 42, pp. 12790-12796, 2017.10.1016/j.ijhydene.2017.01.198Search in Google Scholar
[17] R.K. Munje, M. R. Roda and B.E. Kushare, “Speed control of DC motor using PI and SMC”, IEEE International Conference on Power and Energy, Singapore, pp. 945-950, 2010.10.1109/IPECON.2010.5696985Search in Google Scholar
[18] P. M. Meshram and R. G. Kanojiya, “Tuning of PID controller using Ziegler-Nichols method for speed control of DC motor,” IEEE-International Conference on Advances in Engineering, Science and Management (ICAESM -2012), Nagapattinam, Tamil Nadu, India, pp. 117-122, 2012.Search in Google Scholar
[19] D.C. Chengaiah and K. Venkateswarlu, “Comparative study on DC motor speed control using various controllers”, Global Journal of Researches in Engineering Electrical and Electronics Engineering, vol. 13, pp.19-22, 2013.Search in Google Scholar
[20] C. Kumar, D. Tanti, “Speed control of separately excited D.C. motor,” Second International Conference on Emerging Trends in Engineering and Management Research (ICETEMR-2017), Pune, India, pp. 29-39, 2017.Search in Google Scholar
[21] R. David and H. Alla, Discrete, Continuous, and Hybrid Petri Nets, Springer, Berlin, Germany, 2005.Search in Google Scholar
[22] B.C. Florea, D.A. Stoichescu and V. Stefanescu, “A Petri net approach to multicellular chopper control,” 2011 IEEE 17th International Symposium for Design and Technology in Electronic Packaging (SIITME), Timisoara, pp. 227-230, 2011.10.1109/SIITME.2011.6102723Search in Google Scholar
[23] B. Amghar, M. Darcherif and J.-P. Barbot. “Z(TN)-Observability and control of parallel multicell chopper using Petri nets,” IET Power Electronics, vol. 6, no. 4, pp.710-720, April 2013.10.1049/iet-pel.2012.0374Search in Google Scholar
[24] B.C. Florea, “Petri net modeling for hybrid systems control. Application for a multicellular converter,” 2013 Eighth International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, pp. 1-4, 2013.10.1109/ATEE.2013.6563526Search in Google Scholar
[25] F. Salinas, M. Ghanes, J.P. Barbot, M.F. Escalante, and B. Amghar, “Modeling and control design based on petri nets for serial multicellular choppers,” IEEE Transactions on Control Systems Technology, vol. 23, no. 1, January 2015.10.1109/TCST.2014.2313553Search in Google Scholar
[26] F. Salinas, M. A. González, M. F. Escalante and J. de León Morales, ”Control design strategy for flying capacitor multilevel converters based on Petri nets,” IEEE Transactions on Industrial Electronics, vol. 63, no. 3, pp. 1728-1736, 2016.10.1109/TIE.2015.2494535Search in Google Scholar
[27] K. Benmansour, Réalisation dďun banc dďessai pour la commande et lľobservation des convertisseurs multicellulaires série: Approche hybride, Ph. D. Dissertation, Cergy Pontoise University, France, 2009.Search in Google Scholar
© 2019 M.L. Hamida et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Articles in the same Issue
- Chebyshev Operational Matrix Method for Lane-Emden Problem
- Concentrating solar power tower technology: present status and outlook
- Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
- Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
- Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
- Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
- Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
- Local convergence for an eighth order method for solving equations and systems of equations
- Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
- Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
- A reliable analytical approach for a fractional model of advection-dispersion equation
- Mass transfer around a slender drop in a nonlinear extensional flow
- Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
- A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
- An effective technique for the conformable space-time fractional EW and modified EW equations
- Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
- New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
- Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
- A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
- Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
- Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
- Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
- MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
- Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
- Swirling flow of couple stress fluid due to a rotating disk
- MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
- Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
- Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
- Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
- On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
- An adaptive mesh method for time dependent singularly perturbed differential-difference equations
- On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
- Rational exponential solutions of conformable space-time fractional equal-width equations
- Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
- Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
- Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
- Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
- Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
- Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
- Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
- An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
- New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
- Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
- Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
- Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
- Mathematical model on distributed denial of service attack through Internet of things in a network
- Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
- Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
- MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
- A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
- Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
- Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
- Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
- Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
- Combination synchronization of fractional order n-chaotic systems using active backstepping design
- Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
- Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
- Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
- Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
- Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
- Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
- Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
- A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
- A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
- A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
- The expa function method and the conformable time-fractional KdV equations
- Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
- Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
- MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
- MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel
Articles in the same Issue
- Chebyshev Operational Matrix Method for Lane-Emden Problem
- Concentrating solar power tower technology: present status and outlook
- Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
- Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
- Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
- Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
- Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
- Local convergence for an eighth order method for solving equations and systems of equations
- Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
- Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
- A reliable analytical approach for a fractional model of advection-dispersion equation
- Mass transfer around a slender drop in a nonlinear extensional flow
- Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
- A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
- An effective technique for the conformable space-time fractional EW and modified EW equations
- Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
- New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
- Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
- A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
- Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
- Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
- Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
- MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
- Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
- Swirling flow of couple stress fluid due to a rotating disk
- MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
- Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
- Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
- Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
- On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
- An adaptive mesh method for time dependent singularly perturbed differential-difference equations
- On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
- Rational exponential solutions of conformable space-time fractional equal-width equations
- Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
- Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
- Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
- Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
- Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
- Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
- Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
- An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
- New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
- Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
- Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
- Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
- Mathematical model on distributed denial of service attack through Internet of things in a network
- Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
- Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
- MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
- A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
- Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
- Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
- Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
- Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
- Combination synchronization of fractional order n-chaotic systems using active backstepping design
- Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
- Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
- Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
- Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
- Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
- Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
- Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
- A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
- A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
- A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
- The expa function method and the conformable time-fractional KdV equations
- Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
- Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
- MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
- MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel