Abstract
This study is devoted to investigate the influence of transverse magnetic field as well as suction/injection on MHD natural convection flow of conducting fluid in an inclined micro-porous-channel. The analytical solutions for velocity profile and temperature profile have been obtained considering the velocity slip and temperature jump conditions at the micro-porous-channel walls. The solution obtained for the velocity has been used to compute the skin friction, while the temperature has been used to compute the Nusselt number. The effect of various flow parameters entering into the problem are discussed with the aid of line graphs. Results reveal that the impact of inclination angle on fluid velocity is dependent on the value of the wall ambient temperature difference ratio, hence increase in inclination angle yields an enhancement in fluid velocity within the micro-porous-channel for some selected values of the wall ambient temperature difference ratio whereas it displays a dual character for other values. Also, injecting through the micro-porous channel thickens the thermal boundary layer, resulting to weakening the convective current and consequently decreasing the fluid velocity whereas suction weakens the thermal boundary layer yielding an increase in fluid velocity.
1 Introduction
The mechanics of fluid flow in micro-channels has emerged as an active area of research in view of the enormous applications in various branch of industry such as biomedical industry, computer chip manufacturing and separation processes in chemical industry operations among others. Literatures on convective flow in vertical micro-channel are numerous. Extensive investigation have been conducted recently on micro-geometry flow under different physical situations (Chen and Weng [1], Jha et al. [2], Khadrawi et al. [3], Hadded et al. [4], Buonomo and Manca [5], Weng and Chen [6], Jha et al. [7], Avci and Aydin [8, 9], Jha and Aina [10]).
However, the magnetohydrodynamic (MHD) phenomenon has received considerable attention of engineers and scientists over the last two decades owing to its relevance in many MHD applications like MHD generator, MHD accelerators, electric transformers and cooling of metallic plate in cooling bath. Magnetohydrodynamic (MHD) pumps are already in use in chemical energy technology for pumping electrically conducting fluids at some of the atomic energy centre. Several studies have been reported on MHD convective flow under different physical situations. Record of such investigations can be found in the works of Cramer and Pai [11], Chawla [12], Das et al. [13], Sheikholesslami and Gorgi-Bandpy [14], Sheikholesslami et al. [15], Sheikholesslamiet al. [16], Chauhan and Rastogi [17], Ibrahim and Makinde [18], Farhad et al. [19, 20]. Hasan Nihal Zaidi and Naseem Ahmad [21] have discussed MHD convection flow of two immiscible fluids in an inclined channel with heat generation or absorption. Wang et al. [22] experimentally investigated the effect of inclination angle on the convective boiling performance of a micro-channel heat sink. They found that the heat transfer coefficient for 45∘ upward considerably exceeds other configurations. The combined influence of externally applied transverse magnetic field and suction/injection on steady natural convection flow of conducting fluid in a vertical micro-channel was carried out by Jha et al. [23]. In another work, Jha et al. [24] examined the effect of wall surface curvature on transient MHD free convective flow in vertical micro-concentric-annuli. Jha et al. [25] studied exact solution of steady fully developed natural convection flow of viscous, incompressible, and electrically conducting fluid in a vertical annular micro-channel. Recently, Jha and Aina [26] presented the MHD natural convection flow in a vertical micro-porous-annulus (MPA) in the presence of radial magnetic field. Also, the MHD natural convection flow in vertical micro-concentric-annuli (MCA) in the presence of radial magnetic field has been analyzed by Jha et al. [27]. Farhad et al. [28] investigated the effect of magnetic field on blood flow of Casson fluid in axisymmetric cylindrical tube. Farhad et al. [29] presented a study on the application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’- B fluid model. Hidden phenomena of magnetohydrodynamic time dependent flow in porous medium with heat transfer was carried out by Farhad et al. [30]. In a related work, Sheikh et al. [31] investigated on modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium. Other literatures on the above subject can be found in [32, 33, 34, 35, 36, 37, 38, 39].
Some recent works related to the present investigation are found in the literature [40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52]. Nanofluid treatment in a porous enclosure considering thermal non – equilibrium model under the impact of magnetic field has been analyzed by Sheikholeslami and Shehzad [40]. Sheikholeslami and Seyednezhad [41] numerically studied Fe304-Ethylene glycol nanofluid electrohydrodynamics flow and natural convection heat transfer in a porous medium. Sheikholeslami and Moradi [42] studied the influence of thermal radiation on nanofluid behaviour in existence of Couloumb forces via CVFEM. Sheikholeslami [43] numerically investigate for Cu0-H20 nanofluid flow in a porous channel with magnetic field using mesoscopic method. Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure was carried out by Sheikholeslami [44]. Sheikholeslami and Rokni [45] present numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation. In another related article, Sheikholeslami and Shehzad [46] presented numerical analysis of Fe304-H20 nanofluid flow in permeable media under the effect of external magnetic source. Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method was carried out by Sheikholeslami [47]. The effect of a constant magnetic field on the nanofluid natural convection in a porous media with a Sinusoidal hot cylinder was presented by Sheikholeslami [48]. Recently, Sheikholeslami [49] investigate the impact of Lorentz forces on magnetic nanofluid free convection in a porous media. Sheikholeslami [50] reported a simulation of nanofluid natural convection in a porous enclosure in existence of magnetic field. Sheikholeslami and Moradi [51] examined the influence of thermal radiation on heat transfer of nanfluid in permeable media in presence of variable magnetic field. The effect of Lorentz forces on nanofluid hydrothermal treatment in a porous curved cavity using CVFEM was described by Sheikholeslami [52].
On the other hand, suction or injection of fluid through the bounding surfaces, as, for example, in mass transfer cooling, it can significantly change the flow field and, as a consequence, affect the rate of heat transfer from the bounding surfaces. In general, suction tends to increase the skin-friction and heat transfer coefficients whereas injection acts in the opposite manners. Injection or withdrawal of fluid through porous heated or cooled surface is of general interest in practical problems involving film cooling, control of boundary layers, etc. This can lead to enhanced heating (or cooling) of the system and can help to delay the transition from laminar flow [53].
To date, a lot of work has been conducted on micro-geometry flow under different physical situations in the presence of magnetic field. Nevertheless, to the best of the authors’ knowledge, there is no investigation on the influence of transverse magnetic field as well as suction/injection on MHD natural convection flow in an inclined micro-porous-channel. The main aim of the present work is to present a theoretical study for the MHD convection fluid and heat transfer in an inclined micro-porous-channel.
2 Mathematical Analysis
The flow considered is a fully developed steady natural convection flow of viscous, incompressible, electrically conducting fluid through an inclined micro-porous-channel under the effect of transverse magnetic field. The system under consideration is sketched in Figure 1, where the chosen coordinate’s (X, Z) axes, making an angle α with the horizontal are drawn. The fluid is bounded by porous channel walls separated by b. A magnetic field of uniform strength (0, B0, 0) is assumed to be applied in the direction perpendicular to the direction of flow. It is assumed that the magnetic Reynolds number is very small, which corresponds to negligibly induced magnetic field compared to the externally applied one. Fluid is being injected into the flow region through the cold porous plate and in order to conserve the mass of the fluid in the channel, fluid is being sucked out of the channel at the same rate through the hot porous plate. In addition, the plates are heated asymmetrically with one plate maintained at a temperature T1 while the other plate at a temperature T2 where T1 > T2. Due to this temperature gradient between the porous plates, natural convection flow occurs in the channel. Following Hasan and Naseem [21] and Jha et al. [23], the governing equations for the transport processes in dimensionless form in the presence of velocity slip and temperature jump are given under the Boussinesq’s approximation as follows [21, 23]:
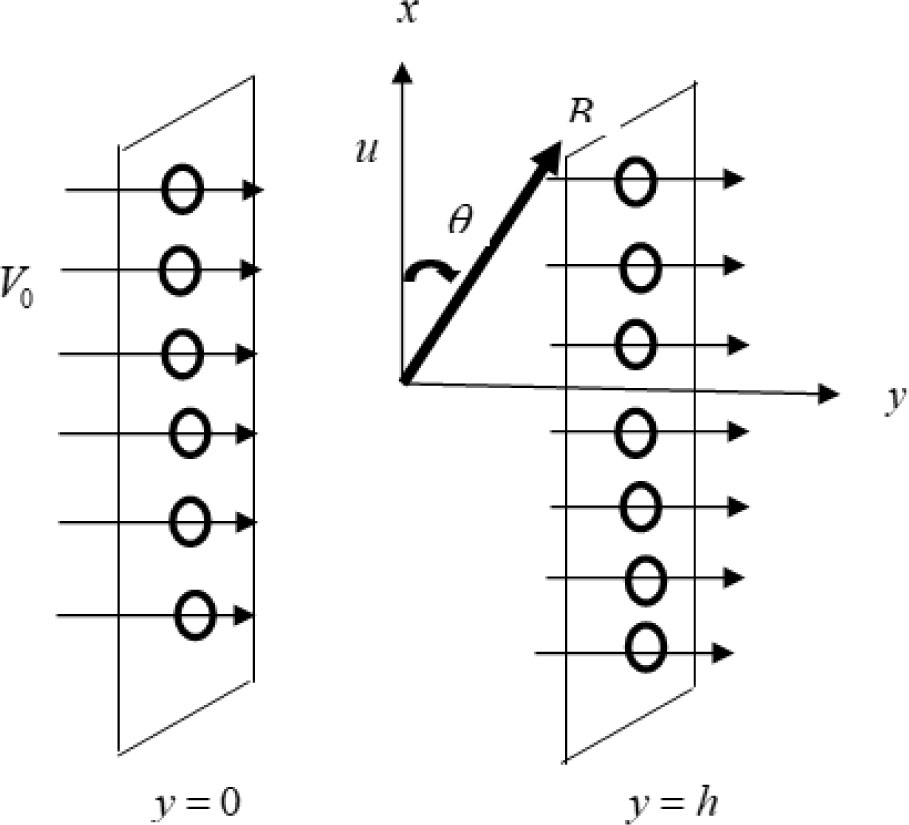
Physical model
The dimensionless quantities used in the above equations are:
The physical quantities used in the above equations are defined in the nomenclature.
The boundary conditions which describe velocity slip and temperature jump conditions at the fluid – wall interface are:
where:
Here ys is the ratio of specific heats, Pr is the Prandtl number, fv and ft are the tangential momentum and thermal accommodation coefficients, respectively, and range from near 0 to 1, λ is the molecular mean free path, Kn is the Knudsen number, ln is the fluid – wall interaction parameter, and ξ is the wall- ambient temperature difference ratio. Referring to the values of fv and ft given in Eckert and Drake [54] and Goniak and Duffa [55], the value of βv is near unity, and the value ofβt ranges from near 1 to more than 100 for actual wall surface conditions and is near 1.667 for many engineering applications, corresponding to fv = 1, ft = 1, ys = 1.4 and Pr = 0.71(βv = 1, βt = 1.667).
By using the method of undetermined coefficients, solutions to Eqns. (1) and (2), subject to the boundary conditions, (4) and (5) have the following exact solutions:
Two important parameters for buoyancy – induced micro-flow and micro-heat transfer are the volume flow rate m and heat transfer rate q, respectively. The dimensionless volume flow rate is:
Substituting equation (6) into equation (8), one obtain
And the rate of heat transfer which is expressed as the Nusselt number is
Therefore:
Using expression (6), we obtain the skin - friction (τ) on the micro-porous-channel walls as follows:
All the constants are defined in Appendix
3 Results and Discussion
In this section, the results obtained for fully developed MHD natural convection flow of electrically conducting fluid in an inclined micro-porous-channel in the presence of suction/injection as well as transverse magnetic field are discussed. The major parameter such as: angle of inclination, rarefaction, fluid wall interaction, suction/injection and Hartmann number on the flow formation are depicted graphically. The present parametric study has been performed in the continuum and slip flow regimes (Kn ≤ 0.1). Also, for air and various surfaces, the values of βν and βt range from near 1 to 1.667 and from near 1.64 to more than 10, respectively. So, this study has been performed over reasonable ranges of 0 ≤ βvKn ≤ 0.1, 0 ≤ M ≤ 2, –2 ≤ S ≤ 2 and 0 ≤ ln ≤ 10 [23] with fixed values βvKn = 0.05, M = 2, S = 0.5, ϕ = 45∘ and ln = 1.667 all arbitrarily chosen to investigate their effect on the micro-porous-channel fluid flow. The product βvKn represents a measure of the departure from the continuum regime while dimensionless parameter ln represents a property of the fluid – wall interaction.
The expression for the temperature in equation (7), the effect of suction/injection (S), rarefaction parameter (βvKn), and fluid-wall interaction parameter (ln) on the temperature profile and rate of heat transfer which is expressed as the Nusselt number are exactly the same as those given by Jha et al. [23]. Therefore, we focus on the effects of angle of inclination, rarefaction, fluid wall interaction, suction/injection and Hartmann number on fluid velocity, volume flow rate and skin friction on the micro-porous channel walls using the aid of line graphs. In the present study, three cases of interest are investigated for different values of the wall ambient temperature difference ratio ξ : ξ = 1 corresponding to the physical case when both micro-porous-channel walls are heated symmetrically, ξ = 0 corresponds to the physical case when one of the walls is heated and other not heated and ξ = –1 implies the physical situation when one of the micro-porous-channel walls is heated and the other cooled.
Using the numerical values of the skin friction on the micro-porous-channel walls, results obtained in the present work was validated with the work of Jha et al. [23] for Gr = 1 and ϕ = 90∘ and presented in Table 1. From the table, it is obvious that an excellent agreement is established.
Comparison of the numerical values of the skin friction at the micro-porous-channel walls (for Gr = 1 and ϕ = 90∘) with the work of Jha et al. [23]
| ξ | βvKn | τ0 (Present work for Gr = 1 and ϕ = 90∘) | τ0 (Jha et al. [23]) | τ1 (Present work for Gr = 1 and ϕ = 90∘) | τ1 (Jha et al. [23]) |
|---|---|---|---|---|---|
| 1 | 0.0 | 0.3551 | 0.3551 | -0.4151 | -0.4151 |
| 0.05 | 0.3429 | 0.3429 | -0.3944 | -0.3944 | |
| 0.1 | 0.3313 | 0.3313 | -0.3760 | -0.3760 | |
| 0 | 0.0 | 0.0963 | 0.0963 | -0.2677 | -0.2677 |
| 0.05 | 0.1032 | 0.1032 | -0.2366 | -0.2366 | |
| 0.1 | 0.1065 | 0.1065 | -0.2136 | -0.2136 | |
| -1 | 0.0 | -0.1624 | -0.1624 | -0.1203 | -0.1203 |
| 0.05 | -0.1365 | -0.1365 | -0.0788 | -0.0788 | |
| 0.1 | -0.1183 | -0.1183 | -0.0511 | -0.0511 |
Figure 2 displays the effect of the inclination angle on the velocity profile under different wall heating conditions. From the figure, it is observed that for symmetric (ξ = 1) and asymmetric heating (ξ = 0) fluid velocity increases with the increase in the inclination angle. This could be attributed to the enhancement in the convective buoyancy force due to increase in the inclination angle. However, when asymmetric heating (ξ = –1) is considered, increase in the inclination angle results to increase in fluid velocity near the hot wall whereas it decreases at the cold wall.
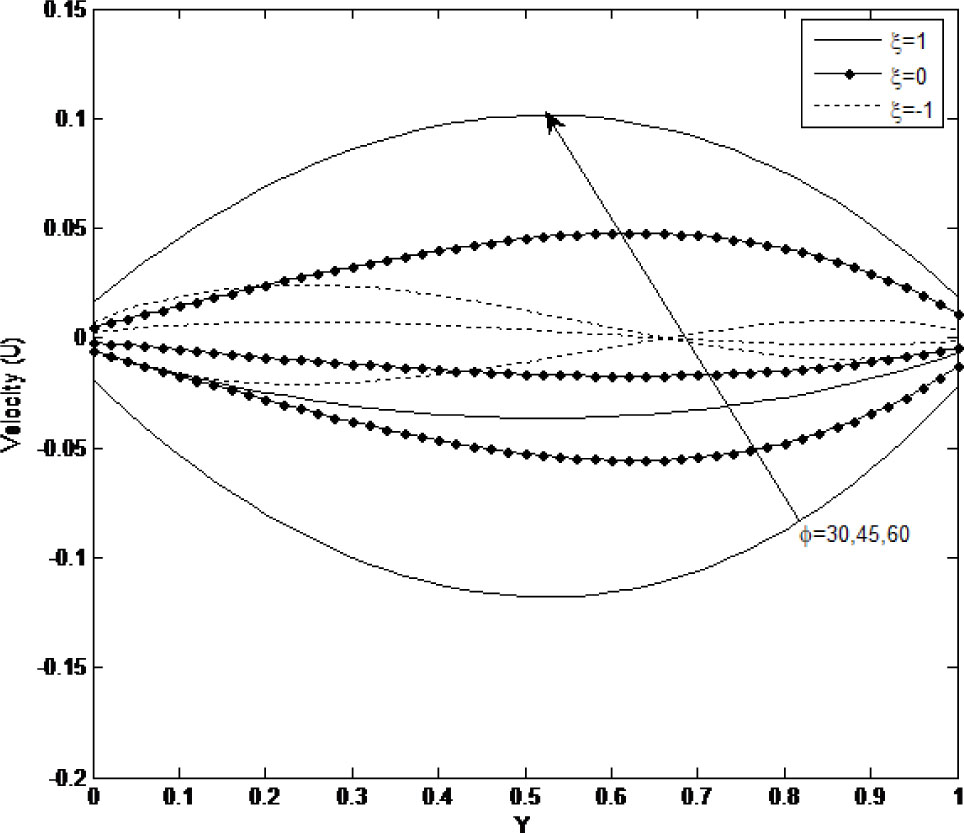
Effect on angle of inclination on velocity profile
Figure 3 illustrates the effect of suction/injection parameter (S) on fluid velocity in an inclined micro-porous channel. The figure reveals the significance of suction or injection on buoyancy induced flow formation in the micro-channel. From the figure, it is obvious that injection (S > 0) thickens the thermal boundary layer, resulting to weakening the convective current and consequently decreasing the fluid velocity whereas suction (S < 0) weakens the thermal boundary layer yielding an increase in fluid velocity.
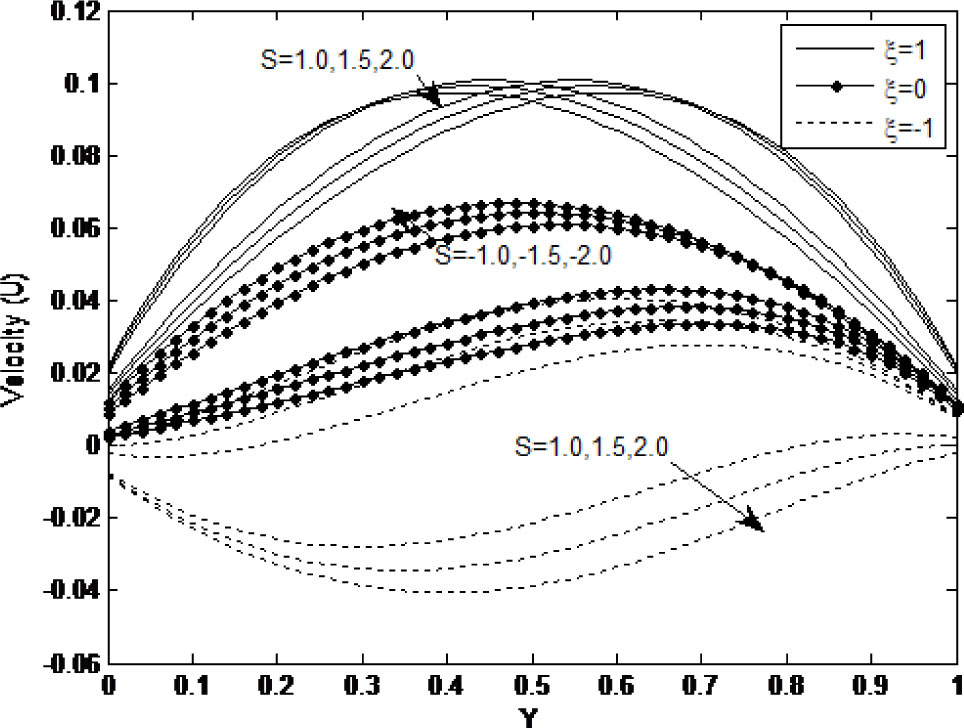
Effect of suction/injection on velocity profile
The influence of the Hartmann number (M) on fluid velocity in an inclined micro-porous channel is displayed in Fig. 4 for both symmetric (ξ = 1) and asymmetric (ξ = 0, –1) heating conditions. From the figure, it is clear that increase in Hartmann number leads to decrease in fluid velocity for all wall heating conditions. This is due to the physical fact that increase in Hartmann number induces a mechanical damping force which acts in the directions opposite to the fluid motion thereby suppressing the fluid velocity within the micro-channel as observed in the Fig. 4.
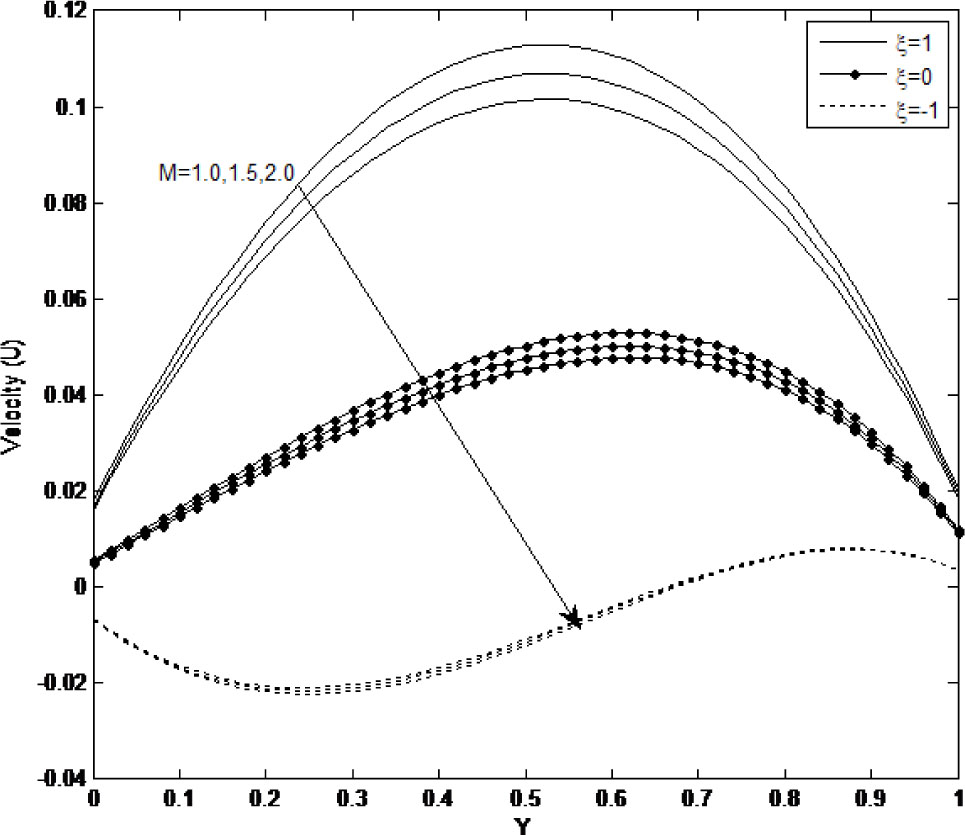
Effect on Hartmann number on velocity profile
The effect of rarefaction parameter (βvKn) on the micro-porous-channel is observed in Figure 5 under different wall heating conditions. It is observed from the figure that, increasing the wall-ambient temperature difference ratio as well as rarefaction parameter leads to enhancement in the velocity slip. This result yields an observable increase in the fluid velocity. In addition, as the wall-ambient temperature difference ratio (ξ) increases, the effect of rarefaction parameter (βvKn) on the inclined micro-porous channel slip velocity becomes significant.
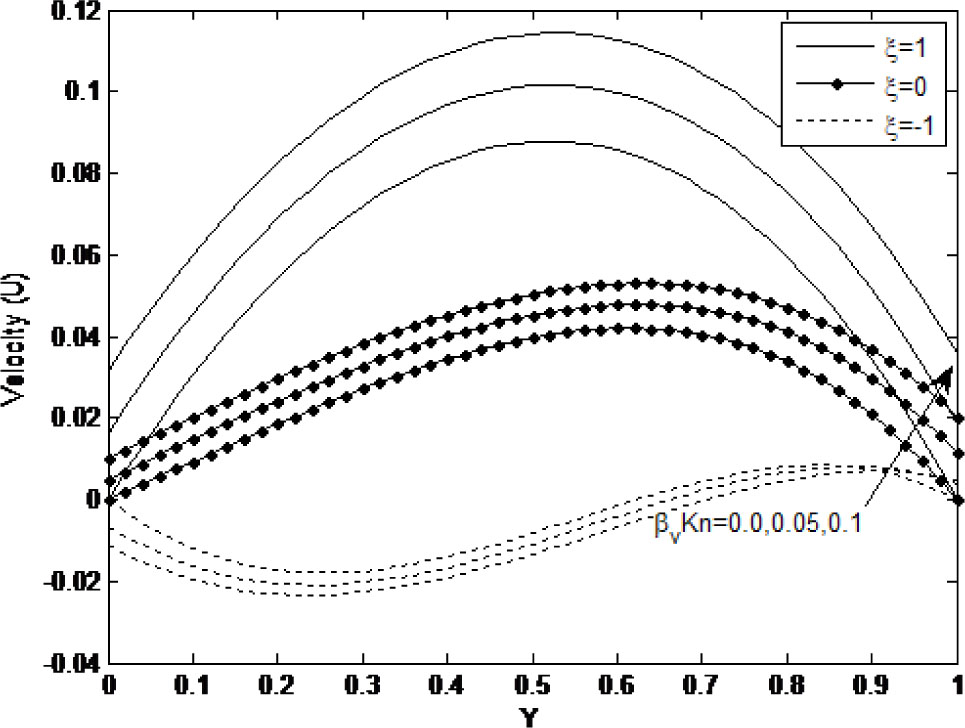
Effect of rarefaction parameter on velocity
Figure 6 displays the effect of fluid wall interaction parameter (ln ) on fluid velocity. From the figure, it is observed that velocity slip increases on the micro-porous-channel surfaces with the increase of fluid wall interaction parameter (ln). Also, it is obvious that for symmetric heating (ξ = 1), increase in ln has no influence on fluid velocity within the micro-porous channel since the temperature of the walls are not changing. However, when asymmetric heating is considered (ξ = 0, –1), the effect of temperature jump induced by increase in ln becomes significant as fluid velocity is observed to increase about the cold wall and decrease about the hot wall.
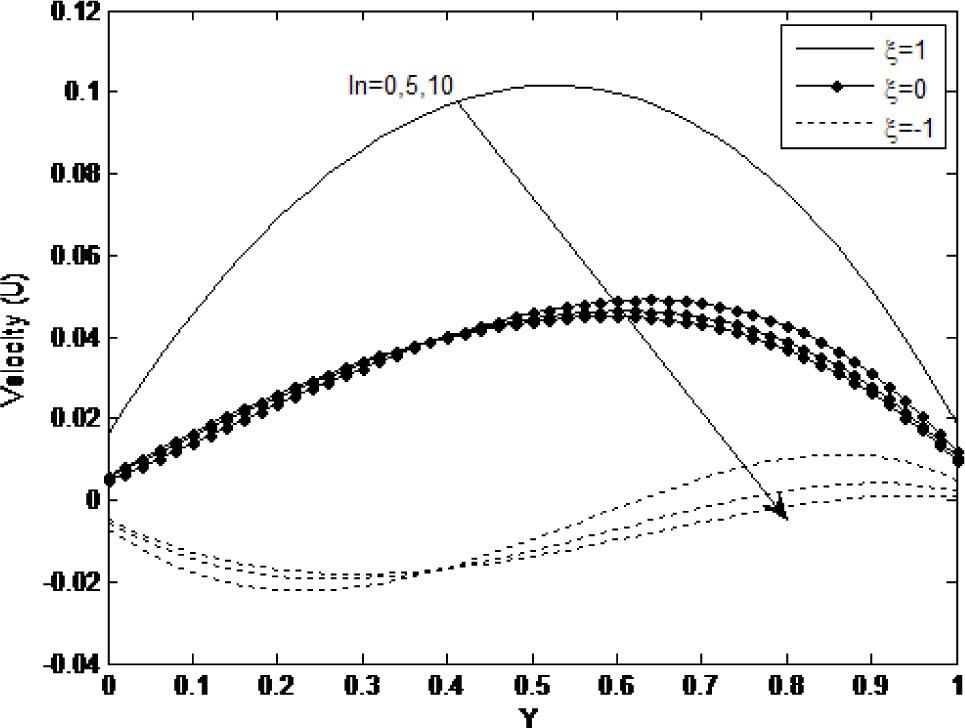
Effect of fluid wall interaction parameter on velocity profile
Figure 7 describes the combined effect of the inclination angle (ϕ), rarefaction parameter (βvKn) and wall ambient temperature difference ratio (ξ) on the micro-porous-channel volume flow rate. It is clear from the figure that increase in the inclination angle yields an observable increase in the volume flow for both symmetric (ξ = 1) and asymmetric heating (ξ = 0, –1) cases. However, this increase in volume flow could be further enhanced by the increase in rarefaction parameter as for the symmetric heating case (ξ = 1). Furthermore, it is also clear that for asymmetric heating (ξ = 0), increase in rarefaction parameter has no significant effect on the volume flow.
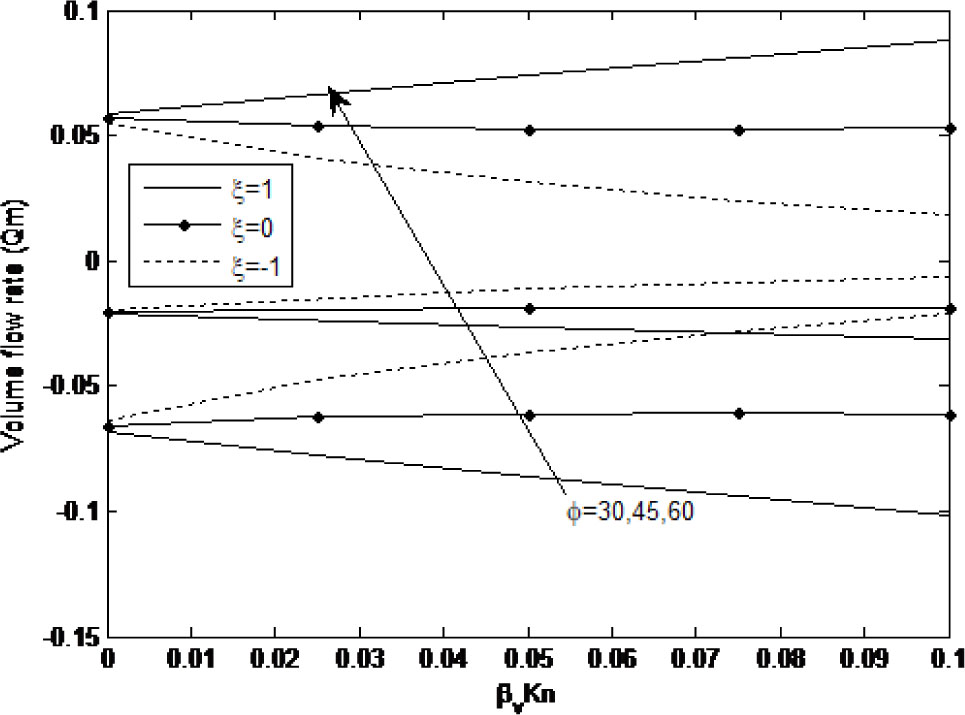
Volume flow rate versus βvKn for different of ϕ
Figure 8 and 9 illustrates the influence of the inclination angle (ϕ), rarefaction parameter (βvKn) and wall ambient temperature difference ratio (ξ) on the skin friction (τ) at the micro-porous-channel walls(Y = 0) and (Y = 1). From Fig. 8, it is observed that the effect of the rarefaction parameter on the skin friction (τ0) becomes more pronounced as βvKn grows for both symmetric (ξ = 1) and asymmetric heating (ξ = 0, –1) cases. Increasing the inclination angle on the other hand yields an observable increase in τ0. A similar phenomenon is observed in Fig. 9.
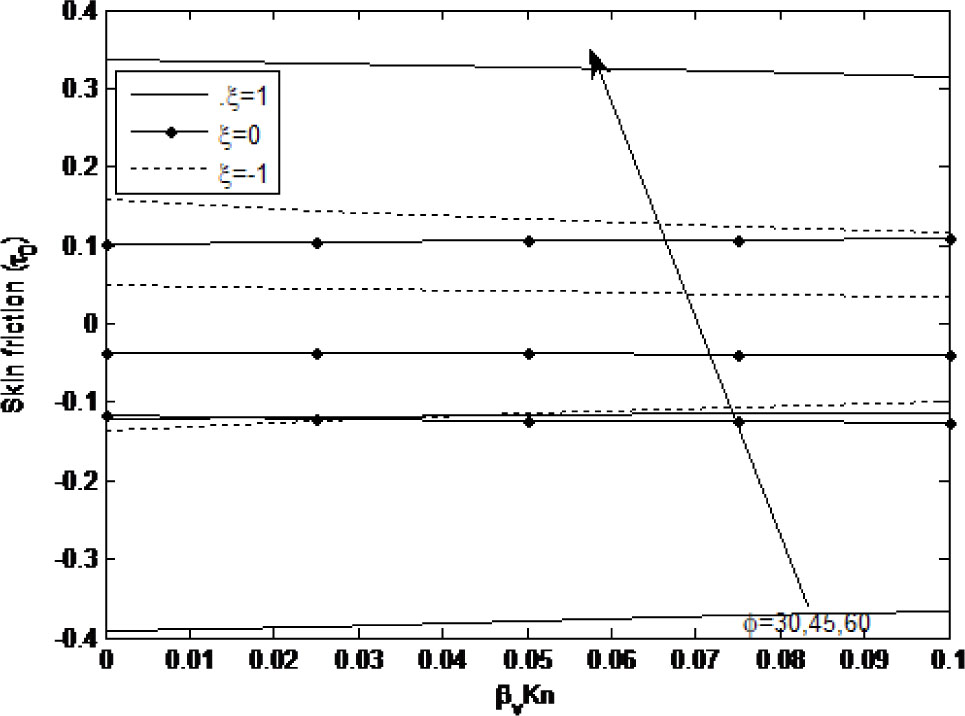
Skin fraction (τ0) versus βvKn for different of ϕ
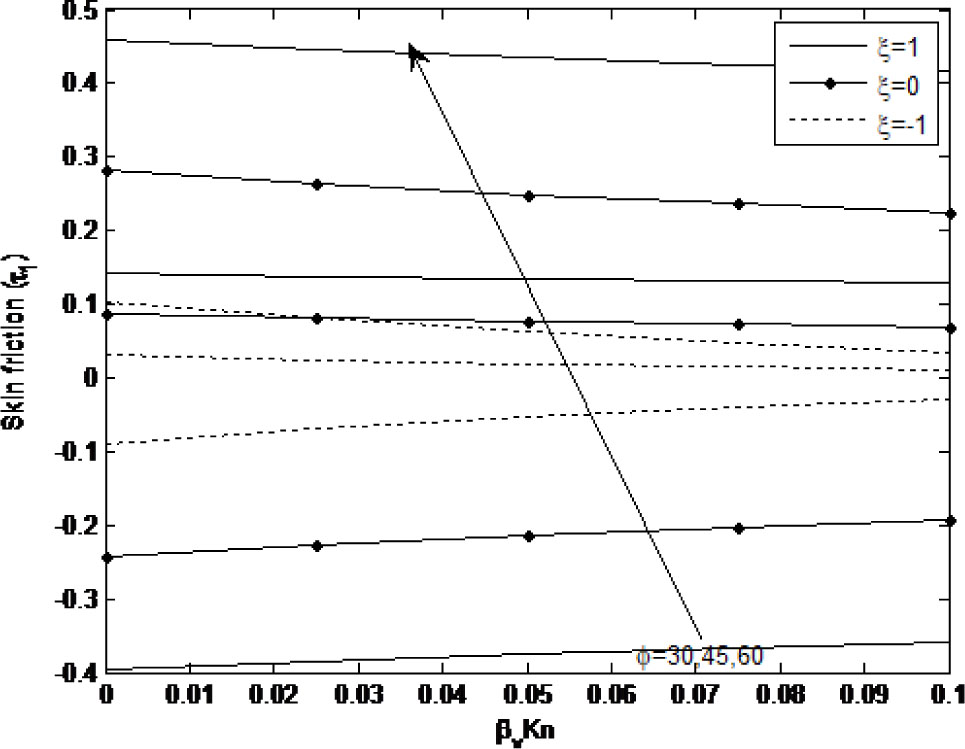
Skin fraction (τ1) versus βvKn for different of ϕ
4 Conclusions
The present paper investigates on the fully developed laminar flow of a viscous incompressible and electrically conducting fluid in an inclined micro-porous-channel subject to a transversely applied magnetic field. The governing equations were solved analytically and expressions for the temperature and velocity profiles where obtained under relevant boundary conditions. Effect of various flow parameters on fluid velocity and volume flow have been highlighted using line graphs and there after discussed. The main findings of the present work are as follows:
Increasing the inclination angle enhances the convective current in the micro-porous-channel resulting to increase in fluid velocity as observed in Figure 2.
It could also be seen from Figure 3 that injection (S > 0) thickens the thermal boundary layer, thereby weakening the convective current and consequently decreasing fluid velocity whereas suction (S < 0) weakens the thermal boundary layer yielding an increase in fluid velocity.
Increase in the inclination angle yields an observable increase in the volume flow for both symmetric (ξ = 1) and asymmetric heating (ξ = 0, –1) cases as observed in Figure 7.
Increasing the inclination angle yields an increase in the skin friction (τ0, τ1) at both boundaries, whereas the effect of the rarefaction parameter on skin friction (τ0, τ1) becomes pronounced as βvKn becomes large.
A Appendix
- Nomenclature
- b
channel width
- Cp, Cv
Specific heats at constant pressure and constant volume, respectively
- ft, fv
thermal and tangential momentum accommodation coefficients, respectively
- g
gravitational acceleration ln fluid- wall interaction parameter, (βt/βv)
- Kn
Knudsen number, (λ/b)
- m
volume flow rate
- Q
dimensionless volume flow rate
- M
Hartmann number
- Nu
dimensionless heat transfer rate (Nusselt number)
- S
suction/injection parameter
- Pr
Prandtl number
- T
temperature of fluid
- T0
reference temperature
- u, v
velocity components in x, y directions
- V0
constant suction/injection velocity
- U
dimensionless velocity
- Greek Letters
- α
thermal diffusivity
- ϕ
angle of inclination
- β
thermal expansion coefficient
- βt, βv
dimensionless variables
- ys
ratio of specific heats (Cp/Cv)
- μ
dynamic viscosity
- θ
dimensionless temperature
- ξ
wall-ambient temperature difference ratio
- ρ
density
- ν
fluid kinematic viscosity
- Subscripts
- 1
hotter wall values
- 2
cooler wall values
References
[1] Chen C. K, and Weng H. C. Natural convection in a vertical micro-channel. J Heat Transfer 2005; 127, pp. 1053-1056.10.1115/1.1999651Search in Google Scholar
[2] Jha, B. K., Babatunde Aina and S. B. Joseph, Natural Convection Flow in vertical Micro-channel with Suction/Injection, Journal of Process Mechanical Engineering, 2014, 228 (3), pp. 171-18010.1177/0954408913492719Search in Google Scholar
[3] Khadrawi A. F, Othman A. and Al-Nimr M. A., Transient free convection fluid flow in a vertical microchannel as decribed by the hyperbolic heat conduction model. Int .J. Thermophys, 2005, 26(3), pp. 905-918.10.1007/s10765-005-5586-2Search in Google Scholar
[4] Haddad, O.M., Abuzaid, M.M., and Al-Nimr, M.A., Developing free-convection gas flow in a vertical open-ended microchannel filled with porous media, Numer. Heat Transf, A: 2005, 26(3), 905-918.10.1080/10407780590968006Search in Google Scholar
[5] Buonomo B., and Manca O., Natural Convection Flow in a Vertical Micro-Channel with Heated at Uniform Heat Flux. Int. J. Therm. Sci. 2012, 49, pp. 1333-134410.1016/j.ijthermalsci.2010.03.005Search in Google Scholar
[6] Weng, H. C., Chen, C. K., Drag reduction and heat transfer enhancement over a heated wall of a vertical annular microchannel. Int. J. Heat Mass Transfer, 2009, 52, pp. 1075–107910.1016/j.ijheatmasstransfer.2008.06.022Search in Google Scholar
[7] Jha, B. K, Babatunde Aina and S. A. Muhammad, Combined Effects of Suction/Injection and Wall Surface Curvature on Natural Convection Flow in a Vertical Annular Micro-channel, Journal of Thermophysics and Aeromechanics, 2015, 22 (2), pp. 217-22810.1134/S0869864315020080Search in Google Scholar
[8] Avci M., Aydin O., Mixed convection in a vertical parallel plate microchannel, J.Heat Transfer Trans. ASME, 2007, 129, 162–166.10.1115/1.2422741Search in Google Scholar
[9] Avci M., Aydin O., Mixed convection in a vertical microannulus between twoconcentric microtubes, J. Heat Transfer Trans. ASME, 2009, 131, 01450210.1115/1.2977552Search in Google Scholar
[10] Jha, B. K. and Aina, Babatunde, Mathematical modelling and exact solution of steady fully developed mixed convection flow in a vertical micro-porous-annulus, Journal of AfrikaMatematika, 2015, 26, pp. 1199-121310.1007/s13370-014-0277-4Search in Google Scholar
[11] Cramer K. R., Pai S., Magneto Fluid Dynamics for Engineers and Applied Physicists. New York: McGraw-Hill; 1973, pp. 204-237.Search in Google Scholar
[12] Chawla S. S., Magnetohydrodynamics Unsteady Free Convection. ZAMM 1967; Vol. 47: pp. 499–508.10.1002/zamm.19670470803Search in Google Scholar
[13] Das S., Jana R. N., Makinde O. D., MHD Boundary Layer Slip Flow and Heat Transfer of Nanofluid past a Vertical Stretching Sheet with non-uniform Heat Generation/Absorption. International Journal of Nanoscience, 2014, Vol. 13, No. 3, 1450019.10.1142/S0219581X14500197Search in Google Scholar
[14] Sheikholeslamia M, Gorji-Bandpy M., Free Convection of Ferro-fluid in a Cavity Heated from below in the Presence of an External Magnetic Field. Powder Technol 2014; Vol.256, pp. 490–8.10.1016/j.powtec.2014.01.079Search in Google Scholar
[15] Sheikholeslamia M, Gorji-Bandpy M, Ganji DD, Rana P, SoleimaniSoheil, Magnetohydrodynamic Free Convection of Al2O3–water Nanofluid Considering Thermophoresis and Brown-ian motion effects. Comput Fluid 2014; Vol. 94, pp. 147–60.10.1016/j.compfluid.2014.01.036Search in Google Scholar
[16] Sheikholeslamia M, Gorji-Bandpy M, Ganji DD. Lattice Boltzmann method for MHD Natural Convection Heat Transfer using Nanofluid. Powder Technol 2014; Vol. 254, pp. 82–93.10.1016/j.powtec.2013.12.054Search in Google Scholar
[17] Chaughan, D., Rastogi, P., 2012. Heat Transfer effects on a Rotating MHD Couette Flow in a ChannelPartially by a Porous Medium with Hall Current, Journal of Applied Science and Engineering, 15 (3), 281-290.Search in Google Scholar
[18] Ibrahim W., and Makinde O. D., Double-diffusive Mixed Convection and MHD Stagnation Point flow of Nanofluid over a Stretching Sheet.Journal of Nanofluids, 2015, Vol.4, pp. 28-37.10.1166/jon.2015.1129Search in Google Scholar
[19] Farhad A., Norzieha M., SSharidan S., Khan I. and Samiuthaq, On Hydromagnetic Rotating Flow in a Porous Medium with Slip Condition and Hall Current, International Journal of the Physical Sciences, 2012, 7(10), pp. 1540-1548.10.5897/IJPS11.1767Search in Google Scholar
[20] Farhad Ali, Ilyas Khan, Samiulhaq, Norzieha Mustapha, and SharidanShafie, Unsteady Magnetohydrodynamic Oscillatory Flow of Viscoelastic Fluids in a Porous Channel with Heat and Mass Transfer, Journal of the Physical Society of Japan, 2012, 81, 06440210.1143/JPSJ.81.064402Search in Google Scholar
[21] Hasan N. Z, Naseem A, MHD convection flow of two immiscible fluids in an inclined channel filled with heat generation/absorption, American j. Applied Mathematics, (2016), 4, 80-91.10.11648/j.ajam.20160402.13Search in Google Scholar
[22] Wang C. C., Chang W. J., Dai C. H., Lin Y. T., Yang K. S., “Effect of inclination on theconvective boiling performance of a microchannel heat sink using HEF – 7100,” J. Experimental Thermal and fluid Science, ( 2012), 36, 143-148,10.1016/j.expthermflusci.2011.09.006Search in Google Scholar
[23] Jha, B. K., Aina, Babatunde and Ajiya A. T., Role of Suction/Injection on MHD Natural Convection Flow in a Vertical Microchannel, International Journal of Energy & Technology 2015, Vol. 7, pp. 30-39.Search in Google Scholar
[24] Jha, B. K., Aina, Babatunde and Sani Isa, Transient Magnetohydrodynamic Free Convective Flow in Vertical Micro-Concentric-Annuli, ProcIMechE Part N: J Nanoengineering and Nanosystems, 10.1177/1740349915578956Search in Google Scholar
[25] Jha, B. K., Aina, Babatunde and Sani Isa, Fully Developed MHD Natural Convection Flow in a Vertical Annular Microchannel: An exact solution, Journal of King Saud university- Science, 2015, 27, pp. 253-259.10.1016/j.jksus.2014.12.002Search in Google Scholar
[26] Basant K. Jha and BabatundeAina, MHD NaturalConvection Flow in a Vertical Micro-Porous- Annulus in the Presence of RadialMagneticField, Journal of Nanofluids, 2016, 10.1166/jon.2016.1204Search in Google Scholar
[27] Basant K. Jha, BabatundeAina and Sani Isa, MHD Natural Convection flow in a Vertical Micro-Concentric-Annuli in the Presence of Radial Magnetic Field: An Exact Solution, Journal of Ain Shams Engineering, 2015, http://dx.doi.org/10.1016/j.asej.2015.07.01010.1016/j.asej.2015.07.010Search in Google Scholar
[28] Farhad Ali, Nadeem Ahmad Sheikh, Ilyas Khan, and Muhammad Saqib. "Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model." Journal of Magnetism and Magnetic Materials 423 (2017): 327-336.10.1016/j.jmmm.2016.09.125Search in Google Scholar
[29] Ali, Farhad, Muhammad Saqib, Ilyas Khan, and Nadeem Ahmad Sheikh. "Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model." The European Physical Journal Plus131, no. 10 (2016): 377.10.1140/epjp/i2016-16377-xSearch in Google Scholar
[30] Farhad Ali, Nadeem Ahmad Sheikh, Muhammad Saqib, and Arshad Khan. "Hidden Phenomena of an MHD Unsteady Flow in Porous Medium with Heat Transfer." Journal of Nonlinear Science: Letter A. (2017): 101-116.Search in Google Scholar
[31] Sheikh, N. A., Ali, F., Khan, I., & Saqib, M. A modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium. Neural Computing and Applications, 1-11.10.1007/s00521-016-2815-5Search in Google Scholar
[32] Saqib, M., Ali, F., Khan, I., & Sheikh, N. A. Heat and mass transfer phenomena in the flow of Casson fluid over an infinite oscillating plate in the presence of first-order chemical reaction and slip effect. Neural Computing and Applications, 1-14.10.1007/s00521-016-2810-xSearch in Google Scholar
[33] Sheikh, N. A., Ali, F., Khan, I., Saqib, M & Khan, A. MHD flow of micro-polar fluid over an oscillating vertical plate embedded in a porous media with constant temperature and concentration. Mathematical Problems in Engineering.Search in Google Scholar
[34] Exact and numerical solutions for unsteady heat and mass transfer problem of Jeffrey fluid with MHD and Newtonian heating effects, Neural Comput & Applic, 10.1007/s00521-017-2935-6.Search in Google Scholar
[35] Effects of MoS2 nanoparticles on MHD slip flow of molybdenum disulphide nanofluid in a porous medium, Journal of Molecular Liquids, http://dx.doi.org/10.1016/j.molliq.2017.03.009.10.1016/j.molliq.2017.03.009Search in Google Scholar
[36] M Saqib, F Ali, I Khan, NA Sheikh, SAA Jan, Exact solutions for free convection flow of generalized Jeffrey fluid: A Caputo-Fabrizio fractional model, Alexandria Engineering Journal.10.1016/j.aej.2017.03.017Search in Google Scholar
[37] MA Imran, I Khan, M Ahmad, NA Shah, M Nazar, Heat and mass transport of differential type fluid with non-integer order time-fractional Caputo derivatives Journal of Molecular Liquids 229, 67-7510.1016/j.molliq.2016.11.095Search in Google Scholar
[38] I Khan, NA Shah, LCC Dennis, A scientific report on heat transfer analysis in mixed convection flow of Maxwell fluid over an oscillating vertical plate Scientific Reports 710.1038/srep40147Search in Google Scholar PubMed PubMed Central
[39] NA Shah, I Khan, Heat transfer analysis in a second grade fluid over and oscillating vertical plate using fractional Caputo–Fabrizio derivatives, The European Physical Journal C 76 (7), 1-11.10.1140/epjc/s10052-016-4209-3Search in Google Scholar
[40] Sheikholeslamia M and Shehzad S.A., Simulation of water based nanofluid convective flow inside a porous enclosure via non-equilibrium model, International Journal of Heat and Mass Transfer 120 (2018) 1200–121210.1016/j.ijheatmasstransfer.2017.12.132Search in Google Scholar
[41] Sheikholeslamia Mohsen and Seyednezhad Mohadeseh, Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM, International Journal of Heat and Mass Transfer 120 (2018) 772–78110.1016/j.ijheatmasstransfer.2017.12.087Search in Google Scholar
[42] Sheikholeslami M., Shamlooei M and Moradi R., Fe3O4-Ethylene glycol nanofluid forced convection inside a porous enclosure in existence of Coulomb force, Journal of molecular liquids, 249 (2018) 429-437.10.1016/j.molliq.2017.11.048Search in Google Scholar
[43] Sheikholeslami M., Numerical investigation for CuO-H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method, Journal of molecular liquids, 249 (2018) 739-746.10.1016/j.molliq.2017.11.069Search in Google Scholar
[44] Sheikholeslami Mohsen, Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure, Journal of molecular liquids, 249 (2018) 1212-1221.10.1016/j.molliq.2017.11.141Search in Google Scholar
[45] Sheikholeslamia Mohsen and Houman B. Rokni, Numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation, International Journal of Heat and Mass Transfer 118 (2018) 823–831.10.1016/j.ijheatmasstransfer.2017.11.041Search in Google Scholar
[46] Sheikholeslamia Mohsen and Shehzad S.A., Numerical analysis of Fe3O4–H2O nanofluid flow in permeable media under the effect of external magnetic source, International Journal of Heat and Mass Transfer 118 (2018) 182–192.10.1016/j.ijheatmasstransfer.2017.10.113Search in Google Scholar
[47] Sheikholeslami M., Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method, Journal of molecular liquids, 234 (2017) 364-374.10.1016/j.molliq.2017.03.104Search in Google Scholar
[48] Sheikholeslami M., CuO-water nanofluid free convection in a porous cavity considering Darcy law, Eur. Phys. J. Plus (2017)132:55.10.1140/epjp/i2017-11330-3Search in Google Scholar
[49] Sheikholeslami M., Influence of Lorentz forces on nanofluid flow in a porous cavity by means of non- Darcy mode, Vol. 34 Issue: 8, pp. 2651-2667, https://doi.org/10.1108/EC-01-2017-000810.1108/EC-01-2017-0008Search in Google Scholar
[50] Sheikholeslami M., Numerical investigation of MHD nanofluid free convective heat transfer in a porous tilted enclosure, Vol. 34 Issue: 6, pp.1939-1955, https://doi.org/10.1108/EC-08-2016-029310.1108/EC-08-2016-0293Search in Google Scholar
[51] Sheikholeslami M., Shamlooei M. and Moradi R., Numerical simulation for heat transfer intensification of nanofluid in a porous curved enclosure considering shape effect of Fe3O4 nanoparticles, Chemical Engineering & Processing: Process Intensification 124 (2018) 71-82.10.1016/j.cep.2017.12.005Search in Google Scholar
[52] Sheikholeslami Mohsen, Numerical simulation of magnetic nanofluid natural convection in porous media, Physics Letters A, 381 (2017) 494-503.10.1016/j.physleta.2016.11.042Search in Google Scholar
[53] Chaudhary M. A, Merkin J. H. The effect of blowing and suction on free convection boundary layers on vertical surfaces with pre-scribed heat flux. J. Eng. Math 1993;27:265 -292.10.1007/BF00128967Search in Google Scholar
[54] Eckert ERG, Drake Jr. RM. Analysis of heat and mass transfer. New York: Mcgraw-Hill; 1972, Chap. 11.Search in Google Scholar
[55] Goniak R, Duffa G. Corrective term in wall slip equations for Knudsen layer. J. Thermophys Heat Transfer 1995;9:383–384.10.2514/3.677Search in Google Scholar
© 2019 B. Aina and P. Bukar Malgwi, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Articles in the same Issue
- Chebyshev Operational Matrix Method for Lane-Emden Problem
- Concentrating solar power tower technology: present status and outlook
- Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
- Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
- Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
- Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
- Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
- Local convergence for an eighth order method for solving equations and systems of equations
- Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
- Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
- A reliable analytical approach for a fractional model of advection-dispersion equation
- Mass transfer around a slender drop in a nonlinear extensional flow
- Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
- A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
- An effective technique for the conformable space-time fractional EW and modified EW equations
- Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
- New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
- Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
- A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
- Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
- Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
- Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
- MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
- Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
- Swirling flow of couple stress fluid due to a rotating disk
- MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
- Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
- Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
- Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
- On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
- An adaptive mesh method for time dependent singularly perturbed differential-difference equations
- On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
- Rational exponential solutions of conformable space-time fractional equal-width equations
- Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
- Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
- Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
- Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
- Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
- Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
- Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
- An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
- New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
- Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
- Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
- Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
- Mathematical model on distributed denial of service attack through Internet of things in a network
- Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
- Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
- MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
- A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
- Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
- Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
- Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
- Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
- Combination synchronization of fractional order n-chaotic systems using active backstepping design
- Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
- Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
- Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
- Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
- Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
- Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
- Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
- A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
- A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
- A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
- The expa function method and the conformable time-fractional KdV equations
- Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
- Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
- MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
- MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel
Articles in the same Issue
- Chebyshev Operational Matrix Method for Lane-Emden Problem
- Concentrating solar power tower technology: present status and outlook
- Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
- Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
- Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
- Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
- Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
- Local convergence for an eighth order method for solving equations and systems of equations
- Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
- Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
- A reliable analytical approach for a fractional model of advection-dispersion equation
- Mass transfer around a slender drop in a nonlinear extensional flow
- Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
- A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
- An effective technique for the conformable space-time fractional EW and modified EW equations
- Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
- New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
- Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
- A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
- Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
- Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
- Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
- MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
- Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
- Swirling flow of couple stress fluid due to a rotating disk
- MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
- Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
- Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
- Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
- On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
- An adaptive mesh method for time dependent singularly perturbed differential-difference equations
- On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
- Rational exponential solutions of conformable space-time fractional equal-width equations
- Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
- Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
- Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
- Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
- Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
- Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
- Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
- An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
- New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
- Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
- Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
- Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
- Mathematical model on distributed denial of service attack through Internet of things in a network
- Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
- Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
- MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
- A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
- Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
- Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
- Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
- Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
- Combination synchronization of fractional order n-chaotic systems using active backstepping design
- Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
- Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
- Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
- Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
- Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
- Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
- Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
- A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
- A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
- A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
- The expa function method and the conformable time-fractional KdV equations
- Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
- Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
- MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
- MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel

