Home On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
Article Open Access

On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation

  • K. Ganesh Kumar , G.K. Ramesh EMAIL logo , B.J. Gireesha and A.M. Rashad
Published/Copyright: September 17, 2018
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 8 Issue 1

Abstract

Present article reports the magnetohydrodynamic flow of Carreau nanofluid in the presence of nonlinear thermal radiation. In this model we incorporated slip condition on heat and mass boundary conditions. Similarity transformations are applied to convert the governing dimensional expressions into non-dimensional forms. Runge-Kutta-Fehlberg method of fourth–fifth order using shooting technique utilized to elaborate the numerical solutions of physical phenomenon.A comparative analysis is presented with the previous published data in special case for the justification of present results. The role of physical constraints on liquid velocity, temperature and concentration are discussed through numerical data and plots.

Keywords: Carreau nanofluid; thermal and solutal slip; nonlinear radiation; magnetic field

1 Introduction

Convective heat transport is a fundamental aspect of various industrial operations. The efficiencies of thermal devices and systems are related to heat transfer rates which in turn depend on the thermal conductivity of the working fluids. With increasingly more sophisticated improvements in nanotechnology and optimization, the request is increasing for more effective and durable heat transfer fluids with significantly greater thermal conductivities than traditional ones. Traditional heat transfer fluids (water, oils and ethylene glycol) applied in the currently thermal systems have relatively low thermal conductivities compared to solids. Nanofluids, an enterprising and clearly more efficient kind of working fluid, are gained by dissolving nanometer-sized particles/fibers between 1 and 100 nm in traditional heat transfer fluids. An excellent literature review on nanofluids transport phenomena and their different applications is reported in Das et al. [1] and Choi [2]. Nield and Kuznetsov [3] used the mathematical nanofluid model suggested by Buongiorno [4] to examine the influence of Brownian motion and thermophoresis on nanofluid natural convection flow over a vertical plate under the improved boundary conditions. Due to the importance of Brownian motion and thermophoresis effects, concentration boundary layer of nanoparticles was considered in their study. Aziz et al. [5] have presented nanofluid natural convection boundary layer flow over a vertical plate subject to the convective boundary conditions. Other studies of the recent evolutions in nanofluid technology have been analyzed and are available in [6, 7, 8, 9].

Lately, various investigations have been communicated extending Buongiorno’s model for the magnetic nanofluid dynamics, which are essentially helpful in biomedicine, magnetic cell separation, cancer treatment, etc. Bég and Ferdows [10] performed a numerical study to discuss the influence of magnetic field on nanofluid flow from an exponential stretching sheet. Ferdows et al. [11] investigated the unsteady MHD free convective and nanofluid flow from a radiate stretching surface. Sudarsana Reddy et al. [12] reported the influence of magnetic field and chemical reaction on nanofluids over a vertical cone. Ruchika et al. [13] have presented the influence of velocity and thermal slip effects on MHD boundary layer flow of nanofluid over an inclined cylinder. Rashad [14, 15] analyzed the MHD slip flow of a nanofluid past a radiate edge and stretching surface, respectively.

Presently many researchers are concentrating on exploration of non-Newtonian liquids, because non-Newtonian fluids have multidisciplinary applications in modern industrial and technological products. Few examples of non-Newtonian materials include food, ketchup, shampoos, slurries, granular suspension, paper pulp, paints, polymer solutions, certain oils, and clay coatings. All the features of non-Newtonian liquids cannot be distinguished by a single mathematical relationship. In view of the above applications Nadeem et al. [16] contemplated the two-dimensional enduring incompressible Oldroyd-B nanofluid stream past an extending sheet. Later they [17, 18] broadened their work on a Jeffrey and Maxwell liquid model. Noor et al. [19] examined the mixed convection boundary layer flow of a micropolar fluid almost a stagnation point along a vertical extending sheet within the sight of nano-particles and slip conditions. Ali and Hayat [20] intoruduced analytical solution for the flow of a Carreau fluid in an asymmetric channel. Olajuwon [21] investigated the convective heat transfer in a MHD Carreau fluid over a vertical radiate plate. Hayat et al. [22, 23] studied the boundary layer flow of Carreau fluid over a stretching surface with convective boundary conditions. As of late numerous analysts [24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34] have studied and discussed about the impacts of slips impacts and nonlinear type of thernmal radiation in the flow of non-Newtonian liquids.

The present problem addresses the impacts of multiple slips, Brownian motion and thermophoresis on MHD flow of Carreau nanofluid over a radiate stretching sheet. The transformed boundary layer equations which represent the flow, temperature and concentration are solved numerically using Runge-Kutta-Fehlberg method of fourth–fifth order using shooting technique. Also comparisons of present result with previously published works was done and are found in excellent agreement.

2 Mathematical formulation

We considered the steady-state incompressible Carreau nanoliquid flow over a stretchable sheet. The x-axis is along the sheet and y-axis normal to it. Here the flow generation is because of linear stretching of surface with distance x, i.e. Uw = bx. A constant magnetic field with strength B0 is implemented in transverse flow direction. Twis the surface temperature at wall and Cw the solutal concentration. At larger distance from surface, temperature and nanoparticle concentration is represented by T∞ and C∞ respectively.

The continuity, momentum, energy and concentration expressions are described as

∂u∂x+∂v∂y=0,(1)
u∂u∂x+v∂u∂y=ν∂2u∂y2+3n−12Γ2∂2u∂y2∂u∂y2−σB02ρu,(2)
u∂T∂x+v∂T∂y=α∂2T∂y2+τDB∂c∂y∂T∂y+DTT∞∂T∂y2−∂qr∂y,(3)
u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2,(4)

with the relevant boundary conditions (see Ibrahim and Shankar [24])

u=uw,v=0,T=Tw+K1∂T∂y,C=Cw+K2∂C∂yaty=0,u→0,T→T∞,C→C∞asy→∞,(5)

where the velocity components are presented by u and v, respectively, α for thermal diffusivity, ν=μρ for kinematic viscosity, ρ for density of fluid, σ for electrical conductivity, τ for ratio of effective heat capacity of the nanoparticle material to the heat capacity of the fluid, K1 and K2 for thermal and concentration slip factor, DBfor Brownian diffusion coefficient and DT for thermophoresis diffusion coefficient, qr for radiative heat flux. Radiation heat flux qr via Rosseland approximation can be set in the form:

qr=−4σ∗3k∗∂T4∂y=−16σ∗3k∗T3∂T∂y(6)

where σ* for Stefan–Boltzmann constant and k* for mean absorption coefficient.

The energy equation with radiation heat flux takes the form

u∂T∂x+v∂T∂y=∂∂yα+16σ∗T∞33k∗∂T∂y+τDB∂c∂y∂T∂y+DTT∞∂T∂y2.(7)

For the mathematical analysis of problem, we use the following transformation

u=bxf′η,v=−bνfη,η=bνy,T=T∞1+(θw−1θ(η)),ϕη=C−C∞Cw−C∞,(8)

where θw=TwT∞,θw>1 being the temperature ratio parameter.

After utilizing equation (8), equation (1) is satisfied identically and equations (2), (4) and (7) takes the following form

f‴η−f′η2+f″ηfη+3(n−1)2Wef″η2f‴η−Mf′η=0,(9)
1+Rddη1+1+θwθ3θ″η+Prfθ′+Nbθ′ϕ′+Ntθ′2=0,(10)
ϕ″+LePrfϕ′+NtNbθ″=0,(11)

with the boundary conditions

f=0,f′=1,θ(0)=1+Bθ′,ϕ(0)=1+Dϕ′atη=0f′=0,θ→0,ϕ→0asη=∞,(12)

where M=σBo2ρb for magnetic parameter, B=K1νb and D=K2νb represents thermal and concentration slip parameters, n for power law index parameter, We=Γ2bUwν for Weissenberg number, Pr=να for Prandtl number, R=16σ∗T∞33kk∗ for radiation parameter, Le=αDB for Lewis number, Nb=τDBCw−C∞ν for Brownian motion parameter, Nt=τDTTw−T∞T∞ν for thermophoresis parameter.

The physical quantities of interest like skin friction coefficient (Cf) local Nusselt number (Nux) and local Sherwood number (Shx) are

cf=τwρUw2,Nux=UwqwkbTw−T∞andShx=Uwqmab(Cw−C∞),

where

τw=μ0∂u∂y+n−1Γ22∂u∂y3η=0qw=−k∂T∂yy=0andqw=−D∂C∂yy=0,

Dimensionless form of local skin friction coefficient (Cf), local Nusselt number (Nux) and local Sherwood number (Shx) are

RexCf=f″0+n−1We2f″03,NuxRe12=−1+Rθw3θ′(0)

and

ShxRe12=−ϕ′(0),

where the local Reynolds number Rex=uw2(x)aν.

3 Numerical Method

Equations (9) to (11) together with the boundary conditions (12) form highly non-linear ordinary differential equations. The reduced set of non-linear ordinary differential equations is solved numerically using Shooting method along with Runge-Kutta-Fehlberg fourth-fifth order scheme. In algebraic package Maple, the Shooting method is implemented as an algorithm called ‘shoot’. This Maple software has been well tested for its accuracy and robustness and this has been used to solve a wide range of non-linear problems. It is most important to choose an appropriate finite value of η∞. In this method, a suitable finite value of η∞ is considered as η6 in such way that the boundary conditions defined at infinity satisfy asymptotically. In addition, the relative error tolerance to 10−6 is considered for convergence and the step size is chosen as Δη = 0.001. Further it is important to mention that as finding the solutions of velocity, temperature and concentration, the CPU time to estimate the values of velocity (1.32 sec) is much less than the CPU time to evaluate the values of temperature (1.74 sec) and the CPU time for concentration is 1.96 sec.

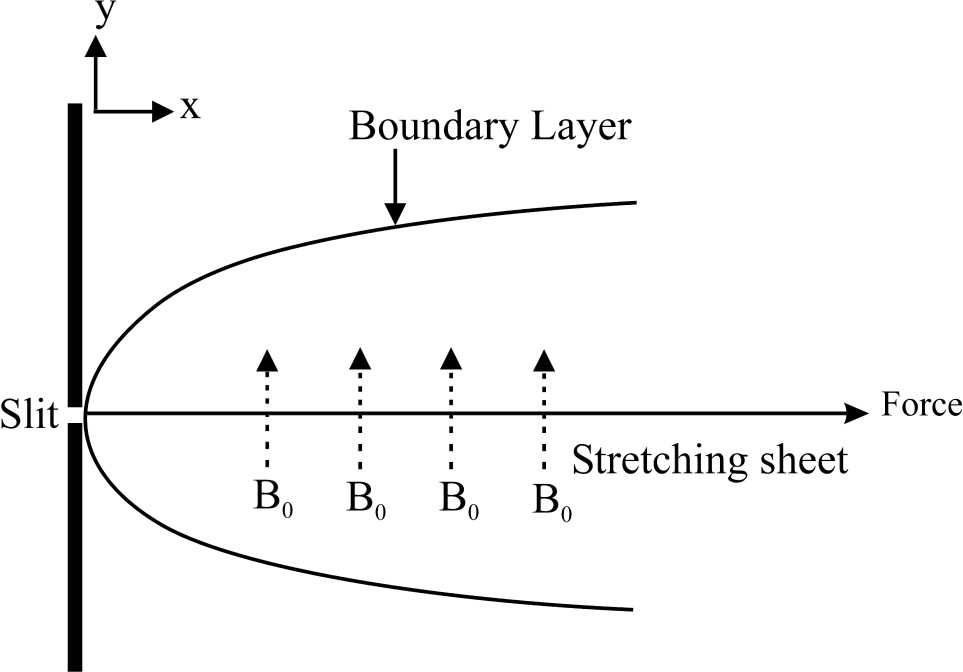
Fig. 1 Schematic representation of the flow diagram.
Fig. 1

Schematic representation of the flow diagram.

4 Results and discussion

In this section, the influences several physical parameters on the velocity, temperature and nanoparticle concentration profiles are analyzed graphically with tabulated results and relevant discussions. Eqs. (7)- (9) with the boundary conditions (10) are solved numerically with fifth-order Runge-Kutta Scheme using shooting scheme for the values of physical parameters like We, n, M, B, D, Nb, Nt, R, θw, Pr, Le. The results are reported graphically in Figures 2-5 and conclusions are drawn to analyze the effects of various physical quantities of interest on velocity, temperature and concentration profiles as well as the local skin friction, heat transfer rate and mass transfer rates that have significant effects. Comparisons, displayed in Tables 1 and 2, the present results with previously published works are performed and excellent agreements have been obtained.

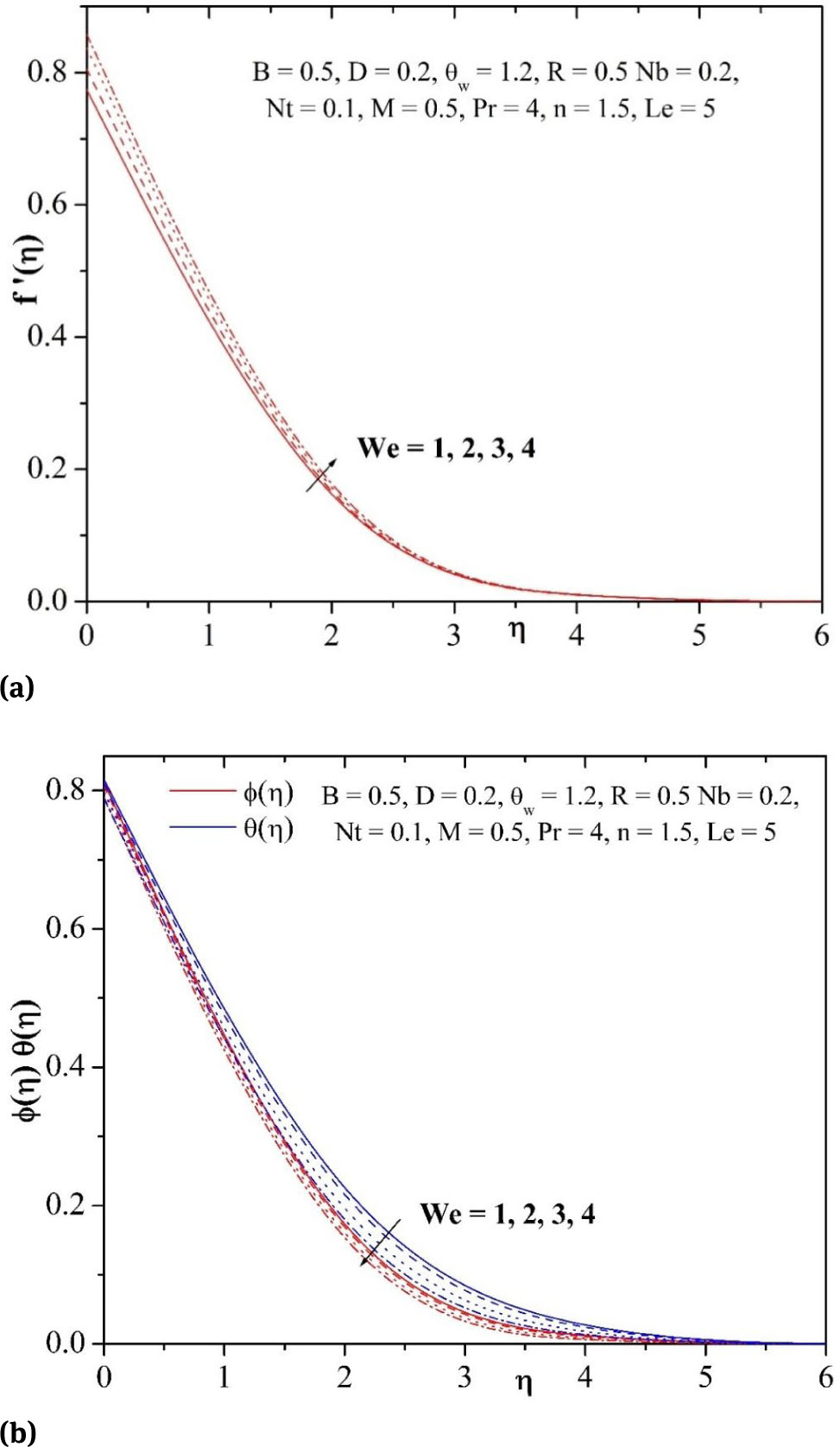
Fig. 2 (a) Influence of We on velocity profile. (b) Influence of We on temperature and concentration profiles.
Fig. 2

(a) Influence of We on velocity profile. (b) Influence of We on temperature and concentration profiles.

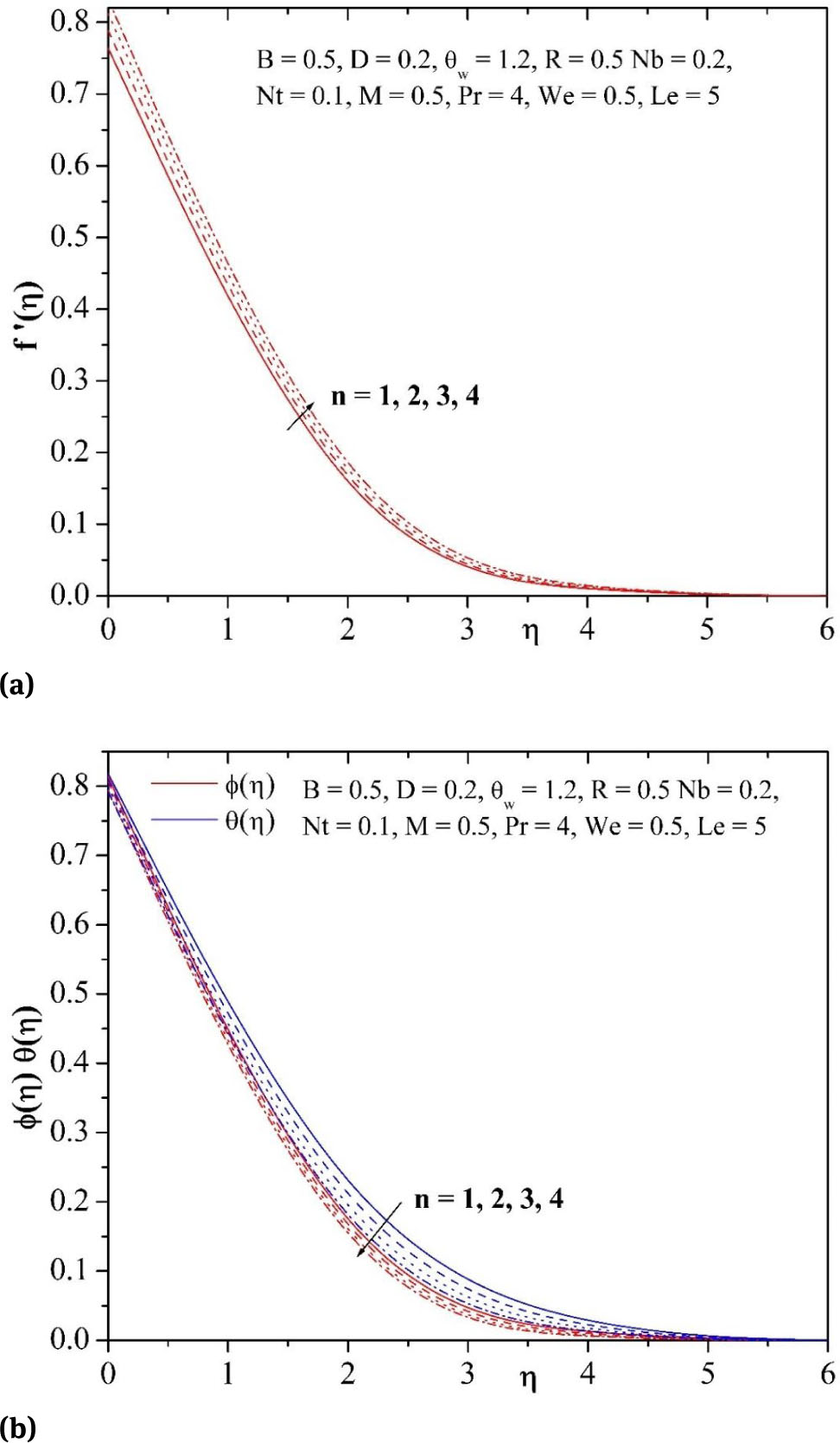
Fig. 3 (a) Influence of n on velocity profile. (b)Influence of n on temperature and concentration profiles.
Fig. 3

(a) Influence of n on velocity profile. (b)Influence of n on temperature and concentration profiles.

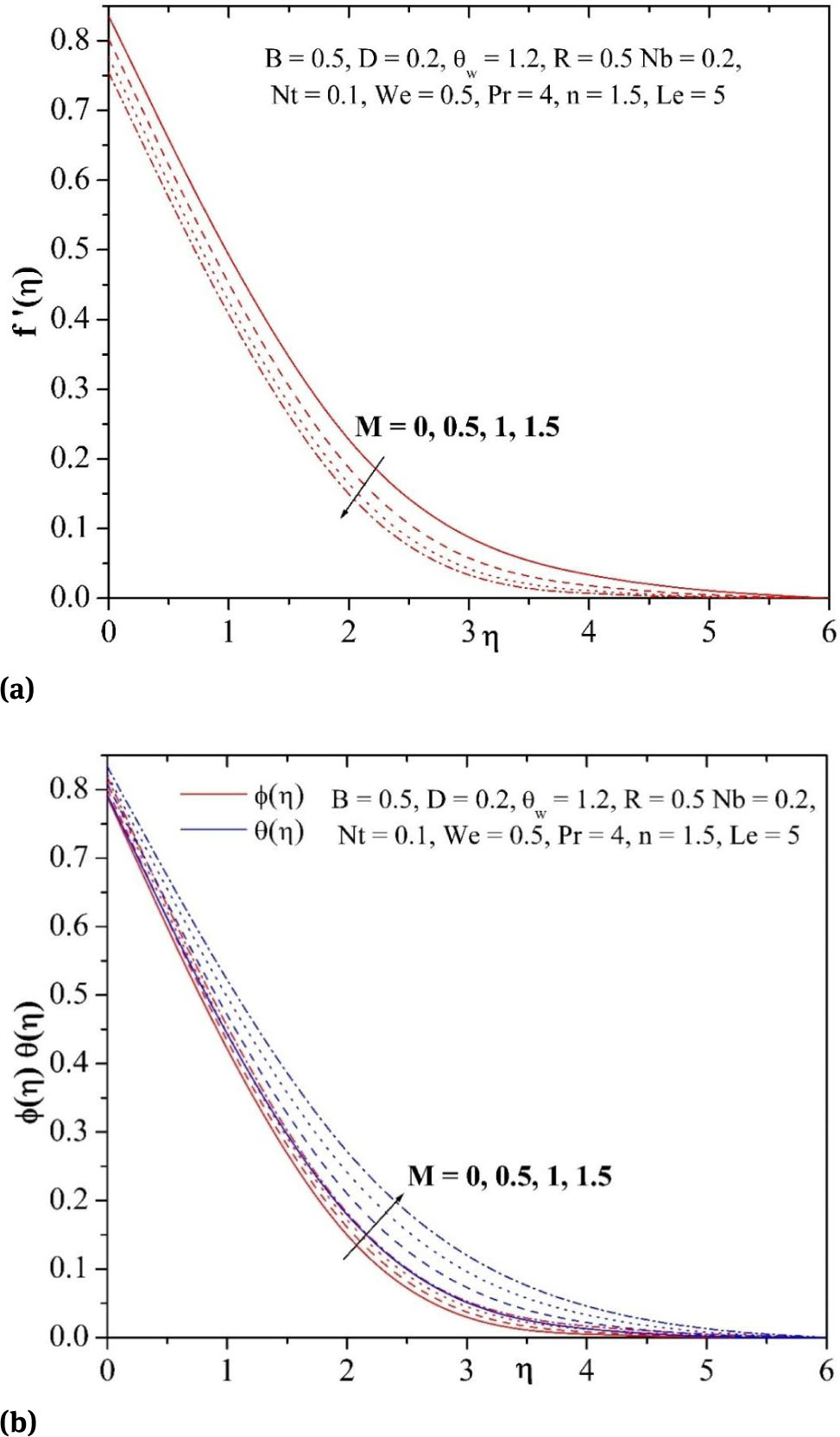
Fig. 4 (a) Influence of M on velocity profile. (b) Influence of M on temperature and concentration profiles.
Fig. 4

(a) Influence of M on velocity profile. (b) Influence of M on temperature and concentration profiles.

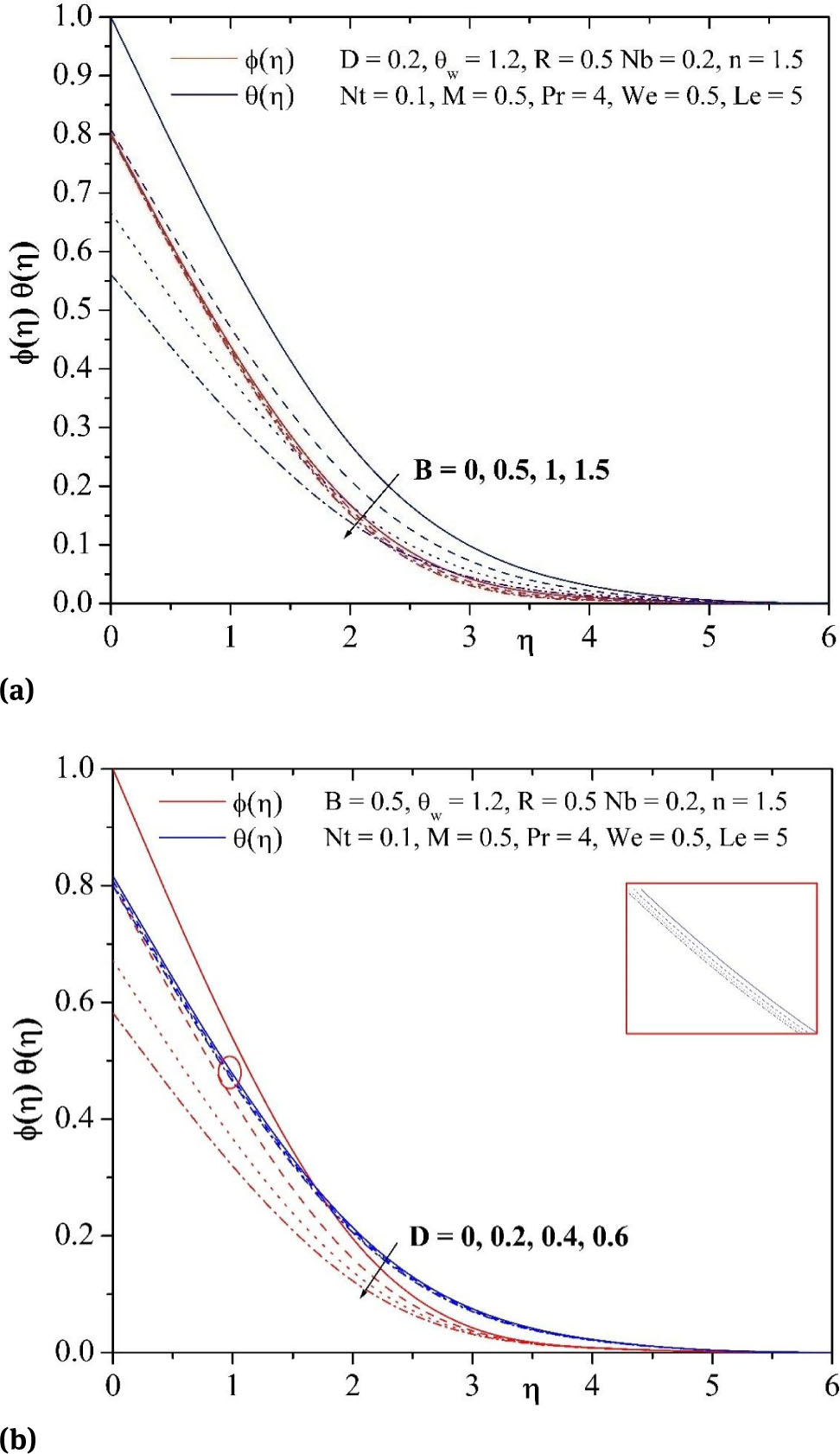
Fig. 5 (a) Influence of B on temperature and concentration profiles. (b) Influence of D on temperature and concentration profiles.
Fig. 5

(a) Influence of B on temperature and concentration profiles. (b) Influence of D on temperature and concentration profiles.

Table 1

Comparison results for the function −f″ (0) for several values of M in the case, We = 0, andn = 0, (absence of temperature and concentration).

Cortell [32]Ramesh et al. [33]Present result
M−f″(0)−f″(0)−f″(0)
01.0001.0001.00006
0.21.0951.0951.09546
0.51.2241.2241.22475
11.4141.4141.41421
1.21.4831.4831.48324
1.51.5811.5811.58114
21.7321.7321.73205

Table 2

Comparison of the result for Nusselt number −θ ′(0) in the absence of We, θw, R, B, D.

PrKhan and Pop [34]Present result (RKF-45 method)
0.70.45390.45357
20.91130.91135
71.89541.89539
203.35393.35387
706.46216.46209

Fig. 2(a)-3(c) show the profiles for velocity f′(η), temperature θ(η) and concentration φ(η) for different values of Weissenberg number We and power law index n. It is observed that an increase in the Weissenberg number We and power law index n leads to increase the fluid velocity and to decrease both the temperature and concentration profiles. The influence of magnetic field parameter M on velocity, temperature and concentration profiles in the boundary layer is displayed in Figs. 4(a)-4(c). It is noticed from these figures that the hydrodynamic boundary layer thickness decelerates whilst thermal boundary layer thickness and solutal boundary layer thickness elevates with enhance in the values of M. This is because of the fact that, the presence of magnetic field in an electrically conducting fluid produces a force called Lorentz force, this force acts versus the flow trend causes the depreciation in velocity profiles Fig. 4(a), and at the same time, to overcome the drag force imposed by the Lorentzian retardation the fluid has to result in extra work; this additional work can be converted into thermal energy which enhances the temperature of the fluid Fig. 4(b) and also enhances the concentration profiles Fig. 4(c).

Effects of thermal slip parameter B and solutal slip parameter D on the dimensionless temperature, nanoparticle volume fraction profiles are displayed in Figs. 5(a)-5(b). As the thermal slip parameter B and solutal slip parameter D enhances, both the temperature and nanoparticle volume fraction reduces near the plate surface. This elucidates that temperature and nanoparticle volume fraction near the surface reduces to a minimum with strong thermal and solutal slips and achieves a maximum with no thermal and solutal slip effects. This behavior happens due to fluid in the boundary layer being insensitive toward the heating effects of the plate surface and hence diminished heat and mass will be transferred from the surface to the nanofluid body.

Fig. 6(a) demonstrates that due to increasing the value of the Brownian parameter Nb, the temperature profile boosts, whereas the opposite trend is noted for the concentration profile. Therfore, the thermal boundary layer thickness increases, whereas the concentration boundary layer thickness decreases. This is due to the fact that the kinetic energy of the nanoparticles promotes due to the strength of this chaotic motion and as a result, the fluids temperature raises. This is because the Brownian motion at the nanoscale and the molecular levels is an important mechanism of the nanoscale level that dominates the thermal behaviors. In systems using nanofluids, the Brownian motion takes place because of the size of nanoparticles which can change the properties of heat transfer. As the scale size of particles approaches the scale of nanometer, the particles Brownian motion and its result on the surrounding liquids play a pivotal role in heat transfer characteristics.

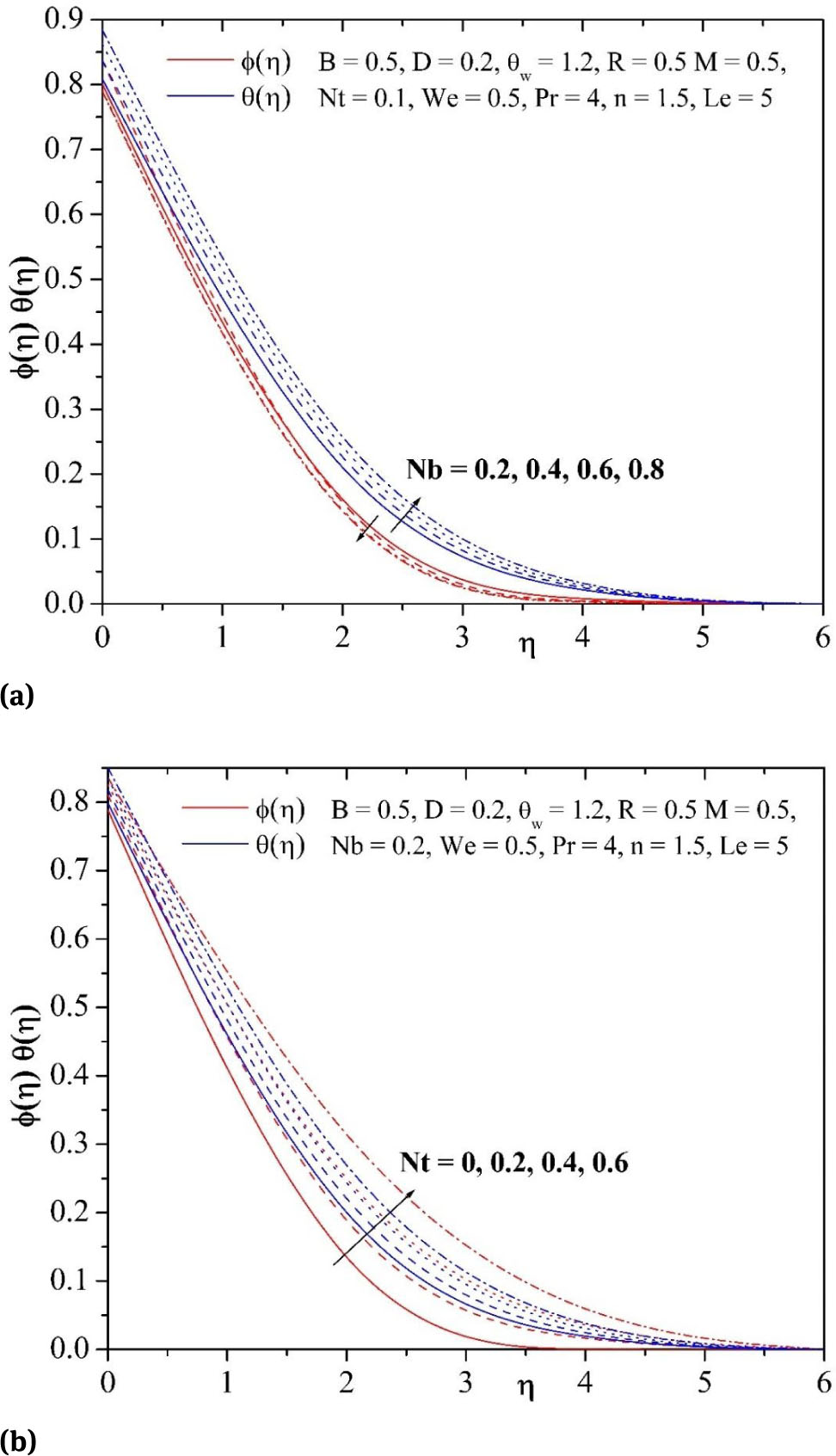
Fig. 6 (a) Influence of Nb on temperature and concentration profiles. (b) Influence of Nt on temperature and concentration profiles.
Fig. 6

(a) Influence of Nb on temperature and concentration profiles. (b) Influence of Nt on temperature and concentration profiles.

Fig. 6(b) reveals the impact of the thermophoresis parameter Nt on the temperature and the concentration of nanoparticle profiles. It is noticed that the temperature profile and the concentration of nanoparticle increase with increasing Nt . This is because diffusion penetrates profounder into the fluid due to boosting values of Nt which produces the thickening of the thermal boundary layer as well as the concentration boundary layer.

The significance of Prandtl number Pr on the temperature profiles is depicted in Fig. 7(a). It is noted that the temperature distributions diminish when Pr values increases. By definition, Prandtl number is defined as the ratio of momentum diffusivity to the thermal diffusivity, raising the values of Pr means higher momentum diffusivity or lesser thermal diffusivity which results in the reduction in the thermal boundary layer thickness. Fig. 7(b) presents the concentration profiles for different values of and Lewis number Le. It is observed that concentration distributions decelerate with elevating values of Le in the entire boundary layer region. The Lewis number defines the ratio of thermal diffusivity to mass diffusivity. Elevating the Lewis number means a higher thermal diffusivity or lower mass diffusivity and this provides thinner concentration boundary layer.

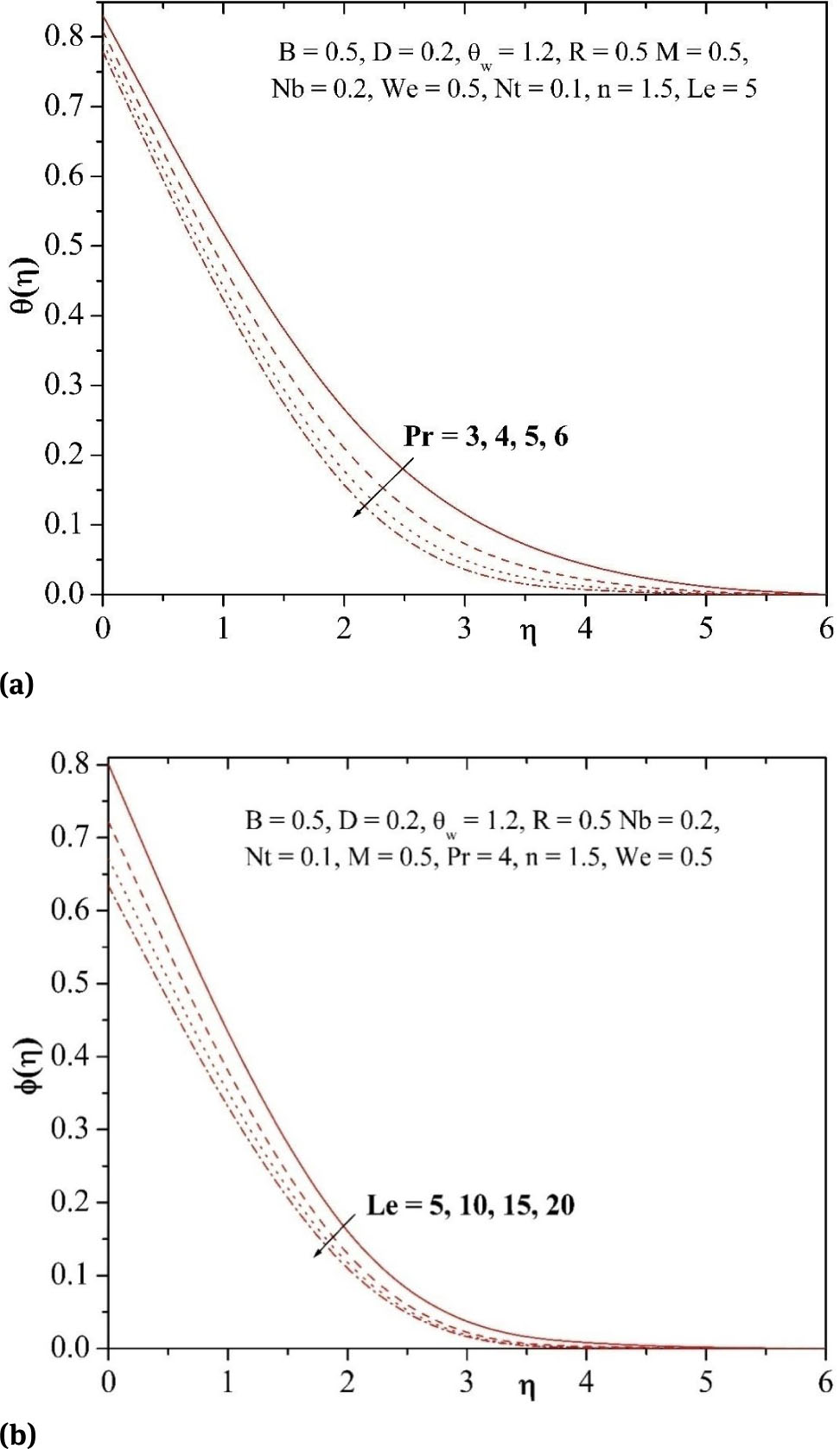
Fig. 7 (a) Influence of Pr on temperature profile. (b) Influence of Le on concentration profile.
Fig. 7

(a) Influence of Pr on temperature profile. (b) Influence of Le on concentration profile.

Figs. 8(a)-8(b) illustrate the influences of temperature ratio parameter θw and radiation parameter R on the temperature profiles, respectively. It is seen that as the values of θw rises the fluid temperarure diminishes significantly and this depreciation is more near the surface than in the far-field regime (free stream of the boundary layer). Furthermore, it is perceived from Fig. 8(b) that as the values of radiation parameter R increases the temperature profiles are also enhanced. This is because of the fact that the mean absorption coefficient reduces with increasing values of radiation parameter; as a result the thermal boundary layer thickness of the nanofluid is promotes.

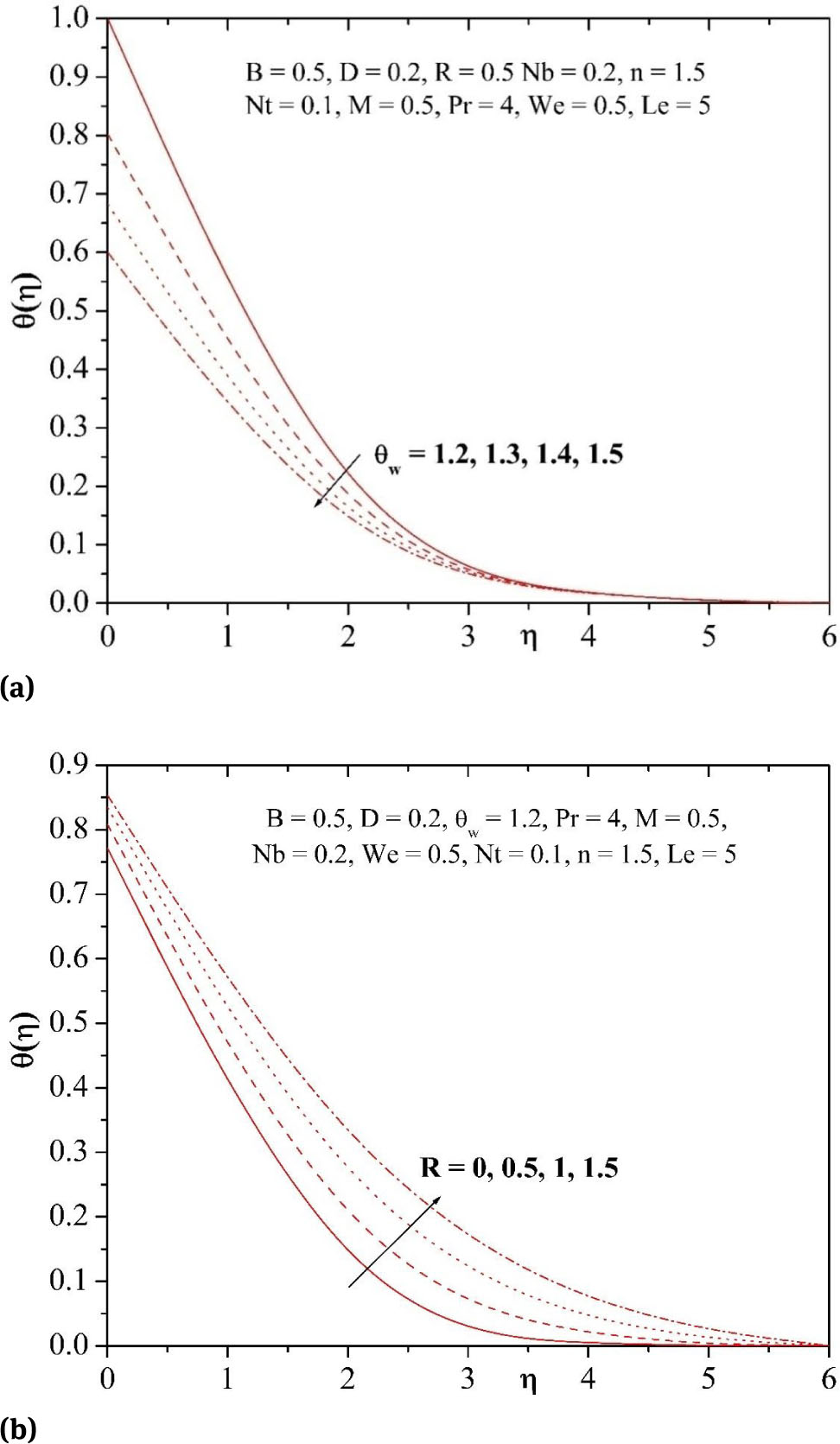
Fig. 8 (a) Influence of θw on temperature profile. (b) Influence of R on temperature profile.
Fig. 8

(a) Influence of θw on temperature profile. (b) Influence of R on temperature profile.

The variations of skin-friction coefficient −f″(0), Nusselt number −θ ′(0) and Sherwood number −ϕ ′(0) for diverse values of governing parameters are calculated and summarized in Tables 3-4. It is clear from these tables that the heat and mass transfer rates are both decelerates, whereas the skin-friction coefficient enhances with the increasing values of magnetic parameter M. It is also evident that the increasing of power law index n leads to escalate all the skin-friction coefficient, Nusselt and Sherwood numbers in the entire nanofluid regime, but reverse trend is noted with rising values of Weissenberg number We. Moreover, increasing the thermal slip parameter B generates a growth in values of Sherwood number and deceleration in the Nusselt number, while the opposite behaviors occurs with the increment in the solutal slip parameter D. Physically, as the thermal slip increases, this decelerates the capability of the nanofluid in the boundary layer to feel the heating impact of the plate surface, and hence, heat transfer rate reduces. Furthermore, the heat and mass transfer are enhanced when Brownian parameter Nb increased, whereas, they are depreciated with higher values of the thermophoresis parameter Nt. It is observed that both Nusselt number enhances and Sherwood numbers diminishes as Prandtl number Pr increases while the reverse trend happens with improving values of Lewis number Le. Finally, It is seen that with the higher values of radiation parameter R and temperature ratio parameter θw, both the Nusselt and Sherwood numbers elevate in the boundary layer regime.

Table 3

Variation of skin friction coefficient, Nusselt number and Sherwood number for different physical parameters.

MWen−RexCf−NuRex−ShRex
00.27080.77421.0521
0.50.42550.71340.9961
10.54750.66290.9493
00.43240.72841.0112
10.32340.71470.9880
20.12170.70450.9801
0-0.97780.69830.9707
10.12580.72841.0112
21.22110.75731.0398

Table 4

Variation of Nusselt number and Sherwood number for different physical parameter.

BDθwLeNbNtPrR−NuRex−ShRex
00.82220.9894
0.50.71340.9961
10.62101.0024
00.68471.2686
0.20.71340.9961
0.40.73240.8199
1.20.71440.9961
1.30.72211.0050
1.40.73251.0125
50.70970.9961
100.71071.3919
150.71341.6437
0.20.68240.8760
0.40.61230.9526
0.60.54361.2344
00.75001.0548
0.20.67860.9468
0.40.61440.8714
30.62981.0037
40.71340.9961
50.77600.9907
00.45610.9845
0.50.71340.9961
10.90111.0051

5 Conclusion

The impacts of multiple slips and thermal radiation on MHD flow of Carreau nanofluid over a stretching sheet with thermal radiation are numerically analyzed in this article. The slip of the heat and mass transfer in this problem is because of Brownian motion and thermophoresis. In the mathematical modeling of the problem effect of Carreau nanofluid, the dynamic effects of nanoparticles, thermophoresis and Brownian motion are taken into the account. The effects of different parameters on velocity, temperature and concentration profiles, as well as skin-friction coefficient, Nusselt number and Sherwood number were analyzed. The results of present study can be summarized as follows:

  1. The Nusselt and Sherwood numbers deteriorate, whereas the skin-friction coefficient is elevates with the higher values of magnetic parameter M.

  2. With the higher values of values of thermophoretic parameter Nt, the heat and mass transfer are reduced.

  3. A rise in Brownian motion parameter Nb improves the heat and mass transfer rates.

  4. All the skin-friction coefficient, Nusselt and Sherwood numbers depreciate when Weissenberg number We is upgrades, whereas, they elevates as the power law index nincreases.

  5. Increasing both the radiation parameter R and temperature ratio parameter θw, both the Nusselt and Sherwood numbers elevate in the boundary layer regime.

Ph: +91 9900981204

Acknowledgement

The authors are very much thankful to the editor and referee for their encouraging comments and constructive suggestions to improve the presentation of this manuscript.

Nomenclature

b

Constants

B0

magnetic field

B and D

thermal and solutal slip parameter

C

nanoparticle volume fraction

Cw

concentration at the wall

C∞

ambient nanofluid volume fraction

Cf

skin friction coefficient

cp

specific heat coefficient

K1 and K2

slip factor

T

fluid temperature

Tw

surface temperature

T∞

ambient surface temperature

DB

Brownian diffusion coefficient

DT

thermophoretic diffusion coefficient

k

thermal conductivity

k*

mean absorption coefficient

Le

Lewis number

Nb

Brownian motion parameter

Nt

thermophoresis parameter

Nux

local Nusselt number

n

Power law index

Pr

Prandtl number

qr

radiative heat flux

qw

heat flux

qm

mass flux

R

radiation parameter

Rex

local Reynolds number

Shx

local Sherwood number

u, v

velocity components

Uw

stretching sheet

We

Weissenberg number

x, y

Coordinates

Greek symbols
θ

dimensionless temperature

θw

temperature ratio parameter

ϕ

dimensionless nanoparticle volume fraction

ν

Kinematic viscosity of the fluid

μ

coefficient of fluid viscosity

σ*

Stefan–Boltzmann constant

τ

ratio of the effective heat capacity of the nanoparticle to that of an ordinary fluid

τw

shear stress along the wall

α

Prandtl parameter

β

elastic parameter

α1

thermal diffusivity of the fluid

ρ

fluid density

References

[1] S. K. Das, S. U. S. Choi, W. Yu and T. Pradeep, Nanofluids-science and technology, John Wiley & Sons Publishers, Hoboken, (2007).10.1002/9780470180693Search in Google Scholar

[2] S. U. S. Choi, Enhancing thermal conductivity of fluids with nanoparticle. in: D.A. Siginer, H.P. Wang (Eds.), Developments and Applications of Non-Newtonian Flows, ASME FED, vol. 231/MD 66 (1995) 99-105.Search in Google Scholar

[3] A.V. Kuznetstov and D.A. Neild, Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model, International journal of thermal sciences, 77(2014) 126-129.10.1016/j.ijthermalsci.2013.10.007Search in Google Scholar

[4] J. Buongiorno, Convective transport in nanofluids, ASME Journal of Heat Transfer, 128 (2006) 240-250.10.1115/1.2150834Search in Google Scholar

[5] A. Aziz and W.A. Khan, Natural convective boundary layer flow of a nanofluid past a convectively heated vertical plate, Int. J. Therm. Sci., 52(2012) 83-90.10.1016/j.ijthermalsci.2011.10.001Search in Google Scholar

[6] A. J. Chamkha, M. Modather, S. M. M. EL-Kabeir and A. M. Rashad, Radiative effects on boundary-layer flow of a nanofluid on a continuously moving or fixed permeable surface, Recent Patents on Mechanical Engineering, 5 (3) (2012) 176-183.10.2174/2212797611205030176Search in Google Scholar

[7] G. K. Ramesh, B. J. Gireesha T. Hayat and A. Alsdedi, Stagnation point flow of Maxwell fluid towards a permeable surface in the presence of nanoparticles, Alexandria Engineering Journal, 53(2016) 857-865.10.1016/j.aej.2016.02.007Search in Google Scholar

[8] A. J. Chamkha and A. M. Rashad, Natural convection from a vertical permeable cone in nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes, International Journal of Numerical Methods for Heat and Fluid Flow, 22(8) (2012) 1073-1085.10.1108/09615531211271871Search in Google Scholar

[9] A. J. Chamkha, S. Abbasbandy, A. M. Rashad and K. Vajravelu, Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid, Meccanica, 48 (2013) 275-285.10.1007/s11012-012-9599-1Search in Google Scholar

[10] O. A. Bég and M. Ferdows, Explicit numerical simulation of magnetohydrodynamic nanofluid flow from an exponential stretching sheet in porous media. Appl Nanosci 2013; 1-15. 10.1007/s13204-013-0275-0.Search in Google Scholar

[11] M. Ferdows, M. S. Khan, O. A. Bég, M. A. K. Azad and M. M. Alam, Numerical study of transient magnetohydrodynamic radiative free convection nanofluid flow from a stretching permeable surface. Proc IMechE, Part E: J Process Mechanical Engineering. Epub ahead of print 25 September 2013. 10.1177/0954408913493406.Search in Google Scholar

[12] P. Sudarsana Reddy and K. V. Suryanarayana Rao, MHD natural convection heat and mass transfer of Al2O3 - water and Ag - water nanofluids over a vertical cone with chemical reaction, Procedia Engineering, 127(2015)476-484.10.1016/j.proeng.2015.11.401Search in Google Scholar

[13] D. Ruchika, Puneet Rana and Lokendra Kumar, MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: Buongiorno’s model, Powder Technology, 288(2016)140-150.10.1016/j.powtec.2015.11.004Search in Google Scholar

[14] A. M. Rashad, Impact of thermal radiation on MHD slip flow of a ferrofluid over a nonisothermal wedge, Journal of Magnetism and Magnetic Materials, 422 (2017) 25-31.10.1016/j.jmmm.2016.08.056Search in Google Scholar

[15] A. M. Rashad, Impact of anisotropic slip on transient three dimensional MHD flow of ferrofluid over an inclined radiate stretching surface, Journal of the Egyptian Mathematical Society, (In Press).10.1016/j.joems.2016.12.001Search in Google Scholar

[16] S. Nadeem, Rizwan Ul Haq, N. S. Akbar, C. Lee and Z. H. Khan, Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet, PLoS ONE 8(8)(2013) e69811. https://doi.org/10.1371/journal.pone.0069811.10.1371/journal.pone.0069811Search in Google Scholar PubMed PubMed Central

[17] S. Nadeem, Rizwan Ul Haq and Z. H. Khan, Numerical solution of non-Newtonian nanofluid flow over a stretching sheet, Applied Nanoscience, 4(5) (2014) 625–631.10.1007/s13204-013-0235-8Search in Google Scholar

[18] S. Nadeem, Rizwan Ul Haq and Z. H. Khan, Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles, Journal of the Taiwan Institute of Chemical Engineers, 45(1)(2014) 121-126.10.1016/j.jtice.2013.04.006Search in Google Scholar

[19] N.F.M. Noor, Rizwan Ul Haq, S. Nadeem and I. Hashim, Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects, Meccanica, 50 (2015) 2007–2022.10.1007/s11012-015-0145-9Search in Google Scholar

[20] N. Ali and T. Hayat, Peristaltic motion of a Carreau fluid in an asymmetric channel Appl. Math. Comput. 193(2007) 535-552.Search in Google Scholar

[21] B. I. Olajuwon, Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion Thermal. Sci. 15(2011) 241-252.Search in Google Scholar

[22] T. Hayat, S. Asad, M. Mustafa and A. Alsaedi, Boundary layer flow of Carreau fluid over a convectively heated stretching sheet, Appl. Math. Comput. 246(2014)12-22.10.1016/j.amc.2014.07.083Search in Google Scholar

[23] T. Hayat, M Waqas, S. A. Shehzad, A. AL-Saedi, Stretched flow of Carreau nanofluid with convective boundary condition, PRAMANA-Journal of Physics, 86 (1) (2016)3-17.10.1007/s12043-015-1137-ySearch in Google Scholar

[24] W. Ibrahim and B. Shankar, MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions Computers and fluids, 75(2013) 1-10.10.1016/j.compfluid.2013.01.014Search in Google Scholar

[25] S.K.Parida, S.Panda, and B.R.Rout, MHD boundary layer slip flow and radiative nonlinear heat transfer over a flat plate with variable fluid properties and thermophoresis, Alexandria Engineering Journal, 54(4)(2015)941-953.10.1016/j.aej.2015.08.007Search in Google Scholar

[26] G.K. Ramesh, Numerical study of the influence of heat source on stagnation point flow towards a stretching surface of a Jeffrey nanoliquid, Journal of Engineering, 2015 (2015), Article ID 382061, 10 pages http://dx.doi.org/10.1155/2015/38206110.1155/2015/382061Search in Google Scholar

[27] Muhammad A Imran, S. Sarwar and Muhammad Imran, Effects of slip on free convection flow of Casson fluid over an oscillating vertical plate, Boundary Value Problems, 2016 (30)( 2016). https://doi.org/10.1186/s13661-016-0538-210.1186/s13661-016-0538-2Search in Google Scholar

[28] Y. S. Daniel, Z.A.Aziz, Z.Ismail and F. Salah, Effects of slip and convective conditions on MHD flow of nanofluid over a porous nonlinear stretching/shrinking sheet, Australian Journal of Mechanical Engineering (2017)1-17. http://dx.doi.org/10.1080/14484846.2017.135884410.1080/14484846.2017.1358844Search in Google Scholar

[29] R. A. Shah, T. Abbas, M. Idrees and M. Ullah, MHD Carreau fluid slip flow over a porous stretching sheet with viscous dissipation and variable thermal conductivity, Boundary Value Problems, 2017(94)( 2017)10.1186/s13661-017-0827-4Search in Google Scholar

[30] K.Ganesh Kumar, N. Rudraswamy, B.J. Gireesha and M.R. Krishnamurthy, Influence of nonlinear thermal radiation and viscous dissipation on three-dimensional flow of Jeffrey nano fluid over a stretching sheet in the presence of Joule heating. Nonlinear Engineering, 6(3) (2017) 207-219.10.1515/nleng-2017-0014Search in Google Scholar

[31] K.Ganesh Kumar, G.K.Ramesh, B.J.Gireesha and R.S.R.Gorla, Characteristics of Joule heating and viscous dissipation on three-dimensional flow of Oldroyd B nanofluid with thermal radiation, Alexandria Engineering Journal, (2017). https://doi.org/10.1016/j.aej.2017.06.00610.1016/j.aej.2017.06.006Search in Google Scholar

[32] R. Cortell, A note on magnetohydrodynamic flow of a power-law fluid over a stretching sheet. Appl. Math. Comput. 168 (2005)557–56610.1016/j.amc.2004.09.046Search in Google Scholar

[33] G. K. Ramesh, B. J. Gireesha and C. S. Bagewadi, Stagnation point flow of a MHD dusty fluid towards a stretching sheet with radiation, Afrika Matematika, 25(1) (2014) 237-249.10.1007/s13370-012-0114-6Search in Google Scholar

[34] W. A. Khan and I, Pop, Boundary-layer flow of a nanofluid past a stretching sheet. Int. J Heat Mass Transfer, 53(2010)2477–2483.10.1016/j.ijheatmasstransfer.2010.01.032Search in Google Scholar

Received: 2017-08-13
Revised: 2018-01-28
Accepted: 2018-04-07
Published Online: 2018-09-17
Published in Print: 2019-01-28

© 2019 K.G. Kumar et al., published by De Gruyter.

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. Chebyshev Operational Matrix Method for Lane-Emden Problem
  2. Concentrating solar power tower technology: present status and outlook
  3. Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
  4. Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
  5. Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
  6. Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
  7. Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
  8. Local convergence for an eighth order method for solving equations and systems of equations
  9. Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
  10. Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
  11. A reliable analytical approach for a fractional model of advection-dispersion equation
  12. Mass transfer around a slender drop in a nonlinear extensional flow
  13. Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
  14. A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
  15. An effective technique for the conformable space-time fractional EW and modified EW equations
  16. Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
  17. New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
  18. Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
  19. A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
  20. Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
  21. Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
  22. Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
  23. MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
  24. Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
  25. Swirling flow of couple stress fluid due to a rotating disk
  26. MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
  27. Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
  28. Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
  29. Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
  30. On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
  31. An adaptive mesh method for time dependent singularly perturbed differential-difference equations
  32. On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
  33. Rational exponential solutions of conformable space-time fractional equal-width equations
  34. Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
  35. Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
  36. Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
  37. Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
  38. Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
  39. Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
  40. Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
  41. An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
  42. New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
  43. Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
  44. Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
  45. Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
  46. Mathematical model on distributed denial of service attack through Internet of things in a network
  47. Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
  48. Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
  49. MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
  50. A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
  51. Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
  52. Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
  53. Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
  54. Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
  55. Combination synchronization of fractional order n-chaotic systems using active backstepping design
  56. Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
  57. Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
  58. Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
  59. Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
  60. Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
  61. Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
  62. Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
  63. A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
  64. A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
  65. A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
  66. The expa function method and the conformable time-fractional KdV equations
  67. Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
  68. Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
  69. MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
  70. MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel
https://doi.org/10.1515/nleng-2017-0120
Keywords for this article
Carreau nanofluid; thermal and solutal slip; nonlinear radiation; magnetic field
Creative Commons
BY 4.0

Articles in the same Issue

  1. Chebyshev Operational Matrix Method for Lane-Emden Problem
  2. Concentrating solar power tower technology: present status and outlook
  3. Control of separately excited DC motor with series multi-cells chopper using PI - Petri nets controller
  4. Effect of boundary roughness on nonlinear saturation of Rayleigh-Taylor instability in couple-stress fluid
  5. Effect of Heterogeneity on Imbibition Phenomena in Fluid Flow through Porous Media with Different Porous Materials
  6. Electro-osmotic flow of a third-grade fluid past a channel having stretching walls
  7. Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation
  8. Local convergence for an eighth order method for solving equations and systems of equations
  9. Numerical techniques for behavior of incompressible flow in steady two-dimensional motion due to a linearly stretching of porous sheet based on radial basis functions
  10. Influence of Non-linear Boussinesq Approximation on Natural Convective Flow of a Power-Law Fluid along an Inclined Plate under Convective Thermal Boundary Condition
  11. A reliable analytical approach for a fractional model of advection-dispersion equation
  12. Mass transfer around a slender drop in a nonlinear extensional flow
  13. Hydromagnetic Flow of Heat and Mass Transfer in a Nano Williamson Fluid Past a Vertical Plate With Thermal and Momentum Slip Effects: Numerical Study
  14. A Study on Convective-Radial Fins with Temperature-dependent Thermal Conductivity and Internal Heat Generation
  15. An effective technique for the conformable space-time fractional EW and modified EW equations
  16. Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation
  17. New exact and numerical solutions for the effect of suction or injection on flow of nanofluids past a stretching sheet
  18. Numerical investigation of MHD stagnation-point flow and heat transfer of sodium alginate non-Newtonian nanofluid
  19. A New Finance Chaotic System, its Electronic Circuit Realization, Passivity based Synchronization and an Application to Voice Encryption
  20. Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions
  21. Application of QLM-Rational Legendre collocation method towards Eyring-Powell fluid model
  22. Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations
  23. MHD nonaligned stagnation point flow of second grade fluid towards a porous rotating disk
  24. Nonlinear Dynamic Response of an Axially Functionally Graded (AFG) Beam Resting on Nonlinear Elastic Foundation Subjected to Moving Load
  25. Swirling flow of couple stress fluid due to a rotating disk
  26. MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source
  27. Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness
  28. Nonhomogeneous porosity and thermal diffusivity effects on stability and instability of double-diffusive convection in a porous medium layer: Brinkman Model
  29. Magnetohydrodynamic(MHD) Boundary Layer Flow of Eyring-Powell Nanofluid Past Stretching Cylinder With Cattaneo-Christov Heat Flux Model
  30. On the connection coefficients and recurrence relations arising from expansions in series of modified generalized Laguerre polynomials: Applications on a semi-infinite domain
  31. An adaptive mesh method for time dependent singularly perturbed differential-difference equations
  32. On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation
  33. Rational exponential solutions of conformable space-time fractional equal-width equations
  34. Simultaneous impacts of Joule heating and variable heat source/sink on MHD 3D flow of Carreau-nanoliquids with temperature dependent viscosity
  35. Effect of magnetic field on imbibition phenomenon in fluid flow through fractured porous media with different porous material
  36. Impact of ohmic heating on MHD mixed convection flow of Casson fluid by considering Cross diffusion effect
  37. Mathematical Modelling Comparison of a Reciprocating, a Szorenyi Rotary, and a Wankel Rotary Engine
  38. Surface roughness effect on thermohydrodynamic analysis of journal bearings lubricated with couple stress fluids
  39. Convective conditions and dissipation on Tangent Hyperbolic fluid over a chemically heating exponentially porous sheet
  40. Unsteady Carreau-Casson fluids over a radiated shrinking sheet in a suspension of dust and graphene nanoparticles with non-Fourier heat flux
  41. An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering
  42. New numerical method based on Generalized Bessel function to solve nonlinear Abel fractional differential equation of the first kind
  43. Numerical Study of Viscoelastic Micropolar Heat Transfer from a Vertical Cone for Thermal Polymer Coating
  44. Analysis of Bifurcation and Chaos of the Size-dependent Micro–plate Considering Damage
  45. Non-Similar Comutational Solutions for Double-Diffusive MHD Transport Phenomena for Non-Newtnian Nanofluid From a Horizontal Circular Cylinder
  46. Mathematical model on distributed denial of service attack through Internet of things in a network
  47. Postbuckling behavior of functionally graded CNT-reinforced nanocomposite plate with interphase effect
  48. Study of Weakly nonlinear Mass transport in Newtonian Fluid with Applied Magnetic Field under Concentration/Gravity modulation
  49. MHD slip flow of chemically reacting UCM fluid through a dilating channel with heat source/sink
  50. A Study on Non-Newtonian Transport Phenomena in Mhd Fluid Flow From a Vertical Cone With Navier Slip and Convective Heating
  51. Penetrative convection in a fluid saturated Darcy-Brinkman porous media with LTNE via internal heat source
  52. Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity
  53. Semitrailer Steering Control for Improved Articulated Vehicle Manoeuvrability and Stability
  54. Thermomechanical nonlinear stability of pressure-loaded CNT-reinforced composite doubly curved panels resting on elastic foundations
  55. Combination synchronization of fractional order n-chaotic systems using active backstepping design
  56. Vision-Based CubeSat Closed-Loop Formation Control in Close Proximities
  57. Effect of endoscope on the peristaltic transport of a couple stress fluid with heat transfer: Application to biomedicine
  58. Unsteady MHD Non-Newtonian Heat Transfer Nanofluids with Entropy Generation Analysis
  59. Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere
  60. Influence of Joule Heating and Non-Linear Radiation on MHD 3D Dissipating Flow of Casson Nanofluid past a Non-Linear Stretching Sheet
  61. Radiative Flow of Third Grade Non-Newtonian Fluid From A Horizontal Circular Cylinder
  62. Application of Bessel functions and Jacobian free Newton method to solve time-fractional Burger equation
  63. A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform
  64. A multiple-step adaptive pseudospectral method for solving multi-order fractional differential equations
  65. A reliable numerical algorithm for a fractional model of Fitzhugh-Nagumo equation arising in the transmission of nerve impulses
  66. The expa function method and the conformable time-fractional KdV equations
  67. Comment on the paper: “Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet, M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, and Rama Subba Reddy Gorla, Nonlinear Engineering 2016, 5(3), 147-159”
  68. Three-Dimensional Boundary layer Flow and Heat Transfer of a Fluid Particle Suspension over a Stretching Sheet Embedded in a Porous Medium
  69. MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution
  70. MHD Convection Fluid and Heat Transfer in an Inclined Micro-Porous-Channel
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 28.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2017-0120/html
Scroll to top button